Coevolutionary Landscape of Kinase Family Proteins: Sequence Probabilities and Functional Motifs

Abstract

The protein kinase catalytic domain is one of the most abundant domains across all branches of life. Although kinases share a common core function of phosphoryl-transfer, they also have wide functional diversity and play varied roles in cell signaling networks, and for this reason are implicated in a number of human diseases. This functional diversity is primarily achieved through sequence variation, and uncovering the sequence-function relationships for the kinase family is a major challenge. In this study we use a statistical inference technique inspired by statistical physics, which builds a coevolutionary “Potts” Hamiltonian model of sequence variation in a protein family. We show how this model has sufficient power to predict the probability of specific subsequences in the highly diverged kinase family, which we verify by comparing the model’s predictions with experimental observations in the Uniprot database. We show that the pairwise (residue-residue) interaction terms of the statistical model are necessary and sufficient to capture higher-than-pairwise mutation patterns of natural kinase sequences. We observe that previously identified functional sets of residues have much stronger correlated interaction scores than are typical.

Introduction

About 2% of the human genome belongs to the protein kinase family and over ${10}^5$ different kinases have been sequenced from many species (1). Protein kinases’ common catalytic role in protein phosphorylation is carried out by a conserved catalytic structural motif, but individual kinases are specialized to phosphorylate particular substrates and are bound by different regulatory partners as part of cell signaling networks. Kinases are implicated in many human diseases, and understanding how a particular kinase’s sequence determines its individual function has clinical applications. The ability to predict the sequence-dependent effect of specific mutations is relevant for the treatment of kinase-related cancers (2), and understanding the differences in functionality between kinases can aid in selective drug design (3).

One approach to understanding the effects of particular kinase sequence variations has been by structural analysis, based on thousands of observed kinase crystal structures and comparison of their sequences. Patterns of structural variation and conservation within and between protein kinase subfamilies has led to the identification of various functional motifs such as the HRD and DFG motifs necessary for catalysis, networks of stabilizing interactions formed in the kinase active catalytic state known as the C-spine and R-spine, and the importance of the C and F helices in acting as rigid foundations on which the catalytic core rests (4, 5, 6, 7, 8, 9, 10). Two conformational states, the catalytically active “DFG-in” and the inactive “DFG-out” states have been discovered to be important in controlling kinase activation and regulation (11). An important goal of these studies is to understand the sequence-dependent ligand-binding properties of different kinases for therapeutic purposes; however, ligand binding affinities are still difficult to predict (12, 13, 14, 15), and crystal structures only give a partial view of kinase function.

Another way to extract information about function from kinase sequence variation is to construct a statistical (Potts) model from a multiple sequence alignment (MSA) of sequences collected from many organisms. The idea of using sequence statistics to understand protein structure and function has been motivated and justified by the observation that strongly covarying positions in an MSA correspond well to contacts in structure, a fact used for protein contact prediction with significant success (16, 17, 18, 19, 20, 21). Using concepts from statistical physics, this idea has evolved and led to the Potts model of protein sequence variation, which is able to capture the pairwise and higher-order mutational correlation patterns, although the model is inferred only from pairwise interaction terms. The Potts model has wider potential applications beyond protein family contact prediction, and can be used to predict sequence-specific properties (22, 23, 24). Statistical energies computed using the Potts model can be used to predict the relative probability of any sequence in the family, including sequences not seen in the data set, and can be used to predict the effect of mutations on the probability of a sequence (25, 26, 27, 28). The probability is often interpreted as a fitness. The sequence-space landscapes predicted by the Potts model have been found to correlate to experimentally measured fitness landscapes and free energy landscapes (24, 29, 30, 31, 32). For example, in human immunodeficiency virus (HIV) sequences, Potts statistical energies correlate well with in vitro fitness measurements for tens of sequence variants with multiple mutations relative to the well-defined wild-type sequence (26, 33), and Potts models inferred on one HIV sequence database predict sequence frequencies in an independent database (25, 34). Similarly, the Potts probability is found to correlate well with measurements of the free energy of folding of proteins in a family (24, 29, 35, 36, 37). This connection between Potts probabilities and fitnesses suggests that the Potts model can be used to predict some features of the relationship between protein sequence and function.

The physical interpretation of the Potts model parameters and the capabilities and limitations of the Potts model are still being explored. Potts model predictions of the effect of mutations in particular sequences have often been limited to a relatively small number of mutations at a time, typically single and double mutants, or in systems with high sequence conservation (29, 33). Other studies have shown that higher-than-pairwise variations are well described by Potts models in a number of biological systems; however, these tests were limited to systems with very small, explicitly enumerable state spaces (38, 39, 40). Modeling the sequence landscape of the highly diverged protein kinase family is a challenge because kinase sequences have an average of only 30% identity to each other, vary at many positions at once, and cover a vast span of sequence space. In this work, we focus on the model’s ability to reconstruct kinase sequence-specific statistics, particularly subsequence probabilities, and illustrate how highly correlated patterns can be associated with functional sets of positions.

We use a previously described Monte Carlo inference method designed to obtain the Potts model parameters for diverse protein families such as the protein kinase family (22). We demonstrate the ability of the inferred model to describe a large sequence landscape by showing that it captures the observed higher-order marginals (subsequence probabilities) of the original MSA, which are not directly fitted. Using in silico tests, we show that when the MSA contains a few thousand effective sequences, the inferred statistical energies of the model are not sensitive to the size of the MSA. Through comparison to site-independent (uncorrelated) models of sequence variation, we show the that epistatic effects of correlations are essential to accurately predict higher-order marginals, i.e., subsequences that vary at many positions simultaneously. We show how well the statistical energies of the Potts model for the kinase family reflects the frequency of subsequences observed in the Uniprot database and in the much larger data set constructed in silico. We then use the subsequence statistics predicted by the Potts model to illustrate how highly correlated patterns can be associated with functional motifs, and to identify motifs within the kinase sequence with strong correlated signals. We illustrate how functional units of kinase family proteins are more conserved and exhibit strong epistatic effects.

Potts covariation analysis

Potts covariation analysis models the distribution $P\left(S\right)$ for the probability of observing a sequence in an MSA of a protein family, incorporating pairwise correlated effects to parametrize the model. $P\left(S\right)$ has been interpreted as a fitness, and sometimes as the probability of the protein’s native fold in thermodynamic equilibrium (24, 29, 41, 42, 43). Because of the enormous size of sequence space (roughly estimated to be ${10}^{140}$ sequences for the kinase family in Supporting Material), this distribution cannot be directly measured from an MSA of only a few thousand sequences. An alternative is to solve for the maximum entropy distribution, subject to the constraints that the univariate and bivariate marginals $f_{\alpha \beta }^{ij}$ of sequences generated from the model (for residues $\alpha ,\beta$ at positions $i,j$) match those of the MSA data set, which can be accurately measured. The maximum entropy distribution is found to be $P\left(S\right)\propto e^{-E\left(S\right)}$ for the Potts Hamiltonian $E\left(S\right)={\sum }_i^L{h}_{S_i}^i+{\sum }_{i<j}^L{J}_{S_i{S}_j}^{ij}$, which contains pairwise “coupling” terms J and single-site “fields” h, which may be solved for by maximum likelihood inference. One could in principle build a Hamiltonian that includes higher-order terms by fitting triplet correlations in the data, but not only is there insufficient data to build such a model, it does not appear to be necessary as we discuss below.

Given a parametrized model, the Hamiltonian $E\left(S\right)$ defines a statistical energy landscape over sequence space, computable for any sequence such that lower values are more favorable, and the coupling parameters $J_{S_i{S}_j}^{ij}$ give information about the statistical interaction between two residues in a sequence. The $J_{S_i{S}_j}^{ij}$ have been related to folding or binding free energy contributions (43, 44). From $P\left(S\right)$ we can estimate the probability of any sequence, and by similar computation we may also predict the probability of subsequences in particular (sub)sets of positions (not necessarily contiguous) of the MSA. The Potts model allows us to explore aspects of the statistics that we do not have the power to measure from the raw data because of sample size. For instance, given a data set of N sequences, it is not possible to directly measure the probability of a (sub)sequence that appears in nature with frequency of roughly $1/N$ or less. This sampling noise (or “shot noise”) issue is particularly a problem for longer sets of positions and for the full-length sequences because the probability of individual subsequences decreases rapidly with increasing number of positions due to the increased size of the sequence space. The correlated nature of the model is also important. The collective effect of the pairwise terms J mean that the statistics of the Potts model can be significantly different from a site-independent or uncorrelated model that ignores correlated effects, particularly for longer sets of positions where more pairwise terms come into play. We will compare the Potts model to the maximum entropy independent model fitted to the univariate marginals of the data, which is exactly solvable and takes a “log odds” form where $h_{\alpha }^i=-\text{log}{f}_{\alpha }^i$ and $J=0$.

Inference of the Potts model parameters is nontrivial. The Potts landscape has primarily been used for the purpose of protein structure contact prediction, and the approximations and algorithms developed to solve for the parameters J have mostly been tailored for this application (19, 36, 45, 46, 47, 48, 49). For the purpose of understanding kinase sequence variation, the distribution $P\left(S\right)$ itself is more central, and more accurate inference techniques are necessary to model this distribution as illustrated in a recent benchmark (43). For this reason, we use a Monte Carlo inference technique that makes fewer approximations (22).

Methods

In this study, we focus on the statistical properties of a Potts model for the kinase family. We use a Potts model and kinase sequence data set that we have previously prepared using methods of parameter inference, MSA preprocessing, alphabet reduction, interaction scoring, and Protein Data Bank (PDB) contact analysis described in (22). These methods are recapitulated in additional detail for this study below. In the current study, we additionally develop methods to analyze the subsequence statistics of this Potts model.

Potts model inference

We use Markov Chain Monte Carlo (MCMC) methods to perform the Potts parameter inference, a method developed in previous studies (33, 36, 50). Our implementation is based on the one described in reference (33). This method makes few analytic approximations such as the weak-coupling approximation used in mean-field methods (49), approximate likelihood functions (19), or truncated cluster entropies (51), at the expense of increased computation time. We compare our results to mean-field methods below. In the MCMC method, we generate sequences from the model according to the equilibrium distribution $P\left(S\right)$ by MCMC, given a trial set of couplings J, and update the parameters J based on the discrepancy between the model and data set bivariate marginals. Our graphic processing unit-based implementation decreases the computation time, and also allows efficient generation and analysis of the large simulated MSAs used in this study. A description of the MCMC algorithm is provided in the Supporting Material of (22). Convergence of the parameters is shown in Fig. S8.

MSA preprocessing

We obtain kinase sequences using HHblits (52) to search the Uniprot database starting from the Pfam kinase family seed (PF00069). We remove any sequences with gaps in the “HRD” or “DFG” triplets, sequences missing the aspartic acid required for Mg²⁺ binding, more than 10 gaps, more than 40 inserts, or with invalid/unknown amino acids, leaving 127,113 sequences of length 241. These sequences are phylogenetically related and sampled with experimental biases, and therefore do not represent independent samples from the distribution $P\left(S\right)$. We correct for this as described in (49) by downweighting similar sequences. We assign a weight $w=1/n$ to each sequence, where n is the number of sequences in the alignment with > 60% sequence identity to it. This cutoff was chosen based on analysis of the distribution of pairwise sequence similarities in the kinase data set (see Supporting Material). This leaves an effective number of sequences $N_{\text{eff}}=\sum w$ of 8149. We then trim the first 5 and last 61 positions from the alignment that contain variable secondary structures, leaving 175 positions.

Alphabet reduction

We reduce the alphabet size q from 21 residue types (20 amino acids plus gap) to 8 in a way that preserves the correlation structure of the MSA, unlike amino acid reduction schemes based on physiochemical properties (53, 54). For each position (processed in random order) we merge the pair of letters that gives the best least-squares fit between the $\left(\begin{array}{c}L\\ 2\end{array}\right)$ Mutual Information (MI) scores across all position pairs of the MSA in the eight-letter and 21-letter alphabets. MI is a measure of correlation strength between two MSA columns $i,j$, given by ${\text{MI}}^{ij}={\sum }_{\alpha \beta }^q{f}_{\alpha \beta }^{ij}\text{log}{f}_{\alpha \beta }^{ij}/f_{\alpha }^i{f}_{\beta }^j$ (55). This merging is repeated until all positions have been reduced to eight letters. In practice, this procedure often first merges the very low-frequency residue types at a position into a single “mutant” residue. After computing bivariate marginals from the weighted eight-letter sequence set, we add a small pseudocount of roughly $1/N$ as a finite size correction.

Alphabet reduction has the benefit of eliminating many small marginals (rare residue types) from the system and thus decreases the computational cost of inference, which scales as $q^2$. For the kinase MSA, we find that reduction to eight letters is a suitable compromise between reducing the problem size and preserving the sequence correlations (Fig. S1 B), and captures almost all the sequence variation; kinase sequences in our data set have 27% average pairwise identity with 21 letters but still only 31% identity after reduction to eight (Fig. S1 A). Further justifying this choice, the mean effective number of amino acids at each position of our raw data set is 8.9, computed by exponentiating the site entropy (see Supporting Material). The Pearson correlation between the 21-letter and eight-letter MI scores is 0.97.

Interaction score: weighted Frobenius norm

A number of different methods have been suggested for obtaining a position pair interaction score from the Potts model parameters, including the “Direct information” (45), Frobenius norm (19), and average product corrected Frobenius norm (56). To control and reduce the contribution of marginals with high sampling error, we score interactions using a weighted Frobenius norm computed as $I^{ij}=\sqrt{{\sum }_{\alpha \beta }{\left(w_{\alpha \beta }^{ij}{J}_{\alpha \beta }^{ij}\right)}^2}$ where $w_{\alpha \beta }^{ij}>0$ are tunable weights. In the case where the weights $w_{\alpha \beta }^{ij}=1$, this reproduces the unweighted Frobenius norm calculation. Both the Frobenius norm and weighted Frobenius norm depend on the choice of “gauge” of the model, referring to the fact that the Potts model described above with $\left(\begin{array}{c}L\\ 2\end{array}\right)q^2$ couplings contains superfluous parameters, such that compensatory transformations of the $J_{\alpha \beta }^{ij}$ parameters can leave the distribution $P\left(S\right)$ unchanged. In fact, there are only $\left(\begin{array}{c}L\\ 2\end{array}\right){\left(q-1\right)}^2+L\left(q-1\right)$ independent parameters, fitted based on an equal number of independent marginals. These gauge transformations have been described in other publications (45, 49, 51). Typically, the Frobenius norm is computed in the “zero-mean” gauge, which minimizes the Frobenius norm and guarantees that uncorrelated positions have an interaction score of 0. For the weighted Frobenius norm, we instead transform the model to a gauge that satisfies the gauge constraint ${\sum }_{\alpha }{w}_{\alpha \beta }^{ij}{J}_{\alpha \beta }^{ij}=0$, which similarly minimizes the weighted norm. To downweight the influence of couplings corresponding to infrequently observed mutant pairs that have high sampling error, we heuristically choose $w_{\alpha \beta }^{ij}=f_{\alpha \beta }^{ij}$, which gives good correspondence between the interaction score and observed contacts in crystal structures (see Fig. S5; Supporting Material).

PDB contact frequency analysis

To measure contact frequencies in the kinase DFG-out and DFG-in conformational states, we obtain 2896 kinase structures from the PDB classified into the DFG-in and DFG-out state collected as described in a previous publication (22) and aligned them to our kinase MSA. A contact is defined as a nearest heavy-atom distance between two residues of less than 6 Å. See reference (22) for further details. When compiling statistics of the residue identities in the sequences of the PDB data set, the sequences are weighted to account for similarity at a 10% similarity threshold after applying the method described above for MSA preprocessing.

In silico sequence data set

We generate our main in silico data set by sampling from the kinase Potts Hamiltonian by MCMC. To roughly simulate the effect of the phylogenetic corrections, we take sequence samples after only a short interval of 175 MCMC steps, giving a nonindependent set of sequences. We then apply the phylogenetic filter at 40% identity, giving 9990 effective sequences. We infer a new in silico set of Potts model parameters using this in silico data set as input, which may differ from the original kinase model due to the effects of finite sampling, phylogeny, and other potential sources of error.

Estimating subsequence frequencies

To test the Potts model’s ability to describe the probability of variations over many positions, we need to estimate the frequency of subsequences (higher-order marginals) predicted by the model. We use two methods to do this. For shorter sets of positions with $L\le 10$, we generate a large in silico MSA of $4\times {10}^6$ sequences by Monte Carlo sampling of the kinase Potts Hamiltonian and simply count the subsequence frequencies. For longer sets of positions, this method is insufficient because the probability of generating a particular subsequence falls far below $1/{10}^6$. Instead, we use a reweighting procedure that allows us to compute relative subsequence frequencies from a generated in silico MSA even if the subsequence does not appear in it. The procedure is described next.

Dividing the MSA into a set of positions whose subsequence probabilities we wish to estimate and a remainder set of “background” positions, the equilibrium probability of a subsequence A is given by $f_A={\sum }_b{p}_b^A$, where $p_b^A$ is the Potts probability of a sequence with background b and subsequence A. Since $p_b^A=e^{-E_b^A}/Z$ and $p_b^B=e^{-E_b^B}/Z$ for subsequence B at the same positions, we can also write $f_A={\sum }_b{p}_b^B{e}^{E_b^B-E_b^A}$. It follows that given a large enough equilibrium sample of sequences $\left\{S\right\}$, we can approximate the frequency of subsequence A as $f_A\propto {\sum }_S{e}^{E_S-E_{A\to S}}$, where $E_S$ is the Potts energy of sequence S and $E_{A\to S}$ is the energy after substituting subsequence A, up to an unknown normalization constant. The ratio of subsequences frequencies, e.g., $f_A/f_B$, can then be unambiguously obtained as the unknown normalization factor cancels. This approximation becomes exact in the limit of large in silico MSAs, and should be valid as long as the distributions of sampled backgrounds for each subsequence, with the subsequence held fixed, would overlap significantly with each other. Using an in silico MSA of size $4\times {10}^6$, we confirm that this approximation is accurate, first for shorter subsequences tested for lengths 2–10 by comparing the frequency predicted by this method to the counted frequency in the raw MSA, and second for longer subsequences of length $L-8$ to L (i.e., those with short backgrounds), by comparing to the exact frequencies computed by enumerating the backgrounds b and summing Potts probabilities as $f_A\propto {\sum }_b{e}^{-E_b^A}$.

Results and Discussion

We infer a model for a data set of $N=8149$ effective kinase sequences of length 175, and quantify the quality of fit through the sum of squared residuals (SSR) of the bivariate marginals. Due to the finite sample size, there is error in each measured bivariate marginal f around its true (unknown) value, and due to this error we estimate an expected SSR of 1.69 between the data set marginals and the (unknown) true marginals. This estimate is obtained by summing over the expected binomial variances of each bivariate marginal of $f\left(1-f\right)/N$ (approximating the observed bivariate marginals as independent), and we also confirm this by generating MSAs of size 8149 from the inferred model and comparing these MSA’s SSR relative to the model’s marginals. The SSR between the inferred Potts model’s marginals and the observed MSA’s marginals is close to 1.69, which suggests that the inferred model approximates the “true” bivariate marginals as well as finite sampling effects allow. In contrast, the SSR of 36.4 between the independent model and the data set is much larger. This shows that the independent model must have significant error in addition to finite sampling error, and demonstrates the importance of modeling correlated effects.

Probability distributions of kinase subsequences

Although the Potts model is fitted to the bivariate marginals of a data set of $N\sim {10}^4$ sequences, it is able to capture higher-order marginals of the data set involving simultaneous variation at many positions. To test this, we would ideally directly compare predicted higher-order marginals (equivalent to subsequence probabilities) to the corresponding frequency observed in an MSA. However, the “shot noise” effect makes this impossible for long sequences, as the probability of seeing an individual kinase sequence of length 175 is always many orders of magnitude smaller than $1/N$ (the smallest observable frequency). We may nevertheless verify the Potts model predictions by examining shorter sets of positions whose MSA statistics can still be measured with reasonable accuracy given the sample size of the data set, but long enough that they encompass a large sequence space. To quantify model error for a set of positions, we measure the Pearson correlation $r_{20}$ between the frequency of the top 20 subsequences most frequently observed at those positions in the kinase family MSA to the probability predicted by the Potts model. We estimate the Potts probability of a subsequence from a generated MSA of $4\times {10}^6$ sequences as described in the Methods. We use the top 20 subsequences for each set of positions in this comparison because the remaining rarer subsequences have high sampling error.

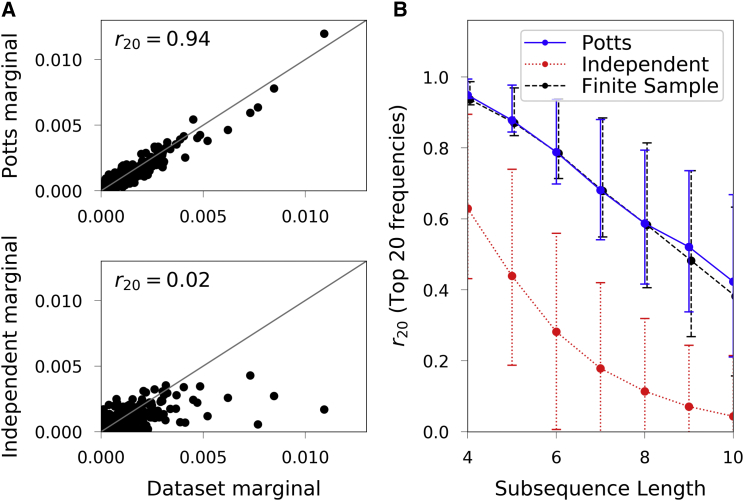
For sets of positions up to about length 10 for which there are sufficient statistics to test the model, the Potts model correctly predicts the observed frequencies and the independent model performs very poorly. In Fig. 1 A we illustrate subsequence frequencies for a specific set of seven positions associated with the DFG-in versus DFG-out conformational transition, described in more detail in another section. The $r_{20}$ score for this set is very high (0.94), which means that the predicted probabilities of the subsequences (seventh-order marginals) agree very well with the corresponding frequencies observed in the data set MSA. In contrast, there is essentially no $r_{20}$ correlation with the independent model.

Figure 1.

Subsequence frequency predictions. (A) Predicted subsequence frequencies for a set of seven positions known to be important for kinase activity, compared to the data set frequencies. The Potts distribution (top) models the observed distribution well, in contrast to the independent model (bottom). (B) Average correlation between observed and predicted frequencies for the top 20 subsequences for large samples of subsequences of varying length, for observed subsequence frequencies with the Potts model (blue), and with the independent model (red, dotted). Circles show the means, and error bars show the range of first to third quartile values (25–75% of sets of positions). The dashed line (black) is an estimate of the expected correlation due only to finite sampling, computed by comparing the subsequence frequencies of a finite synthetic data set MSA of size 8149 to the frequencies of a large MSA of $4\times {10}^6$ sequences generated from a Potts model fitted to the synthetic MSA of size 8149. Both the trend and range of the expected correlations due to the effects of the sample size (8149) are consistent with the correlation between the observed frequencies and those predicted by the Potts model. To see this figure in color, go online.

We verify this more generally by choosing 1000 random sets of positions of length 2–10 from the 175 positions of the full sequence, and compute $r_{20}$, as shown in Fig. 1 B. We also compute the expected $r_{20}$ due to finite sampling alone, by comparing subsequence frequencies in a synthetic MSA of size 8149 generated by the Potts model to those predicted by a second Potts model fitted to this synthetic MSA, estimated from a sample of $4\times {10}^6$ sequences, shown as a dashed line. The Potts model $r_{20}$ correlation decreases for increasing subsequence length, but it closely follows the expected $r_{20}$ due to finite sampling, which shows that this decrease reflects the increasing statistical error in the finite sample data set observed marginals rather than increasing error in the model. Furthermore, the $r_{20}$ between the Potts model and the data set is entirely accounted for by the finite sample size of the data. If third- or higher-order terms affected the subsequence frequency distributions for the lengths we tested, on average, this could manifest as additional error in the model past that we observe due to the finite sample size of the reference data set. For instance, in Fig. 1 B one analogously sees how the lack of second-order terms in the independent model manifests as additional error of this model relative to the finite sample estimate. The absence of such additional error in the Potts model estimates suggests that higher-than-pairwise terms do not play a significant role here. This is a striking result. We note, however, that absence of evidence is not necessarily evidence of absence: It remains possible that a large number of weaker higher-order interaction terms have a small effect for subsequences with $L<10$, but a greater effect for larger L.

Nevertheless, these observations support an interpretation that the collective effects of the pairwise terms of the Potts model are necessary and also sufficient to predict higher-order statistics (marginals) of the data set. The fact that the Potts model captures the higher-order marginals of the data set significantly beyond the pair marginals (up to 10th order, see Fig. 4) which it fits directly supports its use in predicting properties of the sequence space landscape.

Figure 4.

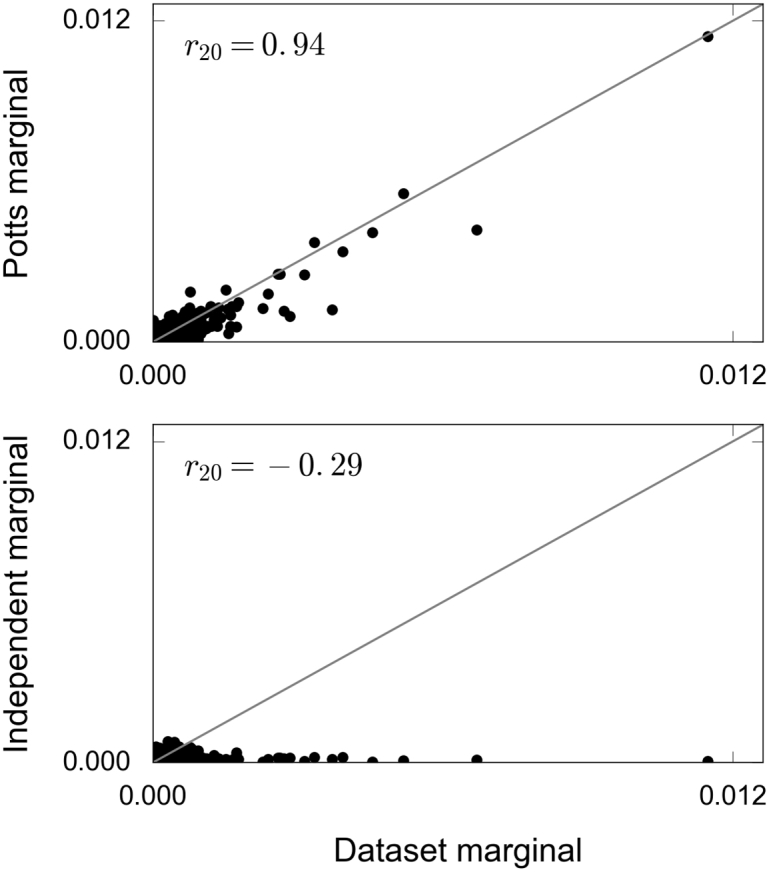
Observed and predicted marginals for a set of six positions in the activation loop. Top: Potts model predictions. Bottom: Independent model predictions. The slightly negative correlation coefficient means that the independent model predicts a low frequency for some of the most frequent subsequences observed in the data, an effect already noted in the discussion of Fig. 2B.

In silico tests: shot noise and importance of pairwise terms

To further demonstrate the ability of the model to describe large sequence spaces for longer sets of positions with $L>10$, we perform in silico tests to show that the statistical energies of sequences are not strongly affected by finite sampling effects given a sequence sample size of ∼10⁴. For longer sequence lengths it is conceivable that the effects of sampling noise in the data or inference errors become more pronounced, as the number of pairwise terms J used in the computation of statistical energy grows quadratically in L. To test this, we generate an in silico data set MSA consisting of 9990 effective sequences generated from the original Potts model as described in the Methods, to which we fit a new in silico Potts model, and then compare the two models. The in silico data set represents a finite resampling process that scrambles small bivariate marginals that have large relative error, and serves to demonstrate that the inferred model is not sensitive to their precise values.

We first examine subsequence statistics of longer position sets. In sets longer than length 10, the subsequence frequencies become minute and cannot be measured even by generating simulated MSAs of up to ∼10⁶ sequences, but instead we are able to compute their relative frequencies using an algorithm described in the Methods. We compute these frequencies using both the original Potts model parameterized on the kinase family MSA and the in silico Potts model, and take the logarithm, giving an effective statistical energy of each subsequence for both models. We find that for subsequences from length 4–175, the two Potts models agree with an average correlation of 0.9 in statistical energy (Fig. S2). The independent model, in contrast, predicts statistical energies for short subsequences of length 4 with similar correlation, but as position set length increases its power drops dramatically, and for sequences of length 128 it has no predictive power $\left(r=0.08\right)$.

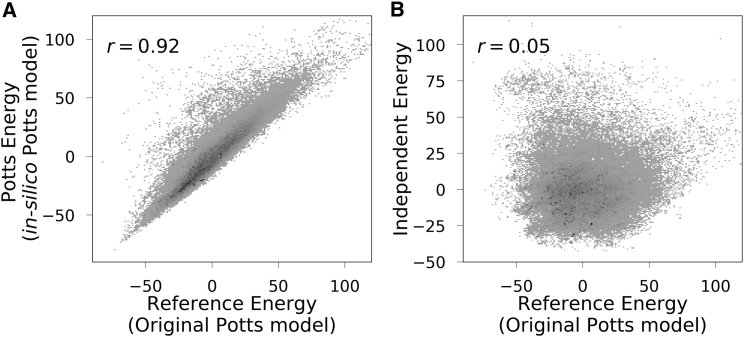
The importance of correlated effects is most pronounced for full kinase sequences varying over all 175 positions. In Fig. 2 A we compare the statistical energies of the 127,113 kinase family sequences of our unweighted data set computed using the in silico Potts model with those computed using the original Potts model (the “reference energy”), finding a Pearson correlation of $r=0.92$. Most of the sequences in this plot are highly dissimilar from the 9990 effective in silico sequences used to parametrize the in silico model. On average, a sequence in the in silico data set has only 52% sequence identity to its most similar sequence in the unweighted kinase data set, and 31% similarity on average to the whole data set, demonstrating the Pott model’s ability to model variation far in sequence space from the sequences it is parametrized with. In contrast, the independent model is unable to predict statistical energies, showing no correlation $\left(r=0.05\right)$ between its predictions and the original statistical energy values (Fig. 2 B). Most dramatically, sequences predicted to be lowest probability (high statistical energy) in the independent model include some of the highest probability (low statistical energy) sequences predicted by the Potts model. These are sequences with multiple rare mutations that the independent model necessarily assigns a low probability, but which the Potts model predicts are very favorably coupled. These results strongly support the importance of the correlated terms and show that they become necessary for predicting statistics of full sequences with many mutations.

Figure 2.

Statistical energies computed for kinase sequences taken from Uniprot. (A) Statistical energies computed using the original Potts model compared to those computed using a Potts model refitted to a finite size in silico sample of 9990 effective sequences generated from the first model, and (B) computed using the original Potts model compared to the those computed using an independent model fit to the in silico sequences. Lower energies are more favorable. The darkness of a plotted point reflects the log of the number of sequences at that point, and most sequences are concentrated near the center of the distribution.

This test does not probe whether triplet and higher-order terms in the Hamiltonian are needed to predict full sequence probabilities because the in silico data set MSA is generated from a pairwise model. However, the lack of a need to parametrize higher-order terms in the Hamiltonian is justified by the results of the previous section for $L<10$. The in silico tests do show that, given such a pairwise model, the statistical energy predictions for sequences with $L>10$, for which sampling error is more significant, are robust given an MSA of thousands of sequences, and the independent model is grossly inadequate.

Although we have focused on the kinase family, we expect these results generalize to other protein families. We have also analyzed the trypsin and photoactive yellow protein families using the same methods as for the kinase family, and obtain similar results (see Fig. S4). We also analyze the kinase in silico data set using the more approximate mean-field methods for parameter inference. We find that the correlation between the energies computed with this model and those computed with the original model is 0.7, compared with 0.92 found by MCMC (Fig. S7, compare to Fig. 2 A).

Identifying highly correlated sets of mutations and functional motifs

Statistical energies calculated from the Potts model can be used to investigate kinase function, and allow us to probe statistics not measurable from the data alone because the finite size of the MSA prevents direct measurement of the frequencies of subsequences or full sequences. As an example, we examine subsequence statistics of particular kinase position sets, and investigate how functional sets of positions (motifs) have strong correlated interactions contributing to their statistical energy, and can be identified because their marginals are more accurately predicted by the Potts model than by the independent model as measured by the $r_{20}$ scores.

To use the $r_{20}$ scores in this way, it is useful to understand that $r_{20}$ scores for a particular position set, in either the independent model or the Potts model, can be lower (reflecting poorer model-data correspondence) due to two different effects. First, due to inaccuracy of the model itself (i.e., due to ignoring correlations), and second, due to sampling error (shot noise) in the data set used as the benchmark for the model predictions, due the finite size of the data MSA.

The degree of model inaccuracy depends on the nature of the correlated interactions within the set of positions. If the “true” Hamiltonian describing the MSA involves higher-order terms than those included in the model (e.g., third-order terms) this will lower the $r_{20}$ score for the Potts model, particularly for sets of positions in which the higher-order interactions contribute significantly to the statistics. At least for $L<10$, our results above suggest that these terms are not important. The independent model does not include second-order terms, so we expect it to perform more poorly for motifs that have functional constraints and therefore correlation is expected to be important. We expect highly correlated (potentially functional) sets of positions to have higher $r_{20}$ score with the Potts model than with the independent model.

Data set sampling error, on the other hand, will often be smaller in functional motifs because they have greater conservation. The sampling error for a subsequence of frequency f can be modeled as the binomial distribution SD $\sqrt{f\left(1-f\right)/N}$ for MSA size N. For small f, the relative error in a statistical energy (obtained by dividing by f) is approximately $\sqrt{1/Nf}$, meaning that higher-frequency subsequences have lower relative statistical error. Highly conserved sets of positions, whose statistics are dominated by a small number of high-frequency subsequences, will therefore have lower sampling error as measured by $r_{20}$. We expect more highly conserved sets of positions to have higher $r_{20}$ scores with both the Potts model and the independent model.

These observations suggest that we can identify strongly correlated motifs by comparing the $r_{20}$ statistics using the Potts model with the corresponding results for the independent model. A high $r_{20}$ score for the Potts model and a low score for the independent model is a sign that the set of positions is more conserved and more correlated than typical, suggesting that it may be an important functional motif.

Previously identified functional set of positions has high correlation

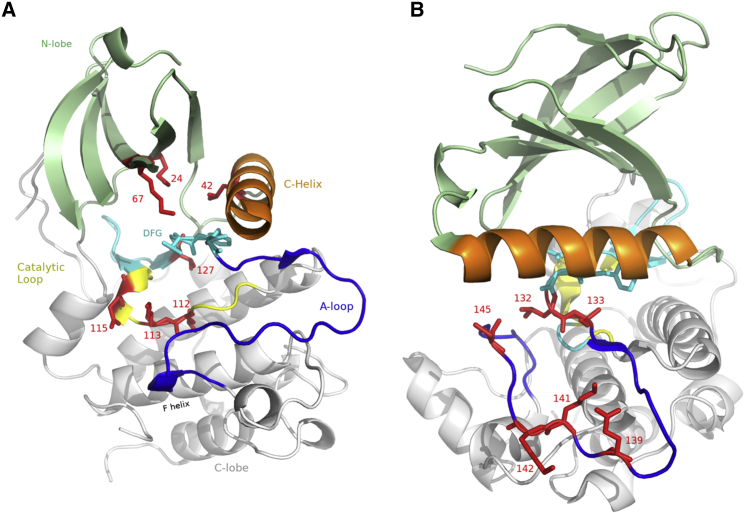
We first examine a motif of length 7 formed from a set positions previously identified in the literature to control kinase function by structure-based analysis (11), illustrated in Fig. 1 A. Its Potts $r_{20}=0.94$ score is much higher than the typical score for sequences of the same length (${\overline{r}}_{20}=0.65$, see Fig. 1 B), yet the independent model’s $r_{20}=0.02$ is much lower than is typical $\left({\overline{r}}_{20}=0.18\right)$. These are the positions 24, 42, 67, 112, 113, 115, and 127 in our alignment, which correspond to PDB residue indices K72, L95, M120, L167, K168, E170, and V182 for the protein kinase A PDB: 2CPK (57), as tabulated in Tables S1 and S2. These seven residues are highlighted in the kinase structure in Fig. 3 A. Residues 112, 113, 115, and 127 form a small subgroup anchoring the catalytic loop, and 24 (known as the β-3 Lysine), 42, and 67 (the gatekeeper residue) form a group on the opposite side of the DFG motif. This example motif demonstrates how sets of positions identified to be important structurally are also found by examining the Potts sequence statistics, and both conservation and correlation are important in the statistics of functional motifs.

Figure 3.

(A) Seven positions (red) identified as important for kinase function in previous literature based on structural analysis shown in crystal structure (PDB: 2CPK), which we identify to be a highly correlated motif. The C-lobe (white) and N-lobe (light green) are shown with the A-loop in blue, the DFG motif and β-7-8 loops in cyan, catalytic loop in yellow, and the α-C helix in orange. The seven positions are shown in red with their alignment index, (B) six positions in the activation loop identified to form a correlated motif (red), and other colors as in (A) (PDB: 2YAC, in the DFG-in state). Residue numbers correspond to positions in our alignment, and map to PDB residue indices as listed in Tables S1 and S2. To see this figure in color, go online.

The Potts model also gives us insights into the important interactions among these residues. The high Potts interaction scores (see Methods) between pairs of these residues suggest that position pairs 112–127 and 113–115 interact strongly, and that the gatekeeper (67) and position 42 on the α-C helix also have a moderate-to-strong interaction. Position 112 is an important residue known to anchor the N-terminal of the catalytic loop to the F-helix (11), whereas position 127 is in the β-8 loop at the N-terminal of the activation loop. The strong Potts interaction score between 112 and 127 suggests a, to our knowledge, new interpretation that the start of the activation loop is indirectly anchored to the F-helix through the intermediary residue 112, thus stabilizing the activation loop. Positions 113 and 115 are known to be involved in catalysis and substrate binding, respectively (11). The predicted interaction between the gatekeeper (67) and position 42, a residue in the α-C helix and part of what is called the “hydrophobic spine,” supports previous results suggesting that the gatekeeper can stabilize this spine (58) and anchor the α-C helix, whose positioning is important for catalysis. The Potts model recapitulates previously identified interactions between important residues, but also suggests, to our knowledge, new interactions among them.

Correlated motif within the activation loop

We next investigate functionality of the activation loop. It is well known that the activation loop conformation consisting of ∼23 residues is important in controlling kinase activation and signaling (22, 56). Phosphorylation of residues in the activation loop causes kinase activation in vivo. The activation loop has different conformations in different functional states (e.g., active, src-like inactive, and DFG-out inactive) and the residues are intricately coupled (Fig. 3 B). In the active state, this loop becomes more structured and stabilizes the catalytic residues in preparation for catalysis, and forms more extensive contacts with other parts of the protein. An important catalytically inactive state is known as DFG-out, in which the activation loop becomes more flexible and frequently cannot be resolved in DFG-out crystal structures, and forms more intraloop contacts and fewer contacts with the rest of the protein. This conformation has clinical significance because certain inhibitors stabilize the DFG-out state, rendering the kinase inactive.

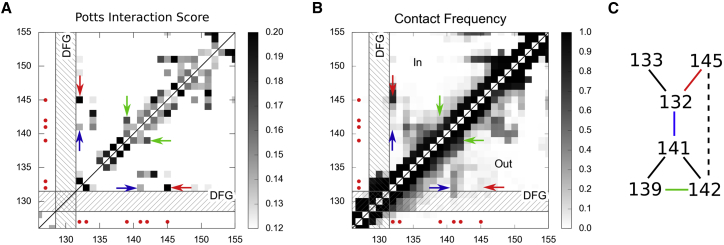
To investigate networks of interactions within the activation loop that are likely to contribute to kinase function, we searched for sets of positions within the loop with the largest differences in $r_{20}$ between the Potts and independent models. These correspond to motifs that are both more conserved and more correlated than observed on average for subsequences of that length, leading us to a motif of six positions, with statistics shown in Fig. 4 and structure shown in Fig. 3 B. To understand the possible functional significance of these residues, we investigated whether they are related to the DFG-in and DFG-out conformational transition, by comparing the interaction scores for pairs of these residues to contact frequencies in the DFG-in and DFG-out conformations measured from a set of 4129 PDB structures, shown in Fig. 5. We find that out of the 15 possible pair interactions, six of these have high interaction scores above a cutoff that is used to distinguish contacts during contact prediction. They are connected together, forming a network illustrated in Fig. 5 C.

Figure 5.

Interaction map and Contact map focusing on the activation loop region. (A) Potts Interaction Score map. The activation loop spans positions 132–151, and is preceded by the DFG motif (which is shown as a hashed area). Position pairs are shaded by their interaction score (see Methods). The six-residue motif identified as highly correlated is marked by red points, and three particular interactions are pointed out with colored arrows: the pair 132,145 (red) is an interaction in the DFG-in state only, and 132,141 (blue) and 139,142 (green) are interactions in the DFG-out state only. (B) Contact frequency map constructed from analysis of the PDB database. The upper triangle shows pair-contact frequency (6 Å closest heavy atom-atom cutoff) in DFG-in conformations, and lower triangle in DFG-out conformation. (C) Network interaction structure of the six-residue motif, showing a link for pairs with high interaction score, or a dotted line for intermediate to weak interaction score. To see this figure in color, go online.

We further investigate the residue pair 132–145, as it has a very strong Potts interaction score and forms a contact in 81% of DFG-in structures and only 8% of DFG-out structures, yet to our knowledge has not been previously identified as functionally important. Position 132 is the DFG + 1 residue, and position 145 is a residue closer to the C-terminal end of the activation loop. An example crystal structure in which this pair is in contact in the DFG-in state (PDB: 2YAC) is shown in Fig. 3 B. To better understand why this interaction may be important, we examine kinase structure and sequence statistics for sequences observed in our sequence data set and in the DFG-in or DFG-out state in the PDB. Interactions between a leucine or phenylalanine at position 132 and cysteine at position 145 are present in ∼20% of DFG-in structures, and none of the DFG-out structures. The “LC” residue combination also gives one of the most positive $C_{\alpha \beta }^{ij}$ correlations from among the 64 possibilities for this position pair in the kinase alignment, as well as one of the most positive contributions to the interaction score (see Fig. S6, D and E). The “FC” residue combination behaves similarly. Crystal structures involving these interactions show that the LC and FC residue combinations often form a hydrophobic interaction, and that the more polar cysteine is more solvent exposed and shields the L or F from solvent. Other residue combinations more prevalent in the DFG-in sequences similarly involve hydrophobic residues (see Fig. S6 B). In total, the 132–145 pair appears to form interactions that stabilize the DFG-in state, based on Potts model scores and crystal structure conformations.

This example illustrates first how functional motifs within a protein might be identified, and second how the Potts model can help suggest the biophysical basis for the functional role of the motif. In future work, we will develop more systematic methods of identifying functional groups of residues. Previous studies have shown how covariation-based techniques can give information about protein architecture and groups of coevolving residues, which have been termed “protein sectors” (59, 60). Our present results suggest that the Potts model may be used in a similar way, in addition to accounting for the collective effects of many pairwise interactions at once.

Conclusions

The protein kinase catalytic domain is one of the most abundant domains across all branches of life. Although kinases share a common core function of phosphoryl-transfer, they also have wide functional diversity, which is primarily achieved through sequence variation. In this study, we use a statistical inference technique to build a maximum entropy coevolutionary Potts Hamiltonian model of sequence variation in the kinase protein family. Our results show that the kinase sequence statistics (higher-order marginals) calculated with a Potts model containing only two-body interactions in the Hamiltonian, and inferred using the MCMC algorithm as we have done, recapitulate the observed marginals for the kinase family up to the observable limit imposed by the shot noise effects inherent in the data because of the sample size. The higher-order marginals (beyond bivariate marginals) are not fitted.

We have shown that the pairwise terms of the Potts model are necessary, and also appear to be sufficient, to model the kinase sequence landscape, particularly for the purpose of modeling the higher-order marginals. The discrepancies we observe between the kinase family subsequence probabilities predicted by the Potts model, with only pairwise terms and the observed subsequence frequency counts in the MSA, can be accounted for by the finite size effect of the MSA. Other groups have explored how shot noise can affect the univariate and bivariate marginals, and individual coupling parameters in toy models (46, 61), and we have previously studied the effects of finite sampling for Potts models fitted to HIV sequence data (40, 62). Here, we examine how shot noise affects the prediction of subsequence probabilities and the statistical energies of full sequences, using real data from the kinase protein family.

Although the finite size of the kinase sequence database and MSA constructed from the database places a limit on the ability of the Potts model to recapitulate the statistics of the higher-order marginals actually observed in the sequence database, it has only a small effect on the statistical energies of the Potts model itself. To show this, we carried out an in silico test. In this test, we used our Potts model of the kinase family to construct an in silico MSA data set, of size ∼8000 sequences. This in silico MSA has only $31\text{\%}$ sequence similarity to the original MSA that we generated from the Uniprot database. We then parameterized a new Potts model from the set of in silico kinase sequences, and showed that the scoring of Uniprot sequences with the new Potts model was highly correlated with that of the original Potts model (see Fig. 2 A).

We propose that kinase family protein functional motifs may be identified as sets of positions where the sequence covariation is much more correlated than is typical for subsequences of that length, and which also exhibit larger than average sequence conservation. Those two criteria can be quantified by identifying sets of positions where the Potts statistical energies are much more favorable than the average Potts statistical energy of a marginal of that same length, whereas the statistical energy of the independent model is much less favorable than the average. We have shown how a set of previously identified functional residues have higher correlation and conservation than typical random sets of positions, and we have also identified a highly correlated and conserved set of positions in the activation loop, which is potentially important in controlling activation loop function. We hope that Potts models used in this and similar ways will help increase our understanding about the deep connections between protein sequence covariation on one hand, and protein structure and function on the other.

Author Contributions

R.M.L and A.H. designed the research. A.H., W.F.F., and P.H. performed the research. R.M.L. and A.H. wrote the manuscript.

Editor: Nathan Baker.