Diffusion in a tube of alternating diameter

Abstract

The paper deals with diffusion of a particle in a tube that consists of alternating wide and narrow sections. At sufficiently long times the particle motion can be coarse-grained and described as effective free-diffusion along the tube axis. In the coarse-grained description all the details of the tube geometry are packed into the effective diffusion coefficient of the particle. We derive a formula for the effective diffusion coefficient, which shows how it depends on the geometric parameters of the tube. To test the accuracy of this formula we compare its predictions with the values of the effective diffusion coefficient found in Brownian dynamics simulations. The comparison shows that the formula is applicable at arbitrary values of the length and radius of the narrow sections on condition that the radius of the wide sections does not exceed their length.

1. Introduction

The model of a particle diffusing in a tube of periodically varying geometry was first considered in the literature on diffusion in porous solids [1]. Later this model has been used to analyze diffusion in different complex media like soils [2], biological tissues [3], neurons [4], and zeolites [5]. Theoretical analysis of controlled drug delivery [6] is another important application of the model [7]. Periodic variations of the tube geometry lead to a slowdown of diffusion along the tube compared to that in free space. This happens because any expanded section of a tube works as an entropy well while any constriction zone works as an entropy barrier [8,9]. To characterize the slowdown consider displacement of the particle, Δx(t) = x(t) − x(0), where x(t) is the particle coordinate measured along the tube axis at time t. At sufficiently long times, when 〈Δx²(t)〉 significantly exceeds the square of the period, l, associated with variations in the tube geometry, 〈Δx²(t)〉 ≫ l², one can introduce a coarse-grained distribution of the displacement. From here on we use the angular brackets, 〈· · ·〉, as a notation of the averaging over both the particle stochastic trajectories and its initial position, which is assumed to be uniformly distributed over the tube. The coarse-grained distribution can be described by means of the effective propagator, G_eff(x, t|x₀) = G_eff(x − x₀, t), where x₀ = x(0) is the initial position of the particle, that satisfies the effective one-dimensional (1-D) free-diffusion equation,

$$\frac{\partial G_{\text{eff}}}{\partial t}=D_{\text{eff}}\frac{{\partial }^2{G}_{\text{eff}}}{\partial x^2}$$ (1)

In this equation all information about the varying tube geometry is packed into the effective diffusion coefficient, D_eff, which may be well below the particle diffusion coefficient in free space.

Then the question about the relation between D_eff and the tube geometry naturally arises. Finding of this relation is a difficult problem that cannot be solved in general. However, the problem can be solved when the tube radius, r(x), is a slowly varying function, |dr(x)/dx| ≪ 1. The point is that in such a case the three-dimensional (3-D) diffusion problem can be reduced to an effective 1-D problem. To find D_eff first one should replace the initial 3-D diffusion equation by an effective 1-D Smoluchowski equation with periodic entropy potential and position-dependent diffusion coefficient. This is so-called modified Fick–Jacobs (F–J) equation [8] that reduces to the regular F–J equation [9] when the position-dependent diffusion coefficient is replaced by the particle diffusion coefficient in free space. Based on the modified F–J equation, one can find D_eff by means of the Lifson–Jackson formula [10] that is an exact result for the 1-D Smoluchowski equation in which both the potential and the position-dependent diffusion coefficient are periodic. This two-step approach has been realized for a tube formed by contacting spherical cavities where an analytical expression for D_eff can be obtained [11]. Although the modified F–J equation was derived by Zwanzig [8a] under the assumption that |dr(x)/dx| ≪ 1, the range of its applicability is much broader – this equation is still applicable when r(x) satisfies |dr(x)/dx| ≤ 1 [12].

The present paper is focused on the effective diffusion coefficient in the opposite limiting case, when the approach based on the modified F–J equation is inapplicable, namely, the paper discusses D_eff in a tube of alternating diameter schematically shown in Fig. 1a. In such a tube the radius changes abruptly, so that dr(x)/dx diverges at the points where the radius makes a jump. Nevertheless, a formula for D_eff can be derived. This formula, which is the main result of the present paper, shows how D_eff depends on the geometric parameters of the tube. In the next section we discuss the obtained expression for D_eff and demonstrate that its predictions are in excellent agreement with D_eff found in Brownian dynamics simulations when the radius of the wide sections of the tube does not exceed their length. We derive this expression in Section 3. Then in Section 4 we compare our result with corresponding result that can be obtained following the way applicable for tubes of slowly varying diameter, i.e., using the modified F–J equation and the Lifson–Jackson formula. Finally, some concluding remarks are made in the last section.

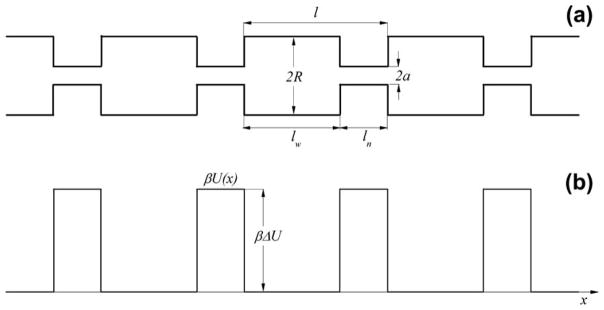
Fig. 1.

Schematic representation of a tube of alternating diameter (panel (a)) and corresponding dimensionless entropy potential (panel (b)). The tube consists of alternating wide and narrow sections of radii R and a whose lengths are equal to l_w and l_n, respectively. The dimensionless entropy potential, βU(x) = 2 ln (R/r(x)), is equal to zero and 2 ln (R/a) in the wide and narrow sections of the tube, respectively. At the boundaries separating the two sections the potential make a jump, βΔU = 2 ln (R/a).

2. Formulation of the result

Consider a particle diffusing in a tube schematically shown in Fig. 1a. The tube consists of alternating narrow (n) and wide (w) sections of radii a and R, whose lengths, respectively, are l_n and l_w. The tube radius, r(x), is a periodic function of the x-coordinate measured along the centerline of the tube, r(x + l) = r(x), where l = l_n + l_w is the tube period. At long times, when the mean squared displacement of the particle, 〈Δx²(t)〉, is much greater than the square of the tube period, 〈Δx²(t)〉 ≫ l², the mean squared displacement linearly grows with time,

$$\langle \mathrm{\Delta }{x}^2(t)\rangle =2D_{\text{eff}}t,t\gg l^2/D_{\text{eff}}$$ (2)

where D_eff is the effective diffusion coefficient. In our analysis we ignore the hydrodynamic interaction of the particle with the tube walls and assume that the value of the particle diffusion coefficient in both sections of the tube is identical to its value in free space, denoted by D.

The slowdown of diffusion is due to the fact that to enter a narrow section the particle has to climb up the entropy barrier to find the entrance. When a ≪ R, this may take the particle a lot of time, since the entropy barrier is high. The main result of the present paper is the expression for the effective diffusion coefficient that shows how D_eff depends on the geometric parameters of the tube, a, R, l_n, and l_w,

$$D_{\text{eff}}=D{\left\{1+\frac{l_n{l}_w}{{(l_n+l_w)}^2}{\left(\frac{R}{a}-\frac{a}{R}\right)}^2+\frac{\pi R^2[l_w+{(a/R)}^2{l}_n]}{2f(v)a{(l_n+l_w)}^2}\right\}}^{-1}$$ (3)

where f(ν) is a function of the radii ratio, ν, given by

$$f(v)=\frac{1+1.37v-0.37v^4}{{(1-v^2)}^2},v=\frac{a}{R}$$ (4)

This function monotonically increases with ν from unity at ν = 0 to infinity as ν → 1, as shown in Fig. 2. Using D as a scale, we can write D_eff in terms of the tortuosity, τ [13], as

Fig. 2.

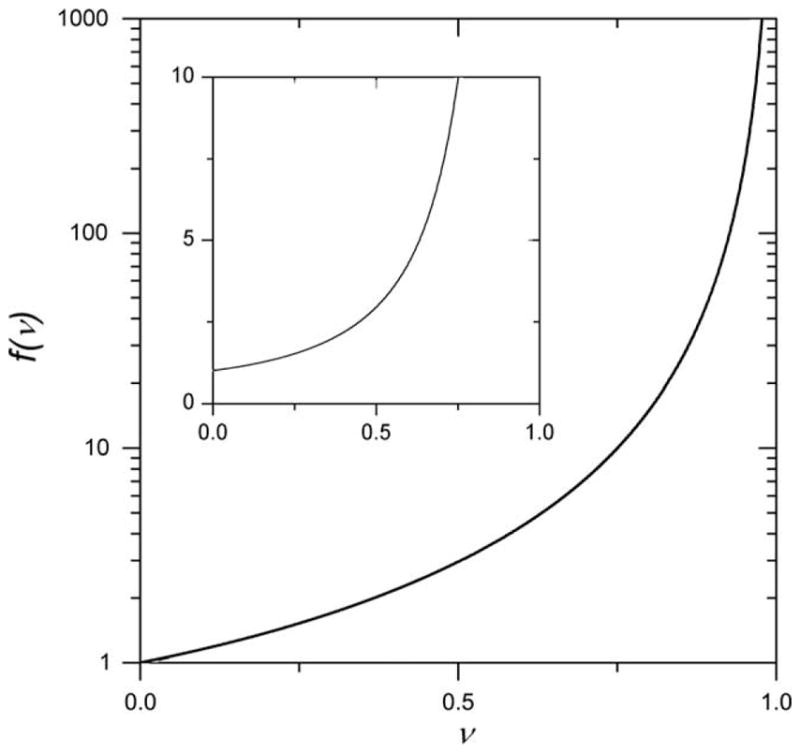
Function f(ν) defined in Eq. (4).

$$\begin{gathered} D_{\text{eff}}=\frac{D}{\tau },\tau =\frac{D}{D_{\text{eff}}} \\ =1+\frac{l_n{l}_w}{{(l_n+l_w)}^2}{\left(\frac{R}{a}-\frac{a}{R}\right)}^2+\frac{\pi (a^2{l}_n+R^2{l}_w)}{2f(v)a{(l_n+l_w)}^2} \end{gathered}$$ (5)

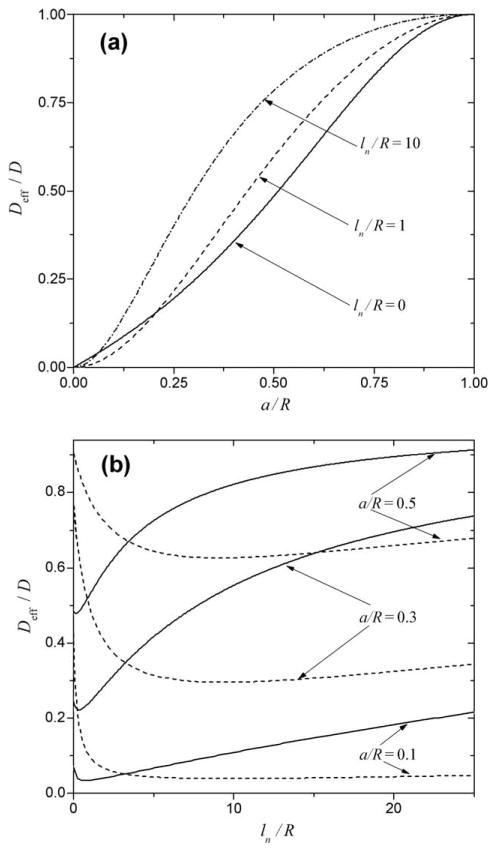
Although the tube is characterized by four parameters, a, R, l_n, and l_w, the tortuosity is a function of three dimensionless parameters. We illustrate the dependence of D_eff on the parameters of the tube in Fig. 3.

Fig. 3.

Dependence of the effective diffusion coefficient on the tube parameters, Eq. (3). (a) D_eff as a function of a/R at l_n/R = 0 (solid curve), l_n/R = 1 (dashed curve), and l_n/R = 10 (dashed-dotted curve). For all the curves l_w/R = 1; (b) D_eff as a function of l_n/R at a/R = 0.1, 0.3, 0.5 for l_w/R = 1 (solid curves) and l_w/R = 10 (dashed curves). One can see that non-monotonic behavior of D_eff is more pronounced at larger values of l_w/R.

The formula for D_eff is applicable at arbitrary length and radius of the narrow sections whereas the length of the wide sections must satisfy

$$l_w\ge R$$ (6)

When the length of the narrow sections tends to zero, l_n → 0, we deal with a tube with infinitely thin periodic partitions that separate the tube into compartments of length l = l_w. The particle can go from one compartment to the other through a circular aperture of radius a located in the center of the partition separating the compartments. In this limiting case the tortuosity takes the form [14b]

$$\tau =1+\frac{\pi R^2}{2f(v)al}$$ (7)

and we recover the expression for D_eff derived recently [14].

As a → R (ν → 1, f(ν) → ∞), the tortuosity, Eq. (5), approaches unity and D_eff, Eq. (3), tends to D as it must be. As a → 0 (ν → 0, f (ν) → 1), the tortuosity diverges and D_eff tends to zero. The small-a asymptotic behavior of τ is given by

$$\tau =\frac{R^2{l}_w(2l_n+\pi a)}{2a^2{(l_n+l_w)}^2},a\to 0$$ (8)

This asymptotic behavior depends on the thickness of the narrow sections of the tube: When l_n is finite τ diverges as 1/a², and D_eff tends to zero as a² while at l_n = 0 (tube separated into compartments by infinitely thin periodic partitions) τ diverges as 1/a, and D_eff tends to zero linearly in a (see Fig. 3a).

We have developed a theory of diffusion in tubes with infinitely thin periodic partitions, l_n = 0, l_w = l, in Ref. [14], where we derived a formula for D_eff and demonstrated excellent agreement between its predictions and D_eff found in Brownian dynamics simulations at all values of the radii ratio, ν = a/R, on condition that the length of the compartments satisfied l = l_w ≥ R. This constraint is quite general and holds true not only when the narrow sections are infinitely thin partitions. With this in mind, we tested the dependence of D_eff, Eq. (3), on the length and radius of the narrow sections at l_w = R and 2R. The results at l_w = R are presented in Table 1, which gives the ratios of the D_eff obtained in Brownian dynamics simulation and predicted by the theory at different values of the radii ratio, ν = 0.1, 0.3, 0.5, 0.7, 0.9, and several values of the length of the narrow sections, l_n/R = 0, 0.5, 1, 2. One can see excellent agreement between the theoretical predictions and the simulation results. Similar comparison at l_w = 2R (the results are not shown) corroborates this conclusion.

Table 1.

Ratios of the effective diffusion coefficients found in Brownian dynamics simulations to their theoretically predicted counterparts, Eq. (3), at different values of the length and radius of the narrow sections. The simulation results were obtained at l_w = R by averaging over 5 × 10⁴ trajectories. The relative errors of these results do not exceed 2%.

Radii ratio, a/R	Length of narrow sections, ln/R
	0	0.5	1	2
0.1	1.00	1.00	1.01	1.01
0.3	0.99	0.99	1.00	1.01
0.5	0.99	0.97	0.99	1.00
0.7	0.99	0.98	0.98	0.99
0.9	0.99	0.99	0.99	0.99

3. Derivation

To derive the formula for D_eff discussed in the previous section we first map diffusive motion of the particle onto the nearest-neighbor continuous-time random walk between periodically spaced tube cross-sections located in the middle of the wide sections of the tube. For the sake of convenience we take that these cross-sections are located at x_n = nl, where n = 0, ±1, ±2,. . ..

Consider a particle that starts from the cross-section located at x_l. When the wide sections of the tube are long enough, the distributions of the particle exit points to the neighboring cross-sections located at x_l±1 are (i) uniform over these cross-sections and (ii) independent of the particle starting position on the initial cross-section. Based on these observations we replace diffusive motion of the particle by continuous-time random walk between neighboring cross-sections. Then we can find D_eff using the relationship [15]

$$D_{\text{eff}}=\frac{l^2}{2\langle t\rangle }$$ (9)

where 〈t〉 is the mean first-passage time of the particle from an initial cross-section to one of the two neighboring cross-sections separated from the initial one by distance l. Thus, derivation of the formula for D_eff reduces to finding the mean first-passage time 〈t〉 as a function of the tube parameters.

To solve this problem consider a particle that starts from the cross-section located at x₁ = l. Our goal is to find the particle mean first-passage time to one of the two neighboring cross-sections located at x₀ = 0 and x₂ = 2l. This mean first-passage time is identical to the mean particle lifetime assuming that the cross-sections located at x₀ = 0 and x₂ = 2l are absorbing, so that the particle trajectory is terminated at the first contact with these cross-sections. Because of the symmetry we can replace the initial cross-section located at x₁ = l by a reflecting wall. Thus we have to find the mean lifetime of the particle that starts from the reflecting wall located at x₁ = l and is trapped at the first contact with the absorbing cross-section located at x₀ = 0.

To reach the absorbing cross-section, the particle has to pass through the narrow section of the tube located between x = l_w/2 and x = l_n + l_w/2 = l − l_w/2. We describe diffusion of the particle in such geometry by means of the effective 1-D description suggested recently [16]. In this approach the free-diffusion equation is used to describe the particle motion in the wide and narrow sections of the tube, and the solutions found in the neighboring sections are matched using the matching conditions introduced in Ref. [16].

Let G(x, t) be the particle propagator, which can be written as

$$G(x,t)=\{\begin{array}{ll}{G}_1(x,t),\hfill & 0<x<l_w/2\hfill \\ G_2(x,t),\hfill & l_w/2<x<l_n+l_w/2\hfill \\ G_3(x,t),\hfill & l_n+l_w/2<x<l\hfill \end{array}$$ (10)

In each of the three intervals the components of the propagator satisfy

$$\frac{\partial G_i(x,t)}{\partial t}=D\frac{{\partial }^2{G}_i(x,t)}{\partial x^2},i=1,2,3$$ (11)

The components of the propagator also satisfy the initial condition

$$G_1(x,0)=G_2(x,0)=0;G_3(x,0)=\delta (x-l)$$ (12)

as well as the absorbing and reflecting boundary conditions at x = 0 and x = l, respectively,

$$G_1(0,t)={\frac{\partial G_3(x,t)}{\partial x}|}_{x=l}=0$$ (13)

At x = l_w/2 and x = l_n + l_w/2 the components satisfy the matching conditions. To write these conditions we introduce two trapping rates, κ_w and κ_n. The former, κ_w, describes transitions of the particle from wide sections to the narrow ones, whereas the latter, κ_n, describes the particle transitions in the opposite direction. The matching conditions have the form [16]

$${D\frac{\partial G_1}{\partial x}|}_{x=l_w/2}={D\frac{\partial G_2}{\partial x}|}_{x=l_w/2}={({\kappa }_n{G}_2-{\kappa }_w{G}_1)\mid }_{x=l_w/2}$$ (14)

and

$${D\frac{\partial G_2}{\partial x}|}_{x=l_n+l_w/2}={D\frac{\partial G_3}{\partial x}|}_{x=l_n+l_w/2}={({\kappa }_w{G}_3-{\kappa }_n{G}_2)\mid }_{x=l_n+l_w/2}$$ (15)

Here the first equalities are the conditions of the flux conservation at the boundaries, while the second equalities establish the relations between the fluxes through the boundaries and the components of the propagator.

The trapping rates κ_w and κ_n are not independent. They are related by the relationship

$${\kappa }_w{R}^2={\kappa }_n{a}^2$$ (16)

which follows from the condition of detailed balance, i.e., from the requirement of no net fluxes at equilibrium. The trapping rate κ_w was found in Ref. [17] using a version of the effective medium approximation called boundary homogenization [18]. The result is [17]

$${\kappa }_w=\frac{4\mathit{Daf}(v)}{\pi R^2}$$ (17)

Respectively, the trapping rate κ_n is given by

$${\kappa }_n=\frac{4Df(v)}{\pi a}$$ (18)

As a → 0 (f(ν) → 1), the trapping rates take the forms κ_w = 4Da/(πR²) and κ_n = 4D/(πa). The former follows from the Berg–Purcell–Shoup–Szabo theory of trapping by patchy surfaces [19] in the low patch surface fraction limit [17,18]. The latter describes escape of a particle diffusing in a cylindrical membrane channel into an infinite semi-space outside the membrane [20]. As a → R (f(ν) → ∞), both κ_w and κ_n diverge, as it must be in a tube of a constant diameter.

Using the propagator, Eq. (10), one can find the particle survival probability, S(t), defined as

$$S(t)={\int }_0^{l}G(x,t)dx={\int }_0^{l_w/2}{G}_1(x,t)dx+{\int }_{l_w/2}^{l_n+l_w/2}{G}_2(x,t)dx+{\int }_{l_n+l_w/2}^l{G}_3(x,t)dx$$ (19)

Then one can find the particle lifetime probability density, φ(t),

$$\phi (t)=-\frac{dS(t)}{dt}$$ (20)

and, finally, the mean lifetime of the particle,

$$\langle t\rangle ={\int }_0^{\infty }t\phi (t)dt={\int }_0^{\infty }S(t)dt$$ (21)

Using Eq. (19) one can write the mean lifetime as a sum of three integrals

$$\langle t\rangle ={\int }_0^{l_w/2}{F}_1(x)dx+{\int }_{l_w/2}^{l_n+l_w/2}{F}_2(x)dx+{\int }_{l_n+l_w/2}^l{F}_3(x)dx$$ (22)

where functions F_i(x), i = 1, 2, 3, are defined as the time integrals of the components of the propagator,

$$F_i(x)={\int }_0^{\infty }{G}_i(x,t)dt,i=1,2,3$$ (23)

As follows from Eqs. (11) and (23), these functions satisfy

$$D\frac{d^2{F}_i(x)}{d{x}^2}=-{\delta }_{i,3}\delta (x-l),i=1,2,3$$ (24)

According to Eqs. (13)–(15), they also satisfy the boundary conditions at x = 0 and x = l,

$$F_1(0)={\frac{d{F}_3(x)}{dx}|}_{x=l}=0$$ (25)

and the matching conditions at x = l_w/2 and x = l_n + l_w/2,

$${D\frac{d{F}_1}{dx}|}_{x=l_w/2}={D\frac{d{F}_2}{dx}|}_{x=l_w/2}={({\kappa }_n{F}_2-{\kappa }_w{F}_1)\mid }_{x=l_w/2}$$ (26)

$${D\frac{d{F}_2}{dx}|}_{x=l_n+l_w/2}={D\frac{d{F}_3}{dx}|}_{x=l_n+l_w/2}={({\kappa }_w{F}_3-{\kappa }_n{F}_2)\mid }_{x=l_n+l_w/2}$$ (27)

One can find functions F_i (x) from Eqs. (24)–(27). The result is

$$F_1(x)=\frac{x}{D},0<x<\frac{l_w}{2}$$ (28)

$$F_2(x)=\frac{D+{\kappa }_w{l}_w/2}{D{\kappa }_n}+\frac{x-l_w/2}{D},\frac{l_w}{2}<x<l_n+\frac{l_w}{2}$$ (29)

$$F_3(x)=\frac{2D+{\kappa }_n{I}_n+{\kappa }_w{I}_w/2}{D{\kappa }_w}+\frac{x-l_n-l_w/2}{D},l_n+\frac{l_w}{2}<x<l$$ (30)

Using these functions when carrying out the integrations in Eq. (22), one obtains

$$\langle t\rangle =\frac{1}{2D}\left[l_n^2+l_w^2+2D\left(\frac{l_n}{{\kappa }_n}+\frac{l_w}{{\kappa }_w}\right)+l_n{l}_w\left(\frac{{\kappa }_w}{{\kappa }_n}+\frac{{\kappa }_n}{{\kappa }_w}\right)\right]$$ (31)

Substituting here κ_w and κ_n defined in Eqs. (17) and (18), one eventually arrives at the expression for the mean lifetime that can be written in terms of the tortuosity τ, Eq. (5), as

$$\langle t\rangle =\frac{l^2\tau }{2D}$$ (32)

Finally, substituting this expression for 〈t〉 into Eq. (9), one recovers the formula for D_eff given in Eq. (3), which is the main result of the present paper.

4. Discussion

It seems interesting to compare the formula for D_eff, Eq. (3), with the result for the effective diffusion coefficient that can be obtained on the basis of the modified F–J equation. In the case under consideration this equation is identical to the regular F–J equation and has the form:

$$\frac{\partial G(x,t\mid x_0)}{\partial t}=D\frac{\partial }{\partial x}\left\{A(x)\frac{\partial }{\partial x}\left[\frac{G(x,t\mid x_0)}{A(x)}\right]\right\}$$ (33)

where G(x, t|x₀) is the particle propagator and A(x) = π[r(x)]² is the tube cross-section area at given x. The entropy potential, U(x), counted from its value in the wide cross-sections (Fig. 1b) is given by

$$U(x)=-k_{B}T\text{ln}\left(\frac{A(x)}{A_w}\right)=2k_{B}T\text{ln}\left(\frac{R}{r(x)}\right)$$ (34)

where k_B and T are the Boltzmann constant and the absolute temperature and A_w = πR² is the cross-section area of the wide sections. Using the entropy potential one can write Eq. (33) as the Smoluchowski equation:

$$\frac{\partial G(x,t\mid x_0)}{\partial t}=D\frac{\partial }{\partial x}\left\{e^{-\beta U(x)}\frac{\partial }{\partial x}[e^{\beta U(x)}G(x,t\mid x_0)]\right\}$$ (35)

where β = 1/(k_BT).

Since the entropy potential is a periodic function of x, U(x + l) = U(x), one can find the corresponding effective diffusion coefficient, D_F–J, by means of the Lifson–Jackson formula [10], according to which

$$\frac{D}{D_{F-J}}={\tau }_{F-J}={\langle \frac{1}{A(x)}\rangle }_l{\langle A(x)\rangle }_l$$ (36)

where τ_F–J is the corresponding tortuosity and 〈f(x)〉_l denotes the average of a periodic function f(x), f(x + l) = f(x), over the period l,

$${\langle f(x)\rangle }_l=\frac{1}{l}{\int }_0^{l}f(x)dx$$ (37)

Carrying out the integrations one obtains

$${\tau }_{F-J}=1+\frac{l_n{l}_w}{{(l_n+l_w)}^2}{\left(\frac{R}{a}-\frac{a}{R}\right)}^2$$ (38)

Note that Michaels obtained this expression for the tortuosity long time ago [1b].

Using τ_F–J we can write the tortuosity given in Eq. (5) as

$$\tau ={\tau }_{F-J}+\frac{\pi (a^2{l}_n+R^2{l}_w)}{2f(v)a{(l_n+l_w)}^2}$$ (39)

The difference between τ and τ_F–J is the most pronounced at small l_n. Indeed, as l_n → 0, τ_F–J tends to unity whereas τ tends to its limiting form given in Eq. (7). The latter is the tortuosity in the tube separated into compartments by infinitely thin periodic partitions. This tortuosity is much larger than unity when a is much smaller than R, more precisely, when the tube parameters satisfy the inequality al ≪ R². To summarize, the formula for τ given in Eq. (5) predicts correct behavior of the tortuosity at small l_n while the formula for τ_F–J, Eq. (38), found on the basis of the F–J equation fails in this limiting case.

5. Concluding remarks

The main result of this paper is the formula for the effective diffusion coefficient of a particle diffusing in a tube of alternating diameter, Eq. (3). The formula is applicable at arbitrary length and radius of the narrow sections of the tube on condition that the radius of the wide sections does not exceed their length. Thus, one can find D_eff not only when the tube radius is a slowly varying function, |dr(x)/dx| ≤ 1, but also in the opposite limiting case when the tube radius changes abruptly. The point is that one can introduce an effective 1-D description of diffusion in a 3-D tube in both cases. In tubes of slowly varying diameter the corresponding 1-D description is formulated in terms of the modified Fick–Jacobs equation, whereas in tubes of alternating diameter this is the 1-D description suggested in Ref. [16]. Finally we indicate that the validity of the Fick–Jacobs equation has been studied recently in Refs. [21,22].