Exploration Disrupts Choice-predictive Signals and Alters Dynamics in Prefrontal Cortex

Summary

In uncertain environments, decision-makers must balance two goals: they must “exploit” rewarding options, but also “explore” in order to discover rewarding alternatives. Exploring and exploiting necessarily change how the brain responds to identical stimuli, but little is known about how these states, and transitions between them, change how the brain transforms sensory information into action. To address this question, we recorded neural activity in a prefrontal sensorimotor area while monkeys naturally switched between exploring and exploiting rewarding options. We found that exploration profoundly reduced spatially selective, choice-predictive activity in single neurons and delayed choice-predictive population dynamics. At the same time, reward learning was increased in brain and behavior. These results indicate that exploration is related to sudden disruptions in prefrontal sensorimotor control and rapid, reward-dependent reorganization of control dynamics. This may facilitate discovery through trial-and-error.

Introduction

In complex environments, reward contingencies are seldom fully known. In these circumstances, there is a limit to the effectiveness of an “exploitative” strategy. Trying to maximize immediate reward by repeatedly choosing known-value options risks missed opportunities to discover better alternatives. Thus, decision-makers occasionally deviate from exploiting in order to “explore”—they sample alternative actions, gather information about the environment, and thereby increase the potential for future rewards (Kaelbling et al., 1996; Sutton and Barto, 1998). Designing a system flexible enough to both exploit and explore is classic problem in reinforcement learning (Sutton and Barto, 1998), and its solution is a prerequisite for intelligent, adaptive behavior in natural decision-makers (Rushworth and Behrens, 2008). However, only a few studies have examined how exploration is implemented in the brain (Daw et al., 2006; Quilodran et al., 2008; Pearson et al., 2009; Kawaguchi et al., 2015), and it remains unclear how the mapping of sensory input onto motor output is adjusted in order to pursue these different strategies in an otherwise identical environment.

The brain is biased towards representing and selecting rewarding options. For example, neurons in oculomotor regions such as the frontal eye field (FEF) (Leon and Shadlen, 1999; Roesch and Olson, 2003; Ding and Hikosaka, 2006; Roesch and Olson, 2007; Glaser et al., 2016) and the lateral intraparietal area (LIP) (Platt and Glimcher, 1999; Sugrue et al., 2004) signal high-value gaze targets more robustly than low-value targets. At the behavioral level, high value targets cause rapid, vigorous orienting responses (Takikawa et al., 2002; Reppert et al., 2015) and previously rewarded options continue to capture gaze and bias attention even when explicitly devalued (Takikawa et al., 2002; Anderson et al., 2011; Hickey and van Zoest, 2012). This bias improves the detection of goal-relevant targets and would help during exploitation. However, it interferes with the goal of exploring alternative options.

How can the brain efficiently overcome its reward-seeking bias in order to discover better options? One way might be to choose more randomly during exploration, perhaps by adding noise or indeterminacy to neural computations involved in choice and attention. This is an efficient way to produce exploration in artificial agent (Sutton and Barto, 1998) and humans also seem to explore largely randomly (Wilson et al., 2014). However, random selection in behavior need not imply an indeterminate selection process in the brain, and there is no empirical evidence for indeterminate selection. Alternatively, the representations of chosen options could be enhanced during exploration, perhaps due to some bias towards uncertain options (Rushworth and Behrens, 2008; Schultz et al., 2008). This latter hypothesis might have cognitive consequences. For example, in regions involved in directing attention, increasing choice-selective representations could increase reward learning, because attention facilitates learning (Pearce and Hall, 1980; Swan and Pearce, 1988; Pearce and Bouton, 2001; Niv et al., 2015). Such an observation could provide a mechanistic basis for normative accounts that predict that learning should increase during exploration (Kaelbling et al., 1996; Sutton and Barto, 1998; Yu and Dayan, 2005; Daw et al., 2006; Cohen et al., 2007; O’Reilly, 2013). Of course, learning could increase during exploration via other mechanisms. It remains unclear whether learning is increased during exploration in biological decision-makers and exploration may just as readily decrease choice selectivity as increase it.

Neural structures involved in directing attention and choice, such as the FEF, are ideally suited to test how the brain implements exploration. FEF neurons are highly spatially selective: their firing rates reliably signal the location of to-be-chosen targets, either presented in isolation or among distractors (Bizzi, 1968; Bruce and Goldberg, 1985; Schall and Hanes, 1993; Umeno and Goldberg, 1997; Schall and Thompson, 1999; Coe et al., 2002). These spatially selective signals are remarkably precise and choice-predictive in comparison to those found in other prefrontal regions (Funahashi et al., 1990; Hayden and Platt, 2010; Purcell et al., 2012; Chen and Stuphorn, 2015). Furthermore, this selective activity in the FEF is both correlatively and causally implicated in the control of both covert attention (Kastner et al., 1998; Moore and Fallah, 2001; Moore and Armstrong, 2003; Moore and Fallah, 2004; Thompson et al., 2005; Armstrong et al., 2009) and saccadic target selection (Bizzi, 1968; Bruce and Goldberg, 1985; Schall and Hanes, 1993; Umeno and Goldberg, 1997; Schall and Thompson, 1999; Coe et al., 2002), making the region ideally suited to address questions about the link between selective attentional signals and changes in learning rates across states. Finally, although choice-predictive spatial-selectivity in the FEF is weakly modulated by the expected value of chosen targets (Leon and Shadlen, 1999; Roesch and Olson, 2003; Ding and Hikosaka, 2006; Roesch and Olson, 2007; Glaser et al., 2016), it remains unclear whether FEF target selectivity will differ across explore and exploit goals.

To test these hypotheses, we trained monkeys on a task that encouraged transitions between exploration and exploitation, namely a restless k-armed bandit (Kaelbling et al., 1996; Sutton and Barto, 1998), while we recorded from small populations of FEF neurons. We first developed a novel method to identify and characterize the monkey’s goal state on each trial, and then examined how spatially selective, choice-predictive signals in the FEF changed across those states. We found that FEF selectivity was profoundly disrupted during exploration and spatially selective, choice-predictive population dynamics are delayed and disorganized, consistent with the hypothesis that indeterminacy may facilitate exploratory choice.

Results

In the task, monkeys made a sequence of choices between 3 physically identical targets, indicating their choice via saccades to one target. Each target location offered some probability of reward, which walked unpredictably and independently over time (figure 1A; STAR Methods). Because monkeys could only infer the current value of each target via selecting it, monkeys were induced to intersperse exploitative, reward-maximizing choices with exploratory choices, in order to learn about the reward contingencies of other targets.

Figure 1. Task design and goal state identification.

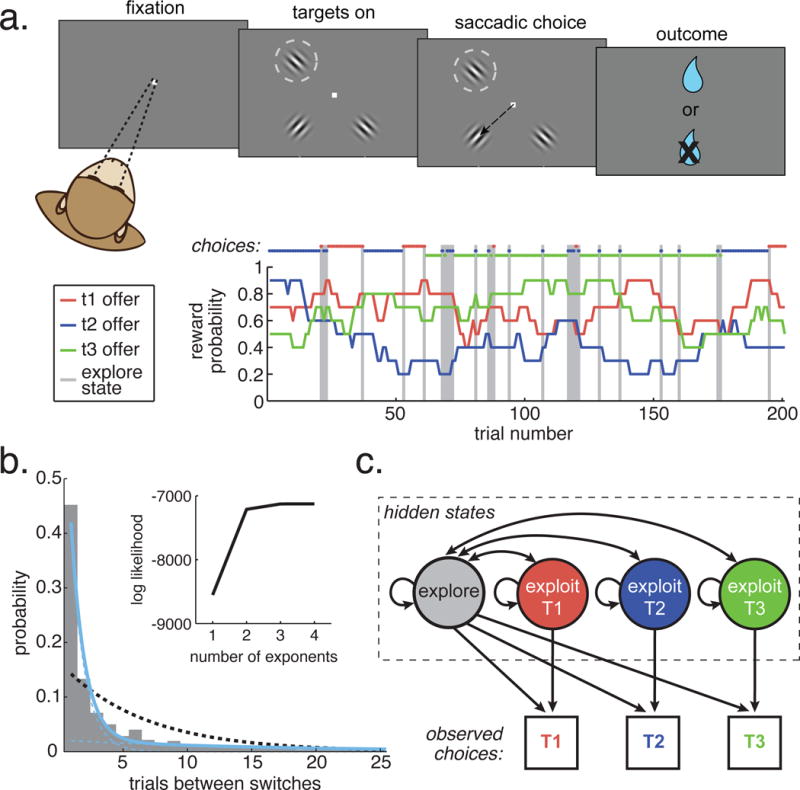
A) The task (top) was to choose between three probabilistically rewarded targets, one of which was placed in the receptive field of an FEF neuron (dotted circle). Bottom: Reward probabilities (lines) and choices (dots) for 200 example trials. Gray bars highlight explore-labeled choices. B) The distribution of times between switch decisions (inter-switch-intervals). A single probability of switching or continuous range of switch probabilities would produce exponentially distributed inter-switch intervals. Dotted black line: the maximum likelihood fit for a single discrete exponential distribution. Solid blue line: a mixture of two exponential distributions, with each component distribution in dotted blue. The two components reflect one fast-switching time constant (average interval: 1.6 trials) and one persistent time constant (17.2 trials). Inset) The log likelihood of mixtures of 1 to 4 exponential distributions. See also figure S1. C) A hidden Markov model, based on the different time constants for switching, was used to infer the goal state on each trial from the sequence of choices. The model included one persistent state for each target (“exploit”) and one state where the subjects’ were equally likely to choose any of the three targets (“explore”).

Monkeys learned about the rewards. They earned a higher rate of reward (83.1% of trials ± 5.7% STD) than would be expected by random choice (70.6%; 10 sessions in monkey B: p < 0.0002, t(9) = 8.5; 17 sessions in monkey O: < 0.0001, t(17) = 8.5) or trial-shuffled choices (72.6%, monkey B: p < 0.0002, t(9) = 6.2; monkey O: < 0.0001, t(17) = 10.0). To determine whether monkeys were tracking reward history, we used cross-validated, multinomial logistic regression to predict choice from past rewards, and estimate subjective value (STAR Methods). The average half-life of a reward outcome was 2.36 trials (figure S2; median = 2, range = 1.5 to 4), and accounting for multiple previous outcomes improved predictions of choice behavior in every session, compared to a 1-trial-back model (a win-stay, lose-shift strategy) or the best-τ model with outcomes shuffled within choices (all AIC and BIC values smaller for the non-shuffled reward-history model; all AIC and BIC weights for the shuffled and one-trial-back models < 0.0001). Thus, monkeys picked the best option more often than chance by integrating reward information over multiple trials.

We developed a novel method to determine whether each choice was exploratory or exploitative. Previous studies (Daw et al., 2006; Pearson et al., 2009; Jepma and Nieuwenhuis, 2011) have fit a delta-rule reinforcement learning (RL) model to behavior, then labeled choices that are inconsistent with the model’s values as “exploratory,” under the rationale that exploration is a non-reward-maximizing goal. This approach produced similar, albeit weaker results to those reported here (delta-rule learning models fit to each monkey with a softmax learning rule, mean target selectivity index during “explore” choices = 0.065, mean during “exploit” choices = 0.077, mean difference within neurons = −0.01, 95% CI = −0.002 to −0.022, paired t-test within neurons, p < 0.02, t(552) = −1.91). However, a non-reward-maximizing goal would produce choices that are orthogonal to value, not the errors of reward-maximization that are identified as exploration in this approach. For this and other reasons (STAR Methods), we looked for other patterns in the choice that could be used to infer latent explore and exploit goals.

Although there are many different algorithms for exploration in artificial agents, one frequent feature is that exploration is implemented via adding some variability to a value-based decision rule (Kaelbling et al., 1996; Sutton and Barto, 1998). That is, exploration occurs when decision noise or additional information causes some choices to deviate from the currently preferred option and towards an alternative. Practically, this means that explore choices are disconnected from their neighboring choices, whose targets otherwise change slowly according to long time scale fluctuations in the value of the options. Indeed, artificial agents, exploring via noisy decision rules, produce sequences of choices in which two distinct time constants are apparent: one short time constant due to fast switching for exploration and one long time constant due to slow switching for reward-maximizing (e.g. figure S1). We found that same structure in the monkeys’ choices (figure 1B). Fitting mixtures of 1-4 components, we found that inter-switch intervals were parsimoniously described as a mixture of two discrete exponential distributions, one slow component with an expected run length of 17.24 trials and one fast component with an expected run length of 1.64 trials (figure 1B). The two-exponential distribution (log likelihood = −5603) was a substantially better fit than a single-exponential distribution (log likelihood = −5963; likelihood ratio test, df = 2, p < 10⁻³²), adding additional distributions to the mixture produced a minimal improvement in model fit (figure S1D and E), and an identical pattern was observed in both monkeys individually. In the monkeys, the fast time constant was close to 1.5 trials: the value we would expect from independent random choices between three options. Although the monkeys’ time constants did not match those from the RL models (monkeys were more persistent and exploitative, figure S1), we could still exploit this shared temporal structure to identify exploratory choices.

Because the order of inter-switch intervals was non-random (STAR Methods, p(short_t | long_t−1) = 77%, greater than all of 1000 permutations, p(short_t | short_t−1) = 68%, less than all of 1000 permutations), we used a hidden Markov model (HMM) to label choices as coming from fast-switching or slow-switching regimes. HMMs allow inference about latent, generative states from temporal structure in observed behavior (Murphy, 2012). This HMM (figure 1C, STAR Methods) had two classes of latent states: an “exploitation” state that produced repeated choices to the same option (slow switching), and an “exploration” state which produced shorter samples of different options (fast switching) (Quilodran et al., 2008). This model was a better fit to the behavior than models containing either more or fewer states (STAR Methods). The emissions structure of the explore state implied random selection between the three options during exploration, an assumption based on the short switching time constant (near 1.5; figure 1A). However, this model also outperformed a model that assumed selection was biased away from previously exploited options during exploration (STAR Methods; lower AIC value 20/28 sessions; lower BIC in 26/28 sessions) and the mutual information (MI) between the previously exploited option and choices made during exploration was quite low (0.04 ± 0.04 STD), significantly lower than we would expect from biased selection (p < 10⁻²², paired t-test, t(27) = −36.11; STAR Methods). Ultimately, the most probable generative state was calculated from this model for each choice and used to label each choice as an “explore” or “exploit” choice (STAR Methods).

Explore choice labels were correlated with whether a decision was a switch decision, but explore choices were not synonymous with switch decisions (mean Spearman’s rho = 0.6, range = 0.43 to 0.7 across 28 sessions). Latent explore and exploit states differed in terms of their rate of switching, but individual explore choices could be either switch or stay choices and the same was true for exploit choices. In all, 32% of switch decisions were also exploit decisions. For example, a switch to a previously exploited option was often an exploit choice (a switch-to-exploit). Additionally, 35% of explore-state decisions were stay decisions. For example, the monkeys could choose the same target twice while in an explore state (a stay-to-explore). Explore/exploit state labels better explained neural activity than did switch/stay decisions (figure S5).

To evaluate the validity of the HMM approach, we asked whether the latent states inferred by the HMM matched the normative definition of exploitation and exploration in other ways. By definition, explore choices are non-reward maximizing decisions (Daw et al., 2006; Wilson et al., 2014) that reduce uncertainty about which option is the best (Daw et al., 2006; Cohen et al., 2007). HMM-labeled explore choices were consistent with this definition, despite the fact that no reward information was used to infer the states. First, in contrast to exploit-labeled choices, explore-labeled choices were nearly orthogonal to option value. Decision-states that are orthogonal to reward maximization should produce equal numbers of choices to high and low value targets: the distribution of choices should match the distribution of rewards in the environment. Indeed, the average subjective value of target chosen during exploration was not different from chance (p = 0.58, t(1,27) = 0.58). The objective values of chosen targets during exploration were also very close to, if slightly below chance (figure 2B). This suggests that explore choices were driven by a goal other than reward-maximization.

Figure 2. Features of explore and exploit-labeled choices.

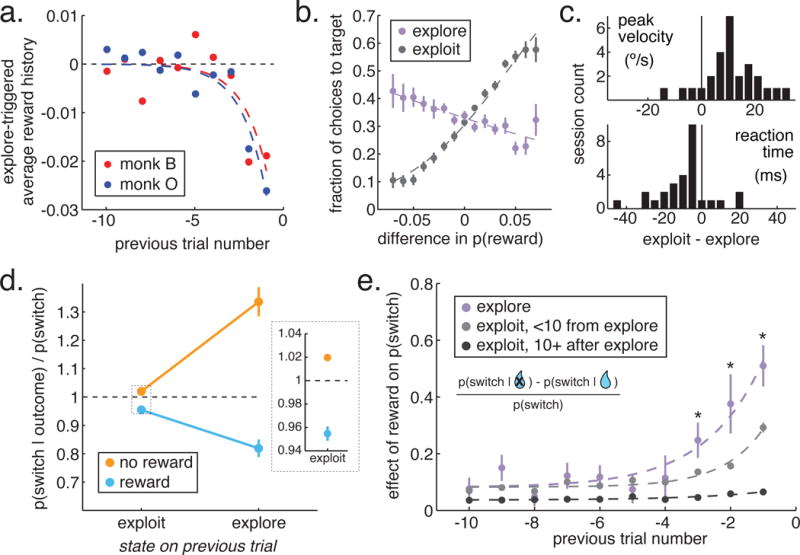
A) The reward history filter preceding transitions into explore states (Wiener kernel analysis). B) Choice as a function of true reward probability for explore and exploit choices. X axis: Difference between each target and the mean of the alternatives. C) Difference in reaction time and peak velocity between explore and exploit choices. D) The probability that the monkeys would switch targets on the next trial, given this trials’ outcome and goal state. Inset: Exploit choices enlarged to show error bars. E) The effect of past reward outcomes on switch decisions as a function of time since the outcome (x-axis) and state at the time of the outcome (colors). * p < 0.05, paired t-test, n = 28 sessions. Data is normalized for illustration only, statistics were run on non-normalized data.

Second, typical markers of reward-seeking, exploitative behavior (e.g. high velocity movements and short reaction times (Takikawa et al., 2002; Kawagoe et al., 2004; Reppert et al., 2015)) were reduced during exploration, compared to exploitation (figure 2C; peak velocity: mean decrease = 9.2°/s ± 11.2°/s STD, p < 0.001, paired-t-test, t(1,27) = 4.77; reaction time: mean increase = 11.9 ms ± 13.5 ms STD, p < 0.0002, t(27) = −4.37; n = 28 sessions). Third, explore choices occurred more often when the rate of reward of the preferred option decreased, reducing certainty about which option was best (figure 2A; significant decrease in Wiener kernel weight for reward outcomes on trials preceding exploration, kernels fit to each of 28 of sessions, 1 trial before exploration: −0.024 ± 0.016 STD, p < 0.0001, t(27) = −7.86, 2 trials: −0.018 ± 0.011 STD, p < 0.0001, t(27) = −8.91; STAR Methods).

Finally, reward learning was increased during explore choices. The outcomes of explore choices influenced subsequent decisions more, both on the next trial (figure 2D; two-way ANOVA, sig. interaction between state and outcome: F(1,111) = 59.02, p < 0.0001; also sig main effects of last reward F(1,111) = 98.55, df = 1, p < 0.0001 and state F(1,111) = 9.38, df = 1, p < 0.003) and several trials into the future (figure 2E; 1 trial back, reward effect = 0.11 ± 0.12 STD, paired t-test, 28 sessions, p < 0.0002, t(27) = 4.61; 2 trials, 0.12 ± 0.24 STD, p < 0.03, t(27) = 2.41; 3 trials, 0.11 ± 0.18 STD, p < 0.02, t(27) = 2.56). Learning rates remained increased for several trials (< 10) after exploration (figure 2E; significant interaction between state and outcomes up to 10 trials in the past, p < 0.004, F(18, 839) = 2.16; also sig. main effect of past trial number: p < 0.0001, F(9,839) = 9.75, and state: p < 0.0001, F(2, 839) = 27.52). Moreover, conditioning learning rates on exploratory states in several delta-rule RL models substantially improved the model fit to behavior, and confirmed that learning rates are increased during and shortly after exploration in both monkeys (Tables S1–2, STAR Methods). Thus, the HMM labeled as “exploratory” choices that were non-reward-maximizing and occurring during periods of uncertainty and enhanced learning, matching the normative definition of exploration.

FEF neuronal activity differed across explore and exploit-labeled choices. During exploit choices, single-neuron activity (figure 3A,D, n = 131), multi-unit activity (figure 3B, n = 443) and the pooled population activity (figure 3C, n = 574) each exhibited strong selectivity for target choices in the neuronal RF, as expected from many previous studies (Bizzi, 1968; Bruce and Goldberg, 1985; Schall and Hanes, 1993; Umeno and Goldberg, 1997; Schall and Thompson, 1999; Coe et al., 2002). During exploit choices, spatially selective, choice-predictive activity was present well before (>200 ms) target onset, and it lasted throughout the choice epoch. In contrast, selectivity was absent until just before (~70 ms) explore choices (figure 3D). This was not due to a change in neuronal tuning or the neural code. Comparing the accuracy of classifiers trained and cross-tested on held out subsets of explore and exploit trials revealed that there was less information about choice in neurons during explore choices (trained on exploit, tested on exploit: 66.6%, +/− 13.0% STD; trained on explore, tested on explore: 56.4% accuracy, +/− 10.4% STD; average of decrease in accuracy of 10% within-session, p < 0.003, signtest sign = 19), even considering a whole-trial epoch that included motor activity. The reduced selectivity during explore choices was due both to a decrease in single-and multi-unit activity for RF choices (figure 3D inset; mean decrease = −0.015 units of normalized firing rate ± 0.083 STD, paired t-test, p < 0.0001, t(496) = −5.48) and to an increase in activity for non-RF choices (mean increase = 0.028, ± 0.054 STD, p < 0.0001, t(542) = 10.26) in both monkeys (monkey B: in RF, p < 0.0001, t(178) = −4.70, out of RF, p < 0.003, t(182) = 3.01; monkey O: in RF, p < 0.002, t(317) = −3.19, out of RF, p < 0.0001, t(354) = 11.16).

Figure 3. Target selectivity during exploration in single units.

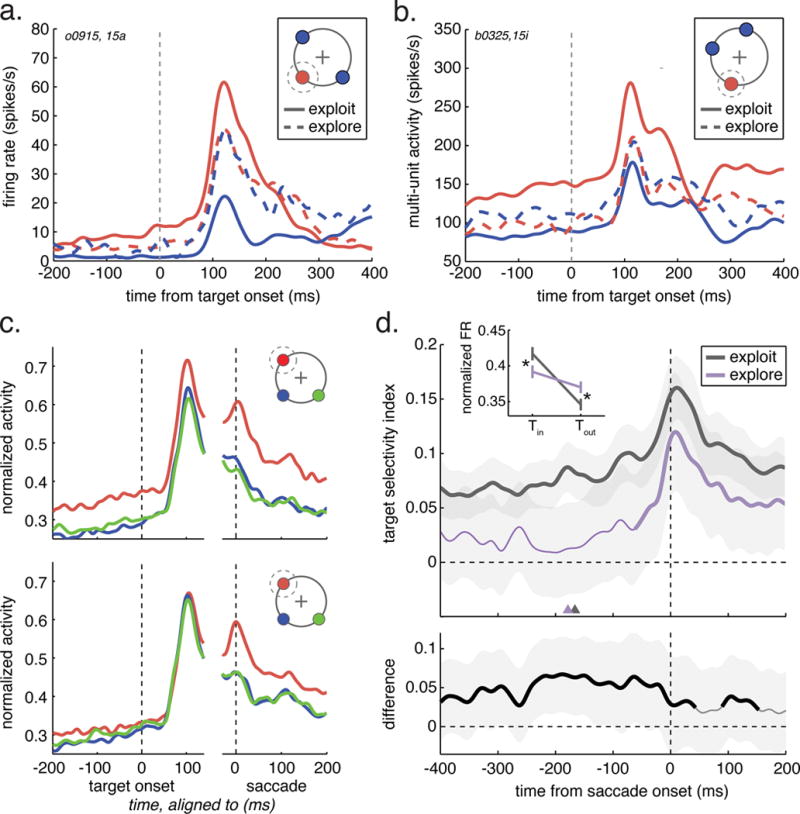
A) A single neuron from monkey O. The cartoon illustrates the relative positions of the RF target (Tin, red) and the two non-RF targets (Tout, blue). Target selective firing rate measured during exploit choices (solid lines) and explore choices (dotted lines). B) Same as A, but for a multi-unit recorded in monkey B. C) Target selectivity across the population of recorded units (n = 574) during exploit choices (top), and explore choices (bottom). Red = Tin, blue = ipsilateral Tout, green = contralateral Tout. D) The target selectivity index averaged over all single neurons (monkey O, n = 83; monkey B, n = 48), plotted across time. Inset: Firing rate was suppressed for Tin choice and increased for Tout choice. Bottom: Difference in the target selectivity index between explore and exploit, averaged over single neurons. Thick lines in both top and bottom: significant difference from 0 in that epoch, p < 0.05, n = 131, shading: ± S.E.M. See also table S3, figure S5.

The difference in target selectivity between explore and exploit choices was not better explained by a range of alternative hypotheses (figure S5, table S3). For example, consistent with previous studies (e.g. (Coe et al., 2002)), we observed greater target selectivity when monkeys repeated the same choice (stay) compared to when they switched (paired, within-unit, t-test: p < 0.0001, t(1,538) = 12.6). However, target selectivity was lower during exploration, controlling for whether any individual choice was switch or stay. Target selectivity was reduced during explore-labeled switch trials, compared to exploit-labeled switches (p < 0.0001, t(1,518) = −5.1) and target selectivity was reduced during explore-labeled stay trials, compared to exploit (p < 0.0001, t(1, 359) = −6.0). As another example, consider the outcome of the last trial (figure S5). There was a small, but significant decrease target selectivity after non-rewarded trials (p < 0.0001, t(1,560) = 5.6) and exploration was more common after omitted rewards (figure 2A). However, significant state differences were observed regardless of whether the monkey was rewarded on the last trial (p < 0.0001, t(1,518) = −5.1, paired within-unit t-test) or not rewarded (p < 0.0001, t(1, 359) = −6.0). Similar observations were made for differences in reward history, the subjective value of the chosen option, the relative value of the chosen option, response time, and saccadic peak velocity (figure S5, table S3): explore state choices had lower target selectivity, even compared to exploit state choices matched for these confounding variables.

Although selective, choice-predictive activity was substantially reduced in single neurons, it remained possible that the population of FEF neurons maintained choice-predictive information, perhaps via small differences in firing rate distributed across neurons. However, we also observed a substantial reduction in choice decoding accuracy from populations of simultaneously recorded neurons (figure S4A and B, STAR Methods; logistic classifier, mean accuracy during the 400 ms epoch before the saccade: exploit choices = 73.5%, explore choices = 48.9%, chance (accuracy with shuffled labels) = 44.0%, mean reduction in accuracy within session = 24.5%, 95% CI = 17.8% to 31.3%, p < 0.0001, t(27) = 7.43, 28 sessions with populations of 14-22 neurons; mean reduction in the probability of the chosen option: 0.18 lower for explore choices, 95% CI = 0.14 to 0.23, p < 0.0001, t(27) = 7.95). To understand how population choice representations changed across states, we used targeted dimensionality reduction (Cohen and Maunsell, 2010; Mante et al., 2013; Cunningham and Yu, 2014). Dimensionality reduction re-represents, in a small number of dimensions, important features of the high-dimensional activity of populations of simultaneously recorded neurons. Unlike principle component analysis, targeted dimensionality reduction selects a low dimensional representation wherein the axes have specific interpretations in terms of the information that is encoded in the population activity. We used multinomial logistic regression to identify a projection where population activity predicted the log odds of choice (figure 4A, S5C and D, STAR Methods). During exploitation, we found that population trajectories fanned out quickly along choice-predictive vectors, becoming increasingly predictive of choice over time (figure 4B, S5C and D). In contrast, trajectories were disorganized during exploration and separated more slowly.

Figure 4. Dynamics of population target selectivity.

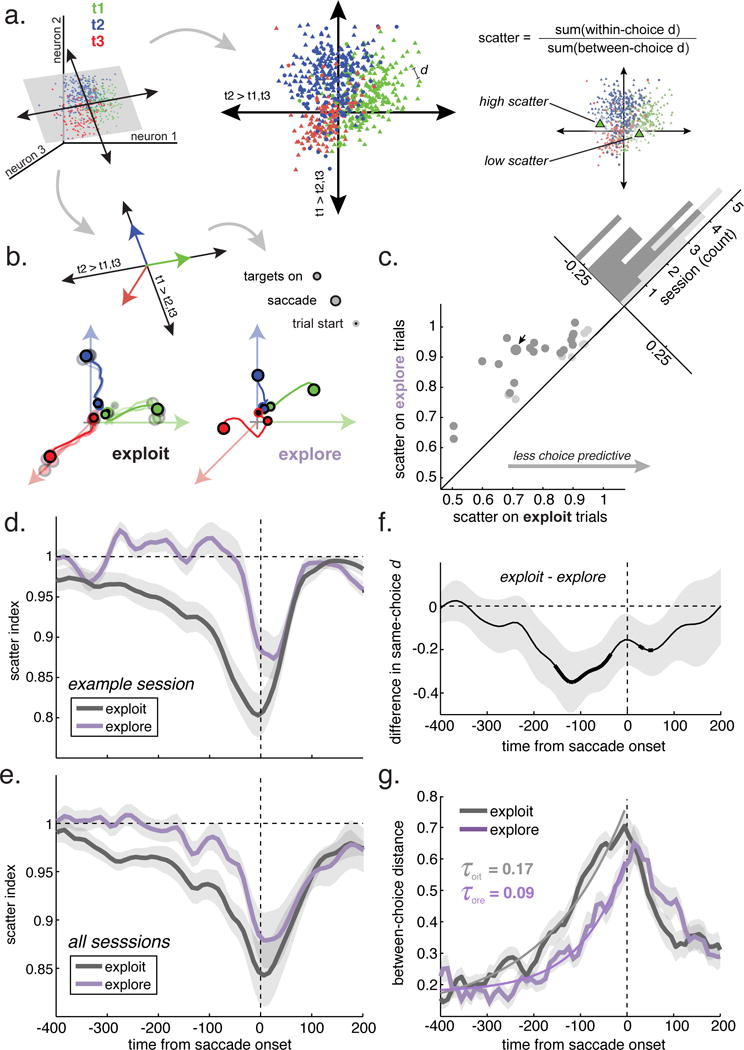
A) Targeted dimensionality reduction. Choice-separating hyperplanes (black arrows: linear combinations of neuronal firing rates) were identified with multinomial logistic regression. Single trial neural activity was projected into the subspace defined by these hyperplanes (gray plane). Middle panel: The distribution of whole-trial positions in the subspace from one example session. Each marker indicates the position of one trial, colored according to whether target 1 (green), 2 (blue), or 3 (red) was chosen. d is the Euclidean distance between two trials in this subspace. Left: The scatter index (top) is a measure of clustering in the choice-predictive subspace. The two highlighted trials are example trials in which target 1 was chosen that have high scatter index (left) and low scatter index (right), respectively. B) Example neural trajectories in the choice-predictive subspace. Top: Because logistic regression was used to calculate the separating hyperplanes, the vectors perpendicular to the axes (colored arrows) reflect increasing confidence that the monkey will make that decision. Bottom left: Average neural trajectories during exploit trials from the example session. Saturated colors = average across all exploit choices. Desaturated = 4 random samples matched to number of explore choices. Bottom right: Trajectories during explore choices. C) Average scatter index for explore and exploit choices in each session. All sessions are above the unity line. Dark gray = individually significant sessions. D) Evolution of the scatter index during the example session, during explore (purple) and exploit (black) choices. E) Same as D, averaged across sessions. F) The difference in within-choice trajectory distance between explore choices and exploit choices, averaged across sessions. Thick lines indicate significant difference from 0 (corrected p < 0.05, rank sum). G) Between-choice divergence in neural trajectories. Exponential model fits overlaid. Shading: ± S.E.M., n = 28 sessions throughout. See also table S3, figures S4–5.

We reasoned that changes in decoding and choice-predictive dynamics could be due to changes in the distribution of selective, choice-predictive population activity across trials. There were clear clusters of same-choice trials in the choice-predictive subspace (figure 4A), so we next asked whether this clustering differed across exploration and exploitation. Clustering was quantified via a “scatter index”, which measured choice-predictive population activity on each trial deviated from other trials where the monkey made the same physical choice (STAR Methods). A scatter index of 1 indicates that neural activity was no more similar to same-choice trials as it was to different choices trials. Conversely, a scatter index less than 1 indicates that the pattern of activity was more similar in same-choice trials. In every single session, we observed greater scatter during exploration (figure 4C). Thus, choice-predictive population activity was substantially more disorganized and variable during exploration.

This did not appear to be due to the influence of previous choices on current-trial choice representations for two reasons. First, as already noted (figure 4), choice-predictive activity on explore trials was further away from other trials where the monkey made the same physical choice (average distance to other same-choice trials; paired t-test, exploit-explore, p < 0.0001, t(1,27) = −6.05). But it was also further away from trials that matched the last choice the monkey made (p < 0.0001, t(1,27) = −7.61) and—critically—closer to trials where the monkey chose an option that was neither the same as the present choice nor the same as the last choice (the “third option”, p < 0.0001, t(1,27) = 5.15). Second, we explicitly tested the hypothesis scatter during explore-choices was comparable to a mixture of previous-choice and last-choice information via creating mixing pseudo-trials (STAR methods). Scatter was substantially higher during explore choices than it would be for mixtures of previous-choice and current-choice information (explore: mean = 0.82 ± 0.05 STE; exploit pseudo-trials: mean = 0.50 ± 0.02 STE; paired t-test, p < 0.0001, t(1,27) = 6.42). Thus, the disorganization of choice-predictive activity during exploration was unlikely to be due to some conflict from previous-choice information held over during exploration.

Moreover, like target selectivity, the difference in population scatter across states was not better explained by a range of alternative explanations. For example, although scatter was lower during stay decisions compared to switches (paired, within-session, t-test: p < 0.0001, t(1,27) = −10.4), there was additional modulation by explore/exploit states. Scatter was increased during explore-labeled switch choices, compared to exploit-labeled switches (p < 0.001, t(1,27) = 3.9) and during explore-labeled stay choices, compared to exploit-labeled stays (p < 0.0001, t(1,27) = 5.4). Significant state differences in scatter were also observed regardless of whether the monkey was rewarded on the last trial (p < 0.0001, t(1,27) = 5.2, paired within-session t-test) or not rewarded (p < 0.0001, t(1,27) = 8.3). Finally, changes in network scatter across decision states were again not better explained by reward history, the subjective value of the chosen option, the relative value of the chosen option, response time, and saccadic peak velocity (figure S5, table S3).

The scatter index decreased leading up to the saccadic choice during both exploration and exploitation, indicating that same-choice patterns of population activity became increasingly clustered before the saccade (example session, figure 4C; all sessions, figure 4D; each monkey separately, figure S4E and F). The scatter index deviated significantly from 1 approximately 225 ms earlier during exploit trials than during explore trials (time difference between the first bin in each condition with p < 0.05, t-test, Holm-Bonferroni corrected). However, choice-predictive activity remained more scattered during exploration throughout the trial, compared to exploitation. This was due to two differences in choice-predictive trajectories: during exploitation, within-choice variability in trajectories was reduced (figure 4F), and between-choice distance was increased (figure 4G; STAR Methods). The divergence of trajectories leading to different choices was best by models in which separation accelerated over time (exponential fits in figure 4G; model comparison in Tables S4 and S5; STAR Methods). Collapsing variability and accelerating divergence are consistent with models describing decisional activity as an attractor dynamic (Wong and Wang, 2006; Mante et al., 2013; Kopec et al., 2015), though it suggests that dynamical attractor regimes may differ across exploration and exploitation.

In order to determine how transitions between these regimes might occur, we examined network scatter evolved across transitions between exploration and exploitation (example session: figure 5A; all sessions: figure 5B). First, scatter was higher during explore choices than the exploit choices both immediately before exploration (p < 0.002, signtest, sign = 24; paired t-test: p < 0.0001, t(27) = 6.1) and immediately after (p < 0.004, signtest, sign = 22; paired t-test: p < 0.0002, t(27) = 4.5), consistent with a good alignment of HMM labels and endogenous states. Over the 10 trials preceding transitions into exploration, scatter was stable (slope = 0.005, p = 0.3, GLM, 10 trial lags across 28 sessions) and transitions into exploration were abrupt. However, following exploration, scatter decreased gradually over the next 10 trials (slope = −0.022, p < 0.0001). There was no trend in the scatter index within bouts of exploration (slope = −0.01, p = 0.16). It was possible that the apparently gradual recovery of scatter after exploration was just due to misalignment of the kind of abrupt transitions that have been reported previously (Durstewitz et al., 2010; Karlsson et al., 2012) and which were observed at the start of exploration (figure 5A,B). However, a comparison of changes in the scatter index across trials (scatter “step sizes,” STAR Methods) revealed that the variance in step sizes during recovery from exploration was lower than would be expected from misalignment of abrupt transitions (paired t-test, observed variance - mean of bootstrapped variance, p < 0.0005, t(27) = 4.24, mean effect size = 0.047, 17 95% CI = 0.024 to 0.069; individually significant decrease in variance in 16/28 sessions, > 57%, one-sided bootstrap test). Furthermore, there was no significant increase in the variance in step sizes post-exploration compared to a period in which the scatter index was largely stationary (during the the 10 trials before exploration; paired t-test, p > 0.5, t(27) = 0.68, mean effect size = 0.005), despite the fact that scatter step sizes were significantly larger and more negative after exploration (mean pre-explore step size = 0.007, mean post-explore step size = −0.015, paired t-test, p < 0.0001, t(27) = 5.98, mean pre - post difference = −0.022, 95% CI = −0.015 to −0.030). Thus, transitions into exploration were abrupt, but recovery from exploration was a more continuous and gradual process.

Figure 5. Target selectivity across trials relative to explore transitions.

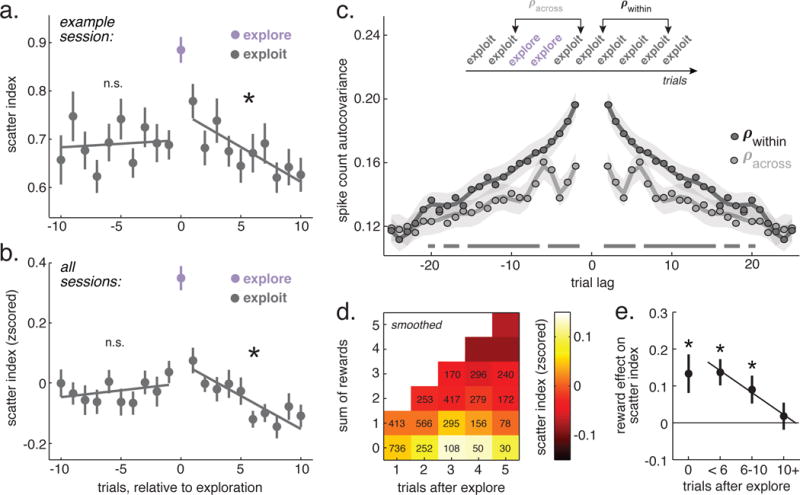
A) Average scatter index on trials before, during, and after exploration from an example session. Lines = GLM fits to the scatter index before and after exploration. Bars ± SEM throughout, * p < 0.05, n = 28 sessions. B) Same as A, across sessions. C) Residual spike count autocorrelation for exploit trials that were (light gray) or were not (dark gray) separated by exploration. Lags at < 2 were not possible for explore-separated trials. Lines represent polynomial fit (order = number of lags ÷ 2), shading ± SEM of the fit. Solid lines along the bottom are significant bins, bootstrapped, p < 0.05, corrected, n = 514 units. D) Scatter index during the first 5 exploit trials following an explore, combined across sessions as a function of both trials since exploration and the rewards accumulated since exploration. Trial counts in each bin are overlaid. E) The difference in the scatter index between trials where reward was received on the last trial and when it was not, separated according to time since exploration, n = 28 sessions.

These complex dynamics could suggest a transient increase in the rate of change or reorganization in FEF activity near exploration. If this were the case, transitions into exploration should disrupt slow, persistent fluctuations in activity across trials. We tested this hypothesis via examining residual spike-count autocorrelation functions ((Bair et al., 2001), STAR Methods). Neuronal spike counts were correlated with themselves on nearby trials (figure 5E). However, when nearby trials were separated by exploration, spike count autocorrelations were reduced. This was true even for within same-choice trials separated by exploration and was not due to differences in sample size (STAR Methods). Instead exploration disrupted slow fluctuations in spike counts that were otherwise observed on the order of 1-10 trials. There were pronounced peaks in the autocorrelation function for explore-separated trials that were not apparent for non-separated trials, suggesting an oscillation (0.05-0.07 Hz) that may be more pronounced near exploration or which may be revealed by the disruption in slow fluctuations associated with exploration. Thus, exploration disrupted slow, persistent fluctuations in network activity, consistent with a rapid reorganization of network dynamics in the vicinity of exploration.

To determine what forces might shape this reorganization, we asked what drove the gradual recovery of choice-predictive organization after exploration. The gradual recovery of the scatter index was not autonomous, occurring inevitably due to the passage of time since exploration (figure 5D). Instead, it was driven by rewards. The number of rewards accumulated since the end of exploration was a better predictor of the decrease in the scatter index (accumulated reward model: AIC = 22538, BIC = 22734; trials since model: relative AIC weight = 0.002, AIC = 22550, relative BIC weight = 0.002, BIC = 22746). Moreover, rewards had more influence on the scatter index during these periods (figure 5E). In general, rewards decreased the scatter index on the next trial (explore trials: mean decrease = −0.04 ± 0.08 STD, p < 0.02, t(27) = 2.6; exploit trials: −0.02 ± 0.03 STD, p < 0.006, t(27) = 3.0, n = 28 sessions). However, reward only affected scatter within the first 10 exploit choices following exploration (figure 5D; 5 or fewer trials: p < 0.0005, t(27) = 3.9; between 5 and 10 trials: p < 0.02, t(27) = 2.42; 10+ trials: p = 0.6, t(27) = 0.5). Thus, rewards had a greater impact both on behavior (figure 2E) and on choice-predictive population dynamics (figure 5E) during and shortly after exploration.

Discussion

The results show that exploration substantially reduces classic patterns of spatially selective, choice-predictive activity in FEF neurons. Despite identical task demands, visual stimuli, and eye movements, there was less information about oculomotor choice in the FEF during exploration, at both the single-neuron and the population level. Exploration also disrupted choice-predictive population dynamics occurring on multiple time scales. During explore periods, FEF neurons conveyed little information about the location of future choices; choice-predictive neural trajectories were delayed and disorganized, and autocorrelations between trials were disrupted. Future work is necessary to determine how population dynamics evolve on single trials, but together, these results suggest that exploration is associated with a sudden disruption of persistent, spatially selective dynamics in prefrontal cortex that would otherwise be maintained over multiple trials. Indeterminate, random selection rules are efficient and sufficient strategies for exploration (Sutton and Barto, 1998; Wilson et al., 2014) and these results suggest that the primate prefrontal cortex implements exploration via a similar strategy.

The present study developed a novel method for identifying individual choices as explore or exploit choices. This method is based on the fact that explore and exploit choices occur on different temporal scales by definition: exploitation is the repeated sampling of a known-good option, while exploration samples briefly from a range of alternative options. Here, we observed that there were also two distinct time constants in the monkeys’ decisions in a classic explore/exploit task, mirroring the pattern of time constants observed in exploratory RL agents. Furthermore, in monkeys, choices labeled according to these time constants were consistent with normative definition of exploration and exploitation: explore choices were non-reward-maximizing choices that reduced uncertainty. By design, this approach made few assumptions about the computations that produce exploration, which makes the approach robust to the field’s current uncertainty about these underlying computations. However future work is necessary to elucidate these computations and develop truly mechanistic models of exploration.

Our observation that explore-exploit state transitions coincide with changes in the fidelity of spatial representations within the FEF raises the important question of their underlying mechanism. A number of studies have surveyed the presence and magnitude of value-based decision signals within primate prefrontal cortex, including both medial and lateral prefrontal areas. Overall, these studies have shown that although value signals are clearly present within the FEF (Leon and Shadlen, 1999; Roesch and Olson, 2003; Ding and Hikosaka, 2006; Roesch and Olson, 2007; Glaser et al., 2016), they are less prevalent than in other prefrontal regions (Leon and Shadlen, 1999; Roesch and Olson, 2003; 2007) and choice signals emerge later in the FEF compared to the supplementary eye field (SEF) (Coe et al., 2002). Perhaps, like value signals, the decision of when and what to explore is also propagated to the FEF from higher-order prefrontal regions. There is compelling evidence that the SEF signals transitions into exploration (Kawaguchi et al., 2015) and tracks decision confidence (Middlebrooks and Sommer, 2012), previous outcomes (Donahue et al., 2013), and reward prediction errors (So and Stuphorn, 2012): it contains the appropriate signals to mediate transitions into exploration. Another candidate region is the anterior cingulate cortex (ACC), which projects directly to the FEF (Barbas and Mesulam, 1981) and is implicated in regulating the stability of reward-maximizing goals (Kennerley et al., 2006; Ebitz and Platt, 2015; Ebitz and Hayden, 2016). Future work will be necessary to establish a clear causal role for such prefrontal areas in explore-exploit state transitions.

What is the significance of these effects on spatial representations within the FEF for attention? Attention, be it overt or covert, is a fundamental competency for decision-making, that shapes reward learning (Pearce and Hall, 1980; Swan and Pearce, 1988; Pearce and Bouton, 2001; Niv et al., 2015) and choice (Krajbich et al., 2010). The FEF is a critical source of selective modulations of peripheral sensorimotor circuitry (Ebitz and Moore, 2017). It plays a direct role both in saccadic target selection (Bizzi, 1968; Bruce and Goldberg, 1985; Schall and Hanes, 1993; Umeno and Goldberg, 1997; Schall and Thompson, 1999; Coe et al., 2002) and in the deployment of visual spatial attention (Kastner et al., 1998; Moore and Fallah, 2001; Moore and Armstrong, 2003; Moore and Fallah, 2004; Thompson et al., 2005; Armstrong et al., 2009). Both functions appear enabled by the precise spatial tuning of FEF neurons (Bruce and Goldberg, 1985; Armstrong et al., 2009), which exceeds that of the SEF (Purcell et al., 2012; Chen and Stuphorn, 2015), dlPFC (Funahashi et al., 1990), or ACC (Hayden and Platt, 2010). In addition, the FEF has direct projections to both dorsal and ventral stream areas of extrastriate visual cortex (Stanton et al., 1995) and to downstream oculomotor structures (Stanton et al., 1988), projections that appear uniquely potent in regulating these circuits (Schlag-Rey et al., 1992; Ekstrom et al., 2008). These facts suggest that the FEF may serve as an interface between the prefrontal regions where decision-related signals might originate, and downstream visual and oculomotor structures, where they shape spatial attention and visually guided saccades. FEF’s unique role in these circuits suggest that the profound changes in FEF selectivity we report here may have consequences for sensorimotor control: altering attentional priorities and the perceptual correlates of attention, though future studies will be needed to test this hypothesis empirically.

During exploration, reward-dependent learning was increased in the behavior and rewards had a larger impact on trial-to-trial reconfiguration of spatially selective, choice-predictive neural activity patterns. This provides empirical support for normative predictions that learning should be enhanced during exploration (Kaelbling et al., 1996; Sutton and Barto, 1998; Yu and Dayan, 2005; Daw et al., 2006; Cohen et al., 2007; O’Reilly, 2013) and are consistent with previous reports of variable learning rates in volatile environments (Behrens et al., 2007; Quilodran et al., 2008; Rushworth and Behrens, 2008; Nassar et al., 2012; O’Reilly, 2013; McGuire et al., 2014). Critically, increased learning rates during exploration also suggest that the monkeys were not simply disengaged from the task during explore choices: despite the profound disruption in prefrontal choice-predictive signals, they learned more about the outcomes of their choices. However, this juxtaposition of results raises the critical question of what cognitive and neural mechanisms might support changes in learning rates. Enhanced selective attention seemed an attractive mechanism—it predicts increased learning via enhancing stimulus associability (Pearce and Hall, 1980; Swan and Pearce, 1988; Pearce and Bouton, 2001; Niv et al., 2015)—but here, learning was paradoxically associated with disorganized activity in a structure implicated in the control of attention (Kastner et al., 1998; Moore and Fallah, 2001; Moore and Armstrong, 2003; Moore and Fallah, 2004; Thompson et al., 2005; Armstrong et al., 2009). Perhaps changes in learning rate are simply another facet of the same indeterminate brain state that permits exploratory choice: a state in which the network is rapidly reconfiguring and more susceptible to the influence of rewards. Future work is necessary to determine how frequently indeterminate brain states co-occur with increases in reward-dependent plasticity, but if these are indeed different features a single, unified, exploratory brain state, it is a state that could both allow the brain to discover unknown opportunities and to rapidly reconfigure to pursue the opportunities that result in reward.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Becket Ebitz (rebitz@gmail.com).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All animal care and experimental procedures were approved by the Stanford University Institutional Animal Care and Use Committee. Two male rhesus macaques (between 5 and 10 years, between 6 and 14 kg) participated in the experiment over the course of 2 years. Monkeys were singly housed in a small (8-10) colony room. In order to allow for neurophysiological recordings, monkeys were surgically prepared with head restraint prostheses, craniotomies, and recording chambers under isoflurane anesthesia. Analgesics were used to minimize discomfort. After recovery, monkeys were acclimated to the laboratory and head restraint, then placed on controlled access to fluids and trained to perform the task. One animal was naïve at the start of the experiment, the second had previously participated in oculomotor and visual attention studies.

METHOD DETAILS

Electrophysiological techniques

Recordings were largely, if not exclusively, made within the FEF. Within 5 days of each recording, we confirmed recording site locations via electrical microstimulation. We lowered low-impedance (< 50 kΩ) tungsten electrodes into the vicinity of the arcuate sulcus. Microstimulation trains were cathode-leading square wave trains, with pulses delivered at a rate of 333 Hz through a pulse stimulator and two stimulus isolators (Grass). Sites were identified as FEF if saccades were evoked in less than 50 ms with currents 50 µA or less (Bruce et al., 1985). The results of the microstimulation (saccadic thresholds, latencies) are described elsewhere (Ebitz and Moore, 2017). Recordings were conducted with 16-channel U-probes (Plexon) placed so that each contact was within the gray matter at a site with saccadic microstimulation thresholds consistent with the FEF. In one monkey, we histologically confirmed the placement of recording electrodes into the anterior bank of the arcuate sulcus (figure S3), both monkeys had similar current thresholds for evoking saccades (figure S3), and similar results were obtained in each (figure S4).

General behavioral techniques

MATLAB was used to display stimuli and collect eye data, which was sampled at 1000 Hz via an infrared eye tracking system (SR Research). Task stimuli were presented against a dark gray background on a 47.5 cm wide LCD monitor (Samsung; 120 Hz refresh rate, 1680 × 1050 resolution), located 34 cm in front of the monkey.

Three-armed bandit task

This was a sequential decision-making task in which the monkeys choose between 3 alternative targets whose values (probability of reward) walked over trials. The monkey first fixated a central fixation square (0.5° stimulus, +/− 1.5-2° of error) for a variable interval (450-750ms). At any point within 2 seconds after the onset of the targets, the monkey indicated his choice by making a saccade to one of the targets and fixating it (3° stimulus, +/− 3°) for a specified period (150 ms). Target eccentricity varied between sessions, between 8° and 12°. The probability of receiving a fluid reward following selection of either target was determined by the current reward probability of the chosen target and was fixed in magnitude within session (0.2-0.4 mL). Reward probabilities changed independently over trials for each of the three targets: on each correct trial, each target had a 10% chance of the reward parameter changing either up or down by a fixed step of 0.1, bounded at 0.1 and 0.9. Because rewards were variable, independent, and probabilistic, monkeys could only infer values through sampling the targets and integrating their experienced reward history over multiple trials.

QUANTIFICATION AND STATISTICAL ANALYSIS

General analysis techniques

Data was analyzed with custom MATLAB scripts. Paired, two-sided across-session t-test were used, unless otherwise specified. If multiple comparisons were made, p values were adjusted with a Holm-Bonferroni correction and compared against the standard α = 0.05 threshold. When an index was calculated (such as for within-cell target selectivity), a minimum of two observations were required for each term in the index or the cell was excluded. As a result, these index-based analyses have variable numbers of observations and degrees of freedom, as noted in the text. For targeted dimensionality analyses, < 8% of cells (n = 45 of 574) were omitted from the population for each session because their mean whole-trial firing rate across all trials was < 2 spikes/s, which lead to unstable beta weights inter-switch for these cells (after (Mante et al., 2013)). No data points were excluded for other reasons and observation counts are reported in figure legends and/or Results. Additional details of statistical analyses reported in following sections and effect sizes and statistical tests are in the Results or in Supplemental Tables.

Behavioral data analysis

Rationale for state labeling approach

In previous studies using restless multi-armed bandit tasks, explore and exploit choices have been labeled according to whether or not they are consistent with subjective values inferred from fitting a delta-rule reinforcement-learning (RL) model (Daw et al., 2006; Pearson et al., 2009; Jepma and Nieuwenhuis, 2011). This approach begins by defining “explore choices” as “non-reward-maximizing.” Then, choices that are consistent with inferred values are labeled as exploit, while choices inconsistent with values are labeled as explore. This approach formally equates exploration with errors of reward-maximization: these are explicitly the choices in which the most valuable option was not chosen. However, exploratory choices are choices in which a different goal—other than reward-maximization—is driving choice. In this view, explore choices should be orthogonal to reward value, not perfectly anti-correlated with it. The previous approach is also sensitive to misspecifications of the RL model: slight differences in the RL model used to generate values can have large consequences for what choices would be labeled exploratory. Yet the relationship between RL models and biological actors’ decision processes is an area of open and active inquiry. Subjective value calculations can differ between species and tasks and there are many schemes for adding exploration to an artificial agent, though it remains unclear which, if any, best match the computations performed by real agents. Therefore, here we develop a new method to identify choices as exploratory or exploitative that did not require we choose a specific model of value-based decision-making or make any assumptions about the computations used to determine when and what to explore.

This method is based on the observation that exploration and exploitation take place on different time scales. For example, in RL agents, exploration is typically implemented via adding noise or indeterminacy to a decision-rule. Thus, the choices that are caused by this noise—the exploratory choices—are shorter duration samples than the choices that depend on option value, which change more slowly over time. Similar observations about the temporal dynamics of exploration and exploitation have been made in biological agents (Pearson et al., 2009). To be concrete, in an RL agent with ε-greedy decision rule, exploratory choices would be very brief choice runs whose duration would be determined by both the (typically small) value of ε and the number of choice options. Conversely, when a good option is found, the agent will make long runs of choices to that particular option—exploiting it. For an ε-greedy agent, the duration of choice runs during exploration would depend on the volatility of target values and the compliment of ε, and the complete distribution of choice run lengths would have both a long and short component (figure S1A). Moreover, simulation shows a mixture of short duration choice runs and long duration choice runs with more complex exploratory schemes, such as softmax exploration (figure S1B) or upper confidence bound sampling. Thus, the distinct time constants of exploration and exploitation provide a starting point for labeling choices that is robust to the particular computations the agent uses to decide when and what to explore.

Exponential mixture model

In order to determine whether the monkeys also had two time scales of decision-making, we analyzed the temporal structure of the monkeys’ choice sequences. If a single time constant (probability of switching) governed the behavior, we would expect to see exponentially distributed inter-switch intervals. That is, the distribution of inter-switch intervals should be well described by the following model:

$$f(x)=\frac{1}{\beta }{e}^{-\frac{x}{\beta }}$$

Where β is the “survival parameter” of the model: the average inter-switch interval. However, although the time between switch decisions was largely monotonically decreasing and concave upwards, the distribution was not well described by a single exponential distribution (figure 1B, S1). The monkeys had more short-latency and more long latency choice runs, indicating that a single switching probability could not have generated the data. Therefore, we next fit mixtures of varying numbers of exponential distributions (1-4) to monkeys (figure 1C, S1) and RL agents (figure S1), in order to infer the number of switching regimes in these choice processes. For continuous-time processes, these mixture distributions would be of the form:

$$f(x)={\displaystyle \sum _{i=1}^n{\pi }_i}\frac{1}{{\beta }_i}{e}^{-\frac{x}{{\beta }_i}}$$

Where 1 ≥ π_i ≥ 0 for all π_i, and Σ_i π_I = 1. Here, each β_i reflects the survival parameter (average inter-switch interval) for each component distribution i and the π_i reflects the relative weight of each component. Because trials were discrete, we fit the discrete analog of this distribution: mixtures of 1-4 discrete exponential (geometric) distributions (Barger, 2006). Mixtures were fit via the expectation-maximization algorithm and we used standard model comparison techniques (Burnham and Anderson, 2002) to determine the most probable number of mixing components (figures 1C, S1, Results).

Randomness of mixing component sequences

To determine whether transitions between explore-like and exploit-like inter-switch intervals were random, we compared real choice sequences to a shuffled sequence of inter-switch intervals. We calculated the max probable generative mixing distribution (the “z label”) from the two-exponential mixture model for each inter-switch interval. This was equivalent to setting a model-based threshold on the inter-switch intervals and labeling all intervals less than this threshold as short runs and all intervals greater than this threshold as long runs. Then, we asked whether the length of the inter-switch interval at time t-1 was predictive of the length of the next interval at time t. Significance was assessed via comparing real conditional probabilities with those calculated via permutation (1000 repetitions of shuffled labels).

Hidden Markov model (HMM)

Because there were two switching regimes in the behavior and transitions between these regimes were structured, we next turned to an HMM to to determine the most probable decision-making regime for each observed choice. HMMs are used to model sequential processes in which observations (i.e. choices) are generated by unobserved latent states (i.e. goals). They are appropriate whenever the latent state dynamics are reasonably Markovian: determined by a fixed probability that does not change across time. Markovian processes produce exponentially-distributed state occupancies, consistent with the structure of the monkeys’ choice behavior here (figures 1C, S1). To produce long, exponentially-distributed runs of repeated choices to a single target, the HMM had one latent exploitative state for each target. To produce short, random run lengths, the HMM had one shared explore state from which decisions to any of the choices were equally likely. To move from exploiting one target to exploiting another, the model enforced a transition through an explore state. However, in an unconstrained model with the same number of latent states, direct transitions between two exploit states as well as other-choice emissions from an exploit state all had paths of < 2%, indicating that an unconstrained model will effectively reduce to the final model here. Thus, HMM-labeled exploit choices occurred during periods in which a single target was repeatedly sampled and explore choices occurred during periods in which any target was likely to be sampled. Moreover, the HMM produced state labels that were consistent with normative definitions of exploration in other ways (figure 2). To account for session-by-session variability in choice biases, the HMM was fit to each session via the Baum-Welch algorithm (Matlab: hmmfit). Then, the Viterbi algorithm (Matlab: hmmviterbi) was used to find maximum a posteriori sequence of states, the most probable of which was taken as the state-label for each trial (examples illustrated in figure 1A).

Choice biases during explore states

The structure of the HMM assumed random selection during exploration, but it remained possible that the monkeys instead only chose between options other than the previously exploited option. We used two methods to evaluate this possibility.

First, if explore choices were biased away from the last exploited option, then knowing the identity of that option would reduce uncertainty about what would be chosen during exploration. With random choices, knowing the last exploited option would not reduce uncertainty. The amount of information about one random variable gained from observing another is the mutual information (MI) between the variables. We calculated the MI between previous exploit choices (S) and current explore choices (C):

$$I(S,C)={\displaystyle \sum _{s\in S}{\displaystyle \sum _{c\in C}p(s,c)}}\text{log}\left(\frac{p(s,c)}{p(s)p(c)}\right)$$

Where s is one of the set of previously exploited options, S, and c is one of the set of possible choices, C. Then, we compared the observed MI to the expected MI given either 1) biased or 2) unbiased (random) selection. Expected MI was calculated via randomly drawing choices that matched monkeys’ distribution of explore choices within each session. The last exploited option was excluded to produce a biased sample or included to produce an unbiased one. If the monkeys excluded the last exploited option from explore choices, MI would be high (0.37 ± 0.04 STD across session simulations). Conversely, MI for unbiased random selection would be very low (0.02 ± 0.02 STD). MI was lower than we would expect from biased selection (see Results), though also greater than purely random selection (p < 0.01, t(27) = 2.88). This could be either due to a small, but real bias in the monkeys’ behavior, or to the fact that the HMM was more likely to erroneously identify a real explore choice to the last exploited option as an exploit choice.

Second, we tested for biased exploration by determining whether a HMM that explicitly assumed biased selection was a better fit to the behavior. The biased HMM was similar to the original model (figure 1C), but included 3 exploratory states. Each exploit state had its own explore state, in which only targets other than the previous exploit option could be chosen. Transitions between different explore states were prohibited to ensure biased exploration. The log likelihood of the anti-bias model was slightly higher (original model = −9599.6, anti-bias model = −9525.7), but the number of parameters was substantially increased in this model (15 parameters in the antibias model vs 8 parameters in the original model) and model comparison did not justify this more complicated model (see Results).

A note on the interpretation and generalization of the state-labeling method

Although we observed evidence for two time constants in the behavior, and the HMM included only discrete states, it remains unclear whether these states are truly discrete. Certainly, the neural activity suggests a gradual recovery of population dynamics after exploration, an observation that is inconsistent with discrete states in the FEF. Future work is necessary to develop more sophisticated models of these sequential choice dynamics and to understand what factors determine their parameters. Moreover, while our task design and reward schedule did not enforce two different time constants for switching, it remains unclear whether two switching time constants would be observed in other tasks that require exploration. The present experiment used a classic explore/exploit dilemma task—a restless three-armed bandit—but other studies of exploratory behavior manipulate reward magnitude rather than probability (Daw et al., 2006; Pearson et al., 2009; Jepma and Nieuwenhuis, 2011), use static bandits (Wilson et al., 2014), or include change-points or volatility manipulations (Behrens et al., 2007; Nassar et al., 2012; McGuire et al., 2014). Perhaps under these circumstances, monkeys would have used a range of switching time constants or set some fixed threshold for the number of samples from each option. If range of switching time constants was used, and these were uniformly distributed, inter-switch intervals would be distributed as a single exponential, with an inverse half-life equal to average probability of switching. If a fixed threshold was used, inter-switch intervals would not be exponentially distributed at all, but instead peaked at the time of the fixed threshold. Future studies are necessary to determine how different task demands and reward schedules determine the temporal dynamics of sequential choice behavior.

Subjective value estimation

We modeled subjective value as an exponentially weighted history of the past outcomes the monkeys observed (figure S2). Monkeys commonly exhibit exponential reward history kernels over past outcomes (Sugrue et al., 2004; Lau and Glimcher, 2005; Kennerley et al., 2006): recent outcomes affect choice more than past outcomes and the weight of previous outcomes decays roughly exponentially. This is exactly equivalent to a dynamic update process, in which new values are calculated as a weighted average of past value and current outcome. In either case, the effect of an outcome decays exponentially. In the dynamic view, the parameter of interest is typically represented as α and referred to as the learning rate. In the kernel view, value updates are typically parameterized using α⁻¹, or the half-life of a reward outcome, denoted τ. Despite these links and the apparent simplicity of the problem, there are a number of different choices to make in formalizing either approach. For example, unchosen option values may also be updated: they may decay to a uniform prior or towards 0, if the monkeys are locally estimating of the rate of reward for each option (e.g. (Kennerley et al., 2006)) or reward outcomes may be transformed into prediction errors before integration. We evaluated each of these possibilities quantitatively and ultimately chose the method for calculating subjective value that best explained the monkey’s choice behavior, as described below.

Here, we used convolution and regression (after (Sugrue et al., 2004)) to calculate the exponentially weighted moving average of reward history. Reward history was coded as a binary vector (1 if they were rewarded for selecting that target on that trial, 0 otherwise) and convolved with an exponential filter of various half lives (22 values of τ, range: 0.5 through 25). Each convolution produced a vector of subjective values under the hypothesis that the filter length the monkey used matched the one used in the convolution. Then, we used multinomial logistic regression to find the best filter by predicting choice from each subjective value vector. The best-fitting τ was identified via finding the filter length that minimized cross-validated (10-fold) model deviance (figure S2). Ultimately, we chose the simplest model (shortest half-life) within 1 standard error of the minimum cross-validated deviance.

In our approach, if an option was not chosen at trial t, its outcome was coded as 0. This is equivalent to saying that the value of unchosen options decayed to 0 and implies that the monkeys were calculating a local rate of return for each option, regardless of selection (a feature of monkey decision-making that has been reported previously (Lau and Glimcher, 2005; Kennerley et al., 2006)). In every single session, the best-τ model in which unchosen options decayed to 0 outperformed the best-τ model in which unchosen values decayed to a uniform prior (unchosen option outcomes set to 0.5, rather than 0; lower AIC and BIC values in every session, all AIC and BIC weights < 0.0001) or were carried forward from the previous time step (lower AIC and BIC values in every session, all AIC and BIC weights < 0.0001).

Of course, our approach also made the strong assumption that monkeys directly incorporated outcomes into values, rather than first transforming them into reward prediction errors (i.e. performing a delta-rule update). To determine if this was true, we directly compared choice-predicting accuracy for values calculated either directly or via a delta-rule update. Again, we found the best τ (α⁻¹) for each approach via choosing the best among 22 subjective value vectors. Directly integrating new outcomes produced subjective values that better explained choice than did delta-rule updates, as indicated by lower AIC and BIC values in the majority of sessions (25/28). Moreover, the final model (in which unchosen values decayed) remained the single best approach, outperforming both of these alternative formulations in every session (28/28, all AIC and BIC weights < 0.0001).

Delta-rule reinforcement learning model

Reinforcement learning models were used for HMM development and validation (figure S1) and to corroborate learning rate effects (figure 2E). In each case, standard delta-rule reinforcement learning models (after (Rescorla and Wagner, 1972)) were fit via maximum likelihood. We assume that the value (v) of a target i, selected at time t is updated according to:

$${\widehat{v}}_{i,t+1}={\widehat{v}}_{i,t}+\alpha {\delta }_t$$

Where v_i,t is the value of option i at time t, α is a fitted learning rate, and the prediction error (δ) is

$${\delta }_t=r_t-{\widehat{v}}_{i,t}$$

To determine whether and how learning rates changed as a function of time since exploration (table S1–S2), we added a second update term, conditioned on exploratory periods:

$${\widehat{v}}_{i,t+1}={\widehat{v}}_{i,t}+\alpha {\delta }_t+S_t\gamma {\delta }_t$$

Where S_t was a logical vector indicating the state of the animal on that trial. S was set to 1 for explore trials (in the explore-only model) or to 1 for both explore trials and exploit trials within 10 trials following an explore trial (explore+10 model). S was 0 otherwise. Thus, γ described the change in learning rate during these special epochs, relative to the global shared learning rate α.

Models with both softmax and ε-greedy decision rules were evaluated for each analysis. The two decision rules each assume the monkeys’ goal is reward-maximization, but that reward-maximizing decisions are noisy (exploratory) in different ways. In the ε-greedy case, the rule assumes that the monkey picks the best target most of the time, but also randomly chooses with some probability (ε):

$$p(i_t=\text{arg}{max}_i({\widehat{v}}_{i,t}))=(1-\epsilon )+\frac{\epsilon }{n}$$

$$p(i_t\ne \text{arg}{max}_i({\widehat{v}}_{i,t}))=\epsilon -\frac{\epsilon }{n}$$

Where n is the number of choice options.

In the softmax case, the inverse temperature parameter (β) describes the steepness of a decision rule that probabilistically maps value comparisons to decisions.

$$p(i_t)=\frac{e^{{\widehat{v}}_{i,t}\beta }}{{\displaystyle \sum _{j=1:n}{e}^{{\widehat{v}}_{j,t}\beta }}}$$

Across all models, the softmax decision rule was a better fit for the data (Table S1–2), but learning rates were similar in both cases. Model fits using both decision rules are reported in the text and Supplemental Tables.

Models were initialized with 100 random seeds and fit via maximum likelihood (minimizing the negative of the log likelihood; fminsearch, MATLAB). Target values were initialized at 0.5. Learning rates (α) were constrained between 0 and 1, but state-conditioned learning rates (γ) were allowed to vary between −1 and 1, to allowing for suppressed learning during exploration.

Explore-triggered reward history

In order to determine if transitions into exploration occur in response to specific reward histories, we asked whether there was any pattern in the sequence of rewards before explore transitions. One method to do this would be to take the average reward history over some period (filter length) before explore transitions. However, random walks like our reward schedule are autocorrelated, so we used a Wiener filter approach to extract the explore-triggered reward history impulse, corrected for these autocorrelations. Wiener filter analysis has previously been used to extract choice-triggered reward-history impulses (Sugrue et al., 2004) and is similar to methods used to examine spike-triggered average stimuli. Briefly, the symmetrical Toepliz autocorrelation matrix of rewards (Θ_rr) is inverted and multiplied against the cross-correlation between transitions into explore and rewards (Θ_tr) to produce the explore-triggered reward history impulse (h):

$$\overline{h}={\mathrm{\Theta }}_{rr}^{-1}{\overline{\mathrm{\Theta }}}_{tr}$$

Here, both time series are binary and centered so the cross correlation (Θ_tr) is simply the explore-triggered average of reward history, without correction for autocorrelations. Note that overbars indicate vectors, rather than matrices. We used a filter length of 10 trials, but changing the filter length did not change the result: transitions to exploration were driven by omitted rewards on the last 2 trials.

Effect of past rewards on choice

To determine whether past reward outcomes would have a state-dependent impact on behavior many trials into the future (increased reward-learning), we calculated the difference in the switch-probability on each trial (t) conditioned on reward outcome on some past trial (r_i):

$$\text{reward effect}=p(\mathit{switch}|r_{t-i}=1)-p(\mathit{switch}|r_{t-i}=0)$$

This quantity was calculated separately within three states (explore choices, exploit choices that occurred within 10 trials following an explore choice, and late exploit choice). For clarity of presentation, the data in figure 2D and 2E are normalized to the probability of switching within each state, but the same pattern was apparent in non-normalized data and statistical tests were run on non-normalized data. This analysis only included past trials in which the animal made the same choice as the most recent (1-back) trial.

Neuronal data analysis

Unless otherwise specified, firing rates were normalized between 0 and 1 by first subtracting the average minimum firing rate (baseline) and then dividing by the baseline-subtracted maximum firing rate across trials. Paired (within-neuron or session) nonparametric tests were used with Holm-Bonferroni corrections for multiple comparisons. Whole-trial epochs ranged from −400 ms to 100 ms aligned to choice (saccade onset). Sliding analyses were conducted using overlapping 25 ms bins (10 ms steps) and p values were corrected for the total number of bins (Holm-Bonferroni). The only exception to this was the separation between different-choice trajectories, in which case bins were nonoverlapping (25 ms steps) due to the need for independent bins for curve fitting.

Target Selectivity

In order to quantify target selectivity in single neurons over time, we first identified each neuron’s preferred target (Tin) as the target which elicited the highest whole-trial firing rate when chosen. For each cell, a target selectivity index was then calculated as the difference between mean firing rate for preferred-target choices and the mean of firing rates for the alternative choices (together: Tout).

Imputation for population analyses

Analyses of simultaneously recorded neurons require an observation for each combination of neuron and trial, but some cells were not held for the whole duration of the session. Because we did not want to discard these neurons or trials and these data were missing at random (no systematic biases in choices or states for missing data), we imputed the mean firing rate for the trials preceding or following a loss of isolation (after (Friedman et al., 2001)). The mean firing rate was calculated across all choices, so this procedure effectively decreased the impact of these neurons on the targeted dimensionality analyses without entirely excluding them. Some imputation was done for 12% of neurons, and constituted approximately 3% of observations. Excluding trials with any missing neurons or neurons with any missing trials produced similar results, though statistical power was lower.

Targeted dimensionality reduction

To determine how choice-predictive network states evolved across trials, we used a form of targeted dimensionality reduction based on multinomial logistic regression (after (Cohen and Maunsell, 2010; Mante et al., 2013)). This allowed us to identify a choice-predictive subspace in the activity of simultaneously recorded neurons and to examine how goal states altered choice-predictive population dynamics.

Briefly, within the axes defined by the firing rates of simultaneously recorded neurons, we used one-vs-all multinomial logistic regression (mnrfit, MATLAB) to find the hyperplanes (weighted combinations of neuronal firing rates) that best predicted the choice the monkey would make. These weights of simultaneously recorded neurons then formed the bases of our choice-predicitive subspace and we projected each trial’s neural activity into the choice-predictive subspace.

The approach starts by finding binary classifiers that separate the pattern of neural activity that predicts one choice from the pattern that predicts other two options. In general, logistic regression finds the separating hyperplane (linear combination of feature weights) that best differentiates, in the maximum likelihood sense, observations that belong to a class (labeled true) from observations that do not (labeled false). One classifier is needed to differentiate two classes, and in K-multi-class one-vs-all classification, K-1 classifiers are needed to fully separate the observations. The final Kth choice serves as the reference against which the other K-1 choices are compared and the true observations for the final Kth choice are the false observations for all of the other choices. We fit a system of K-1 independent binary classifiers of the form:

$$p(\text{choice}=i|X)=\left(\frac{1}{1+e^{-(X{\beta }_i)}}\right)$$

Where X is the trials by neurons matrix of firing rates of simultaneously recorded neurons, including a first column of ones for the intercept. Equivalently, we can invert the logistic link function:

$$\text{log}\left(\frac{p(\text{choice}=i|X)}{1-p(\text{choice}=i|X)}\right)=X{\beta }_i$$

Fitting the classifier (finding the maximum likelihood solution for β_i) finds the separating hyperplane within neuron-dimensional space that best differentiates neural activity on trials in which option i is chosen from neural activity on other trials. The separating hyperplane for each choice i satisfies:

$$X{\beta }_i=0$$

If there were only two neurons (features for classification), the choice-predictive vector would be the vector orthogonal to the separating hyperplane. That is, the choice-predictive vector is the one along which increasing distance from the origin reflects increasing log odds that a target will be chosen (for positive values) or not chosen (for negative values). The position of each trial along this choice-predictive vector is calculated via scalar projection. Each trial is represented as a column vector of firing rates, x_i, and then its projection onto the unit vector orthogonal to the separating hyperplane is:

$$d_i=\left(\frac{1}{\Vert {\beta }_i\Vert }\right){\beta }_i^T{x}_0$$

In more than two dimensions, there are many orthogonal vectors, but this same scalar projection gives the shortest distance from each trial to the separating hyperplane: that is, the projection of the trial onto the choice-predictive vector from this classifier. In matrix notation:

$$d_i=\left(\frac{1}{\Vert {\beta }_i\Vert }\right)X{\beta }_i$$

At this point, it should be clear that this projection is proportional to the log odds of making that choice, up to a factor determined by the magnitude of β. That is:

$$X{\beta }_i=d_i\Vert {\beta }_i\Vert =\text{log}\left(\frac{p(\text{choice}=i|X)}{1-p(\text{choice}=i|X)}\right)$$

To preserve the intuitive relationship between subspace position and the log odds of choice, we drop the scaling factor and calculate each trial’s projection along choice-predictive axis i as:

$$\mathit{pro}{j}_i=X{\beta }_i$$

One regression was used to find the projection onto the vector that predicts target 1 choices and a second was used to find the projection onto the vector that predicts target 2 choices. These defined the bases of the choice-predictive subspace (figure 4B). Here, the vector predicting target 3 choices is the negative of both the target 1 and target 2 axes (that is, the vector that predicts target 3 choices is the one along which we have increasing confidence that neither target 1 nor target 2 will be chosen).

For all targeted dimensionality reduction analyses, the separating hyperplanes were calculated based on the average firing rates across the whole-trial epoch. For clarity in the illustration in figure 4B, separating hyperplanes were re-calculated within each time bin, but fixed bases calculated from whole-trial firing rate were used in all analyses.

Relationship between targeted dimensionality reduction and decoding

It should be clear that the same regression that is used to perform targeted dimensionality reduction can also be used to decode choice from the neural activity. To decode choice, we calculate the regression coefficients and the Xβ_I for each choice, at each time point before the saccade, just as in the targeted dimensionality reduction. Next, calculate the probability of each of the three options from the multinomial regression model (Friedman et al., 2001) and take the maximally probable choice as the prediction for each trial. Finally, we evaluate decoding accuracy by asking how often the choice predicted by the model coincides with the choice the monkey made.

The timecourse of decoding accuracy was similar to the results of targeted dimensionality reduction and is illustrated in figure S4. However, converting to choice probability requires a nonlinear transformation of the neuronal representation of each choice, which can obfuscate real differences in neural activity. For example, while decoding accuracy is largely flat for ~200 ms before the saccade, the peak of the Xβ_I (log odds) of the chosen and unchosen options is at the time of the saccade (compare figure S4A and B with C and D). This occurs because an equivalent change in choice-predictive neural activity has different effects on decoded choice probability, depending on the baseline level (i.e. a comparatively large effect when choice probability is close to chance, and a comparatively small effect when choice probability is close to 0 or 1). Because choice probability is strongest at the time of the saccade, the effects of the nonlinearity will also be most pronounced at this time. For these reasons, we performed most of our population analyses in the untransformed space, where changes in firing rate had an equivalent effect on our dependent measures, no matter the current baseline level of choice-predictive information.

Availability of choice information during exploration

In order to directly ask whether less information about upcoming choice was available during exploration (rather than a change in tuning, for example) we used multinomial logistic regression (MATLAB: mnrfit) as before to predict choice from neural activity during explore choices and count-matched subsets of exploit choices (to control for any effect of trial number). Models were trained only on exploit trials or only on explore trials, then tested on held out subsets of those trials (tested on 10 held out trials, 30 repetitions of training and testing). Models were fit to the whole-trial epoch, which included the motor-related activity.

Scatter index

In order to calculate how much neural activity on each trial was typical of other trials in which the monkey made the same choice, we used a typical measure of clustering.

$$\text{scatter}=\frac{d_{\mathit{within}}}{d_{\mathit{between}}}$$

Where d was the average Euclidean distance between points in the choice-predictive subspace. The scatter index was thus close to 1 (high scatter) when choice-predictive neural activity was not more similar to other trials were the monkey made the same physical choice, compared to trials where the monkey chose one of the other two options. Conversely, a scatter index less than 1 (low scatter) indicates that neural activity clusters with other trials where the monkey made the same physical choice.

Mixing pseudo-trials

Because choices were autocorrelated, “choice-predictive” activity might not simply reflect the decision-making process on the present trial, but instead could also incorporate information about the last choice that was made. Exploit choices tended to be repeat choices, so the combination of this-choice and last-choice activity reduce scatter in exploit trials (and vice versa for explore trials). To evaluate the hypothesis that scatter was reduced during explore choices because population activity reflected a mixture of information about the previous choice and the current choice, we created pseudo-trials that were a mixture (average) of the choice-predictive activity from pairs of randomly selected exploit trials. A different sample of pseudo-trials was constructed for each possible permutation of the different options (n = 6 for 3 choice options). The number of pseudo-trials matched the number of explore trials in each condition (where a condition was a combination of the present choice and the last choice). The scatter index was then calculated as before, with the distances to same-condition-choices (matching both the present trial and the last trial) in the numerator and distance to the third (non-matching) choice trials in the denominator. This procedure created a distribution of scatter indices under the hypothesis that neural activity on explore trials was simply a mixture of two different types of exploit-like trials: one reflecting the current choice, and one reflecting the previous choice.

Method for evaluating alternative explanations

Explore and exploit choices differed in a number of continuous dimensions (e.g. figure 2). To determine whether any of these variables better explained the results, we fit the following GLM to both single-unit target selectivity and the single-trial network scatter:

$$\widehat{y}={\beta }_0+{\beta }_1(S)+{\beta }_2(\varphi )+{\beta }_3(\varphi S)$$

Where S is a logical vector indicating whether a trial was exploratory (1), ϕ is a vector of centered and scaled observations of the confounding variable, and y is target selectivity or neural scatter. β1 thus captures the offset between exploration and exploitation (state effect), accounting for any main effect of or interaction with the confounding variable. Fitted beta weights and p values for a number of confounds are reported in table S3 and illustrated in figure S5.

For within-cell target selectivity, the model was fit to binned data: each session’s trials were separated into 5 quantile bins and target selectivity was calculated within each cell, within each state (explore and exploit). Five bins were selected to minimize the number of empty bins per cell, but results were identical with either more (10) or fewer (3) bins. For predicting within-trial neural scatter, the model was fit to raw data and additional dummy terms were included to account for any main effect of session (one term for each session minus one).

Divergence in neural trajectories

In order to estimate the rate of divergence in the neural trajectories, we fit linear, exponential, and piecewise linear models to predict the between-choice distance in presaccadic neural trajectories (d) as a function of time before the choice (t; in milliseconds). Then, standard model comparison techniques were used to identify the most probable model (figure S4–5). The models were formulated as follows. Linear:

$$\widehat{d}={\beta }_0+{\beta }_{1}t$$

Where B₀ and B₁ are offset and slope parameters. Exponential:

$$\widehat{d}={\beta }_0+{\beta }_1{e}^{t/\tau }$$

Where B₀ and B₁ are offset and scale parameters, respectively, and τ is the time constant of exponential divergence in trajectory distances. Piece-wise linear:

$$\widehat{d}=\{\begin{array}{cc}{\beta }_0+{\beta }_{1}t& t<c\\ {\beta }_0+{\beta }_{1}c+\tau (t-c)& t\ge 0\end{array}$$

Where B₀ and B₁ are offset and slope parameters, c is a fitted parameter identifying the time point at which the rate of separation increases, and τ is the change in the rate after time c. All three models were fit with a nonlinear least squares cost function and the models’ log likelihoods, AIC and BIC values are:

$$\text{log}(\mathrm{l})=-(n/2)·\text{log}(\mathit{SSE}/n)$$

$$\mathit{AIC}=-2·\text{log}(\mathrm{l})+2(k+1)$$

$$\mathit{BIC}=-2·\text{log}(\mathrm{l})+(k+1)·\text{log}(n)$$

Where SSE is the sum of squared errors, n is the number of observations, and k is the number of parameters in each model (see (Burnham and Anderson, 2002)). To calculate the relative likelihood of the two models, we calculated the AIC and BIC values and weights (Burnham and Anderson, 2002) and the results from this analysis are reported in table S4.

Spike count autocorrelation

In order to determine how transitions into exploration affected persistent patterns of activity in the FEF, we calculated the spike count autocorrelation function separately for exploit trials that were and were not separated by explore choices. For each single neuron and multiunit where a minimum of 5 trial pairs was observed in each bin (where a bin was a combination of trial lag and condition, n = 514 units), we calculated the autocorrelation at each possible trial lag τ (τ > 1, t ≤ 25).

$$\rho (\tau )=\frac{\mathrm{E}[N_t{N}_{t+\tau }]-\mathrm{E}[N_t]\mathrm{E}[N_{t+\tau }]}{{\sigma }_{N_t}^2}$$

Where E is the expected value, N is the observed spike count at time t and time t+τ, and σ is the standard deviation of the spike count, computed across all trials for the choices made at each time point t and t+τ. Spike counts were calculated from a whole-trial epoch, ranging from 200 ms before stimulus onset to 400 ms after, though the results were insensitive to the specific choice of epoch. In order to isolate the residual variance in spike count that could not be accounted for by differences in mean firing rate or variance across trials, spike counts were z-scored within-choice (after (Bair et al., 2001)). After this normalization, EN_t = EN_t+τ = 0, and σ = 1, so the equation simplifies to:

$$\rho (\tau )=\mathrm{E}[N_t{N}_{t+\tau }]$$

The normalization was designed to isolate the residual variance in the spike count from any contribution of choice information. We confirmed that this was the case empirically. Following normalization, correlations were not significantly higher for randomly selected same-choice exploit trials than for different-choice exploit trials (paired t-test, p > 0.7). Moreover, qualitatively similar results to those reported in figure 5C were obtained using only same-choice explore-separated trials, though the power of this analysis was substantially lower, owing to fewer neurons with a sufficient number of observations and fewer observations per trial lag.

Significant differences between explore-crossing and non-explore crossing correlations were assessed at each time lag via bootstrapping. The observations were resampled, with replacement, 1000 times. Resampling was done without respect to the original labels and count matched to the number of observations for each label. The 1000 repetitions produced 1000 differences in correlation values for each time lag: a distribution of effect sizes under the null hypothesis that there was no difference in spike-count correlations between explore-separated and non-explore-separated trials. If the autocorrelation function of explore-separated trials was not different from the autocorrelation of non-separated trial pairs, we would expect the explore-separated autocorrelation function to fall within this null distribution. Therefore, significance (figure 5C) was assessed as the fraction of bootstrapped samples that were as big or bigger than the real difference observed at each time lag and corrected for multiple comparisons.

Process dynamics of scatter recovery

When averaged across trials, neural scatter decreased slowly after exploration (figure 5A, B). This was in contrast to the sudden increase in scatter at the start of exploration and the sudden changes in strategic or rule-related neural activity that have been reported in other tasks (Durstewitz et al., 2010; Karlsson et al., 2012). However, it was possible that the slow changes in trial-averaged scatter were caused by abrupt changes within trial sequences. A simple misalignment across sequences would make scatter appear to recover slowly, despite a generative process of discrete jumps. We evaluated this possibility via examining the distribution of changes in scatter (“scatter step sizes”).

In a jump process, scatter step sizes would by highly variable because they would contain a mixture of large jumps and small, steady-state adjustments. Conversely, in a continuous process, the variance in the distribution of step sizes would be lower. In the present dataset, it was possible to benchmark the variance in scatter step sizes from a jump process via examining the variance in scatter step sizes during transitions into exploration—a period in which discrete jumps in the scatter index obviously occurred (figure 5A and B). To create reference distributions under this hypothesis, we calculated the scatter step sizes during transitions into exploration (on explore trials and the 10 trials preceding exploration). Scatter step sizes were then downsampled with replacement to match the number of post-exploration trials (within 10 trials following exploration). This procedure created 1000 reference distributions for the scatter step sizes that would be observed if post-explore adjustments were caused by a jump process similar to the one observed during transitions into exploration.

DATA AND SOFTWARE AVAILABILITY

Data and software are available upon request to the Lead Contact (Becket Ebitz, rebitz@gmail.com). Code for some analyses (discrete exponential mixture models, Wiener filter, etc.) is available on the Lead Contact’s webpage (https://rebitz.github.io/code.html).