Evidence of directional and stabilizing selection in contemporary humans

Significance

Combining high-throughput molecular genetic data with extensive phenotyping enables the direct study of natural selection in humans. We see firsthand how and at what rates contemporary human populations are evolving. Here we demonstrate that the genetic variants associated with several traits, including age at first birth in females and body-mass index in males, are also associated with reproductive success. In addition, for several traits, we demonstrate that individuals at either extreme of the phenotypic range have reduced fitness—the hallmark of stabilizing selection. Overall, the data are indicative of a moving optimum model for contemporary evolution of human quantitative traits.

Abstract

Modern molecular genetic datasets, primarily collected to study the biology of human health and disease, can be used to directly measure the action of natural selection and reveal important features of contemporary human evolution. Here we leverage the UK Biobank data to test for the presence of linear and nonlinear natural selection in a contemporary population of the United Kingdom. We obtain phenotypic and genetic evidence consistent with the action of linear/directional selection. Phenotypic evidence suggests that stabilizing selection, which acts to reduce variance in the population without necessarily modifying the population mean, is widespread and relatively weak in comparison with estimates from other species.

Natural selection can strongly affect patterns of phenotypic variation. This fact has led to considerable interest in understanding how natural selection and other evolutionary forces combined to shape the allelic spectrum underlying variation within and between populations. Most of this work has focused on searching the genome for signatures of past selective events (1). Yet selection fundamentally acts on phenotypes, not genotypes. Therefore, the relationships between phenotypes and fitness must be studied in contemporary populations to observe natural selection directly. In doing so, we can gain insights about the direction and magnitude of phenotypic evolution. Theoretically, such observations allow one to predict future evolutionary change, and they can serve as points of comparison with inferences of selection obtained from other sources of data. Here we report observational evidence that is consistent with the action of natural selection in a contemporary human population.

Directional selection results in a covariance between the trait and fitness and can lead to changes in the mean value of a trait in a population (2–4). Further, if phenotypic variation for the trait is caused by genetic factors, then directional selection can result in changes in the genetic composition of a population. Phenotypes may also be subject to stabilizing selection or disruptive selection, which are both nonlinear forms of selection. The key distinction between stabilizing and disruptive selection is whether the relationship between fitness and a phenotype is concave down or up, respectively. Stabilizing selection, which is commonly invoked in theoretical studies of quantitative traits (5–9), will tend to reduce phenotypic variation while disruptive selection will tend to increase it. In a seminal paper on the direct study of natural selection, Lande and Arnold (10) put forth a statistical framework by which the magnitude of both directional and nonlinear selection could be estimated from observational data via regression of fitness onto phenotypes and their squared values.

Application of the Lande and Arnold (10) framework to human populations has yielded evidence consistent with the action of directional selection on physiology, life-history, and body-size traits in both pre- and postindustrial societies (11). While important differences between the studied populations exist (12, 13), a few interesting trends have emerged. Multiple studies have suggested that directional selection has acted to lower the age at first birth in females (14–19), increase the age at menopause (14, 17), increase weight in females (17, 18, 20), and decrease height in females (13, 17, 18, 20, 21) in contemporary postindustrial populations.

Direct evidence for the action of stabilizing selection in humans is scarcer. Birth weight is one reported example of a human trait under stabilizing selection (22), although the intensity of selection has decreased in postindustrial societies (23). A twin study of female reproductive life-history traits showed evidence for a phenotypic optimum for age at menarche (14). Additionally, phenotypic evidence has been presented that is indicative of the simultaneous action of directional and stabilizing selection on height in the Dutch (24). However, a recent study in the contemporary United States found no evidence for any nonlinear selection (25)—although sample size may have limited the power to detect such effects. While selection acts on phenotypes, evolution requires genetic variation. The genetic covariance between a phenotype and fitness determines the expected evolutionary change (2–4) of that phenotype in a population. Genetic covariances between traits can be estimated from pedigree information or directly from molecular genetic data (26).

The use of molecular genetic data has multiple advantages over traditional sources of data for the study of contemporary selection (19, 25, 27). The most obvious advantage is the availability of data; genetic data from large samples of unrelated individuals are increasingly accessible to many researchers. Another advantage comes from the ability to control for possible cultural transmission of traits, which is generally confounded with genetics in observational studies because parents pass both on to their offspring (11). This issue can be partially mitigated by accounting for population structure (28) and geography in samples of unrelated individuals.

In the first attempt to use SNP-array data to study contemporary natural selection on complex traits, Tropf et al. (19) found a negative genetic correlation between relative lifetime reproductive success (rLRS)—the individual lifetime reproductive success divided by the mean—and age at first birth, using a bivariate linear mixed-modeling approach (26, 29). However, Beauchamp (25) noted that the bivariate analyses are underpowered with modest sample sizes and chose to analyze genetic predictors derived from the results of independent large genome-wide association studies (GWAS). Significant negative correlations between polygenic prediction scores for female educational attainment and rLRS have been found in the populations of the contemporary United States (25) and Iceland (27). But reliance on external GWAS summary statistics limits analyses to traits that have already been thoroughly characterized at the genetic level.

Here, we analyze the phenotypic and genetic correlates of rLRS in the UK Biobank (UKB). The UKB is a large population-based prospective study of the genetic and environmental determinants of aging-related disease (30). The dataset consists of over 500,000 individuals from the United Kingdom who have been genotyped at common SNPs and clinically phenotyped for many different traits. These data provide paired genotype and phenotype samples large enough to accurately measure additive genetic correlation between many heritable complex traits (31).

First, we apply the Lande and Arnold (10) framework through regression analyses of the relationship between a suite of phenotypes and a proxy for fitness, rLRS, in 217,728 females and 158,638 males. Then, the genetic data available from 157,807 female and 115,902 male unrelated samples are used to estimate genetic correlations between the phenotypes and rLRS through linkage disequilibrium (LD)-score regression analysis (32, 33). This analysis was supported by the observation that rLRS had a low, but measurable heritability. Our analyses replicate the main results of other recent studies (19, 25, 27) and uncover a host of other significant genetic correlations with rLRS. We also report estimates of quadratic relationships with rLRS, which may be interpreted as evidence consistent with stabilizing or disruptive selection, informing efforts to model the processes that maintain heritable variation in human complex traits (34–43). Our observations are consistent with the action of weak directional and stabilizing selection and limited disruptive selection in the UK Biobank population.

Phenotypic Observations

We estimate linear ($\beta$) and quadratic ($\gamma$) selection gradients by regressing rLRS onto phenotypes and squared phenotypes (10). Because of possible heterogeneity in selection pressures and rLRS measurement precision—documented number of live births in females vs. self-reported number of children fathered in males—all analyses were performed on a sex-specific basis. In total, we analyzed 37 traits in females and 33 traits in males; the traits and results are listed in Dataset S1. The histogram of $\widehat{\beta }$ (SI Appendix, Fig. S1A) shows that the observed signals of directional selection are weaker than what has been found in other species (44). Such weak selection gradients are unlikely to lead to large changes in phenotypic distributions over clinically or socially relevant timescales (25, 27). However, it is important to note that the measured rLRS may be biased because it is conditional on survival to postreproductive age and may not be completed rLRS for males. Despite the weak signal, we find that 23 female traits and 21 male traits have significant nonzero directional selection gradients ($\widehat{\beta }$) at a family-wise error rate (FWER) $\le 0.05$. However, many of these traits are highly correlated (SI Appendix, Figs. S4 and S5) and should not be viewed as separable axes of selection.

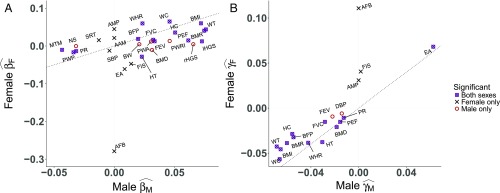
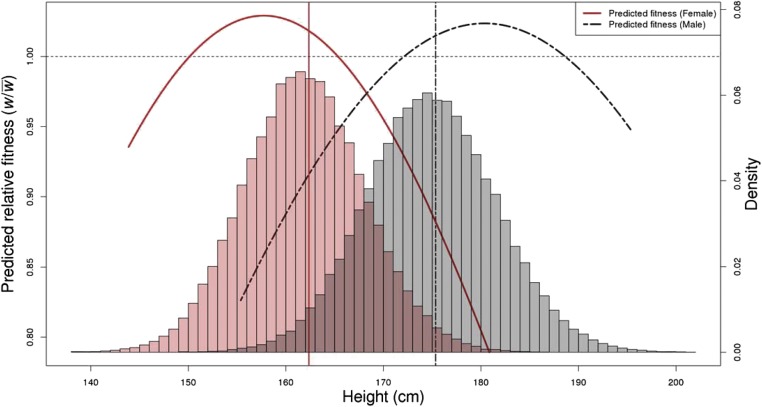
The $\widehat{\beta }$ estimates for traits with a significant estimate in at least one sex are shown in Fig. 1A. Overall, the $\widehat{\beta }$ estimates were not highly correlated between sexes. This implies that there is some sex-specific selection acting on these phenotypes, consistent with recent work on the genetic and phenotypic correlates of viability (45). In many instances, the difference between sexes is driven by a large difference in the magnitude, not the sign, of $\widehat{\beta }$. For example, the estimate for educational attainment in females is ${\widehat{\beta }}_{\mathit{EA},F}=-0.0612\pm 0.0022(P<{10}^{-172})$ while the estimate in males is ${\widehat{\beta }}_{\mathit{EA},M}=-0.0086\pm 0.003(P\approx {10}^{-2.3})$. Conversely, the estimate for birth weight in males, ${\widehat{\beta }}_{\mathit{BW},M}=0.021\pm 0.0038(P<{10}^{-7})$, is much larger than the estimate in females of ${\widehat{\beta }}_{\mathit{BW},F}=0.0047\pm 0.0027(P=0.084)$. Height is the only trait we studied for which the data indicate sexually antagonistic selection. In females ${\widehat{\beta }}_{\mathit{HT},F}=-0.028\pm 0.0021(P<{10}^{-39})$, while in males ${\widehat{\beta }}_{\mathit{HT},M}=0.022\pm 0.0025(P<{10}^{-18})$. Fig. 2 further illustrates that the predicted phenotypic optimum is above and below the population mean height for males and females, respectively, consistent with multiple previous studies showing a difference in contemporary selection pressures on height between males and females (13). Further, the empirical relationship between LRS and height, illustrated in SI Appendix, Fig. S2, is very similar to that predicted by a Gaussian stabilizing selection model (SI Appendix, Fig. S3).

Fig. 1.

(A and B) Scatterplot showing the magnitude of (A) linear selection gradients $\widehat{\beta }$ and (B) quadratic selection gradients $\widehat{\gamma }$ for a selection of traits in females and males. Traits were selected on the basis of being significant (FWER$\le 0.05$) in at least one sex. Estimates are on the z-score scale for theoretical interpretation and consistency across traits. Points are labeled with the following abbreviated trait descriptions: age at menarche (AAM), age at first birth (AFB), age at menopause (AMP), body-fat percentage (BFP), bone mineral density (BMD), body-mass index (BMI), basal metabolic rate (BMR), birth weight (BW), diastolic blood pressure (DBP), educational attainment (EA), forced expiratory volume (FEV), fluid intelligence score (FIS), forced vital capacity (FVC), hip circumference (HC), hand grip strength (HGS), height (HT), mean time to correctly identify matches (MTM), neuroticism score (NS), peak expiratory flow (PEF), pulse rate (PR), pulse-wave arterial stiffness index (PWA), pulse-wave peak-to-peak time (PWP), pulse-wave reflection index (PWRI), systolic blood pressure (SBP), speech reception threshold (SRT) estimate, waist circumference (WC), waist-to-hip ratio (WHR), and weight (WT). Note that data on AFB, AMP, and AAM are not available for males and their regression values were set to zero.

Fig. 2.

Predicted relative fitness as a function of height. Linear and quadratic selection gradients were converted into parameters of a Gaussian fitness function. Using the parameterized Gaussian fitness function, relative fitness values across the observed phenotypic range are predicted and shown by solid red (female) and dashed black (male) lines. The population means are indicated by vertical solid red (female) and dashed black (male) lines. Histograms of female (red) and male (gray) phenotypes are overlaid with an axis on the right-hand side. The horizontal dashed line indicates a relative predicted fitness of 1.

In contrast to a recent study (25), 12 traits in females and 14 traits in males have a significant nonlinear selection gradient estimate ($\widehat{\gamma }$). It is important to note that the sample size available in ref. 25 was nearly two orders of magnitude smaller than that of the present study. The histogram of $\widehat{\gamma }$ values in SI Appendix, Fig. S1B shows a skew toward negative values. Specifically, 47 of the 64 sex–trait combinations examined show a negative quadratic selection gradient (median $\widehat{\gamma }=-0.0059$), of which 26 were significant. Twenty-four sex–trait pairs had a nonzero $\widehat{\beta }$ and a significant negative $\widehat{\gamma }$, which is indicative of the simultaneous action of directional and stabilizing selection.

Fig. 1B shows that, unlike many of the $\widehat{\beta }$ estimates, the estimates of $\widehat{\gamma }$ were quite similar in both sexes. For example, the estimates for height are ${\widehat{\gamma }}_{\mathit{HT},F}=-0.0189\pm 0.0014(P<{10}^{-37})$ in females and ${\widehat{\gamma }}_{\mathit{HT},M}=-0.015\pm 0.0017(P<{10}^{-17})$ in males, respectively. Fig. 1B shows that among traits with significant $\widehat{\gamma }$ in both sexes the male estimate tends to be farther from zero (with height being an exception). We find no traits with significant $\widehat{\gamma }$ in both sexes with opposite signs.

Fig. 1B shows that age at menopause, fluid intelligence score, and age at first birth (AFB) all have a positive $\widehat{\gamma }$ in females. In addition, the $\widehat{\gamma }$ for educational attainment is positive in both sexes. A positive value of $\gamma$ can be interpreted as evidence of disruptive selection. However, our results for AFB are more indicative of a plateauing of directional selection toward the upper phenotypic extreme rather than true disruptive selection (SI Appendix, Fig. S6). The situation is somewhat less clear for the other phenotypes with a significant positive $\widehat{\gamma }$ (SI Appendix, Figs. S7, S9, and S10) and these results should be followed up more closely in future work.

A multiple-regression analysis provided a more conservative perspective on the phenotypic correlates of rLRS. Due to multicollinearity (SI Appendix, Figs. S4 and S5) and nonoverlapping missing data, we had to choose only a subset of traits for the multiple regression. The full multiple-regression results are included in Dataset S1 and are summarized in SI Appendix, Table S1. In males, the estimates of $\beta$ for hand-grip strength, pulse rate, body-mass index (BMI), and systolic blood pressure are significant in the multiple regression and retain their direction of association from the single-trait regression models. In females, the estimates of $\beta$ for educational attainment (EA), AFB, age at menarche, bone mineral density, systolic blood pressure, and waist-to-hip ratio are significant in the multiple-regression model. However, the direction of the association between EA and rLRS in females is positive in the multiple-regression setting. This stands in sharp contrast to the separate regression results and strongly points away from a simple linear relationship between EA and increased rLRS. Rather, it appears that correlated factors, such as AFB, drive the apparent selection (46) on EA.

To further explore the relationship between AFB, EA, and rLRS we fitted a reduced multiple-regression model with EA, AFB, and their interaction. In the reduced model, all three terms (two linear and one interaction) were highly significant (SI Appendix, Table S1). As in the initial multiple regression, the direction of association for EA is positive in the reduced model. In addition, the interaction term between EA and AFB is strongly positive ($\widehat{{\beta }_{\mathit{AFB}\text{:}\mathit{EA}}}=0.03\pm 0.0016(P<{10}^{-112})$). One hypothesis consistent with this observation is that the effect of EA on rLRS becomes more positive as AFB increases and that the negative regression coefficient in the EA-alone model can be fully explained by the strong negative association between AFB and rLRS. In simpler terms these results suggest that among females who have children later in life, those individuals with higher EA will tend to have more children. This is despite the fact that people with higher EA tend to have fewer children overall and is consistent with prior work in the Icelandic population (27).

The estimates of $\gamma$ were much less significant in the multiple regression compared with the separate regressions. For females, the estimates of $\gamma$ for age at first live birth and BMI were significant—with the BMI estimate reversing direction to be positive. In males, the estimates of $\gamma$ for EA and BMI were significant—with both retaining their direction of association.

Genetic Correlations with rLRS

The phenotypic results are consistent with the action of natural selection, but for adaptation to occur there must be effects on the genetic level. To this end, we analyzed genetic data from 157,807 female and 115,902 male unrelated samples. Estimates of the genetic correlations between several traits and rLRS, $r_{g\text{,}\mathit{rLRS}}$, were obtained from the data, using LD-score regression (32, 33). LD-score regression uses the regression of the cross-products of z statistics onto a measure of LD in a genomic window (the LD score), assuming a polygenic architecture, to estimate genetic covariance components from GWAS results. We also analyzed the UKB interim data release, using a linear mixed-modeling (LMM) approach. This approach was not computationally feasible on the full dataset; we report the results on the full dataset using LD-score regression in the main text, but see SI Appendix for a discussion of the LMM results. All genetic variance and covariance estimates are contained in Dataset S2.

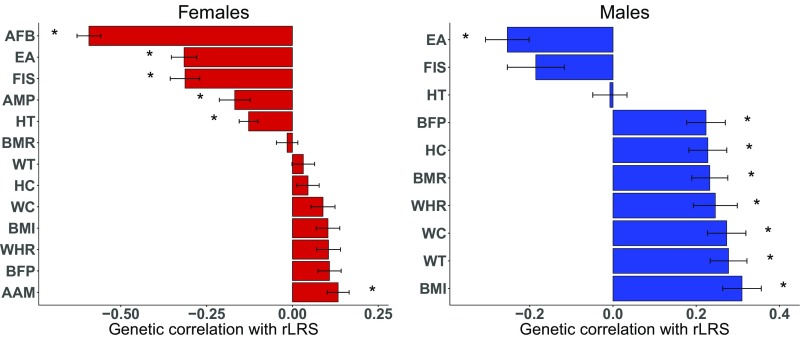
Theory predicts that traits highly correlated with fitness will have low heritability (47). As expected, rLRS has a low but significant SNP heritability in the UKB dataset, which means that we have power to detect strong genetic correlations. Specifically, the LD-score regression estimates of $h_{\mathit{SNP}\text{,}\mathit{rLRS}}^2$ were 0.056 and 0.033 in females and males, respectively, with respective standard errors of 0.0046 and 0.0054. Fig. 3 shows ${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ for the subset of traits for which an estimate was marginally significant (P $\le {10}^{-3}$) in at least one sex.

Fig. 3.

Bar plots showing genetic correlations between a selection of traits and rLRS for females (red) and males (blue). Traits were selected on the basis of being marginally significant (P $\le 0.001$) in at least one sex and were sorted in ascending order of the estimate for each sex. Data are displayed as the correlation estimate plus or minus the SE ($\sim P\le 0.001$, *FWER $\le 0.05$). Bars are labeled with the following abbreviated trait descriptions: age at menarche (AAM), age at first birth (AFB), age at menopause (AMP), body-fat percentage (BFP), body-mass index (BMI), basal metabolic rate (BMR), educational attainment (EA), fluid intelligence score (FIS), hip circumference (HC), height (HT), waist circumference (WC), waist-to-hip ratio (WHR), and weight (WT).

The estimated genetic correlation with rLRS was significant for several anthropometric traits. For example, the estimates of ${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ for height are $-0.1278\pm 0.0274(P<{10}^{-5})$ in females and $-0.0074\pm 0.0412(P=0.18)$ in males. Recall that we estimated a significant negative selection gradient in females with a small but significant positive selection gradient in males. The phenotypic results are in agreement with prior studies in Western populations (13), suggesting that selection on reproductive success favors shorter females and taller males. However, because we see no evidence for a genetic correlation between height and rLRS in males, we do not predict that the observed phenotypic selection in males would induce a response to selection (in a single generation).

BMI provides another important example of evidence for directional selection on an anthropometric trait. We estimate that the ${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ for BMI is $0.104\pm 0.0344(P={10}^{-2.6})$ in females and $0.31\pm 0.046(P<{10}^{-10})$ in males. These results are qualitatively similar to our phenotypic results which indicated positive directional selection in both sexes with a larger estimate in males. Although the genetic result for females did not pass our study-wise significance threshold, the results are consistent with the hypothesis that contemporary selection on reproduction favors higher BMI in males and support exploration of the same hypothesis in females.

The genetic correlation estimate for AFB in females was the strongest observed in our study. We estimate that the ${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ for AFB is $-0.593\pm 0.035(P<{10}^{-16})$. This result is consistent both with our phenotypic observations and with prior pedigree-based results (17). EA is also strongly negatively correlated with rLRS; we estimate the ${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ for EA to be $-0.316\pm 0.037(P<{10}^{-16})$ in females and $-0.2539\pm 0.052(P<{10}^{-5})$ in males. However, the most likely explanation for these genetic results is something very similar to what we observed on the phenotypic level for these two traits, which would agree with work on contemporary selection in an Icelandic population (27).

Another interesting aspect of the observed negative directional selection on AFB is that it would suggest selection for increased female reproductive lifespan. However, the evidence is less clear when we compare the results on AFB to other female reproductive life-history traits such as the age at menarche (AAM) and age at menopause (AMP). In fact, we estimate that the genetic correlation with rLRS is positive for AAM (${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ = $0.133\pm 0.032(P<{10}^{-4.4})$) and negative for AMP (${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ = $-0.168\pm 0.045(P<{10}^{-3.7})$). The genetic result for AMP is particularly unexpected because it is inconsistent with both our phenotypic result (even though the phenotypic correlation is very small, 0.02) and a prior result obtained in a pedigree study (17). Further, we estimate that the genetic correlation between AAM and AFB is strongly positive despite the fact that signs of the ${\widehat{r}}_{g\text{,}\mathit{rLRS}}$ estimates for the two traits are opposite. We intuitively expect a positive relationship between AAM and AFB because the latter requires the former. However, the positive genetic correlation between rLRS and AAM is less explicable.

Estimation of the genetic evidence of nonlinear selection was not performed because of lack of statistical power. Theory predicts that the additive genetic variance for a squared phenotype is likely to be very small and, when present, is confounded with genetic control of phenotypic variability. In addition, the empirical heritability estimates for squared phenotypes are small (SI Appendix, Fig. S19). Despite the lack of power, a polygenic predictor for height, constructed from a meta-analysis of the Genetic Investigation of Anthropometric Traits (GIANT)–UKB joint dataset, did show a marginally significant negative quadratic regression coefficient in females (see SI Appendix for details).

Discussion

Estimates of linear and quadratic selection gradients were obtained via simple linear regression of a broad set of phenotypes onto a proxy for fitness. The results suggest that many traits measured in the UKB are under the influence of directional and stabilizing selection. However, many of the selection gradient estimates were not significant in a multiple-regression setting, implicating apparent selection (46). However, the population genetic architecture of a trait may still be modified by apparent selection.

For example, the direction of association between female EA and rLRS is positive in the multiple regression, which opposes results from our single-trait regressions, genetic correlation analyses, and multiple other published results (16, 25, 27, 48–50). Our findings lead to the prediction that variants with a positive effect on female EA would decrease in frequency over time even if variance in EA itself does not directly cause variance in reproductive success. Consistent with this prediction, recent work demonstrated that the mean polygenic score for EA has declined over time in the Icelandic population (27), but also suggest that this trend may be explained by factors like female AFB.

Consistent with previous studies, our results support a hypothesis of strong negative selection on female AFB (14–19, 51–54). We also observed a small but positive relationship between AMP in females and rLRS on the phenotypic level, which agrees with previous results (11, 14, 17, 54). However, we find support for a negative genetic relationship between rLRS and AMP. Further, both genetic and phenotypic data suggest a positive correlation between AAM and rLRS. Thus, it is unclear whether the total reproductive lifespan is positively or negatively correlated with rLRS in our data. As larger samples from diverse populations become available, we may gain a more clear view of the selective forces acting on reproductive traits in contemporary humans.

There is clear evidence for correlation between rLRS and several anthropometric traits. Our findings are consistent with previous reports of selection for increased BMI (17, 25). Additionally, the data suggest that the relationship between rLRS and height is more negative in females than in males, which agrees with other results in the literature (18, 24, 25).

Our estimates are conditional on survival to postreproductive ages, so the intensity of selection could be different for traits that strictly influence survival. Birth weight is a classic example of a trait under strong stabilizing selection, where high and low birth weights are correlated with reduced survival in both males and females (22). Yet we find no evidence for stabilizing selection on birth weight in males and only a mrginally significant estimate of $\widehat{\gamma }=-0.0057\pm 0.0019(P<{10}^{-2})$ in females.

There are a few other important caveats and limitations to our present analyses. All of our results are conditional on the suite of phenotypes that we have measured; there is a real possibility that there are unmeasured phenotypes that drive or confound some of our results. This issue is related to the phenomenon of apparent selection and should always be kept in mind when studying phenotypic selection (46). In addition, the genetic correlations are estimated using common SNP markers (minor allele frequency > 0.01), which may be a source of bias because the genetic variants with deleterious effects on fitness are likely to be rare and thus absent from our analyses. However, this should simply reduce the power of our analyses. Further, there is evidence that the population of the UKB may not be perfectly representative of the whole population of the United Kingdom (55). The potential ascertainment bias (heathy participant bias) in the UKB is important to consider and may have a quantitative effect on our estimates, but the bias is not likely to be large enough (55) to disrupt the conclusions of our work in a qualitative way.

The distributions of $\widehat{\beta }$ and $\widehat{\gamma }$ provide a useful context for considering the types and strengths of selective forces at play in contemporary human populations (44). These insights support ongoing efforts to use theoretical evolutionary models to understand the maintenance of heritable variation for complex traits in humans (5–9, 34–43). The estimates of $\beta$ and $\gamma$ are qualitatively consistent with estimates from other species (44), but the quantitative range is an order of magnitude smaller. However, the selection gradients from our study are estimated with much more precision than those in other species, where the sampling variance may have inflated the range of estimated coefficients. So, while the signal of selection appears to be statistically significant, we do not expect that selection can explain the observed secular trends in the phenotypes we studied.

Stabilizing selection appears to be the more common form of nonlinear selection. The most common model of stabilizing selection used in evolutionary quantitative genetics is the Gaussian stabilizing selection model (56). One of the most important parameters of the Gaussian stabilizing selection model is the inverse selection intensity normalized by the phenotypic variance, $\frac{V_S}{V_P}$. This ratio quantifies how fast fitness, modeled by a Gaussian function, decreases as a function of distance to the theoretical fitness optimum. $\frac{V_S}{V_P}$ can be estimated by the negative reciprocal of the quadratic selection gradient (46). Based on the first and third quartile values of $\widehat{\gamma }$, we estimate that a reasonable range for human phenotypes is $\frac{V_S}{V_P}\sim 28-173$ with a median of 65, which would be considered weak, but nontrivial in a theoretical context (9). Theoretical arguments suggest that a thorough characterization of the effects of stabilizing at the genetic level will require larger sample sizes and/or methods of interrogating nonadditive genetic variance to directly observe stabilizing selection acting on genetic variation in a population sample like the UKB.

We have shown the power of combining high-throughput molecular genetic data with extensive phenotyping to study the ongoing dynamics of human evolution (11). Our work supports further study of a dynamic moving-optimum model for the evolution of complex traits in humans. Presently, we do not know whether the genetic architectures of complex traits are commensurate with equilibrium models parameterized by their contemporary selection gradients. If they are not, further research is needed to better understand how contemporary evolutionary forces differ from the ones that shaped the genetic architecture of the trait.

Materials and Methods

Phenotypic and genetic data were obtained from the UKB and may be accessed by all bona fide researchers from the UKB Access Management System. Only data from samples of self-reported white-British ancestry over the ages of 45 y for females and 50 y for men were used in all analyses, unless otherwise noted. Phenotypic analyses were performed using linear regression in R (57). Genetic correlations were calculated using LD-score regression software according to the protocol developed in ref. 33. Statistical significance was determined using Bonferroni-corrected P values at a family-wise error rate of 0.05. The Northwest Multicentre Research Ethics Committee approved the study and all participants in the UKB study provided written informed consent. For detailed descriptions of the data preparation and analyses, see SI Appendix, Supporting Materials and Methods.