Structure of sexual networks determines the operation of sexual selection

Significance

Sexual selection is a powerful evolutionary force, but debate persists over its strength and quantification. We argue that current approaches ignore the structure of the sexual network. We capture this network structure with a metric we call “mating assortment” that precisely and exhaustively captures the indirect as well as direct relationship between a male’s promiscuity and that of his sexual partners. We show that mating assortment is highly variable in nature and use simulations to reveal that such variation plays a key—but so far unappreciated—role in determining the strength of sexual selection on males. Our results provide a clear and quantitative method for studying sexual selection in the many mating systems in which both polygyny and polyandry co-occur.

Abstract

Sexual selection is a fundamental evolutionary process but remains debated, particularly in the complexity of polyandrous populations where females mate with multiple males. This lack of resolution is partly because studies have largely ignored the structure of the sexual network, that is, the pattern of mate sharing. Here, we quantify what we call mating assortment with network analysis to specify explicitly the indirect as well as direct relationships between partners. We first review empirical studies, showing that mating assortment varies considerably in nature, due largely to basic properties of the sexual network (size and density) and partly to nonrandom patterns of mate sharing. We then use simulations to show how variation in mating assortment interacts with population-level polyandry to determine the strength of sexual selection on males. Controlling for average polyandry, positive mating assortment, arising when more polygynous males tend to mate with more polyandrous females, drastically decreases the intensity of precopulatory sexual selection on male mating success (Bateman gradient) and the covariance between male mating success and postcopulatory paternity share. Average polyandry independently weakened some measures of sexual selection and crucially also impacted sexual selection indirectly by constraining mating assortment through the saturation of the mating network. Mating assortment therefore represents a key—albeit overlooked—modulator of the strength of sexual selection. Our results show that jointly considering sexual network structure and average polyandry more precisely describes the strength of sexual selection.

Darwin suggested that male reproductive success is typically limited by competitive access to fertilization opportunities and that sexual selection drives the evolution of traits conferring an advantage in intrasexual competition (1). Darwin’s view of sexual selection on males was limited to competition over mating opportunities. The realization that, across many sexually reproducing taxa, females often mate with multiple males so that their ejaculates overlap at the time of fertilization (polyandry) (e.g., refs. 2 and 3), has revolutionized our understanding of sexual selection (4, 5). Polyandry extends sexual selection on males after mating (postcopulatory), via sperm competition (6) and cryptic female choice (7, 8), by generating variation in the proportion of a female’s eggs fertilized by her sexual partners (paternity share). Polyandry therefore adds complexity to the architecture of male reproductive success through variance in paternity share and covariance with precopulatory success: that is, the number of females mated (mating success) and their fecundity (9–14). This complexity directly affects the overall strength of sexual selection and the way different selective episodes target male traits (9, 10, 14–18). Integrating episodes of precopulatory and postcopulatory sexual selection represents a fundamental challenge for understanding the evolution of sexually selected traits and reproductive strategies (14, 18, 19).

A rapidly growing body of research has focused on the link between polyandry and the operation of sexual selection on males. This effort, however, has produced contradicting results. Some studies, often of species displaying low levels of polyandry, have suggested that increasing average polyandry may strengthen sexual selection on males, by allowing a subset of males to increase their reproductive success by mating with more females (20–23). For example, polyandry has been suggested to drive the evolution of exaggerated sexual ornaments with which males attract partners across (24, 25) and even within species of socially monogamous birds (refs. 23 and 26; see ref. 27). In contrast, other studies, often of more polyandrous species, have suggested that increasing average polyandry may in fact weaken sexual selection (10, 28). These studies predict that polyandry should reduce variance in male mating success and limit the potential strength of precopulatory sexual selection because the reproductive benefits of mating with additional females are reduced when paternity is shared among multiple males. Thus, polyandry may weaken the relationship between male mating success and reproductive success (i.e., the Bateman gradient), and thus erode precopulatory sexual selection on male mating success (4, 10, 11, 16).

Behavioral studies investigating the relationship between precopulatory male mating success and postcopulatory paternity share have yielded similarly inconsistent results (14). A positive relationship between a male’s mating success and his paternity share, which would be expected to reinforce sexual selection on male mating success (14), has been found in several species, including junglefowl, Gallus gallus, guppies, Poecila reticulata, and fruit flies, Drosophila melanogaster (10, 29–32). In other taxa, however, this relationship may be negative (33–35), indicating that precopulatory and postcopulatory episodes represent alternative pathways to male reproductive success, thereby creating opportunities for alternative male mating tactics. Finally, in other species, episodes of precopulatory and postcopulatory sexual selection are largely independent (17, 36, 37).

A potential reason underpinning these inconsistencies is that these studies have largely focused on the average level of polyandry in a population or group, ignoring the details of how polyandry varies among females and is distributed across males within a group. We call this quantitative structure of variation in polyandry among females and across males “mating assortment.” The crucial point is whether highly polygynous males tend to mate with more monogamous females (negative assortment) or with more polyandrous females (positive assortment). By describing the relationship between the polygyny of males and the polyandry of their sexual partners, mating assortment modulates the relationship between male mating success (precopulatory) and the intensity of sperm competition (postcopulatory), and thus can play a crucial role in determining variation in male reproductive success and the strength of precopulatory and postcopulatory sexual selection (32, 38–46). Consider, for example, a population where males that mate with many females also tend to mate with the most polyandrous females. This may result in those males with greatest mating success (i.e., most polygynous) suffering the highest intensity of sperm competition. Consider now the opposite scenario, where males with higher mating success experience less sperm competition because the females with whom they mate are less polyandryous. In the former scenario, positive mating assortment between male polygyny and female polyandry weakens the relationship between the mating success of a male and his reproductive success (Bateman gradient), thus reducing precopulatory sexual selection on male mating success. In the latter scenario, negative mating assortment increases the reproductive returns that a male derives by mating with additional females, thus strengthening precopulatory sexual selection (39, 41–43).

Here, we demonstrate that quantifying patterns of mating assortment is fundamental to assessing the impact of polyandry on male sexual selection. We first review the empirical literature to characterize variation in patterns of mating assortment across taxa. We then clarify how mating assortment and population-level polyandry interact to mold the operation of sexual selection on males. To do so, we adopt a network-based approach that represents sexually reproducing populations as a network of individuals (nodes) connected by links (copulations) (40, 41, 47–49). A unique property of network analysis is its ability to capture both direct and indirect relations between interacting entities (39, 50–53). By its very nature, mating assortment requires quantification of indirect as well as direct measures of sexual partnership. Only by considering indirect interactions can we capture the true interplay between the polygyny of a male and the polyandry of his partners. We use a recently developed sexual network metric of mating assortment, the sperm competition intensity correlation (SCIC) (43), and simple simulations to generate basic qualitative predictions. Crucially, our approach dissects the effect of assortative mating patterns on sexual selection independently of changes in population-level polyandry.

We show that (i) estimates of mating assortment vary widely across empirical studies of different organisms, (ii) variation in mating assortment directly affects the strength of sexual selection, and (iii) the effect of mating assortment on sexual selection is partly determined by how it interacts with average polyandry. We conclude that focusing exclusively on the average level of polyandry, without considering its interaction with mating assortment, does not accurately capture the impact of polyandry on sexual selection. Our explicit quantification of mating assortment provides a more integrative framework for understanding the impact of polyandry on sexual selection, and the evolution of, and variation in, sexually selected traits in nature.

Results

Empirical Patterns of Mating Assortment.

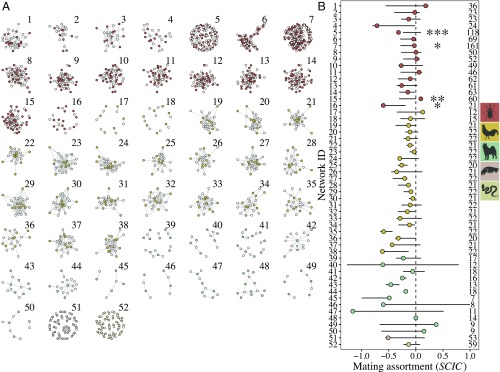
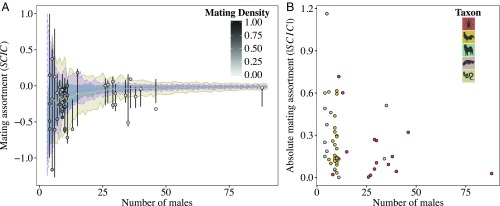
We built sexual networks (Fig. 1A) and calculated SCIC from empirical studies of freely mating groups in both natural and laboratory populations of a broad range of species (Table 1 and Materials and Methods). Mating assortment in these networks vary considerably, from positive to negative (Fig. 1B and Table 1). In most networks, the observed SCIC did not differ significantly from the null distribution of values generated from randomizations. This indicates that mating assortment can vary substantially even when mating between males and females occurs at random, given simple properties of the network such as network size (i.e., the number of male and female nodes), mating density (number of mating pairs/total number of possible mating pairs), and the variation in male and female mating success (Fig. 1B). Randomizations of smaller networks, that is, those with fewer males and females, had less continuous null distributions of SCIC values as a consequence of the limited number of possible permutations (SI Appendix, Fig. S1). Confirming previous theoretical predictions (43), our results show that for small networks both empirical estimates of SCIC and their respective null distributions tended to reach more extreme values (Fig. 2A and SI Appendix, Fig. S2). As networks become larger, empirical SCIC values, and their randomized null distributions, become less variable and absolute deviations from zero tend to decrease (Fig. 2 and SI Appendix, Fig. S2). This is because, in larger networks, SCIC estimates are impacted less by small random deviations in mating patterns, whereas, in small networks, relatively minor changes in the organization of matings between males and females can result in large changes in SCIC values (43). The size of networks varied across taxonomic groups, such that mammals tended to be represented by smaller groups, insects by the largest networks, and birds by intermediate-sized networks (Figs. 1A and 2B and Table 1).

Fig. 1.

Mating assortment (SCIC) varies considerably across empirical populations. (A) Visualizations of the 52 empirical sexual networks obtained from the literature. Nodes represent males and females and the links connect mating pairs. White nodes represent females, and colored nodes represent males. Colors designate the taxonomic group of the species of each sexual network (red, arthropods; yellow, birds; green, mammals; pink, molluscs; tan, reptiles). (B) Points show the observed values of sperm competition intensity correlation (SCIC) for 52 empirical sexual networks obtained from the literature. Colors designate the taxonomic group of the species of each sexual network (red, arthropods; yellow, birds; green, mammals; pink, molluscs; tan, reptiles). Estimates are ordered Top to Bottom by taxonomic group. Error bars represent the 95% range of SCIC values based on 1,000 randomizations of each empirical network. SCIC estimates significantly different from simulated null distributions are highlighted with asterisks (***P < 0.001, **P < 0.01, *P < 0.05). The estimate of network ID 5 remained significant after correcting for false-discovery rate using the Benjamini–Hochberg procedure. Numbers on Right of the plot represent total group size (n males + n females). Estimates were obtained from the following studies [sexual network number (reference)]: 1 (17), 2–4 (84), 5 (45), 6–7 (46), 8–15 (85), 16 (86), 17–18 (87), 19–38 (32), 39–40 (88), 41 (89), 42 (90), 43 (91), 44 (92), 45–47 (93), 48 (94), 49–50 (95), 51 (96), and 52 (97).

Table 1.

Levels of mating assortment (SCIC) and average polyandry estimated from empirical studies across different taxa

Taxonomic group	Mean SCIC (range)	Mean group size (range)	Mean polyandry (±SE)	Mean mating density (±SE)	No. of estimates (studies)	Species (alphabetical)	Refs. (chronological)
Arthropod	−0.143 (−0.717 to 0.182)	57.375 (21–161)	3.824 (0.295)	0.174 (0.025)	16 (6)	Aquarius remigis	17, 45, 46, 84–86
						Gryllus campestris, Laupala cerasina, Rhynchophorus ferrugineus, Serracutisoma proximum
Bird	−0.206 (−0.616 to 0.127)	20.682 (12–22)	5.16 (0.378)	0.544 (0.036)	22 (2)	Gallinago media, Gallus gallus	32, 87
Mammal	−0.294 (−1.163 to 0.375)	12.667 (7–18)	2.01 (0.303)	0.34 (0.027)	12 (8)	Alouatta caraya, Canis familiaris, Cryptoprocta ferox, Lemur catta, Macaca fascicularis, Mandrillus sphinx, Saimiri oestedi,	88–95
Mollusc	−0.511 (—)	53 (—)	2.111 (—)	0.06 (—)	1 (1)	Sepia apama	96
Reptile	−0.134 (—)	59 (—)	1.8 (—)	0.053 (—)	1 (1)	Agkistrodon contortrix	97

Mating assortment (Sperm competition intensity correlation; SCIC) calculated from 52 empirical sexual networks provided in 18 studies, grouped by taxon along with the population/group size, average polyandry, average mating density, species name and reference.

Fig. 2.

The relationship between empirical estimates of SCIC and mating density and the number of competing males. (A) Each point represents the relationship between the number of competing males and observed values of sperm competition intensity correlation (SCIC) for 52 empirical sexual networks obtained from the literature. The shading of points indicates mating density (number of mating pairs/number of possible mating pairs). Black vertical lines provide 95% range of simulated SCIC values based on 1,000 randomizations of each empirical network. Colored lines and shaded areas show the mean and 95% range of null expectations for SCIC from randomly mating populations with differing number of competing males at three mating densities (tan/solid, ∼0.25; pink/dashed, ∼0.5; blue/dotted, ∼0.75). Null expectations are generated from 100 randomly mating populations for each group size and density combination, where each population has an equal sex ratio. (B) The relationship between the absolute magnitude of SCIC values and the number of competing males for 52 empirical sexual networks obtained from the literature. Colors designate the taxonomic group of the species of each sexual network (red, arthropods; yellow, birds; green, mammals; pink, molluscs; tan, reptiles).

Importantly, while the majority of empirical SCIC values could be parsimoniously explained as random, given the observed variation in individual male and female mating success, network size, and mating density, in a minority of cases, SCIC values are more extreme than expected by chance (Fig. 1B). This suggests that mating assortment may in some cases arise through nonrandom mechanisms, for example, nonrandom spatial variation in mating rates or phenotypic preferences between individual partners. We next use a theoretical simulation approach to explore how such variation in SCIC values affects sexual selection under different levels of average polyandry.

Simulations.

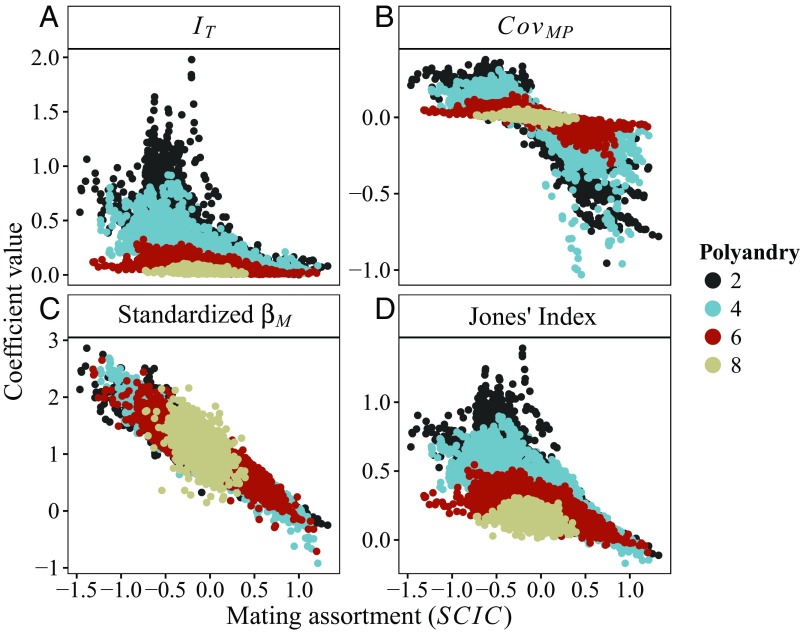
The average level of polyandry of a population had two distinct effects. First, increasing average polyandry tended to consistently reduce the absolute maximum value of all measures of sexual selection (Fig. 3). Second, increasing average polyandry resulted in a progressive contraction in the range of random SCIC variation, such that, at high polyandry, simulations were less likely to reach strongly positive or negative SCIC values due to a progressive saturation of the network (i.e., increasing mating density; Fig. 3 and SI Appendix, Fig. S3).

Fig. 3.

Mating assortment (SCIC) and average population polyandry combine to modulate the potential for sexual selection. Results for mating assortment simulations. Each point represents one simulated population. Plots show the relationship between mating assortment, measured as the sperm competition intensity correlations (SCIC), and four population level measures including (A) the opportunity for selection (I_T), (B) standardized covariance between male mating success and paternity share (COV_MP), (C) standardized male Bateman gradients (${\beta }_M$), and the (D) maximum precopulatory selection differential (Jones’ index). Colors show the average polyandry of populations. Polyandry levels of 2, 4, 6, and 8 correspond to mating densities (total number mating pairs/total number of possible mating pairs) of 0.2, 0.4, 0.6, and 0.8, respectively.

Independently of average polyandry, increasingly positive levels of mating assortment (SCIC) reduced total variation in male reproductive success (i.e., I_T; Fig. 3A and Table 2), and led to a more negative covariance between male mating success and paternity share (i.e., COV_MP; Fig. 3B and Table 2, using the Pearson’s correlation coefficient between M and P also yielded qualitatively similar results; SI Appendix, Fig. S4). Consequently, increasing SCIC also weakened precopulatory sexual selection, measured as male Bateman gradients (i.e., β_M). Instead, the effects of average polyandry on COV_MP and β_M when controlling for SCIC, were much weaker and close to zero (Fig. 3 B and C and Table 2). The weak effect of average polyandry on COV_MP and β_M is driven by a contraction in the range of absolute SCIC values: at low average polyandry, mating networks are relatively sparse, allowing for more negative assortments, while at higher average polyandry, networks become increasingly saturated producing less extreme negative assortments (SI Appendix, Fig. S3). Average polyandry and SCIC had similarly negative impacts on the maximum potential selection differential on precopulatory traits (i.e., Jones’ index; Fig. 3D and Table 2). The strong reductive effect of average polyandry on the Jones’ index was driven largely by the reduction in the standardized variation in male mating success with increasing polyandry (i.e., opportunity for sexual selection, I_s; Materials and Methods and SI Appendix, Fig. S5), whereas the effect of SCIC on all measures remained strong after controlling for variation in male mating success (SI Appendix, Fig. S6). Finally, increasing average polyandry interacted with SCIC such that, at higher mating densities, the effect of SCIC on all measures was reduced. High levels of polyandry therefore reduced the impact of mating assortment on patterns of selection.

Table 2.

The effect of mating assortment (SCIC) and average polyandry on measures of sexual selection

Parameter	IT	COVMP	βM	Jones’ index
SCIC	−0.560 (0.003)	−0.084 (0.001)	−0.409 (0.002)	−0.111 (0.001)
Average polyandry	−0.701 (0.016)	0.012 (0.001)	0.010 (0.003)	−0.108 (0.004)
SCIC*Average polyandry	0.071 (0.004)	0.072 (0.001)	0.032 (0.002)	0.055 (0.001)

Linear mixed model results for the effects of population-level average polyandry and sperm competition intensity correlation (SCIC) on the opportunity for selection (I_T), the standardized covariance between mating success and paternity share (COV_MP), mean-standardized Bateman gradients (${\beta }_M$), and the maximum precopulatory selection differential (Jones’ index). Fixed effects are scaled to have a mean of zero and SD of 1 and so are comparable within models. Effects are shown with SEs in brackets; all main effects and interactions were significant at the <0.001 level.

We confirmed the generality of these results using complementary simulations, where (i) SCIC was variance-standardized rather than mean-standardized (i.e., where T and M were standardized to have a mean of zero and SD of 1; equal to the correlation coefficient between T and M, 43), (ii) females produce only one ovum, and (iii) using larger populations (100 males and 100 females) with the same range average of polyandry and, separately, with corresponding mating densities. All of these complementary simulations produced qualitatively similar results (SI Appendix, Figs. S7–S10), confirming that the roles of mating assortment and average polyandry in male sexual selection are broadly robust to variation in SCIC variance, female fecundity, and population size.

Discussion

In polyandrous populations, males must compete for fertilization both before and after mating. Polyandry is thus expected to be a strong modulator of the strength of precopulatory and postcopulatory sexual selection on males (4, 9–12, 15, 17, 36). Nevertheless, understanding sexual selection in polyandrous populations and the interplay between precopulatory and postcopulatory episodes of selection has remained incomplete because we lack a quantitative metric for the relationship between male mating success and the polyandry of female partners (38–43). We have utilized a method to link the polygyny of males and the polyandry of their partners (mating assortment) based on a network approach that provides the requisite quantification of both direct and indirect effects.

Here, we present a survey of mating assortment across empirical studies of freely mating groups of different organisms. To measure mating assortment, we used a recently proposed measure called the SCIC (43). Our survey shows that SCIC is highly variable and ranges from positive to negative across species and populations. Assortative mating patterns may arise through both stochastic processes in randomly mating populations and as emergent properties of nonrandom mating due to individual strategies and ecological factors (32, 43–46, 54, 55). We used randomizations to generate null expectations of SCIC arising in a group as a simple consequence of random mating given a certain network structure (group size, average polyandry, and variation in individual mating success). We show that much of the variation in mating assortment is consistent with such null expectations and can be explained by such simple properties of the network (e.g. strongly negative SCIC is driven by the skew in male mating success). Importantly, however, our randomizations suggest that, even under conditions of random mating, stochastic variation in mating assortment can generate nondirectional biases in estimates of sexual selection, particularly when groups are small, as is often the case in detailed studies of mating behaviors. However, we also show that, in some cases, SCIC values may be more extreme than null expectations, suggesting potential for nonrandom patterns of assortative mating where the most successful (i.e., highly polygynous) males mate with the most (or least) polyandrous females, more than expected by chance.

Several behavioral mechanisms may drive nonrandom mating assortment. For example, in Soay sheep (Ovis aries), dominant rams with high mating success (M) can exclude subdominant males from mating with high-quality females, resulting in many less successful males (with low M) mating with a shared subset of relatively few females (56). This is predicted to generate strongly negative patterns of mating assortment (most polygynous males paired with least polyandrous females). Generally, positive covariances between male mating success and mate guarding ability may drive negative assortment (44). Females may also actively drive assortative patterns. For example, if mate discrimination and resistance to mating are costly, only high-quality females may be able to mate with a small number of highly successful, preferred males. In contrast, low-quality females may not be able to discriminate, leading to high polyandry linked to the low polygyny of the less successful males. Positive assortment may arise when trade-offs result in a negative relationship between a male’s ability to mate guard and his mating success. For example, in many species characterized by low-level polyandry, those polygynous males who travel to mate with other females, may themselves lose paternity to polygynous competitors (57). As we have demonstrated, positive assortment erodes the benefits of male mating success and negates precopulatory sexual selection on males (41, 58). Similarly, local variation in environmental conditions, group size, densities, or phenotypic variation may drive local variation in polyandry and the intensity of sperm competition and ultimately population-level patterns of SCIC (14, 59–62). For example, local variation in density may result in some highly polygynandrous groups and other less dense, more monogamous groups, and positive mating assortment may arise at the population level (60, 61). Therefore, both random and nonrandom mechanisms are likely to generate range of mating structures in natural populations.

We used simulations to disentangle the effect of average polyandry and mating assortment on the operation of sexual selection. Our simulations confirm previous suggestions that average polyandry has a direct effect on sexual selection on males, largely by negating the strength of precopulatory sexual selection (10, 12). Importantly, these simulations also reveal a critical role of mating assortment independent of polyandry: for any given level of polyandry, a negatively assorted mating network, with high polygyny linked to low polyandry, reinforces selection on male mating success (i.e., Bateman gradients). Steeper Bateman gradients arise as a consequence of an increased positive covariance between male mating success (M) and paternity share (P, i.e., COV_MP), which in turn contributes to the covariance between mating success and male reproductive success (T, i.e., COV_MT). Average polyandry is often predicted to reduce sexual selection on male M by diminishing the correlation between M and P (16). Our results stress that these effects may be obscured or reversed by differences in mating assortment across populations and therefore have key implications for studies of sexual selection across groups and populations that vary in mating assortment (39). Importantly, while this is of most interest to populations with nonrandom mating assortment, variation in assortment may obscure the effects of average polyandry on sexual selection even in randomly mating populations where mating assortment is determined by stochastic processes.

Thus, for any given level of average polyandry and variation in male mating success (opportunity for sexual selection; I_s), mating assortment is a key additional parameter of mating systems that can shape sexual selection on males. Moreover, our simulations indicate that the role of mating assortment is indirectly modulated by the average polyandry of a population. As average polyandry increases, the mating network becomes increasingly saturated, limiting the range of possible mating assortment and thus reducing the scope for SCIC to influence variation in male reproductive success.

More broadly, our results shed light on the utility of the Bateman gradient as an indicator of sexual selection on males. A recent study identified the Bateman gradient as a relatively poor indicator of sexual selection on males (63) and advocated the Jones’ index as a better indicator of the strength of sexual selection (63). Our results suggest that the Bateman gradient and the Jones’ index provide complementary information. Bateman gradients are typically standardized by dividing both T and M by their respective means (64–68). The slope of a mean standardized Bateman gradient of 1 can be interpreted as follows: “a 100% increase in relative mating success results in a 100% increment in relative reproductive success” (64, 66, 68). In contrast, the Jones’ index, which represents the maximum potential selection differential on a trait predicting male mating success (63, 65), is equivalent to a variance-standardized Bateman gradient (i.e., M is standardized by subtracting its mean and dividing by its SD). The Jones’ index thus measures selection on M in units of SDs (64, 66, 68, 69). By measuring the strength of selection on mating success in isolation from changes in variation in male mating success, the mean-standardized Bateman gradient reveals that increasing the average polyandry of a population alone does not necessarily change the functional relationship between male M and T. Instead, our results demonstrate that mating assortment is a key modulator of this relationship. In comparison, the Jones’ index reveals how the reduced variation in male M, associated with high mating densities (high polyandry), combines with increasing SCIC to accentuate the reduction in the potential strength of precopulatory selection on male traits. These results should be useful in interpreting and reconciling the findings of previous studies that used either variance- (10, 70) or mean-standardized Bateman gradients (65, 71). Taken together, both measures (i.e., Bateman gradient and Jones’ index) provide a fuller understanding of how polyandry shapes sexual selection on males and consideration of SCIC clarifies the complementarity of Bateman gradients and the Jones’ index.

Our simulations are necessarily a deliberate simplification of nature, where male reproductive success is often determined by the complex interaction of multiple factors, and polyandry can dynamically feed back into male strategies (72, 73). For example, our simulations do not incorporate variation in male fertilization efficiency or sperm limitation, which may affect paternity distributions for any given pattern of assortative mating (15, 74, 75). Nor did we consider that male ejaculate expenditure and female polyandry can dynamically affect each other (19), and will modulate male differential investment in precopulatory versus postcopulatory competition. Importantly, mating assortment may interact with such postcopulatory processes to mediate the scope for sexual conflict. For example, if highly polygynous males are constrained in their ejaculate expenditure and thereby unable to fertilize all of the ova of their female partners (76), negative mating assortment may accentuate variation in female fertility. Supporting this prediction, in feral fowl (Gallus domesticus), dominant old males provide fewer and lower-quality ejaculates to female partners but are able to exclude other male competitors from mating, compromising the fertility of females in the group (77).

Taken together, these empirical and simulation results provide predictions about sexual selection in polyandrous populations. As networks become increasingly more saturated, we expect average polyandry to become a key driver of sexual selection through its direct effect on variance in male reproductive success and indirect effects via mating assortment. All else being equal, small populations and groups might be more vulnerable to saturation, because a certain level of average polyandry is more likely to saturate the network than in larger populations. In larger populations, on the other hand, mating densities will likely be relatively low because the absolute number of possible mating pairs increases multiplicatively with the number of males and females. Larger populations may therefore offer more opportunities for different mating structures and more potential for nonrandom patterns of mating assortment. These results therefore generate helpful null expectations concerning the influence of mating assortment and average polyandry on sexual selection. These expectations should help reconcile previous empirical studies suggesting diverse effects of polyandry on male Bateman gradients and the covariance between precopulatory and postcopulatory episodes of sexual selection (14). For example, predictions that increasing average polyandry should strengthen sexual selection on males often arise from studies of species displaying low levels of polyandry, such as socially monogamous birds (20–23). Our results suggest that an increase might in principle be observed in some measures of sexual selection (e.g., I_T) when modest increments in average polyandry (i.e., from low to intermediate) are associated with negative SCIC (i.e., more polygynous males are better able to prevent female polyandry). Further increments in average polyandry in these populations may increasingly saturate the network, ultimately increasing the polyandry of most females, and resulting in a less negative SCIC. Indications that average polyandry may weaken sexual selection on males often come from studies of highly polyandrous populations (10, 28). As we show, high polyandry constrains variation in SCIC, and increments in average polyandry under such conditions are likely to weaken sexual selection and further limit the relative role of SCIC. Future empirical work should seek to explore these predictions.

Mating assortment patterns may also contribute to explain variation in ornament exaggeration and sexual dimorphism. All else being equal, we might expect that, for a given level of average polyandry, populations that are consistently negatively assorted might evolve more exaggerated male ornaments than positively assorted populations. One should be cautious, however, about predicting evolutionary responses based on contemporary patterns of mating assortment because mating assortment is likely to change dynamically across multiple breeding seasons and generations. Future studies should investigate socioecological parameters underpinning these temporal dynamics and characterize their impact on sexual selection. Doing so will help us understand the way assortative mating patterns influence contemporary evolutionary change and ultimately patterns of exaggeration of precopulatory and postcopulatory traits. A crucial next step will be to understand how patterns of mating assortment relate to variation in male reproductive success and patterns of sexual selection in nature. A particularly interesting focus will be to understand how different sperm competition mechanisms (e.g., fair versus loaded raffles; ref. 75) and variation in male traits generate deviations from the qualitative expectations set out here and whether mating patterns themselves have stronger role in different systems.

Future work should also seek to understand how local differences in environmental conditions, population densities, group size, and phenotypic variation may drive local variation in polyandry and the intensity of sperm competition (59–61), and how these in turn translate into mating assortment at the population level. Recent studies have argued that a key goal in sexual selection research is to understand how the social and environmental variation within and across populations shape covariances between precopulatory and postcopulatory episodes of sexual selection (14). Our results highlight that understanding how such socioecological variation shapes assortative mating patterns in nature will form an important component of this goal. As fine-grain data on mating behavior become more readily available, an important aspect of this pursuit will be to investigate and compare the link between social and sexual organization across taxa, from invertebrates to primates (61, 62, 78). Information on patterns of mating assortment and underpinning social drivers may also help evolutionary and epidemiological studies of human societies (e.g., refs. 79 and 80).

In conclusion, the present study helps to clarify ongoing debate on the role of polyandry in sexual selection (16, 38–40, 44–46). We demonstrate that mating assortment varies widely across populations and that such variation, together with population-level average polyandry, dictates the potential for sexual selection on males (9, 16, 38). Collectively, our results reveal that mating assortment constitutes a potentially key facet of mating systems, which modifies the postcopulatory competitive landscape and can drive variation in the operation of sexual selection across populations.

Materials and Methods

Calculating SCIC, Polyandry, and Mating Density.

SCIC measures the relationship between a male’s mating success (M) and the mating success of his partners [i.e., his partners’ polyandry (43)]. To estimate SCIC, we first calculate each male’s “sperm competition intensity” (SCI) as the harmonic mean mating success of each female mated with a given male [i.e., the average polyandry of this male’s partners (16, 43, 44); note that this index includes the focal male within the polyandry of his partners]. The SCIC is then measured as the least-squares regression of male SCI against male mating success (M) [where both parameters are standardized at the population level by their respective means (43)]. Negative values of SCIC describe a tendency for males with high mating success to mate with females with few mating partners. Positive values describe a positive correlation between a male’s mating success and the mating success of his female partners. Only those individuals that copulated are included in network measures.

We calculated average polyandry as the mean number of unique mating partners across copulating females. The mating density of networks was calculated as the total number mating pairs divided by total number of possible mating pairs. For any given population, increasing polyandry will always result in an increase in density. However, similar levels of polyandry will result in differing mating densities across populations with different numbers of males and females (i.e., network size). For example, in a population with eight males and eight females, an average polyandry of 4 corresponds to a density of 0.5 (i.e., 50% of all possible pairs of males and females mate). However, in a population of 16 males and 16 females, average polyandry of 4 corresponds to a mating density of 0.25.

Empirical Review.

To obtain measures of SCIC from empirical studies in the literature, we conducted multiple searches on Web of Science (wok.mimas.ac.uk). We were interested in studies that published data of behavioral observations, providing information on which males copulated with which females so we could construct the relevant sexual networks. Because our focus was on sperm competition, whenever information allowed it, we considered females that mated with multiple males within a period that—given the reproductive biology of the species—could result in sperm competition (SI Appendix, Table S1). If a study contained multiple datasets (i.e., multiple discreet social units and/or multiple breeding seasons), we considered each separate individual dataset in our analysis.

Our first search used the TOPIC field and contained the following search terms (“Bateman* gradient*”) OR (“Bateman* slope*”) OR (“Bateman* principle*”) OR (“opportunit* for selection”) OR (“opportunit* for sexual selection”) on February 14, 2017. This resulted in 440 records. We chose these search terms as studies calculating Bateman gradients and variation in mating success were thought likely to have data on individual mating patterns. Of these, we excluded records based on the title and/or abstract that indicated the study would not provide appropriate data. A small number of papers were not available to the authors. Other studies were excluded if they omitted the required information in the manuscript, supporting material, or on associated data repository websites (e.g., Dryad). Furthermore, we excluded datasets with trivial group sizes of up to only two males and/or females, or where males and females were not allowed to freely interact and copulate (i.e., enforced sequential monogamy) and where there was no variation in male mating success. Similarly, we excluded those studies in which mating success was only inferred from molecular parentage. This is because any mating patterns based on molecular parentage exclude males that mate but never sire any offspring (especially so in species with low fecundity). Thus, the observed mating patterns may likely represent the result of sperm competitive processes rather than male sperm competitive environments per se (43, 70). This resulted in only two papers that provided raw male and female behavioral pairings that fit our criteria.

Our second search followed the same procedure as above using the search terms (sexual network* OR social network*) AND (sexual selection OR mating system). This search returned 58 records, of which three papers provided data that fit our criteria. Our third search contained the terms (mating* or copulat*) AND (behavio*) AND (observ*), restricting our search to the journals Animal Behavior, Behavioral Ecology, and Behavioral Ecology and Sociobiology. This returned 697 records of which six studies provided appropriate datasets.

We complemented these searches with additional datasets obtained via references in other papers, any datasets already known to the authors from previous searches and through ad hoc searches in relation to mating patterns and sexual behavior via Google. We excluded one study in which all females were monogamous with the exception of one female who remated with another male only after her current mate was killed by the study. A second study in which most females were monogamous was eliminated because it was hard to distinguish between copulations and copulation attempts. This selection process generated 52 datasets across 18 studies (SI Appendix, Table S1). The final data do not therefore reflect an exhaustive review of mating patterns across the animal kingdom, being limited by (i) taxonomic bias, (ii) a tendency to rely on genetic parentage assignment as a proxy for mating success rather than behavioral observations, and (iii) limited availability of raw data of male–female combinations.

For each dataset, we then estimated SCIC as above, average polyandry, and mating density. We include mating density as a comparable measure of the levels of polyandry and polygyny in a group as empirical networks vary in both the number of males and females. Importantly, populations are likely to show nonzero values of SCIC by chance (43). We therefore investigated the extent to which empirical estimates of SCIC may be driven by nonrandom patterns of assortative mating using randomizations of each empirical network to generate null expectations for SCIC for each network. Specifically, we generated a null distribution of mating structures (SCIC) for each empirical mating network using an approach that randomly shuffles copulating pairs of males and females in the network, maintaining the mating density of the network, and therefore average polyandry, constant within each population (81). Furthermore, this approach also holds constant the variation in male and female mating success [i.e., the opportunity for sexual selection $\left(I_s={\sigma }_M^2/{\overline{M}}^2\right)$ for both males and females (65)]. This approach thus allows us to assess whether observed values of SCIC were more or less than would be expected by chance under random mating, given the observed variation in male and female mating success, network size, and average polyandry. If observed SCIC values are not more extreme than can be expected by chance given these constraints, this would suggest that an explanation beyond these more basic properties of the network need not be invoked when accounting for observed SCIC values. Using this randomization approach, we generated 1,000 randomized versions of each of the 52 networks, resulting in 52,000 randomized networks. Importantly, while this approach allows us to ask whether empirical values of SCIC are more or less extreme than may be expected in a randomly mating population with a given basic structure, we are not able consider the individual details of each dataset. These details may include, for example, whether all individuals overlapped in time. Therefore, in some cases, randomizations may generate pairings not possible in nature. With this is mind, our approach can establish whether given mating patterns are particularly extreme given key aspects of the empirical sexual network, and inspection of methodologies in each published study suggests that such improbable pairings may only represent a minority of the data collected.

All randomizations and analyses were carried out using R statistical software (82).

Simulations.

To assess the effects of mating assortment on sexual selection, we first generated artificial populations with 10 males and 10 females. For each population, we fixed the average polyandry so that females mated with two, four, six, or eight males on average. To achieve this, we randomly selected male and female pairs to copulate with each other, ensuring a set number of male–female pairs copulated. In all cases, each pair copulated once, and all individuals had at least one mating partner. Because populations were fixed to 10 males and 10 females, these four levels of polyandry correspond to mating densities (total number mating pairs/total number of possible mating pairs) of 0.2, 0.4, 0.6, and 0.8, respectively. In total, we generated 100 populations for each level of average polyandry (i.e., average population polyandry, 2, 4, 6, and 8; totaling 400 populations). We then generated a range of mating structures by conducting randomizations of each of our 400 simulated populations so that we either increased or decreased the correlation between a male’s mating success and the mating success of his female partners. This was achieved by randomly selecting two copulating pairs within a population and swapping mating partners between these mating pairs. We did this in a stepwise fashion for each population by making one pairwise swap at a time, retaining each newly assorted population for analysis. We repeated this process for each population in two directions, either by continuously increasing positive assortment one swap at a time or by continuously increasing negative assortment one swap at a time, until we could no longer increase or decrease the correlation between male and female mating success (i.e., no swap could be made that increased or decreased mating assortment after 25,000 attempts). This approach holds both average polyandry and variation in male and female mating success [i.e., the opportunity for sexual selection ($I_s$)] constant across each randomization of a given population. This process resulted in a broad spectrum of mating patterns for each level of average polyandry (SI Appendix, Fig. S3). We then simulated sperm competition for every population, where each female produced 100 ova and all males that mate with a female have a probability of fertilizing an ovum proportional to the number of males mating with that female [e.g., if four males mated with a female, each male has 25% chance of fertilizing each ovum (19)].

For each male in each population, we then calculated his reproductive success (T) as the number of ova fertilized, his mating success (M) as the number of unique females he mated with, and his paternity share (P) as the proportion of his partners’ ova that he fertilized. We then measured the relationship between a male’s mating success (M) and the mating success of his partners (i.e., his partners’ polyandry) using the SCIC (43).

We assessed the effects of SCIC on sexual selection on males, using linear mixed models across all simulated populations (totaling 9,558 populations). Response variables in models were (i) the standardized variation in reproductive success (opportunity for selection; $I_T={\sigma }_T^2/{\overline{T}}^2$); (ii) the standardized covariance between male mating success and male paternity share (COV_MP), which represents the contribution of the covariance between M and P to variation in male reproductive success; (iii) standardized male Bateman gradients calculated as the slope of male reproductive success on male mating success where both are standardized by their respective means (β_M; also denoted β_ss); and (iv) the maximum potential precopulatory selection differential (i.e., the Jones’ index) (9, 65). The Jones’ index quantifies the maximum potential strength of precopulatory sexual selection (through M) on a male trait as the product of standardized Bateman gradient and the opportunity for sexual selection on male mating success (i.e., ${\beta }_M\sqrt{I_s}={\beta }_M\sqrt{{\sigma }_M^2/{\overline{M}}^2}$) and has recently been identified as useful proxy measure for precopulatory sexual selection on phenotypic traits (63). Note that $\sqrt{I_s}$ is equal to the coefficient of variation in male mating success ($C{V}_M$) and so the Jones’ index is equal to the variance-standardized Bateman gradient (${\beta }_M^{\sigma }$), where M is standardized to have a mean of 0 and SD of 1 (i.e., ${\beta }_M^{\sigma }={\beta }_{M}C{V}_M={\beta }_M\sqrt{{\sigma }_M^2/{\overline{M}}^2}$). Fixed effects in all models included SCIC, the average polyandry of the population, and their interaction. The identity of the original random mating population was included as a random effect. Statistical significance of interaction terms was assessed using likelihood ratio tests to compare a model with the interaction to a model with only main effects. Statistical significance of main effects was assessed using likelihood ratio tests to compare a model with both main effects to model with the focal main effect removed. The opportunity for selection (I_T) was log-transformed to meet model assumptions. We scaled explanatory variables by subtracting the mean and dividing it by its SD to facilitate comparisons between the effect of average polyandry and SCIC within models. All simulations and statistical analyses were carried out using R statistical software (82) and mixed-effects models using lme4 (83). Data used in this study are provided as Datasets S1 and S2.