Toward a unified theory of efficient, predictive, and sparse coding

Significance

Sensory neural circuits are thought to efficiently encode incoming signals. Several mathematical theories of neural coding formalize this notion, but it is unclear how these theories relate to each other and whether they are even fully consistent. Here we develop a unified framework that encompasses and extends previous proposals. We highlight key tradeoffs faced by sensory neurons; we show that trading off future prediction against efficiently encoding past inputs generates qualitatively different predictions for neural responses to natural visual stimulation. Our approach is a promising first step toward theoretically explaining the observed diversity of neural responses.

Abstract

A central goal in theoretical neuroscience is to predict the response properties of sensory neurons from first principles. To this end, “efficient coding” posits that sensory neurons encode maximal information about their inputs given internal constraints. There exist, however, many variants of efficient coding (e.g., redundancy reduction, different formulations of predictive coding, robust coding, sparse coding, etc.), differing in their regimes of applicability, in the relevance of signals to be encoded, and in the choice of constraints. It is unclear how these types of efficient coding relate or what is expected when different coding objectives are combined. Here we present a unified framework that encompasses previously proposed efficient coding models and extends to unique regimes. We show that optimizing neural responses to encode predictive information can lead them to either correlate or decorrelate their inputs, depending on the stimulus statistics; in contrast, at low noise, efficiently encoding the past always predicts decorrelation. Later, we investigate coding of naturalistic movies and show that qualitatively different types of visual motion tuning and levels of response sparsity are predicted, depending on whether the objective is to recover the past or predict the future. Our approach promises a way to explain the observed diversity of sensory neural responses, as due to multiple functional goals and constraints fulfilled by different cell types and/or circuits.

Sensory neural circuits perform a myriad of computations, which allow us to make sense of and interact with our environment. For example, neurons in the primary visual cortex encode information about local edges in an image, while neurons in higher-level areas encode more complex features, such as textures or faces. A central aim of sensory neuroscience is to develop a mathematical theory to explain the purpose and nature of such computations and ultimately, predict neural responses to stimuli from first principles.

The influential “efficient coding” theory posits that sensory circuits encode maximal information about their inputs given internal constraints, such as metabolic costs and/or noise (1–4); similar ideas have recently been applied in genetic and signaling networks (5, 6). While conceptually simple, this theory has been extremely successful in predicting a host of different neural response properties from first principles. Despite these successes, however, there is often confusion in the literature, due to a lack of consensus on (i) what sensory information is relevant (and thus, should be encoded) and (ii) the internal constraints (determining what information can be encoded).

One area of potential confusion is between different ideas of why and how neural networks may need to make predictions. For example, given low noise, efficient coding predicts that neurons should remove statistical dependencies in their inputs so as to achieve nonredundant, statistically independent responses (3, 4, 7–9). This can be implemented within a recurrent network where neurons encode a prediction error equal to the difference between their received inputs and an internally generated expectation, hence performing “predictive coding” (10–13). However, Bialek and coworkers (14, 15) recently proposed an alternative theory, in which neurons are hypothesized to preferentially encode sensory information that can be used to predict the future, while discarding other nonpredictive information (14–17). While both theories assume that neural networks make predictions, they are not equivalent: one describes how neurons should compress incoming signals, and the other describes how neurons should selectively encode only predictive signals. Signal compression requires encoding surprising stimuli not predicted by past inputs; these are not generally the same as predictive stimuli, which are informative about the future (16).

Another type of code that has been studied extensively is “sparse coding”: a population code in which a relatively small number of neurons are active at any one time (18). While there are various reasons why a sparse code may be advantageous (19–21), previous work has shown that sparse coding emerges naturally as a consequence of efficient coding of natural sensory signals with a sparse latent structure (i.e., generated by combining many sensory features, few of which are present at any one time) (22). Sparse coding has been successful in predicting many aspects of sensory neural responses (23, 24), notably the orientation and motion selectivity of neurons in the primary visual cortex (25–29). Nonetheless, it is unclear how sparse coding is affected by other coding objectives, such as efficiently predicting the future from past inputs.

An attempt to categorize the diverse types of efficient coding is presented in SI Appendix, Efficient Coding Models. To consistently organize and compare these different ideas, we present a unifying framework based on the information bottleneck (IB) (30). In our work, a small set of optimization parameters determines the goals and constraints faced by sensory neurons. Previous theories correspond to specific values of these parameters. We investigate the conditions under which different coding objectives have conflicting or synergistic effects on neural responses and explore qualitatively unique coding regimes.

Efficient Coding with Varying Objectives/Constraints

We consider a temporal stimulus, $x_{-\mathrm{\infty }:t}\equiv (\dots ,x_{t-1},x_t)$, which elicits neural responses, $r_{-\mathrm{\infty }:t}\equiv (\dots ,r_{t-1},r_t)$. We seek a neural code described by the probability distribution $p(r_t|x_{-\mathrm{\infty }:t})$, such that neural responses within a temporal window of length $\tau$ encode maximal information about the stimulus at lag $\mathrm{\Delta }$ given fixed information about past inputs (Fig. 1A). This problem can be formalized using the IB framework (30–32) by seeking a code, $p(r_t|x_{-\mathrm{\infty }:t})$, that maximizes the objective function:

$$L_{p(r_t|x_{-\mathrm{\infty }:t})}=I(R_{t-\tau :t};X_{t+\mathrm{\Delta }})-\gamma I(R_t;X_{-\mathrm{\infty }:t}),$$ [1]

where the first term (to be maximized) is the mutual information between the responses between $t-\tau$ and $\tau$ and the stimulus at time $t+\mathrm{\Delta }$, while the second term (to be constrained) is the mutual information between the response at time $t$ and past inputs (which we call the coding capacity, $C$). A constant, $\gamma$, controls the tradeoff between coding fidelity and compression. This objective function can be expanded as

$$L_{p(r_t|x_{-\mathrm{\infty }:t})}={⟨\log p(x_{t+\mathrm{\Delta }}|r_{t-\tau :t})-\log p\left(x_{t+\mathrm{\Delta }}\right)-\gamma \log p(r_t|x_{t-\mathrm{\infty }:t})+\gamma \log p\left(r_t\right)⟩}_{p(r,x)}.$$ [2]

Previously, we showed that, in cases where it is not possible to compute this objective function directly, one can use approximations of $p(x_{t+\mathrm{\Delta }}|r_{t-\tau :t})$ and $p(r_t)$ to obtain a lower bound, $\stackrel{\sim }{L}\le L$, that can be maximized tractably (31) (SI Appendix,General Framework).

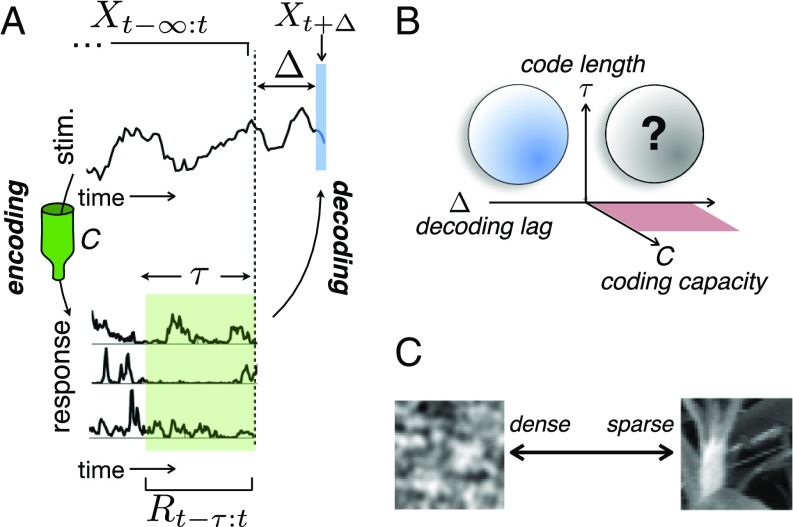
Fig. 1.

Schematic of modeling framework. (A) A stimulus (stim.) (Upper) elicits a response in a population of neurons (Lower). We look for codes where the responses within a time window of length $\tau$ maximize information encoded about the stimulus at lag $\mathrm{\Delta }$, subject to a constraint on the information about past inputs, $C$. (B) For a given stimulus, the optimal code depends on three parameters: $\tau$, $\mathrm{\Delta }$, and $C$. Previous work on efficient temporal coding generally looked at $\tau >\mathrm{\hspace{0.17em}0}$ and $\mathrm{\Delta }<0$ (blue sphere). Recent work posited that neurons encode maximal information about the future ($\mathrm{\Delta }>0$) but only treated instantaneous codes $\tau \sim \mathrm{\hspace{0.17em}0}$ (red plane). Our theory is valid in all regimes, but we focus in particular on $\mathrm{\Delta }>0$ and $\tau >\mathrm{\hspace{0.17em}0}$ (black sphere). (C) We further explore how optimal codes change when there is a sparse latent structure in the stimulus (natural image patch; Right) vs. when there is none (filtered noise; Left).

From Eqs. 1 and 2, we see that the optimal coding strategy depends on three factors: the decoding lag, $\mathrm{\Delta }$; the code length, $\tau$; and the coding capacity, $C$ (determined by $\gamma$). Previous theories of neural coding correspond to specific regions within the 3D parameter space spanned by $\mathrm{\Delta }$, $\tau$, and $C$ (Fig. 1B). For example, temporal redundancy reduction (3, 33) occurs (i) at low internal noise (i.e., high $C$), (ii) where the objective is to encode the recent past ($\mathrm{\Delta }<0$), and (iii) where information about the stimulus can be read out by integrating neural responses over time ($\tau \gg 0$). Increasing the internal noise (i.e., decreasing $C$) results in a temporally redundant “robust” code (34–37) (blue sphere in Fig. 1B). Recent work positing that neurons efficiently encode information about the future ($\mathrm{\Delta }>0$) looked exclusively at near-instantaneous codes, where $\tau \sim 0$ (red plane in Fig. 1B) (15, 38–40). Here, we investigate the relation between these previous works and focus on the (previously unexplored) case of neural codes that are both predictive ($\mathrm{\Delta }>0$) and temporal ($\tau >\mathrm{\hspace{0.17em}0}$) and have varying signal to noise (variable $C$) (black sphere in Fig. 1B).

To specialize our theory to the biologically relevant case, we later investigate efficient coding of natural stimuli. A hallmark of natural stimuli is their sparse latent structure (18, 22, 25, 26): stimulus fragments can be constructed from a set of primitive features (e.g., image contours), each of which occurs rarely (Fig. 1C). Previous work showed that, in consequence, redundancy between neural responses is minimized by maximizing their sparsity (SI Appendix, Efficient Coding Models) (22). Here, we investigated what happens when the objective is not to minimize redundancy but rather, to efficiently predict future stimuli given finite coding capacity.

Results

Dependence of Neural Code on Coding Objectives.

Our initial goal was to understand the influence of different coding objectives in the simplest scenario, where a single neuron linearly encodes a 1-d input. In this model, the neural response at time $t$ is $r_t={\sum }_{k==0}^{{\tau }_w}{w}_k{x}_{t-k}+{\eta }_t$, where $w=(w_0,\dots ,w_{{\tau }_w})$ are the linear coding weights and ${\eta }_t$ is a Gaussian noise with unit variance.^∗

With 1-d stimuli that have Gaussian statistics, the IB objective function takes a very simple form:

$$L=-\frac{1}{2}\log ⟨{\left(x_{t+\mathrm{\Delta }}-\sum _{k=0}^{\tau }{u}_k{r}_{t-k}\right)}^2⟩-\gamma \frac{1}{2}\log ⟨r_t^2⟩,$$ [3]

where $u=(u_0,\dots ,u_{\tau })$ are the optimal linear readout weights used to reconstruct the stimulus at time $t+\mathrm{\Delta }$ from the responses between $t-\tau$ and $t$. Thus, the optimal code is the one that minimizes the mean-squared reconstruction error at lag $\mathrm{\Delta }$, constrained by the variance of the neural response (relative to the noise variance).^†

Initially, we investigated “instantaneous” codes, where $\tau =\mathrm{\hspace{0.17em}0}$, so that the stimulus at time $t+\mathrm{\Delta }$ is estimated from the instantaneous neural response at time $t$ (Fig. 2A). We considered three different stimulus types, which are shown in Fig. 2B. With a “Markov” stimulus (Fig. 2B, Top and SI Appendix, Methods for Simulations in the Main Text), with a future trajectory that depended solely on the current state, $x_t$, the neurons only needed to encode $x_t$ to predict the stimulus at a future time, $x_{t+\mathrm{\Delta }}$. Thus, when $\tau =\mathrm{\hspace{0.17em}0}$, we observed the trivial solution where $r_t\propto x_t$, irrespective of the decoding lag, $\mathrm{\Delta }$ (Fig. 2 C and D and SI Appendix, Fig. S2A).

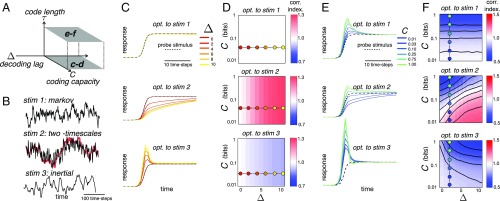
Fig. 2.

Dependence of optimal code on decoding lag, $\mathrm{\Delta }$; code length, $\tau$; and coding capacity, $C$. (A) We investigated two types of code: instantaneous codes, where $\tau =\mathrm{\hspace{0.17em}0}$ (C and D), and temporal codes, where $\tau >\mathrm{\hspace{0.17em}0}$ (E and F). (B) Training stimuli (stim.) used in our simulations. Markov stimulus: future only depends on the present state. Two-timescale stimulus: sum of two Markov processes that vary over different timescales (slow stimulus component is shown in red). Inertial stimulus: future depends on present position and velocity. (C) Neural responses to probe stimulus (dashed lines) after optimization (opt.) with varying $\mathrm{\Delta }$ and $\tau =\mathrm{\hspace{0.17em}0}$. Responses are normalized by the final steady-state value. (D) Correlation (corr.) index after optimization with varying $\mathrm{\Delta }$ and $C$. This index measures the correlation between responses at adjacent time steps normalized by the stimulus correlation at adjacent time steps (i.e., $⟨r_t{r}_{t+1}⟩/⟨r_t^2⟩$ divided by $⟨x_t{x}_{t+1}⟩/⟨x_t^2⟩$). Values greater/less than one indicate that neurons temporally correlate (red)/decorrelate (blue) their input. Filled circles show the parameter values used in C. (E and F) Same as C and D but with code optimized for $\tau \gg 0$. Plots in E correspond to responses to probe stimulus (dashed lines) at varying coding capacity and fixed decoding lag (i.e., $\mathrm{\Delta }=3$; indicated by dashed lines in F).

With a “two-timescale” stimulus constructed from two Markov processes that vary over different timescales (Fig. 2B, Middle), the optimal solution was a low-pass filter to selectively encode the predictive, slowly varying part of the stimulus. The strength of the low-pass filter increased monotonically with $\mathrm{\Delta }$ (Fig. 2 C and D and SI Appendix, Fig. S2A).

Finally, with an “inertial” stimulus, with a future trajectory that depended on both the previous state, $x_t$, and velocity, $x_t-x_{t-1}$ (Fig. 2B, Bottom), the optimal solution was a high-pass filter so as to encode information about velocity. The strength of this high-pass filter also increased monotonically with $\mathrm{\Delta }$ (Fig. 2 C and D and SI Appendix, Fig. S2A, Bottom).

With an instantaneous code, varying the coding capacity, $C$, only rescales responses (relative to the noise amplitude) so as to alter their signal-to-noise ratio. However, the response shape is left unchanged (regardless of the stimulus statistics) (Fig. 2D). In contrast, with temporally extended codes, where $\tau >\mathrm{\hspace{0.17em}0}$ (so the stimulus at time $t+\mathrm{\Delta }$ is estimated from the integrated responses between time $t-\tau$ and $t$) (Fig. 2A), the optimal neural code varies with the coding capacity, $C$. As with previous efficient coding models, at high $C$ (i.e., high signal-to-noise ratio), neurons always decorrelated their input, regardless of both the stimulus statistics and the decoding lag, $\mathrm{\Delta }$ (to achieve nonredundant responses) (SI Appendix, Efficient Coding Models), while decreasing $C$ always led to more correlated responses (to achieve a robust code) (SI Appendix, Efficient Coding Models) (36). However, unlike previous efficient coding models at low to intermediate values of $C$ (i.e., intermediate to low signal-to-noise ratio), the optimal code was qualitatively altered by varying the decoding lag, $\mathrm{\Delta }$. With the Markov stimulus, increasing $\mathrm{\Delta }$ had no effect; with the two-timescale stimulus, it led to low-pass filtering, and with the inertial stimulus, it led to stronger high-pass filtering.

Taken together, “phase diagrams” for optimal, temporally extended codes show how regimes of decorrelation/whitening (high-pass filtering) and of smoothing (low-pass filtering) are preferred depending on the coding capacity, $C$, and decoding lag, $\mathrm{\Delta }$. We verified that a qualitatively similar transition from low- to high-pass filtering is also observed with higher dimensional stimuli and/or more neurons. Importantly, we show that these phase diagrams depend in an essential way on the stimulus statistics already in the linear Gaussian case. We next examined what happens for non-Gaussian, high-dimensional stimuli.

Efficient Coding of Naturalistic Stimuli.

Natural stimuli exhibit a strongly non-Gaussian statistical structure, which is essential for human perception (22, 41). A large body of work has investigated how neurons could efficiently represent such stimuli by encoding their nonredundant or independent components (4). Under fairly general conditions (e.g., that stimuli have a sparse latent structure), this is equivalent to finding a sparse code: a form of neural population code, in which only small fractions of neurons are active at any one time (22). For natural images, this leads to neurons that are selective for spatially localized image contours, with receptive fields (RFs) that are qualitatively similar to the RFs of V1 simple cells (25, 26). For natural movies, this leads to neurons selective for a particular motion direction, again similar to observations in area V1 (27).

However, an independent (sparse) temporal code has only been shown to be optimal (i) when the goal is to maximize information about past inputs (i.e., $\mathrm{\Delta }<0$) and (ii) at low noise (i.e., at high capacity; $C\gg 0$). We were interested, therefore, in what happens when these two criteria are violated: for example, when neural responses are optimized to encode predictive information (i.e., for $\mathrm{\Delta }\ge 0$).

To explore these questions, we modified the objective function of Eq. 3 to deal with multidimensional stimuli and non-Gaussian statistics of natural images (SI Appendix, General Framework). Specifically, we generalized the second term of Eq. 3 to allow optimization of the neural code with respect to higher-order (i.e., beyond covariance) response statistics. This was done by approximating the response distribution $p(r)$ by a Student t distribution, with shape parameter, $\nu$, learned directly from data (SI Appendix, Eq. S5) (31). Crucially, our modification permits—but does not enforce by hand—sparse neural responses (42). For nonsparse, Gaussian stimuli, the IB algorithm returns $\nu \to \mathrm{\infty }$, so that the Student t distribution is equivalent to a Gaussian distribution, and we obtain the results of the previous section; for natural image sequences, it replicates previous sparse coding results in the limit $\mathrm{\Delta }<0$ and $C\gg \mathrm{\hspace{0.17em}0}$ (SI Appendix, Fig. S5), without introducing any tunable parameters.

We investigated how the optimal neural code for naturalistic stimuli varied with the decoding lag, $\mathrm{\Delta }$, while keeping coding capacity, $C$, and code length, $\tau$, constant. Stimuli were constructed from 10 $\times$ 10-pixel patches drifting stochastically across static natural images (Fig. 3A, SI Appendix, Methods for Simulations in the Main Text, and SI Appendix, Fig. S3). Gaussian white noise was added to these inputs (but not the decoded variable, $X_{t+\mathrm{\Delta }}$) (SI Appendix, Methods for Simulations in the Main Text). Neural encoding weights were optimized with two different decoding lags: for $\mathrm{\Delta }=-6$, the goal was to encode past stimuli, while for $\mathrm{\Delta }=1$, the goal was to predict the near future. Fig. 3B confirms that the codes indeed are optimal for recovering either the past ($\mathrm{\Delta }=-6$) or future ($\mathrm{\Delta }=1$) as desired.

Fig. 3.

Efficient coding of naturalistic stimuli. (A) Movies were constructed from a 10 $\times$ 10-pixel patch (red square), which drifted stochastically across static natural images. (B) Information encoded [i.e., reconstruction (recon.) quality] by neural responses about the stimulus at varying lag (i.e., reconstruction lag) after optimization with $\mathrm{\Delta }=-6$ (blue) and $\mathrm{\Delta }=1$ (red). (C) Spatiotemporal encoding filters for four example neurons after optimization with $\mathrm{\Delta }=-6$. (D) Same as C for $\mathrm{\Delta }=1$. (E) Directionality index of neural responses after optimization with $\mathrm{\Delta }=-6$ and $\mathrm{\Delta }=1$. The directionality index measures the percentage change in response to a grating stimulus moving in a neuron’s preferred direction vs. the same stimulus moving in the opposite direction.

After optimization at both values of $\mathrm{\Delta }$, individual neurons were selective to local oriented edge features (Fig. 3 C and D) (25). Varying $\mathrm{\Delta }$ qualitatively altered the temporal features encoded by each neuron, while having little effect on their spatial selectivity. Consistent with previous results on sparse temporal coding (27), with $\mathrm{\Delta }=-6$, single cells were responsive to stimuli moving in a preferred direction as evidenced by spatially displaced encoding filters at different times (Fig. 3C and SI Appendix, Fig. S6 A–C) and a high “directionality index” (Fig. 3E). In contrast, with $\mathrm{\Delta }=1$, cells responded equally to stimuli moving in either direction perpendicular to their encoded stimulus orientation. This was evidenced by spatiotemporally separable RFs (SI Appendix, Fig. S6 D–F) and directionality indexes near zero. This qualitative difference between the two types of code for naturalistic movies was highly surprising, and we sought to understand its origins.

Tradeoff Between Sparsity and Predictive Power.

To gain an intuitive understanding of how the optimal code varies with decoding lag, $\mathrm{\Delta }$, we constructed artificial stimuli from overlapping Gaussian bumps, which drifted stochastically along a single spatial dimension (Fig. 4A and SI Appendix, Methods for Simulations in the Main Text). While simple, this stimulus captured two key aspects of the naturalistic movies. First, Gaussian bumps drifted smoothly in space, resembling stochastic global motion over the image patches; second, the stimulus had a sparse latent structure.

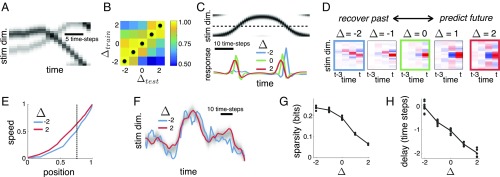
Fig. 4.

Efficient coding of a “Gaussian-bump” stimulus. (A) Stimuli (stim.) consisted of Gaussian bumps that drifted stochastically along a single spatial dimension (dim.) (with circular boundary conditions). (B) Information encoded by neural responses about the stimulus at varying lag, ${\mathrm{\Delta }}_{\mathrm{test}}$, after optimization with varying ${\mathrm{\Delta }}_{\mathrm{train}}$. Black dots indicate the maximum for each column. (C) Response of example neuron to a test stimulus (Upper) and after optimization with $\mathrm{\Delta }=-2$ (blue), $\mathrm{\Delta }=0$ (green), and $\mathrm{\Delta }=2$ (red; Lower). (D) Spatiotemporal encoding filters for an example neuron after optimization with different $\mathrm{\Delta }$. (E) Circular correlation between the reconstructed speed of a moving Gaussian blob and its true speed vs. the circular correlation between the reconstructed position and its true position obtained from neural responses optimized with $\mathrm{\Delta }=\pm 2$ (red and blue curves). Curves were obtained by varying $\gamma$ in Eq. 3 to find codes with different coding capacities. (F) Linear reconstruction of the stimulus trajectory obtained from neural responses optimized with $\mathrm{\Delta }=\pm 2$ (red and blue curves). The full stimulus is shown in grayscale. While coding capacity was chosen to equalize the mean reconstruction error for both models (vertical dashed line in E), the reconstructed trajectory was much smoother after optimization with $\mathrm{\Delta }=2$ than with $\mathrm{\Delta }=-2$. (G) Response sparsity (defined as the negentropy of neural responses) vs. $\mathrm{\Delta }$ (dots indicate individual neurons; the line indicates population average). (H) Delay between stimulus presented at a neuron’s preferred location and each neuron’s maximum response vs. $\mathrm{\Delta }$.

We optimized the neural code with $\mathrm{\Delta }$ ranging from $-2$ to $2$, holding the coding capacity, $C$, and code length, $\tau$, constant. Fig. 4B confirms that highest performance was achieved when the reconstruction performance was evaluated at the same lag for which each model was trained. This simpler setup recapitulated the surprising result that we obtained with naturalistic stimuli: namely, when $\mathrm{\Delta }<0$, neurons were selective to a single preferred motion direction, while when $\mathrm{\Delta }\ge 0$, neurons responded equally to stimuli moving from either direction to their RF (Fig. 4 C and D).

Predicting the future state of the stimulus requires estimating its current motion direction and speed. How is it possible then that optimizing the code for predictions ($\mathrm{\Delta }>0$) results in neurons being unselective to motion direction? This paradox is resolved by realizing that it is the information encoded by the entire neural population that counts, not the information encoded by individual neurons. Indeed, when we looked at the information encoded by the neural population, we did find what we had originally expected: when optimized with $\mathrm{\Delta }>0$, the neural population as a whole encoded significantly more information about the stimulus velocity than its position (relative to when $\mathrm{\Delta }<0$), despite the fact that individual neurons were unselective to motion direction (Fig. 4 E and F).

The change in coding strategy that is observed as one goes from encoding the past ($\mathrm{\Delta }<0$) to the future ($\mathrm{\Delta }>\mathrm{\hspace{0.17em}0}$) is in part due to a tradeoff between maintaining a sparse code and cells responding quickly to stimuli within their RF. Intuitively, to maintain highly selective (and thus, sparse) responses, neurons first have to wait to process and recognize the “complete” stimulus feature; unavoidably, however, this entails a processing delay, which leads to poor predictions. This can be seen in Fig. 4 G and H, which shows how both the response sparsity and delay to stimuli within a cell’s RF decrease with $\mathrm{\Delta }$. In SI Appendix, Supplementary Simulations, we describe in detail why this tradeoff between efficiency and prediction leads to direction-selective filters when $\mathrm{\Delta }<0$ but not when $\mathrm{\Delta }>0$ (SI Appendix, Fig. S7).

Beyond the effects on the optimal code of various factors explored in detail in this paper, our framework further generalizes previous efficient and sparse coding results to factors listed in SI Appendix, Table S1 and discussed in SI Appendix, Supplementary Simulations. For example, decreasing the capacity, $C$ (while holding $\mathrm{\Delta }$ constant at $-2$), resulted in neurons being unselective to stimulus motion (SI Appendix, Fig. S8A), with a similar result observed for increased input noise (SI Appendix, Fig. S8B). Thus, far from being generic, traditional sparse temporal coding, in which neurons responded to local motion, was only observed in a specific regime (i.e., $\mathrm{\Delta }<0$, $C\gg 0$, and low input noise).

Discussion

Efficient coding has long been considered a central principle for understanding early sensory representations (1, 3), with well-understood implications and generalizations (23, 37). It has been successful in predicting many aspects of neural responses in early sensory areas directly from the low-order statistics of natural stimuli (7, 22, 32, 43, 44) and has even been extended to higher-order statistics and central processing (45, 46). However, a criticism of the standard theory is that it treats all sensory information as equal, despite empirical evidence that neural systems prioritize behaviorally relevant (and not just statistically likely) stimuli (47). To overcome this limitation, Bialek and coworkers (14, 15) proposed a modification to the standard efficient coding theory, positing that neural systems are set up to efficiently encode information about the future given fixed information about the past. This is motivated by the fact that stimuli are only useful for performing actions when they are predictive about the future.

The implications of such a coding objective have remained relatively unexplored. Existing work only considered the highly restrictive scenario where neurons maximize information encoded in their instantaneous responses (15, 38, 40). In this case (and subject to some additional assumptions, such as Gaussian stimulus statistics and instantaneous encoding filters), predictive coding is formally equivalent to slow feature analysis (39). This is the exact opposite of standard efficient coding models, which (at low noise/high capacity) predict that neurons should temporally decorrelate their inputs (3, 33).

We developed a framework to clarify the relation between different versions of the efficient coding theory (14, 30, 31). We investigated what happens when the neural code is optimized to efficiently predict the future (i.e., $\mathrm{\Delta }>0$ and $\tau >\mathrm{\hspace{0.17em}0}$) (Fig. 1B). In this case, the optimal code depends critically on the coding capacity (i.e., signal-to-noise ratio), which describes how much information the neurons can encode about their input. At high capacity (i.e., low noise), neurons always temporally decorrelate their input. At finite capacity (i.e., mid to high noise), however, the optimal neural code varies qualitatively depending on whether the goal is to efficiently predict the future or reconstruct the past.

When we investigated efficient coding of naturalistic stimuli, we found solutions that are qualitatively different from known sparse coding results, in which individual neurons are tuned to directional motion of local edge features (27). In contrast, we found that neurons optimized to encode the future are selective for motion speed but not direction (Fig. 3 and SI Appendix, Fig. S6). Surprisingly, however, the neural population as a whole encodes motion even more accurately in this case (Fig. 4E). We show that these changes are due to an implicit tradeoff between maintaining a sparse code and responding quickly to stimuli within each cell’s RF (Fig. 4 G and H).

It is notable that, in our simulations, strikingly different conclusions are reached by analyzing single-neuron responses vs. the population responses. Specifically, looking only at single-neuron responses would lead one to conclude that, when optimized for predictions, neurons did not encode motion direction; looking at the neural population responses reveals that the opposite is true. This illustrates the importance of population-level analyses of neural data and how, in many cases, single-neuron responses can give a false impression of which information is represented by the population.

A major challenge in sensory neuroscience is to derive the observed cell-type diversity in sensory areas from a normative theory. For example, in visual area V1, one observes a range of different cell types, some of which have spatiotemporally separable RFs and others do not (48, 49). The question arises, therefore, whether the difference between cell types emerges because different subnetworks fulfill qualitatively different functional goals. One hypothesis, suggested by our work, is that cells with separable RFs have evolved to efficiently encode the future, while cells with nonseparable RFs evolved to efficiently encode the past. More generally, the same hypothesis could explain the existence of multiple cell types in the mammalian retina, with each cell type implementing an optimal code for a particular choice of optimization parameters (e.g., coding capacity or prediction lag).

Testing such hypotheses rigorously against quantitative data would require us to generalize our work to nonlinear encoding and decoding models (SI Appendix, Table S1). Here, we focused on a linear decoder to lay a solid theoretical foundation and permit direct comparison with previous sparse and robust coding models, which also assumed a linear decoder (25–27, 35, 36). In addition, a linear decoder forces our algorithm to find a neural code for which information can be easily extracted by downstream neurons performing biologically plausible operations. While the linearity assumptions simplify our analysis, the framework can easily accommodate nonlinear encoding and decoding. For example, we previously used a “kernel” encoding model, where neural responses are described by a nonparametric and nonlinear function of the input (31). Others have similarly used a deep convolutional neural network as an encoder (50).

As mentioned earlier, predictive coding has been used to describe several different approaches. Clarifying the relationship between inequivalent definitions of predictive coding and linking them mathematically to coding efficiency provided one of the initial motivations for our work. In past work, alternative coding theories are often expressed using very different mathematical frameworks, impeding comparison between them and sometimes leading to confusion. In contrast, by using a single mathematical framework to compare different theories—efficient, sparse, and predictive coding—we were able see exactly how they relate to each other, the circumstances under which they make opposing or similar predictions, and what happens when they are combined.