Weyl–Kondo semimetal in heavy-fermion systems

Significance

While electronic states with nontrivial topology have traditionally been known in insulators, they have been evidenced in metals during the past 2 years. Such Weyl semimetals show topological protection while conducting electricity both in the bulk and on the surface. An outstanding question is whether topological protection can happen in metals with strong correlations. Here, we report theoretical work on a strongly correlated lattice model to demonstrate the emergence of a Weyl–Kondo semimetal. We identify Weyl fermions in the bulk and Fermi arcs on the surface, both of which are associated with the many-body phenomenon called the Kondo effect. We determine a key signature of this Weyl–Kondo semimetal, which is realized in a recently discovered heavy-fermion compound.

Abstract

Insulating states can be topologically nontrivial, a well-established notion that is exemplified by the quantum Hall effect and topological insulators. By contrast, topological metals have not been experimentally evidenced until recently. In systems with strong correlations, they have yet to be identified. Heavy-fermion semimetals are a prototype of strongly correlated systems and, given their strong spin-orbit coupling, present a natural setting to make progress. Here, we advance a Weyl–Kondo semimetal phase in a periodic Anderson model on a noncentrosymmetric lattice. The quasiparticles near the Weyl nodes develop out of the Kondo effect, as do the surface states that feature Fermi arcs. We determine the key signatures of this phase, which are realized in the heavy-fermion semimetal Ce₃Bi₄Pd₃. Our findings provide the much-needed theoretical foundation for the experimental search of topological metals with strong correlations and open up an avenue for systematic studies of such quantum phases that naturally entangle multiple degrees of freedom.

Strongly correlated electrons represent a vibrant field that continues to expand its horizon. In heavy-fermion systems, strong correlations make their ground states highly tunable and give rise to a rich phase diagram that features antiferromagnetic order, Kondo-screened, and other paramagnetic phases, and beyond-Landau quantum-phase transitions (1, 2). In the simplest cases, these systems can be considered in terms of the local moments originating from the $f$ electrons that Kondo couple to the spins of the conduction electrons. The interaction generates the Kondo spin-singlet ground state; the ensuing entanglement with the conduction electrons converts the local moments into quasiparticles that can hybridize with the conduction electrons. This leads to a metal with a large, strongly renormalized effective carrier mass, which is the hallmark of the heavy-fermion system classification. The resulting state could be a heavy-fermion metal or a Kondo insulator, depending on whether the chemical potential lies within or falls between the hybridized bands (3–5). Electronically intermediate between the two cases are heavy-fermion semimetals (6–13). Several of these have a broken inversion symmetry, including CeRu₄Sn₆ (6, 7) and Ce₃Bi₄Pd₃ (9).

Semimetal systems are being theoretically studied in the noninteracting limit with spin-orbit coupling, which plays an essential role in obtaining topological phases of electronic matter (14–17). The Weyl semimetal in three dimensions (3D) was recently evidenced experimentally (18–20). It possesses bulk excitations in the form of chiral fermions, with massless relativistic dispersions near pairs of nodal points in the momentum space, as well as surface states in the form of Fermi arcs (21–24). Because both the bulk and surface states are gapless, one can expect that the Weyl semimetals are particularly susceptible to the influence of electron correlations. Moreover, strong correlations in nonperturbative regimes typically mix different degrees of freedom in generating low-energy physics; thus, in any strongly correlated Weyl semimetal, the low-energy electronic excitations are expected to involve degrees of freedom such as spin moments, which may be harnessed for such purposes as information storage and retrieval.

In this work, we report the discovery of a Weyl–Kondo semimetal (WKSM) phase in a concrete microscopic model on a 3D noncentrosymmetric lattice. This model contains the strongly correlated $4f$ electrons and a band of conduction $spd$ electrons, respectively. It is realistic in that it captures the inversion-symmetry breaking and spin-orbital coupling in a tunable way. In the regime where the electron–electron repulsion is much larger than the width of the conduction-electron band, the interaction-induced renormalization factor can be very large. In addition, because the inversion-symmetry breaking term, spin-orbit coupling, and other electronic couplings are renormalized in very different ways, it is a priori unclear whether any Weyl state can be realized in a robust way. Our work advances an affirmative answer in this well-defined microscopic model. Moreover, we demonstrate the key signatures of the WKSM phase, which turn out to be realized in several heavy-fermion compounds.

The Hamiltonian for the periodic Anderson model to be studied is

$$H=H_d+H_{cd}+H_c.$$ [1]

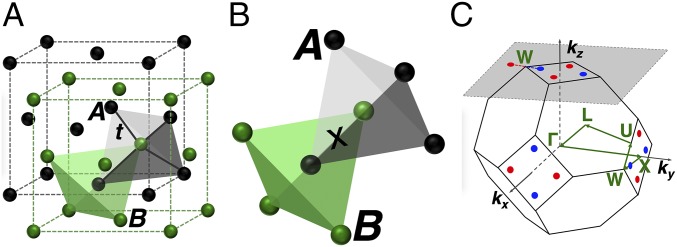
For a proof-of-concept demonstration, we consider a cubic system in which the breaking of inversion symmetry can be readily incorporated. This is a diamond lattice, which comprises two interpenetrating face-centered cubic lattices A and B (Fig. 1A). We choose this lattice because it is nonsymmorphic, and, in the case of noninteracting electrons, band touching is enforced by its space-group symmetry (25). The model contains $d$ and $c$ electrons, corresponding to the physical $4f$ and $spd$ electrons, respectively. The first term, $H_d$, describes the $d$ electrons with an energy level $E_d$ and a Coulomb repulsion $U$. The coupling between the two species of electrons is described by a bare hybridization of strength $V$. The conduction-electron Hamiltonian $H_c$ realizes a modified Fu–Kane–Mele model (26). Each unit cell has four species of conduction electrons, denoted by sublattices $A$ and $B$ and physical spins $\uparrow$ and $\downarrow$: ${\mathrm{\Psi }}_{\text{𝐤}}^T=\left(\begin{array}{cccc}\hfill c_{\text{𝐤}\uparrow ,A}\hfill & \hfill c_{\text{𝐤}\uparrow ,B}\hfill & \hfill c_{\text{𝐤}\downarrow ,A}\hfill & \hfill c_{\text{𝐤}\downarrow ,B}\hfill \end{array}\right)$. There is a nearest-neighbor hopping $t$ (chosen as our energy unit) and a Dresselhaus-type spin-orbit coupling of strength $\lambda$. The broken inversion symmetry, Fig. 1B, is captured by an onsite potential $m$ that staggers between the A and B sublattices (17, 27). The band basis is arrived at by applying a canonical transformation on $H_c$ written in the sublattice and spin basis. It corresponds to a pseudospin basis (27), defined by the eigenstates $|\pm D⟩$. We fix the $d$-electron level to below the conduction-electron band and consider the case of a quarter filling, corresponding to one electron per site. Further details of the model are given in Materials and Methods.

Fig. 1.

The 3D noncentrosymmetric lattice and associated Brillouin zone (BZ). (A) Diamond lattice with hopping $t$ and onsite energy $\pm m$ differentiating $A,B$ sublattices. The solid lines connect nearest neighbors. (B) Interlocking tetrahedral sublattice cells illustrating how the distinction between the A and B sublattices (zincblende structure) invalidates the inversion center lying on the point marked “X.” (C) The BZ of the diamond lattice, with Weyl nodes shown in blue/red and high symmetry contour used for Fig. 2 in green.

We consider the regime with the onsite interaction $U$ being large compared with the bare $c$-electron bandwidth ($U/t\to \mathrm{\infty }$). We approach the prohibition of $d$ fermion double occupancy by an auxiliary-particle method (28): $d_{i\sigma }^{†}=f_{i\sigma }^{†}{b}_i$. Here, the $f_{i\sigma }^{†}$ ($b_i$) are fermionic (bosonic) operators, which satisfy a constraint that is enforced by a Lagrange multiplier $\mathrm{\ell }$. This approach leads to a set of saddle-point equations, where $b_i$ condenses to a value $r$, which yields an effective hybridization between the $f$ quasiparticles and the conduction $c$ electrons. The details of the method are described in Materials and Methods.

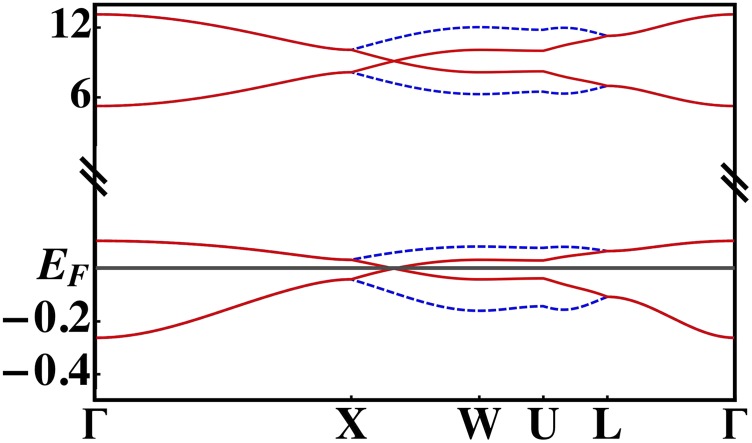
The corresponding quasiparticle band structure is shown in Fig. 2. Nodal points exist at the Fermi energy, in the bands for which the pseudospin (defined earlier) has an eigenvalue $-D$. They occur at the wave vectors ${\text{𝐤}}_W$, determined in terms of the hybridized bands,

$${\mathcal{E}}_{-D}^{(+,+)}({\text{𝐤}}_W)={\mathcal{E}}_{-D}^{(-,+)}({\text{𝐤}}_W),{\mathcal{E}}_{-D}^{(+,-)}({\text{𝐤}}_W)={\mathcal{E}}_{-D}^{(-,-)}({\text{𝐤}}_W),$$ [2]

for the upper and lower branches, respectively. The Weyl nodes appear along the Z lines (lines connecting the X and W points) in the three planes of the BZ, as illustrated in Fig. 1C. This is specific to the zincblende lattice. For other types of lattices, the Weyl nodes may occur away from the high-symmetry parts of the BZ.

Fig. 2.

Energy dispersion of the bulk electronic states. Shown here is the energy vs. wave vector k along a high-symmetry path in the BZ, defined in Fig. 1C. The bottom four bands near $E_F$ show a strong reduction in the bandwidth. The bare parameters are $(t,\lambda ,m,E_d,V)=(1,0.5,1,-6,6.6)$. In the self-consistent solution, $r\simeq 0.259$ and $\mathrm{\ell }\simeq 6.334$.

We note that the bands near the Fermi energy have a width much reduced from the noninteracting value. This width is given by the Kondo energy. Compared with the bare width of the conduction-electron band, the reduction factor corresponds to $r^2$ (which is $\sim$0.067 in the specific case shown in Fig. 2). We remark that, in the absence of the hybridization between the $f$ and conduction electrons, the ground state would be an insulator instead of a semimetal: The $f$ electrons would be half-filled and form a Mott insulator, while the conduction electrons would be empty, forming a band insulator. All these imply that the nodal excitations develop out of the Kondo effect.

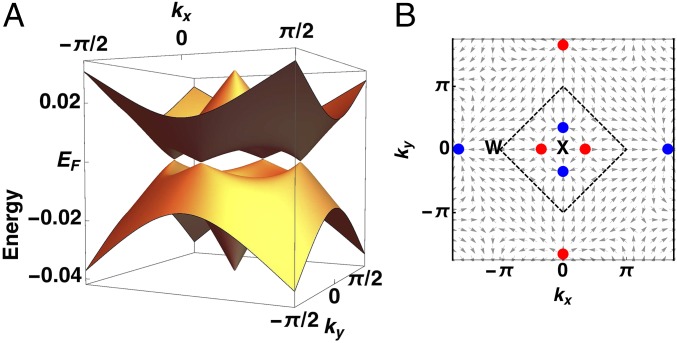
To demonstrate the monopole flux structure of the Weyl nodes, we calculate the Berry curvature in the strong coupling regime. We show the results at the ${\text{𝐤}}_z=\mathrm{\hspace{0.17em}2}\pi$ boundary of the 3D BZ, in the gray plane of Fig. 1C, whose dispersion is shown in Fig. 3B. In Fig. 3B, the arrows represent the field’s unit-length 2D projection onto the ${\text{𝐤}}_x{\text{𝐤}}_y$-plane, $\widehat{\mathrm{\Omega }}({\text{𝐤}}_x,{\text{𝐤}}_y,2\pi )={|\overrightarrow{\mathrm{\Omega }}({\text{𝐤}}_x,{\text{𝐤}}_y,2\pi )|}^{-1}\left(\begin{array}{c}\hfill {\mathrm{\Omega }}_{yz}({\text{𝐤}}_x,{\text{𝐤}}_y,2\pi ),{\mathrm{\Omega }}_{zx}({\text{𝐤}}_x,{\text{𝐤}}_y,2\pi )\hfill \end{array}\right)$. The Weyl node locations (blue/red circles) are clearly indicated by the arrows flowing in or out, representing negative or positive monopole “charge.”

Fig. 3.

Characterization of the Weyl nodes. The plots are in the $({\text{𝐤}}_x,{\text{𝐤}}_y)$ plane of the four Weyl nodes at ${\text{𝐤}}_z=\mathrm{\hspace{0.17em}2}\pi$ (gray plane in Fig. 1C). (A) Energy dispersion, showing the band degeneracies at the Weyl node points and a strong reduction of the bandwidth. (B) The distribution of the Berry curvature field. The bare parameters are the same as in Fig. 2.

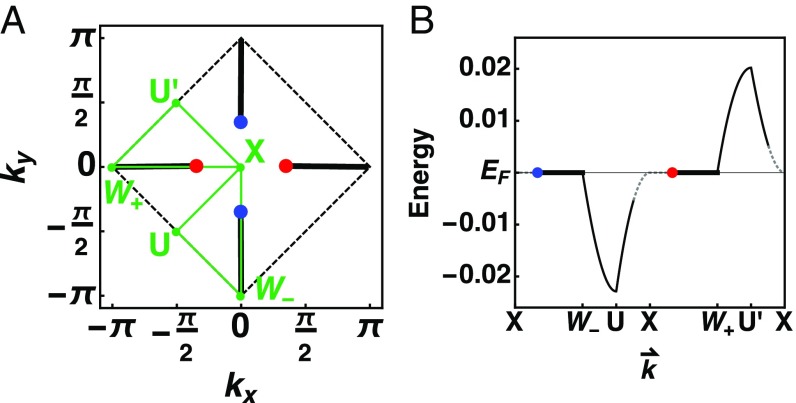
We next analyze the surface states. Focusing on the $(001)$ surface, we find the following energy dispersion for the surface states:

$$𝔈(k_x,k_y)=-2\sin \left(\frac{k_x}{4}\right)\sin \left(\frac{k_y}{4}\right)+\frac{V_s^2+{(E_s)}^2}{2E_s}-\sqrt{{\left(2\sin \left(\frac{k_x}{4}\right)\sin \left(\frac{k_y}{4}\right)-\frac{V_s^2-{(E_s)}^2}{2E_s}\right)}^2+V_s^2},$$ [3]

where we define the parameters $(V_s,E_s,{\mu }_s)=(rV,E_d+\mathrm{\ell },-{(rV)}^2/(E_d+\mathrm{\ell }))$. (For the derivation, see Supporting Information.) In Fig. 4, we show the energy dispersion along a high-symmetry path in the k space. The solid lines represent the surface states, and the dashed lines show where they merge with the bulk states and can no longer be sharply distinguished. The surface electron spectrum has a width that is similarly narrow as the bulk electron band (compare Fig. 4B with Fig. 3A), implying that the surface states also come from the Kondo effect. The surface Fermi arcs (where $𝔈({\text{𝐤}}_x,{\text{𝐤}}_y)=\mathrm{\hspace{0.17em}0}$) connect the Weyl nodes along ${\text{𝐤}}_x=\mathrm{\hspace{0.17em}0}$ and ${\text{𝐤}}_y=\mathrm{\hspace{0.17em}0}$, separating the positive and negative energy surface patches, marked by the solid black lines in Fig. 4A.

Fig. 4.

Energy dispersion of the surface electronic states. The spectrum shows the (anti-)Weyl nodes marked with blue (red). The solid black lines connecting the nodes represent Fermi arcs, and black dashed lines represent the BZ around the $X$ point. (A) High-symmetry k-space contour taken on the BZ boundary at ${\text{𝐤}}_z=\mathrm{\hspace{0.17em}2}\pi$. (B) Energy dispersion of the surface state along the path specified in A; the gray dotted line denotes the decay of the surface states into the bulk states. The parameters are the same as in Fig. 2.

As is typical for strongly correlated systems, the most dominant interactions in heavy-fermion systems are onsite, making it important to study them in lattice models (as opposed to the continuum limit). Our explicit calculations have been possible using a well-defined model on a diamond lattice that permits inversion-symmetry breaking. Nonetheless, we expect our conclusion to qualitatively apply to other noncentrosymmetric 3D systems. Finally, the WKSM is expected to survive the effect of a time-reversal symmetry breaking term, such as a magnetic field; this is illustrated in Supporting Information.

We now turn to the implications of our results for heavy-fermion semimetals. The entropy from the bulk Weyl nodes will be dictated by the velocity $v^{\ast }$, and the corresponding specific heat per unit volume has the following form (Supporting Information):

$$c_v\sim {(k_{B}T/\mathrm{\hslash }{v}^{\ast })}^3{k}_B.$$ [4]

We stress that this expression is robust against the residual interactions of the nodal excitations (Supporting Information). The utility of thermodynamical quantities as a key signature reflects an important distinction of the WKSM from weakly correlated Weyl semimetals. The Kondo temperature of typical heavy-fermion systems is considerably smaller than the Debye temperature. This is to be contrasted with the weakly correlated systems, in which the bandwidth of the conduction electrons is much larger than the Debye temperature. Therefore, in a WKSM, the nodal contributions to the entropy would dominate over the phonon component. The corresponding form of entropy also implies that the nodal excitations will have large contributions to the thermopower.

Eq. 4 can be readily tested, given that there is a considerable number of semimetallic heavy-fermion compounds (4). A noncentrosymmetric heavy-fermion system Ce₃Bi₄Pd₃ has recently been discovered to display semimetal behavior based on transport measurements, and its specific heat is well described in terms of Eq. 4 (9). A fit in terms of our theoretical expression Eq. S29 (Supporting Information) reveals an effective velocity, $v^{\ast }$, that is three orders of magnitude smaller than that expected for weakly correlated systems, reflecting the reduction in the energy scale—the Kondo temperature for Ce₃Bi₄Pd₃—from the bandwidth of the latter by a similar order of magnitude (9). This analysis provides strong evidence that Ce₃Bi₄Pd₃ is a candidate WKSM system with strongly correlated Weyl nodes and provides the motivation for further studies on such quantities as magnetotransport and high-resolution angle-resolved photoemission spectroscopy in this system. More recently, Eq. 4 has been used to fit the specific heat of another heavy-fermion system, YbPtBi, suggesting it be another candidate WKSM system (29).

Our theoretical results provide guidance in the search for Weyl semimetals in other heavy-fermion systems. For instance, in the $4f$-based system CeSb, Weyl physics has been suggested based on magnetotransport measurements (30, 31). Even though any nodes in this system are likely away from the Fermi energy, the fact that it is a Kondo system with low-energy scales leads to the expectation that they can be tuned toward the Fermi energy by pressure or chemical doping, and we propose specific heat measurements and our Eq. 4 as a means of ascertaining the role of the $4f$ electrons in this system. In addition, the noncentrosymmetric CeRu₄Sn₆ also displays semimetal properties (6) and has been discussed as a potential topological system (7). Its electronic structure has been studied by ab initio calculations combined with dynamical mean field theory (6, 32) or the Gutzwiller projection method (33). While the two types of calculations disagree on the low-energy dispersion and the latter study does not appear to capture the strong renormalizations expected in a Kondo system, the existence of linearly dispersing nodes and their Weyl nature have been suggested in the latter study. The low-temperature specific heat in single crystalline CeRu₄Sn₆ (34) implies the importance of the $4f$ electrons to the low-energy physics but does not appear to have the form of Eq. 4. Our theoretical results suggest that further thermodynamic and thermoelectrical studies will be instructive in ascertaining the potential WKSM nature of CeRu₄Sn₆.

We close with several observations. First, we have focused on a model defined on an nonsymmorphic diamond lattice, in which, for noninteracting electrons, the crystallographic space group symmetry allows for a filling-enforced semimetal state (21, 25). Our study here demonstrates that for Kondo systems defined on such a lattice and in the presence of inversion-symmetry breaking, the WKSM phase arises in a robust way. On the other hand, for noninteracting systems in 3D, a Dirac semimetal can also arise at the phase transition between topologically distinct insulating states. It will therefore be instructive to search for the WKSM state at topological phase transitions in Kondo systems; we leave this matter for future studies.

Second, our work provides a proof-of-principle demonstration for the emergence of a WKSM phase in a Kondo lattice with inversion symmetry breaking. This makes it likely that such a phase arises in inversion-symmetry-breaking 3D Kondo lattices with other crystallographic symmetries. The candidate WKSM material Ce₃Bi₄Pd₃ has a nonsymmorphic space group (220), and its Kondo-driven Weyl nodes may very well be enforced by its crystallographic symmetry and electron filling. Our findings here motivate further studies that incorporate the realistic electronic structure of Ce₃Bi₄Pd₃.

Third, in the WKSM state advanced here, the electron correlations produce a zeroth-order effect given that the localized moments of the $4f$ electrons underlie the Weyl excitations. Correspondingly, the renormalization factors (for the nodal velocity) are extremely large, typically on the order of ${10}^2-{10}^3$. This distinguishes the WKSM from other types of interacting Weyl semimetals discussed previously. The large renormalization factor is responsible for the possibility of using thermodynamics to probe the Weyl nodes. Our work also sets the stage for calculations of additional signature properties for the Weyl physics, such as the optical conductivity and related dynamical quantities.

Fourth, the context of heavy-fermion systems links the WKSM phase advanced here with the topological Kondo insulators (5) and the physics of their surface states (35). Nonetheless, the WKSM as a state of matter is distinct: In the bulk, it features strongly renormalized Weyl nodes instead of being fully gapped; on the surface, it hosts Fermi arcs from a band with a width of the Kondo energy, which are to be contrasted with the surface Dirac nodes of the topological Kondo insulators. This also dictates that the WKSM will be realized in heavy-fermion materials that are quite different from those for the topological Kondo insulators, as exemplified by the aforementioned Ce₃Bi₄Pd₃.

Finally, the emergence of a WKSM makes it natural for quantum-phase transitions in heavy-fermion systems from such a topological semimetal to magnetically ordered and other correlated paramagnetic states. Moreover, the existence of Weyl nodes also enhances the effect of long-range Coulomb interactions. While the density fluctuations of the $f$ electrons are strongly suppressed in the local-moment regime, it still will be instructive to explore additional nearby phases such as charge-density-wave order (36); other types of long-range interactions could produce topologically nontrivial Mott insulators (37). As such, the study of WKSM and related semimetals promises to shed new light on the global phase diagram of quantum critical heavy-fermion systems (4) and other strongly correlated materials (38).

In summary, we have demonstrated an emergent WKSM phase in a model of heavy-fermion systems with broken inversion symmetry and have determined the surface electronic spectra which reveal Fermi arcs. The nodal excitations of the WKSM phase develop out of the Kondo effect. This leads to unique experimental signatures for such a phase, which are realized in a noncentrosymmetric heavy-fermion system. Our results are expected to guide the experimental search for $f$-electron-based Weyl semimetals. In general, they open the door for studying topological semimetals in the overall context of quantum phases and their transitions in strongly correlated electron systems and, conversely, broaden the reach of strongly correlated gapless and quantum critical states of matter.

Materials and Methods

The 3D Periodic Anderson Model.

The three terms in the model of Eq. 1 are presented here in more detail. The strongly correlated $d$ electrons are specified by

$$H_d=E_d\sum _{i,\sigma }{d}_{i\sigma }^{†}{d}_{i\sigma }+U\sum _i{n}_{i\uparrow }^d{n}_{i\downarrow }^d.$$ [5]

The hybridization term is as follows:

$$H_{cd}=V\sum _{i,\sigma }\left(d_{i\sigma }^{†}{c}_{i\sigma }+\text{H.c.}\right).$$ [6]

In the above two equations, the site labeling $i$ means $i=(\text{𝐫},a)$, where r runs over the Bravais lattice of unit cells and $a$ runs over the two sites, $a=A,B$, in the unit cell.

The conduction electron Hamiltonian $H_c$ realizes a modified Fu–Kane–Mele model (26) and is expressed as $H_c={\sum }_{\text{𝐤}}{\mathrm{\Psi }}_{\text{𝐤}}^{†}{h}_{\text{𝐤}}{\mathrm{\Psi }}_{\text{𝐤}}$, where ${\mathrm{\Psi }}_{\text{𝐤}}^T=\left(\begin{array}{cccc}\hfill c_{\text{𝐤}\uparrow ,A}\hfill & \hfill c_{\text{𝐤}\uparrow ,B}\hfill & \hfill c_{\text{𝐤}\downarrow ,A}\hfill & \hfill c_{\text{𝐤}\downarrow ,B}\hfill \end{array}\right)$, and

$$h_{\text{𝐤}}={\sigma }_0\left(u_1(\text{𝐤}){\tau }_x+u_2(\text{𝐤}){\tau }_y+m{\tau }_z\right)+\lambda \left(\text{𝐃}(\text{𝐤})\cdot 𝝈\right){\tau }_z.$$ [7]

Here, $𝝈=({\sigma }_x,{\sigma }_y,{\sigma }_z)$ and $𝝉=({\tau }_x,{\tau }_y,{\tau }_z)$ are the Pauli matrices acting on the spin and sublattice spaces, respectively, and ${\sigma }_0$ is the identity matrix. In the first term, $u_1(\text{𝐤})$ and $u_2(\text{𝐤})$ are determined by the conduction electron hopping, $t_{⟨ij⟩}=t$ between nearest-neighbor sites ($⟨ij⟩$). The second term specifies a Dresselhaus-type spin-orbit coupling between the second-nearest-neighbor sites ($⟨⟨ij⟩⟩$), which is of strength $\lambda$ and involves vector $\text{𝐃}(\text{𝐤})=\left(\begin{array}{c}\hfill D_x(\text{𝐤}),D_y(\text{𝐤}),D_z(\text{𝐤})\hfill \end{array}\right)$. Specifically,

$$u_1(\text{𝐤})=t\left(1+\sum _{n=1}^3\cos (\text{𝐤}\cdot {\text{𝐚}}_n)\right),$$ [8]

$$u_2(\text{𝐤})=t\sum _{n=1}^3\sin (\text{𝐤}\cdot {\text{𝐚}}_n),$$ [9]

$$D_x(\text{𝐤})=\sin (\text{𝐤}\cdot {\text{𝐚}}_2)-\sin (\text{𝐤}\cdot {\text{𝐚}}_3)-\sin (\text{𝐤}\cdot ({\text{𝐚}}_2-{\text{𝐚}}_1))+\sin (\text{𝐤}\cdot ({\text{𝐚}}_3-{\text{𝐚}}_1)),$$ [10]

and $D_y,D_z$ are obtained by permuting the fcc primitive lattice vectors ${\text{𝐚}}_n$. The canonical (unitary) transformation, ${\breve{\mathrm{\Psi }}}_{\text{𝐤}}=S_{\sigma }^{†}{\mathrm{\Psi }}_{\text{𝐤}}$, leads to

$$H_c=\sum _{\text{𝐤}}{\breve{\mathrm{\Psi }}}_{\text{𝐤}}^{†}\left(\begin{array}{cc}\hfill h_{\text{𝐤}+}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill h_{\text{𝐤}-}\hfill \end{array}\right){\breve{\mathrm{\Psi }}}_{\text{𝐤}},$$ [11]

$$h_{\text{𝐤}\pm }=u_1(\text{𝐤}){\tau }_x+u_2(\text{𝐤}){\tau }_y+(m\pm \lambda D(\text{𝐤})){\tau }_z.$$ [12]

We have used a pseudospin basis (27), defined by the eigenstates $|\pm D⟩$ with eigenvalues

$$\frac{\text{𝐃}\cdot 𝝈}{D}|\pm D⟩=\pm |\pm D⟩$$ [13]

where $D(\text{𝐤})\equiv |\text{𝐃}(\text{𝐤})|$. The eigen energies of the $|\pm D⟩$ sectors are simply obtained to be

$${\epsilon }_{\pm D}^{\tau }=\tau \sqrt{u_1{(\text{𝐤})}^2+u_2{(\text{𝐤})}^2+{(m\pm \lambda D(\text{𝐤}))}^2}$$ [14]

where $\tau =(+,-)$. We use this transformation on the full Anderson model in the strong coupling limit, at the saddle-point level where the Lagrange multiplier ${\mathrm{\ell }}_i$, which enforces the local constraint $b_i^{†}{b}_i+{\sum }_{\sigma }{f}_{i\sigma }^{†}{f}_{i\sigma }=\mathrm{\hspace{0.17em}1}$, takes a uniform value, $\mathrm{\ell }$. This corresponds to ${\breve{\mathrm{\Xi }}}_{\text{𝐤}}=S_{\sigma }^{†}{\mathrm{\Xi }}_{\text{𝐤}}$. Anticipating the separability of the $|\pm D⟩$ sectors by specifying ${\breve{\mathrm{\Psi }}}_{\text{𝐤}}^T=\left(\begin{array}{c}\hfill {\breve{\psi }}_{\text{𝐤}+}^T,{\breve{\psi }}_{\text{𝐤}-}^T\hfill \end{array}\right)$, ${\breve{\mathrm{\Xi }}}_{\text{𝐤}}^T=\left(\begin{array}{c}\hfill {\breve{\xi }}_{\text{𝐤}+}^T,{\breve{\xi }}_{\text{𝐤}-}^T\hfill \end{array}\right)$, where ${\breve{\psi }}_{\text{𝐤}\pm }^T=\left(\begin{array}{c}\hfill {\breve{\psi }}_{\text{𝐤}\pm ,A},{\breve{\psi }}_{\text{𝐤}\pm ,B}\hfill \end{array}\right)$ and ${\breve{\xi }}_{\text{𝐤}\pm }^T=\left(\begin{array}{c}\hfill {\breve{\xi }}_{\text{𝐤}\pm ,A},{\breve{\xi }}_{\text{𝐤}\pm ,B}\hfill \end{array}\right)$, we obtain the strong coupling Hamiltonian

$$H^s=\sum _{\text{𝐤},a=\pm }\left(\begin{array}{cc}\hfill {\breve{\psi }}_{\text{𝐤}a}^{†}\hfill & \hfill {\breve{\xi }}_{\text{𝐤}a}^{†}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill h_{\text{𝐤}a}-\mu {\mathbb{1}}_2\hfill & \hfill rV{\mathbb{1}}_2\hfill \\ \hfill rV{\mathbb{1}}_2\hfill & \hfill (E_d+\mathrm{\ell }){\mathbb{1}}_2\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\breve{\psi }}_{\text{𝐤}a}\hfill \\ \hfill {\breve{\xi }}_{\text{𝐤}a}\hfill \end{array}\right),$$ [15]

which separates as $H^s={\mathcal{H}}_{+}^s+{\mathcal{H}}_{-}^s$. We obtain the full spectra of the eight hybridized bands,

$${\mathcal{E}}_{\pm D}^{(\tau ,\alpha )}(\text{𝐤})=\frac{1}{2}\left[E_s+{\stackrel{\sim }{\epsilon }}_{\pm D}^{\tau }+\alpha \sqrt{{\left(E_s-{\stackrel{\sim }{\epsilon }}_{\pm D}^{\tau }\right)}^2+4V_s^2}\right],$$ [16]

where $\alpha =(+,-)$ indexes the upper/lower quartet of bands, ${\stackrel{\sim }{\epsilon }}_{\pm D}^{\tau }={\epsilon }_{\pm D}^{\tau }-\mu$, and $(E_s,V_s)=(E_d+\mathrm{\ell },rV)$. In Supporting Information, we prove that the $|+D⟩$ sector is always gapped, whereas the $|-D⟩$ sector allows Weyl nodes when $0<\frac{m}{4|\lambda |}<\mathrm{\hspace{0.17em}1}$, and determine $\mu =-V_s^2/E_s$, which fixes the Fermi energy at the Weyl nodes.

To determine $r,\mathrm{\ell }$, $H^s$ must be solved self-consistently from the saddle-point equations

$$\frac{1}{2N_u}\sum _{\text{𝐤},a=\pm }⟨{\breve{\xi }}_{\text{𝐤}a}^{†}{\breve{\xi }}_{\text{𝐤}a}⟩+r^2=\mathrm{\hspace{0.17em}1},\frac{V}{4N_u}\sum _{\text{𝐤},a=\pm }\left[⟨{\breve{\psi }}_{\text{𝐤}a}^{†}{\breve{\xi }}_{\text{𝐤}a}⟩+\text{H.c.}\right]+r\mathrm{\ell }=\mathrm{\hspace{0.17em}0},$$ [17]

where $N_u$ is the number of the unit cell. The equations are solved on a $64\times 64\times 64$ cell of the diamond lattice, with error $ϵ\le \mathcal{O}({10}^{-5})$.