Enzyme leaps fuel antichemotaxis

Significance

Challenging the traditional view that enzyme kinetics are only a matter of catalyzing chemical reactions, there is mounting evidence that the enzyme catalysis enhances enzyme mobility. This is significant to programming spatio-temporal patterns of molecular response to chemical stimulus, which is common to living matter as well as to significant chemical technology. This paper shows that the enhanced diffusivity of enzymes is a “run-and-tumble” process analogous to that performed by swimming microorganisms, executed in this situation by molecules that lack the decision-making machinery of microorganisms. The result is that enzymes display “antichemotaxis” when they turn over substrate; they migrate in the direction of lesser reactant concentration.

Abstract

There is mounting evidence that enzyme diffusivity is enhanced when the enzyme is catalytically active. Here, using superresolution microscopy [stimulated emission-depletion fluorescence correlation spectroscopy (STED-FCS)], we show that active enzymes migrate spontaneously in the direction of lower substrate concentration (“antichemotaxis”) by a process analogous to the run-and-tumble foraging strategy of swimming microorganisms and our theory quantifies the mechanism. The two enzymes studied, urease and acetylcholinesterase, display two families of transit times through subdiffraction-sized focus spots, a diffusive mode and a ballistic mode, and the latter transit time is close to the inverse rate of catalytic turnover. This biochemical information-processing algorithm may be useful to design synthetic self-propelled swimmers and nanoparticles relevant to active materials. Executed by molecules lacking the decision-making circuitry of microorganisms, antichemotaxis by this run-and-tumble process offers the biological function to homogenize product concentration, which could be significant in situations when the reactant concentration varies from spot to spot.

Not enough is known about how the nanoscale action of individual molecules [especially, elementary chemical reaction kinetics catalyzed by enzymes (1, 2)] connects with the emergent macroscale nonequilibrium properties of living matter itself. We are interested here with programming macroscopic movement to respond to chemical stimuli. For swimming microorganisms, one mechanism is the “run-and-tumble” foraging algorithm of a biased random walk in the direction of higher chemical concentration (“chemotaxis”); in the presence of food, bacteria move from spot to spot by the run-and-tumble process with reorientational “tumbles” punctuated by long “runs” in the direction of higher food concentration, without sensing the chemical gradient (3–5). Inspired by pioneering reports that catalytically active enzymes diffuse more rapidly than in the absence of reactant (6, 7), we have tested how enzyme concentration responds to a gradient of substrate concentration, employing superresolution fluctuation microscopy to access length scales close to the size of the moving enzyme itself.

Results

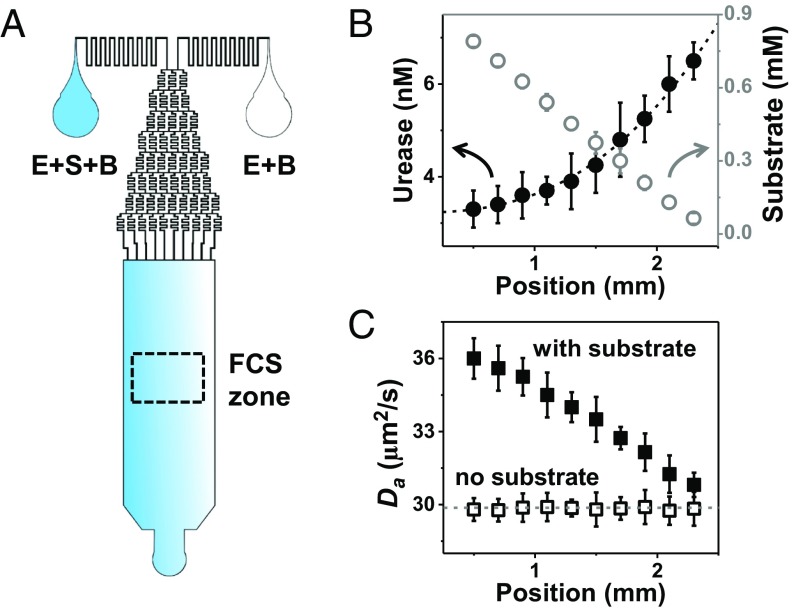
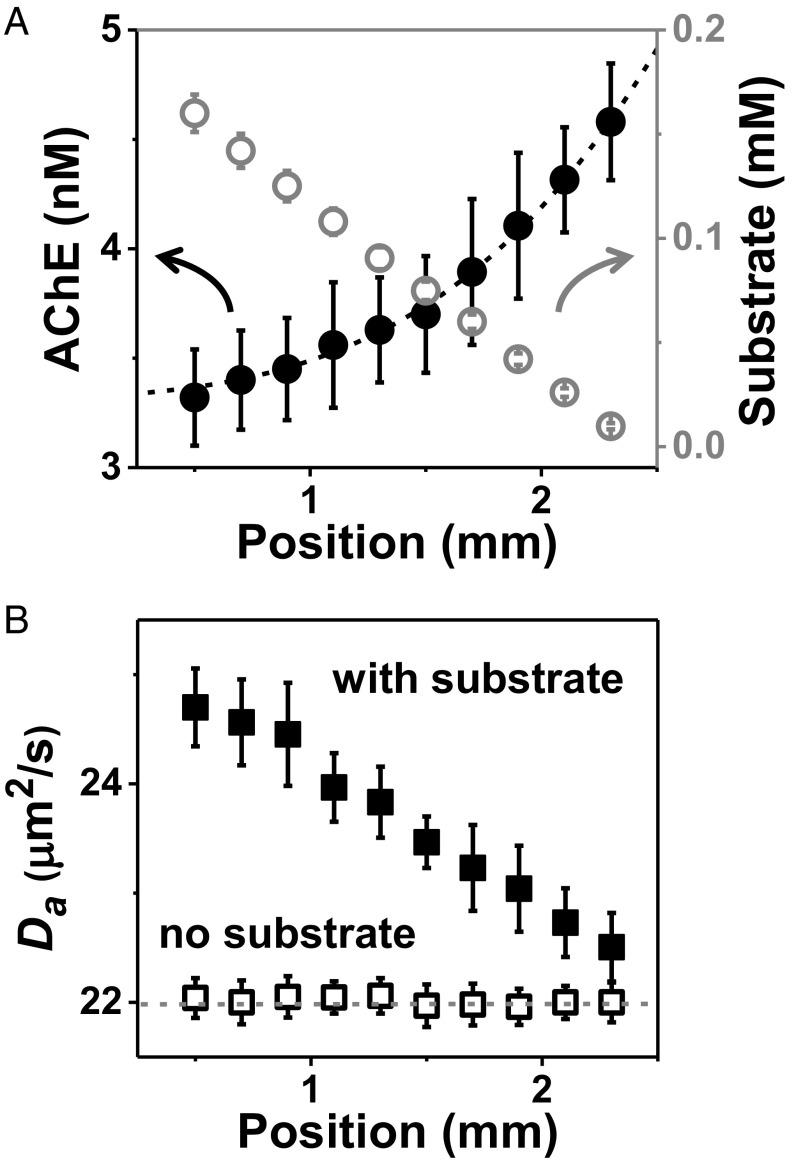
Our microfluidic device produces at the inlet of the test channel a homogeneous enzyme concentration accompanied by a linear gradient of substrate concentration, using sequential dilution from two parent reservoirs (Fig. 1A and Fig. S1). Tagging optically a small fraction of the enzymes with a fluorescent dye, we monitor local concentration by fluorescence correlation spectroscopy (FCS) (8, 9) at locations downstream from the channel entry, having produced a well-developed concentration profile (measurements made 10 min after entry with laminar flow of 50 µL/h) with enzyme concentration chosen to be in the concentration-dependent regime of kinetics. Fig. 1B shows that the initially uniform concentration of urease, an enzyme that hydrolyzes urea, now adopts the inverse concentration profile as substrate such that the product of enzyme concentration and substrate concentration is roughly uniform. The enzyme’s apparent diffusion coefficient is proportional to substrate concentration (Fig. 1C). A second enzyme (acetylcholinesterase, which hydrolyzes acetylcholine) likewise displays such antichemotaxis (Fig. 2A) and proportionality of the apparent diffusion coefficient to substrate concentration (Fig. 2B). Showing that enzyme activity is required for antichemotaxis, enzyme diffusivity is independent of position in the channel when no substrate is present (Figs. 1C and 2B).

Fig. 1.

Antichemotaxis of urease when it catalyzes urea hydrolysis in a microfluidic channel. (A) Design scheme of the microfluidic chip. The enzyme–substrate–buffer (E+S+B) enters one inlet, and the substrate-free enzyme solution in buffer (E+B) enters another, producing constant enzyme concentration across the channel but a linear gradient of its substrate. (B) Urease concentration extracted from FCS autocorrelation fitting to Eq. 1 (solid circles) and calibrated urea concentration (open circles) are plotted against position across channel with error bars showing SD of five repeated measurements. Dotted line through the data is the hyperbolic profile predicted by the model. (C) The enzyme diffusion coefficient (D_a) extracted from FCS autocorrelation fitting with a diffraction-limited spot size, plotted against position in the channel, in the presence (solid squares) and absence (open squares) of substrate.

Fig. 2.

Antichemotaxis of acetylcholinesterase (AChE) when it catalyzes acetylcholine hydrolysis in a microfluidic channel. (A) Substrate concentration (open circles) and enzyme concentration (solid circles) are plotted against horizontal position with error bars showing SD of five repeated measurements. (B) The enzyme diffusion coefficient (D_a) extracted from FCS autocorrelation fitting with a diffraction-limited spot size, plotted against position in the channel, in the presence (solid squares) and absence (open squares) of substrate.

While our studies confirm recent reports (6, 7) that the apparent diffusion coefficient (D_a) speeds up with increasing substrate concentration (Figs. 1C and 2B), the earlier claims of standard chemotaxis (10, 11) were consistent with the alternative explanation of diffusion-induced mixing, and antichemotaxis was not reported previously. Earlier studies employed diffraction-limited optics, however. Therefore, we undertook superresolution microscopy experiments to investigate how enzyme dynamics are coupled to activity on small length scales.

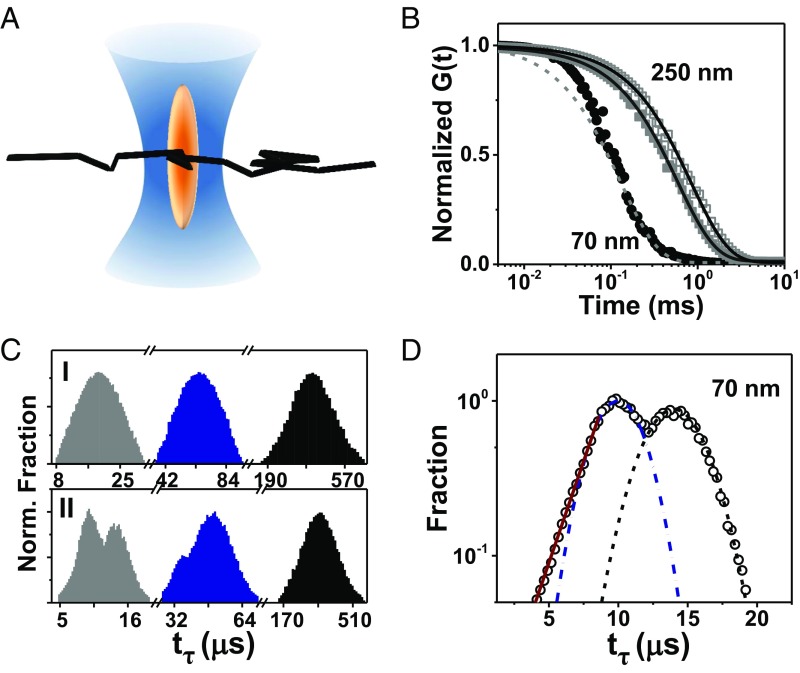
Overcoming the diffraction-limited resolution of normal confocal microscopy using stimulated emission-depletion (STED) (12, 13), and combining this with FCS, we evaluated enzyme mobility critically by varying the “beam waist” (w), the diameter of the needle-shaped optical structure perpendicular to the focal plane sketched schematically in Fig. 3A. This is the length scale of the problem as fluorescence fluctuations are dominated by passage through the beam waist, the shortest path through the optical structure. After confirming the excellent fit of intensity–intensity autocorrelation curves with substrate absent to the standard FCS model based on Fickian diffusion (14, 15), experiments were repeated with substrate present, finding that when w ≤ 150 nm, the autocorrelation function decayed too abruptly to fit the standard diffusive model at times shorter than ∼0.1 ms (Fig. 3B). Inspecting transit times (t_τ) for fluorophores to transit the beam waist, we found these distributions to be Gaussian regardless of w in the absence of substrate but bimodal with substrate present, provided that w ≤ 150 nm. This held for urease in buffer (Fig. 3C) and also when 20% Ficoll was added to urease as a crowding agent (Fig. S2); Ficoll, a polysaccharide, has hydrodynamic radius [∼2–7 nm (16)] similar to that of the enzyme [∼7 nm (17)]. For the extreme case of the smallest w achievable in our experimental setup, a logarithmic scale of counts emphasizes that two modes exist with substrate present: a Gaussian mode and a faster exponential mode (Fig. 3D). This bimodal family of transit times contrasts sharply with the single Gaussian distribution observed without substrate.

Fig. 3.

STED-FCS measurements. (A) Experimental geometry in which STED narrows the hourglass-shaped confocal spot to be elliptical. (B) Normalized autocorrelation function G(t) plotted against logarithmic time lag with w = 70 nm (circles) and 250 nm (squares), with solid and open symbols showing substrate and substrate-free, respectively. Dotted line illustrates poor fit to Fickian diffusion. (C) Transit time distribution t_τ without (C, I) and with (C, II) substrate, w = 70 nm, 100 nm, and 250 nm from left to right. Bin size, 0.5 ms. (D) Log-linear plot of transit time distribution, w = 70 nm, deconvoluted into fast and slow components with Gaussian fits near the peak shown by dotted lines.

Discussion

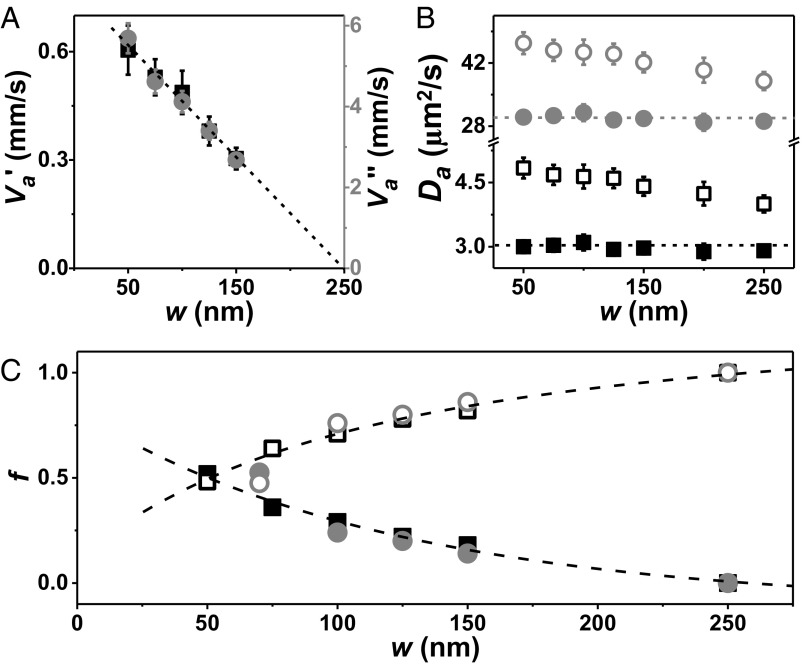
Intriguingly, the enzyme’s fast peak transit time ∼0.01 ms for w = 70 nm is close to its inverse rate of catalytic turnover (18) and is inconsistent with passive diffusion. The similar time scales suggest that the ballistic length scale is similar to the beam waist. In control experiments, we mixed tracer dyes with substrate in the enzyme solution, finding that dye mobility likewise speeds up and adopts FCS autocorrelation functions likewise inconsistent with Fickian diffusion (Fig. S3). This implies that catalytic activity creates hydrodynamic flow, a generic feature of active matter (19). If nevertheless one were to calculate an apparent diffusion coefficient, it would grow with decreasing w but there is no evidence that the elementary steps execute a random walk with dependence on length scale. Tentatively, we identify the fast component at small w with impulsive, ballistic motion and we estimate its apparent speed, the quotient of w and fast peak transit time, for enzyme in buffer (v_a′′) and enzyme in buffer–Ficoll mixture (v_a′). In Fig. 4A, v_a is plotted against w; decreasing linearly with increasing w, it extrapolates to zero at the diffraction limit. However, for the slow component of transit time the implied diffusion coefficient D_a evaluated from the quotient of squared beam width and transit time in the standard way for a random-walk model (8, 9) is independent of w without substrate and also is nearly independent of w with substrate present (Fig. 4B), so both cases are diffusive or nearly diffusive. The trend is for the fast transit time component to dominate as w approaches the size of the enzyme (Fig. 4C). The growing fraction of fast component implies growing importance of a ballistic mode.

Fig. 4.

Transit time distribution. (A) Ratio of beam waist to peak time of the fast component, plotted against w in buffer with 20% Ficoll as crowding agent (black, v_a′) and in buffer (gray, v_a′′). (B) Ratio of w² to peak time of the slow component (when w ≤ 150 nm) or peak unimodal time (larger w) plotted against w without (solid symbols) and with (open symbols) substrate in buffer (gray) and buffer–Ficoll solution (black). (C) Ratio of ballistic to diffusive (solid symbols) and diffusive to ballistic (open symbols) of transit time distribution, plotted against w in buffer with same symbols as in B. Dashed lines through the points are a guide to the eye.

Furthermore, treating the enzyme as a nanoswimmer, the force owing to the leap or kick on the enzyme of radius a in the medium of viscosity η is roughly estimated as the Stokes drag force $f=6\pi \eta a{v}_a\simeq 1\hspace{0.17em}\text{pN},$ and the work dissipated is $W=f\cdot l\simeq 10-20\hspace{0.17em}{\text{k}}_{\text{B}}\text{T,}$ where the leap length was taken as l ∼ 50–100 nm based on the observed ballistic behavior on this scale. Indeed, independently we also biochemically estimate the kick length from the enhanced diffusion curves $D_a\left(c\right)$ evaluated over large, diffraction-limited spots (Figs. 1C and 2B); using theoretical arguments below based on Michaelis–Menten kinetics, they give the same range as the optical measurement, l ∼ 50–100 nm. These are upper bounds of leap length because what we express here as ballistic speed likely consists of a sequence of shorter steps that have not yet randomized, but as we have no direct information relevant to this, following Occam’s razor this line of reasoning was not pursued. In the context of seeking to explain enhanced diffusion, others have suggested possible connections to the enthalpy of reaction as well as possible mechanisms but these scenarios are speculative (7, 11, 20). In this paper, we simply emphasize this experimental phenomenology in the subdiffraction region where measurements were not made previously. Indeed, while the propulsion mechanism remains elusive, the energy scale of the implied kicks is typical of enzyme biochemistry.

This chemically driven leaping motion, fueled by catalytic activity, suggests that enzyme thermally driven diffusion is speeded up by stochastic impulsive leaps which produce directional motion when the substrate–enzyme complex releases a product. In addition to turnover rate, it is plausible to expect that the relevant parameter is the available Gibbs free energy of the chemical reaction, in the low–Reynolds-number regime where considerations of momentum conservation and inertia are not expected to matter much. That number is a scalar and asymmetry, presented by binding sites at specific locations, will generate vectorial motion. Tentatively, we attribute the fast component in Fig. 4A to a sequence of ballistic leaps with reorientation between them, akin to the run and tumble known for bacteria (3–5). To explore the dependence on substrate concentration (the source of kicks), we reduced the substrate concentration by a factor of 10 and found that the fast component of the transit time distribution appeared only over a narrower range of w ≤ 70 nm (Fig. S4), consistent with the expectation that in this case a smaller fraction of the enzyme population engages in ballistic motion, but apparent speed was the same. For a different enzyme, acetylcholinesterase, all of these patterns were confirmed. Acetylcholinesterase with substrate present also displays bimodal transit time distribution when w ≤ 100 nm accompanied by the same trends in v_a and D_a (Fig. S5), in addition to antichemotaxis (Fig. 2A).

These physically motivated expectations imply the simple model that enzyme diffusion is augmented by episodic stochastic kicks at the frequency at which the enzyme turns over substrate. The total diffusivity D_a(c) is therefore the sum of two independent processes, Brownian motion and run and tumble, $D_a\left(c\right)=D_0+D_T\left(c\right),$ where D₀ is the Fickian component without substrate as described in Materials and Methods. The active diffusivity $D_T\left(c\right)$ is proportional to the catalytic rate, $D_T\left(c\right)=\frac{1}{3}{l}^2\left[k_{\text{cat}}c/\left(k_M+c\right)\right],$ where l is the kick length, c is the substrate concentration, k_cat is the turnover rate constant, and k_M is the Michaelis constant. Here, for urease (18) k_M = 3 mM, k_cat = 17,000 s⁻¹, and l ∼ 60 nm estimated from the discussion above. To analyze the antichemotaxis gradient demonstrated experimentally in Figs. 1B and 2A, consider the flux of enzyme across the substrate gradient, $J=\nabla \left(D\left(c\right)\cdot \rho \right),$ where ρ is the enzyme concentration. Down the channel, the enzyme concentration profile reaches a steady state where flux $=0,$ which implies a simple inverse spatial dependence, $\rho \left(c\right)\propto 1/D\left(c\right).$ This theoretical curve with no fit parameters except a normalization factor of the average enzyme concentration agrees with the data in Fig. 1B.

These experiments demonstrate that enzymes can transduce chemical reactions into spatial motility that on length scales ≤150 nm contains ballistic character. These stochastic leaps are more frequent as the substrate (“food”) concentration rises, driving enzymes to migrate into zones of lesser substrate concentration where the local mobility is less and causing enzymes to accumulate where they move most slowly (“antichemotaxis”). This can be biologically useful because it homogenizes the spatial distribution of the enzymatic production, which is essential in the crowded milieu of the cell. Here we have restricted our analysis to enzyme mobility in vitro. We believe, however, that this work opens unique routes to understand enzyme activity in living systems and also to generalize these principles in potential synthetic systems (19) involving active particles and nanoparticles.

Materials and Methods

Enzymes and Enzyme Dye Labeling.

Urease from jack bean, purchased from Sigma, was labeled at the amine residue with dylight488 maleimide dye by a protocol involving 150 mM phosphate buffer (pH 7.0) with added 2 µM urease and 40 µM fluorescent dye solution, stirred for 6 h at room temperature. Acetylcholinesterase from Electrophorus electricus, purchased from Sigma, was labeled at its carboxyl residue by dylight488-NHS (N-hydroxysuccinimide) dye by a protocol in which 30 µM dye solution and 1 µM enzyme were added to a mixture of 80% phosphate buffer solution (PBS) and 20% dimethyl sulfoxide (DMSO) before 6 h of stirring at room temperature. Finally, the dye-labeled enzymes were purified by removing the free dye by membrane dialysis (Amicon ultra-4 centrifugal filter; Millipore).

The enzyme hydrolysis reactions were observed sometimes in buffer solution and sometimes in 10 cP solution. The latter was achieved by mixing 20% Ficoll 70 (Sigma) in 150 mM phosphate buffer with pH adjusted to 7.2. To this, 1 mM urea (Sigma) and 10 nM dye-labeled enzyme were added at room temperature. When studying acetylcholinesterase enzymatic action, 20% Ficoll was added to 100 mM phosphate buffer with pH adjusted to 8.0. To this, 50 µL of 0.5 mM 5,5′-dithiobis-(2-nitrobenzoic acid) (DTNB), 0.2 mM acetylcholine (Sigma), and dye-labeled enzyme were added at room temperature.

For STED-FCS measurements, dye-labeled enzyme was introduced at a concentration of roughly 0.1%. To a parent solution of 10 µM enzyme, 10 nM of dye-labeled enzyme was added. For FCS without STED, 2 nM of dye-labeled enzyme and 8 nM of dye-free enzyme were added. Therefore, total enzyme concentration was 10 nM in all experiments.

Microfluidic Gradient Platform.

The microfluidic chip is composed of two sample inlets, concentration gradient generator (CGG) (21) and FCS observation zone, and an outlet. The width and the height of the serpentine channels in CGG are 100 μm. The microfluidic chip was fabricated in polydimethylsiloxane (PDMS) (Sylgard 184; Dow Corning), using standard soft-lithography methods (22).

Enzyme Concentration Determination.

Confocal FCS with calibrated beam waist 250 nm was used to measure the local concentration of dye-labeled urease. Variations across the microfluidic channel of the amplitude of the autocorrelation function G(t) are known to be inversely proportional to the concentration of fluorescent molecules by standard analysis. The urea concentration gradient was calculated by binning of line scans of luminescence image (Fig. S1). As shown in Fig. 1B, the urease concentration increases in inverse proportion to the substrate concentration. Using acetylcholinesterase the same measurements and line binning were performed (Fig. 2A).

STED-FCS Measurements.

FCS measurements were performed using a STED-FCS (Leica TCS SP8X), using a 100× oil immersion objective lens with numerical aperture N.A. = 1.4 and pinhole size equal to 1 airy unit. Measurements were averaged for about 10 min and typically this was repeated about five times. We employed excitation wavelength 488 nm with depletion wavelength 592 nm, excitation at 80 MHz, and a pulse width of 80 ps. Before each measurement, the excitation laser and the depletion laser were superposed and the system was freshly aligned. The excitation power was controlled up to 5 µW. The maximum depletion power in the objective back aperture was 200 mW. Emitted fluorescence was collected using an avalanche photodiode (APD) (Micro Photon Devices; PicoQuant) through a 500- to 550-nm bandpass filter. The APD signal was recorded using a time-correlated single–photon-counting (TCSPC) detection unit (Picoharp 300; PicoQuant).

To see that beam waist is the length scale of this problem, consider the extreme case of passage through an optical structure in the shape of a cylinder, an infinitely long needle of width W. For this case, the average length of a path through the center of the circular cross-section of the needle is (π/2)*W ∼ 1.57 W, where the average is over all possible directions of the path. For a finite needle, an ellipsoid of aspect ratio q, the average length is less than this: It is W*q*ArcSec(q)/(q² − 1)^1/2 ∼ (π/2 − 1/q)*W and q ∼ 10 for a beam waist of 50 nm. A further decrease will result from paths that cross off center. To conclude, at most the average path length is about 1.5 times larger than the minimum waist and in practice, the actual factor is closer to the minimum waist because off-center paths are shorter.

For comparison with the single-component Fickian diffusion model, autocorrelation curves G(t) were fitted to the standard relation for free diffusion through a 3D Gaussian volume with radial and axial extensions w and h,

$$\text{G}\left(\text{t}\right)=\frac{1}{N}{\left(1+\frac{t}{t_{\tau }}\right)}^{-1}{\left(1+\frac{w^2}{h^2}\frac{t}{t_{\tau }}\right)}^{-1/2},$$ [1]

where N is average number of fluorophores in the observation volume, and t_τ is an average transit time of fluorophores through the observation volume. The diffusion coefficient D can be inferred from the relation $D=w^2/4t_{\tau }.$

Antichemotaxis Formula.

To account for the enhanced diffusion of the enzymes, we add to the thermally induced Fickian diffusivity D₀ a concentration-dependent stochastic process with a diffusivity $D_T\left(c\right).$ The enzyme kicks whenever it catalyzes a substrate at the average turnover rate given by the Michaelis–Menten kinetics $f_{kick}=k_{\text{cat}}c/\left(k_M+c\right),$ where k_cat is the catalytic rate and k_M is the Michaelis constant. The active diffusivity $D_T\left(c\right)$ is $D_T\left(c\right)=\frac{1}{3}{l}^2{f}_{kick},$ where l is the average kick length. The total diffusivity D_a(c) is therefore the sum $D_a\left(c\right)=D_0+D_T\left(c\right)=D_0+\frac{1}{3}{l}^2\left[k_{\text{cat}}c/\left(k_M+c\right)\right].$ Previous theoretical consideration of enhanced diffusion due to hydrodynamic interactions showed (23) that as long as the two stochastic processes (in the case considered, thermal and hydrodynamic forces) are uncorrelated, the overall diffusion coefficient is the sum of the two diffusion constants, the standard one together with the active diffusion coefficient. The same general consideration applies in our case. This linear approximation would fail if thermal fluctuations and kicks were correlated, but we observe no evidence for such correlation. Therefore, the enzyme flux is $J=-\nabla \left(D_a\left(c\right)\cdot \rho \right)$ with a continuity equation $\partial \rho /\partial t=-\nabla J={\nabla }^2\left(D\left(c\right)\cdot \rho \right).$ The microfluidic channel is designed to let the enzyme concentration reach a steady-state downstream $J=const.$ Since there is no flux through the boundaries, it follows that $J=-\nabla \left(D_a\left(c\right)\cdot \rho \right)=0.$ The direct outcome is the inverse concentration profile, $\rho \left(c\right)\propto 1/D_a\left(c\right)$. The substrate gradient across the channel is approximately linear $c\left(x\right)=c_0\left(1+Ax\right),$ which yields a spatial enzyme profile, $1/\rho \left(x\right)\propto 1/C+1/\left[B+1/\left(1+Ax\right)\right],$ where $C=\frac{1}{3}{l}^2{k}_{\text{cat}}/D_0$ and $B=k_M/c_0.$