Significance
Thermotropic liquid crystals (LCs) are central to a wide range of commercial and emerging technologies. Lyotropic, aqueous-based LCs are common in nature, but applications have been scarce. The current understanding of their behavior is limited, and manipulating their mechanical and dynamic characteristics has been challenging. Here we show that the elasticity and temporal evolution of biopolymer-based nematic systems can be inferred from simple optical microscopy measurements, and that their mechanical properties can be manipulated by adjusting certain molecular characteristics, such as the product of length and concentration. It is also shown that the dynamic evolution of the resulting materials can be understood and predicted on the basis of a free energy functional originally developed for the study of thermotropic systems.
Keywords: lyotropic liquid crystal, actin, topological defects, microtubule, elasticity
Abstract
Achieving control and tunability of lyotropic materials has been a long-standing goal of liquid crystal research. Here we show that the elasticity of a liquid crystal system consisting of a dense suspension of semiflexible biopolymers can be manipulated over a relatively wide range of elastic moduli. Specifically, thin films of actin filaments are assembled at an oil–water interface. At sufficiently high concentrations, one observes the formation of a nematic phase riddled with topological defects, characteristic of a two-dimensional nematic system. As the average filament length increases, the defect morphology transitions from a U shape into a V shape, indicating the relative increase of the material’s bend over splay modulus. Furthermore, through the sparse addition of rigid microtubule filaments, one can gain additional control over the liquid crystal’s elasticity. We show how the material’s bend constant can be raised linearly as a function of microtubule filament density, and present a simple means to extract absolute values of the elastic moduli from purely optical observations. Finally, we demonstrate that it is possible to predict not only the static structure of the material, including its topological defects, but also the evolution of the system into dynamically arrested states. Despite the nonequilibrium nature of the system, our continuum model, which couples structure and hydrodynamics, is able to capture the annihilation and movement of defects over long time scales. Thus, we have experimentally realized a lyotropic liquid crystal system that can be truly engineered, with tunable mechanical properties, and a theoretical framework to capture its structure, mechanics, and dynamics.
Recent advances have extended applications of nematic liquid crystals (LCs) onto realms that go beyond display technologies (1) and elastomers (2, 3) to colloidal/molecular self-assembly (4–6), pathogen sensing (7, 8), photonic devices (9), drug delivery (10), and microfluidics (11). In LCs, topological defects correspond to locally disordered regions where the orientation of the mesogens (12) (the units that form an LC mesophase) changes abruptly. Defects exhibit unique optical and other physicochemical characteristics, and serve as the basis for many of the applications of these materials. The microstructure of an LC, the so-called “director field,” is determined by a delicate interplay between elastic forces, geometrical constraints, and the influence of applied external fields (13, 14). That microstructure dictates optical and mechanical response of the LC to external cues. Thus, the ability to control and optimize the LC elasticity is essential for emerging applications. The most widely used low-molecular-weight LCs are thermotropic (LC phases emerge at a certain temperature), and exhibit a nematic phase within a certain, relatively narrow temperature range. In such LCs, the defect size is small ( nm) (15), thereby placing severe constraints on applications that might rely on defects to perform certain functions [e.g., absorption and transport of colloidal particles (5)]. Furthermore, in thermotropic systems, there is a limited range of accessible microstructures that are only achieved with significant changes in temperature (12).
Lyotropic materials in which LC phases emerge at certain solute concentrations circumvent some of these shortcomings. In addition, certain lyotropic LCs are not toxic to many microbial species (16) and neutral to antibody–antigen binding (17), providing a possibility for biological applications (18). Here we rely on suspensions of biopolymers to form lyotropic LCs, where long and semiflexible mesogens lead to the formation of nematic phases at sufficiently high concentrations. More specifically, we use filamentous actin (F-actin), with a width of 7 nm and persistence length of 10 m to 17 m (19, 20). F-actin suspensions exhibit a nematic phase when the concentration rises above the Onsager limit (21, 22). Here we deplete F-actin onto an oil–water interface, thereby forming a quasi-two-dimensional (2D) nematic system (23). F-actin’s average contour length can be tuned from m to m by addition of variable concentrations of a capping protein that limits polymer growth (22, 24). Because the typical core size of corresponding topological defects that arise in nematic actin is on the order of micrometers, they can be visualized by optical microscopy. We demonstrate an approach to extract precise measurements of elastic moduli by examining the morphology of the defects (25). We find that, as the filament length increases from 1 m to 2 m, the defect morphology transitions from a U shape to a V shape, indicating that the nematic LC changes from a splay-dominant into a bend-dominant LC material. We also demonstrate that the formation of a composite LC by addition of sparse concentrations of a more rigid mesogen leads to an increase of the bend elasticity of the resulting composite LC that grows linearly with its number density and average length.
Our 2D nematic system provides an ideal platform for detailed studies of the dynamics of defects in lyotropic LCs. To engineer lyotropic systems containing topological defects for emerging applications, it is essential that a quantitative formalism be advanced with which to predict the dynamics of lyotropic LCs. Here we combine a Landau–de Gennes free energy model and the underlying momentum conservation equations and show that such an approach is capable of describing dynamic processes in polydisperse, semiflexible biopolymer systems, paving the way for elucidating its nonequilibrium dynamics.
Results and Discussion
The local average orientation of the mesogens is denoted by n, which is a position-dependent (unit) vector field that obeys nematic (head–tail) symmetry, i.e., n and n are undistinguishable. When an LC transitions from an isotropic phase to a nematic phase, topological defects emerge and annihilate over time as the material undergoes thermal equilibration. Those defects can be categorized by their winding number or topological charge (26). Fig. 1B provides an illustration of defects. The long-range order of nematic LCs is often characterized by the Frank–Oseen elastic theory (27), where the elastic energy density is given by
| [1] |
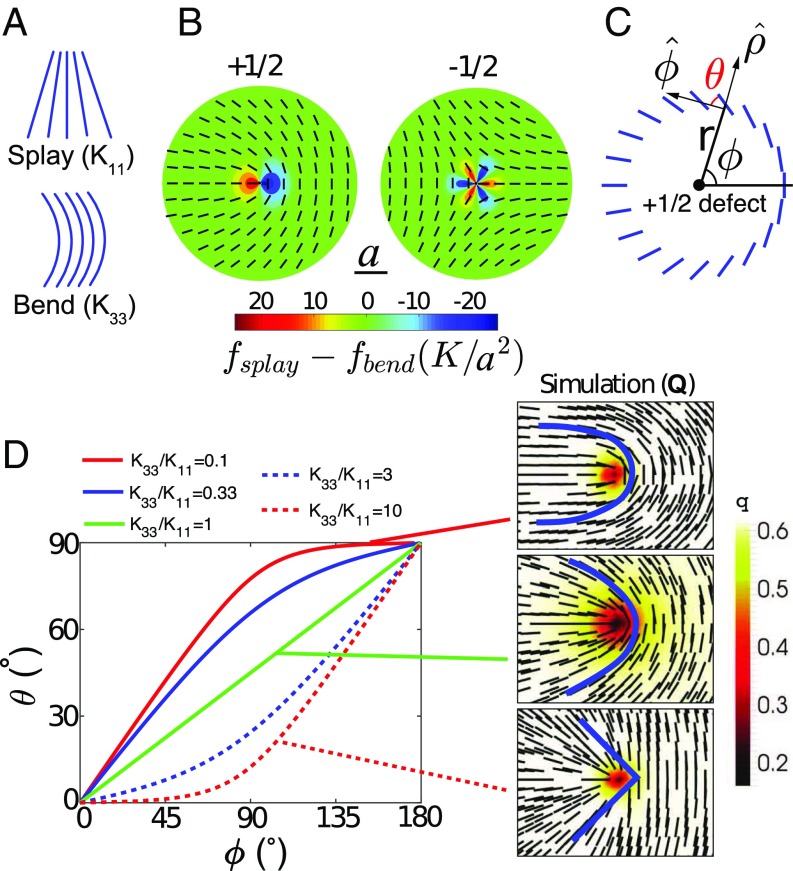
Here the four prefactors penalize splay (), twist (), bend (), and saddle-splay () deformations, respectively. A widely used simplification of the above expression is provided by the so-called “one-constant approximation,” which assumes . In that case, Eq. 1 reduces to (using Einstein notation summing all repeating indices) , and captures many qualitative physics of nematic LCs. In a 2D nematic system, mesogens are constrained to lie in a plane, and the twist () and saddle-splay () deformation modes are irrelevant. Therefore, the splay () and bend () influence the structure of topological defects, depicted in Fig. 1A. By minimizing the system’s total elastic energy over an area ( with respect to n), an analytical expression for the director field near a defect is obtained. Introducing an elastic distortion energy density according to and , we quantify the distribution of splay and bend distortions near a defect. In Fig. 1B, near defects is plotted under the one-constant approximation, demonstrating that the defect has twofold symmetry, whereas the defect has threefold symmetry.
Fig. 1.
Morphology of defects. (A) Illustration of splay and bend distortion in nematic LC. (B) The director fields of and defect under one-elastic-constant approximation. The color indicates the difference in splay and bend energy density; is the unit length scale. (C) Quantitative description of defect morphology: is the polar coordinate; is the angle between the director and the angular vector . (D) The morphology of defects as a function of elastic constant ratio . Right images are the Q-tensor–based simulation results. Blue curves following the local director field are added to guide the eye.
To better account for nematic symmetry, one can also construct a second-order, symmetric, traceless tensor Q based on n. The Q tensor (under a uniaxial assumption) is defined by , where is the scalar order parameter that characterizes how well aligned the mesogens are. The nematic symmetry is automatically satisfied when a Q tensor is introduced. Eq. 1 can be written in terms of the Q tensor and incorporated into the Landau–de Gennes free energy model, and a Ginzburg–Landau approach is implemented to arrive at the LC’s equilibrium structure (see Materials and Methods). To explore the fine structure of the topological defect, we go beyond the one-constant approximation and consider the bend-to-splay ratio . We find that the analytical expressions derived are consistent with the results from full Q-tensor simulations (see Fig. S1). To quantify the director field near a defect, one can introduce an angle (illustrated in Fig. 1C) in a polar coordinate system , such that the director can be expressed as . In Fig. 1D, is plotted for various values of . These calculations show that the defect morphology adopts a U shape when () and a V shape when (). When , splay distortion is more energetically demanding, whereas bend distortion is easier. The system therefore tries to squeeze any high-splay regions and expand high-bend regions. The resulting directors are more horizontal, leading to a U-shape morphology. In contrast, if , splay distortions become energetically easier and bend distortions become more demanding; the system is therefore stretched in the opposite direction. It tries to spread high-splay regions and suppress high-bend regions, resulting in a V-shape director field. One can also examine the core shape of a defect by varying (see Fig. S1).
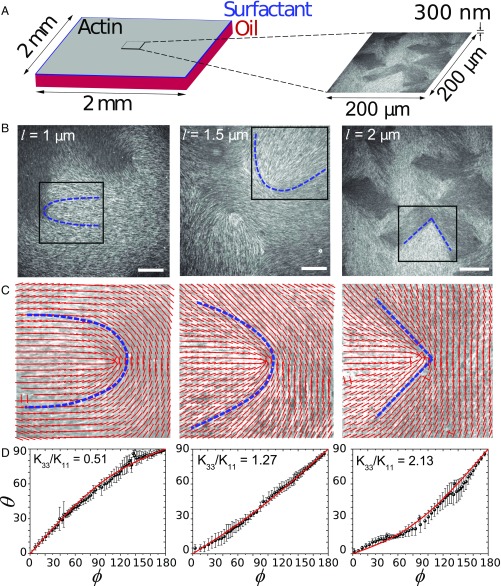
We next demonstrate experimentally that it is possible to vary and visualize the material’s elasticity by constructing LCs comprised of the biopolymer F-actin with variable filament length. The filaments are polymerized starting from a 2-M solution of monomeric actin (G-actin), of which are fluorescently labeled. The filament length is varied from 1 m to 2 m in the presence of variable concentrations of capping protein (see Materials and Methods). Actin filaments are crowded onto an oil–water interface stabilized by surfactant molecules by using methylcellulose as a depletion agent. Over a duration of 30 min to 60 min, a dense film of actin filaments forms a nematic phase (see Movie S1), evidenced by the appearance of several defects, reminiscent of the Schlieren texture of a thermotropic LC after a sudden temperature quench (12). Fig. 2A shows that, as the filament length is increased from m to m, the defect transitions from a U-shape to a V-shape morphology (see auxiliary dashed lines in Fig. 2A). The corresponding director field of these images is obtained through image analysis (28) (see Materials and Methods), and the structural changes of these defects are shown in Fig. 2B. We have, therefore, realized an experimental system in which a dramatic transition in defect morphology is present and optically observed, and, in fact, is captured quantitatively by the theory described above (Fig. 1C). According to the Onsager type model (29), the increase in mesogen length systematically increases of an LC suppressing bend distortion in the nematic director (30). This suggests that the underlying mechanism of defect morphogenesis is due to the change in LC’s elastic constants. As we will elaborate further, the agreement between Figs. 1D and 2 demonstrates that the nematic elasticity theory can describe polydisperse, semiflexible biopolymer suspensions. Our experiments also demonstrate that the mechanical properties of actin-based nematic LCs are highly tunable through biochemical control of semiflexible polymer length.
Fig. 2.
Experiments on changing and visualizing actin-based LC’s elasticity by varying filament length. (A) Schematic illustration of experimental setup. Short F-actin is crowded to the oil–water interface supported by a layer of surfactant molecules. The small region in the middle represents the camera’s field of view used to image actin LC. (B) Fluorescent images of F-actin nematic LC on an oil–water interface. Filament length increases from left to right. Dashed lines highlight the shape of the +1/2 defects. (Scale bar, 30 m.) The director field within the black box is shown in C. (C) Red lines indicate the local director fields near defects highlighted in A. (D) Quantitative measurements of the director fields for the above defects in terms of plots.
To quantify the LC mechanics, we plot the angle against as a function of distance from the defect core, (Fig. 1C). We average over a range of where it remains relatively constant (Fig. S2) and extract by fitting to the theory. The calculations shown in Fig. 2C indicate that actin LCs exhibit from to as increases from m to m. It is known that holds for hard-rod calamitic LCs, and is seen for common disk-like discotic LCs (31). Therefore, in contrast to the behavior of traditional small-molecule thermotropic LCs, one can access both a bend-dominant calamitic regime () and a splay-dominant discotic regime () with the same material by using different mesogen lengths. According to the excluded volume theory for rigid-rod LCs, and , where is the rod length and is the volume fraction (29, 32). Therefore, . Our experiments are consistent with this scaling law: As the average filament length is doubled, increases by a factor of ∼. F-actin is a semiflexible biopolymer, with persistence length m (20). Thus, as polymer length increases, one should expect deviations due to its semiflexible nature. For polymer length m, we find good agreement with rigid-rod theory. However, for lengths m, the semiflexible nature becomes increasingly important as ceases to increase.
When the filament length is comparable to its persistence length, the bend-to-splay ratio ceases to increase and instead declines (see Fig. S3), consistent with previous work in poly--benzylglutamate-based lyotropic LC (33, 34). Therefore, there is limitation on varying the LC’s elasticity by solely relying on changing the length of a semiflexible mesogen.
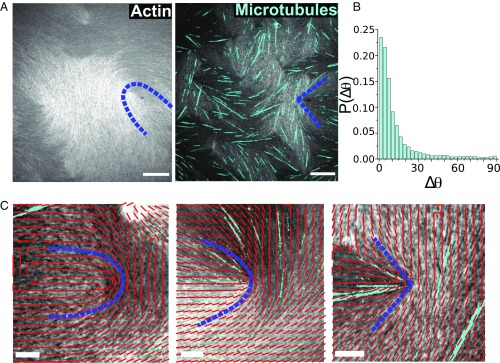
To explore the possibility of accessing a larger range of LC elasticity, we created composite LCs consisting of concentrated actin suspensions interdispersed with sparse concentration of microtubules, which are more rigid biopolymers ( 1 mm). Intuitively, microtubules, if sufficiently sparse, should not affect the splay constant but should increase the bend elasticity of the LC. We explore this possibility by constructing a simple model, based on three assumptions: (i) Microtubules are well dispersed in the actin, (ii) microtubules are relatively short and only weakly bent in the LC, and (iii) microtubule density is sufficiently small to render self-interactions negligible. We observe that microtubules are aligned with the local director field (Fig. 3B). This substantiates our intuition that the rigid polymers should only suppress the bend mode (increase ) without penalizing splay mode ( unchanged). The free energy penalty associated with microtubule bending can be incorporated into the bend distortion term in the Frank–Oseen expression, such that the change in bend constant is a linear function of microtubule number density (see Simple Theory on the Elasticities of Microtubule Doped Actin LC),
| [2] |
where is the average microtubule length, is the microtubule flexural rigidity (19, 35), and is the film thickness. Our measurements estimate nm (see Fig. S4).
Fig. 3.
Experiments on changing actin-based LC’s elasticity by adding rigid microtubules. (A) Optical images of actin LC without and with microtubules. Blue dashed lines highlight the change in defect shape from U to V. (Scale bar, 30 m.) (B) Probability distribution of the angle between microtubule orientations and the local F-actin director fields. (C) Optical images of defects overlaid with the corresponding director field. Microtubule number density increases from left to right followed by the defect shape change from U to V. (Scale bar, 10 m.)
Guided by the considerations outlined above, we add a small concentration of taxol-stabilized microtubules to the solution of actin filaments. Consistent with our hypothesis, we observe that the addition of microtubules has a significant effect on defect morphology. Fig. 3A shows optical images of a system with and without microtubules. In the absence of microtubules, the +1/2 defects’ morphology is U-shaped, as outlined by the blue dashed line, and a significant amount of bending is also visible. When microtubules are added, all defects adopt a V-shape morphology, and bending is suppressed. In Fig. 3C, we find that the number of microtubules, shown in cyan, has a direct influence on the shape of +1/2 defects, which undergoes a gradual transition from a U- to a V-shape morphology, as highlighted by the director field around the defect core. Eq. 2 indicates that the change in the composite LC’s elasticity should only be a function of , which is namely microtubule’s linear density.
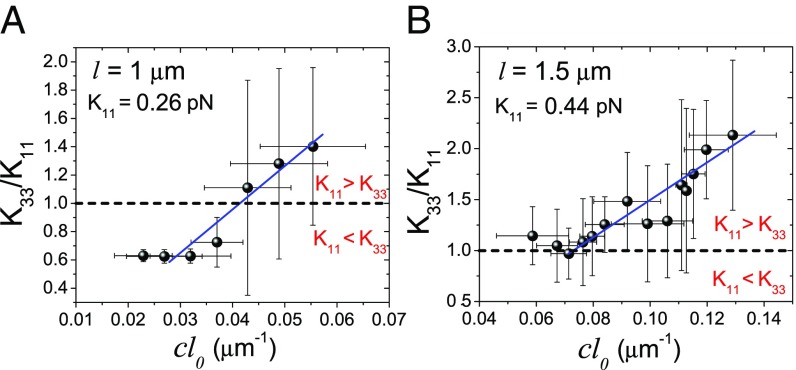
To test this prediction, we inspect several tens of defects for two independent experimental sets. The microtubule’s linear density is determined by measuring and in the vicinity of each individual defect (see Materials and Methods). We measure by fitting the defect morphology to the theory, and we then plot it against . In Fig. 4, we find that both independent sets of experiments show a linear trend between and above a threshold of microtubule’s linear density. In Fig. 4A, the transition from a splay-dominated into a bend-dominated regime that occurs at is observed, exhibiting the high tunability of the composite LC.
Fig. 4.
Experiments on changing actin-based LC’s elasticity by adding rigid microtubules. The two plots are two independent experimental sets, each of which plots the fitted elastic constant ratio as a function of for (A) =1 m for defects and (B) = 1.5 m for 20 defects. The slope gives the direct measure of the splay elastic constant . The error bars correspond to the SD.
Having validated the theory, this framework can be used to measure the absolute values of and . Since the elastic constant ratio is measured before and after microtubules are added, is known. Using Eq. 2 to determine , can be evaluated from . Our calculations indicate that, for actin LCs with m, pN, and, for actin LCs with m, pN and pN. These measured constants are one order of magnitude smaller than those of thermotropic LCs, and also smaller than the few values that have been reported for lyotropic LCs (32, 33, 36). The fact that the long-filament system has a higher elastic constant and higher is also consistent with the Onsager-type model. Note that, in the limit of high concentration of microtubules, the composite’s properties will deviate from the linear equation and approach those of a pure microtubule LC.
Traditional LC elasticity measurements rely on external fields or calibrations (12, 32, 36), a limitation overcome by the use of this protocol. Microtubules in the system play the role of “elastic dopants,” analogous to the chiral dopants that are added to nematic materials to increase chirality (37). Our results provide a framework within which one can simultaneously visualize, tune, and measure the material’s elasticity. We emphasize here that the idea of measuring a material’s mechanical properties by observing defects can be generalized to other ordered systems. Defects are singularity regions in an otherwise ordered material, where different elastic modes compete against each other. Thus, we expect the framework developed here could be extended to characterization of the morphology and statistics of defects, disclinations, or dislocations as a means of probing the elastic properties of other types of materials.
The results presented thus far serve to establish that the theoretical framework adopted here can, in fact, describe the equilibrium structure of lyotropic biopolymers. For emerging applications involving nonequilibrium processes, it is important that such a formalism be also able to describe the dynamics of such systems. In what follows, we therefore turn our attention to the more challenging task of characterizing and predicting the coupling between structure and dynamics that arises in actin-based LCs. When a thermotropic LC is quenched from an isotropic into a nematic state, defects emerge and annihilate each other over time. The interplay between LC elasticity, viscosity, and defect structure (configurations) determines the dynamics of annihilation events. Note that recent efforts have addressed the coupling of structure and dynamics in free-standing smectic LCs (38). In contrast to that work, our actin-based LC system represents a true nematic LC which is free of confining walls (39). As such, it offers a unique 2D platform on which to explore structure-based dynamics.
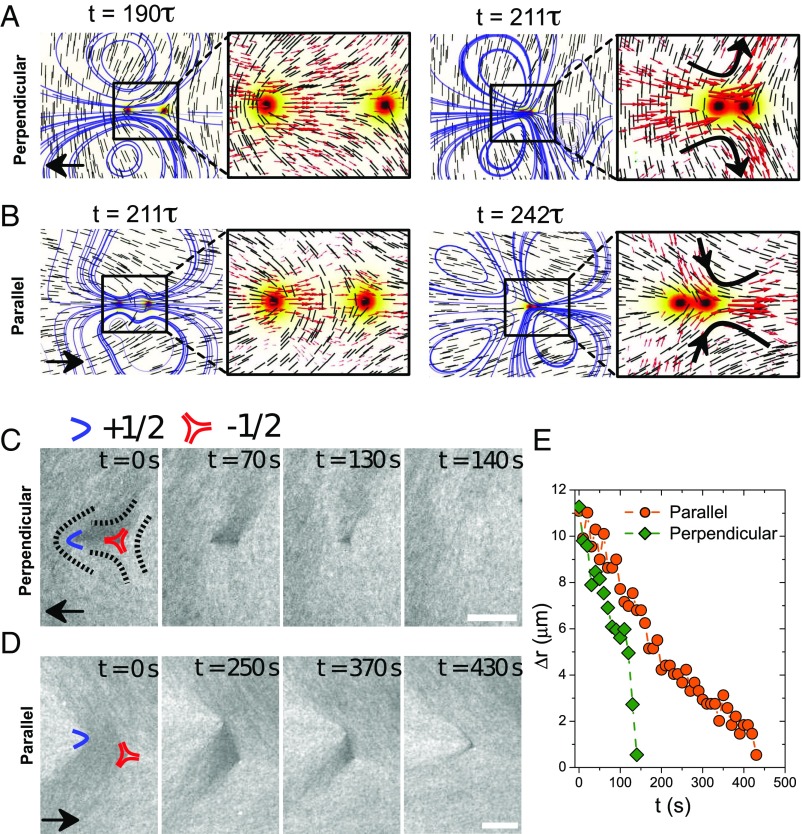
In Fig. 5, we show two typical defect configurations, which differ in the angle between the line connecting the defect cores and the nematic far field. For simplicity, and without loss of generality, we consider two opposite, symmetric cases. In the first, the defect line is parallel to a well-defined far field; in the second, it is perpendicular (Fig. 5 A and B). In both situations, the defects attract each other to lower the system’s total elastic free energy. Thus, in the “perpendicular” case, the defect should move opposite to its orientation, whereas, in the “parallel” case, the defect should move along its orientation (see Movie S2). This is exactly what is observed in our experiments, as shown in Fig. 5 C and D for the perpendicular and parallel cases, respectively, and in Movie S3. Interestingly, in the case of the parallel far field (Fig. 5D), the +1/2 defect deviates from a straight head-on approach to the −1/2 defect. Therefore, we have observed and analyzed two distinct types of defect annihilation events, thanks to the unique optical feature of our nematic system in which defects are optically distinguishable.
Fig. 5.
Two scenarios of defect annihilation events. (A and B) Simulations of defect annihilation with two different defect configurations; black arrows indicate the orientations of defects approaching −1/2 defect from left, short lines show the director field, and curves are the streamlines. Background color corresponds to the order parameter, using the same colorbar as in Fig. 1D. In zoom-in frames, black arrows indicate the inward/outward flows upon annihilation, and red arrows represent the velocity field. (C and D) Time sequence of annihilation as seen in the experiments for perpendicular and parallel case, respectively. Blue boomerangs and red triangles represent +1/2 and −1/2 defects, respectively. (Scale bar, 10 m.) (E) Defect separation, measured in experiment, , plotted as function of time.
We use our theoretical model to investigate how the flow field generated by the defect motion depends on the LC’s elastic constants and the underlying configuration. When two defects approach and eventually annihilate each other, hydrodynamic effects play a key role in the dynamics. In particular, past work has suggested that the defect always moves faster than the defect (40). Our hydrodynamic simulations and experimental observations, however, indicate that this is not the complete story. When one takes into account elasticity and defect configurations, the opposite can be true: A defect may move faster than a defect (see Defect Annihilation). In Fig. 5, we show the effect of defect configurations on an isolated annihilation event. We find that the perpendicular case annihilates faster than the parallel case. If one ignores hydrodynamic effects, the two cases would proceed in an identical manner (under the one-constant assumption). The inclusion of hydrodynamics breaks that symmetry. As shown in Fig. 5, the flow fields corresponding to the two configurations are markedly different. For the perpendicular case, there are two symmetric vortices on the two sides of the defect line (indicated by blue lines in Fig. 5A with an outward transverse flow upon annihilation), whereas, for the parallel case, upon defect annihilation, an extensional flow is produced, and the transverse flow is inward. Because the director field at the defect line in the perpendicular case is aligned with the flow, the corresponding viscosity is low, and the enhanced hydrodynamic flow accelerates the defects’ motion. In the parallel case, the flow direction is perpendicular to the local director field, and the high viscosity suppresses such flow, leading to slower dynamics. The horizontal separation of two defects, r, can be plotted as a function of time as shown in Fig. 5E. Our experiments indicate that, on average, the perpendicular case clearly exhibits faster dynamics than the parallel case, confirming our predictions. Taken together, these results establish that defect structure influences dynamics, a feature that could be exploited to manipulate the transport of cargo in an LC by creating different flow patterns as defects annihilate.
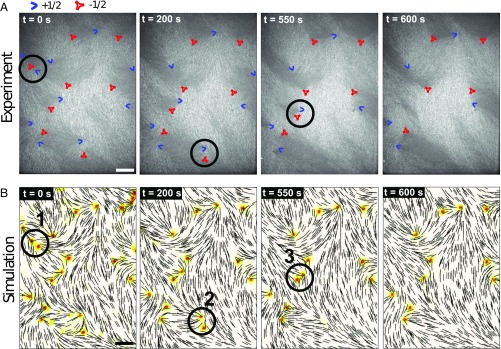
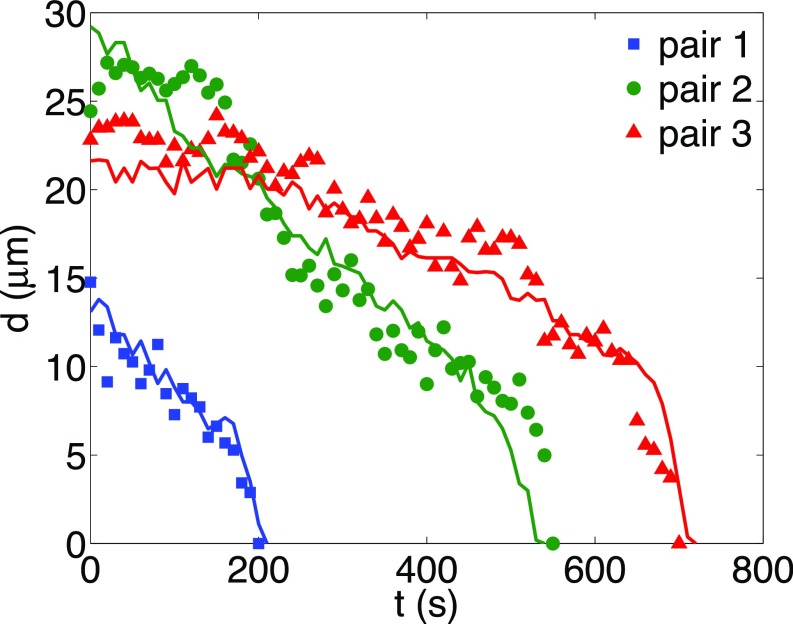
The results presented in Fig. 5 are limited to two isolated defects, and only two ideal, extreme cases (parallel and perpendicular defect configuration) are considered. The question that emerges then is whether the simple formalism adopted here can describe dynamics in the more common case in which multiple defects with nearly arbitrary relative orientations interact with each other (41, 42). To address this question, we now consider a system of area containing tens of defects. We measure the director field from the experiments and use it as the initial condition for a 3D simulation (see Materials and Methods). We run the simulation over an extended period, and examine whether the model can capture the temporal evolution of defects that is observed in the experiments over laboratory time scales (minutes to hours). Our computer simulation can be viewed as analogous to weather forecasting: We take a pattern (director field) as the initial condition, and we rely on a simulation to predict its structure at a future time. In our quasi-2D nematic system, we show four images comparing simulations and experiments at four consecutive times, separated by a time interval of ∼200 s. As shown in Fig. 6 and in Movie S4, the model predicts the three annihilation events in correct chronological order (see the circled defects in Fig. 6), and the individual defect positions after 10 min. Shown in Fig. 7, simulations have also quantitatively captured defect separations for the three annihilating defect pairs. This agreement, which is simply based on the initial defect structure, along with our previous work using the same model to successfully describe active nematics (43), serves to underscore that the hydrodynamic formalism adopted here is able to capture key aspects of the structure and dynamics of lyotropic, polydisperse, actin-based 2D nematic systems. Despite the fact that the LC’s elastic structure and hydrodynamics are both long-ranged and nonlinearly coupled, its defect dynamics can be accurately predicted by our athermal model, implying that such defect dynamics are deterministic.
Fig. 6.
Actin-based LC “weather map.” (A) Consecutive optical images from actin LC equilibration process; blue boomerangs represent defects, and red triangles indicate defects. (B) Consecutive simulation images corresponding to the experiments; black lines depict the local director field, and the background color indicates scalar order parameter (adopting the same colorbar as in Fig. 1). The circled defects annihilate in the next frame. (Scale bars, m.)
Fig. 7.
Metric of the weather map. Defect separation as a function of time for three annihilating defect pairs marked by numbers in Fig. 6. Symbols are experimental measurements, and curves are from simulation.
In conclusion, we have demonstrated a semiflexible biopolymer-based 2D nematic system, which exhibits highly tunable elasticity, and could be useful for future LC technologies relying on topological defects. Its elastic constants can be tuned either by varying the average filament length or by doping it with a sparse concentration of rigid polymers. We show a method to infer the ratio of splay and bend constant by visualizing the morphology of defects. Using this, we find that the bend-to-splay ratio can range from to , such that the material transitions from a splay-dominant to a bend-dominant system. For rigid-polymer doped composites, our simple theoretical model predicts that the change in bend constant is proportional to the linear density of rigid polymers, and enables measurement of the absolute values of bend and splay constants. We further show that the hydrodynamic model of nematic LCs developed in our work describes defect dynamics of this highly structured viscoelastic fluid over extended periods of time. In particular, we have predicted and confirmed experimentally that the annihilation time of a defect pair depends on the defect configuration, a feature that could potentially be used to engineer molecular transport systems that rely on autonomous defect motion.
Materials and Methods
Theory and Modeling.
The bulk free energy of the nematic LC, , is defined as
| [3] |
where is the short-range free energy, is the long-range elastic energy, and is the surface free energy due to anchoring. The is given by a Landau-de Gennes expression of the form (12, 44)
| [4] |
Parameter controls the magnitude of , namely the equilibrium scalar order parameter via . The elastic energy is written as ( means )
| [5] |
If the system is uniaxial, the s in Eq. 5 can be mapped to the s in Eq. 1 via
| [6] |
By assuming a one-elastic-constant , one has and . Pointwise, n is the eigenvector associated with the greatest eigenvalue of the Q tensor at each lattice point.
To obtain the static morphology of topological defects, we minimize Eq. 3 with respect to the Q tensor via a Ginzburg–Landau algorithm (45). To simulate the LC’s nonequilibrium dynamics, a hybrid lattice Boltzmann method is used to simultaneously solve a Beris–Edwards equation and a momentum equation which accounts for the backflow effects. By introducing a velocity gradient , strain rate , vorticity , and a generalized advection term
| [7] |
one can write the Beris–Edwards equation (46) according to
| [8] |
The constant is related to the material’s aspect ratio, and is related to the rotational viscosity of the system by (47). The molecular field H, which drives the system toward thermodynamic equilibrium, is given by
| [9] |
where is a symmetric and traceless operator. When velocity is absent, i.e., , the Beris–Edwards equation, Eq. 8, reduces to Ginzburg–Landau equation
To calculate the static structures of defects, we adopt the above equation to solve for the Q tensor at equilibrium.
Degenerate planar anchoring is implemented through a Fournier–Galatola expression (48) that penalizes out-of-plane distortions of the Q tensor. The associated free energy expression is given by
| [10] |
where and . Here P is the projection operator associated with the surface normal as . The evolution of the surface Q field is governed by (49)
| [11] |
where with , namely nematic coherence length. The above equation is equivalent to the mixed boundary condition given in ref. 50 for steady flows.
Using an Einstein summation rule, the momentum equation for the nematics can be written as (47, 51)
| [12] |
The stress is defined as
| [13] |
where is the isotropic viscosity, and the hydrostatic pressure is given by (52)
| [14] |
The temperature is related to the speed of sound by . We solve the evolution equation, Eq. 8, using a finite difference method. The momentum equation, Eq. 12, is solved simultaneously via a lattice Boltzmann method over a D3Q15 grid (53). The implementation of stress follows the approach proposed by Guo et al. (54). Our model and implementation were validated by comparing our simulation results to predictions using the Ericksen–Leslie–Parodi theory (55–57). The units are chosen as follows: The unit length is chosen to be m, characteristic of the filament length; the characteristic viscosity is set to ; and the force scale is made to be N. , , and lead to and . Other parameters are chosen to be , , , , and , leading to . The simulation is performed in a rectangular box. The boundary conditions in the plane are periodic. Two confining walls are introduced in the dimension, with strong degenerate planar anchoring, ensuring a quasi-2D system. In the weather map simulation, m and m, larger than the experimental image, to suppress boundary effects; m is chosen to correspond to the sample thickness, mimicking the hydrodynamic screening effects of the substrates in the experiments. We refer the reader to ref. 49 for additional details on the numerical methods used here.
Experimental Methods.
Proteins.
Monomeric actin is purified from rabbit skeletal muscle acetone powder (58) (Pel-Freez Biologicals) stored at °C in G-buffer (2 mM Tris HCL pH 8.0, 0.2 mM APT, 0.2 mM CaCl2, 0.2 mM DTT, NaN3). Fluorescent labeling of actin was done with a tetramethylrhodamine-6-maleimide dye (Life Technologies). Capping protein [mouse, with a HisTag, purified from bacteria (59); gift from the Dave Kovar laboratory, The University of Chicago, Chicago] is used to regulate actin filament length. The 1:10 ratio of fluorescently labeled tubulin (cat TL488M; Cytoskeleton) and unlabeled tubulin (cat HTS03; Cytoskeleton) were incubated at 4 °C in PEM-100 (100 mM Na-PIPES, 1 mM MgSO4,1 mM EGTA, pH 6.8) at 5 mg/mL. The mixture was centrifuged at 4 °C at 30,000 × g for 10 min, and the supernatant was incubated in PEM-100 at 37 °C in the presence of 1 mM GMPCPP (cat #NU-405L; Jena Biosciences) for 20 min. Taxol was added to stabilize polymers to 50 μM final concentration. The microtubule length was shortened by shearing through Hamilton Syringe (Mfr #81030, Item #EW-07939-13) before adding 3 μL of volume to the actin polymers.
Experimental assay and microscopy.
The actin is polymerized in 1X F-buffer (10 mM imidazole, pH 7.5, 50 mM KCL, 0.2 mM EGTA, 1 mM MgCl2, and 1 mM ATP). To prevent photobleaching, an oxygen scavenging system [4.5 mg/mL of glucose, 2.7 mg/mL of glucose oxidase (cat 345486, Calbiochem), 17,000 units/mL of catalase (cat 02071, Sigma), and 0.5 vol -mercaptaethanol] is added; 0.3 wt 15 cP methylcellulose is added as the crowding agent. Actin from frozen stocks stored in G-buffer is added to a final concentration of 2 M with a ratio 1:5 TMR-maleimide labeled:unlabeled actin monomer. To control the filament length, frozen capping protein stocks are thawed on ice and are added at the same time (0.3 mol to 0.17 mol ). We call this assay “polymerization mixture” from hereon.
The experiment is done in a cylindrical chamber which is a glass cylinder glued to a coverslip (60). Coverslips are sonicated clean with water and ethanol. The surface is treated with triethoxy(octyl)silane in isopropanol to produce a hydrophobic surface. To prepare a stable oil–water interface, PFPE-PEG-PFPE surfactant (cat 008, RAN Biotechnologies) is dissolved in Novec-7500 Engineered Fluid (3M) to a concentration of 2 wt . To avoid flows at the surface, a small mm teflon mask is placed on the treated coverslip before exposing it to UV/ozone for 10 min. The glass cylinder is thoroughly cleaned with water and ethanol before gluing it to the coverslip, using instant epoxy. Then L of oil–surfactant solution is added into the chamber, and quickly pipetted out to leave a thin coating. The thickness of the resulting oil film is ∼50 m, and our results are independent of its small variations. When the oil is spread on the glass surface, it often shows a slight bulge (5 m) in the middle. Therefore, the sample is always imaged in the middle of the film over the camera field of view, which is ∼200 m 200 m, to make sure that the sample remains in focus over this area, which is far away from the edges. Imaging close to the edges is avoided. The polymerization mixture is immediately added afterward. For experiments on defect shape change as a function of microtubule concentration, taxol-stabilized microtubules were added to 1 g/mL of the final concentration. We waited for a period of 30 min to 60 min before acquiring images.
The sample is imaged using an inverted microscope (Eclipse Ti-E; Nikon) with a spinning disk confocal head (CSU-X; Yokagawa Electric), equipped with a Complementary metal-oxide semiconductor camera (Zyla-4.2 USB 3; Andor). A 40 1.15 NA water-immersion objective (Apo LWD; Nikon) was used for imaging. Images were collected using 568-nm and 647-nm excitation for actin and microtubules, respectively. Image acquisition was controlled by Metamorph (Molecular Devices).
Image analysis.
To extract the director field, the optical images were band-pass filtered and unsharp masked in the ImageJ software (61) to remove noise and spatial irregularities in brightness.
The resulting images were analyzed using an algorithm as described in methods of Cetera et al. (28). In short, the algorithm computes 2D fast Fourier transform of a small local square section (of side ) of the image and uses an orthogonal vector to calculate the local actin orientation. The sections were overlapped over a distance to improve statistics. The and are varied over 15 m to 30 m and 1 m to 3 m, respectively, for different images to minimize errors in the local director without changing the final director field.
The microtubule number density () and average length () are estimated using ImageJ. The image around a +1/2 defect is cropped to a rectangular shape of area centered at its core (Fig. 3C). The resulting image is then thresholded to separate all of the microtubule bundles whose is extracted from the major axis of the fitted ellipse. To extract , we plot the distribution of background-corrected microtubule intensity and assign the single microtubule intensity () to the value where the distribution shows a peak. The bundle intensity was scaled with to extract (=), which is the number of microtubules in a bundle. The was later estimated by calculating , where denotes the sum over all of the bundles.
Supplementary Material
Acknowledgments
N.K. thanks Dr. Kimberly Weirich for useful discussions and purified proteins, Dr. Samantha Stam for assisting with experiments, and Dr. Patrick Oakes for helping in director field analysis. R.Z. acknowledges helpful discussions with Dr. Shuang Zhou and Dr. Takuya Yanagimachi, and is grateful for the support of the University of Chicago Research Computing Center for assistance with the calculations carried out in this work. This work was supported primarily by the University of Chicago Materials Research Science and Engineering Center, which is funded by the National Science Foundation (NSF) under Award DMR-1420709. M.L.G. and J.L.R. acknowledge support from NSF Grant MCB-1344203. J.J.d.P. acknowledges support from NSF Grant DMR-1710318. The design of tubulin–actin composites in the J.L.R. and J.J.d.P. group was supported by the US Army Research Office through the Multidisciplinary University Research Initiative (MURI Award W911NF-15-1-0568). N.K. acknowledges the Yen Fellowship of the Institute for Biophysical Dynamics, The University of Chicago.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1713832115/-/DCSupplemental.
References
- 1.Chen RH. Liquid Crystal Displays: Fundamental Physics and Technology. Wiley; New York: 2011. [Google Scholar]
- 2.Warner M, Terentjev EM. Liquid Crystal Elastomers. Vol 120 Oxford Univ Press; Oxford: 2003. [Google Scholar]
- 3.Camacho-Lopez M, Finkelmann H, Palffy-Muhoray P, Shelley M. Fast liquid-crystal elastomer swims into the dark. Nat Mater. 2004;3:307–310. doi: 10.1038/nmat1118. [DOI] [PubMed] [Google Scholar]
- 4.Muševič I, Škarabot M, Tkalec U, Ravnik M, Žumer S. Two-dimensional nematic colloidal crystals self-assembled by topological defects. Science. 2006;313:954–958. doi: 10.1126/science.1129660. [DOI] [PubMed] [Google Scholar]
- 5.Rahimi M, et al. Nanoparticle self-assembly at the interface of liquid crystal droplets. Proc Natl Acad Sci USA. 2015;112:5297–5302. doi: 10.1073/pnas.1422785112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang X, Miller DS, Bukusoglu E, de Pablo JJ, Abbott NL. Topological defects in liquid crystals as templates for molecular self-assembly. Nat Mater. 2015;15:106–112. doi: 10.1038/nmat4421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lin I-H, et al. Endotoxin-induced structural transformations in liquid crystalline droplets. Science. 2011;332:1297–1300. doi: 10.1126/science.1195639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sadati M, et al. Liquid crystal enabled early stage detection of beta amyloid formation on lipid monolayers. Adv Funct Mater. 2015;25:6050–6060. [Google Scholar]
- 9.Humar M, Ravnik M, Pajk S, Muševič I. Electrically tunable liquid crystal optical microresonators. Nat Photon. 2009;3:595–600. [Google Scholar]
- 10.Zhang R, et al. Controlled deformation of vesicles by flexible structured media. Sci Adv. 2016;2:e1600978. doi: 10.1126/sciadv.1600978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sengupta A, Herminghaus S, Bahr C. Liquid crystal microfluidics: Surface, elastic and viscous interactions at microscales. Liq Cryst Rev. 2014;2:73–110. [Google Scholar]
- 12.de Gennes P, Prost J. The Physics of Liquid Crystals. Oxford Univ Press; Oxford: 1995. [Google Scholar]
- 13.Tomar V, Hernández SI, Abbott NL, Hernandez-Ortiz JP, de Pablo JJ. Morphological transitions in liquid crystal nanodroplets. Soft Matter. 2012;8:8679–8689. [Google Scholar]
- 14.Miller DS, Abbott NL. Influence of droplet size, pH and ionic strength on endotoxin-triggered ordering transitions in liquid crystalline droplets. Soft Matter. 2013;9:374–382. doi: 10.1039/C2SM26811F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rahimi M, et al. Segregation of liquid crystal mixtures in topological defects. Nat Commun. 2017;8:15064. doi: 10.1038/ncomms15064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Woolverton CJ, Gustely E, Li L, Lavrentovich OD. Liquid crystal effects on bacterial viability. Liq Cryst. 2005;32:417–423. [Google Scholar]
- 17.Luk YY, Jang CH, Cheng LL, Israel BA, Abbott NL. Influence of lyotropic liquid crystals on the ability of antibodies to bind to surface-immobilized antigens. Chem Mater. 2005;17:4774–4782. [Google Scholar]
- 18.Park H-S, Lavrentovich OD. Liquid Crystals Beyond Displays: Chemistry, Physics, and Applications. Wiley; New York: 2012. [Google Scholar]
- 19.Blanchoin L, Boujemaa-Paterski R, Sykes C, Plastino J. Actin dynamics, architecture, and mechanics in cell motility. Physiol Rev. 2014;94:235–263. doi: 10.1152/physrev.00018.2013. [DOI] [PubMed] [Google Scholar]
- 20.Ott A, Magnasco M, Simon A, Libchaber A. Measurement of the persistence length of polymerized actin using fluorescence microscopy. Phys Rev E. 1993;48:R1642–R1645. doi: 10.1103/physreve.48.r1642. [DOI] [PubMed] [Google Scholar]
- 21.Viamontes J, Oakes PW, Tang JX. Isotropic to nematic liquid crystalline phase transition of F-actin varies from continuous to first order. Phys Rev Lett. 2006;97:118103. doi: 10.1103/PhysRevLett.97.118103. [DOI] [PubMed] [Google Scholar]
- 22.Weirich KL, et al. Liquid behavior of cross-linked actin bundles. Proc Natl Acad Sci USA. 2017;114:2131–2136. doi: 10.1073/pnas.1616133114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sanchez T, Chen DTN, DeCamp SJ, Heymann M, Dogic Z. Spontaneous motion in hierarchically assembled active matter. Nature. 2012;491:431–434. doi: 10.1038/nature11591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Weeds A, Maciver S. F-actin capping proteins. Curr Opin Cell Biol. 1993;5:63–69. doi: 10.1016/s0955-0674(05)80009-2. [DOI] [PubMed] [Google Scholar]
- 25.Hudson SD, Thomas EL. Frank elastic-constant anisotropy measured from transmission-electron-microscope images of disclinations. Phys Rev Lett. 1989;62:1993–1996. doi: 10.1103/PhysRevLett.62.1993. [DOI] [PubMed] [Google Scholar]
- 26.Kleman M, Lavrentovich OD. Soft Matter Physics. Springer; New York: 2001. [Google Scholar]
- 27.Frank FC. I. liquid crystals. on the theory of liquid crystals. Discuss Faraday Soc. 1958;25:19–28. [Google Scholar]
- 28.Cetera M, et al. Epithelial rotation promotes the global alignment of contractile actin bundles during drosophila egg chamber elongation. Nat Commun. 2014;5:5511. doi: 10.1038/ncomms6511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Odijk T. Elastic constants of nematic solutions of rod-like and semi-flexible polymers. Liq Cryst. 1986;1:553–559. [Google Scholar]
- 30.Narayan V, Menon N, Ramaswamy S. Nonequilibrium steady states in a vibrated-rod monolayer: Tetratic, nematic, and smectic correlations. J Stat Mech Theory Exp. 2006;2006:P01005. [Google Scholar]
- 31.Demus D, Goodby JW, Gray GW, Spiess HW, Vill V. Handbook of Liquid Crystals, Low Molecular Weight Liquid Crystals I: Calamitic Liquid Crystals. Wiley; New York: 2011. [Google Scholar]
- 32.Zhou S, et al. Elasticity, viscosity, and orientational fluctuations of a lyotropic chromonic nematic liquid crystal disodium cromoglycate. Soft Matter. 2014;10:6571–6581. doi: 10.1039/c4sm00772g. [DOI] [PubMed] [Google Scholar]
- 33.Lee S-D, Meyer RB. Light scatting measurements of anisotropic viscoelastic coefficients of a main-chain polymer nematic liquid crystal. Liq Cryst. 1990;7:15–29. [Google Scholar]
- 34.Lee SD, Meyer RB. Liquid Crystallinity in Polymers: Principles and Fundamental Properties. Wiley; New York: 1991. [Google Scholar]
- 35.Hawkins TL, Sept D, Mogessie B, Straube A, Ross JL. Mechanical properties of doubly stabilized microtubule filaments. Biophys J. 2013;104:1517–1528. doi: 10.1016/j.bpj.2013.02.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhou S, et al. Elasticity of lyotropic chromonic liquid crystals probed by director reorientation in a magnetic field. Phys Rev Lett. 2012;109:037801. doi: 10.1103/PhysRevLett.109.037801. [DOI] [PubMed] [Google Scholar]
- 37.Xu F, Crooker PP. Chiral nematic droplets with parallel surface anchoring. Phys Rev E. 1997;56:6854–6860. [Google Scholar]
- 38.Stannarius R, Harth K. Defect interactions in anisotropic two-dimensional fluids. Phys Rev Lett. 2016;117:157801. doi: 10.1103/PhysRevLett.117.157801. [DOI] [PubMed] [Google Scholar]
- 39.Yanagimachi T, Yasuzuka S, Yamamura Y, Saito K. Cell gap dependence of nematic backflow around annihilating disclination pair. J Phys Soc Jpn. 2012;81:074603. [Google Scholar]
- 40.Tóth G, Denniston C, Yeomans JM. Hydrodynamics of topological defects in nematic liquid crystals. Phys Rev Lett. 2002;88:105504. doi: 10.1103/PhysRevLett.88.105504. [DOI] [PubMed] [Google Scholar]
- 41.Vromans AJ, Giomi L. Orientational properties of nematic disclinations. Soft Matter. 2016;12:6490–6495. doi: 10.1039/c6sm01146b. [DOI] [PubMed] [Google Scholar]
- 42.Tang X, Selinger JV. Orientation of topological defects in 2D nematic liquid crystals. Soft Matter. 2017;13:5481–5490. doi: 10.1039/c7sm01195d. [DOI] [PubMed] [Google Scholar]
- 43.Zhang R, Zhou Y, Rahimi M, de Pablo JJ. Dynamic structure of active nematic shells. Nat Commun. 2016;8:13483. doi: 10.1038/ncomms13483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Landau L, Lifshitz E. Statistical Physics. 3rd Ed Pergamon; Oxford: 1980. [Google Scholar]
- 45.Ravnik M, Žumer S. Landau-de gennes modelling of nematic liquid crystal colloids. Liq Cryst. 2009;36:1201–1214. [Google Scholar]
- 46.Beris AN, Edwards BJ. Thermodynamics of Flowing Systems with Internal Microstructure. Oxford Univ Press; New York: 1994. [Google Scholar]
- 47.Denniston C, Orlandini E, Yeomans JM. Lattice Boltzmann simulations of liquid crystal hydrodynamics. Phys Rev E. 2001;63:056702. doi: 10.1103/PhysRevE.63.056702. [DOI] [PubMed] [Google Scholar]
- 48.Fournier J, Galatola P. Modeling planar degenerate wetting and anchoring in nematic liquid crystals. Europhys Lett. 2005;72:403–409. [Google Scholar]
- 49.Zhang R, Roberts T, Aranson I, de Pablo JJ. Lattice Boltzmann simulation of asymmetric flow in nematic liquid crystals with finite anchoring. J Chem Phys. 2016;14:084905. doi: 10.1063/1.4940342. [DOI] [PubMed] [Google Scholar]
- 50.Batista VMO, Blow ML, Telo da Gama MM. The effect of anchoring on the nematic flow in channels. Soft Matter. 2015;11:4674–4685. doi: 10.1039/c5sm00249d. [DOI] [PubMed] [Google Scholar]
- 51.Denniston C, Marenduzzo D, Orlandini E, Yeomans JM. Lattice Boltzmann algorithm for three-dimensional liquid-crystal hydrodynamics. Philos Trans R Soc Lond A. 2004;362:1745–1754. doi: 10.1098/rsta.2004.1416. [DOI] [PubMed] [Google Scholar]
- 52.Fukuda J, Yokoyama H, Yoneya M, Stark H. Interaction between particles in a nematic liquid crystal: Numerical study using the landau-de gennes continuum theory. Mol Cryst Liq Cryst. 2005;435:63–74. [Google Scholar]
- 53.Guo Z, Shu C. Lattice Boltzmann Method and its Applications in Engineering. 1st Ed World Sci; Singapore: 2013. [Google Scholar]
- 54.Guo Z, Zheng C, Shi B. Discrete lattice effects on the forcing term in the lattice boltzmann method. Phys Rev E. 2002;65:046308. doi: 10.1103/PhysRevE.65.046308. [DOI] [PubMed] [Google Scholar]
- 55.Ericksen JL. Continuum theory of liquid crystals of nematic type. Mol Cryst Liq Cryst. 1969;7:153–164. [Google Scholar]
- 56.Leslie FM. Some constitutive equations for anisotropic fluids. Q J Mech Appl Math. 1966;19:357–370. [Google Scholar]
- 57.Parodi O. Stress tensor for a nematic liquid crystal. J Phys France. 1970;31:581–584. [Google Scholar]
- 58.Spudich JA, Watt S. The regulation of rabbit skeletal muscle contraction: I. Biochemical studies of the interaction of the tropomyosin-troponin complex with actin and the proteolytic fragments of myosin. J Biol Chem. 1971;246:4866–4871. [PubMed] [Google Scholar]
- 59.Palmgren S, Ojala PJ, Wear MA, Cooper JA, Lappalainen P. Interactions with PIP2, ADP-actin monomers, and capping protein regulate the activity and localization of yeast twinfilin. J Cell Biol. 2001;155:251–260. doi: 10.1083/jcb.200106157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Stam S, et al. Filament rigidity and connectivity tune the deformation modes of active biopolymer networks. Proc Natl Acad Sci USA. 2017;114:E10037–E10045. doi: 10.1073/pnas.1708625114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Rasband WS. Imagej (US Natl Inst Health, Bethesda), Tech Rep 1997-2009.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.