Summary
Head direction cells form an internal compass signaling head azimuth orientation even without visual landmarks. This property is generated by a neuronal ring attractor that is updated using rotation velocity cues. The properties and origin of this velocity drive remain, however, unknown. We propose a quantitative framework whereby this drive represents a multisensory self-motion estimate computed through an internal model that uses sensory prediction error of vestibular, visual, and somatosensory cues to improve on-line motor drive. We show how restraint-dependent strength of recurrent connections within the attractor can explain differences in head direction cell firing between free foraging and restrained passive rotation. We also summarize recent findings on how gravity influences azimuth coding, indicating that the velocity drive is not purely egocentric. Finally, we show that the internal compass may be three-dimensional and hypothesize that the additional vertical degrees of freedom use global allocentric gravity cues.
eTOC
Laurens and Angelaki present a quantitative model of how multisensory self-motion signals update the firing rate of head direction cells to maintain a sense of orientation in light or darkness, during active or passive motion, and during three-dimensional movements.
INTRODUCTION
Our ability to navigate through the environment is an essential cognitive function, which is subserved by specialized brain regions dedicated to processing spatial information (O’Keefe and Nadel, 1978; Mittelstaedt and Mittelstaedt, 1980). Of these spatial representations, head direction (HD) cells form an internal compass and are traditionally characterized by an increase in firing when the head faces a preferred direction (PD) in the horizontal plane (Taube et al., 1990a,b; Sharp et al., 2001a; Taube, 2007). In the rodent, the largest concentration of HD cells is found in the anterior thalamus (Taube, 1995; Taube and Burton, 1995), which supplies HD signals to other areas of the limbic system (Goodridge and Taube, 1997; Winter et al., 2015). The HD network is highly influenced by visual allocentric landmarks that serve as reference (Taube, 2007; Yoder et al., 2011), but is also able to maintain and update head direction in the absence of visual cues, e.g., when an animal explores an environment in darkness, by integrating rotation velocity signals over time. It is broadly accepted that these properties are generated through recurrent connections that form a neuronal attractor, which integrates rotation velocity signals (Redish et al., 1996; Skaggs et al., 1995; Zhang, 1996; Stringer et al., 2002). Although neuronal recordings support this concept (Peyrache et al., 2015; Kim et al., 2017), the underlying physiology remains poorly understood.
Lesions of the vestibular system disrupt HD responses, indicating that central vestibular networks are a major source of self-motion information (Stackman et al., 2002; Muir et al., 2009, Yoder and Taube, 2009; reviewed by Clark and Taube, 2012). However, the computational principles of how vestibular cues influence HD cells have never been worked out. Efforts to understand these principles have been hindered by the lack of a theoretical perspective that unites well-defined (but traditionally segregated) principles about (1) how a neuronal attractor works, (2) basic vestibular computations (particularly those related to three dimensional orientation) and visual-vestibular interactions, (3) how vestibular cues and efference motor copies are integrated during voluntary, self-generated head movements, and (4) recent findings on how HD networks encode head orientation in three dimensions (3D) (Calton and Taube, 2005; Finkelstein et al., 2015; Page et al. 2017). This review aims at presenting such a missing quantitative perspective, linking vestibular function relevant to spatial orientation with the properties of HD cells and the underlying attractor network. Our presentation is organized into four main sections.
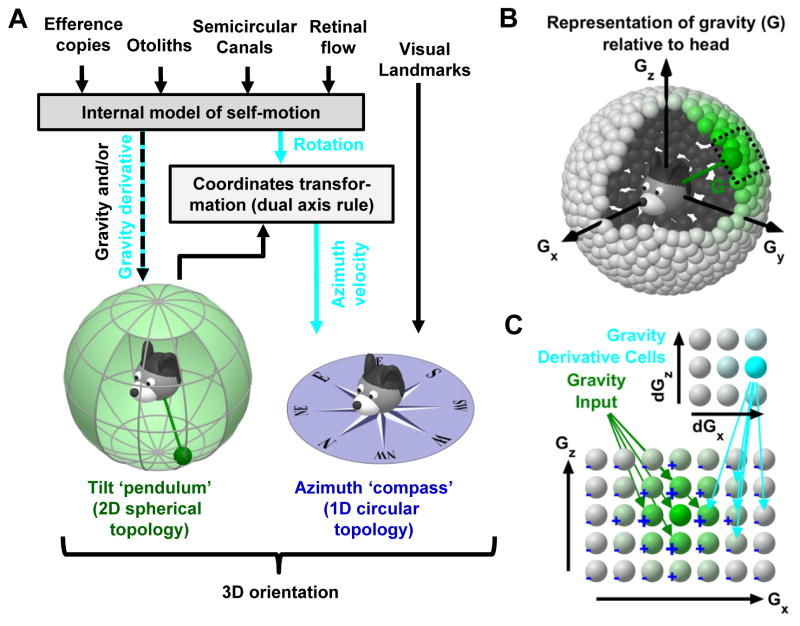
First, we provide some intuition about the vestibular system’s role during actively-generated versus passive, unpredictable head movements, including a quantitative perspective of how rotational self-motion cues from vestibular, visual, somatosensory and efference motor copies interact (details can be found in Laurens and Angelaki, 2017). We then unite this self-motion model with a standard model of the head direction attractor in a single conceptual framework. We highlight that vestibular nuclei (VN) neurons with attenuated responsiveness during active head movements (reviewed in Cullen, 2012; 2014) carry sensory prediction error signals. Thus, they are inappropriate for driving the HD ring attractor, which explains why there are no direct projections from the VN to the lateral mammillary and dorsal tegmental nuclei (Biazoli et al., 2006; Clark et al., 2012), areas whose bi-directional connectivity is assumed to house the HD attractor (Basset et al., 2007; Clark and Taube, 2012; Sharp et al., 2001a). Instead, we propose that the attractor velocity drive comes from the final self-motion estimate, which includes contributions of visual, vestibular, somatosensory and efference copy cues (Laurens and Angelaki, 2017). We discuss the implications of these properties for studying HD cells in freely moving or restrained animals, as well as in virtual reality. We highlight the role of the vestibular sensors and why, although the HD attractor drive is not exclusively driven by a sensory vestibular signal, vestibular lesions are detrimental to its directional properties.
Second, we summarize the fundamental properties of attractor networks, such that we can then disentangle the functional role of two factors: changes in the gain of self-motion velocity inputs to the attractor, and changes in the strength of recurrent connections within the attractor itself. We show through simulations that restraint-dependent changes on HD cell response properties, including experimentally reported decreases in HD cell modulation during passive/restrained versus active/unrestrained movements (Shinder and Taube, 2011; 2014a), can be reproduced through changes in the strength of recurrent connections within the HD attractor network. In contrast, changes in the gain of self-motion drive can explain the “bursty” activity, with drifting PD tuning, which has been reported previously in canal-lesioned animals (Muir et al., 2009) and recently produced by optogenetic inhibition of the nucleus prepositus (Butler et al. 2017).
Third, we summarize recent findings on how and why the animal’s orientation relative to gravity influences the properties of HD cells, including the loss or reversal of HD tuning in upside-down orientations (Finkelstein et al., 2015; Calton and Taube, 2005). We show that these experimental findings are readily explained by a recently proposed re-definition of the concept of azimuth during three-dimensional motion and of the three-dimensional properties of the self-motion signal that drives the HD attractor network (Page et al. 2017). In fact, this framework shows that egocentric velocity (e.g., yaw signals from the horizontal semicircular canals) alone cannot update the HD attractor. Instead, additional self-motion components encoding earth-horizontal azimuth velocity are necessary.
Fourth, we highlight recent findings that HD cells may constitute a 3D (rather than azimuth-tuned only) compass (Finkelstein et al., 2015) and hypothesize that the additional vertical degrees of freedom may also have their primary drive from the vestibular system: in this case, by coding head orientation relative to gravity (Laurens et al., 2016).
Finally, we summarize recent findings that arthropods possess a neuronal representation of HD whose properties and dependence on self-motion input resembles the HD system of mammals.
Collectively, this review provides a quantitative framework that forms a working hypothesis on how multisensory self-motion cues update the HD attractor. Most importantly, we show that HD cell properties in both freely moving and restrained animals, as well as during planar exploration and 3D motion, are readily interpreted when these multiple elements, which are for the first time collectively presented together, are considered.
NEURONAL ATTRACTOR
To begin, it is important to establish that there are three major components of the HD attractor (Redish et al., 1996; Skaggs et al., 1995; Zhang, 1996; Stringer et al., 2002; Peyrache et al., 2015; Kim et al., 2017), which are fundamental for understanding HD responses (Fig. 1A–C):
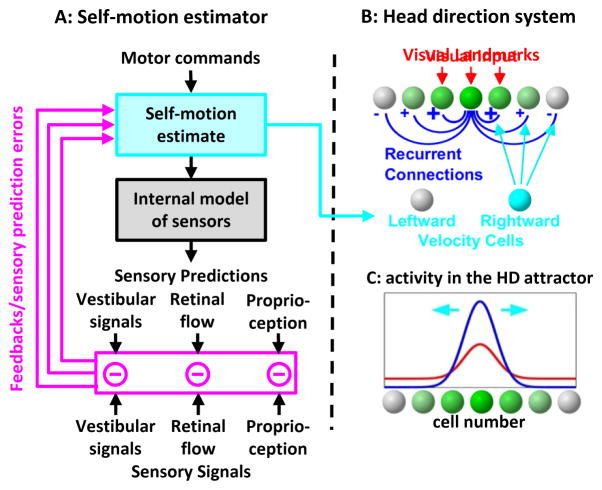
Figure 1. Self-motion drive to the head direction system.
(A, B) Schematic of the self-motion estimator, where actual sensory signals (vestibular, proprioceptive, retinal flow) are compared with the corresponding predictions (generated through an internal model of the sensors) to generate sensory prediction errors (A, magenta) that improve the self-motion estimate (cyan). It is this final self-motion estimate, and neither the motor command nor the sensory prediction error (magenta), that has the appropriate properties (see simulations in Fig. 2) for updating the HD ring attractor (B), which is also anchored to visual landmarks. (C) Simulations of a HD ring attractor (Stringer et al., 2002) during random exploration. Activity of one neuron of the head direction attractor, under the influence of visual inputs alone (red) or with the additional influence of recurrent connections (blue). Self-motion signals result in a sideward shift of the hill of activity (cyan arrows).
A ‘landmark signal’ originating from the visual system activates cells whose PD corresponds to the animal’s current orientation in the environment (Fig. 1B).
Recurrent connections whereby neighboring cells activate each other and inhibit distant cells. Through mutual excitation, cells that are initially activated by the visual landmark signal activate each other even further, while inhibiting other cells. This mechanism amplifies the hill of activity and confers it the ability to sustain itself in the absence of visual inputs (Fig. 1C).
Self-motion velocity signals are thought to be conveyed by ‘velocity cells’ that influence the network by reinforcing recurrent connections in one direction, causing the hill of activity to slide in the corresponding direction (Fig. 1A,B, ‘self-motion signal’). This mechanism allows the attractor to integrate angular velocity over time.
A NEEDLESS CONUNDRUM
We continue by discussing the properties of this self-motion velocity signal that provides the input to the HD cell attractor. In particular, we will address a confusion that exists in the field. As summarized above, lesions of the vestibular system disrupt HD responses, and head direction cell tuning disappears in vestibular deficient animals (Stackman et al., 2002; Muir et al., 2009, Yoder and Taube, 2009; reviewed by Clark and Taube, 2012), indicating that vestibular signals are required for the HD network to operate. On the other hand, actively-exploring animals generally have stronger HD tuning than passively-rotating, restrained animals (reviewed in Shinder and Taube 2014a,b), a property that has been interpreted as evidence that efference copies of motor commands are also a critical component of the velocity input to the HD ring attractor. Yet, normal HD tuning can be measured in restrained animals when they are rotated rapidly (Shinder and Taube 2011, 2014a), a fact that, again, suggests that vestibular signals play a primordial role in generating HD responses. Together, these observations create a puzzle that has never been clearly resolved.
To make matters worse, there is a widespread misconception that vestibular signals are functionally unimportant in actively moving animals. This notion has been created by inappropriately interpreting the functional implications of the fact that a particular (but prevalent) cell type in the VN shows reduced motion sensitivity during actively-generated rotations and translations (reviewed by Cullen 2012; 2014). The misinterpretation of the implications of this experimental observation has led to the conundrum: if the vestibular pathway does not encode self-motion during active movements, how is the HD signal computed, and why does the HD network appear to require a functional vestibular system (Cullen, 2012; Cullen and Taube, 2017; Shinder and Taube, 2014b)? Up to date, no solution to the conundrum, that would explain experimental findings in both freely moving and restrained animals or following vestibular lesions, has been proposed. Furthermore, no study has attempted to address this question in the light of a quantitative, computational framework.
To begin with, we stress that to understand the role of the vestibular system and other multisensory self-motion cues on the updating of the HD signal, it is important to gain insight from computational principles that govern the dynamics of self-motion estimation. As will be shown next, the conundrum introduced by Cullen and Taube (2017) (see also Shinder and Taube, 2014b) disappears when the interpretation that “vestibular self-motion signals are attenuated during active motion” is removed. In the only up-to-date modeling effort to understand how vestibular and extra-vestibular cues are combined during actively-generated head movements, we (Laurens and Angelaki, 2017) have proposed that the vestibular system is not only functioning, but also critically useful and important, for accurate self-motion sensation during both passive and active head movements. By considering a dynamical model of self motion processing that operates in unison during any type (active or passive) of motion, we are thus bridging a noticeable gap between the vestibular, motor control and navigation fields, as summarized next.
INTERNAL MODELS, SENSORY PREDICTION AND ACTIVE VERSUS PASSIVE MOTION IN THE VESTIBULAR SYSTEM
Our insights come from a simple Kalman filter model, where we have extended a well established framework developed previously for the optimal processing of passive vestibular signals using internal models (Laurens 2006; Laurens and Droulez, 2007; 2008; Laurens et al. 2010, 2011a; Laurens and Angelaki, 2011; Laurens et al. 2013a,b; Oman, 1982; 1989; Borah et al., 1988; Glasauer 1992; Merfeld, 1995; Glasauer and Merfeld 1997; Bos and Bles 2002; Zupan and Merfeld, 2002) to actively-generated head movements by incorporating motor commands (Fig. 1A; Laurens and Angelaki, 2017).
An important step in this model of multisensory self-motion estimation is the computation of sensory prediction errors (i.e., difference between actual and predicted sensory signals; Fig. 2B vs. 2C) that are used to correct the self-motion estimates. During active motion, motor commands can be used to predict head and body motion and anticipate the corresponding sensory re-afference, such that sensory prediction error is minimal (Fig 2D, top; Laurens and Angelaki, 2017). In contrast, sensory activity cannot be anticipated during passive/unpredictable motion, resulting in non-zero sensory prediction errors, which then drive the self-motion estimate (Fig. 2D, middle). We have shown that the simulated sensory prediction error mimics the properties of VN neurons with attenuated responsiveness during active motion (Cullen 2012; 2014). Importantly, even though sensory prediction errors differ, the final self-motion estimate is identical to the true head motion, irrespective of whether motion is active or passive, at least during short-lasting movements (Fig. 2E). Furthermore, if a passive motion (or a motor error) occurs during active movement (Fig. 2A–E, bottom), the vestibular organs will sense the total head motion (Fig. 2B, bottom). The internal model output will predict the active component (Fig. 2C, bottom) whereas some VN neurons will encode specifically the passive component (or the motor error; Fig. 2D, bottom). The final self-motion signal (Fig. 2E, bottom) is the sum of the prediction (output of the internal model; Fig. 2C, bottom) and the error signal (Fig. 2D, bottom). The three simulations shown in the three rows of Fig. 2A–E also illustrate how the final motion estimate will ultimately be nearly identical (see Laurens and Angelaki 2017 for details) to the sensory signal (compare Fig. 2B and E) during short duration movements.
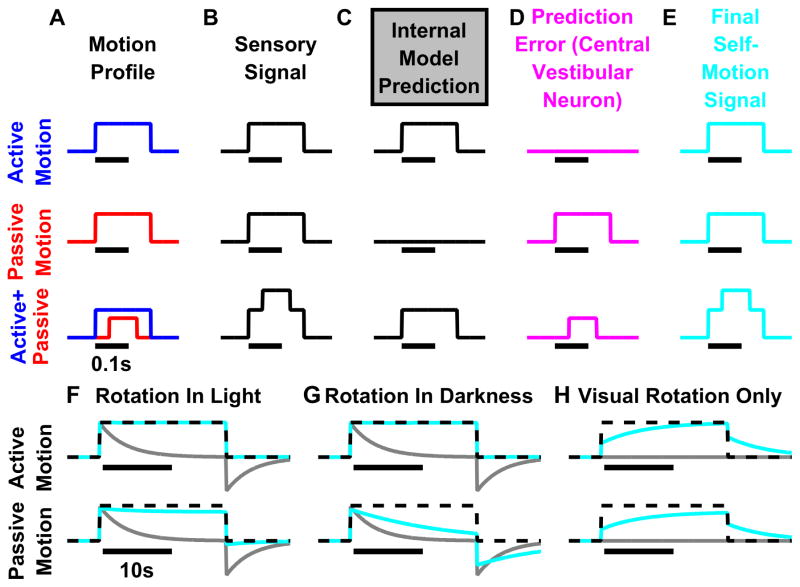
Figure 2. Internal model simulations during active and passive motion.
(A–E) Fast head movements. (A) Two movements with identical velocity profiles (broken black lines) are performed actively (top), passively (middle) or a combination thereof (bottom). During active motion (top), the internal model uses the motor command to generate an accurate prediction of both self-motion velocity and sensory signal (C, top). The predicted sensory signal matches the actual signal, and therefore the sensory prediction error is null (D, top; magenta). During passive motion (middle), both the predicted self-motion velocity and predicted sensory signal are null (C, middle), as there is no motor command. Therefore, the sensory prediction error is equal to the sensory signal (D, middle; magenta), which is transformed into a feedback that drives an accurate self-motion estimate. Thus, although the central vestibular neurons recorded by Cullen and colleagues, which encode sensory prediction error (Brooks et al., 2015), are largely suppressed during active motion (top line) compared to passive motion (middle line), the final self-motion estimate is identical (and matches the stimulus) during both active and passive motion. For short rotations, simulation results are identical in light and darkness. Bottom line: Combination of active (blue) and passive (red) motion. The sensory signal (B) encodes the total (active+passive) motion. The internal model predicts the active component (C) and the sensory prediction error corresponds to the passive (D) component. The final self motion estimate is identical to the total motion. (F–H) Long-duration movements (illustrated as constant velocity). Due to the mechanical properties of the vestibular sensors, the rotation signal (gray lines) decreases with a time constant of ~4s (in macaques) and exhibit an after-effect when rotation stops. The internal model of the sensors improves the self-motion estimate to a limited extent (Laurens and Angelaki, 2011; 2017). During rotation in light (F), visual rotation velocity cues create a sustained self-motion signal, thus the final self-motion estimate matches the stimulus during both active and passive motion. An accurate final self-motion estimate is also computed during active rotation in darkness (G, top). However, during passive rotation in darkness (G, bottom), the internal model cannot entirely compensate (see Laurens and Angelaki, 2011; 2017), and the final self-motion estimate decreases over time. (H) In visual virtual reality (VR; in this case, a rotating visual surround), the final self-motion estimate is inaccurate unless in steady-state (constant velocity) when the actual vestibular (canal) signal is null. Importantly, presenting the same visual stimulus while the animal attempts to rotate actively (but without simultaneous activation of the vestibular system) would induce a similarly inaccurate final self-motion estimate (G, top), even if other sensory cues (visual, somatosensory) and motor commands are available. These simulations highlight why the HD (and likely grid) signal is lost in VR. Simulations are based on the Kalman filter model of Laurens and Angelaki (2017).
The model of Laurens and Angelaki (2017) eliminates the misconception that vestibular signals are unimportant during self-generated, active head movements. The attenuated VN responses recorded by Cullen and colleagues (reviewed in Cullen, 2012; 2014) carry sensory prediction errors and are thus inappropriate to drive the HD attractor. In fact, there is currently no evidence to link VN response properties directly to HD cells, as there are no direct projections from the VN to the brain areas thought to house the HD attractor (Biazoli et al., 2006; Clark et al., 2012), exactly as it should be, given that these VN responses are inappropriate for driving the HD updating.
Instead, we propose that the multisensory self-motion estimate (Fig. 2D), rather than the sensory prediction error (Fig. 2C), updates the ring attractor (Fig. 1A, B). In fact, the model nicely explains and clarifies, for the first time, why vestibular cues are critical for HD tuning and why HD cells lose their spatial tuning properties in the absence of functioning vestibular signals, even during active head movements. This occurs because vestibular signals are continuously monitored to correct the internal model output and, without intact vestibular organs, the self motion estimate which drives the HD attractor, would no longer be accurate during either active or passive motion. Thus, not only are vestibular sensory cues important, but also absolutely necessary for accurate self-motion computation during actively-generated movements.
The previous literature on HD cells has long recognized that proprioceptive and motor efference cues should participate, together with vestibular signals, to track head direction over time (e.g., see Clark and Taube, 2012: ‘internally generated information, or idiothetic cues (i.e. vestibular, proprioception, and motor efference), can be utilized to keep track of changes in directional heading over time’). However, a quantitative conceptual framework that describes the interplay between these sources of self-motion information has been lacking. The model of Laurens and Angelaki (2017; simplified in Fig. 1A and 2) provides the missing theoretical framework of how multiple signals are combined to construct an appropriate multisensory self motion estimate under all conditions (during active motion, as well as during passive motion, in light and in darkness) that then updates the HD cell attractor. Importantly, each cue’s contribution to the final self-motion estimate can be precisely predicted and quantitatively estimated based on the Bayesian framework.
Note that the final self-motion estimates are always identical during active and passive rotations in the light (Fig. 2E, F). However, during passive long-duration rotation in darkness (i.e., in the absence of motor commands, somatosensory and visual cues), the final self-motion estimate is inaccurate (Fig. 2G, bottom), because the vestibular sensors are poor at sensing low-frequency rotations. Accordingly, HD cells drift more during complex passive motion stimuli in darkness (Stackman et al., 2003). In contrast, during actively-generated movements, motor commands and/or available somatosensory cues improve rotation estimation and ensure HD stability even during long (several minutes) active foraging sessions in darkness.
Commonly-used rodent virtual reality (VR) environments, where the animal runs in place without the expected natural vestibular activation predicted by the internal model, lead to conflict conditions, where the vestibular sensory afferent signal does not match the sensory prediction. In this case, the final self-motion velocity (assumed to drive the HD ring attractor) is strongly underestimated during fast (high frequency) movements (Fig. 2H, early response). During slower or steady-state (low frequency) motion, however, retinal flow signals dominate self-motion perception and may mitigate the absence of vestibular signals (Fig. 2H, late response). This explains why HD and other spatial cell properties are altered in two-dimensional VR (i.e., simulating locomotion on a plane; Aghajan et al., 2015; Ravassard et al., 2013). In contrast, spatial properties are less affected in VR simulating a linear track (no rotation conflict), or in the presence of task-relevant landmarks (no need for path integration). Furthermore, this framework also explains why results can be variable across studies and laboratories, depending on the visual VR stimuli (how strong landmark cues are) and the running behavior of the animals (faster speeds lead to larger visual/vestibular conflict).
In summary, understanding how the HD cell attractor is updated requires an understanding of the computational principles that govern self-motion estimation and the fundamental role of vestibular cues and sensory internal models. Although seemingly complex (and a bit engineering-inspired), there is a clear, quantitative, and logical framework that governs the roles of vestibular cues and their internal model in relationship to other multisensory self-motion cues for computing veridical self-motion estimates that are necessary to generate the spatial properties of HD, place and grid cells.
RECURRENT CONNECTIVITY STRENGTH AMPLIFIES HD FIRING AND IS MODULATED BY RESTRAINT
Next we offer a new interpretation to link experimentally reported decreases in HD cell modulation during passive/restrained versus active/unrestrained movements and vestibular self-motion signals. Shinder and Taube (2011; 2014a) recorded HD responses when (1) animals foraged freely, (2) animals were restrained (head and body) and rotated rapidly and continuously (>100°/s), (3) animals were restrained and placed statically (0°/s) in various orientations. In conditions (1) and (2), HD cells exhibited large firing rate modulation, firing in bursts (average 56 spk/s) when the animal faced the cell’s PD, and being almost silent (average 1 spk/s) when the animals faced away from it (Fig. 3A, blue and green curves). In condition (3), HD cells retained their PD, but their modulation range was reduced to 23 spk/s (in the PD) - 5 spk/s (away from the PD), (Fig. 3A, red symbols). Which property can account for and explain these experimental findings?
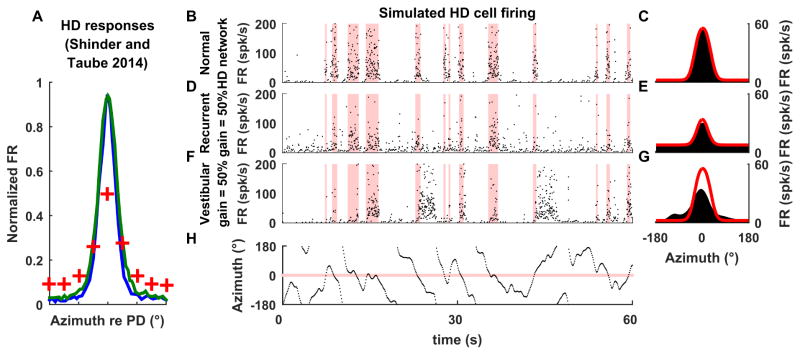
Figure 3. Restraint-dependent firing properties of HD cells.
(A) Neuronal activity in HD cells reported in Shinder and Taube (2014a) when the animal moves freely (blue), is restrained and rotated rapidly (green) or restrained and placed at various static orientations (red crosses). (B–H) Simulated responses of a ring attractor cell under three conditions (B,C) when the unrestrained animal moves actively and freely, thus the attractor operates normally, (D, E) when recurrent connection strength is decreased by 50% (but self-motion velocity input remains the same), and (F, G) when the self-motion input gain that drives the ring attractor is decreased by 50% (but recurrent connection strength remains the same). Panels on the left illustrate simulated spiking activity (instantaneous firing rate). Pink bands indicate when head direction is within 30° of the cell’s PD. Panels on the right illustrate tuning curves reconstructed from the simulated firing on the left panels (black) or from simulations where the animal is placed statically in various orientations (red). Simulations are based on the model of Stringer et al. (2002); see Suppl. Methods. Note that when the animal moves freely, sharp bursts of firing occur when the head faces the cell’s PD, and the cell is nearly silent otherwise. When recurrent connection strength is reduced by 50% (D,E), the simulated model cell exhibits a higher background firing rate and lower modulation. When the gain of the self-motion velocity input signals is reduced by 50% (F,G), the activity in the HD attractor drifts relative to actual head direction. Thus, the cell’s burst of activity coincide only occasionally with the cell’s PD. (H) Motion profile used in the simulations in B,D,F.
Previous work (Cullen and Taube, 2017; Shinder and Taube, 2014b) has proposed that the attenuation of HD responses under restraint/passive motion conditions is related to the attenuation of neuronal responses in central vestibular pathways during active (as compared to passive) self-motion. However, several arguments can be raised against this interpretation.
As illustrated in Fig. 2 (and easily verified by behavioral studies; see Laurens and Angelaki 2017), under most circumstances the final self-motion estimate, which is the signal that should update the ring attractor, is identical during active and passive motion.
Neuronal firing in the VN is attenuated during active motion (Cullen 2012; 2014), when HD cells respond consistently and not during passive motion, when HD responses may be attenuated (Shinder and Taube 2014a,b). Thus, the effects in the two cell types are opposite.
HD responses are attenuated in restrained animals, when placed statically in different directions (Shinder and Taube 2014a), but are not attenuated in freely-moving animals that pause facing different directions. Yet, self-motion signals originating from the vestibular organs are equal to zero in both of these situations, regardless of whether or not the animal is restrained. Thus, this difference cannot be explained by considerations about the attenuation of VN responses during passive motion.
Indeed, notions of “passive motion” and “restrained animals” are often confounded. While all experiments on restrained animals use passive motion, passive motion can also be applied to freely moving, as well as, restrained animals. For example, Blair and Sharp (1996) rotated the platform onto which animals walked, and found that HD cells can track motion applied in this manner. Thus, ‘passive’ motion is not the problem for appropriate HD updating; restraint appears to be the problem.
Finally, but most importantly, the restrained/passive motion findings of Shinder and Taube (2011; 2014a) are inconsistent with simulations based on an attenuated self-motion signal, as shown next.
Recall that recurrent connections within the ring attractor amplify HD responses by allowing cells with similar PDs to activate each other while inhibiting other cells (Fig. 1C). This property is further highlighted in Fig. 3B–G, which simulates both the instantaneous firing (left panels) and average azimuth tuning (right panels; black) of a HD cell. In a simulation where the strength of all recurrent connections is lowered by 50% (see Suppl. Methods), the HD cell retains its PD, but its peak firing rate is reduced and its baseline firing rate increases (compare Fig. 3D,E vs. 3B,C). Importantly, the cell exhibits the same response curve in a simulation where the animal is positioned statically for several seconds at each orientation (black vs. red curves).
In contrast, when the strength of recurrent connections remains unchanged but the self-motion velocity drive is “attenuated” by 50% (thus, inducing a mismatch between the velocity input to the ring attractor and the animal’s velocity), the packet of activity drifts relative to the actual head direction and coincides only occasionally with the cell’s PD (Fig. 3F, red vertical bars). The corresponding tuning (Fig. 3G, black) exhibits a weak peak at the cell’s PD (in this particular simulation, bursting occurs more often in the PD because visual information anchors the cell’s response to some extent). Although the average tuning curves in Fig. 3E and Fig. 3G (black) are somewhat similar, the instantaneous pattern of activity burst firing in Fig. 3D and Fig. 3F are entirely different.
We can now compare these simulations with the experimental findings of Shinder and Taube (2011; 2014a). The reduced responses observed in restrained/passive rotation experiments (Shinder and Taube 2014a), where HD cells respond consistently when the animal faces the PD but with a lower modulation amplitude, resemble the predictions of Fig. 3D (changes in the strength of recurrent connections), and not Fig. 3F (changes in the magnitude of input drive). Thus, we reason that restraining animals results in a decrease of recurrent connection strength in the HD attractor, probably though a tonic modulatory process. This recurrent activity may be restored by moving the animal rapidly (interestingly, even head translation may improve HD cell responses in the restrained animal; Shinder and Taube, 2011).
Although these simulations provide a theoretical interpretation of the Taube and colleagues’ experimental findings, how and where such tonic modulatory is implemented remains unknown. The simulations in Fig. 3 are based on a simplified version of Stringer et al. (2002) (see Suppl. Methods), in which the reduction of the hill of activity is achieved by lowering the strength of both excitatory and inhibitory connections. From a theoretical point of view, there are multiple mechanisms through which a tonic modulation of the network properties may reproduce the consequence of restraining (see e.g. Song and Wang 2005). In this respect, it is also noteworthy that neuronal responses in the dorsal tegmental nucleus, which is thought to be part of the HD attractor, are profoundly altered (and often suppressed) in restrained rats (Sharp et al. 2001b).
Importantly, one should not necessarily conclude that vestibular signals are necessary to maintain recurrent connection strength. First, HD cells respond vigorously in unrestrained animals even when they stop moving for short periods of time (Shinder and Taube, 2014a; Taube, 1995; Taube et al., 1990a). Second, a study in sleeping rodents (Peyrache et al., 2015) indicates that the bursting activity in the HD network is identical during REM sleep and when animals are awake and freely-moving. In fact, the simplified attractor model of Fig. 3 can reproduce the REM sleep findings of Peyrache et al. (2015) by disconnecting the attractor from its updating velocity inputs and introducing a small amount of neuronal noise to make it drift.
The simulated firing pattern of Fig. 3F,G can also explain the findings of Muir et al. (2009) and Yoder and Taube (2009) in animals with vestibular lesions (Table 1). These studies reported “bursty” cells that alternate between periods of inactivity and short bursts of activity but bear little relationship to head direction. The alternation of inactivity and bursting resembles the activity of a neuronal attractor that would be decoupled from its velocity input and drift randomly (Clark and Taube, 2012), in line with the simulations in Fig. 3F. This activity can be further interpreted in light of the model in Fig. 1, which assumes that the final self-motion signal drives the HD attractor. We have reasoned that, although in principle this is a multisensory signal, vestibular lesions would lead to a mismatch with the sensory predictions during active head movements, thus destroy the normal correction feedback. As a result, the brain loses its ability to estimate self-motion accurately (accordingly, lesioned animals exhibit pronounced locomotor deficits), even though other sensory cues remain intact. In a recent elegant study, Butler et al. (2017) recently induced the HD attractor to drift in freely moving healthy animals by optogenetically inactivating the nucleus prepositus.
Table 1.
Effect of vestibular manipulations on HD tuning and interpretation in light of the present theoretical framework.
| Vestibular Manipulation | HD findings | hypothesized effect |
|---|---|---|
| Canal plugging (Muir et al 2009) | bursty cells, no HD tuning | Ring attractor intact, self-motion estimate compromised because sensory prediction error is incorrect (Fig. 1A, 3E). |
| Tilted mutant (Yoder & Taube 2009) | bursty cells, unstable HD tuning | Ring attractor intact, self-motion estimate mismatch (missing allocentric gravity component; see Fig. 6). |
| Passive fast motion (Blair & Sharp 1996; Shider & Taube 2011;2014a) | normal HD tuning | Ring attractor intact, self-motion internal model intact. |
| Restrained animal (Shinder & Taube 2014a) | reduced HD tuning | Reduced recurrent collaterals of ring attractor, self-motion estimate intact. |
In summary, the HD activity attenuation observed in some studies is most likely due to the restraining (not the self-motion signal itself) altering the strength of recurrent connections of the ring attractor. Furthermore, collectively the simulations of Fig. 1–3 illustrate that the issue of activity attenuation in some central vestibular neurons during active and passive motion (Cullen, 2012; 2014) is unrelated to the factors that contribute to HD cell activity during active vs. passive motion, or in restrained vs. freely moving animals.
Having, as we hope, corrected the mis-representations of what the important issues are in linking vestibular and, more generally, multisensory self-motion signals to HD tuning, we next highlight further challenges regarding the properties of the self-motion drive of the HD attractor by showing that this multisensory self-motion velocity input to the HD attractor has more complex spatial properties that originally envisioned.
GENERALIZED DEFINITION OF AZIMUTH COMPASS THAT MAINTAINS ALLOCENTRIC ORIENTATION DURING THREE-DIMENSIONAL MOVEMENT
Recall that HD cells have been traditionally recorded during motion in an earth horizontal plane. As such, the issue of reference frames was trivial. For example, self-motion cues updating the ring attractor could be purely egocentric; e.g., yaw velocity signals from the horizontal semicircular canals (Calton and Taube, 2005; Taube, 2007), as long as visual landmark cues anchor HD tuning to the allocentric local environment (Taube, 2007). Importantly, when limited to the horizontal plane, the local and global (the latter defined as the earth’s surface) allocentric frames coincide.
More recently, a few studies have allowed animals to move in 3D (Calton and Taube, 2005; Finkelstein et al., 2015; Page et al. 2017), thus forcing the question of whether self-motion velocity signals that update the HD attractor are represented in egocentric or allocentic reference frames (Jeffery et al. 2013; 2015; Taube and Shinder, 2013). But before we summarize experimental findings, one must first appreciate that neither solution is without problems.
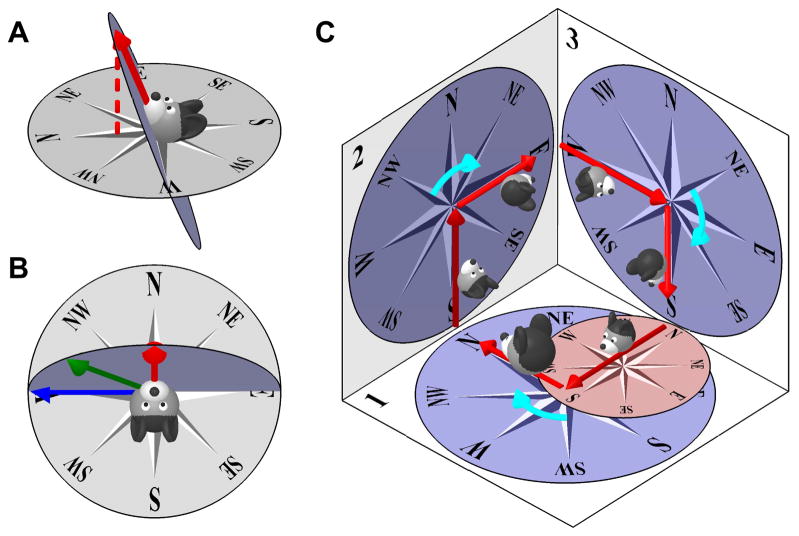
Let’s consider an allocentric azimuth updating rule first (Fig. 4A). One way to define azimuth during 3D head motion could be to project the direction the head faces (red arrow) onto a compass in the earth-horizontal plane. However, this solution distorts the angles between points in the head-horizontal plane. This is illustrated in Fig. 4B, where the diagram in A is viewed from the top. Red, blue and green arrows represent 0°, 90° and 45° leftward directions on the head-horizontal plane. When projected onto the earth-horizontal plane, the red and blue arrow will point North and West, i.e. 90° apart, but the green arrow will point between West and North-West, i.e. 71° from the red and 29° from the blue arrow. Thus, defining azimuth by projecting directions onto an earth-horizontal plane induces a distortion that would severely complicate the ability to orient oneself when navigating on a sloped surface, because the orientation of various landmarks in a visual reference frame, or the amplitude of head rotations in the sloped surface’s plane, would not correspond to the azimuth signal stored in the HD network. Furthermore, earth-vertical surfaces, like walls of a box, would not be represented at all.
Figure 4. Earth-horizontal (Allocentric updating) vs. Head-horizontal (Egocentric updating) azimuth models.
(A), (B) Earth-horizontal azimuth model, illustrating the distortion produced. The larger the tilt angle of the head away from the earth-horizontal surface, the larger the distortion between egocentric and allocentric reference frames. (C) Head-horizontal (yaw-only) azimuth model, with the compass attached to the head horizontal plane. After completing a 3D trajectory and returning to surface n∘1, the head-fixed compass (small red compass on surface n∘1) is no longer consistent with its orientation at the beginning of the trajectory (large compass on surface n∘1). Therefore, a purely egocentric azimuth compass can’t track head orientation during motion in 3D.
One may then hypothesize that the solution is to use an egocentric azimuth updating rule (Calton and Taube, 2005; Taube and Shinder, 2013) where azimuth would be updated based on egocentric yaw rotation signals only, and remain unchanged during pitch and roll movements. Unfortunately, as pointed out by Jeffery and colleagues (Jeffery et al. 2013, 2015; Page et al. 2017), this solution would also fail, this time even more seriously. This is illustrated by a hypothetical motion trajectory (Fig. 4C), where the rodent is initially facing North on an earth-horizontal surface (n∘1 in Fig. 4C, large head) and then moves across two earth-vertical surfaces (n∘2 and n∘3) before coming back to its initial orientation. When an animal initially faces North on an earth-horizontal surface (n∘1) and pitches nose-up, the compass would simply follow the rotation of the head and the North axis would now point upward. This solution would allow the animal to navigate naturally on the vertical surface. Then the animal turns East to proceed along surface n∘3 and pitches 90° when it enters it. At this point, he faces East (since azimuth is not updated when he pitches from surface n∘2 to n∘3), and the compass on surface n∘3 is drawn according to this orientation. The animal turns again and faces South, goes through another pitch of 90° in order to return to surface n∘1. At this point, the internal azimuth signal (small red compass on surface n∘1) would incorrectly encode a Southward orientation, although the animal is in fact facing West. When the animal returns to its initial orientation (large head on surface n∘1), it will have performed exactly three 90° rightward horizontal turns (cyan arrows, when on each surface), interleaved with another three 90° nose up pitch turns (when it transitions from one surface to another). A purely egocentric azimuth model (updated by horizontal canal signals only) would update during the horizontal turns, such that the total rotation registered by the HD attractor would be 3×90=270°. However, the correct attractor should have registered 360°. What went wrong in the arithmetic? This example illustrates that a purely egocentric azimuth updating rule (using yaw velocity signals only) cannot track head orientation during 3D motion.
Given that both egocentric and allocentric azimuth updating rules face serious limitations (Fig. 4), which solution is used by the brain? We summarize the experimental findings next (Fig. 5).
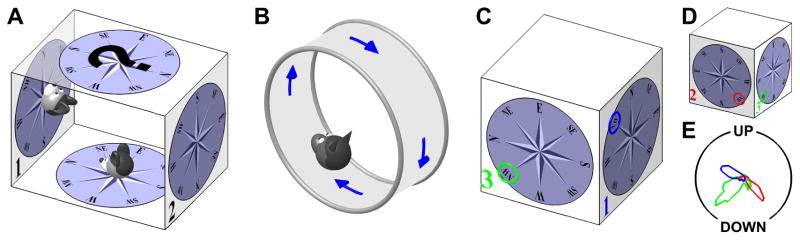
Figure 5. Summary of experimental findings on HD responses during locomotion on surfaces that are not earth-horizontal.
(A) Experiment by Calton and Taube (2005). Rats are placed inside a box and walk on the floor, two vertical walls (n∘1 and n∘2) and ceiling. HD tuning is maintained and anchored to the head-horizontal compass; except when walking on the ceiling. (B) Experiment by Finkelstein et al. (2015). Bats crawl along a vertically oriented circular track. (C), (D) Experiment by Page et al. (2017), where rodents walk on the walls of a cube. Three surfaces are numbered (n∘1, 2, 3) and color-coded. The NW direction is indicated by a colored circle on each surface. (D shows the same cube as in C, seen from another angle to display side n∘2.) (E) Polar representation of the tuning curves of an example HD cell (data courtesy from Kate Jeffery), on sides n∘ 1–3 (color-coded), as seen from a camera outside the cube. Note that the cell’s PD on various sides corresponds to different directions in space. However, these directions correspond to the same azimuth (NW) in the tilted reference frame defined in Fig. 6.
Calton and Taube (2005; see also Stackman et al., 2000) trained rats to walk along the inner surface of a box. Starting from the bottom surface, they walked up one wall (marked n∘1 in Fig. 5A), then walked upside down across the ceiling, climbed down the opposite wall (marked n∘2), and reached the bottom floor again to receive a reward. HD cells in the anterior thalamus, which were first characterized on the bottom surface of the box, also responded when the animals walked on both vertical walls. When an animal walked facing North onto wall n∘1, its orientation continued to be coded as North. Furthermore, when the animal descended wall n∘2, its orientation still coded North. The authors concluded that HD cells encoded orientation as if the entire surface of the bottom and walls were a single continuous and flat surface (‘locomotion plane’), which is consistent with the egocentric updating rule (e.g., from the horizontal semicircular canals). When animals walked upside-down on the ceiling, HD tuning was either lost or bore no relation with the HD tuning recorded on the floor (see also Gibson et al. 2013).
Finkelstein et al. (2015) recorded HD cells in the dorsal pre-subiculum of bats that crawled around the inner surface of a vertically oriented circular track (Fig. 5B). In agreement with Calton and Taube (2005), they found that, if the animal faced a cell’s PD on the bottom of the track, the cell would exhibit a large response during the entire motion along the track, including at the top. Thus, when walking upside-down, some HD cells appear to reverse PD (since, in an allocentric frame of reference, the animal faces opposite directions on the floor and on the ceiling), whereas other cells lost their tuning. The finding that azimuth tuning reverses in inverted animals persisted when animals were wrapped in a towel and displaced manually upside-down.
Finally, a major breakthrough came with the experiments of Page et al. 2017, who trained rats to walk on top and along all two or three vertical walls of a cube (Fig. 5C–E). When neuronal responses were recorded on opposite walls of the cube, PDs reversed (in allocentric coordinates), as in previous experiments. When animals transited between adjacent sides of the cube (e.g. from surface n∘1 to n∘3 in Fig. 5C), PD changed by 90° (Fig. 5E), in contrast to the predictions of the purely egocentric updating rule, which would predict no change. Similar results were recently obtained in a variation of this task by Dumont et al. (Soc. Neurosci. Conf. 2017, 427.11). Why does this happen and what do these findings suggest regarding the updating rule for the HD ring attractor?
Recall that an egocentric azimuth solution fails because it loses its allocentric invariance when moving outside the earth-horizontal plane (Fig. 4C). Page et al. (2017) proposed that the HD system resolves this problem by using a “dual-axis” updating rule. We describe this solution next, and we refer to the azimuth signal computed by this rule as the “tilted azimuth compass” reference frame.
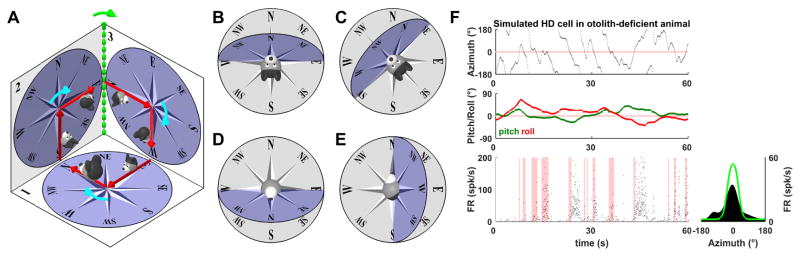
Page et al. (2017) reasoned that the correct (tilted azimuth) compass must be updated when animals transition from one earth-vertical surface to another (i.e., when the head-horizontal plane rotates around an earth-vertical axis). In Fig. 6A (replotted from Fig. 4C), for example, this includes the transition from surfaces n∘2 to n∘3 (but not the transitions from surfaces n∘1 to n∘2 or n∘3 to n∘1). This is because, although the animal is facing East on surface n∘2, it faces South when it enters surface n∘3. With this 90° correction (which clearly HD cells register; Fig. 5E), the ring attractor would correctly update by 360° in the trajectory of Fig. 6A. Therefore, the correct input drive to the azimuth ring attractor should include two components (Page et al. 2017): (1) a head-horizontal (yaw) rotation velocity (i.e., rotation in the head horizontal plane), as originally assumed; and (2) an earth-horizontal rotation velocity (i.e., rotation around an earth-vertical axis; Fig. 6A, broken green line and green arrow).
Figure 6. Definition of tilted azimuth model.
(A) Consistency of the tilted azimuth compass with both egocentric and allocentric reference frames during 3D motion (multiple surfaces). Starting from a north orientation on an earth-horizontal surface (initial position marked by a large head), the animal follows a trajectory and comes back to its initial orientation (as in Fig. 4C). The trajectory includes three right-hand turns (in the head-horizontal plane, cyan arrows), each of which changes head azimuth by 90°. Azimuth must also be changed by 90° when the animal moves from surface n∘2 to n∘3 (rotation about an earth-horizontal axis, green) to ensure a 360° total azimuth change when the animal returns to its initial orientation. (B–D) Comparison of the tilted azimuth model (blue; Page et al. 2017) and the earth-horizontal frame (gray). (B) Example orientation, where the N, S, E and W directions of the head-horizontal and earth-horizontal compasses match, but not the NE and NW (as well as SE and SW). (C) The head-horizontal plane now intersects the earth-horizontal plane along the NE–SW axis. Accordingly, the two compasses now match along these directions, as well as in the NW direction, but not along the N and S directions. (D) Illustration of a pitch movement exceeding 90°, where the azimuth reverses along the N–S axis: the N direction of the head-horizontal compass is now aligned with the earth-horizontal S direction. (E) Illustration of a roll movement exceeding 90°, where azimuth reverses along the E–W (and not N–S axes). Note that, if the movements in (D) and (E) are continued until the head is upside-down, the compasses lie in the same “inverted” earth-horizontal plane but are oriented differently (the N–S axis is reversed in D and the E–W axis is reversed in E). As a result, the tilted azimuth model can’t be defined unequivocally in inverted orientation (hence the singularity). (F) Simulation of a HD cell (as in Fig. 3) when the animal tilts its head (pitch/roll) assuming that the rotation drive signal to the HD ring attractor doesn’t account for head tilt (i.e., head-horizontal azimuth compass, updated only by yaw rotations). Cell firing doesn’t correspond to the cell’s PD consistently, resulting in drifts, as reported in otolith-deficient mice (Yoder and Taube, 2009). Light green: azimuth tuning curve obtained if head tilt is accurately accounted for (as is the case with the tilted azimuth model).
An alternative way to define the tilted azimuth reference frame is to use the following rules: (1) the tilted compass is always aligned with the head’s horizontal plane, and (2) the azimuth on the earth-horizontal (Fig. 6B–D, gray) and tilted compasses (Fig. 6B–D, blue) always remain anchored along a line where the two planes intersect (i.e. E–W axis in Fig. 6B,D, NE–SW axis in Fig. 6C). The compromise, however, is that increasing tilt angle beyond 90° leads to a reversal of azimuth, i.e. the North direction in the head-horizontal compass (Fig. 6D, blue) is now aligned with the South direction in the earth-horizontal compass (gray). This reversal occurs because, in Fig. 6D, the East and West directions are anchored to the earth-horizontal East and West directions. In contrast, the North and South directions in the tilted frame are not earth-horizontal. As a result, instead of being anchored to earth-horizontal directions, they are defined relative to East and West. By definition, North lies 90° CW relative to West and 90° CCW relative to East in the plane of the compass. Placing it in the corresponding location in Fig. 6D results in North pointing in a Southward direction in the earth-horizontal plane. As illustrated in Fig. 5A, this framework also explains why the compass seems to extend to the whole locomotion plane in the experiments of Calton and Taube (2005). They only tested transitions from earth-horizontal to earth-vertical surfaces, but not from an earth-vertical to another earth-vertical plane; under these conditions, the tilted compass will simply rotate together with the plane of locomotion.
These same principles apply when an animal walks on a horizontal surface but tilts its head. To illustrate the importance of this transformation, we simulated the same cell as in Fig. 3 but assumed that the head was tilting randomly (Fig. 6E, top) and the brain was not compensating for this tilt, but instead the HD attractor was updated by only egocentric rotation signals in the head-horizontal plane. Similar to the cell in Fig. 3E, the cell in Fig. 6E fires in bursts of activity that are inconsistently aligned with the cell’s PD. This simulation may explain findings in otolith-deficient mice (Yoder and Taube, 2009) where ADN neurons exhibited the pattern of “bursty” activity described in Fig. 6F, indicating that the HD signal was unstable. We propose that the lack of functioning otolith organs in these animals prevented the spatial transformation of rotation signals and the computation of the allocentric velocity component. This would induce a mismatch between the velocity input to the ring attractor and the animal’s velocity, resulting in activity bursts that drift relative to actual head direction, exactly as demonstrated experimentally by Yoder and Taube (2009). The tilted azimuth framework also accounts for the observation that the direction-specific discharge of HD cells was usually not maintained when the rat locomoted on the vertical wall or ceiling in 0-G (parabolic flight; Taube et al., 2004).
One limitation of the tilted azimuth framework is that it is not defined in upside-down orientation, where the tilted azimuth can’t be defined, because: (i) the head yaw axis and the earth-vertical axis are opposite, such that the dual axis rule can’t be implemented (Page et al. 2017), and (ii) it is impossible to define a unique line along which the two planes intersect. Note also that the tilted azimuth reverses compared to the earth-horizontal azimuth when pitching but not when rolling (Fig. 6D,E). As a consequence, the tilted compasses attained when starting upright and pitching or rolling to upside-down would be incompatible. For these reasons the tilted azimuth frame faces a singularity around upside-down orientations. As pointed out by Page et al. (2017), this issue may explain why HD tuning in upside-down orientation varies across studies; i.e. why it inverts in half of the population in bats (Finkelstein et al. 2015) and vanishes in rodents (Calton and Taube 2005).
Thus, in summary, the velocity self-motion signal updating the azimuth compass (i.e., the drive to the HD ring attractor) is more complex than originally envisioned. Because of the need for continuous matching between head-horizontal and earth-horizontal (allocentric) compasses, the animal’s orientation relative to gravity must be monitored and used to transform self-motion rotation signals. Vestibular signals are critical for this transformation too. Specifically, to update the azimuth ring attractor, the velocity drive to the HD circuit must include spatially-transformed, allocentrically (gravity)-defined self-motion signals. Gravity-referenced signals are indeed found in both the VN and cerebellum (Angelaki et al., 2004; Yakusheva et al., 2007; Laurens et al., 2013a,b). In fact, it was a decade ago when Yakusheva et al. (2007) first proposed that earth-horizontal angular velocity (computed from head-fixed horizontal canal signals that are processed by gravity information) within and/or downstream of the caudal cerebellar vermis provides a critical signal for spatial navigation (see Fig. 1 of Yakusheva et al. 2007). Specifically, we proposed: “As in man-made inertial guidance systems, inertial self-motion detection involves computation of rotational and translational components expressed relative to an earth-fixed reference. However, because our motion sensors are fixed to the head, they measure the linear acceleration and angular rotation within a reference frame that is head- and not earth-centered“.
Indeed, evidence that the vestibular system computes the earth-referenced components of rotation can be found in both eye movement (Angelaki and Hess, 1995a) and perceptual responses (Day and Fitzpatrick, 2005). Notably, after lesion of the caudal cerebellar vermis, reflexive eye movements during rotation no longer show evidence for spatial (earth-centered) reference frame transformations (Angelaki and Hess, 1995a,b; Wearne et al., 1998). Thus, the vestibulo-cerebellum is likely critically involved in the computation of the gravity-referenced signal for the dual axis updating rule for tilted azimuth. Yet, for years, these important results for understanding spatial orientation in 3D had remained outside the mainstream of the navigation community. These coordinate transformations (Yakusheva et al. 2007) will be outlined in Fig. 7, such as to define the updating vestibular/multisensory velocity inputs to the HD attractor, but first we need to discuss the existence of a 3D compass, that expands the concept of the tilted azimuth (still a planar compass) to 3D orientation.
Figure 7. Conceptual model of 3D head orientation compass.
(A) 3D orientation may be decomposed into 2D tilt and 1D azimuth compasses. Tilt signals are symbolized by a head-fixed pendulum (green). The end of this pendulum may reach any position on a sphere drawn around the head, with each position representing one possible head tilt (spherical topology). Self-motion signals (gravity and/or gravity derivative; and azimuth velocity, cyan) are computed by an internal model of self-motion (Fig. 1A). Note that egocentric rotation signals must be further transformed by gravity to compute allocentric azimuth velocity, necessary to update the ring attractor during 3D rotations (tilted azimuth model). This is because the velocity input to the azimuth compass (HD ring attractor) must include both head-horizontal and earth-horizontal components. (B), (C) Model of 2D attractor that computes 2D tilt. Spherical topology of the proposed model (B), with a portion of the model expanded to show connectivity within the network (C). Cells receive gravity signals (green) and activate neighbors while inhibiting distant cells (‘+’ and ‘−’). A gravity-derivative cell tuned to dGx>0 activates rightward connections between gravity-tuned cells, causing the activity to shift. Note the common principles with the 1D model in Fig. 1B. Whether the computation of tilt orientation uses an attractor network remains to be tested experimentally.
To motivate the next section, note that, in Fig. 6A, the azimuth is North if the head faces upward on surface n∘2 but East if it faces upward on surface n∘3 – which seems paradoxical since the head is facing the same allocentric direction. This is because the tilted azimuth does not encode “upward” or “downward” directions, nor does it encode head tilt (although tilt signals are required to update it). Thus, in addition to the tilted azimuth compass, which needs gravity signals, the HD system may depend on gravity even more, as it may monitor the animal’s 3D orientation in the world. Next we summarize what little is currently known about the 3D properties of HD cells.
IS THERE A THREE-DIMENSIONAL COMPASS – AND DOES IT DEPEND ON GRAVITY?
Can the HD system represent all three dimensions of head orientation in space, or is it just an one-dimensional (tilted) azimuth compass that can maintain its allocentric reference? For example, in Fig. 6A, the animal faces North when it looks upward on surface n∘2, and East if it looks upward on surface n∘3. If a 3D compass exists, then some HD cells should fire preferentially when the animal faces upward, independently of azimuth.
Indeed, a recent study in bats showed that HD cells in the pre-subiculum are tuned in 3D. Specifically, some cells signal the angular orientation of the head in pitch and roll (i.e. 2D head tilt), independently of azimuth, and some cells carry both tilt and azimuth signals (Finkelstein et al., 2015). However, Finkelstein et al (2015) did not consider reference frames (Fig. 4, 6) and mathematical issues related to computing 3D orientation and instead restricted their analysis by excluding tilt movements to the side (e.g. roll).
Note that encoding 3D head orientation in a 3D attractor would raise a “combinatory explosion” issue (because of the large number of cells required to represent 3D orientations, and the large number of connections required to encode all possible rotations from one orientation to another). One solution to avoid this mathematical complexity is to encode head azimuth independently from the two other degrees of freedom, and use gravity to define these remaining degrees of freedom, i.e. vertical head tilt orientation. In fact, since correctly updating the azimuth HD ring attractor requires knowledge of orientation relative to gravity (Fig. 6), this solution does not require much additional computation or neural hardware.
Indeed, Laurens et al. (2016) have recently described pitch- and roll- coding cells that were anchored to gravity, and not visual cues, in the macaque anterior thalamus. Preliminary findings show gravity-tuned cells in the anterior dorsal thalamus of mice, with many cells being jointly tuned to both azimuth and gravity (Cham et al. Soc. Neurosci. Conf. 2017, 427.01; Laurens et al. Soc. Neurosci. Conf. 2017, 427.02), exactly as previously described in the bat presubicculum (Finkelstein et al., 2015).
Thus, as outlined in Fig. 7A, we propose that the HD system may form a 3D compass, where two dimensions are defined by gravity (2D tilt, spherical topology, green) and the other dimension by the tilted azimuth compass (circular topology implemented by the ring attractor, blue). Importantly, gravity signals influence computations for both the 2D tilt and tilted azimuth updating. In fact, the same internal model computations for self-motion estimation shown in Fig. 1 can also simultaneously compute tilt and gravity signals (Laurens et al., 2013a,b; Laurens and Angelaki, 2017). The vestibular system on its own can sense head tilt unequivocally (but only if there is no translation; see Yakusheva et al. 2007; Laurens et al. 2013a, b)- but not head azimuth. This explains why visual landmarks are necessary to anchor azimuth (the azimuth signal stored in the attractor will eventually drift if an animal walks in complete darkness), but are not necessary for tilt signals (Laurens et al., 2016).
It should be stressed that this framework is entirely compatible with the toroid model proposed by Finkelstein et al. (2015) as long as only pitch movements are considered. Indeed, we propose that head tilt (in pitch and roll) and head azimuth are two independent dimensions. The toroid model makes the same assumption but considers only pitch. Furthermore, the toroid model assumes that pitch movements do not change azimuth, and the dual axis rule that underlies the tilted azimuth model agrees with this assumption as long as the head doesn’t roll. However, we and Page et al. (2017) extend the toroidal model since: (1) we account for the fact that some tilt neurons are tuned to roll (Laurens et al. 2016; see also Finkelstein et al. 2015; Cham et al. Soc. Neurosci. Conf. 2017, 427.01; Laurens et al. Soc. Neurosci. Conf. 2017, 427.02) and (2) the tilted azimuth model generalizes the definition of azimuth using the dual axis rule, where azimuth depends on pitch and roll movements (e.g. when moving from surface n∘2 to n∘3 in Fig. 6A), indicating that tilt and azimuth compasses are no longer independent (as the toroid pitch-only model assumes). Thus, the azimuth compass in the current model (see also Page et al. 2017) is distinct from the toroid azimuth (Finkelstein et al. 2015) when all 3 degrees of freedom are considered. The dual axis rule also implies that tilted azimuth reverses relative to earth-horizontal azimuth when the head pitches more than 90° but not when it rolls more than 90° (Fig. 6D,E). Finally, the tilted compass has a singularity in upside-down orientation, unlike the toroid model.
An important question for future research is whether tilt signals are processed by a neuronal attractor, similar to azimuth velocity cues. A neuronal attractor for tilt would have a two-dimensional spherical geometry (Fig. 7B), and could integrate inputs that encode the time derivative of gravity in order to track gravity (Fig. 7C). Both of these signals have been identified in the macaque anterior thalamus (Laurens et al., 2016). Yet, it remains unknown whether gravity signals are computed elsewhere and relayed to the anterior thalamus, or computed within a circuit that includes the anterior thalamus itself.
In summary, the importance of gravity to life on earth, the existence of 3D HD cells in flying mammals, and the presence of gravity-referenced signals in the macaque (Laurens et al., 2016) and rodent (Cham et al., 2017) anterior thalamus support the hypothesis that vertical orientation is defined by gravity and computed at or downstream of the brainstem/cerebellar circuit that processes gravito-inertial acceleration (Laurens et al., 2013a,b). HD cells may carry only tilt, only azimuth, or both signals (Finkelstein et al., 2015; Cham et al., 2017; Laurens et al., 2017). How these signals interact in individual cells remains to be determined in future experiments.
MAMMALIAN NEURAL PATHWAYS
There have been many reviews (Taube 2007; Shinder and Taube 2010; Clark and Taube, 2012; Yoder and Taube 2014) of the potential pathways that could carry vestibular signals from the medial VN to the lateral mammillary (LMN) and dorsal tegmental nuclei (DTN). Candidate areas carrying vestibular signals to DTN include the nucleus prepositus hypoglossi and the supragenual nucleus (Biazoli et al., 2006; Brown et al., 2005; Butler and Taube, 2015). However, it is possible that vestibular projections influencing HD computation may also arise from the rostral fastigial nuclei, which respond to vestibular stimuli as strongly as the VN (Angelaki et al., 2004; Brooks and Cullen, 2009; Brooks et al. 2015; Shaikh et al., 2005). Projections to DTN and LMN can also arise from reticular nuclei, such as the mesencephalic reticular nucleus, the paragigantocellular reticular nucleus and the gigantocellular reticular nucleus (Brown et al., 2005), which project to the nucleus prepositus hypoglossal (Ohtake 1992) and supragenual nucleus (Biazoli et al., 2006) (reviewed in Shinder and Taube 2010). In fact, fastigiofugal fibers from the rostral part of the fastigial nuclei innervate heavily the nucleus gigantocellularis (NRG) and other reticular nuclei (Homma et al., 1995). Neurons in NRG respond to sensory stimuli of multiple modalities, including vestibular (Martin et al., 2010). Furthermore, electrical stimulation of the rostral NRG evokes ipsilateral horizontal head rotations (Quessy and Freedman, 2004). Preliminary recordings from the dorsal paragigantocellular reticular formation reported neurons modulating similarly during active and passive yaw rotations (Wu Zhou, personal communication), possibly reflecting the total self-motion signal of Fig. 2. Future studies must characterize neuronal properties in these areas, particularly whether they relate to the gravity-dependent properties of the velocity drive to the HD network. In addition, further physiological studies should elucidate whether recurrent activity in the HD networks is modulated under restraining, or more generally, in a restraint-dependent manner.
HEAD DIRECTION SYSTEM IN INSECTS
Interestingly, insect species possess a HD system, which is located in the ellipsoid body and protocerebral bridge of the central complex, and which bears a striking similarity with the mammalian HD system (Seelig and Jayaraman, 2015). The ellipsoid body is a ring-link structure in which neighboring neurons fire together, forming a ‘bump’ of activity whose position on the ring varies as a function of head direction. Neuronal activity in the ellipsoid body has been studied in tethered flies (Drosophila melanogaster) in virtual reality environments, either when walking on an air-supported ball (Seelig and Jayaraman, 2015; Green et al., 2017; Turner-Evans et al., 2017) or during simulated flight (Kim et al., 2017). Although the flies are immobilized, their turning motor actions can be measured through the rotation of the ball (when walking) or the difference of cumulated wingbeat amplitude between the right and left wing (when flying). Similar to mammalian HD cells, the position of the bump is anchored to visual landmarks when available. Interestingly, the bump can also track the fly’s simulated turning movements when walking in darkness but not during simulated flying.
These findings are readily explained by the computational framework outlined here. Flies, which lack a mammalian-type vestibular organ, sense rotations using miniature hindwings called halteres (Pringle et al. 1948; Dickinson 1999). These halteres beat during flight, and the interaction of beating movements and body rotations creates Coriolis forces that are sensed by mechanoreceptors. Kim et al. (2017) proposed that the bump of activity in the ellipsoid body doesn’t track the fly’s motor actions during tethered flight because the halteres don’t detect any motion and therefore conflict with motor commands (similar to rodent VR). The Kalman filter framework (see also Laurens and Angelaki 2017) agrees with this interpretation: when a motor command is performed but the corresponding sensory reafference is zero, the final motion estimate follows the sensory reafference and should also be zero. Importantly, Drosophila beat their halteres during flight only, and not when walking (Hall et al. 2015), and therefore halteres are switched out when walking. In this situation, the Kalman framework predicts that the final motion estimate follows the motor command. Accordingly, neuronal activity in the ellipsoid body can track turning movements in tethered flies walking in darkness.
Flies rely more heavily on visual self-motion signals than on halteres when flying (Sherman and Dickinson 2003). This explains that the bump of activity tends to follow visual cues when available, even when these cues conflict with motor commands or sensory signals from the halteres. For instance, Seelig and Jayaraman (2015) manipulated visual signals in order to decouple them from motor actions in walking flies, and found that the bump of activity followed visual cues. Furthermore, Kim et al. (2017) found that the bump of activity followed visual cues during tethered flying, despite the absence of reafference from the halteres.
Recent calcium imaging and optogenetic studies (Kim et al., 2017; Green et al., 2017; Turner-Evans et al., 2017) have been remarkably successful at demonstrating that neuronal activity within the ellipsoid body has the properties of an attractor network, and at uncovering the neuronal mechanisms whereby the protocerebral bridge may provide rotation velocity signals to the ellipsoid body. The similarity between the neuronal mechanisms that encode head direction in mammals and insects, the fact that flies can also sense rotations (as well as gravity; Kamikouchi et al. 2009), raise the exciting possibility that some of the computational principles discussed in this perspective may apply to the HD system of insects as well.
Finally, it is important to disentangle a potentially confusing association: the observation that the bump of activity in head-fixed walking flies can be correctly updated using visual cues cannot be considered similar or comparable to the directional responses reported by Acharya et al. (2016) in the rat CA1 (there are currently no published studies of rodent HD cells in VR). Specifically, Acharya et al. (2016) reported normal head-direction modulation (but compromised place-coding) in VR and concluded “this directional modulation does not require robust vestibular cues”. Indeed, the VR conditions that lead to directional responses in the study of Acharya et al. (2016) had strong distal landmarks, which could drive directional responses directly, thus compensating for the absence of accurate path integration (which requires vestibular cues for correct estimation of rotation velocity). Importantly, the directional responses were eliminated in VR depicting a virtual world where distal visual cues were absent (Acharya et al. 2016), a condition where path integration through optic flow cues is not accurate enough to replace landmark navigation. Thus, the Acharya et al. (2016) experimental findings actually show that vestibular cues are necessary for accurate angular path integration (when it is engaged in the absence of visual landmarks); rotational optic flow cues are insufficient on their own.
CONCLUSIONS
We have proposed a quantitative framework for how vestibular signals, and other self-motion cues, contribute to a multisensory estimate of allocentric self-motion, which we hypothesize updates the HD ring attractor (and possibly influences grid cell tuning too). This azimuth velocity signal is influenced by efference copies, canal, visual, somatosensory, as well as gravity signals, thus it requires extensive processing before it can be integrated by the ring attractor. The only way to test this proposed framework qualitatively would be to experimentally identify the source and properties of this multisensory self-motion estimate, as well as its neuronal correlates along the entire network of regions that carry self-motion signals to the navigation system. Virtual Reality setups, which provide the ability to independently manipulate visual, vestibular and efference motor/somatosensory signals can be particularly helpful in this regard.
STAR Methods
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jean Laurens (jean.laurens@gmail.com).
METHOD DETAILS
We designed and simulated an attractor model based on Stringer at al. (2002). The network included N = 100 HD cells with evenly spaced preferred directions (PD). Each neuron receives excitatory visual inputs V whose strength is maximal when the head faces the neurons’ PD (Fig. 1B, red). Each neuron sends excitatory inputs (E) to those other neurons that have similar PD. Finally, each neuron sends inhibitory inputs to all other neurons (presumably though an intermediate interneurons population, which is not explicitly modelled here). The summation of local excitatory and global inhibitory connections (E and I) forms the pattern of connectivity illustrated in Fig. 1B (blue). Altogether, the synaptic input of each neuron i is the sum of the three following components:
| (eq.1) |
| (eq. 2) |
| (eq. 3) |
where N(x,σ) is a Gaussian function centered on 0, with standard deviation σ and scaled such that N(0,σ)=1 and HD is the direction of the head at time t. Parameters ϕV, ϕE and ϕI are gain factors. The weights of the recurrent excitatory connections are encoded by matrix wij = N(PDi−PDj, σw), whereas all inhibitory connections have the same weight. To simulate the integration of rotation velocity signals Ω, we simplified eq. 10 in (Stringer at al. 2002) and assumed that the net effect of velocity cells is to offset the pattern of recurrent excitatory connections; i.e. we replaced (eq. 2) by:
| (eq. 2′) |
with wΩ ij = N(PDi−PDj−kΩ.Ω, σw). Thus, if Ω>0 (counterclockwise rotation; CCW), then neuron j will activate preferentially other neurons whose PD is located CCW relative to its own PD; which will cause the activity in the attractor to shift in the CCW direction.
Given these inputs, the firing rate ri of each cell is computed in two steps (as in Stringer at al. 2002):
| (eq. 4) |
| (eq. 5) |
where h is an activation function designed to simulate leaky integrator neurons and τ is a time constant. We used δt = 0.1s, σV = 15°, σw = 8.6°, τ = 0.1s, ϕV = 17, ϕE = 6.24, ϕI = 1.56, α = 30, β = 0.022. Given these parameters, we performed preliminary simulations to determine how rapidly the hill of activity slides as a function of kΩ.Ω (in the absence of visual inputs). Based on these simulations, we determined that, using the value kΩ = 1.46s, the hill of activity would shift at a velocity equal to Ω. We computed the average firing rate of all 100 neurons as a function of time, and displayed the activity of one neuron (with a PD of 0°) in Fig. 3 and 6. Simulated spike trains were obtained by drawing spikes randomly, assuming a Poisson distribution.
We simulated the consequences of reducing recurrent activity by dividing both ϕE and ϕI by 2. We simulated a reduction of the vestibular gain by dividing kΩ by 2.
DATA AND SOFTWARE AVAILABILITY
Matlab code generated to simulate the attractor network can be found at: https://github.com/JeanLaurens/Laurens_Angelaki_Brain_Compass_2017
HIGHLIGHTS.
We show how visual, vestibular and motor cues update head direction (HD) cells
The properties of the HD system are identical during passive and active motion
HD azimuth uses a reference frame that depends on head tilt relative to gravity
HD cells may encode three dimensional head orientation
Acknowledgments
This study was supported by National Institutes of Health grants R21 NS098146 and R01-DC004260.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests
AUTHORS CONTRIBUTIONS
Conceptualization: J.L. and D.E.A.; Methodology: J.L.; Writing – Original Draft: J.L. and D.E.A.; Writing – Review and Editing: J.L. and D.E.A.; Funding Acquisition: J.L. and D.E.A.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aghajan ZM, Acharya L, Moore JJ, Cushman JD, Vuong C, Mehta MR. Impaired spatial selectivity and intact phase precession in two-dimensional virtual reality. Nature neuroscience. 2015;18(1):121–128. doi: 10.1038/nn.3884. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Hess BJ. Inertial representation of angular motion in the vestibular system of rhesus monkeys. II. Otolith-controlled transformation that depends on an intact cerebellar nodulus. Journal of Neurophysiology. 1995a;73(5):1729–1751. doi: 10.1152/jn.1995.73.5.1729. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Hess BJ. Lesion of the nodulus and ventral uvula abolish steady-state off-vertical axis otolith response. Journal of Neurophysiology. 1995b;73(4):1716–1720. doi: 10.1152/jn.1995.73.4.1716. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Shaikh AG, Green AM, Dickman JD. Neurons compute internal models of the physical laws of motion. Nature. 2004;430(6999):560. doi: 10.1038/nature02754. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Gu Y, DeAngelis GC. Multisensory integration: psychophysics, neurophysiology, and computation. Current opinion in neurobiology. 2009;19(4):452–458. doi: 10.1016/j.conb.2009.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biazoli CE, Goto M, Campos AMP, Canteras NS. The supragenual nucleus: a putative relay station for ascending vestibular signs to head direction cells. Brain research. 2006;1094(1):138–148. doi: 10.1016/j.brainres.2006.03.101. [DOI] [PubMed] [Google Scholar]
- Blair HT, Sharp PE. Visual and vestibular influences on head-direction cells in the anterior thalamus of the rat. Behavioral neuroscience. 1996;110(4):643. doi: 10.1037//0735-7044.110.4.643. [DOI] [PubMed] [Google Scholar]
- Borah J, Young LR, Curry RE. Optimal estimator model for human spatial orientation. Annals of the New York Academy of Sciences. 1988;545(1):51–73. doi: 10.1111/j.1749-6632.1988.tb19555.x. [DOI] [PubMed] [Google Scholar]
- Bos JE, Bles W. Theoretical considerations on canal–otolith interaction and an observer model. Biological cybernetics. 2002;86(3):191–207. doi: 10.1007/s00422-001-0289-7. [DOI] [PubMed] [Google Scholar]
- Brooks JX, Cullen KE. Multimodal integration in rostral fastigial nucleus provides an estimate of body movement. Journal of Neuroscience. 2009;29(34):10499–10511. doi: 10.1523/JNEUROSCI.1937-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks JX, Carriot J, Cullen KE. Learning to expect the unexpected: rapid updating in primate cerebellum during voluntary self-motion. Nature neuroscience. 2015;18(9):1310–1317. doi: 10.1038/nn.4077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JE, Card JP, Yates BJ. Polysynaptic pathways from the vestibular nuclei to the lateral mammillary nucleus of the rat: substrates for vestibular input to head direction cells. Experimental brain research. 2005;161(1):47–61. doi: 10.1007/s00221-004-2045-4. [DOI] [PubMed] [Google Scholar]
- Butler WN, Taube JS. The nucleus prepositus hypoglossi contributes to head direction cell stability in rats. Journal of Neuroscience. 2015;35(6):2547–2558. doi: 10.1523/JNEUROSCI.3254-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler WN, Smith KS, van der Meer MA, Taube JS. The Head-Direction Signal Plays a Functional Role as a Neural Compass during Navigation. Current Biology. 2017;27(9):1259–1267. doi: 10.1016/j.cub.2017.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calton JL, Taube JS. Degradation of head direction cell activity during inverted locomotion. Journal of Neuroscience. 2005;25(9):2420–2428. doi: 10.1523/JNEUROSCI.3511-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark BJ, Taube JS. Vestibular and attractor network basis of the head direction cell signal in subcortical circuits. Frontiers in neural circuits. 2012:6. doi: 10.3389/fncir.2012.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark BJ, Brown JE, Taube JS. Head direction cell activity in the anterodorsal thalamus requires intact supragenual nuclei. Journal of neurophysiology. 2012;108(10):2767–2784. doi: 10.1152/jn.00295.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cullen KE. The vestibular system: multimodal integration and encoding of self-motion for motor control. Trends in neurosciences. 2012;35(3):185–196. doi: 10.1016/j.tins.2011.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cullen KE. The neural encoding of self-generated and externally applied movement: implications for the perception of self-motion and spatial memory. Frontiers in integrative neuroscience. 2014:7. doi: 10.3389/fnint.2013.00108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cullen KE, Taube JS. Our Sense of Direction: Progress, Controversies, and Challenges. Nature Neuroscience. 2017 doi: 10.1038/nn.4658. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day BL, Fitzpatrick RC. Virtual head rotation reveals a process of route reconstruction from human vestibular signals. The Journal of physiology. 2005;567(2):591–597. doi: 10.1113/jphysiol.2005.092544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickinson MH. Haltere–mediated equilibrium reflexes of the fruit fly, Drosophila melanogaster. Philosophical Transactions of the Royal Society of London B: Biological Sciences. 1999;354(1385):903–916. doi: 10.1098/rstb.1999.0442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkelstein A, Derdikman D, Rubin A, Foerster JN, Las L, Ulanovsky N. Three-dimensional head-direction coding in the bat brain. Nature. 2015;517(7533):159–164. doi: 10.1038/nature14031. [DOI] [PubMed] [Google Scholar]
- Gibson B, Butler WN, Taube JS. The head-direction signal is critical for navigation requiring a cognitive map but not for learning a spatial habit. Current Biology. 2013;23(16):1536–1540. doi: 10.1016/j.cub.2013.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasauer S. Das Zusammenspiel von Otolithen und Bogengangen im Wirkungsgefuge der Subjektiven vertikale. Lehrstuhl fur Nachrichtentechnik der Technischen Universitat Munchen; 1992. [Google Scholar]
- Glasauer S, Merfeld DM. Modelling three-dimensional vestibular responses during complex motion stimulation. Three-dimensional kinematics of eye, head and limb movements. 1997:387–398. [Google Scholar]
- Goodridge JP, Taube JS. Interaction between the postsubiculum and anterior thalamus in the generation of head direction cell activity. Journal of Neuroscience. 1997;17(23):9315–9330. doi: 10.1523/JNEUROSCI.17-23-09315.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green J, Adachi A, Shah KK, Hirokawa JD, Magani PS, Maimon G. A neural circuit architecture for angular integration in Drosophila. Nature. 2017;546(7656):101–106. doi: 10.1038/nature22343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall JM, McLoughlin DP, Kathman ND, Yarger AM, Mureli S, Fox JL. Kinematic diversity suggests expanded roles for fly halteres. Biology letters. 2015;11(11):20150845. doi: 10.1098/rsbl.2015.0845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homma Y, Nonaka S, Matsuyama K, Mori S. Fastigiofugal projection to the brainstem nuclei in the cat: an anterograde PHA-L tracing study. Neuroscience research. 1995;23(1):89–102. [PubMed] [Google Scholar]
- Jeffery KJ, Jovalekic A, Verriotis M, Hayman R. Navigating in a three-dimensional world. Behavioral and Brain Sciences. 2013;36(5):523–543. doi: 10.1017/S0140525X12002476. [DOI] [PubMed] [Google Scholar]
- Jeffery KJ, Wilson JJ, Casali G, Hayman RM. Neural encoding of large-scale three-dimensional space—properties and constraints. Frontiers in psychology. 2015:6. doi: 10.3389/fpsyg.2015.00927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamikouchi A, Inagaki HK, Effertz T, Hendrich O, Fiala A, Gopfert MC, Ito K. The neural basis of Drosophila gravity-sensing and hearing. Nature. 2009;458(7235):165. doi: 10.1038/nature07810. [DOI] [PubMed] [Google Scholar]
- Kim SS, Rouault H, Druckmann S, Jayaraman V. Ring attractor dynamics in the Drosophila central brain. Science. 2017;356(6340):849–853. doi: 10.1126/science.aal4835. [DOI] [PubMed] [Google Scholar]
- Laurens J. Doctoral dissertation. Paris: 2006. Modelisation Bayesienne des interactions visuo-vestibulaires; p. 6. [Google Scholar]
- Laurens J, Droulez J. Bayesian processing of vestibular information. Biological cybernetics. 2007;96(4):389–404. doi: 10.1007/s00422-006-0133-1. [DOI] [PubMed] [Google Scholar]
- Laurens J, Droulez J. Bayesian modelling of visuo-vestibular interactions. Probabilistic reasoning and decision making in sensory-motor systems. 2008:279–300. [Google Scholar]
- Laurens J, Straumann D, Hess BJ. Processing of angular motion and gravity information through an internal model. Journal of neurophysiology. 2010;104(3):1370–1381. doi: 10.1152/jn.00143.2010. [DOI] [PubMed] [Google Scholar]
- Laurens J, Strauman D, Hess BJ. Spinning versus wobbling: how the brain solves a geometry problem. Journal of Neuroscience. 2011;31(22):8093–8101. doi: 10.1523/JNEUROSCI.5900-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Angelaki DE. The functional significance of velocity storage and its dependence on gravity. Experimental brain research. 2011;210(3–4):407–422. doi: 10.1007/s00221-011-2568-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Meng H, Angelaki DE. Computation of linear acceleration through an internal model in the macaque cerebellum. Nature neuroscience. 2013a;16(11):1701–1708. doi: 10.1038/nn.3530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Meng H, Angelaki DE. Neural representation of orientation relative to gravity in the macaque cerebellum. Neuron. 2013b;80(6):1508–1518. doi: 10.1016/j.neuron.2013.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Kim B, Dickman JD, Angelaki DE. Gravity orientation tuning in macaque anterior thalamus. Nature neuroscience. 2016;19(12):1566–1568. doi: 10.1038/nn.4423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens J, Angelaki DE. A unified internal model theory to resolve the paradox of active versus passive self-motion sensation. eLife. 2017;2017(6):e28074. doi: 10.7554/eLife.28074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin EM, Pavlides C, Pfaff D. Multimodal Sensory Responses of Nucleus Reticularis Gigantocellularis and the Responses9 Relation to Cortical and Motor Activation. Journal of neurophysiology. 2010;103(5):2326–2338. doi: 10.1152/jn.01122.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittelstaedt ML, Mittelstaedt H. Homing by path integration in a mammal. Naturwissenschaften. 1980;67(11):566–567. [Google Scholar]
- Merfeld DM. Modeling the vestibulo-ocular reflex of the squirrel monkey during eccentric rotation and roll tilt. Experimental Brain Research. 1995;106(1):123–134. doi: 10.1007/BF00241362. [DOI] [PubMed] [Google Scholar]
- Muir GM, Brown JE, Carey JP, Hirvonen TP, Della Santina CC, Minor LB, Taube JS. Disruption of the head direction cell signal after occlusion of the semicircular canals in the freely moving chinchilla. Journal of Neuroscience. 2009;29(46):14521–14533. doi: 10.1523/JNEUROSCI.3450-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’keefe J, Nadel L. The hippocampus as a cognitive map. Oxford: Clarendon Press; 1978. [Google Scholar]
- Oman CM. A heuristic mathematical model for the dynamics of sensory conflict and motion sickness. Acta Oto-Laryngologica. 1982;94(sup392):4–44. [PubMed] [Google Scholar]
- Oman CM. NASA technical report. 1989. Sensory conflict in motion sickness: an observer theory approach. [Google Scholar]
- Ohtake T. Ascending projections from the gigantocellular reticular and dorsal paragigantocellular nuclei of the medulla oblongata in the rat: an anterograde PHA-L tracing study. Neuroscience research. 1992;14(2):96–116. doi: 10.1016/0168-0102(92)90086-r. [DOI] [PubMed] [Google Scholar]
- Page HJ, Wilson JJ, Jeffery KJ. A dual-axis rotation rule for updating the head direction cell reference frame during movement in three dimensions. Journal of Neurophysiology. 2017:jn-00501. doi: 10.1152/jn.00501.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyrache A, Lacroix MM, Petersen PC, Buzsaki G. Internally organized mechanisms of the head direction sense. Nature neuroscience. 2015;18(4):569–575. doi: 10.1038/nn.3968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pringle JWS. The gyroscopic mechanism of the halteres of Diptera. Philosophical Transactions of the Royal Society of London B: Biological Sciences. 1948;233(602):347–384. [Google Scholar]
- Quessy S, Freedman EG. Electrical stimulation of rhesus monkey nucleus reticularis gigantocellularis. Experimental brain research. 2004;156(3):342–356. doi: 10.1007/s00221-003-1787-8. [DOI] [PubMed] [Google Scholar]
- Ravassard P, Kees A, Willers B, Ho D, Aharoni D, Cushman J, … Mehta MR. Multisensory control of hippocampal spatiotemporal selectivity. Science. 2013;340(6138):1342–1346. doi: 10.1126/science.1232655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redish AD, Elga AN, Touretzky DS. A coupled attractor model of the rodent head direction system. Network: Computation in Neural Systems. 1996;7(4):671–685. [Google Scholar]
- Seelig JD, Jayaraman V. Neural dynamics for landmark orientation and angular path integration. Nature. 2015;521(7551):186–191. doi: 10.1038/nature14446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaikh AG, Ghasia FF, Dickman JD, Angelaki DE. Properties of cerebellar fastigial neurons during translation, rotation, and eye movements. J Neurophysiol. 2005;93(2):853–63. doi: 10.1152/jn.00879.2004. [DOI] [PubMed] [Google Scholar]
- Sharp PE, Blair HT, Cho J. The anatomical and computational basis of the rat head-direction cell signal. Trends in neurosciences. 2001a;24(5):289–294. doi: 10.1016/s0166-2236(00)01797-5. [DOI] [PubMed] [Google Scholar]
- Sharp PE, Tinkelman A, Cho J. Angular velocity and head direction signals recorded from the dorsal tegmental nucleus of gudden in the rat: implications for path integration in the head direction cell circuit. Behavioral neuroscience. 2001b;115(3):571. [PubMed] [Google Scholar]
- Sherman A, Dickinson MH. A comparison of visual and haltere-mediated equilibrium reflexes in the fruit fly Drosophila melanogaster. Journal of Experimental Biology. 2003;206(2):295–302. doi: 10.1242/jeb.00075. [DOI] [PubMed] [Google Scholar]
- Shinder ME, Taube JS. Differentiating ascending vestibular pathways to the cortex involved in spatial cognition. Journal of Vestibular Research. 2010;20(1, 2):3–23. doi: 10.3233/VES-2010-0344. [DOI] [PubMed] [Google Scholar]
- Shinder ME, Taube JS. Active and passive movement are encoded equally by head direction cells in the anterodorsal thalamus. Journal of neurophysiology. 2011;106(2):788–800. doi: 10.1152/jn.01098.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinder ME, Taube JS. Self-motion improves head direction cell tuning. Journal of neurophysiology. 2014a;111(12):2479–2492. doi: 10.1152/jn.00512.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinder ME, Taube JS. Resolving the active versus passive conundrum for head direction cells. Neuroscience. 2014b;270:123–138. doi: 10.1016/j.neuroscience.2014.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skaggs WE, Knierim JJ, Kudrimoti HS, McNaughton BL. A model of the neural basis of the rat’s sense of direction. Advances in neural information processing systems. 1995:173–180. [PubMed] [Google Scholar]
- Song P, Wang XJ. Angular path integration by moving “hill of activity”: a spiking neuron model without recurrent excitation of the head-direction system. Journal of Neuroscience. 2005;25(4):1002–1014. doi: 10.1523/JNEUROSCI.4172-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stackman RW, Tullman ML, Taube JS. Maintenance of rat head direction cell firing during locomotion in the vertical plane. Journal of Neurophysiology. 2000;83(1):393–405. doi: 10.1152/jn.2000.83.1.393. [DOI] [PubMed] [Google Scholar]
- Stackman RW, Clark AS, Taube JS. Hippocampal spatial representations require vestibular input. Hippocampus. 2002;12(3):291–303. doi: 10.1002/hipo.1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stackman RW, Golob EJ, Bassett JP, Taube JS. Passive transport disrupts directional path integration by rat head direction cells. Journal of neurophysiology. 2003;90(5):2862–2874. doi: 10.1152/jn.00346.2003. [DOI] [PubMed] [Google Scholar]
- Stringer SM, Trappenberg TP, Rolls ET, Araujo I. Self-organizing continuous attractor networks and path integration: one-dimensional models of head direction cells. Network: Computation in Neural Systems. 2002;13(2):217–242. [PubMed] [Google Scholar]
- Taube JS, Muller RU, Ranck JB. Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. Journal of Neuroscience. 1990a;10(2):420–435. doi: 10.1523/JNEUROSCI.10-02-00420.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taube JS, Muller RU, Ranck JB. Head-direction cells recorded from the postsubiculum in freely moving rats. II. Effects of environmental manipulations. Journal of Neuroscience. 1990b;10(2):436–447. doi: 10.1523/JNEUROSCI.10-02-00436.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taube JS. Head direction cells recorded in the anterior thalamic nuclei of freely moving rats. Journal of Neuroscience. 1995;15(1):70–86. doi: 10.1523/JNEUROSCI.15-01-00070.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taube JS, Burton HL. Head direction cell activity monitored in a novel environment and during a cue conflict situation. Journal of Neurophysiology. 1995;74(5):1953–1971. doi: 10.1152/jn.1995.74.5.1953. [DOI] [PubMed] [Google Scholar]
- Taube JS, Stackman RW, Calton JL, Oman CM. Rat head direction cell responses in zero-gravity parabolic flight. Journal of neurophysiology. 2004;92(5):2887–2997. doi: 10.1152/jn.00887.2003. [DOI] [PubMed] [Google Scholar]
- Taube JS. The head direction signal: origins and sensory-motor integration. Annu Rev Neurosci. 2007;30:181–207. doi: 10.1146/annurev.neuro.29.051605.112854. [DOI] [PubMed] [Google Scholar]
- Taube JS, Shinder M. On the nature of three-dimensional encoding in the cognitive map: Commentary on Hayman, Verriotis, Jovalekic, Fenton, and Jeffery. Hippocampus. 2013;23(1):14–21. doi: 10.1002/hipo.22074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner-Evans D, Wegener S, Rouault H, Franconville R, Wolff T, Seelig JD, … Jayaraman V. Angular velocity integration in a fly heading circuit. eLife. 2017;6:e23496. doi: 10.7554/eLife.23496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wearne S, Raphan T, Cohen B. Control of spatial orientation of the angular vestibuloocular reflex by the nodulus and uvula. Journal of neurophysiology. 1998;79(5):2690–2715. doi: 10.1152/jn.1998.79.5.2690. [DOI] [PubMed] [Google Scholar]
- Winter SS, Clark BJ, Taube JS. Disruption of the head direction cell network impairs the parahippocampal grid cell signal. Science. 2015;347(6224):870–874. doi: 10.1126/science.1259591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yakusheva TA, Shaikh AG, Green AM, Blazquez PM, Dickman JD, Angelaki DE. Purkinje cells in posterior cerebellar vermis encode motion in an inertial reference frame. Neuron. 2007;54(6):973–985. doi: 10.1016/j.neuron.2007.06.003. [DOI] [PubMed] [Google Scholar]
- Yoder RM, Taube JS. Head direction cell activity in mice: robust directional signal depends on intact otolith organs. Journal of Neuroscience. 2009;29(4):1061–1076. doi: 10.1523/JNEUROSCI.1679-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoder RM, Clark BJ, Taube JS. Origins of landmark encoding in the brain. Trends in neurosciences. 2011;34(11):561–571. doi: 10.1016/j.tins.2011.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoder RM, Taube JS. The vestibular contribution to the head direction signal and navigation. Frontiers in integrative neuroscience. 2014:8. doi: 10.3389/fnint.2014.00032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K. Representation of spatial orientation by the intrinsic dynamics of the head direction cell ensemble: a theory. Journal of Neuroscience. 1996;16(6):2112–2126. doi: 10.1523/JNEUROSCI.16-06-02112.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zupan LH, Merfeld DM, Darlot C. Using sensory weighting to model the influence of canal, otolith and visual cues on spatial orientation and eye movements. Biological cybernetics. 2002;86(3):209–230. doi: 10.1007/s00422-001-0290-1. [DOI] [PubMed] [Google Scholar]