Diffraction-Free Bloch Surface Waves

Abstract

In this article, we demonstrate a diffraction-free Bloch surface wave sustained on all-dielectric multilayers that does not diffract after being passed through three obstacles or across a single mode fiber. It can propagate in a straight line for distances longer than 110 μm at a wavelength of 633 nm and could be applied as an in-plane optical virtual probe, both in air and in an aqueous environment. The ability to be used in water, its long diffraction-free distance, and its tolerance to multiple obstacles make this wave ideal for certain applications in areas such as the biological sciences, where many measurements are made on glass surfaces or for which an aqueous environment is required, and for high-speed interconnections between chips, where low loss is necessary.

ToC graphic

Diffraction free and self-healing propagation of Bloch Surface Wave in water.

Bloch surface waves (BSWs) are electromagnetic surface waves excited at the interface between a truncated periodic dielectric multilayer with a photonic band gap (PBG) and its surrounding medium. They can be considered to be the dielectric analogue of surface plasmon polaritons (SPPs), except with lower losses and longer propagation lengths. ^{1, 2} Similar to SPPs, BSWs have been applied in nanoscale optical circuits, bio-sensing, gas sensing, fluorescence emission enhancement or sorting, and surface enhanced Raman scattering. ^3–7 BSWs possess specific properties that differentiate them from SPPs. They are not subject to losses caused by metal absorption, which allows for BSW resonance with high quality factor and long propagation length. ⁸ There are many choices for the dielectric materials for BSWs, which allows this dielectric multilayer to be used from deep ultraviolet (UV) to near-infrared (NIR) wavelengths; ⁹ meanwhile SPPs suffer considerably higher propagation losses in the UV and visible region. So, various methods have been proposed to increase the propagation lengths of SPPs, ^{10, 11} that is still not long enough for practical applications. Additionally, fluorophores can be quenched near metallic surfaces, which does not occur with dielectric surfaces. Further, the moderate localization of a BSW mode compared with that of a SPP mode is favorable for applications where a large volume of the adjacent material needs to interact with the dielectric multilayer.

Both SPPs and BSWs undergo diffraction in the plane of the interface, which will induce coupling losses between the on-chip components as the wave packet spreads laterally during propagation. In recent years, with the rapid development of plasmonic technology, many methods have been proposed to construct diffraction-free SPPs, ¹² such as plasmonic Airy beams (PABs) generated by spatial light modulators, ¹³ in-plane diffraction from metallic hole arrays, ¹⁴ Cosine-Gauss plasmon beams created by two sets of metallic gratings, ¹⁵ and efficient manipulation of PABs in linear optical potentials produced by wedged metal–dielectric–metal structures. ¹⁶ The evolution from free-space three dimensional (3D) diffraction-free optical waves (such as Bessel and Airy beams) into two dimensional (2D) surface waves, is not only of fundamental interest, but could also facilitate the development of devices that utilize these waves. One of the main advantages of this technique is that 2D elements can have arbitrary shapes—something that is difficult to achieve in 3D. ¹⁷ This is also one of the reasons why research is shifting from metamaterials to meta-surfaces.^{18, 19}

Previously, little to no effort had been devoted to constructing diffraction-free surface waves in an aqueous environment and in the visible light band, which is more favorable for biological applications. Many biological and clinical assays are performed on glass surfaces, including assays involving DNA, ²⁰ proteins, ²¹ and HIV, ²² as well as a wide range of immunoassays. ²³ More recently these assays are being modified to use multiplexing based on multiple excitation and emission channels. ^{24, 25} The ability to generate and control diffraction-free light waves on glass surfaces could have a large impact on the biosciences and result in other formats for diagnostic devices. Such applications are more difficult to achieve with metallic structures because of the high propagation losses at the metal/water interface. The propagation loss of a SPP at a metal/water interface is higher than that of a SPP at a metal/air interface, notably in the visible spectrum, such as for a wavelength of 633 nm. For a BSW with dielectric multilayers, the propagation losses are much lower (both in water and air), and their effective indices can be tuned by varying the thickness of the top dielectric layer. ²⁶ Using an axicon (or conical lens element^27–29), free-space Bessel beams, which are also a diffraction-free beam, can be generated; this has been reported in free space optics (3D optics). In the present report, we demonstrate both experimentally and theoretically that diffraction-free BSWs can be generated on an all-dielectric multilayer with simple dielectric gratings. Owing to the low loss of BSWs, diffraction-free behavior can be preserved even after the wave encounters either three obstacles or a single mode silicon fiber along the propagation path.

RESULTS AND DISCUSSION

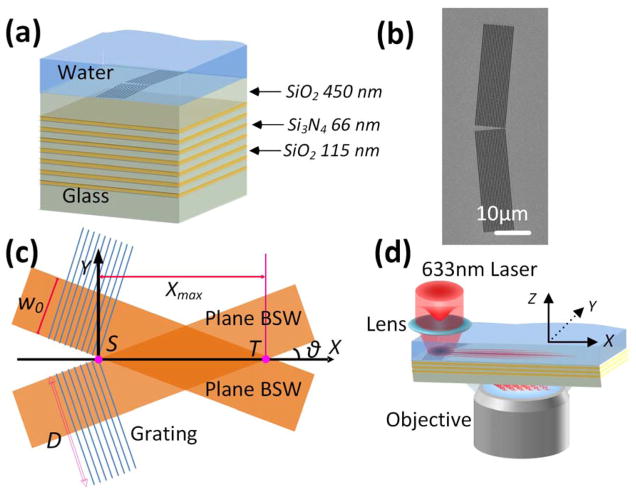
The dielectric multilayer is made of alternating layers of SiO₂ and Si₃N₄, with the number of layers shown in Figure 1a. Except for the top SiO₂ layer, which was 450 nm thick (refractive index n = 1.46), the SiO₂ layers were 110 nm thick. The thickness of the Si₃N₄ (Si Rich+) layers was approximately 66 nm (refractive index n = 2.6). With this multilayer structure, BSWs can be populated at the water/SiO₂ interface (Supplementary Figure 1). Two dielectric gratings (Figure 1b) with a period of 460 nm were inscribed on the top SiO₂ layer with a focused ion beam (FIB); the grating’s period was matched with the physical wavelength of the BSWs at the SiO₂/water interface (Figure 1b, which shows that the crossing angle of the two gratings were designed to be either 10° or 170°). Subsequently, the multilayer was coated with a drop of water. With the aid of the grating for momentum matching, BSWs were excited with a normally incident, focused Gaussian beam from a laser with linear polarization parallel to the Y-axis at a wavelength of 633 nm. ³⁰ The laser beam was focused onto the center of the two gratings. The plane BSWs of equal amplitude launched by the pair of gratings are expected to interfere constructively to form DF-BSWs for a distance X_max = w₀/sin (θ) = 115 μm, where θ was designed to be 5° and the beam waist of the incident beam was w₀, which was set to 10 μm. The length of the grating (D) was 30 μm and thus larger than the beam waist (Figure 1c). It should be noted that the calculation of the maximum non-diffraction distance was based on the assumption that BSWs propagate without loss (from point S to point T, where point S was set to be the zero point of the X–Y axis). Although the non-diffracting BSW was realized in air environment and at the telecommunication wavelength, with the aid of a nano-thin 2D axicon, ³¹ our configuration with gratings is more compact where the gratings can work as both the coupler and shaping component. The advantages of BSW over SPP in the terms of propagation loss and real application is more obvious in the visible light band and aqueous environment. The optical field intensity distribution of the generated BSWs was then measured with a home-built leakage radiation microscope (LRM, Fig. 1d). ³²

Figure 1. Schematic diagram of the samples and of the optical setup.

(a) Dielectric multilayer with intersecting gratings fabricated on the top SiO₂ layer. The top surface of the sample was immersed in deionized water. (b) A scanning electron microscope (SEM) image of the grating in which the cross-angle of the two gratings is 170°. The period of the gratings was 460 nm. (c) Formation of the DF-BSW. The cross-angle of the two gratings is defined as (π-2θ = 170°); X_max represents the longest diffraction-free distance; D represents the length of the grating; w₀ is the beam waist; and S represents the zero point of the X–Y axis. (d) Optical setup of the LRM. The Gaussian beam was focused onto the two gratings and then launches the DF-BSW, whose leakage radiation is collected by the objective.

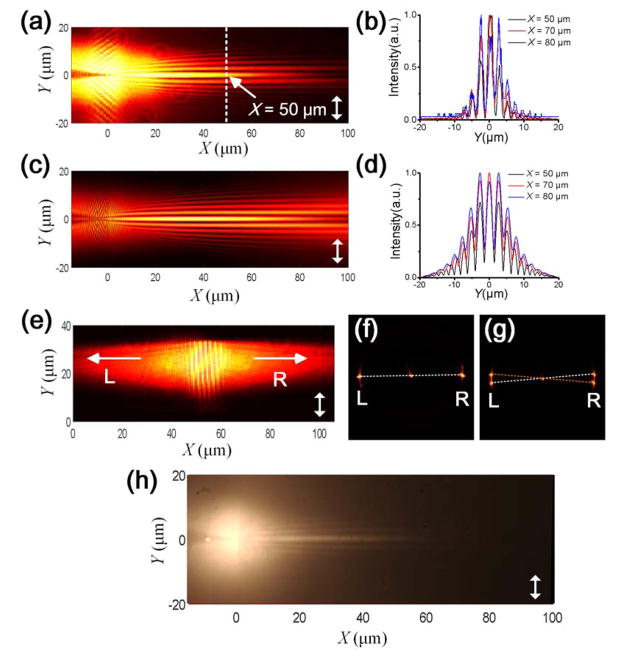
Figure 2a shows a front focal plane (FFP) image of the LRM; in it, a significant main lobe and several parallel side lobes appear and propagate toward the right side. A numerical simulation of the electric filed distribution on the top surface of the dielectric layer (SiO₂/water interface, Figure 1a) was performed with the finite-difference time-domain (FDTD) method (Figure 2c). ³³ The numerical mode is the same as the Figure 1a, where the layer thicknesses, grating parameters, beam waist, and incident wavelength were the same as those used in the experiments (Figure 1). Consistent with the LRM image, a strong main lobe and several weak parallel side lobes are visible in the simulated image. Because of the scattering caused by the roughness around the gratings, the intensity is brighter in the areas of excitation in the experimental image (Figure 2a) than in the simulated one (Figure 2c). To assess the diffraction-free properties, we plotted the intensity profiles along the white dashed lines at three distances X (X = 50, 70, and 80 μm, where the position of the starting point S was set to be X = 0 μm (Figure 1c); for clarity, only one dashed line is shown at X = 50 μm) for both the experimental (Figure 2b) and simulated (Figure 2d) images. The beam presents a narrow profile, and the full-width at half-maximum of the main lobe was about 2 μm at all three distances (or X-positions) in both the numerical and experimental results. Similar to the main lobe, the transverse profiles (or beam shapes) of the side lobes were also preserved for the surface waves propagating along the propagating direction. For the cosine-Gauss SPP wave, ¹⁵ only the main lobe appeared and retained diffraction-free owing to the high loss of the SPPs. Another difference is that BSWs can be populated with either transverse electric (TE) or transverse magnetic (TM) polarized light if the correct layer thicknesses are chosen, ³⁴ which yields even more polarization choices. In this work, the DF-BSW was excited with an incident beam with a polarization along the Y-axis (Figure 2a and 2b) causing the BSW to be TE polarized (the DF-BSW here cannot be excited with TM polarized light as demonstrated by the image in Supplementary Figure 2). In contrast, for diffraction-free SPPs, the excitation field and propagation field must be TM polarized (SPPs can only be generated with TM polarized light, as shown in Supplementary Figure 3, where the incident polarization direction is along the X-axis). For comparison, the electric field distribution of the diffraction-free SPPs at the silver/water interface originating from the two gratings was also simulated with FDTD at the same wavelength, i.e. at 633 nm (Supplementary Figure 3); this shows that the propagation distance is considerably reduced.

Figure 2. DF-BSW at a dielectric/water interface.

(a) Recorded DF-BSW image on the FFP of the LRM. (c) Simulated field distribution of the DF-BSW. (b) Recorded beam shapes at different transverse positions (X = 50, 70, and 80 μm). (d) Simulated beam shapes at the same positions (X = 50, 70, and 80 μm). (e) Recorded FFP-LRM image of a BSW launched by a single grating. The grating’s direction (long axis of the grating line) is vertical, so the propagating direction of the launched BSW is perpendicular to the grating’s direction. (f) Corresponding BFP-LRM image of the image in panel (e), where the left and right spots represent the BSW propagating to left and right, respectively. (g) Corresponding BFP-LRM image of the image in panel (a), where the right two spots represent the two BSW plane waves propagating to the right; these then interfere and form a DF-BSW. (h) FFP-LRM fluorescence image of the DF-BSW; the water is doped with the dye Fluorescent red 646 reactive (which can be excited by a laser with a wavelength of 633 nm). A long pass filter (cut-on wavelength at 650 nm) was used to reject the excitation wavelength. The double-headed white arrows in panels (a), (c), (e), and (h) indicate the orientation of the incident polarization.

To clearly show the formation of the DF-BSW, the laser beam was focused onto a single grating where plane BSWs that propagate both toward the right and left sides are generated (Figure 2e). The corresponding back focal plane (BFP) image (Figure 2f) shows three points. The center one represents the transmitted laser beam. Normally, the dielectric multilayer would reflect all light with a wavelength of 633 nm because of its PBG, meaning no light would pass through the multilayer at normal incidence. Because of the inscribed gratings on the top SiO₂ layer (the gratings can be seen as defects in the multilayer), the PBG of the multilayer is broken and therefore the light can be transmitted, which results in the center spot on the BFP image. The BFP image represents the distribution of the wave-vector or divergence of the corresponding optical waves. If the spot on the BFP image is large, it means that the corresponding wave propagates in a wide range of directions (i.e. it has a large divergence). Hence, the known numerical aperture (NA) of the objective (NA of 1.49) and the size of the center spot divergence can be derived at approximately 2°, meaning that the exciting light is essentially of normal incidence. Similarly, the left and right spots correspond to BSWs from a single grating; the BSWs propagate toward both the left and the right side. From the BFP image, we can deduce that the propagation directions are both perpendicular to the long axis of the grating. The two spots in the image are very small, corresponding to an angular divergence of approximately 3°; hence, they can be seen as belonging to an approximately planar surface wave (Figure 1c). The distance between the right and left spots indicates the wavenumber (or effective index) of the excited BSW. The larger the distance, the larger the wavenumber is. The wavenumber was derived to be 1.38 K₀ in this case, which is consistent with the findings from the white light BFP image (Supplementary Figure 1). Here the K₀ is the wavenumber of light at the same frequency in vacuum.

For comparison, the BFP image shows two pairs of spots (Figure 2g, relative to the FFP image in Figure 2a). Two dashed lines connecting a pair of spots both pass through the center spot. Based on the above description, the two pairs of spots (on each dashed line) demonstrate that the two gratings each generate a BSW. Owing to the different orientations of the gratings (their cross-angle was either 170° or 10°, Figure 1), the propagation direction (illustrated by the two dashed lines) of the BSWs originating from each grating will be different, which results in the four spots visible in Figure 2g. The cross-angle of the launched planar BSWs, represented by the cross-angle of the two dashed lines, was 10°, which is consistent with the cross-angle of the two designed gratings (Figure 1b, 2θ = 10°; the propagation direction of the launched BSW was perpendicular to the grating). The BSWs launched by each grating interfere when they overlap spatially, as illustrated in Figure 1c (the BSWs propagating to the right side). Our BFP images confirm the formation of the diffraction-free surface waves, which originate from the interference of the two planar surface waves caused by the one-dimensional gratings. This information cannot be resolved only from the FFP image (Figure 2g).

The penetration of the DF-BSW into water was simulated as shown in Supplementary Figure 4 (which shows the electric-field distribution in the Y-Z plane at different X positions). The evanescent field of BSW can reach the X-Y plane at Z= 400 nm as shown in Supplementary Figure 4. The decay length along the Z- direction can be increased or decreased by either decreasing or increasing the top SiO₂ layer, respectively. ²⁶ The penetration of the DF-BSW into water can be used for fluorescence imaging. The dye-labelled cells are suspended in cell culture media, which are aqueous solutions. To demonstrate this, we doped the water with the dye Fluorescent red 646 reactive (from Fluka), which can be excited at a wavelength of 633 nm and which fluorescence at 660 nm. The fluorescence image (Figure 2h) shows that the fluorophores along the main lobe of the DF-BSW can be excited. This phenomenon suggests that the DF-BSW can work as an in-plane optical virtual probe. By using this dielectric multilayer, the out of plane virtual probe also can be generated by the focused BSW. ³⁵ These virtual probes can be used in different applications, from sensing to fluorescence imaging. For example, here, if a labeled cell in a microfluidic system flows across the DF-BSW, it will be excited and can then be counted or detected or sorted. Here, the DF-BSW is trapped on the surface and propagates far away from the focal point, so there is little contribution from the directly incident light, resulting in a low background noise. What is more, given the small distance of the evanescent penetration compared with the free space laser beam, the DF-BSW has the potential to be used for single molecule detection where the molecules are located far from the incident light. The fluorescence coupling efficiency appears to be low based on the relative brightness of the directly excited fluorescence and the DF-BSW. This may be the result of having used a thick layer of the fluorophore containing water, which may reduce surface-selective fluorophore binding.

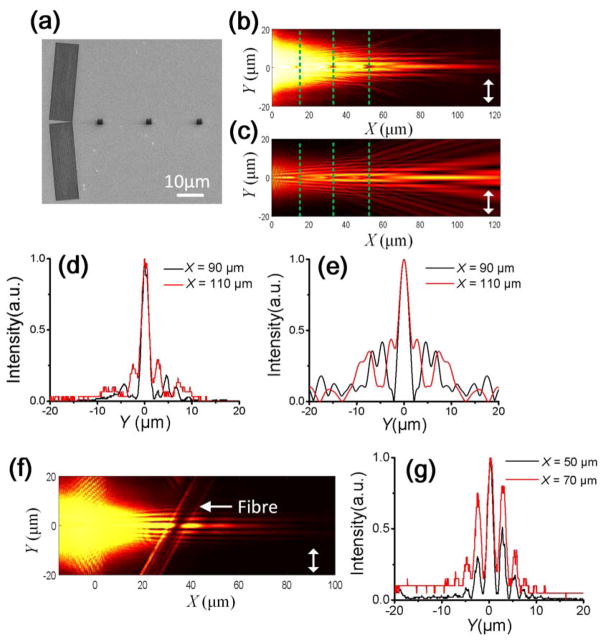
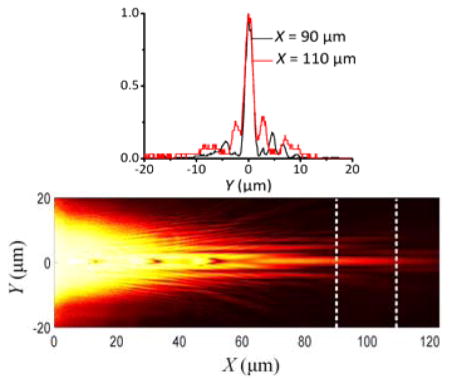
An important advantage of this low loss dielectric multilayer is that the diffraction-free can be preserved even after passing several obstacles (such as the three obstacles shown in Figure 3a, which were 2 μm × 2 μm square holes positioned at X = 16 μm, 34 μm, and 52 μm, respectively, these holes were fabricated with FIB, with the similar process as the fabrication of the coupling gratings on Figure 1b); this had not previously been demonstrated experimentally for any diffraction-free SPPs. We conclude that one reason this had not previously been shown is the high absorption losses in metal; another reason being the high scattering loss of SPP waves caused by obstacles. Figure 3b and 3c clearly illustrate that the main lobe of the BSWs still propagates along a straight line after passing the three obstacles, even when the distance between the starting point (S) and the third obstacle reaches around 52 μm. The intensity profiles at X = 90 μm and 110 μm (Figure 3d and 3e) clearly demonstrate that the diffraction-free behavior of the main lobe is maintained after the three obstacles (it also was named as self-healing property). The diffraction-free distance thus approaches the maximum theoretical value (Xmax = w₀/sin (θ) = 115 μm), which demonstrates that a BSW can propagate much further than a SPP. The main lobe becomes more distinct than the side lobe after the obstacles—this is true in both in the simulated and experimental images. In contrast, the main lobe is weaker than the side lobe at long distances (such as at X = 100 μm, Figure 2a and 2c) in the absence of obstacles. What is more, a comparison of Figures 3c and 2c shows that BSWs propagate further when obstacles are present. In Figure 2c the maximum intensity of the main lobe occurs around X = 40 μm, whereas in Figure 3c, it occurs around X = 90 μm. These properties potentially provide a way to obtain a strong main lobe for the diffraction-free surface waves. In addition to the regular obstacles designed along the travel path of the main lobe, a single mode silicon fiber with a diameter of about 9 μm and longer than 50 μm was placed on the multilayer (Figure 3f). While one might expect that this would block the propagation of both the BSW’s main and side lobes, Figure 3g shows that the main and side lobes of the BSW preserve their diffraction-free property after passing through the fiber. Due to the transparence of the silica fiber at the wavelength of 633 nm, the BSW can perform the refractive passing through the fiber and maintain the diffraction free property. To the best of our knowledge, there is no previous report of diffraction-free SPPs that can pass through an obstacle that is so large.

Figure 3. Recovery of the DF-BSW at the dielectric/water interface.

(a) SEM image of the dielectric gratings and three square obstacles inscribed via FIB on the top SiO₂ layer. The distance between the obstacles was 18 μm, and the distance between the last obstacle and the starting point S was 52 μm. The FFP-LRM image (b) and the simulated image (c) of the DF-BSW shows it propagating around the three obstacles. The dashed lines in panels (b) and (c) show the positions of the obstacles. Panel (d) shows the LRM recorded beam shapes at different positions (X = 90 and 110 μm). Panel (e) shows the simulated beam shapes at the same positions (X = 90 and 110 μm). Panel (f) shows an FFP-LRM image of the BSW propagating across a silica fiber attached to the dielectric multilayer, while panel (g) shows the beam shape of the BSW after the fiber at X = 50 and 70 μm. The double-headed white arrows in panels (b), (c), and (f) indicate the orientation of the incident polarization.

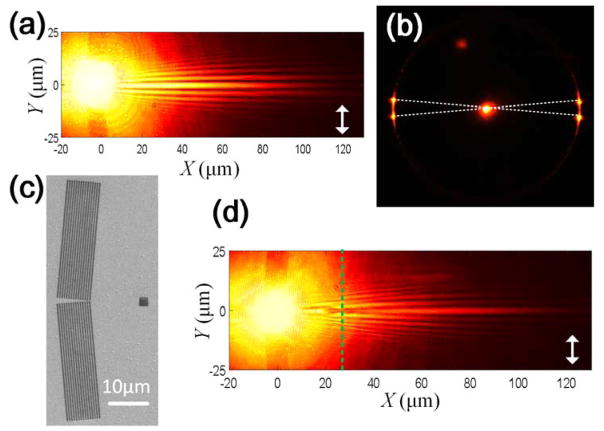
Similar to a BSW at the dielectric/water interface, a BSW at a dielectric/air interface can also be generated on a dielectric multilayer (Supplementary Figure 5a). In this case, a BSW with a smaller wavenumber than when using water is observed (smaller dark ring in the BFP images, Supplementary Figure 5b). With the aid of two gratings (Supplementary Figure 5c, grating period of 590 nm to match the wavelength of the BSW at the air/SiO₂ interface), DF-BSWs are generated as shown in the FFP image of the LRM (Figure 4a, captured with a 60× objective with a NA of 1.20), in which both the main lobe and side lobes appear simultaneously. The BFP image (Figure 4b) also shows two pairs of spots on the left and right sides, where the cross-angle is also 10°. When a square obstacle with a size of 2 μm ×2 μm was placed in the propagating path (Figure 4c), the BSWs showed self-healing, and the main lobe became more dominant after the obstacle (Figure 4d). The DF-BSWs in air can thus be used to detect atmospheric particles that flow close to the surface of the dielectric multilayer. The advantage of this approach is that the particle can cause a signal on a dark background, which is much easier to detect than a small decrease in a high intensity signal.

Figure 4. DF-BSW at the dielectric/air interface.

(a) FFP-LRM image of the DF-BSW, and (b) corresponding BFP image of (a). (c) SEM image of the gratings with a single obstacle. The cross-angle of the gratings was 170°. The period of the grating was 590 nm. (d) Corresponding FFP-LRM image of (c) in which the dashed line represents the position of the obstacle (X = 28 μm); the size of the square obstacle was 2 μm × 2 μm. The double-headed white arrows in panels (a) and (d) indicate the orientation of the incident polarization.

From Figure 4a it can be seen that the propagation of the DF-BSW can exceed a distance of 110 μm from starting point S at a wavelength of 633 nm. For a SPP with a wavelength of 785 nm, the diffraction-free surface waves can only travel 80 μm; ¹⁵ this distance will be further decreased if the incident wavelength were decreased to 633 nm, i.e. to the same wavelength as used for the BSW (Supplementary Figure 3). As described by the equation X_max =w₀/sin (θ), we can increase the non-diffraction distance X_max by increasing w₀ or by decreasing θ, which does not change the intrinsic propagation loss of the SPPs or BSWs—however, the SPPs and BSWs may lose their energy before they reach the terminal point T, in which case this equation cannot be used. The diffraction-free distance of the surface waves generated by the intersecting gratings is strongly correlated with the intrinsic propagation loss of the plane BSWs or SPPs. For a SPP at an Ag/water interface, the theoretical propagation length is approximately 8.5 μm for a wavelength of 633 nm, regardless of the roughness of the silver film and the leakage radiation loss used for imaging. ³⁶ Whereas, for the BSW shown on Figure 2e, the experimental propagation length can be calibrated to be as long as 38 μm at the same wavelength, based on intensity trace fitting with an exponential function. The smaller the loss of the BSWs compared with that of SPPs, the more favorable it is for increasing the real diffraction-free distance and also its tolerance to obstacles, as demonstrated in Figures 2, 3, and 4. It should be noted in the discussions of Figures 2, 3, and 4, we do not use the definition “propagation length” for the DF-BSW, because the intensity decay along the X-axis (propagation direction of the DF-BSW) is not exponential (its maximum intensity appears at nearly the center of the BD-BSW beam). Whereas, for a BSW excited by a single grating (Figure 2e), the excited BSW propagating to the left or right is a diffracting beam and is exponentially dampened during propagation.

CONCLUSIONS

In conclusion, we have experimentally and numerically demonstrated DF-BSWs, in water environment and at visible light band. The lower loss of the dielectric multilayer compared with a metal film, especially in the visible spectrum, makes BSWs more favorable than SPPs for the formation of diffraction-free surface waves, with the advantage of being diffraction-free over long distances and can be re-formed after passing through larger or smaller obstacles. Because of these advantages, DF-BSWs have potential applications in areas such as on-chip optical circuits, ^{17, 37,} where the signal may encounter obstacles as the devices become more complex. DF-BSWs may also find use for the optical nano-manipulation of molecules in liquids ^{38, 39} or as a light source for cell counting in flow cytometry. ⁴⁰ Since a DF-BSW has an evanescent field, DF-BSWs can be used for cell imaging for cells located on surfaces as an alternative to total internal reflection, which requires a coupling prism. ⁴¹ Additionally, with the exception of the DF-BSWs demonstrated here, all other intensity or shape controllable surface waves, such as those generated by linearly focusing beams, ⁴² de-multiplexing waves, ⁴³ in-plane Airy beams, ¹⁴ trapping light that mimics gravitational lensing, ⁴⁴ and wave-front shaping by exploiting general relativity (GR) and its effects, ⁴⁵ can be attained with this platform, which consists of all-dielectric multilayers with water or air as the surrounding medium. We believe that our findings will inspire further intriguing phenomena to be discovered and that additional practical applications in beam engineering and nanophotonic manipulations will be uncovered.

METHODS

Leakage radiation microscopy

The incident laser beam (633 nm wavelength) was coupled into a single mode fiber and then collimated by an optical expander. The collimated beam was focused by a lens onto the dielectric gratings (Figure 1d, with a beam waist of 10 μm). An oil or water immersed objective (for oil: 100× magnification and NA of 1.49 from Nikon for a BSW at a dielectric/water interface, see Figures 2 and 3 as well as Supplementary Figure 2; for water: 60× magnification and NA of 1.20 From Nikon for a BSW at a dielectric/water interface, see Figure 4) was used to collect the leakage signals of the BSWs. By changing the position and focal length of the tube lens, either the FFP or BFP of the objective can be imaged by a CCD camera (Retiga 6000 from QImaging). A polarizer and a half wave plate can be inserted between the fiber-expander and the top focal lens to tune the incident polarization.

Fabrication of the dielectric multilayers and gratings

The dielectric multilayers were fabricated via plasma-enhanced chemical vapor deposition (PECVD, Oxford System 100) of SiO₂ and Si₃N₄ on a standard microscope cover glass (0.17 mm thickness) at a vacuum pressure of <0.1 mTorr and a temperature of 300 °C. For the BSWs in water, the refractive index of the (high index) dielectric layer Si₃N₄ (Si Rich+) was n = 2.60, and for the BSWs in air it was n = 2.14. The low refractive index dielectric layer was SiO₂ (n = 1.46). The thicknesses of these layers are shown in Figure 1a and in Supplementary Figure 5a, respectively. There were fourteen layers in total. The dielectric multilayer was then coated with a gold film of 20 nm thickness by magnetron sputtering (Sputter-Lesker Lab18); this gold film was then used to create two gratings on the top SiO₂ layer using FIB (Helios NanoLab 650) lithography. After the lithography step, the gold film was removed with aqua regia, and then the dielectric multilayer was cleaned with acetone and then with nanopure deionized water and dried with an N₂ stream. The square holes on Figure 3a were fabricated with the same way.