Abstract
Transcription factors (TFs) are able to associate to their binding sites on DNA faster than the physical limit posed by diffusion. Such high association rates can be achieved by alternating between three-dimensional diffusion and one-dimensional sliding along the DNA chain, a mechanism-dubbed facilitated diffusion. By studying a collection of TF binding sites of Escherichia coli from the RegulonDB database and of Bacillus subtilis from DBTBS, we reveal a funnel in the binding energy landscape around the target sequences. We show that such a funnel is linked to the presence of gradients of AT in the base composition of the DNA region around the binding sites. An extensive computational study of the stochastic sliding process along the energetic landscapes obtained from the database shows that the funnel can significantly enhance the probability of TFs to find their target sequences when sliding in their proximity. We demonstrate that this enhancement leads to a speed-up of the association process.
INTRODUCTION
Transcription factors (TFs) are able to bind short target sequences on the DNA, where they can promote or impede the binding of RNA-Polymerase (RNAP) and, consequently, activate or repress transcription (1). Fast and accurate control of gene expression is crucial for many biological functions, and relies on the ability of TFs to rapidly find their transcription factor binding site (TFBS) among a multitude of competing DNA sequences, and to establish with it a stable complex.
A mechanism to achieve fast target search is facilitated diffusion (FD). FD was postulated by Berg and Von Hippel (2–4), based on earlier theoretical ideas (5,6), to explain the fact that the association rate of Escherichia coli Lac repressor to its binding site is two orders of magnitude faster than the diffusion-limited rate (7). In FD, TFs alternate between different modes of exploration of the DNA chain. When associated to the DNA, they can slide along it with weak specificity for its base composition. When detached from DNA, TFs diffuse in the cytosol before reassociating to the chain, either at long distance (jumps) or at short distance (hops) from the detachment site (8). Further, in compact DNA conformations, TFs can bind to two non-contiguous DNA branches and thus pass from one branch to the other (intersegmental transfer) (9,10). Even though all the above mechanisms play a role in FD, sliding is key (11), as it effectively extends the size of the target to the sliding length—the antenna effect (12). Although FD is nowadays a broadly accepted mechanism, some works have questioned its effectiveness in physiological conditions (13,14), see (15) for a review. Sliding of Lac repressor was recently demonstrated in vivo by single molecule experiments (16).
The energetics of the sliding process presents a conceptual difficulty. The TF binding energy profiles along the genome are highly fluctuating and characterized by many sequences close in binding energy to the target (17–19). A TF tightly bound to the DNA, with high specificity to the base composition, would suffer of a highly reduced sliding effectiveness due to energetic traps in the fluctuating energy landscape (20), leading to a severe slowing down of the search process. Conversely, a loosely bound TF would slide more easily, but with a reduced stability at the target, leading to a loss of reliability. This tradeoff is often referred to as the speed-stability paradox (17–19). Slutsky and Mirny (17), building upon previous ideas (21,22), proposed that a TF bound to DNA and alternating between two conformations, a highly specific recognition mode and a weakly specific search mode, can both quickly find its binding site and form with it a stable complex (see also (18,19,23)).
The mechanism of FD suggests that the genetic background, i.e. the DNA sequences surrounding a given target, can influence the search kinetics. Some indications in this direction have been obtained for the RNAP and its σ-factors. RNAP, while sliding along λ-phage DNA, tends to spend more time bound to AT-rich regions, where dissociation rates are smaller (24). Further, the average binding energy landscape of E. coli σ70 factor displays lower values with respect to the DNA average in a wide region extending over 500 bp around the target sites (25). It was speculated that such low-energy regions could be related to their AT-richness (25). It is tempting to interpret such characteristic landscape as an energetic funnel that can increase the accessibility and, eventually, speed up the search of the target site, similarly to what happens in protein folding (26). This interpretation is particularly engaging if it can be extended to generic TFs. The possibility of speed-up due to a funnel has been already proposed in the literature. A theoretical study of RNAP, ignoring the effects of fluctuations, showed that energy gradients directly translate into a deterministic bias toward the target (27). A computational study, based on Brownian dynamics simulations of a coarse-grained model of the TF–DNA complex, demonstrated that organizing binding energies in a funnel reduces the search time with respect to the case of randomly organized binding energies (28). An energetic funnel, on a much shorter length scale, was argued to emerge from electrostatic complementarity of positive and negative charges on the TF and DNA respectively (29). Funnels originating from low entropy non-target sequences were proposed to affect TF–DNA binding preferences for different eukaryotes (30–32).
In this paper, we scrutinize the role of the binding energy landscape in the sliding kinetics of a large set of TFs of E. coli. The first question we address is whether generic TF binding sites are embedded in an energetic funnel. For the paradigmatic example of the Lac repressor, the energy landscape around the target appears uncorrelated (22). However, energy gradients can be hard to detect because of fluctuations and become apparent only by averaging over many target regions. Analyzing the average genetic background of 1544 TFBS from the RegulonDB database (33), we demonstrate the presence of a funnel extending over more than 300 bp both upstream and downstream of the TFBSs. Performing an analysis of the base composition around the TFBSs, we show that the funnel is related to gradients in AT composition, that are present in regions up to 1000 bp upstream of the transcription start site (34,35).
The second question is whether the funnel can speed-up target search. We present an extensive computational study of a two-state model for sliding TFs similar to that of (17,18) on the binding energy landscapes obtained from the database of TFBSs. We show that, despite the fluctuations of the energy landscape that were neglected in previous studies (27,28), the funnel significantly increases the probability of finding the target. We estimate the effect of the funnel on the total search time. We confirm the main finding also in Bacillus subtilis, for which we analyzed a set of TFBSs from the DBTBS database (36).
MATERIALS AND METHODS
Database of TFBSs of E. coli
We consider a set of 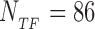 TFs of E. coli K12 (strain MG1655) from RegulonDB version 7.4 (33). Position-specific scoring matrices (PSSMs) for these TFs are built from their annotated binding sites (37). The PSSMs are 4 × Lα matrices, where 4 is the number of nucleotides (A,C,G,T) and Lα the number of bases which the TF α binds to. For most TFs, one finds Lα ≈ 15–20 bp, though in the database (DB) there are examples with Lα = 5 − 7 bp and Lα ≥ 30 bp, see Supplementary Table S1. Each entry of a PSSM represents the probability, Pα(s, j) that a nucleotide s is present at position j among the target sequences of the TF α. Such probability is inferred from the number of sequences, nα(s, j) in the DB having a nucleotide s at position j via the formula (19)
TFs of E. coli K12 (strain MG1655) from RegulonDB version 7.4 (33). Position-specific scoring matrices (PSSMs) for these TFs are built from their annotated binding sites (37). The PSSMs are 4 × Lα matrices, where 4 is the number of nucleotides (A,C,G,T) and Lα the number of bases which the TF α binds to. For most TFs, one finds Lα ≈ 15–20 bp, though in the database (DB) there are examples with Lα = 5 − 7 bp and Lα ≥ 30 bp, see Supplementary Table S1. Each entry of a PSSM represents the probability, Pα(s, j) that a nucleotide s is present at position j among the target sequences of the TF α. Such probability is inferred from the number of sequences, nα(s, j) in the DB having a nucleotide s at position j via the formula (19)
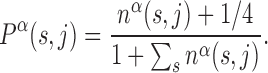 |
(1) |
The factor 1/4 corresponds to assuming a Bayesian prior of equal probabilities for all bases to mitigate the effect of small sample sizes (19).
RegulonDB also lists the putative targets for each TF, including sequences with strong (experimental) and weak (only computational) evidence of being target sites for the TF. Over the whole set of TFs, the database collects 1913 such sequences. We searched each sequence on the E. coli genome and its reverse complement, and excluded from the set those that appear more than once in order to limit our analysis only to potentially functional binding sites. After this selection we are left with 1544 target sequences belonging to a set of 76 TFs with Lα in the range 10 to 37 bp. The list of the TFs with their Lα and number of unique target sequences Mα (α = 0, …, NTF − 1) is presented in Supplementary Table S1. Further information on the database of target sequences is reported in a Supplementary File.
Binding energy from position-specific scoring matrices
From the PSSMs, binding free energies can be estimated with standard procedures based on equilibrium measurements (38,39). Notice that, in this paper, we refer to the free energy of binding, including structural degrees of freedom not explicitly included in the model, simply as ‘binding energy’. We approximate the binding energy of a TF α to a given DNA sequence starting at position x along the DNA as a sum of independent contributions ϵα(s, j) from each base s at position x + j, with j = 0…Lα − 1. The coordinate x can be either in the forward or reverse genome and is measured in the direction from 5′ to 3′. The ϵα(s, j)’s are obtained from the PSSMs by identifying the statistical weights with the Boltzmann weights, ϵα(s, j) = −ln Pα(s, j), where we measure energy in units of the thermal energy so that kBT = 1, with kB the Boltzmann constant and T the temperature. We set the average binding energy of each TF α over the entire DNA to zero. The binding energy of TF α therefore reads:
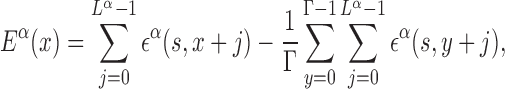 |
(2) |
where Γ is the genome length. The independent base approximation adopted in Equation (2) is the simplest way of estimating binding energies, and more sophisticated methods have been proposed. Comparisons with direct measurements, e.g. by protein binding microarray, show that, in most cases, non-independent base correction terms are small, so that Equation (2) works very well (40).
Modeling TF–DNA interaction
Two-state sliding model
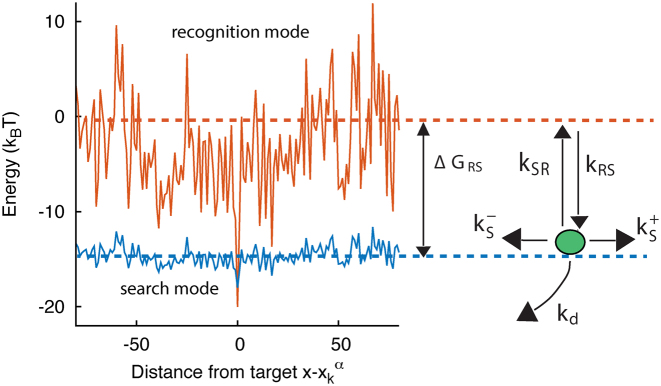
Following (17,18), we assume that the TF–DNA complex can switch between two states: recognition (R) and search (S). The switching is associated to major conformational changes in the TF–DNA complex (41,42), related to e.g. local folding (43) and hydrophobic effects (44), as observed for zinc-finger proteins (45) and p53 (46,47).
In the R state, the TF tightly binds to the DNA experiencing the energy landscape Eα(x) that we obtained from the PSSMs via Equation (2). Fluctuations of the binding energy are characterized by a standard deviation in the range σR ∼ 4 − 7. These fluctuations strongly inhibit sliding, that can be effectively neglected, see Supplementary Section S1.
In the S state, the binding energy landscape is dominated by unspecific electrostatic attractions (22,48), modulated by weak-specific interactions leading to milder fluctuations of the binding energy, still allowing for effective sliding (17,18). The energy of the search mode is the sum of a sequence-dependent contribution and a non-specific one. Following (17), we assume that the former is simply proportional to Eα(x). The latter, 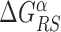 , represents the average energy difference between the R and S conformations of the TF–DNA complex. For sequences strongly differing from the target one, the R state should be energetically unfavorable (17): otherwise, the TF would spend too much time tightly bound to non-target sequences, slowing down the search process. Therefore, the binding energy landscape of TF α in S state reads
, represents the average energy difference between the R and S conformations of the TF–DNA complex. For sequences strongly differing from the target one, the R state should be energetically unfavorable (17): otherwise, the TF would spend too much time tightly bound to non-target sequences, slowing down the search process. Therefore, the binding energy landscape of TF α in S state reads  with
with 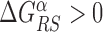 and 0 ≤ ρ ≤ 1. The limiting cases ρ = 0, 1 correspond to the S state being completely unspecific or as specific as the R state, respectively. Effective sliding requires limited ruggedness of the energy landscape with values of σS ≈ 2 or less (see Supplementary Equation (S3)). Since σS = ρσR and based on the observation that σR ≈ 4 − 7, we shall only consider values of ρ ≤ 0.3. The kinetic rates for the full process, sketched in Figure 1, are:
and 0 ≤ ρ ≤ 1. The limiting cases ρ = 0, 1 correspond to the S state being completely unspecific or as specific as the R state, respectively. Effective sliding requires limited ruggedness of the energy landscape with values of σS ≈ 2 or less (see Supplementary Equation (S3)). Since σS = ρσR and based on the observation that σR ≈ 4 − 7, we shall only consider values of ρ ≤ 0.3. The kinetic rates for the full process, sketched in Figure 1, are:
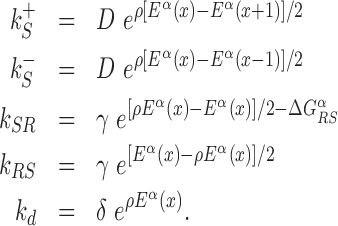 |
(3) |
Figure 1.
Graphical representation of the two-state model. The two continuous curves represent the energy levels of the two modes of a TF, equal to Eα(x) (recognition mode, top curve) and 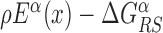 (search mode, bottom curve). The dashed lines denote the average energy in the two modes. The arrows represent the transitions in the stochastic model, characterized by the rates in Equation (3).
(search mode, bottom curve). The dashed lines denote the average energy in the two modes. The arrows represent the transitions in the stochastic model, characterized by the rates in Equation (3).
The rates 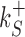 and
and 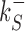 control the sliding transitions between adjacent bases along the DNA, ruled by the sequence-dependent energy differences in S state and the diffusion rate constant D. The rates kRS and kSR regulate the transitions from recognition to search state and vice versa, respectively. Their value in the absence of an energetic difference between the two states is γ. The factor 1/2 in the rates of Equation (3) ensures the detailed balance condition. It derives from assuming that the height of the activation barrier between pairs of states is proportional to their average energy up to an additive constant (see Supplementary Section S2B). Finally, kd is the dissociation rate from the DNA. We assume that TFs can detach only in the S state. Dissociation is controlled by the rate constant δ, including all contributions from the non-specific binding energy. Notice that ρ appears in Equation (3) as an inverse temperature. However, the analogy is only formal as, at fixed temperature, ρ depends on the details of the contacts between TF and DNA when the TF is in the search conformation.
control the sliding transitions between adjacent bases along the DNA, ruled by the sequence-dependent energy differences in S state and the diffusion rate constant D. The rates kRS and kSR regulate the transitions from recognition to search state and vice versa, respectively. Their value in the absence of an energetic difference between the two states is γ. The factor 1/2 in the rates of Equation (3) ensures the detailed balance condition. It derives from assuming that the height of the activation barrier between pairs of states is proportional to their average energy up to an additive constant (see Supplementary Section S2B). Finally, kd is the dissociation rate from the DNA. We assume that TFs can detach only in the S state. Dissociation is controlled by the rate constant δ, including all contributions from the non-specific binding energy. Notice that ρ appears in Equation (3) as an inverse temperature. However, the analogy is only formal as, at fixed temperature, ρ depends on the details of the contacts between TF and DNA when the TF is in the search conformation.
To reduce the number of free parameters in (3), we make the simplifying assumption that D, γ, δ and ρ do not depend on the TF.
Model parameters
Theoretical studies (49,50), based on the observation that proteins spin around the DNA helix while sliding (51), estimated the one-dimensional diffusion constant of TFs depending on the size of the protein and its center-of-mass average distance from the DNA helix axis (50). For examples, the theory predicts D1D ≈ 3 × 10−13m2 s−1 for a relatively large protein like LacI, and D1D ≈ 10−12m2 s−1 for the smaller hOgg1. Experiments show systematically smaller values, e.g. D1D ≈ 2.1–4.6 × 10−14m2 s−1 for LacI (52,53) and D1D ≈ 5 × 10−13m2 s−1 for hOgg1 (50,51). A possible cause for this discrepancy is the fluctuating energy landscape, see Supplementary Equation (S3). We choose the diffusion rate constant D = 107bp2s−1, corresponding to D1D = 10−12m2 s−1 for a flat landscape. In the presence of weak fluctuations, σ ≈ 1–2 as expected in the search state, the resulting diffusion constant ranges in 10−13 − 10−15m2 s−1, in agreement with the experimentally measured values.
The parameter γ characterizes the transition rate between search and recognition state. For example, observed transition rates between weakly and tightly bound configurations in the Lac repressor are on the order of 107s−1 (42). In general, theory suggests that this transition should be quite fast to avoid slowing down of the search process (18,54). We fix γ = 107s−1, and later show that our results are robust upon varying the value of γ.
The energy difference 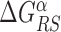 controls the delicate balance between search and recognition. Since the fluctuations of the energy landscape can significantly vary among TFs, we fix a different value of
controls the delicate balance between search and recognition. Since the fluctuations of the energy landscape can significantly vary among TFs, we fix a different value of 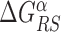 for each TFs. In particular, we determine
for each TFs. In particular, we determine 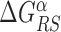 by imposing that, for the weakest binding sequence of TF α and for the largest considered value of ρ = 0.3, the R and S states have the same energy. In formulas, we set
by imposing that, for the weakest binding sequence of TF α and for the largest considered value of ρ = 0.3, the R and S states have the same energy. In formulas, we set 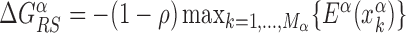 with ρ = 0.3, where
with ρ = 0.3, where 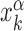 is the position of TFBS k of TF α.
is the position of TFBS k of TF α.
The dissociation rate δ is the main determinant of the average sliding length ℓS. Experimental and theoretical estimates of the sliding length in the literature range from about or slightly less than 100 bp (16,55) to 200–500 bp (18) or more (53). We fixed δ = 103s−1 yielding ℓS in a range 150–190 bp with an average value of about 170 bp.
Model simulation
The stochastic rate model (3) is implemented using a standard Gillespie algorithm (56). We consider three different setups for the sliding events: (i) in proximity of consensus sequences; (ii) in proximity of consensus sequences, placed in random positions on the DNA; and (iii) in a random region of the genome far from any target sequence. In setup (i), in each realization we initialize the TF α in the search state and place it with a uniform probability in a region [ − W, W] around the position 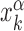 of its kth binding sequence. In setup (ii), for each realization we copy a target sequence at a random position
of its kth binding sequence. In setup (ii), for each realization we copy a target sequence at a random position 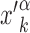 of the genome, far from other target sequences. The initial condition is chosen as in setup (i) with
of the genome, far from other target sequences. The initial condition is chosen as in setup (i) with 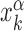 replaced by
replaced by 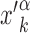 . In both setups (i) and (ii), we fixed W = 1000, sufficiently larger than the average sliding length, so that the probability of finding the target when associating at a distance larger than W is negligible, see Supplementary Figure S4. In setup (iii), the TF is initialized in the search state with uniform probability at any position on the genome, with the only requirement to be sufficiently far from other known TFBS.
. In both setups (i) and (ii), we fixed W = 1000, sufficiently larger than the average sliding length, so that the probability of finding the target when associating at a distance larger than W is negligible, see Supplementary Figure S4. In setup (iii), the TF is initialized in the search state with uniform probability at any position on the genome, with the only requirement to be sufficiently far from other known TFBS.
RESULTS
Energetic funnel around TF binding sites: evidence and origin
We start by investigating the binding energy landscape around the TFBSs in the DB (see ‘Materials and Methods’ section). The binding energy landscape around single TFBS appears uncorrelated (22) (see also Supplementary Figure S1). To reveal its features, we average it over the whole set of TFBSs. To this aim, we define the normalized mean binding energy as a function of the distance r from the target
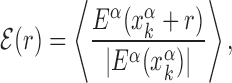 |
(4) |
where, 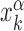 is the position on the DNA chain of the kth target site of the αth TF. In the above expression, 〈Y〉 denotes the average of a quantity
is the position on the DNA chain of the kth target site of the αth TF. In the above expression, 〈Y〉 denotes the average of a quantity 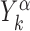 over all target sequences, i.e.
over all target sequences, i.e. 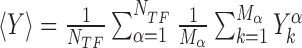 . The normalization in (4) rescales at the same level targets with different energies, so that
. The normalization in (4) rescales at the same level targets with different energies, so that 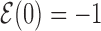 . The function
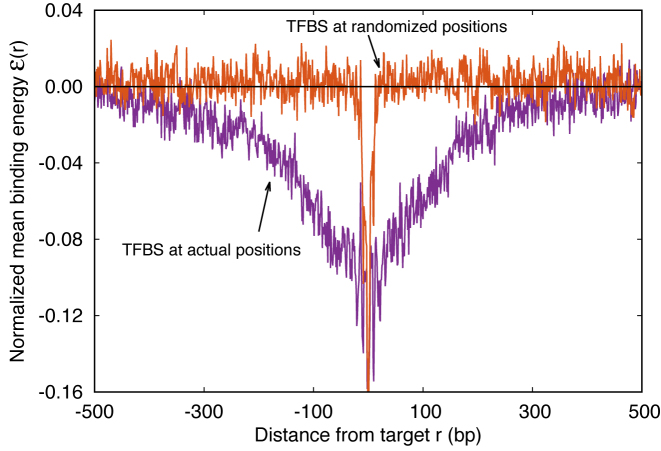
. The function 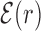 reveals a wide, nearly symmetric funnel extending up to a distance of about 300 bp, both upstream and downstream of the TFBS, as represented in Figure 2. As also shown in Figure 2, when repeating the analysis by randomizing the position of each target sequences, the energy landscape becomes a ‘golf course’ with
reveals a wide, nearly symmetric funnel extending up to a distance of about 300 bp, both upstream and downstream of the TFBS, as represented in Figure 2. As also shown in Figure 2, when repeating the analysis by randomizing the position of each target sequences, the energy landscape becomes a ‘golf course’ with 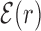 significantly different from zero only very close to the target. We have also computed the average (4) by randomly reshuffling the TFBS, i.e. by placing each target sequence at the coordinate of a randomly chosen target sequence of a different TF. In this case, a funnel is still visible even if its strength is reduced, see Supplementary Figure S2. This means that the origin of the funnel should be, at least to some degree, common to all TFs.
significantly different from zero only very close to the target. We have also computed the average (4) by randomly reshuffling the TFBS, i.e. by placing each target sequence at the coordinate of a randomly chosen target sequence of a different TF. In this case, a funnel is still visible even if its strength is reduced, see Supplementary Figure S2. This means that the origin of the funnel should be, at least to some degree, common to all TFs.
Figure 2.
Average normalized binding energy 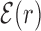 (4) as a function of the distance r from the target. The curve labeled TFBS at actual position displays
(4) as a function of the distance r from the target. The curve labeled TFBS at actual position displays 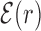 computed over the whole set of 1544 unique target sequences in the DB (see ‘Materials and Methods’ section). The other curve represents the
computed over the whole set of 1544 unique target sequences in the DB (see ‘Materials and Methods’ section). The other curve represents the 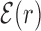 computed with TFBS at randomized positions (as labeled) on the DNA. The randomized coordinates are drawn with uniform probability on the DNA, with the only constraint of being at least 1000 bp away from any other target sequence in the DB.
computed with TFBS at randomized positions (as labeled) on the DNA. The randomized coordinates are drawn with uniform probability on the DNA, with the only constraint of being at least 1000 bp away from any other target sequence in the DB.
As the binding energy is directly inferred from the base composition of the binding sequences, via Equation (2), the funnel must depend on features of the base composition background around the TFBS. Sequences in the promoter region around the target display a positive gradient of AT bases (34,35,57), whereas the genome-averaged frequency of AT of E. coli is FAT = 0.492103. To quantify this unbalance, we define the AT frequency bias β(x) = I(x) − FAT, with I(x) equal to 1 if the base at genome coordinate x is either A or T, and 0 otherwise. We then average the AT frequency bias over the whole set of TFBSs in the database:
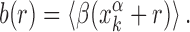 |
(5) |
The average AT frequency bias b(r) measures the difference between the average AT concentration at distance r from a target site with respect to the genome-averaged AT concentration. As shown in Figure 3, the shape of the function b(r) closely resembles the normalized binding energy landscape (Figure 2), apart from the sign. In the inset of Figure 3 we directly compare 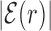 and b(r). For |r| > 0, both curves are well fitted by an exponential ∼exp ( − |r|/ℓf) with the distance ℓf ≈ 120 bp being of the order of the DNA bending persistence length (about 150 bp, (58)). The function b(r) computed for randomized positions, also shown in Figure 3, is significantly different from zero only close to r = 0, as the target sequences themselves are biased in AT concentration.
and b(r). For |r| > 0, both curves are well fitted by an exponential ∼exp ( − |r|/ℓf) with the distance ℓf ≈ 120 bp being of the order of the DNA bending persistence length (about 150 bp, (58)). The function b(r) computed for randomized positions, also shown in Figure 3, is significantly different from zero only close to r = 0, as the target sequences themselves are biased in AT concentration.
Figure 3.
AT frequency bias b(r) (5) as a function of distance r from the target. The curve labeled TFBS at actual position displays b(r) computed over the whole set of 1544 unique target sequences in the DB (see ‘Materials and Methods’ section). The other curve represents the same quantity computed with TFBS at randomized positions (as labeled) on the DNA. The randomized computation is performed as in Figure 2. Inset: comparison between 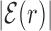 and b(r), as in the legend, in linear-log scale. The white thick lines are an exponential fit aexp ( − |r|/ℓf), yielding ℓf ≈ 120 bp and a ≈ 0.128.
and b(r), as in the legend, in linear-log scale. The white thick lines are an exponential fit aexp ( − |r|/ℓf), yielding ℓf ≈ 120 bp and a ≈ 0.128.
The relation between the AT frequency bias b(r) and the energetic funnel (Figure 3) suggests to use the average AT frequency bias in the neighborhood of each TFBS as a proxy for the local funnel strength. To this aim, we define the background frequency bias Bbkg(k, α) as the AT frequency bias in a region of size 2N around the kth target of the α-th TF normalized by the genome-averaged AT frequency,
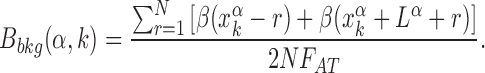 |
(6) |
The background frequency bias measures the relative difference between the average AT concentration in the region of size N upstream and downstream of the target sequence (which is excluded) with respect to the genome-averaged AT concentration. We fix N = 100, on the order of the funnel range ℓf. We verified that Bbkg(α, k) is a good proxy for the funnel strength by computing the normalized binding energy over subsets of TFBS characterized by backgrounds with different degrees of AT frequency bias, see Supplementary Figure S3.
In this section, by analyzing the database of TF binding sites, we have shown that an average energetic funnel is present in the proximity of the TF binding sites. However, TFs do not experience the average landscape but the individual ones, where fluctuations can in principle overwhelm the funnel, see Supplementary Figure S1. It is thus important to assess whether, despite these fluctuations, the funnel plays a relevant role on the sliding kinetics around individual target sequences. In the following two sections, we answer this question by means of numerical simulations of the stochastic sliding model introduced in ‘Materials and Methods’ section, using the individual, non-averaged energy landscapes.
Effect of the funnel on probability to reach the target
By simulating the two-state model (3) as described in ‘Materials and Methods’ section, we estimate, for all target sequences in the DB, the success probabilities Ps(α, k) as the fraction of sliding rounds next to each target 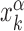 in which the target is reached with the TF in recognition state before detachment occurs. To compare with a null case in which the funnel is absent, we also compute
in which the target is reached with the TF in recognition state before detachment occurs. To compare with a null case in which the funnel is absent, we also compute 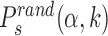 , which is defined as Ps(α, k) but with the target placed at random positions, see ‘Materials and Methods’ section. For each target sequence, we quantify the effect of the funnel by the relative gain in success probability respect to the randomized case:
, which is defined as Ps(α, k) but with the target placed at random positions, see ‘Materials and Methods’ section. For each target sequence, we quantify the effect of the funnel by the relative gain in success probability respect to the randomized case:
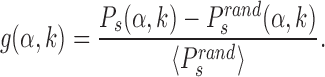 |
(7) |
Notice that while Ps depends on the initial window size W (see ‘Materials and Methods’ section), the relative gain g is independent of it, see Supplementary Figure S4.
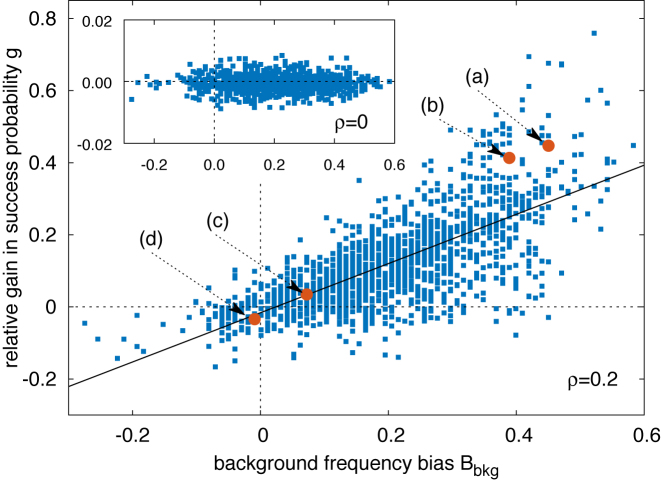
The gain g(α, k) is shown in Figure 4 for ρ = 0.2 as a function of the funnel-strength proxy Bbkg(α, k) (6) for all TFBSs in the database. A clear correlation is observed (slope ≈0.68 with Pearson correlation coefficient r ≈ 0.72). This effect depends crucially on the specificity of the energy landscape in search mode, tuned by the parameter ρ (see ‘Materials and Methods’ section). For ρ = 0 the energy landscape in search mode is flat, so that the funnel can not drive the sliding motion toward the target and the correlation disappears, as shown in the inset of Figure 4. As discussed in the next section, for larger ρ the effect of the funnel is stronger but the diffusivity is also reduced. The correlation in Figure 4 is robust against varying the parameter γ as demonstrated in Supplementary Figure S5. We obtained qualitatively similar results with a simplified single-state model, see Supplementary Figure S6. A variant of Equation (3) implementing a Metropolis rule similar to Ref. (17) also leads to similar results, see Supplementary Figure S7 and Section S2B. This shows that exploitation of the funnel is robust against changing the details of the model, provided that the sliding process has some degree of specificity.
Figure 4.
Scatter plot of the relative success-probability gain g(α, k) [Equation (7)] to find the target versus the background frequency bias Bbkg(α, k) [Equation (6)]. The success probabilities for each TFBS and its randomized counterparts have been estimated by averaging over 106 realizations of the stochastic model, with the TF initialized as described in ‘Materials and Methods’ section. ρ = 0.2 and the other parameters are fixed as in ‘Materials and Methods’ section. The black solid line is the result of a linear regression giving g = 0.68 Bbkg − 0.016 with Pearson correlation coefficient r = 0.72. Filled circles labeled as (a–d) correspond to the specific sequences analyzed in Figure 6: (a) TATTGCTCCACTGTTTA for PhoP; (b) GTAAAAATATATAAA for CpxR; (c) AAGCAAAGCGCAG for Ada; (d) TGCGTGAAAAACTGTC for PhoB. Inset: same scatter plot as in the main figure but with ρ = 0, i.e. without specificity in the S state. In this case, no gain in success probability is observed (notice the scale on the y axis).
The increase in success probability due to the AT concentration gradients relies on the fact that TFs have high affinity to AT-rich regions. This affinity can significantly vary among TFs, so that some TFs can exploit AT concentration gradients better than others. To quantify this idea, we study the relative gain in probability of success averaged over the target sequences of each TF, 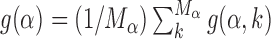 , and its correlation with the average base composition of the target sequences. We quantify the latter introducing the normalized AT frequency bias per TF
, and its correlation with the average base composition of the target sequences. We quantify the latter introducing the normalized AT frequency bias per TF
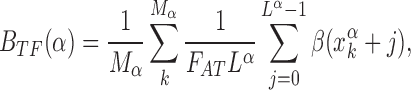 |
(8) |
which measures the mean relative difference between the average AT concentration of the target sequences of TF α and the genome-averaged AT concentration.
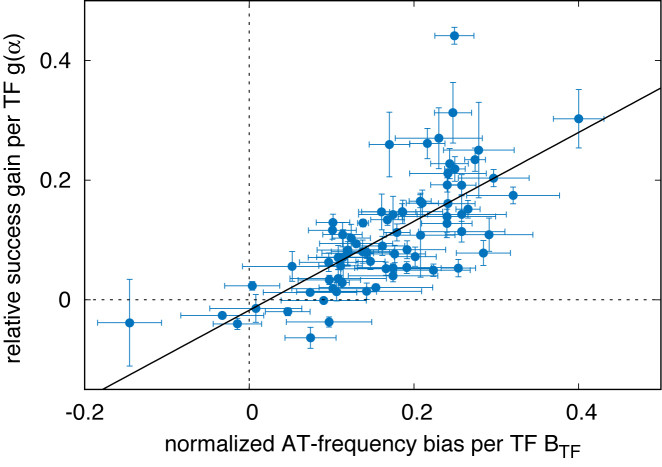
Figure 5 shows that g(α) is positively correlated with BTF(α), confirming that TFs having a strong propensities for AT-rich regions can efficiently exploit AT-concentration gradients and, therefore, find their binding sequence more easily when embedded in an AT concentration gradient.
Figure 5.
Classification of TFs according to their AT frequency bias and target finding success. Relative gain in probability of success per TF (averaged over their target sequences), g(α), as a function of the AT relative frequency bias per TF, BTF(α), see Equation (8). The error bars represent the standard error over the sample of Mα TFBS of TF α. The line is the linear regression g = 0.74BTF − 0.018 with Pearson correlation coefficient r ≈ 0.71.
Since several TFBSs are close to each other and TFBSs tend to be AT-rich, one may suspect that the funnel and the resulting gain in probability of success is mostly due to clustering of TFBSs. To exclude this scenario, in Supplementary Figure S8 we show that the basic features of the scatter plot of Figure 4 are preserved when considering only isolated TFBSs, i.e. target sequences that are far from other TFBSs in the DB.
Influence of the funnel on the total search time
Exploitation of the energetic funnel requires some degree of specificity in search mode, which is tuned by the parameter ρ. Incrementing ρ increases the success probability, but slows down 1D diffusion due to the enhanced fluctuations of the binding energy landscape in search mode, see Supplementary Section S1. Given this tradeoff, it is non-trivial to assess the net effect of the funnel on the total target search time, which is the relevant quantity for fast transcription regulation.
To clarify this issue, we consider a TF in the cytosol that finds its target by alternating between 3D and 1D diffusion. For simplicity, we neglect other mechanisms such as hopping and intersegmental transfer. The average total search time can be estimated as:
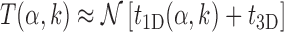 |
(9) |
where, t1D(α, k) and t3D are the average duration of sliding and 3D diffusion rounds, respectively, and 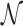 is the average number of 1D/3D diffusion rounds necessary to find the target.
is the average number of 1D/3D diffusion rounds necessary to find the target.
The standard approach to analyze Equation (9) is to evaluate 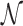 as the ratio between the total genome length Γ and the average sliding length ℓS that, for a diffusion process, is proportional to
as the ratio between the total genome length Γ and the average sliding length ℓS that, for a diffusion process, is proportional to 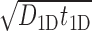 . This estimation procedure predicts a minimum total search time T for t1D = t3D (17,18,48). It also suggests that the energetic funnel would not significantly affect T since such time is dominated by the 1D/3D diffusion rounds away from the target (17).
. This estimation procedure predicts a minimum total search time T for t1D = t3D (17,18,48). It also suggests that the energetic funnel would not significantly affect T since such time is dominated by the 1D/3D diffusion rounds away from the target (17).
However, this argument does not take into account that 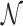 is not determined by the average sliding length but by the accessibility of the target, i.e. how easy it is to find it when sliding in its proximity. Note that the probability of reaching the target is the product of the probability of landing within a distance W from it (equal to (2W + 1)/Γ, where Γ is the genome length) times the previously studied probability Ps(α, k) of finding it when sliding in its proximity. The average number of rounds
is not determined by the average sliding length but by the accessibility of the target, i.e. how easy it is to find it when sliding in its proximity. Note that the probability of reaching the target is the product of the probability of landing within a distance W from it (equal to (2W + 1)/Γ, where Γ is the genome length) times the previously studied probability Ps(α, k) of finding it when sliding in its proximity. The average number of rounds 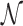 is the inverse of this probability. Substituting in Equation (9) we obtain:
is the inverse of this probability. Substituting in Equation (9) we obtain:
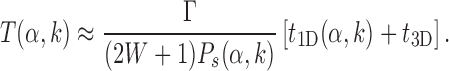 |
(10) |
In the above expression, the quantity (2W + 1)Ps(α, k) is independent of W (for large enough W) and can be interpreted as the effective sliding length in proximity of the target, which is larger than the average sliding length thanks to the funnel, see Supplementary Figure S4.
The tradeoff discussed at the beginning of the section can be restated in the light of Equation (10). In the presence of a funnel, increasing the specificity ρ in search mode enhances Ps(α, k) but decreases D1D, due to the stronger fluctuations, and consequently increases t1D. Therefore, it is not obvious to assess the net effect of changing ρ on the search time T(α, k).
To shed light on this issue, we estimate T(α, k) and study its dependence on ρ using Equation (10) and simulations of the two-state model. We compute the probability PS(α, k) as in the previous section. The average duration of a sliding round t1D(α, k) is evaluated by simulating the model in randomly chosen regions of the genome far from the target. Simulating the 3D diffusion process to estimate t3D is out of the scope of this work. We therefore choose t3D as a fraction of the value of t1D for ρ = 0, ranging from t3D = t1D as suggested by Equation (9) to t3D = t1D/10 as suggested by experimental measurements of the Lac repressor (52).
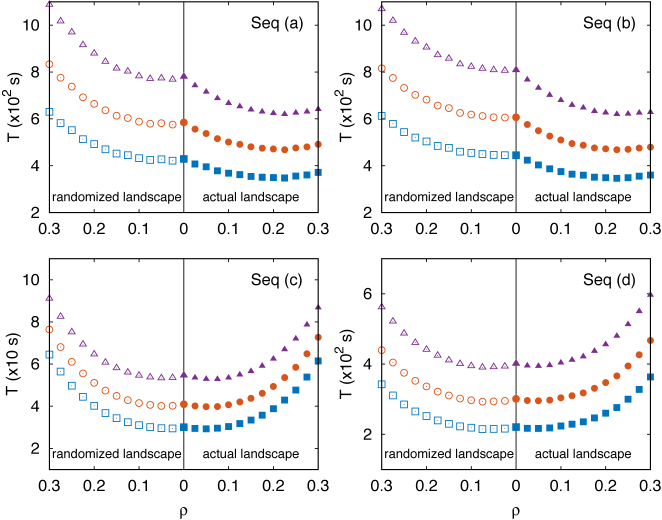
Results are illustrated in Figure 6 for four representative binding sequences of different TFs. These sequences were chosen because they have strong evidence in RegulonDB and are located in different regions of the scatter plot of Figure 4. In particular, sequences (a) and (b) are in the upper right region of the scatter-plot, therefore being surrounded by a pronounced and effective funnel, whereas sequences (c) and (d) are close to the origin of the scatter-plot, corresponding to a weak or absent funnel.
Figure 6.
Total search time T, computed as in Equation (10), versus ρ for four target sequences of four different TFs as labeled in Figure 4. In each panel, the three curves correspond to different assumptions for the average duration of a 3D diffusion round t3D = νt1D(ρ = 0): (boxes) ν = 0.1, (circles) ν = 0.5 (triangles) ν = 1. Filled symbols (on the right of the vertical solid line) refer to computation of the success probability Ps(α, k) performed with the target sequences at their actual positions. Empty symbols on the left correspond to the computation performed by randomizing the positions of the TFBSs. Each symbol is obtained by an average over 106 realizations. The average sliding time t1D is estimated by simulating 106 sliding events at random locations far from the target sequence.
For sequences (a) and (b), the search time T displays a minimum for ρ ≈ 0.2, where T is about 20% smaller than in the randomized landscape. We find that, at equal values of ρ > 0, the search time for the actual landscape is systematically lower than for the randomized one. In particular, for ρ = 0.3, the larger specificity we considered, the search time is about half of the value obtained for the randomized landscape. This result should be contrasted with sequences (c) and (d) for which the search time in the actual and randomized landscapes are basically indistinguishable. Notice that T seems to be smaller for sequences (c) and (d). However, quantitative comparisons between search times of different TFs should be taken with care, as the results might depend on the approximation of fixing the same rates for all TFs. Instead, the qualitative difference between sequences (a), (b) and (c), (d) is a robust finding, that does not depend on this approximation.
Energetic funnel in Bacillus subtilis
To test the generality of our results besides the gram-negative E. coli K12, we repeated part of the analysis in the gram-positive B. subtilis that is characterized by different niches (59) and evolutionary histories (60,61). We considered 30 TFs for a total of 313 TFBSs from the DBTBS database (36), see Supplementary Section S3A and Table S2. We found that the average normalized binding energy 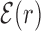 , Equation (4), displays a funnel, see Supplementary Figure S9, comparable to that observed in E. coli (Figure 2), though more noisy due to the smaller dataset. As in Figure 3, the base composition around the TFBS is characterized by gradient in AT frequency similar to
, Equation (4), displays a funnel, see Supplementary Figure S9, comparable to that observed in E. coli (Figure 2), though more noisy due to the smaller dataset. As in Figure 3, the base composition around the TFBS is characterized by gradient in AT frequency similar to 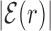 , see Supplementary Figure S10. Notice that in B. subtilis the genome-averaged AT frequency is FAT = 0.564856. We simulated the two-state model described in the ‘Materials and Methods’ section, with the same parameters used for E. coli but for
, see Supplementary Figure S10. Notice that in B. subtilis the genome-averaged AT frequency is FAT = 0.564856. We simulated the two-state model described in the ‘Materials and Methods’ section, with the same parameters used for E. coli but for 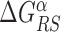 that has been fixed as discussed in ‘Materials and Methods’ section. We computed the success probability comparing it against the randomized null model. The scatter plot of the relative gain, g(α, k), as a function of the relative AT frequency bias Bbkg(α, k) (Supplementary Figure S11) displays features similar to those observed in E. coli (Figure 4) but with a weaker correlation, confirming the generality of our findings.
that has been fixed as discussed in ‘Materials and Methods’ section. We computed the success probability comparing it against the randomized null model. The scatter plot of the relative gain, g(α, k), as a function of the relative AT frequency bias Bbkg(α, k) (Supplementary Figure S11) displays features similar to those observed in E. coli (Figure 4) but with a weaker correlation, confirming the generality of our findings.
DISCUSSION AND CONCLUSION
Nature and role of the energetic funnel
In this work, we revealed the existence of an energetic funnel surrounding TFBSs in E. coli and B. subtilis. We related this energetic funnel to gradients of AT content around binding sequences. Our numerical simulations show that the funnel can significantly increase the probability to find a TFBS when sliding close to it, leading to shorter search times even in the presence of realistic binding energy fluctuations.
The presence of gradients in base composition in the promoter regions, containing most TFBS, is a widespread feature common to most organisms ranging from bacteria to multicellular eukaryotes (34,35,57). In particular, AT-rich gradients characterize bacteria and unicellular eukaryotes whereas GC-rich gradients are prevalent in multicellular eukaryotes (35). Although FD in eukaryotes is more complex because of chromatin packaging, it would be interesting to explore whether the GC-rich gradients can be related to energetic funnels similar to those we revealed in this work.
The base composition of a DNA segment can influence conformational properties such as bending, breathing of the double helix, flexibility and, in eukaryotes, nucleosome positioning (62–64), and correlates with the promoter strength (65) and binding of certain nucleoid-associated proteins, further affecting DNA conformation (66). All these properties play a key role in protein–DNA interaction (64,67). It has been proposed that the base composition pattern in bacterial genome arises partly from the necessity for the DNA to bend or twist in the proximity of binding sites (68), see also (69). Further, AT-rich regions are more likely to form denaturation bubbles (70). Our results, combined with these observations, point to a scenario in which the nucleotide content in the promoter region has evolved under multiple selective forces, dictated by the kinetics of TF search process, the conformational properties of the DNA and the thermodynamics of TF–DNA interactions. These evolutionary forces often point in the common direction of increasing AT content around promoters. However, contrasting effects can also be present. For example it has been recently argued that (positive or negative) funnel structures may emerge in the free binding-energy landscape of yeast TFs also due to low entropy properties of repeated homo-oligonucleotide tracts (30–32).
Role of hopping, intersegmental transfer and DNA conformation
We estimated the target-search time by only considering 1D sliding and 3D diffusion, i.e. jumps of the TF to distant portions of the DNA chain. In principle, also short-distance jumps (hops) may be present. However, in vivo measurements (11) have found a negligible role of hopping. Numerical simulations confirm that for low salt concentration, as in vivo, the main mechanism is sliding (71,72). For compact DNA conformations, TFs with multiple binding sites can transiently bind to two contiguous DNA segments, far apart along the chain, favoring intersegmental transfer (55). Though this mechanism may be important (9), it is not clear whether it applies to TF with a single binding domain, which are the majority in our database. In cases where hops or intersegmental transfer are relevant, we expect a reduction of t3D in (10) as a main effect, which would not not affect qualitatively our results.
When considering realistic compact DNA conformations, the effectiveness of FD has been questioned (13). However, molecular dynamics simulations in (28) showed that a funnel would positively impact the search time even taking into account DNA conformation.
Experimental predictions
Our results can be experimentally tested using techniques to monitor the in vivo association rate of TFs to a promoter (16,52,73). For example, the experiment in (16) provided a direct evidence of sliding of the Lac repressor by engineering E. coli strains with two identical Lac operators placed at different distances from each other, and comparing the total association rate with that predicted by 1D random walk theory. With similar techniques, one can modify the genetic background around a given TFBS, for example copying sequences with different AT concentration, and measure the change in association rates. The scatter plots in Figures 4 and 5, and the corresponding dataset provided as Supplementary File can be used to identify TFs and corresponding target sequences for which the effect is expected to be most significant. In vitro experiments can also be designed to assess the association and dissociation rates as a function of the base composition as done for RNAP in (24). These experiments could test the affinity of a given TF to a specific natural or engineered base composition pattern around a binding site, potentially leading to novel design strategies for synthetic promoters, see e.g. (74).
Generalizations
In our computational study, we considered each TF independently. In crowded situation, possibly including roadblocks (11,75–77) the role of an energetic funnel is less clear to assess. It has been speculated that, in such situation, a genetic background that helps reaching the target could make traffic more severe and that a ‘negative design’, making the target less accessible by sliding, would be instead preferable (32). It will be of interest to generalize the study presented here to the case of many proteins competing for the same target. Another interesting perspective is to extend our analysis to other organisms, and to classify different TFBS according to their biological functions and base composition of their genetic background.
In prokaryots, genes that express a TF are often close along the DNA to the TF binding site. This colocalization can speed up the target finding, provided the sliding rounds are not completely independent (78–80). Since, as shown by our study, the presence of an energetic funnel increases the probability to locate the target when the TF attaches in its proximity, it will be interesting to explore a possible link between intensity of funnels and colocalization.
Supplementary Material
ACKNOWLEDGEMENTS
We thank S. Brown, F. Cecconi and L. Peliti for a critical reading of the manuscript. We acknowledge Y. Makita for providing us with the DBTBS dataset on B. subtilis.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Funding for open access charge: OIST core funding for the Biological Complexity Unit.
Conflict of interest statement. None declared.
REFERENCES
- 1. Alberts B., Johnson A., Lewis J., Raff M., Roberts K., Walter P.. Molecular Biology of the Cell, Garland Science. 2007; 5th edn, NY: Taylor & Francis Group. [Google Scholar]
- 2. Berg O., Winter R., von Hippel P.H.. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochem. 1981; 20:6929–6948. [DOI] [PubMed] [Google Scholar]
- 3. Berg O.G., Winter R.B., von Hippel P.H.. How do genome-regulatory proteins locate their DNA target sites?. Trends Biochem. Sci. 1982; 7:52–55. [Google Scholar]
- 4. von Hippel P.H., Berg O.. Facilitated target location in biological systems. J. Biol. Chem. 1989; 264:675–678. [PubMed] [Google Scholar]
- 5. Adam G., Delbrück M.. Rich A, Davidson N. Reduction of dimensionality in biological diffusion processes. Structural Chemistry and Molecular Biology. 1968; 198:San Francisco: Freeman; 198–215. [Google Scholar]
- 6. Richter P.H., Eigen M.. Diffusion controlled reaction rates in spheroidal geometry: application to repressor-operator association and membrane bound enzymes. Biophys. Chem. 1974; 2:255–263. [DOI] [PubMed] [Google Scholar]
- 7. Riggs A., Bourgeois S., Cohn M.. The lac repressor-operator interaction: III. Kinetic studies. J. Mol. Biol. 1970; 53:401–417. [DOI] [PubMed] [Google Scholar]
- 8. Lomholt M.A., van den Broek B., Kalisch S.-M.J., Wuite G.J., Metzler R.. Facilitated diffusion with DNA coiling. Proc. Natl. Acad. Sci. U.S.A. 2009; 106:8204–8208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Hu T., Shklovskii B.. How a protein searches for its specific site on DNA: the role of intersegment transfer. Phys. Rev. E. 2007; 76:051909. [DOI] [PubMed] [Google Scholar]
- 10. Sheinman M., Kafri Y.. The effects of intersegmental transfers on target location by proteins. Phys. Biol. 2009; 6:016003. [DOI] [PubMed] [Google Scholar]
- 11. Mahmutovic A., Berg O.G., Elf J.. What matters for lac repressor search in vivo–sliding, hopping, intersegment transfer, crowding on DNA or recognition?. Nucleic Acids Res. 2015; 43:3454–3464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Hu T., Grosberg A.Y., Shklovskii B.. How proteins search for their specific sites on DNA: the role of DNA conformation. Biophys. J. 2006; 90:2731–2744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Florescu A.-M., Joyeux M.. Comparison of kinetic and dynamical models of DNA-protein interaction and facilitated diffusion. J. Phys. Chem. A. 2010; 114:9662–9672. [DOI] [PubMed] [Google Scholar]
- 14. Koslover E.F., de la Rosa M. A.D., Spakowitz A.J.. Theoretical and computational modeling of target-site search kinetics in vitro and in vivo. Biophys. J. 2011; 101:856–865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Kolomeisky A.B. Physics of protein–DNA interactions: mechanisms of facilitated target search. Phys. Chem. Chem. Phys. 2011; 13:2088–2095. [DOI] [PubMed] [Google Scholar]
- 16. Hammar P., Leroy P., Mahmutovic A., Marklund E.G., Berg O.G., Elf J.. The lac repressor displays facilitated diffusion in living cells. Science. 2012; 336:1595–1598. [DOI] [PubMed] [Google Scholar]
- 17. Slutsky M., Mirny L.A.. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophys. J. 2004; 87:4021–4035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Mirny L., Slutsky M., Wunderlich Z., Tafvizi A., Leith J., Kosmrlj A.. How a protein searches for its site on DNA: the mechanism of facilitated diffusion. J. Phys. A. 2009; 42:434013. [Google Scholar]
- 19. Sheinman M., Bénichou O., Kafri Y., Voituriez R.. Classes of fast and specific search mechanisms for proteins on DNA. Rep. Progr. Phys. 2012; 75:026601. [DOI] [PubMed] [Google Scholar]
- 20. Bouchaud J.-P., Georges A.. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 1990; 195:127–293. [Google Scholar]
- 21. Von Hippel P.H., Berg O.G.. On the specificity of DNA-protein interactions. Proc. Natl. Acad. Sci. U.S.A. 1986; 83:1608–1612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Gerland U., Moroz J.D., Hwa T.. Physical constraints and functional characteristics of transcription factor–DNA interaction. Proc. Natl. Acad. Sci. U.S.A. 2002; 99:12015–12020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Zhou H.-X. Rapid search for specific sites on DNA through conformational switch of nonspecifically bound proteins. Proc. Natl. Acad. Sci. U.S.A. 2011; 108:8651–8656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Harada Y., Funatsu T., Murakami K., Nonoyama Y., Ishihama A., Yanagida T.. Single-molecule imaging of RNA polymerase-DNA interactions in real time. Biophys. J. 1999; 76:709–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Weindl J., Hanus P., Dawy Z., Zech J., Hagenauer J., Mueller J.C.. Modeling DNA-binding of Escherichia coli σ70 exhibits a characteristic energy landscape around strong promoters. Nucleic Acids Res. 2007; 35:7003–7010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Bryngelson J.D., Onuchic J.N., Socci N.D., Wolynes P.G.. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 1995; 21:167–195. [DOI] [PubMed] [Google Scholar]
- 27. Weindl J., Dawy Z., Hanus P., Zech J., Mueller J.C.. Modeling promoter search by E. coli RNA polymerase: one-dimensional diffusion in a sequence-dependent energy landscape. J. Theor. Biol. 2009; 259:628–634. [DOI] [PubMed] [Google Scholar]
- 28. Brackley C., Cates M., Marenduzzo D.. Facilitated diffusion on mobile DNA: configurational traps and sequence heterogeneity. Phys. Rev. Lett. 2012; 109:168103. [DOI] [PubMed] [Google Scholar]
- 29. Cherstvy A., Kolomeisky A., Kornyshev A.. Protein- DNA interactions: reaching and recognizing the targets. J. Phys. Chem. B. 2008; 112:4741–4750. [DOI] [PubMed] [Google Scholar]
- 30. Afek A., Lukatsky D.B.. Genome-wide organization of eukaryotic preinitiation complex is influenced by nonconsensus protein-DNA binding. Biophys. J. 2013; 104:1107–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Afek A., Cohen H., Barber-Zucker S., Gordân R., Lukatsky D.B.. Nonconsensus protein binding to repetitive DNA sequence elements significantly affects eukaryotic genomes. PLoS Comp. Biol. 2015; 11:e1004429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Afek A., Lukatsky D.B.. Positive and negative design for nonconsensus protein-DNA binding affinity in the vicinity of functional binding sites. Biophys. J. 2013; 105:1653–1660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Salgado H., Peralta-Gil M., Gama-Castro S., Santos-Zavaleta A., Muñiz-Rascado L., García-Sotelo J.S., Weiss V., Solano-Lira H., Martínez-Flores I., Medina-Rivera A. et al. RegulonDB v8.0: omics data sets, evolutionary conservation, regulatory phrases, cross-validated gold standards and more. Nucleic Acids Res. 2013; 41:D203–D213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Aerts S., Thijs G., Dabrowski M., Moreau Y., De Moor B.. Comprehensive analysis of the base composition around the transcription start site in Metazoa. BMC Genomics. 2004; 5:34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Calistri E., Livi R., Buiatti M.. Evolutionary trends of GC/AT distribution patterns in promoters. Mol. Phylogen. Evol. 2011; 60:228–235. [DOI] [PubMed] [Google Scholar]
- 36. Makita Y., Nakao M., Ogasawara N., Nakai K.. DBTBS: database of transcriptional regulation in Bacillus subtilis and its contribution to comparative genomics. Nucleic Acids Res. 2004; 32:D75–D77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Medina-Rivera A., Abreu-Goodger C., Thomas-Chollier M., Salgado H., Collado-Vides J., van Helden J.. Theoretical and empirical quality assessment of transcription factor-binding motifs. Nucleic Acids Res. 2011; 39:808–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Berg O.G., von Hippel P.H.. Selection of DNA binding sites by regulatory proteins: Statistical-mechanical theory and application to operators and promoters. J. Mol. Biol. 1987; 193:723–743. [DOI] [PubMed] [Google Scholar]
- 39. Stormo G.D., Fields D.S.. Specificity, free energy and information content in protein–DNA interactions. Trends Biochem. Sci. 1998; 23:109–113. [DOI] [PubMed] [Google Scholar]
- 40. Zhao Y., Stormo G.D.. Quantitative analysis demonstrates most transcription factors require only simple models of specificity. Nat. Biotech. 2011; 29:480–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Garvie C.W., Wolberger C.. Recognition of specific DNA sequences. Mol. Cell. 2001; 8:937–946. [DOI] [PubMed] [Google Scholar]
- 42. Kalodimos C.G., Boelens R., Kaptein R.. A residue-specific view of the association and dissociation pathway in protein–DNA recognition. Nat. Struct. Mol. Biol. 2002; 9:193–197. [DOI] [PubMed] [Google Scholar]
- 43. Spolar R.S., Record M.T. Jr. Coupling of local folding to site–specific binding of proteins to DNA. Science. 1994; 263:777–784. [DOI] [PubMed] [Google Scholar]
- 44. Ha J.-H., Spolar R.S., Record M.T.. Role of the hydrophobic effect in stability of site-specific protein-DNA complexes. J. Mol. Biol. 1989; 209:801–816. [DOI] [PubMed] [Google Scholar]
- 45. Zandarashvili L., Esadze A., Vuzman D., Kemme C.A., Levy Y., Iwahara J.. Balancing between affinity and speed in target DNA search by zinc-finger proteins via modulation of dynamic conformational ensemble. Proc. Natl. Acad. Sci. U.S.A. 2015; 112:E5142–E5149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Tafvizi A., Huang F., Fersht A.R., Mirny L.A., van Oijen A.M.. A single-molecule characterization of p53 search on DNA. Proc. Natl. Acad. Sci. U.S.A. 2011; 108:563–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Leith J.S., Tafvizi A., Huang F., Uspal W.E., Doyle P.S., Fersht A.R., Mirny L.A., van Oijen A.M.. Sequence-dependent sliding kinetics of p53. Proc. Natl. Acad. Sci. U.S.A. 2012; 109:16552–16557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Halford S.E., Marko J.F.. How do site-specific DNA-binding proteins find their targets?. Nucleic Acids Res. 2004; 32:3040–3052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Schurr J.M. The one-dimensional diffusion coefficient of proteins absorbed on DNA: Hydrodynamic considerations. Biophys. Chem. 1979; 9:413–414. [PubMed] [Google Scholar]
- 50. Bagchi B., Blainey P.C., Xie X.S.. Diffusion constant of a nonspecifically bound protein undergoing curvilinear motion along DNA. J. Phys. Chem. B. 2008; 112:6282–6284. [DOI] [PubMed] [Google Scholar]
- 51. Blainey P.C., Luo G., Kou S., Mangel W.F., Verdine G.L., Bagchi B., Xie X.S.. Nonspecifically bound proteins spin while diffusing along DNA. Nat. Struct. Mol. Biol. 2009; 16:1224–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Elf J., Li G.-W., Xie X.S.. Probing transcription factor dynamics at the single-molecule level in a living cell. Science. 2007; 316:1191–1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Wang Y., Austin R.H., Cox E.C.. Single molecule measurements of repressor protein 1D diffusion on DNA. Phys. Rev. Lett. 2006; 97:048302. [DOI] [PubMed] [Google Scholar]
- 54. Murugan R. Theory of site-specific DNA-protein interactions in the presence of conformational fluctuations of DNA binding domains. Biophys. J. 2010; 99:353–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Winter R.B., Berg O.G., Von Hippel P.H.. Diffusion-driven mechanisms of protein translocation on nucleic acids. 3. The Escherichia coli lac repressor–operator interaction: kinetic measurements and conclusions. Biochemistry. 1981; 20:6961–6977. [DOI] [PubMed] [Google Scholar]
- 56. Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977; 81:2340–2361. [Google Scholar]
- 57. Calistri E., Buiatti M., Livi R.. Variation and constraints in species-specific promoter sequences. J. Theor. Biol. 2014; 363:357–366. [DOI] [PubMed] [Google Scholar]
- 58. Hagerman P.J. Flexibility of DNA. Ann. Rev. Biophys. Biophys. Chem. 1988; 17:265–286. [DOI] [PubMed] [Google Scholar]
- 59. Nakano M.M., Zuber P.. Anaerobic growth of a ‘strict aerobe’ (Bacillus subtilis). Ann. Rev. Microbiol. 1998; 52:165–190. [DOI] [PubMed] [Google Scholar]
- 60. Ciccarelli F.D., Doerks T., Von Mering C., Creevey C.J., Snel B., Bork P.. Toward automatic reconstruction of a highly resolved tree of life. Science. 2006; 311:1283–1287. [DOI] [PubMed] [Google Scholar]
- 61. Yang S., Doolittle R.F., Bourne P.E.. Phylogeny determined by protein domain content. Proc. Natl. Acad. Sci. U.S.A. 2005; 102:373–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Abeel T., Saeys Y., Bonnet E., Rouzé P., Van de Peer Y.. Generic eukaryotic core promoter prediction using structural features of DNA. Genome Res. 2008; 18:310–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Filesi I., Cacchione S., De Santis P., Rossetti L., Savino M.. The main role of the sequence-dependent DNA elasticity in determining the free energy of nucleosome formation on telomeric DNAs. Biophys. Chem. 2000; 83:223–237. [DOI] [PubMed] [Google Scholar]
- 64. Lavery R., Zakrzewska K., Beveridge D., Bishop T.C., Case D.A., Cheatham T., Dixit S., Jayaram B., Lankas F., Laughton C. et al. A systematic molecular dynamics study of nearest-neighbor effects on base pair and base pair step conformations and fluctuations in B-DNA. Nucleic Acids Res. 2010; 38:299–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Tang G.-Q., Bandwar R.P., Patel S.S.. Extended upstream AT sequence increases T7 promoter strength. J. Biol. Chem. 2005; 280:40707–40713. [DOI] [PubMed] [Google Scholar]
- 66. Dillon S.C., Dorman C.J.. Bacterial nucleoid-associated proteins, nucleoid structure and gene expression. Nat. Rev. Microbiol. 2010; 8:185–195. [DOI] [PubMed] [Google Scholar]
- 67. Araúzo-Bravo M.J., Fujii S., Kono H., Ahmad S., Sarai A.. Sequence-dependent conformational energy of DNA derived from molecular dynamics simulations: toward understanding the indirect readout mechanism in protein–DNA recognition. J. Am. Chem. Soc. 2005; 127:16074–16089. [DOI] [PubMed] [Google Scholar]
- 68. Mitchison G. The regional rule for bacterial base composition. Trends Gen. 2005; 21:440–443. [DOI] [PubMed] [Google Scholar]
- 69. Johnson S., Chen Y.-J., Phillips R.. Poly (dA: dT)-rich DNAs are highly flexible in the context of DNA looping. PLoS One. 2013; 8:e75799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Jeon J.-H., Adamcik J., Dietler G., Metzler R.. Supercoiling induces denaturation bubbles in circular DNA. Phys. Rev. Lett. 2010; 105:208101. [DOI] [PubMed] [Google Scholar]
- 71. Givaty O., Levy Y.. Protein sliding along DNA: dynamics and structural characterization. J. Mol. Biol. 2009; 385:1087–1097. [DOI] [PubMed] [Google Scholar]
- 72. Guardiani C., Cencini M., Cecconi F.. Coarse-grained modeling of protein unspecifically bound to DNA. Phys. Biol. 2014; 11:026003. [DOI] [PubMed] [Google Scholar]
- 73. Yu J., Xiao J., Ren X., Lao K., Xie X.S.. Probing gene expression in live cells, one protein molecule at a time. Science. 2006; 311:1600–1603. [DOI] [PubMed] [Google Scholar]
- 74. Scranton M.A., Ostrand J.T., Georgianna D.R., Lofgren S.M., Li D., Ellis R.C., Carruthers D.N., Dräger A., Masica D.L., Mayfield S.P.. Synthetic promoters capable of driving robust nuclear gene expression in the green alga Chlamydomonas reinhardtii. Algal Res. 2016; 15:135–142. [Google Scholar]
- 75. Li G.-W., Berg O.G., Elf J.. Effects of macromolecular crowding and DNA looping on gene regulation kinetics. Nat. Phys. 2009; 5:294–297. [Google Scholar]
- 76. Bauer M., Rasmussen E.S., Lomholt M.A., Metzler R.. Real sequence effects on the search dynamics of transcription factors on DNA. Sci. Rep. 2015; 5:10072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Brackley C., Cates M., Marenduzzo D.. Intracellular facilitated diffusion: searchers, crowders, and blockers. Phys. Rev. Lett. 2013; 111:108101. [DOI] [PubMed] [Google Scholar]
- 78. Kolesov G., Wunderlich Z., Laikova O.N., Gelfand M.S., Mirny L.A.. How gene order is influenced by the biophysics of transcription regulation. Proc. Natl. Acad. Sci. U.S.A. 2007; 104:13948–13953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Bauer M., Metzler R.. In vivo facilitated diffusion model. PLoS One. 2013; 8:e53956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Pulkkinen O., Metzler R.. Distance matters: the impact of gene proximity in bacterial gene regulation. Phys. Rev. Lett. 2013; 110:198101. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.