Direct Reconstruction of Parametric Images for Brain PET with Event-by-Event Motion Correction: Evaluation in Two Tracers Across Count Levels

Abstract

Parametric images for dynamic positron emission tomography (PET) are typically generated by an indirect method, i.e., reconstructing a time series of emission images, then fitting a kinetic model to each voxel time activity curve. Alternatively, “direct reconstruction,” incorporates the kinetic model into the reconstruction algorithm itself, directly producing parametric images from projection data. Direct reconstruction has been shown to achieve parametric images with lower standard error than the indirect method. Here, we present direct reconstruction for brain PET using event-by-event motion correction of list-mode data, applied to two tracers.

Event-by-event motion correction was implemented for direct reconstruction in the Parametric Motion-compensation OSEM List-mode Algorithm for Resolution-recovery reconstruction. The direct implementation was tested on simulated and human datasets with tracers [¹¹C]AFM (serotonin transporter) and [¹¹C]UCB-J (synaptic density), which follow the 1-tissue compartment model. Rigid head motion was tracked with the Vicra system. Parametric images of K₁ and distribution volume (V_T=K₁/k₂) were compared to those generated by the indirect method by regional coefficient of variation (CoV). Performance across count levels was assessed using sub-sampled datasets.

For simulated and real datasets at high counts, the two methods estimated K₁ and V_T with comparable accuracy. At lower count levels, the direct method was substantially more robust to outliers than the indirect method. Compared to the indirect method, direct reconstruction reduced regional K₁ CoV by 35–48% (simulated dataset), 39–43% ([¹¹C]AFM dataset) and 30–36% ([¹¹C]UCB-J dataset) across count levels (averaged over regions at matched iteration); V_T CoV was reduced by 51–58%, 54–60% and 30–46%, respectively. Motion correction played an important role in the dataset with larger motion: correction increased regional V_T by 51% on average in the [¹¹C]UCB-J dataset.

Direct reconstruction of dynamic brain PET with event-by-event motion correction is achievable and dramatically more robust to noise in V_T images than the indirect method.

1. Introduction

Kinetic modeling of dynamic positron emission tomography (PET) can produce parametric images characterizing tracer uptake rates, useful in studying a wide variety of physiological functions such as metabolism and receptor pharmacology. Parametric images are typically obtained from dynamic PET data by reconstructing images at multiple time frames, then fitting a kinetic model to each voxel time activity curve (TAC). Often, due to high voxel noise, multiple methods are used to reduce voxel noise in order to produce parametric images with acceptable noise levels [1–4]. An alternative method, “direct reconstruction,” produces parametric images directly from raw data by incorporating the kinetic model into the reconstruction algorithm. Because the image-domain noise distribution is difficult to model, direct reconstruction, using the Poisson model, can achieve lower-variance parameter estimates than the indirect method. Direct reconstruction has been the focus of much recent attention, as computational power has grown to support this large estimation problem; please see recent reviews [5–8].

Motion correction is critical for dynamic brain PET of awake subjects [9, 10]. However, there are very few examples in the literature for which direct reconstruction of brain data has included motion correction. Gravel et al. [11] presented a method for correcting inter-frame motion in direct reconstruction, and evaluated their method in simulated data but not in real data. Jiao et al. [12] also developed a direct reconstruction algorithm to estimate inter-frame motion and kinetic parameters simultaneously from PET sinogram data. Neither of these methods addresses intra-frame motion or takes advantage of measurements from an external motion tracking device, which can be made accurately with high temporal resolution [9]. The work of Jin et al. [10] suggests that, while frame-based motion correction is sufficient for small intra-frame motions (< 5 mm), event-by-event motion correction has universally good performance.

Most published demonstrations of direct reconstruction use sinogram data (e.g., [13–15]), but list mode data is better suited for event-by-event motion correction since continuous motion information can be used [10]. When using list mode data, exact computation of the sensitivity image – the sum of the system matrix, including attenuation and normalization, over all possible lines-of-response (LOR) – is difficult since the locations of the lines-of-response are continuously changing with motion. For the sake of computational feasibility, approximations must be made, particularly when correcting for motion [16, 17]. In this work, we extend the Parametric Motion-compensation OSEM List-mode Algorithm for Resolution-recovery reconstruction for the one-tissue model (PMOLAR-1T) [18–20] to include event-by-event motion for direct reconstruction; this requires a modified approach for estimating the sensitivity image. In the previous initial evaluation of PMOLAR-1T on human data, this effect was ignored for simplicity.

The magnitude by which direct reconstruction outperforms the indirect method will depend on, among other factors, the kinetics of the PET tracer, noise level, kinetic model, and kinetic parameter of interest (see Figure 11 in [8]). Here, we evaluate the performance of this algorithm for two tracers whose kinetics can be modeled with the1-tissue compartment (1T) model, [¹¹C]AFM and [¹¹C]UCB-J. [¹¹C]AFM [21] targets the serotonin (5HT) transporter protein (SERT) and has been applied to the study of psychiatric disorders such as depression and post-traumatic stress disorder. [¹¹C]UCB-J is a new tracer targeting the synaptic vesicle glycoprotein 2A [22] and can be used to measure synaptic density, relevant to a wide range of diseases including epilepsy and Alzheimer’s disease. We quantify the benefit of direct reconstruction, as compared to the indirect method, for each tracer, over a range of count levels. Here we take advantage of list-mode data, which permits the generation of lower-count noise realizations by selectively retaining varying fractions of the events during reconstruction.

2. Methods

2.1 Algorithm

2.1.1 Emission Image Reconstruction

For the indirect approach, an emission image for each frame of the dynamic PET data is independently reconstructed. The list mode EM update equation [23, 24] for the activity λ of each voxel j for a frame f of duration T as implemented in MOLAR [16, 25] is:

$${\lambda }_{jf}^{\left(n+1\right)}=\frac{{\lambda }_j^{\left(n\right)}}{T{Q}_j}{\displaystyle \sum _k\frac{c_{kj}{A}_k{N}_k{L}_t}{{\displaystyle {\sum }_{j\prime }{c}_{kj\prime }{A}_k{N}_k{L}_t{\lambda }_{j^{\prime }f}^{\left(n\right)}}+R_k+S_k}}$$ (1)

where variable definitions are given in Table 1; note that the list mode event index k maps to a particular LOR i and time t within frame f. The terms c_kj and A_k are time-dependent to account for motion: each event’s LOR is transformed according to the measured motion at corresponding time index t. Each voxel of the global sensitivity image

$$Q_j={\displaystyle \sum _{it}{c}_{\mathit{ijt}}{A}_{it}{N}_i,}$$ (2)

is pre-computed using a large number of random LORs as described in [16, 25].

Table 1.

Variable definitions.

Variable	Unit	Description
Ait	–	Attenuation along LOR I at time index t
cijt	mm	Contribution of voxel j to LOR i at time index t (includes geometry, resolution, solid angle, and motion effects)
Δt	s	Duration of each time bin (for direct reconstruction; time interval for discretization of the kinetic model, which can theoretically be as small as 1 ms, the timing resolution of the list mode file)
f	–	Frame index (for indirect reconstruction)
G	–	Number of k2 values used to compute sensitivity images with motion correction (Eqs. 16 and 17)
i	–	LOR index
j	–	Voxel index
k	–	List mode event index
K1,j	mL/min/cm3	Inflow rate constant of 1T model at voxel j
k2,j	1/min	Outflow rate constant of 1T model at voxel j
Lt	–	Decay factor
λj	Bq/mL	Value of emission image at voxel j
$M_{\mathit{ijt}\tau }^{\left(n\right)}$	counts	Conditional expectation of complete data at iteration n
n	–	Iteration number
Ni	(counts/s)/(Bq/mL·mm)	Normalization factor for LOR i (in terms of absolute sensitivity)
Pτ	Bq/mL	Value of input function to 1T model at time index τ
Qj	(counts/s)/(Bq/mL)	Sensitivity of voxel j
Rit	counts/s	Randoms rate for LOR i at time index t
Sit	counts/s	Scatter rate for LOR i at time index t
t	–	Time bin index, relative to injection time
T	s	Duration of an emission time frame (for indirect reconstruction)
τ	–	Time bin index of tracer delivery (for discretization of convolution integral)
Xijtτ	counts	Random variable representing counts detected on LOR i at time t, emitted from voxel j for tracer delivered at time index τ (xijtτ denotes a realization of this random variable)
ξijtτ	1/s	Rate parameter of the Poisson distribution of Xijtτ
Yit	counts	Random variable representing counts detected on LOR i at time index t (yit denotes a realization of this random variable)

2.1.2 Direct Parametric Reconstruction

The 1T compartment model describing tissue activity concentration C_T(t), parameterized by influx and efflux rate constants K₁ and k₂, is

$$C_T\left(t\right)=C_A\left(t\right)\otimes K_1{e}^{-k_{2}t},$$ (3)

where C_A(t) is the arterial input function (the time-varying tracer concentration in the plasma) and ⊗ is the convolution operator with integration beginning at t=0. The underlying kinetic model, i.e., the emission time course, is not represented as truly continuous, but rather per time epoch Δt. While Δt can be as small as the list mode resolution (1 ms), in this work we set Δt = 6s, which is more than sufficient for normal rates of tracer kinetics based on sampled input functions. PMOLAR-1T (previously described in [20] and reviewed here) is a direct reconstruction algorithm based on expectation maximization (EM), in which update equations are analytically derived for the 1T model. For mathematical clarity, we present the equations for sinogram-based reconstruction, which can be generalized to list mode (the results in this manuscript were generated by the list mode approach). The adaptation to list mode is most simply achieved by directly processing the list mode data of each time bin, where each event index k maps to a particular LOR i and time t, and the count y_it=1. The EM complete data space is given by the random emissions detected along LOR i from voxel j at time index t, from tracer input delivered at time τ. Note that for list mode reconstruction, t has the time resolution of the list mode data (1 ms). This random variable X_ijtτ describing the EM complete data space is assumed to be Poisson distributed

$$X_{\mathit{ijt}\tau }~\text{Poisson}({\xi }_{\mathit{ijt}\tau })$$ (4)

with rate parameter

$${\xi }_{\mathit{ijt}\tau }=\mathrm{\Delta }t{c}_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{K}_{1,j}{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}.$$ (5)

(Refer to Table 1 for all variable definitions.) This complete data space decomposes the total counts along LOR i into its spatial components (as in the static EM algorithm) and into its temporal components (based on the convolution equation). The complete-data log likelihood for this Poisson random variable (omitting constant terms) is given by

$$\log f\left(x|K_1,k_2\right)={\displaystyle \sum _{\mathit{ijt}\tau }(x_{\mathit{ijt}\tau }\ln {\xi }_{\mathit{ijt}\tau }-{\xi }_{\mathit{ijt}\tau })},$$ (6)

and the expectation of the complete data at iteration n, including randoms rate R_it and scatter rate S_it, is

$$E\left[X_{\mathit{ijt}\tau }|Y_{it},K_1^{\left(n\right)}{k}_2^{\left(n\right)},R_{it},S_{it}\right]=\frac{y_{it}{\xi }_{\mathit{ijt}\tau }^{\left(n\right)}}{{\displaystyle {\sum }_{j^{\prime }{\tau }^{\prime }}{\xi }_{i{j}^{\prime }t{\tau }^{\prime }}^{\left(n\right)}+R_{it}+S_{it}}}:=M_{\mathit{ijt}\tau }^{\left(n\right)}$$ (7)

The EM surrogate function is the conditional expectation of the kinetic parameters in each voxel, given their current estimates:

$$E\left[\log f\left(X|K_1,k_2\right)|y,K_1^{\left(n\right)},k_2^{\left(n\right)},R_{it},S_{it}\right]={\displaystyle \sum _{\mathit{ijt}\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}\text{ln}{\xi }_{\mathit{ijt}\tau }-{\xi }_{\mathit{ijt}\tau }$$ (8)

The update equation for K₁ is found by maximizing the right-hand side of (8) with respect to K₁, which gives:

$$K_{1,j}^{\left(n+1\right)}=\frac{{\displaystyle {\sum }_{it\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}}{\mathrm{\Delta }t{\displaystyle {\sum }_{it\tau }{c}_{\mathit{ijt}}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,j}^{\left(n+1\right)}\left(t-\tau \right)}}$$ (9)

To find the update equation for k₂, the partial derivative of (8) with respect to k₂ is set to 0 to obtain the intermediate result:

$${\displaystyle \sum _{it\tau }\left(t-\tau \right)}\mathrm{\Delta }t{c}_{\mathit{ijt}}{A}_{it}{N}_t{L}_t{K}_{1,j}{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}={\displaystyle \sum _{it\tau }\left(t-\tau \right)}{M}_{\mathit{ijt}\tau }^{\left(n\right)}$$ (10)

Substituting the result for K_1,j from (9) into (10) yields the following:

$$\frac{{\displaystyle {\sum }_{it\tau }\left(t-\tau \right)}{M}_{\mathit{ijt}\tau }^{\left(n\right)}}{{\displaystyle {\sum }_{it\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}}=\frac{{\displaystyle {\sum }_{it\tau }\left(t-\tau \right)c_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}}{{\displaystyle {\sum }_{it\tau }{c}_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}}$$ (11)

Here, we define a function H(k₂) as the right-hand side of (11):

$$H\left(k_{2,j}\right)=\frac{{\displaystyle {\sum }_{it\tau }\left(t-\tau \right)c_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}}{{\displaystyle {\sum }_{it\tau }{c}_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}},$$ (12)

Because the left-hand side of (11) is dependent only on the data and current parameter estimates, the update equation for k₂ is:

$$k_{2,j}^{\left(n+1\right)}=H^{-1}\left(\frac{{\displaystyle {\sum }_{it\tau }\left(t-\tau \right)M_{\mathit{ijt}\tau }^{\left(n\right)}}}{{\displaystyle {\sum }_{it\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}}\right).$$ (13)

As done previously [20], in the absence of motion, c_ijt and A_it are independent of time, so the update equation for K₁ (9) can be simplified to:

$$K_{1,j}^{\left(n+1\right)}=\frac{{\displaystyle {\sum }_{it\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}}{\mathrm{\Delta }t{Q}_j{\displaystyle {\sum }_{t\tau }{L}_t{P}_{\tau }{e}^{-k_{2,j}^{\left(n+1\right)}\left(t-\tau \right)}}}$$ (14)

and H(k₂) (12) can be simplified to:

$$H\left(k_{2,j}\right)=\frac{{\displaystyle {\sum }_i{c}_{ij}{A}_i{N}_i{\displaystyle {\sum }_{t\tau }\left(t-\tau \right)L_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}}}{{\displaystyle {\sum }_i{c}_{ij}{A}_i{N}_i{\displaystyle {\sum }_{t\tau }{L}_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}}}=\frac{{\displaystyle {\sum }_{t\tau }{L}_t\left(t-\tau \right)P_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}}{{\displaystyle {\sum }_{t\tau }{L}_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}}.$$ (15)

The terms ${\displaystyle {\sum }_{t\tau }{L}_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}$ and ${\displaystyle {\sum }_{t\tau }\left(t-\tau \right)L_t{P}_{\tau }{e}^{-k_{2,j}\left(t-\tau \right)}}$ can be pre-computed at a set of k₂ values for computational efficiency (with the approximation of ignoring time-varying live time correction). Note that H(k_2,j) is a monotonically decreasing function; refer to Appendix A in the Supplemental File for the proof.

Here, we have extended the implementation to include motion. Specifically, when there is motion, the sums ${\displaystyle {\sum }_{it\tau }{c}_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,j}^{\left(n+1\right)}\left(t-\tau \right)}}$ and ${\displaystyle {\sum }_{it\tau }\left(t-\tau \right)c_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,j}^{\left(n+1\right)}\left(t-\tau \right)}}$ from (9) and (12) are not factorable into a sensitivity term Q_j and a kinetic model term which is a function of k₂. Therefore, we incorporated the kinetic model term into the sensitivity image to produce a “kinetic-sensitivity image” by computing the denominator and numerator terms:

$$Q_{j,k_{2,g}}^{\prime }={\displaystyle \sum _{it\tau }{c}_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,g}\left(t-\tau \right)}}$$ (16)

and

$$Q_{j,k_{2,g}}^{″}={\displaystyle \sum _{it\tau }\left(t-\tau \right)c_{\mathit{ijt}}{A}_{it}{N}_i{L}_t{P}_{\tau }{e}^{-k_{2,g}\left(t-\tau \right)}}$$ (17)

at a set of G coarsely sampled k₂ values (where subscript g denotes the index into this set), to get two sets of kinetic sensitivity images. This results in a spatially variant $H_j^{\prime }\left(k_2\right)$:

$$H_j^{\prime }\left(k_{2,j}\right)=\frac{Q_{j,k_2}^{″}}{Q_{j,k_2}^{\prime }}.$$ (18)

The Q′ and Q″ images are pre-computed for G k₂ values; then $H_j^{\prime }$ is computed for these G k₂ values (see Supplementary figure S13), and a linear interpolation between the two values of $H_j^{\prime }$ nearest to $\frac{{\displaystyle {\sum }_{it\tau }\left(t-\tau \right)M_{\mathit{ijt}\tau }^{\left(n\right)}}}{{\displaystyle {\sum }_{it\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}}$ is used to solve the following update equation:

$$k_{2,j}^{\left(n+1\right)}=H_j^{\prime -1}\left(\frac{{\displaystyle {\sum }_{it\tau }\left(t-\tau \right)M_{\mathit{ijt}\tau }^{\left(n\right)}}}{{\displaystyle {\sum }_{it\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}}\right)$$ (19)

The inverse of H′ is implemented as piecewise linear between each pair of k_2,g values. In principle, higher order interpolation could be used, but for this application, linear interpolation is likely sufficient (H′(k₂) is well approximated by piecewise linear functions for the k₂ spacing we selected). See Supplemental Figure S13, which gives an example of H′(k₂) for a representative voxel.

The K₁ update equation in the presence of motion is then

$$K_{1,j}^{\left(n+1\right)}=\frac{{\displaystyle {\sum }_{it\tau }{M}_{\mathit{ijt}\tau }^{\left(n\right)}}}{\mathrm{\Delta }t{Q}_{j,k_{2,j}}^{\prime }},$$ (20)

where again interpolation within the table of G k₂ values is used to find Q′ at the current k₂ estimate.

2.2 Data Simulation

A 4D simulation (3D + kinetics) was performed to validate the updated equations, specifically the inclusion of the kinetic term in the sensitivity image, in the presence of motion, and to characterize bias in parametric images generated by the indirect and direct methods. Note that nonlinear parameter estimation methods can produce bias simply due to noise. A list mode file was simulated for a 2-hour scan based on [¹¹C]AFM kinetics and the HRRT scanner geometry. Template parametric K₁ and k₂ images were generated by intensity-based segmentation of parametric images from a real human [¹¹C]AFM scan. These parametric images were used in conjunction with an input function from a human acquisition to calculate the activity image at 6-second intervals, according to the 1T model.

At each timestamp (in ms intervals), a random sampling of LORs was forward projected through the ground truth activity image. This forward projection step yielded an expected value for the counts of each LOR, consistent with the spatial and temporal distribution of activity. Since the LORs are undersampled, an adjustment must be made to the expected value. First, note that a Poisson random variable compounded with a Bernoulli random variable (i.e. an undersampling operator) results in another Poisson random variable. Thus, since the LOR selection process can be approximated as a Poisson random variable, a Bernoulli variate was then produced for each random LOR. The probability parameter of each Bernoulli distribution was specified by the expected value of the counts along that LOR, scaled by the LOR undersampling rate. To improve efficiency, LORs were grouped by similar expected values (approximated from a coarse forward projection of the activity image at regular time intervals), and non-uniformly sampled such that groups with higher expected values were sampled more heavily. LOR sampling rates were set high enough such that the Bernoulli parameter never exceeded 1. Thus, the LOR sampling process varied in space and time to capture the tracer kinetics as well as motion, which was simulated based on Vicra measurements from a real human acquisition, and applied event-by-event. A more detailed description of the simulation methodology can be found in Appendix B presented in the Supplemental file. Randoms and scatter modeling were not included. Attenuation inside the brain was assumed to be uniform. The simulated list mode file contained 837 million true events, which was then downsampled to 5, 10, and 20% count levels as described below for the human datasets.

2.3 Human Data Acquisition

This study is a retrospective analysis of previously acquired datasets of two healthy male subjects, one using tracer [¹¹C]AFM and the other with [¹¹C]UCB-J (see Table 2). Both PET scans were acquired on the high-resolution research tomograph (HRRT) (Siemens Medical Solutions, Knoxville, TN, USA). Transmission scans were acquired for attenuation correction. Input functions were obtained by arterial blood sampling at the radial artery, continuously collected for the first 7 minutes of the PET acquisition at 4 mL/min (PBS-101, Veenstra Instruments, Joure, The Netherlands). Fifteen manual samples were collected over the remainder of the acquisition. Corrections were made for metabolites, decay, dispersion, and delay. The Polaris Vicra tracking system (NDI Systems, Waterloo, Ontario, Canada) [26] was used to measure rigid motion of the head throughout each scan at a frequency of ~30 Hz. These measurements formed a priori knowledge of the motion field, which were provided as input to the reconstruction algorithm as previously described [10, 25]. During reconstruction (both indirect and direct methods), the endpoints of each line of response are corrected according to the most recent measurement from the external tracking device.”

Table 2.

Summary of human acquisitions.

	Subject 1	Subject 2
Tracer	[11C]AFM	[11C]UCB-J
Dose (MBq)	832	650
Scan Duration (h)	2	2
Counts (×109)	1.2	2.3

Each list mode file was down-sampled to 5, 10, and 20% of the total counts by applying a repeating sequence of 50 ms gates for the 2-hour scan duration. Respectively, each 20^th, 10^th, or 5^th gate was kept per replicate. Five replicates were reconstructed for each case, as well as the original (full count) datasets.

Reconstruction and Kinetic Modeling

For the indirect method, each frame was initialized to the 1T model evaluated at the frame midpoint with k₂=0.02 min⁻¹, K₁=0.5 mL/min/cm³. For the direct method, reconstruction initial conditions were set to k₂=0.02 min⁻¹, K₁=0.5 mL/min/cm³. Both methods used 4 iterations of 20 subsets. Events were sequentially assigned to subsets in the order read in from the list mode file.

To estimate Q or Q′ and Q″ (Eq. 2 for indirect; Eq. 16 and 17 for direct) sensitivity images, random LORs were selected. The number of random LORs was chosen in proportion to the number of events included in the reconstruction (e.g., such that the 10% count level reconstructions used half the number of random LORs for Q estimation as the 20% count level reconstructions). This approach, to scale the number of random LORs based on the number of actual events in the reconstruction, has been shown to balance the amount of noise added by the random Q process vs. computation time. For each real event in the list mode file, a random LOR was chosen, to achieve time-varying sampling according to count rate. To verify that this approach was appropriate, for the [¹¹C]AFM dataset only, the 10% count level datasets were additionally reconstructed with Q generated using double the number of random LORs as list mode events, and the 5% count level datasets with quadruple the number of random LORs (i.e., the same number of random LORs as used in the 20% count level reconstructions). These reconstructions were used to evaluate the impact of the number of LORs used to estimate the sensitivity image on the noise of the parametric images.

For the direct method, Q′ and Q″ (Eqs. 16 and 17) were computed for 12 k₂ values distributed linearly between 0.0001 min⁻¹ and 0.078 min⁻¹.

Randoms were estimated based on time-varying block singles rates. Scatter was estimated across coarsely sampled detector space at 10 time points using the single-scatter simulation (SSS) method [27], and iteratively updated at subsets 0, 4, and 10 of the first iteration. Global scatter scale factors for each time point were determined as the ratio between scatter measured outside the attenuation volume and calculated scatter estimate. To determine the scatter estimate for each event, linear interpolation among the 10 estimated timepoints was used [18, 19].

For each down-sampled replicate, dynamic PET sequences of 17 temporal frames (4×30s, 1×1min, 2×2min, 2×5min, 1×7min, 3×10min, 3×15min, 1×20min) beginning one minute after scan start were reconstructed using MOLAR [16], for the indirect method. Post-reconstruction of each iteration of 20 subsets, the 1T model was fit to each voxel using the basis function method [28, 29] with weights based on noise-equivalent counts. The minimal and maximal allowed values of k₂ were 0.0001 min⁻¹ and 0.078 min⁻¹, respectively. In previous analyses of these tracers with a more lenient maximum k₂ (1.0), fewer than 0.1% of voxels exceeded the maximum set here.

2.4 Quantitative Analysis

The parameters of interest in this study were K₁ and volume of distribution, V_T=K₁/k₂, which contains the receptor-related information [30]. Quantitative metrics were summarized regionally, for 8 regions (amygdala, caudate, cerebellum, frontal lobe, hippocampus, occipital lobe, putamen, and thalamus) from the automated anatomical labeling (AAL) template [31] in the Montreal Neurological Institute (MNI) space, which was transformed to the PET space independently for each subject based on co-registered MR images. Regions were eroded by one voxel, and all regions besides the subcortical regions (caudate, putamen, and thalamus) were masked to include only voxels corresponding to gray matter, as determined from the co-registered MRI. For simulated data, percent bias in K₁ and V_T with respect to the true values was calculated per voxel from the average of the 5 replicates, per count level. Mean parametric images were generated by averaging replicates for each count level, which was followed by averaging within region of interest. Voxelwise coefficient of variation (CoV) for V_T could not be reliably estimated using the mean and standard deviations across 5 replicates, due in part to large outliers. Instead, the voxelwise covariance matrix of K₁ and k₂ was estimated across replicates per count level, and voxelwise V_T CoV was estimated by propagation of uncertainty, using the full-count images from direct reconstruction (due to high bias in lower count and indirect images) for the mean voxelwise values of K₁ and k₂:

$$Co{V}_{V_T}=\sqrt{{\left(\frac{{\sigma }_1}{K_1}\right)}^2}+{\left(\frac{{\sigma }_2}{k_2}\right)}^2-\frac{2{\sigma }_{12}}{K_1{k}_2}$$ (17)

where σ₁ is the K₁ standard deviation, σ₂ is the k₂ standard deviation, and σ_1,2 is the covariance of K₁ and k₂. Standard deviation images were calculated as standard deviation across 5 replicates, per voxel. The covariance images were computed across 5 replicates, using a 3×3×3 neighborhood at each voxel (for a total of 135 values contributing to the covariance estimate at each voxel). To quantify the advantage of the direct method over the indirect method, we computed the percent reduction in regional V_T CoV from indirect to direct, at matched iteration and count level:

$$\%\mathrm{Re}\text{duction}=100\%.\frac{Co{V}_{\mathit{indirect}}-Co{V}_{\mathit{direct}}}{Co{V}_{\mathit{indirect}}}.$$ (18)

3. Results

Changes in regional K₁ and k₂ means over the final two iterations at the 100% count level for both the indirect and direct methods were small (−1.9±1.5%, see Supplemental Tables S1 and S2); accordingly, whenever results are not shown for all iterations, they are summarized at iteration 2. Most results are presented for a single representative brain region (frontal lobe), with additional regions presented in the Supplemental Data.

3.1 Simulated Data

Simulated and reconstructed images are shown in Fig. 1. The K₁ image shows differences based on higher and lower blood flow in gray matter and white matter, respectively. The V_T image shows the distribution of serotonin transporter binding which is lowest in the cerebellum and highest in subcortical and midbrain regions.

Figure 1.

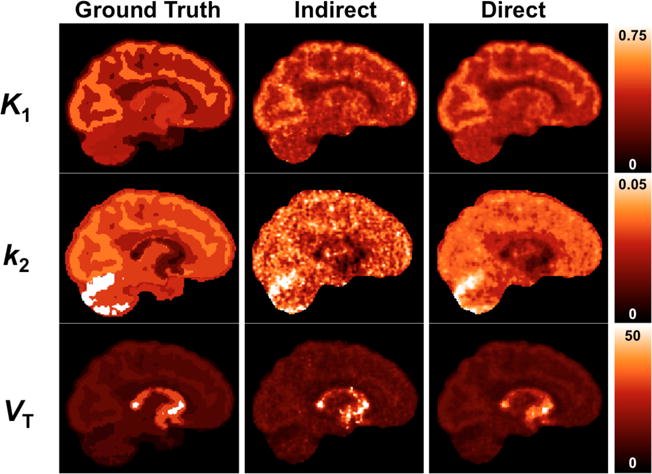
Simulated parametric images. First column shows true images. Second and third columns show reconstructed parametric images by the indirect and direct methods, respectively, at Iteration 2 (20 subsets). These results use the full list mode file (100%-count level). No smoothing has been applied. For a comparison with and without motion correction, see Supplemental Figure S1.

At the full count level, K₁ and V_T images (Fig. 1) are qualitatively similar between the direct and indirect methods, though indirect had slightly higher noise. The k₂ image has notable differences in texture between indirect and direct, with the indirect k₂ image showing much higher variability. At iteration 2, the mean regional biases of K₁ and V_T in the frontal lobe for the full-count dataset were <1% for both the indirect and direct methods (Tables 3 and 4). Bias tended to increase with iteration, particularly for the indirect method. Several small regions (amygdala, caudate, putamen) exhibited significant bias in V_T even for the full-count dataset, by the indirect method but not the direct method (Supplemental Tables S3–S5).

Table 3.

Mean bias of K₁ in the frontal cortex for the simulated dataset, per count level and iteration, for direct and indirect methods.

		Iter 1	Iter 2	Iter 3	Iter 4
100% Counts	Indirect	−0.7	0.4	1.1	1.7
	Direct	−1.6	−0.6	−0.1	0.1
20% Counts	Indirect	0.6	3.2	4.8	5.9
	Direct	−1.4	−0.03	0.6	1.0
10% Counts	Indirect	2.3	5.3	7.1	8.6
	Direct	−1.2	0.4	1.3	1.9
5% Counts	Indirect	4.0	7.4	9.9	12
	Direct	−1.4	1.0	2.6	3.5

Table 4.

Mean bias of V_T in the frontal cortex for the simulated dataset, per count level and iteration, for direct and indirect methods.

		Iter 1	Iter 2	Iter 3	Iter 4
100% Counts	Indirect	−0.3	0.8	3.2	10
	Direct	−0.4	0.2	0.5	0.6
20% Counts	Indirect	5.2	116	327	554
	Direct	−0.3	0.5	1.3	2.1
10% Counts	Indirect	49	420	779	1072
	Direct	−0.2	1.2	4.1	7.9
5% Counts	Indirect	322	996	1446	1740
	Direct	2.0	35	157	261

Across all count levels, bias in frontal lobe K₁ was relatively low by both methods across iterations (Table 3): even at iteration 4 at the 5% count level the bias from the indirect method was only 12%. Some other regions showed greater bias in K₁ at low counts, even at iteration 2 (Supplemental Table S3).

Results were different for V_T (K₁/k₂). At the subsampled count levels, extreme outliers cause large positive bias in V_T images generated by the indirect method, which worsen with increasing iteration and decreasing count level (Fig. 2a, 3a; Table 4). These outliers are due to k₂ values approaching the lower bound imposed in model fitting. At the 5% count level, the mean bias in V_T in the frontal cortex is ~1000% by the indirect method at iteration 2, however the median V_T bias is 15%, due to the asymmetric distribution of estimated values. Bias in V_T is much better controlled by the direct method (Fig. 2b, Fig. 3b), and only the 5% count level has significant outliers (mean V_T bias at iteration 2 is 35% and median is 4%). Mean and median V_T bias for other regions are given in Supplemental Tables S4 and S5. The regions exhibiting greatest bias were primarily those with higher V_T values (due to higher concentrations of transporter) and thus very low k₂, where errors introduce large bias in V_T.

Figure 2.

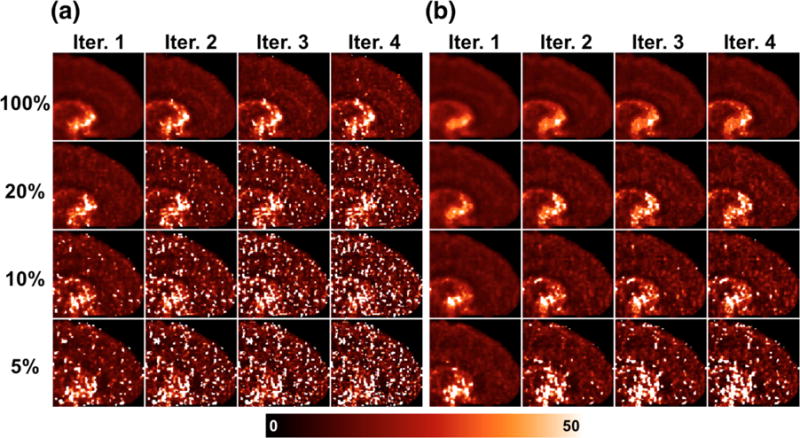
V_T parametric maps of one replicate of simulated [¹¹C]AFM dataset per count level (rows), across 4 iterations (columns). (a) Generated by the indirect method. (b) Generated by the direct method.

Figure 3.

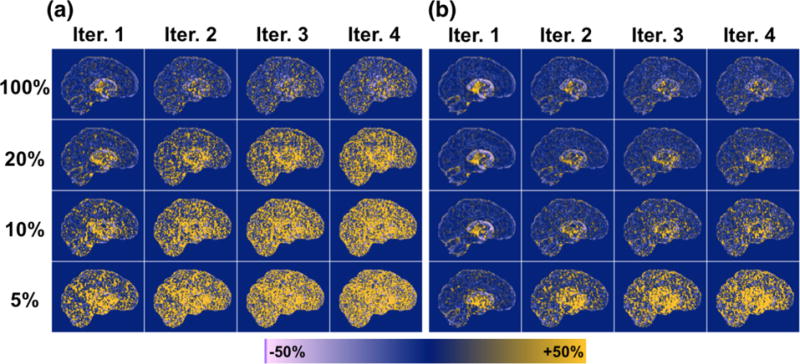
Voxelwise percent bias in V_T parametric images, computed from average across 5 replicates of simulated data (except for the 100% count level, which used 1 replicate), per count level (rows) and iteration (columns). (a) Generated by the indirect method. (b) Generated by the direct method.

Fig. 4a shows the regional CoV values for V_T in the frontal lobe. Direct reconstruction shows much lower noise than the indirect method. For example, at iteration 2, V_T CoV is lower for the 5% count level by direct reconstruction (21%) than that with quadruple the counts by the indirect method (25%) (Fig. 4a). At iteration 2, the percent reduction in regional V_T CoV (in the frontal cortex) afforded by direct reconstruction compared to indirect is similar across count levels, ranging from 59% to 64% (Fig. 4b). Percent reduction in V_T CoV was similar for other regions, 51–58% (averaged separately per count level, across regions). Percent reduction in K₁ CoV was smaller, 35–48% averaged across regions.

Figure 4.

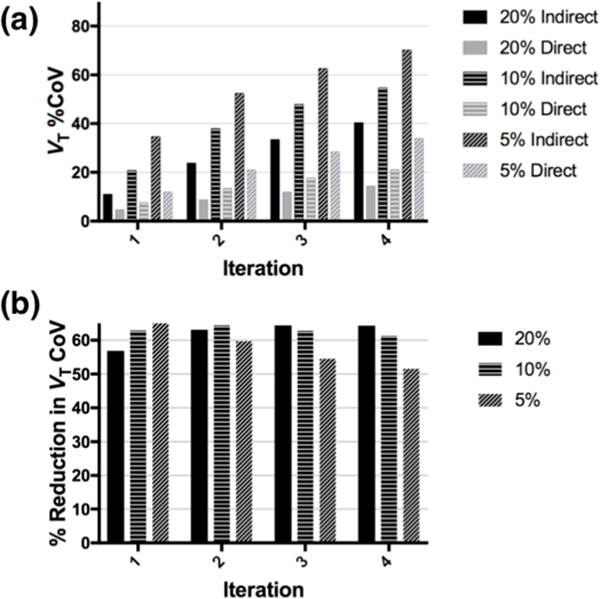
(a) Regional V_T %CoV (in the frontal cortex) by iteration and count level for the indirect and direct methods, for the simulated dataset. (b) Percent reduction in regional V_T CoV of the direct method relative to the indirect method, by iteration and count level, for the simulated dataset.

3.2 Human Data

To demonstrate the importance of motion correction, one replicate at the 20% count level for each dataset was reconstructed by the direct method, both with and without motion correction (Fig. 5). Motion magnitude over the 2-hour scan duration was summarized quantitatively according to Equation 3 in [10] for each dataset; the average motion was 2.86 mm for the [¹¹C]AFM dataset and 20.1 mm for the [¹¹C]UCB-J dataset. The large motion for the [¹¹C]UCB-J dataset is primarily due to a shift that occurred in the 56^th minute. Only subtle differences are present between the corrected and uncorrected images for the [¹¹C]AFM dataset, consistent with the relatively small motion in this acquisition (Fig. 5a). The average V_T in the frontal cortex at iteration 2 is 14.6 mL/cm³ without motion correction, and 15.9 mL/cm³ with motion correction. Motion correction had a more pronounced effect on the [¹¹C]UCB-J parametric images when correction was not applied (Fig. 5b). A large vertical shift is evident in the k₂ image, which was more greatly impacted by motion than the K₁ image. When left uncorrected, the motion in the [¹¹C]UCB-J study results in severe artifacts and widespread elevation in k₂, which in turn lowers V_T: at iteration 2, the average V_T in the frontal lobe is 15.2 mL/cm³ without motion correction, and 25.5 mL/cm³ with motion correction. See Supplemental Table S6 and S7 for other regional values for K₁, k₂, and V_T with and without motion correction.

Figure 5.

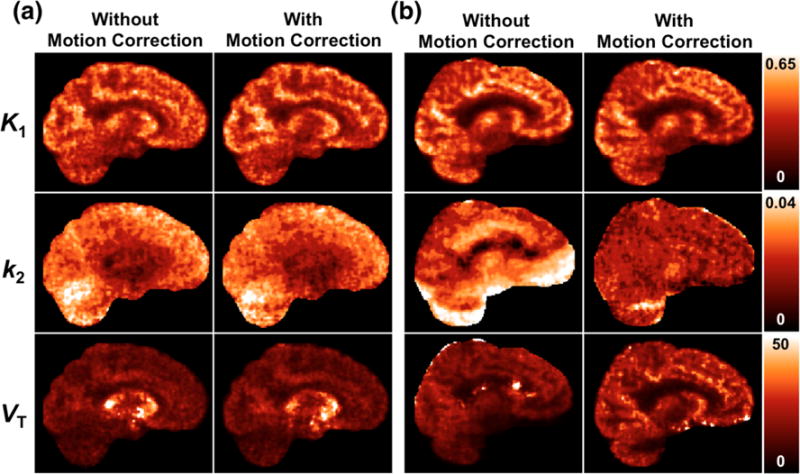
Parametric images generated via direct reconstruction, without and with motion correction. Results are shown at iteration 2, for one replicate at the 20% count level. (a) [¹¹C]AFM dataset (b) [¹¹C]UCB-J dataset

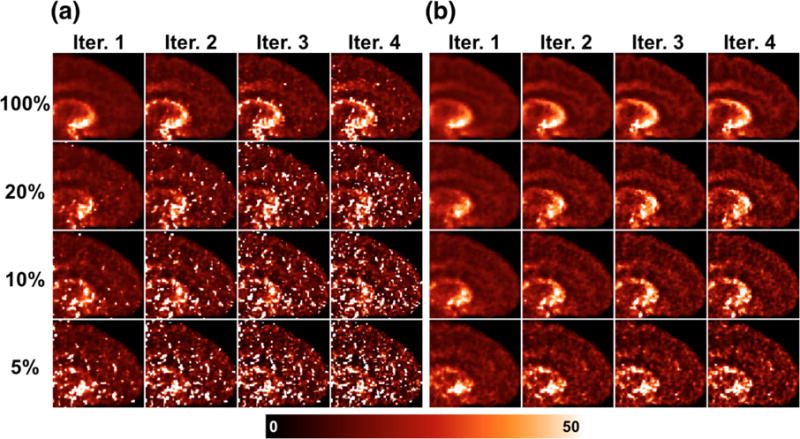
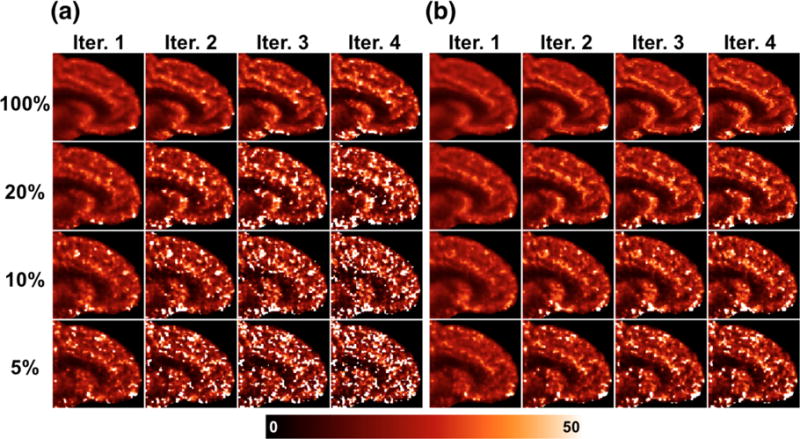
Parametric V_T images of single replicates of the [¹¹C]AFM and [¹¹C]UCB-J datasets are shown, respectively in Figures 6 and 7, at each count level and iteration. See Supplemental Figures S2–S5 for K₁ and k₂ parametric images of each tracer. K₁ images are similar between the [¹¹C]AFM and [¹¹C]UCB-J datasets, as they both reflect cerebral blood flow. The k₂ image is more uniform across the brain in [¹¹C]UCB-J due to uniformity of binding to synaptic vesicles in gray matter.

Figure 6.

V_T parametric maps of one replicate of human [¹¹C]AFM dataset per count level (rows), across 4 iterations (columns). (a) Generated by the indirect method. (b) Generated by the direct method.

Figure 7.

V_T parametric maps of one replicate of human [¹¹C]UCB-J dataset per count level (rows), across 4 iterations (columns). (a) Generated by the indirect method. (b) Generated by the direct method.

Full-count images by both methods are mostly free of outliers. Predictably, noise becomes systematically worse with increasing iteration and decreasing count level, and is always higher for the indirect method than the direct method at matched count level and iteration. For both tracers, the noise advantage of the direct method over the indirect method is more visibly apparent in the k₂ images than K₁.

Mean regional K₁ and V_T values at iteration 2 for the frontal lobe (averaged across replicates and within region) for the 2 tracers are given in Tables 5 and 6; see Supplemental Tables S8–S11 for other regions. In both datasets, mean K1 values are similar between direct and indirect methods across all count levels, with only slightly greater differences between direct and indirect K₁ at the 5% count level compared to the 100% count level. This is consistent with the simulation study, for which bias in K₁ was low in all regions for both methods, increasing modestly with decreasing count level for the indirect method (Supplemental Table S3). However, mean V_T values are similar between direct and indirect only for the full-count reconstructions. The mean V_T is stable across count level for the direct method, with a slight increase at the lowest count levels for [¹¹C-]UCB-J. Mean V_T estimated by the indirect method becomes larger with decreasing count level, as a result of noise-induced bias: higher variance in k₂ produces more k₂ values approaching the lower bound for k₂, and thus much higher V_T values. Median V_T values are less biased since they are less affected by these outliers.

Table 5.

Summary of regional K₁ and V_T values from [¹¹C]AFM dataset in the frontal lobe at iteration 2 for each count level. Mean and median are computed within region from the mean image across replicates.

		[11C]AFM K1			[11C]AFM VT
		Mean	Median	%CoV	Mean	Median	%CoV
100% Counts	Indirect	0.45	0.45	–	14.8	14.5	–
	Direct	0.44	0.44	–	15.9	15.6	–
20% Counts	Indirect	0.46	0.46	17	26.1	15.0	19
	Direct	0.44	0.44	9	15.9	15.6	10
10% Counts	Indirect	0.47	0.46	24	62.5	15.6	33
	Direct	0.45	0.44	13	16.0	15.7	14
5% Counts	Indirect	0.48	0.47	32	125	16.3	49
	Direct	0.45	0.45	18	16.1	15.8	21

Table 6.

Summary of regional K₁ and V_T values from [¹¹C]UCB-J dataset in the frontal lobe at iteration 2 for each count level. Mean and median are computed within region from the mean image across replicates.

		[11C]UCB-J K1			[11C]UCB-J VT
		Mean	Median	%CoV	Mean	Median	%CoV
100% Counts	Indirect	0.43	0.43	–	25.4	25.0	–
	Direct	0.43	0.43	–	25.0	24.7	–
20% Counts	Indirect	0.43	0.44	11	30.5	25.8	17
	Direct	0.43	0.43	7	25.9	25.2	12
10% Counts	Indirect	0.44	0.44	16	54.3	26.6	27
	Direct	0.43	0.43	10	26.7	25.3	17
5% Counts	Indirect	0.45	0.45	23	120	28.4	44
	Direct	0.43	0.43	15	30.6	25.8	23

Qualitative image assessments of noise from Figs. 6 and 7 show clear noise advantage of the direct method; this assessment is supported by the regional estimates of V_T %CoV (across replicates) in the frontal lobe (Figs. 8a and 8b). K₁ %CoV was lower than V_T %CoV, but followed the same trends (Supplemental Figure S6a and b). V_T %CoV was relatively uniform throughout most of the brain (see Supplemental Figures S7 and S8 for V_T CoV images of each tracer across count levels and iterations), although subcortical V_T %CoV appeared to be higher (since V_T values there are higher). For [¹¹C]AFM, the direct method at the 5% count level has similar regional V_T CoV in the frontal lobe at iteration 2 (21%) as the indirect method at the 20% count level (19%), i.e., with quadruple the counts (Fig. 8a). This agreed well with the simulation results, for which the direct method gave V_T CoV of 21% at the 5% count level and the indirect method gave V_T CoV of 24% at the 20% count level. For [¹¹C]UCB-J (Fig. 8b), the direct method gives similar regional V_T CoV at iteration 2 (23% for the 5% count level, 17% for the 10% count level) as the indirect method does with double the counts (27% for the 10% count level, 17% for the 20% count level).

Figure 8.

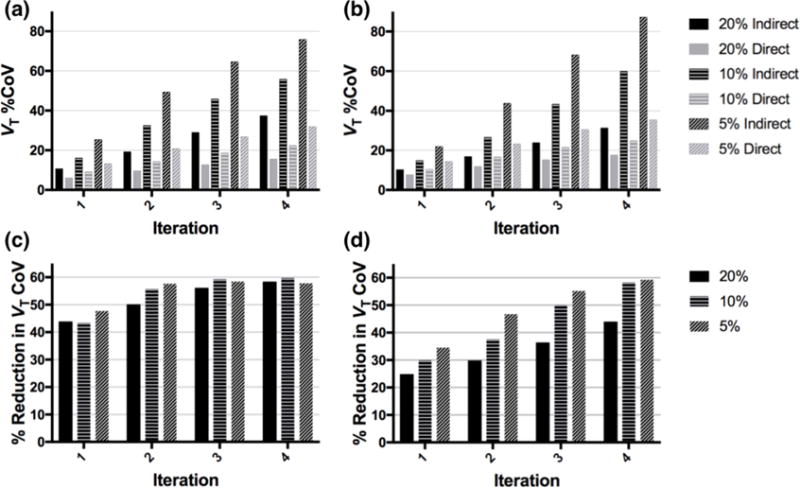
(a,b) Regional V_T %CoV (in the frontal cortex) by iteration and count level for the indirect and direct methods, for (a) [¹¹C]AFM and (b) [¹¹C]UCB-J. (c,d) Percent reduction in regional V_T CoV of the direct method relative to the indirect method, by iteration and count level, for (c) [¹¹C]AFM and (d) [¹¹C]UCB-J.

For the [¹¹C]AFM dataset, the advantage of direct reconstruction in terms of regional V_T CoV reduction, compared to the indirect method, is similar across count levels, for matched iteration (Fig 8c). In the [¹¹C]UCB-J dataset, the advantage of direct reconstruction is consistently greatest for the lowest count level, across all iterations (Fig 8d). The reduction in K₁ CoV of direct reconstruction compared to the indirect method followed similar trends (Supplemental Figure S6c,d). At iteration 2, the percent reduction in regional K₁ CoV in the frontal lobe between direct and indirect was 43–46% for [¹¹C]AFM and 30–36% for [¹¹C]UCB-J; the percent reduction in regional V_T CoV between direct and indirect ranged from 50% to 58% for [¹¹C]AFM, and 30% to 47% for [¹¹C]UCB-J. Similar results were obtained across other regions (Supplemental Figures S9 and S10).

4. Discussion

4.1 Summary

In this work, we demonstrate the application of direct reconstruction with event-by-event motion compensation to simulated and real brain PET data for two tracers with 1T kinetics, across multiple count levels. The primary outcome measure is distribution volume coefficient of variation, which is compared regionally between the direct and indirect methods. Both methods gave comparable regional estimates for K₁ across all count levels. The direct method produced more stable estimates of V_T across count levels. The direct method consistently gave parametric images with lower CoV than the indirect method.

4.2 Relative Advantage of Direct Reconstruction

While direct reconstruction yielded substantial improvements in CoV for both datasets, the benefit of direct over indirect was greater for the [¹¹C]AFM dataset than for the [¹¹C]UCB-J dataset. The [¹¹C]UCB-J dataset had double the counts of the [¹¹C]AFM dataset, which might contribute to the difference in performance. The weighted least squares fitting used in the indirect method assumes Gaussian noise in image space, which likely becomes a better approximation at higher counts, allowing the indirect method to achieve variance closer to the theoretical minimum.

The benefit of direct reconstruction over the indirect method in terms of parameter CoV, as determined in this study, falls within the range of those previously reported (e.g., see Figure 11 of [8]). However, a more thorough comparison of these results to those in the literature is difficult due to the dependence on tracer, model, parameter of interest, and count level, as well as the inclusion of other factors, such as randoms, scatter, and motion.

4.3 Motion

In previous work using PMOLAR-1T, as well as most other published studies on direct reconstruction, motion has been avoided or ignored. In our data, the parametric images from one of the two evaluated human datasets were not greatly affected by motion (9% increase in frontal lobe V_T with motion correction, compared to uncorrected), while those from the second were more severely affected (68% increase in frontal lobe V_T with motion correction, compared to uncorrected). Motion can have variable impact on parametric images, depending on motion magnitude, frequency, and time of occurrence. For instance, motion towards the end of an acquisition might be more likely to affect k₂ than K₁, because the early data has a larger impact on K₁ estimation, and the later data have greater sensitivity to k₂; this is consistent with the results from the [¹¹C]UCB-J study, which had a large motion an hour into the scan.

4.4 Outlying V_T Estimates

The primary outcome measure used here is V_T (=K₁/k₂), a measure of total tracer binding to the target. Because V_T is calculated as a ratio, it is prone to large outliers, and increasingly so at lower count levels. Note that in both indirect and direct methods, a fixed range for k₂ is established in advance, thus, V_T can be constrained by setting a relatively high lower bound for k₂, which would result in more visually appealing images. The k₂ images from direct reconstruction have much greater precision than those from the indirect method, so the distribution of k₂ values did not extend as close to 0 as in the indirect method, despite sharing the same imposed lower bound on k₂. Therefore, unlike the lower count indirect V_T images, the direct V_T images had very few outliers at any count level.

4.5 Stopping Iteration

To determine a stopping criterion for iterative reconstruction methods without regularization, it is common to estimate from simulations the iteration that, for instance, minimizes root-mean-square error, combining the effects of bias and noise. Such an approach was not viable for this application, because both CoV and regional bias in V_T increased with each iteration, for all count levels and methods. Moreover, biases at full counts were extremely small at iterations 1 and 2, suggesting that convergence had been reached, at least for the ROIs examined here. Also, we used subsets for computational practicality, so we cannot assess convergence with much granularity. While in some places we have used iteration 2 results as a reasonable stopping point, we do not present any formal stopping criterion for this work.

4.6 Sampling for Sensitivity Image Estimation

In routine reconstructions of HRRT data with MOLAR, in order to properly model continuous motion, the sensitivity image (Eqs. 2, 16, and 17) is determined by sampling LORs, and it is standard practice to use the same number of LORs for estimating the sensitivity image as events in the list mode file, in order to balance noise vs. computation time. Increasing LOR sampling affected indirect and direct V_T CoV equally. Iteration 2 regional V_T CoV decreases by ~15% for both methods at the 5% count level when the number of sampled LORs is quadrupled; regional V_T CoV decreases by 11% for both methods at the 10% count level when the number of sampled LORs is doubled (Supplemental Figure S11). Quadrupling (at the 5% count level) or doubling (at the 10% count level) the number of LORs sampled for estimation of the sensitivity image resulted in a ~20% decrease, in each case, in regional mean V_T at iteration 2 for the indirect method, reflecting a reduction in the magnitude of outliers. For the direct method, which did not produce many outlying V_T values, increasing the LOR sampling results in virtually no change in mean V_T. While increasing the LOR sampling for sensitivity image estimation can indeed reduce noise, the effect is modest, and much smaller than that gained from using direct reconstruction over indirect for matched conditions.

4.7 Limitations

One shortcoming of this work is the limited number of replicates reconstructed per condition. Because replicates were obtained by downsampling real list mode files, we were restricted to 5 (independent) replicates for the 20% count level. At the lower count levels, the decision to use only 5 replicates was driven by considerations for computational burden. The same approach was taken by Gravel and Reader [32] in a similar work evaluating direct reconstruction of binding potential images for raclopride PET. With so few replicates, voxelwise estimates of standard deviation will tend to be biased downwards (sample variances will be unbiased). However, comparing results generated by either 5 or 15 replicates for the simulated data at the 5% count level, we find that regional averages of the voxelwise V_T CoV estimates are not greatly affected by number of replicates (see Supplemental Fig. S12). At iteration 2, the V_T CoV in the frontal lobe was 12% greater when estimated with 15 replicates versus 5 replicates for the indirect method, and 7% greater for the direct method. Moreover, the pattern of CoV with respect to count level or method was not affected by the small number of replicates.

Because the low count replicates in this study are sub-sampled from real list mode datasets, the randoms rates are still consistent with full count acquisitions. True low count acquisitions would be expected to have fewer random events. Therefore, this approach represents a conservative estimate of performance at low counts.

Inaccurate model specification can cause propagation of bias from regions where the model does not fit, to regions where it should, when parametric images are generated by direct reconstruction [33]. The 1T model has been validated for use in both [¹¹C]AFM and [¹¹C]UCB-J, though some lack of fit was observed for [¹¹C]AFM in regions with relatively low binding [21]. If the regions with poor fits are indeed only those with low activity, the relative magnitude of the residuals due to lack of fit will also likely be low, and error propagation is expected to be minimal. For the full count datasets, there were no substantial differences in regional K₁ and k₂ values between the indirect and direct methods, suggesting that error propagation is unlikely to be significant.

The 1T compartment model is of course not suitable for modeling the kinetics of all tracers. In principle, the algorithm presented here can be easily extended to the two tissue compartment model by adding a dimension to the EM complete data space specifying compartment number (with an ordering constraint to enforce parameter identifiability), though convergence rate might suffer due to increased parameter correlations. This extension would be similar to what we have previously implemented for direct reconstruction of cardiac PET [34], for which two linear parameters were added to the 1T model to accommodate spillover from the right and left ventricles into myocardial tissue.

5. Conclusion

These results demonstrate the first use of event-by-event motion correction in the direct reconstruction of real PET data. The advantage of direct reconstruction over indirect was substantial at a given iteration and was similar or increased slightly with decreasing count level, as quantified by mean regional V_T CoV. Additionally, the direct method was more robust to outliers even at extremely low count levels, where the indirect method suffers from noise-induced bias. The advantage of direct reconstruction is substantial enough to permit greatly reduced doses, compared to what would be required for similar quality parametric images generated by the indirect method.