Abstract
Multiport catheters and catheters with a porous surface have been proposed for intraparenchymal infusions of therapeutics in fluid suspensions. Target diseases include brain cancer and serious neurodegenerative diseases, as well as peripheral tumors, for example in the prostate and the liver. We set up the theory for infusions from such devices, in particular the fluid flow equations which demand a coupling between the flow within the catheter and that in tissue. (Such a coupling is not necessary in the theory of infusion from single port catheters.) The new feature of such catheters, treated by our model, is revealed by infusions into inhomogeneous media. Multiport designs have the potential to overcome the limitation of single port catheters, for which the path of the fluid leaving the port is dominated by the inhomogeneities. We solve these equations for some simple cases to illustrate the key design features of porous catheters that show such advantages. The mathematics required for numerical solution with more realistic assumptions is also developed. We confirm the robustness of such catheters, when the ports are sufficiently resistive, against leakage paths that would compromise the infusions from catheters with one or a few large ports. The methods of this paper can be incorporated into a larger planning system for intraparenchymal infusions involving such devices.
1. Introduction
Direct infusion of drugs into the brain parenchyma using convection-enhanced delivery (CED) results in the treatment of large regions of tissue and concentrates the infusate therein, thereby circumventing the delivery obstacles posed by the blood-brain barrier and dilution of infusate in the blood [1]. CED is a technique that relies on pressure gradients to establish bulk flow over time, resulting in continuous convective flow and widespread distribution of the infusate in the brain. It has been used in several clinical trials including large volume infusions in brain cancer, with, however, the trials failing to reach their goals for successful introduction of the drug (see e.g., [2]). As that reference indicates, there is strong evidence that the failure to deliver the therapeutic dose to the intended target regions may alone be sufficient to account for the failure of efficacy (as measured by survival of the patient) in the trials, though of course the studies could not evaluate the efficacy of the drug. The point is that such efficacy could not be evaluated, being confounded by the inadequacy of the delivery. The mainstay for delivery device in these trials has been a simple end-port catheter, (see e.g., [3]) which has a single port of efflux. While there is no evidence to suggest that a better catheter would have resulted in a different outcome, there is a need to overcome some of the known limitations of such catheters. Without pretence at completeness, these include: (i) at high flow rates, excessive pressure may develope at one place (e.g., the tip) which may be undesirable in itself and also may result in deleterious backflow; and (ii) the placement of such catheters is rather critical since sinks, sulci, blood vessels are often in the proximity and act as siphons for fluid flow (this is further discussed at the end of the next section). In fact, when attempting a large volume distribution, the advance from a ‘point’ source may easily encounter such sinks. It may in fact be an advantage not to have a catheter that strongly limits backflow in such circumstances, as has been reiterated recently [4]. In any case, to overcome some of the limitations of such catheters, people have proposed multiport catheters, which, if the ports are large, have well-known pitfalls, namely a tendency for all the efflux to come out of one of the ports (see e.g., Figure 10 and accompanying text in [5] or, in a different context, [6]). These pitfalls are brought out by the mathematical model in this paper and are discussed further – see end of Section 3 and also later. Catheters with small pores, and porous membrane catheters (for the latter, see [7]), were proposed in part to overcome these limitations, and such catheters are the subject of this paper. In the next section we give some of the background and rationale for the introduction of such catheters with extended fluid sources. Following that, we first point out the characteristic resistances that determine the nature of the outflow from a simple discrete two-port catheter. Then we proceed immediately to a simple approximation for porous catheters that allow us to exhibit its behavior with just integrations of analytic expressions. The theory bears out the expectations and the considerations for design of such catheters. Apart from concluding discussions, we have also introduced appendices where we exhibit the expressions needed for a more exact treatment of such catheters. We also remark that we have only referenced non-standard or recent materials, which seems appropriate at the present time, when searches are easily performed. Thus for example, we use the phrase “Hilbert transform” without explanation or reference. That implies that entering these words into a search engine will easily retrieve an accurate description of the term.
2. Background
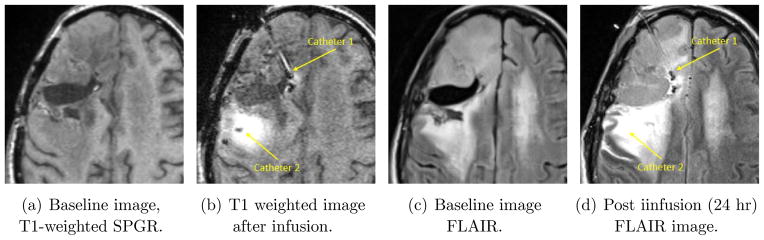
We recapitulate some of the reasons why one might consider catheters such as we are treating in this paper. However, we emphasize that the purpose of the paper is to develop a useful mathematical model for such catheters. Justification for the clinical use of such catheters must rely on experimental and empirical evidence and is beyond the scope of this paper. We mention in particular that the catheter is currently being considered only for acute infusions. (There is a well-known need for chronic infusions in brain disease as well [8], [9] but the current porous devices are intended for only 7 –day or less use with only intraoperative or implant indications and only after adequate testing of potential therapeutic occlusion.) As stated above, end port catheters have been used in human brain cancer patients. A representative example of the variability of infusions and the problems that can arise is shown in Figure 1. There are two pairs of images, obtained by different magnetic resonance imaging (MRI) sequences. A contrast reagent, Magnevist™, which shows up with high intensity in the two images – Figures 1(a) and (b) – comprising the first pair, was infused at a concentration of 1 mM (millimoles per liter) at a rate of for 24 hours from two catheters. Figure 1(a) shows a baseline image; while (b) is the image where the presence of the reagent shows up as high intensity. Little or no infusate is visible from the first catheter (in-plane) in tissue. (The second catheter is partially in-plane, with the tip more medial and inferior from the visible portion in this slice. A large distribution of tracer is visible around this catheter.) There are too many fluid spaces such as sulci and CSF regions near the site of infusion for effective distribution from the first catheter. Evidence for this assertion is provided by Figures 1(c) and (d). These are exactly the same time and space slices as the left pair, but the MR sequence used (called FLAIR) is sensitive to tracer in the cerebro-spinal fluid (CSF). The resection cavity shows leakage of tracer, with most of the infusate from the first catheter having leaked. Even when detailed guidelines are provided, such catheters provide inadequate delivery, as was discussed in the post-hoc analysis referred to [2]. Now, distributing large volumes in at least the hemisphere of the the brain where tumor is present has been a goal for a number of years in brain tumor therapies delivered intraparenchymally. More recently, an important need for improved delivery has emerged with the promise of disease-modifying therapies, such as small interfering RNA (siRNA)-based strategies, for neurodegenerative diseases such as Parkinson’s or Huntington’s.
Figure 1.
Infusion in human brain cancer (Dr. John Sampson’s laboratory at Duke University.)
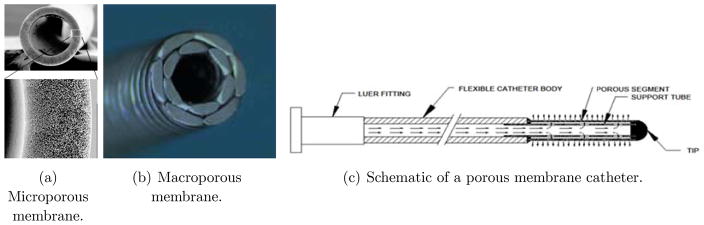
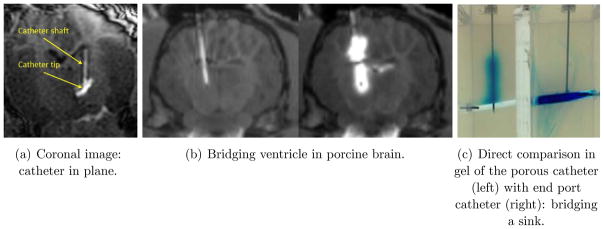
With either direct delivery of these molecules, or through an adeno-associated viral (AAV) carrier, there is an emphasis on global delivery of these agents to the brain. In these and other target diseases, current “point source” methods of delivery have limitations just described that limit their clinical utility without placement of a large number of catheters. People have therefore proposed multiport catheters to allow efflux from an entire length of catheter, and, in particular where a certain length of catheter is porous [7], which may be considered as a catheter with a very large number of small (and thus high fluid- resistivity) ports, and which is the principal subject of this paper. (We shall mention more conventional multiport catheters and their limitations in the next section. Also, methods such as laser drilling of holes or track-etching processes using heavy ion accelerators, both of which result in large numbers of small ports in a catheter – albeit smaller and more numerous for the etching process – are within the purview of our theories.) There are of course alternate designs for infusing larger volumes, such as an array of catheters that are deployed from a single point of entry (a modern version of this is being tested as the Cleveland Multiport Catheter™), or infusing along a trajectory as a single port is advanced or withdrawn (see [10] for a discussion of this: in any case this is not a useful method for large volume infusions where each infusion will be required to last many hours). Existing models for single port catheters suffice to simulate such designs. Our purpose here is to develop a model for porous catheters for which the model of the single port catheter does not suffice. Figure 2 shows views of both so-called microporous (a) and macroporous configurations (b). The port sizes are of the order of a 100 nm for the former, and of the order of several micrometers for the latter. A schematic layout of such a catheter is shown in the figure (c), where the length of the region containing the myriad of microports can be customized. The fact that a single port of efflux can result in the infusate being directed away from target because the flow encountered is illustrated in Figure 3 (a) which shows a coronal view (where the catheter is in-plane) at a particular instant of an in-vivo infusion in the thalamus of a pig brain conducted at the laboratory of Dr. Walter Block at the University of Wisconsin. (While not directly relevant to the phenomenon we are discussing, this was an infusion conducted at 1 μL min for 100 min (see [11] for the protocol used for this and related experiments). The infusate from the catheter, which happened to be placed near a blood vessel in the thalamus, is carried mostly out into CSF. On the other hand, in a porcine infusion conducted at the University of Virginia at the laboratory of Dr. Jaime Mata with the microporous catheter, Figure 3 (b), it may be seen that the catheter placed deliberately through a ventricle, infuses the tissue successfully on either side of the fluid sink. (This was an entirely different experiment: the infusion rate was ramped up from 1 μL/min to 6 μL/min for a total of 1 mL of infusate). This would not be possible with a single end-port catheter, although we did not do a control comparison during this study. Such a study was performed in vitro and is shown in Figure 3 (c). This is a direct comparison between such a catheter and an endport catheter and the the “bridging” property is displayed, though this time in gel, with bromophenol blue dye being the infusate for visibility. A fluid filled gap was created in gel, with the distal end of both catheters just penetrating tissue past the gap. The endport catheter immediately backflowed [12] into the gap and filled it. The porous catheter, on the other hand, distributes along its entire length. A small amount not easily visible does of course enter the gap, but the porous gel material is successfully infused. (Both infusions were performed at 5 μL/min for a total of two hours.)
Figure 2.
Porous membrane type catheters.
Figure 3.
The “bridging” effect: porous versus end-port catheters.
While it may be objected that careful planning allows trajectories not to bridge a ventricle, the points that we are emphasizing is that (i) a length of porous catheter obviates the need for infusing several times along a trajectory which in any case becomes impracticable as mentioned for large infusions; (ii) placement near blood vessels, sulci, and many other ‘siphons’ for flow is not always or even usually practicable even if ventricular traversal can be avoided; and (iii) in any case it can be argued that it is useful to have a device that is robust against such ‘errors’ in placement.
3. The two-port catheter
Below, we treat the porous catheter as the limit of a multiport catheter with a large number of ports of small diameter. To facilitate comparison with that limit, we shall first treat a two port catheter. The distal end of the catheter is in the negative portion of the z–axis, so that z increases vertically “upwards” as is conventional. We have chosen the position of the ports so that they will be symmetrically situated with respect to the ends of the porous length which we shall take below to extend from z = −L/2 to z = L/2. Thus the two ports will be situated at z = −L/4 (distal port) and at z = L/4 (proximal end). When we present numerical results, we shall considered a layered medium with two layers with very different fluid conductivities, one for z < 0, and another conductivity for z > 0: hence our choice of coordinates and positioning of the catheter so that the ports are always symmetrically situated with respect to the two layers. In the case of a uniform medium of course, the choice would be immaterial.
Denote Q =AV0 to be the flow rate through the catheter, where A is the internal cross-section of the catheter accessible to the fluid, so thatV0 is the incoming axial velocity. Let q1 = av1 be the outflow rate across the first port of cross-sectional area a with outflow velocity v1. For simplicity, we take the areas of all the ports to be equal, so that we don’t have to index these. Then, the axial flow speed past the first port isV1, with
| (1) |
Further, let us denote the pressure at the pump to be p0, and that at the first port be p1: the distance between these two positions is denoted L0. We thus also have
| (2) |
with Kcath being the hydraulic permeability (with dimensions of area) of the catheter. For a circular cylindrical lumen, this would be R2/8, from the equation for Poiseuille flow, while for a catheter with a stylet in place, it would be more appropriate to use the permeability for annular Poiseuille flow between two cylinders. With similarly defined quantities for the second and final port, we have
| (3) |
along with
| (4) |
Further, denoting the pressures in the tissue just outside the ports, in tissue, by corresponding capital letters,
| (5) |
where t is the width of the port and Kport its hydraulic permeability. Thus if we know the external pressures, we may solve for p0, p1, p2 from the above three different expressions (2), and the two equations in (4), upon using (5) for q1,q2. The remaining unknowns P1,P2 may also be determined from Darcy’s law in porous media if we know the medium properties. First, assuming the tissue conductivity is uniform, we get, by the method of images,
| (6) |
In a two layer medium we retain the symbol K for the tissue conductivity at the proximal port (at positive z). However, we confine our attention to the case where the distal port is facing fluid (infinite conductivity), as would occur if this port of the catheter were in the ventricle or a blood vessel. Then the pressures in tissue at the two ports for a double layer medium simplify to
| (7) |
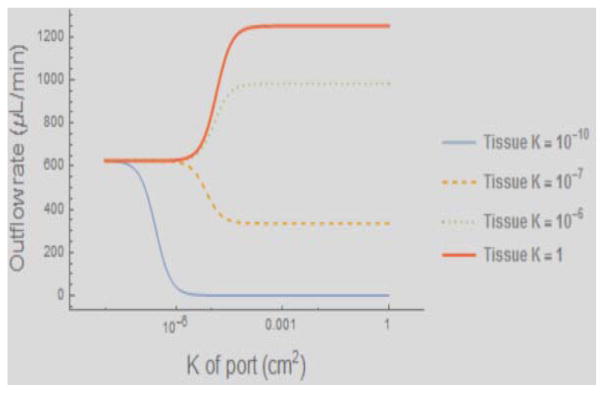
Equations (6) or (7) as the case may be substituted into equations (5) give us two equations for the four unknowns (the efflux rates q and the port pressures p at the two ports), while (3) substituted into the rightmost term in (4) give us two more, so we may obtain unique results for all the quantities concerned. Although these equations are linear and their solutions may be explicitly obtained, in Figure 4 we only show the plots of the outflow rates from the catheters, evaluated from (5) after substituting the solutions obtained for the pressures, by the above method. The interesting quantities are the outflow rates from the two ports, and a significant determinant of these is the resistance of the ports. So we plot the outflow from the port facing the tissue (the outflow through the other is just the total flow rate less the flow rate through the first port) as a function of hydraulic permeability of the port in cm2. The curves displayed are for the tissue permeabilities (the inverse of the resistivities) of 10−10, 10−7, 10−6, and 1, (cm2) respectively as shown in the legend. At the extreme left, all curves begin with the flows being balanced (equal out of each port) due essentially to the high port resistivity compared with any of the tissue resistivities used in the plot. The ideal case would be when all the graphs are horizontal: in that case the efflux would be uniform from each port no matter what the permeability of the tissue facing the ports. K refers to the permeability of the tissue. The total outflow rate is always 1250 microliters/minute, so the port not shown has efflux that is simply the displayed rate subtracted from the total. At the extreme left therefore (very high port resistance) the flow from the two ports are equal, despite the fact that one is in tissue, and the other in water. This modeling shows that for the lowest tissue permeability, there is equal flow out of both ports even though the second port faces fluid; however as the port resistance drops, the zero resistance of the fluid facing the second port wins out and there is no flow out of the first port. In contrast, if we consider the condition of low tissue resistance, while the beginning of the curve indicates equal outflow from both ports, the port facing tissue wins out even for low resistance ports (at least for the numerical values here chosen for the permeabilities). The reason now is that the tissue resistance is so low that the resistance of the catheter lumen sufficiently disfavors the second port, which is situated in our case further downstream of the flow within the catheter. Intermediate values of the tissue resistance display intermediate behaviors. There is thus a tissue resistance that balances with the lumen and port resistances so that equal outflow occurs from both ports. Thus, in general, we expect an interplay between these three kinds of resistances in determining the outflow rates. The clinical implication is that smaller pores will result in equal flow out of the pores, while large pore outflow is influenced by the position of the pore relative to the pressure source (proximal to distal on the catheter) and the hydraulic conductivity of the tissue adjacent to the pore. If all else were equal, one would opt for the highest port resistances. However, this has two deleterious consequences: the intraluminal pressures can be very high and can become dangerous to the mechanical integrity of the catheter components; and secondly, high resistances means very small pores, and the therapeutic particle may not be able to traverse through the ports into the tissue which it needs to treat. In practice, therefore, a compromise has to be made.
Figure 4.
Outflow from the port facing tissue in a two-port catheter, the other port facing fluid. The X-axis is the hydraulic permeability (inverse of the resistivity) of the port: high resistance is to the left (near the origin) and low resistance to the right. See text for detailed explanation.
4. The porous catheter
It is clear that the above equations can be generalized to any number of ports (for a specialized case for these where however the external pressures are assumed to be known, see [13]). However, both as a practical matter (since the parameters of all the ports will not be available) and for theoretical convenience, we shall proceed to a continuum limit that obtains when the number of ports increases without limit while the size of the ports decreases and a certain quantity (see below) has a finite limit. We expect that this would be a good approximation with a sufficiently large number of small diameter ports. The basic geometry of this catheter has already been described above. The problem of laminar flow in a tube or channel with porous walls and with suction or efflux through these walls has been the subject of a rich literature with some remarkable phenomena that occur [14]. For numerical evaluation, we shall take the parameters to be as in Table 1. The equations needed to describe simple outflow from an array of ports can be immediately written down from the above two-port case. The symbols Q, A, a, t, Kport, and K retain their meanings from before (see also Table 1). So, for simplicity, we assume all the ports are identical. We denote the cross-sectional-averaged fluid velocity within the lumen of the catheter, and at a point z along its axis, as V (z). As mentioned before, the distal end (next to the tip, see Figure 2(c)) of the porous length is at z = −L/2 while the proximal end is at z = L/2. The end of the tube is closed. Further notation: let the ports be numbered i, ranging from 1 to N, and let their centers be at z = Li, and the average fluid speed across a port entering tissue is denoted vi. We also denote the distances between the centers of the ports directly below one another along the axis to be Δ and all uniform.
Table 1.
Parameter values for theoretical calculations.
| Symbol | Meaning | Value | |
|---|---|---|---|
| r0 | Inner radius of catheter | 0.03 cm | |
| rc | outer radius of catheter | 0.045 cm | |
| w | diameter of stylet | 2 × 0.02 cm | |
| K | hydraulic permeability of tissue | 10−9 cm2 | |
| L | length of porous region of catheter | 5 cm | |
| Q | total flow rate out of catheter | 1.25 mL/min | |
| η | viscosity of fluid (water) | 0.01@25C dyne – sec/cm2 | |
| A | (internal) area of catheter lumen | 0.096 mm2 | |
| Kcath | hydraulic permeability of catheter lumen | 0.038 mm2 | |
| Λ | boundary value (see text) |
|
Then, from Darcy–type laws arising directly from Poiseuille flow,
| (8) |
In the second of the equations, δpi is the pressure drop P – p between the pressure P in the tissue facing the port and the pressure p within the catheter just inside. We denote V (z) at port i by Vi. In the region between pump and the first port, the average velocity of fluid flow for a fixed flow rate Q is constant, say V0. We thus have
| (9) |
Denote
| (10) |
and its continuum limit, q(z). Subtracting equation(9) from a similar one for i+1, and replacing Vi by its discretized Darcy expression from (8), taking Δ → 0, and setting the ambient pressure outside the catheter in the fluid to be P (z), we get
| (11) |
Since the efflux via from the ports goes like 1/N, and thus taking the limit N → ∞ as well, we must have a finite non-zero limit for
| (12) |
| (13) |
At z = L/2, we know that V0 = −Q/A in the direction of increasing z, so
| (14) |
and the second boundary condition holds since all the fluid has exited out of the catheter by there.
Consolidating we have
| (15) |
where the positive parameter λ is defined to be
| (16) |
along with the boundary conditions (14). We emphasize that this is a continuum limit of the case of discrete ports and so holds only if the conditions noted above are satisfied. The general solution for p is
| (17) |
with C1 and C2 being the integration constants evaluated by imposing (14). We select the lower limit for the integral to be z = −L/2. The value for λ has to be obtained from other considerations (see below), but since it depends on the catheter construction, it does not change according the boundary conditions. The equations for C1, C2 are explicitly
| (18) |
| (19) |
We now look at some special cases. In case P (z) = 0 everywhere (e.g., if there is only fluid outside the catheter), this gives
| (20) |
We proceed as for the two-port catheter to solve for the more general case where there is a medium with known hydraulic permeability outside. We shall present numerical results for two simple cases. One for a uniform medium, and the other for a two layer medium where the distal half of the catheter faces pure fluid. The mathematics required for computing the pressure in tissue due to outflow at a rate q(z) per unit length from a cylinder of finite radius is complicated. We give the method in Appendix A but defer its numerical implementation for later. To show the qualitative phenomena however, we may adopt the model of a thin wire rather than that of a cylindrical catheter surface of non-zero radius, taking care to evaluate the resulting expressions only for radial distances from the wire larger than the catheter radius (i.e., for r > rc). In that case the solution are standard from analogous problems in electrostatics and we may write the pressure outside the catheter in a uniform medium, subject to the boundary condition that the flow is radially out into the medium, as
| (21) |
| (22) |
for r > rc, which is the convolution of the kernel shown with the flux density q(z)/(4πK/η). For the rest of this paper we shall set α = 0 which means we are neglecting any efflux of water out of the tissue due to capillary losses, ductal systems etc. If we need to consider these, then we shall have to include the exponential in the kernel. However, to highlight the special features of such catheters, it is simpler to neglect this for the present.
We now have equations for the internal and external pressures at the catheter (at least for a uniform medium): (17) and (21) along with (15). Abstractly we can write
| (23) |
where L1,2 are linear integral operators that do however also depend on λ as can be seen from their defining equations. The solution for p for example is formally
| (24) |
A solution method that suggests itself is to write (1 − x)−1 ~ 1 + x + x2 + ···, or by iterating the pair of equations in (23). Viewed this way it is clear that large λ (or, rather, large λL which is dimensionless) poses a problem since the mappings back and forth may fail to be contractions and hence may not result in a convergent solution. We have not conducted a mathematical investigation of these equations, but proceed to show solutions constructed by iteration, where they clearly converge, and we shall make remarks on large λ further on.
Uniform medium
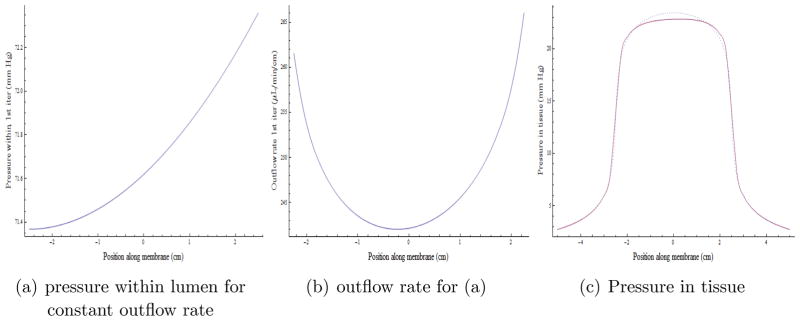
First, we consider the case where the flow rate out of the catheter is uniform: q(z) = const = Q/L, 0 ≤ z ≤ L and zero otherwise. This gives us the external pressure P(z) along the catheter as we have already seen in equation (21). Then we can use this to compute the integration constants from (18),(19). This allows us to compute the pressure inside the catheter from (17), which in turn allows us to compute the flow rate from (13), using (15) for the second derivative of the pressure. This process may then be iterated. If the mappings (17) and the composite mapping (15) followed by (21) are contractions, we may hope for convergence from this iteration. The results are shown in Figure 5. The outflow is reasonably uniform along the length. Assuming a constant flow rate per unit length throughout the porous length, the pressure in the tissue is shown as the dotted curve in (c) of the figure. The solution for the internal lumen pressure from equation (17) then is plotted in Figure 5 (a), which in turn determines a revised outflow rate plotted in (b). We see that the outflow rate is fairly uniform but not constant (for the parameter values chosen, see Table 1); and this outflow rate can in turn be used to calculate a new pressure in the tissue in the second iteration: this is plotted as the solid curve in (c). We see that it is quite close to the starting curve, and we expect that the iteration is already close to convergence. We have checked this.
Figure 5.
Iterative solution for the pressure and flow from a porous membrane catheter for uniform tissue outside. The fluid is entering the catheter from the positive (right) side. Pressure within the lumen (a) and outflow (b) are fairly constant along the length of the catheter (+2.5 to − 2.5) and falls off quickly proximally and distally in the 10 cms of the abscissa shown in (c).
Two layer medium
For different hydraulic conductivities in tissue at the ports, K+, K−, say, where the interface is at z = 0, we can show, by the method of images, that the pressure in the tissue is given by
| (25) |
We should mention that the above formula is correct only for a two layer system, so K(z) = K± according to whether z > 0 or z < 0. We chose K = 10−9 cm2 in the upper layer, a reasonable value for brain tissue. We choose the lower layer to be water with a formally infinite hydraulic conductivity. This immediately gives the pressure for negative z to be zero. The reason is that Darcy’s law is a reduction of the equations of viscous flow near solid surfaces when the only effect of the viscosity is at the interface: the viscosity of fluid in the bulk plays no role. Thus even with outflow, there is no pressure gradient in the bulk fluid. This is of course incorrect, but qualitatively does not make much difference due to the very high resistivity of the porous medium in comparison. In any case if we let K− → ∞, the prefactor in the second term is just −1 for z > 0, the only region where (25) needs to be evaluated. It should also be noted that the range of the integral is only from ζ = 0 to L/2: when |ζ| > L/2, q is zero (no ports), while in this particular case since P is evaluated (and is non-zero) only for z ≥ 0, the second fraction for ζ ≤ 0 is the same as the first, and cancels with it because of the negative sign. Of course, all these just noted simplifications occur only in this particular case due to the singularity of the fluid conductivity in the lower layer.
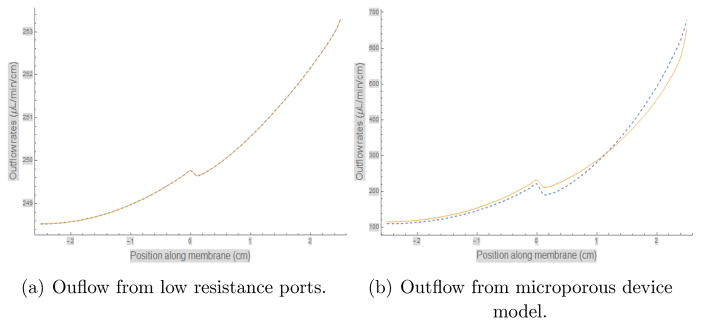
In Figure 6(a), we show two iterations of the outflow rate (beyond the zero’th where we assume it to be a constant) for the case λL/2 = 0.1, a value small enough to hope for convergence. Indeed the two iterations (dotted for the first and a solid line for the second) are indistinguishable. Note that the range of the ordinate is very small and the flow rates are essentially uniform with a small variation around the mean of 250 μL/min/cm of porous length. This is quite remarkable considering that the lower layer is water with infinite conductivity. To get a feeling for the value of this for catheters that have been made, we use some unpublished data from infusions in water where the outside pressure can be set to zero, and the pressure at the pump for a given flow rate was observed. We can then use equation (20) for the lumen pressure, neglecting the small pressure differential due to the tubing and lumen from the pump to the proximal end of the porous catheter. Using the internal diameters of the catheters and other known parameters such as the radius of stylets used during the infusion, we obtained λL/2 ≃ 1.325 and 6.55 for the micro- and macro-porous catheters, respectively. The results for the outflow after iterating for the microporous catheter is given in Figure 6(b). The figure (b) shows that while there is certainly loss into the fluid, there remains substantial flow into the tissue (the positive z portion of the X –axis). The flow rate however shows considerably more variation now. The two iterations are still close together, and so demonstrate convergence of the iteration scheme mentioned. On the other hand our iteration scheme does not work for the macroporous catheter: the ports are of such low resistance that fluid is actually sucked in from the tissue and ejected into the fluid. We hope to report on more robust numerical methods later, but there is a physical basis to this behavior as well, namely the low resistance of the catheter can lead to very sub-optimal behavior. It has been previously shown (see, e.g., examples shown in [15]) that multiport catheters with large ports often have an “all or nothing” behavior even when the variation in conductivity of the tissue or gel medium is minimal.
Figure 6.
Outflow rate computation in two layer media. Two iterations of the outflow rate beyond the starting assmption of uniform flow using the method described in the text are shown in (a) and (b): the dotted one is the first and the solid line the second iteration. The iterative method is useful for the case where there are a large number of small ports, and is described by a dimensionless number described in the text. In (a) this number was chosen to be 0.1, while (b) is the number appropriate for the microporous catheter, which turns out to be > 1. However the iterations still converge well for this device.
5. Suction and fluid removal
In the above discussion we have focused on acute intraparenchymal infusions into the tissue. Following an initial evaluation of membrane dialysis as a method of fluid removal, [16], such porous catheters have also been proposed for this purpose [17], [18], [19], [20]. We emphasize again that our purpose is to indicate how the model might be used for reversed flow, but consideration of blockage and other such potential problems is beyond the scope of this paper. The model may be used in calculations only if we assume there is no blockage. If we simply reverse the sign of the flow, we will obtain exactly the same solution as shown above, albeit with negative pressure (with respect to the CSF pressure, say). However, when using the device for such a purpose we cannot set the flow rate, but rather we run it with a specified negative pressure at the pump, say pA where pA is negative with respect to resting interstitial tissue pressure (which, rather than atmospheric pressure, has throughout been taken to be zero). If the pump pressure is set at z = A > L/2 (since it is the length that reaches up to L/2, and there is a further length of tubing that reaches to the pump), that means simply that we replace the first boundary condition of the pair in (14) with
| (26) |
the second in that pair remaining the same. The second term on the left hand side is the small drop of pressure in the length between pump and the beginning of the porous length, and can usually be neglected. We have verified that the same iteration process as above encounters no difficulties in similar cases, so we omit displaying the curves that result, since they are qualitatively as before. The theory above is adequate to deal with fluid removal with negative pressure but we should mention that the inventors of the porous device now favor a different approach to fluid removal from brain tissue, see [21], [22].
6. Conclusions
We have provided the theoretical framework for computing the behavior of infusions from both discrete multiport catheters (already contained in part in [13]) as well as a continuum limit which allows us to examine porous catheters. Without this limit, a simulation would demand detailed knowledge of the geometry of the pores, an essential impossibility. This is the first treatment of such devices and applications as far as we know. The computation demands that we calculate also the fluid flow and pressure within the lumen of the catheter. We have illustrated simple cases of the performance of such catheters: full implementation of the calculational scheme in an extension of our approach to simulations of fluid and particulate flow in tissue [23] is under way at the time of this writing. We have also shown that the same method can also be used for the use of such catheters in fluid removal. In addition, the appendices below describe (i) the substantial extension required to treat the catheter body as a finite radius cylinder, confirming the model used in the main body of the paper in the suitable limit of small radius; and (ii) an approach to treating backflow at the same level of approximation as the previous simple model developed for single port catheters [12]. While the class of problems encountered fall within the rubric of potential theory in classical physics such as electrostatics, the details differ and the particular geometries and boundary conditions have not been treated before, again as far as we know (see also Appendix 1). Our calculations confirm the expectations of the inventors of such devices [7], namely that they significantly ameliorate the “all or nothing” behavior seen so often in single port catheters (and discussed above), and that the fluid resistivity of the ports of the catheter relative to that of the tissue plays a critical role in ensuring the superior performance of such devices when faced with tissue of varying resistivity. Such behavior is of particular advantage in large volume infusions, where one can infuse simultaneously from a large surface (over the length of the porous region of the catheter) as opposed to a single port. Studies of precisely such infusions are being concluded at the present time in a separate project, and the results will be reported upon. It is also obvious from the formulas in this paper (and as has been checked with the numerical simulations) that the pressure at any point of tissue facing the catheter is correspondingly smaller than from a single port infusing at the same total rate, since the pressure here is distributed over a much larger surface area. For high infusion rates, this could also be of advantage.
In previous work [23] we have described a patient-specific planning system for targeted drug delivery and argued [24] for its importance in helping ensure effective delivery, and by extension, in helping the success of clinical trials and administration of such therapies. The models of infusions hitherto have been restricted entirely to single port catheters. The treatment here allows one to extend the modeling to multiport and porous catheters, and to extend the range of planning systems to these. We hope to incorporate these advances into the next generation of mathematical models and software for planning CED to infuse large volumes of therapeutic solutions into brain, liver and other tissue.
Acknowledgments
The research described in this paper was supported by grant number R44RDK085810 of the National Institutes of Health of the U. S. A., with Jim Stice of Twin Star Medical (TS) as Principal Invesigator. We thank him for making the funds available and for encouragement. The second author RMO is a founder of TS, and he and the company have a commercial interest in the device and its applications. The first author RR has no conflicts to report concerning this research.
Appendix A. Outflow from a cylinder
The purpose of this appendix is first, to describe the mathematics required to compute the pressure distribution in tissue for a specified outflow rate from a length of catheter which is a cylinder of non-zero radius, and secondly, to show that the wire model we have used in the main text results by taking suitable limits for the expressions put forth here. In addition, we indicate an iteration scheme for solving the equations for the finite radius catheters beginning with the limiting case of zero radius. The setup of the problem belongs to the venerable tradition of the “methods of mathematical physics” [25], and to applications of potential theory to physics, but the particular geometry and boundary conditions are not available in the classical texts.
We now reset the distal closed end of the catheter at z = 0. It was convenient in the main body of the paper to set that at z = −L/2 since we wished to display results for when half the catheter was in fluid and half in tissue. Here, our treatment is general, and it will be simpler to choose the origin of the axes at the distal catheter end. As before places with negative z coordinates are entirely in tissue while the catheter shaft is along the positive z axis. Our starting point is the porous flow equation in cylindrical coordinates with azimuthal symmetry assumed in the wire model,
| (A.1) |
where α has been defined earlier, equation (22). For simplicity we set this to zero here as well, although the following development goes through with its inclusion. Separable solutions of the form
| (A.2) |
will then lead to
| (A.3a) |
| (A.3b) |
for some constant k independent of the coordinates. Let the semi-infinite catheter of outer radius rc occupy the half space z ≥ 0, the space z < 0 being open. The solution to Laplace’s equation must exist in the region I ⊕ II where
| (A.4) |
| (A.5) |
In region I the asymptotic condition at infinity, namely that the pressure approaches zero (though a constant will do if it would be convenient for us to have zero solutions at other locations), implies rejecting the growing exponentials exp (|kz|) and I0(|k|r). This means that in region I we can take the solution to be of the form exp (ikz) K0(|k|r), using real k, which would form a complete set of solutions satisfying the boundary condition at infinity. In region II we demand regularity at r = 0 and finiteness as z → −∞, thus limiting ourselves to solutions of the form exp (|k|z) J0(kr) or exp (ikz) I0(|k|r).
Consequently, in region I we posit the solution
| (A.6) |
subject to the Neumann boundary condition specifying the outflow rate for z > 0
| (A.7) |
where H(z) the Heaviside, or unit step, function
| (A.8) |
and the other symbols have the same meaning as in the text. (The value at z = 0 is chosen between 0 and 1 according to convenience.) We are also employing the following notation for any function g
| (A.9) |
At the closed base of the catheter, z = 0 and r < r1, we invoke Neumann boundary conditions.
| (A.10) |
We then posit
| (A.11) |
with the coefficients required to satisfy
| (A.12) |
Since I0(|k|r) is an even function of k, this requires β̃(k) to be an even function of k with β̃(0) = 0. (We do not need the form of solution expressed by the J0–type Bessel functions, due to the homogeneous boundary condition at the end cap appropriate to the type of catheters we are treating here: had there been a non-homogeneous condition of either Dirichlet or Neumann type, then we would need to augment the forms chosen with products of first kind Bessel functions and real exponentials. These would be used to satisfy the inhomogeneous boundary condition, while the rest of the approach below would continue to hold, with the appropriate modifications.) To obtain the solution of Laplace equation valid everywhere for z < 0, the solution should be continuous at a boundary and its gradient have the requisite discontinuity determined by the boundary. But the boundary between regions I and II is purely fictitious (mathematical), hence demanding the continuity and differentiability of the solution at that boundary renders it a regular solution of the Laplace equation. One can observe this directly from eq. (A.1), as well. Continuity and differentiability of p at r1 would make the ∂rp and terms equal for pI and pII at the boundary, so that the Laplace equation would render continuous at that boundary as well. Applying an analogous argument while taking higher derivatives of eq. A.1 would render higher derivatives of the solution continuous at the boundary as well, thus guaranteeing a regular solution. The continuity and differentiability of the solution at the I/II boundary is expressed via
| (A.13) |
| (A.14) |
The first of these equations is satisfied by setting
| (A.15) |
The Fourier transform of H(−z) g(z) is and conversely, where ℋ denotes the Hilbert transform, so the Fourier transform of the second equation reads
| (A.16) |
Substitution of α̃(k) from the previous equation results in an inhomogeneous singular integral equation for β̃(k). This is a form of integral equation that has received attention in the literature, and, in general, there are numerical schemes available to solve such equations. We shall not pursue solution of these equations here, although the iterative approach we describe below could also be used with this equation, but we note that in the limit the catheter approaches an infinitely-thin semi-infinite wire, region II disappears and the full solution is given via eq. (A.6), i.e.
| (A.17) |
the second equation coming from the convolutional property of the Fourier transform and the fact that the Fourier transform of in k is . Strictly speaking, even with this wire approximation, we should solve the Neumann boundary condition at the catheter radius, namely
| (A.18) |
for a. This too is a singular integral equation. In the main text, we further simplified the approach by noting that
| (A.19) |
becomes a delta function in the limit r →0, since
| (A.20) |
This is also apparent from the Fourier transform from which Δ(z, r) was derived, namely
| (A.21) |
and the fact that
| (A.22) |
So that taking this limit we obtained simply
| (A.23) |
which is the approximation we have used in the text: equation (21) with α set to zero. However, we show that this is a reasonable approximation by proposing a series solution for the integral equation (which, as we remarked, may also be used with the more difficult integral equation for the finite cylinder above). If we define the convolution operator in the z variable as
| (A.24) |
then
| (A.25) |
where r = r1 is assumed, needs to be solved for a Now define
| (A.26) |
Thus eqs. (A.25) and (A.26) imply that
| (A.27) |
must be solved for a where we recall that a = a+. Defining the operator ℒ through the relation
| (A.28) |
we see that
| (A.29) |
Other than using standard methods to solve for this integral equation, we could also attempt a series solution for a assuming that the norm of the operator ℒ < 1:
| (A.30) |
with
| (A.31) |
and so on. By definition of the operator ℒ in eq. (A.28) and W+ being non-zero only for z > 0, it is clear that the series solution in eq. (A.30) respects this property for the resulting a, i.e. a = a+ as well. In order to examine the convergence of the series, we consider the expansion of the Bessel function:
( is the digamma function.) The Fourier transform in z of the kernel Δ is
| (A.32) |
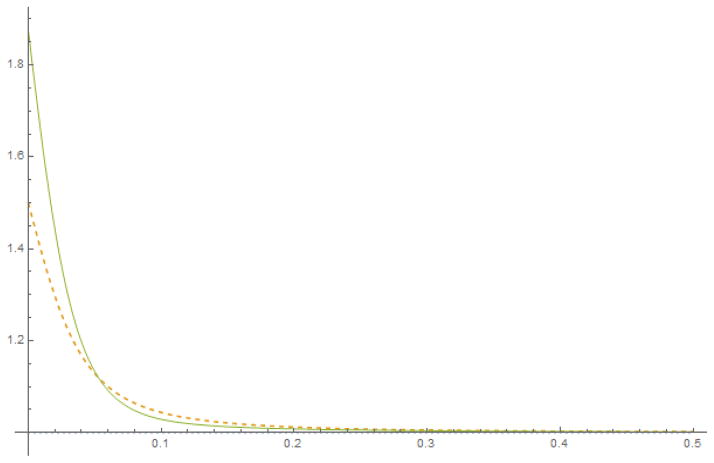
so that the term (Δ1 * W) is the Fourier transform of . So is at most 𝒪(r2|k|2). We can then confine ourselves to the first few terms of the series expansion if is principally confined to long wavelengths, in particular compared to the catheter radius. We show two iterations in the figure, showing excellent convergence outside of the end: it should be noted that the curve is symmetrical around the mid point of the porous length, and only one end of it is shown. We leave such explorations to the future.
Figure A1.
Iterating the integral equation
Appendix B. Backflow
In the treatment of multiport catheters in this paper, we have ignored backflow. In general for the flow rates encountered, there is little flow beyond the extent of the porous length itself, particularly when the latter is large. As mentioned in the Introduction, there is a priori an argument to be made for having a larger length of porous catheter for infusing large regions, so that in applications where this catheter is particularly advantageous, this length can be several centimeters. Nevertheless, it may be useful to indicate, following the theory of our earlier paper, how backflow may be computed in the present model. This appendix is not self-contained, and relies on an understanding of backflow and how to model it as discussed in [12]. In the simplest model for backflow, which we called the NIH model for sound historical reasons, there were a pair of equations to be solved for Q, p where Q was the flow rate up the catheter, in the thin annular fluid-filled layer surrounding the catheter, and p is the pressure at the boundary of the catheter that drives flow into the tissue. In the current treatment, we have used the quantities q(z) to be the flow per unit length radially outward from the catheter, and P to be the pressure at the catheter surface. (We have used the lower case p to be the pressure, and similarly we used Q to denote the flow, within the catheter lumen itself.) Let us therefore denote Qb to be the flow rate on the outside flowing up the catheter. Furthermore, the radially outward flow in the treatment above was equal to the flow coming in through the port, which is no longer the case. So let us now denote the flow into the port to be qin, i.e., qin in is defined to be the right hand side of the first equation in (15). We then have
| (B.1) |
Therefore we may proceed with the backflow theory as outlined previously. There are now five unknown functions of z, in contrast to the two for the simpler endport case, namely, (omitting the argument z), p, qin, q, P and Qb. The relation between (what is now denoted) P and Qb for Poiseuille flow is as before, see equation (6) in [12] – with the notational replacements noted – while the pressure P is computed as a function of q as shown in the present paper. The internal pressure p in the lumen which determine q, has also been described in this paper. Finally, the fourth equation we have is (B.1), and we may numerically compute the four functions from these four equations. The final backflow obtained will be subject to similar limitations as described in [12], except that the most important of these limitations, namely, that for the pressure in the tissue along the catheter length has been correctly described here. We hope to develop this computation in the future, though in practice, very little backflow has been observed for the infusion rates employed in experiments so far. The reason for this is undoubtedly the smaller pressure over any unit surface area (as mentioned in the Conclusions above) with corresponding reduction in the backflow that would otherwise result.
References
- 1.Bobo RH, Laske DW, Akbasak A, Morrison PF, Dedrick RL, Oldfield EH. Convection–enhanced delivery of macromolecules in the brain. Proceedings of the National Academy of Sciences U S A. 1994;91:2076–2080. doi: 10.1073/pnas.91.6.2076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sampson JH, Archer GE, Pedain C, Wembacher-Schroder E, Westphal M, Kunwar S, Vogelbaum MA, Coan A, Herndon JE, Raghavan R, Brady ML, Reardon DA, Friedman AH, Friedman HS, Rodriguez-Ponce I, Chang S, Mittermeyer S, Croteau D, Puri R. Poor drug distribution as a possible explanation for the results of the PRECISE trial. Journal of Neurosurgery. 2010;113:301–309. doi: 10.3171/2009.11.JNS091052. [DOI] [PubMed] [Google Scholar]
- 3.Raghavan Raghu. Intraparenchymal delivery and its discontents. Neuromethods. 2010;45:85–135. Issue title: Drug Delivery to the Central Nervous System. [Google Scholar]
- 4.Bankiewicz Krystof S, Sudhakar Vivek, Samaranch Lluis, Sebastian Waldy San, Bringas John, Forsayeth John. AAV viral vector delivery to the brain by shape-conforming MR-guided infusions. Journal of Controlled Release. 2016;240:434–442. doi: 10.1016/j.jconrel.2016.02.034. [DOI] [PubMed] [Google Scholar]
- 5.Raghavan Raghu, Brady Martin L, Rodriguez-Ponce Maria Inmaculada, Hartlep Andreas, Pedain Christoph, Sampson John H. Convection-enhanced delivery of therapeutics for brain disease, and its optimization. Journal of Neurosurgery. 2006;20:1–13. doi: 10.3171/foc.2006.20.4.7. [DOI] [PubMed] [Google Scholar]
- 6.Campolo M, Molin D, Rawal N, Soldati A. Protocols to compare infusion distribution of wound catheters. Medical and Engineering Physics. 2012;34:326–332. doi: 10.1016/j.medengphy.2011.07.033. [DOI] [PubMed] [Google Scholar]
- 7.Oh S, Odland RM, Wilson SR, Kroeger KM, Liu C, Lowenstein PR, Castroad MG, Hall WA, Ohlfest JR. Improved distribution of small molecules and viral vectors in the murine brain using a hollow fiber catheter. Journal of Neurosurgery. 2007;107:568–577. doi: 10.3171/JNS-07/09/0568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bienemann A, White E, Woolley M, Castrique E, Johnson DE, Wyatt M, Murray G, Taylor H, Barua N, Gill SS. The development of an implantable catheter system for chronic or intermittent convection-enhanced delivery. Journal of Neuroscience Methods. 2012;203:284–291. doi: 10.1016/j.jneumeth.2011.10.002. [DOI] [PubMed] [Google Scholar]
- 9.Lewis Owen, Woolley Max, Johnson David, Rosser Anne, Barua Neil U, Bienemann Alison S, Gill Steven S, Evans Sam. Chronic, intermittent convection-enhanced delivery devices. Journal of Neuroscience Methods. 2016;259:47–56. doi: 10.1016/j.jneumeth.2015.11.008. [DOI] [PubMed] [Google Scholar]
- 10.Sillay K, Hinchman A, Kumbier L, Schomberg D, Ross C, Kubota K, Brady M, Brodsky E, Miranupuri G, Raghavan R. Strategies for the delivery of multiple collinear infusion clouds in convection-enhanced delivery in the treatment of Parkinson’s disease. Stereotactic and Functional Neurosurgery. 2013;91:153–161. doi: 10.1159/000345270. [DOI] [PubMed] [Google Scholar]
- 11.Emborg ME, Joers V, Fisher R, Brunner K, Carter V, Ross C, Raghavan R, Brady M, Raschke J, Kubota K, Alexander A. Intraoperative intracerebral MRI-guided navigation for accurate targeting in non-human primates. Cell Transplantation. 2010;19:1587–1597. doi: 10.3727/096368910X514323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Raghavan Raghu, Mikaelian Samuel, Brady Martin, Chen Zhi-Jian. Fluid infusions from catheters into elastic tissue I: azimuthally symmetric backflow in homogeneous media. Physics in Medicine and Biology. 2010;55:281–304. doi: 10.1088/0031-9155/55/1/017. [DOI] [PubMed] [Google Scholar]
- 13.Raghavan Raghu, Poston Timothy, Viswanathan Raju. Drug delivery and catheter systems, apparatus and processes. 6,464,662. United States Patent. Issued October 15, 2002.
- 14.Berman Abraham S. Laminar flow in channels with porous walls. Journal of Applied Physics. 1953;24:1232–1235. [Google Scholar]
- 15.Bauman MA, Gillies GT, Raghavan R, Brady ML, Pedain C. Physical characterization of neurocatheter performance in a brain phantom gelatin with nanoscale porosity: steady-state and oscillatory flows. Nanotechnology. 2004:92–97. [Google Scholar]
- 16.Odland Rick M, Umeda Alvin, Stevens Scott, Heinrich James, Rowe Mark. Reduction of Tissue Edema by Microdialysis. Archives for Otolaryngology and Heand and Neck Surgery. 1995;121:662–666. doi: 10.1001/archotol.1995.01890060060012. [DOI] [PubMed] [Google Scholar]
- 17.Odland Rick M, Rheuark Daryl, Ispirescu Scott, Kizziar Ron. The effect of capillary ultrafiltration probes on skin flap edema. Otollaryngology - Head and Neck Surgery. 2002;128:210–214. doi: 10.1067/mhn.2003.69. [DOI] [PubMed] [Google Scholar]
- 18.Odland Rick M, Scott Panter S, Rockswold Gaylan L. Effect of tissue ultrafiltration on skin flap survival. Journal of Neurotrauma. 2004;131:296–299. doi: 10.1016/j.otohns.2004.03.005. [DOI] [PubMed] [Google Scholar]
- 19.Odland Rick M, Schmidt Andrew H, Hunter Brian, Kidder Lou, Bechtold Joan E, Linzie Bradley M, Pedowitz Robert A, Hargens Alan R. Use of Tissue Ultrafiltration for Treatment of Compartment Syndrome. Journal of Orthpedic Trauma. 2005;19:267–275. doi: 10.1097/01.bot.0000155308.20133.71. [DOI] [PubMed] [Google Scholar]
- 20.Odland Rick M, Schmidt Andrew H. Compartment Syndrome Ultrafiltration Catheters: Report of a Clinical Pilot Study of a Novel Method for Managing Patients at Risk of Compartment Syndrome. Journal of Orthopedic Trauma. 2011;25:358–365. doi: 10.1097/BOT.0b013e3181f9aba9. [DOI] [PubMed] [Google Scholar]
- 21.Odland Rick M, Scott Panter S, Rockswold Gaylan L. The Effect of Reductive Ventricular Osmotherapy on the Osmolarity of Artificial Cerebrospinal Fluid and the Water Content of Cerebral Tissue Ex Vivo. Journal of Neurotrauma. 2011;28:135–142. doi: 10.1089/neu.2010.1282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Odland Rick M, Venugopal Sandya, Borgos John, Coppes Valerie, McKinney Alexander M, Rockswold Gaylan, Shi Jian, Panter Scott. Efficacy of Reductive Ventricular Osmotherapy in a Swine Model of Traumatic Brain Injury. Neurosurgery. 2012;70:445–455. doi: 10.1227/NEU.0b013e318230ee5e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Raghavan Raghu, Brady Martin. Predictive models of pressure-driven infusions into brain parenchyma. Physics in Medicine and Biology. 2011;56:1–26. doi: 10.1088/0031-9155/56/19/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Raghavan Raghu, Brady Martin L, Sampson John H. Delivering therapy to target: improving the odds for successful drug development. Therapeutic Delivery. 2016;7:457–481. doi: 10.4155/tde-2016-0016. [DOI] [PubMed] [Google Scholar]
- 25.Morse Philip M, Feshbach Herman. Methods of Theoretical Physics Parts I and II. McGraw Hill; 1953. [Google Scholar]