Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Jan 23;51(4):2186–2196. doi: 10.1021/acs.est.6b04030

Modeling Biphasic Environmental Decay of Pathogens and Implications for Risk Analysis

Andrew F Brouwer †,*, Marisa C Eisenberg †, Justin V Remais ‡, Philip A Collender ‡, Rafael Meza †, Joseph N S Eisenberg †
PMCID: PMC5789392  PMID: 28112914

Abstract

graphic file with name es-2016-04030j_0007.jpg

As the appreciation for the importance of the environment in infectious disease transmission has grown, so too has interest in pathogen fate and transport. Fate has been traditionally described by simple exponential decay, but there is increasing recognition that some pathogens demonstrate a biphasic pattern of decay—fast followed by slow. While many have attributed this behavior to population heterogeneity, we demonstrate that biphasic dynamics can arise through a number of plausible mechanisms. We examine the identifiability of a general model encompassing three such mechanisms: population heterogeneity, hardening off, and the existence of viable-but-not-culturable states. Although the models are not fully identifiable from longitudinal sampling studies of pathogen concentrations, we use a differential algebra approach to determine identifiable parameter combinations. Through case studies using Cryptosporidium and Escherichia coli, we show that failure to consider biphasic pathogen dynamics can lead to substantial under- or overestimation of disease risks and pathogen concentrations, depending on the context. More reliable models for environmental hazards and human health risks are possible with an improved understanding of the conditions in which biphasic die-off is expected. Understanding the mechanisms of pathogen decay will ultimately enhance our control efforts to mitigate exposure to environmental contamination.

Introduction

Many infectious pathogens are transmitted between hosts via environmental media, including water, air, food, and fomites. Pathogens occupying these media are subject to environmental stresses, transport, and senescence, and the persistence of pathogens in these settings is of great interest when considering interventions that target environmental media (including water treatment, surface decontamination, and hand hygiene) as well as strategies for meeting regulatory thresholds for environmental protection.1 When pathogens persist in the environment, their movement through various media, water in particular, can facilitate transmission over long distances.2 Various modeling frameworks that describe pathogen persistence and transport via surface water—so-called fate and transport models—have been used to gain insight into the environmental dynamics of infectious disease risk (e.g., refs (3−7)).

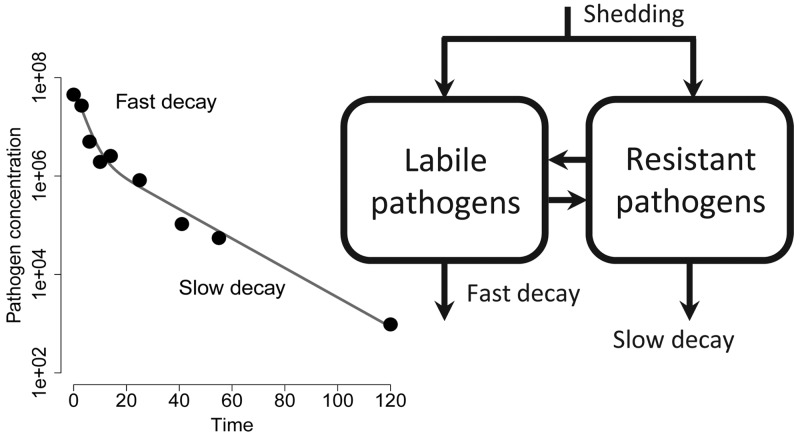
A critical feature of fate and transport models is the representation of pathogen attenuation over time or distance, which is generally expressed as an exponential, monophasic decay of pathogen concentration over time. While long-tailed deviations from monophasic decay have been known since the early 20th century, assumptions of first-order kinetics remain overwhelmingly the norm.8−12 Some pathogens, Escherichia coli in particular, exhibit a biphasic pattern—a period of faster decay (labile regime) followed by a period of slower decay (resistant regime); see Hellweger et al.13 for a review. Studies that have characterized biphasic decay (e.g., refs (13−15)) generally consider one of two empirical models: the piecewise log–linear function12

graphic file with name es-2016-04030j_m001.jpg 1

or the biexponential model11,16−18

graphic file with name es-2016-04030j_m002.jpg 2

Other models have also been used, such as the Weibull

graphic file with name es-2016-04030j_m003.jpg 3

which can be used to represent a heterogeneous distribution of stress tolerance and has been used predominantly in the context of the inactivation of foodborne pathogens.19,20 Another kind of biphasic behavior is also seen in some contexts: a phase of relative population stability, or even growth, followed by faster decay. This phenomenon is also important from a risk perspective, but is beyond the scope of our study, as it is typically modeled using very different strategies from those used to address slow-decaying tails. See, for example, Phaiboun et al.21 for a starvation kinetics model capable of reproducing this behavior.

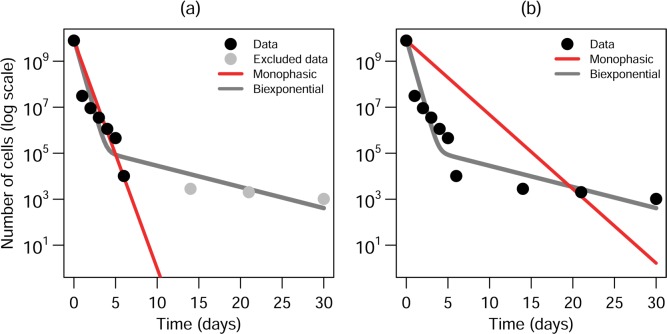
The additional parameter or parameters that must be estimated in biphasic models—and the additional longitudinal data necessary to estimate them—explain in part why biphasic decay is rarely incorporated into fate and transport models. Modelers have tended to superimpose monophasic models on biphasic data. For example, monophasic decay parameters are sometimes fit only to the labile regime (e.g., ref (22)), which can happen if sampling studies end prematurely (Figure 1a). In this case, the resulting model will consistently underestimate underlying biphasic pathogen concentrations. Alternatively, a monophasic model can be fit to an entire biphasic data set (Figure 1b) (e.g., ref (23−25)). In this case, pathogen concentrations will be substantially overestimated initially but underestimated after a certain point. Yet another approach is to fit the model only to the first and last data points (e.g., ref (26)).

Figure 1.

Figure 1

Open in a new tab

Two monophasic models for a population of Shigella sonnei undergoing biphasic decay in seawater at room temperature27 and a biexponential fit (eq 5). (a) A monophasic model fit only to labile regime, providing relatively accurate estimates for the initial phase but underestimating pathogen survival at later time points. (b) A monophasic model fit to all data, overestimating initial pathogen survival and underestimating survival after about 20 days. All models fit by log-transformed least-squares and with a set intercept.

To date, all data on biphasic decay have come from observational studies in which media (either in a laboratory or in the environment) are sampled over time to estimate pathogen population and die-off. Further, consideration of biphasic decay in exposure and risk assessment has been confined to pathogens on agricultural products, particularly in regard to delay of harvesting time after wastewater application.28−30 We know of no studies incorporating biphasic decay in an analysis of disease risk at the population scale or in a hydrological fate and transport context.

Various hypotheses have been proposed to explain the observation of biphasic dynamics.13,14,31 We categorize these hypotheses into four—not necessarily mutually exclusive—categories:

  • 1.

    Population heterogeneity. The pathogen population is composed of distinct subpopulations, some more susceptible to environmental decay. These populations might be different strains, the result of a new mutation, or populations in different phases of growth, etc. This hypothesis is frequently used, for example, to explain the observed biphasic decay of E. coli populations.

  • 2.

    Hardening off. Once exposed to the environment, the pathogen converts to a hardier phenotype through altered gene expression or other mechanisms. This hypothesis is particularly relevant for pathogens that exhibit microbial dormancy or quiescence, a kind of bet-hedging strategy in which cells limit growth in exchange for environmental resilience.32,33 Such states are thought to explain, for example, antibiotic-resistant persistor cells and certain chronic infections.

  • 3.

    VBNC. The pathogen enters a viable-but-not-culturable (VBNC) state that cannot be detected by usual culturing methods. This hypothesis is closely related to the dormancy discussed above, but, here, the resistant cells are not measured, typically because their metabolic profiles have changed in a way that renders them incapable of growth on the cell culture media used in quantification. Under this hypothesis, biphasic decay can be observed even if the two pathogen types decay at the same rate and thus could be an artifact of data collection methods. VBNC states have been observed for E. coli, H. pylori, V. cholerae, Salmonella, and Shigella, among others.34

  • 4.

    Density effects. Pathogen decay rates are tied to pathogen density, possibly because of substrate concentration or quorum sensing. Previous results suggest that the decay of E. coli in surface water is not a density effect,13 but this mechanism could be relevant for other pathogens or for other kinds of biphasic phenomena.21 Our mathematical framework does not consider density effects.

Our analysis has two broad aims. First, we show that the biexponential model can arise from mechanistic assumptions and thus should be preferred to purely empirical models such as the piecewise log–linear model. Longitudinal pathogen concentration data, however, cannot distinguish between several variants of the mechanistic model presented. Through identifiability analysis, we identify the parametric information available in these sampling studies and show how this information can be interpreted in the context of different underlying mechanisms. Our analysis is not a validation of any specific mechanistic model; indeed, we show that such validation is impossible—beyond demonstrating that a biexponential curve may fit biphasic data—when only cell concentration data are available. The second aim is to emphasize that biased estimates of risk can result when a monophasic model is used to analyze a biphasic decay process. We provide two case studies in support of this aim. First, we show that assuming monophasic decay when the pathogen exhibits biphasic decay can substantially underestimate disease risk. Second, we explore the effect of biphasic decay in hydrological fate and transport modeling, showing that monophasic approximations to biphasic data may over- or underestimate concentrations depending on how the approximations are formulated.

Materials and Methods

Model

We consider a family of linear, two-compartmental models that encompasses several possible mechanisms of biphasic decay. Let E1(t) and E2(t) be populations of pathogens of type 1 (labile) and type 2 (resistant) in the environment, and let E(t) = E1(t) + E2(t) be the total pathogen population. Let u(t) be the total addition of pathogens into the environment (e.g., shedding). We consider models of the form

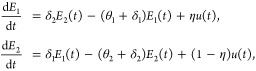graphic file with name es-2016-04030j_m004.jpg 4

with initial conditions E1(0) = ρω and E2(0) = (1−ρ) ω, where the seven model parameters are listed in Table 1.

Table 1. Parameters for the General Pathogen-Decay Model Given in Eq 4.

symbol parameter
θ1, θ2 decay rate coefficients for labile and resistant pathogens, respectively
δ1 rate coefficient for transition to resistant state (e.g., entering dormancy)
δ2 rate coefficient for transition to labile state (e.g., resuscitation)
ω initial population of pathogens
ρ initial fraction of pathogens that are labile
η fraction of introduced pathogens that are labile
u(t) time-varying input of pathogens to the system
Open in a new tab

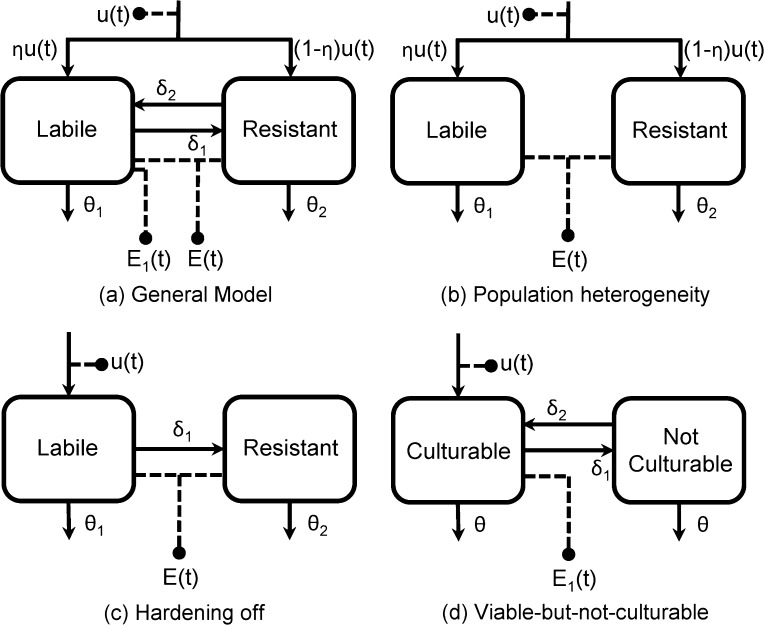
Although biphasic decay can mathematically occur from a number of different configurations of a two-state linear compartmental model (Figure 2a), we will ground our analysis in three plausible models of pathogen decay. The models shown in Figure 2b–d correspond to the first three hypotheses listed in the Introduction. In the population heterogeneity model (Figure 2b), pathogens are inherently of two different types that decay at different rates, but we observe only the total population (δ1 = δ2 = 0; observed data is E(t)). In the hardening-off model (Figure 2c), all pathogens are initially of one type but begin to convert to a hardier, possibly dormant, form once in the environment with negligible resuscitation (δ2 = 0, η = 1; observed data is E(t)). In the viable-but-not-culturable model (Figure 2d), pathogens all decay at the same rate and interconvert between measurable and unmeasurable forms (η = 1, θ2 = θ1; observed data is E1(t)). Although it is likely that the nonculturable pathogens do not decay at the same rate as the cultivable ones, this submodel demonstrates that observed biphasic behavior does not necessarily imply different pathogen decay rates. Although we are grounding our analysis in these three models, the truth may very well be a blend of mechanisms dependent on the pathogen and environmental conditions.

Figure 2.

Figure 2

Open in a new tab

General model of biphasic decay and three mechanistic submodels. Solid lines are transfer of pathogens, and the dashed lines indicate measurement.

Identifiability

A necessary consideration for estimation of model parameters from data is identifiability. A model parameter is said to be identifiable if it can be uniquely determined from observed data. The model is said to be identifiable only if all model parameters are identifiable (more formal definitions are presented elsewhere35−37). As an example, consider the linear model y = (m1 + m2) x + b. This model is unidentifiable when the data are (x, y) pairs because, although b is identifiable, m1 and m2 cannot be uniquely determined.

Identifiability of a model is dependent on both the parametrization and the data measured. There may problems estimating parameters uniquely because of the inherent specification of the model (e.g., trying to separately estimate m1 and m2 in the linear model above) or because of issues relating to data quality, frequency of sampling, etc. (e.g., trying to model a sinusoid when the resolution of the data is only once per period at the same point in its phase). The study of inherent identifiability problems (as in the linear model example), which would exist even with continuous, perfectly measured, and error-free data, is called structural identifiability; the study of identifiability problems related to the data (as in the sinusoid example) is called practical identifiability.38

If a model is structurally unidentifiable, one can identify the parametric information available in the data in the form of identifiable parameter combinations,37 e.g. m1 + m2 is an identifiable parameter combination in the linear model above. It is sometimes possible to make unidentifiable models identifiable by reparameterizing the model in terms of identifiable combinations (e.g., setting m = m1 + m2 in the linear example above) or by measuring different data (e.g., measuring a sinusoid at different points in its phase).

In this paper, structural identifiability analysis is done by a differential algebra approach.39−41 We note that many of the identifiability results in this paper are recontextualizations of results or build from prior work in the field of pharmacokinetics,35,42,43 but pathogen decay presents a novel context and interpretation.

Results

We present results—both theoretical analysis and numerical case studies—relating to the model presented in eqs 4, which considers both sampling studies with no input (u = 0) and experiments with measured pathogen inputs (u ≢ 0).

Five technical results are first presented to provide insight into the properties of the model. Proposition 1 proves that the biexponential model describes the behavior of the family of considered mechanisms. Proposition 2 states that the apparent parameters of the biexponential model can be uniquely determined from pathogen concentration data (i.e., are identifiable). In contrast, Proposition 3 proves that the general mechanistic model is unidentifiable, and it considers what combinations of the mechanistic model parameters can be identified under various assumptions about which data are measured. Corollary 1, which follows directly from Proposition 3, gives these identifiable combinations in the context of the population heterogeneity, hardening-off, and viable-but-not-culturable models. Proposition 4 states that it is impossible to distinguish from the shape of the data alone whether we are measuring all pathogens or only a culturable fraction.

Finally, we illustrate these results through examples demonstrating that data obtained from sampling studies alone cannot elucidate the mechanism of decay and through case studies exploring the implications of biphasic decay in risk assessment and hydrological fate and transport modeling.

Theoretical Results

Proposition 1. Except for degenerate parameter combinations, the model given in eq 4 displays biphasic behavior in the labile fraction E1(t) and in the total pathogen population E(t) = E1(t) + E2(t). That is, for some parameter combinations a, b, c, d, and h, E(t) and E1(t) have the form

graphic file with name es-2016-04030j_m005.jpg 5

where

graphic file with name es-2016-04030j_m006.jpg 6

is a forcing function where υ(t) = u(t) for E(t) and υ(t) = ηu(t) for E1(t).

Take-away: Any of the mechanisms modeled in Figure 2 can produce biphasic dynamics.The proof of Proposition 1 is left to the supplement. When the total population E(t) is observed, a degeneracy (that is, decay is not biphasic) occurs when there is no difference in the labile and resistant decay rates (θ1 = θ2); when only the labile fraction E1(t) is observed, there is a degeneracy when resistant pathogens cannot be resuscitated and cultured (δ2 = 0).

Parameters a, b, c, d, and h have meaning in the shape of the observed decay and are most easily interpreted as if the underlying mechanism was population heterogeneity (and thus we call them “apparent” parameters): a is the apparent labile decay rate, b is the apparent resistant decay rate, c is the apparent initial fraction of labile pathogens, d is the initial total concentration of pathogens, and h is the apparent fraction of newly introduced pathogens that are labile. In terms of the mechanistic parameters,

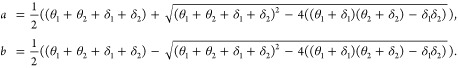graphic file with name es-2016-04030j_m007.jpg 7

For the total pathogen population E(t),

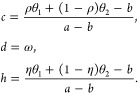graphic file with name es-2016-04030j_m008.jpg 8

For the labile pathogen population E1(t),

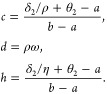graphic file with name es-2016-04030j_m009.jpg 9

Correct association of the values of a and b with mechanistic model parameter combinations does not depend on whether the environmental compartment measured is in truth E(t) or E1(t) because a and b are associated with the same parameter combinations regardless. However, c, d, and h are associated with different parameter combinations depending on whether E(t) or E1(t) is measured and thus will be misspecified if the environmental compartment is not correctly identified (e.g., only observing one type of pathogen when there are really two). For example, if one assumes that one is measuring E(t) but is in truth measuring E1(t), then one is implicitly assuming that ca + (1 – c) b is the weighted decay rates ρθ1 + (1 – ρ) θ2 when that quantity is actually θ1 + δ1 + δ2(1–1/ρ).

Proposition 2. The parameter combinations a, b, c, d, and h in Proposition 1 are identifiable.

Take-away: When observing biexponential decay, one can uniquely determine the apparent decay rates, the proportion of the population attributed to each type, the initial population, and, if there is shedding, the proportion of shed pathogens apparently of each type.

That the coefficients and exponents of an observed sum of exponentials are identifiable is known from identifiability theory42,44 and can be used to generate this result. It is also a straightforward application of the differential algebra approach to identifiability, which we include in the supplement.

We still want to know the extent to which we can uniquely determine the parameters of the underlying mechanistic models in Figure 2. However, the apparent parameters in Proposition 2 are complicated functions of the mechanistic parameters. In Proposition 3, we manipulate the apparent parameters into a different set of identifiable combinations that express equivalent information but are much simpler expressions of the mechanistic parameters. Note that the number of identifiable combinations of mechanistic parameters is the same as the number of identifiable apparent parameters.

Proposition 3. The full model given in eq 4 with data E(t) = E1(t) + E2(t) is unidentifiable. If θ1 ≠ θ2, then

  • when there is no pathogen input (u(t) ≡ 0), the identifiable combinations are θ1 + θ2 + δ1 + δ2 (the sum a + b), (θ1 + δ1) (θ2 + δ2) – δ1δ2 (the product ab), ρθ1 + (1 – ρ) θ2 (decay rates weighted by initial fractions, ca+(1– c) b), and ω (the total initial pathogen population, d);

  • when pathogen input over time is measured (υ(t) = u(t) ≢ 0), one can additionally identify ηθ1 + (1−η) θ2 (decay rates weighted by input fractions, ha + (1 – h) b).

The model given in eq 4 with data E1(t) is unidentifiable. If δ2 ≠ 0, then

  • when there is no pathogen input (u(t) ≡ 0), the identifiable combinations are θ1+θ2+δ1+δ2 and (θ1+δ1) (θ2+δ2) – δ1δ2, θ1+δ1+δ2(1–1/ρ), and ρω (again found by a + b, ab, ac+(1– c) b, and d, respectively).

  • when pathogen addition over time is measured (υ(t) = ηu(t) ≢ 0), one can additionally identify θ1+δ1+δ2(1–1/η) (again ha+(1– h) b).

Take-away: The full linear, compartmental model (Figure 2a) has six parameters (seven, if υ ≢ 0 and is known), including initial conditions, but the pathogen survival data contains only four (five, if υ ≢ 0 and is known) pieces of parametric information. In other words, the model given the data could be made identifiable if information about two parameters is independently known, although the choice of which two parameters is not entirely arbitrary; only certain pairs of parameters, dependent on the identifiable parameter combinations given above, will resolve the unidentifiability problem, e.g. knowing, a priori, both decay rates θ1 and θ2 resolves the unidentifiability but knowing the dormancy rate δ1 and initial fraction ρ does not.

The proof is the same as that of Proposition 2 and may be found in the supplement. Note that we expressed the mechanistic identifiable combinations as the same functions of the apparent parameters in Proposition 3 whether the data is E(t) or E1(t) but that these combinations represent different underlying process.

Now that we have the identifiable parameter combinations for the full mechanistic model, it is straightforward to simplify the identifiable combinations under the assumptions of the submodels.

Corollary 1

In the sampling framework (u(t) ≡ 0),

  • the population heterogeneity model is identifiable with parameters θ1, θ2, ρ, and ω (respectively a, b, c, and d);

  • the hardening-off model is unidentifiable with identifiable combinations θ1+δ1, θ2, ρ(θ1–θ2), and ω (respectively a, b, c(a– b), and d);

  • the viable-but-not-culturable model is unidentifiable with identifiable combinations θ, δ1 + δ2, δ2/ρ, and ρω (respectively b, a – b, (1 – c) (a – b), and d).

In the measured-input framework (u(t) ≢ 0),

  • when u(t) is known, the population heterogeneity model is identifiable with parameters θ1, θ2, ρ, ω, and η (respectively a, b, c, d, and h);

  • when u(t) is known, the hardening-off model is identifiable with parameters θ1, δ1, θ2, ρ, and ω (respectively ha + (1– h) b, (1 – h) (a – b), b, c/h, and d);

  • when ηu(t) is known, the viable-but-not-culturable model is identifiable with parameters θ, δ1, δ2, ρ, and ω (respectively b, h(a– b), (1– h) (a – b), (1 – h) /(1 – c), and (1 – c) d/(1 – h))

Take-away: Making assumptions about mechanism simplifies the parameter combinations identified in Proposition 3.

We illustrate this corollary in Examples 1 and 2. In particular, this corollary demonstrates that the mechanistic submodels are identifiable if we measure the input to the system. We use a thought experiment to explore this possibility in Example 2.

When measuring pathogen concentrations, one does not necessarily know if technique is capturing a representation of the whole population, or only of a culturable subsample. This next proposition tells us that the shape of the data alone cannot resolve this issue.

Proposition 4. When measuring a pathogen concentration (where it is unknown a priori whether it is E(t) = E1(t) + E2(t) or E1(t)) and, possibly, an input υ(t) (including υ(t) ≡ 0), it cannot be determined a posteriori whether (i)E(t) is measured and υ(t) = u(t) or (ii) E1(t) is measured and υ(t) = ηu(t).

Take-away: One cannot tell from the pathogen concentration alone whether one is measuring all of the pathogens or only a subpopulation of them.

A single example of indistinguishability suffices as proof, and we illustrate this in Example 2.

Examples

In this section, we provide four examples. In Example 1, we fit models to observations of pathogen population over time when there is no additional input to the system. In Example 2, we use simulated data to fit models to observations of pathogen population over time when there is a known, continuous addition of pathogen. In Example 3, we examine the implications of biphasic decay in a risk assessment. Finally, in Example 4, we explore the biases introduced by the misapplication of monophasic models in a hydrological fate and transport model.

Example 1: Modeling pathogen concentration samples over time

In this example, we use data from a study by Rogers et al.,14 in which known concentrations of transformed green fluorescent protein E. coli O157:H7/pZs were added to manure-amended soil with 80% field capacity moisture content and incubated at 25 °C for 120 days. The piecewise log–linear model (eq 1) used by the authors, the Weibull model (eq 3), and biexponential model (eq 5) all fit the data well (Figure 3); the Weibull and biexponential models are fit by minimizing the log-transformed least-squares difference in R (v. 3.0.1) using optim.

Figure 3.

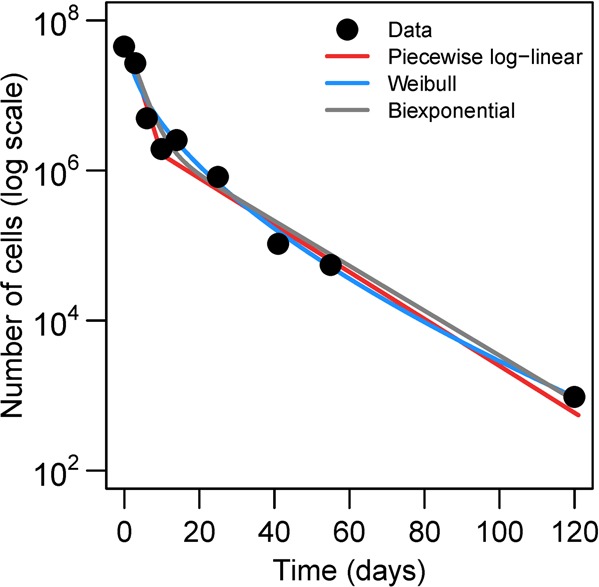
Figure 3

Open in a new tab

Fitting (log-transformed least-squares) piecewise log–linear, Weibull, and biexponential models of biphasic decay to population of E. coli over time in Rogers et al.14 The best fit estimates are a = 0.37, b = 0.072, t* = 9 for the piecewise log–linear model (eq 1), α = 2.1 and β = 0.59 for the Weibull model (eq 3), and a = 0.36, b = 0.069, and c = 0.93 for the biexponential model (eq 5).

Although both the piecewise log–linear and biexponential models can estimate the apparent labile a and resistant b pathogen decay rates, the biexponential model identifies c, the initial fraction attributable to the labile group. From a control perspective, c can be a useful parameter; the expected fraction of resistant pathogens may be a crucial consideration in water treatment strategies. The best-fit break point t* obtained from the piecewise log–linear model, on the other hand, is likely determined by several experiment-specific factors, and is not directly interpretable as a simple biological quantity with control relevance. Similarly, although the parameters α (hazard rate) and β (shape parameter) of the Weibull model define a distribution of stress tolerances in the population, such a distribution is quite abstract and difficult to interpret in mechanistic biological terms.

We purposefully do not include a goodness-of-fit comparison. We argue that such a statistical comparison of these models does not provide information about mechanism and would thus, as all of the models fit reasonably well, be of limited use and distract from the main point. The piecewise log–linear model is purely empirical, while the biexponential model arises from mechanistic assumptions, and is thus, we argue, preferable. The Weibull model, while rooted in assumptions about distributions of stress tolerance in the pathogen population, is also, ultimately, empirical, as its parameters are not measurable quantities.

Of our mechanistic submodels, only the population heterogeneity model is identifiable (θ1 = 0.36, θ2 = 0.07, and ρ = 0.93). The hardening off model only partially resolves the parameter values (θ1 + δ1 = 0.36, θ2 = 0.07, ρ(θ1 – θ2) = 0.27). This is also true of the VBNC model (θ = 0.069, δ1 + δ2 = 0.29, and δ2/ρ = 0.02). The observed dynamics can arise from any of the mechanisms—with identical fits—demonstrating that the data do not inform the specific mechanism.

Example 2: Modeling populations over time with a measured input

In Corollary 1, we saw that all three of the mechanistic submodels are identifiable if the pathogen input to the system is measured. In this example, we consider a thought experiment of a pathogen decay study with a measured, continuous input; since we know of no comparable pathogen decay study, we use simulated data. Although we imagine it here as a possible lab experiment, it could also apply to a situation where a number of sick individuals are shedding at a known rate into some environmental medium that is subsequently sampled. We begin with an initial population of 0, a constant input u(t), and parameter set of (θ1, θ2, δ1, δ2, η)=(0.4, 0.1, 0.2, 0.3, 0.9). As indicated by Proposition 4, the same data can be generated by setting u(t) = 1000 and observing E(t) as by setting η = 0.566 and u(t) = 1000/0.566 and observing E1(t). Hence, from the data, it is impossible to tell, a posteriori, whether one is measuring E(t) and υ(t) = u(t) or E1(t) and υ(t) = ηu(t). We fit each of the submodels to this data after a normally distributed error was applied. We then plot the best-fit lines (numerical least-squares) for the population heterogeneity, hardening off, and viable-but-not-culturable models, which are seen to be identical in Figure 4. (Note that the error is added for simulated realism only; each model could fit the exact data).

Figure 4.

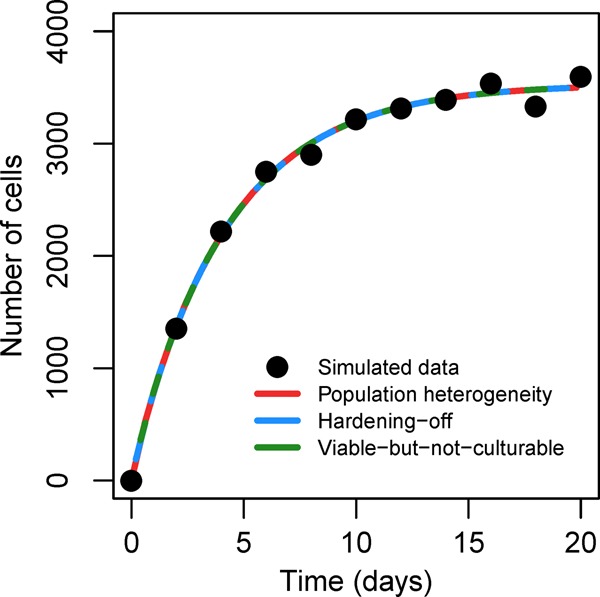
Figure 4

Open in a new tab

Simulated biphasic dynamics of E. coli with continuous input. See Example 2 in text.

All three models fit the data equally well. However, comparing the true parameter values used to generate the data with each parameter set estimated (Table 2), we see that each model is misspecified. This is because we choose to generate data from the full model. All parametric information in the data can be summarized by the estimated apparent parameter combinations a = 2.15, b = 0.23, and h = 0.19 (Proposition 2). Comparing these to the true values of a = 0.76, b = 0.24, and h = 0.25, we see that this study actually provides insufficient data to accurately measure the apparent labile decay rate.

Table 2. Parameters Estimated from the Simulated Data in Figure 4 by the Different Mechanistic Submodels.

model θ1 θ2 δ1 δ2 η
true values underlying the simulated data 0.4 0.1 0.2 0.3 0.9
population heterogeneity estimates 2.15 0.23 — — 0.19
hardening off estimates 0.60 0.23 1.56 — —
viable-but-not-culturable estimates 0.23 — 0.37 1.56 —
Open in a new tab

Each of the submodels make assumptions about how these estimated parameter combinations a, b, and h relate to the underlying parameters. These assumptions allow all three models to be identifiable. However, the models are also indistinguishable and do not accurately reflect the generating parameters. This example thus illustrates the important distinction between identifiability and distinguishability. As the analytical results in the previous section show, even if identifiable parameters are estimated, the model may be misspecified, making these estimates incorrect or even meaningless (e.g., if the estimated parameter does not appear in the true underlying mechanism).

Example 3: Consequences of neglecting biphasic decay in a risk assessment

We extend a prior risk assessment of drinking water exposure to Cryptosporidium(45) to investigate the potential impact on risk when accounting for biphasic pathogen decay. Decay rates for Cryptosporidium vary in the range of 0.005–0.04 log10 units per day and appear relatively insensitive to temperature between 0 and 20 °C.23,46−49 Although Cryptosporidium is not known for exaggerated biphasic decay behavior, there have been suggestions that certain forms are hardier than others. Permeability of oocysts to the fluorescent vital dye 4′,6-diamidino-2-phenylindole (DAPI) correlates with viability, and it has been hypothesized, given that oocysts can interconvert between DAPI± forms, that impermeability may confer environmental protection.47,50,51 Indeed, Campbell, Robertson, and Smith observed this in one of their studies50 but not a subsequent one.47 Hence, there may be environmental conditions in which biphasic decay occurs for some types of Cryptosporidium, even if it is not typical more generally. That such long-tail survival might not be expected only highlights the possibility of risk misestimation.

For the purposes of this example, assume that a population of Cryptosporidium can be written as

graphic file with name es-2016-04030j_m010.jpg 10

a reparameterization of eq 5 that emphasizes the decay half-lives. Here, half-lives of 10 and 60 days correspond to decays of 0.03 and 0.005 log10 units per day, a range consistent with the literature but more conservative than that considered by Eisenberg et al.52 When c = 1, the population consists solely of labile pathogens, and, when c = 0, the population is solely resistant pathogens.

Suppose that a wastewater treatment plant measures daily concentrations of Cryptosporidium in its inflow that are lognormally distributed with mean 2.12 and standard deviation 4.48 organisms/L and that water is then held for 10 days before treatment (at which point the distribution would be identical to that estimated in Eisenberg et al.52 under fully fast decay). Then, the concentration of organisms immediately before treatment is consistent with the distribution of organisms in the source water considered in the prior risk assessment when c = 1.45 Consistent with the prior risk assessment, (1) treatment efficacy of sedimentation and filtration was modeled as a Weibull distribution with mean 3.84 and standard deviation 0.59 log10 unit removal, (2) the volume of tap water consumption was assumed to be log-normal with mean 1.2 and standard deviation 1.2 L/day, (3) the dose–response relationship was assumed to be an exponential cumulative probability function f with parameter k = 0.004078, and (4) the moribidity ratio M, the fraction of infected who become ill, was assumed to be 0.39.45,53 We treat the c parameter in two ways. First, we characterize risk as a function of c, and, second, we sample c daily from a uniform (0,1) distribution.

For each day i, we (1) sample from the distribution of Cryptosporidium concentrations 10 days prior, and let Pi be the concentration of Cryptosporidium on day i, that is, after 10 days of holding, and (2) sample the treatment efficiency Ti on day i. For each person on each day, we (1) draw a volume of water consumed Vij, (2) draw a number of pathogens Nij consumed by person j on day i from a Poisson distribution with mean PiTiVij, (3) calculate the probability of illness as πij = M · f(Nij), (4) draw a number uij from a uniform distribution on (0,1), and 5) let the indicator Iij of illness for person j on day i be 1 if uij < πij and 0 otherwise. Then, the sum of Ii,j is the total number of cases experienced by the population in one year.

In Figure 5, we present a heat map of yearly cases of illness attributable to Cryptosporidium over 1,000 simulations as a function of c, the fraction of fast decaying pathogens, and when c is randomly sampled on each day. The sample means are also plotted. When all pathogens decay at the faster rate, the average is 3.3 case per year per 10 000 with a standard deviation of 2.5 and a maximum of 23; when all pathogens decay slowly (c = 0), the average number of cases is 6.0, nearly double that of the first case, with a standard deviation of 4.7 and a maximum of 107. When c is sampled each day, the average number of cases is 4.8 with a standard deviation of 3.1 and a maximum of 31. Biphasic decay increases both the mean and the variance of the number of cases.

Figure 5.

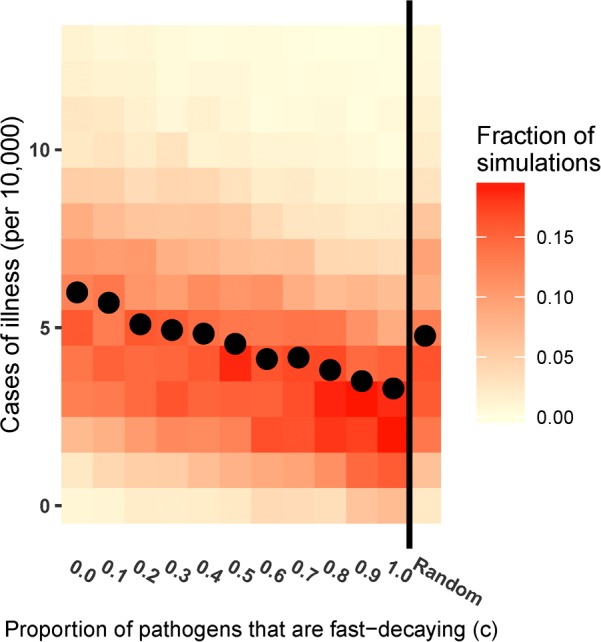
Figure 5

Open in a new tab

Heatmap displaying the fraction of simulations that have each number of cases of illness in a year in a population of 10 000, both as a function of c, the proportion of pathogens that are fast decaying, and with c chosen randomly each day. The mean number of cases is shown with a dot.

Example 4: Consequences of neglecting biphasic decay in a hydrological fate and transport model

To explore the potential biases introduced through the incorrect assumptions of monophasic decay within a hydrological fate and transport model, we simulate the extent of bacteriological impairment downstream of a wastewater treatment outfall on the Sonora river in Mexico, using a simplification of a previously published E. coli transport model.54 Specifically, using Markov chain Monte Carlo methods, we compared predictions of downstream bacterial concentrations in three scenarios: (1) when using a biexponential model, (2) when using a monophasic model fit only to the labile regime, and (3) when using a monophasic model fit to the full biphasic experimental data (Figure 2 of Hellweger et al.13).

We assume that E. coli originating from the Baviacora wastewater treatment plant decay and grow in a biphasic manner (eq 5) with parameters a and b normally distributed (μa = 1.94, σa = 0.23, μb = −0.15, σb = 0.04; note that a negative μb indicates growth of the resistant fraction) and c beta-distributed (αc = 784.29, βc = 10.87) to be consistent with the experimental results of Hellweger et al.13 A sedimentation rate coefficient was estimated from our biphasic decay rate and the total removal rate estimated by Robles-Morua et al.54 Back calculating from Figure 7 of Robles-Morua et al.,54 we estimate the average streamflow velocity below the Baviacora outfall to be 16.75 km/day; discharge and flow velocity downstream of the Baviacora outfall is observed to be relatively constant over 60 km. Assuming, as in Robles-Morua et al.,54 an initial E. coli concentration of 24.63 times the EPA standard for bathing water of 126 colony forming units (cfu) per 100 mL,55 we estimate the downstream extent of water impairment up to 60 km under the three scenarios. Additional details on the methods (determination of monophasic decay rate and sedimentation rate) are available in the Supporting Information.

In the baseline scenario—Scenario 1—compliance was achieved within 60 km in 61% of simulations, with the median simulation achieving compliance in 37.7 km (minimum 16.7 km), though once compliant, simulations did not necessarily stay so because of the growth of the resistant fraction of E. coli. Over 99.8% of simulations in Scenario 2 achieved compliance within 60 km, with the median achieving compliance at 21.0 km (minimum 15.4 km). For Scenario 3, only 23% of simulations achieved compliance within 60 km, with the median simulation achieving compliance at 78.3 km (assuming river conditions remain constant past 60 km; minimum 25.4 km).

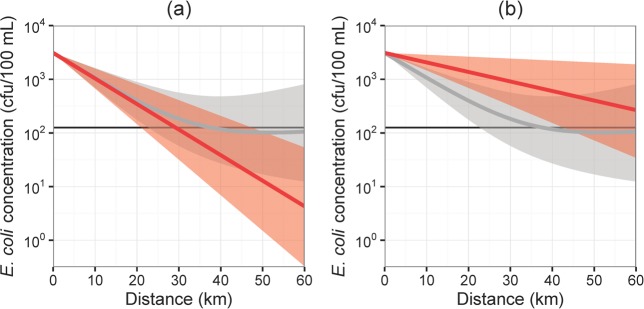
In order to characterize the biases of Scenarios 1 and 3 over the spatiotemporal scale, we plot the simulations up to a distance of 60 km in Figure 6. The median estimated E. coli concentration is always an underestimate for Scenario 2 relative to Scenario 1, which highlights the danger of fitting monophasic curves only to the labile regime and is especially problematic in a regulatory context. For Scenario 3, the median concentration is an overestimate over the considered range (up to 76 km if river conditions remain constant, after which it is an underestimate; additional details in appendix). Hence, for considering compliance within 60 km, Scenario 3 can be thought of as a conservative simplification of the biphasic model. The greatest overestimation occurs at around 36 km, where the median of Scenario 3 is 5.3 times that of Scenario 1. Neither Scenario 2 nor Scenario 3 can capture the regrowth dynamic in the biphasic scenario.

Figure 6.

Figure 6

Open in a new tab

Comparative simulation results for (a) Scenarios 1 (biphasic, in gray) and 2 (monophasic fit to the labile regime, in red) and (b) Scenarios 1 (biphasic, in gray) and 3 (monophasic fit to entire data, in red). Each scenario shows the median and 95% CI simulated E. coli concentrations over 60 km of hydrologic transport. The black line gives the EPA regulatory compliance threshold of 126 cfu/100 mL.

Discussion

The predominant assumption in the risk assessment and transmission modeling literature is that pathogens in the environment decay through a monophasic exponential process. Increasingly, however, we are recognizing that a biphasic framework for understanding pathogen decay provides a more accurate description of observed die-off for certain pathogens, environmental/experimental conditions, and time-scales. Our identifiability analysis highlights the limitations of current sampling data in informing the specific mechanisms associated with observed biphasic decay and provides guidance on future empirical studies that can inform intervention strategies. Our case studies highlight the fact that biases associated with the misspecificiation of the pathogen decay process can lead to either over- or underestimates of risk depending on how the data are used to estimate a first-order die-off process. Although we considered only fast–slow biphasic decay in this study, future work may be able to further elucidate the slow–fast decay observed in certain scenarios and considered by Phaiboun et al.21 The following sections discuss modelidentifiability and risk misestimation in more detail.

Identifiability

The biexponential model arises from a mechanistic description of pathogen decay and should be preferred to purely empirical models; nevertheless, one should be careful to not overinterpret the biexponential model’s apparent parameters. Although previous literature has often attributed a population heterogeneity mechanism to biphasic decay, identical dynamics can arise from a number of other mechanisms, including hardening off and the existence of viable-but-not-culturable states. Full identifiability of the general model (Figure 2a) parameters—and thus determination of mechanism—requires that the labile and resistant populations be measured separately. This separation might be accomplished through genomic, expressomic, or proteomic analysis of the pathogen population.

Sampling studies that observe overall pathogen concentrations, however, do allow for the identification of combinations of model parameters. Propositions 2 and 3 demonstrate that four pieces of information (degrees of freedom) are embedded in the observation of biphasic decay, most easily understood in terms of the parameters of Proposition 1: the apparent decay rates a and b, the total population d, and the apparent initial fraction of labile pathogens c. An additional piece of information, represented by h, can be obtained when pathogens are added to the system at a measured rate; however, as an additional parameter must also be estimated, this additional information does not resolve the identifiability issues illustrated here. The full model in eq 4 contains six (with no input) or seven (with measured input) parameters, and hence two parameteric constraints or pieces of information, as might be available from independent experimental studies, are need to make the model identifiable.

Our results also provide guidance on what independent information will resolve the unidentifiability of the model, as the independent determination of two parameters arbitrarily may not be sufficient. Each of the models in shown in Figures 2b–d have two constraints. But, as we see in Example 1 and the first part of Corollary 1, despite having four pieces of information and two constraints, the six parameters are not individually identifiable in the hardening-off and VBNC models. However, in the experimental context (Example 2), with five pieces of information and two constraints, all seven parameters may be uniquely estimated for each of the three models (second part of Corollary 1). Moreover, that each of the models is fully identifiable in the latter context highlights the difference between structural identifiability of a model (i.e., whether the parameters may be determined from data) and whether structure of the model (and thus mechanism) can be identified.

Our work highlights the usefulness of identifiability in the hydrologic and microbial modeling contexts. Structural identifiability and distinguishability analysis developed out of problems in engineering and pharmacokinetics35,42,44 and has also found an increasing range of applications in hydrology-related fields such as water quality56 and water treatment,57 among others.58−60 There, as here, it provides a tool to assist in experiment design, evaluate uncertainty, and assess modeling assumptions. Indeed, the comparison of alternative models of biphasic decay (both mechanistic and nonmechanistic) has strong parallels to the problems encountered when using multiexponential, noncompartmental, and compartmental models to assess drug distribution and elimination in pharmacokinetics.61−63

Risk Estimation

If a monophasic decay model is estimated from the labile regime of biphasic decay data, risks will always be underestimated. The degree of underestimation, as shown in Example 3, will depend on the distribution of labile and resistant pathogens in the environment. In this risk assessment case study, the mean risk doubled as the pathogen population moved from wholly labile to wholly resistant, and the maximum simulated burden nearly quadrupled because of the increased variance. We see this again in Example 4, where the mispecified monophasic model fit to the labile regime (Scenario 2) predicted compliance within 60 km in 98% of simulations while the biphasic model (Scenario 1) predicted compliance in only 61% of simulations. Hence, not accounting for the possibility of biphasic decay can potentially result in appreciable underestimation. On the other hand, when using a monophasic model fit to the entirety of the biphasic data (Scenario 3), we found that the model modestly overestimated bacterial concentrations on the scale of our hydrological transport case study, so that only 25% of simulations achieved compliance within 60 km. Bacterial concentrations further downstream were underestimated.

In Example 4, neither monophasic parametrization could capture the regrowth dynamic of the resistant fraction of the bacteria. While our results suggest that certain monophasic parametrizations may be conservative for some environmentally relevant scenarios, it is important to remember that we only considered decay in one environmental medium. If one considers die-off in manure prior to washout, transport, and decay in a river, the relevant time scales would likely extend beyond the point at which any monophasic approximation might yield conservative results.

The potential for biphasic pathogen die-off should be considered in all risk assessments, and the biexponential model should be used when appropriate. This model arises from mechanistic models but is not limited to any one mechanism. To effectively incorporate biphasic decay and understand the potential for intervention, targeted studies are needed to inform the mechanisms underlying biphasic dynamics. Further, because biphasic dynamics are likely a function of the interaction of mechanism and environmental factors—such as temperature, pH, or salinity—understanding mechanism will be important to characterizing the environmental conditions conducive to biphasic decay. Ultimately, these improved models will drive the design of more effective intervention strategies.

Acknowledgments

This work was funded under Models of Infectious Disease Agent Study (MIDAS) program within the National Institute of General Medical Sciences of the National Institutes of Health (grant U01GM110712). JVR and PAC acknowledge support from the National Institute of Allergy and Infectious Diseases (grant K01AI091864), the National Science Foundation Water Sustainability and Climate Program (grant 1360330), and the National Institutes of Health/National Science Foundation Ecology of Infectious Disease program funded by the Fogarty International Center (grant R01TW010286).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.est.6b04030.

  • Proofs of the theoretical results and additional details for the hydrological fate and transport case study (PDF)

The authors declare no competing financial interest.

Supplementary Material

es6b04030_si_001.pdf (222.4KB, pdf)

References

  1. Benham B.; Baffaut C.; Zeckoski R.; Douglas-Mankin K.; Pachepsky Y. A.; Sadeghi A. M.; Brannan K. M.; Soupir M. L.; Habersack M. J. Modeling bacteria fate and transport in watershed models to support TMDLs. Transactions of the ASABE 2006, 49, 987–1002. 10.13031/2013.21739. [DOI] [Google Scholar]
  2. Walters E.; Schwarzwälder K.; Rutschmann P.; Müller E.; Horn H. Influence of resuspension on the fate of fecal indicator bacteria in large-scale flumes mimicking an oligotrophic river. Water Res. 2014, 48, 466–77. 10.1016/j.watres.2013.10.002. [DOI] [PubMed] [Google Scholar]
  3. de Brauwere A.; Ouattara N. K.; Servais P. Modeling fecal indicator bacteria concentrations in natural surface waters: a review. Crit. Rev. Environ. Sci. Technol. 2014, 3389, 2380–2453. 10.1080/10643389.2013.829978. [DOI] [Google Scholar]
  4. Ferguson C.; de Roda Husman A. M.; Altavilla N.; Deere D.; Ashbolt N. Fate and Transport of Surface Water Pathogens in Watersheds. Crit. Rev. Environ. Sci. Technol. 2003, 33, 299–361. 10.1080/10643380390814497. [DOI] [Google Scholar]
  5. Jamieson R.; Gordon R.; Joy D.; Lee H. Assessing microbial pollution of rural surface waters: A review of current watershed scale modeling approaches. Agricultural Water Management 2004, 70, 1–17. 10.1016/j.agwat.2004.05.006. [DOI] [Google Scholar]
  6. Kazama S.; Aizawa T.; Watanabe T.; Ranjan P.; Gunawardhana L.; Amano A. A quantitative risk assessment of waterborne infectious disease in the inundation area of a tropical monsoon region. Sustainability Science 2012, 7, 45–54. 10.1007/s11625-011-0141-5. [DOI] [Google Scholar]
  7. Mari L.; Bertuzzo E.; Finger F.; Casagrandi R.; Gatto M.; Rinaldo A. On the predictive ability of mechanistic models for the Haitian cholera epidemic. J. R. Soc., Interface 2015, 12, 20140840. 10.1098/rsif.2014.0840. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Madsen T.; Nyman M. Zur Theorie der Desinfektion I. Med. Microbiol. Immunol. 1907, 57, 388–404. 10.1007/BF02140521. [DOI] [Google Scholar]
  9. Chick H. An Investigation of the Laws of Disinfection. J. Hyg. 1908, 8, 92–158. 10.1017/S0022172400006987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chick H. The Process of Disinfection by Chemical Agencies and Hot Water. J. Hyg. 1910, 10, 237–286. 10.1017/S0022172400042959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cerf O. Tailing of survival curves of bacterial spores. J. Appl. Bacteriol. 1977, 42, 1–19. 10.1111/j.1365-2672.1977.tb00665.x. [DOI] [PubMed] [Google Scholar]
  12. Crane S. R.; Moore J. A. Modeling enteric bacterial die-off: A review. Water, Air, Soil Pollut. 1986, 27, 411–439. 10.1007/BF00649422. [DOI] [Google Scholar]
  13. Hellweger F. L.; Bucci V.; Litman M. R.; Gu a. Z.; Onnis-Hayden a. Biphasic Decay Kinetics of Fecal Bacteria in Surface Water Not a Density Effect. J. Environ. Eng. 2009, 135, 372–376. 10.1061/(ASCE)0733-9372(2009)135:5(372). [DOI] [Google Scholar]
  14. Rogers S. W.; Donnelly M.; Peed L.; Kelty C. A.; Mondal S.; Zhong Z.; Shanks O. C. Decay of bacterial pathogens, fecal indicators, and real-time quantitative PCR genetic markers in manure-amended soils. Appl. Environ. Microbiol. 2011, 77, 4839–4848. 10.1128/AEM.02427-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Zhang Q.; He X.; Yan T. Differential Decay of Wastewater Bacteria and Change of Microbial Communities in Beach Sand and Seawater Microcosms. Environ. Sci. Technol. 2015, 49, 8531–8540. 10.1021/acs.est.5b01879. [DOI] [PubMed] [Google Scholar]
  16. Frost W. H.; Streeter H. W.. Study of Pollution and Natural Purification of the Ohio River: 2. Report on Surveys and Laboratory Studies Public Health Bulletin No. 143; U.S. Public Health Service: Washington DC, 1924. [Google Scholar]
  17. Phelps E. B.Stream Sanitation; John Wiley & Sons, Inc.: New York, 1944. [Google Scholar]
  18. Velz C. J.Applied Stream Sanitation, 2nd ed.; Wiley: New York, 1984. [Google Scholar]
  19. Franz E.; Semenov A. V.; Termorshuizen A. J.; De Vos O. J.; Bokhorst J. G.; Van Bruggen A. H. C. Manure-amended soil characteristics affecting the survival of E. coli O157:H7 in 36 Dutch soils. Environ. Microbiol. 2008, 10, 313–327. 10.1111/j.1462-2920.2007.01453.x. [DOI] [PubMed] [Google Scholar]
  20. Van Boekel M. A. J. S. On the use of the Weibull model to describe thermal inactivation of microbial vegetative cells. Int. J. Food Microbiol. 2002, 74, 139–159. 10.1016/S0168-1605(01)00742-5. [DOI] [PubMed] [Google Scholar]
  21. Phaiboun A.; Zhang Y.; Park B.; Kim M. Survival Kinetics of Starving Bacteria Is Biphasic and Density-Dependent. PLoS Comput. Biol. 2015, 11, e1004198. 10.1371/journal.pcbi.1004198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Blaustein R. A.; Pachepsky Y.; Hill R. L.; Shelton D. R.; Whelan G. Escherichia coli survival in waters: Temperature dependence. Water Res. 2013, 47, 569–578. 10.1016/j.watres.2012.10.027. [DOI] [PubMed] [Google Scholar]
  23. Peng X.; Murphy T.; Holden N. M. Evaluation of the effect of temperature on the die-off rate for Cryptosporidium parvum oocysts in water, soils, and feces. Appl. Environ. Microbiol. 2008, 74, 7101–7107. 10.1128/AEM.01442-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Pérez-López M. E.; Del Socorro González-Elizondo M.; López-González C.; Martínez-Prado A.; Cuevas-Rodríguez G. Aquatic macrophytes tolerance to domestic wastewater and their efficiency in artificial wetlands under greenhouse conditions. Hidrobiológica 2009, 19, 233–244. [Google Scholar]
  25. Yang Y.; Chan W. Y.; Wu C. L.; Kong R. Y. C.; Lai a. C. K. Minimizing the exposure of airborne pathogens by upper-room ultraviolet germicidal irradiation: an experimental and numerical study. J. R. Soc., Interface 2012, 9, 3184–95. 10.1098/rsif.2012.0439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Franz E.; Schijven J.; de Roda Husman A. M.; Blaak H. Survival of commensal and pathogenic Escherichia coli in soil and water: a systematic review and meta-regression analysis. Environ. Sci. Technol. 2014, 48, 6763–6771. 10.1021/es501677c. [DOI] [PubMed] [Google Scholar]
  27. Ellafi A.; Denden I.; Abdallah F. B.; Souissi I.; Bakhrouf A. Survival and adhesion ability of Shigella spp. strains after their incubation in seawater microcosms. World J. Microbiol. Biotechnol. 2009, 25, 1161–1168. 10.1007/s11274-009-9995-4. [DOI] [Google Scholar]
  28. Petterson S. R.; Ashbolt N. J. Viral risks associated with wastewater reuse: Modeling virus persistence on wastewater irrigated salad crops. Water Sci. Technol. 2001, 43, 23–26. [PubMed] [Google Scholar]
  29. Seidu R.; Sjølander I.; Abubakari A.; Amoah D.; Larbi J. A.; Stenström T. A. Modeling the die-off of E. coli and Ascaris in wastewater-irrigated vegetables: implications for microbial health risk reduction associated with irrigation cessation. Water Sci. Technol. 2013, 68, 1013. 10.2166/wst.2013.335. [DOI] [PubMed] [Google Scholar]
  30. McKellar R. C.; Peréz-Rodríguez F.; Harris L. J.; Moyne A.-l.; Blais B.; Topp E.; Bezanson G.; Bach S.; Delaquis P. Evaluation of different approaches for modeling Escherichia coli O157:H7 survival on field lettuce. Int. J. Food Microbiol. 2014, 184, 74–85. 10.1016/j.ijfoodmicro.2014.04.026. [DOI] [PubMed] [Google Scholar]
  31. Easton J. H.; Gauthier J. J.; Lalor M. M.; Pitt R. E. Die-off of pathogenic E. coli O157:H7 in sewage contaminated waters. J. Am. Water Resour. Assoc. 2005, 41, 1187–1193. 10.1111/j.1752-1688.2005.tb03793.x. [DOI] [Google Scholar]
  32. Jones S. E.; Lennon J. T. Dormancy contributes to the maintenance of microbial diversity. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 5881–5886. 10.1073/pnas.0912765107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rittershaus E. S. C.; Baek S. H.; Sassetti C. M. The normalcy of dormancy: Common themes in microbial quiescence. Cell Host Microbe 2013, 13, 643–651. 10.1016/j.chom.2013.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Ramamurthy T.; Ghosh A.; Pazhani G. P.; Shinoda S. Current Perspectives on Viable but Non-Culturable (VBNC) Pathogenic Bacteria. Frontiers in Public Health 2014, 2, 103. 10.3389/fpubh.2014.00103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Bellman R.; Åström K. J. On structural identifiability. Math. Biosci. 1970, 7, 329–339. 10.1016/0025-5564(70)90132-X. [DOI] [Google Scholar]
  36. Rothenberg T. J. Identification in Parametric Models. Econometrica 1971, 39, 577–591. 10.2307/1913267. [DOI] [Google Scholar]
  37. Cobelli C.; DiStefano J. J. Parameter and structural identifiability concepts and ambiguities: a critical review and analysis. Am. J. Physiol. 1980, 239, R7–R24. [DOI] [PubMed] [Google Scholar]
  38. Raue A.; Kreutz C.; Maiwald T.; Bachmann J.; Schilling M.; Klingmüller U.; Timmer J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. 10.1093/bioinformatics/btp358. [DOI] [PubMed] [Google Scholar]
  39. Saccomani M. P.; Audoly S.; Bellu G.; D’Angio L. A new differential algebra algorithm to test identifiability of nonlinear systems with given initial conditions. Proceedings of the 40th IEEE Conference on Decision and Control 2001, 4, 3108–3113. 10.1109/CDC.2001.980295. [DOI] [Google Scholar]
  40. Audoly S.; Bellu G.; D’Angiò L.; Saccomani M. P.; Cobelli C. Global identifiability of nonlinear models of biological systems. IEEE Trans. Biomed. Eng. 2001, 48, 55–65. 10.1109/10.900248. [DOI] [PubMed] [Google Scholar]
  41. Meshkat N.; Eisenberg M.; Distefano J. J. An algorithm for finding globally identifiable parameter combinations of nonlinear ODE models using Gröbner Bases. Math. Biosci. 2009, 222, 61–72. 10.1016/j.mbs.2009.08.010. [DOI] [PubMed] [Google Scholar]
  42. Anderson D. H.Compartmental Modeling and Tracer Kinetics, Lecture Notes in Biomathematics; Springer-Verlag, 1983; Vol. 50. [Google Scholar]
  43. Godfrey K. R.; Jones R. P.; Brown R. F. Identifiable pharmacokinetic models: the role of extra inputs and measurements. J. Pharmacokinet. Biopharm. 1980, 8, 633–648. 10.1007/BF01060058. [DOI] [PubMed] [Google Scholar]
  44. DiStefano J., IIIDynamic Systems Biology Modeling and Simulation; Academic Press, 2015. [Google Scholar]
  45. Eisenberg J. N. S.; Hubbard A.; Wade T. J.; Sylvester M. D.; LeChevallier M. W.; Levy D. A.; Colford J. M. Inferences drawn from a risk assessment compared directly with a randomized trial of a home drinking water intervention. Environ. Health Perspect. 2006, 114, 1199–1204. 10.1289/ehp.8682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Chauret C.; Chen P.; Springthrope S.; Sattar S.. Effect of environmental stressors on the survival of Cryptosporidium oocysts. In Proceedings of the American Water Works Association Water Quality Technology Conference; New Orleans, 1995. [Google Scholar]
  47. Robertson L. J.; Campbell A. T.; Smith H. V. Survival of Cryptosporidium parvum Oocysts under Various Environmental Pressures. Appl. Environ. Microbiol. 1992, 58, 3494–3500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Medema G.; Bahar M.; Schets F. M. Survival of cryptosporidium parvum, escherichia coli, faecal enterococci and clostridium perfringens in river water: influence of temperature and autochthonous microorganisms. Water Sci. Technol. 1997, 35, 249–252. 10.1016/S0273-1223(97)00267-9. [DOI] [Google Scholar]
  49. Chauret C.; Nolan K.; Chen P.; Springthorpe S.; Sattar S. Aging of Cryptosporidium parvum oocysts in river water and their susceptibility to disinfection by chlorine and monochloramine. Can. J. Microbiol. 1998, 44, 1154–1160. 10.1139/cjm-44-12-1154. [DOI] [PubMed] [Google Scholar]
  50. Campbell A. T.; Robertson L. J.; Smith H. V. Viability of Cryptosporidium parvum oocysts: Correlation of in vitro excystation with inclusion or exclusion of fluorogenic vital dyes. Appl. Environ. Microbiol. 1992, 58, 3488–3493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Robertson L. J.; Campbell A. T.; Smith H. V. In vitro excystation of Cryptosporidium parvum. Parasitology 1993, 106, 13–19. 10.1017/S003118200007476X. [DOI] [PubMed] [Google Scholar]
  52. Eisenberg J. N. S.; Lei X.; Hubbard A. H.; Brookhart M. A.; Colford J. M. The role of disease transmission and conferred immunity in outbreaks: Analysis of the 1993 Cryptosporidium outbreak in Milwaukee, Wisconsin. Am. J. Epidemiol. 2005, 161, 62–72. 10.1093/aje/kwi005. [DOI] [PubMed] [Google Scholar]
  53. DuPont H. L.; Chappell C. L.; Sterling C. R.; Okhuysen P. C.; Rose J. B.; Jakubowski W. The Infectivity of Cryptosporidium parvum in Healthy Volunteers. N. Engl. J. Med. 1995, 332, 855–859. 10.1056/NEJM199503303321304. [DOI] [PubMed] [Google Scholar]
  54. Robles-Morua A.; Mayer A. S.; Auer M. T.; Vivoni E. R. Modeling riverine pathogen fate and transport in Mexican rural communities and associated public health implications. J. Environ. Manage. 2012, 113, 61–70. 10.1016/j.jenvman.2012.08.035. [DOI] [PubMed] [Google Scholar]
  55. United States Environmental Protection Agency. Ambient Water Quality Criteria for Bacteria, 1986.
  56. Beck M. B. Water quality modeling: a review of the analysis of uncertainty. Water Resour. Res. 1987, 23, 1393–1442. 10.1029/WR023i008p01393. [DOI] [Google Scholar]
  57. Dochain D.; Vanrolleghem P.. Dynamical Modelling and Estimation in Wastewater Treatment Processes; IWA publishing, 2001. [Google Scholar]
  58. Wagener T.; McIntyre N.; Lees M.; Wheater H.; Gupta H. Towards reduced uncertainty in conceptual rainfall-runoff modelling: Dynamic identifiability analysis. Hydrol. Processes 2003, 17, 455–476. 10.1002/hyp.1135. [DOI] [Google Scholar]
  59. Liu Y.; Gupta H. V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, 1–18. 10.1029/2006WR005756.20300476 [DOI] [Google Scholar]
  60. Brun R.; Reichert P.; Künsch H. R. Practical identifiability analysis of large environmental simulation models. Water Resour. Res. 2001, 37, 1015–1030. 10.1029/2000WR900350. [DOI] [Google Scholar]
  61. DiStefano J.; Landaw E. Multiexponential, multicompartmental, and noncompartmental modeling. I. Methodological limitations and physiological interpretations. Am. J. Physiol.: Regul., Integr. Compar. Physiol. 1984, 246, R651–R664. [DOI] [PubMed] [Google Scholar]
  62. Landaw E.; DiStefano J. J. Multiexponential, multicompartmental, and noncompartmental modeling. II. Data analysis and statistical considerations. Am. J. Physiol.: Regul., Integr. Compar. Physiol. 1984, 246, R665–R677. [DOI] [PubMed] [Google Scholar]
  63. Cobelli C.; Toffolo G. Compartmental vs. noncompartmental modeling for two accessible pools. Am. J. Physiol.: Regul., Integr. Compar. Physiol. 1984, 247, R488–R496. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

es6b04030_si_001.pdf (222.4KB, pdf)

Articles from Environmental Science & Technology are provided here courtesy of American Chemical Society

RESOURCES