Abstract
Obstacles to inferring species trees from whole genome data sets range from algorithmic
and data management challenges to the wholesale discordance in evolutionary history found
in different parts of a genome. Recent work that builds trees directly from genomes by
parsing them into sets of small 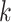 -mer strings holds promise
to streamline and simplify these efforts, but existing approaches do not account well for
gene tree discordance. We describe a “seed and extend” protocol that finds nearly exact
matching sets of orthologous
-mer strings holds promise
to streamline and simplify these efforts, but existing approaches do not account well for
gene tree discordance. We describe a “seed and extend” protocol that finds nearly exact
matching sets of orthologous 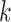 -mers and extends them to construct data
sets that can properly account for genomic heterogeneity. Exploiting an efficient suffix
array data structure, sets of whole genomes can be parsed and converted into phylogenetic
data matrices rapidly, with contiguous blocks of
-mers and extends them to construct data
sets that can properly account for genomic heterogeneity. Exploiting an efficient suffix
array data structure, sets of whole genomes can be parsed and converted into phylogenetic
data matrices rapidly, with contiguous blocks of 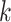 -mers
from the same chromosome, gene, or scaffold concatenated as needed. Phylogenetic trees
constructed from highly curated rice genome data and a diverse set of six other eukaryotic
whole genome, transcriptome, and organellar genome data sets recovered trees nearly
identical to published phylogenomic analyses, in a small fraction of the time, and
requiring many fewer parameter choices. Our method’s ability to retain local homology
information was demonstrated by using it to characterize gene tree discordance across the
rice genome, and by its robustness to the high rate of interchromosomal gene transfer
found in several rice species.
-mers
from the same chromosome, gene, or scaffold concatenated as needed. Phylogenetic trees
constructed from highly curated rice genome data and a diverse set of six other eukaryotic
whole genome, transcriptome, and organellar genome data sets recovered trees nearly
identical to published phylogenomic analyses, in a small fraction of the time, and
requiring many fewer parameter choices. Our method’s ability to retain local homology
information was demonstrated by using it to characterize gene tree discordance across the
rice genome, and by its robustness to the high rate of interchromosomal gene transfer
found in several rice species.
Keywords: k-mer, lineage sorting, Oryza, phylogenomics, suffix array
Construction of a phylogenetic tree from even a single gene is “hard” from the standpoint of
algorithm theory (Felsenstein 2004), yet trees are now
being inferred from entire transcriptomes (Wickett et al.
2014) or genomes (Neafsey et al. 2015) at a
scale up to a million times larger than this—across taxa as diverse in scope as land plants
(Wickett et al. 2014), viral epidemics (Worobey et al. 2014), and cancer tumors (Zhao et al. 2016). In addition to data set size, genomic
data add complexities of annotation, orthology detection, and sequence alignment
upstream of tree construction, and discordant gene trees caused by gene
duplication, deep coalescence, and lateral transfer detected downstream of
tree construction (Maddison et al. 1997; Fontaine et al. 2015; Liu
et al. 2015; Nater et al. 2015). Phylogenomic
analysis pipelines have accordingly become parameter-rich mash-ups of diverse algorithms and
toolkits (Misof et al. 2014; Wickett et al. 2014; Neafsey et al.
2015; Prum et al. 2015; Zhao et al. 2016). Moreover, although some of these upstream components
contribute substantial information about genomes, they can also introduce their own biases
into phylogenetic inference proper. For example, Zwickl et al.
(2014) highlighted annotation errors in rice phylogenomics that introduced “block
shifts” into multiple sequence alignments of genes. These affected the overall frequency
spectrum of gene trees and the final species tree reconstruction. Recent methods that avoid
annotation, alignment, and even assembly, by recoding genomes as sets of short
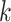 -mer strings, have shown promise to streamline
and speed up inference and make its assumptions more robust and reproducible (Gardner and Hall 2013; Bertels et al. 2014; Chan et al. 2014; Leimeister and Morgenstern 2014; Fan et al. 2015; Haubold et al.
2015).
-mer strings, have shown promise to streamline
and speed up inference and make its assumptions more robust and reproducible (Gardner and Hall 2013; Bertels et al. 2014; Chan et al. 2014; Leimeister and Morgenstern 2014; Fan et al. 2015; Haubold et al.
2015).
Using 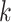 -mers sampled from sequences has been a mainstay
of several core bioinformatic tools, especially alignment and database search, for many years
(Gusfield 1997). Early attempts to use
-mers sampled from sequences has been a mainstay
of several core bioinformatic tools, especially alignment and database search, for many years
(Gusfield 1997). Early attempts to use
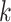 -mers for phylogenetic inference did not perform
well (Hohl and Ragan 2007), which led to a wave of
modifications to allow inexact
-mers for phylogenetic inference did not perform
well (Hohl and Ragan 2007), which led to a wave of
modifications to allow inexact 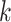 -mer matching (Leimeister and Morgenstern 2014), to include genome coordinate information between
matches (Haubold et al. 2015), and to correct
-mer matching (Leimeister and Morgenstern 2014), to include genome coordinate information between
matches (Haubold et al. 2015), and to correct
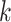 -mer-based distances for multiple hits (Fan et al. 2015; Haubold et
al. 2015). However, almost all these approaches estimate pairwise distances from
numbers of shared
-mer-based distances for multiple hits (Fan et al. 2015; Haubold et
al. 2015). However, almost all these approaches estimate pairwise distances from
numbers of shared 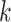 -mers, and distance-based phylogenetic methods
lose information about homology, especially positional homology, during data reduction, which
may decrease statistical robustness in tree reconstruction (Huelsenbeck 1995). Even if the magnitude of this impact is small, a potentially more
significant concern is that by reducing two genomes to a single pairwise distance, fine scale
signal about discordant phylogenetic histories across the genome is discarded, which is
inadvisable given the widespread occurrence of such discordance (Pollard et al. 2006; White et al.
2009; Zwickl et al. 2014; Nater et al. 2015).
-mers, and distance-based phylogenetic methods
lose information about homology, especially positional homology, during data reduction, which
may decrease statistical robustness in tree reconstruction (Huelsenbeck 1995). Even if the magnitude of this impact is small, a potentially more
significant concern is that by reducing two genomes to a single pairwise distance, fine scale
signal about discordant phylogenetic histories across the genome is discarded, which is
inadvisable given the widespread occurrence of such discordance (Pollard et al. 2006; White et al.
2009; Zwickl et al. 2014; Nater et al. 2015).
To keep the speed and simplicity of 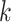 -mer based approaches but
retain information about positional homology, we combined and extended several well-tested
ideas in new ways (Gardner and Hall 2013; Leimeister and Morgenstern 2014; Fan et al. 2015; Haubold et al.
2015) and leveraged recent improvements in engineering of a key data structure (Rajasekaran and Nicolae 2014). From a set of
-mer based approaches but
retain information about positional homology, we combined and extended several well-tested
ideas in new ways (Gardner and Hall 2013; Leimeister and Morgenstern 2014; Fan et al. 2015; Haubold et al.
2015) and leveraged recent improvements in engineering of a key data structure (Rajasekaran and Nicolae 2014). From a set of
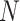 genomes, which may be at various stages of
assembly, our algorithm builds short multiple sequence alignments, or
“
genomes, which may be at various stages of
assembly, our algorithm builds short multiple sequence alignments, or
“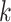 -mer blocks,” starting from approximately
matching
-mer blocks,” starting from approximately
matching 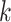 -mer “seeds” (Fig. 1) and adding adjacent short flanking sequences. Because a
-mer “seeds” (Fig. 1) and adding adjacent short flanking sequences. Because a
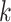 -mer block is typically too short to contain
sufficient phylogenetic information for tree construction itself, it can be pooled by gene,
contig, scaffold, chromosome, and so forth, into one or more concatenated alignments, or
“supermatrices.” At the limit, all
-mer block is typically too short to contain
sufficient phylogenetic information for tree construction itself, it can be pooled by gene,
contig, scaffold, chromosome, and so forth, into one or more concatenated alignments, or
“supermatrices.” At the limit, all 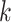 -mer blocks discovered across
the genome can be grouped into one supermatrix, but it will often be more informative to
construct sets of supermatrices in which smaller pools of
-mer blocks discovered across
the genome can be grouped into one supermatrix, but it will often be more informative to
construct sets of supermatrices in which smaller pools of 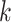 -mer blocks
reflect the local coordinates in the genome. This allows discovery of different gene tree
histories across the genome, species tree inference based on sets of “gene trees” (Liu et al. 2015; Edwards et
al. 2016), and other inferences about reticulation, hybridization, or introgression
(Huson et al. 2010).
-mer blocks
reflect the local coordinates in the genome. This allows discovery of different gene tree
histories across the genome, species tree inference based on sets of “gene trees” (Liu et al. 2015; Edwards et
al. 2016), and other inferences about reticulation, hybridization, or introgression
(Huson et al. 2010).
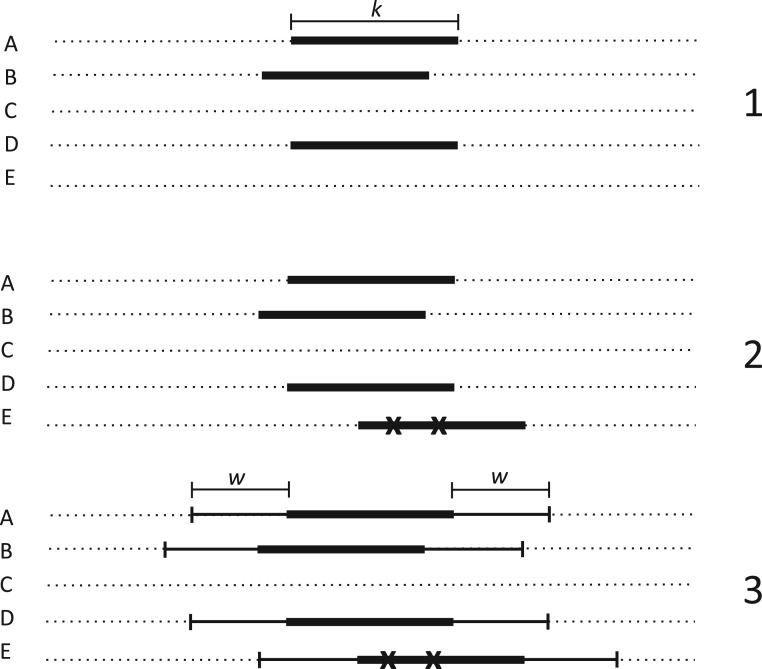
Figure 1.
Seed and extend strategy to construct 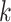 -mer blocks. Step 1: a
set of identical
-mer blocks. Step 1: a
set of identical 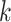 -mers is found in taxa A, B, and D. Step
2: this
-mers is found in taxa A, B, and D. Step
2: this 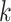 -mer block is extended in the taxon
dimension by finding additional
-mer block is extended in the taxon
dimension by finding additional 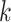 -mers that have at most
-mers that have at most
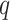 mismatches (here
mismatches (here
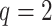 ; the black x’s) relative to the
; the black x’s) relative to the
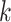 -mers found in Step 1; here block
extended to include taxon E. Step 3: the four-taxon
-mers found in Step 1; here block
extended to include taxon E. Step 3: the four-taxon 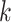 -mer
block is then extended in the genome dimension upstream and downstream of each
-mer
block is then extended in the genome dimension upstream and downstream of each
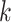 -mer by a short distance,
-mer by a short distance,
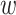 , nucleotides. Together these two
extensions yield an ungapped alignment suitable for phylogenetic analysis.
, nucleotides. Together these two
extensions yield an ungapped alignment suitable for phylogenetic analysis.
The layout of the article is as follows. First, we describe the algorithm and its
implementation details (reserving a full description of its relationship to existing methods
for discussion). Next we describe simulation experiments designed to characterize the
distribution of 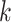 -mer blocks that may be expected in
genome-scale data sets, to predict properties of the resulting phylogenetic data sets. To
complement this, we also examine the genomic context of
-mer blocks that may be expected in
genome-scale data sets, to predict properties of the resulting phylogenetic data sets. To
complement this, we also examine the genomic context of 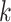 -mer blocks
discovered in a well-annotated set of complete genome sequences for rice and its wild
relatives in Oryza. Then, we examine the actual performance of the method in
seven whole genome data sets at various levels of sequence divergence, by comparing results we
obtain with published work for these taxa. This part is undertaken with supermatrix
comparisons, which still provides a useful benchmark in the literature. However, we return to
the discovery of gene tree discordance by examining collections of gene trees built from the
Oryza data, and comparing the frequency distribution of discordant
alternative trees inferred by our method compared to a more conventional approach using
annotated and aligned genes. Finally, we consider limitations of the method and possible
extensions.
-mer blocks
discovered in a well-annotated set of complete genome sequences for rice and its wild
relatives in Oryza. Then, we examine the actual performance of the method in
seven whole genome data sets at various levels of sequence divergence, by comparing results we
obtain with published work for these taxa. This part is undertaken with supermatrix
comparisons, which still provides a useful benchmark in the literature. However, we return to
the discovery of gene tree discordance by examining collections of gene trees built from the
Oryza data, and comparing the frequency distribution of discordant
alternative trees inferred by our method compared to a more conventional approach using
annotated and aligned genes. Finally, we consider limitations of the method and possible
extensions.
MATERIALS AND METHODS
Overview of Algorithm for Finding Homologous k-mer Blocks
Our algorithm uses a “seed and extend” strategy to build sets of orthologous sequences in
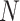 related species. The seed consists of a
set of exact matching
related species. The seed consists of a
set of exact matching 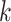 -mers, where
-mers, where 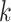 is
chosen large enough so that a
is
chosen large enough so that a 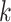 -mer is unique in its own genome (to avoid
paralogy), but small enough that it is present in at least
-mer is unique in its own genome (to avoid
paralogy), but small enough that it is present in at least 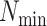 taxa (Fig. 1). The seed is then extended in taxon space by using an algorithm
that efficiently finds
taxa (Fig. 1). The seed is then extended in taxon space by using an algorithm
that efficiently finds 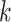 -mers in additional taxa that have at most
-mers in additional taxa that have at most
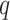 mismatches relative to the
mismatches relative to the
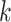 -mers in the original block, where
-mers in the original block, where
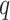 is small relative to
is small relative to
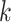 . Together these
. Together these 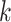 -mers
form an ungapped alignment. This is then extended in genome space by appending and
prepending
-mers
form an ungapped alignment. This is then extended in genome space by appending and
prepending 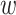 nucleotides upstream and downstream to
it, where
nucleotides upstream and downstream to
it, where 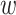 is of length on the order of
is of length on the order of
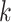 . This final ungapped alignment is called
a “
. This final ungapped alignment is called
a “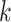 -mer block.” By choosing
-mer block.” By choosing
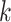 relatively large, but keeping
relatively large, but keeping
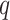 and
and 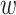 small
we limit inclusion of paralogous sequences, cap sequence divergence, and increase the
reliability of the ungapped alignment as an approximation to full optimization-based
multiple sequence alignment (Gusfield 1997).
small
we limit inclusion of paralogous sequences, cap sequence divergence, and increase the
reliability of the ungapped alignment as an approximation to full optimization-based
multiple sequence alignment (Gusfield 1997).
Implementation
To scale this algorithm to gigabase genomes, running time and memory usage are both
critical. To find the initial exact-matching 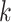 -mer seeds, the
-mer seeds, the
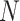 sequences, each of length
sequences, each of length
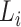 , are concatenated into a string,
, are concatenated into a string,
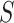 , of length
, of length 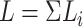 . If reverse complements are
included, these are simply concatenated to the end of this string, now with length
2
. If reverse complements are
included, these are simply concatenated to the end of this string, now with length
2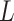 . The string is stored as a
memory-efficient-sorted suffix array containing the coordinates of all
. The string is stored as a
memory-efficient-sorted suffix array containing the coordinates of all
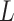 (or 2
(or 2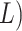 suffixes. This data structure requires
suffixes. This data structure requires 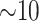 bytes/nucleotide.
This array is constructed by a new, fast sorting method that is highly scalable (Rajasekaran and Nicolae 2014), having worst case run
times of
bytes/nucleotide.
This array is constructed by a new, fast sorting method that is highly scalable (Rajasekaran and Nicolae 2014), having worst case run
times of 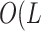 log
log 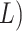 and
usually much better than this in practice. Once the suffix array is sorted, exact
and
usually much better than this in practice. Once the suffix array is sorted, exact
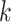 -mer matches form contiguous blocks in the
array. The entire data set can then be processed merely by traversing the array from
beginning to end, checking to see if
-mer matches form contiguous blocks in the
array. The entire data set can then be processed merely by traversing the array from
beginning to end, checking to see if 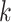 -mers are (i) unique in
their genomes, (ii) present in
-mers are (i) unique in
their genomes, (ii) present in 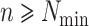 genomes, and (iii) not overlapping with any
genomes, and (iii) not overlapping with any 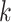 -mer blocks that have
already been found.
-mer blocks that have
already been found.
The first extension to include additional taxa with up to 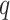 mismatches is done by “filtration” (Pevzner and Waterman
1995). For any
mismatches is done by “filtration” (Pevzner and Waterman
1995). For any 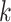 -mer that matches at most
-mer that matches at most
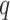 times with another
times with another
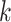 -mer, there must exist at least one
substring of length
-mer, there must exist at least one
substring of length 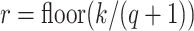 that matches
exactly between the two. Thus, mismatches can be found by looking for exact matches of
length
that matches
exactly between the two. Thus, mismatches can be found by looking for exact matches of
length 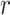 in the suffix array, extending them the
appropriate distance in the genome sequence and checking to see if indeed there are
in the suffix array, extending them the
appropriate distance in the genome sequence and checking to see if indeed there are
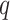 or fewer mismatches. Lookups in the
suffix array for an arbitrary
or fewer mismatches. Lookups in the
suffix array for an arbitrary 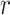 -mer are done efficiently with a binary
search.
-mer are done efficiently with a binary
search. 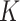 -mers that satisfy the mismatch criteria
are also checked for uniqueness and lack of overlap with other blocks. Extension to add
the flanking sequences of each
-mers that satisfy the mismatch criteria
are also checked for uniqueness and lack of overlap with other blocks. Extension to add
the flanking sequences of each 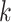 -mer is achieved
trivially by fetching the coordinates of the
-mer is achieved
trivially by fetching the coordinates of the 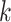 -mers in the
-mers in the
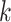 -mer block and referring back to the
original stored genome sequence,
-mer block and referring back to the
original stored genome sequence, 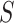 .
.
Genomes may be input as a set of chromosomes, scaffolds, contigs, or other assembly
units. The start and stop coordinates of each are maintained so that
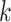 -mer blocks can later be pooled according
to these assembly units if desired. Low complexity
-mer blocks can later be pooled according
to these assembly units if desired. Low complexity 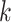 -mers
are detected from the frequency spectrum of three-mer frequencies (Morgulis et al. 2006), and excluded to limit fruitless enumeration of
matches in highly repetitive regions.
-mers
are detected from the frequency spectrum of three-mer frequencies (Morgulis et al. 2006), and excluded to limit fruitless enumeration of
matches in highly repetitive regions.
A software implementation hakmer (“ omology-
omology- ware
k-mers”) is free and open source C/C
ware
k-mers”) is free and open source C/C code
(http://sourceforge.net/projects/hakmer/). Generic 64 bit
C
code
(http://sourceforge.net/projects/hakmer/). Generic 64 bit
C code for the suffix array library is
also available (https://github.com/mariusmni/radixSA64).
code for the suffix array library is
also available (https://github.com/mariusmni/radixSA64).
Parameters Affecting 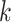 -mer Block Discovery
-mer Block Discovery
Here we define several terms to let us quantify properties of the data sets produced by
building 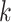 -mer blocks. These properties depend on
the sequence input and the parameter choices in hakmer, including
-mer blocks. These properties depend on
the sequence input and the parameter choices in hakmer, including
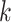 -mer length,
-mer length, 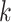 ; the
maximum number of mismatches,
; the
maximum number of mismatches, 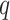 ; minimum required taxonomic coverage,
; minimum required taxonomic coverage,
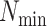 ; and width of flanking
sequence,
; and width of flanking
sequence, 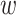 . The output, consisting of
. The output, consisting of
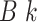 -mer blocks, can be characterized by
three quantities. The first is data use efficiency,
-mer blocks, can be characterized by
three quantities. The first is data use efficiency,
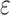 , which is the fraction of the
, which is the fraction of the
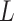 bases in the input that are present in
the
bases in the input that are present in
the 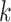 -mer blocks in the output. The second is
taxon coverage,
-mer blocks in the output. The second is
taxon coverage, 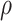 , the number of
elements out of the
, the number of
elements out of the 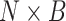 set of sequences possibly found
among the
set of sequences possibly found
among the 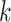 -mer blocks that actually are present,
since some taxa may not contain all
-mer blocks that actually are present,
since some taxa may not contain all 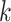 -mers found in other taxa
in a
-mers found in other taxa
in a 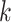 -mer block. It is guaranteed to be at
least
-mer block. It is guaranteed to be at
least 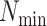 /
/ but may
be more. Taxon coverage is an important predictor of impacts of missing data on
phylogenomic inference (Sanderson et al. 2010,
2011, 2015).
but may
be more. Taxon coverage is an important predictor of impacts of missing data on
phylogenomic inference (Sanderson et al. 2010,
2011, 2015).
Low taxon coverage can induce “terraces” in phylogenetic inference, which are sets of
trees with identical likelihood or parsimony scores (Sanderson et al. 2011, 2015). For a given
collection of  -mer blocks and its pattern of taxon
coverage, it is possible to compute the size of the terrace in which any particular tree
is imbedded. More generally, however, the probability that terraces will exist is a
function of the coverage, the number of taxa, and number of
-mer blocks and its pattern of taxon
coverage, it is possible to compute the size of the terrace in which any particular tree
is imbedded. More generally, however, the probability that terraces will exist is a
function of the coverage, the number of taxa, and number of  -mer
blocks. In particular, the number of blocks needed to ensure less than a 5% chance that
terraces exist for any unrooted tree is given by
-mer
blocks. In particular, the number of blocks needed to ensure less than a 5% chance that
terraces exist for any unrooted tree is given by
(Sanderson et al. 2010, theorem 2). Based on this idea,
we define a third quantity, the k-mer block differential ,
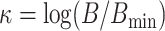 , which is
positive when there are sufficient number of blocks discovered to avoid terraces and
negative when terraces are more likely.
, which is
positive when there are sufficient number of blocks discovered to avoid terraces and
negative when terraces are more likely.
Expected Distributions of 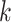 -mer Blocks:
Simulations
-mer Blocks:
Simulations
To assay the impact of algorithm parameters on the distribution of
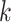 -mer blocks discovered, genome sequences
were simulated on a star phylogeny with 50 leaves using an HKY model in Seq-Gen 1.3.3
(Rambaut and Grassly 1997). Sequence lengths were
set to 1 Mb, and sequence divergence between root and each leaf was set to range from 0.01
to 0.10 substitutions/site, with equal divergences for all edges. A star phylogeny is the
worst case scenario for
-mer blocks discovered, genome sequences
were simulated on a star phylogeny with 50 leaves using an HKY model in Seq-Gen 1.3.3
(Rambaut and Grassly 1997). Sequence lengths were
set to 1 Mb, and sequence divergence between root and each leaf was set to range from 0.01
to 0.10 substitutions/site, with equal divergences for all edges. A star phylogeny is the
worst case scenario for 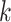 -mer block discovery since all sequences
are maximally divergent from each other. These data sets were then run in
hakmer across a range of parameter values to characterize patterns in
their
-mer block discovery since all sequences
are maximally divergent from each other. These data sets were then run in
hakmer across a range of parameter values to characterize patterns in
their 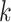 -mer block structure (Figs. 2–4).
-mer block structure (Figs. 2–4).
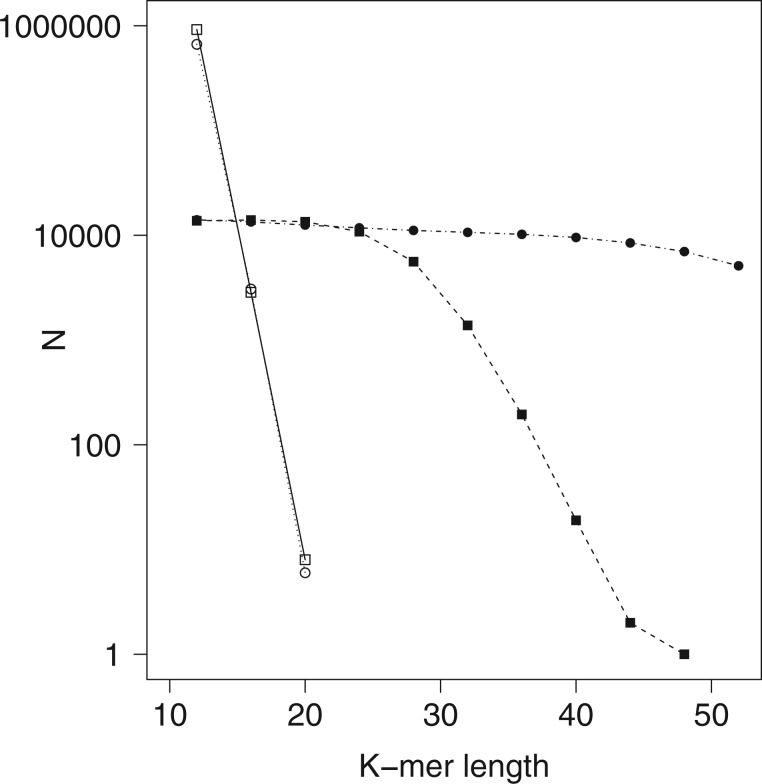
Figure 2.
Effect of 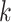 -mer length on number of
-mer length on number of
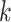 -mer blocks discovered (closed
shapes) or number of paralogs (open shapes) in simulations. Circles: sequence
-mer blocks discovered (closed
shapes) or number of paralogs (open shapes) in simulations. Circles: sequence
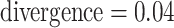 ; squares:
sequence
; squares:
sequence 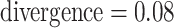 .
.
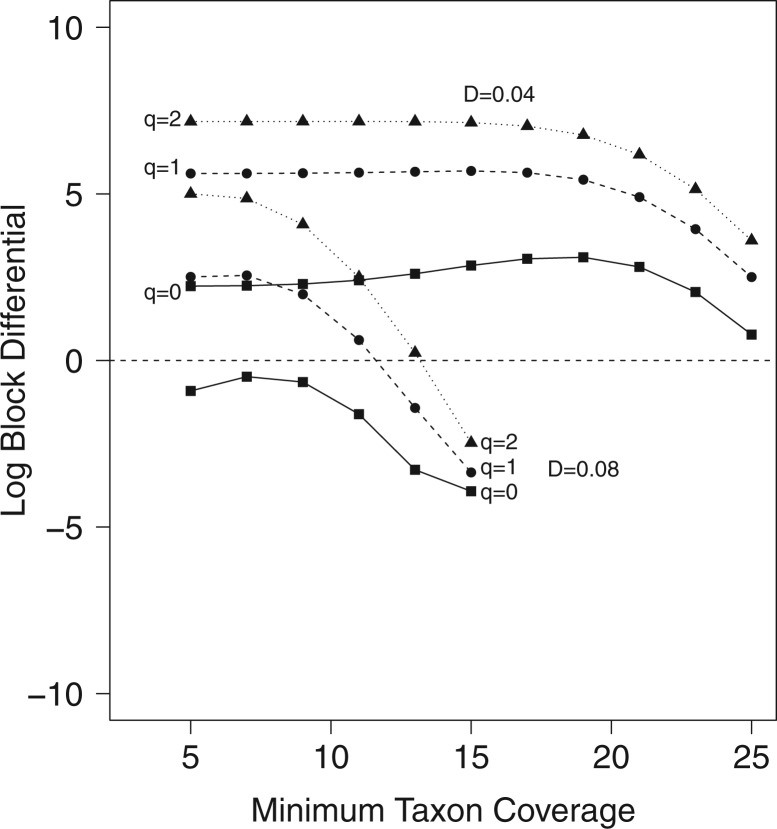
Figure 4.
Log block differential, 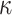 , versus
minimum taxon coverage,
, versus
minimum taxon coverage, 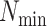 , in
simulations, for two levels of sequence divergence,
, in
simulations, for two levels of sequence divergence, 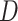 ,
and three levels of allowed mismatches,
,
and three levels of allowed mismatches, 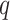 .
.
Distribution of 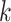 -mer Blocks in Oryza Complete Genome
Sequences
-mer Blocks in Oryza Complete Genome
Sequences
We used genome annotations for Oryza species (downloaded from the
Gramene website: ftp://ftp.ensemblgenomes.org/pub/plants/release-27/gff3/) to identify the
genomic context for each 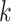 -mer block. Custom PERL scripts were used
to match
-mer block. Custom PERL scripts were used
to match 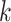 -mer coordinates with chromosome number
and other features identified in the GFF files. In particular, we checked whether
-mer coordinates with chromosome number
and other features identified in the GFF files. In particular, we checked whether
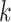 -mers were associated with genes and, more
strictly, with coding sequences of protein-coding genes. We also tracked whether each
sequence from a species was found on the same chromosome in different species or,
alternatively, whether interchromosomal transfers had occurred.
-mers were associated with genes and, more
strictly, with coding sequences of protein-coding genes. We also tracked whether each
sequence from a species was found on the same chromosome in different species or,
alternatively, whether interchromosomal transfers had occurred.
Phylogenomic Analyses of Seven Genome-Scale Data Sets
To gauge downstream performance of our algorithm in reconstructing species trees from
genome data, we constructed seven genome data sets spanning different time depths in the
tree of life, different classes of genomic data, and input sizes ranging from 31 million
to 9.4 billion base pairs and from 8 to 663 taxa (Table
1). These included two plant organellar genome data sets, a whole transcriptome
data set for the angiosperm order Caryophyllales, and four whole genome data sets, three
from angiosperms and one from Anopheles mosquitoes. In our first
analyses, we focused on comparing global supermatrices built from
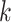 -mers across the genome to results on
supermatrix phylogenomic analyses in the published work. Our data sets were constructed to
streamline data retrieval from GenBank and maximize taxon sampling, and our taxon samples,
therefore, did not match exactly taxon sampling in the larger published analyses.
-mers across the genome to results on
supermatrix phylogenomic analyses in the published work. Our data sets were constructed to
streamline data retrieval from GenBank and maximize taxon sampling, and our taxon samples,
therefore, did not match exactly taxon sampling in the larger published analyses.
Table 1.
Genomic data sets used in this study (sorted by increasing data set size)
| Clade | Data | Time depth (Ma) | No. of taxa | No. of bases (millions) | No. of sequences
|
Data source |
|---|---|---|---|---|---|---|
| Land plants | Mitochondrial genomes | 450
|
93 | 31.3 | 93 | GenBank |
| Angiosperms | Plastid genomes | 139
|
663 | 98.3 | 663 | GenBank |
| Caryophyllales | Transcriptomes | 107
|
67 | 1388.2 | 1.61 million | Dryad |
| Oryza | Whole genomes | 15
|
11 | 3731.9 | 20,071 | Gramene rel. 27 |
| Anopheles | Whole genomes | 100
|
17 | 3871.0 | 148,163 | GenBank |
| Fabaceae (Papilionoideae) | Whole genomes | 60
|
8 | 5168.4 | 130,672 | GenBank |
| Eudicots | Whole genomes | 136
|
24 | 9402.8 | 298,907 | Phytozome 10.3 |
 That is, genomes, chromosomes, scaffolds, contigs, treated as
disjoint assembly units;
That is, genomes, chromosomes, scaffolds, contigs, treated as
disjoint assembly units;  ages
from Sanderson and Doyle (2001),
ages
from Sanderson and Doyle (2001),
 Magallón et al. (2015),
Magallón et al. (2015),  Tang et al. (2010),
Tang et al. (2010),  Neafsey et al. (2015), and
Neafsey et al. (2015), and  Lavin et al. (2005).
Lavin et al. (2005).
Genome sequences were input without any preprocessing. For each data set, a variety of parameter sets were examined to identify an optimal set of run conditions that would minimize paralogy, maximize data use efficiency, and minimize terrace problems (Table 2). The reverse complement option was used in all data sets except for the plastid genome data sets, where the (usual) presence of a large inverted repeat was frequently bypassed by the algorithm’s protocol to avoid paralogy. Thus, ignoring reverse complements actually increased the amount of data extracted.
Table 2.
Selected  -mer block algorithm parameter
settings and resulting data set characteristics obtained for each genome data
set
-mer block algorithm parameter
settings and resulting data set characteristics obtained for each genome data
set
| Clade |
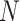
|
 (index
(index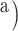
|
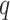
|
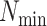
|
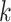 -mer blocks
-mer blocks |
Alignment length |
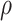
|
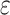
|
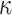
|
|---|---|---|---|---|---|---|---|---|---|
| Land plant mitochondrial | 93 | 24 (0) | 2 | 10 | 2279 | 145,856 | 0.25 |
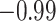
|
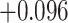
|
| Angiosperm plastid | 663 | 28 (5) | 2 | 100 | 1711 | 116,348 | 0.51 |
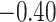
|
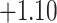
|
| Caryophyllales | 67 | 28 (0) | 2 | 15 | 684 | 46,512 | 0.58 |
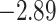
|
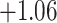
|
| Oryza | 11 | 32 (0) | 0 | 11 | 35,646 | 2,566,512 | 1.00 |

|
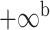
|
| Anopheles | 17 | 32 (0) | 2 | 12 | 38,648 | 2,782,656 | 0.89 |
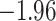
|
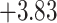
|
| Fabaceae | 8 | 32 (1) | 2 | 4 | 33,609 | 2,419,848 | 0.82 |
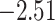
|
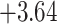
|
| Eudicots | 24 | 28 (0) | 2 | 5 | 31,897 | 2,168,996 | 0.36 |
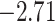
|
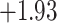
|
 Index indicates the numeral in the supermatrix file name
corresponding to this run and these parameters (see Supplementary Materials
available on Dryad);
Index indicates the numeral in the supermatrix file name
corresponding to this run and these parameters (see Supplementary Materials
available on Dryad);  Undefined, because
Undefined, because
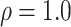 .
.
Phylogenetic Tree Construction
Sets of 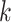 -mer blocks were concatenated as
supermatrices, either across all blocks identified from the genome sequence data, or in
some cases at more local scales within genomes, determined by genome coordinates. All
phylogenetic trees were inferred using maximum likelihood implemented in RAxML v. 8.04
(Stamatakis 2014), with the default rapid hill
climbing algorithm and a GTRGAMMA model used for data sets with
-mer blocks were concatenated as
supermatrices, either across all blocks identified from the genome sequence data, or in
some cases at more local scales within genomes, determined by genome coordinates. All
phylogenetic trees were inferred using maximum likelihood implemented in RAxML v. 8.04
(Stamatakis 2014), with the default rapid hill
climbing algorithm and a GTRGAMMA model used for data sets with 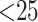 taxa and the GTRCAT model used for the two genome data sets with
taxa and the GTRCAT model used for the two genome data sets with 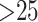 taxa. Bootstrap estimates of support for clades were obtained using the RAxML -b option
(full, slow bootstrap), except for the two taxon-rich data sets which used the faster -x
bootstrap option (Supplementary Figs.
1–8 available on Dryad at http://datadryad.org/resource/doi:10.5061/dryad.96b0h).
taxa. Bootstrap estimates of support for clades were obtained using the RAxML -b option
(full, slow bootstrap), except for the two taxon-rich data sets which used the faster -x
bootstrap option (Supplementary Figs.
1–8 available on Dryad at http://datadryad.org/resource/doi:10.5061/dryad.96b0h).
Discovery and Characterization of Intra-genomic Discordance
We constructed sets of gene trees in the Oryza data set by concatenating
neighboring 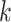 -mer blocks into data sets of
-mer blocks into data sets of
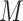 blocks each, where
blocks each, where
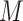 was 25, 100, or 1000. Bootstrap majority
rule ML trees for the 1426 data sets for
was 25, 100, or 1000. Bootstrap majority
rule ML trees for the 1426 data sets for 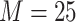 set were constructed
using RAxML (raxmlHPC-AVX -m GTRGAMMA -x seed2 -# 100 -s alignmentFile -n outfilesname -p
seed1). Each of these data sets comprised
set were constructed
using RAxML (raxmlHPC-AVX -m GTRGAMMA -x seed2 -# 100 -s alignmentFile -n outfilesname -p
seed1). Each of these data sets comprised 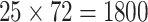 bp
alignments. The discordance pattern among these gene trees was quantified and visualized
as a consensus network in SplitsTree v. 4.10 (Kloepper and
Huson 2008), with a threshold setting of 0.05 on split frequencies. This diagram
captures the set of alternative gene tree splits that occur in at least 5% of all input
gene trees.
bp
alignments. The discordance pattern among these gene trees was quantified and visualized
as a consensus network in SplitsTree v. 4.10 (Kloepper and
Huson 2008), with a threshold setting of 0.05 on split frequencies. This diagram
captures the set of alternative gene tree splits that occur in at least 5% of all input
gene trees.
To compare these results to a benchmark, we inferred the same kind of consensus network for the 6015 gene trees assembled for the same taxa in Stein J.C. et al. (submitted for publication). That set comprised alignments of whole gene regions (introns, exons, and flanking gene sequence), aligned with PRANK (Loytynoja and Goldman 2008), for which optimal trees were constructed using ML in GARLI (Zwickl 2006), with short length branches collapsed into polytomies. We compared both the graph structure of the consensus network and the split frequencies along sets of parallel edges in the network (Fig. 5).
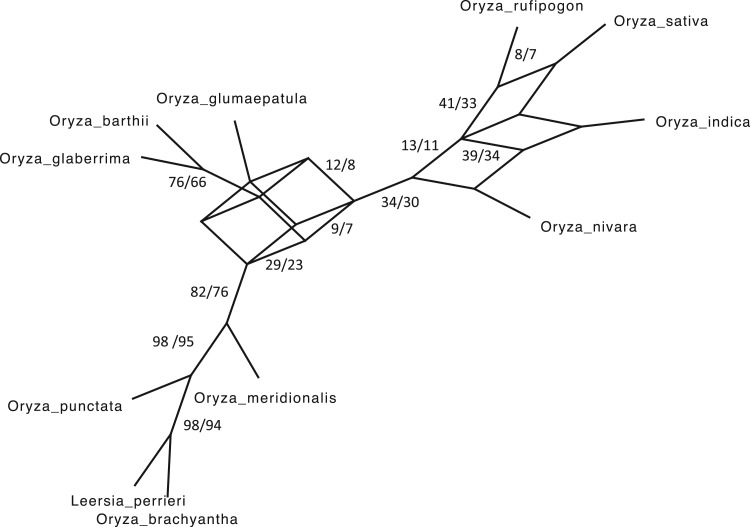
Figure 5.
Similarity of Oryza gene tree discordance patterns across the
whole genome inferred using our 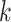 -mer block method
versus conventional phylogenomic pipeline. Diagram is a consensus network of gene
trees (Huson et al. 2010) (threshold
-mer block method
versus conventional phylogenomic pipeline. Diagram is a consensus network of gene
trees (Huson et al. 2010) (threshold
 0.05), and has the same topology
whether constructed from 1426 sets of 25 contiguous
0.05), and has the same topology
whether constructed from 1426 sets of 25 contiguous 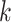 -mer blocks or from trees inferred from
alignments of 6015 annotated rice genes (Stein J.C. et al., submitted for
publication). Branch lengths are labeled with pairs of support values obtained in
the
-mer blocks or from trees inferred from
alignments of 6015 annotated rice genes (Stein J.C. et al., submitted for
publication). Branch lengths are labeled with pairs of support values obtained in
the 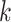 -mer data set (left number) and
phylogenomic data set (right), indicating the frequency of splits supported among
the collection of gene trees.
-mer data set (left number) and
phylogenomic data set (right), indicating the frequency of splits supported among
the collection of gene trees.
Interchromosomal Transfers in Oryza
For the Oryza analysis, each 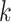 -mer block was recoded
as an ordered list of 11 integers, such that, for each, the first integer is the
chromosome number for the block’s sequence in Leersia, the second the
chromosome number in O. barthii, and so on in lexical order of the 11
taxon names: for example, 1-1-1-1-1-1-1-1-1-3-1 (chromosome 1 in Leersia,
chromosome 1 in O. barthii, etc.). Then this list of lists was sorted
according to chromosome, and then within chromosome by the start coordinate position of
the Leersia
-mer block was recoded
as an ordered list of 11 integers, such that, for each, the first integer is the
chromosome number for the block’s sequence in Leersia, the second the
chromosome number in O. barthii, and so on in lexical order of the 11
taxon names: for example, 1-1-1-1-1-1-1-1-1-3-1 (chromosome 1 in Leersia,
chromosome 1 in O. barthii, etc.). Then this list of lists was sorted
according to chromosome, and then within chromosome by the start coordinate position of
the Leersia -mer block sequence. Runs of consecutive
identical integer patterns were identified for any pattern having more than one chromosome
number: these represent potentially homologous sequence transferred between chromosomes.
The length of these runs in the list was then translated into corresponding genome
coordinates determined from the start positions of the
-mer block sequence. Runs of consecutive
identical integer patterns were identified for any pattern having more than one chromosome
number: these represent potentially homologous sequence transferred between chromosomes.
The length of these runs in the list was then translated into corresponding genome
coordinates determined from the start positions of the  -mer
sequences in Leersia. Finally, the five longest of these runs was
extracted for further analysis, which corresponded to runs spanning
-mer
sequences in Leersia. Finally, the five longest of these runs was
extracted for further analysis, which corresponded to runs spanning
 250,000 nt in Leersia
(Supplementary Table 1
available on Dryad). Phylogenetic trees were reconstructed using RAxML (as described
above) for the concatenated sets of
250,000 nt in Leersia
(Supplementary Table 1
available on Dryad). Phylogenetic trees were reconstructed using RAxML (as described
above) for the concatenated sets of  -mer blocks for each of
the five runs of
-mer blocks for each of
the five runs of 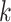 -mer blocks (Supplementary Fig. 8 available on
Dryad).
-mer blocks (Supplementary Fig. 8 available on
Dryad).
RESULTS
Distribution of k-mer Blocks: Simulation Results
Simulation experiments showed that the length of 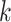 -mers
must be large enough to make matches within the same genome due to paralogy (or chance)
low, but if
-mers
must be large enough to make matches within the same genome due to paralogy (or chance)
low, but if 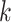 was too large, few
was too large, few
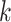 -mer blocks having at least
-mer blocks having at least
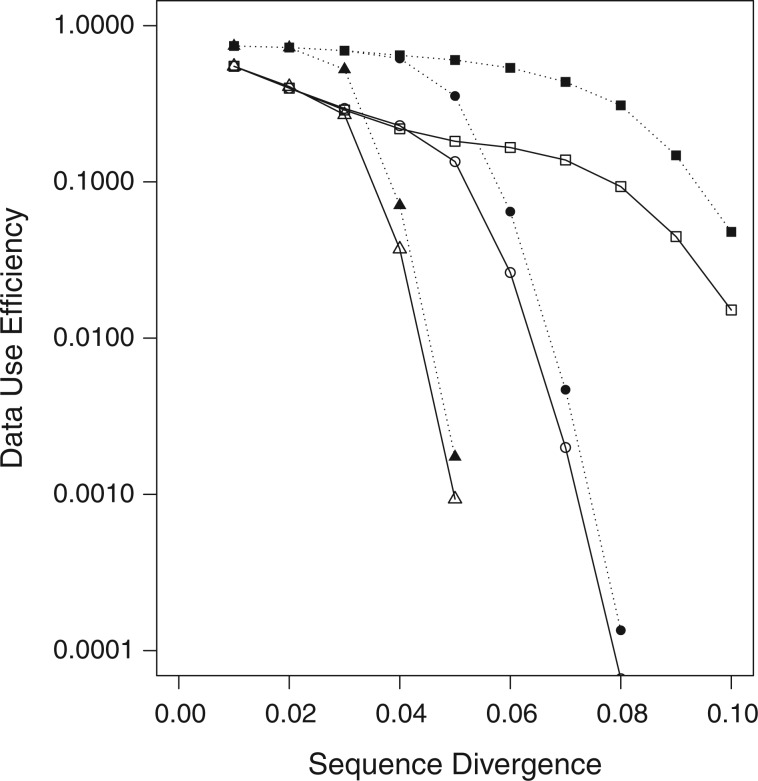
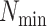 taxa were found (Fig. 2). Data use efficiency,
taxa were found (Fig. 2). Data use efficiency, 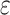 , was very high for low levels of
sequence divergence (
, was very high for low levels of
sequence divergence (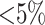 ), but dropped off quickly above
that (Fig. 3). However, the reduction in
), but dropped off quickly above
that (Fig. 3). However, the reduction in
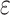 at higher sequence divergences
was ameliorated by reducing
at higher sequence divergences
was ameliorated by reducing 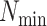 , the minimum required taxon
coverage, and increasing the number of mismatches allowed,
, the minimum required taxon
coverage, and increasing the number of mismatches allowed, 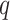 (Fig. 3).
(Fig. 3).
Figure 3.
Data use efficiency versus sequence divergence in simulations at differing levels
of taxon coverage and mismatches. Squares: 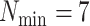 ; circles:
; circles:
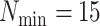 ; triangles:
; triangles:
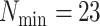 . Open shapes:
. Open shapes:
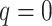 ; closed shapes:
; closed shapes:
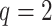 .
.
If 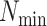 is less than
is less than
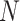 , however, there will likely be
, however, there will likely be
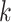 -mer blocks with data missing for some
taxa, which can introduce terraces of trees with equal optimality scores (Sanderson et al. 2011, 2015). However, the probability of terraces emerging from our protocol,
estimated from the log block differential,
-mer blocks with data missing for some
taxa, which can introduce terraces of trees with equal optimality scores (Sanderson et al. 2011, 2015). However, the probability of terraces emerging from our protocol,
estimated from the log block differential, 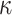 , is high only
when there is a combination of high sequence divergence and high minimum taxon coverage.
These conditions lead to a drop in the number of
, is high only
when there is a combination of high sequence divergence and high minimum taxon coverage.
These conditions lead to a drop in the number of 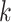 -mer
blocks found, making terraces more likely for a given level of missing data. However,
increasing data use efficiency, reducing
-mer
blocks found, making terraces more likely for a given level of missing data. However,
increasing data use efficiency, reducing 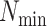 , or allowing
more mismatches reduces the probability of terraces (Fig.
4).
, or allowing
more mismatches reduces the probability of terraces (Fig.
4).
Distribution of 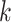 -mer Blocks: Genomes of Oryza
-mer Blocks: Genomes of Oryza
Of the 35,646 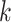 -mer blocks having unique exact matches in
all 10 species of Oryza (plus outgroup, Leersia), 95.5%
of these mapped to assembled chromosomes in all 11 species. Of these, 76.6% of blocks were
found on homologous chromosomes in all species, with the remaining 23.4% having a
nonhomologous chromosome in at least one species. Most of the latter were in O.
nivara and O. meridionalis. These putative interchromosomal
transfers often involved contiguous runs of
-mer blocks having unique exact matches in
all 10 species of Oryza (plus outgroup, Leersia), 95.5%
of these mapped to assembled chromosomes in all 11 species. Of these, 76.6% of blocks were
found on homologous chromosomes in all species, with the remaining 23.4% having a
nonhomologous chromosome in at least one species. Most of the latter were in O.
nivara and O. meridionalis. These putative interchromosomal
transfers often involved contiguous runs of 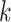 -mer blocks, with the
largest spanning some 415 kb (as measured in Leersia). Furthermore, the
intrachromosomal locations of
-mer blocks, with the
largest spanning some 415 kb (as measured in Leersia). Furthermore, the
intrachromosomal locations of 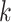 -mer blocks were not
random. Among the
-mer blocks were not
random. Among the 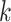 -mer blocks mapping to chromosomes, 88% of
-mer blocks mapping to chromosomes, 88% of
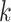 -mers proper were located within genes,
and 71% of the
-mers proper were located within genes,
and 71% of the 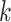 -mer blocks consisted of
-mer blocks consisted of
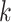 -mers located in genes in all 11 species.
Most of the latter (70%) were localized within genes to CDS (coding) regions, as opposed
to UTRs or introns. On average only 34% of genome length is annotated as genic in these 11
species, so
-mers located in genes in all 11 species.
Most of the latter (70%) were localized within genes to CDS (coding) regions, as opposed
to UTRs or introns. On average only 34% of genome length is annotated as genic in these 11
species, so 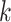 -mer blocks are clearly enriched in these
more conserved regions.
-mer blocks are clearly enriched in these
more conserved regions.
Phylogenomic Analyses of Seven Genome-Scale Data Sets
Running times to construct data sets for further phylogenetic analysis ranged from a few
minutes to a few hours for the largest input. The latter required substantial memory
(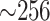 GB), but this is comparable to
the memory required to assemble its genomes from raw sequence read data in the first
place, but with trivial running times by comparison. Weeks or months of conventional
informatics processing upstream of tree building were reduced to minutes to hours by
sidestepping annotation and alignment.
GB), but this is comparable to
the memory required to assemble its genomes from raw sequence read data in the first
place, but with trivial running times by comparison. Weeks or months of conventional
informatics processing upstream of tree building were reduced to minutes to hours by
sidestepping annotation and alignment.
Data use efficiency ranged from 40% in the plastid genome analysis to 0.1% in the
transcriptome data, but the number of 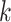 -mer blocks retained by
the algorithm remained large, ranging from
-mer blocks retained by
the algorithm remained large, ranging from 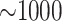 in the smaller
organellar genomes and transcriptome data sets to
in the smaller
organellar genomes and transcriptome data sets to 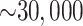 in all the whole genome data
sets (Table 2). In the largest, eudicot, data set
18.3 million nucleotides were present in the final concatenated “supermatrix” of
in all the whole genome data
sets (Table 2). In the largest, eudicot, data set
18.3 million nucleotides were present in the final concatenated “supermatrix” of
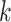 -mer blocks (24 taxa
-mer blocks (24 taxa
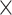 2.16 million bp, not counting
missing data from partial taxon coverage), despite this representing just 0.2% of the
original sequence data in these genomes.
2.16 million bp, not counting
missing data from partial taxon coverage), despite this representing just 0.2% of the
original sequence data in these genomes.
Phylogenetic trees constructed by maximum likelihood methods using supermatrices of all
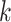 -mer blocks in each data set recovered
trees nearly identical to published trees in all seven data sets, including close
agreement with bootstrap estimates of statistical significance of clades (Supplementary Figs. 1–8 available on
Dryad). The few exceptions were revealing. For example, a few placements of taxa in the
eudicot whole genome tree (Supplementary Fig. 7 available on Dryad) are at odds with widely cited
relationships based largely on plastid genome data (Soltis
et al. 2011), but these apparent oddities are actually quite consistent with
recent phylogenomic studies using nuclear or mitochrondrial data (Sun et al. 2015). See Appendix for full discussion of each case
study.
-mer blocks in each data set recovered
trees nearly identical to published trees in all seven data sets, including close
agreement with bootstrap estimates of statistical significance of clades (Supplementary Figs. 1–8 available on
Dryad). The few exceptions were revealing. For example, a few placements of taxa in the
eudicot whole genome tree (Supplementary Fig. 7 available on Dryad) are at odds with widely cited
relationships based largely on plastid genome data (Soltis
et al. 2011), but these apparent oddities are actually quite consistent with
recent phylogenomic studies using nuclear or mitochrondrial data (Sun et al. 2015). See Appendix for full discussion of each case
study.
Discovery and Characterization of Intragenomic Discordance
A high level of intragenomic phylogenetic discordance in the Oryza data,
not detectable in the supermatrix analysis of all data (Supplementary Fig. 4 available on
Dryad), was easily detectable by pooling small contiguous sets of
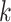 -mer blocks to build local phylogenies of
different genomic regions. The spectrum of 1426 local trees, each built from a
concatenation of 25 neighboring
-mer blocks to build local phylogenies of
different genomic regions. The spectrum of 1426 local trees, each built from a
concatenation of 25 neighboring 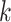 -mer blocks, was
characterized using a consensus network (Fig. 5;
Huson et al. 2010), which indicated that most of
this conflict is within the species group closest to O. sativa,
especially involving the South American species O.glumaepatula, which is
likely to have undergone extensive introgression (Stein J.C. et al., submitted for
publication). The consensus network structure matches exactly the network derived from an
independent set of 6015 gene trees constructed using conventional phylogenomic methods for
the same taxa from the same raw genome sequence data (Stein J.C. et al., submitted for
publication), and the frequency distribution of conflicting splits was very similar
between the two (Fig. 5).
-mer blocks, was
characterized using a consensus network (Fig. 5;
Huson et al. 2010), which indicated that most of
this conflict is within the species group closest to O. sativa,
especially involving the South American species O.glumaepatula, which is
likely to have undergone extensive introgression (Stein J.C. et al., submitted for
publication). The consensus network structure matches exactly the network derived from an
independent set of 6015 gene trees constructed using conventional phylogenomic methods for
the same taxa from the same raw genome sequence data (Stein J.C. et al., submitted for
publication), and the frequency distribution of conflicting splits was very similar
between the two (Fig. 5).
A second example supports the overall robustness of the 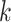 -mer
method to structural changes in the genome. We followed up on the discovery of significant
numbers of interchromosomal gene transfers by reconstructing phylogenetic trees for the
five transfers having sequence lengths
-mer
method to structural changes in the genome. We followed up on the discovery of significant
numbers of interchromosomal gene transfers by reconstructing phylogenetic trees for the
five transfers having sequence lengths 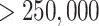 nt (Supplementary Table 1 available on
Dryad). In each case, despite genome sequence having been translocated to another
chromosome in at least one species, the trees obtained from the orthologous regions on
these different chromosomes were consistent with trees from genomic regions not exhibiting
these transfers, mirroring in particular the discordant placement of O.
glumaepatula seen in Figure 5 (see also
Supplementary Fig. 8 available
on Dryad).
nt (Supplementary Table 1 available on
Dryad). In each case, despite genome sequence having been translocated to another
chromosome in at least one species, the trees obtained from the orthologous regions on
these different chromosomes were consistent with trees from genomic regions not exhibiting
these transfers, mirroring in particular the discordant placement of O.
glumaepatula seen in Figure 5 (see also
Supplementary Fig. 8 available
on Dryad).
DISCUSSION
In this article, we developed and tested a method for quickly building phylogenetic data
sets from whole genomes at large scale. The core of the method is the enumeration of
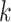 -mer blocks, which are sets of nearly exact
matching
-mer blocks, which are sets of nearly exact
matching 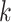 -mers and their flanking sequence. If chosen
correctly, these have a high probability of orthology. The method can find tens of thousands
of
-mers and their flanking sequence. If chosen
correctly, these have a high probability of orthology. The method can find tens of thousands
of 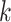 -mer blocks in whole genomes in minutes to
hours of computing time, avoiding compute-expensive data processing steps of annotation and
alignment, and controlling for limitations caused by sequence divergence and missing data.
Genome sequence data can be input “as is” from assemblies at contig, scaffold, or whole
chromosome scales, or any mixture thereof.
-mer blocks in whole genomes in minutes to
hours of computing time, avoiding compute-expensive data processing steps of annotation and
alignment, and controlling for limitations caused by sequence divergence and missing data.
Genome sequence data can be input “as is” from assemblies at contig, scaffold, or whole
chromosome scales, or any mixture thereof.
Our approach to testing the performance of this method was two-fold: first, we used
simulation together with highly annotated genome test data from Oryza to
discover the properties of sets of 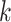 -mer blocks generated by
our protocol; and second, we evaluated the performance of tree inference per se from these
-mer blocks generated by
our protocol; and second, we evaluated the performance of tree inference per se from these
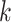 -mer blocks by analysis of seven diverse
genomic data sets and comparison to published phylogenetic trees for the same taxa. A key
finding of our simulations was that
-mer blocks by analysis of seven diverse
genomic data sets and comparison to published phylogenetic trees for the same taxa. A key
finding of our simulations was that 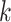 -mer block discovery will
eventually be degraded at high levels of sequence divergence through a combination of
finding fewer
-mer block discovery will
eventually be degraded at high levels of sequence divergence through a combination of
finding fewer 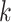 -mers blocks, and, in those that are found,
having matches to fewer taxa (and hence more missing data). However, the simulations also
indicated the extent to which these problems could be ameliorated by changing
-mers blocks, and, in those that are found,
having matches to fewer taxa (and hence more missing data). However, the simulations also
indicated the extent to which these problems could be ameliorated by changing
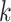 , increasing the number of allowed mismatches,
, increasing the number of allowed mismatches,
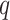 , and increasing the tolerance for
, and increasing the tolerance for
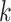 -mer blocks with missing taxa, but doing so in
such a way that problems with phylogenetic terraces are avoided (Sanderson et al. 2011, 2015). Not
surprisingly, when we examined where
-mer blocks with missing taxa, but doing so in
such a way that problems with phylogenetic terraces are avoided (Sanderson et al. 2011, 2015). Not
surprisingly, when we examined where 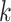 -mer blocks were found in
a well-annotated test case of Oryza complete genome sequence, they are
clearly concentrated in conserved coding regions, but they are not exclusively found there.
Thus, to the extent that conventional annotation-based phylogenomic work tends to focus
exclusively on protein-coding genes, this method is able to go beyond these regions to
include other highly conserved parts of the genome.
-mer blocks were found in
a well-annotated test case of Oryza complete genome sequence, they are
clearly concentrated in conserved coding regions, but they are not exclusively found there.
Thus, to the extent that conventional annotation-based phylogenomic work tends to focus
exclusively on protein-coding genes, this method is able to go beyond these regions to
include other highly conserved parts of the genome.
Analyses of seven empirical studies suggested that the method works well over a range of
phylogenomic scales at various time depths in the tree of life. To some extent this
reflected trade-offs between average substitution rates in different kinds of genomes and
the size of those genomes. Conserved plant mitochondrial and plastid genomes, for example,
could be pushed to time depths of hundreds of millions of years, when combined with small
mismatch allowances, 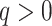 , because their average substitution rates
are so slow. Though relatively small genomes, these rates and parameter settings still led
to discovery of enough
, because their average substitution rates
are so slow. Though relatively small genomes, these rates and parameter settings still led
to discovery of enough 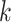 -mer blocks to infer a high-quality tree. In
whole nuclear genome data sets, the faster average rates might be anticipated to make up for
the difficulty in finding
-mer blocks to infer a high-quality tree. In
whole nuclear genome data sets, the faster average rates might be anticipated to make up for
the difficulty in finding 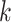 -mer blocks at higher sequence divergences,
and indeed this was true. There were no issues discovering vast numbers of
-mer blocks at higher sequence divergences,
and indeed this was true. There were no issues discovering vast numbers of
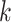 -mer blocks in rice and
Anopheles, the ages of which are only
-mer blocks in rice and
Anopheles, the ages of which are only 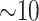 –15 Ma, but it was also still possible to
find a reasonable number in angiosperms at time depths ranging from 50 to 100 Ma.
–15 Ma, but it was also still possible to
find a reasonable number in angiosperms at time depths ranging from 50 to 100 Ma.
We judged performance by comparing simple supermatrix data sets obtained by concatenating
all 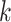 -mer blocks to results of supermatrix analyses
published in the literature. Topologies and support values were remarkably consistent
between published trees relying on conventional annotation/alignment data processing and
those we obtained using
-mer blocks to results of supermatrix analyses
published in the literature. Topologies and support values were remarkably consistent
between published trees relying on conventional annotation/alignment data processing and
those we obtained using 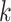 -mers blocks. The very few areas of
disagreement were almost all mirrored by alternative data sets and analyses found in the
literature, especially those obtained from different genomes, such as plastid versus nuclear
genome data sets for angiosperms (Soltis et al. 2011;
Sun et al. 2015). Taxon samples were different
between our trees and trees from the literature. We opted to sample the largest sets of
whole genome sequences currently in GenBank, rather than the exact sample from the article
in the literature. This made comparisons using something like a tree–tree distance
problematic, as we would have to delete many taxa unique to one or the other tree. The
extensive exposition in the Appendix is meant to leverage our experience with some of these
phylogenetic problems and provides a hopefully more interpretable and falsifiable set of
conclusions about performance.
-mers blocks. The very few areas of
disagreement were almost all mirrored by alternative data sets and analyses found in the
literature, especially those obtained from different genomes, such as plastid versus nuclear
genome data sets for angiosperms (Soltis et al. 2011;
Sun et al. 2015). Taxon samples were different
between our trees and trees from the literature. We opted to sample the largest sets of
whole genome sequences currently in GenBank, rather than the exact sample from the article
in the literature. This made comparisons using something like a tree–tree distance
problematic, as we would have to delete many taxa unique to one or the other tree. The
extensive exposition in the Appendix is meant to leverage our experience with some of these
phylogenetic problems and provides a hopefully more interpretable and falsifiable set of
conclusions about performance.
However, the results of supermatrix analyses in phylogenomics studies may well typically only reflect a “first order” approximation to the species phylogeny that is most accurate in regions of the tree in which biological sources of discordance such as incomplete lineage sorting are absent. To obtain a better, “second order” approximation it is now clear that reconstruction of individual gene trees, by which we mean any appropriately local region in a genome, is necessary. Numerous methods of inferring species trees from such gene trees are now available (Liu et al. 2015), but rather than examining such methods explicitly in these data sets, we focused on characterizing the discordance in the gene trees proper, as this is ultimately a key determinant of the species tree. We took a similar tack in phylogenomic analysis of data for the chromosome 3 short arm in Oryza (Zwickl et al. 2014) to understand the sources of biases in these gene tree discordance patterns. Moreover, in both that study and our more recent whole genome phylogenomic analysis of Oryza using conventional annotation/alignment pipelines (Stein J.C. et al., submitted for publication), supermatrix methods and species tree inference using gene trees as input returned the same results.
Because rice genome data exhibit widespread gene tree discordance (Zou et al. 2008; Cranston et al.
2010; Zhang et al. 2014; Zwickl et al. 2014; Stein J.C. et al., submitted for
publication), we used it to test the power of our 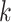 -mer block method to
retain critical information about homology in the context of discordance. We examined (i)
intragenomic conflict in phylogenetic signal and (ii) interchromosomal transfers identified
via the
-mer block method to
retain critical information about homology in the context of discordance. We examined (i)
intragenomic conflict in phylogenetic signal and (ii) interchromosomal transfers identified
via the 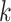 -mer blocks. The frequency distribution of
gene trees obtained by Stein J.C. et al. (submitted for publication) using conventional
methods, and by using pools of nearby
-mer blocks. The frequency distribution of
gene trees obtained by Stein J.C. et al. (submitted for publication) using conventional
methods, and by using pools of nearby 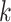 -mer blocks, was nearly
identical (Fig. 5), suggesting that the full arsenal of
species tree inference methods now available could be used with
-mer blocks, was nearly
identical (Fig. 5), suggesting that the full arsenal of
species tree inference methods now available could be used with 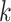 -mer
block data sets. The only caveat to this is that enough coordinate information must be
available to allow pooling of nearby
-mer
block data sets. The only caveat to this is that enough coordinate information must be
available to allow pooling of nearby 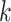 -mer blocks (see below in
“Limitations, Extensions, and Prospects” section).
-mer blocks (see below in
“Limitations, Extensions, and Prospects” section).
The potential of the 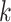 -mer block method to grapple with data sets
having complex discordant signals, however, was well illustrated by examining patterns of
interchromosomal transfer in Oryza. A few species of Oryza
exhibit large numbers of regions on certain chromosomes that evidently are homologous to
regions on different chromosomes in the remaining species. This complex pattern of homology
(or conceivably assembly errors in some cases) is evident in pairwise global alignments of
all chromosomes across Oryza (see Gramene rel. 50 at http://www.gramene.org), but how to exploit it has not been so clear. Runs of
-mer block method to grapple with data sets
having complex discordant signals, however, was well illustrated by examining patterns of
interchromosomal transfer in Oryza. A few species of Oryza
exhibit large numbers of regions on certain chromosomes that evidently are homologous to
regions on different chromosomes in the remaining species. This complex pattern of homology
(or conceivably assembly errors in some cases) is evident in pairwise global alignments of
all chromosomes across Oryza (see Gramene rel. 50 at http://www.gramene.org), but how to exploit it has not been so clear. Runs of
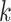 -mer blocks having the same chromosomal
distribution patterns were easy to find and their pooled phylogenetic histories were quite
similar to the gene tree distributions found in gene trees not undergoing transfers. This
indicates that
-mer blocks having the same chromosomal
distribution patterns were easy to find and their pooled phylogenetic histories were quite
similar to the gene tree distributions found in gene trees not undergoing transfers. This
indicates that 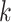 -mer blocks can be used to directly uncover
new sources of gene tree discordance within a genome, and yet are robust enough that the
gene trees inferred from them correctly mimic those from regions of the genome not
undergoing transfers.
-mer blocks can be used to directly uncover
new sources of gene tree discordance within a genome, and yet are robust enough that the
gene trees inferred from them correctly mimic those from regions of the genome not
undergoing transfers.
Relationship of hakmer to Other Methods
Our method uses some techniques found in previous work, including especially the use of
approximate 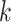 -mer matching (though we use a different
implementation), and the anchors together with flanking ungapped alignments, but it also
differs from all of them in key ways. Most importantly, it builds ungapped multiple
sequence alignments rather than distance matrices, thus preserving information about local
homologies within the genome, and it effectively insures orthology between species by
forcing exact or approximate
-mer matching (though we use a different
implementation), and the anchors together with flanking ungapped alignments, but it also
differs from all of them in key ways. Most importantly, it builds ungapped multiple
sequence alignments rather than distance matrices, thus preserving information about local
homologies within the genome, and it effectively insures orthology between species by
forcing exact or approximate 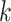 -mer matches to be long enough to be
single copy within a genome (Fig. 2).
-mer matches to be long enough to be
single copy within a genome (Fig. 2).
Hakmer is similar to kSNP in certain respects (Gardner and Hall 2013; Gardner et al.
2015). Their method is aimed at SNP detection for phylogenetic reconstruction and
other problems. It finds 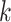 -mers (with
-mers (with 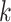 odd)
having exactly one mismatch that is flanked symmetrically by (
odd)
having exactly one mismatch that is flanked symmetrically by (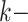 1)/2
exact matches on either side, and uses the mismatch as phylogenetic information. In
contrast, hakmer finds
1)/2
exact matches on either side, and uses the mismatch as phylogenetic information. In
contrast, hakmer finds 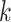 -mers with up to
-mers with up to
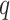 mismatches and then uses both the
mismatches and then uses both the
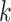 -mers and flanking regions of length
-mers and flanking regions of length
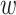 in the multiple sequence alignment.
Hakmer should, therefore, be useful to deeper phylogenetic depths, and
less prone to paralogy problems, because hakmer allows
in the multiple sequence alignment.
Hakmer should, therefore, be useful to deeper phylogenetic depths, and
less prone to paralogy problems, because hakmer allows
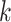 to be set large enough to essentially
guarantee a single match per genome, while also allowing more than just a single mismatch
in the extended block, and including additional flanking regions for additional
phylogenetic information. kSNP uses MUMmer’s suffix tree data structures (Kurtz et al. 2004) to find additional matches among
genomes, which requires more memory than our suffix array to index positions of matches
across all genomes without any speed improvement (Leimeister and Morgenstern 2014).
to be set large enough to essentially
guarantee a single match per genome, while also allowing more than just a single mismatch
in the extended block, and including additional flanking regions for additional
phylogenetic information. kSNP uses MUMmer’s suffix tree data structures (Kurtz et al. 2004) to find additional matches among
genomes, which requires more memory than our suffix array to index positions of matches
across all genomes without any speed improvement (Leimeister and Morgenstern 2014).
Chan et al. (2014) reviewed the performance of
several pairwise distance methods, which use functions of the number of exact
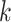 -mer matches between genomes of different
species. They compared performance to what would be obtained from multiple sequence
alignments using sequence data simulated under a wide variety of interesting evolutionary
models. Fan et al. (2015) estimate a pairwise
distance based on the number of shared exact matching
-mer matches between genomes of different
species. They compared performance to what would be obtained from multiple sequence
alignments using sequence data simulated under a wide variety of interesting evolutionary
models. Fan et al. (2015) estimate a pairwise
distance based on the number of shared exact matching 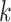 -mers,
but they also attempt to correct for multiple hits in the same
-mers,
but they also attempt to correct for multiple hits in the same 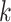 -mer by
reference to both a Poisson process model of base substitution and a model generating
homoplasy in the
-mer by
reference to both a Poisson process model of base substitution and a model generating
homoplasy in the 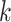 -mers that depends on
-mers that depends on
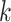 -mer frequencies and structure.
-mer frequencies and structure.
Not all pairwise distance methods require 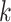 -mers of fixed length.
Ulitsky et al. (2006) compute the pairwise
distance between genomes as the average over all start positions in sequence 1 of the
lengths of the longest exact matches in sequence 2. Leimeister and Morgenstern (2014) extended this method by allowing up to
-mers of fixed length.
Ulitsky et al. (2006) compute the pairwise
distance between genomes as the average over all start positions in sequence 1 of the
lengths of the longest exact matches in sequence 2. Leimeister and Morgenstern (2014) extended this method by allowing up to
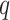 mismatches. They implemented this with an
“extended” suffix array data structure. Haubold et al.
(2015) compute pairwise distances by finding two anchor points between two
genomes, where an anchor is a maximal exact match found in both genomes. They then use the
ungapped alignment between anchors to compute a corrected distance measure.
mismatches. They implemented this with an
“extended” suffix array data structure. Haubold et al.
(2015) compute pairwise distances by finding two anchor points between two
genomes, where an anchor is a maximal exact match found in both genomes. They then use the
ungapped alignment between anchors to compute a corrected distance measure.
Several methods use unassembled short read sequence data aligned to reference genomes to build alignments and then trees. Bertels et al. (2014) criticized potential biases of some such methods that align reads to a single reference genome, which they attempt to correct by identifying SNPs from reads mapped to several reference genomes simultaneously. These approaches require computationally relatively expensive short read aligners at their core, which limits scalability. Moreover, avoiding paralogous sequences in the same genome is fundamentally difficult in unassembled data, and Bertels et al. (2014) try to limit this by a weighting scheme based on how aligned reads map to multiple places in reference genomes. To achieve the level of performance seen in large genome data sets, we found it necessary to work with assembled genomes with hakmer.
Limitations, Extensions, and Prospects
Our method is designed to gain a rapid and accurate phylogenetic foothold in large and
complex genomic data sets across taxa at moderate levels of sequence divergence. It is not
ideal when sequence divergence is so large that there are few 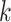 -mers
shared by a substantial fraction of taxa and/or flanking regions are so diverged that they
require formal multiple alignment algorithms. By the same token, in deep phylogenies there
may well be issues with composition bias or saturation that require careful model fitting
that may be degraded by having samples of short stretches of the genome rather than long
aligned blocks. Nor is our method necessary when taxa are so closely
related that very long stretches of exact matches are frequent between genomes (much
longer than our
-mers
shared by a substantial fraction of taxa and/or flanking regions are so diverged that they
require formal multiple alignment algorithms. By the same token, in deep phylogenies there
may well be issues with composition bias or saturation that require careful model fitting
that may be degraded by having samples of short stretches of the genome rather than long
aligned blocks. Nor is our method necessary when taxa are so closely
related that very long stretches of exact matches are frequent between genomes (much
longer than our 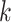 -mers); these can be discovered by
existing exact algorithms such as those in MUMmer (Kurtz
et al. 2004), or by invoking very fast heuristics like BLAST (Altschul et al. 1997), which will perform well at such
high levels of sequence identity.
-mers); these can be discovered by
existing exact algorithms such as those in MUMmer (Kurtz
et al. 2004), or by invoking very fast heuristics like BLAST (Altschul et al. 1997), which will perform well at such
high levels of sequence identity.
Several possible strategies may increase the domain of reasonable problem instances for
this method. Increasing 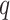 , the mismatch limit, obviously detects
more divergent
, the mismatch limit, obviously detects
more divergent 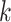 -mers, and running times for algorithms
for matching
-mers, and running times for algorithms
for matching 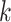 -mers with
-mers with 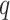 mismatches increase with
mismatches increase with 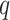 sublinearly (Nicolae and Rajasekaran 2015; in fact at best at
sublinearly (Nicolae and Rajasekaran 2015; in fact at best at
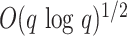 ), but in our
implementation this is combined with binary searches of the whole suffix array, which adds
considerable overhead. Increasing
), but in our
implementation this is combined with binary searches of the whole suffix array, which adds
considerable overhead. Increasing 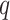 runs the risk of
finding
runs the risk of
finding 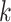 -mer blocks with highly divergent flanking
sequences as well, necessitating gapped alignment protocols. It might be more productive
to increase the length of the flanking regions,
-mer blocks with highly divergent flanking
sequences as well, necessitating gapped alignment protocols. It might be more productive
to increase the length of the flanking regions, 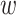 , directly, which adds
phylogenetically variable sites roughly at a rate proportional to
, directly, which adds
phylogenetically variable sites roughly at a rate proportional to
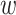 . One strategy to avoid the inevitable
alignment problems that also increase in probability with
. One strategy to avoid the inevitable
alignment problems that also increase in probability with
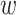 would be to trigger a formal multiple
sequence alignment algorithm if
would be to trigger a formal multiple
sequence alignment algorithm if 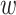 exceeds some threshold.
Running time for this often scales as
exceeds some threshold.
Running time for this often scales as 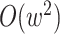 in
practice, however, and would get quite expensive unless the number of taxa is kept low.
Alternatively, the extension length could be chosen adaptively using techniques like those
used in sequence database searches, such as extending the
in
practice, however, and would get quite expensive unless the number of taxa is kept low.
Alternatively, the extension length could be chosen adaptively using techniques like those
used in sequence database searches, such as extending the 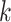 -mer
block as an ungapped alignment until the running alignment score drops by some threshold
amount from its peak value, as in BLAST (Altschul et al.
1997).
-mer
block as an ungapped alignment until the running alignment score drops by some threshold
amount from its peak value, as in BLAST (Altschul et al.
1997).
In general, sets of genomes are mixtures of less and more conserved regions, so our
analyses based on 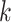 -mer matches preferentially extracts a
subset of these genomes, the properties of which might be biased with respect to
phylogenetic inference. This sort of ascertainment bias seems much more likely to affect
inferences derived from branch lengths or associated with rates, including
coalescent-based species tree inference perhaps, than it does simple gene tree topology
reconstruction (Costa et al. 2016), but this remains
to be investigated for our method.
-mer matches preferentially extracts a
subset of these genomes, the properties of which might be biased with respect to
phylogenetic inference. This sort of ascertainment bias seems much more likely to affect
inferences derived from branch lengths or associated with rates, including
coalescent-based species tree inference perhaps, than it does simple gene tree topology
reconstruction (Costa et al. 2016), but this remains
to be investigated for our method.
To fully exploit the power of species tree inference methods that allow gene tree
discordance, we expect that pooling of nearby 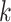 -mer blocks will be
needed. This means in general that multiple
-mer blocks will be
needed. This means in general that multiple 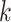 -mer blocks must be
available at the scaffold level in genome assemblies to make pooling worthwhile. If
sequence divergence is high, there may be too few
-mer blocks must be
available at the scaffold level in genome assemblies to make pooling worthwhile. If
sequence divergence is high, there may be too few 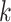 -mer
blocks present on the average scaffold for pooling. This was not a problem in the
Oryza or Anopheles data sets, which have large N50
values, but would have been more problematic in the other whole genome data sets having
more heterogeneity in assembly quality, and certainly in the transcriptome data set, which
is intrinsically limited in the length of its assembly unit by the size of a transcript.
The same remedies for high sequence divergence described above can be helpful to reduce
the average distance between blocks, by increasing the number of blocks discovered per
unit coordinate distance.
-mer
blocks present on the average scaffold for pooling. This was not a problem in the
Oryza or Anopheles data sets, which have large N50
values, but would have been more problematic in the other whole genome data sets having
more heterogeneity in assembly quality, and certainly in the transcriptome data set, which
is intrinsically limited in the length of its assembly unit by the size of a transcript.
The same remedies for high sequence divergence described above can be helpful to reduce
the average distance between blocks, by increasing the number of blocks discovered per
unit coordinate distance.
In conclusion, our experience with this 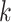 -mer based phylogenomic
approach on real data sets suggests that it is a rapid and effective way to tease apart
not just the primary phylogenetic signal one would obtain from more conventional
supermatrix analyses but also more nuanced signals arising from discordant histories in
the genomes. Though both simulations and empirical analyses suggest it ultimately is
limited by sequence divergence, the phylogenetic scope of its applicability appears to be
quite broad. In plant data sets, it provided useful results for nuclear genome data to
depths of 50–100 Ma and for slower evolving plastid and mitochondrial genomes back to the
origin of angiosperms and land plants at 140/450 Ma, respectively. The method offers
dramatically increased speed, reproducibility, and simplicity of data analysis, but it is
not without cost. Only further experience will demonstrate whether this kind of
high-throughput phylogenomics can be applied sufficiently broadly in the tree of life (and
with sufficient accuracy) to compete with more exhaustive conventional approaches.
-mer based phylogenomic
approach on real data sets suggests that it is a rapid and effective way to tease apart
not just the primary phylogenetic signal one would obtain from more conventional
supermatrix analyses but also more nuanced signals arising from discordant histories in
the genomes. Though both simulations and empirical analyses suggest it ultimately is
limited by sequence divergence, the phylogenetic scope of its applicability appears to be
quite broad. In plant data sets, it provided useful results for nuclear genome data to
depths of 50–100 Ma and for slower evolving plastid and mitochondrial genomes back to the
origin of angiosperms and land plants at 140/450 Ma, respectively. The method offers
dramatically increased speed, reproducibility, and simplicity of data analysis, but it is
not without cost. Only further experience will demonstrate whether this kind of
high-throughput phylogenomics can be applied sufficiently broadly in the tree of life (and
with sufficient accuracy) to compete with more exhaustive conventional approaches.
SUPPLEMENTARY MATERIAL
Data available from the Dryad Digital Repository: http://datadryad.org/resource/doi:10.5061/dryad.96b0h.
FUNDING
This work was supported by the US National Science Foundation [PGRP-1026200 to M.J.S.; DEB-1353815 to M.J.S. and M.M.M.].
Supplementary Material
Acknowledgments
We thank Dan Gusfield for suggesting suffix arrays; XSEDE for computational resources; and Mike Steel, Derrick Zwickl, Carlos Machado, and the entire Oryza Genome Evolution group for advice and criticism.
Appendix: Detailed Results of Phylogenomic Analyses of Seven Data Sets
Land plants: mitochondrial genomes.
Our bootstrap tree (Supplementary Fig. 1 available on Dryad) for 87 taxa has areas of strong and weak support. We can compare it to the 41-gene mitochondrial analysis of Liu et al. (2014), by pruning our tree to the taxa found in theirs. Only two differences emerged. In their tree, Oryza is one nearest neighbor interchange (NNI) closer to Triticum, and in their tree the hornworts are sister to vascular plants, whereas in ours hornworts are sister to mosses, albeit with weak support. The uncertain position of hornworts figured prominently in Liu et al.’s (2014) arguments for the need to compensate for convergent base compositional shifts causing conflicting phylogenetic signals in the deeper part of land plant phylogeny (cf. their figure 1). In an analysis of 17 chloroplast genes primarily for bryophytes, Chang and Graham (2014) agreed with the remaining relationships within the mosses indicated by our tree, although they also found the hornworts sister to vascular plants.
Within angiosperms, there are two areas of poor to medium support in our tree. The first
is associated with the position of Vaccinium macrocarpon, which although
is near its traditionally accepted place as sister to the rest of the asterids (Soltis et al. 2011) in our tree, it is in a polytomy.
In the RAxML optimal tree (data not shown), it is found on a short branch within that
clade, as sister to our representatives from Asterales (Helianthus and
Daucus). A more surprising outlier is the aberrant position of the
clubmoss Selaginella, which should be sister to the other clubmoss in our
sample, Huperzia. Instead, in our bootstrap tree, it is in a polytomy
with asterid and rosid angiosperms. More precisely, in the RAxML optimal tree (data not
shown), it is nested within the genus Cucumis (cucumber). Bootstrap
support in this entire area of the tree is low, suggesting that
Selaginella is behaving as a “rogue taxon” (Aberer et al. 2013), which is also supported by the fact that it is
present in very few  -mer blocks, indicating low homology with
other genomes in our data set. Because it hits with 99% identity (and 84% overlap) to the
Selaginella chloroplast genome, it may be a scaffold mistakenly
annotated as mitochondrial when it is in fact plastid (Banks et al. 2011). The cucumber sample (GenBank accession NC_016004.1) with
which this problematic Selaginella genome grouped in the optimal tree is
also unusual, as it is from a second mitochondrial chromosome found in that species. It
also has few
-mer blocks, indicating low homology with
other genomes in our data set. Because it hits with 99% identity (and 84% overlap) to the
Selaginella chloroplast genome, it may be a scaffold mistakenly
annotated as mitochondrial when it is in fact plastid (Banks et al. 2011). The cucumber sample (GenBank accession NC_016004.1) with
which this problematic Selaginella genome grouped in the optimal tree is
also unusual, as it is from a second mitochondrial chromosome found in that species. It
also has few  -mer blocks, indicating low homology to
the rest of the data.
-mer blocks, indicating low homology to
the rest of the data.
Like our tree based on nuclear genomes of eudicots (Supplementary Fig. 7 available on
Dryad), our mitochondrial genome tree weakly suggests Vitis is outside
asterids  rosids and that the
“Celastrales–Oxalidales–Malpighiales” (COM) clade (represented here only by
Ricinus) is again closer to malvids than to rosids (see below for
further discussion).
rosids and that the
“Celastrales–Oxalidales–Malpighiales” (COM) clade (represented here only by
Ricinus) is again closer to malvids than to rosids (see below for
further discussion).
Angiosperms: plastid genomes.
Our tree (Supplementary Fig. 2
available on Dryad) for 663 taxa had strong support throughout. Major relationships along
the backbone, as well as among the approximately 42 orders represented, were nearly
identical to those in recently published phylogenies derived from multiple genomic
compartments (Soltis et al. 2011) or from plastid
genomes (Ruhfel et al. 2014) with fewer taxa.
Exceptions include that our tree placed Ceratophyllum as sister to the
monocots with weak support, instead of sister to eudicots (Moore et al. 2007; Soltis et al. 2011;
Ruhfel et al. 2014), although support for that
placement in other studies is also generally weak and sensitive to the data partitioning
scheme (Moore et al. 2007; Ruhfel et al. 2014). Our only sample from Pandanales, the
mycoheterotrophic Sciaphila densiflora, was on a very long branch in the
RAxML optimal ML tree (data not shown) and placed in a polytomy with Asparagales and the
commelinid clade. Sciaphila was also found on a long branch in the
original analysis associated with the publication of its highly unusual reduced plastid
genome, which is only 21 kbp in length (Lam et al.
2015). The only other significant departure from previous published phylogenies
is for Cypripedium macranthos (Orchidaceae). Unlike the other two members
of this genus represented in our tree, this taxon is grouped outside the orchids (but
still within the Asparagales), with Eustrephus (Asparagaceae). A
megablast search against GenBank’s nucleotide database shows equally good hits to members
of Arecaceae, Bromeliaceae, and Asparagaceae with 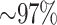 identity over
identity over
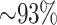 its length, and it has been found
on a long branch in previous trees (Luo et al.
2014). Our other plastid genomes from Cypripedium all hit to
members of Orchidaceae in BLAST searches, indicating that the plastid genome for
C. macranthos is an outlier. A handful of other genera were not
monophyletic in our bootstrap tree, but in each case a few NNI moves would restore
monophyly. Plastid genome evolution is so slow that it is rarely used for species-level
relationships within genera; it is certainly possible that whole plastid genomes sampled
via
its length, and it has been found
on a long branch in previous trees (Luo et al.
2014). Our other plastid genomes from Cypripedium all hit to
members of Orchidaceae in BLAST searches, indicating that the plastid genome for
C. macranthos is an outlier. A handful of other genera were not
monophyletic in our bootstrap tree, but in each case a few NNI moves would restore
monophyly. Plastid genome evolution is so slow that it is rarely used for species-level
relationships within genera; it is certainly possible that whole plastid genomes sampled
via  -mers are also not ideal at such a low
taxonomic level.
-mers are also not ideal at such a low
taxonomic level.
Caryophyllales: transcriptomes.
Our bootstrap tree of 67 taxa (Supplementary Fig. 3 available on Dryad) was fully resolved and all but six
clades were supported  90% (most 100%). This tree agreed with
that of Yang et al. (2015: their figure S1) at
every node but one, this involving a simple NNI within the genus involving
Portulaca cryptopetala within Portulaca. Yang et al.’s
analysis was based on 1122 putative orthologous loci identified from the set of all
transcriptomes.
90% (most 100%). This tree agreed with
that of Yang et al. (2015: their figure S1) at
every node but one, this involving a simple NNI within the genus involving
Portulaca cryptopetala within Portulaca. Yang et al.’s
analysis was based on 1122 putative orthologous loci identified from the set of all
transcriptomes.
Oryza: whole genomes.
Our bootstrap tree (Supplementary Fig. 4 available on Dryad) for 10 species of Oryza and the outgroup Leersia is identical to that obtained by Stein J.C. et al. (submitted for publication) for the same species, including the 100% bootstrap support estimates at each node of the tree. Stein et al. used 6015 single copy orthologous genes across all 12 chromosomes. They obtained the same tree whether using a supermatrix of all loci, or the MP-EST species tree inference method (Liu et al. 2010), which uses the set of gene trees as input instead and optimizes across gene tree coalescent histories. Our tree also agrees with a considerably smaller analysis (Zwickl et al. 2014) of 473 genes obtained from the short arm of chromosome 3, except that in their tree O. rufipogon is switched from the sister group of O. sativa to be the sister group of O. nivara and O. indica. They obtained the same results with concatenation and species tree inference methods.
Anopheles: whole genomes.
Our bootstrap tree (Supplementary Fig. 5 available on Dryad) was fully resolved with 100% support at each node. We compared our tree with two recently published genome-scale phylogenomic studies of Anopheles: Neafsey et al. (2015), which has a broad sample across the genus with outgroups, and Fontaine et al. (2015), which focuses on the A. gambiae complex. Neafsey et al. (2015) identified 1085 “relaxed” single copy orthologs and estimated trees using concatenated amino acid sequences and a PROTGAMMAJTT model. Our tree agrees with theirs (their figures 1 and S4) except within the A. gambiae complex, where our tree is resolved but theirs is not. They did not report bootstrap values, but all of ours were 100%. Fontaine et al. (2015) inferred a complex phylogenetic history within the A. gambiae complex in which whole genome trees disagreed with inferences from the X chromosome alone (they argued the latter were more accurate). Our tree agrees with their whole genome tree (their figure S17), except in their tree A. melas is the sister group of A. merus. Their support values were 100% at each node. On the other hand, our tree was identical to their X chromosome tree with respect to these two species, but disagreed with respect to the position of A. gambiae within the complex (in accord with the disagreement they observed between autosomes and the X chromosome).
Fabaceae: whole genomes.
Our bootstrap tree (Supplementary Fig. 6 available on Dryad) was fully resolved with 100% support at each node. No whole genome trees have been published for Fabaceae, so we compared our tree with the three-gene taxon-rich analysis of the family presented in Bruneau et al. (2013). Our tree agrees with that tree at each node. Whether Lupinus or Arachis is the correct outgroup (or both are) is unclear, requiring further taxa to be sampled for resolution. Our tree also agrees with the large plastid-genome-based phylogenomic tree described above (Supplementary Fig. 2 available on Dryad). In that tree Lupinus and Arachis are sister groups, jointly acting as outgroups to the remaining six taxa in our whole genome tree.
Eudicots: whole genomes.
Our bootstrap tree for 24 taxa (Supplementary Fig. 7 available on Dryad) has only two nodes with less than 90% bootstrap support. Comparisons to previously published phylogenies suggest agreement within relatively closely related clades, such as Brassicaceae (Huang et al. 2016), but possible disagreement in the placement of three leaf taxa (Vitis, Cucumis, and Eucalyptus) as well as the position of the COM clade, represented here by Euphorbiaceae (Riccinus, Manihot), Salicaceae (Populus), and Linaceae (Linum). Soltis et al. (2011), in a combined analysis of 17 nuclear-ribosomal, mitochondrial, and chloroplast genes, found strong support for the placement of Vitaceae (Vitis) as sister to the Rosid clade (sister to all but Solanum and Mimulus in our analysis, after rooting on Aquilegia; one NNI move on our tree). However, placement of Vitis, and the support for that placement, varies across trees generated using nuclear nonribosomal data (Zhang et al. 2012), mitochondrial data (Zhu et al. 2007), and chloroplast data (Sun et al. 2015). In another discrepancy with the large 17-gene combined analysis (Soltis et al. 2011), we found support for Cucumis (Cucurbitaceae) to be phylogenetically closer to Fabales than to Rosales. This placement (again, one NNI move away on our tree) is consistent with the five-gene nuclear data set (Zhang et al. 2012) and some cpDNA analyses (Sun et al. 2015). Similarly, mitochondrial data (Zhu et al. 2007; Sun et al. 2015) and nuclear data (Zhang et al. 2012), reanalyzed in Sun et al. (2015), support our unexpected position of Myrtales (Eucalyptus) as sister to the rest of the rosids. Our most substantial discrepancy involves the COM clade, which has been considered part of the fabids (Soltis et al. 2011), but our analysis provides strong support for its placement closer to the malvids. However, Sun et al. (2015) reanalyzed several data sets to elucidate relationships among the fabid, malvid, and COM clades, and also found strong support from the mitochondrial and nuclear genomes for this placement. In all of these cases, the previously accepted phylogenetic placement was almost entirely derived from chloroplast data, whereas our results are consistent with at least some nuclear and mitochondrial genome analyses.
References
- Aberer A.J.,, Krompass D.,, Stamatakis A. 2013. Pruning rogue taxa improves phylogenetic accuracy: an efficient algorithm and webservice. Syst. Biol. 62:162–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F.,, Madden T.L.,, Schaffer A.A.,, Zhang J.,, Zhang Z.,, Miller W.Q.,, Lipman D.J. 1997. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 25:3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banks J.A.,, Nishiyama T.,, Hasebe M.,, Bowman J.L.,, Gribskov M.,, de Pamphilis C.,, Albert V.A.,, Aono N.,, Aoyama T.,, Ambrose B.A.,, Ashton N.W.,, Axtell M.J.,, Barker E.,, Barker M.S.,, Bennetzen J.L.,, Bonawitz N.D.,, Chapple C.,, Cheng C.Y.,, Correa L.G.G.,, Dacre M.,, DeBarry J.,, Dreyer I.,, Elias M.,, Engstrom E.M.,, Estelle M.,, Feng L.,, Finet C.,, Floyd S.K.,, Frommer W.B.,, Fujita T.,, Gramzow L.,, Gutensohn M.,, Harholt J.,, Hattori M.,, Heyl A.,, Hirai T.,, Hiwatashi Y.,, Ishikawa M.,, Iwata M.,, Karol K.G.,, Koehler B.,, Kolukisaoglu U.,, Kubo M.,, Kurata T.,, Lalonde S.,, Li K.J.,, Li Y.,, Litt A.,, Lyons E.,, Manning G.,, Maruyama T.,, Michael T.P.,, Mikami K.,, Miyazaki S.,, Morinaga S.,, Murata T.,, Mueller-Roeber B.,, Nelson D.R.,, Obara M.,, Oguri Y.,, Olmstead R.G.,, Onodera N.,, Petersen B.L.,, Pils B.,, Prigge M.,, Rensing S.A.,, Riano-Pachon D.M.,, Roberts A.W.,, Sato Y.,, Scheller H.V.,, Schulz B.,, Schulz C.,, Shakirov E.V.,, Shibagaki N.,, Shinohara N.,, Shippen D.E.,, Sorensen I.,, Sotooka R.,, Sugimoto N.,, Sugita M.,, Sumikawa N.,, Tanurdzic M.,, Theissen G.,, Ulvskov P.,, Wakazuki S.,, Weng J.K.,, Willats W.,, Wipf D.,, Wolf P.G.,, Yang L.X.,, Zimmer A.D.,, Zhu Q.H.,, Mitros T.,, Hellsten U.,, Loque D.,, Otillar R.,, Salamov A.,, Schmutz J.,, Shapiro H.,, Lindquist E.,, Lucas S.,, Rokhsar D.,, Grigoriev I.V. 2011. The Selaginella genome identifies genetic changes associated with the evolution of vascular plants. Science 332:960–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertels F.,, Silander O.K.,, Pachkov M.,, Rainey P.B.,, van Nimwegen E. 2014. Automated reconstruction of whole-genome phylogenies from short-sequence reads. Mol. Biol. Evol. 31:1077–1088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruneau A.,, Doyle J.J.,, Herendeen P.,, Hughes C.,, Kenicer G.,, Lewis G.,, Mackinder B.,, Pennington R.T.,, Sanderson M.J.,, Wojciechowski M.F.,, Boatwright S.,, Brown G.,, Cardoso D.,, Crisp M.,, Egan A.,, Fortunato R.H.,, Hawkins J.,, Kajita T.,, Klitgaard B.,, Koenen E.,, Lavin M.,, Luckow M.,, Marazzi B.,, McMahon M.M.,, Miller J.T.,, Murphy D.J.,, Ohashi H.,, de Queiroz L.P.,, Rico L.,, Sarkinen T.,, Schrire B.,, Simon M.F.,, Souza E.R.,, Steele K.,, Torke B.M.,, Wieringa J.J.,, van Wyk B.E., Legume Phylogeny Working Group. 2013. Legume phylogeny and classification in the 21st century: progress, prospects and lessons for other species-rich clades. Taxon 62:217–248. [Google Scholar]
- Chan C.X.,, Bernard G.,, Poirion O.,, Hogan J.M.,, Ragan M.A. 2014. Inferring phylogenies of evolving sequences without multiple sequence alignment. Sci. Rep. 4:6504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang Y.,, Graham S.W. 2014. Patterns of clade support across the major lineages of moss phylogeny. Cladistics 30:590–606. [DOI] [PubMed] [Google Scholar]
- Costa I.R.,, Prosdocimi F.,, Jennings W.B. 2016. In silico phylogenomics using complete genomes: a case study on the evolution of hominoids. Genome Research 26:1257–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cranston K.A.,, Hurwitz B.,, Sanderson M.J.,, Ware D.,, Wing R.A.,, Stein L. 2010. Phylogenomic analysis of BAC-end sequence libraries in Oryza (Poaceae). Syst. Bot. 35:512–523. [Google Scholar]
- Edwards S.V.,, Xi Z.X.,, Janke A.,, Faircloth B.C.,, McCormack J.E.,, Glenn T.C.,, Zhong B.J.,, Wu S.Y.,, Lemmon E.M.,, Lemmon A.R.,, Leache A.D.,, Liu L.,, Davis C.C. 2016. Implementing and testing the multispecies coalescent model: a valuable paradigm for phylogenomics. Mol. Phylog. Evol. 94:447–462. [DOI] [PubMed] [Google Scholar]
- Fan H.,, Ives A.R.,, Surget-Groba Y.,, Cannon C.H. 2015. An assembly and alignment-free method of phylogeny reconstruction from next-generation sequencing data. BMC Genom. 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. 2004. Inferring phylogenies. Sunderland (MA): Sinauer Press. [Google Scholar]
- Fontaine M.C.,, Pease J.B.,, Steele A.,, Waterhouse R.M.,, Neafsey D.E.,, Sharakhov I.V.,, Jiang X.F.,, Hall A.B.,, Catteruccia F.,, Kakani E.,, Mitchell S.N.,, Wu Y.C.,, Smith H.A.,, Love R.R.,, Lawniczak M.K.,, Slotman M.A.,, Emrich S.J.,, Hahn M.W.,, Besansky N.J. 2015. Extensive introgression in a malaria vector species complex revealed by phylogenomics. Science 347:42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner S.N.,, Hall B.G. 2013. When whole-genome alignments just won’t work: kSNP v2 software for alignment-free snp discovery and phylogenetics of hundreds of microbial genomes. PLoS One 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner S.N.,, Slezak T.,, Hall B.G. 2015. kSNP3.0: SNP detection and phylogenetic analysis of genomes without genome alignment or reference genome. Bioinformatics 31:2877–2878. [DOI] [PubMed] [Google Scholar]
- Gusfield D. 1997. Algorithms on strings, trees and sequences. New York:Cambridge University Press. [Google Scholar]
- Haubold B.,, Klotzl F.,, Pfaffelhuber P. 2015. andi: fast and accurate estimation of evolutionary distances between closely related genomes. Bioinformatics 31:1169–1175. [DOI] [PubMed] [Google Scholar]
- Hohl M.,, Ragan M.A. 2007. Is multiple-sequence alignment required for accurate inference of phylogeny? Syst. Biol. 56:206–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C.-H.,, Sun R.,, Hu Y.,, Zeng L.,, Zhang N.,, Cai L.,, Zhang Q.,, Koch M.A.,, Al-Shehbaz I.,, Edger P.P.,, Pires J.C.,, Tan D.-Y.,, Zhong Y.,, Ma H. 2016. Resolution of Brassicaceae phylogeny using nuclear genes uncovers nested radiations and supports convergent morphological evolution. Mol. Biol. Evol. 33:394–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck J.P. 1995. The robustness of 2 phylogenetic methods - 4-taxon simulations reveal a slight superiority of maximum-likelihood over neighbor joining. Mol. Biol. Evol. 12:843–849. [DOI] [PubMed] [Google Scholar]
- Huson D.H.,, Rupp R.,, Scornavacca C. 2010. Phylogenetic networks: concepts, algorithms, and applications. Cambridge, UK:Cambridge University Press. [Google Scholar]
- Kloepper T.H.,, Huson D.H. 2008. Drawing explicit phylogenetic networks and their integration into SplitsTree. BMC Evol. Biol. 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurtz S.,, Phillippy A.,, Delcher A.L.,, Smoot M.,, Shumway M.,, Antonescu C.,, Salzberg S.L. 2004. Versatile and open software for comparing large genomes. Genome Biol. 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam V.K.Y.,, Gomez M.S.,, Graham S.W. 2015. The highly reduced plastome of mycoheterotrophic Sciaphila (Triuridaceae) is colinear with its green relatives and is under strong purifying selection. Genome Biol. Evol. 7:2220–2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavin M.,, Herendeen P.S.,, Wojciechowski M.F. 2005. Evolutionary rates analysis of Leguminosae implicates a rapid diversification of lineages during the tertiary. Syst. Biol. 54:575–594. [DOI] [PubMed] [Google Scholar]
- Leimeister C.A.,, Morgenstern B. 2014. kmacs: the k-mismatch average common substring approach to alignment-free sequence comparison. Bioinformatics 30:2000–2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L.,, Xi Z.X.,, Wu S.Y.,, Davis C.C.,, Edwards S.V. 2015. Estimating phylogenetic trees from genome-scale data. In: Mousseau T.A.,, Fox C.W.,editors. Year in evolutionary biology. p. 36–53. [DOI] [PubMed] [Google Scholar]
- Liu L.A.,, Yu L.L.,, Edwards S.V. 2010. A maximum pseudo-likelihood approach for estimating species trees under the coalescent model. BMC Evol. Biol. 10:18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y.,, Cox C.J.,, Wang W.,, Goffinet B. 2014. Mitochondrial phylogenomics of early land plants: mitigating the effects of saturation, compositional heterogeneity, and codon-usage bias. Syst. Biol. 63:862–878. [DOI] [PubMed] [Google Scholar]
- Loytynoja A.,, Goldman N. 2008. Phylogeny-aware gap placement prevents errors in sequence alignment and evolutionary analysis. Science 320:1632–1635. [DOI] [PubMed] [Google Scholar]
- Luo J.,, Hou B.W.,, Niu Z.T.,, Liu W.,, Xue Q.Y.,, Ding X.Y. 2014. Comparative chloroplast genomes of photosynthetic orchids: Insights into evolution of the Orchidaceae and development of molecular markers for phylogenetic applications. PLoS One 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddison W.P. 1997. Gene trees in species trees. Syst. Biol. 46:523–536. [Google Scholar]
- Magallón S.,, Gómez-Acevedo S.,, Sánchez-Reyes L.L.,, Hernández-Hernández T. 2015. A metacalibrated time-tree documents the early rise of flowering plant phylogenetic diversity. New Phytol. 437–453 [DOI] [PubMed] [Google Scholar]
- Misof B.,Liu S.L.,Meusemann K.,Peters R.S.,Donath A.,Mayer C.,Frandsen P.B.,Ware J.,Flouri T.,Beutel R.G.,Niehuis O.,Petersen M.,Izquierdo-Carrasco F.,Wappler T.,Rust J.,Aberer A.J.,Aspock U.,Aspock H.,Bartel D.,Blanke A.,Berger S.,Bohm A.,Buckley T.R.,Calcott B.,Chen J.Q.,Friedrich F.,Fukui M.,Fujita M.,Greve C.,Grobe P.,Gu S.C.,Huang Y.,Jermiin L.S.,Kawahara A.Y.,Krogmann L.,Kubiak M.,Lanfear R.,Letsch H.,Li Y.Y.,Li Z.Y.,Li J.G.,Lu H.R.,Machida R.,Mashimo Y.,Kapli P.,McKenna D.D.,Meng G.L.,Nakagaki Y.,Navarrete-Heredia J.L.,Ott M.,Ou Y.X.,Pass G.,Podsiadlowski L.,Pohl H., von Reumont B.M.,Schutte K.,Sekiya K.,Shimizu S.,Slipinski A.,Stamatakis A.,Song W.H.,Su X.,Szucsich N.U.,Tan M.H.,Tan X.M.,Tang M.,Tang J.B.,Timelthaler G.,Tomizuka S.,Trautwein M.,Tong X.L.,Uchifune T.,Walzl M.G.,Wiegmann B.M.,Wilbrandt J.,Wipfler B.,Wong T.K.F.,Wu Q.,Wu G.X.,Xie Y.L.,Yang S.Z.,Yang Q.,Yeates D.K.,Yoshizawa K.,Zhang Q.,Zhang R.,Zhang W.W.,Zhang Y.H.,Zhao J.,Zhou C.R.,Zhou L.L.,Ziesmann T.,Zou S.J.,Li Y.R.,Xu X.,Zhang Y.,Yang H.M.,Wang J.,Wang J.,Kjer K.M.,Zhou X.. 2014. Phylogenomics resolves the timing and pattern of insect evolution. Science 346:763–767. [DOI] [PubMed] [Google Scholar]
- Moore M.J.,, Bell C.D.,, Soltis P.S.,, Soltis D.E. 2007. Using plastid genome-scale data to resolve enigmatic relationships among basal angiosperms. Proc. Natl Acad. Sci. USA: 104:19363–19368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgulis A.,, Gertz E.M.,, Schaffer A.A.,, Agarwala R. 2006. A fast and symmetric DUST implementation to mask low-complexity DNA sequences. J. Comp. Biol. 13:1028–1040. [DOI] [PubMed] [Google Scholar]
- Nater A.,, Burri R.,, Kawakami T.,, Smeds L.,, Ellegren H. 2015. Resolving evolutionary relationships in closely related species with whole-genome sequencing data. Syst. Biol. 64:1000–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neafsey D.E.,Waterhouse R.M.,Abai M.R.,Aganezov S.S.,Alekseyev M.A.,Allen J.E.,Amon J.,Arca B.,Arensburger P.,Artemov G.,Assour L.A.,Basseri H.,Berlin A.,Birren B.W.,Blandin S.A.,Brockman A.I.,Burkot T.R.,Burt A.,Chan C.S.,Chauve C.,Chiu J.C.,Christensen M.,Costantini C.,Davidson V.L.M.,Deligianni E.,Dottorini T.,Dritsou V.,Gabriel S.B.,Guelbeogo W.M.,Hall A.B.,Han M.V.,Hlaing T.,Hughes D.S.T.,Jenkins A.M.,Jiang X.F.,Jungreis I.,Kakani E.G.,Kamali M.,Kemppainen P.,Kennedy R.C.,Kirmitzoglou I.K.,Koekemoer L.L.,Laban N.,Langridge N.,Lawniczak M.K.N.,Lirakis M.,Lobo N.F.,Lowy E., MacCallum R.M.,Mao C.H.,Maslen G.,Mbogo C.,McCarthy J.,Michel K.,Mitchell S.N.,Moore W.,Murphy K.A.,Naumenko A.N.,Nolan T.,Novoa E.M., O’Loughlin S.,Oringanje C.,Oshaghi M.A.,Pakpour N.,Papathanos P.A.,Peery A.N.,Povelones M.,Prakash A.,Price D.P.,Rajaraman A.,Reimer L.J.,Rinker D.C.,Rokas A.,Russell T.L.,Sagnon N.,Sharakhova M.V.,Shea T.,Simao F.A.,Simard F.,Slotman M.A.,Somboon P.,Stegniy V.,Struchiner C.J.,Thomas G.W.C.,Tojo M.,Topalis P.,Tubio J.M.C.,Unger M.F.,Vontas J.,Walton C.,Wilding C.S.,Willis J.H.,Wu Y.C.,Yan G.Y.,Zdobnov E.M.,Zhou X.F.,Catteruccia F.,Christophides G.K.,Collins F.H.,Cornman R.S.,Crisanti A.,Donnelly M.J.,Emrich S.J.,Fontaine M.C.,Gelbart W.,Hahn M.W.,Hansen I.A.,Howell P.I.,Kafatos F.C.,Kellis M.,Lawson D.,Louis C.,Luckhart S.,Muskavitch M.A.T.,Ribeiro J.M.,Riehle M.A.,Sharakhov I.V.,Tu Z.J.,Zwiebel L.J.,Besansky N.J.. 2015. Highly evolvable malaria vectors: the genomes of 16 Anopheles mosquitoes. Science 347:43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolae M.,, Rajasekaran S. 2015. On string matching with mismatches. Algorithms 8:248–270. [Google Scholar]
- Pevzner P.A.,, Waterman M.S. 1995. Multiple filtration and approximate pattern-matching. Algorithmica 13:135–154. [Google Scholar]
- Pollard D.A.,, Iyer V.N.,, Moses A.M.,, Eisen M.B. 2006. Widespread discordance of gene trees with species tree in Drosophila: evidence for incomplete lineage sorting. PLoS Genet. 2:1634–1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prum R.O.,, Berv J.S.,, Dornburg A.,, Field D.J.,, Townsend J.P.,, Lemmon E.M.,, Lemmon A.R. 2015. A comprehensive phylogeny of birds (Aves) using targeted next-generation DNA sequencing. Nature 526:569–573. [DOI] [PubMed] [Google Scholar]
- Rajasekaran S.,, Nicolae M. 2014. An elegant algorithm for the construction of suffix arrays. J. Disc. Algor. 7:21–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A.,, Grassly N.C. 1997. Seq-Gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. CABIOS 13:235–238. [DOI] [PubMed] [Google Scholar]
- Ruhfel B.R.,, Gitzendanner M.A.,, Soltis P.S.,, Soltis D.E.,, Burleigh J.G. 2014. From algae to angiosperms-inferring the phylogeny of green plants (Viridiplantae) from 360 plastid genomes. BMC Evol. Biol. 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanderson M.J.,, Doyle J.A. 2001. Sources of error and confidence intervals in estimating the age of angiosperms from rbcL and 18S rDNA data. Am. J. Bot. 88:1499–1516. [PubMed] [Google Scholar]
- Sanderson M.J.,, McMahon M.M.,, Stamatakis A.,, Zwickl D.J.,, Steel M. 2015. Impacts of terraces on phylogenetic inference. Syst. Biol. 64:709–726. [DOI] [PubMed] [Google Scholar]
- Sanderson M.J.,, McMahon M.M.,, Steel M. 2010. Phylogenomics with incomplete taxon coverage: the limits to inference. BMC Evol. Biol. 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanderson M.J.,, McMahon M.M.,, Steel M. 2011. Terraces in phylogenetic tree space. Science 333:448–450. [DOI] [PubMed] [Google Scholar]
- Soltis D.E.,, Smith S.A.,, Cellinese N.,, Wurdack K.J.,, Tank D.C.,, Brockington S.F.,, Refulio-Rodriguez N.F.,, Walker J.B.,, Moore M.J.,, Carlsward B.S.,, Bell C.D.,, Latvis M.,, Crawley S.,, Black C.,, Diouf D.,, Xi Z.X.,, Rushworth C.A.,, Gitzendanner M.A.,, Sytsma K.J.,, Qiu Y.L.,, Hilu K.W.,, Davis C.C.,, Sanderson M.J.,, Beaman R.S.,, Olmstead R.G.,, Judd W.S.,, Donoghue M.J.,, Soltis P.S. 2011. Angiosperm phylogeny: 17 genes, 640 taxa. Am. J. Bot. 98:704–730. [DOI] [PubMed] [Google Scholar]
- Stamatakis A. 2014. RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun M.,, Soltis D.E.,, Soltis P.S.,, Zhu X.Y.,, Burleigh J.G.,, Chen Z.D. 2015. Deep phylogenetic incongruence in the angiosperm clade Rosidae. Mol. Phylog. Evol. 83:156–166. [DOI] [PubMed] [Google Scholar]
- Tang L.,, Zou X.H.,, Achoundong G.,, Potgieter C.,, Second G.,, Zhang D.Y.,, Ge S. 2010. Phylogeny and biogeography of the rice tribe (Oryzeae): evidence from combined analysis of 20 chloroplast fragments. Mol. Phylog. Evol. 54:266–277. [DOI] [PubMed] [Google Scholar]
- Ulitsky I.,, Burstein D.,, Tuller T.,, Chor B. 2006. The average common substring approach to phylogenomic reconstruction. J. Comp. Biol. 13:336–350. [DOI] [PubMed] [Google Scholar]
- White M.A.,, Ane C.,, Dewey C.N.,, Larget B.R.,, Payseur B.A. 2009. Fine-scale phylogenetic discordance across the house mouse genome. PloS Genet. 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickett N.J.,Mirarab S.,Nguyen N.,Warnow T.,Carpenter E.,Matasci N.,Ayyampalayam S.,Barker M.S.,Burleigh J.G.,Gitzendanner M.A.et al.. 2014. Phylotranscriptomic analysis of the origin and early diversification of land plants. Proc. Natl Acad. Sci. USA: 111:E4859–E4868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worobey M.,, Han G.Z.,, Rambaut A. 2014. A synchronized global sweep of the internal genes of modern avian influenza virus. Nature 508:254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y.,, Moore M.J.,, Brockington S.F.,, Soltis D.,, Wong G.K.,, Carpenter E.J.,, Zhang Y.,, Chen L.,, Yan Z.,, Xie Y.,, Sage R.F.,, Covshoff S.,, Hibberd J.M.,, Nelson M.N.,, Smith S.A. 2015. Dissecting molecular evolution in the highly diverse plant clade Caryophyllales using transcriptome sequencing. Mol. Biol. Evol. 32:2001–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang N.,, Zeng L.P.,, Shan H.Y.,, Ma H. 2012. Highly conserved low-copy nuclear genes as effective markers for phylogenetic analyses in angiosperms. New Phytol. 195:923–937. [DOI] [PubMed] [Google Scholar]
- Zhang Q.J.,, Zhu T.,, Xia E.H.,, Shi C.,, Liu Y.L.,, Zhang Y.,, Liu Y.,, Jiang W.K.,, Zhao Y.J.,, Mao S.Y.,, Zhang L.P.,, Huang H.,, Jiao J.Y.,, Xu P.Z.,, Yao Q.Y.,, Zeng F.C.,, Yang L.L.,, Gao J.,, Tao D.Y.,, Wang Y.J.,, Bennetzen J.L.,, Gao L.Z. 2014. Rapid diversification of five Oryza AA genomes associated with rice adaptation. Proc. Natl Acad. Sci. USA: 111:E4954–E4962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Z.-M.,, Zhao B.,, Bai Y.,, Iamorina A.,, Gaffney S.G.,, Schlessinger J.,, Lifton R.P.,, Rimm D.L.,, Townsend J.P. 2016. Early and multiple origins of metastatic lineages within primary tumors. Proc. Natl Acad. Sci. USA: 113:2140–2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X.Y.,, Chase M.W.,, Qiu Y.L.,, Kong H.Z.,, Dilcher D.L.,, Li J.H.,, Chen Z.D. 2007. Mitochondrial matR sequences help to resolve deep phylogenetic relationships in rosids. BMC Evol. Biol. 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou X.H.,, Zhang F.M.,, Zhang J.G.,, Zang L.L.,, Tang L.,, Wang J.,, Sang T.,, Ge S. 2008. Analysis of 142 genes resolves the rapid diversification of the rice genus. Genome Biol. 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwickl D.J. 2006. Genetic algorithm approaches for the phylogenetic analysis of large biological sequence datasets under the maximum likelihood criterion [dissertation]. [Austin (TX)]:University of Texas at Austin. [Google Scholar]
- Zwickl D.J.,, Wing R.,, Stein J.,, Ware D.,, Sanderson M.J. 2014. Disentangling methodological and biological sources of gene tree discordance on Oryza (Poaceae) chromosome 3. Syst. Biol. 63:645–659. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.