An M-estimator for reduced-rank system identification

Abstract

High-dimensional time-series data from a wide variety of domains, such as neuroscience, are being generated every day. Fitting statistical models to such data, to enable parameter estimation and time-series prediction, is an important computational primitive. Existing methods, however, are unable to cope with the high-dimensional nature of these data, due to both computational and statistical reasons. We mitigate both kinds of issues by proposing an M-estimator for Reduced-rank System IDentification ( MR. SID). A combination of low-rank approximations, ℓ₁ and ℓ₂ penalties, and some numerical linear algebra tricks, yields an estimator that is computationally efficient and numerically stable. Simulations and real data examples demonstrate the usefulness of this approach in a variety of problems. In particular, we demonstrate that MR. SID can accurately estimate spatial filters, connectivity graphs, and time-courses from native resolution functional magnetic resonance imaging data. MR. SID therefore enables big time-series data to be analyzed using standard methods, readying the field for further generalizations including non-linear and non-Gaussian state-space models.

1. Introduction

High-dimensional time-series data are becoming increasingly abundant across a wide variety of domains, spanning economics [13], neuroscience [10], and cosmology [28]. Fitting statistical models to such data, to enable parameter estimation and time-series prediction, is an important computational primitive. Linear dynamical system (LDS) models are amongst the most popular and powerful, because of their intuitive nature and ease of implementation [15]. The famous Kalman Filter-Smoother is one of the most popular and powerful tools for time-series prediction with an LDS, given known parameters [14].

In practice, however, for many LDS’s, the parameters are unknown and must be estimated in a process often called system identification [17]. To the best of our knowledge, currently there does not exist a methodology that provides parameter estimates and predictions for ultra-high-dimensional time-series data (e.g. the dimension of the time series, p > 10, 0 0 0).

The challenges associated with high-dimensional time-series estimation and prediction are multifold. First, naïvely, such models include dense p × p matrices, which are often too large to store, much less invert in memory. Several recent efforts to invert large sparse matrices using a series of computational tricks show promise, though they are still extremely computationally expensive [4,12].

Second, estimators behave poorly due to numerical instability. Reduced-rank LDS models can partially address this problem by reducing the number of latent states. [7]. However, without further constraints, the dimensionality of the latent states would be reduced to such an extent that it would significantly decrease the predictive capacity of the resulting model. Third, even after addressing these problems, the time to compute all the necessary quantities can be overly burdensome. Distributed memory implementations, such as those built with Spark, might help overcome this problem. However, it would lead to additional costs and set-up burden, as it would require a Spark cluster [29].

We address all three of these issues with our M-estimator for Reduced-rank System IDentification ( MR. SID). By assuming the dimensionality of the latent state space is small (i.e. reduced-rank), relative to the observed space dimensionality, we can significantly improve computational tractability and estimation accuracy. By further penalizing the estimators, with ℓ₁ and/or ℓ₂ penalties, via utilizing prior knowledge on the structure of the parameters, we gain further estimation accuracy in this high-dimensional but relatively low-sample size regime. Finally, by employing several numerical linear algebra tricks, we can reduce the computational burden significantly.

These three techniques combined enable us to obtain highly accurate estimates in a variety of simulation settings. MR. SID is, in fact, a generalization of the now classic Baum-Welch expectation maximization algorithm, commonly used for system identification in much lower dimensional linear dynamical systems [20]. We show numerically that the hyperparameters can be selected to minimize prediction error on held-out data. Finally, we use MR. SID to estimate functional connectomes from the motor cortex. MR. SID enables us to estimate the regions, rather than imposing some prior parcellation on the data, as well as estimate sparse connectivity between regions. MR. SID reliably estimates these connectomes, as well as predicts the held-out time-series data. To our knowledge, this is the first time a single unified approach has been used to estimate partitions and functional connectomes directly from the high-dimensional data.

This work presents a new analysis of a model which has only been implemented in low-dimensional settings, and paves the way for high-dimensional implementation. Though primitive, it is a first step for essentially any high-dimensional time series analysis, control system identification, and spatiotemporal analysis. To enable extensions, generalizations, and additional applications, the code for the core functions and generating each of the figures is freely available on Github (https://github.com/shachen/PLDS/).

2. The model

In statistical data analysis, one often encounters some observed variables, as well as some unobserved latent variables, which we denote as Y = (y₁,…, y_T) and X = (x₁,…, x_T) respectively. By the Bayes rule, the joint probability of X and Y is P(X, Y) = P(Y|X)P(X). The conditional distribution P(Y|X) and prior P(X) can both be represented as a product of marginals:

$$P(\mathit{Y}|\mathit{X})={\displaystyle \prod _{t=1}^{T}P({\mathit{y}}_t|{\mathit{y}}_0,\dots ,{\mathit{y}}_{t-1},{\mathit{x}}_0,\dots ,{\mathit{x}}_{t-1})},$$

$$P(\mathit{X})=P({\mathit{x}}_0){\displaystyle \prod _{t=1}^{T}P({\mathit{x}}_t|{\mathit{x}}_0,\dots ,{\mathit{x}}_{t-1})}.$$

The generic time-invariant state-space model (SSM) makes the following simplifying assumptions:

$$P({\mathit{y}}_t|{\mathit{y}}_0,\dots ,{\mathit{y}}_{t-1},{\mathit{x}}_0,\dots ,{\mathit{x}}_t)\approx P({\mathit{y}}_t|{\mathit{x}}_t),$$

$$P({\mathit{x}}_t|{\mathit{x}}_0,\dots ,{\mathit{x}}_{t-1})\approx P({\mathit{x}}_t|{\mathit{x}}_{t-1}).$$ (1)

A linear dynamical system (LDS) further assumes that both terms in (1) are linear Gaussian functions, which when written as an iterative random process, yield the standard matrix update rules:

$${\mathit{x}}_{t+1}=A{\mathit{x}}_t+{\mathbf{w}}_t,{\mathbf{w}}_t~N(\mathbf{0},Q),{\mathit{x}}_0~N({\pi }_0,V_0),$$

$${\mathit{y}}_t=C{\mathit{x}}_t+{\mathbf{v}}_t,{\mathbf{v}}_t~N(\mathbf{0},R),$$

where A is a d × d state transition matrix and C is a p × d generative matrix. x_t is a d × 1 vector and y_t is a p × 1 vector. The output noise covariance R is p × p, while the state noise covariance Q is d × d. Initial state mean π₀ is d × 1 and covariance V₀ is d × d.

The model can be thought of as a continuous version of the hidden Markov model (HMM), where the columns of C stand for the hidden states and one observes a single state at time t. Unlike HMM, LDS (1) allows one to observe a linear combination of multiple states. A is the analogy of the state transition matrix, which describes how the weights x_t evolve over time. Another difference is that LDS contains two white noise terms, which are captured by the Q and R matrices.

Without applying further constraints, the LDS model itself is unidentifiable. Three minimal constraints are introduced for identifiability:

• Constraint 1: Q is the identity matrix

• Constraint 2: the order of C′ s columns is fixed based on their norms

• Constraint 3: V₀ = 0

Note that the first two constraints follow directly from Roweis and Ghahramani (1999), which try to eliminate the degeneracy in the model. Additionally, V₀ is set to zero, meaning the starting state x₀ = π₀ is an unknown constant instead of a random variable. We put this constraint on, because in the application that follows only one single chain of time series observed. To estimate V₀, multiple series of observations are required.

The following three constraints are further applied to achieve a more useful model:

• Constraint 4: R is a diagonal matrix

• Constraint 5: A is sparse

• Constraint 6: C has smooth columns

The constraint on R is natural. Consider the case where the observations are high dimensional, which means that the R matrix is very large. One cannot accurately estimate the many free parameters in R with a limited amount of observations. Therefore, some constraints on R will help with inferential accuracy, by virtue of significantly reducing variance while not adding too much bias. For example, R can be set to multiples of the identity matrix, or more generally, a diagonal matrix. A static LDS model with a diagonal R is equivalent to Factor Analysis, while one with multiples of the identity R matrix leads to Principal Component Analysis (PCA) [21].

The A matrix is the transition matrix of the hidden states. In many applications, it is desirable for A to be sparse. An ℓ₁ penalty on A is used to impose the sparsity constraint. In the applications that follow, A is a central construct of interest representing a so-called connectivity graph, and the graph is expected to be sparse.

Similarly, in many applications, it is desirable for the columns of C to be smooth. For example, in neuroimaging data analysis, each column of C can be a signal in the brain. Having the signals spatially smooth can help extract meaningful information from the noisy neuroimaging data. In this context, an ℓ₂ penalty on columns of C is used to enforce smoothness.

With all those constraints, the model becomes:

$${\mathit{x}}_{t+1}=A{\mathit{x}}_t+{\mathbf{w}}_t,{\mathbf{w}}_t~N(\mathbf{0},\mathbf{I}),{\mathit{x}}_0={\pi }_0,$$

$${\mathit{y}}_t=C{\mathit{x}}_t+{\mathbf{v}}_t,{\mathbf{v}}_t~N(\mathbf{0},R),$$ (2)

where A is a sparse matrix and C has smooth columns.

Let θ = {A, C, R, π₀} represent all unknown parameters, while P(X, Y) represents the full likelihood. Then, combining model 2 and the constraints on A and C leads us to an optimization problem:

$$\widehat{\theta }=\underset{\theta }{\text{arg}min}\left\{-\text{log}{P}_{\theta }(\mathit{X},\mathit{Y})+{\lambda }_1{\Vert A\Vert }_1+{\lambda }_2{\Vert C\Vert }_2^2\right\}$$ (3)

where λ₁ and λ₂ are tuning parameters and ‖·‖_p represents the p-norm of a vector. Equivalently, this problem has the following dual form:

$$\begin{array}{ll}\text{minimize}\hfill & \{-\text{log}{P}_{\theta }(\mathit{X},\mathit{Y})\}\hfill \\ \text{subject to:}\hfill & \alpha {\Vert A\Vert }_1+(1-\alpha ){\Vert C\Vert }_2^2\le \phi \text{for some}\phi ;A\in {\mathcal{A}}_{d\times d},C\in {\mathcal{C}}_{p\times d},{\mathcal{R}}_{p\times d},{\pi }_0\in {\pi }_{d\times 1}\hfill \end{array}$$

where $\alpha =\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}$. ${\mathcal{A}}_{d\times d}$ and ${\mathcal{C}}_{p\times d}$ are d × d and p × d dimensional matrix spaces respectively. ${\mathcal{R}}_{p\times p}$ is the p × p diagonal matrix space and π_d×1 is the d dimensional vector space.

3. Parameter estimation

Replacing log P(X, Y) in problem (3) with its concrete form, one gets

$$\widehat{\theta }=\underset{\theta }{\text{arg}min}\left\{{\displaystyle \sum _{t=1}^T\left(\frac{1}{2}{[{\mathit{y}}_t-C{\mathit{x}}_t]}^{\top }{R}^{-1}[{\mathit{y}}_t-C{\mathit{x}}_t]\right)-\frac{T}{2}\text{log}\left|R\right|}+{\displaystyle \sum _{t=1}^T(\frac{1}{2}{[{\mathit{x}}_t-A{\mathit{x}}_{t-1}]}^{\top }[{\mathit{x}}_t-A{\mathit{x}}_{t-1}])-\frac{T}{2}\text{log}\left|\mathbf{I}\right|-\text{log}({𝟙}_{{\pi }_0}({\mathit{x}}_0))+{\lambda }_1{\Vert A\Vert }_1+{\lambda }_2{\Vert C\Vert }_2^2}\right\}$$ (4)

Denote the target function in the curly braces as Φ(θ, Y, X). Then a parameter estimation algorithm is one that optimizes Φ(θ, Y, X) with regard to θ = {A, C, R, π₀}.

Parameter estimation for LDS has been investigated extensively in statistics, machine learning, control theory, and signal processing research. For example, in machine learning, the exact and variational inference algorithms for general Bayesian networks can be applied to LDS. In control theory, the corresponding area of study is known as system identification.

Specifically, one way to search for the maximum likelihood estimation (MLE) is through iterative methods such as Expectation-Maximization (EM) [22]. The EM algorithm for a standard LDS is detailed in Zoubin and Geoffrey (1996) [11]. An alternative is to use subspace identification methods such as N4SID and PCA-ID, which give asymptotically unbiased closed-form solutions [8,27]. In practice, determining an initial solution with subspace identification and then refining it with EM is an effective approach [6].

However, the above approaches are not directly applicable to optimization problem (3) due to the introduced penalty terms. We therefore developed an algorithm called M-estimation for Reduced-rank System IDentification ( MR. SID), as described below. MR. SID is a generalized Expectation-Maximization (EM) algorithm.

3.1. E Step

The E step of EM requires computation of the expected log likelihood, Г = E[ log P(X, Y)|Y]. This quantity depends on three expectations: E[x_t|Y], $E[{\mathit{x}}_t{\mathit{x}}_t^{\top }|\mathit{Y}]$ and $E[{\mathit{x}}_t{\mathit{x}}_{t-1}^{\top }|\mathit{Y}]$. for simplicity, we denote their finite sample estimators by:

$${\widehat{\mathit{x}}}_t\equiv E[{\mathit{x}}_{\mathit{t}}|\mathit{Y}],{\widehat{P}}_t\equiv E[{\mathit{x}}_t{\mathit{x}}_t^{\top }|\mathit{Y}],{\widehat{P}}_{t,t-1}\equiv E[{\mathit{x}}_t{\mathit{x}}_{t-1}^{\top }|\mathit{Y}].$$ (5)

Expectations (5) are estimated with a Kalman filter/smoother (KFS), which is detailed in the Appendix. Notice that all expectations are taken with respect to the current estimations of parameters.

3.2. M Step

Each of the parameters in θ = {A, C, R, π₀} is estimated by taking the corresponding partial derivatives of Φ(θ, Y, x), setting them to zero, and then solving the equations. The details of derivations can be found in the Appendix.

Let the estimations from the previous step be denoted as ${\theta }^{\text{old}}=\{A^{\text{old}},C^{\text{old}},R^{\text{old}},{\pi }_0^{\text{old}}\}$, and the current estimations as ${\theta }^{\text{new}}=\{A^{\text{new}},C^{\text{new}},R^{\text{new}},{\pi }_0^{\text{new}}\}$. The estimation for the R matrix has a closed form, as follows:

$$R^{\text{new}}=\text{diag}\left\{\frac{1}{T}{\displaystyle \sum _{t=1}^T({\mathit{y}}_t{\mathit{y}}_t^{\top }-C^{\text{new}}{\widehat{\mathit{x}}}_t{\mathit{y}}_t^{\top })}\right\}$$ (6)

where diag extracts the diagonal of the in-bracket term, as we constrain R to be diagonal in Constraint 4.

The estimation for π₀ has a closed form. The relevant term $\text{log}({𝟙}_{{\pi }_0}({\widehat{\mathit{x}}}_0))$ is minimized only when ${\pi }_0^{\text{new}}={\widehat{\mathit{x}}}_0$.

The estimation for the C matrix also has a closed form. Using a vectorization trick as in [25], one can derive C’s closed form solution with the Tikhonov regularization [24]

$$C^{\text{new}}=\text{Solve}\text{with}\text{Tikhonov}\text{regularization}$$ (7)

For matrix A, its estimation is similar to that of C, but slightly more complex. The complexity is that A does not have a closed form solution due to the ℓ₁ penalty term. However, it can be solved numerically with a Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) [5]. The FISTA algorithm is detailed in the Appendix.

With FISTA, matrix A updates as follows:

$$A^{\text{new}}=\text{Solve}\text{with}\text{FISTA}$$ (8)

The parameters in the EM algorithm are initialized with the singular value decomposition (SVD). In addition, several matrix computation techniques are utilized to make the algorithm highly efficient and scalable. The details can be found in the Appendix. Combining the initialization, E-step, and M-step, a complete EM algorithm for MR. SID is addressed in Table 1.

Table 1.

The complete EM algorithm.

Algorithm EM Algorithm for MR. SID
1.	Initialize θ = {A, C, R, π0} with SVD
2.	While convergence criteria are unmet E Step
3.	Update the expectations in Eq. (5) with the KFS M Step
4.	$R^{\text{new}}=\text{diag}\left\{\frac{1}{T}{\displaystyle \sum _{t=1}^T({\mathit{y}}_t{\mathit{y}}_t^{\top }-C^{\text{old}}{\widehat{\mathit{x}}}_t{\mathit{y}}_t^{\top })}\right\}$, as in Eq. 6
5.	${\pi }_0^{\text{new}}={\widehat{\mathit{x}}}_0$
6.	Update Cnew, as in Eq. (7)
7.	Update Anew with FISTA, as in Eq. (8)

4. Simulations

4.1. Simulation setup

Two simulations of different dimensions are performed to demonstrate the parameter estimations, computational efficiency, and predicting ability of MR. SID. In the low dimensional setting, p = 300, d = 10, and T = 100. A is first generated from a random matrix, then elements with small absolute values are truncated to zero to make it sparse. Afterwards, a multiple of the identity matrix is added to A. Finally, A is scaled to make sure its eigenvalues fall within [−1, 1], thus avoiding diverging time series. Matrix C is then generated as follows. Each column contains random samples from a standard Gaussian. Then, each column is sorted in ascending order. Covariance Q is the identity matrix and covariance R is a multiple of the identity matrix. Initial state π₀ = 0 is a zero vector. Pseudocode for data generation can be found in the Appendix.

In the high-dimensional setting, p = 10000, d = 30, and T = 100. The parameters are generated same in the manner. To evaluate the accuracy of estimations, we elect to define the distance between two matrices A and B as

$$d_{A,B}=\underset{P\in P(n)}{\text{arg}min}\left\{\text{log}\left[\frac{n}{\text{Trace}(P\times C_{A,B})}\right]\right\}$$ (9)

where C_{A, B} is the correlation matrix between columns of A and B, P(n) is a collection of all the permutation matrices of order n, and P is a permutation matrix.

Both the standard LDS and MR. SID are applied to the simulation data. Estimation accuracies are plotted against penalty sizes in Fig. 1. From the plot, one sees that the prediction accuracy first improves, then drops when the penalties increase. MR. SID is also used for time series prediction, and the result is plotted in Fig. 2. The prediction accuracy peaks when the penalty coefficients λ_A and λ_C are around 10⁻³. This makes sense, as the same (λ_A, λ_C) pair also gives the best estimations of A and C, as seen in Fig. 1. The latter observation provides us a way to pick tuning parameters in real applications: one can use a collection of tuning parameter pairs (λ_A, λ_C) for estimations (with train data) and subsequently for predictions (with test data). The pair that gives the most accurate out-of-sample predictions is picked. This trick is used in Section 5.

Fig. 1.

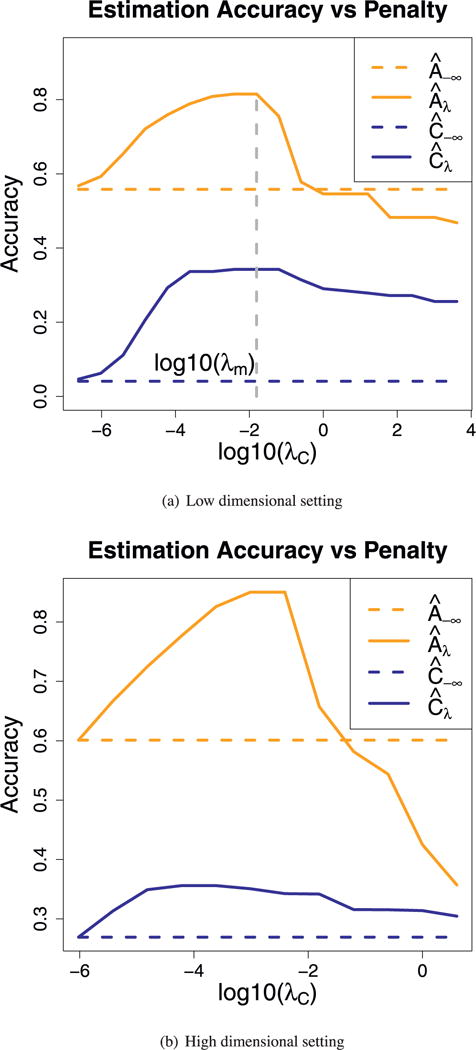
x axis is tuning parameter λ_C under log scale and y axis is the distance between truth and estimations; λ_A is increasing proportionally with λ_C. One can see that in both the low dimensional and hight dimensional setting, estimation accuracies for A and C first increase then decrease as penalty increases.

Fig. 2.

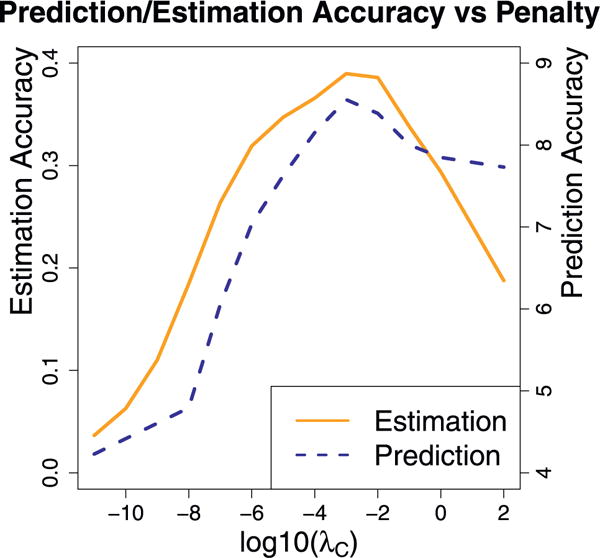
Estimation and prediction accuracies. The x-axis represents the penalty size on a log scale. The y-axis represents the estimation and prediction accuracies. Note that the penalty which yields the most accurate estimation also gives the best prediction.

5. Application

5.1. Data and motivation

MR. SID is applied to two datasets in this section: the Kirby 21 data and the Human Connectome Project (HCP) data.

The Kirby 21 data were acquired from the FM Kirby Research Center at the Kennedy Krieger Institute, an affiliate of Johns Hopkins University [16]. Twenty-one healthy volunteers with no history of neurological disease each underwent two separate resting state fMRI sessions on the same scanner. The data are preprocessed with FSL, a comprehensive library of analysis tools for fMRI, MRI, and DTI brain imaging data [23]. Specifically, FSL is used for spatial smoothing with a Gaussian kernel. Then MR. SID was applied on the smoothed data. The number of scans was T = 210.

The Human Connectome Project (HCP) is a systematic effort to map macroscopic human brain circuits and their relationship to behavior in a large population of healthy adults [9,18,26]. All scans consist of 1200 time points. A comprehensive introduction of the dataset is given by [26].

Extensive research has been done to analyze the above datasets. Methods such as PCA and ICA (Independent Component Analysis) have been applied to obtain spatial decompositions of the brain, as well as the functional connectivity among the decomposed regions. Thus, for our first application, we applied MR. SID to the Kirby 21 data with the intent of obtaining both a spatial decomposition graph and a connectivity graph. As a second application, MR. SID was applied to the HCP data to predict brain activities. For both datasets, the motor cortex, which contains p = 7396 voxels, is analyzed instead of the whole brain.

5.2. Results

MR. SID is first applied to two subjects (four scans) from the Kirby 21 dataset. To pick the optimal penalty size, different values of λ_A = λ_C were attempted. Their values range from 10⁻¹⁰ to 10⁴. Then the estimated models with each combination were used to make predictions. We use the value of 10⁻⁵, as it gives the most accurate out-of-sample predictions. To determine the number of latent states, d, the profile likelihood method proposed by Zhu et al. [30] is utilized. The method assumes the eigenvalues of the data matrix follow a Gaussian mixture, and uses profile likelihood to pick the optimal number of latent states. Apply the method to all four scans, the numbers of latent states are 11, 6, 14 and 15 respectively. Their average, d = 11, is used.

First, let’s look at the estimations of A matrix. Let A₁₂ stand for the estimated A matrix for the second scan of subject one. Similar logic applies to the A₁₁, A₂₁, A₂₂, and C matrices. These matrices contain subject-specific information. 4 matrices leads to 6 unique pairs. Intuitively, the pair (A₁₁, A₁₂) and (A₂₁, A₂₂) should have the highest similarity, as each comes from two scans of the same subject. This idea is validated by Table 2, which summarize similarities among the 4 matrices. The distance measure in Eq. (9) was used. The Amari error [2], which is another permutation-invariant measure of similarity, is also provided. A smaller d(A, B) or Amari error means higher similarity.

Table 2.

Similarities among estimated A matrices.

dA, B	A11	A12	A21	A22
A11	0
A12	0.076(0.88)	0
A21	0.105(1.05)	0.095(1.08)	0
A22	0.095(1.02)	0.095(1.09)	0.085(0.98)	0

Next, let’s look at the C matrices. 3D renderings of the columns of C₁₁ are shown in Fig. 3. The 3D regions in the plot are comparable to existing parcellations of the motor cortex. As an example, the blue region in Fig. 3 accurately matches the dorsomedial (DM) parcel of the five-region parcellation proposed by Nebel MB et al. [19].

Fig. 3.

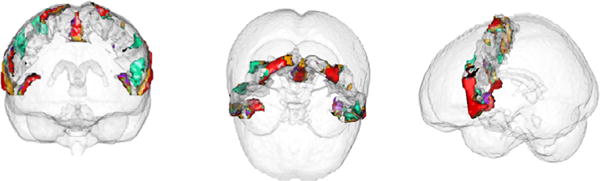
3D rendering of columns of matrix C₁₁: estimation for the first scan of subject one.

Matrix A and C have natural interpretation here. Each y_t is a snapshot of brain activity at time t. The columns of C are interpreted as time-invariant brain “point spread functions”. At each time point, the observed brain image, y_t, is a linear mixture of latent co-assemblies of neural activity x_t. Matrix A describes how x_t evolves over time. A is a directed graph if one treats each neural assembly as a vertex. Each neural assembly is spatially smooth, and connectivity across them is empirically sparse. This naturally fits into the sparsity and smoothness assumptions of MR. SID.

To summarize, MR. SID gives a spatial decomposition of the motor cortex, as well as the sparse connectivity among the decomposed regions. The connectivity graph contains subject-specific information and can correctly group scans by subject. The decomposed regions are spatially smooth and are comparable to existing parcellations of the motor cortex.

As a second application, MR. SID is applied to the HCP data. The goal is to predict future brain signals using historical data. HCP data has T = 1200 time points. The first N = 1000 (about 80%) were used as training data, while the rest were used for out-of-sample test. For comparison purposes, the PCA/SVD method (to initialize MR. SID) and the LDS/HMM model are also fitted. Parameter estimations are first performed for all three methods, then the estimated parameters were fed into Eq. (2) to make k-step predictions into the future. Pseudocode for k-step ahead predictions is given in the Appendix.

The prediction accuracies are shown in Fig. 4. From the top panel, one can see that MR. SID has significantly higher prediction accuracies than SVD for the first 150 steps. Considering that SVD is used to initialize MR. SID, this observation demonstrates that MR. SID makes real improvement on top of SVD. The middle panel is a sample plot of the true time series and predictions. MR. SID gives more accurate predictions and its prediction interval covers the true signal. Note that the interval gets wider for longer term predictions, as the errors from each step accumulate. The bottom panel compares MR. SID models of different penalties: when there is no penalty, MR. SID gives identical result as LDS/HMM; with the optimal penalty picked with training data, it gives more accurate predictions than LDS.

Fig. 4.

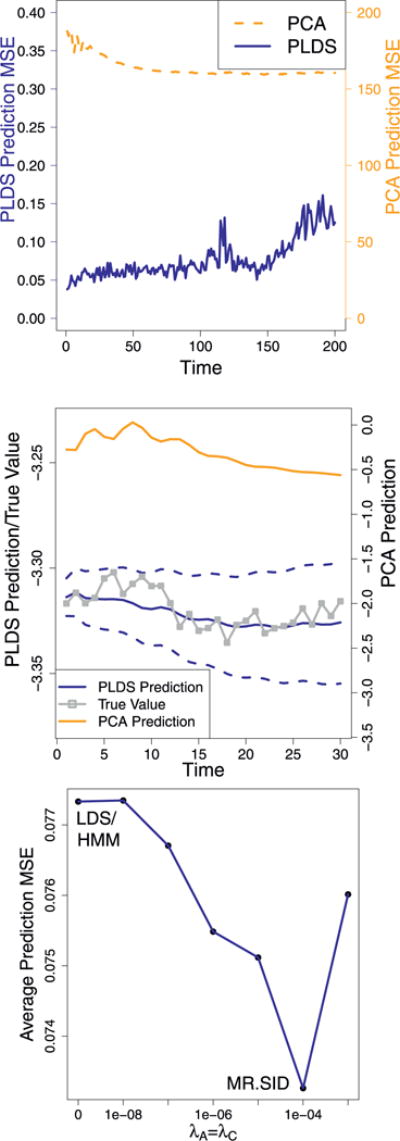
Predictions on HCP data: (1) MR. SID and SVD predictions over time, with accuracies measured as mean squared error (MSE). (2) Sample time series plot. True signals and predictions are both averaged over a sample of 20 voxels. The dotted blue lines represents the 60% prediction interval of MR. SID. Values were log-scaled for plotting. (3) Prediction accuracies of LDS/HMM and MR. SID.

6. Discussion

We have taken a first step towards the modeling and estimation of high-dimensional time-series data. The proposed method balances both statistical and computational considerations. Indeed, much like the Kalman Filter-Smoother for modeling time-series data, and the Baum-Welch algorithm for system identification act as “primitives” for time-series data analysis, MR. SID can act as a primitive for similar time-series analysis when the dimensionality is significantly larger than the number of time steps. Via simulations we demonstrated the efficacy of our methods. Then, by applying the proposed approach to fMRI scans of the motor cortex of healthy adults, we identified limited sub-regions (networks) from the motor cortex.

In the future, this work could be extended in two important directions. First, the assumption of conditionally independent observations given latent states remains a challenge. The covariance structures in the observation equation, R, should be generalized and prior knowledge could be incorporated into it [1]. The idea is that R should be general enough to be flexible, but sufficiently restricted to make the model useful. Many other methods, e.g. those that use tridiagonal and upper triangular matrices, could also be considered. Mohammad et al. have discussed the impact of autocorrelation on functional connectivity, which also provides some direction for extension [3]. In addition, the work can also be extended on the application side. Currently, only data from a few subjects have been analyzed. As a next step, the model can generalize to a group version and be used to analyze more subjects. The A matrix estimated by MR. SID could potentially be used as a measure of fMRI scan reproducibility.