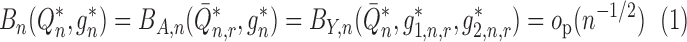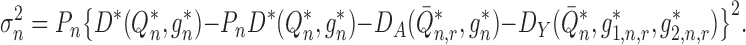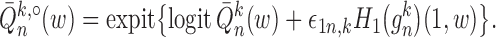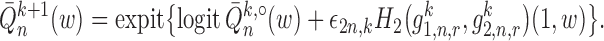Summary
Doubly robust estimators are widely used to draw inference about the average effect of a treatment. Such estimators are consistent for the effect of interest if either one of two nuisance parameters is consistently estimated. However, if flexible, data-adaptive estimators of these nuisance parameters are used, double robustness does not readily extend to inference. We present a general theoretical study of the behaviour of doubly robust estimators of an average treatment effect when one of the nuisance parameters is inconsistently estimated. We contrast different methods for constructing such estimators and investigate the extent to which they may be modified to also allow doubly robust inference. We find that while targeted minimum loss-based estimation can be used to solve this problem very naturally, common alternative frameworks appear to be inappropriate for this purpose. We provide a theoretical study and a numerical evaluation of the alternatives considered. Our simulations highlight the need for and usefulness of these approaches in practice, while our theoretical developments have broad implications for the construction of estimators that permit doubly robust inference in other problems.
Keywords: Adaptive estimation, Doubly robust estimation, Efficient influence function, Targeted minimum loss-based estimation
1. Introduction
In recent years, doubly robust estimators have gained immense popularity in many fields, including causal inference. An estimator is said to be doubly robust if it is consistent for the target parameter of interest when any one of two nuisance parameters is consistently estimated. This property gives doubly robust estimators a natural appeal: any possible inconsistency in the estimation of one nuisance parameter may be mitigated by the consistent estimation of the other. In many problems, doubly robust estimators arise naturally in the pursuit of asymptotic efficiency. Locally efficient estimators often exhibit double robustness due to the form of the efficient influence function of the estimated parameter in the statistical model considered. For many parameters that arise in causal inference, the efficient influence function assumes a doubly robust form, which may explain why doubly robust estimators arise so frequently in that area. For example, under common causal identification assumptions, the statistical parameter identifying the mean counterfactual response under a point treatment yields a doubly robust efficient influence function in a nonparametric model (Robins et al., 1994). Thus, locally efficient estimators of this statistical target parameter are naturally doubly robust. General frameworks for constructing locally efficient estimators can therefore be utilized to generate estimators that are doubly robust.
While the conceptual appeal of doubly robust estimators is clear, questions remain about how they should be constructed in practice. It has long been noted that finite-dimensional models are generally too restrictive to permit consistent estimation of nuisance parameters (Bang & Robins, 2005), but much current work on double robustness involves parametric working models and maximum likelihood estimation. Kang & Schafer (2007) showed that doubly robust estimators can be poorly behaved if both nuisance parameters are inconsistently estimated, leading to recent proposals for estimators that minimize bias resulting from misspecification (Vermeulen & Vansteelandt, 2014, 2016). While providing an improvement over conventional techniques, these estimators rely upon consistent estimation of at least one nuisance parameter using a parametric model. An alternative approach is to employ flexible, data-adaptive estimation techniques for both nuisance parameters to reduce the risk of inconsistency (van der Laan & Rose, 2011).
A general study of the behaviour of doubly robust estimators under inconsistent estimation
of a nuisance parameter is needed in order to understand how to perform robust inference.
This topic has not received much attention, perhaps because the problems arising from
misspecification are well understood when parametric models are used. For example, if
nuisance parameters are estimated using maximum likelihood, the resulting estimator of the
parameter of interest is asymptotically linear even if one of the nuisance parameter models
has been misspecified. Although in this scenario the asymptotic variance of the estimator
may not be easy to calculate explicitly, resampling techniques may be employed for
inference. When the estimator is the solution of an estimating equation, robust
sandwich-type variance estimators may also be available. In contrast, when nuisance
parameters are estimated using data-adaptive approaches, the implications of inconsistently
estimating one nuisance parameter are much more serious. Generally, the resulting estimator
is irregular, exhibits large bias and has a convergence rate slower than
root-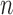 . As we show below, the implications for
inference are dire: regardless of nominal level, the coverage of naïve two-sided confidence
intervals tends to zero and the Type I error rate of two-sided hypothesis tests tends to
unity as the sample size increases. This phenomenon cannot simply be avoided by better
variance estimation, and it occurs even when the true variance of the estimator is known
exactly. Neither is the nonparametric bootstrap a remedy, as, due to the use of
data-adaptive procedures, it is not generally valid for inference.
. As we show below, the implications for
inference are dire: regardless of nominal level, the coverage of naïve two-sided confidence
intervals tends to zero and the Type I error rate of two-sided hypothesis tests tends to
unity as the sample size increases. This phenomenon cannot simply be avoided by better
variance estimation, and it occurs even when the true variance of the estimator is known
exactly. Neither is the nonparametric bootstrap a remedy, as, due to the use of
data-adaptive procedures, it is not generally valid for inference.
In view of these challenges, investigators may believe it simpler to use to parametric models. However, this is unappealing since both nuisance parameters, and hence also the parameter of interest, are then likely to be inconsistently estimated. The use of flexible data-adaptive techniques, such as ensemble machine learning, appears necessary if one is to have any reasonable expectation of consistency for any of the nuisance parameter estimators (van der Laan & Polley, 2007). However, because such methods are highly adaptive, research is needed into developing appropriate methods for doubly robust inference that use such tools.
A first theoretical study of the problem of doubly robust nonparametric inference is the
work of van der Laan (2014), who focused on the
counterfactual mean under a single time-point intervention and considered targeted minimum
loss-based estimation. As the average treatment effect is the difference between two
counterfactual means under different treatments, it too was directly addressed. The
estimators proposed therein were shown to be doubly robust with respect to not only
consistency but also asymptotic linearity. Furthermore, under regularity conditions, the
analytic form of the influence function in van der Laan
(2014) is known, paving the way for the construction of doubly robust confidence
intervals and 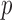 -values. The proposed procedure is quite
complex and has never been implemented. We are therefore motivated to study theoretically
and numerically the following three questions about doubly robust nonparametric inference on
an average treatment effect or, equivalently, on a counterfactual mean:
-values. The proposed procedure is quite
complex and has never been implemented. We are therefore motivated to study theoretically
and numerically the following three questions about doubly robust nonparametric inference on
an average treatment effect or, equivalently, on a counterfactual mean:
1. How badly does inconsistent nuisance parameter estimation affect inference using data-adaptive estimators, and how do estimators that allow doubly robust inference perform?
2. Can existing targeted minimum loss-based estimators be improved by new versions that require estimation of lower-dimensional nuisance parameters?
3. Can simpler alternatives to targeted minimum loss-based estimation be used to construct estimators that are doubly robust for inference and also easier to implement?
As we shall demonstrate in § 5, the answer to question 1 is that na§vely constructed confidence intervals can have very poor coverage, whereas intervals constructed based on appropriate correction procedures have coverage near their nominal level. This suggests that the methods discussed in the present paper are truly needed and may be quite useful. For question 2, we show that it is possible to reduce the dimension of the nuisance parameters introduced in the quest for doubly robust inference, which can provide finite-sample benefits relative to van der Laan (2014). More importantly, this methodological advance is likely to be critical to any extension of the methods discussed here to the setting of treatments defined by multiple time-point interventions. For question 3, we show that the most popular alternative framework to targeted minimum loss-based estimation, the so-called one-step approach, may not be used to theoretically guarantee doubly robust inference unless one knows which nuisance parameter is consistently estimated.
2. Doubly robust estimation
2.1. Notation and background
Suppose that the observed data unit is 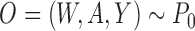 , where
, where
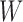 is a vector of baseline covariates,
is a vector of baseline covariates,
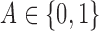 is a binary treatment,
is a binary treatment,
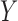 is an outcome, and
is an outcome, and
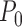 is the true data-generating
distribution, known only to lie in some model
is the true data-generating
distribution, known only to lie in some model 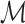 . We take
. We take
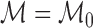 , where
, where
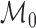 is a nonparametric model,
although arbitrary restrictions on the distribution of
is a nonparametric model,
although arbitrary restrictions on the distribution of 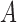 given
given
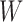 are allowed without affecting our
derivations. We focus on the parameter
are allowed without affecting our
derivations. We focus on the parameter 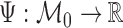 defined as
defined as
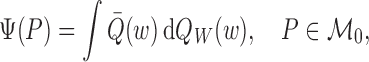 |
where 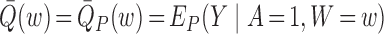 is the so-called outcome regression and
is the so-called outcome regression and 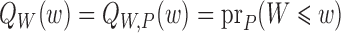 is
the distribution function of the covariate vector. The parameter value
is
the distribution function of the covariate vector. The parameter value
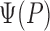 represents the treatment-specific,
covariate-adjusted mean outcome implied by
represents the treatment-specific,
covariate-adjusted mean outcome implied by 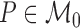 . Under
additional causal assumptions, it can be interpreted as the mean counterfactual outcome
under the treatment corresponding to
. Under
additional causal assumptions, it can be interpreted as the mean counterfactual outcome
under the treatment corresponding to 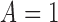 (Rubin, 1974). Because all developments below immediately apply to the
(Rubin, 1974). Because all developments below immediately apply to the
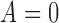 case, and therefore to the average
treatment effect, without loss of generality we explicitly examine only the case where
case, and therefore to the average
treatment effect, without loss of generality we explicitly examine only the case where
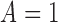 .
.
As the parameter of interest depends on 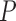 only through
only through
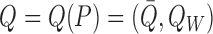 , we will at times
write
, we will at times
write 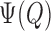 in place of
in place of
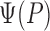 . We will denote
. We will denote
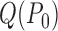 by
by 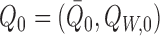 for short, where
for short, where
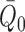 is the true outcome regression
and
is the true outcome regression
and 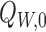 the true distribution of
the true distribution of
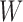 . The propensity score, defined as
. The propensity score, defined as
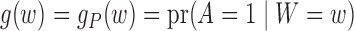 , plays
an important role, and throughout this paper the true propensity score
, plays
an important role, and throughout this paper the true propensity score
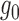 is assumed to satisfy
is assumed to satisfy
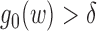 for some
for some
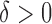 and all
and all 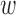 in the
support of
in the
support of 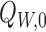 . Below, we make use of empirical
process notation, letting
. Below, we make use of empirical
process notation, letting 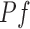 denote
denote 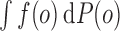 for each
for each
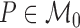 and
and
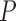 -integrable function
-integrable function
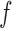 . We also denote by
. We also denote by
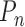 the empirical distribution function
based on
the empirical distribution function
based on 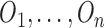 , so
, so
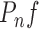 is the average
is the average
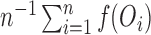 .
.
Recall that a regular estimator 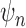 of
of
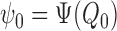 is asymptotically linear
if and only if it can be written as
is asymptotically linear
if and only if it can be written as 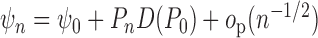 ,
where
,
where 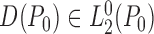 is a gradient of
is a gradient of
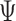 at
at 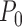 relative to model
relative to model 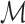 . Here, for each
. Here, for each
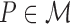 , we denote by
, we denote by
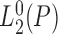 the Hilbert space of all
real-valued functions with zero mean and finite variance defined on the support of
the Hilbert space of all
real-valued functions with zero mean and finite variance defined on the support of
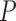 endowed with the covariance inner
product. The function
endowed with the covariance inner
product. The function 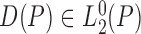 is said to be a gradient
of
is said to be a gradient
of 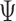 at
at 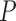 relative to
relative to 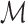 if
if
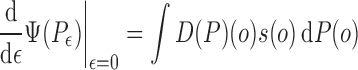 |
for any regular one-dimensional parametric submodel
 with
score
with
score 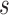 for
for 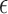 at
at 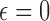 and such that
and such that
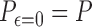 . In the nonparametric
case, where
. In the nonparametric
case, where 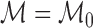 , an example of
such a submodel is given by
, an example of
such a submodel is given by 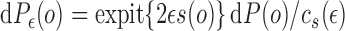 ,
where
,
where 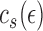 is a normalizing constant and
is a normalizing constant and
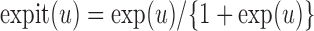 for
any
for
any 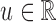 . Under sampling from
. Under sampling from
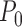 , a regular and asymptotically linear
estimator is efficient if and only if its influence function is the efficient influence
function
, a regular and asymptotically linear
estimator is efficient if and only if its influence function is the efficient influence
function 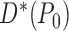 . The efficient influence function
is the unique gradient that lies in the tangent space
. The efficient influence function
is the unique gradient that lies in the tangent space 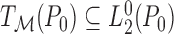 of
of 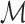 at
at 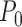 , and
it is a crucial ingredient in the construction of asymptotically efficient estimators. For
an overview of efficiency theory, see Bickel et al.
(1997).
, and
it is a crucial ingredient in the construction of asymptotically efficient estimators. For
an overview of efficiency theory, see Bickel et al.
(1997).
The efficient influence function of 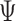 at
at
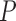 relative to
relative to 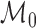 is
is
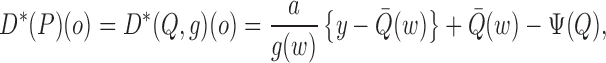 |
with 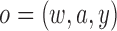 denoting a
realized value of
denoting a
realized value of 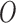 (van der
Laan & Robins, 2003).
(van der
Laan & Robins, 2003).
2.2. Doubly robust consistency
Suppose that 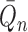 and
and 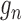 are
estimators of
are
estimators of 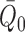 and
and 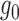 ,
respectively, and denote by
,
respectively, and denote by 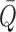 and
and 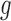 their
respective in-probability limits. We write
their
respective in-probability limits. We write 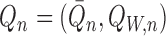 ,
where
,
where 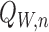 is the empirical distribution based
on observations
is the empirical distribution based
on observations 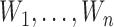 . A linearization of the
parameter allows us to write
. A linearization of the
parameter allows us to write
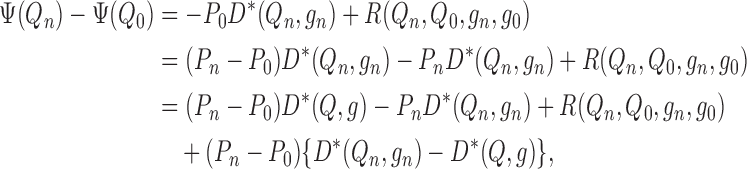 |
where 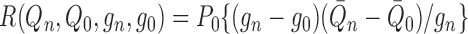 .
The first equality is expected because
.
The first equality is expected because 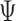 is strongly
differentiable in the sense of Pfanzagl (1982). As
shorthand, we will write
is strongly
differentiable in the sense of Pfanzagl (1982). As
shorthand, we will write 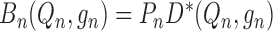 and
and
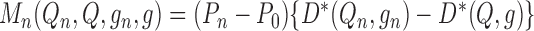 .
Using this notation, we can express
.
Using this notation, we can express 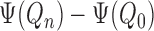 as
as
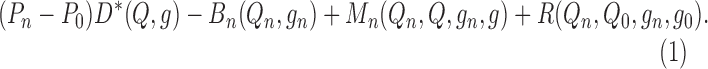 |
(1) |
This representation reduces the analysis of the plug-in estimator
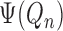 to the consideration of four
terms. The first term,
to the consideration of four
terms. The first term, 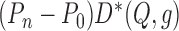 , is the average of
, is the average of
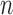 independent draws of the random variable
independent draws of the random variable
 , which has mean
zero if either
, which has mean
zero if either 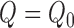 or
or 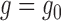 .
This observation is a simple but fundamental fact underlying doubly robust estimation.
Since
.
This observation is a simple but fundamental fact underlying doubly robust estimation.
Since 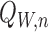 is known to converge to
is known to converge to
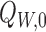 , the statement
, the statement
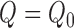 is equivalent to
is equivalent to
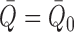 . The second term,
. The second term,
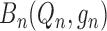 , is a first-order bias term
that must be accounted for to allow
, is a first-order bias term
that must be accounted for to allow 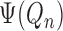 to be
asymptotically linear. The third term is an empirical process term that is often
asymptotically negligible, that is,
to be
asymptotically linear. The third term is an empirical process term that is often
asymptotically negligible, that is, 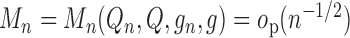 .
This is true, for example, if
.
This is true, for example, if 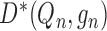 falls in a
falls in a
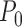 -Donsker class with probability tending
to 1 and
-Donsker class with probability tending
to 1 and 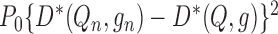 converges
to zero in probability. For a comprehensive reference on empirical processes, we refer
readers to van der Vaart & Wellner (1996).
Finally, the fourth term,
converges
to zero in probability. For a comprehensive reference on empirical processes, we refer
readers to van der Vaart & Wellner (1996).
Finally, the fourth term, 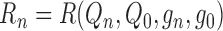 , is the remainder
from the linearization. By inspection, this term tends to zero at a rate determined by how
fast the nuisance functions
, is the remainder
from the linearization. By inspection, this term tends to zero at a rate determined by how
fast the nuisance functions 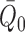 and
and 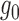 are
estimated.
are
estimated.
To correct for the first-order bias term 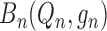 , two
general strategies may be used: the one-step Newton–Raphson approach and targeted minimum
loss-based estimation. The first, hereafter called the one-step approach, suggests
performing an additive correction for the first-order bias, leading to the estimator
, two
general strategies may be used: the one-step Newton–Raphson approach and targeted minimum
loss-based estimation. The first, hereafter called the one-step approach, suggests
performing an additive correction for the first-order bias, leading to the estimator
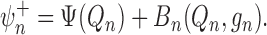 |
This approach appeared in Ibragimov & Has’minskii
(1981) and Pfanzagl (1982), and is the
infinite-dimensional extension of the one-step Newton–Raphson technique for efficient
estimation in parametric models. In this paper, the efficient influence function is a
linear function of the parameter of interest. As such, the one-step estimator equals the
solution of the optimal estimating equation for this parameter and is therefore equivalent
to the so-called augmented inverse probability of treatment estimator (Robins et al., 1994; van der Laan & Robins, 2003). Owing to their simple construction, one-step
estimators are generally computationally convenient, though this convenience comes at a
cost, as the one-step correction may produce estimates outside the parameter space, such
as probability estimates either below zero or above one. Targeted minimum loss-based
estimation, formally developed in van der Laan & Rubin
(2006) and comprehensively discussed in van der
Laan & Rose (2011), provides an algorithm to convert
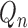 into a targeted estimator
into a targeted estimator
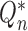 of
of 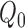 such
that
such
that 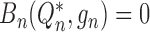 , which may then be used to
define the targeted plug-in estimator
, which may then be used to
define the targeted plug-in estimator 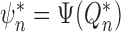 . The
first update of
. The
first update of 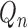 in this recursive scheme consists of
the minimizer of an empirical risk over a least favourable submodel through
in this recursive scheme consists of
the minimizer of an empirical risk over a least favourable submodel through
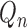 . The process is iterated using updated
versions of
. The process is iterated using updated
versions of 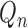 until convergence to yield
until convergence to yield
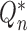 . In the problem considered here,
convergence occurs in a single step. By virtue of being a plug-in estimator,
. In the problem considered here,
convergence occurs in a single step. By virtue of being a plug-in estimator,
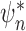 may exhibit improved finite-sample
behaviour relative to its one-step counterpart (Porter et
al., 2011).
may exhibit improved finite-sample
behaviour relative to its one-step counterpart (Porter et
al., 2011).
The large-sample properties of both 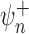 and
and
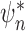 can be studied through (1). As above, suppose that the empirical
process term
can be studied through (1). As above, suppose that the empirical
process term 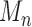 is asymptotically negligible. If both
is asymptotically negligible. If both
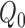 and
and 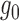 are
estimated consistently, so that
are
estimated consistently, so that 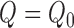 and
and
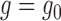 , and if estimation of these nuisance
functions is fast enough to ensure that the remainder term
, and if estimation of these nuisance
functions is fast enough to ensure that the remainder term 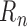 is
asymptotically negligible, then
is
asymptotically negligible, then 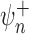 is
asymptotically linear with influence function equal to
is
asymptotically linear with influence function equal to 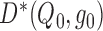 , and thus it is asymptotically
efficient. The same can be said of
, and thus it is asymptotically
efficient. The same can be said of 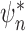 if the same
conditions on
if the same
conditions on 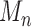 and
and 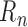 hold
with
hold
with 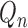 replaced by
replaced by 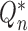 .
If only one of
.
If only one of 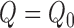 or
or 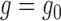 holds, it is impossible to guarantee the asymptotic negligibility of the remainder term,
even if both
holds, it is impossible to guarantee the asymptotic negligibility of the remainder term,
even if both 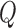 and
and 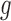 lie in
parametric models. Nevertheless, provided
lie in
parametric models. Nevertheless, provided 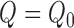 or
or
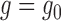 , under very mild conditions, the
remainder term
, under very mild conditions, the
remainder term 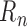 based on either
based on either
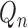 or
or 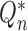 tends to zero in probability, and the empirical process term
tends to zero in probability, and the empirical process term 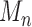 remains asymptotically negligible. Since
remains asymptotically negligible. Since 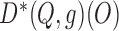 has mean zero
if either
has mean zero
if either 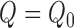 or
or 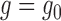 and has finite variance, the central limit theorem implies that
and has finite variance, the central limit theorem implies that 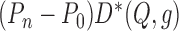 is
is
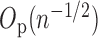 , so both
, so both
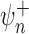 and
and 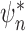 are consistent estimators of
are consistent estimators of 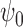 . This is so-called double
robustness: consistent estimation of
. This is so-called double
robustness: consistent estimation of 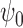 if either of the
nuisance functions
if either of the
nuisance functions 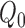 or
or 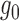 is
consistently estimated.
is
consistently estimated.
2.3. Doubly robust asymptotic linearity
Doubly robust asymptotic linearity is a more stringent requirement than doubly robust
consistency. It is also arguably more important, since without it the construction of
valid confidence intervals and tests may be very difficult, if not impossible. A careful
study of 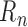 is required to determine how doubly
robust inference may be obtained.
is required to determine how doubly
robust inference may be obtained.
When both the outcome regression and the propensity score are consistently estimated,
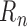 is a second-order term consisting of
the product of two differences, both tending to zero. Hence, provided
is a second-order term consisting of
the product of two differences, both tending to zero. Hence, provided
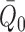 and
and 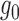 are
estimated sufficiently fast,
are
estimated sufficiently fast, 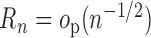 . This holds,
for example, if both
. This holds,
for example, if both 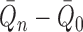 and
and
 are
are 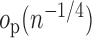 with respect to the
with respect to the
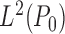 -norm. If only one of the outcome
regression or propensity score is consistently estimated, one of the differences in
-norm. If only one of the outcome
regression or propensity score is consistently estimated, one of the differences in
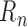 does not tend to zero. Consequently,
does not tend to zero. Consequently,
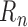 is either of the same order as or tends
to zero more slowly than
is either of the same order as or tends
to zero more slowly than 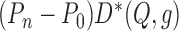 . As such,
. As such,
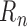 at least contributes to the first-order
behaviour of the estimator and may determine it entirely. If a correctly specified
parametric model is used to estimate either
at least contributes to the first-order
behaviour of the estimator and may determine it entirely. If a correctly specified
parametric model is used to estimate either 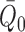 or
or
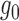 , the delta method generally implies
that
, the delta method generally implies
that 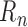 is asymptotically linear. In this case,
both
is asymptotically linear. In this case,
both 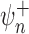 and
and 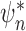 are also asymptotically linear, though their influence function is the sum of two terms:
are also asymptotically linear, though their influence function is the sum of two terms:
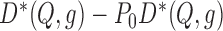 and the influence
function of
and the influence
function of 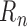 as an estimator of zero. Correctly
specifying a parametric model is seldom feasible in realistic settings, however, so it may
be preferable to use adaptive estimators of the nuisance functions. In such a situation,
whenever one nuisance parameter is inconsistently estimated, the remainder term
as an estimator of zero. Correctly
specifying a parametric model is seldom feasible in realistic settings, however, so it may
be preferable to use adaptive estimators of the nuisance functions. In such a situation,
whenever one nuisance parameter is inconsistently estimated, the remainder term
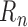 tends to zero slowly and thus dominates
the first-order behaviour of the estimator of
tends to zero slowly and thus dominates
the first-order behaviour of the estimator of  . Therefore, in
this case the one-step and targeted minimum loss-based estimators are doubly robust with
respect to consistency but not with respect to asymptotic linearity.
. Therefore, in
this case the one-step and targeted minimum loss-based estimators are doubly robust with
respect to consistency but not with respect to asymptotic linearity.
To illustrate the deleterious effect of the remainder on inference in these situations,
suppose that we construct an asymptotic level-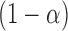 two-sided
Wald-type confidence interval for
two-sided
Wald-type confidence interval for 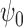 based on a
consistent estimator
based on a
consistent estimator 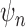 , say with true standard error
, say with true standard error
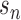 . Suppose further that
. Suppose further that
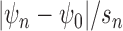 tends to
tends to
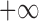 in probability, which often occurs
when the bias of
in probability, which often occurs
when the bias of 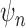 tends to zero more slowly than its
standard error. Denoting by
tends to zero more slowly than its
standard error. Denoting by 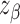 the
the 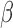 quantile of the standard normal distribution, the coverage of the oracle Wald-type
interval
quantile of the standard normal distribution, the coverage of the oracle Wald-type
interval 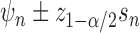 is such that
is such that
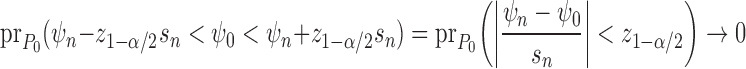 |
as 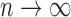 . This remains true if
we replace
. This remains true if
we replace 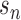 by any random sequence that converges
to zero at the same rate or faster. If asymptotic linearity were preserved under
inconsistent estimation of one of the nuisance parameters,
by any random sequence that converges
to zero at the same rate or faster. If asymptotic linearity were preserved under
inconsistent estimation of one of the nuisance parameters, 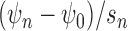 would instead tend to a
standard normal variate. The oracle Wald-type intervals, and in fact any Wald-type
interval using a consistent standard error estimator, would have correct asymptotic
coverage. This argument therefore stresses the benefit of constructing estimators that are
doubly robust with respect to asymptotic linearity for the sake of obtaining confidence
intervals and tests whose validity is doubly robust.
would instead tend to a
standard normal variate. The oracle Wald-type intervals, and in fact any Wald-type
interval using a consistent standard error estimator, would have correct asymptotic
coverage. This argument therefore stresses the benefit of constructing estimators that are
doubly robust with respect to asymptotic linearity for the sake of obtaining confidence
intervals and tests whose validity is doubly robust.
3. Doubly robust inference via targeted minimum loss-based estimation
3.1. Existing construction
van der Laan (2014) proposed a targeted minimum
loss-based estimator of 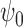 that is not only locally efficient
and doubly robust for consistency but also doubly robust for asymptotic linearity. To do
so he showed that, with some additional bias correction,
that is not only locally efficient
and doubly robust for consistency but also doubly robust for asymptotic linearity. To do
so he showed that, with some additional bias correction, 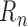 may
be rendered asymptotically linear with a well-described influence function. This requires
approximating the first-order behaviour of
may
be rendered asymptotically linear with a well-described influence function. This requires
approximating the first-order behaviour of 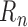 using additional
nuisance parameters, which consist of a bivariate and a univariate regression, defined
respectively as
using additional
nuisance parameters, which consist of a bivariate and a univariate regression, defined
respectively as
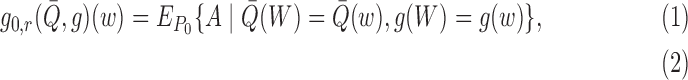 |
(2) |
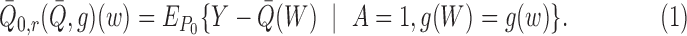 |
(3) |
Expression (2) is the bivariate
regression of the true propensity of treatment on an outcome regression and a propensity
score, whereas (3) is the univariate
regression of the residual from an outcome regression on a propensity score in the treated
subgroup. The subscript 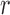 emphasizes that these nuisance parameters
are of reduced dimension relative to
emphasizes that these nuisance parameters
are of reduced dimension relative to 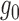 and
and
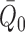 . This dimension reduction is
critical since it essentially guarantees that consistent estimators of these parameters
can be constructed in practice. For example, we may be unable to consistently estimate
. This dimension reduction is
critical since it essentially guarantees that consistent estimators of these parameters
can be constructed in practice. For example, we may be unable to consistently estimate
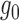 , which is a function of the entire
vector of potential confounders; however, we can guarantee consistent estimation of
, which is a function of the entire
vector of potential confounders; however, we can guarantee consistent estimation of
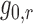 , which involves only a bivariate
summary of
, which involves only a bivariate
summary of 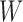 .
.
Key to the study of how these additional nuisance parameters may be used to approximate
the first-order behaviour of the remainder term 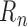 are the functions
are the functions
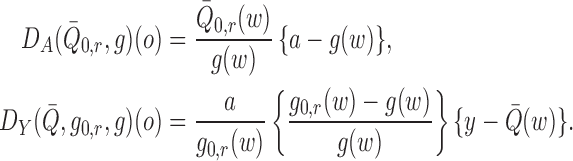 |
In Appendix A, we show that the remainder term
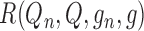 can be represented as
can be represented as
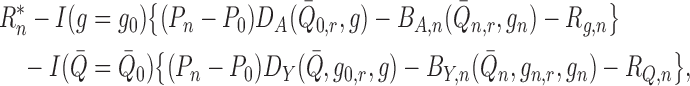 |
(4) |
where 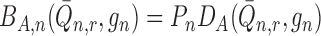 and
and 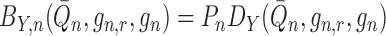 are bias terms, and
are bias terms, and  ,
,  and
and  are second-order terms. The
specific form of these terms is provided in Appendix
A, where we also discuss sufficient conditions for ensuring their asymptotic
negligibility. Just as the bias term in (1) had to be accounted for to achieve doubly robust consistency, so too must the
bias terms in (4) to achieve doubly
robust asymptotic linearity.
are second-order terms. The
specific form of these terms is provided in Appendix
A, where we also discuss sufficient conditions for ensuring their asymptotic
negligibility. Just as the bias term in (1) had to be accounted for to achieve doubly robust consistency, so too must the
bias terms in (4) to achieve doubly
robust asymptotic linearity.
The iterative targeted minimum loss-based estimation algorithm proposed in Theorem 3 of
van der Laan (2014) produces estimators
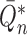 ,
, 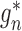 ,
,
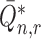 and
and
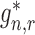 from initial estimators
from initial estimators
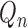 and
and 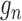 in
such a manner as to ensure that
in
such a manner as to ensure that
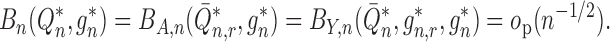 |
In view of (1) and (4), 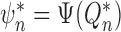 is asymptotically linear
with influence function
is asymptotically linear
with influence function
 |
provided either 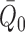 or
or
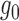 is estimated consistently. If
is estimated consistently. If
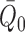 and
and 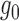 are
estimated consistently, then
are
estimated consistently, then 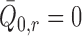 and
and
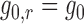 . In this case,
. In this case,
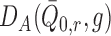 and
and
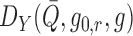 are identically
zero, which establishes local efficiency of
are identically
zero, which establishes local efficiency of 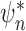 .
.
3.2. Novel reduced-dimension construction
We now show how to theoretically improve upon the proposal of van der Laan (2014) through an alternative formulation of a targeted minimum loss-based estimator. We derive an approximation of the remainder that relies on alternative nuisance parameters of lower dimension than those presented in § 3.1. This makes the estimation problem involved more feasible and may also pave the way to a generalization of this work to settings with longitudinal treatments.
In Appendix B, we argue that the remainder term in
(4) can be represented using
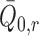 as previously defined and the
additional nuisance parameters
as previously defined and the
additional nuisance parameters
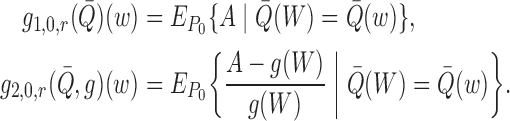 |
These are univariate regressions, in contrast to the bivariate regression
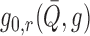 described in § 3.1 and used in van
der Laan (2014). Nonparametric estimators of these univariate parameters often
achieve better rates than those proposed therein. Use of this alternative representation
yields estimators guaranteed to be asymptotically linear under weaker conditions than
previously required.
described in § 3.1 and used in van
der Laan (2014). Nonparametric estimators of these univariate parameters often
achieve better rates than those proposed therein. Use of this alternative representation
yields estimators guaranteed to be asymptotically linear under weaker conditions than
previously required.
Here, we state the main result describing the behaviour of the estimator implied by this parameterization of the remainder term; we also discuss an iterative implementation of the estimator. Redefining
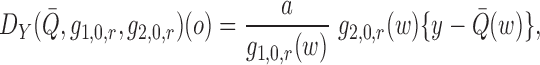 |
we have the following result.
Theorem 1.
Suppose that either
or
. Provided that the nuisance estimators
satisfy
(5) and that the second-order terms
and
described in Appendix B are
, the plug-in estimator
is asymptotically linear with influence function
. Furthermore,
converges in law to a zero-mean normal random variable with variance estimated consistently by
An algorithm to construct nuisance estimators that satisfy (5) can be devised based on targeted minimum loss-based estimation.
Without loss of generality, suppose 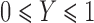 . Defining
. Defining
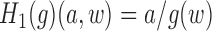 ,
,
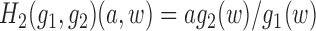 and
and
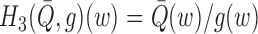 , we
implement the following recursive procedure.
, we
implement the following recursive procedure.
Step 1.
Construct initial estimates
and
of
and
, and set
.
Step 2.
Define
and
; fit a logistic regression with outcome
, covariate
and offset
using only data points with
; set
as the estimated coefficient of
; and define
Step 3.
Construct estimates
and
of
and
based on
and
.
Step 4.
Define
and
; fit a logistic regression with outcome
, covariate
and offset
using only data points with
; set
as the estimated coefficient of
; and define
Step 5.
Construct estimates
of
based on
and
.
Step 6.
Define
and
; fit a logistic regression with outcome
, covariate
and offset
; set
as the estimated coefficient of
; and define
Step 7.
Set
and iterate Steps 1–6 until
is large enough that
.
Step 8.
Set
,
,
,
and
.
Theorem 1 implies that doubly robust confidence intervals and tests can readily be
crafted. For example, the Wald construction 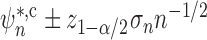 is a doubly robust
is a doubly robust 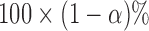 asymptotic confidence
interval for
asymptotic confidence
interval for 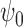 , and prescribing rejection of the
null hypothesis
, and prescribing rejection of the
null hypothesis 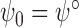 versus the alternative
versus the alternative
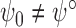 only when
only when
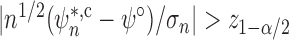 constitutes a doubly robust hypothesis test with asymptotic level
constitutes a doubly robust hypothesis test with asymptotic level
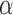 . Thus, valid statistical inference
is preserved when one nuisance parameter is inconsistently estimated, in contrast to
conventional doubly robust estimation, wherein only consistency is preserved.
. Thus, valid statistical inference
is preserved when one nuisance parameter is inconsistently estimated, in contrast to
conventional doubly robust estimation, wherein only consistency is preserved.
4. Doubly robust inference via one-step estimation
In § 2 we discussed the construction of doubly
robust, locally efficient estimators of 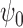 and argued that both
the one-step approach and targeted minimum loss-based estimation can be used for bias
correction. For the sake of constructing asymptotically efficient estimators, these two
strategies are generally considered to be alternatives, with targeted minimum loss-based
estimation possibly delivering better finite-sample behaviour but the one-step approach
often simpler to implement. In § 3, we outlined how
the bias-correction feature of the targeted minimum loss-based estimation framework could be
leveraged to achieve doubly robust asymptotic linearity and thus perform doubly robust
inference. Since targeted minimum loss-based estimation can be more complicated to implement
than the one-step correction procedure, it is natural to wonder whether a one-step approach
could also account for the additional bias terms that result from the inconsistent
estimation of either
and argued that both
the one-step approach and targeted minimum loss-based estimation can be used for bias
correction. For the sake of constructing asymptotically efficient estimators, these two
strategies are generally considered to be alternatives, with targeted minimum loss-based
estimation possibly delivering better finite-sample behaviour but the one-step approach
often simpler to implement. In § 3, we outlined how
the bias-correction feature of the targeted minimum loss-based estimation framework could be
leveraged to achieve doubly robust asymptotic linearity and thus perform doubly robust
inference. Since targeted minimum loss-based estimation can be more complicated to implement
than the one-step correction procedure, it is natural to wonder whether a one-step approach
could also account for the additional bias terms that result from the inconsistent
estimation of either 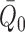 or
or 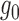 . If
so, the resulting one-step estimator could provide a computationally convenient alternative
to the algorithm described in § 3.2.
. If
so, the resulting one-step estimator could provide a computationally convenient alternative
to the algorithm described in § 3.2.
We recall that the doubly robust, locally efficient one-step estimator
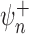 was constructed by adding the bias
term
was constructed by adding the bias
term 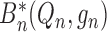 to the initial plug-in
estimator
to the initial plug-in
estimator 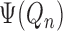 . By extension, it seems sensible to
investigate whether the estimator
. By extension, it seems sensible to
investigate whether the estimator
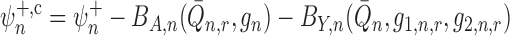 |
(6) |
is doubly robust with respect to asymptotic linearity. By (1) and (4), the estimator
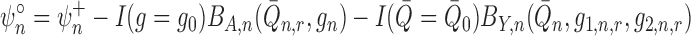 |
is asymptotically linear with influence function
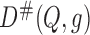 , just as the targeted minimum
loss-based estimators in the previous section. Therefore,
, just as the targeted minimum
loss-based estimators in the previous section. Therefore, 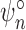 is locally efficient and doubly
robust with respect to asymptotic linearity. Nevertheless, to compute
is locally efficient and doubly
robust with respect to asymptotic linearity. Nevertheless, to compute
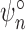 , the analyst must know which
nuisance parameter, if any, is inconsistently estimated. Such information will generally not
be available, except in the case of a randomized trial, where
, the analyst must know which
nuisance parameter, if any, is inconsistently estimated. Such information will generally not
be available, except in the case of a randomized trial, where 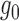 may be
known to the experimenter. To study the properties of
may be
known to the experimenter. To study the properties of 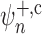 , we note that
, we note that
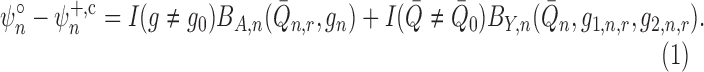 |
(7) |
The one-step estimator 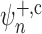 corrects for both
inconsistent estimation of
corrects for both
inconsistent estimation of 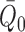 and inconsistent estimation of
and inconsistent estimation of
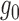 . However, for consistent estimation of
. However, for consistent estimation of
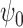 , no more than one of these two
nuisance parameters can in reality be inconsistently estimated. In this case there is
necessarily overcorrection in
, no more than one of these two
nuisance parameters can in reality be inconsistently estimated. In this case there is
necessarily overcorrection in 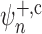 , and it is not a priori
obvious whether this may be detrimental to the behaviour of the estimator. Elucidating this
issue requires a careful study of each of the two bias-correction terms in settings where
they are not in fact needed. For example, the term
, and it is not a priori
obvious whether this may be detrimental to the behaviour of the estimator. Elucidating this
issue requires a careful study of each of the two bias-correction terms in settings where
they are not in fact needed. For example, the term 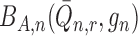 , used to correct
for bias resulting from inconsistent estimation of
, used to correct
for bias resulting from inconsistent estimation of 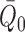 ,
must be analysed in the scenario where it is actually
,
must be analysed in the scenario where it is actually 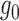 that
has been inconsistently estimated.
that
has been inconsistently estimated.
In Appendix C, we show that under reasonable conditions, we can represent the first summand on the right-hand side of (7) as
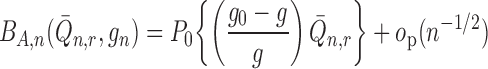 |
when 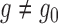 , and we can
represent the second summand as
, and we can
represent the second summand as
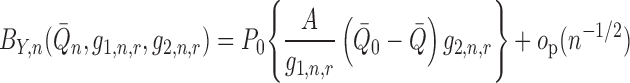 |
when 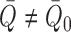 . This
implies that the first-order behaviour of
. This
implies that the first-order behaviour of  is
driven by these terms. In particular, the rate of convergence of
is
driven by these terms. In particular, the rate of convergence of  is determined by that of the
estimators
is determined by that of the
estimators 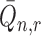 ,
, 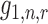 and
and 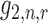 of the reduced-dimension nuisance
parameters. In practice, these terms are unlikely to be estimable at the parametric rate,
since this would require the correct specification of a parametric model for a complex
object, and adaptive techniques are likely to be used. Because the rates achieved by these
techniques are generally slower than
of the reduced-dimension nuisance
parameters. In practice, these terms are unlikely to be estimable at the parametric rate,
since this would require the correct specification of a parametric model for a complex
object, and adaptive techniques are likely to be used. Because the rates achieved by these
techniques are generally slower than 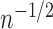 , the estimator
, the estimator
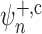 fails to be
root-
fails to be
root-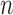 consistent and hence doubly robust with
respect to asymptotic linearity. Using an argument identical to that in § 2.3, we can show that Wald-type confidence intervals
for
consistent and hence doubly robust with
respect to asymptotic linearity. Using an argument identical to that in § 2.3, we can show that Wald-type confidence intervals
for 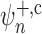 have similarly poor
asymptotic coverage. Therefore, at least theoretically, the one-step construction does not
appear helpful.
have similarly poor
asymptotic coverage. Therefore, at least theoretically, the one-step construction does not
appear helpful.
This warrants further discussion. The above theory shows that the targeted minimum loss-based estimation framework is able to simultaneously account for inconsistent estimation of either the outcome regression or the propensity score without the need to know which is required. In contrast, the one-step approach requires knowledge of which nuisance parameter is possibly inconsistently estimated to achieve doubly robust asymptotic linearity. Without this knowledge, asymptotic linearity cannot be guaranteed in a doubly robust fashion. This is relevant for future work to derive procedures for doubly robust inference on other parameters admitting doubly or multiply robust estimators.
5. Simulation study
5.1. Data-generating mechanism and crossvalidation set-up
In each of the simulations below, the baseline covariate vector 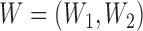 had independent components
with
had independent components
with 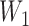 distributed according to a uniform
distribution over the interval
distributed according to a uniform
distribution over the interval 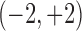 and
and
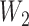 distributed as a binary random variable
with success probability
distributed as a binary random variable
with success probability 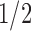 . The conditional probability of
. The conditional probability of
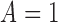 given
given 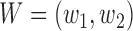 was
was 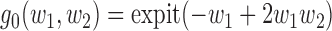 .
The outcome
.
The outcome 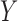 was a binary random variable whose
conditional probability of occurrence given
was a binary random variable whose
conditional probability of occurrence given 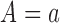 is
is
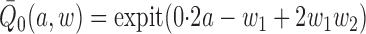 .
.
We implemented and compared the performance of the following six estimators:
(i) the standard, uncorrected targeted minimum loss-based estimator;
(ii) the corrected targeted minimum loss-based estimator using bivariate nuisance regression, as proposed by van der Laan (2014);
(iii) the corrected targeted minimum loss-based estimator using univariate nuisance regressions, as introduced in Theorem 1;
(iv) the standard, uncorrected one-step estimator, commonly referred to as the augmented inverse probability weighted estimator;
(v) the corrected one-step estimator using bivariate nuisance regression;
(vi) the corrected one-step estimator using univariate nuisance regressions, as given in (6).
We evaluated these estimators in the following three scenarios.
I. Only the outcome regression is consistently estimated.
II. Only the propensity score is consistently estimated.
III. Both the outcome regression and the propensity score are consistently estimated.
The consistently estimated nuisance parameter, either the outcome regression or the
propensity score, was estimated using a bivariate Nadaraya–Watson estimator with bandwidth
selected by crossvalidation, while the inconsistently estimated nuisance parameter was
estimated using a logistic regression model with main terms only, thus ignoring the
interaction between 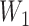 and
and 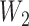 . The
reduced-dimension nuisance parameters required for the additional correction procedure
involved in computing estimators (ii), (iii), (v) and (vi) were estimated using the
Nadaraya–Watson estimator with bandwidth selected by leave-one-out crossvalidation (Racine & Li, 2004). For scenarios I and II, we
considered sample sizes
. The
reduced-dimension nuisance parameters required for the additional correction procedure
involved in computing estimators (ii), (iii), (v) and (vi) were estimated using the
Nadaraya–Watson estimator with bandwidth selected by leave-one-out crossvalidation (Racine & Li, 2004). For scenarios I and II, we
considered sample sizes 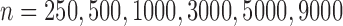 . For
scenario III, theory dictates that all estimators considered should be asymptotically
equivalent, so we used only the sample sizes
. For
scenario III, theory dictates that all estimators considered should be asymptotically
equivalent, so we used only the sample sizes 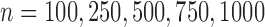 . For each
. For each
 we generated 5000 datasets. We summarized
estimator performance in terms of bias, bias times
we generated 5000 datasets. We summarized
estimator performance in terms of bias, bias times  ,
coverage of 95% confidence intervals, and accuracy of the standard error estimator, which
we assessed by comparing the Monte Carlo variance of the estimator and the average
estimated variance across simulations. We examined the following hypotheses based on our
theoretical work.
,
coverage of 95% confidence intervals, and accuracy of the standard error estimator, which
we assessed by comparing the Monte Carlo variance of the estimator and the average
estimated variance across simulations. We examined the following hypotheses based on our
theoretical work.
(A) In scenarios I and II, the bias of estimators (i), (iv), (v) and (vi) tends to zero more slowly than
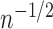 , whereas that of estimators
(ii) and (iii) does so faster than
, whereas that of estimators
(ii) and (iii) does so faster than 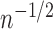 .
.(B) In scenarios I and II, the slow convergence of the bias for estimators (i), (iv), (v) and (vi) adversely affects the nominal confidence interval coverage, whereas the corrected targeted minimum loss-based estimators (ii) and (iii) have asymptotically nominal coverage.
(C) In scenarios I and II, influence function-based variance estimators are accurate for the corrected estimators (ii), (iii), (v) and (vi), but not for the uncorrected estimators (i) and (iv).
(D) In scenario III, all estimators exhibit approximately the same behaviour.
5.2. Results
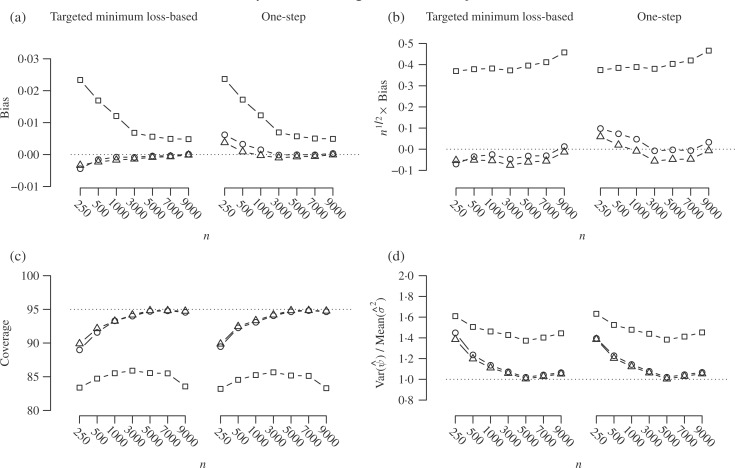
We first focus on the results for scenario I, in which only the outcome regression is
consistently estimated. In Fig. 1(a), the bias of
each estimator tends to zero, illustrating the conventional double robustness of these
estimators. However, Fig. 1(b) supports hypothesis
(A), as the bias of the uncorrected estimators tends to zero at a slower rate than
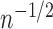 , while the bias of the corrected
targeted minimum loss-based estimators tends to zero faster. The bias of the corrected
one-step estimators is reduced relative to the uncorrected estimators, and for the sample
sizes considered we do not yet see the expected divergence in the bias when inflated by
, while the bias of the corrected
targeted minimum loss-based estimators tends to zero faster. The bias of the corrected
one-step estimators is reduced relative to the uncorrected estimators, and for the sample
sizes considered we do not yet see the expected divergence in the bias when inflated by
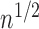 . Figure 1(c) indicates strong support for hypothesis (B): the coverage of
intervals based on the uncorrected estimators is not only far from the nominal level but
also U-shaped, suggesting worsening coverage in larger samples, as is expected based on
our arguments in § 2.3. Intervals based on the
corrected estimators have approximately nominal coverage in moderate and large samples.
Figure 1(d) indicates that the variance estimators
for the uncorrected estimators are liberal, which contributes to the poor coverage of
intervals. The variance estimators for the corrected estimators are approximately accurate
in larger samples, thus supporting hypothesis (C).
. Figure 1(c) indicates strong support for hypothesis (B): the coverage of
intervals based on the uncorrected estimators is not only far from the nominal level but
also U-shaped, suggesting worsening coverage in larger samples, as is expected based on
our arguments in § 2.3. Intervals based on the
corrected estimators have approximately nominal coverage in moderate and large samples.
Figure 1(d) indicates that the variance estimators
for the uncorrected estimators are liberal, which contributes to the poor coverage of
intervals. The variance estimators for the corrected estimators are approximately accurate
in larger samples, thus supporting hypothesis (C).
Fig. 1.
Simulation results when only the outcome regression is consistently estimated, with
the following performance measures plotted against the sample size
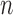 : (a) bias; (b)
: (a) bias; (b)
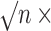 bias; (c) coverage of
95% confidence intervals; (d) accuracy of the standard error estimator. Squares
represent estimators that do not account for inconsistent nuisance parameter
estimation, circles represent estimators using the bivariate correction of van der Laan (2014), and triangles represent
estimators using the proposed univariate corrections.
bias; (c) coverage of
95% confidence intervals; (d) accuracy of the standard error estimator. Squares
represent estimators that do not account for inconsistent nuisance parameter
estimation, circles represent estimators using the bivariate correction of van der Laan (2014), and triangles represent
estimators using the proposed univariate corrections.
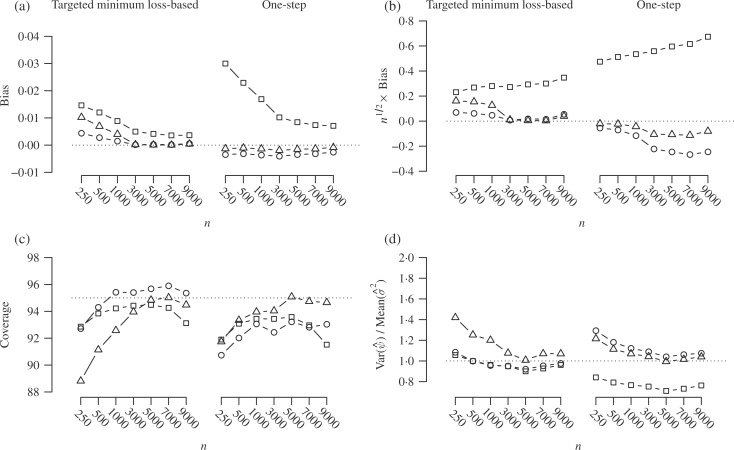
Figure 2 summarizes the results for scenario II. In
Fig. 2(b) we again see that the bias of the
uncorrected estimators tends to zero more slowly than 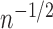 ; this is also true of the corrected
one-step estimators. In contrast, the bias of the corrected targeted minimum loss-based
estimators appears to converge to zero faster than
; this is also true of the corrected
one-step estimators. In contrast, the bias of the corrected targeted minimum loss-based
estimators appears to converge to zero faster than 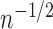 . Figure
2(c) partially supports hypothesis (B): intervals based on the uncorrected
estimators achieve near-nominal coverage for moderate and large sample sizes in spite of
the large bias. However, we again find the expected U-shape, with an eventual downturn in
coverage as the sample size increases further. Intervals based on the corrected targeted
minimum loss-based estimators using bivariate nuisance regression have improved coverage
throughout, and intervals based on either corrected targeted minimum loss-based estimator
have nearly nominal coverage in larger samples. Intervals based on the corrected one-step
estimator with the univariate correction achieve approximately nominal coverage, while
those based on the one-step estimator with bivariate correction do not, probably due to
larger bias. Figure 2(d) shows that the variance
estimator for the uncorrected one-step estimator is conservative, whereas that based on
the uncorrected targeted minimum loss-based estimator is approximately accurate. The
variance estimators based on the corrected one-step or targeted minimum loss-based
estimators appear to be valid throughout, although that based on the latter using
univariate nuisance regressions appears to be liberal in smaller samples.
. Figure
2(c) partially supports hypothesis (B): intervals based on the uncorrected
estimators achieve near-nominal coverage for moderate and large sample sizes in spite of
the large bias. However, we again find the expected U-shape, with an eventual downturn in
coverage as the sample size increases further. Intervals based on the corrected targeted
minimum loss-based estimators using bivariate nuisance regression have improved coverage
throughout, and intervals based on either corrected targeted minimum loss-based estimator
have nearly nominal coverage in larger samples. Intervals based on the corrected one-step
estimator with the univariate correction achieve approximately nominal coverage, while
those based on the one-step estimator with bivariate correction do not, probably due to
larger bias. Figure 2(d) shows that the variance
estimator for the uncorrected one-step estimator is conservative, whereas that based on
the uncorrected targeted minimum loss-based estimator is approximately accurate. The
variance estimators based on the corrected one-step or targeted minimum loss-based
estimators appear to be valid throughout, although that based on the latter using
univariate nuisance regressions appears to be liberal in smaller samples.
Fig. 2.
Simulation results when only the propensity score is consistently estimated: (a)
bias, (b) 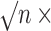 bias, (c) coverage of
95% confidence intervals, and (d) accuracy of the standard error estimator plotted
against
bias, (c) coverage of
95% confidence intervals, and (d) accuracy of the standard error estimator plotted
against 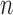 . Squares represent estimators that do
not account for inconsistent nuisance parameter estimation, circles represent
estimators using the bivariate correction of van der
Laan (2014), and triangles represent estimators using the proposed univariate
corrections.
. Squares represent estimators that do
not account for inconsistent nuisance parameter estimation, circles represent
estimators using the bivariate correction of van der
Laan (2014), and triangles represent estimators using the proposed univariate
corrections.
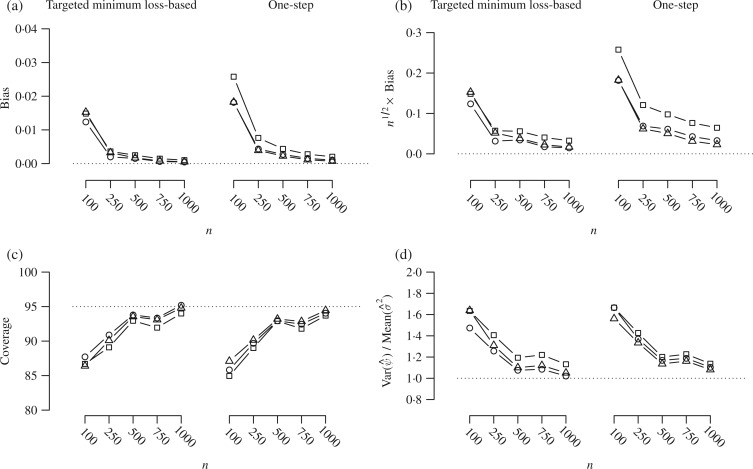
Finally, Fig. 3 supports hypothesis (D): when both the propensity score and the outcome regression are consistently estimated, all of the estimators perform approximately equally well, even in smaller samples. This suggests that implementing the correction procedures needed to achieve doubly robust asymptotic linearity and inference does not come at the cost of estimator performance in situations where the additional corrections are not needed.
Fig. 3.
Simulation results when both the outcome regression and the propensity score are
consistently estimated: (a) bias, (b) 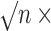 bias, (c) coverage of 95%
confidence intervals, and (d) accuracy of the standard error estimator plotted against
bias, (c) coverage of 95%
confidence intervals, and (d) accuracy of the standard error estimator plotted against
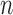 . Squares represent estimators that do
not account for inconsistent nuisance parameter estimation, circles represent
estimators using the bivariate correction of van der
Laan (2014), and triangles represent estimators using the proposed univariate
corrections.
. Squares represent estimators that do
not account for inconsistent nuisance parameter estimation, circles represent
estimators using the bivariate correction of van der
Laan (2014), and triangles represent estimators using the proposed univariate
corrections.
The run-times for the targeted minimum loss-based estimators (ii) and (iii) are on average two to three times as long as those of their one-step counterparts. The run-time required for the bivariate correction of estimators (ii) and (v) is on average one and a half times as long as the univariate correction for estimators (iii) and (iv). Two additional simulation studies in the Supplementary Material compare the proposed estimators with existing doubly robust estimators. The results demonstrate the advantage of estimators that allow for flexible nuisance parameter estimation in complex data-generating mechanisms. Results from a simulation study including a greater number of covariates, reported in the Supplementary Material, suggest a potential reduction in finite-sample bias for the proposed univariate-corrected targeted minimum loss-based estimator relative to the bivariate-corrected estimator of van der Laan (2014).
6. Concluding remarks
An interesting finding of this work is that it is possible to theoretically guarantee doubly robust inference under mild conditions using targeted minimum loss-based estimation, though not with the one-step approach. While we have found the corrected one-step estimators to perform relatively well in simulations, we cannot expect this in all scenarios, since theory suggests otherwise. Therefore, the preferred approach to providing doubly robust inference, in spite of its computational complexity, may be targeted minimum loss-based estimation. These methods are implemented in the R (R Development Core Team, 2017) package drtmle, available from the Comprehensive R Archive Network (Benkeser, 2017).
It may be fruitful to incorporate universally least favourable parametric submodels (van der Laan, 2016) into the targeted minimum loss-based estimation algorithms used here. Such submodels facilitate the construction of estimators using minimal data-fitting in the bias-reduction step of the algorithm. Rather than requiring iterations to perform bias reduction, use of these submodels would yield algorithms that converge in only a single step. This could yield improved performance in finite samples, particularly in extensions of this work to more complex parameters, such as average treatment effects defined by longitudinal interventions.
Supplementary Material
Acknowledgement
The authors thank the associate editor and reviewer for helpful suggestions. This work was a portion of the PhD thesis of Benkeser, supervised by Carone and Gilbert and funded by the Bill and Melinda Gates Foundation. Carone, van der Laan and Gilbert were partially funded by the National Institute of Allergy and Infectious Diseases. Carone was also funded by the University of Washington Department of Biostatistics Career Development Fund.
Supplementary material
Supplementary material available at Biometrika online includes results from an additional simulation study.
Appendix A
First-order expansion of the remainder
We derive equation (4) and sufficient conditions under which it holds. Note that
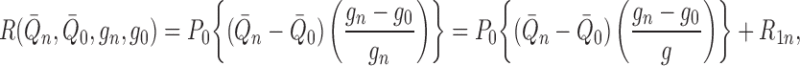 |
where we define the second-order remainder term by
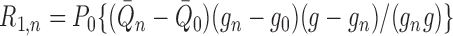 .
Adding and subtracting
.
Adding and subtracting  and
and  and
simplifying, we find that
and
simplifying, we find that
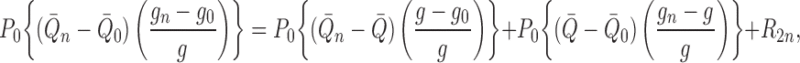 |
where the second-order remainder term is
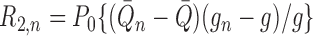 .
Assuming that either
.
Assuming that either 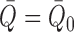 or
or
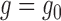 , we can write
, we can write
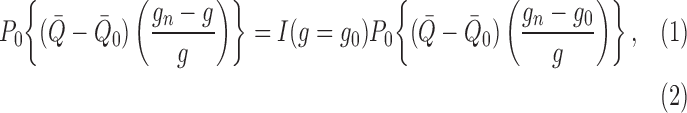 |
(A1) |
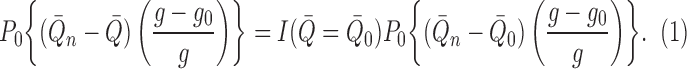 |
(A2) |
Examining (A1), and with some abuse of notation, we observe that
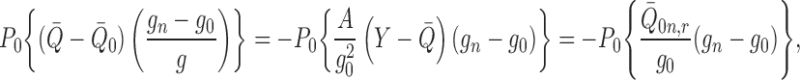 |
where we have set 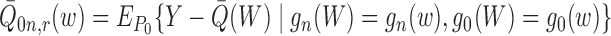 .
Then we may write
.
Then we may write
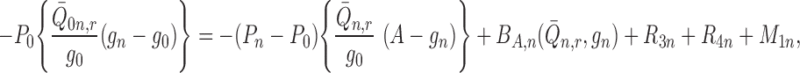 |
where we define
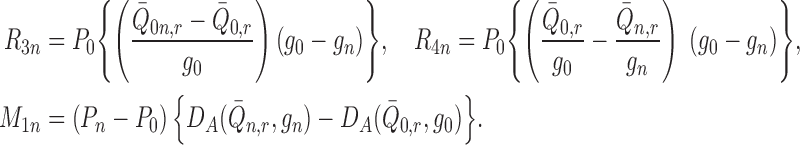 |
If, for example, each of 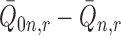 ,
,
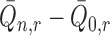 and
and
 is
is 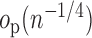 in the
in the
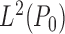 -norm, then
-norm, then
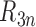 and
and 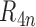 are
are 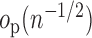 . Furthermore, if
. Furthermore, if
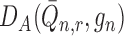 falls in a
falls in a
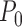 -Donsker class with probability tending
to one and
-Donsker class with probability tending
to one and 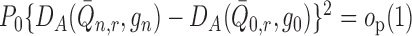 ,
then
,
then 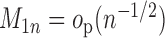 .
.
Examining (A2) and again allowing some abuse of notation, we find that
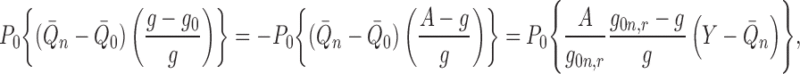 |
where the additional nuisance parameter is defined as
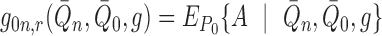 .
Some algebraic manipulation allows us to write
.
Some algebraic manipulation allows us to write
 |
where we define
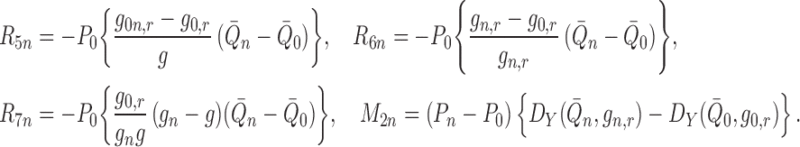 |
If, for example, each of 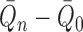 ,
,
 and
and
 is
is
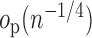 in the
in the
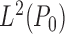 -norm, then
-norm, then
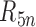 ,
, 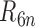 and
and 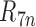 are
are 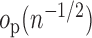 . Furthermore, if
. Furthermore, if
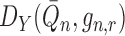 falls in a
falls in a
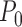 -Donsker class with probability tending
to one and
-Donsker class with probability tending
to one and 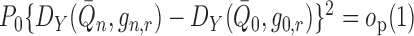 ,
then
,
then  . Thus, we have
shown that (4) holds with
. Thus, we have
shown that (4) holds with
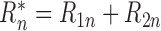 ,
,
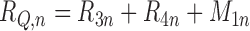 and
and
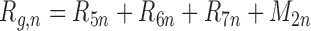 .
.
Appendix B
Derivation of the reduced-dimension remainder representation
We proceed similarly to the derivations above, but now, with regard to (A2) and with some abuse of notation, we have
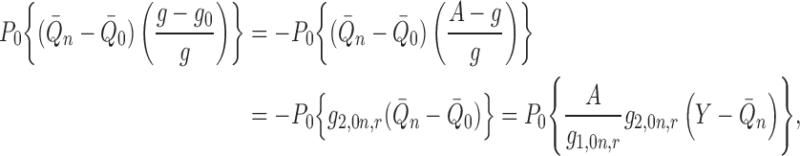 |
where we define the nuisance terms
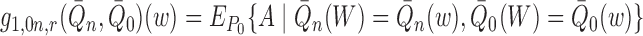 and
and 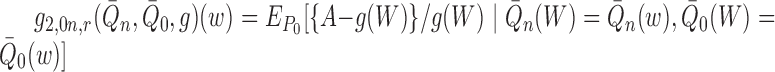 .
We can then write
.
We can then write
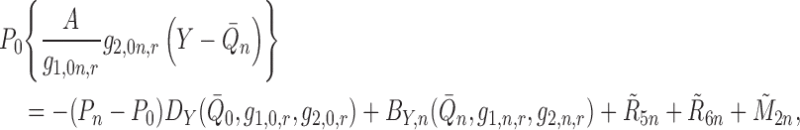 |
where
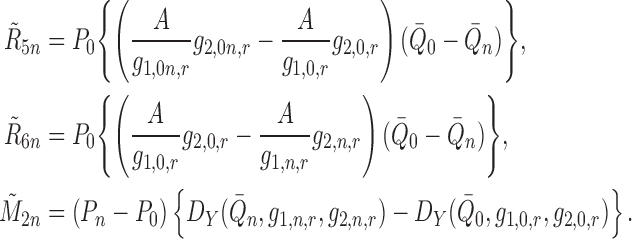 |
If, for example, each of 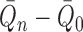 ,
,
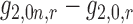 and
and
 is
is
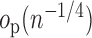 in the
in the
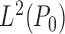 -norm, it generally follows that
-norm, it generally follows that
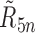 and
and
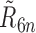 are
are
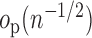 . Furthermore, if
. Furthermore, if
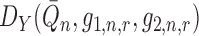 falls
in a
falls
in a 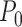 -Donsker class with probability tending
to one and
-Donsker class with probability tending
to one and 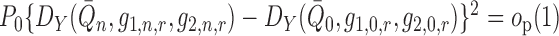 ,
it also follows that
,
it also follows that 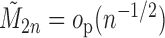 . This
implies that (4) holds with
. This
implies that (4) holds with
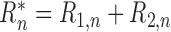 ,
,
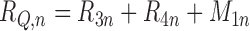 and
and
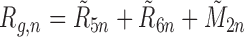 when the alternative reduced-dimension parameterization of the remainder is used.
when the alternative reduced-dimension parameterization of the remainder is used.
Appendix C
Behaviour of unnecessary correction terms
We first examine the behaviour of 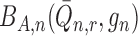 when
when
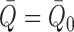 . We note that
. We note that
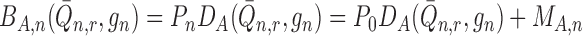 ,
where we define the empirical process term
,
where we define the empirical process term 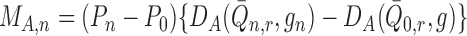 ,
which can reasonably be assumed to be
,
which can reasonably be assumed to be 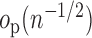 . The
second equality is a consequence of the fact that
. The
second equality is a consequence of the fact that 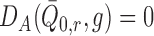 for all
for all
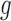 , because
, because 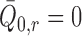 . With some abuse of
notation, we can write
. With some abuse of
notation, we can write
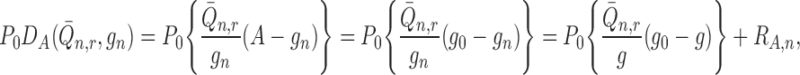 |
where
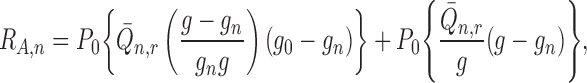 |
which is 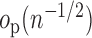 under
the rate conditions outlined in Appendices A and B.
under
the rate conditions outlined in Appendices A and B.
We next examine the behaviour of 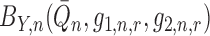 when
when
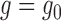 . We have
. We have
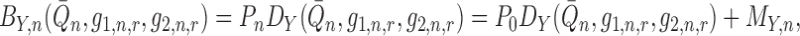 |
where we define the empirical process term
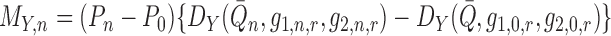 ,
which can reasonably be assumed to be
,
which can reasonably be assumed to be 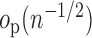 . As
above, the second equality is a consequence of the fact that
. As
above, the second equality is a consequence of the fact that 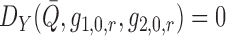 for
all
for
all 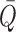 , because
, because 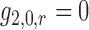 when
when 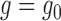 .
With some abuse of notation we can write
.
With some abuse of notation we can write
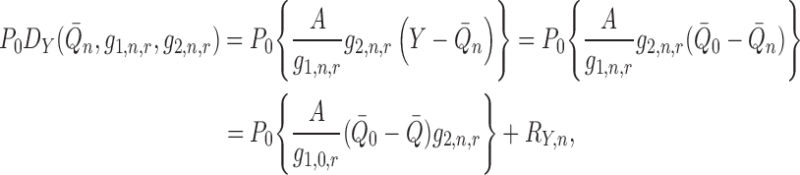 |
where
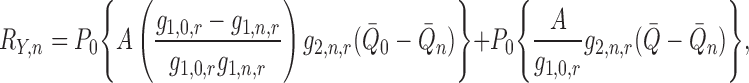 |
which is 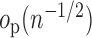 under
the rate conditions above.
under
the rate conditions above.
References
- Bang H. & Robins J. M. (2005). Doubly robust estimation in missing data and causal inference models. Biometrics 61, 962–73. [DOI] [PubMed] [Google Scholar]
- Benkeser D. (2017). drtmle: Doubly-Robust Nonparametric Estimation and Inference. R package version 1.0.0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickel P., Klaassen C., Ritov Y. & Wellner J. (1997). Efficient and Adaptive Estimation for Semiparametric Models. Baltimore, Maryland: Johns Hopkins University Press. [Google Scholar]
- Ibragimov I. A. & Has’minskii R. Z. (1981). Statistical Estimation: Asymptotic Theory, vol. 2.New York: Springer. [Google Scholar]
- Kang J. D. & Schafer J. L. (2007). Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statist. Sci. 22, 523–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfanzagl J. (1982). Contributions to a General Asymptotic Statistical Theory. New York: Springer. [Google Scholar]
- Porter K. E., Gruber S., van der Laan M. J. & Sekhon J. S. (2011). The relative performance of targeted maximum likelihood estimators. Int. J. Biostatist. 7, 1–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team (2017). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing,Vienna, Austria: ISBN 3-900051-07-0.http://www.R-project.org. [Google Scholar]
- Racine J. & Li Q. (2004). Nonparametric estimation of regression functions with both categorical and continuous data. J. Economet. 119, 99–130. [Google Scholar]
- Robins J. M., Rotnitzky A. & Zhao L. P. (1994). Estimation of regression coefficients when some regressors are not always observed. J. Am. Statist. Assoc. 89, 846–66. [Google Scholar]
- Rubin D. B. (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. J. Educ. Psychol. 66, 688–701. [Google Scholar]
- van der Laan M. J. (2014). Targeted estimation of nuisance parameters to obtain valid statistical inference. Int. J. Biostatist. 10, 29–57. [DOI] [PubMed] [Google Scholar]
- van der Laan M. J. (2016). One-step targeted minimum loss-based estimation based on universal least favorable one-dimensional submodels. Int. J. Biostatist. 12, 351–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Laan M. J. & Polley E. C. (2007). Super learner. Statist. Appl. Genet. Molec. Biol. 6, 1–23. [DOI] [PubMed] [Google Scholar]
- van der Laan M. J. & Robins J. M. (2003). Unified Methods for Censored Longitudinal Data and Causality. New York: Springer. [Google Scholar]
- van der Laan M. J. & Rose S. (2011). Targeted Learning: Causal Inference for Observational and Experimental Data. New York: Springer. [Google Scholar]
- van der Laan M. J. & Rubin D. (2006). Targeted maximum likelihood learning. Int. J. Biostatist. 2, 1–40. [Google Scholar]
- van der Vaart A. W. & Wellner J. A. (1996). Weak Convergence and Empirical Processes: With Applications to Statistics. New York: Springer. [Google Scholar]
- Vermeulen K. & Vansteelandt S. (2014). Bias-reduced doubly robust estimation. J. Am. Statist. Assoc. 110, 1024–36. [DOI] [PubMed] [Google Scholar]
- Vermeulen K. & Vansteelandt S. (2016). Data-adaptive bias-reduced doubly robust estimation. Int. J. Biostatist. 12, 253–82. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.