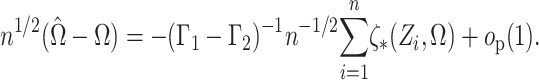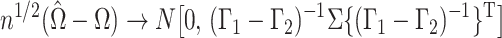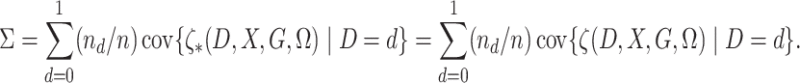Summary
Many methods have recently been proposed for efficient analysis of case-control studies of gene-environment interactions using a retrospective likelihood framework that exploits the natural assumption of gene-environment independence in the underlying population. However, for polygenic modelling of gene-environment interactions, which is a topic of increasing scientific interest, applications of retrospective methods have been limited due to a requirement in the literature for parametric modelling of the distribution of the genetic factors. We propose a general, computationally simple, semiparametric method for analysis of case-control studies that allows exploitation of the assumption of gene-environment independence without any further parametric modelling assumptions about the marginal distributions of any of the two sets of factors. The method relies on the key observation that an underlying efficient profile likelihood depends on the distribution of genetic factors only through certain expectation terms that can be evaluated empirically. We develop asymptotic inferential theory for the estimator and evaluate its numerical performance via simulation studies. An application of the method is presented.
Keywords: Case-control study, Gene-environment interaction, Genetic epidemiology, Pseudolikelihood, Retrospective study, Semiparametric method
1. Introduction
Recent genome-wide association studies indicate that complex diseases, such as cancers, diabetes and heart diseases, are in general extremely polygenic (Chatterjee et al., 2016; Fuchsberger et al., 2016). Genetic predisposition to a single disease may involve thousands of genetic variants; each of these may have a very small effect individually, but in combination they can explain substantial variation in risk in the underlying population. As discoveries from genome-wide association studies continue to enhance understanding of complex diseases, in the future it will be critical to elucidate how these genetic factors interact with environmental risk factors, in order to better understand disease mechanisms and to develop public health strategies for disease prevention.
Because of its sampling efficiency, the case-control design is widely popular for conducting studies of genetic associations and gene-environment interactions. A variety of analytical methods have been proposed to increase the efficiency of analysis of case-control data for studies of gene-environment interactions by exploiting an assumption of gene-environment independence in the underlying population. It has been shown that under the assumptions of gene-environment independence and rare disease, the interaction odds-ratio parameters of a logistic regression model can be estimated efficiently based on cases alone (Piegorsch et al., 1994). A general logistic regression model can be fitted to case-control data under the gene-environment independence assumption using a log-linear modelling framework (Umbach & Weinberg, 1997) or a semiparametric retrospective profile likelihood framework (Chatterjee & Carroll, 2005). More recently, the assumption of gene-environment independence has been exploited to propose a variety of powerful hypothesis testing methods for conducting genome-wide scans of gene-environment interactions (Mukherjee & Chatterjee, 2008; Murcray et al., 2009; Hsu et al., 2012; Mukherjee et al., 2012; Gauderman et al., 2013; Han et al., 2015).
We consider developing methods for efficient analysis of case-control studies for modelling gene-environment interactions that involve multiple genetic variants simultaneously. To develop parsimonious models for joint effects, many studies have focused on developing models for gene-environment interactions using underlying polygenic risk scores that could be defined by all known genetic variants associated with the disease (Meigs et al., 2008; Wacholder et al., 2010; Chatterjee et al., 2013; Dudbridge, 2013; Chatterjee et al., 2016). Further, to obtain improved biological insights and to enhance statistical power for detection, one may often wish to model gene-environment interactions using multiple variants within genomic regions and/or biologic pathways (Chatterjee et al., 2006; Jiao et al., 2013; Lin et al., 2013, 2015). In standard prospective logistic regression analysis, which conditions on both the genetic and the environmental risk factor status of the individuals, handling multiple genetic variants is relatively straightforward. In contrast, with so-called retrospective methods, which aim to exploit the assumption of gene-environment independence, the task becomes complicated because all currently existing methods require parametric modelling of the distribution of the genetic or environmental variables.
We propose a computationally simple method for fitting general logistic regression models to case-control data under the assumption of gene-environment independence, but without requiring any further modelling assumptions about the distributions of the genetic or environmental variables. We extend the Chatterjee–Carroll profile likelihood framework, which originally considered modelling gene-environment interactions using single genetic variants for which genotype status could be specified using parametric multinomial models. The new method relies on the observation that the profile likelihood itself can be estimated based on an empirical genotype distribution that is estimable from a case-control sample. We develop the asymptotic theory of the resulting estimator under a semiparametric inferential framework. Simulations and an example illustrate the properties of the new method.
2. Model, method and theory
2.1. Background, model and method
In the following, we use notation similar to that in Chatterjee & Carroll (2005). We will denote disease status, genetic
information and environmental risk factors by  ,
,
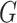 and
and 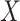 ,
respectively. Here
,
respectively. Here 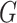 may correspond to a complex multivariate
genotype associated with multiple genetic variants or to a continuous polygenic risk score
that is defined a priori based on known associations of the genetic variants with the
disease. We assume that the risk of the disease given genetic and environmental factors in
the underlying population can be specified using a model of the form
may correspond to a complex multivariate
genotype associated with multiple genetic variants or to a continuous polygenic risk score
that is defined a priori based on known associations of the genetic variants with the
disease. We assume that the risk of the disease given genetic and environmental factors in
the underlying population can be specified using a model of the form
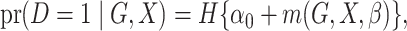 |
(1) |
where 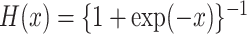 is the logistic
distribution function and
is the logistic
distribution function and  is a parametrically specified
function that defines a model for the joint effect of
is a parametrically specified
function that defines a model for the joint effect of 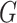 and
and
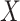 on the logistic-risk scale. The goal of the
gene-environment interaction study is to make inference on the parameters
on the logistic-risk scale. The goal of the
gene-environment interaction study is to make inference on the parameters
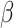 in (1), including interaction parameters.
in (1), including interaction parameters.
Let 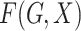 denote the joint distribution of
denote the joint distribution of
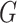 and
and 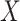 in the
underlying population. The key assumption that genetic factors,
in the
underlying population. The key assumption that genetic factors, 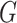 , and
environmental factors,
, and
environmental factors, 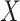 , are independently distributed in the
underlying population can be mathematically stated as
, are independently distributed in the
underlying population can be mathematically stated as
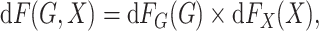 |
where 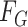 and
and 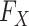 denote the underlying marginal distributions of
denote the underlying marginal distributions of 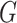 and
and
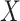 , respectively. In the Supplementary Material we discuss
how to weaken this assumption by suitable conditioning on additional stratification
factors. In contrast to the existing literature, here we assume that the marginal
distributions
, respectively. In the Supplementary Material we discuss
how to weaken this assumption by suitable conditioning on additional stratification
factors. In contrast to the existing literature, here we assume that the marginal
distributions 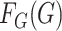 and
and 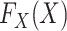 are both completely unspecified.
are both completely unspecified.
We consider a population-based case-control study, in which 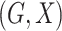 are
sampled independently from individuals with the disease, called cases, and those without
the disease, called controls. Suppose there are
are
sampled independently from individuals with the disease, called cases, and those without
the disease, called controls. Suppose there are 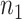 cases and
cases and
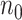 controls. Standard prospective logistic
regression analysis, which is equivalent to maximum likelihood estimation when
controls. Standard prospective logistic
regression analysis, which is equivalent to maximum likelihood estimation when
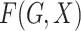 is allowed to be completely
unspecified, yields consistent estimates of
is allowed to be completely
unspecified, yields consistent estimates of 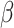 (Prentice & Pyke, 1979).
(Prentice & Pyke, 1979).
The retrospective likelihood is the probability of observing the genetic and environmental variables, given the subject’s disease status. Under gene-environment independence in the underlying population, the retrospective likelihood is
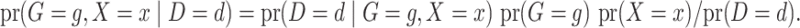 |
Let 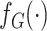 and
and 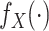 represent the density or mass
functions of
represent the density or mass
functions of 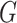 and
and 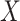 ,
respectively. The retrospective likelihood is
,
respectively. The retrospective likelihood is
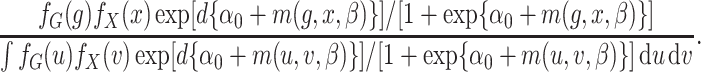 |
(2) |
Chatterjee & Carroll (2005) profiled out
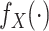 by treating it as discrete on
the set of distinct observed values
by treating it as discrete on
the set of distinct observed values 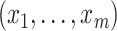 of
of
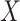 with probabilities
with probabilities
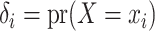 , and then
maximizing (2) over
, and then
maximizing (2) over
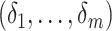 , leading
eventually to the semiparametric profile likelihood described as follows. Define
, leading
eventually to the semiparametric profile likelihood described as follows. Define
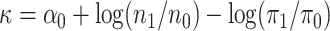 ,
where
,
where 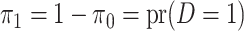 is defined
as the probability of the disease in the underlying population. Define
is defined
as the probability of the disease in the underlying population. Define
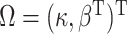 .
Also let
.
Also let
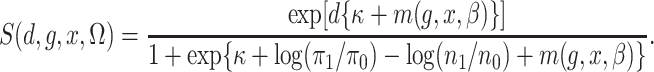 |
Then, with this notation, the semiparametric profile likelihood is
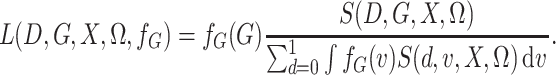 |
(3) |
While the representation in (3) does
not involve the unknown density of 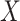 , it does involve the
unknown density of
, it does involve the
unknown density of 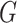 . This is a major reason that methods in
the current literature specify a parametric distribution for
. This is a major reason that methods in
the current literature specify a parametric distribution for 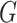 . Our
aim in this paper is to dispense with the need to give a parametric form for the
distribution function of
. Our
aim in this paper is to dispense with the need to give a parametric form for the
distribution function of 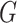 , so that analysis can be performed with
respect to potentially complex multivariate genotype data for which parametric modelling
can be difficult and cumbersome.
, so that analysis can be performed with
respect to potentially complex multivariate genotype data for which parametric modelling
can be difficult and cumbersome.
Here is our key insight, which we discuss first in the context that
 is known or at least can be estimated
well. For case-control studies that are conducted within well-defined populations,
relevant probabilities of the disease can be ascertained using population-based disease
registries. When case-control studies are conducted by the sampling of subjects within a
larger cohort study, the probability of the disease in the underlying population can be
estimated using the disease incidence rate observed in the cohort.
is known or at least can be estimated
well. For case-control studies that are conducted within well-defined populations,
relevant probabilities of the disease can be ascertained using population-based disease
registries. When case-control studies are conducted by the sampling of subjects within a
larger cohort study, the probability of the disease in the underlying population can be
estimated using the disease incidence rate observed in the cohort.
Our key insight in treating the distribution of 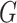 as
nonparametric concerns the term in the denominator of (3), defined as
as
nonparametric concerns the term in the denominator of (3), defined as
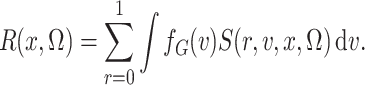 |
This is simply the expectation, in the source population, of 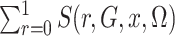 ; that is,
; that is,
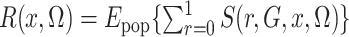 ,
where the subscript pop emphasizes that the expectation is in the source population, not
in the case-control study. However, crucially,
,
where the subscript pop emphasizes that the expectation is in the source population, not
in the case-control study. However, crucially,
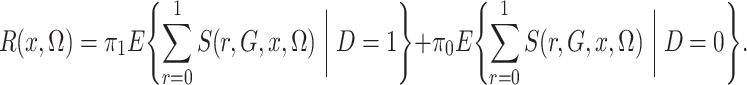 |
(4) |
Of course, 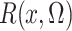 is unknown, but we estimate it
unbiasedly and nonparametrically by
is unknown, but we estimate it
unbiasedly and nonparametrically by
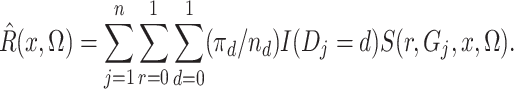 |
(5) |
In the Supplementary Material,
we show that  is an unbiased estimate
of
is an unbiased estimate
of 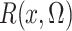 which is
which is
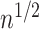 -consistent, and that it is
asymptotically normally distributed.
-consistent, and that it is
asymptotically normally distributed.
Ignoring the leading term 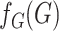 in (3), which is not estimated, and taking logarithms leads us to an
estimated loglikelihood in
in (3), which is not estimated, and taking logarithms leads us to an
estimated loglikelihood in 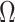 across the data as
across the data as
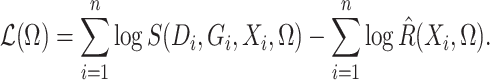 |
(6) |
Define 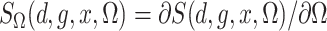 and similarly for
and similarly for 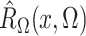 . Then the
estimated score function, a type of estimated estimating equation, is
. Then the
estimated score function, a type of estimated estimating equation, is
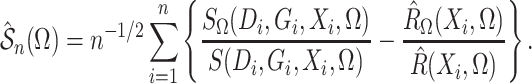 |
(7) |
Define
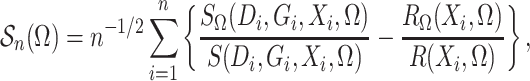 |
which is the profile loglikelihood score function when the
distribution of 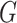 is known. Since the profile loglikelihood
score of Chatterjee & Carroll (2005) would have
mean zero if the distribution of
is known. Since the profile loglikelihood
score of Chatterjee & Carroll (2005) would have
mean zero if the distribution of 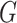 were known, it follows
that
were known, it follows
that
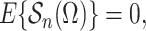 |
(8) |
where the expectation in (8) is taken in the case-control study, not in the source population. Thus, since
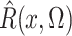 and
and
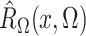 converge in
probability to
converge in
probability to 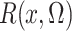 and
and 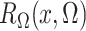 , respectively, a
consistent estimate of
, respectively, a
consistent estimate of 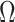 can be obtained by solving
can be obtained by solving
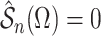 . This estimate
. This estimate
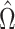 , which maximizes the
semiparametric pseudolikelihood (6),
will be referred to as the semiparametric pseudolikelihood estimator.
, which maximizes the
semiparametric pseudolikelihood (6),
will be referred to as the semiparametric pseudolikelihood estimator.
2.2. Rare diseases when 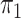 is unknown
is unknown
When the probability of disease in the source population is unknown, one can invoke a
rare disease assumption which is often reasonable for case-control studies (Piegorsch et al., 1994; Modan et al., 2001; Epstein & Satten,
2003; Zhao et al., 2003; Lin & Zeng, 2006; Kwee et al., 2007). If we assume that 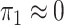 , then
, then
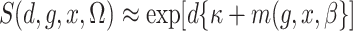 ,
and the expectation involved in the calculation of
,
and the expectation involved in the calculation of 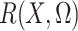 can be evaluated based on only
the sample of controls, with
can be evaluated based on only
the sample of controls, with 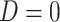 . In this case, the estimates of
. In this case, the estimates of
 converge not to
converge not to
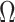 itself but to
itself but to
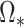 , the solution to (8) with
, the solution to (8) with 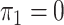 .
Typically, except when the sample size is very large and hence standard errors are
unusually small, the small possible bias of the rare disease approximation is of little
consequence and coverage probabilities of confidence intervals remain near nominal; see §
3 for examples. The asymptotic theory of § 2.3 below is then unchanged.
.
Typically, except when the sample size is very large and hence standard errors are
unusually small, the small possible bias of the rare disease approximation is of little
consequence and coverage probabilities of confidence intervals remain near nominal; see §
3 for examples. The asymptotic theory of § 2.3 below is then unchanged.
In the Supplementary Material, we show that the score and the Hessian take simple forms in this case, and that the Hessian is negative semidefinite. Computation is thus very efficient.
2.3. Asymptotic theory
To state the asymptotic results, we first make the definitions
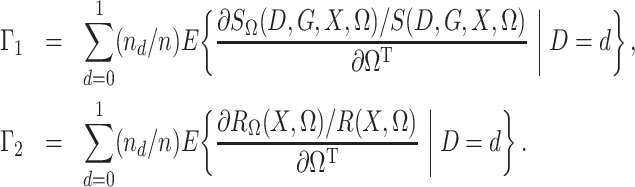 |
In addition, define 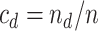 ,
, 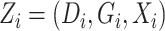 ,
,
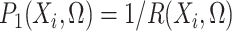 and
and
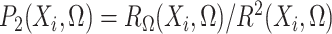 .
.
We use the notational convention that for arbitrary functions 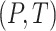 ,
,
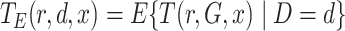 .
Also, we use the convention that
.
Also, we use the convention that
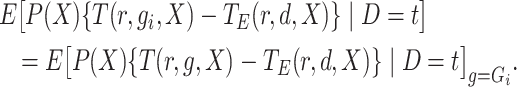 |
Define
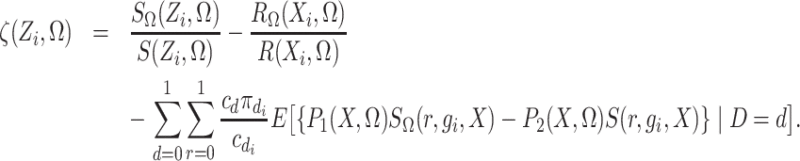 |
Finally, define 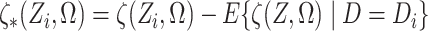 .
.
Theorem 1.
Suppose that
, where
, and that
is known. Then
Therefore, since the
are independent and
, as
,
in distribution, where
In § 2.2, when 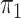 is
unknown and the disease is relatively rare, the same result holds upon setting
is
unknown and the disease is relatively rare, the same result holds upon setting
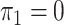 .
.
3. Simulations
3.1. Overview
In our simulations, 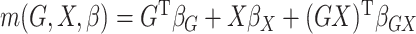 and the value of
and the value of 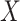 is binary with population frequency
is binary with population frequency
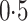 . There are either three or five
correlated single nucleotide polymorphisms within a region; we report on the latter case,
but the results for the former case are similar. Each single nucleotide polymorphism takes
on the values 0, 1 or 2 following a trinomial distribution that follows the Hardy–Weinberg
equilibrium, i.e., the
. There are either three or five
correlated single nucleotide polymorphisms within a region; we report on the latter case,
but the results for the former case are similar. Each single nucleotide polymorphism takes
on the values 0, 1 or 2 following a trinomial distribution that follows the Hardy–Weinberg
equilibrium, i.e., the 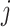 th component of
th component of 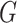 equals
0, 1, 2 with probabilities
equals
0, 1, 2 with probabilities 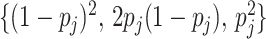 ,
respectively. The values of the
,
respectively. The values of the 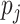 are described
below.
are described
below.
To generate correlation among the single nucleotide polymorphisms, we first generated a
3- or 5-variate multivariate normal variate, with mean 0 and standard deviation 1, and a
correlation matrix with correlation between the 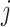 th and
th and
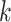 th components being
th components being
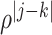 , where
, where
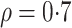 . After generating these
random variables, we trichotomized them with appropriate thresholds so that the
frequencies of 0, 1 and 2 matched those specified by the allele frequency
. After generating these
random variables, we trichotomized them with appropriate thresholds so that the
frequencies of 0, 1 and 2 matched those specified by the allele frequency
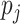 and Hardy–Weinberg equilibrium.
and Hardy–Weinberg equilibrium.
In both simulations, the logistic intercept 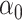 was chosen so
that the population disease rate
was chosen so
that the population disease rate 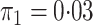 .
However additional simulations with
.
However additional simulations with 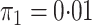 yielded very similar results in terms of coverage, efficiency gains, and unbiasedness. See
§ 3.3 and the Supplementary Material for a
discussion of additional simulations. In the simulation reported here,
yielded very similar results in terms of coverage, efficiency gains, and unbiasedness. See
§ 3.3 and the Supplementary Material for a
discussion of additional simulations. In the simulation reported here,
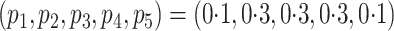 ,
,
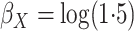 ,
,
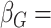
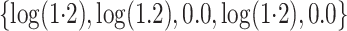 and
and 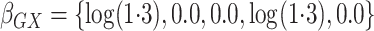 .
Here
.
Here 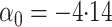 .
.
3.2. Results
The standard error estimators used in our simulation were based on the asymptotic theory described in Theorem 1; we also used the bootstrap and obtained very similar results. The appropriate bootstrap in a case-control study is to resample the cases and controls separately, thus maintaining the sample sizes for each.
The simulation results are presented in Table 1.
Our semiparametric pseudolikelihood estimator shows little bias and has coverage
percentages near the nominal level. Both with a rare disease approximation and with
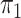 known, our semiparametric
pseudolikelihood estimator achieves approximately a 25% increase in mean squared error
efficiency over ordinary logistic regression for the main effects in both
known, our semiparametric
pseudolikelihood estimator achieves approximately a 25% increase in mean squared error
efficiency over ordinary logistic regression for the main effects in both
 and
and  .
.
Table 1.
Results of 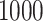 simulations as described
in
simulations as described
in
 3: mean bias, coverage probabilities
of a
3: mean bias, coverage probabilities
of a 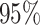 nominal confidence interval,
and mean squared error efficiency of our semiparametric pseudolikelihood estimator
compared with ordinary logistic regression; the simulationsc were performed with
nominal confidence interval,
and mean squared error efficiency of our semiparametric pseudolikelihood estimator
compared with ordinary logistic regression; the simulationsc were performed with
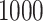 cases and
cases and
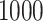 controls
controls
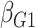
|
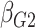
|

|
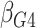
|

|
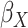
|
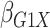
|
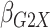
|
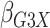
|
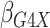
|
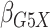
|
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| True | 0.18 | 0.18 | 0.00 | 0.18 | 0.00 | 0.41 | 0.26 | 0.00 | 0.00 | 0.26 | 0.00 |
| Logistic: 1000 cases | |||||||||||
| Bias | 0.00 | 0.01 | 0.00 | 0.01 | –0.01 | 0.01 | 0.01 | –0.01 | 0.00 | 0.00 | 0.01 |
| CI (%) | 94.3 | 95.2 | 95.7 | 95.1 | 94.7 | 94.6 | 94.9 | 94.2 | 94.5 | 96.0 | 94.2 |
| SPMLE Rare: 1000 cases | |||||||||||
| Bias | 0.01 | 0.00 | 0.00 | 0.02 | –0.01 | 0.02 | –0.02 | –0.01 | 0.01 | –0.02 | 0.01 |
| CI (%) | 95.2 | 95.4 | 96.4 | 95.8 | 95.3 | 95.1 | 95.4 | 94.8 | 96.1 | 95.5 | 94.9 |
| Avg MSE Eff | All  :
1 :
1 28 28 |
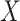 : 1
: 1 26 26 |
All 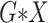 :
2 :
2 18 18 |
||||||||
SPMLE 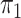 known:
1000 cases known:
1000 cases | |||||||||||
| Bias | 0.00 | 0.00 | 0.00 | 0.01 | –0.01 | 0.01 | 0.00 | –0.01 | 0.01 | –0.01 | 0.01 |
| CI (%) | 95.1 | 95.5 | 96.4 | 95.8 | 95.0 | 95.5 | 95.6 | 94.6 | 95.9 | 95.2 | 94.5 |
| Avg MSE Eff | All 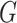 :
1 :
1 28 28 |
All 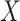 :
1 :
1 28 28 |
All 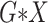 :
2 :
2 07 07 |
||||||||
Logistic, ordinary logistic regression; SPMLE Rare, our estimator using the rare
disease approximation with unknown 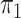 (§ 2.2); SPMLE
(§ 2.2); SPMLE 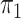 known, our estimator when
known, our estimator when
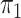 is known in the source
population (§ 2.1); CI, coverage of a
nominal 95% confidence interval, calculated using the asymptotic standard error;
Avg MSE Eff, mean squared error efficiency of our method compared to logistic
regression averaged over
is known in the source
population (§ 2.1); CI, coverage of a
nominal 95% confidence interval, calculated using the asymptotic standard error;
Avg MSE Eff, mean squared error efficiency of our method compared to logistic
regression averaged over  (All
(All
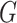 ), over
), over 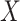 (All
(All 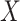 ) or over all
) or over all
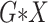 interactions (All
interactions (All
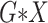 ).
).
Strikingly, the mean squared error efficiency of our semiparametric pseudolikelihood
estimators compared to ordinary logistic regression is approximately
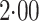 for all the interaction terms,
thus demonstrating that our methods, which do not model the distribution of either
for all the interaction terms,
thus demonstrating that our methods, which do not model the distribution of either
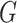 or
or 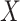 ,
achieve numerically significant increases in efficiency.
,
achieve numerically significant increases in efficiency.
3.3. Additional simulations
The Supplementary Material
presents a series of additional simulations. These include the results of a simulation to
evaluate the robustness of our method with respect to misspecification of the population
disease rate; we found a surprising robustness with respect to disease rate
misspecification. Additionally, we performed simulations to examine the robustness of our
method with respect to violations of the gene-environment independence assumption. Those
simulation studies show that there will be bias in the estimates of gene-environment
interaction parameters for the specific single nucleotide polymorphisms that violate
gene-environment independence, but the average mean squared error for parameter estimates
across all the different single nucleotide polymorphisms could still be substantially
lower than that obtained from prospective logistic regression analysis. We also show in
the Supplementary Material how
to remove this bias when 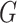 and
and 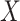 are
independent conditional on a discrete stratification variable. Mukherjee & Chatterjee (2008) and Chen et al. (2009) show how to use empirical Bayes methods to provide additional
robustness with respect to violations of the gene-environment independence assumption.
are
independent conditional on a discrete stratification variable. Mukherjee & Chatterjee (2008) and Chen et al. (2009) show how to use empirical Bayes methods to provide additional
robustness with respect to violations of the gene-environment independence assumption.
4. Data analysis
In this section, we apply our method to a case-control study for breast cancer arising from
a large prospective cohort at the National Cancer Institute: the Prostate, Lung, Colorectal
and Ovarian cancer screening trial (Canzian et al.,
2010). The design of this study is described in detail by Prorok et al. (2000) and Hayes et al.
(2000). The cohort data consisted of 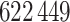 women, of whom
3
women, of whom
3 56% developed breast cancer (Pfeiffer et al., 2013). The case-control study analysed
here consists of 753 controls and 658 cases. Although
56% developed breast cancer (Pfeiffer et al., 2013). The case-control study analysed
here consists of 753 controls and 658 cases. Although 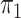 is
known in this population, we analyse the data both with
is
known in this population, we analyse the data both with 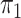 known and with
known and with 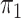 unknown but using a rare disease
approximation.
unknown but using a rare disease
approximation.
We had data available on genotypes for 21 single nucleotide polymorphisms that have been
previously associated with breast cancer based on large genome-wide association studies. The
polygenic risk score was defined by a weighted combination of the genotypes, with the
weights defined by log-odds-ratio coefficients reported in prior studies. We examined the
interaction of the polygenic risk score with age at menarche, 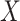 , a known
risk factor for breast cancer, defined as the binary indicator of whether the age at
menarche exceeds 13 or not. We also adjust the model for age as a continuous variable,
denoted here by
, a known
risk factor for breast cancer, defined as the binary indicator of whether the age at
menarche exceeds 13 or not. We also adjust the model for age as a continuous variable,
denoted here by  , so that the model fitted is
, so that the model fitted is
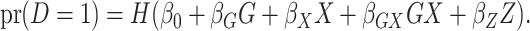 |
Results when age was categorized as 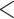 35, 35–40, 40–45,
35, 35–40, 40–45,
 75 were similar.
75 were similar.
We also performed analyses to check the gene-environment independence assumption. Since
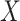 is binary, we ran a
is binary, we ran a  -test of
the polygenic risk score against the levels of
-test of
the polygenic risk score against the levels of 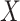 , of course among the
controls only. The
, of course among the
controls only. The 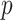 -value was 0
-value was 0 91,
indicating almost no genetic effect. We also ran chi-squared tests for the 21 individual
genes, finding no significant association after controlling the false discovery rate: the
minimum
91,
indicating almost no genetic effect. We also ran chi-squared tests for the 21 individual
genes, finding no significant association after controlling the false discovery rate: the
minimum 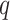 -value was 0
-value was 0 09.
In addition, we checked for correlation, known as linkage disequilibrium, between the 21
loci used to create the polygenic risk score and 32 loci that are known to influence age at
menarche (Elks et al., 2010). The data available to
us do not contain the necessary information to analyse linkage disequilibrium between the
two sets of loci.
09.
In addition, we checked for correlation, known as linkage disequilibrium, between the 21
loci used to create the polygenic risk score and 32 loci that are known to influence age at
menarche (Elks et al., 2010). The data available to
us do not contain the necessary information to analyse linkage disequilibrium between the
two sets of loci.
Using phased haplotypes from subjects of European descent from the 1000 Genomes Project
(The 1000 Genomes Project Consortium, 2015) and
HapMap (Gibbs et al., 2003), no evidence of linkage
disequilibrium was found: the maximum  was
0
was
0 1 and the minimum
1 and the minimum
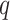 -value was 0
-value was 0 85.
Finally, a 2014 study examined the relationship between age at menarche and 10 of the 21
single nucleotide polymorphisms used to create our polygenic risk score, none of which were
found to influence age at menarche (Andersen et al.,
2014).
85.
Finally, a 2014 study examined the relationship between age at menarche and 10 of the 21
single nucleotide polymorphisms used to create our polygenic risk score, none of which were
found to influence age at menarche (Andersen et al.,
2014).
Table 2 presents the results for the cases where
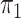 is unknown and known; as remarked upon
previously, the results are very similar. Because of the very different scales of the
variables, to provide a basis for comparison the variable age at baseline was standardized
to have mean zero and standard deviation one. In addition, we standardized some of the
coefficient estimates so that
is unknown and known; as remarked upon
previously, the results are very similar. Because of the very different scales of the
variables, to provide a basis for comparison the variable age at baseline was standardized
to have mean zero and standard deviation one. In addition, we standardized some of the
coefficient estimates so that 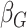 was multiplied by the standard
deviation of the polygenic risk score, and
was multiplied by the standard
deviation of the polygenic risk score, and  was multiplied
by the standard deviation of
was multiplied
by the standard deviation of 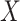 times the polygenic risk score.
times the polygenic risk score.
Table 2.
Results of the analysis of the Prostate, Lung, Colorectal and Ovarian cancer screening trial data
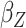
|
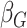
|
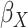
|
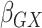
|
|
|---|---|---|---|---|
| Logistic | ||||
| Estimate | 0 018 018 |
0 297 297 |
 0
0 165 165 |
0 124 124 |
| Std err | 0 054 054 |
0 064 064 |
 0
0 132 132 |
0 068 068 |
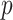 -value
-value |
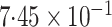
|
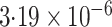
|
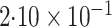
|
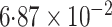
|
| SPMLE Rare | ||||
| Estimate | 0 024 024 |
0 321 321 |
 0
0 175 175 |
0 138 138 |
| Std err (asymptotic) | 0 054 054 |
0 067 067 |
 0
0 134 134 |
0 055 055 |
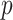 -value (asymptotic)
-value (asymptotic) |
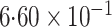
|
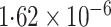
|
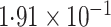
|
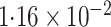
|
SPMLE 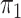 known known |
||||
| Estimate | 0 022 022 |
0 313 313 |
 0
0 174 174 |
0 141 141 |
| Std err (asymptotic) | 0 054 054 |
0 065 065 |
 0
0 133 133 |
0 055 055 |
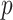 -value (asymptotic)
-value (asymptotic) |
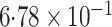
|
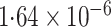
|
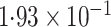
|
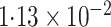
|
Logistic, ordinary logistic regression; SPMLE Rare, our method using the rare
disease approximation with unknown 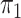 ; SPMLE
; SPMLE
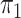 known, our method when the
disease rate is known in the source population (
known, our method when the
disease rate is known in the source population (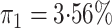 ); Std err, the
asymptotic standard error estimate;
); Std err, the
asymptotic standard error estimate; 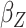 , the main
effect for age;
, the main
effect for age; 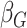 and
and
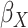 , the main effects for the
polygenic risk score (
, the main effects for the
polygenic risk score (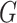 ) and the environmental variable
) and the environmental variable
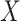 (age at menarche
(age at menarche
 13), respectively;
13), respectively;
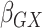 , the gene-environment
interaction.
, the gene-environment
interaction.
As expected from the known association of the single nucleotide polymorphisms with risk of
breast cancer, the polygenic risk score was strongly associated with breast cancer status of
the women in the study. Standard logistic regression analysis reveals some evidence for
interaction of the polygenic risk score with age at menarche, but the result was not
statistically significant at the 0 05 level. When the
analysis was done under the gene-environment independence assumption, the evidence for
interaction appeared to be stronger.
05 level. When the
analysis was done under the gene-environment independence assumption, the evidence for
interaction appeared to be stronger.
The coefficient estimate for the interaction term is slightly larger for our semiparametric methods than for logistic regression. Also, the asymptotic standard error estimate of logistic regression is approximately 23% larger than that for our methods, indicating a variance increase of approximately 50%. Although not listed here, the bootstrap mentioned in § 3.2 has very similar standard error estimates. In that bootstrap, 33% of the time the logistic interaction estimate was actually greater than that of the disease-rate-known estimate.
5. Discussion and extensions
We have proposed a general method for using retrospective likelihoods to study gene-environment interactions involving multiple markers, an approach that does not require any distributional assumption on the multivariate genotype distribution. Sometimes, one may consider modelling multimarker gene-environment interactions using an underlying polygenic risk score, which is a weighted combination of numerous genetic markers where the weights are predetermined from previous association studies. In such situations, the polygenic risk score might be assumed to follow approximately a normal distribution in the underlying population, and the profile likelihood method of Chatterjee & Carroll (2005) can be used with appropriate modification by replacing the parametric multinomial distribution for a single nucleotide polymorphism genotype with a parametric normal distribution for the polygenic risk score; see also Chen et al. (2008) and Lin & Zeng (2009). In general, however, if one wishes to explore complex models for multivariate gene-environment interactions retaining separate parameters for distinct single nucleotide polymorphisms or for distinct genetic profiles defined by combinations of correlated single nucleotide polymorphisms, then one cannot avoid dealing with complex multivariate genotype distributions, something that is not easy to specify through parametric models.
Our methods are types of semiparametric plug-in estimators, and thus have certain features
in common with the work of Newey (1994), namely that
the profile likelihood has the nonparametric component 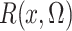 in (4) that is estimated by (5). Generally, however, such plug-in estimators are not
semiparametric efficient. We believe it will be possible to create an efficient
semiparametric estimator by modifying the work of Ma
(2010); we are exploring this and its computational aspects, which may be
daunting.
in (4) that is estimated by (5). Generally, however, such plug-in estimators are not
semiparametric efficient. We believe it will be possible to create an efficient
semiparametric estimator by modifying the work of Ma
(2010); we are exploring this and its computational aspects, which may be
daunting.
Supplementary Material
Acknowledgement
Stalder and Asher should be considered joint first authors. Carroll is also Distinguished Professor at the University of Technology Sydney. Chatterjee is also Bloomberg Professor of Oncology at the Johns Hopkins University. Stalder was supported by a fellowship from the Fondation Ernest Boninchi. Ma was supported by the U.S. National Science Foundation and National Institute of Neurological Disorders and Stroke. Asher, Liang and Carroll were supported by the National Cancer Institute. Chatterjee’s research was partially funded through a Patient-Centered Outcomes Research Institute Award. The statements and opinions in this article are solely the responsibility of the authors and do not necessarily represent the views of the Patient-Centered Outcomes Research Institute, its Board of Governors or Methodology Committee.
Supplementary material
Supplementary Material available at Biometrika online contains proofs, skewness and kurtosis and Q-Q plots for the simulation in Table 1, a discussion of how to modify our methods to account for strata, results of additional simulations, and software written in R. The data used in § 4 are available from the National Cancer Institute via a data transfer agreement.
References
- Andersen S. W., Trentham-Dietz A., Gangnon R. E., Hampton J. M., Skinner H. G., Engelman C. D., Klein B. E., Titus L. J., Egan K. M. & Newcomb P. A. (2014). Breast cancer susceptibility loci in association with age at menarche, age at natural menopause and the reproductive lifespan. Cancer Epidemiol. 38, 62–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canzian F., Cox D. G., Setiawan V. W., Stram D. O., Ziegler R. G., Dossus L., Beckmann L., Blanché H., Barricarte A., Berg C. D.. et al. (2010). Comprehensive analysis of common genetic variation in 61 genes related to steroid hormone and insulin-like growth factor-I metabolism and breast cancer risk in the NCI breast and prostate cancer cohort consortium. Hum. Molec. Genet. 19, 3873–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee N. & Carroll R. J. (2005). Semiparametric maximum likelihood estimation in case-control studies of gene-environment interactions. Biometrika 92, 399–418. [Google Scholar]
- Chatterjee N., Kalaylioglu Z., Moslehi R., Peters U. & Wacholder S. (2006). Powerful multilocus tests of genetic association in the presence of gene-gene and gene-environment interactions. Am. J. Hum. Genet. 79, 1002–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee N., Shi J. & García-Closas M. (2016). Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nature Rev. Genet. 17, 392–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee N., Wheeler B., Sampson J., Hartge P., Chanock S. J. & Park J.-H. (2013). Projecting the performance of risk prediction based on polygenic analyses of genome-wide association studies. Nature Genet. 45, 400–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y. H., Chatterjee N. & Carroll R. J. (2008). Retrospective analysis of haplotype-based case-control studies under a flexible model for gene-environment association. Biostatistics 9, 81–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y. H., Chatterjee N. & Carroll R. J. (2009). Shrinkage estimators for robust and efficient inference in haplotype-based case-control studies. J. Am. Statist. Assoc. 104, 220–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudbridge F. (2013). Power and predictive accuracy of polygenic risk scores. PLoS Genet. 9, e1003348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elks C. E., Perry J. R. B., Sulem P., Chasman D. I., Franceschini N., He C., Lunetta K. L., Visser J. A., Byrne E. M., Cousminer D. L.. et al. (2010). Thirty new loci for age at menarche identified by a meta-analysis of genome-wide association studies. Nature Genet. 42, 1077–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein M. P. & Satten G. A. (2003). Inference on haplotype effects in case-control studies using unphased genotype data. Am. J. Hum. Genet. 73, 1316–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchsberger C., Flannick J., Teslovich T. M., Mahajan A., Agarwala V., Gaulton K. J., Ma C., Fontanillas P., Moutsianas L., McCarthy D. J.. et al. (2016). The genetic architecture of type 2 diabetes. Nature 536, 41–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Gauderman W. J., Zhang P., Morrison J.
L. & Lewinger J.
P. (2013).
Finding novel genes by testing G
 E interactions in a genome-wide
association study. Genet. Epidemiol. 37,
603–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
E interactions in a genome-wide
association study. Genet. Epidemiol. 37,
603–13. [DOI] [PMC free article] [PubMed] [Google Scholar] - Gibbs R. A., Belmont J. W., Hardenbol P., Willis T. D., Yu F., Yang H., Ch’ang L.-Y., Huang W., Liu B., Shen Y.. et al. (2003). The International HapMap Project. Nature 426, 789–96. [DOI] [PubMed] [Google Scholar]
- Han S. S., Rosenberg P. S., Ghosh A., Landi M. T., Caporaso N. E. & Chatterjee N. (2015). An exposure-weighted score test for genetic associations integrating environmental risk factors. Biometrics 71, 596–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes R. B., Reding D., Kopp W., Subar A. F., Bhat N., Rothman N., Caporaso N., Ziegler R. G., Johnson C. C., Weissfeld J. L.. et al. (2000). Etiologic and early marker studies in the prostate, lung, colorectal and ovarian (PLCO) cancer screening trial. Contr. Clin. Trials 21, 349S–55S. [DOI] [PubMed] [Google Scholar]
- Hsu L., Jiao S., Dai J. Y., Hutter C., Peters U. & Kooperberg C. (2012). Powerful cocktail methods for detecting genome-wide gene-environment interaction. Genet. Epidemiol. 36, 183–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiao S., Hsu L., Bézieau S., Brenner H., Chan A. T., Chang-Claude J., Le Marchand L., Lemire M., Newcomb P. A., Slattery M. L.. et al. (2013). SBERIA: Set-based gene-environment interaction test for rare and common variants in complex diseases. Genet. Epidemiol. 37, 452–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwee L. C., Epstein M. P., Manatunga A. K., Duncan R., Allen A. S. & Satten G. A. (2007). Simple methods for assessing haplotype-environment interactions in case-only and case-control studies. Genet. Epidemiol. 31, 75–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D. Y. & Zeng D. (2006). Likelihood-based inference on haplotype effects in genetic association studies. J. Am. Statist. Assoc. 101, 89–104. [Google Scholar]
- Lin D. Y. & Zeng D. (2009). Proper analysis of secondary phenotype data in case-control association studies. Genet. Epidemiol. 33, 256–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin X., Lee S., Christiani D. C. & Lin X. (2013). Test for interactions between a genetic marker set and environment in generalized linear models. Biostatistics 14, 667–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin X., Lee S., Wu M. C., Wang C., Chen H., Li Z. & Lin X. (2015). Test for rare variants by environment interactions in sequencing association studies. Biometrics 72, 156–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma Y. (2010). A semiparametric efficient estimator in case-control studies. Bernoulli 16, 585–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meigs J. B., Shrader P., Sullivan L. M., McAteer J. B., Fox C. S., Dupuis J., Manning A. K., Florez J. C., Wilson P. W., D’Agostino Sr R. B.. et al. (2008). Genotype score in addition to common risk factors for prediction of type 2 diabetes. N. Engl. J. Med. 359, 2208–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Modan B., Hartge P., Hirsh-Yechezkel G., Chetrit A., Lubin F., Beller U., Ben-Baruch G., Fishman A., Menczer J., Struewing J. P.. et al. (2001). Parity, oral contraceptives, and the risk of ovarian cancer among carriers and noncarriers of a BRCA1 or BRCA2 mutation. N. Engl. J. Med. 345, 235–40. [DOI] [PubMed] [Google Scholar]
- Mukherjee B., Ahn J., Gruber S. B. & Chatterjee N. (2012). Testing gene-environment interaction in large-scale case-control association studies: Possible choices and comparisons. Am. J. Epidemiol. 175, 177–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee B. & Chatterjee N. (2008). Exploiting gene-environment independence for analysis of case–control studies: An empirical Bayes-type shrinkage estimator to trade-off between bias and efficiency. Biometrics 64, 685–94. [DOI] [PubMed] [Google Scholar]
- Murcray C. E., Lewinger J. P. & Gauderman W. J. (2009). Gene-environment interaction in genome-wide association studies. Am. J. Epidemiol. 169, 219–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newey W. K. (1994). The asymptotic variance of semiparametric estimators. Econometrica 62, 1349–82. [Google Scholar]
- Pfeiffer R. M., Park Y., Kreimer A. R., Lacey Jr J. V., Pee D., Greenlee R. T., Buys S. S., Hollenbeck A., Rosner B., Gail M. H.. et al. (2013). Risk prediction for breast, endometrial, and ovarian cancer in white women aged 50 y or older: Derivation and validation from population-based cohort studies. PLoS Med. 10, e1001492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piegorsch W. W., Weinberg C. R. & Taylor J. A. (1994). Non-hierarchical logistic models and case-only designs for assessing susceptibility in population based case-control studies. Statist. Med. 13, 153–62. [DOI] [PubMed] [Google Scholar]
- Prentice R. L. & Pyke R. (1979). Logistic disease incidence models and case-control studies. Biometrika 66, 403–11. [Google Scholar]
- Prorok P. C., Andriole G. L., Bresalier R. S., Buys S. S., Chia D., Crawford E. D., Fogel R., Gelmann E. P., Gilbert F., Hasson M. A.. et al. (2000). Design of the prostate, lung, colorectal and ovarian (PLCO) cancer screening trial. Control. Clin. Trials 21, 273S–309S. [DOI] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium (2015). A global reference for human genetic variation. Nature 526, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umbach D. M. & Weinberg C. R. (1997). Designing and analysing case-control studies to exploit independence of genotype and exposure. Statist. Med. 16, 1731–43. [DOI] [PubMed] [Google Scholar]
- Wacholder S., Hartge P., Prentice R., Garcia-Closas M., Feigelson H. S., Diver W. R., Thun M. J., Cox D. G., Hankinson S. E., Kraft P.. et al. (2010). Performance of common genetic variants in breast-cancer risk models. N. Engl. J. Med. 362, 986–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao L. P., Li S. S. & Khalid N. (2003). A method for the assessment of disease associations with single-nucleotide polymorphism haplotypes and environmental variables in case-control studies. Am. J. Hum. Genet. 72, 1231–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.