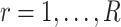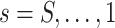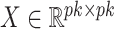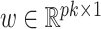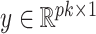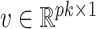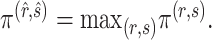Summary
Bayesian sparse factor models have proven useful for characterizing dependence in multivariate data, but scaling computation to large numbers of samples and dimensions is problematic. We propose expandable factor analysis for scalable inference in factor models when the number of factors is unknown. The method relies on a continuous shrinkage prior for efficient maximum a posteriori estimation of a low-rank and sparse loadings matrix. The structure of the prior leads to an estimation algorithm that accommodates uncertainty in the number of factors. We propose an information criterion to select the hyperparameters of the prior. Expandable factor analysis has better false discovery rates and true positive rates than its competitors across diverse simulation settings. We apply the proposed approach to a gene expression study of ageing in mice, demonstrating superior results relative to four competing methods.
Keywords: Expectation-maximization algorithm, Factor analysis, Shrinkage prior, Sparsity, Variable selection
1. Introduction
Factor analysis is a popular approach to modelling covariance matrices. Letting 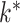 ,
, 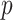 and
and 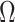 denote the true number of factors, number of dimensions and
denote the true number of factors, number of dimensions and 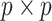 covariance matrix, respectively, factor models set
covariance matrix, respectively, factor models set 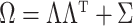 , where
, where 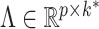 is the loadings matrix and
is the loadings matrix and 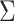 is a diagonal matrix of positive residual variances. To allow computation to scale to large
is a diagonal matrix of positive residual variances. To allow computation to scale to large 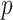 ,
, 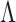 is commonly assumed to be of low rank and sparse. These assumptions imply that
is commonly assumed to be of low rank and sparse. These assumptions imply that 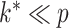 and the number of nonzero loadings is small. A practical problem is that
and the number of nonzero loadings is small. A practical problem is that 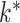 and the locations of zeros in
and the locations of zeros in 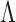 are unknown. A number of Bayesian approaches exist to model this uncertainty in
are unknown. A number of Bayesian approaches exist to model this uncertainty in  and sparsity (Carvalho et al., 2008; Knowles & Ghahramani, 2011), but conventional approaches that rely on posterior sampling are intractable for large sample sizes
and sparsity (Carvalho et al., 2008; Knowles & Ghahramani, 2011), but conventional approaches that rely on posterior sampling are intractable for large sample sizes 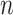 and dimensions
and dimensions 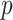 . Continuous shrinkage priors have been proposed that lead to computationally efficient sampling algorithms (Bhattacharya & Dunson, 2011), but the focus is on estimating
. Continuous shrinkage priors have been proposed that lead to computationally efficient sampling algorithms (Bhattacharya & Dunson, 2011), but the focus is on estimating 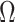 , with
, with 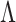 treated as a nonidentifiable nuisance parameter. Our goal is to develop a computationally tractable approach for inference on
treated as a nonidentifiable nuisance parameter. Our goal is to develop a computationally tractable approach for inference on 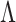 that models the uncertainty in
that models the uncertainty in 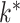 and the locations of zeros in
and the locations of zeros in 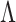 . To do this, we propose a novel shrinkage prior and a corresponding class of efficient inference algorithms for factor analysis.
. To do this, we propose a novel shrinkage prior and a corresponding class of efficient inference algorithms for factor analysis.
Penalized likelihood methods provide computationally efficient approaches for point estimation of 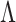 and
and 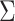 . If
. If 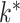 is known, then many such methods exist (Kneip & Sarda, 2011; Bai & Li, 2012). Sparse principal components analysis estimates a sparse
is known, then many such methods exist (Kneip & Sarda, 2011; Bai & Li, 2012). Sparse principal components analysis estimates a sparse 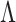 assuming
assuming 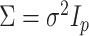 , where
, where 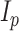 is the
is the 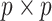 identity matrix (Jolliffe et al., 2003; Zou et al., 2006; Shen & Huang, 2008; Witten et al., 2009). The assumptions of spherical residual covariance and known
identity matrix (Jolliffe et al., 2003; Zou et al., 2006; Shen & Huang, 2008; Witten et al., 2009). The assumptions of spherical residual covariance and known 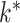 are restrictive in practice. There are several approaches to estimating
are restrictive in practice. There are several approaches to estimating 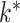 . In econometrics, it is popular to rely on test statistics based on the eigenvalues of the empirical covariance matrix (Onatski, 2009; Ahn & Horenstein, 2013). It is also common to fit the model for different choices of
. In econometrics, it is popular to rely on test statistics based on the eigenvalues of the empirical covariance matrix (Onatski, 2009; Ahn & Horenstein, 2013). It is also common to fit the model for different choices of 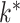 , and choose the best value based on an information criterion (Bai & Ng, 2002). Recent approaches instead use the trace norm or the sum of column norms of
, and choose the best value based on an information criterion (Bai & Ng, 2002). Recent approaches instead use the trace norm or the sum of column norms of 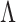 as a penalty in the objective function to estimate
as a penalty in the objective function to estimate 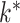 (Caner & Han, 2014). Alternatively, Ročková & George (2016) use a spike-and-slab prior to induce sparsity in
(Caner & Han, 2014). Alternatively, Ročková & George (2016) use a spike-and-slab prior to induce sparsity in 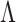 with an Indian buffet process allowing uncertainty in
with an Indian buffet process allowing uncertainty in 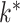 ; a parameter-expanded expectation-maximization algorithm is then used for estimation.
; a parameter-expanded expectation-maximization algorithm is then used for estimation.
We propose a Bayesian approach for estimation of a low-rank and sparse 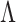 , allowing
, allowing 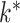 to be unknown. Our approach relies on a novel multi-scale generalized double Pareto prior, inspired by the generalized double Pareto prior for variable selection (Armagan et al., 2013) and by the multiplicative gamma process prior for loadings matrices (Bhattacharya & Dunson, 2011). The latter approach focuses on estimation of
to be unknown. Our approach relies on a novel multi-scale generalized double Pareto prior, inspired by the generalized double Pareto prior for variable selection (Armagan et al., 2013) and by the multiplicative gamma process prior for loadings matrices (Bhattacharya & Dunson, 2011). The latter approach focuses on estimation of 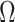 , but does not explicitly estimate
, but does not explicitly estimate 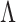 or
or 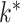 . The proposed prior leads to an efficient and scalable computational algorithm for obtaining a sparse estimate of
. The proposed prior leads to an efficient and scalable computational algorithm for obtaining a sparse estimate of 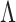 with appealing practical and theoretical properties. We refer to our method as expandable factor analysis because it allows the number of factors to increase as more dimensions are added and as
with appealing practical and theoretical properties. We refer to our method as expandable factor analysis because it allows the number of factors to increase as more dimensions are added and as 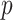 increases.
increases.
Expandable factor analysis combines the representational strengths of Bayesian approaches with the computational benefits of penalized likelihood methods. The multi-scale generalized double Pareto prior is concentrated near low-rank matrices; in particular, a high probability is placed around matrices with rank 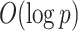 . Local linear approximation of the penalty imposed by the prior equals a sum of weighted
. Local linear approximation of the penalty imposed by the prior equals a sum of weighted 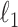 penalties on the elements of
penalties on the elements of 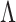 . This facilitates maximum a posteriori estimation of a sparse
. This facilitates maximum a posteriori estimation of a sparse 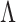 using an extension of the coordinate descent algorithm for weighted
using an extension of the coordinate descent algorithm for weighted 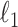 -regularized regression (Zou & Li, 2008). The hyperparameters of our prior are selected using a version of the Bayesian information criterion for factor analysis. Under the theoretical set-up for high-dimensional factor analysis in Kneip & Sarda (2011), we show that the estimates of loadings are consistent and that the estimates of nonzero loadings are asymptotically normal.
-regularized regression (Zou & Li, 2008). The hyperparameters of our prior are selected using a version of the Bayesian information criterion for factor analysis. Under the theoretical set-up for high-dimensional factor analysis in Kneip & Sarda (2011), we show that the estimates of loadings are consistent and that the estimates of nonzero loadings are asymptotically normal.
2. Expandable factor analysis
2.1. Factor analysis model
Consider the usual factor model. Let 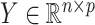 ,
, 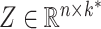 and
and 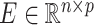 be the mean-centred data matrix, latent factor matrix and residual error matrix, respectively, where
be the mean-centred data matrix, latent factor matrix and residual error matrix, respectively, where 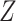 and
and 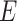 are unknown. We use index
are unknown. We use index 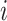 for samples, index
for samples, index 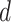 for dimensions, and index
for dimensions, and index 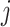 for factors. If
for factors. If 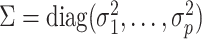 is the residual error variance matrix, then the factor model for
is the residual error variance matrix, then the factor model for 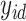 is
is
| (1) |
where 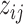 and
and 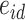 are independent
are independent 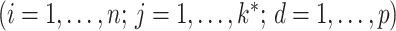 . Equivalently,
. Equivalently,
| (2) |
for sample 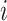 and
and 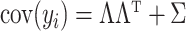
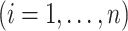 . Similarly, model (1) reduces to regression in the space of latent factors
. Similarly, model (1) reduces to regression in the space of latent factors
| (3) |
for dimension 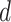
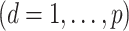 . Unlike usual regression, the design matrix
. Unlike usual regression, the design matrix 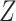 in (3) is unknown.
in (3) is unknown.
Penalized estimation of 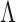 is typically based on (2) or (3). The loss is estimated as the regression-type squared error after imputing
is typically based on (2) or (3). The loss is estimated as the regression-type squared error after imputing 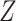 using the eigendecomposition of the empirical covariance matrix
using the eigendecomposition of the empirical covariance matrix 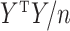 or an expectation-maximization algorithm. The choice of penalty on
or an expectation-maximization algorithm. The choice of penalty on 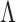 presents a variety of options. If the goal is to select factors that affect any of the
presents a variety of options. If the goal is to select factors that affect any of the 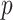 variables, then the sum of column norms of
variables, then the sum of column norms of 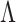 can be used as a penalty; a recent example is the group bridge penalty,
can be used as a penalty; a recent example is the group bridge penalty, 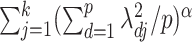 , where
, where 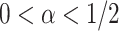 and
and 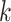 is an upper bound on
is an upper bound on 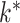 . The selected factors correspond to the nonzero columns of the estimated
. The selected factors correspond to the nonzero columns of the estimated 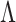 (Caner & Han, 2014). To further obtain elementwise sparsity, a nonconcave variable selection penalty can be applied to the elements in
(Caner & Han, 2014). To further obtain elementwise sparsity, a nonconcave variable selection penalty can be applied to the elements in 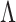 . The estimate of
. The estimate of 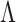 depends on the choice of criterion for selecting the tuning parameters (Hirose & Yamamoto, 2015).
depends on the choice of criterion for selecting the tuning parameters (Hirose & Yamamoto, 2015).
Our expandable factor analysis differs from this typical approach in several important ways. We start from a Bayesian perspective, and place a prior on 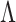 that is structured to allow uncertainty in
that is structured to allow uncertainty in 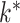 while shrinking towards loadings matrices with many zeros and
while shrinking towards loadings matrices with many zeros and 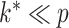 . If
. If 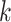 is an upper bound on
is an upper bound on 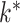 , then the prior is designed to automatically allow a slow rate of growth in
, then the prior is designed to automatically allow a slow rate of growth in 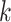 as the number of dimensions
as the number of dimensions 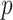 increases by concentrating in neighbourhoods of matrices with rank bounded above by
increases by concentrating in neighbourhoods of matrices with rank bounded above by 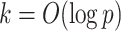 . To our knowledge, this is a unique feature of our approach, justifying its name. Expandability is an appealing characteristic, as more factors should be needed to accurately model the dependence structure as the dimension of the data increases.
. To our knowledge, this is a unique feature of our approach, justifying its name. Expandability is an appealing characteristic, as more factors should be needed to accurately model the dependence structure as the dimension of the data increases.
2.2. Multi-scale generalized double Pareto prior
We would like to design a prior on 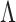 such that maximum a posteriori estimates of
such that maximum a posteriori estimates of 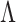 have the following four characteristics:
have the following four characteristics:
(a) the estimate of a loading with large magnitude should be nearly unbiased;
(b) a thresholding rule, such as soft-thresholding, is used to estimate the loadings so that loadings estimates with small magnitudes are automatically set to zero;
(c) the estimator of any loading is continuous in the data to limit instability; and
(d) the
 -norm of the
-norm of the 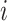 th column of the estimated
th column of the estimated 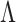 does not increase as
does not increase as 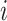 increases.
increases.
The first three properties are related to nonconcave variable selection (Fan & Li, 2001). Properties (b) and (d) together ensure existence of a column index after which all estimated loadings are identically zero. Automatic relevance determination and multiplicative gamma process priors satisfy (d) but fail to satisfy (b). No existing prior for loadings matrices satisfies properties (a)–(d) simultaneously (Carvalho et al., 2008; Bhattacharya & Dunson, 2011; Knowles & Ghahramani, 2011).
In order to satisfy these four properties and obtain a computationally efficient inference procedure, it is convenient to start with a prior for a loadings matrix 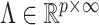 having infinitely many columns; in practice, all of the elements will be estimated to be zero after a finite column index that corresponds to the estimated number of factors. Bhattacharya & Dunson (2011) showed that the set of loadings matrices
having infinitely many columns; in practice, all of the elements will be estimated to be zero after a finite column index that corresponds to the estimated number of factors. Bhattacharya & Dunson (2011) showed that the set of loadings matrices 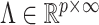 that leads to well-defined covariance matrices is
that leads to well-defined covariance matrices is
We propose a multi-scale generalized double Pareto prior for 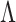 having support on
having support on 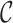 . This prior is constructed to concentrate near low-rank matrices, placing high probability around matrices with rank at most
. This prior is constructed to concentrate near low-rank matrices, placing high probability around matrices with rank at most 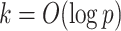 .
.
The multi-scale generalized double Pareto prior on 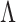 specifies independent generalized double Pareto priors on
specifies independent generalized double Pareto priors on 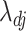 (
(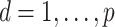 ;
; 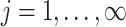 ) so that the density of
) so that the density of 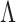 is
is
| (4) |
where 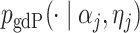 is the generalized double Pareto density with parameters
is the generalized double Pareto density with parameters 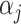 and
and 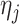 (Armagan et al., 2013). This prior on
(Armagan et al., 2013). This prior on 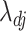 ensures that properties (a)–(c) are satisfied. Property (d) is satisfied by choosing parameter sequences
ensures that properties (a)–(c) are satisfied. Property (d) is satisfied by choosing parameter sequences 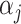 and
and 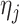 (
(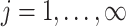 ) such that two conditions hold: the prior measure
) such that two conditions hold: the prior measure 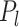 on
on 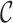 has density
has density 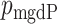 in (4), and
in (4), and 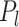 has
has 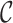 as its support. These conditions hold for the form of
as its support. These conditions hold for the form of 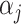 and
and 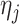 (
(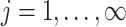 ) specified by the following lemma.
) specified by the following lemma.
Lemma 1
If
,
(
) and
, then
.
The proof is given in the Supplementary Material, along with the other proofs.
As in Bhattacharya & Dunson (2011), we truncate to a finite number of columns for tractable computation. This truncation is accomplished by mapping 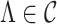 to
to 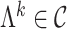 , with
, with 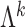 retaining the first
retaining the first 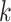 columns of
columns of 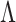 . The choice of
. The choice of 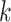 is such that
is such that 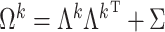 is arbitrarily close to
is arbitrarily close to 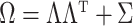 , where distance between
, where distance between 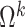 and
and 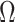 is measured using the
is measured using the 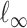 -norm of their elementwise difference. In addition, for computational convenience, we assume that the hyperparameters
-norm of their elementwise difference. In addition, for computational convenience, we assume that the hyperparameters 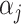 and
and 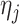 (
(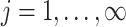 ) are analytic functions of the parameters
) are analytic functions of the parameters 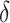 and
and 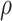 , respectively, with these functions satisfying the conditions of Lemma 1.
, respectively, with these functions satisfying the conditions of Lemma 1.
The following lemma defines the forms of 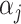 and
and 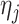 (
(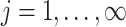 ) in terms of
) in terms of 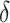 and
and 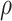 .
.
Lemma 2
If
,
,
and
for
, then
, where
has density
in (4) with hyperparameters
and
(
). Furthermore, given
, there exists a positive integer
for every
such that for all
,
,
(
) and
, we have that
where
.
The penalty imposed on the loadings by the prior grows exponentially with 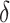 as the column index increases. This property of the prior ensures that all the loadings are estimated to be zero after a finite column index, which corresponds to the estimated number of factors.
as the column index increases. This property of the prior ensures that all the loadings are estimated to be zero after a finite column index, which corresponds to the estimated number of factors.
3. Estimation algorithm
3.1. Expectation-maximization algorithm
We rely on an adaptation of the expectation-maximization algorithm to estimate 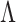 and
and 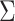 . Choose a positive integer
. Choose a positive integer 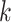 of order
of order 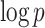 as the upper bound on
as the upper bound on 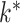 ; the estimate of the number of factors will be less than or equal to
; the estimate of the number of factors will be less than or equal to 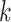 . The results are not sensitive to the choice of
. The results are not sensitive to the choice of 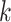 due to the properties of the multi-scale generalized double Pareto prior, provided
due to the properties of the multi-scale generalized double Pareto prior, provided 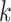 is sufficiently large. If
is sufficiently large. If 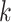 is too small, then the estimated number of factors will be equal to the upper bound, suggesting that this bound should be increased. Given
is too small, then the estimated number of factors will be equal to the upper bound, suggesting that this bound should be increased. Given 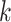 , define
, define 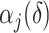 and
and 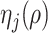 (
(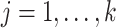 ) as in Lemma 2, with
) as in Lemma 2, with 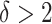 and
and 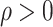 being prespecified constants.
being prespecified constants.
We present the objective function as a starting point for developing the coordinate descent algorithm and provide derivations in the Supplementary Material. Let 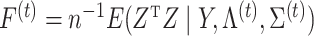 and
and 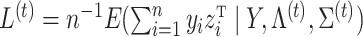 , where the superscript
, where the superscript 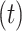 denotes an estimate at iteration
denotes an estimate at iteration 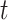 and
and 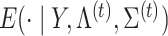 denotes the conditional expectation given
denotes the conditional expectation given 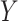 ,
, 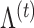 and
and 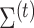 based on (1). The objective function for parameter updates in iteration
based on (1). The objective function for parameter updates in iteration 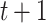 is
is
| (5) |
where 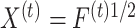 and
and 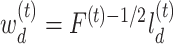 (
(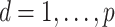 ).
).
3.2. Estimating parameters using a convex objective function
The objective (5) is written as a sum of 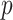 terms. The
terms. The 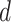 th term corresponds to the objective function for the regularized estimation of the
th term corresponds to the objective function for the regularized estimation of the 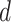 th row of the loadings matrix,
th row of the loadings matrix, 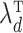 , with a specific form of log penalty on
, with a specific form of log penalty on 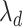 (Zou & Li, 2008). Local linear approximation at
(Zou & Li, 2008). Local linear approximation at 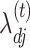 of the log penalty on
of the log penalty on 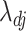 in (5) implies that each row of
in (5) implies that each row of 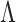 is estimated separately at iteration
is estimated separately at iteration 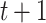 :
:
| (6) |
This problem corresponds to regularized estimation of regression coefficients 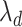 with
with 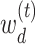 as the response,
as the response, 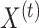 as the design matrix,
as the design matrix, 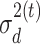 as the error variance, and a weighted
as the error variance, and a weighted 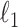 penalty on
penalty on 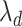 .
.
The solution to (6) is found using block coordinate descent. Let column 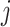 of
of 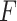 and row
and row 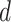 of
of 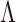 without the
without the 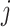 th element be written as
th element be written as 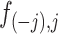 and
and 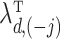 . Then the update to estimate
. Then the update to estimate 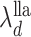 is
is
| (7) |
where 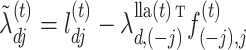 and
and 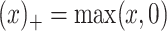 . Fix
. Fix 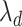 at
at 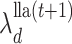 in (5) to update
in (5) to update 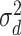 in iteration
in iteration 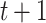 as
as
| (8) |
If any root-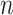 -consistent estimate of
-consistent estimate of 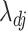 is used instead of
is used instead of 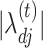 in (6), then it acts as a warm starting point for the estimation algorithm. This leads to a consistent estimate of
in (6), then it acts as a warm starting point for the estimation algorithm. This leads to a consistent estimate of 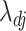 in one step of coordinate descent (Zou & Li, 2008). An implementation of this approach for known values of
in one step of coordinate descent (Zou & Li, 2008). An implementation of this approach for known values of 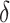 and
and 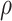 is summarized in steps (i)–(iv) of Algorithm 1 using the R (R Development Core Team, 2017) package glmnet (Friedman et al., 2010).
is summarized in steps (i)–(iv) of Algorithm 1 using the R (R Development Core Team, 2017) package glmnet (Friedman et al., 2010).
Algorithm 1
Estimation algorithm for expandable factor analysis.
Notation :
1.
is the diagonal matrix containing diagonal elements of a symmetric matrix
.
2. Chol(
) is the upper triangular Cholesky factorization of a symmetric positive-definite matrix
.
3.
is a block-diagonal matrix with
forming the diagonal blocks.
4.
, where
.
Input :
1. Data
and upper bound
on the rank of the loadings matrix.
2. The
-
grid with
grid indices (
;
).
Do :
1. Centre data about their mean
(
;
).
2. Let
. Then estimate eigenvalues and eigenvectors of
:
and
.
3. Define
to be the matrix
.
4. Begin estimation of
,
and
across the
-
grid:
For
For
(i) Define
,
if
, and
if
(
).
(iv) Estimate
in (7) and
in (8) using the R package glmnet in three steps:
result
glmnet
x =
, y =
, weights =
, intercept = FALSE,
standardize = FALSE, penalty.factor =
.

coef
result, s =
, exact = TRUE
[-1, ].

(
).
(v) Set
,
,
, and estimate the posterior weight
in (10).
End for.
Set
.
End for.
5. Obtain grid index
for the estimate of
, where
Return :
,
and
.
The estimate of 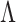 obtained using (7) satisfies properties (a)–(d) described earlier. The adaptive threshold
obtained using (7) satisfies properties (a)–(d) described earlier. The adaptive threshold 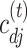 in (7) ensures that property (a) is satisfied. The soft-thresholding rule to estimate
in (7) ensures that property (a) is satisfied. The soft-thresholding rule to estimate 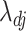 ensures that property (b) is satisfied. The local linear approximation (6) has continuous first derivatives in the parameter space excluding zero, so property (c) is also satisfied (Zou & Li, 2008). The
ensures that property (b) is satisfied. The local linear approximation (6) has continuous first derivatives in the parameter space excluding zero, so property (c) is also satisfied (Zou & Li, 2008). The 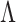 estimate satisfies property (d) due to the structured penalty imposed by the prior.
estimate satisfies property (d) due to the structured penalty imposed by the prior.
We comment briefly on the choice of prior and uncertainty quantification. We build on the generalized double Pareto prior instead of other shrinkage priors not only because the estimate of 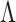 satisfies properties (a)–(d), but also because local linear approximation of the resulting penalty has a weighted
satisfies properties (a)–(d), but also because local linear approximation of the resulting penalty has a weighted 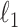 form. We exploit this for efficient computations and use a warm starting point to estimate a sparse
form. We exploit this for efficient computations and use a warm starting point to estimate a sparse 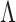 in one step using Algorithm 1. Uncertainty estimates of the nonzero loadings are obtained from Laplace approximation, and the remaining loadings are estimated as zero without uncertainty quantification.
in one step using Algorithm 1. Uncertainty estimates of the nonzero loadings are obtained from Laplace approximation, and the remaining loadings are estimated as zero without uncertainty quantification.
3.3. Root-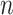 -consistent estimate of
-consistent estimate of 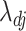
The root-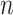 -consistent estimate of
-consistent estimate of 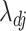 exists under Assumptions A0–A4 given in the Appendix. If
exists under Assumptions A0–A4 given in the Appendix. If 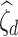 and
and 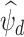 (
(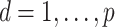 ) are the eigenvalues and eigenvectors of the empirical covariance matrix
) are the eigenvalues and eigenvectors of the empirical covariance matrix 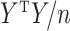 , then
, then 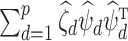 is the eigendecomposition of
is the eigendecomposition of 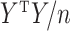 . It is known that
. It is known that 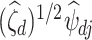 is a root-
is a root-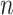 -consistent estimator of
-consistent estimator of 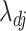 if
if 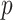 is fixed and
is fixed and 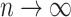 . If
. If 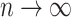 ,
, 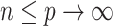 and
and 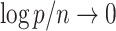 , then
, then 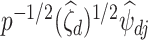 is a root-
is a root-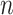 -consistent estimator of
-consistent estimator of 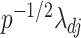 ; see the Supplementary Material for a proof. Scaling by
; see the Supplementary Material for a proof. Scaling by 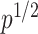 is required because the largest eigenvalue of
is required because the largest eigenvalue of 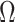 tends to infinity as
tends to infinity as 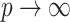 (Kneip & Sarda, 2011). This scaling does not change our estimation algorithm for
(Kneip & Sarda, 2011). This scaling does not change our estimation algorithm for 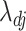 in (7), except that
in (7), except that 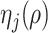 is changed to
is changed to 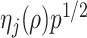 (
(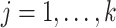 ).
).
3.4. Bayesian information criterion to select 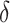 and
and 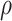
The parameter estimates in (7) and (8) depend on the hyperparameters through 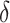 and
and 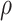 , both of which are unknown. To estimate
, both of which are unknown. To estimate 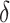 and
and 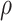 , we use a grid search. Let
, we use a grid search. Let 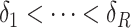 and
and 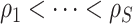 form a
form a 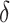 -
-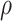 grid. If
grid. If 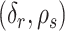 is the value of (
is the value of (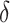 ,
, 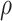 ) at grid index
) at grid index 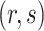 , then
, then 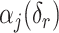 and
and 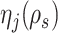
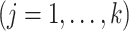 are the hyperparameters of our prior defined using Lemma 2, and
are the hyperparameters of our prior defined using Lemma 2, and 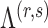 and
and 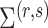 are the parameter estimates based on this prior. Algorithm 1 first estimates
are the parameter estimates based on this prior. Algorithm 1 first estimates 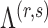 and
and 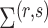 for every
for every 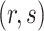 by choosing warm starting points and then estimates (
by choosing warm starting points and then estimates (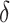 ,
, 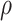 ) using all the estimated
) using all the estimated 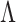 and
and 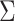 . These two steps in the estimation of (
. These two steps in the estimation of (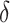 ,
, 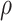 ) are described next.
) are described next.
The structured penalty imposed by our prior implies that 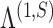 has the maximum number of nonzero loadings. Algorithm 1 exploits this structure by first estimating
has the maximum number of nonzero loadings. Algorithm 1 exploits this structure by first estimating 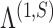 and then other loadings matrices along the
and then other loadings matrices along the 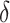 -
-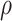 grid by successively thresholding nonzero loadings in
grid by successively thresholding nonzero loadings in 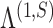 to 0. Let
to 0. Let 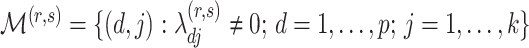 be the set that contains the locations of nonzero loadings in
be the set that contains the locations of nonzero loadings in 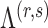 . The estimation path of Algorithm 1 across the
. The estimation path of Algorithm 1 across the 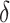 -
-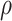 grid is such that
grid is such that 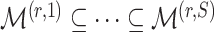 (
(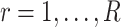 ) and
) and  .
.
After the estimation of 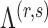 and
and 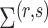
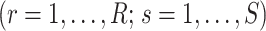 ,
, 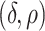 is set to
is set to 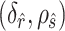 if
if 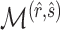 has the maximum posterior probability. Let
has the maximum posterior probability. Let 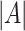 be the cardinality of set
be the cardinality of set 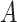 . Given
. Given 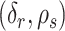 , there are
, there are 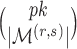 loadings matrices that have
loadings matrices that have 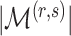 nonzero loadings but differ in the locations of the nonzero loadings. Assuming that each of these matrices is equally likely to represent the locations of nonzero loadings in the true loadings matrix, the prior for
nonzero loadings but differ in the locations of the nonzero loadings. Assuming that each of these matrices is equally likely to represent the locations of nonzero loadings in the true loadings matrix, the prior for 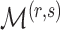 is
is
| (9) |
Let 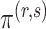 be the posterior probability of
be the posterior probability of 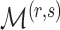 . Then an asymptotic approximation to
. Then an asymptotic approximation to 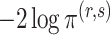 is
is
| (10) |
if terms of order smaller than 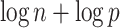 are ignored, where
are ignored, where 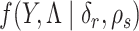 is the joint density of
is the joint density of 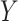 and
and 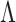 based on (1). The first term in (10) measures the goodness-of-fit, and the last two terms penalize complexity of a factor model with
based on (1). The first term in (10) measures the goodness-of-fit, and the last two terms penalize complexity of a factor model with 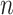 samples and
samples and 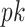 loadings with the locations of nonzero loadings in
loadings with the locations of nonzero loadings in 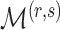 . Theorem 3 in the next section shows that
. Theorem 3 in the next section shows that 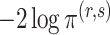 and
and 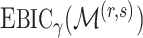 have the same asymptotic order under certain regularity assumptions, where
have the same asymptotic order under certain regularity assumptions, where 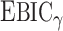 is the extended Bayesian information criteria of Chen & Chen (2008) and
is the extended Bayesian information criteria of Chen & Chen (2008) and 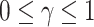 is an unknown constant. The analytic forms of
is an unknown constant. The analytic forms of 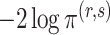 and
and 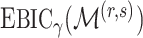 are the same when
are the same when 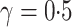 and terms of order smaller than
and terms of order smaller than 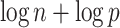 are ignored, so we use
are ignored, so we use 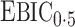 for estimating
for estimating 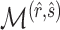 in our numerical experiments.
in our numerical experiments.
4. Theoretical properties
Let 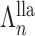 and
and 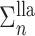 be the fixed points of
be the fixed points of 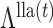 and
and 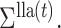 The updates (7) and (8) define the map
The updates (7) and (8) define the map 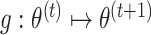 , where
, where 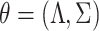 . The following theorem shows that our estimation algorithm retains the convergence properties of the expectation-maximization algorithm.
. The following theorem shows that our estimation algorithm retains the convergence properties of the expectation-maximization algorithm.
Theorem 1
If
represents the objective (5), then
does not decrease at every iteration. Let
be the local linear approximation of (5). Assume that
only for stationary points of
; then the sequence
converges to its stationary point
.
Let 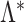 be the true loadings matrix and
be the true loadings matrix and 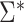 the residual variance matrix. We define
the residual variance matrix. We define 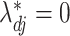 (
(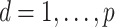 ;
; 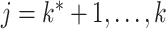 ) and express
) and express 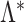 as having
as having 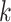 columns. The locations of true nonzero loadings are in the set
columns. The locations of true nonzero loadings are in the set 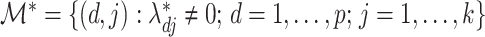 . Let
. Let 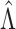 and
and 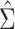 be the estimates of
be the estimates of 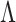 and
and 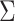 obtained using our estimation algorithm for a specific choice of
obtained using our estimation algorithm for a specific choice of 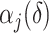 and
and 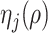 (
(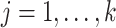 ); then
); then 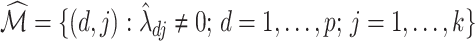 is an estimator of
is an estimator of 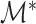 . If
. If 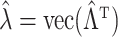 and
and 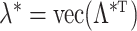 , then
, then 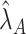 and
and 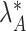 retain elements of
retain elements of 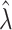 and
and 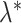 with indices in the set
with indices in the set 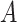 . The following theorem specifies the asymptotic properties of
. The following theorem specifies the asymptotic properties of 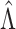 ,
, 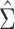 and
and 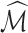 .
.
Theorem 2
Suppose that Assumptions A0–A6 in the Appendix hold and that
,
and
. Then, for any
and
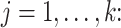
(i)
,
and
are consistent estimators of
,
and
, respectively
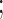
(ii)
and
in distribution, where
is a
symmetric positive-definite matrix and
.
Theorem 2 holds for any multi-scale generalized double Pareto prior with hyperparameters 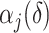 and
and 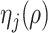 (
(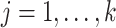 ) that satisfies Assumption 5. In practice, the estimate of
) that satisfies Assumption 5. In practice, the estimate of 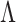 depends on the choice of
depends on the choice of 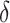 and
and 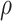 . Restricting the search to the hyperparameters indexed along the
. Restricting the search to the hyperparameters indexed along the 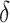 -
-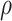 grid, Algorithm 1 sets the values of the hyperparameters to
grid, Algorithm 1 sets the values of the hyperparameters to 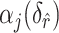 and
and 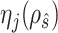 (
(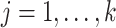 ), where
), where 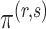 achieves its maximum at grid index
achieves its maximum at grid index 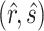 . The following theorem justifies this method of selecting hyperparameters and shows the asymptotic relationship between
. The following theorem justifies this method of selecting hyperparameters and shows the asymptotic relationship between 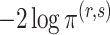 and
and 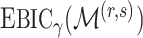 .
.
Theorem 3
Suppose that the generalized double Pareto prior with hyperparameters defined using
leads to estimation of
. Let
be another set that contains the locations of nonzero loadings in an estimated
for a given
. Define
and
. If Assumptions A0–A7 in the Appendix hold, then for any
such that
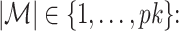
(i)
in probability as
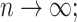
(ii)
as
.
Let 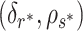 be a point on the
be a point on the 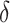 -
-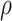 grid that leads to estimation of
grid that leads to estimation of 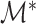 . Then, Theorem 3 shows that Algorithm 1 selects
. Then, Theorem 3 shows that Algorithm 1 selects 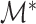 with probability tending to 1 because
with probability tending to 1 because 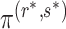 will be larger than any
will be larger than any 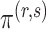 where
where 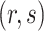 is such that
is such that 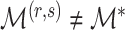 .
.
5. Data analysis
5.1. Set-up and comparison metrics
We compared our method with those of Caner & Han (2014), Hirose & Yamamoto (2015), Ročková & George (2016) and Witten et al. (2009). The first competitor was developed to estimate the rank of 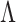 , and the last three competitors were developed to estimate
, and the last three competitors were developed to estimate  . We used two versions of Roǎková and George’s method. The first version uses the expectation-maximization algorithm developed in Ročková & George (2016), and the second version adds an extra step in every iteration of the algorithm that rotates the loadings matrix using the varimax criterion.
. We used two versions of Roǎková and George’s method. The first version uses the expectation-maximization algorithm developed in Ročková & George (2016), and the second version adds an extra step in every iteration of the algorithm that rotates the loadings matrix using the varimax criterion.
We evaluated the performance of the methods for estimating 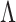 on simulated data using the root mean square error, proportion of true positives, and proportion of false discoveries:
on simulated data using the root mean square error, proportion of true positives, and proportion of false discoveries:
where 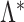 and
and 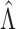 are the true and estimated loadings matrices and
are the true and estimated loadings matrices and 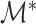 and
and 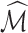 are the true and estimated locations of nonzero loadings. We assume that
are the true and estimated locations of nonzero loadings. We assume that 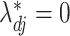 for any
for any 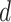 and
and 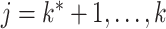 . Since
. Since 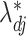 and
and  could differ in sign, mean square error compared their magnitudes.
could differ in sign, mean square error compared their magnitudes.
5.2. Simulated data analysis
The simulation settings were based on examples in Kneip & Sarda (2011). The number of dimensions varied among 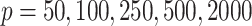 . The rank of every simulated loadings matrix was fixed at
. The rank of every simulated loadings matrix was fixed at 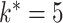 . The magnitudes of nonzero loadings in a column were equal and decreased as
. The magnitudes of nonzero loadings in a column were equal and decreased as 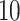 ,
, 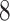 ,
, 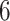 ,
, 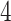 and
and 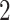 from the first to the fifth column. The signs of the nonzero loadings were chosen such that the columns of any loadings matrix were orthogonal, with a small fraction of overlapping nonzero loadings between adjacent columns:
from the first to the fifth column. The signs of the nonzero loadings were chosen such that the columns of any loadings matrix were orthogonal, with a small fraction of overlapping nonzero loadings between adjacent columns:
The error variances  increased linearly from
increased linearly from 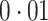 to
to 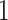 for
for 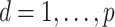 . With varying sample sizes
. With varying sample sizes 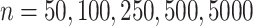 , data were simulated using model (1) for all combinations of
, data were simulated using model (1) for all combinations of 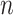 and
and 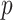 . The simulation set-up was replicated ten times and all five methods were applied in every replication by fixing the upper bound on the number of factors at
. The simulation set-up was replicated ten times and all five methods were applied in every replication by fixing the upper bound on the number of factors at 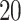 . The
. The 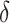 -
-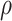 grid had dimensions
grid had dimensions 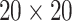 , and
, and 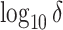 increased linearly from
increased linearly from 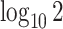 to
to 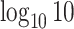 while
while 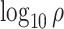 increased linearly from
increased linearly from 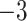 to
to 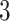 when
when 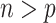 and from
and from 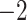 to
to 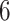 when
when 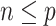 .
.
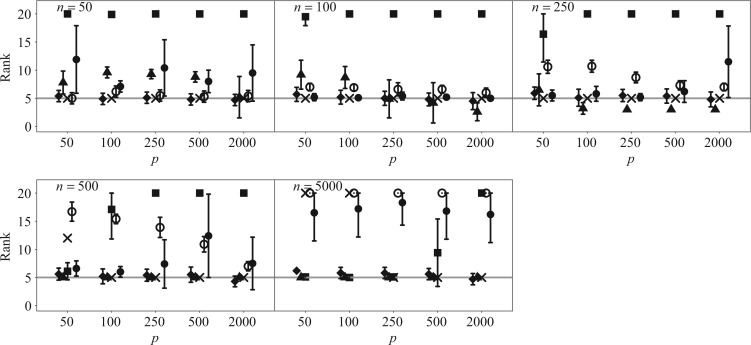
All five methods had the same computational complexity of 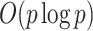 for one iteration, but their runtimes differed depending on their implementations, with the method of Witten et al. (2009) being the fastest. Figure 1 shows that Hirose and Yamamoto’s method and both versions of Roǎková and George’s method significantly overestimated
for one iteration, but their runtimes differed depending on their implementations, with the method of Witten et al. (2009) being the fastest. Figure 1 shows that Hirose and Yamamoto’s method and both versions of Roǎková and George’s method significantly overestimated 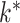 for large
for large 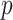 . The method of Witten et al. slightly overestimated
. The method of Witten et al. slightly overestimated 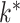 across all settings. Caner and Han’s method showed excellent performance and accurately estimated
across all settings. Caner and Han’s method showed excellent performance and accurately estimated 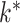 across all simulation settings, except when
across all simulation settings, except when 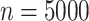 and
and 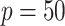 or
or 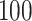 . When
. When 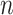 was larger than 500, Assumption A4 was satisfied and our method accurately estimated
was larger than 500, Assumption A4 was satisfied and our method accurately estimated 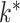 as 5 in every setting, performing better than Caner and Han’s method when
as 5 in every setting, performing better than Caner and Han’s method when 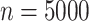 .
.
Fig. 1.
Rank estimate averaged across simulation replications for the methods of Caner & Han (2014) (crosses), Hirose & Yamamoto (2015) (squares), Ročková & George (2016) varimax-free version (empty circles), Ročková & George (2016) varimax version (filled circles) and Witten et al. (2009) (diamonds), as well as our estimation algorithm (triangles). In each panel the horizontal grey line represents the true number of factors; error bars represent Monte Carlo errors.
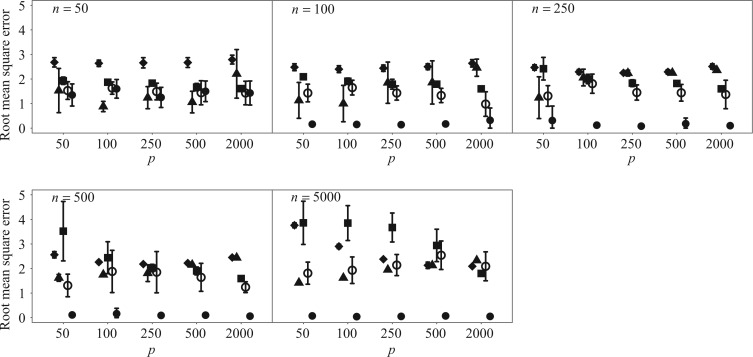
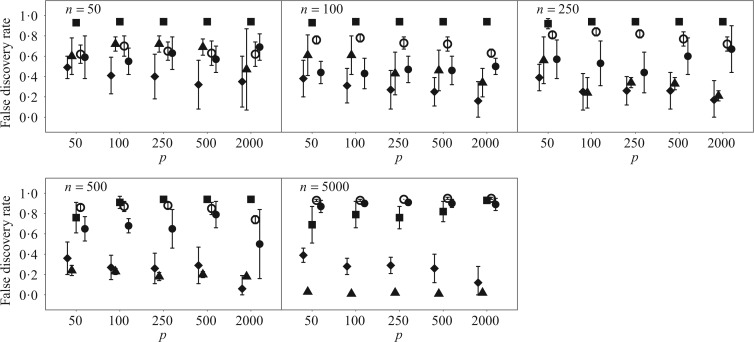
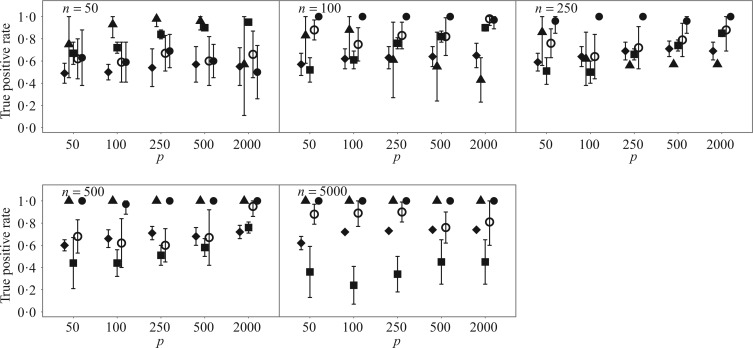
The four methods for estimating 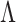 differed significantly in their root mean square errors, true positive rates, and false discovery rates; see Figs 2–4. Hirose and Yamamoto’s method had the highest false discovery rates and the lowest true positive rates across most settings. Both versions of Roǎková and George’s method estimated an overly dense
differed significantly in their root mean square errors, true positive rates, and false discovery rates; see Figs 2–4. Hirose and Yamamoto’s method had the highest false discovery rates and the lowest true positive rates across most settings. Both versions of Roǎková and George’s method estimated an overly dense 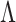 across most settings, resulting in high true positive rates and high false discovery rates. The extra rotation step in the second version of Roǎková and George’s method resulted in excellent mean square error performance; however, varimax rotation is a post-processing step. A similar step to reduce the mean square error could be added to our method, for example by including a step to rotate the
across most settings, resulting in high true positive rates and high false discovery rates. The extra rotation step in the second version of Roǎková and George’s method resulted in excellent mean square error performance; however, varimax rotation is a post-processing step. A similar step to reduce the mean square error could be added to our method, for example by including a step to rotate the 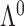 in step 3 of Algorithm 1 using the varimax criterion. When
in step 3 of Algorithm 1 using the varimax criterion. When 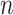 and
and 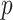 were small, the method of Witten et al. achieved the lowest false discovery rates while our method achieved the highest true positive rates. When
were small, the method of Witten et al. achieved the lowest false discovery rates while our method achieved the highest true positive rates. When 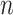 and
and 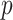 were larger than 250 and 100, respectively, Assumption A4 was satisfied and our method simultaneously achieved the highest true positive rates and lowest false discovery rates while maintaining competitive mean square errors relative to the rotation-free methods.
were larger than 250 and 100, respectively, Assumption A4 was satisfied and our method simultaneously achieved the highest true positive rates and lowest false discovery rates while maintaining competitive mean square errors relative to the rotation-free methods.
Fig. 2.
Root mean square error averaged across simulation replications for the methods of Hirose & Yamamoto (2015) (squares), Ročková & George (2016) varimax-free version (empty circles), Ročková & George (2016) varimax version (filled circles) and Witten et al. (2009) (diamonds), as well as our estimation algorithm (triangles). Error bars represent Monte Carlo errors.
Fig. 4.
False discovery rate averaged across simulation replications for the methods of Hirose & Yamamoto (2015) (squares), Ročková & George (2016) original version (empty circles), Ročková & George (2016) varimax version (filled circles) and Witten et al. (2009) (diamonds), as well as our estimation algorithm (triangles). Error bars represent Monte Carlo errors.
Fig. 3.
True positive rate averaged across simulation replications for the methods of Hirose & Yamamoto (2015) (squares), Ročková & George (2016) varimax-free version (empty circles), Ročková & George (2016) varimax version (filled circles) and Witten et al. (2009) (diamonds), as well as our estimation algorithm (triangles). Error bars represent Monte Carlo errors.
5.3. Microarray data analysis
We used gene expression data on ageing in mice from the AGEMAP database (Zahn et al., 2007). There were 40 mice aged 1, 6, 16 and 24 months in this study. Each age group included five male and five female mice. Tissue samples were collected from 16 different tissues, including the cerebrum and cerebellum, for every mouse. Gene expression levels in every tissue sample were measured on a microarray platform. After normalization and removal of missing data, gene expression data were available for all 8932 probes across 618 microarrays. We used a factor model to estimate the effect of latent biological processes on gene expression variation.
AGEMAP data were centred before analysis following Perry & Owen (2010). Gene expression measurements were represented by 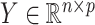 , where
, where 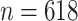 and
and 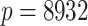 . Further, age
. Further, age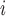 represented the age of mouse
represented the age of mouse 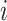 and gender
and gender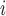 was 1 if mouse
was 1 if mouse 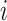 was female and 0 otherwise. Least-squares estimates of the intercept, age effect and gender effect in the linear model
was female and 0 otherwise. Least-squares estimates of the intercept, age effect and gender effect in the linear model 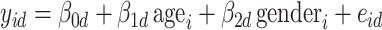 (
(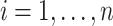 ), with idiosyncratic error
), with idiosyncratic error 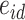 , were represented as
, were represented as 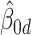 ,
, 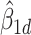 and
and 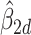 . Using these estimates for
. Using these estimates for 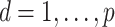 , the mean-centred data were defined as
, the mean-centred data were defined as
Four mice were randomly held out, and all tissue samples for these mice in 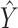 were used as test data. The remaining samples were used as training data. This set-up was replicated ten times. All four methods were applied to the training data in every replication by fixing the upper bound on the number of factors at 10. The
were used as test data. The remaining samples were used as training data. This set-up was replicated ten times. All four methods were applied to the training data in every replication by fixing the upper bound on the number of factors at 10. The 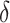 -
-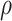 grid had dimensions
grid had dimensions 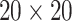 , and
, and 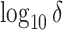 increased linearly from
increased linearly from 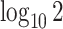 to
to 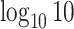 while
while 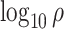 increased linearly from
increased linearly from 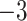 to
to 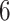 .
.
The results for all five methods were stable across all ten folds of crossvalidation. Caner and Han’s method, Hirose and Yamamoto’s method, both versions of Roǎková and George’s method, the method of Witten et al. and our method selected 10, 10, 10, 4 and 1, respectively, as the number of latent biological processes 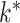 across all folds. Our result matched the result of Perry & Owen (2010), who confirmed the presence of one latent variable using rotation tests. Our simulation results and the findings in Perry & Owen (2010) strongly suggest that our method accurately estimated
across all folds. Our result matched the result of Perry & Owen (2010), who confirmed the presence of one latent variable using rotation tests. Our simulation results and the findings in Perry & Owen (2010) strongly suggest that our method accurately estimated 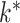 and the other methods overestimated
and the other methods overestimated 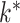 .
.
We also estimated the factors for the test data. With 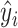 denoting test datum
denoting test datum 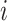 and
and 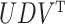 denoting the singular value decomposition of
denoting the singular value decomposition of 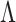 , the factor estimate of test datum
, the factor estimate of test datum 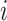 was
was 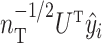 , where
, where 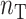 denotes the number of samples in the training data. Perry & Owen (2010) found that factor estimates for the tissue samples from cerebrum and cerebellum, respectively, had bimodal densities. We used the density function in R with default settings to obtain kernel density estimates of the factors. Hirose and Yamamoto’s method and both versions of Roǎková and George’s method estimated the number of factors as 10, which made the results challenging to interpret. The method of Witten et al. recovered bimodal densities in all four factors for both tissue samples, but it was unclear which of these four factors corresponded to the factor estimated by Perry & Owen (2010). Our method estimated the number of factors to be 1 and recovered the bimodal density in both tissue samples.
denotes the number of samples in the training data. Perry & Owen (2010) found that factor estimates for the tissue samples from cerebrum and cerebellum, respectively, had bimodal densities. We used the density function in R with default settings to obtain kernel density estimates of the factors. Hirose and Yamamoto’s method and both versions of Roǎková and George’s method estimated the number of factors as 10, which made the results challenging to interpret. The method of Witten et al. recovered bimodal densities in all four factors for both tissue samples, but it was unclear which of these four factors corresponded to the factor estimated by Perry & Owen (2010). Our method estimated the number of factors to be 1 and recovered the bimodal density in both tissue samples.
Supplementary Material
Acknowledgement
This work was supported by the U.S. National Institute of Environmental Health Sciences, National Institutes of Health, and National Science Foundation. We are grateful to the referees, associate editor, and editor for their comments and suggestions.
Supplementary material
Supplementary material available at Biometrika online includes derivation of the expectation-maximization algorithm, proofs of Lemmas 1 and 2 and Theorems 1–3, supporting figures for the results in § 5.3, and the R code used for data analysis.
Appendix
Assumptions
Assumptions A0–A4 follow from the theoretical set-up for high-dimensional factor models in Kneip & Sarda (2011). Assumption 5 is based on results in Zou & Li (2008) for variable selection.
Assumption A0.
Let
,
,
,
,
,
and
(
).
Assumption A1.
There exist finite positive constants
,
and
such that
,
and
(
;
).
Assumption A2.
There exists a constant
such that
,
,
and
are
-sub-Gaussian for every
. A random variable
is
-sub-Gaussian if
for any
.
Assumption A3.
Let
be the eigenvalues of
; then there exists a
such that
,
,
, and
.
Assumption A4.
The sample size
and dimension
are large enough that
and
.
Assumption A5.
Let
be the upper bound on
and let
,
,
and
(
) be defined as in Lemma 2. Then
,
,
and
(
) as
,
and
.
Assumption A6.
The elements of the set
are fixed and do not change as
or
increases to
.
Model (2) is recovered upon substituting 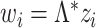 into Assumption A0. Assumption A1 ensures that
into Assumption A0. Assumption A1 ensures that 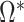 is positive definite. Assumption A2 ensures that the empirical covariances are good approximations of the true covariances. Specifically, for any
is positive definite. Assumption A2 ensures that the empirical covariances are good approximations of the true covariances. Specifically, for any 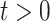 ,
,
hold simultaneously with probability at least 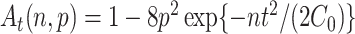 . If
. If 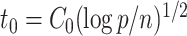 , then
, then 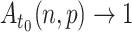 as
as 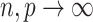 and
and 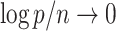 . Assumption A3 guarantees identifiability of
. Assumption A3 guarantees identifiability of  when
when 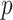 is large and
is large and 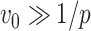 . Assumption A4 is required to ensure that
. Assumption A4 is required to ensure that 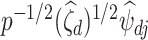 is a root-
is a root-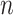 -consistent estimator of
-consistent estimator of 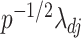 as
as 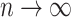 ,
, 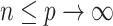 and
and 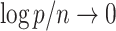 .
.
One additional assumption is required to relate 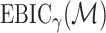 and
and 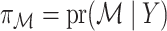 .
.
Assumption A7
Let
for a fixed constant
such that
.
Assumption A7 and equation (4.6) in Theorem 3 of Kneip & Sarda (2011) imply that 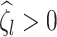 for any
for any 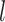 such that
such that 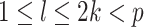 , because
, because 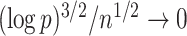 as
as 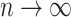 .
.
References
- Ahn S. C. & Horenstein A. R. (2013). Eigenvalue ratio test for the number of factors. Econometrica 81,1203–27. [Google Scholar]
- Armagan A., Dunson D. B. & Lee J. (2013). Generalized double Pareto shrinkage. Statist. Sinica 23,119–43. [PMC free article] [PubMed] [Google Scholar]
- Bai J. & Li K. (2012) Statistical analysis of factor models of high dimension. Ann. Statist. 40,436–65. [Google Scholar]
- Bai J. & Ng S. (2002). Determining the number of factors in approximate factor models. Econometrica 70,191–221. [Google Scholar]
- Bhattacharya A. & Dunson D. B. (2011). Sparse Bayesian infinite factor models. Biometrika 98,291–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caner M. & Han X. (2014). Selecting the correct number of factors in approximate factor models: The large panel case with group bridge estimators. J. Bus. Econ. Statist. 32,359–74. [Google Scholar]
- Carvalho C. M., Chang J., Lucas J. E., Nevins J. R., Wang Q. & West M. (2008). High-dimensional sparse factor modeling: Applications in gene expression genomics. J. Am. Statist. Assoc. 103,1438–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J. & Chen Z. (2008). Extended Bayesian information criteria for model selection with large model spaces. Biometrika 95,759–71. [Google Scholar]
- Fan J. & Li R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Statist. Assoc. 96,1348–60. [Google Scholar]
- Friedman J. H., Hastie T. J. & Tibshirani R. J. (2010). Regularization paths for generalized linear models via coordinate descent. J. Statist. Software 33,1–22. [PMC free article] [PubMed] [Google Scholar]
- Hirose K. & Yamamoto M. (2015). Sparse estimation via nonconcave penalized likelihood in factor analysis model. Statist. Comp. 25,863–75. [Google Scholar]
- Jolliffe I. T., Trendafilov N. T. & Uddin M. (2003). A modified principal component technique based on the LASSO. J. Comp. Graph. Statist. 12,531–47. [Google Scholar]
- Kneip A. & Sarda P. (2011). Factor models and variable selection in high-dimensional regression analysis. Ann. Statist. 39,2410–47. [Google Scholar]
- Knowles D. & Ghahramani Z. (2011). Nonparametric Bayesian sparse factor models with application to gene expression modeling. Ann. Statist. 5,1534–52. [Google Scholar]
- Onatski A. (2009). Testing hypotheses about the number of factors in large factor models. Econometrica 77,1447–79. [Google Scholar]
- Perry P. O. & Owen A. B. (2010). A rotation test to verify latent structure. J. Mach. Learn. Res. 11,603–24. [Google Scholar]
- R Development Core Team (2017). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.ISBN 3-900051-07-0.http://www.R-project.org. [Google Scholar]
- RokĉovÁ V. & George E. I. (2016). Fast Bayesian factor analysis via automatic rotations to sparsity. J. Am. Statist. Assoc. 111,1608–22. [Google Scholar]
- Shen H. & Huang J. Z. (2008). Sparse principal component analysis via regularized low rank matrix approximation. J. Mult. Anal. 99,1015–34. [Google Scholar]
- Witten D. M., Tibshirani R. J. & Hastie T. J. (2009). A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics 10,515–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahn J. M., Poosala S., Owen A. B., Ingram D. K., Lustig A., Carter A., Weeraratna A. T., Taub D. D., Gorospe M., Mazan-Mamczarz K. et al. (2007). AGEMAP: A gene expression database for aging in mice. PLoS Genet. 3,e201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H., Hastie T. J. & Tibshirani R. J. (2006). Sparse principal component analysis. J. Comp. Graph. Statist. 15,265–86. [Google Scholar]
- Zou H. & Li R. (2008). One-step sparse estimates in nonconcave penalized likelihood models. Ann. Statist. 36,1509–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.