Self-healing hydrogels formed by complexation between calcium ions and bisphosphonate-functionalized star-shaped polymers

Abstract

Star-shaped poly(ethylene glycol) (PEG) chain termini were functionalized with alendronate to create transient networks with reversible crosslinks upon addition of calcium ions. The gelation ability of alendronate-functionalized PEG was greatly dependent on the number of arms and arm molecular weight. After mixing polymer and calcium solutions, the formed hydrogels could be cut and then brought back together without any visible interface. After 2 minutes of contact, their connection was strong enough to allow for stretching without tearing through the previous fracture surface. Oscillatory rheology showed that the hydrogels recovered between 70 and 100% of the original storage and loss modulus after rupture. Frequency sweep measurements revealed a liquid-like behavior at lower frequencies and solid-like at high frequencies. Shifting frequency curves obtained at different calcium and polymer concentrations, all data collapsed in a single common master curve. This time-concentration superposition reveals a common relaxation mechanism intrinsically connected to the calcium-bisphosphonate complexation equilibrium.

Graphical Abstract

INTRODUCTION

Hydrogels are materials composed of hydrophilic polymer strands connected to each other at crosslinking points. The resulting three-dimensional network can be regarded as a huge macromolecule that spans the entire volume of the system. Due to the hydrophilic nature of the constituting polymeric chains, hydrogels can absorb considerable amounts of water. This feature makes them appropriate for a wide variety of technological applications, including biomaterials for drug delivery and tissue regeneration. Traditionally, hydrogels are created by irreversible bonds between the polymer chains that form permanent networks. An important feature of these materials is that their stiffness falls within the range of soft biological tissues.¹ Nevertheless, a permanent network cannot recover its initial integrity after rupture. For applications in regenerative medicine, non-degradable permanent networks do not allow cellular migration. To obviate this problem, hydrogels were designed with star shaped multi-arm PEG macromers crosslinked through peptide sequences susceptible to degradation by matrix metalloproteinases.^2,3 However, cellular infiltration is achieved at the expense of the original network integrity. In biological tissues, nature solves this problem by continuously breaking down and reconstructing the extracellular matrix. The complexity and degree of sophistication of these natural materials is still far beyond the current state of the art of synthetic materials.

A simple approach that holds great potential to overcome this problem is the creation of transient networks, in which polymer strands are connected by reversible bonds. Several types of reversible chemical bonds of different strength have been used to design self-healing PEG hydrogels, such as reversible covalent bonds,^4,5 hydrogen bonding^6,7 and coordination bonds.^8–12 These transient hydrogels are structurally similar to a permanent network, but dynamically different since the network configuration is constantly being reshaped. In this way, transient networks are self-healing, which mean that they possess the ability to recover the integrity and, at least to some extent, the original properties after damage. Hydrogels formed by reversible bonds are expected to respond to cell-induced stress by rapidly breaking and reforming elastically active crosslinks. Such systems facilitate complex cellular functions, while retaining the overall mechanical environment. For instance, cell spreading, proliferation, and osteogenic differentiation of mesenchymal stem cells (MSCs) were all enhanced in hydrogels with faster bond dynamics.^13,14

To fully harness the benefits of self-healing soft materials, it is essential to obtain quantitative understanding of the macromolecular dynamics relationship to the stress relaxation behavior of the network. However, this is often complicated by convoluted effects of complex supramolecular organization, heterogeneous polymeric structures or other competing interactions. To overcome these limitations, regular star-shaped poly(ethylene glycol) (PEG) polymers end-capped with reactive moieties have been used to create transient networks with well-defined architectures.^6,9–12,15 The rheological behavior of the simple star-shape geometry is well described by classical polymer physics theory,^16,17 facilitating analysis of the dynamic network connectivity in terms of crosslinking reaction kinetics and equilibrium. Recently, we found that catechol-modified star-shaped PEGs can be crosslinked through metal-coordination with Al³⁺, Fe³⁺ and V³⁺ ions, while the viscoelastic properties of these materials were mainly determined by variations in the kinetics of metal-catechol coordination bonds.¹² Although several examples of transient PEG networks based on metal coordination bonds have been described previously, most metals described are too toxic for biomedical applications. In the current study, we describe a material based on biologically compatible components created by modifying the chain-ends of star-shaped PEGs with a bisphosphonate (alendronic acid). Bisphosphonate drugs are currently used to treat osteoporosis, Paget’s disease of bone, malignancies metastatic to bone, multiple myeloma, and hypercalcemia of malignancy.^18–20 They inhibit bone resorption^19,20, interact strongly with calcium at the surface of bone hydroxyapatite, and form complexes with calcium ions in aqueous solution.^20–22 Herein, the complexation equilibrium between bisphosphonate end-groups and calcium ions provides the rationale for the design of transient crosslinks. We modified the free-chain ends of star-shaped PEGs comprising different number of arms and arm molecular weight to evaluate the effect of the macromolecular architecture on hydrogel network formation, stress relaxation and self-healing properties. We also studied how changes in the reaction equilibrium and kinetics, induced by changes in either calcium or polymer concentration, influenced network dynamics.

EXPERIMENTAL SECTION

Materials

Star-shaped PEG-OH molecules (8-arm with a tripentaerythritol core and 10, 20 or 40 kDa; 4-arm with a pentaerythritol core and 10 kDa) were purchased from JenKem Technology USA Inc. Alendronic acid (98%) was acquired from AK Scientific Inc. Phosphate buffered saline (PBS) solutions were prepared containing 2.67 mM KCl and 137.9 mM NaCl (pH=7.4). Regular PBS solution was prepared with a total buffer concentration of 10 mM, and it is referred only as PBS throughout the manuscript. Strongly buffered PBS solution was prepared with a phosphate buffer concentration of 100 mM, referred as PBS(100 mM) solution. 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide hydrochloride (EDC) was purchased from TCI America. N-hydroxysuccinimide (NHS), pyridine and all divalent salts were purchased from Sigma.

Synthesis of alendronate-terminated PEG

Alendronate-terminated PEGs were synthesized by a three-step procedure (Fig. SI-1). First, N-hydroxysuccinimide-terminated PEGs (PNHS) were synthesized in two steps as previously described.²³ Briefly, PEG-OH was dissolved in chloroform (1 g/ml) together with 5 equiv. of glutaric anhydride. Pyridine (5 equiv.) was added dropwise, and the reaction was refluxed at 80°C under inert atmosphere for 24 h. The reaction product was diluted in MeOH, precipitated at −20°C for 1 h and centrifuged at −5°C, followed by discarding the supernatant and repeating the procedure two more times. A white powder was obtained after diethyl ether precipitation and vacuum drying overnight (97% yield and ~100% conversion of the arm ends). Subsequently, the obtained glutaric acid terminated PEG (PG) was dissolved in DMSO (0.5 g/ml) and reacted with an excess of NHS (10 equiv.) and EDC (10 equiv.) for 30 min at room temperature. The NHS activated PEG (PNHS) was purified again by consecutive precipitation in MeOH and diethyl ether. A white powder was obtained after vacuum drying. PNHS with 97% conversion of its arms was obtained with 81% yield.

Finally, alendronic acid was reacted with PNHS to produce alendronate terminated PEG (PAA). A small test reaction was previously performed in an NMR tube using PBS (100 mM) solution in D₂O. We followed the reaction kinetics for 3 h by ¹H-NMR (Fig. SI-2) to determine the optimum pH to minimize competing hydrolysis of NHS, therefore maximizing coupling of AA. Finally, alendronic acid was dissolved at 80 mM in PBS (100 mM) solution and the pH was readjusted to 7.4 by adding 1 N NaOH solution. PNHS (1 wt%) was dissolved in the alendronic acid solution and reacted for 4h at room temperature. The solution was dialyzed for 36 h against water, and freeze-dried. The degree of modification was determined by proton nuclear magnetic resonance (¹H-NMR) and is described in Table 1.

Table 1.

Summary of multi-arm PEGs modified with alendronic acid at the chain termini: molecular weight (M_w), number of arms (f), arm molecular weight (M_a), and overlapping concentration (C*).

Polymer	Mw (kDa)	f	Ma (kDa)	Yield (1H-NMR)	C*=1/[η] (wt%)
P(8)10-AA	10	8	1.25	84%	12.3
P(8)20-AA	20	8	2.5	87%	7.5
P(8)40-AA	40	8	5	85%	4.6
P(4)10-AA	10	4	2.5	87%	7.4

Specific viscosity [η] was calculated from Mark-Houwink-Sakurada parameters (α = 0.716, and K as function of f).²⁴

Preparation of self-healing hydrogels

Each sample was prepared by mixing equal volumes of a PAA solution in PBS with a CaCl₂ aqueous solution. The concentration of each of these solutions was chosen to obtain gels with final concentrations of polymer from 10 to 20 wt%, and final calcium concentrations from 25 to 500 mM (see Table 2). The various formulations were named after the number of arms (X), polymer M_w (Y) and modification (AA stands for alendronic acid), using the nomenclature P(X)Y-AA. The mixture was stirred vigorously with a spatula to form homogenous moldable gels. Subsequently, gelation was monitored by visual inspection.

Table 2.

Visual screening of gelation at different polymer and CaCl₂ concentrations

			[Ca2+]/mM
Polymer	Concentration (wt%)	[AA]/mM	25	50	100	200	500
P(8)10-AA	10	80	✖	✖	✖	✖	✖
	15	120	✖	✖	✖	✖	✖
	20	160	•	•	✓	✓	✓
P(8)20-AA	10	40	✖	•	✓	✓	✓
	15	60	✓	✓	✓	✓	✓
	20	80	✓	✓	✓	✓	✓
P(8)40-AA	10	20	✖	✖	✖	✖	✖
	15	30	✖	✖	✖	✖	✖
	20	40	✖	✖	✖	✖	✖
P(4)10-AA	10	40	✖	✖	✖	✖	✖
	15	60	✖	✖	✖	✖	✖
	20	80	✖	✖	✖	✖	✖

Legend: (✖) viscous solution; (•) weak gels or very viscous solution; and (✓) gel formation. Grey table cells indicate dilute-regime. Polymers are in the semidilute regime for all other conditions.

Oscillatory rheology

The viscoelastic properties of the gels were tested by oscillatory rheology using an AR2000 Advanced Rheometer (TA Instruments) with parallel plate geometry (20 mm diameter) at a fixed gap size of 500 μm. In general, the rheological properties of the gels were analyzed after being homogenized for 3 min and incubated overnight into sealed test tubes. An independent measurement was performed with freshly prepared gels (~3 min) to analyze if a large curing time was required for gel attaining equilibrium viscoelastic properties. Strain sweep tests were performed to determine the linear viscoelastic region, which was found to be greater than 100% for most conditions (Fig. SI-3).

Frequency sweeps were performed at a constant strain of 5% by varying the angular frequency between 0.1 and 100 rad/s). Prior to each frequency sweep test, a time sweep was performed for 5 min at 10 rad/s frequency and 5% strain to guarantee gel equilibration. Storage modulus (G′), loss modulus (G″), and damping factor (and tan δ) were determined for star-shaped PEG polymers of different molecular weight (M_w) and number of arms (f). Polymer and calcium concentrations were varied around the arbitrary reference values of 15 wt% and 100 mM, respectively. All measurements were performed at least in triplicate at constant temperature (20°C) and under controlled humidity.

Self-healing behavior

Macroscopic self-healing properties of polymer gels were evaluated visually by observing gel recovery after cutting a gel into two pieces with a surgical knife and followed by fusing the two pieces without the application of a continuous external pressure. Gels were also stained with either orange or black dyes to facilitate visualization. After cutting these differently colored gels into pieces, the procedure was repeated by fusing gel pieces of different colors.

Rheological failure-recovery tests were performed by applying large amplitude strains to break the gel integrity followed by monitoring gel recovery. Initial viscoelastic properties were measured at 5% strain and 10 rad/s angular frequency. After 5 min, strain was ramped until 1000% in 3 min to assure gel network disruption. After loss of gel integrity, the initial testing conditions were restored to follow the time-dependent recovery of gel integrity for 10 min. Several failure-recovery cycles were applied consecutively and the recovery was quantified by comparing the storage modulus and damping factor before and after each rupture. All measurements were performed at least in triplicate at constant temperature (20°C) and under controlled atmospheric moisture.

RESULTS AND DISCUSSION

Synthesis of star-shaped PEG-alendronate

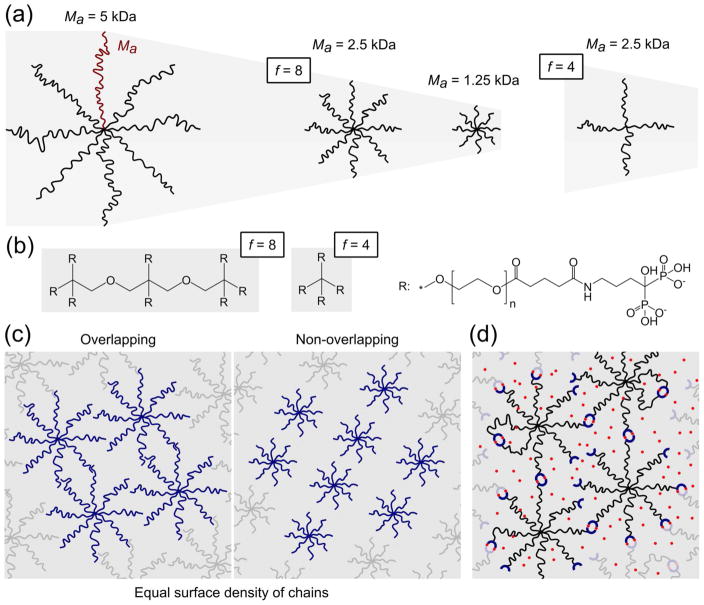
The terminus of each chain of star-shaped PEG polymers was functionalized with alendronic acid (AA) (see Fig. 1b and Fig. SI-1 for a detailed reaction scheme). Since alendronic acid is insoluble in most common organic solvents but soluble in water at neutral and basic pH, the synthesis was performed in aqueous solutions. However, in water the hydrolysis of NHS competes with coupling of AA, and the rates of both reactions increase with pH. In order to determine suitable reaction conditions, we followed the reaction kinetics for 3 h by ¹H-NMR. When using PBS buffer in D₂O, the AA coupling reaction was complete in about 2 h (about 85% for all tested polymers, Fig. SI-2, Table 1), whereas the remaining PEG-NHS was fully hydrolyzed (about 15%). PEGs with different number of arms (f) and molecular weights (M_w) were designated as P(X)Y-AA, where X is the value of f, Y is the nominal M_w in kDa, and AA refers to the functionalization with alendronic acid (see Fig. 1a). The effect of arm length on gelation was investigated by comparing 8-arm PEGs of different molecular weight (M_a = 1.25, 2.5, or 5 kDa), while the effect of the number of arms was studied by comparing star-shaped PEGs of similar arm length (M_a = M_w/f = 2.5 kDa) but different number of arms (f = 4 or 8) (Table 1).

Figure 1.

(a) PEG chains are represented by lines proportional in length to the molecular weight. (b) Chemical drawing of eight and four-arm PEG molecular cores and of an arm modified with alendronate. (c) Schematic representation of P(8)20-AA and P(8)10-AA solutions. The density of lines is constant, and depicts a polymer concentration where P(8)20-AA macromers overlap in solution. At the same concentration, P(8)10-AA molecules cannot fill the entire space and do not form a transient network. (d) Transient network showing free ends, intramolecular (loops) and intermolecular (crosslinks) associations. Calcium ions and alendronate moieties are represented by red dots and blue half-rings, respectively.

Visual observation of gelation

Star-shaped PEGs functionalized with AA were soluble in water (and PBS) in the absence of Ca²⁺. Mixing equal volumes of polymer and CaCl₂ solutions at final polymer concentrations between 10 and 20 wt% and Ca²⁺ concentrations between 25 and 500 mM (Table 2) yielded either viscous solutions or solid-like self-standing materials, herein referred as self-healing hydrogels. At the polymer concentration range used in this work, most solutions are in the semidilute regime, with the exception of P(8)10-AA solutions at 10 wt% (see Table 2). The overlapping concentration (C*), which defines the transition between the dilute and semidilute regimes, was calculated using the relation:¹⁷

$$C^{\ast }=\frac{1}{[\eta ]}$$

where [η] is the intrinsic viscosity. This can be calculated using the Mark-Houwink-Sakurada equation:

$$[\eta ]=K·{M_v}^{\alpha }$$

We used the parameters determined by Comanita et al.²⁴ for star-shaped PEGs in water with varying number of arms (α = 0.716 as it would be expected for a good solvent, and K is a function of f). The calculated C* values are shown in the Table 1. Moreover, we can safely assume that the transient networks were free of entanglements. The dependence of the molecular weight between entanglements (M_e) on the volume fraction (φ) was described by Colby and Rubinstein as:²⁵

$$M_e(\phi )=M_e(\phi =1)\times {\phi }^{-4/3}$$

The molecular weight between entanglements for the polymer melt (φ = 1, 100 %) is reported to be 2.2 kDa.²⁶ As a result, at a polymer concentration between 10 and 20 wt% as used in our experiments, an arm molecular weight of at least 20 kDa would be required to create one entanglement. Therefore, besides the referred exception at the dilute regime (P(8)10-AA solutions at 10 wt%), all other conditions are in the unentangled semidilute regime.

Gelation depended strongly on molecular weight (M_w), number of arms (f) and the Ca²⁺ concentration. Eight-arm PEGs with a molecular weight 20 kDa (P(8)20-AA) displayed the most pronounced gelation behavior. In fact, at 15 and 20 wt% polymer concentration, hydrogels were formed for the entire range of tested Ca²⁺ concentrations, while a final polymer concentration of 10 wt% required a Ca²⁺ concentration higher than 100 mM for gelation. Hydrogels were not obtained for most of the other AA functionalized PEGs except for P(8)10-AA, which only formed hydrogels at high polymer (20 wt%) and Ca²⁺ concentrations (above 100 mM). Generally, increasing both polymer and calcium concentrations formed stronger hydrogels. Moreover, we found that either a lower number of arms (f = 4) or a higher molecular weight (M_w = 40 kDa) hampered the formation of self-standing hydrogels.

Influence of number of arms (f) on gelation

We hypothesized that the ability of star-shaped PEG-alendronate macromers to form a transient network would increase with the number of functional groups per macromolecular precursor. A higher f corresponds to a greater probability of a macromolecule to participate simultaneously in multiple crosslinks. This is clearly manifested by comparing polymers with the same M_a, such as P(8)20-AA and P(4)10-AA), or with the same M_w, such as P(8)10-AA and P(4)10-AA. In both cases, decreasing the number of arms by a factor of 2 hampered the formation of an effective network (see Table 2). Therefore, a threshold f value between 4 and 8 exists below which network formation is inhibited for the conditions tested.

In reversibly crosslinked networks, the equilibrium concentration of intermolecular bonds determines the effective number of crosslinks per macromolecular precursor (f′). If p_inter is the probability of an arm forming an intermolecular bond, the number of effective crosslinks per PEG precursor is given by f′ = p_inter × f/2. In our system, the formation of competing intramolecular bonds with a certain probability p_intra cannot be ruled out. For strong interactions, the equilibrium is pushed towards fully completion and the probability of free arms is neglectable (p_free ≅ 0). However, for weaker interactions p_free ≠ 0 and:

$$p_{\mathit{inter}}+p_{\mathit{intra}}+p_{\mathit{free}}=1$$

We assume that in the semidilute unentangled regime the interception of two different loops to create mechanically interlocked chains is unlikely. Thus, the formation of intramolecular bonds should mainly lead to elastically inactive loops in our experimental conditions (see Fig. 1d). Therefore, only the intermolecular bonds are expected to create actual crosslinks.

As depicted in Table 2, P(8)20-AA and P(4)10-AA have the same molar concentration of AA for all polymer concentrations, as well as similar overlapping concentration (Table 1). This particular case allows for a more direct comparison of the underlying equilibrium, because samples can be prepared with different number of arms but equal polymer, calcium and AA concentrations, alongside the same concentration regime. While intramolecular bonds are strongly favored in the dilute regime, at the vicinity of the overlapping concentration this effect is progressively attenuated by the closer proximity of chains belonging to different molecules. Therefore, an identical overlapping concentration means that the probability of forming an intermolecular bond (p_inter) should be very similar in both cases, and the difference in number of effective crosslinks per PEG molecule (f′)derives primarily from the difference in the number of arms (f). We found that hydrogels cannot be formed from P(4)10-AA, even at around 10 times excess of calcium. The random bond percolation model predicts that gelation does not occur at conditions when p_inter(f − 1) < 1.^17,27 As such, it is possible to estimate an upper limit for the intermolecular bond frequency (p_inter < 0.34) for these two polymers. On the other hand, P(8)20-AA polymer forms hydrogels and therefore p_inter(f − 1) > 1, which allows calculation of a lower limit p_inter > 0.14 for the crosslinking frequency. This result shows that the crosslinking reaction extension is relatively low, both for polymers with the best gelation properties (P(8)20-AA) and for polymers that do not gel at all (P(4)10-AA). Therefore, the stronger multivalency effect provided by a higher number of arms determines the gelation behavior of star-shaped PEG crosslinked through alendronate-Ca²⁺ complexation. Moreover, it also indicates that the existence of free arms and intramolecular bonds cannot be disregarded. This conclusion can be generalized for all other conditions, which were tested for comparable AA and calcium concentration ranges.

Influence of arm length (M_a) on gelation

At a constant number of arms and polymer concentration, a larger arm length results in a decreased molar concentration of polymer ends, resulting into a decreased p_inter. Accordingly, the effective number of crosslinks (f′) is also reduced. By comparing P(8)20-AA and P(8)40-AA at the same polymer concentration (see Table 2), it can be observed that a two-fold increase in arm length, and consequently a two-fold decrease in the molar concentration of AA, is enough to suppress gelation. The susceptibility of gelation to AA concentration is consistent with the low intermolecular bond frequency described in the previous section, even for hydrogel-forming polymer P(8)20-AA. Adding Ca²⁺ to P(8)40-AA solutions still resulted in a noticeable increase in the solution viscosity, revealing that polymer aggregates were formed, but the number of interchain associations was insufficient to create a macroscopic hydrogel.

On the other hand, decreasing the arm length was also detrimental for the gelation capability of the eight-arm PEG polymers. In fact, for P(8)10-AA macromolecules of shortest arm length, the threshold polymer concentration for gelation (20 wt%) was two times higher than for P(8)20-AA (10 wt%). Interestingly, the critical gelation concentration for both polymers (Table 2) was about 1.3 higher than the calculated overlapping concentration (Table 1). Below the overlapping concentration the bond percolation theory cannot describe the network connectivity. Instead, the number of intermolecular bonds (p_inter) required to form a continuous macromolecular network increases with decreasing polymer concentration.²⁸ This means that P(8)10-AA did not form hydrogels at lower polymer concentrations due to a direct effect of the macromolecular configuration rather than an indirect effect related to the crosslinking extent (see Fig. 1c), which in this case was expected to be higher since the concentration of AA is also higher.

The macromer with highest gelation capacity, P(8)20-AA, was tested in more detail using oscillatory rheology in order to obtain insight in the viscoelastic properties and self-healing ability of the formed hydrogels.

Self-healing behavior

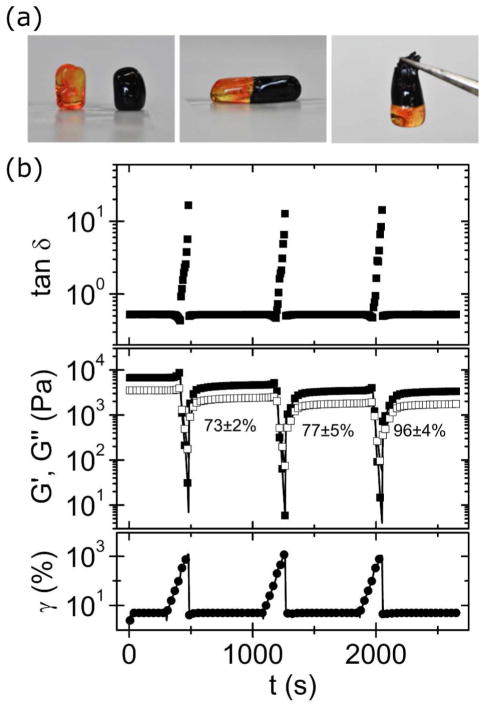
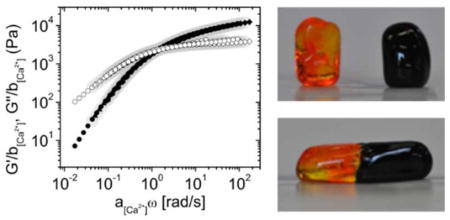
Transparent, homogenous and moldable hydrogels were immediately formed when P(8)20-AA and Ca²⁺ solutions were mixed. The hydrogels formed through the interaction of star-shape PEG-AA with calcium ions possessed self-healing capability. As can be seen in Fig. 2a, cylinders composed of 15 wt% polymer and 100 mM CaCl₂ stained with different dyes were cut in two pieces, and then brought back together. No obvious border was observed after fusing both parts of the gel, and after 2 min of contact their connection was strong enough to allow for stretching without tearing through the previous fracture surface. This phenomenon was repeatable and effective irrespective of the position of the cut or fusion. Moreover, no liquid flow was detected through the interface at the bare eye, as colors did not mix or fade within the experimental timescale (up to six hours). This revealed that the observed macroscopic self-healing was a local interfacial phenomenon. Nonetheless, self-healing also occurred at these materials bulk as shown in Fig. 2b, which depicts the quantification of self-healing behavior of the same gels by oscillatory rheology. In this experiment, a strain from 5 to 1000% was applied to cause gel failure, as manifested by a sudden increase in the damping factor, accompanied by a decrease in both storage and loss modulus. When strain was brought to its initial value, a very fast recovery was observed for each of these three variables. Failure-recovery cycles were repeated several times without a measurable loss of the self-healing capability. In fact, the storage modulus recovery was 73 ± 2, 77 ± 5, and 96 ± 4 % after the first, second and third failure cycle, respectively. This is comparable to other star-shaped PEG self-healing hydrogels reported in the literature.^10,15,29,30 Furthermore, the damping factor returned to its original level almost instantaneously for every cycle. A similar self-healing capability was observed for all P(8)20-AA gelation conditions tested irrespective of the polymer or Ca²⁺ concentrations (see Fig. SI-4).

Figure 2.

Self-healing behavior of the hydrogel formed from 15 w% P8(20)-AA and 100 mM CaCl₂. (a) The gel was formed into a cylinder, cut in two pieces (left), fused together (center) and stretched without fracture (right). The pieces were stained with dyes of different color to improve visualization of the healing process. (b) Failure-recovery tests where gel failure was induced by an increase in strain from 5 to 1000%. The recovery of the storage modulus for each cycle is shown in the picture. Measurements were performed at 20°C and a constant angular frequency of 10 rad/s.

Effect of polymer concentration on viscoelastic properties

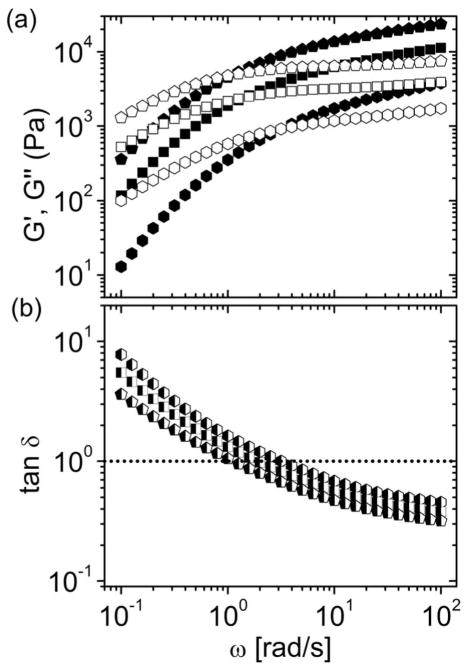
Frequency sweep experiments were performed both on freshly prepared hydrogels (~3 min) and after incubation overnight in a sealed test tube. The rheological properties were not affected by aging (Fig. SI-5), revealing that crosslinking was a fast process reaching equilibrium in less than 3 minutes. Frequency sweep experiments revealed solid-like properties (G′ > G″) at high frequencies and viscous liquid-like behavior (G′ < G″) properties at lower frequencies for all samples (Fig. 3). As expected, an increase in polymer concentration resulted into higher G′ and G″, and simultaneously lower tan δ values at the same frequency. The plateau modulus (G₀ ~ 4 x 10⁴ Pa for 15 wt%) was comparable to other transient networks based on star-shaped PEG hydrogels as reported in the literature.^4,9,11

Figure 3.

Frequency sweeps of P(8)20-AA ionic gels formed at polymer concentrations of 10 (hexagons), 15 (squares) and 20 wt% (pentagons) at a calcium concentration of 100 mM: (a) Storage (G′) and loss (G″) moduli are represented with solid and open symbols, respectively; (b) Damping factor (tan δ). All measurements were performed at 20°C and 5% strain.

In Figure 3 a systematic shift of G′, G″ and tan δ curves can be observed with increasing polymer concentration (C_p). We shifted the dynamic data of Figure 3 both horizontally (a_Cp) and vertically (b_Cp) to build a polymer concentration-invariant master curve, according to the following equations:

$$\begin{gathered} G^{\prime }(\omega )=b_{C_p}·G_{\mathit{ref}}^{\prime }\left(a_{C_p}·\omega \right) \\ {G}^{″}(\omega )=b_{C_p}·G_{\mathit{ref}}^{″}\left(a_{C_p}·\omega \right) \end{gathered}$$

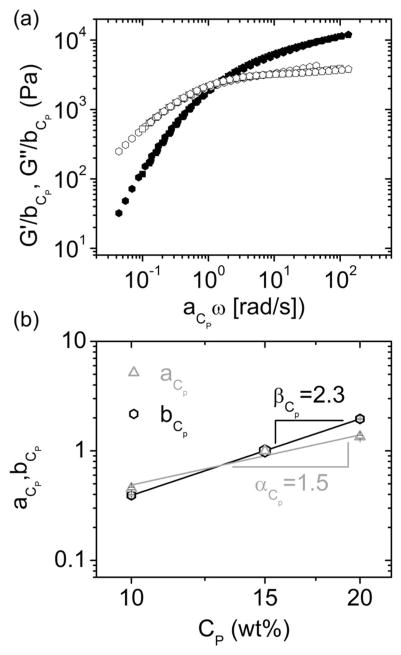
where $G_{\mathit{ref}}^{\prime }$ and $G_{\mathit{ref}}^{″}$ are the storage and loss modulus of the reference data, respectively. We used the method proposed by Honerkamp and Weese³¹ and a reference polymer concentration of 15 wt%. Running a global fitting (R² = 0.998, χ² = 0.714), all data collapsed in a single master curve (Fig. 4a). The shift factors are plotted against polymer concentration in Figure 4b (symbols) and simple scaling laws were found (lines in Fig. 4b). The vertical shift factor accounts for variations in the plateau elastic modulus due to changes in polymer concentration (G₀ ~ b_Cp), whereas the horizontal shift factor reflects the dependence of the characteristic network relaxation time on polymer concentration (τ ~ a_Cp), therefore:

$$\begin{gathered} \tau ~a_{C_p}~{C_p}^{\alpha } \\ {G}_0~b_{C_p}~{C_p}^{\beta } \end{gathered}$$

with α = 1.5 and β = 2.3. The zero-shear viscosity (η₀) dependence on polymer concentration is described by the power law:

$${\eta }_0=\tau ·G_0~{C_p}^{(\alpha +\beta )}={C_p}^{3.8}$$

Figure 4.

Superposition of frequency sweep data for polymer concentrations ranging from 10 to 20 wt% (as shown in Figure 3). (a) Polymer concentration invariant master curves of P(8)20-AA ionic gels formed at a calcium concentration of 100 mM. Storage (G′) and loss (G″) moduli are represented by the same symbols as in Figure 2a. (b) Horizontal (a_Cp) and vertical (b_Cp) shifts were determined from the superposition fitting, and are shown as a function of polymer concentration.

Although there is a growing interest in self-healing hydrogels based on star-shaped polymers crosslinked through reversible interactions at the chains termini,^{5,9–12,15,30,32} a rheological model which describes the stress relaxation behavior of this well-defined architecture is not yet available. The Maxwell model was tentatively used to fit our rheological data, but not used further due to a large deviation from Maxwellian behavior. Poor fitting is also depicted in many literature reports, where a strong mismatch between fitted single Maxwell element models and data is often shown both at high and low frequencies.^32–34

In semidilute solutions in a good solvent, the relationship between G₀ and C_p is described for both reversibly and irreversibly crosslinked networks by:^35,36

$$G_0~C_p^{9/4}$$

At higher frequencies, transient networks behave similarly to permanent ones. Consequently, the plateau elastic modulus has the same polymer concentration dependence for both cases. The plateau modulus of our system follows this expected scaling behavior.

On the other hand, there is not such a general relationship for τ and η₀ scaling behavior. Rubinstein and Semenov developed the so-called sticky Rouse³⁷ and sticky reptation³⁸ models to describe the chain dynamics of reversibly associating linear polymers with “sticky” points distributed along the chain. For unentangled conditions in a good solvent, the sticky Rouse model predicts 3 regimes with distinct concentration dependence of zero-shear viscosity (η₀ ~ C_p^1.1–5.9).^37,38 In turn, the sticky reptation model predicts 4 regimes for entangled conditions in a good solvent (η₀ ~ C_p^3.75–8.5).³⁸ Both models assume strong association between “sticky” points, and provide expressions for a renormalized bond lifetime that account for a change in the relaxation time in conditions where there are almost no free chains in solution. In such conditions, dissociated chains recombine several times before being able to find different chain partners, which effectively increases the relaxation time of the network. There is a remarkable similarity for the viscosity dependence on polymer concentration between our PEG hydrogels and the predictions made by the sticky reptation model for entangled networks mostly composed of intermolecular bonds (η₀ ~ C_p^3.75, G₀ ~ C_p^2.3 and τ ~ C_p^1.45).³⁸ However, our unentangled hydrogels do not fulfill the assumptions of the model and regime, besides the existence of reversible crosslinks, precluding any analogy. For instance, an increased apparent bond lifetime can be ruled out since our system is not strongly associated but coexists with intramolecular bonds and free polymer ends. In these conditions, we expect the network relaxation time to have a weak or non-dependence on bond formation rate (1/τ_off), but to depend mostly on bond lifetime (τ_on). Craig and coworkers found that the characteristic relaxation time of transient networks based on poly(4-vinylpyridine) is primarily governed by bond dissociation rates and not equilibrium constants.^34,39

An alternative model developed by Cates³⁵ describes the dynamics of entangled linear polymers in the presence of reversible chain-scission reactions, predicting η₀ ~ C_p^3.5 and τ ~ C_p^1.25 when breaking of flexible chains is much faster than reptation time (τ_rep ≫ τ_on). Although the model assumption of entangled linear chains is also not valid, the star-shaped molecules can still be seen as chains entangled at the branching point with an extremely high reptation time, such that bond breaking time dominates network stress relaxation. We found similar, but slightly stronger dependencies for η₀ and τ.

Manakker et al³³ also found slightly stronger dependences (η₀ ~ C_p^4.2 and τ ~ C_p^1.6) at similar polymer concentration range for hydrogels based on inclusion complexes between a 8-arm star-shaped PEG with chain ends modified with cholesterol and a telechelic linear PEG modified with β-cyclodextrin. Rossow et al⁹ modified star-shaped PEG with terpyridine to create transient networks based on coordination complexes. Network stress relaxation was tuned adding divalent ions with different affinities (Co²⁺ and Zn²⁺) and varying solvent polarity, which resulted in various types of scaling behavior (η₀ ~ C_p^2.0–3.1 and τ ~ C_p^0.4–1.2). Therefore, although the polymer concentration dependencies found in this and other works³³ display similarity to Cate’s assumptions and predictions,³⁵ it seems that this behavior cannot be extrapolated to different concentration regimes and/or association strengths. The development of theoretical models to predict stress-relaxation of star-shaped transient networks will be highly valuable to the understanding and engineering of this type of soft materials.

Effect of calcium concentration on viscoelastic properties

The effect of calcium concentration on the rheological properties of the transient networks was also studied at constant polymer concentration (15 wt%). The G′ and G″ curves resulting from frequency sweep measurements presented shape similarity for the entire range of tested calcium concentrations. These curves were shifted both horizontal and vertically by means of the procedure described above, but with shift factors as a function of [Ca²⁺].

$$\begin{gathered} G^{\prime }(\omega )=b_{[{\text{Ca}}^{2+}]}·G_{\mathit{ref}}^{\prime }(a_{[{\text{Ca}}^{2+}]}·\omega ) \\ {G}^{″}(\omega )=b_{[{\text{Ca}}^{2+}]}·G_{\mathit{ref}}^{″}(a_{[{\text{Ca}}^{2+}]}·\omega ) \end{gathered}$$

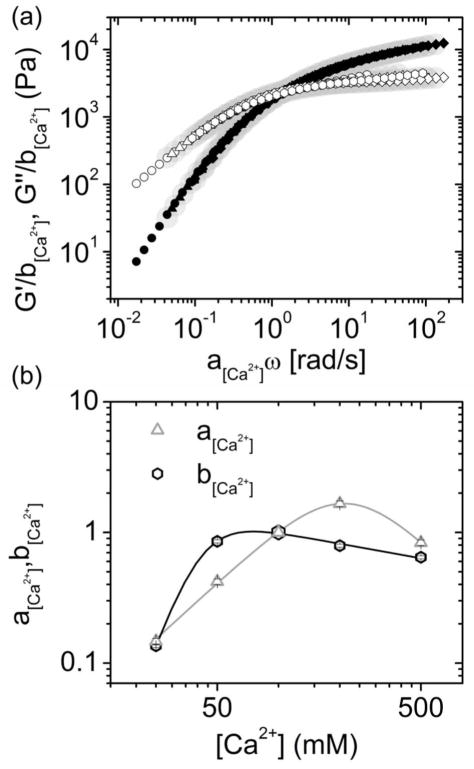
All calcium concentration dependent data fitted into a common master curve as depicted in Figure 5a, where the curve for a calcium concentration of 100 mM was used as reference. The calcium dependent shift factors are plotted in Figure 5b.

Figure 5.

Superposition of frequency sweeps for calcium concentrations ranging from 25 to 500 mM. (a) Calcium concentration invariant master curves of P(8)20-AA ionic gels formed at a polymer concentration of 15 wt%. Polymer concentration invariant master curves from figure 3 and shown as grey large background symbols. (b) Horizontal (a_[Ca²⁺]) and vertical (b_[Ca²⁺]) shift factors were determined from the superposition fitting, and are shown as function of Calcium concentration.

The horizontal shift factor a_[Ca²⁺] accounts for changes in the relaxation time, and thus in network connectivity dynamics. This means that the horizontal shift factor dependence on calcium concentration derives primarily from the way this concentration affects both the dissociation reaction rate (1/τ_on) and the number of bonds (f × p_inter) that should be disrupted to allow the displacement of the star-shaped molecules. Figure 5b shows that the horizontal shift factor increased up to a calcium concentration of 200 mM, indicating that the relaxation spectrum was displaced to longer times (lower frequencies) with increasing calcium concentration. In turn, above 200 mM the relaxation spectrum shifted back to shorter relaxation times (higher frequencies), and consequently a_[Ca²⁺] decreased with increasing calcium concentration. This behavior at high calcium concentration can be explained by the formation of complexes with different stoichiometry and stability. It was reported that bisphosphonates can form chelates of different stoichiometry with calcium.²¹ Moreover, at pH 7.2 alendronate forms salts with different stoichiometry and solubility depending on the ratio between calcium and alendronate. Interestingly the alendronate solubility decreases up to a ratio of 1.5, and increases thereafter.⁴⁰ This indicates that complexes formed at higher calcium concentration are less stable, which agrees with the observed shift of the stress relaxation spectrum to shorter times above a calcium concentration threshold of around 200 mM.

A vertical shift factor b_[Ca²⁺] was also introduced to account for differences in the equilibrium elastic modulus (G₀), which could originate from different concentrations of elastically effective chains. In this case, variations of G₀ do not arise from variations of the polymer concentration since this variable was kept constant for the entire dataset. In figure 5b it can be observed that b_[Ca²⁺] increased sharply up to a calcium concentration of 50 mM, and remained approximately constant at higher concentrations. The vertical shift accounts for variation in the equilibrium elastic modulus, and represents an instantaneous snap-shot of the network, because at higher frequencies bonds do not have time to dissociate and crosslinks behave as permanent associations. Therefore, the vertical shift depends on the equilibrium density of crosslinks, but should be insensitive to the individual rate constants of association and dissociation, provided that the ratio between the two rate constants remain constant. The mismatch between the dependence of both shift factors on the calcium concentration relies on their different physical meanings (see Figure 5b). The stress relaxation depends on the collective disruption of network bonds, which is independent on the instantaneous network connectivity that determines the equilibrium elastic modulus.

In figure 5a, we also presented the polymer concentration invariant master curve (background gray spots) for comparison with the calcium concentration master curve. The superposition between both curves is remarkable, revealing that the relaxation mechanisms in the network all scale similarly with both polymer and calcium concentrations. This is similar to what was recently observed for catechol-modified star-shaped PEGs crosslinked through metal-coordination (Al³⁺, Fe³⁺ and V³⁺).¹² In that study, the coordinating metal ion strongly influenced the viscoelastic relaxation spectra, which were superimposed to form a coordination metal-invariant master curve. Consequently, the differences in viscoelastic behavior were mainly determined by variations in the dynamics of metal-catechol coordination bonds.¹¹ Our results are in line with this previous study, which suggests that stress relaxation in self-healing hydrogels based on star-shaped polymers is determined primarily by variations in bonding dynamics, and that the underlying phenomena can be generalized. The development of specific models to describe this class of materials will be crucial to understand and fully harness their applicability as advanced materials.

CONCLUSIONS

Star-shaped poly(ethylene glycol) macromolecules with different geometric features (in terms of number of arms and arm molecular weight) were successfully end-functionalized with alendronate. The gelation behavior upon addition of calcium ions was highly dependent on this macromolecular architecture. Macromolecules containing four arms of 2.5 kDa each did not form hydrogels, indicating a low degree of chain association. On the other hand, polymers with same arm molecular weight but with twice as many arms formed self-healing hydrogels. However, gelation of eight arm polymers with shorter arms (1.25 kDa) was only observed for higher polymer concentrations (20 wt%), and gelation was completely hindered for higher arm molecular weight (5 kDa). Therefore, gelation occurred only in a small experimental window of number of arms and molecular weight. This peculiar behavior was explained by two opposite effects of increasing the arm molecular weight: first, it decreases the overlapping concentration, increasing likelihood of intermolecular bonds; second, it decreases the actual concentration of reactive chain ends, decreasing the likelihood of intermolecular bonds. For this reason, we have found an optimum intermediate arm molecular weight. When formed, the hydrogels could be cut and fused together within few minutes without any visible interface. Oscillatory rheology showed that the hydrogels recovered around 90% of the original storage and loss modulus after being ruptured by applying an extreme strain. Frequency sweeps revealed a liquid-like behavior at lower frequencies and solid-like behavior at high frequencies. The relaxation spectrum depended on both calcium and polymer concentrations. Storage and loss modulus curves could be shifted both horizontally and vertically to create a common master curve for both calcium and polymer concentrations. This time-concentration superposition revealed a common relaxation mechanism intrinsically connected to the complexation equilibrium, which suggested that stress relaxation in our self-healing hydrogels based on alendronate-functionalized star-shaped PEGs is governed primarily by variations in bonding dynamics. These insights contribute to a better understanding of the self-healing behavior of PEG-based materials and may be a source of inspiration for the design of advanced materials in application areas such as regenerative medicine and bioprinting.