Model selection for univariable fractional polynomials

Abstract

Since Royston and Altman’s 1994 publication (Journal of the Royal Statistical Society, Series C 43: 429–467), fractional polynomials have steadily gained popularity as a tool for flexible parametric modeling of regression relationships. In this article, I present fp_select, a postestimation tool for fp that allows the user to select a parsimonious fractional polynomial model according to a closed test procedure called the fractional polynomial selection procedure or function selection procedure. I also give a brief introduction to fractional polynomial models and provide examples of using fp and fp_select to select such models with real data.

1. Introduction

Since Royston and Altman’s 1994 publication, fractional polynomials (fps) have steadily gained popularity as a tool for flexible parametric modeling of regression relationships in both univariable and multivariable settings. A recent inquiry in Google Scholar (17 January 2017) yielded 1,289 citations of Royston and Altman (1994) to date. For those unfamiliar with fps, I provide a brief introduction below. For a much wider view, please see Royston and Sauerbrei (2008), the multivariable fractional polynomials website at http://mfp.imbi.uni-freiburg.de, and the articles cited therein.

An fp is a special type of polynomial that might include logarithms, noninteger powers, and repeated powers. Every time a power repeats in an fp function of x, it is multiplied by another ln (x). One may write an fp in x as

$$x^{\left(p_1,p_2,\dots ,p_m\right)\prime }\beta$$

where the positive integer m is known as the degree or dimension of the fp. For example, an fp in x with powers (−1, 0, 0.5, 3, 3) and coefficients β has the following form:

$$x^{{\left(-1,0,0.5,3,3\right)}^{\prime }}\beta ={\beta }_1{x}^{-1}+{\beta }_2\text{ln}\left(x\right)+{\beta }_3{x}^{0.5}+{\beta }_4{x}^3+{\beta }_5{x}^3\text{ln}\left(x\right)$$

In the above example, the dimension of the fp is m = 5.

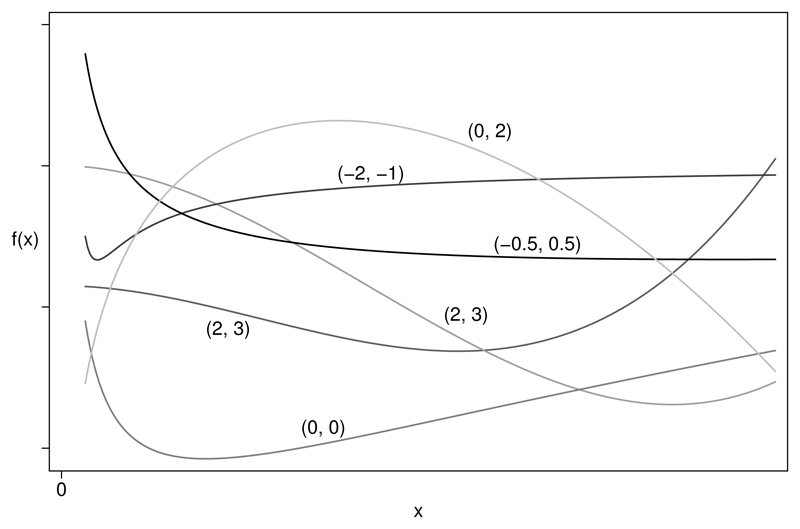
Despite their somewhat dry definition, fps are not just a mathematical abstraction. With a suitable range of powers, they provide a considerable range of functional forms in x that are useful in regression models of real data. The default set of powers from which fp powers are selected is {−2, −1, −0.5, 0, 0.5, 1, 2, 3}, with 0 signifying log (that is, ln). In practice, even fp1 and fp2 functions (fps of dimension 1 and 2) offer much more flexibility than polynomials of the same degree, that is, linear or quadratic functions. See, for example, figure 1, which shows schematically some fp2 functions with various powers (p₁, p₂) and coefficients (β₁, β₂).

Figure 1.

Examples of some functional forms available with fp2 functions with various powers (p₁, p₂)

The aim of flexible regression models for a single continuous covariate x is to provide a succinct and accurate approximation of the relationship between x and a response y without resorting to “categorization” (discretization) of the covariate into groups. Further material on fps, including a discussion of the pitfalls of categorization and the motivation and potential advantages of fps, may be found at http://mfp.imbi.uni-freiburg.de/fp, along with a real example.

Univariable fp regression models have been available in official Stata for two decades following the release of the fracpoly command in Stata 5 (1997). After a ground-up rewrite, the current official implementation of univariable fps as fp appeared in Stata 12 (2011). Using a revised command syntax and fp search algorithm, fp extended the types of regression model in which fps could be fit.

An important concept in flexible regression modeling is “parsimony”: the need to remove “dead wood” from a model, mainly to avoid overfitting and improve the inter-pretability of the selected model. An example of dead wood in univariable fp modeling is the inclusion of high-dimensional fp terms not supported by the data. Such terms would likely produce “wiggly” fit curves that exhibit uninterpretable local features (recognized as an issue also when fitting standard polynomials of high dimension). For an example of the curve instability that can result from overfit spline models (another type of smoother), see Royston and Sauerbrei (2008) figure 3.3.

With fp modeling, one can use the function selection procedure (fsp), which, if possible, simplifies an fp model to one of lesser complexity by appropriate statistical testing. In this article, I outline how the fsp works and introduce a new fp postestimation command, fp_select, that implements the fsp. I illustrate fp_select in an example with real data.

2. The FSP

An important (default) option of fp is compare. The table of fp model comparisons presented with compare contains all the elements needed to select a preferred model according to the fsp, an ordered sequence of hypothesis tests. The fsp has the flavor of a closed test procedure (Marcus, Peritz, and Gabriel 1976) that (approximately) protects the “familywise” type 1 error probability for selecting an fp transformation of x at some nominal value, α, such as 0.05. For further details of the closed test aspect, see the description of the fsp in Ambler and Royston (2001), there called “procedure RA2”. Although fp (and fracpoly) supply the necessary information on which the fsp operates, neither program actually indicates which model the fsp would choose at a given α level.

The fsp starts with an fp model of maximal allowed complexity, defined by its dimension, say, m₀. By default in fp, m₀ = 2, that is, an fp2 (fp of dimension or degree 2). The fsp attempts to simplify the model to an fp1 or linear function of x by applying a specific sequence of tests. The sequence of tests for m₀ = 2 is described under the heading Methods of FP model selection in the Stata manual entry for mfp (see [r] mfp). See also Royston and Sauerbrei (2008, 82–84).

In general terms, the fsp has two parts. The maximum permissible fp degree, m₀, is chosen by the analyst a priori and is usually 2. The first part of the fsp is a test for including an fp-transformed continuous covariate x in the model. Let us call the corresponding significance level α_select. Conventionally, if α_select = 1, no test occurs and x (possibly fp transformed) is included in the model anyway, with the final choice of the functional form being determined by the subsequent steps of the fsp. If α_select < 1, the best-fitting fpm₀ model is tested against the model omitting x on 2m₀ degrees of freedom (d.f.) at significance level α_select. If the test is significant, the algorithm continues as described below; otherwise, x is “omitted” (taken as uninfluential) and the procedure ends.

Let the critical significance level for the tests of functional form in the fsp be α (0 < α < 1). Assuming the inclusion test at level α_select is “passed”, the remaining steps for general m₀ ≥ 1 are as follows:

1. Test fpm₀ against linear (a straight line) in x on 2m₀ − 1 d.f. at level α. If significant, continue; otherwise, stop, with the chosen model for x being a straight line.

2. If m₀ > 1, test fpm₀ against fp1 on 2 (m₀ − 1) d.f. at level α. If significant, continue; otherwise, stop, with the chosen model for x being fp1.

3. If m₀ > 2, test fpm₀ against fp2 on 2 (m₀ − 2) d.f. at level α. If significant, continue; otherwise, stop, with the chosen model for x being fp2.

4. Continue in this manner until the test of fpm₀ against fp(m₀ − 1). If significant, the selected model is fpm₀; otherwise, it is fp(m₀ − 1). This is the end of the procedure.

In some situations, one might have reason to vary the significance levels α_select and α, the two “tuning” constants of the fsp. In an observational study, for example, where possible overfitting of the variables in a confounder model is not necessarily a critical issue, one might choose α_select = 1 and α = 0.2 to select the functional form for a continuous confounder.

3. Example

3.1. Data and preliminary analysis

As an example, I use the IgG data (Isaacs et al. 1983), which may be loaded into Stata by typing webuse igg. The aim is to model y = sqrtigg, the square root of the serum immunoglobulin-G (IgG) concentration in 298 children as a function of x = age, a child’s age in years. I square-root transform the response to stabilize the variance and normalize the residuals.

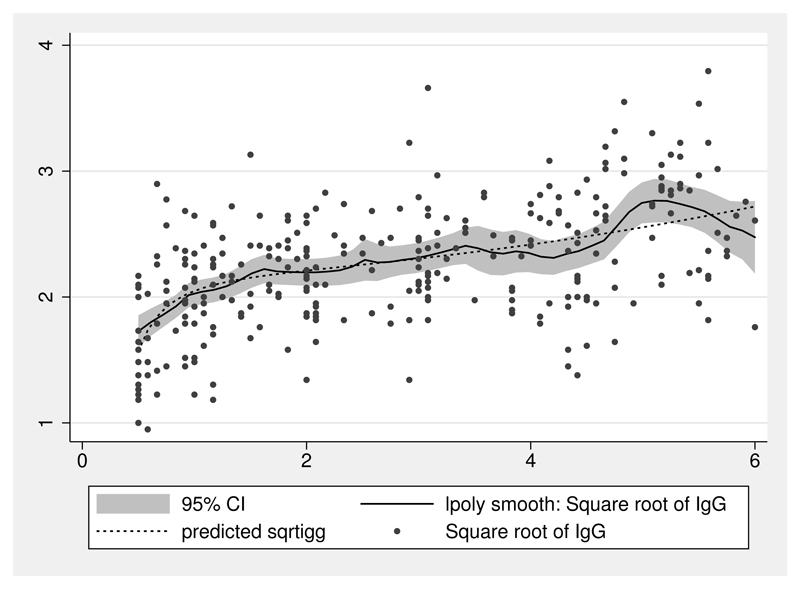
Figure 2 is a smoothed scatterplot of y against x.

Figure 2.

IgG data with local polynomial and fp smoothing

The solid line is a local polynomial fit created by Stata’s lpolyci graph subcommand with a relatively narrow bandwidth of 0.2, hence the rather “wiggly” curve. Nevertheless, a visual indication of nonlinearity is present. The dashed line is the best-fitting fp2 curve as computed by the fpfit subcommand. The commands that created the figure are as follows:

     . webuse igg
     . set scheme sj
     . graph twoway (lpolyci sqrtigg age, bwidth(0.2)) (fpfit sqrtigg age)
     > (scatter sqrtigg age, msymbol(o) msize(*0.75))

A biological argument suggests that because IgG is a blood protein reflecting the maturity of the immune system from birth on, the underlying curve should be monotone increasing. The fit fp2 curve is in fact monotone. It indicates a rapid rise in IgG in the youngest children followed by a gentler rate of increase. By contrast, the “nonparametric” local polynomial fit is nonmonotone, with local features that evidently are present in the data but are unlikely to be real in the population.

3.2. FP model selection

I now consider fp model selection for the IgG dataset. Below is the output from running fp with the default dimension(2) setting.

     . fp <age>: regress sqrtigg <age>
     (fitting 44 models)
     (....10%....20%....30%....40%....50%....60%....70%....80%....90%....100%)
     Fractional polynomial comparisons: 



age
df
Deviance
Res. s.d.
Dev. dif.
P(*)
Powers



omitted
0
427.539
0.497
108.090
0.000



linear
1
337.561
0.428
 18.113
0.000
1


m = 1
2
327.436
0.421
 7.987
0.020
0


m = 2
4
319.448
0.416
 0.000
--
−2 2

(*) P = sig. level of model with m = 2 based on F with 293 denominator dof. 


Source
SS
df
MS
Number of obs
=
298



F(2, 295)
=
64.49


Model
22.2846976
2
11.1423488
Prob > F
=
0.0000


Residual
50.9676492
295
.172771692
R-squared
=
0.3042



Adj R-squared
=
0.2995


Total
73.2523469
297
.246640898
Root MSE
=
.41566



sqrtigg
Coef.
Std. Err.
     t
P > |t|
[95% Conf. Interval]



age_1
−.1562156
  .027416
−5.70
0.000
−.2101713
−.10226


age_2
.0148405
.0027767
 5.34
0.000
 .0093757
.0203052


_cons
2.189242
 .0473835
46.20
0.000
 2.095989
2.282495

As seen for m = 2 in the table titled Fractional polynomial comparisons, the best-fitting fp2 powers of age are (−2, 2). This fp2 transformation of age is represented by the two variables age_1 and age_2 that appear in the table of regression estimates.

Although the results are suggestive, the output is not explicit as to whether an fp2 model is really needed or whether a simpler model (fp1 or linear) would suffice at significance level 0.05. Using fp_select (described in section 4) with α_select = α = 0.05 immediately after fp, we obtain the following result:

     . fp_select, alpha(.05) select(.05)
     selected fp model: powers = (-2 2), df = 4

The output confirms that when m₀ = 2, an fp2 model is selected at the 0.05 significance level. The selected model can be fit as follows using results (best fp powers) stored by fp_select in ‘r(powers)’:

     . fp <age>, fp(‘r(powers)´) replace: regress sqrtigg <age>
     -> regress sqrtigg age_1 age_2 


Source
SS
df
MS
Number of obs
=
298



F(2, 295)
=
64.49


Model
22.2846976
2
11.1423488
Prob > F
=
0.0000


Residual
50.9676492
295
.172771692
R-squared
=
0.3042



Adj R-squared
=
0.2995


Total
73.2523469
297
.246640898
Root MSE
=
.41566





sqrtigg
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]



age_1
-.1562156
.027416
-5.70
0.000
-.2101713
-.10226


age_2
.0148405
.0027767
5.34
0.000
.0093757
.0203052


_cons
2.189242
.0473835
46.20
0.000
2.095989
2.282495

Because in this case the fp2 model was not simplified by fp_select, the result is the same as that reported by fp for the default m₀ = 2 model.

3.3. Impact of complexity on model selection

Let us see what happens if a more complex model with m₀ = 4 is taken as the starting point for model selection:

     . fp <age>, dimension(4) replace: regress sqrtigg <age>
     (fitting 494 models)
     (....10%....20%....30%....40%....50%....60%....70%....80%....90%....100%)
     Fractional polynomial comparisons: 


age
df
Deviance
Res. s.d.
Dev. dif.
P(*)
Powers



omitted
0
427.539
0.497
109.795
0.000


linear
1
337.561
0.428
19.818
0.007
1


m = 1
2
327.436
0.421
9.692
0.149
0


m = 2
4
319.448
0.416
1.705
0.798
-2 2


m = 3
6
319.275
0.416
1.532
0.476
-2 1 1


m = 4
8
317.744
0.416
0.000
--
0 3 3 3

(*) P = sig. level of model with m = 4 based on F with 289 denominator dof. 


Source
SS
df
MS
Number of obs
=
298



F(4, 293)
=
32.63


Model
22.5754541
4
5.64386353
Prob > F
=
0.0000


Residual
50.6768927
293
.172958678
R-squared
=
0.3082



Adj R-squared
=
0.2987


Total
73.2523469
297
.246640898
Root MSE
=
.41588





sqrtigg
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]



age_1
.8761824
.1898721
4.61
0.000
.5024962
1.249869


age_2
-.1922029
.0684934
-2.81
0.005
-.3270044
-.0574015


age_3
.2043794
.074947
2.73
0.007
.0568767
.3518821


age_4
-.0560067
.0212969
-2.63
0.009
-.097921
-.0140924


_cons
2.240866
.1019331
21.98
0.000
2.040252
2.44148

The m₀ = 4 model has powers (0, 3, 3, 3). Next, we apply model selection:

     . fp_select, alpha(0.05) select(0.05)
     selected fp model: powers = (0), df = 2

Instead of fp2, the selected model is now an fp1 with power (0), that is, β₀ +β₁ ln (x).

Table 1 shows p-values from the fsp with increasing maximum complexity. Taking α_select = α = 0.05, it shows model comparisons in the fsp pathways for m₀ = 1, 2, 3, 4.

Table 1.

p-values and selected models arising from fp model comparisons with the IgG data

Comparisons with fpm0 model	Maximum fp complexity, m0
	1	2	3	4
Not in model	0.000	0.000	0.000	0.000
Linear	0.002	0.000	0.003	0.007
m = 1	−	0.020	0.092	0.149
m = 2	−	−	0.919	0.798
m = 3	−	−	−	0.476
Selected model	m = 1	m = 2	m = 1	m = 1

For all four values of m₀, the test of fpm₀ against x “Not in model” is highly significant (p < 0.0005)—see the third row of table 1. This confirms that sqrtigg is associated with age. All tests of fpm₀ against linear (fourth row) are also significant, providing evidence that the relationship is nonlinear.

With maximum complexity m₀ = 2, the test of fp2 against fp1 is significant at the 5% level, resulting in the selection of an fp2 model (as already seen). This is not the case for m₀ = 3 and m₀ = 4, where an fp1 model is chosen instead. However, there is no evidence that more complex models with dimension 3 or 4 fit better than fp2. For example, a test of m = 3 against m = 2 has p = 0.919, and a test of m = 4 against m = 2 has p = 0.798 (see table 1).

The reason why an fp1 function, rather than an fp2 function, is selected when m₀ > 2 is presumably an increase in the type 2 error probability (that is, reduced statistical power) because of redundant parameters being estimated in the models with dimensions greater than 2. See Royston and Sauerbrei (2008, sec. 4.16) for further discussion of the power issue.

4. The fp_select command

4.1. Syntax

The syntax of fp_select is as follows:

fp_select, alpha(#) [select(#)]

You must run fp to fit fp models before using fp_select.

4.2. Description

Taking the results from the most recent run of fp, fp_select tries to simplify the most complex reported fp model by applying an ordered sequence of significance tests. The aim is to reduce possible overfitting. The sequence, known as the FSP, approximates a closed test procedure. See the foregoing sections for further details.

4.3. Options

alpha(#) defines the significance level for testing less complex models against the most complex fp model that was fit, fpm₀. A typical value of # might be 0.05 or 0.01. alpha() is required.

select(#) defines the significance level for testing whether the covariate is influential. Specifically, if m₀ is the dimension (degree) of the most complex fit fp model, the test is of fpm₀ against the “null” model that omits the covariate. If the covariate is not significant at level # < 1, the procedure terminates. Otherwise, testing continues. The default is select(1), meaning the selection test is not performed and the covariate is automatically included.

4.4. Examples

Fit default fp2 model:

   webuse igg
   fp <age>: regress sqrtigg <age>
   fp_select, select(0.05) alpha(0.05)
   display "‘r(powers)´"

Fit a more complex fp model:

 fp <age>, dimension(4) replace: regress sqrtigg <age>
 fp_select, alpha(0.2)
 display "‘r(powers)´"

A multiequation example:

 sysuse auto
 fp <weight>: sureg (price foreign <weight> length) (mpg foreign <weight>) ///
   (displ foreign <weight>)
 fp_select, select(0.05) alpha(0.05)
 display "‘r(powers)´"

5. Comments

fp_select fills a gap in the ability of fp to select a parsimonious model. It removes the need to use mfp (searching on one continuous covariate) to select such a model. Note that fp requires that a model return a log likelihood, whereas mfp can fit some additional models (see help on mfp).

About the author

Patrick Royston is a biostatistician with 40 years of experience and with a strong interest in biostatistical methods and statistical computing and algorithms. He works largely in methodological issues in the design and analysis of clinical trials and observational studies. He is currently focusing on alternative outcome measures in trials with a time-to-event outcome; on problems of model building and validation with survival data, including prognostic factor studies and treatment-covariate interactions; on parametric modeling of survival data; and on novel clinical trial designs.