Reference-based sensitivity analysis via multiple imputation for longitudinal trials with protocol deviation

Abstract

Randomized controlled trials provide essential evidence for the evaluation of new and existing medical treatments. Unfortunately, the statistical analysis is often complicated by the occurrence of protocol deviations, which mean we cannot always measure the intended outcomes for individuals who deviate, resulting in a missing-data problem. In such settings, however one approaches the analysis, an untestable assumption about the distribution of the unobserved data must be made. To understand how far the results depend on these assumptions, the primary analysis should be supplemented by a range of sensitivity analyses, which explore how the conclusions vary over a range of different credible assumptions for the missing data. In this article, we describe a new command, mimix, that can be used to perform reference-based sensitivity analyses for randomized controlled trials with longitudinal quantitative outcome data, using the approach proposed by Carpenter, Roger, and Kenward (2013, Journal of Biopharmaceutical Statistics 23: 1352–1371). Under this approach, we make qualitative assumptions about how individuals’ missing outcomes relate to those observed in relevant groups in the trial, based on plausible clinical scenarios. Statistical analysis then proceeds using the method of multiple imputation.

1. Introduction

Randomized controlled trials that collect longitudinal response data are widely used in medical research because they provide essential evidence for the evaluation of new and existing treatments. Unfortunately, protocol deviations—such as treatment withdrawal, unblinding, or loss to follow-up—are unavoidable during the full course of a trial. Consequently, we often cannot measure what we intended for deviating individuals. Planned outcomes may be unobtainable because of the type of deviation. In addition, depending on the nature of the analysis, even values that were recorded postdeviation may be best regarded as missing. The result is a missing-data problem, complicating the analysis.

Complexity arises because—as in any analysis with missing data—we are forced to make an assumption about the distribution of the unobserved data that crucially cannot be verified from the observed data. Therefore, to understand how far the results depend on these assumptions, the primary analysis should be supplemented by a range of sensitivity analyses, which explore how the conclusions vary over a range of different credible assumptions for the missing data (White et al. 2011).

The importance of sensitivity analysis in this context is highlighted in recent regulatory guidelines from the European Medicines Agency (Committee for Medicinal Products for Human Use 2010) and the U.S. National Research Council (2010), which recommends that “examining sensitivity to the assumptions about the missing data mechanism should be a mandatory component of reporting.” Ideally, inferences will be stable across sensitivity analyses, indicating that the impact of the missing data does not seriously affect the interpretation of results. However, it is even more important to report the results of sensitivity analyses when they are contradictory.

When framing a sensitivity analysis, we need to consider carefully both the quantity we wish to estimate and the population for which we wish to estimate it. Following the National Research Council (2010) report, the term estimand is used to describe both the target of inference and the population in which this is estimated. Thus, with missing observations, we need to specify the statistical distribution of individuals’ postdeviation responses. This is often done by specifying one or more parameters that relate individuals’ predeviation and postdeviation data (for example, see Carpenter and Kenward [2013, chap. 10]). However, with reference-based sensitivity analysis, such statements are made by reference to other groups of individuals in the trial (typically to individuals in different treatment arms), obviating the need for explicit parameter specification (Carpenter, Roger, and Kenward 2013).

Before describing this approach further, we follow Carpenter, Roger, and Kenward (2013) and distinguish between two main classes of estimands. The first considers the estimated treatment effect when we assume that postdeviation individuals continue to follow the trial “rules”—that is, abide by the protocol. This is referred to as a de jure estimand. The second explores robustness of inferences to various assumptions about what might have happened—in other words, various de facto scenarios.

Under both de jure and de facto assumptions, we specify the joint distribution of each individual’s predeviation and postdeviation data by reference to relevant groups of individuals in the study. We can then calculate the distribution of each individual’s postdeviation data given his or her predeviation data and use this to multiply impute m completed datasets, fitting our substantive scientific model to each in turn and combining the results for inference using Rubin’s rules (Rubin 1987; Carpenter and Kenward 2013).

A natural assumption for the de jure estimand is that, in each treatment arm, conditional distributions of later follow-up data given earlier follow-up data are the same, whether or not an individual deviates. This corresponds to Rubin’s (1976) missing at random (mar) assumption that, conditional on observed variables, missing data are equal in distribution to observed data. Under mar, it is assumed that postdeviation individuals continued to abide by the protocol. Hence, we refer to it as “randomized-arm mar” below. Under this assumption, the resulting estimates and inferences may also be obtained by fitting a saturated repeated-measures model with separate covariance matrices for each treatment arm (Carpenter and Kenward 2007, chap. 3).

For de facto estimands, we may wish to explore a range of assumptions, described in more detail below. For example, we may assume that postdeviation individuals behave as if they were on a reference (or control) treatment or that the responses stabilize postdeviation. In this context, a distinct advantage of multiple imputation (mi) is that it provides a convenient pathway for sensitivity analysis, because the imputation model need not be formally consistent with the analysis model. Thus, Carpenter, Roger, and Kenward (2013) extend the usual mar-based mi approach and build on the ideas of Little and Yau (1996) to define a collection of mi methods for the inference under a range of contextually relevant de facto assumptions.

The approach falls into the pattern-mixture modeling framework (Little 1993, 1994), where different distributions are specified for fully and partially observed cases such that the overall outcome distribution is a mixture of the two. Each de facto assumption typically corresponds to a different missing not at random data mechanism (Rubin 1976), where conditional distributions of later follow-up data given earlier follow-up data differ between individuals who do and do not deviate. In this setting, some thought has to be given to the appropriate variance of the mi estimator. We have argued elsewhere (Carpenter et al. 2014) that Rubin’s (1987) rules give an appropriate estimate of the variance, inflating the variance that would have been seen—had postdeviation data followed the assumption and been observed—to allow for the information lost because of the missing data.

The purpose of this article is to describe a new command, mimix, that can be used to implement the reference-based sensitivity analyses described by Carpenter, Roger, and Kenward (2013) for quantitative longitudinal data. This command can therefore be used to perform sensitivity analyses for longitudinal continuous clinical trials under a range of qualitative assumptions about the postdeviation behavior.

In the next section, we give more details about the methodology of Carpenter, Roger, and Kenward (2013) and present their generic algorithm for a continuous outcome. In section 3, we outline the syntax of the mimix command. In section 4, we demonstrate the mimix command by using data from a randomized double-blind controlled trial of budesonide delivered by Turbuhaler for the treatment of adult patients with chronic asthma. We discuss and conclude in section 5.

2. Methodology

In this section, we present the methodology of Carpenter, Roger, and Kenward (2013) underlying the mimix command.

Consider a randomized clinical trial with continuous longitudinal follow-up and two treatment arms, active and reference. Let i = 1, … , n index individuals, and let T_i denote the randomized treatment arm. Let j = 0, … , J index the J scheduled observation times, with j = 0 denoting the baseline; then, the outcome for each individual i at time j we denote by Y_ij. We assume that all individuals are observed at baseline, and following protocol deviation, data are missing. For simplicity, we also assume that there are no interim missing values, that is, no individuals with missing data at some point in the follow-up that are later observed. Define D_i as the last observation time prior to deviation for each individual; D_i therefore can take values 0, … , J. The column vector Y_Oi = (Y_i0, … , Y_iDi)^T denotes an individual’s observed outcomes up to D_i, and if D_i < J, then the column vector Y_Mi = (Y_i(Di+1), … , Y_iJ)^T denotes the missing outcomes at times D_i + 1, … , J.

For imputation, for each deviating individual where D_i < J, we require the distribution of missing outcomes given their observed outcomes, treatment arm, and deviation time, denoted as

$$({\mathbf{\text{Y}}}_{Mi}|{\mathbf{\text{Y}}}_{Oi},D_i,T_i,\eta )$$ (1)

where η are the parameters of this distribution whose values we must first estimate before we can impute missing data from (1). Under mar, (1) does not depend on D_i and is simply (Y_Mi|Y_Oi, T_i, η). However, where missing data are missing not at random, this distribution will depend on D_i, and we define a form for (1) that reflects a specific assumption. Given this, mi is used for inference (Rubin 1987; Schafer 1997). That is, we create m complete datasets by drawing from the appropriate Bayesian posterior distribution of (η|Y_O), and we then draw the missing data from (1) by using the current draw of η.

To obtain η, we must choose a model for the observed data. With quantitative longitudinal response data measured at scheduled times, we assume the data can be modeled using the multivariate normal (mvn) distribution. In particular, we assume an unstructured mvn model, with a separate mean for each timepoint in each arm and a separate unstructured covariance matrix in each arm, to allow for the correlation between repeated measures.

The generic algorithm of Carpenter, Roger, and Kenward (2013) that is implemented by the mimix command can be summarized as follows:

1. Separately for each treatment arm, take all the observed data, assume mar, and fit an mvn distribution with an unstructured mean (that is, a separate mean for each of the baseline and the postrandomization observation times) and a variance– covariance matrix using a Bayesian approach with an improper prior for the mean and an uninformative Jeffreys prior for the covariance matrix.

2. Draw a mean vector and covariance matrix from the posterior distribution for each treatment arm. Specifically, we use the Markov chain Monte Carlo (mcmc) method to draw from the appropriate Bayesian posterior, with a sufficient burn-in, and we update the chain sufficiently in between to ensure that subsequent draws are independent. The sampler is initiated using the expectation maximization (em) algorithm. Refer to Carpenter and Kenward (2013) and Gilks, Richardson, and Spiegelhalter (1996) for a more in-depth discussion of mcmc methods and their applications to missing data, and refer to Schafer (1997) for a description of the applicable em algorithm.

3. Use the draws in step 2 to form the joint distribution for each deviating individual’s observed and missing outcome data as required. This can be done under a range of assumptions to explore the robustness of inference about treatment effects. The five options available in the software are described in detail in section 2.1.

4. Construct the conditional distribution of missing (postdeviation) given observed outcome data (1) for each individual who deviated, using the individual’s joint distribution formed in step 3. Sample the missing postdeviation data from this conditional distribution to create a completed dataset.

5. Repeat steps 2–4 m times, resulting in m imputed datasets.

We use this algorithm to generate m imputed datasets. The substantive model of interest is then fit to each imputed dataset in turn, and the results are summarized for inference using Rubin’s rules. For example, the substantive analysis model is often an analysis of covariance in which the final outcome is regressed on a randomized group and adjusted for baseline. For a single scalar parameter of interest, θ, estimates θ̂_m are obtained with standard error σ̂_m. Results across imputations can then be combined using Rubin’s (1987) rules to estimate the overall treatment effect and its associated standard error under the given assumption.

Because Rubin’s rules condition on the number of imputations, estimates, confidence intervals, and inferences will be sensible with two or more imputations. However, with a small number of imputations, results will be imprecise (Rubin 1987). As discussed by Carpenter and Kenward (2007), 5–10 imputations is sufficient to get a reasonably accurate answer for most applications. For more critical inferences, at least 100 imputations are recommended (Carpenter and Kenward 2013).

2.1. Constructing the joint distributions

The proposed framework revolves around the construction of appropriate joint distributions for the observed and unobserved data for deviating individuals. These joint distributions imply conditional distributions for the missing data given the observed data, which are required for imputation (1). The five options described below were proposed by Carpenter, Roger, and Kenward (2013), and they are available in the software.

Randomized-arm MAR. The joint distribution of an individual’s observed and missing outcome data is mvn with a mean and covariance matrix from the individual’s randomized treatment group. This option is natural for a de jure estimand.

Jump to reference (J2R). The joint distribution of an individual’s observed and missing outcome data is mvn with a mean vector from the individual’s randomized group up to his or her last observation time before deviating. Postdeviation, the individual’s mean response profile follows that observed for a reference (typically the control) group. The covariance matrix matches that from the randomized arm for the predeviation measurements and the reference arm for the conditional components for the postdeviation given the predeviation measurements. For individuals in the reference group with missing data, this means that the joint distribution of those individuals’ observed and missing outcome data is formed as mvn with a mean and covariance matrix from the individual’s randomized treatment for predeviation and postdeviation measurements (as under randomized-arm mar). This option is appropriate when the postdeviation individuals ceased their randomized treatment and started treatment similar to that available in one of the other trial arms (the reference).

Last mean carried forward. The joint distribution of an individual’s observed and missing outcome data is mvn with a mean vector from the individual’s randomized group up to his or her last observed time before deviating. Postdeviation, the individual’s means are set equal to the value of the marginal mean for his or her randomized treatment group at the last predeviation measurement. The covariance matrix remains that from the individual’s randomized treatment group. This is an appropriate option when the effect of treatment is maintained, on average, postdeviation.

Copy increments in reference (CIR). The joint distribution of an individual’s observed and missing outcome data is mvn with a mean vector from the individual’s randomized group up to his or her last observation time before deviating. Postdeviation, the individual’s mean increments follow those from a reference (typically the control) group. The covariance matrix is the same as for j2r. For individuals in the reference group with missing data, this means that the joint distribution of those individuals’ observed and missing outcome data is formed as under randomized-arm mar. This is an appropriate assumption when we wish to assume that, postdeviation, the disease resumes the course observed in the reference arm.

Copy reference (CR). The joint distribution of an individual’s observed and missing outcome data is mvn with a mean and covariance matrix from a reference (typically the control) group, regardless of deviation time. For individuals in the reference group with missing data, this means that the joint distribution of those individuals’ observed and missing outcome data is formed as under randomized-arm mar. This is a natural option for individuals who in fact followed a different (reference) treatment from their randomized allocation.

For the j2r, cir, and cr options, we need to specify a reference group (typically the control arm). In many settings, it is then appropriate to impute missing data for individuals in the reference group under randomized-arm mar, and this is the default in the software.

Full technical details on the construction of the appropriate covariance structure can be found in Carpenter, Roger, and Kenward (2013) and Carpenter and Kenward (2013). There is great flexibility for contextually appropriate sensitivity analysis because different assumptions about the missing data can be made for different groups or specific individuals.

We have not yet discussed interim missing data, which is when individuals have missing data at some point in the follow-up but data are observed later. Interim missing values can also be imputed under any of the assumptions outlined above following the generic algorithm of Carpenter, Roger, and Kenward (2013). In some circumstances, the assumption made for interim missing values may be different from that specified for postdeviation data, and mimix allows for this. Interim missing observations may often be reasonably imputed under randomized-arm mar.

3. The mimix command

3.1. Syntax

The mimix command conducts mi under the distinct treatment arm–based assumptions for missing data outlined in section 2.1. Optionally, two substantive models can also be fit to each imputed dataset and the results summarized using Rubin’s (1987) rules. The two substantive model options in mimix are a) a linear regression of the final timepoint on treatment and baseline or b) a saturated repeated-measures model (that is, including treatment crossed with visit and baseline crossed with visit) with separate covariance matrices for each treatment arm. Other substantive models can be fit to the imputed data in the usual way by using mi estimate.

The syntax of the mimix command is the following:

mimix depvar treatvar, id(varname) time(varname) [clear

      saving(filename[ , replace ]) covariates(varlist) interim(string)

      iref(string) {method(string) | methodvar(varname)} mixed

      {refgroup(string) | refgroupvar(varname)} regress burnbetween(#)

      burnin(#) m(#) seed(#) ]

Data are required in long format with one record per individual per timepoint, where depvar is the numeric outcome variable with missing data in the existing dataset and treatvar identifies the treatment group variable in the existing dataset and may be either a numeric or string variable.

id(varname) specifies the variable identifying individuals in the existing dataset. id() is required and may be either a numeric or a string variable.

time(varname) specifies the variable identifying units of time in the original dataset. time() is required and must be a numeric variable.

clear specifies that the original data in memory be cleared and replaced by the imputed dataset. The imputed dataset must be saved manually if required. One of clear or saving() is required.

saving(filename[ , replace ]) saves the imputed datasets. A new filename is required unless replace is also specified. replace allows the filename to be overwritten with new data. One of clear or saving() is required.

covariates(varlist) specifies any additional baseline covariates to be included in the mi model and analysis if either the regress or the mixed option is specified. Any specified covariates must be fully observed numerical variables. Dummy variables must be generated for any factor covariates.

interim(string) specifies an alternative imputation method for all interim missing values (where the individual has data observed later). string may be mar, j2r, lmcf, cir, or cr (not case sensitive). See section 3.3 for further details on specifying the imputation method.

iref(string) specifies the level of treatvar chosen for the reference for all interim missing values (where the individual has data observed later). iref() is required when using the j2r, cir, or cr imputation method. See section 3.3 for further details on specifying the imputation method.

method(string) defines the imputation method for all individuals. string may be mar, j2r, lmcf, cir, or cr (not case sensitive). method() and methodvar() are mutually exclusive; specifying both will return an error message. See section 3.3 for further details on specifying the imputation method.

methodvar(varname) specifies the variable in the original dataset that contains the individual-specific imputation method(s). This option should be used if different imputation methods are required for different individuals. methodvar() must be a string variable containing one of mar, j2r, lmcf, cir, or cr (not case sensitive) for each individual. methodvar() and method() are mutually exclusive; specifying both will return an error message. See section 3.3 for further details on specifying the imputation method.

mixed uses mi estimate with Stata’s default options to fit a saturated repeated-measures model using restricted maximum likelihood—with a separate mean for each treatment and time, full covariate–time interactions for any included covariates(), and a separate unstructured covariance matrix for each arm—to each of the imputed datasets. mixed combines results using Rubin’s (1987) rules for inference. This option may add substantially to the postimputation computation time if a large number of imputations have been specified.

refgroup(string) specifies the level of treatvar chosen for the reference for all individuals. This option is required when using the j2r, cir, or cr imputation method. refgroup() and refgroupvar() are mutually exclusive; specifying both will return an error message. See section 3.3 for further details on specifying the imputation method.

refgroupvar(varname) specifies the variable in the original dataset that identifies the level of treatvar chosen for the reference for each individual. This option is required when using the j2r, cir, or cr imputation method. refgroupvar() and refgroup() are mutually exclusive; specifying both will return an error message. See section 3.3 for further details on specifying the imputation method.

regress uses mi estimate with Stata’s default options to fit a linear regression of depvar at the final timepoint on treatvar, and any included covariates(), to each of the imputed datasets. It combines results using Rubin’s (1987) rules for inference.

burnbetween(#) specifies the number of iterations between pulls for the posterior in the mcmc. The default is burnbetween(100).

burnin(#) specifies the number of iterations in the mcmc burn-in. The default is burnin(100).

m(#) specifies the number of imputations required. The default is m(5).

seed(#) specifies the seed for the random-number generator. The default is seed(0), meaning that no seed is specified by the user and so the current value of Stata’s random-number seed will be used; this will result in different sets of imputations for multiple program runs. To reproduce a set of imputations, the same random-number seed should be used with the original data sorted in exactly the same order.

3.2. Implementation details

Required data format

Data are required in long format with one record per individual per timepoint. If data are in wide format, consult [d] reshape to convert data into long format.

Baseline covariates

Any additional included baseline covariates are required to be complete. Individuals with missing covariate information will be highlighted for the user by mimix and will be discarded in the imputation process and any requested analysis.

Potential error with sparse data

Stata’s mi impute mvn command (which uses the mcmc method initialized by the em algorithm to impute missing values) is used to complete steps 1 and 2 of the general procedure, as detailed in section 2. If the response variable of interest is measured at an occasion with only a few complete cases, mi impute mvn may terminate with an error message if there is not enough information in the observed data to reliably estimate aspects of the covariance structure in the required mvn model. If this is the case, we advise the user to explore an alternative viable mvn model for the data by using the mi impute mvn command. The response at the occasion with few observed outcomes may need to be excluded from the analysis and mimix rerun.

Data output

The imputed datasets are produced in long format, with one record per individual per timepoint per imputation, and are mi set in flong style, ready to analyze using mi estimate. The imputed datasets are output in memory if clear is specified, and they are saved in filename.dta if saving() is specified.

Analysis options

If the regress or mixed analysis option is specified, Stata’s mi estimate command is used with default options to fit the specified analysis model to each imputed dataset and to combine results using Rubin’s (1987) rules (see [mi] mi estimate). The usual output will be displayed in the Results window. If alternative mi estimate options or other substantive models are required following the completion of mimix, then mi estimate can be used in the usual way for further analysis.

Use of data preserve

Because of extensive manipulation of the data, mimix uses the preserve and restore commands. While mimix can be successfully run on data that are already preserved, we recommend that users cancel any previous data preserve by using restore, not to ensure the clear and saving() options of mimix work as intended.

3.3. Specifying the imputation method

The mimix command must contain either the method() option or the methodvar() option. method() indicates which imputation method should be employed for all individuals, while methodvar() indicates which imputation method should be employed for each individual. method() and methodvar() are mutually exclusive options; specifying both will return an error message.

If the method() option is used to request the same imputation method for all individuals, then values specified in method() must be one of those presented in table 1 (not case sensitive). If the methodvar() option is used to request different imputation methods for different individuals, then a new variable that contains individual-specific imputation methods must be generated and specified in methodvar(). The variable that holds the individual imputation methods must only contain values presented in table 1 (not case sensitive), and the method specification cannot vary within an individual over time.

Table 1.

Specifying the imputation method

Method name	Name to specify in method() or methodvar()
Randomized-arm MAR	mar
Jump to reference	j2r
Last mean carried forward	lmcf
Copy increments in reference	cir or ciir
Copy reference	cr

If the j2r, cir, or cr imputation method is used, then either the refgroup() option must also be used to specify the reference level of the treatvar for all individuals or the refgroupvar() option must also be used to indicate the reference level of the treatvar for each individual. Together, these variables allow for the required assumptions outlined in section 2.1. If one of the imputation methods that includes a reference group is specified for all individuals (or for specific individuals via methodvar()), then missing data for individuals in that reference group (with the reference-imputation specification) are imputed under randomized-arm mar.

The interim() option specifies the imputation method for all interim missing values. If this option is not used, any interim missing values will be imputed following the method specified by the methodvar() or method() option, in the same way as missing postdeviation data.

3.4. Stored results

mimix stores the following in r():

Scalars
r(N)	total sample size
r(Nmiss)	total number of individuals with incomplete data
r(Ncomp)	total number of individuals with complete data
r(M)	number of imputations
r(burnin)	number of MCMC burn-in iterations
r(bbetween)	number of MCMC burn-between iterations
Macros
r(depvar)	name of dependent variable
r(treatvar)	name of treatment group variable
r(covariates)	names of covariates
r(method)	imputation method (with method() only)
r(methodvar)	imputation method variable (with methodvar() only)
r(rgroup)	name of reference group (with refgroup() only)
r(rgroupvar)	name of reference group variable (with refgroupvar() only)
r(rseed)	random-number seed
Matrices
r(Ntreat)	sample size in each treatment group
r(Ntreat_mis)	number of individuals with incomplete data in each treatment group
r(Ntreat_comp)	number of individuals with complete data in each treatment group
r(Ntreat_pat)	number of unique missing-value patterns in each treatment group
r(niter_em)	number of iterations EM takes to converge in each treatment group
r(lpobs_em)	observed log posterior in EM in each treatment group
r(conv_em)	convergence flag for EM in each treatment group

If the regress or mixed analysis option is used, then mi estimate is called within the program run and the associated mi estimate results will also be stored in e() (see [mi] mi estimate). If both regress and mixed are specified, then only the mi estimate results of mixed will be stored in e().

4. Example

Here we demonstrate the mimix command with data from a randomized double-blind clinical trial of budesonide delivered by Turbuhaler for the treatment of adult patients with chronic asthma (Busse et al. 1998). A total of 473 individuals were randomized to a daily dose of either 200, 400, 800, or 1,600µg of budesonide or a placebo. The primary outcome—measured at weeks 0 (baseline), 2, 4, 8, and 12—was forced expiratory volume in one second (fev₁), recorded in liters (L); however, several individuals deviated and did not complete the full 12-week follow-up.

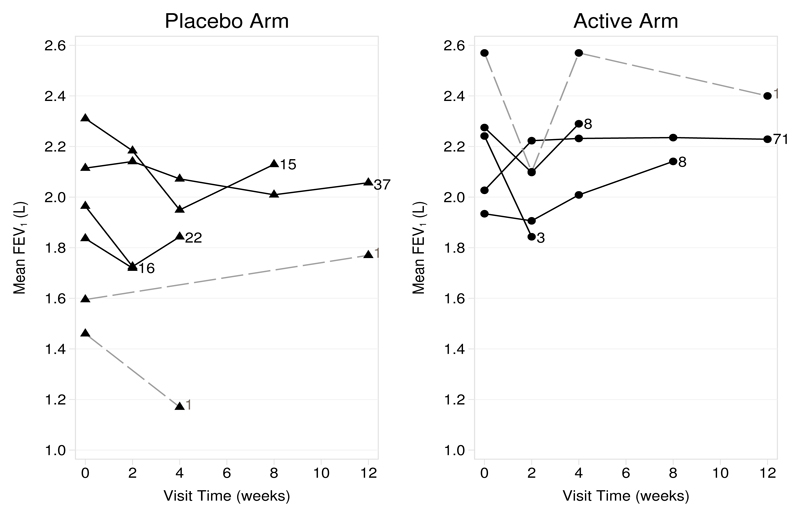
In this article, we focus our attention on only the placebo and the lowest dose active arm (200µg budesonide) for sensitivity analysis. The observed mean profiles by treatment arm and the various missing-data patterns are shown in figure 1. Only 38 of the 92 individuals in the placebo arm (41%) and 72 of the 91 individuals in the active arm (79%) remained in the trial at 12 weeks; 3 individuals (2 placebo and 1 active) had interim missing data.

Figure 1.

Observed mean fev₁ by treatment arm and deviation profile against time. Solid lines join observed means at each timepoint for the various deviation (withdrawal) patterns; dashed lines join observed means of the three individuals with interim missing data. Numbers indicate the counts of individuals with the associated profile.

The primary analysis of the original trial consisted of a linear regression of the 12-week fev₁ outcome on the treatment group, adjusted for baseline fev₁, using data from the 110 individuals measured at week 12. This gives a treatment effect of 0.239 L, p = 0.017. We will use mimix to assess the robustness of the results to various postdeviation assumptions outlined in section 2.1. The interim missing outcomes will be imputed under mar.

In the following output, we describe the variables in the asthma trial dataset and list their contents for one arbitrarily selected deviating individual.

. use asthma
. describe
Contains data from asthma.dta
  obs:           732
 vars:             5                  12 Feb 2015 10:18
 size:        11,712 


variable name
storage
type
display
format
value
label
variable label



id
     int
%8.0g

Patient ID


time
     byte
%9.0g

Measurement time (weeks)


treat
     byte
%8.0g
treat1
Randomised treatment assignment


base
     double
%12.0g

Baseline FEV1 (L)


fev
     float
%9.0g

FEV1 (L)


Sorted by: id
. list in 37/40, noobs sepby(id) 


id
time
treat
base
fev



5030
2
Placebo
1.14
.85


5030
4
Placebo
1.14
1.51


5030
8
Placebo
1.14
.


5030
12
Placebo
1.14
.

id is the unique individual identifier, and treat is the randomized treatment assignment to placebo (treat = 2) or active (treat = 3). fev is the postbaseline fev₁ measurement (L), and time is the time of the fev₁ measurement in weeks. base is the baseline fev₁ measurement. The dataset is already in long format with one observation per individual per timepoint, as required for mimix. We can see that the selected individual deviated sometime between week 4 and week 8; consequently, the individual has missing outcomes for weeks 8 and 12.

4.1. Sensitivity analysis using the mimix command

In this section, we perform a sensitivity analysis using each of the five options listed in section 2.1 for constructing joint distributions. Results of these analyses are summarized in table 2.

Table 2.

Sensitivity analysis results

Analysis	Treatment estimate (L)	Standard error	p-value
De jure
Primary analysis (analysis of covariance)	0.239	0.099	0.017
Randomized-arm mar	0.323	0.104	0.002
De facto
Jump to placebo	0.226	0.103	0.029
Jump to active	0.128	0.095	0.181
Last mean carried forward	0.296	0.096	0.003
Copy increments in placebo	0.281	0.103	0.007
Copy increments in active	0.277	0.082	0.001
Copy placebo	0.289	0.101	0.005
Copy active	0.251	0.082	0.003

We first analyze the data under the randomized-arm mar assumption for all individuals, in other words, the de jure assumption that—postdeviation—individuals continued on their randomized treatment as specified in the protocol. We create 50 imputations and take the default mcmc burn-in of 100 iterations and burn-between of 100 iterations. We include the baseline fev₁ measure in the imputation model as a covariate, but if this fully observed variable were used as an outcome, the results would be stochastically identical. We use the regress option to specify that the substantive analysis is a linear regression of 12-week fev₁ on randomized treatment and baseline fev₁. Imputation with the (randomized-arm) mar option automatically means the interim missing values will be imputed under mar in each treatment group.

. mimix fev treat, id(id) time(time) method(mar) covariates(base) regress m(50)
> clear seed(101)
Performing imputation procedure for group 1 of 2…
Performing imputation procedure for group 2 of 2…
Performing regress procedure …
i.treat	          _Itreat_2-3	      (naturally coded; _Itreat_2 omitted)
Multiple-imputation estimates		        Imputations	  =	    50
Linear regression	                        Number of obs	  =	   183
                                                Average RVI       =	0.4106
                                                Largest FMI       =	0.3495
                                                Complete DF	  =	   180
DF adjustment:	 Small sample	                DF:	min	  =	 91.39
                                                        avg	  =	 99.15
                                                        max	  =	105.79
Model F test:	    Equal FMI	                F(    2, 149.8)   =	 40.69
Within VCE type:          OLS	                Prob > F	  =     0.0000 


fev
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]



_Itreat_3
.3230728
.1042794
3.10
0.002
.1163241
.5298215


base
.7240691
.0861441
8.41
0.000
.5531672
.8949709


_cons
.3959986
.1971734
2.01
0.048
.0043602
.787637


Imputed dataset now loaded in memory
Imputed data created in variable fev using mar

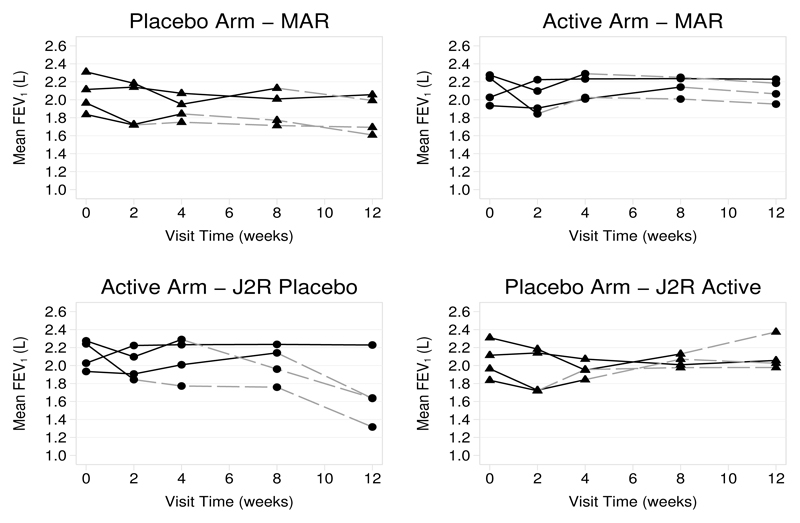
The output displays the results from the requested analysis, along with a description of the variable that now contains imputed data. Under randomized-arm mar, the treatment estimate is increased from the complete records regression reported above, to 0.323 L with a p-value of 0.002. The results of this analysis are shown in the top panel of figure 2.

Figure 2.

Mean fev₁ against time, by treatment arm, for the four different deviation (withdrawal) patterns under randomized-arm mar (top panel) and j2r (bottom panel). Solid lines join observed means before deviation, and dashed lines join the means of the imputed data for that pattern.

Because we used the clear option, the imputed dataset is stored in memory. The imputed data are output using mi set flong. Note that the imputed dataset has not yet been saved. If the saving() option is specified, then the imputed data will be saved when the command is executed.

We now reimpute the asthma trial under the j2r assumption for all individuals, with the placebo arm (treat = 2) first set as the reference. The interim() option is included to impute the interim missing values under randomized-arm mar. Including the interim() option here does not actually affect the results because our substantive model of interest considers the treatment effect at the final timepoint. Imputation of interim values under mar will have an impact when the mixed option is specified to fit a saturated repeated-measures model, using all follow-up outcomes, to estimate a separate baseline-adjusted treatment effect at each follow-up time.

. mimix fev treat, id(id) time(time) method(j2r) refgroup(2) covariates(base)
> interim(mar) regress m(50) clear seed(101)
Performing imputation procedure for group 1 of 2…
Performing imputation procedure for group 2 of 2…
Performing regress procedure …
i.treat	          _Itreat_2-3	      (naturally coded; _Itreat_2 omitted)
Multiple-imputation estimates		        Imputations	  =	   50
Linear regression	                        Number of obs	  =	  183
                                                Average RVI       =    0.4483
                                                Largest FMI       =    0.3510
                                                Complete DF       =       180
DF adjustment:   Small sample                   DF:     min       =     91.07
                                                        avg       =    109.09
                                                        max       =    140.18
Model F test:       Equal FMI                   F(   2,  156.9)   =     32.45
Within VCE type:          OLS                   Prob > F          =    0.0000 


fev
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]



_Itreat_3
.2261827
.1028346
2.20
0.029
.0228754
.42949


base
.6894261
.0933944
7.38
0.000
.5040403
.8748119


_cons
.4669997
.2112431
2.21
0.030
.0473954
.8866041


Imputed dataset now loaded in memory
Imputed data created in variable fev using j2r
Interim missing data imputed using mar

The results of the j2r analysis with placebo as the reference are summarized in table 2 along with the results of a j2r analysis with active as the reference. These address the de facto assumption, when postdeviation individuals not randomized to the reference treatment change to the reference treatment. Both of these analyses result in a reduced treatment estimate relative to the de jure randomized-arm mar assumption. However, while j2r with placebo as the reference still gives a treatment effect that is statistically significant at the 5% level, j2r with active as the reference does not. This is because more individuals deviate in the placebo arm than in the active arm (figure 1), and they tend to be individuals whose lung function is lower. The effect of this versus analysis under randomized-arm mar is shown in figure 2. The change in placebo individuals under j2r-active reduces the treatment estimate by the greatest amount.

Our next analysis is last mean carried forward. Figure 1 shows that the arm-specific means begin to stabilize quite early in the follow-up. It is therefore to be expected that last mean carried forward gives a slightly reduced estimate relative to randomized-arm mar, with a slightly higher p-value (see table 2). If we wish to assume that individuals’ lung function at deviation is broadly maintained postdeviation, then last mean carried forward would be appropriate.

The next two analyses are both cir. In the first, the reference is the placebo, and in the second, the reference is the active arm. Because more individuals deviate in the placebo arm than in the active arm and because the placebo arm profiles tend to decrease while those of the active arm increase, we again see a slightly larger treatment estimate when the reference arm is placebo (see table 2). cir with placebo reference is appropriate if, postdeviation, we wish to assume that active individuals’ lung function starts to decline from its current value at the same rate as seen in the placebo arm. cir with active reference is appropriate if, postdeviation, we wish to assume that postdeviation placebo individuals access an active treatment and their lung function increases from its current value at the rate seen in the active arm.

Finally, we consider cr with placebo reference and with active reference. Under this assumption, an individual’s postdeviation data are imputed as if they had always belonged to the reference arm. cr with placebo reference may be an appropriate de facto assumption for individuals who could not tolerate the active treatment. Under cr, predeviation individual-specific residuals about the mean are typically greater than under j2r. This means that postdeviation profiles typically change less abruptly than with j2r, which is what we observe here (see table 2). For cr with active reference, the treatment estimate is greater than both treatment estimates under j2r but less than the treatment estimates for all the other de facto assumptions.

We therefore conclude that if, postdeviation, medication has a comparable effect with the lowest active dose, then individuals will have comparable lung function at the end of the study. Otherwise, the sensitivity analysis is consistent with the primary analysis of the trial in identifying a significant beneficial effect of treatment relative to placebo.

5. Discussion

In this article, we introduced the mimix command to implement the reference-based sensitivity analysis approach described by Carpenter, Roger, and Kenward (2013). This approach sets out to provide contextually relevant sensitivity analysis of a longitudinal clinical trial with continuous outcome data subject to individual deviation. As we described, the approach constructs each individual’s joint predeviation and postdeviation data distribution by reference to treatment groups and then imputes the individual’s missing postdeviation data accordingly. The mimix program automates the steps of constructing the required joint distributions and the corresponding imputation distributions under a range of assumptions. Further, if desired, the program will automatically fit one of two substantive models to the resulting imputed data and combine the results by using Rubin’s (1987) rules. The available substantive models are either a linear regression of the final timepoint on baseline or treatment or a saturated repeated-measures model, as detailed above.

This method is appealing for sensitivity analysis because it does not require the formal specification of any sensitivity parameters, which is notoriously difficult (White et al. 2007). Rather than requiring quantitative assumptions, it asks for qualitative assumptions in respect to certain study arms. The associated quantitative assumptions are then estimated from the data and used to produce imputations. Different qualitative assumptions can be made for different individuals (or similar groups of individuals), and the mimix command allows this flexibility through the methodvar() option, providing contextually plausible sensitivity analyses.

Interim missing data, which in practice are likely to be inevitable to some extent, are also accommodated by mimix. These may be imputed under randomized-arm mar (often the most appropriate assumption) or one of the alternative reference-based assumptions.

The approach can be used for individuals who deviate immediately, that is, for those who have no outcome data, as long as these individuals are included in the original dataset. The relevant postdeviation distribution is constructed as outlined in section 2 for such individuals, and all outcome data are imputed from it.

Recall that we are modeling data from a clinical trial where patient outcome data are collected according to a prespecified common schedule. The imputation model is mvn, with a separate unstructured covariance matrix for each trial arm and a separate mean for each timepoint. This is the most general, and by far the most appropriate, model for such data (Molenberghs and Kenward 2007, chap. 5.6). If individual patients’ data are collected irregularly, the unstructured covariance matrix is no longer as natural of an option, and other options may be considered. While it is possible that this may encounter convergence difficulties with a very large number of timepoints and limited number of patients, in our experience this is not common. In such situations, one may need to consider alternative, more structured, forms of covariance matrix, but this is beyond our current scope. If the data are skewed, one can consider transformation to approximate normality, and then impute and transform back. Schafer (1997, chap. 6.4), however, reports simulations showing that imputation drawn under the mvn model are robust to moderate skewness.

If we have several baseline covariates on which we wish to condition the imputations, then a current restriction is that these must be fully observed. Moreover, at the imputation step they are formally treated as continuous in the mvn imputation. Fully binary variables can simply be included as they are (however they are coded). However, fully observed c-level categorical variables must be included as (c − 1) dummy indicator variables.

Following the general algorithm of Carpenter, Roger, and Kenward (2013), separate models for the predeviation data are required in each treatment arm. Any covariates potentially including the baseline response are consequently fit separately in each arm prior to the construction stage, where the treatment arm parameters may be mixed for subsequent imputation. If the covariates are markedly imbalanced across treatment arms, this may result in inappropriate data distributions. However, in the randomized controlled trial setting, the expected distribution of the covariates in the two arms will be the same. Randomization should therefore ensure any covariates are well matched and clinically similar in the two arms.

Throughout this article, we focused on the two-arm randomized clinical trial setting; however, this is not a constraint. mimix can be used to conduct reference arm–based imputation for trials with more than two arms.

To summarize, the mimix command provides a computationally accessible tool for reference-based sensitivity analysis. The assumptions available in the program correspond to both de jure and de facto estimands, allowing sensitivity analysis that explores the effect of contrasting assumptions concerning the individual’s postdeviation outcomes. We hope that this implementation will remove a barrier to trialists performing sensitivity analysis in practice.

Biographies

About the authors

Suzie Cro is a PhD student at the London School of Hygiene and Tropical Medicine. Her thesis topic is relevant accessible sensitivity analysis for clinical trials with missing data. She is funded by the mrc Clinical Trials Unit at University College London, where she also works part-time as a medical statistician.

Tim P. Morris is a medical statistician with eight years of experience. He is interested in statistical methods for improving the design and analysis of randomized trials and meta-analysis. His PhD was on practical methods for mi. He is a Stata enthusiast.

Michael G. Kenward has been GlaxoSmithKline professor of biostatistics at the London School of Hygiene and Tropical Medicine since 1999 and has been a consultant in biostatistics for over 25 years. His research interests include longitudinal data analysis and the problem of missing data.

James R. Carpenter holds a joint appointment at the London School of Hygiene and Tropical Medicine and the mrc Clinical Trials Unit at University College London. He has a longstanding interest in longitudinal data, MI, and trials, and he is comaintainer of http://www.missingdata.org.uk.