Outcome-Dependent Sampling with Interval-Censored Failure Time Data

Summary

Epidemiologic studies and disease prevention trials often seek to relate an exposure variable to a failure time that suffers from interval-censoring. When the failure rate is low and the time intervals are wide, a large cohort is often required so as to yield reliable precision on the exposure-failure-time relationship. However, large cohort studies with simple random sampling could be prohibitive for investigators with a limited budget, especially when the exposure variables are expensive to obtain. Alternative cost-effective sampling designs and inference procedures are therefore desirable. We propose an outcome-dependent sampling (ODS) design with interval-censored failure time data, where we enrich the observed sample by selectively including certain more informative failure subjects. We develop a novel sieve semiparametric maximum empirical likelihood approach for fitting the proportional hazards model to data from the proposed interval-censoring ODS design. This approach employs the empirical likelihood and sieve methods to deal with the infinite-dimensional nuisance parameters, which greatly reduces the dimensionality of the estimation problem and eases the computation difficulty. The consistency and asymptotic normality of the resulting regression parameter estimator are established. The results from our extensive simulation study show that the proposed design and method works well for practical situations and is more efficient than the alternative designs and competing approaches. An example from the Atherosclerosis Risk in Communities (ARIC) study is provided for illustration.

1. Introduction

In many epidemiologic studies and disease prevention trials, the outcome of interest is a failure time that suffers from interval-censoring, i.e., the failure time cannot be exactly observed but only an interval that it belongs to is known or observed (e.g. Sun, 2006; Chen et al., 2012). One example of interval-censored failure time data arises from HIV preventive vaccine trials where investigators are interested in assessing the association between antibody responses to a vaccine and the incidence of HIV infection (e.g. Gilbert et al., 2005). In this case, since the study subjects are tested for HIV infection only at discrete clinic visits instead of being continuously monitored, the time to HIV infection is known only to fall between two consecutive visits rather than being exactly observed and thus only interval-censored data on the infection time are available. When the failure rate is low and the observation time intervals are wide, such as in the HIV vaccine trials mentioned above, a large cohort is often required so as to yield reliable precision on the exposure-failure-time relationship. Compounding to this issue, measurements of the exposure variable of interest are often expensive or difficult to obtain, such as the antibody levels measured by complex assays in the HIV vaccine trials above. As a consequence, large cohort studies with simple random sampling could be prohibitively expensive to conduct for investigators with a limited budget. Alternative cost-effective sampling designs and inference procedures with interval-censored failure time data are therefore desirable, and this motivates the research in this paper.

Outcome-dependent sampling (ODS) is a cost-effective sampling scheme that enhances the efficiency and reduces the cost of a study by allowing the probability of acquiring the exposure measurement to depend on the observed value of the outcome. The case-control study with a binary outcome is a simple and well-known example of ODS design and it has been extensively studied and used over the past decades (e.g. Cornfield, 1951; Whittemore, 1997). In recent years, the more general ODS design with a continuous outcome has been an important research area (e.g. Zhou et al., 2002; Chatterjee et al., 2003; Weaver and Zhou, 2005). The fundamental idea of such a design is to oversample observations from the segments of the population, usually the two tails of the response variable’s distribution, that are believed to be more informative regarding the exposure-response relationship. Recent references on ODS design with a continous outcome include Zhou et al. (2007), Song et al. (2009) and Zhou et al. (2011), among others. The case-cohort design is a well-known biased-sampling scheme for censored failure time data. Under this design, measurements of the exposure are obtained for a random sample of the study cohort, called subcohort, and for all subjects who experience the failure regardless of whether or not they are in the subcohort (e.g. Prentice, 1986; Self and Prentice, 1988; Chen and Lo, 1999; Lu and Tsiatis, 2006; Kong and Cai, 2009; Zeng and Lin, 2014). When the failure is non-rare, the generalized case-cohort design has been proposed where besides a subcohort, the exposure measurements are assembled only on a subset of the failure subjects instead of all failure subjects (e.g. Cai and Zeng, 2007; Kang and Cai, 2009). Reaping the benefits of both ODS and case-cohort designs, Ding et al. (2014) and Yu et al. (2015) considered a general failure-time dependent sampling design where a simple random sample of the cohort is enriched by selectively including certain more informative failure subjects. An overview of failure-time dependent sampling designs can be found in Ding et al. (2017).

We note that the existing cost-effective sampling designs for failure time data were primarily developed for traditional censored data where the failure time is either exactly observed or right-censored. We found only a few papers that discussed biased-sampling designs for interval-censored failure time data. Gilbert et al. (2005) considered a biased-sampling design for a phase 3 HIV-1 preventive vaccine trial where the outcome of interest is the time to HIV infection that suffers from interval-censoring. In particular, they defined the infection time as the midpoint of the dates between the last negative and first positive tests and then employed the case-cohort design for traditional censored data. Li et al. (2008) considered the same HIV vaccine trial as in Gilbert et al. (2005) and they simplified the structure of interval-censored data by assuming that the test dates are fixed and the same for all study subjects and then extended the case-cohort design to fit in the resulting data. Li and Nan (2011) studied the case-cohort design with current status data, a special case of interval-censored data, which arise when each study subject is examined only once for the occurrence of the failure and thus the failure time is either left- or right-censored at the only examination. Recently, Zhou et al. (2017) developed the case-cohort design and an inference procedure for failure time data subject to general interval-censoring. The case-cohort design samples all the failure subjects and applies mainly to rare events. In this paper, we propose an outcome-dependent sampling (ODS) design with general interval-censored failure time data, that applies primarily to non-rare or not-so-rare events where it may not be feasible to sample all the failure subjects. Under the proposed interval-censoring ODS design, we enrich a simple random sample by selectively including certain more informative failure subjects. Specifically, we supplement a simple random sample of the study cohort with certain subjects who are known to experience the failure (i.e. the observed interval containing the failure time has a finite right endpoint) and who are believed to be more informative in terms of the exposure-failure-time relationship (i.e. the observed interval belongs to the two tails of the failure time’s distribution). The idea of oversampling from the tails stems from the intuition that if the outcome Y is positively associated with the exposure X, then high (low) Y would be associated with high (low) X; enriching the observed sample with subjects who have high or low Y could potentially enhance the efficiency in evaluating the association between Y and X. This intuition can easily be justified in simple linear regression.

We develop a semiparametric likelihood-based procedure for fitting the proportional hazards model to data from the proposed interval-censoring ODS design. Due to the complicated data structure and the fact that the failure time is never exactly observed, the analysis of interval-censored data is in general much more challenging than that of right-censored data both theoretically and computationally. For example, for regression analysis of interval-censored data, one usually needs to deal with or estimate the finite-dimensional regression parameter and the infinite-dimensional nuisance parameter simultaneously as no tools like the partial likelihood commonly used for right-censored data is available anymore. In particular, regression analysis of interval-censored data, obtained by simple random sampling, under the proportional hazards model remains a popular research topic over the past three decades. Among others, Finkelstein (1986) considered the parametric maximum likelihood estimation with a discrete baseline hazard assumption; Huang (1996) and Zeng et al. (2016) studied the fully semiparametric maximum likelihood estimation for current status data and mixed-case interval-censored data, respectively; Satten (1996) proposed a marginal likelihood approach which avoids estimating the baseline hazard but is still computationally intensive; Pan (2000) suggested a multiple imputation approach which is semiparametric but did not provide theoretical justification; Lin et al. (2015) and Wang et al. (2016) developed efficient algorithms for computing the maximum likelihood estimates via two-stage Poisson data augmentations from Bayesian and Frequentist perspectives, respectively; Zhang et al. (2010) and Zhou et al. (2016) proposed sieve semiparametric maximum likelihood methods and proved the asympotic normality and efficiency of the regression parameter estimators. As discussed by Zhang et al. (2010) and Zhou et al. (2016), the sieve method enjoys both theoretical and computational advantages compared to the alternative methods. Under the proposed interval-censoring ODS design, the likelihood function with the observed data involves two sets of infinite-dimensional nuisance parameters, i.e. the cumulative baseline hazard function and the distributions of examination times and covariates. Following Zhou et al. (2016), we employ a Bernstein-polynomial-based sieve method to deal with the cumulative baseline hazard function. For handling the distributions of examination times and covariates, we adopt the empirical likelihood method considered by Vardi (1985) and Qin (1993) for biasedsampling problems. Both the sieve and empirical likelihood methods yield great dimension reduction on the estimation problem and thus significantly ease the computational difficulty.

The remainder of this paper is organized as follows. In Section 2, we introduce the proposed interval-censoring ODS design and describe the likelihood function. In Section 3, we develop a sieve semiparametric maximum empirical likelihood estimation appr oach, where we employ the empirical likelihood and sieve methods to deal with the infinite-dimensional nuisance parameters. We also establish the asymptotic properties of the resulting estimator. In Section 4, we evaluate the performance of the proposed design and estimator through an extensive simulation study. In Section 5, an illustrative example from the ARIC study is provided. Final remarks are given in Section 6.

2. Interval-Censoring ODS design and Likelihood Function

Let T denote the failure time of interest and Z a p-dimensional covariate vector that may affect T. Suppose that the failure time is subject to interval-censoring and the observation can be represented by

$$Y=\{U,V,{\mathrm{\Delta }}_1=I(T\le U),{\mathrm{\Delta }}_2=I(U<T\le V)\},$$

where U and V are two random examination times, and (Δ₁, Δ₂, 1 − Δ₁ − Δ₂) indicate left-, interval- and right-censored observations, respectively.

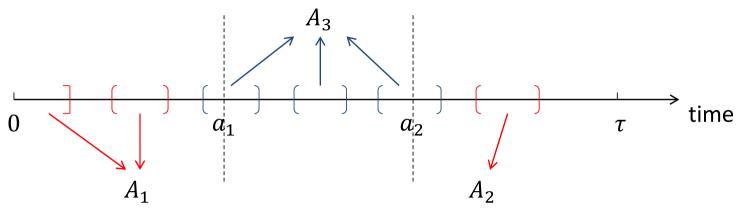
Now we describe our ODS design with interval-censored failure time data. Let τ denote the length of study and a₁ and a₂ two known constants satisfying 0 < a₁ < a₂ < τ. The fundamental idea of ODS design is to oversample observations that are believed to be more informative regarding the exposure-response relationship. Following this idea, we oversample subjects who experience the failure (i.e. Δ₁ +Δ₂ = 1) and who have the failure time falling within either the tail (0, a₁) or (a₂, τ). Specifically, we partition the failures A = {Y : Δ₁ + Δ₂ = 1} into three mutually exclusive and exhaustive strata: A_k, k = 1, 2, 3, defined as

$$\begin{gathered} A_1=\{Y:\{{\mathrm{\Delta }}_1=1,U<a_1\}\text{or}\{{\mathrm{\Delta }}_2=1,V<a_1\}\}, \\ {A}_2=\{Y:{\mathrm{\Delta }}_2=1,U>a_2\}, \\ {A}_3=A\cap {(A_1\cup A_2)}^c, \end{gathered}$$ (1)

where ∩ and ∪ denote the intersection and union of sets, respectively, and B^c the complement of a set B. Figure 1 provides an illustration of the partitions A_k, k = 1, 2, 3. One can see that subjects with Y ∈ A₁ have the failure time falling in the lower tail (0, a₁) while subjects with Y ∈ A₂ have the failure time belong to the upper tail (a₂, τ). Our ODS sample consists of a simple random sample (SRS) of size n₀ and two supplemental samples of sizes n₁ and n₂ from A₁ and A₂, respectively. Let n = n₀ + n₁ + n₂ denote the size of the ODS sample, and I_v, I₀ and I_k the index set of the ODS sample, the SRS sample, and the supplemental sample from A_k, respectively. Then the data structure can be represented by

Figure 1.

An illustration of the partitions {A_k, k = 1, 2, 3} of failures under the interval-censoring ODS design

$$\begin{gathered} \text{The}\text{SRS}\text{sample:}(Y_i,Z_i),i\in I_0; \\ \text{The}\text{supplemental}\text{samples:}\{\begin{array}{l}(Y_i,Z_i\mid Y_i\in A_1),i\in I_1,\text{from}\text{the}\text{lower}\text{tail};\hfill \\ (Y_i,Z_i\mid Y_i\in A_2),i\in I_2,\text{from}\text{the}\text{upper}\text{tail.}\hfill \end{array} \end{gathered}$$ (2)

where Y_i = {U_i, V_i, Δ_1i = I(T_i ≤ U_i), Δ_2i = I(U_i < T_i ≤ V_i)} for i ∈ I_v = I₀ ∪ I₁ ∪ I₂. We remark that the proposed design and method will work for the following two scenarios: (i) a two-phase design where the first-phase data on Y are observed for a well-documented parent cohort and the second-phase data on Z are collected for those sampled into I₀, I₁ and I₂ from the cohort; (ii) a design where the information on the parent cohort is unknown, e.g., the subjects in each of I₀, I₁ and I₂ are recruited from a clinic and the recruitment will stop after a target number of subjects is met. In Scenario (ii), the sampling proportions are unknown and one would not have any information on the underlying population other than those in I₀, I₁ and I₂. We assume that independent Bernoulli sampling is used, and the SRS sample is selected first and then the supplemental samples are chosen.

Suppose that the failure time T follows the proportional hazards model with the conditional cumulative hazard function on Z given by

$$\mathrm{\Lambda }(t\mid Z)=\mathrm{\Lambda }(t)exp({\beta }^{\prime }Z),$$ (3)

where Λ(t) is the unspecified cumulative baseline hazard function and β is the p-dimensional regression parameter of primary interest. We assume that T is conditionally independent of the examination times (U, V) given Z and the joint distribution of (U, V, Z) does not involve the parameters (β, Λ). The likelihood function can then be written as

$$\begin{gathered} L(\beta ,\mathrm{\Lambda },Q)=\left\{\prod _{i\in I_0}f(Y_i,Z_i)\right\}·\left\{\prod _{k=1}^2\prod _{i\in I_k}f(Y_i,Z_i\mid Y_i\in A_k)\right\} \\ =\prod _{i\in I_0}\left\{{(1-S(U_i\mid Z))}^{{\mathrm{\Delta }}_{1i}}{(S(U_i\mid Z_i)-S(V_i\mid Z_i))}^{{\mathrm{\Delta }}_{2i}}S{(V_i\mid Z_i)}^{1-{\mathrm{\Delta }}_{1i}-{\mathrm{\Delta }}_{2i}}q(U_i,V_i,Z_i)\right\} \\ ·\prod _{i\in I_1}\left\{\frac{{(1-S(U_i\mid Z_i))}^{{\mathrm{\Delta }}_{1i}}{(S(U_i\mid Z_i)-S(V_i\mid Z_i))}^{{\mathrm{\Delta }}_{2i}}q(U_i,V_i,Z_i)}{P(Y_i\in A_1)}\right\} \\ ·\prod _{i\in I_2}\left\{\frac{(S(U_i\mid Z_i)-S(V_i\mid Z_i))q(U_i,V_i,Z_i)}{P(Y_i\in A_2)}\right\}, \end{gathered}$$ (4)

where S(t|z) = exp{−Λ(t)e^β′z} is the survival function of T given Z = z, Q(·) and q(·) denote the joint distribution function and density function of (U, V, Z), respectively, which do not depend on (β, Λ), and P(Y ∈ A_k) represents the probability that an interval-censored observation Y = {U, V, Δ₁, Δ₂} belongs to A_k, k = 1, 2, given by

$$\begin{gathered} P(Y\in A_1)=P({\mathrm{\Delta }}_1=1,U<a_1)+P({\mathrm{\Delta }}_2=1,V<a_1) \\ =\int \left\{I(u<a_1)(1-S(u\mid z))+I(v<a_1)(S(u\mid z)-S(v\mid z))\right\}dQ(u,v,z), \\ P(Y\in A_2)=P({\mathrm{\Delta }}_2=1,U>a_2)=\int \left\{I(u>a_2)(S(u\mid z)-S(v\mid z))\right\}dQ(u,v,z). \end{gathered}$$

The nonparametric components (Λ, Q) cannot be separated from the above likelihood function. Thus, to estimate the regression parameter β, one has to deal with the infinite-dimensional nuisance parameters (Λ, Q). To handle this challenging task, we develop a sieve semiparametric maximum empirical likelihood approach without specifying (Λ, Q).

3. Sieve Semiparametric Maximum Empirical Likelihood Approach

First note that based on the observed data from the interval-censoring ODS design

$$O_i=\left\{Y_i=\{U_i,V_i,{\mathrm{\Delta }}_{1i}=I(T_i\le U_i),{\mathrm{\Delta }}_{2i}=I(U_i<T_i\le V_i)\},Z_i\right\},i\in I_v,$$

the log-likelihood function can be written as

$$l(\beta ,\mathrm{\Lambda },Q)=logL(\beta ,\mathrm{\Lambda },Q)=\sum _{i\in I_v}{l}_1(O_i;\beta ,\mathrm{\Lambda })+\sum _{i\in I_v}logq(U_i,V_i,Z_i)-\sum _{k=1}^2{n}_{k}log{\pi }_k,$$ (5)

where L(β, Λ, Q) is given by (4),

$$l_1(O_i;\beta ,\mathrm{\Lambda })={\mathrm{\Delta }}_{1i}log(1-S(U_i\mid Z_i))+{\mathrm{\Delta }}_{2i}log(S(U_i\mid Z_i)-S(V_i\mid Z_i))+(1-{\mathrm{\Delta }}_{1i}-{\mathrm{\Delta }}_{2i})logS(V_i\mid Z_i),$$

and π_k = ∫ G_k(u, v, z; β, Λ)dQ(u, v, z) with G_k, k = 1, 2, defined as

$$\begin{gathered} G_1(u,v,z;\beta ,\mathrm{\Lambda })=I(u<a_1)(1-S(u\mid z))+I(v<a_1)(S(u\mid z)-S(v\mid z)), \\ {G}_2(u,v,z;\beta ,\mathrm{\Lambda })=I(u>a_2)(S(u\mid z)-S(v\mid z)). \end{gathered}$$

In the above, S(t|z) = exp{−Λ(t)e^β′z} is the survival function of T given Z = z.

Maximizing l(β, Λ, Q) with respect to β without specifying (Λ, Q) is not straightforward as one has to handle the infinite-dimensional nuisance parameters (Λ, Q). For this, we propose a novel two-step procedure by first employing the empirical likelihood method to deal with Q and then using the sieve method to address Λ. This approach greatly reduces the dimensionality of the estimation problem and relieves the computational burden. In the following, we describe the proposed two-step procedure in details and also establish the asymptotic properties of the resulting estimator.

3.1 Empirical Likelihood Method

We first employ the empirical likelihood method to profile out Q for fixed (β, Λ) in the log-likelihood function (5) (e.g. Vardi, 1985; Qin, 1993; Zhou et al., 2002; Ding et al., 2014). To find a distribution function Q that maximizes l(β, Λ, Q), it is easy to see that we can restrict our search to the class of discrete distribution functions which have positive jumps only at the observed data points {(U_i, V_i, Z_i) i ∈ I_v}. Let p_i = q(U_i, V_i, Z_i) = dQ(U_i, V_i, Z_i), i ∈ I_v. Then for fixed (β, Λ), the log-likelihood function (5) can be written as

$$l(\beta ,\mathrm{\Lambda },\{p_i\})=\sum _{i\in I_v}{l}_1(O_i;\beta ,\mathrm{\Lambda })+\sum _{i\in I_v}log{p}_i-\sum _{k=1}^2{n}_{k}log\left\{\sum _{i\in I_v}{G}_k(U_i,V_i,Z_i;\beta ,\mathrm{\Lambda })p_i\right\}.$$ (6)

We want to search for {p̂_i} that maximize (6) under the constraints {Σ_{i∈I_v} p_i = 1, p_i ≥ 0, i ∈ I_v}. To solve this constrained optimization problem, we use the Lagrange multiplier method by considering the following Lagrange function

$$H(\beta ,\mathrm{\Lambda },\{p_i\},\rho )=\sum _{i\in I_v}{l}_1(O_i;\beta ,\mathrm{\Lambda })+\sum _{i\in I_v}log{p}_i-\sum _{k=1}^2{n}_{k}log\left\{\sum _{i\in I_v}{G}_k(U_i,V_i,Z_i;\beta ,\mathrm{\Lambda })p_i\right\}+\rho \left\{1-\sum _{i\in I_v}{p}_i\right\},$$

where ρ is the Lagrange multiplier. Taking the derivative of H with respect to p_i, we obtain

$$\frac{\partial H}{\partial p_i}=\frac{1}{p_i}-\sum _{k=1}^2{n}_k\frac{G_k(U_i,V_i,Z_i;\beta ,\mathrm{\Lambda })}{{\sum }_{i\in I_v}{G}_k(U_i,V_i,Z_i;\beta ,\mathrm{\Lambda })p_i}-\rho =0.$$

Solving this equation, we have

$$\widehat{\rho }=n_0\text{and}{\widehat{\rho }}_i={\left[n_0\left\{1+\sum _{k=1}^2\frac{n_k}{n_0{\pi }_k}{G}_k(U_i,V_i,Z_i;\beta ,\mathrm{\Lambda })\right\}\right]}^{-1},i\in I_v.$$

Plugging {p̂_i} back into l(β, Λ, {p_i}) in (6), we have the resulting profile likelihood function

$$l(\theta )=\sum _{i\in I_v}{l}_1(O_i;\beta ,\mathrm{\Lambda })-\sum _{i\in I_v}log\left[n_0\left\{1+\sum _{k=1}^2\frac{n_k}{n_0{\pi }_k}{G}_k(U_i,V_i,Z_i;\beta ,\mathrm{\Lambda })\right\}\right]-\sum _{k=1}^2{n}_{k}log{\pi }_k,$$ (7)

where θ = (ξ, Λ) and ξ = (β′, π₁, π₂)′. After applying the empirical likelihood method, we have greatly reduced the dimensionality associated with Q and only need to deal with (7).

3.2 Sieve Method

We now consider the estimation of unknown parameters θ = (ξ, Λ) based on the profile likelihood function l(θ) in (7). Let θ = {θ = (ξ, Λ) ∈ ℬ ⊗ ℳ} denote the parameter space of θ. Here ℬ = {ξ = (β′, π₁, π₂)′ ∈ R^p+2 : ||β|| ≤ M, π_k ∈ [c, d], k = 1, 2} with p being the dimension of β, M a positive constant and c < d two constants in (0, 1), and ℳ is the collection of all continuous nondecreasing and nonnegative functions over the interval [σ, τ], where σ and τ are known constants usually taken as the lower and upper bounds of all examination times in practice.

Maximizing the profile likelihood function (7) with respect to ξ is still not straightforward as one still has to deal with the infinite-dimensional nuisance parameter Λ. Note that only the values of Λ at the examination times {U_i, V_i : i = 1, …, n} matter in (7), one may follow the conventional approach by taking the nonparametric maximum likelihood estimator of Λ as a right-continuous nondecreasing step function with jumps only at the examination times and then maximizing (7) with respect to ξ and the jump sizes (Huang, 1996). However, it is apparent that such fully semiparametric estimation method could involve a large number of parameters if there are no ties among {U_i, V_i : i = 1, …, n}. To ease the computation difficulty, by following Zhang et al. (2010) and Zhou et al. (2016), we propose to employ the sieve estimation method. Specifically, we define the sieve space as

$${\mathrm{\Theta }}_n=\left\{{\theta }_n=(\xi ,{\mathrm{\Lambda }}_n)\in \mathcal{B}\otimes {\mathcal{M}}_n\right\},$$

where ℬ is defined above and

$${\mathcal{M}}_n=\left\{{\mathrm{\Lambda }}_n(t)=\sum _{k=0}^m{\varphi }_k{B}_k(t,m,\sigma ,\tau ):0\le {\varphi }_0\le {\varphi }_1\le \dots \le {\varphi }_m\text{and}\sum _{k=0}^m\mid {\varphi }_k\mid \le M_n\right\}$$

with B_k(t, m, σ, τ) being Bernstein basis polynomials of degree m = o(n^ν) for some ν ∈ (0, 1),

$$B_k(t,m,\sigma ,\tau )=\left(\begin{array}{c}m\\ k\end{array}\right){\left(\frac{t-\sigma }{\tau -\sigma }\right)}^k{\left(1-\frac{t-\sigma }{\tau -\sigma }\right)}^{m-k},k=0,\dots ,m,$$

and M_n = O(n^a) for some a > 0 controlling the size of the sieve space. The constraints on the Bernstein coefficients ϕ_k’s in ℳ_n are imposed to guarantee that the estimate of the cumulative baseline hazard function Λ(t) is nonnegative and nondecreasing. In fact, one can show that any Λ(t) can be approximated by a Bernstein polynomial Λ_n(t) with the coefficients ϕ_k = Λ(σ + (k/m)(τ − σ)) arbitrarily well as n → ∞, i.e., the sieve space Θ_n approximates the parameter space Θ arbitrarily well as n → ∞ (Lorentz, 1986; Shen, 1997; Wang and Ghosh, 2012). We define the sieve semiparametric maximum empirical likelihood estimator ${\widehat{\theta }}_n=({\widehat{\xi }}_n,{\widehat{\mathrm{\Lambda }}}_n)=({\widehat{\beta }}_n,{\widehat{\pi }}_{1n},{\widehat{\pi }}_{2n},{\sum }_{k=0}^m{\widehat{\varphi }}_{kn}{B}_k(·,m,\sigma ,\tau ))$ of θ to be the value of θ that maximizes the sieve log-likelihood function l_n(θ) over Θ_n, where

$$l_n(\theta )=\sum _{i=1}^n[{\mathrm{\Delta }}_{1i}log(1-S_n(U_i\mid Z_i))+{\mathrm{\Delta }}_{2i}log(S_n(U_i\mid Z_i)-S_n(V_i\mid Z_i))+(1-{\mathrm{\Delta }}_{1i}-{\mathrm{\Delta }}_{2i})log{S}_n(V_i\mid Z_i)-log\left\{n_0\left(1+\sum _{k=1}^2\frac{n_k}{n_0{\pi }_k}{G}_k(U_i,V_i,Z_i;\beta ,{\mathrm{\Lambda }}_n)\right)\right\}-\sum _{k=1}^2\frac{n_k}{n}log{\pi }_k].$$ (8)

In the above, S_n(t|z) = exp{−Λ_n(t)e^β′z} is the survival function of T given Z = z and

$$\begin{gathered} G_1(u,v,z;\beta ,{\mathrm{\Lambda }}_n)=I(u<a_1)(1-S_n(u\mid z))+I(v<a_1)(S_n(u\mid z)-S_n(v\mid z)), \\ {G}_2(u,v,z;\beta ,{\mathrm{\Lambda }}_n)=I(u>a_2)(S_n(u\mid z)-S_n(v\mid z)). \end{gathered}$$

Compared to the fully semiparametric estimation method, the sieve method significantly reduces the dimensionality of the optimization problem and relieves the computation burden as the number of Bernstein bases needed to reasonably approximate the unknown function Λ grows much slower as the sample size increases. Bernstein polynomial basis has several advantages compared to other bases such as piecewise linear function and spline. First, it can model the monotonicity and nonnegativity of the cumulative baseline hazard function with simple restrictions that can easily be removed through reparameterization. Second, Bernstein polynomial is easier to work with as it does not require the specification of interior knots.

3.3 Asymptotic Properties

The asymptotic properties of the proposed estimator θ̂_n will be established in Theorems 1 and 2. Denote G(u, v) the joint distribution function of the two random examination times (U, V) and define a distance on the parameter space Θ = ℬ ⊗ ℳ as

$$d({\theta }^1,{\theta }^2)={\left\{{\Vert {\xi }^1-{\xi }^2\Vert }^2+{\Vert {\mathrm{\Lambda }}^1-{\mathrm{\Lambda }}^2\Vert }_2^2\right\}}^{1/2},$$

for any θ¹ = (ξ¹, Λ¹) ∈ Θ and θ² = (ξ², Λ²) ∈ Θ, where ||v|| denote the Euclidean norm for a vector v and ${\Vert {\mathrm{\Lambda }}^1-{\mathrm{\Lambda }}^2\Vert }_2^2=\int \{{({\mathrm{\Lambda }}^1(u)-{\mathrm{\Lambda }}^2(u))}^2+{({\mathrm{\Lambda }}^1(v)-{\mathrm{\Lambda }}^2(v))}^2\}dG(u,v)$. Let θ₀ = (ξ₀, Λ₀) = (β₀, π₁₀, π₂₀, Λ₀) denote the true value of θ and assume that n₀/n → ρ₀ > 0 and n_k/n → ρ_k ≥ 0, k = 1, 2, as n → ∞. The following theorems give the consistency and asymptotic normality of the proposed estimator θ̂_n when n → ∞. The regularity conditions needed for these theorems are given in the Web Appendix.

Theorem 1

Assume that Conditions (C1) – (C4) given in the Web Appendix hold. Then we have that d(θ̂_n, θ₀) → 0 almost surely and d(θ̂_n, θ₀) = O_p(n^{−min{(1−ν)/2, νr/2}}), where ν ∈ (0, 1) such that m = o(n^ν) and r is defined in Condition (C3).

Theorem 2

Assume that Conditions (C1) – (C4) given in the Web Appendix hold. If ν > 1/2r, we have $\sqrt{n}({\widehat{\xi }}_n-{\xi }_0){\to }_{d}N(0,\mathrm{\sum })$, where Σ = Γ⁻¹ΨΓ⁻¹ with $\mathrm{\Gamma }={\sum }_{k=0}^2{\rho }_k{J}_k({\xi }_0)$ and $\mathrm{\Psi }={\sum }_{k=0}^2{\rho }_k{\mathit{var}}_k(h_k({\xi }_0,{\mathrm{\Lambda }}_0;O))$.

The proofs of Theorems 1 and 2 will be sketched in the Web Appendix. J_k(ξ) and h_k(ξ, Λ; O) in Theorem 2 are the information and efficient score of ξ corresponding to the k-th stratum, k = 0, 1,2 (k = 0 corresponds to the whole population), and they will be further discussed in the Web Appendix. Following Huang et al. (2012), we can obtain a consistent variance estimator of ξ̂_n by treating the log-likelihood function l_n(θ) in (8) as if it is a function of the (p + m + 3)-dimensional parameter θ = (ξ_(p+2)×1, ϕ_(m+1)×1) and then replacing the large-sample quantities in Σ given above with the corresponding small-sample quantities.

We now make a few remarks on the implementation of the proposed estimation procedure. First, it should be noted that there are some restrictions on the parameters due to boundedness and monotonicity. On the other hand, they can easily be removed through reparameterization. For example, we could reparameterize the parameters π_k as $1/(1+exp(-{\pi }_k^{\ast }))$, k = 1, 2, and {ϕ₀, …, ϕ_m} as the cumulative sums of { $exp({\varphi }_0^{\ast }),\dots ,exp({\varphi }_m^{\ast })$}. This reparameterization is a simple one-to-one transformation and does not complicate the computation. Regarding the restriction ${\sum }_{k=0}^m\mid {\varphi }_k\mid \le M_n$, since M_n = O(n^a) is imposed mainly for technical purposes and can be chosen reasonably large for fixed sample size in practice, we do not need to consider this restriction in computation. Thus, to obtain the proposed estimator θ̂_n, many existing unconstrained optimization methods can be used and for the numerical studies in Sections 4 and 5, we employ the Nelder-Mead simplex algorithm built in fminsearch in Matlab. Also for the implementation of the proposed estimation procedure, one needs to determine the degree of Bernstein polynomials m which controls the smoothness of the sieve approximation. For this, we suggest to consider several different values of m and choose the one that minimizes

$$\mathit{AIC}=-2l_n({\widehat{\theta }}_n)+2(p+m+3).$$ (9)

4. A Simulation Study

We carry out an extensive simulation study to evaluate the finite-sample performance of the proposed interval-censoring ODS design and estimator, including the comparison of our ODS design with the SRS and generalized case-cohort designs and the comparison of our estimator with other naive or adapted estimators. Specifically, we generated the covariate Z ~ N(0, 1) and the failure time T from the proportional hazards model given Z:

$$\mathrm{\Lambda }(t\mid Z)=\mathrm{\Lambda }(t)exp({\beta }^{\prime }Z)$$

with the cumulative baseline hazard Λ(t) = 0.1t and regression parameter β = 0 or log2.

To generate the interval-censored observation Y = {U, V, Δ₁ = I(T ≤ U), Δ₂ = I(U < T ≤ V)}, we mimicked medical or epidemiologic follow-up studies. Suppose that a subject was scheduled to be examined at a sequence of time points in [0, τ] generated as cumulative sums of uniform random variables on [0, δ] until τ, where τ is the length of study and 0 < δ < τ. At each of these time points, it was assumed that the subject could miss the scheduled examination with probability ζ, independent of the examination results at other time points. If T was smaller than the first examination time (i.e. left-censored), we defined U as the first examination time, V the second examination time and (Δ₁, Δ₂) = (1, 0); if T was larger than the last examination time (i.e. right-censored), we defined U as the second to the last examination time, V the last examination time and (Δ₁, Δ₂) = (0, 0); otherwise, U and V were defined as the two consecutive examination times bracketing T and (Δ₁, Δ₂) = (0, 1). In the simulation study, we adjusted the values of τ, δ and ζ according to the desired proportion of failures (0.1, 0.2 or 0.3). Here the proportion of failures, denoted by Pr(failure), refers to the proportion of subjects who experience the failure.

The ODS sample consists of a SRS sample of size n₀ and two supplemental samples of sizes n₁ and n₂ from the lower tail A₁ and upper tail A₂, respectively. For the cutpoints (a₁, a₂) that define A₁ and A₂, we considered the (10, 90)- or (20, 80)-th percentiles. In Table 1, five estimators of β were compared under (n₀, n₁, n₂) = (470, 40, 40): (i) the sieve maximum likelihood estimator based only on the SRS portion of the ODS sample, denoted by β̂_{SRS_n0}; (ii) the sieve maximum likelihood estimator based on a SRS sample of the same size as the ODS sample, denoted by β̂_{SRS_n}; (iii) the sieve weighted estimator based on the generalized case-cohort sample that consists of a subcohort of size n₀ and a SRS of size n₁ +n₂ selected from the remaining cases (i.e. failure subjects), denoted by β̂_GCC; (iv) the inverse probability weighted estimator (Breslow and Wellner, 2007) based on the ODS sample, denoted by β̂_IPW; (v) the proposed estimator, denoted by β̂_P. The degree of Bernstein polynomial used in the sieve estimation was taken as m = 3. The simulation results include “Bias” calculated as the average of point estimates minus the true value, “SSD” the sample standard deviation, “ESE” the average of estimated standard errors, “CP” the empirical coverage proportion of 95% confidence interval and “RE” the sample relative efficiency with respect to β̂_{SRS_n} calculated as [SSD(β̂_{SRS_n})/SSD(β̂)]². The results were based on 1000 replicates.

Table 1.

Simulation results for the estimation of β when (n₀, n₁, n₂) = (470, 40, 40)

Pr(failure)	cutpoints		β = 0					β = log2
			Bias	SSD	ESE	CP	RE	Bias	SSD	ESE	CP	RE
0.1	(20%, 80%)	β̂SRS<sub>n0</sub>	−0.000	0.150	0.145	0.94	0.84	0.000	0.163	0.149	0.93	0.89
		β̂SRS<sub>n</sub>	−0.003	0.137	0.134	0.95	1.00	−0.004	0.154	0.138	0.93	1.00
		β̂GCC	−0.001	0.111	0.111	0.95	1.53	−0.002	0.132	0.131	0.95	1.36
		β̂IPW	0.000	0.127	0.121	0.94	1.18	−0.005	0.152	0.139	0.93	1.03
		β̂P	0.004	0.100	0.098	0.94	1.89	−0.008	0.106	0.106	0.94	2.11
	(10%, 90%)	β̂SRS<sub>n0</sub>	−0.001	0.148	0.145	0.95	0.86	0.001	0.160	0.149	0.94	0.97
		β̂SRS<sub>n</sub>	0.004	0.138	0.133	0.94	1.00	−0.002	0.158	0.137	0.93	1.00
		β̂GCC	−0.001	0.115	0.112	0.95	1.42	−0.003	0.137	0.132	0.94	1.32
		β̂IPW	−0.003	0.136	0.130	0.94	1.02	0.002	0.148	0.148	0.94	1.13
		β̂P	0.001	0.105	0.100	0.94	1.71	−0.004	0.103	0.105	0.93	2.32
0.2	(20%, 80%)	β̂SRS<sub>n0</sub>	−0.000	0.106	0.103	0.94	0.81	0.006	0.110	0.107	0.94	0.81
		β̂SRS<sub>n</sub>	−0.002	0.096	0.095	0.95	1.00	0.002	0.099	0.099	0.95	1.00
		β̂GCC	−0.008	0.108	0.107	0.95	0.79	0.010	0.113	0.113	0.94	0.77
		β̂IPW	0.001	0.095	0.092	0.94	1.00	0.004	0.098	0.097	0.94	1.01
		β̂P	0.001	0.084	0.083	0.95	1.28	−0.010	0.086	0.086	0.94	1.33
	(10%, 90%)	β̂SRS<sub>n0</sub>	0.002	0.103	0.103	0.95	0.92	0.003	0.106	0.107	0.95	0.92
		β̂SRS<sub>n</sub>	0.003	0.098	0.095	0.94	1.00	0.002	0.102	0.099	0.95	1.00
		β̂GCC	0.000	0.111	0.106	0.94	0.79	0.008	0.114	0.113	0.94	0.79
		β̂IPW	0.001	0.098	0.097	0.94	1.00	0.004	0.100	0.101	0.95	1.04
		β̂P	0.003	0.084	0.084	0.94	1.37	−0.004	0.083	0.086	0.95	1.50
0.3	(20%, 80%)	β̂SRS<sub>n0</sub>	0.001	0.087	0.084	0.95	0.85	0.007	0.095	0.091	0.93	0.87
		β̂SRS<sub>n</sub>	0.001	0.080	0.078	0.94	1.00	0.001	0.088	0.084	0.95	1.00
		β̂GCC	−0.003	0.099	0.101	0.94	0.65	0.005	0.112	0.109	0.94	0.62
		β̂IPW	0.001	0.081	0.078	0.94	0.97	0.008	0.086	0.084	0.94	1.06
		β̂P	0.002	0.076	0.072	0.93	1.10	−0.016	0.082	0.076	0.93	1.15
	(10%, 90%)	β̂SRS<sub>n0</sub>	−0.003	0.087	0.084	0.94	0.78	0.002	0.089	0.091	0.96	0.95
		β̂SRS<sub>n</sub>	0.003	0.077	0.078	0.96	1.00	0.004	0.086	0.083	0.94	1.00
		β̂GCC	−0.004	0.100	0.101	0.96	0.59	0.006	0.105	0.108	0.95	0.67
		β̂IPW	−0.004	0.082	0.081	0.95	0.89	0.004	0.085	0.087	0.95	1.03
		β̂P	−0.004	0.077	0.076	0.94	1.00	−0.008	0.077	0.078	0.95	1.24

β̂_{SRS_n0}, the sieve MLE based only on the SRS portion of the ODS sample; β̂_{SRS_n}, the sieve MLE based on a SRS sample of the same size as the ODS sample; β̂_GCC, the estimator based on the generalized case-cohort sample; β̂_IPW, the inverse probability weighted estimator based on the ODS sample; β̂_P, the proposed estimator based on the ODS sample.

From Table 1, one can see that for all situations considered: (i) the proposed estimator under the interval-censoring ODS design is virtually unbiased; (ii) the standard error estimates are close to the empirical standard deviations; (iii) the empirical coverage proportions are close to 95%, which indicates that the normal approximation to the distribution of the proposed estimator is reasonable; (iv) the proposed ODS design (β̂_P) is more efficient than the alternative SRS designs (β̂_{SRS_n0} and β̂_{SRS_n}); for example, when the failure rate is 0.1, the cutpoints are (10, 90)-th percentiles and β = log 2, it achieves 132% efficiency gain compared to β̂_{SRS_n}; (v) the proposed estimator is more efficient than the estimator based on the generalized case-cohort sample; for example, when the failure rate is 0.1, the cutpoints are (10, 90)-th percentiles and β = log 2, the relative efficiency of β̂_P compared to β̂_GCC is (0.137/0.103)² = 1.77; (vi) the proposed estimator β̂_P is more efficient than the inverse probability weighted estimator β̂_IPW that is routinely used to accommodate sampling bias; for example, when the failure rate is 0.1, the cutpoints are (10, 90)-th percentiles and β = log 2, the relative efficiency of β̂_P compared to β̂_IPW is (0.148/0.103)² = 2.06. In practice, sampling without replacement is often used to select random samples. Therefore, we conducted some additional simulations to examine the performance of our proposed estimator in the situation when sampling without replacement is used. We considered the same setup and parameter values as those for Table 1 and the results are presented in Web Table 1. The results show that the proposed estimator under the sampling without replacement situation performs similarly to that under independent Bernoulli sampling.

To evaluate the performances of the proposed ODS design and estimator under different sizes of n₀, n₁ and n₂, we conducted additional simulations with (n₀, n₁, n₂) = (530, 10, 10), (500, 25, 25) and (1000, 50, 50) and presented the results in Table 2. The simulation setups in Table 2 are the same as those in Table 1 except for the sizes of n₀, n₁ and n₂. Also the cutpoints, (10, 90)-th percentiles, are used in Table 2. One can see from Table 2 that (i) for a fixed overall ODS sample size n = n₀ + n₁ + n₂, as we allocate more samples to the tails, the efficiency of the proposed estimator β̂_P improves; for example, when the failure rate is 0.1, the cutpoints are (10, 90)-th percentiles and β = log 2, as we change (n₀, n₁, n₂) from (530, 10, 10) to (500, 25, 25) or to (470, 40, 40), the efficiency improves by (0.124/0.116)² = 1.14 or (0.124/0.107)² = 1.34; (ii) as we increase the overall ODS sample size, the efficiency of β̂_P improves as expected; for example, when the failure rate is 0.1, the cutpoints are (10, 90)-th percentiles and β = log 2, as we increase (n₀, n₁, n₂) from (500, 25, 25) to (1000, 50, 50), the efficiency improves by (0.116/0.081)² = 2.05.

Table 2.

Simulation results for the estimation of β using the proposed method under different sample sizes

(n0, n1, n2)	Pr(failure)	β = 0				β = log2
		Bias	SSD	ESE	CP	Bias	SSD	ESE	CP
(530, 10, 10)	0.1	−0.002	0.124	0.121	0.94	−0.001	0.124	0.124	0.95
	0.2	0.000	0.087	0.090	0.95	−0.012	0.092	0.096	0.94
	0.3	−0.007	0.076	0.075	0.94	−0.008	0.082	0.084	0.94
(500, 25, 25)	0.1	−0.003	0.104	0.104	0.95	−0.006	0.116	0.113	0.95
	0.2	0.001	0.085	0.086	0.95	−0.002	0.089	0.091	0.94
	0.3	−0.005	0.076	0.075	0.94	−0.010	0.084	0.078	0.93
(470, 40, 40)	0.1	0.003	0.097	0.098	0.95	−0.001	0.107	0.102	0.94
	0.2	0.005	0.085	0.084	0.95	−0.006	0.088	0.088	0.95
	0.3	−0.005	0.078	0.075	0.93	−0.004	0.079	0.078	0.95
(1000, 50, 50)	0.1	0.001	0.072	0.072	0.96	−0.006	0.081	0.078	0.94
	0.2	−0.001	0.063	0.061	0.94	−0.005	0.066	0.063	0.94
	0.3	0.001	0.054	0.053	0.94	−0.009	0.059	0.058	0.92

5. Analysis for Diabetes from the ARIC Study

In this section, we illustrate the proposed interval-censoring ODS design and inference procedure by analyzing a dataset on incident diabetes from the Atherosclerosis Risk in Communities (ARIC) study (The ARIC Investigators, 1989). The ARIC study is a longitudinal epidemiologic observational study conducted in four US field centers (Forsyth County, NC (Center-F), Jackson, MS (Center-J), Minneapolis Suburbs, MN (Center-M) and Washington County, MD (Center-W)). The study began in 1987 and each field center recruited a cohort sample of approximately 4000 men and women aged 45–64 from their community. Forsyth County, Minneapolis Suburbs, and Washington County include white participants, and Forsyth County and Jackson Center include African American participants. Each participant received an extensive examination at recruitment, including medical, social, and demographic data, and was scheduled to be re-examined on average of every three years with the first examination (baseline) occurring in 1987–89, the second in 1990–92, the third in 1993–95 and the fourth in 1996–98. Since the incidence of diabetes can be determined only between two consecutive examinations, the observed data were subject to interval-censoring.

We illustrate the proposed interval-censoring ODS design and inference procedure by assessing the effect of high-density lipoprotein (HDL) cholesterol level on the risk of diabetes after adjusting for confounding variables and other risk factors in white men younger than 55 years. In particular, we constructed the ODS sample as follows. The cohort of interest consists of 2110 white men younger than 55 years and 244 were observed to have developed diabetes during the study. We took a simple random sample of size n₀ = 520 from the cohort and selected two supplemental samples of sizes n₁ = n₂ = 15 from the strata A₁ and A₂ defined in (1), where a₁ = 1092 (days) and a₂ = 2127 (days) are approximate (25, 75)-th percentiles of the cohort, respectively. Thus, the ODS sample had total n = 550 subjects. We considered the following proportional hazards model

$$\mathrm{\Lambda }(t\mid Z)=\mathrm{\Lambda }(t)exp(Z^{\prime }\beta ),$$

where the vector of covariates Z included HDL cholesterol level, total cholesterol level, body mass index (BMI), age, smoking status, and indicators for field centers (Center-M was chosen as reference). We compared three estimators: (i) the proposed estimator; (ii) the inverse probability weighted (IPW) estimator; (iii) the sieve maximum likelihood estimator based on only the SRS portion of the ODS sample. Regarding the choice of the degree of Bernstein polynomial used in the sieve estimation, we considered the integers m = 3 to 8 and the AIC criterion (9) suggested to choose m = 3 for all three estimators. From the results in Table 3, one can see that (i) the proposed and IPW methods indicate that higher HDL cholesterol level is significantly associated with lower risk of diabetes in white men younger than 55 years; (ii) the proposed method yielded smaller standard error and more significant result compared to the other methods; in particular, the regression coefficient estimate for HDL cholesterol level based on the proposed method is −0.0272, the standard error estimate is 0.0126, and the P-value is 0.0311; (iii) all three methods suggest that lower BMI level is significantly associated with lower risk of diabetes in white men younger than 55 years.

Table 3.

Analysis results for diabetes data from the ARIC study

Variable	Proposed method			IPW method			SRS portion only
	β̂	SE	P-value	β̂	SE	P-value	β̂	SE	P-value
HDL Cholesterol	−0.0272	0.0126	0.0311	−0.0271	0.0133	0.0426	−0.0228	0.0150	0.1273
Total Cholesterol	0.0003	0.0031	0.9364	0.0016	0.0032	0.6137	0.0029	0.0037	0.4360
BMI	0.1145	0.0273	0.0000	0.1094	0.0372	0.0032	0.1244	0.0328	0.0001
Age	−0.0544	0.0217	0.0120	−0.0324	0.0407	0.4257	−0.0089	0.0546	0.8703
Current smoking	−0.0649	0.2563	0.8001	−0.0862	0.1990	0.6648	−0.2679	0.3478	0.4411
Center-F	−0.0429	0.3150	0.8917	−0.1214	0.1897	0.5224	−0.1619	0.3770	0.6676
Center-W	0.0245	0.2730	0.9285	−0.2077	0.2166	0.3376	−0.1475	0.3240	0.6488

6. Discussion

We proposed an innovative and cost-effective sampling design with interval-censored failure time outcome, i.e., the interval-censoring ODS design, which enables investigators to make more efficient use of their study budget by selectively collecting more informative failure subjects. For analyzing data from the proposed interval-censoring ODS design, we developed an efficient and robust sieve semiparametric maximum empirical likelihood method. As shown in the simulation study, the proposed design and method is more efficient than the SRS and generalized case-cohort designs as well as the IPW method.

We provide some remarks on the practical use of the proposed ODS design. To implement this design, one needs to determine the cutpoints (a₁, a₂) and the allocations of the SRS and supplemental samples. For the cutpoints, we suggest to take the lower and upper k-th percentiles of all examination times and recommend k between 10 and 35. For the allocations of the SRS and supplemental samples, it seems from the simulation results that the more supplemental subjects are sampled from the tails, the more efficient the proposed method could be. However, one also needs to keep the SRS sample large enough so as to maintain the adequate representativeness of the ODS sample on the whole population. Due to these considerations and our simulation experiences, we recommend the ratio of SRS size and total supplemental sample size to be at least 5 : 1. Another aspect of the ODS design is the selection of the SRS and supplemental samples. The asymptotic properties of our proposed estimator are derived based on independent Bernoulli sampling. In practice, sampling without replacement is often used. The asymptotic properties can be derived under sampling without replacement, but the derivation would be much more tedious. Based on the literature for case-cohort designs (e.g. Breslow and Wellner, 2007), we expect the difference in asymptotic variance to be very small if there is any. We conducted additional simulations to examine the effect of using sampling without replacement on our proposed estimator. The results show that our proposed estimator performs well even though sampling without replacement is used for selecting the ODS samples in the practical situations we considered.

We also make some comments on the proposed inference procedure. First, regarding the number of Bernstein basis polynomials m, in theory, it depends on the sample size n with m = o(n^ν). However, we found that m does not need to be very large for the results to be satisfying. In practice, based on our numerical experiences, we recommend to consider the values of m to be from 3 to 8 and choose the one that minimizes the AIC. On the other hand, we focused on the proportional hazards model in this paper for its good interpretation and wide application. In fact, the proposed method could easily be extended to other semiparametric models, such as the proportional odds model and transformation model.