Ultrafast imaging of cell elasticity with optical microelastography

Significance

In wave physics, and especially seismology, uncorrelated vibrations could be exploited using “noise correlation” tools to reconstruct images of a medium. By using a high-frequency vibration, a high-speed tracking device, and a reconstruction technique based on temporal correlations of travelling waves we conceptualized an optical microelastography technique to map elasticity of internal cellular structures. This technique, unlike other methods, can provide an elasticity image in less than a millisecond, thus opening the possibility of studying dynamic cellular processes and elucidating new mechanocellular properties. We call this proposed technique “cell quake elastography.”

Abstract

Elasticity is a fundamental cellular property that is related to the anatomy, functionality, and pathological state of cells and tissues. However, current techniques based on cell deformation, atomic force microscopy, or Brillouin scattering are rather slow and do not always accurately represent cell elasticity. Here, we have developed an alternative technique by applying shear wave elastography to the micrometer scale. Elastic waves were mechanically induced in live mammalian oocytes using a vibrating micropipette. These audible frequency waves were observed optically at 200,000 frames per second and tracked with an optical flow algorithm. Whole-cell elasticity was then mapped using an elastography method inspired by the seismology field. Using this approach we show that the elasticity of mouse oocytes is decreased when the oocyte cytoskeleton is disrupted with cytochalasin B. The technique is fast (less than 1 ms for data acquisition), precise (spatial resolution of a few micrometers), able to map internal cell structures, and robust and thus represents a tractable option for interrogating biomechanical properties of diverse cell types.

The ability to measure the elasticity of a cell provides information about its anatomy, function, and pathological state. For example, cell biomechanical properties are related to the cytoskeletal network arrangement and water content (1). The cell membrane can harden or soften to modulate passage of biomolecules (2). Electrochemical activation can induce rapid contraction and mechanical modulation of cell properties in electrophysiology and neurology. Notably, tumor cells are characterized by a change of elasticity (3) and therapies inducing fibrosis, necrosis, and apoptosis are also accompanied by changes in tissue elasticity. Cytoskeleton reorganization is also linked to the activation process of immune cells and critical for effective cell–cell interactions, formation of immunological synapses, and migration processes (4). These are just a few examples that emphasize the importance of cell biomechanics in biology.

Many techniques have been proposed to measure a cell’s mechanical properties, especially its elasticity. Most need a very accurate model of the cell characteristics but the chosen model may impact the measurement accuracy. Moreover, current measurements take seconds to hours to perform, during which biological processes can modify the cell elasticity, and they necessitate fixing the cell on a substrate. Variations in elasticity by a factor of two can occur within a few seconds (5).

In this study we propose an elasticity measurement technique based on elastic wave propagation. This technique performs local measurement of the speed c_s of a shear wave, a type of elastic wave. The shear modulus $\mu$ (elasticity) is given by $\rho c_s^2$, with $\rho$ the medium density, by assuming a purely linear elastic medium and negligible preloads. Here, we show that the shear wave elastography technique can perform micrometer-scale measurements and that it can extract local elasticity on a whole cell. Three main technological challenges needed to be met to achieve this: (i) developing an efficient way to induce kilohertz-range high-frequency shear waves in cells, (ii) finding a robust method to track these waves, and (iii) extracting elasticity from the observed traveling elastic waves.

Results

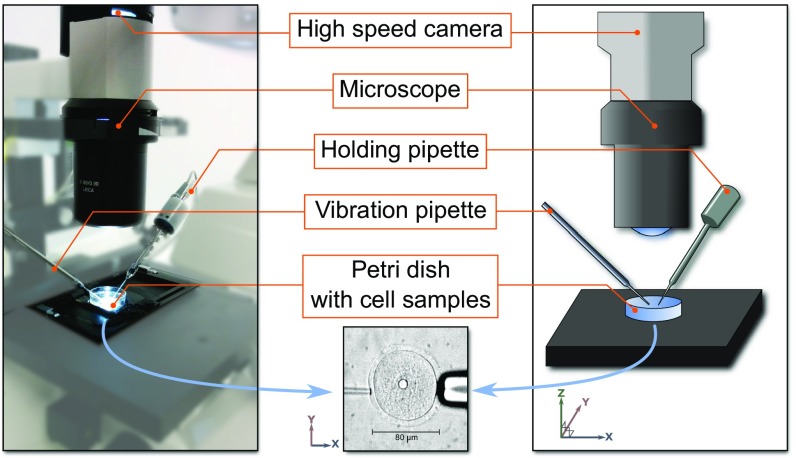
We first set out to demonstrate that high-frequency shear waves can be induced in cells. The key components of the experimental setup are as follows (Fig. 1): a cell held by a first micropipette and excited by contact with a second micropipette vibrating at 15 kHz, a 100× microscope magnification to observe the cell, and a 200,000-frames-per-second camera fixed on the microscope to acquire optical images over time. The 15-kHz vibration represents a compromise between a high-frequency stimulation to have a wavelength smaller than the cell size and a low-frequency excitation to reduce wave attenuation, especially in such a soft medium. The experiment was applied on spherical mouse oocytes (80 µm in diameter), which are well-characterized and easy to manipulate ex vivo. A finite element simulation with a 15-kHz vibration occurring on the side of a soft solid was also built to validate the technique.

Fig. 1.

Illustration of the experiment (Left: picture; Right: scheme). A cell placed in a Petri dish is held by a holding pipette and vibration is applied using a second pipette attached to a piezo-drive unit. Vibration is applied to the zona pellucida of the oocyte. Images of the cell are acquired by a high-speed camera through a microscope.

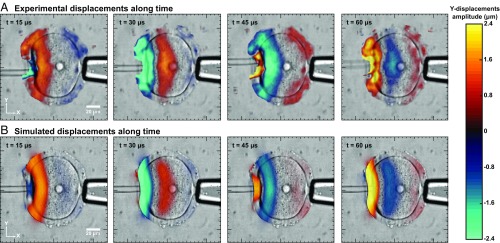
Using an optical flow algorithm (6), displacements can be seen propagating left to right, with good agreement between experiment (Fig. 2A) and simulation (Fig. 2B). Attenuation is strong but displacements can nevertheless be observed on the right side of the cell. Almost no displacement is seen in the surrounding fluid. These displacements propagate at a speed of 1.1 $\pm$ 0.1 m/s, under the form of elastic waves. Elastic waves are often decomposed in bulk waves (i.e., compression and shear waves) and surface waves (i.e., Rayleigh and Love waves). Any compression waves cannot be seen here, as a 15-kHz compression wave has a wavelength of ∼10⁵ μm in such a medium, which is 1,000 times larger than the oocyte diameter. As the oocyte is surrounded by a fluid of similar density, we made the hypothesis of an infinite medium, a common hypothesis in shear wave elastography. Besides, Rayleigh and Love waves typically propagate at a speed close to the shear wave speed (about 10% slower depending on conditions). Consequently, we approximated observed elastic waves as shear waves propagating at a speed c_s.

Fig. 2.

Experimental (A) and simulated (B) Y-displacement maps, at t = 15, 30, 45, and 60 μs, respectively, superimposed on the optical images of the cell. Displacements with amplitude approximately from −2.4 to 2.4 μm propagating from the left vibrating pipette toward the right side of the cell can be observed.

To map cell elasticity from observed shear waves we explored methods proposed in the field of shear wave elastography, such as time of flight (7), elastodynamic equation inversion (8, 9), and optimal control (10). In this study the best reconstruction was obtained using the “passive” elastography algorithm (11, 12), inspired by the seismology field (see Materials and Methods for details). It primarily calculates the shear wave speed, which then allows estimating the shear elasticity modulus.

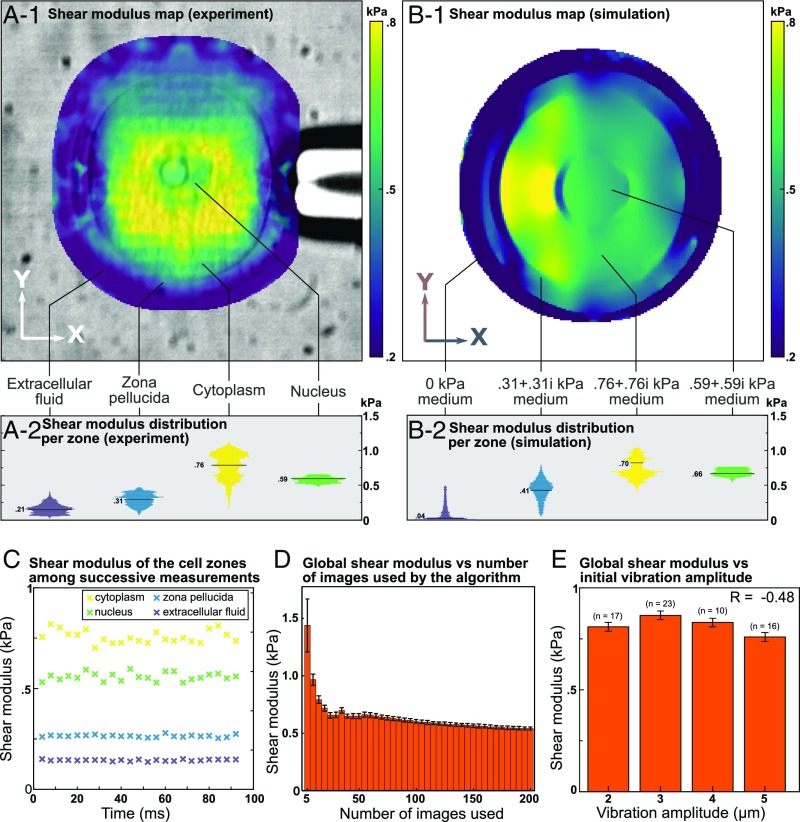
On experimental elasticity maps (Fig. 3A), for analysis purposes, we segmented the oocyte into three functionally distinct zones: the zona pellucida (median of 0.31 kPa), the cytoplasm (median of 0.76 kPa), and the nucleus (median of 0.59 kPa). A median shear modulus was estimated at 0.21 kPa for the extracellular fluid (which should theoretically be zero), but this is attributed to displacements surrounding the cell interpreted by the elastography algorithm as shear waves. Each of these values is pairwise significantly different (P < 0.05, Mann–Whitney U test). Displacements could, however, not be properly estimated by the particle imaging velocimetry algorithm near the pipettes due to the high mechanical contrast of these objects. Consequently, the elasticity could not be calculated in a 10- to 20-μm layer around the holding pipette and the actuator.

Fig. 3.

(A) Elasticity map estimated from experimental displacements superimposed on the microscopy image (A-1) and corresponding distribution of elasticity with median values (A-2) of a mouse oocyte. (B) Elasticity map estimated from simulated displacements superimposed on the microscopy image (B-1) and corresponding distribution of elasticity with median values (B-2) of a soft medium mimicking a mouse oocyte. Nucleus, cytoplasm, zona pellucida, and extracellular fluid can be easily distinguished on both images; artifacts are observed in the zona pellucida. (C) Median shear moduli for successive measures within different zones (cytoplasm, nucleus, zona pellucida, and extracellular fluid). No time evolution is observed. (D) Average median shear moduli of the whole cell among 23 successive measurements as a function of the number of optical images used. Error bars correspond to the SD among successive measurements. (E) Effect of the vibration amplitude on oocyte shear modulus median, obtained by averaging 10–23 measures. Error bars correspond to the SD among successive measurements. Pearson’s correlation coefficient R is too low to show any correlation between the measured shear modulus and the vibration amplitude.

These elasticity values were used as inputs of a simulated medium comprising four concentric circles (Fig. 3B) representing the different cellular zones. The nucleus is quite homogeneous and has a median elasticity of 0.66 kPa (10% difference with input); the cytoplasm is not homogeneous along the x axis, especially around the actuator, but has a median elasticity of 0.7 kPa (10% difference with input); the zona pellucida is around the resolution limit and has some artifacts around the actuator and the holding pipette and has a median elasticity of 0.41 kPa (difference of 25% with input); finally, apart from some specific outliers, the extracellular fluid elasticity is very small (0.04-kPa median value). Hence, we can state that the reconstruction process leads to a few artifacts, mainly in the vicinity of the actuator and the holding pipette, but it can nevertheless estimate shear moduli in four different zones, with medians close to input values.

To assess reproducibility of the technique, 23 successive measurements were made every 2.5 ms (with 200 images per measurement). Such quick repetition of the measure ensured absence of confounding time-dependent hardening or softening of the cell. Fig. 3C illustrates the median shear modulus within different zones (cytoplasm, nucleus, zona pellucida, and extracellular fluid). No time evolution could be observed in any part of the cell, indicating excellent reproducibility of the technique.

Next, we applied the elasticity reconstruction algorithm using 5–200 frames for each of the 23 measurements to test robustness. Mean elasticity quickly decreased by using 5–50 images then continued to slowly decrease (<10%) with 50–160 images, to reach a plateau with around 160 images (Fig. 3C). This implies that at 200,000 frames per second reliable measures of cell elasticity require ∼0.8 ms.

Finally, we studied the impact of the vibration amplitude on the elasticity estimation. With four pipette vibration amplitudes (as measured on optical images) we estimated the shear modulus of one oocyte (Fig. 3E). The shear modulus did not depend on the cell vibration amplitude within the range of 2–5 µm. This result may facilitate future implementation of the technique as it demonstrates that the vibration amplitude is not a critical parameter to consider.

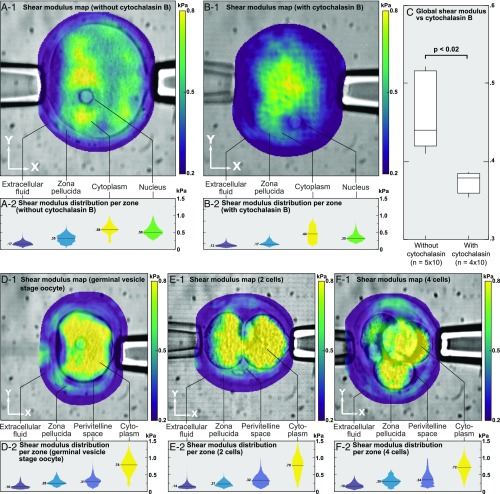
Next, we studied the effect of disrupting the actin cortex of the oocyte upon cell elasticity. Cytochalasin B is a toxin known to block polymerization and the elongation of actin, and we thus expected oocyte softening. Examination of the cortex using Alexa-labeled phalloidin and confocal microscopy revealed a major reduction in actin labeling in the oocyte cortex, confirming the expected action of the drug (SI Materials and Methods). Notably, using optical microelastography, a decrease in shear modulus (softening) was observed when comparing normal and cytochalasin-treated oocytes, both in the cytoplasm and nucleus (Fig. 4 A and B). An artifactual decrease in elasticity within the zona pellucida was observed due to the proximity with the cytoplasm. With a total of 90 measurements on five normal cells and four cytochalasin-treated cells we observed a significant decrease (P < 0.02 with a Mann–Whitney rank sum test) of the mean shear modulus of the whole cells (Fig. 4C).

Fig. 4.

Elasticity map superimposed on the microscopy image (A-1 and B-1) and corresponding distribution of elasticity with median values (A-2 and B-2) of a normal mouse oocyte (A) and a mouse oocyte softened by cytochalasin B (B). Elasticity decreased in all functional areas. (C) Box plot of whole oocyte shear modulus without and with cytochalasin B, showing a significant decrease in elasticity. Elasticity map superimposed on the microscopy image (1) and corresponding distribution of elasticity with median values (2) of a germinal vesicle-stage oocyte (D), a two-cell mouse embryo (E), and a four-cell mouse embryo (F).

We also observed the shear modulus of cells at different stages of maturation: a germinal vesicle-stage oocyte (Fig. 4D), a two-cell embryo (Fig. 4E), and a four-cell embryo (Fig. 4F). The four-cell embryo cytoplasm was difficult to segment, as the fourth cell in the background degraded the shear wave displacement estimation. We could nevertheless measure almost the same elasticity at the three stages.

Discussion

Compared with existing elasticity mapping techniques the cellular imaging method presented in this study may become a viable alternative. Indeed, most cell elasticity measurement techniques are based on static cell deformation under an external force, using aspiration micropipettes (13), magnetic bead twisting (14), and optical tweezers or stretcher (15). The deformation is estimated from optical images acquired before and after applying the force. While global elasticity is easily calculated by dividing the applied force intensity by the measured deformation, localized internal cell structure elasticity is more difficult, because the local deformation depends strongly on the internal distribution of stress. Thus, localized elasticity estimation needs a descriptive model of the cell mechanics, which is difficult to validate and may explain the variability observed among different studies (16–18).

In atomic force microscopy, local elasticity is estimated from the penetration depth of a small probe (19–21). This technique is able to map elasticity with a submicrometric spatial resolution. However, measurements are performed at the cell surface only, so that elasticity of internal structures cannot be determined. Besides, elasticity estimation highly depends on the chosen model. In particular, the probe shape must be precisely calibrated, as a change of shape due to probe aging, for example, can have an important impact. In most implementations, acquisitions are rather slow, taking typically at least a few minutes to acquire a full set of data, thus potentially increasing susceptibility to time-dependent confounding biological processes. Moreover, one needs to attach the cell on a substrate to avoid its displacement, thus imposing boundary conditions that must be taken into account in the model to avoid biased elasticity measures.

An alternative strategy is to inject fluorescent nanoparticles within the cell and to measure the mean random displacement of these particles when the cell is subjected to a shear motion (22). This technique gives access to elasticity and viscosity, but at the location of nanoparticles only, so it does not produce images of the cell’s viscoelasticity. It also requires a few minutes to make a measurement, and this approach is invasive by nature.

Brillouin scattering microscopy, more recently introduced (23, 24), consists of transmitting a laser beam through the cell, where internal mechanical waves shift the laser frequency. Measurement of this shift allows estimating the medium bulk modulus. However, the bulk modulus offers a much smaller contrast than Young’s or shear modulus for similar changes in cell elasticity. For example, Scarcelli et al. (23) found a bulk modulus increase of only 16% when the Young’s modulus raised by about 500% for the same experimentation. As for abovementioned technologies, acquisitions are rather slow, on the order of an hour.

Contrary to existing methods, the proposed technique does not require a stress distribution model and allows localized absolute elasticity measures (i.e., elasticity in kilopascals). As is done in shear wave elastography of whole organ systems, our method may be expanded to provide viscous properties (25, 26). Although we observed some artifacts on reconstructed elasticity maps, median values in each zone can be considered as accurate (differences of about 10% with input values in the simulation). This accuracy could nevertheless be improved, notably by working on the reconstruction process.

Reported measurements could distinguish internal structures of an oocyte based on their elasticity differences. To our knowledge, no measurement of oocyte elasticity has been previously reported at the frequency we used (15 kHz). Most biological tissues exhibit a frequency-dependent elasticity behavior (27), so our measurements lack a gold standard to be compared with. We can nevertheless state that elasticity values reported in our study are reproducible and consistent with finite element simulations. The closest measurement found in the literature has been done by Othman et al. (28) using a 550-Hz vibration frequency (one order of magnitude lower than in our experiments). They measured a global shear modulus of 0.3 kPa for a frog oocyte, which is in the same order of magnitude as our experiments.

An important advantage of the proposed method is the speed of acquisition, on the order of a millisecond. No confounding biological processes, such as cross-linking, could occur during the acquisition time. Future validations of the ultrafast optical microelastography technique may allow demonstrating the capability of this method to follow dynamic cellular processes inducing elasticity changes.

Spatial resolution in shear wave elastography is not directly related to the shear wavelength but depends on many parameters, such as the frame rate, reconstruction algorithm, and shear wave shape. In the current implementation, variations of elasticity could be observed in the nucleus or in the perivitelline space—so we estimate an average resolution on the order of 10 μm. The spatial resolution could be improved, for example with higher vibration frequencies or better imaging analysis algorithms, with the imaging apparatus resolution as the highest achievable—in this case the pixel size (0.57 μm). Different vibrating devices could be conceptualized as multiple harmonic sources and would facilitate the elasticity map reconstruction with the proposed method (11, 12). Three-dimensional mapping is also achievable simply by repeating the experiment at different microscope focusing depths.

Finally, the experimental apparatus is rather simple, consisting of a standard microscope, micropipettes, and a high-speed camera. Phase-contrast optical methods might be used for better contrast and resolution. It may also improve displacement estimation because phase information is available. The resolution of the microscope is not a critical parameter: The technique needs mainly to observe and track displacements inside the cell. The camera minimum speed of acquisition has to be tuned to the experiment as the shear wave velocity is related to the cell elasticity: We have to observe the shear wave propagation over a few images. A slower, less expensive camera could also be employed using a stroboscopic effect (i.e., by repeating synchronized image acquisitions and taking pictures with increasing delays).

Thanks to its speed, robustness, and relative simplicity, we therefore envision that this optical microelastography technique could become an alternative for mapping biomechanical properties of cells. It could open the possibility of studying dynamic cellular processes and elucidating new mechanobiology cellular properties, including cell division and migration.

Materials and Methods

Experimental Setup.

The ultrafast camera (model v2512; Phantom Research) acquired 256- × 256-pixel windows at 200,000 images per second. The frame rate could be lowered down to 30,000 images per second (Nyquist–Shannon limit for a 15-kHz vibration), but oversampling allowed a better tracking of the shear wave propagation. With microscope amplification (Leica DMi1 with 100× lens), each square pixel had a lateral size of 0.57 µm. Cells used were mouse germinal vesicle-stage oocytes. Oocytes were collected as described previously (29) and kept in M2 medium (M-7167; Sigma Aldrich) supplemented with 200 nM 3-isobotyl-1-methyl-xanthine (I-5879; Sigma Aldrich) during observation. Experiments were performed shortly after oocytes were harvested. Cytochalasin B toxin (C-6762; Sigma-Aldrich) was used to depolymerize the actin cortex in some experiments, as described. Experimental procedures were conducted in accordance with guidelines of the Institutional Animal Care Committee of the University of Montreal Hospital Research Center. The investigation conformed with guidelines of the Canadian Council on Animal Care and the Guide for the Care and Use of Laboratory Animals.

To apply vibration, the oocyte was immobilized using a standard holding pipette. A glass vibration pipette was positioned on the zona pellucida of the oocyte, in an area where the zona pellucida was contacting the plasmalemma. The vibration was created by a piezoelectric device (piezo impact drive unit; Prime Tech Ltd.), moving along the y axis with a peak-to-peak amplitude of 20 µm at 15 kHz. The pipette was “rubbing” the cell, so the transmitted displacement was much lower, at about 5.0 ± 0.1 µm (in the Y direction), at the pipette contact. The point here is to induce in-plane pipette displacement with sufficient amplitude to allow tracking vibrations all over the cell.

It would be difficult to use a lower vibration frequency because it would lead to a shear wavelength close to the medium size (around 100 µm), making reconstruction more difficult. However, using a higher vibration frequency to improve resolution would lead to a stronger attenuation and more difficult displacement tracking.

Finite Element Simulation.

The wave equations were solved using COMSOL (version 3.5a) with a structural mechanics module, assuming plane strain. The Navier equation was solved in the frequency domain. We used a 2D model with a manual segmentation of internal structures based on one optical image. The oocyte has an almost spherical shape, symmetrical along the z axis, surrounded by fluid of almost equal density, and we assumed that any out-of-plane border effect had minimal impact. Three zones were segmented: the nucleus, a 20-μm-diameter circle; the cytoplasm, an 80-μm-diameter circle around the nucleus; and the zona pellucida, a 10-μm layer around the cytoplasm. The whole simulated cell was placed in a 200- × 200-μm² space filled with isotonic saline water. We set the bulk modulus for all zones to 2.2 GPa (water compressibility) and the shear modulus elasticity at 0.59 + 0.59i kPa for the nucleus, 0.76 + 0.76i kPa for the cytoplasm, 0.31 + 0.31i kPa for the zona pellucida, and 0 Pa for the surrounding fluid. The shear moduli were extracted from the experimental results, and the loss moduli were set to the same values—we found that this selection gave wave attenuation very comparable to experiments. We tested different sets of parameters but simulated displacements were very different. The nodes on the left side of the zona pellucida were fixed (no displacement in X and Y directions) to simulate the holding pipette, and a vertical prescribed 10-μm harmonic displacement at 15 kHz was applied to the nodes on the left side of the zona pellucida. The continuity of displacement and strain was ensured by the finite element model code at all other interfaces. The model converged using 330,000 degrees of freedom using 75,000 quadratic triangular elements, with a low dependence on the number of elements or degrees of freedom.

Elasticity Derived from Shear Wave Speed.

The proposed technology is inspired by pioneering work in shear wave elastography developed for organ elasticity imaging (7, 8, 30, 31). Considering a medium as elastic, linear, isotropic, and infinite with respect to the wavelength, Navier’s equation governs the displacement $\mathbf{u}$ at each point of the cell:

$$\rho \frac{{\partial }^2\mathbf{u}}{\partial t^2}=\left(K+\frac{4}{3}\mu \right)\nabla \left(\nabla .\mathbf{u}\right)+\mu \nabla \times \left(\nabla \times \mathbf{u}\right),$$

where $\rho$ is the medium density, $\mathbf{u}$ the local displacement, K the bulk modulus, and $\mu$ the shear modulus. Using Helmholtz decomposition $\mathbf{u}={\mathbf{u}}_{\mathbf{p}}+{\mathbf{u}}_{\mathrm{s}}$, where ${\mathbf{u}}_{\mathrm{p}}$ and ${\mathbf{u}}_{\mathrm{s}}$ are, respectively, curl-free and divergence-free vector fields, two elastic waves can be retrieved: (i) a compression wave, which obeys the equation $\rho {\partial }^2{\mathbf{u}}_{\mathrm{p}}/\partial t^2=c_{\mathrm{p}}^2\mathrm{\Delta }{\mathbf{u}}_{\mathbf{p}}$, where $c_p=\sqrt{\left(K+4/3\mu \right)/\rho }$ is the compression wave speed; and (ii) a shear wave, which obeys the equation $\rho {\partial }^2{\mathbf{u}}_{\mathrm{s}}/\partial t^2=c_s^2\mathrm{\Delta }{\mathbf{u}}_{\mathrm{s}}$, where $c_{\mathrm{s}}=\sqrt{\mu /\rho }$ is the shear wave speed. Hence, measuring the shear wave speed locally allows the estimation of the shear modulus (i.e., elasticity).

Shear Wave Speed Estimation.

Once optical images were acquired, displacements along X and Y were estimated using a 2D particle image velocimetry algorithm (6). This algorithm is based on a Lucas–Kanade-based optical flow method with an affine displacement in each block. Shear wave speed was then estimated on the Y-displacement maps using a “passive” elastography algorithm (11, 12). In this algorithm, the temporal cross-correlation between a point $\left(x_0,y_0\right)$ and all other points $\left(x,y\right)$ of the image is calculated to create a 2D+t image $C_{\left(x_0,y_0\right)}\left(x,y;t\right)$ for each position considered $\left(x_0,y_0\right)$. Cross-correlation images typically look like a cross, showing a converging wave for $t<0$, a refocusing at $t=0$ with a maximum of amplitude, and a diverging wave for $t>0$. Curvature of the focal spot is then evaluated on the resulting image, as the focal spot size is directly linked to the wavelength $\lambda$ of the shear wave. Shear wave speed $c_s$ is then estimated by multiplying the wavelength with the shear wave frequency $f$: $c_s=\lambda \times f$ (see SI Materials and Methods for an illustration of the algorithm). The wave correlation technique used here for the inverse problem solution (11, 12) is advantageous because the more diffuse the wavefield the better the reconstruction quality.