Significance
Alignment of cells in response to mechanical cues plays an important role in a wide range of physiologic processes. Multiple cell types orient perpendicular to applied cyclic stretch in 2D culture but parallel to stretch in 3D culture, and the mechanisms underlying this behavior remain elusive. We tested a promising hypothesized mechanism called strain avoidance and showed that it cannot explain cell alignment across the conditions that we examined. By contrast, a computational model of stress fiber kinetics incorporating the influence of traction boundary conditions and altered strain transmission in soft gels reproduced all of our experimental results as well as published 2D stretch experiments. These findings could improve understanding, modeling, and therapeutic modulation of tissue development, regeneration, and repair.
Keywords: cell mechanics, cytoskeleton, stress fibers, computational modeling, fibroblast orientation
Abstract
The ability of cells to orient in response to mechanical stimuli is essential to embryonic development, cell migration, mechanotransduction, and other critical physiologic functions in a range of organs. Endothelial cells, fibroblasts, mesenchymal stem cells, and osteoblasts all orient perpendicular to an applied cyclic stretch when plated on stretchable elastic substrates, suggesting a common underlying mechanism. However, many of these same cells orient parallel to stretch in vivo and in 3D culture, and a compelling explanation for the different orientation responses in 2D and 3D has remained elusive. Here, we conducted a series of experiments designed specifically to test the hypothesis that differences in strains transverse to the primary loading direction give rise to the different alignment patterns observed in 2D and 3D cyclic stretch experiments (“strain avoidance”). We found that, in static or low-frequency stretch conditions, cell alignment in fibroblast-populated collagen gels correlated with the presence or absence of a restraining boundary condition rather than with compaction strains. Cyclic stretch could induce perpendicular alignment in 3D culture but only at frequencies an order of magnitude greater than reported to induce perpendicular alignment in 2D. We modified a published model of stress fiber dynamics and were able to reproduce our experimental findings across all conditions tested as well as published data from 2D cyclic stretch experiments. These experimental and model results suggest an explanation for the apparently contradictory alignment responses of cells subjected to cyclic stretch on 2D membranes and in 3D gels.
Alignment of cells in response to mechanical cues plays an important role in a wide range of physiologic responses from sensing of shear stress by endothelial cells to production of aligned collagen in developing tendons. One of the most intriguing observations to emerge from studying these responses is that cells plated on a flexible 2D substrate orient perpendicular to an applied uniaxial cyclic stretch (1–6), while cells embedded in a 3D gel orient parallel to that stretch (7–13). Recently, Obbink-Huizer et al. (14) proposed an attractive hypothesis to explain this discrepancy. They postulated that the dominant cellular response in both situations is strain avoidance, in which net disassembly of stress fibers (SFs) parallel to an applied strain produces cytoskeletal alignment perpendicular to that strain. According to this hypothesis, cells in 3D gels align parallel to applied cyclic stretch because they are able to compact these gels perpendicular to the stretch direction, producing compaction strains that are much larger than the applied cyclic strains; in other words, cells in gels align with applied stretch only because they are avoiding much larger transverse compaction strains.
To date, only limited experimental data are available to assess this hypothesis. Foolen et al. (8) designed a collagen gel loading system that allowed them to perform either uniaxial cyclic stretching (in the x1 direction with x2 left free to compact) or strip uniaxial cyclic stretching (in the x1 direction with x2 constrained). However, this experimental system simultaneously varied both compaction and boundary conditions in the x2 direction. To specifically test the hypothesis that transverse compaction explains cell alignment parallel to stretch in 3D culture, we developed a system that allowed us to independently control compaction in the loading and transverse directions before and during the application of cyclic uniaxial stretch. Experiments with this system suggested that traction boundary conditions—rather than compaction per se—govern the alignment of cardiac fibroblasts cultured in statically restrained collagen gels. Cyclic uniaxial stretch could modify this alignment, but only at frequencies an order of magnitude greater than required to induce perpendicular alignment in published 2D stretching experiments. We then modified a thermodynamic model of SF dynamics published recently by Vigliotti et al. (15) and were able to reproduce these experimental findings as well as previously published data from 2D cyclic stretching experiments. These experiments and model results suggest a framework for understanding the apparently contradictory alignment responses of cells subjected to cyclic stretch on 2D membranes and in 3D gels.
Results and Discussion
Cellular Alignment in the Presence of Transverse Compaction.
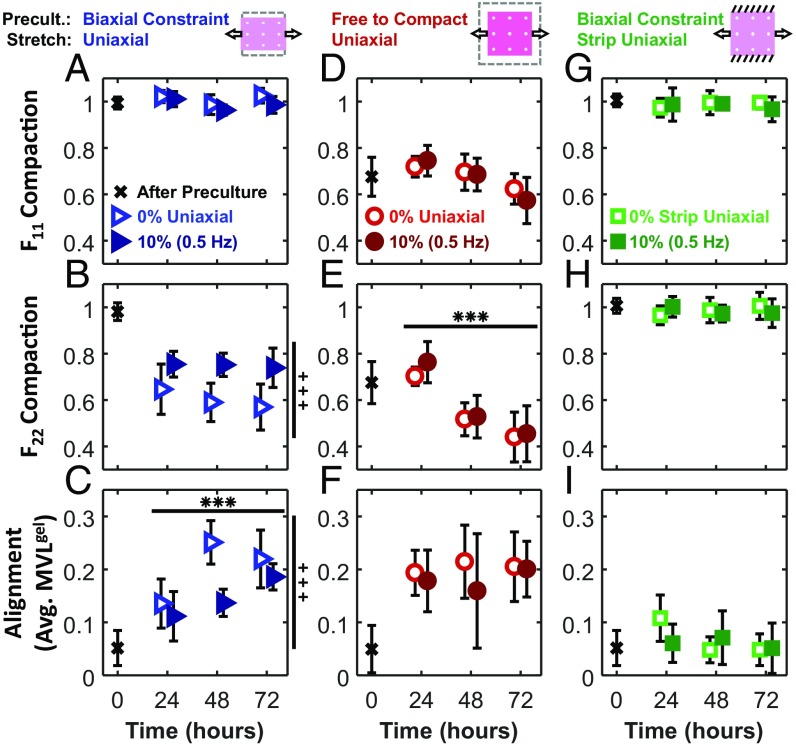
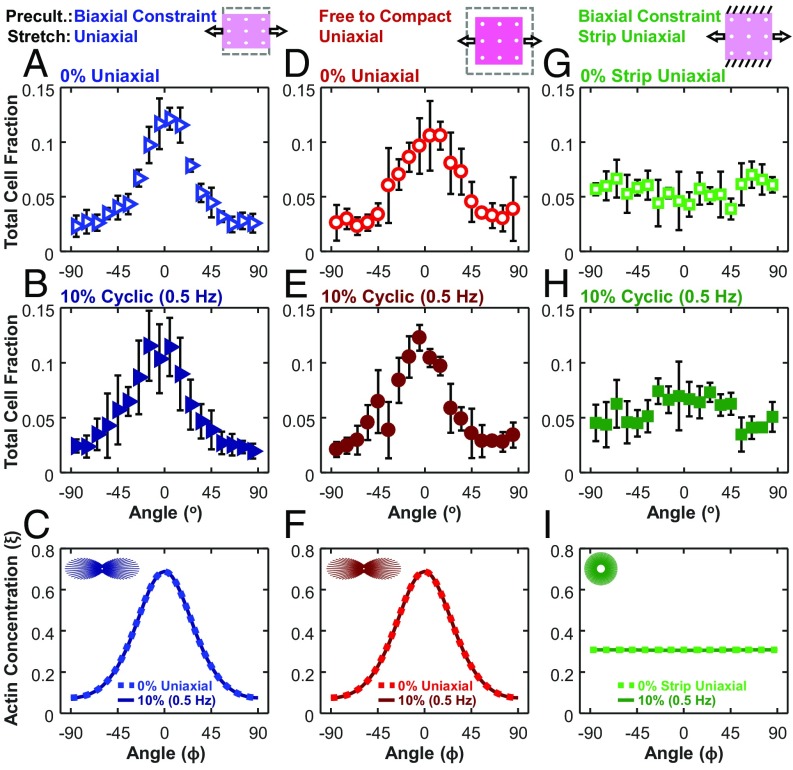
To separate the effects of compaction and boundary conditions, we subjected collagen gels containing primary adult cardiac fibroblasts to different combinations of experimental conditions during a 24-h preculture period and subsequent cyclic stretch periods (Fig. 1). In one group, we restrained gels during preculture and then left the x2 direction free while we imposed low-frequency uniaxial stretch (10%; 0.5 Hz) or restraint (0% stretch) in the x1 direction (Fig. 1C). Marker-based measurements of deformation in the central region of these gels confirmed the presence of substantial transverse compaction (Fig. 2B). Fibroblasts were randomly aligned after the preculture phase but aligned strongly in the x1 direction (parallel to stretch) during the stretching phase (Figs. 2C and 3 A and B). This experiment replicates the classic 3D results described previously by multiple groups, wherein cells in 3D culture align parallel to an imposed stretch (7, 8, 16). Unfortunately, this experiment alone provides limited insight into the factors governing cell alignment, because so many potential determinants covary. Cells could be aligning parallel to the imposed stretch or restraint or perpendicular to the compaction strains; furthermore, since transverse compaction generates collagen alignment parallel to a uniaxial restraint (7, 11, 16, 17), cells could also be aligning along the local collagen fiber direction.
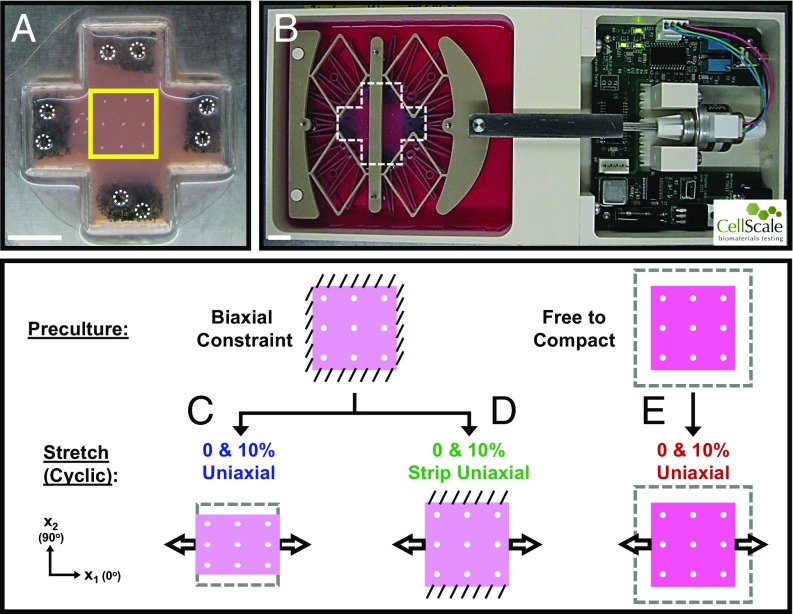
Fig. 1.
Experimental setup and test conditions. (A) Fibroblast-populated collagen gels with sponges embedded in the arms. During an initial preculture period, gel arms would be either biaxially constrained with pins (circled) or left to float freely in media and isotropically compact. Square box indicates region of interest painted with nine TiO2 dots to track gel deformations and later imaged to assess cell alignment. (B) Collagen gel (cruciform-shaped box) pinned in CellScale device. (Scale bars: 1 cm.) (C and D) Collagen gels initially cultured under biaxial constraint before being subjected to (C) 0 or 10% uniaxial stretch in the x1 direction (x2 left free) or (D) 0 or 10% strip uniaxial stretch in x1 (x2 held fixed). (E) Collagen gels initially allowed to compact isotropically before being subjected to either 0 or 10% uniaxial stretch in x1. Diagonal lines indicate constraint; arrows indicate direction of cyclic stretch, and dashed boxes indicate original gel size before compaction.
Fig. 2.
Time course of gel deformation and cell alignment at 24, 48, and 72 h. After an initial preculture period (black x), collagen gels were subjected to either 0% stretch (open symbols) or 10% (0.5 Hz) stretch (solid symbols). Compaction deformations in the x1 (F11; A, D, and G) and x2 (F22; B, E, and H) directions were measured using titanium oxide markers. Average MVL (MVLgel; C, F, and I) describes the strength of cell alignment. MA of all uniaxial cases was 0°. Each data point is representative of five independent experiments and expressed as the mean ± SD. ***ANOVA P < 0.001 difference over time; +++ANOVA P < 0.001 difference between 0 and 10% groups.
Fig. 3.
In all uniaxial cases, cells aligned with similar strength in the direction of stretch, regardless of the pattern of compaction (anisotropic vs. isotropic) or the presence of cyclic stretch. Angular histograms of cell orientation for 0% stretch (open symbols; A, D, and G) or 10% (0.5 Hz) stretch (solid symbols; B, E, and H) at 72-h time points. Each data point is representative of five independent experiments and expressed as the mean ± SD. Angular histograms of SF orientation from computational simulations of our test conditions (C, F, and I). In agreement with the experimental findings, the model predicted highly aligned SFs along the x1 axis under uniaxial stretch (C and F) and uniformly distributed SFs under strip uniaxial stretch (I). Dotted lines indicate 0% stretch, and solid lines indicate 10% cyclic (0.5 Hz) stretch. Insets show circular histogram representations of SFs for 0% cases.
Cellular Alignment in the Presence of Isotropic Compaction.
To better separate these potentially confounding variables, we took advantage of the fact that collagen gel compaction is very rapid during the first few hours and then slows dramatically (Fig. 1E) (18). Thus, when we left gels unconstrained in both directions for 24 h, they compacted isotropically, inducing no net cell alignment (Fig. 2 D–F). Twenty-four hours of subsequent uniaxial restraint or low-frequency cyclic stretch (10%; 0.5 Hz) along the x1 direction produced no additional transverse compaction in the x2 direction, but cells aligned strongly over that same time period; thus, it seems clear that compaction strains could not be the primary driver of cell alignment in this experiment. We note that, with longer culture periods in this experimental group, we did see some additional x2 compaction. However, this compaction was not associated with higher levels of cell alignment (Figs. 2 D–F and 3 D and E), again showing a lack of correlation between the degree of transverse compaction and the degree of cell alignment.
Cellular Alignment in the Absence of Compaction.
In other gels, we prevented transverse compaction by constraining gels biaxially during the preculture period and then applying “strip uniaxial” stretch conditions: stretching (10%; 0.5 Hz) or restraining (0% stretch) gels in the x1 direction while preventing deformation in the x2 direction (Fig. 1D). As expected, these gels displayed no transverse compaction (Fig. 2H). According to the strain avoidance hypothesis, this experiment should produce similar results as those observed with cells cultured on 2D stretchable membranes: in the absence of transverse compaction, cells should avoid the imposed 10% cyclic strain and orient perpendicular to the loading direction. In contrast to this expectation, we found that average fibroblast alignment remained low at all time points in these gels (Fig. 2I), and histograms showed similar numbers of cells oriented in all directions (Fig. 3 G and H).
These results are consistent with most previous reports using 3D gels, but there are some inconsistencies. In agreement with our findings, Foolen et al. (8) reported that vascular-derived cells cultured in collagen/matrigel gels developed random orientations during an initial biaxial constraint and that subsequent 10% strip uniaxial cyclic stretch at 0.5 Hz caused no change in the orientation within the core of the gel. However, they also reported that cells on the top and bottom surfaces of their gels aligned perpendicular to the direction of stretch (8); by contrast, cells at the surface and within the core of our gels showed similar alignment responses in all conditions. In another study, de Jonge et al. (19) reported that myofibroblasts and collagen in 3D fibrin gels subjected to 5% strip uniaxial cyclic stretch at 1 Hz oriented perpendicular to the stretch direction, which seems to contradict both our data and those of Foolen et al. (8).
Effect of Stretching Frequency on Cellular Alignment in 3D Gels.
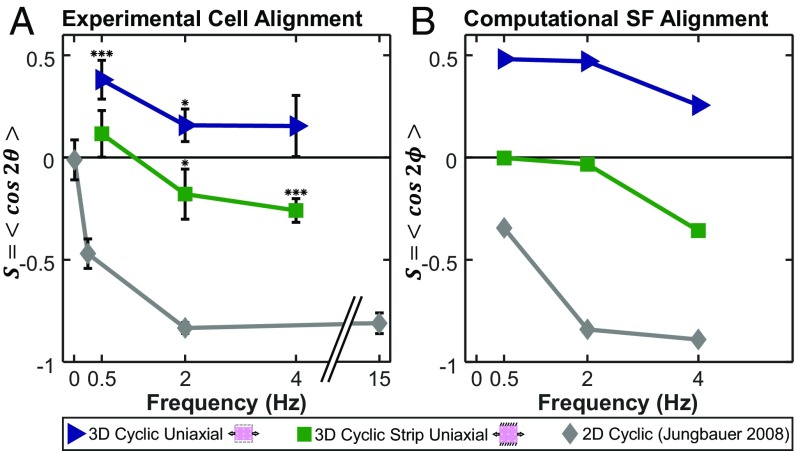
Published data suggest that cells on 2D elastic membranes subjected to cyclic uniaxial stretch align perpendicular to stretch only above a critical frequency of ∼0.1 Hz (20–22). Therefore, we tested the possibility that higher frequencies might induce perpendicular alignment in our strip uniaxial gels; for comparison, we imposed the same stretch conditions on uniaxially stretched gels. We plotted an order parameter that quantifies alignment (1 = parallel, −1 = perpendicular, 0 = random) (Eq. 5) as a function of frequency alongside published 2D data (22) from cyclically stretched rat embryonic fibroblasts (Fig. 4A). Cells in gels subjected to strip uniaxial stretch showed no alignment at 0.5 Hz, modest but statistically significant perpendicular alignment at 2 Hz, and clear perpendicular alignment at 4 Hz (orientation histograms for each case are provided in Fig. S2). Thus, under strip uniaxial conditions, it was possible to induce perpendicular alignment similar to that commonly observed in 2D, but the transition frequency at which this occurred was an order of magnitude higher in our gel experiments than has been reported in 2D. Cells in gels subjected to uniaxial stretch with the x2 direction left free showed clear parallel alignment at 0.5 Hz, modest but statistically significant alignment at 2 Hz, and no significant alignment at 4 Hz (Fig. 4A and Fig. S2).
Fig. 4.
The model captures alignment trends across a range of frequencies and boundary conditions in both 3D and 2D culture conditions. We plotted the order parameter S = <cos2θ> that quantifies alignment (1 = parallel, −1 = perpendicular, 0 = random) as a function of frequency in 3D uniaxial cyclic stretch (blue triangles), 3D strip uniaxial cyclic stretch (green squares), and 2D cyclic stretch on silicone elastomer membranes (gray diamonds) in experimentally measured cell orientations (A) and computationally predicted SF orientations (B). Each data point for the experimental conditions is expressed as the mean ± SD. 3D data points represent five independent experiments (except uniaxial 4 Hz; n = 4), while 2D data points represent 30–50 cells measured by Jungbauer et al. (22) in rat embryonic fibroblasts at 8% cyclic stretch. *P < 0.05; ***P < 0.001 for presence of significant alignment.
Mechanical Determinants of Cell Alignment in 2D and 3D.
Our experimental results suggest thinking about the mechanical factors that influence cell alignment on two different timescales. On the timescale of individual stretch and release cycles, sufficiently rapid or large strains do appear to modify cell alignment in 3D, inducing perpendicular alignment under conditions where static culture would produce randomly oriented cells and reducing parallel alignment under conditions where static culture would produce it. These observations are generally consistent with previous models (14, 23), in which high strain rates either reduce SF assembly or promote disassembly. However, any model that aims to simultaneously capture both 2D and 3D responses must explain why the transition frequency for perpendicular alignment seems to differ in these settings (Fig. 4A). We have incorporated one hypothesis to explain this discrepancy in the computational model presented below.
On the timescale of hours to days over which compaction of 3D gels occurs, we found that strain avoidance could not explain the alignment responses that we observed. When cultured statically or at frequencies too low to induce reorientation, cells in gels restrained in the x1 direction aligned just as strongly regardless of whether they compacted only in the x2 direction or equally in both directions (Figs. 2 and 3). Thus, we believe that the data presented here support the alternate hypothesis that cell alignment in these experiments was primarily determined by the presence or absence of a restraining boundary condition. This alternate hypothesis fits better with prior observations that cells in collagen gels actively remodel the surrounding collagen as well as their attachments to it on a timescale of hours to days, making it difficult to imagine how cells would “remember” compaction strains over these longer times. The boundary condition hypothesis would also be consistent with a prior study by Lee et al. (7), which allowed cell and collagen alignment to develop in uniaxially restrained collagen gels and then switched the direction of restraint from x1 to x2. After the switch, cells reoriented rapidly in the new direction of restraint (and away from the dominant collagen fiber direction) and then gradually began reorienting collagen fibers toward the new preferred cell direction. This result suggested that the cells could sense and respond to a change in the direction of restraint independent of the alignment cues provided by surrounding collagen fibers but did not directly address the role of compaction strains vs. restraint.
Computational Predictions of Cell Alignment.
To explore potential mechanisms that might explain the experimental results reported here, we modified a previously published model by Vigliotti et al. (15) that predicts the steady-state distribution of SFs by accounting for the effects of imposed stretch and shortening on the kinetics of SF assembly and disassembly. The equations and details of the modified model are presented in Supporting Information, but conceptually, we made two modifications that reflect our proposed explanations for the findings presented above.
Our first modification to the original model by Vigliotti et al. (15) was to assume that cells can remodel the surrounding collagen, their attachments to that collagen, and their cytoskeleton over timescales much longer than an individual loading cycle to achieve a state at which the increase in elastic energy due to stretching the cell beyond its reference configuration was balanced by the decrease in cytoskeletal free energy due to SF assembly (Fig. S1). As noted above, there is ample experimental evidence that cells embedded in collagen gels do remodel the surrounding collagen and their attachments (24–26), but the hypothesis that this remodeling minimizes the free energy of the cell remains to be tested. When both the x1 and x2 directions were restrained as in our strip uniaxial stretching experiments, cells reached this minimum energy state at stretches F11 = 1.062, F22 = 1.062 (Fig. S1A). By contrast, when the x1 direction was constrained and the x2 direction was left free as in our uniaxial stretching experiments, cells reached equilibrium at stretches F11 = 1.075, F22 = 0.7893 (Fig. S1 B and C). Importantly, these stretches depended on the presence/absence of restraint in each direction but not on the compaction history, because the cells in the model respond to compaction or stretch by shortening or lengthening individual SFs to hold the strain in each actomyosin subunit constant. Integrating these equilibrium stretches into the model by Vigliotti et al. (15) resulted in nearly isotropic predicted SF distributions for strip uniaxial stimulations of static and low-frequency stretch conditions (Fig. 3I). By contrast, in all uniaxial simulations where the x2 boundary of the gels was left free, the model predicted strong SF alignment in the x1 direction (Fig. 3 C and F), consistent with the experimentally measured cell orientation distributions.
Our second modification accounts for the fact that, when cells are embedded in very soft gels, the cells and gel act as springs in series, and the cells experience only a fraction of the stretch applied globally to the gel (27). In the model by Vigliotti et al. (15), large negative strain rates lead to lower SF forces due to the force–velocity behavior of myosin, discouraging parallel assembly and encouraging perpendicular assembly. Assuming that cells experience all of the global applied stretch in 2D but only a fraction of that stretch in a soft 3D gel, the model predicted that higher frequencies (or higher stretches) are required to modify SF distributions in 3D vs. 2D, in agreement with our 3D experiments and published 2D data (Fig. 4B; orientation histograms for 3D simulations are provided in Fig. S2 D and H). Together, these two modifications to the model by Vigliotti et al. (15) allowed it to correctly predict not only the classic frequency-dependent perpendicular orientation response for 2D cyclic stretch experiments but also the following alignment responses reported here. (i) Under uniaxial restraint, cells in gels align parallel to the restraint, regardless of the degree of transverse compaction. (ii) Superimposing uniaxial cyclic stretch decreases the strength of that alignment in a frequency-dependent manner. (iii) Under biaxial restraint, cells in gels align randomly. (iv) Superimposing uniaxial cyclic stretch promotes perpendicular alignment in a frequency-dependent manner.
A number of published models have addressed the effects of mechanical stretch on cell orientation (14, 15, 23, 28, 29). Several of these are conceptually similar: they use a set of differential equations to track the assembly and disassembly of SF families or subsets oriented in different directions and then introduce experimentally motivated phenomenologic terms that modify the assembly or disassembly rates. For example, Kaunas and Hsu (28) assumed that stretch or shortening of an SF relative to its preferred homeostatic length promotes disassembly; in this model, cyclic stretching induces cell alignment perpendicular to the stretch direction by forcing SF disassembly in that direction. Deshpande et al. (23) assumed that stress within the SFs reduces the disassembly rate, so that cells develop more SFs on stiffer substrates and along the local direction of greatest resistance to cell contraction; in their model, uniaxial cyclic stretch reduces stress in SFs parallel to the stretch direction through the force–velocity behavior of the actomyosin subunits, resulting in disassembly of parallel SFs and net cell orientation perpendicular to the stretch. Obbink-Huizer et al. (14) constructed a similar model but assumed that higher SF tension promotes SF assembly rather than inhibits disassembly. They included not only force–velocity but also, force–length behavior of the SFs, such that active stress generation by the SFs decreased with either stretch or shortening (14); as a consequence, cells in their model turn perpendicular to an applied cyclic stretch or to a cell-induced compaction strain, with the larger strain dominating when both are present. The model by Vigliotti et al. (15) used here incorporates some of the key components of previous models (such as force–length and force–velocity behaviors of actomyosin) into a thermodynamically motivated framework, in which stresses or deformations influence SF assembly by altering the free energy of bound actomyosin subunits (15).
All of these models capture the experimental observation that cells on 2D substrates align parallel to a static stretch but perpendicular to an applied uniaxial cyclic stretch. Adding our assumption that only a fraction of the globally applied stretch is transferred to cells in soft gels would likely allow several of these models to also capture the difference in transition frequency between 2D and 3D experiments (Fig. 4). Of these models, only the model by Obbink-Huizer et al. (14) and the model by Vigliotti et al. (15) correctly predict that cells embedded in a 3D gel align parallel to uniaxial cyclic stretch, but both models rely on the magnitude of transverse compaction strains to make this prediction. In the model by Obbink-Huizer et al. (14), compaction strains perpendicular to the stretch direction reduce perpendicular SF assembly much more than the cyclic stretching reduces parallel SF assembly. In the model by Vigliotti et al. (15), SFs rapidly add or subtract actomyosin subunits along their length to hold the strain on individual subunits constant; large compaction strains perpendicular to stretch produce very short SFs in that direction, which are thermodynamically less stable than the longer SFs that persist in the stretch direction. Based on the experimental data presented here, our revised model proposes a slightly different mechanism: in the absence of external restraint, the minimum energy equilibrium state for a cell embedded in a soft gel is one with very short, unstable SFs, while in the presence of restraint, equilibrium is achieved with longer, more stable SFs. In the presence of anisotropic boundary conditions, the SFs in different directions achieve a mix of these states, and perturbations due to cyclic stretch are then superimposed on this basal state. One conceptual advantage of this mechanism is that it does not assume that cells remember compaction strains that may have occurred days or weeks earlier or even that changes induced in the cytoskeleton by compaction are maintained over long times; rather, it assumes only that the cell will continually remodel its cytoskeleton, surrounding ECM, and/or connections to that ECM to seek a minimum energy state.
Limitations and Sources of Error.
Most models of the effects of stretch on cell orientation (including the one used here) predict distributions of SFs within a single hypothetical cell. However, most experiments quantify the alignment of many cells subjected to a given experimental condition to account for biologic variability and stochasticity that may not be represented in models. Thus, we do not expect model-predicted SF distributions to precisely match experimentally measured cell orientation distributions (Fig. 3 and Fig. S2). Instead, we focused on features, such as mean orientation and strength of alignment, that we expected to be more comparable. To test whether these features are, in fact, comparable between SF and cell orientation distributions, we measured SF and cell orientations in the same subset of cells. The mean orientation computed from SFs within each cell [mean angle of SF (MASF)] correlated almost 1:1 with the alignment of that same cell computed from the cell boundary (MAcell), increasing our confidence in comparisons between model-predicted mean SF orientation and experimentally measured mean cell orientation (Fig. S3A). The strength of alignment computed from analyzing SFs [mean vector length of SF (MVLSF)] also correlated with but was consistently lower than that computed from the cell boundary (MVLcell) (Fig. S3B). On a cell by cell basis, this observation reflects the fact that, even in cells that were clearly spindle-shaped and strongly aligned in a preferred direction, we frequently observed individual SFs oriented away from the primary cell axis.
Limitations of the computational model presented here include the fact that we validated its predictions of cell alignment responses against experimental results for cyclic stretch at a range of frequencies from 0 to 4 Hz and amplitudes ranging from 0 to 10%, but predictions for other frequencies and amplitudes remain to be validated. In addition, although we expect that collagen gels that compacted more in the x2 than in the x1 direction in our experiments also developed some degree of collagen fiber alignment along the x1 axis, we did not measure those collagen orientations or include them in our computational model of cell alignment. Our primary justification for this omission is that prior studies have clearly shown that isotropic compaction maintains random collagen orientation in the x1–x2 plane in these gels (11), yet some of our gels developed very strong cell alignment in the presence of isotropic compaction strains (i.e., the 24-h group in Fig. 2 D–F). Thus, while contact guidance is certainly an important alignment cue in many settings, in our experiments, it does not seem to be the dominant mechanism underlying cell alignment. Finally, the free energy minimization approach used here to compute the equilibrium strain state of simulated cells ignored exchange of nutrients and heat with the surrounding bath and neglected the entropy and distribution of states observed in actual cell populations.
Materials and Methods
Fabrication and Loading of Fibroblast-Populated Collagen Gels.
We isolated and cultured adult rat cardiac fibroblasts and generated fibroblast-populated collagen hydrogels as previously published (17, 30); details are provided in Supporting Information. Gels containing a final concentration of 200,000 cells per 1 mL and 2 mg/mL collagen were polymerized and constrained in both directions or left to compact isotropically during a 24-h preculture period before transfer to the loading system (Fig. 1A). We used CellScale MechanoCulture B1 devices (CellScale) to either statically or dynamically load the cell-populated collagen hydrogels (Fig. 1B). These devices included a “dry” side, housing a circuit board and motor that could be programmed for a variety of amplitudes or frequencies of stretch (Fig. 1B, Right) connected by a stainless steel bridge to a “wet” side filled with 10% FBS-containing media. Three interconnected deformable polyether ether ketone plastic layers transferred linear motion of the bridge into stretch of an inner circle (3.6-cm diameter) of 24 pins. We pinned the arms of the collagen gels in the x1 direction and either pinned the arms in the x2 direction to prevent compaction (strip uniaxial stretch) or cut them off to allow compaction (uniaxial stretch).
We transferred gels initially cultured under biaxial constraint to the B1 devices and subjected them to 0% uniaxial stretch (x1 direction constrained, x2 direction left free to compact), 10% cyclic uniaxial stretch (stretch applied in the x1 direction, x2 direction left free to compact) (Fig. 1C), 0% strip uniaxial stretch (both directions constrained), or 10% cyclic strip uniaxial stretch (stretch applied in the x1 direction, x2 direction held fixed) (Fig. 1D). In this paper, we use “0% strip uniaxial stretch” and “0% uniaxial stretch” (synonymous to biaxial and uniaxial constraint, respectively) to differentiate these loading conditions in the stretcher from the preculture conditions. We also transferred the gels that initially floated freely in media and compacted isotropically to CellScale devices and subjected them to either 0% uniaxial stretch or 10% cyclic uniaxial stretch (Fig. 1E). We mapped the time course of the static (0%) and low-frequency (10%; 0.5 Hz) responses using 15 gels for each of these six conditions: 5 gels stretched for 24 h, 5 gels stretched for 48 h, and 5 gels stretched for 72 h. We explored the effect of higher frequencies by stretching gels for 72 h under each of the following conditions: 10% cyclic uniaxial stretch at 2 Hz (n = 5), 10% cyclic uniaxial stretch at 4 Hz (n = 4), 10% cyclic strip uniaxial stretch at 2 Hz (n = 5), and 10% strip cyclic uniaxial stretch at 4 Hz (n = 5). The five gels in any one experimental group contained cells from five separate rat fibroblast isolations. In addition to the 109 gels listed above, 8 gels underwent the initial preculture step only (n = 4 biaxial constraint, n = 4 isotropic compaction).
Quantification of Gel Compaction.
We applied nine titanium oxide paint dots, consisting of 1 g/mL Titanium(IV) oxide powder (Sigma-Aldrich) mixed with PBS, on the surface of the central region of the gel (box in Fig. 1A) with a 7-0 nylon suture (1647G; Ethicon) and used these markers to track compaction over the course of the experiment. We used a digital camera to image the markers before the preculture period, after the preculture period before the onset of loading, and at the end of each loading protocol. All images were taken when the stretching devices were at the 0% strain position, and therefore, marker positions in these images reflected the deformations due to gel compaction. We used the markers to compute a single homogeneous deformation gradient tensor F that provided the least squares best fit mapping of the nine marker positions from the undeformed (X, beginning of experiment) to deformed (x) positions by solving the overdetermined matrix equation:
| [1] |
where p is an arbitrary vector included to account for translation between images.
Microscopy and Quantification of Cell Alignment.
After the stretch protocols, we fixed the gels in 10% formalin, stained the F actin with Alexa Fluor 488 Phalloidin (A12379; Thermo Fisher Scientific), and used a confocal microscope with a 10× objective to capture z stacks consisting of one image every 2.5 µm through the gel thickness at three locations in the central region. Within each z stack, we created 2D projections (Fig. S4A) by combining sets of 10 consecutive images separated by 25 µm, allowing for analysis of nonoverlapping cells at different depths below the gel surface. Using MATLAB, we converted each 2D projection to binary (Fig. S4B, fluorescent pixels = white, dark pixels = black) and analyzed white pixel clusters above a size threshold of 15 × 15 µm (Fig. S4B).
We tracked the orientation and strength of alignment of fibroblasts using mean vectors calculated using Eqs. 2–4, consistent with circular statistics theory for the analysis of angular data (31):
| [2] |
| [3] |
| [4] |
For each cell, we constructed 400 vectors from the centroid to equally spaced points around the cell boundary. We used the lengths and angles of these vectors ( and , with j = 1,2,…N and n = 400) to compute a vector with length, MVLcell, that indicated strength of alignment (ranging from MVLcell = 0 for a circular cell to MVLcell = 1 for a highly aligned, spindly cell), and MA, MAcell, that indicated orientation (Fig. S4C). The 2 terms in Eq. 2 and 1/2 term in Eq. 4 account for the fact that the full range of possible angles is only 180°, since a cell oriented horizontally could be correctly described as oriented at 0° or at 180° (31). We then combined the individual cell vectors for all cells in each gel and used Eqs. 2–4 to compute a mean vector that reflected the mean strength of cell alignment within each gel (MVLgel; ranging from MVLgel = 0, all cells aligned randomly, to MVLgel = 1, all cells aligned in the same direction) and direction (MAgel) for the entire gel (Fig. S4D). Finally, we averaged MVLgel values across the n = 5 gels for each experimental condition.
Quantification of Parallel vs. Perpendicular Alignment of Cells and SFs.
To quantitatively compare the alignment and directionality of experimentally measured cells and computationally simulated SFs at different frequencies, we used an order parameter (21, 22):
| [5] |
where represents the probability distribution histogram of cells or SFs in each angular bin. S ranges from S = 1, all cells or SFs aligned completely parallel to the stretch (x1) direction, to S = −1, all cells or fibers aligned completely perpendicular to stretch, with S = 0 representing random alignment.
Experimental Measurements of Cell Alignment in 2D.
Jungbauer et al. (22) explored the effects of various stretch amplitudes and frequencies on cells cultured on top of 2D silicone elastomer membranes and used the same S = <cos2θ> order parameter (Eq. 5) to measure cell alignment. We digitized their figures for rat embryonic fibroblasts subjected to 30 × 103 s (8.33 h) of 8% uniaxial cyclic stretch at 0.01, 0.25, 2, and 15 Hz to obtain their mean ± SD alignment values for 30–50 cells per tested frequency.
Statistics.
We used a two-way ANOVA to assess whether transverse compaction (F22) or alignment (MVL) varied significantly across the stretch amplitudes (0, 10%; 0.5 Hz) and durations (24, 48, 72 h) tested (Prism; GraphPad Software). We used a one-sample t test to assess whether alignment (either parallel for S > 0 or perpendicular for S < 0) varied significantly from a hypothetical mean of S = 0 (random alignment) at each of our experimentally tested frequencies. We did not run statistics on any of the measurements taken from the work by Jungbauer et al. (22).
Computational Model.
As detailed in Supporting Information, we modified a previously published model by Vigliotti et al. (15) and used it to simulate the experiments reported here. The model represents the thermodynamics of SF assembly and disassembly and was previously shown to reproduce a number of experimentally observed cellular responses to a range of cyclic stretch waveforms applied to cells cultured on deformable 2D substrates. The model incorporates the fundamental observation that tension promotes SF assembly by assuming that tension reduces the free energy of subunits in the bound state. It also incorporates force–length and force–velocity behavior for actomyosin, allowing it to capture phenomena, such as the disassembly of SFs in response to rapid shortening (15). The model by Vigliotti et al. (15) was designed to simulate the response of a single cell to known applied strains. However, cells embedded in collagen gels can locally remodel both the collagen fibers and their attachments to the collagen (7, 24–26) over timescales of minutes to hours, so that the effective cell strain at any time point in our experiments likely differed from the gross compaction strains that we measured using markers. Therefore, we introduced the additional assumption that, over long timescales, the cell maintains an average stress state that minimizes its free energy. Furthermore, embedded cells and the surrounding gel are mechanically in series, so that in very soft gels, the cells experience only a fraction of the applied cyclic strain (27). Therefore, we assumed that only a fraction of the applied cyclic strain was transmitted to cells when simulating 3D stretch, whereas the full applied cyclic strain was transmitted to cells when simulating 2D stretch.
Supplementary Material
Acknowledgments
This work was supported by NIH Grant T32 GM008715 (to K.C.) and National Science Foundation Civil, Mechanical, and Manufacturing Innovation Grant 1332530 (to J.W.H.). A.V. acknowledges support from the Royal Society’s Newton International Fellowship Alumni Program.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1715059115/-/DCSupplemental.
References
- 1.Huang C, et al. Biological effects of cellular stretch on human dermal fibroblasts. J Plast Reconstr Aesthet Surg. 2013;66:e351–e361. doi: 10.1016/j.bjps.2013.08.002. [DOI] [PubMed] [Google Scholar]
- 2.Moretti M, Prina-Mello A, Reid AJ, Barron V, Prendergast PJ. Endothelial cell alignment on cyclically-stretched silicone surfaces. J Mater Sci Mater Med. 2004;15:1159–1164. doi: 10.1023/B:JMSM.0000046400.18607.72. [DOI] [PubMed] [Google Scholar]
- 3.Kaunas R, Nguyen P, Usami S, Chien S. Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proc Natl Acad Sci USA. 2005;102:15895–15900. doi: 10.1073/pnas.0506041102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ives CL, Eskin SG, McIntire LV. Mechanical effects on endothelial cell morphology: In vitro assessment. In Vitro Cell Dev Biol. 1986;22:500–507. doi: 10.1007/BF02621134. [DOI] [PubMed] [Google Scholar]
- 5.Karlon WJ, et al. Measurement of orientation and distribution of cellular alignment and cytoskeletal organization. Ann Biomed Eng. 1999;27:712–720. doi: 10.1114/1.226. [DOI] [PubMed] [Google Scholar]
- 6.Hsu HJ, Lee CF, Kaunas R. A dynamic stochastic model of frequency-dependent stress fiber alignment induced by cyclic stretch. PLoS One. 2009;4:e4853. doi: 10.1371/journal.pone.0004853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lee EJ, Holmes JW, Costa KD. Remodeling of engineered tissue anisotropy in response to altered loading conditions. Ann Biomed Eng. 2008;36:1322–1334. doi: 10.1007/s10439-008-9509-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Foolen J, Deshpande VS, Kanters FMW, Baaijens FPT. The influence of matrix integrity on stress-fiber remodeling in 3D. Biomaterials. 2012;33:7508–7518. doi: 10.1016/j.biomaterials.2012.06.103. [DOI] [PubMed] [Google Scholar]
- 9.Matsumoto T, et al. Three-dimensional cell and tissue patterning in a strained fibrin gel system. PLoS One. 2007;2:e1211. doi: 10.1371/journal.pone.0001211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Roby T, Olsen S, Nagatomi J. Effect of sustained tension on bladder smooth muscle cells in three-dimensional culture. Ann Biomed Eng. 2008;36:1744–1751. doi: 10.1007/s10439-008-9545-5. [DOI] [PubMed] [Google Scholar]
- 11.Bellows CG, Melcher AH, Aubin JE. Association between tension and orientation of periodontal ligament fibroblasts and exogenous collagen fibres in collagen gels in vitro. J Cell Sci. 1982;58:125–138. doi: 10.1242/jcs.58.1.125. [DOI] [PubMed] [Google Scholar]
- 12.Hu J-J, Humphrey JD, Yeh AT. Characterization of engineered tissue development under biaxial stretch using nonlinear optical microscopy. Tissue Eng Part A. 2009;15:1553–1564. doi: 10.1089/ten.tea.2008.0287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pang Y, Wang X, Lee D, Greisler HP. Dynamic quantitative visualization of single cell alignment and migration and matrix remodeling in 3-D collagen hydrogels under mechanical force. Biomaterials. 2011;32:3776–3783. doi: 10.1016/j.biomaterials.2011.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Obbink-Huizer C, et al. Computational model predicts cell orientation in response to a range of mechanical stimuli. Biomech Model Mechanobiol. 2014;13:227–236. doi: 10.1007/s10237-013-0501-4. [DOI] [PubMed] [Google Scholar]
- 15.Vigliotti A, Ronan W, Baaijens FPT, Deshpande VS. A thermodynamically motivated model for stress-fiber reorganization. Biomech Model Mechanobiol. 2016;15:761–789. doi: 10.1007/s10237-015-0722-9. [DOI] [PubMed] [Google Scholar]
- 16.Costa KD, Lee EJ, Holmes JW. Creating alignment and anisotropy in engineered heart tissue: Role of boundary conditions in a model three-dimensional culture system. Tissue Eng. 2003;9:567–577. doi: 10.1089/107632703768247278. [DOI] [PubMed] [Google Scholar]
- 17.Thomopoulos S, Fomovsky GM, Chandran PL, Holmes JW. Collagen fiber alignment does not explain mechanical anisotropy in fibroblast populated collagen gels. J Biomech Eng. 2007;129:642–650. doi: 10.1115/1.2768104. [DOI] [PubMed] [Google Scholar]
- 18.Knezevic V, Sim AJ, Borg TK, Holmes JW. Isotonic biaxial loading of fibroblast-populated collagen gels: A versatile, low-cost system for the study of mechanobiology. Biomech Model Mechanobiol. 2002;1:59–67. doi: 10.1007/s10237-002-0005-0. [DOI] [PubMed] [Google Scholar]
- 19.de Jonge N, Kanters FMW, Baaijens FPT, Bouten CVC. Strain-induced collagen organization at the micro-level in fibrin-based engineered tissue constructs. Ann Biomed Eng. 2013;41:763–774. doi: 10.1007/s10439-012-0704-3. [DOI] [PubMed] [Google Scholar]
- 20.Terracio L, Miller B, Borg TK. Effects of cyclic mechanical stimulation of the cellular components of the heart: In vitro. In Vitro Cell Dev Biol. 1988;24:53–58. doi: 10.1007/BF02623815. [DOI] [PubMed] [Google Scholar]
- 21.Hsu H-J, Lee C-F, Locke A, Vanderzyl SQ, Kaunas R. Stretch-induced stress fiber remodeling and the activations of JNK and ERK depend on mechanical strain rate, but not FAK. PLoS One. 2010;5:e12470. doi: 10.1371/journal.pone.0012470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jungbauer S, Gao H, Spatz JP, Kemkemer R. Two characteristic regimes in frequency-dependent dynamic reorientation of fibroblasts on cyclically stretched substrates. Biophys J. 2008;95:3470–3478. doi: 10.1529/biophysj.107.128611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Deshpande VS, McMeeking RM, Evans AG. A bio-chemo-mechanical model for cell contractility. Proc Natl Acad Sci USA. 2006;103:14015–14020. doi: 10.1073/pnas.0605837103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Moon AG, Tranquillo RT. Fibroblast‐populated collagen microsphere assay of cell traction force. Part 1. Continuum model. AIChE J. 1993;39:163–177. doi: 10.1115/1.2795998. [DOI] [PubMed] [Google Scholar]
- 25.Pizzo AM, Kokini K, Vaughn LC, Waisner BZ, Voytik-Harbin SL. Extracellular matrix (ECM) microstructural composition regulates local cell-ECM biomechanics and fundamental fibroblast behavior: A multidimensional perspective. J Appl Physiol (1985) 2005;98:1909–1921. doi: 10.1152/japplphysiol.01137.2004. [DOI] [PubMed] [Google Scholar]
- 26.Kim A, Lakshman N, Petroll WM. Quantitative assessment of local collagen matrix remodeling in 3-D culture: The role of Rho kinase. Exp Cell Res. 2006;312:3683–3692. doi: 10.1016/j.yexcr.2006.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ujihara Y, et al. Computational studies on strain transmission from a collagen gel construct to a cell and its internal cytoskeletal filaments. Comput Biol Med. 2015;56:20–29. doi: 10.1016/j.compbiomed.2014.10.015. [DOI] [PubMed] [Google Scholar]
- 28.Kaunas R, Hsu HJ. A kinematic model of stretch-induced stress fiber turnover and reorientation. J Theor Biol. 2009;257:320–330. doi: 10.1016/j.jtbi.2008.11.024. [DOI] [PubMed] [Google Scholar]
- 29.De R, Zemel A, Safran SA. Dynamics of cell orientation. Nat Phys. 2007;3:655–659. [Google Scholar]
- 30.Rouillard AD, Holmes JW. Mechanical boundary conditions bias fibroblast invasion in a collagen-fibrin wound model. Biophys J. 2014;106:932–943. doi: 10.1016/j.bpj.2013.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Batschelet E. Circular Statistics in Biology. Academic; London: 1981. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.