Electron mean-free-path filtering in Dirac material for improved thermoelectric performance

Significance

Using ab initio simulations, we uncover the electron mean-free-path (MFP) spectrum in Dirac material and specifically show how the thermoelectric efficiency can greatly benefit from a distinct, monotonically decreasing trend of electron MFPs arising from the linear energy-momentum dispersion implied by the Dirac band topology. In the past, it was generally assumed that for the nanostructuring approach to be effective, one should design nanostructures to have characteristic length larger than the electron MFP but smaller than the phonon MFP to reduce thermal conductivity. Our results show that enhancement in thermoelectric performance can be achieved in Dirac materials even when they are smaller than the electron MFP by selectively filtering out long-MFP electrons that are harmful to the Seebeck coefficient.

Abstract

Recent advancements in thermoelectric materials have largely benefited from various approaches, including band engineering and defect optimization, among which the nanostructuring technique presents a promising way to improve the thermoelectric figure of merit (zT) by means of reducing the characteristic length of the nanostructure, which relies on the belief that phonons’ mean free paths (MFPs) are typically much longer than electrons’. Pushing the nanostructure sizes down to the length scale dictated by electron MFPs, however, has hitherto been overlooked as it inevitably sacrifices electrical conduction. Here we report through ab initio simulations that Dirac material can overcome this limitation. The monotonically decreasing trend of the electron MFP allows filtering of long-MFP electrons that are detrimental to the Seebeck coefficient, leading to a dramatically enhanced power factor. Using SnTe as a material platform, we uncover this MFP filtering effect as arising from its unique nonparabolic Dirac band dispersion. Room-temperature zT can be enhanced by nearly a factor of 3 if one designs nanostructures with grain sizes of ∼10 nm. Our work broadens the scope of the nanostructuring approach for improving the thermoelectric performance, especially for materials with topologically nontrivial electronic dynamics.

Charge transport underlies the operation of modern devices, to name just a few, from transistors to photovoltaic cells to thermoelectric modules. The mean free path (MFP) of the electrons—the average distance the electron can travel before being scattered—provides fundamental knowledge of the energy flow in such devices (1, 2). A large MFP value is often the target parameter as it implies high electron mobility, which leads to better device performance. In practice, however, a single MFP value does not suffice to describe the electron transport, as the electron MFP can be highly energy dependent. Resolving the electron MFP spectrum is therefore of paramount significance for understanding the charge transport and eventually optimizing the device efficiency.

Knowledge of the electron MFPs has gained growing interest in recent years owing to the development of thermoelectric materials. Thermoelectric devices can directly convert heat into electricity without moving parts (3‒10), and their energy conversion efficiency is usually characterized by the material’s figure of merit zT, defined as $\sigma S^{2}T/({\kappa }_e+{\kappa }_{\text{ph}}),$ where σ is the electrical conductivity, S is the Seebeck coefficient, κ_e and κ_ph are the electron and phonon contributions to the thermal conductivity, respectively, and T is the absolute temperature. To improve zT, one often seeks to partially decouple the electron and phonon transport, which is aimed at either increasing the electrical properties or reducing the lattice thermal conductivity. Among various strategies, the band structure approach has led to several high-zT thermoelectric materials (11), by manipulating the electronic structure to enhance either the electrical conductivity or the Seebeck coefficient, through, for example, engineering the effective mass (12), band convergence (13), nestification (14), resonant impurity doping (5, 15), and deformation potential (16).

Another successful strategy has been using nanostructures (4, 9), which benefits from the fact that phonons normally have longer MFPs than electrons’ in many materials (17). For the nanostructureing approach to be effective, it is generally believed that the characteristic length of nanostructures should be in between the electron and phonon MFPs so that phonons are scattered much stronger, leading to reduced thermal conductivity while the electrical conduction is barely affected. This idea has been applied to various material systems over a broad temperature range to achieve enhanced thermoelectric efficiency, e.g., in PbTe (9), and Bi_1−xSb_x (4), Si_1−xGe_x (18), and Pb_1−xSn_xTe (19) alloys. The improved thermoelectric efficiency is attributed to the lowered thermal conductivity due to increased phonon scatterings at grain boundaries and interfaces, while maintaining the electrical transport. The common wisdom of the nanostructuring approach, however, ignores any possible enhancement in the Seebeck coefficient due to filtering of electrons when nanostructure sizes are comparable to those of electron MFPs. While traditional semiconductors like Si possess simple parabolic band structure with a nearly constant electron MFP, complex materials may offer unique opportunities regarding the MFP spectrum. In particular, several of the best thermoelectric materials such as SnTe (13, 15, 20, 21) and the Bi_1−xSb_x alloy (4) show topologically nontrivial Dirac band structure, with highly nonparabolic band dispersion. This feature could potentially lead to a significant energy-dependent electron MFP that defies traditional models and allow for enhancement in thermoelectric efficiency, especially in the electrical part (the power factor σS²), even when nanostructure sizes approach those of dominant electron MFPs. In fact, the nanostructuring approach has seen success in certain materials when the sizes are pushed down to tens of nanometers (22). Even so, the reason behind the efficiency enhancement remains unclear, particularly hindered by the unknown electron MFPs.

Experimentally resolving the electron MFP requires characterization techniques that can distinguish different states with mode-level details. Although the energy-resolved spectrum is now routinely obtained by spectroscopic methods (e.g., angle-resolved photoemission spectroscopy for electrons) (23, 24), the requirement of single crystals often limits their applications. Furthermore, to estimate MFPs one needs to derive the scattering rate based on the spectral linewidth, which is usually complicated by extrinsic events (instruments, measurement procedures, etc.). Until now, no report has existed for the energy-dependent electron MFPs in low thermal conductivity thermoelectric materials at room temperature. On the other hand, predictions of electron MFPs as well as transport properties using ab initio methods received greater attention only recently due to the development of an efficient interpolation scheme based on Wannier functions for evaluating the electron–phonon (e-ph) coupling matrix (25‒27), which is the key limiting factor for the electron transport. Despite the successful demonstrations in a series of benchmarked materials, including Si (28‒30), GaAs (31, 32), perovskites (33, 34), and 2D materials (35‒39), obtaining the electron MFPs for most good thermoelectric materials, in particular the Dirac materials like SnTe and Bi_1−xSb_x alloy, still presents a challenge. One major difficulty comes from the fact that they often possess complex band structure or phonon dispersion, which requires ultradense meshes to reach the convergence for the transport calculation.

Here we take on the challenge of studying the thermoelectric transport properties (σ, S, κ_e, and κ_ph) in p-type SnTe—a member of the chalcogenide thermoelectric system as well as a representative Dirac material, characterizing topologically nontrivial Dirac band dispersion. This study fully evaluates the thermoelectric property for a practical material within first principles and presents significant progress in understanding the electron transport toward complex systems. Using ab initio simulation, we study the electron MFPs in Dirac materials. The energy dependence of the spectrum differs from that of conventional semiconductors, which is a result of the linear band dispersion induced by the strong spin-orbit coupling (SOC) that mixes the conduction and valence manifolds (40, 41), in stark contrast to the typical parabolic shape seen in conventional semiconductors. Remarkably, we show that this MFP spectrum allows one to filter out long-MFP electrons that are detrimental to the Seebeck coefficient in the degenerate regime, thereby improving the power factor even when nanostructure sizes are comparable to those of electron MFPs. This strategy focuses on selectively scattering electrons based on their MFPs, thereby contrasting with the traditional concept based on “electron energy filtering” (42, 43), where the power factor enhancement is due to the thermionic emission contributed by high-energy electrons. Our study suggests a different direction in improving the thermoelectric performance of materials possessing unique electronic dynamics through the electron MFP filtering effect and potentially leads to discovery of a better thermoelectric system by extending the nanostructuring approach to a larger scope.

Results and Discussion

Ab Initio Scattering Rates and Transport Properties.

Electron transport properties crucially depend on the band structure. For rock-salt structures (e.g., SnTe) with band edge at the L point, the band structure near the band edge can be well characterized by the k·p Hamiltonian, which is given by Mitchell and Wallis (44),

$$H\left(k\right)=m{s}_z{\sigma }_z+\left(v_{f,1}{k}_1{s}_y-v_{f,2}{k}_2{s}_x\right){\sigma }_x+v_{f,3}{k}_3{\sigma }_y,$$ [1]

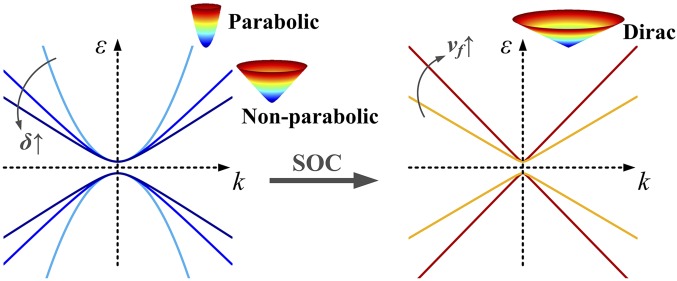
where σ_j is the Pauli matrix, and s_j = ±1 denotes the spin polarization. m is the Dirac mass generated by broken mirror symmetry, with an energy gap of 2|m|, and v_f,i is the Fermi velocity in the ith direction. The electron energy of the Dirac band structure derived from Eq. 1 is ε = ±$\sqrt{m^2+{\mathrm{\Sigma }}_i{v}_{f,i}^2{k}_i^2}$. Both m and v_f,i depend on the SOC strength and inevitably affect the band shape. In Fig. 1, we compare the Dirac bands with linear dispersion (Fig. 1, Right) to the conventional semiconductors commonly with typical nonparabolic band structures (Fig. 1, Left). The nonparabolic band is modeled as a Kane band, ε(1 + δε) = ħ²|k|²/2m_eff, where m_eff is the effective mass of the electron and δ is the band nonparabolicity (δ = 0 corresponds to the parabolic band) (45). The nonparabolicity appears in the band structure in many kinds of semiconductors, for instance, in Si δ = 0.50 and in GaAs δ = 0.61 (46). In this viewpoint, the Dirac band is also not parabolic; the linear energy-momentum relation is induced by the relativistic SOC effect, which usually happens in narrow-gap semiconductors consisting of heavy atoms. The band nonparabolicity has been shown to have profound impact on transport behaviors (47). In this work, we further illustrate that the SOC-induced nonparabolicity is the cornerstone of the electron MFP filtering effect for improving thermoelectric properties and show that the materials with the Dirac band have more benefit for applying this filtering concept in the degenerate regime where most thermoelectric materials reside.

Fig. 1.

A schematic illustration of electronic band structures with different dispersion relations. (Left) Light to dark blue lines show the evolution of the Kane band due to increasing nonparabolicity. (Right) The yellow line indicates the linear dispersion relation of the Dirac band, and the dark red line displays the band shape with a higher Fermi velocity. The rainbow colors on the cones indicate the constant energy contours from a low (colored in blue) to a high (in red) energy level.

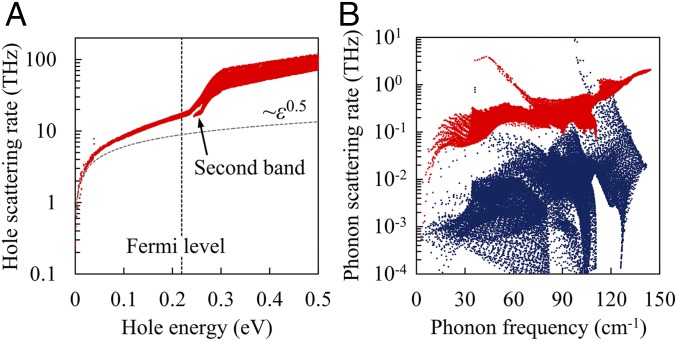
First, we discuss the ab initio scattering rates of holes and phonons in p-type SnTe as they are the key determining factors for the thermoelectric properties. The density-functional theory band structures, e-ph coupling strength, and hole mobility can be seen in Fig. S1, and the convergence tests are shown in Fig. S2. The mathematical and simulation details of our ab initio computational framework are provided in SI Notes, Carriers’ Interactions and Transport Properties and Simulation Details, respectively. Fig. 2A shows the energy-dependent scattering rates of a hole in the valence band within the energy range of 0.5 eV at a carrier concentration of 1.0 × 10²⁰ cm⁻³. Near the band edge, the energy dependence of the scattering rate significantly deviates from the trend of the parabolic band (τ⁻¹ ∼ $\sqrt{\epsilon }$) (46). It is known that acoustic phonons can affect the trend of the scattering rate once their dispersion relations no longer follow linearity near the Brillouin zone center; however, it is not the case for SnTe (see Fig. S1B for phonon dispersion). The deviation is more an indication of the nonparabolic feature inherent in SnTe due to the strong SOC between lowest Sn and upper Te orbitals. This linear energy-momentum relation in Dirac materials leads to a larger slope of scattering rates compared with that of the parabolic band. Furthermore, the polar-optical-phonon scattering is weak in SnTe because of its large dielectric response (ε_∞ = 45 for high-frequency and ε_s = 1,770 for static response) (48), leading to effective suppression of the long-range dipole field. We further decompose the scattering rates into contributions from different phonon branches (Fig. S3). The dominant scattering comes from the deformation potential associated with the longitudinal-optical phonons, while transverse-optical and acoustic phonons have weaker scatterings. This is characteristic of a weakly polar material and is very different from GaAs (a typical strongly polar material) whose electron transport is mainly limited by electron–LO–phonon couplings. The unique Dirac band structure in SnTe and its dielectric response as mentioned above have a significant impact on the electron transport, as we discuss later. For the optimization of zT, we have also performed ab initio calculations for the phonon transport in p-type SnTe. We computed the phonon–phonon (ph-ph) scattering rates and added the phonon–electron (ph-e) scattering rates based on Matthiessen’s rule at different carrier concentrations. The ph-e scattering rates are one order of magnitude smaller than the ph-ph scattering even at high carrier concentrations as shown in Fig. 2B, indicating a smaller effect of e-ph interaction on the lattice thermal conductivity of SnTe.

Fig. 2.

Carriers’ scattering rates of p-type SnTe with carrier concentration 1.0 × 10²¹ cm⁻³ at 300 K. (A) Energy-dependent hole scattering rates. Zero point refers to the valence band maximum. The red dots are obtained by ab initio calculations, and the dashed gray line shows the trend (∼$\sqrt{\epsilon }$) given by deformation-potential scattering in the parabolic band. (B) Frequency-dependent phonon scattering rates due to lattice anharmonicity (colored in red) and ph-e interactions (colored in blue).

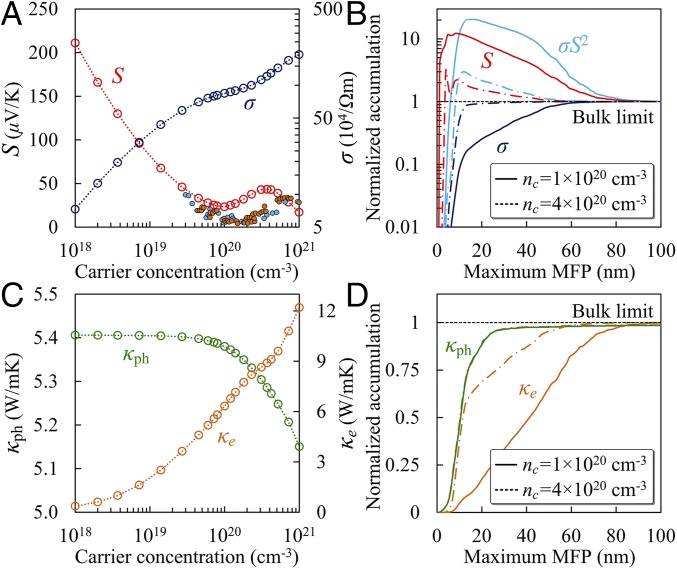
With the ab initio scattering rates, we have obtained the full thermoelectric properties (S, σ, κ_e, and κ_ph) by solving the Boltzmann transport equation. In Fig. 3 we plot these transport properties, along with their accumulation functions with respect to the MFPs. The electrical conductivity increases monotonically as the carrier concentration becomes larger. However, the Seebeck coefficient exhibits a hump at a carrier concentration around 4.0 × 10²⁰ cm⁻³, which comes from the contribution of the second valley located along the Σ line (Г → K) in the valence band. Employing the constant relaxation time approximation (CRTA) here will largely overestimate the Seebeck coefficient at high carrier concentrations; the Seebeck coefficient at the local minima point given by CRTA is 87.1 μV/K, while the ab initio calculation leads to 22.3 μV/K, a more reasonable value compared with experimental measurements (49‒51). This difference is due to the oversimplification of CRTA that ignores the energy dependence of the scattering rates, while as we have seen in Fig. 2A, the scattering rates vary rapidly as a function of energy, and in particular, the appearance of the second valley creates additional intervalley scattering channels between the first and second valleys. These results emphasize the importance of capturing the mode-level details of e-ph couplings in computing the transport properties for thermoelectric materials. In Fig. 3C we also report the room-temperature lattice and electronic thermal conductivity at different carrier concentrations. The lattice thermal conductivity slightly decreases as carrier concentration increases (5% reduction at a carrier concentration of 1.0 × 10²¹ cm⁻³), due to the minor effect of ph-e scattering on phonon transport, which is very different from the case of heavily doped p-type Si (up to 45% reduction in thermal conductivity) where most holes are populated at the Г valley (52). On the other hand, the electronic thermal conductivity shows a similar trend to that of the electrical conductivity, which is consistent with the Wiedemann–Franz law with a nearly constant Lorenz number in the degenerate regime (Fig. S4).

Fig. 3.

Thermoelectric properties and MFP spectrum of p-type SnTe with respect to different carrier concentrations at 300 K. (A) Seebeck coefficient (colored in red) and electrical conductivity (colored in blue). The solid circles are experimental data by Rogers (50) and Zhou et al. (51). (B) Spectral distributions of Seebeck coefficient and electrical conductivity at two representative carrier concentrations. The spectrum for the power factor is colored in light blue. (C) Lattice thermal conductivity (colored in green) and electronic thermal conductivity (colored in orange). (D) Spectral distributions of lattice thermal conductivity and electronic thermal conductivity at two representative carrier concentrations.

The calculations of transport properties in this work are performed on idealized SnTe. The stoichiometric sample, however, generally contains about 2–4% of Sn vacancies (49‒51, 53). In this regard, a comprehensive study on SnTe (53) has indicated that the crystal structure can be substantially affected by the disorder and shows strong sample dependence due to the high mosaicity and residual strain in the grain domains. Therefore, it is necessary to have a detailed discussion on the discrepancies in the crystal structure and transport properties between the pristine and stoichiometric SnTe, which is provided in SI Notes, Comparisons for ab Initio Results with Experiments.

Electron MFP Filtering Effect.

Electron and phonon MFP spectra are crucial quantities for evaluating the nanostructuring technique, but have been missing in past literature so far for materials with inherently low thermal conductivity. Fig. 3 B and D shows the room-temperature MFP spectra for the four thermoelectric transport properties at two carrier concentrations—1.0 × 10²⁰ and 4.0 × 10²⁰ cm⁻³, corresponding to different Fermi-level positions that are deep inside the band. At carrier concentration 1.0 × 10²⁰ cm⁻³, the dominant electrons in electrical transport (S, σ, and κ_e) have a broader MFP spectrum up to 100 nm. However, at higher carrier concentrations (4.0 × 10²⁰ cm⁻³), these electron MFPs are reduced to around 10 nm, due to more available scattering channels for e-ph interaction. In comparison, the dominant phonon MFPs are not very sensitive to the carrier concentration and are between 10 nm and 30 nm, which are in fact in the same range as the electron MFPs. This raises the question of how effective the nanostructuring technique can be, as it normally relies on the fact that phonon MFPs are much longer than electron MFPs. In the following we show that the nanostructuring strategy can still be very effective due to the electron MFP filtering effect, which drastically enhances the Seebeck coefficient despite the reduced electrical conductivity when the nanostructure sizes become comparable to those of the dominant electron MFPs.

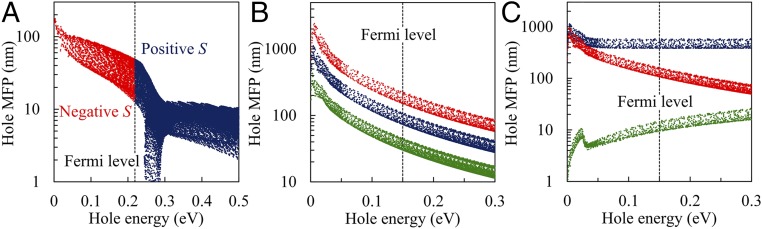
As seen in Fig. 3B, the cumulative Seebeck coefficient can be significantly larger than its bulk limit only if electrons with MFPs up to certain values are considered for the transport, which translates into a much larger power factor compared with the corresponding bulk limit (an enhancement ratio of 20 at a carrier concentration of 1.0 × 10²⁰ cm⁻³ and of 3 at 4.0 × 10²⁰ cm⁻³). This can be understood if we plot the energy-dependent hole MFP, as displayed in Fig. 4A. The MFPs generally decrease as the hole energy increases. At a high carrier concentration, the Fermi level is located inside the valence band (dashed line in Fig. 4A), with holes on the two sides contributing to the Seebeck coefficient with opposite signs because their contributions per carrier are proportional to $\epsilon -{\epsilon }_f$ (46). Limiting the hole MFPs up to a certain value is therefore equivalent to cutting off the holes that are closer to the band edge. This filters out holes with negative contributions to the Seebeck coefficient and as a result remarkably boosts the power factor.

Fig. 4.

Energy-dependent MFPs of different types of band structures. (A) Hole MFPs of p-type SnTe computed by ab initio calculations with carrier concentration 1.0 × 10²⁰ cm⁻³ at 300 K. The blue dots represent the states that will contribute a positive Seebeck coefficient while the red dots will provide a negative contribution. (B) Hole MFPs computed by a semiempirical model with respect to different Fermi velocity. The values of (v_f, ${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}$) shown by green, blue, and red lines are (0.8v_f, 10⁻⁴), (1.0v_f, 10⁻⁴), and (1.2v_f, 10⁻⁴), respectively. (C) Hole MFPs computed by a semiempirical model with respect to different band nonparabolicity δ and ${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}.$ The values of (δ, ${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}$) shown by green, blue, and red lines are (0, 10⁻¹), (0, 10⁻⁴), and (3, 10⁻⁴), respectively. In modeling, the Fermi level is set to be 0.15 eV and the temperature is 300 K; for other parameters refer to SI Notes, Model for Studying Electron MFP Filtering.

This large electron MFP filtering effect is unique for SnTe and arises from its strong band nonparabolicity due to significant SOC and can be promoted by the large dielectric response. To illustrate this point, a theoretical model considering various scattering mechanisms and different band shapes (including Dirac and nonparabolic Kane bands) is used to study the effectiveness of the MFP filtering approach on the enhancement of the power factor in the spectrum. In this model, the acoustic-deformation potential, optical-deformation potential, and polar-optical-phonon interactions are taken into account to evaluate the e-ph scattering rates and power factor (refer to SI Notes, Model for Studying Electron MFP Filtering for mathematical details and parameters). The polar scattering has a factor ${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}$ that measures the strength of the phonon-induced dipole field in terms of the magnitude of dielectric constants (46). It is generally believed that the deformation-potential scattering dominates when ${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}$ is very small. The band shapes of Dirac and nonparabolic bands are, respectively, controlled by the Fermi velocity and the nonparabolicity parameter as introduced above. At each given temperature and Fermi level, one can find an optimal cutoff MFP (λ_opt) that gives the largest cumulative power factor, denoted here as ${\sigma }_{opt}{S}_{opt}^2.$

We illustrate the effect of Dirac band shape by showing the enhancement ratio of the power factor, ${\sigma }_{opt}{S}_{opt}^2/{\sigma }_{bulk}{S}_{bulk}^2,$ with respect to Fermi velocity v_f with varying ${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}$ (Fig. S5A). Strong SOC often leads to a band structure resembling a Dirac band, which is usually described by two parameters: the Dirac mass m and Fermi velocity v_f, both of which depend on the SOC strength (54). Because Dirac mass is more relevant to the band inversion (from m < 0 to m > 0), here we keep m = 0.09 eV (that matches the band gap of SnTe at 300 K) and change the Fermi velocity from 0.8v_f to 1.2v_f. Under strong dielectric screening (${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}$ is small), we find that the enhancement ratio can be as high as 50 and decreases only slightly as the Fermi velocity goes up due to the lower density of states. This implies that the highly nonparabolic feature in Dirac band structure of SnTe, as endowed by the SOC, is the underlying reason for SnTe to exhibit a large enhancement of power factor based on the electron MFP filtering strategy. One can better understand this correlation by looking at the energy-dependent hole MFPs for different cases as shown in Fig. 4B. The energy-dependent hole MFPs show a monotonically decreasing trend (λ ∼ ε⁻², caused by linear dispersion), which indicates the fact that a suitably chosen cutoff MFP (one that meets the Fermi level at the MFP curve) can exclude states that have negative contributions to the Seebeck coefficient while preserving those with positive contributions.

To more explicitly demonstrate the effect of nonparabolicity in band structure on the electron MFP filtering, we show the enhancement ratio of the power factor for the Kane band by varying the nonparabolicity parameter δ and ${\mathit{ϵ}}_{\infty }^{-1}-{\mathit{ϵ}}_s^{-1}$ (Fig. S5B). For a nearly parabolic band, as the dielectric screening becomes stronger, the enhancement ratio increases but only moderately, suggesting that the MFP filtering approach is more effective when the polar scattering is screened and deformation-potential scattering is dominant. When the band becomes highly nonparabolic (δ > 1 in this case), much greater enhancement can be found, particularly at regions where dielectric screening is also strong. This fact can be again seen from the modeled MFP profiles shown in Fig. 4C. The green dots display the hole MFP profile for a parabolic band when e-ph interaction is dominated by polar scattering. In this case, the MFP should be proportional to εT⁻¹ after the phonon-absorption process fully takes over the scattering channel (ε > ħω_LO). These features are in accordance with previous first-principles and theoretical predictions (32, 55). With increased dielectric constant, the polar scattering starts to be suppressed, leading to a MFP profile given by the blue dots. The MFP is nearly a constant at a high-energy regime, which is the same as the trend given by a semiempirical formula once deformation-potential scattering dominates the e-ph interactions in a parabolic band (46). For both cases, because holes with long MFPs appear both above and below the Fermi level, it will be difficult to achieve any improvement of power factor through MFP filtering since both the positive and negative contributions to the Seebeck coefficient will be filtered out simultaneously when we shrink the nanostructure size. However, when significant nonparabolicity is introduced into the band, the MFP profile follows the trend of (1 + 2δε)⁻² as shown by the red dots in Fig. 4C, and the monotonic decreasing trend fits the requirement for filtering out long-MFP holes as we have explained above.

The nonparabolic band shape essentially makes such monotonic behavior much more evident and therefore enhances the effectiveness of the MFP filtering approach. In SnTe the nonparabolicity results from the linear dispersion due to the strong SOC, which explains its significant electron MFP filtering effect. By comparison with the Kane band, it is found that the Dirac band always processes a greater slope of energy-dependent MFP profile, which is beneficial to the concept of MFP filtering. They have the same trend only when δ approaches infinity. These results reveal that the Dirac material is a promising material platform for further advancing the nanostructuring approach by improving the power factor via engineering the electron MFP spectrum.

Improved zT Value Through MFP Filtering.

The remarkable enhancement in power factor by limiting long-MFP holes in p-type SnTe suggests a possible route to enhance the thermoelectric performance via the MFP filtering effect. Here we evaluate the effectiveness of this nanostructuring approach by modeling the effect of the scatterings for both electrons and phonons due to the small length scales of the nanostructures. Instead of sharply cutting off the holes whose MFPs are greater than λ_opt, as done in Fig. S5 (providing the upper bound for the MFP filtering effect), here we demonstrate the improvement of zT value through limiting the MFPs of both holes and phonons by imposing appropriate boundary scattering. In this case, we assume that the carriers are subject to totally diffusive scattering at the ends of the nanostructure (Casimir limit) (56) and that the effective MFP can be estimated via Mathiessen’s rule, ${\lambda }_{eff}^{-1}={\lambda }_{e\text{-ph}}^{-1}+l_{GB}^{-1},$ where λ_e-ph is the ab initio scattering rate due to e-ph interaction and l_GB is the characteristic length of the nanostructure.

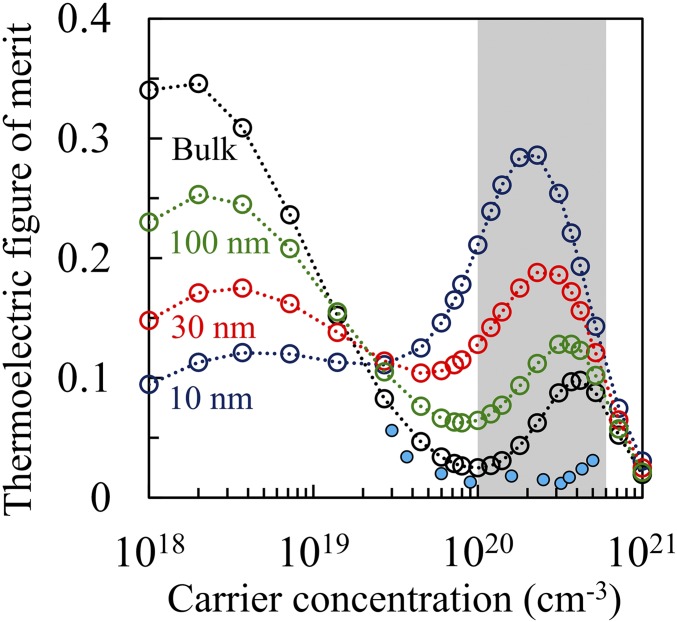
The discrepancy of the zT value between our ab initio calculations and experimental measurements can be attributed to the defect scattering that is not included in our modeling, as well as the smaller calculated energy offset between the first and second valence bands. Despite the fact that SnTe exhibits low thermoelectric efficiency from experiments at room temperature, our simulation results indicate that its zT value can be potentially significantly improved when the carrier concentration is around 1.0 × 10²⁰ cm⁻³ through the nanostructuring approach owing to the selective scatterings to electron and phonon with long MFPs (see Fig. S6 for the reduction of carriers’ MFPs). Although the maximum bulk zT appears at very low carrier concentration (∼1.0 × 10¹⁸ cm⁻³), SnTe behaves as a heavily doped p-type semiconductor owing to its large amount of Sn vacancies introduced in the crystal, and even current state-of-the-art techniques, such as Sn self-compensation, can decrease the carrier concentration only down to 5.0 × 10¹⁹ cm⁻³ (associated with alloying Cd) (13). Therefore, the doping concentration typically achievable in experiments for p-type SnTe falls in the range between 1.0 × 10²⁰ cm⁻³ and 6.0 × 10²⁰ cm⁻³ shown by the shaded region in Fig. 5 (13, 15, 20, 21, 49‒51). In this range, our calculation shows that the zT value can be largely improved by reducing the grain size, particularly benefiting from the improved Seebeck coefficient as a result of the MFP filtering effect, in addition to the reduced electronic and lattice thermal conductivity. In the degenerate regime, the peak zT occurs around a carrier concentration of 2.0 × 10²⁰ cm⁻³ when the grain size is shrunk to 10 nm, which shows 190% enhancement compared with the peak value in bulk SnTe occurring at ∼4.0 × 10²⁰ cm⁻³.

Fig. 5.

Enhancement of zT of p-type SnTe with different carrier concentrations at 300 K due to the MFP filtering effect. The black open circles are bulk zT without boundary scattering. The green, red, and blue open circles are zT calculated under boundary scattering when the characteristic lengths l_GB = 100 nm, 30 nm, and 10 nm are, respectively, applied. The solid circles are experimental values of bulk SnTe by Zhou et al. (51). The shaded region shows the carrier concentration between 1.0 × 10²⁰ cm⁻³ and 6.0 × 10²⁰ cm⁻³, which is the typical regime that can achieve high zT in experiments.

We further note that Heremans et al. (57) previously observed an enhanced Seebeck coefficient in PbTe nanostructures—a similar compound to SnTe—when the characteristic length falls within 30–50 nm. They speculated that this enhancement results from the boundary scattering of long-MFP electrons due to reduced grain size. Now with ab initio calculations we are able to pinpoint the power factor enhancement as arising from the electron MFP filtering effect in the case of p-type SnTe. Our results clearly signify the role of the highly nonparabolic band shape inherent in Dirac materials governing the MFP spectrum, for which the MFP filtering approach can lead to large enhancement of power factor and zT value.

Conclusion

In summary, we have performed ab initio calculations of the full thermoelectric transport properties for a representative Dirac material, SnTe, based on full consideration of the e-ph, ph-e, and ph-ph interactions, with SOC and long-range polar interaction included in the computational framework. We show that the unique electronic dynamics in SnTe, represented by its highly nonparabolic band arising from the strong SOC between conduction and valence bands as well as its large dielectric coefficient, lead to significant energy dependence in the electron scattering rates and particularly the electron MFP spectrum. The distinct electron MFP profile allows one to significantly enhance the Seebeck coefficient in p-type SnTe beyond its bulk value by filtering out long-MFP electrons. We found that in the degenerate regime the peak enhancement of zT at room temperature can be as high as 190% if the nanostructure sizes are reduced down to around 10 nm. Our work not only opens a unique route in using nanostructures to improve zT but also stimulates discovering more thermoelectric systems by looking for a topologically nontrivial electronic band structure that allows a significant electron MFP filtering effect.

Methods

Here we briefly describe our procedures in calculating the electrical, thermal, and thermoelectric transport properties from first principles. For electrons at normal temperatures, their intrinsic scattering rates (or inverse of relaxation times) are governed by e-ph interactions, while for phonons, we have taken into account scatterings both by phonons and by electrons at elevated carrier density. The e-ph interactions are obtained by evaluating the perturbation of atomic displacement on the electronic potential. The ph-ph interactions, on the other hand, are calculated with the knowledge of force constants, which are fitted from force-displacement data. We refer readers to SI Notes, Carriers’ Interactions and Transport Properties and Simulation Details for the detailed calculation procedure and parameters and to SI Notes, Model for Studying Electron MFP Filtering for the model for studying electron MFP filtering.