A Bayesian Approach for Analyzing Zero-Inflated Clustered Count Data with Dispersion

SUMMARY

In practice, count data may exhibit varying dispersion patterns and excessive zero values; additionally, they may appear in groups or clusters sharing a common source of variation. We present a novel Bayesian approach for analyzing such data. In order to model these features, we combine the Conway-Maxwell-Poisson distribution which allows both over- and under-dispersion with a hurdle component for the zeros and random effects for clustering. We propose an efficient Markov chain Monte Carlo sampling scheme to obtain posterior inference from our model. Through simulation studies, we compare our hurdle CMP model with a hurdle Poisson model to demonstrate the effectiveness of our CMP approach. Furthermore, we apply our model to analyze an illustrative dataset containing information on the number and types of carious lesions on each tooth in a population of 9-year-olds from the Iowa Fluoride Study, which is an ongoing longitudinal study on a cohort of Iowa children that began in 1991.

1. Introduction

Zero inflation arises when the parametric model for the counts underestimates the proportion of zeros in the data.^1–4 A new component is introduced to the model so that data are drawn from a mixture model containing the count distribution and a binary component providing additional zeros. An alternative model structure is the hurdle model. The hurdle model is a conditional model that first determines if the count will be zero or non-zero. Conditional on the observation being non-zero, the count is drawn from a distribution with support on the positive integers.^5–7

In practice, we often face situations where such count data are not independent and exhibit dependence between observations within clusters. The failure to appropriately account for dependence in the responses can lead to inefficient parameter estimates and invalid hypothesis tests. For analyzing this type of data, zero-inflated modelings have been developed to incorporate correlations in the marginal regression (i.e., GEE) framework.^8–12 There are also mixed effects models for zero-inflated clustered data that use random effects to introduce dependence.^13–19 However, these methods are typically limited to the equidispersed or overdispersed cases due to the properties of Poisson and negative binomial distributions.

On the other hand, the Conway-Maxwell-Poisson (CMP) distribution, introduced by Conway and Maxwell,²⁰ can model a wide range of dispersion from underdispersion to overdispersion and includes the usual Poisson distribution as a special case. Motivated by this versatility of the CMP distribution, Barriga and Louzada²¹ introduced a Bayesian approach to zero-inflated dispersed data based on a CMP distribution. However, their work only considers independent data and not clustered data. On the other hand, Choo-Wosoba and Datta²² developed statistical methodology with a CMP distribution for analyzing clustered data with excessive zero counts. In their paper, a mixed effects model approach is applied to handle the correlations within clusters. However, this frequentist approach typically is limited to equicorrelation through a single random component due to the difficulty of the Laplace approximation to the likelihood.²³

The development of methodology in this paper is partially motivated by the Iowa Fluoride Study.²⁴ The Iowa Fluoride Study is a longitudinal study with the goal of identifying risk and protective factors for dental health in children. Information about the study is available at http://www.dentistry.uiowa.edu/preventive-fluoride-study. This data contains the caries experience score (CES) for each of the patient’s teeth; the CES is a count variable with a higher scores indicating a more damaged tooth. Obviously, teeth within a child’s mouth share the same dental environment, which implies that the CESs will be correlated within patient. Furthermore, most teeth are healthy (no cavities) leading to excessive zero counts in CES (Figure 1).

Figure 1.

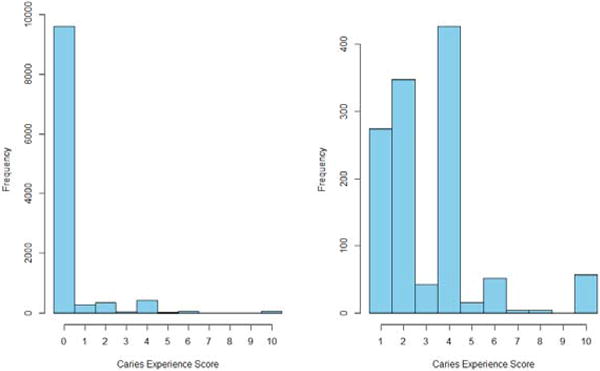
Frequency histograms of the entire caries experience scores (CES) (left panel) and the non-zero CES(right panel) of the nine-year-old children’s dataset from the Iowa Fluoride Study.

To deal with these issues, we propose a Bayesian CMP model that will simultaneously accommodate the common challenges mentioned previously: zero-inflation, clustering, and both over- and underdispersion. Our paper is unique in that we can handle all three in a fully likelihood-based approach. In our previous work, we considered a frequentist approach by using a marginal GEE specification²⁵ and a mixed effects model.²² For the mixed effects model, the Laplacian/quadrature methods used for estimation struggle to estimate correlation structure more complex than equicorrelation. By relying on a Bayesian estimation scheme, we have more flexibility in specifying the dependence across teeth; in particular, we allow differing levels of correlation between different classes of teeth (molar and non-molar). While Barriga and Louzada²¹ does use a Bayesian zero-inflated CMP distribution, they do not model dependence/clustering which is clearly needed in this application. Additionally, we develop our model using a hurdle framework to account for the excess zeros, instead of a zero-inflation model. This provides more natural interpretations as there are separate models for those factors that cause/prevent cavities and those that lead to more/less severe cavities when they appear.

We introduce our Bayesian model in Section 2. Section 3 describes the Markov chain Monte Carlo (MCMC) sampling scheme used for inference. The application to the Iowa Fluoride Study data is undertaken and discussed in Section 4. We perform two simulations and compare the results with a Bayesian Poisson model in Section 5. The paper ends with a discussion in Section 6.

2. The Bayesian Model

In this section, we describe our model structure. We begin with the following general notation which will be used throughout the manuscript. Let N denote the total number of clusters (i.e., children for our illustrative data example), i = 1, …, N is the cluster level index, n_i is the sample size (number of teeth) in the i^th cluster, j indexes the observations (teeth) within the i^th cluster (j = 1, …, n_i), and Y_ij represents the response (CES score) of the j^th observation in the i^th cluster.

To describe the role of the zeros in the data, we use a hurdle model instead of a zero-inflation component, due to its more natural interpretation. This Bayesian hurdle model consists of two different parts, the presence model and the severity model. The presence model considers a binary random variable for the non-zero outcome, i.e., whether there is any caries present on the tooth. The severity model, based on the CMP, describes the positive counts, that is, how much caries is on an involved tooth (how much decay there is quantified by the number of tooth surfaces affected). While we use the terms presence and severity for interpretation of the dental application, these can be considered generally as the zero model and the positive count model.

The presence model is based on a probit regression with both fixed and random effects terms. The probability that an outcome is positive (non-zero) is modeled through $P\left(Y_{ij}>0\right)=\mathrm{\Phi }\left(X_{ij,\beta }^T\beta +U_{ij,\delta }^T{\delta }_i\right)$. This model is associated with fixed effects covariates X_ij and coefficient vector β. Clustering comes from the random effects vector δ_i with corresponding design matrix U_i,δ. The choice of the design matrix U_{i, δ} determines the form of the clustering, allowing many common choices such as equicorrelation, multiple classes, etc.

The Conway-Maxwell-Poisson distribution²⁰ is given by

$$P\left(Y=y\right)=\frac{{\mathrm{\lambda }}^y}{{\left(y!\right)}^{\upsilon }\mathcal{Z}\left(\mathrm{\lambda },\upsilon \right)},y=0,1,2,\cdots ,$$

where $\mathcal{Z}\left(\mathrm{\lambda },\upsilon \right)={\displaystyle \sum _{s=0}^{\infty }\frac{{\mathrm{\lambda }}^s}{{\left(s!\right)}^{\upsilon }}}$ is the normalizing constant, λ is a positive shape parameter, and υ is a non-negative dispersion parameter. The parameter υ yields underdispersion if υ > 1, overdispersion if 0 < υ < 1, or equidispersion if υ = 1. When υ = 1, $\mathcal{Z}\left(\mathrm{\lambda },1\right)=e^{\mathrm{\lambda }}$, which implies that CMP distribution is the same as the Poisson distribution with mean λ. Interpretations from CMP modeling are guided by the result²⁶ that E(Y^υ) = λ.

As the hurdle model is specified through P (Y = y|Y > 0), we use a CMP restricted to the positive integers,

$$P\left(Y_{ij}=y|Y_{ij}>0\right)=\frac{{\left({\mathrm{\lambda }}_{ij}\right)}^y}{{\left(y!\right)}^{\upsilon }{\mathcal{Z}}^{\ast }\left({\mathrm{\lambda }}_{ij},\upsilon \right)},y=1,2,\cdots ,$$ (1)

where the new normalizing constant is ${\mathcal{Z}}^{\ast }\left({\mathrm{\lambda }}_{ij},\upsilon \right)=\mathcal{Z}\left({\mathrm{\lambda }}_{ij},\upsilon \right)-1$. Thus, our severity model uses a truncated CMP distribution which excludes zero. The response-specific shape parameter λ_ij is modeled through $\mathit{log}{\mathrm{\lambda }}_{ij}=X_{ij,\alpha }^T\alpha +U_{ij,\gamma }^T{\gamma }_i$. The regression coefficients α describe the fixed effects, whereas the random effect vector γ_i accounts for clustering. The severity model may or may not use the same random effects design matrix U_i,δ as the presence model. The full distribution of Y_ij (conditional on random effects) can be written as

$$P\left(Y_{ij}=y\right)=\{\begin{array}{ll}1-\mathrm{\Phi }\left(X_{ij,\beta }^T\beta +U_{ij,\delta }^T{\delta }_i\right),& y=0\\ \mathrm{\Phi }\left(X_{ij,\beta }^T\beta +U_{ij,\delta }^T{\delta }_i\right)\times \frac{\mathit{exp}\left\{y\left(X_{ij,\alpha }^T\alpha +U_{ij,\gamma }^T{\gamma }_i\right)\right\}}{{\left(y!\right)}^{\upsilon }{\mathcal{Z}}^{\ast }\left({\mathrm{\lambda }}_{ij},\upsilon \right)},& y=1,2,\cdots \end{array}$$ (2)

where ${\mathcal{Z}}^{\ast }\left({\mathrm{\lambda }}_{ij},\upsilon \right)={\displaystyle \sum _{s=1}^{\infty }\mathit{exp}\left\{s\left(X_{ij,\alpha }^T\alpha +U_{ij,\gamma }^T{\gamma }_i\right)\right\}/{\left(s!\right)}^{\upsilon }}$.

In Equation 2, clustering across outcomes is induced by the random effects δ_i from the presence model and γ_i from the severity model. We assume they jointly follow a multivariate normal distribution: (δ_i, γ_i)^T ~ MV N (0, Σ). As previously noted, the form of the dependence in U is determined by the choice of the random effect design matrices U_δ and U_γ.

For the regression coefficients, we use proper and disperse priors β ~ MV N (0, Ω_β) and α ~ MV N (0, Ω_α). For the covariance matrix of the random effects, we use the conjugate inverse Wishart prior:

$$\sum =\left[\begin{array}{cc}{\sum }_{\delta \delta }& {\sum }_{\delta ,\gamma }\\ {\sum }_{\gamma ,\delta }& {\sum }_{\gamma \gamma }\end{array}\right]\sim IW\left(c,\mathrm{\Psi }\right).$$

As the $\mathcal{Z}$ function of a CMP distribution is not available in a closed form, a conjugate prior for the dispersion is not available. We recommend the prior distribution of the dispersion parameter υ be a lognormal distribution (LN, hereafter) with a median of υ at 1, so that our model is centered at equidispersion. We choose the variance of log(υ) to be 0.5² so that, with 95% probability, υ is a priori between 0.38 to 2.66, representing a reasonable range of dispersions. That is, υ ~ LN(0, 0.5²). Values for the hyperparameters can be taken based on subject matter experience. When none is available, we use proper, weakly-informative priors determined by Ω_α = Ω_β = 10 × I_q, σ_υ = 0.5; c = p + 2, and Ψ = I_p, where q is the number of fixed effect variables, p is the number of random effect variables and I_p is the p dimensional identity matrix. In the prior on Σ, we choose c such that E(Σ) = I_p. Additionally, we perform a brief sensitivity analysis and find that our results are robust to these prior choices (see Web Appendix A).

3. Details of Markov chain Monte Carlo Sampling

As inference is not available in a closed-form, we use iterative MCMC sampling methods. To improve mixing through the sampling process, we introduce continuous latent variables to correspond with whether Y_ij is zero or positive. To that end, we can equivalently express our probit model through the conditionally independent latent variables $Z_{ij}\sim N\left(X_{ij}^T\beta +U_{ij}^T{\delta }_i,1\right)$ where Y_ij > 0 if Z_ij > 0 and Y_ij = 0 if Z_ij < 0. This data augmentation scheme provides conjugate sampling in the presence model and speeds mixing for this component.²⁷

The sampling algorithm iterates between the following steps.

1. Presence model latent variable Z_ij: If Y_ij = 0, then we sample Z_ij from a normal with mean $X_{ij}^T\beta +U_{ij}^T{\delta }_i$ and unit variance, truncated to support (− ∞, 0]. If Y_ij > 0, then we sample from the previous normal distribution truncated to (0, ∞).

2. Presence model regression coefficient β and random effects δ: A naïve Gibbs sampler that samples from p(z|β, δ,⋯), p(β|z, δ,⋯), and p(δ|z, β,⋯) will demonstrate high autocorrelation and slow mixing. To alleviate this, we jointly update β and δ through p(β, δ_i| z, ⋯) = p(β|z, γ) × p(δ_i|β, γ). This is a partially collapsed Gibbs sampler.²⁸

   Note that the sampling distribution for β (marginal over the random effects δ) is

   $$\beta |z,\gamma \sim MVN\left({\left[\left\{{\displaystyle \sum _{i=1}^N{X}_i^T{\left(I\left(n_i\right)+U_i{\sum }_{\delta |\gamma }{U}_i^T\right)}^{-1}{X}_i}\right\}+{\mathrm{\Omega }}_{\beta }^{-1}\right]}^{-1}\times \left\{{\displaystyle \sum _{i=1}^N{X}_i^T{\left(I\left(n_i\right)+U_i{\sum }_{\delta |\gamma }{U}_i^T\right)}^{-1}\left(z_i-U_i{\sum }_{\delta ,\gamma }{\sum }_{\gamma \gamma }^{-1}{\gamma }_i\right)}\right\},{\left[\left\{{\displaystyle \sum _{i=1}^N{X}_i^T{\left(I\left(n_i\right)+U_i{\sum }_{\delta |\gamma }{U}_i^T\right)}^{-1}{X}_i}\right\}+{\mathrm{\Omega }}_{\beta }^{-1}\right]}^{-1}\right),$$

   where I(a) denotes the a-dimensional identity matrix and ${\sum }_{\delta |\gamma }={\sum }_{\delta \delta }-{\sum }_{\delta ,\gamma }{\sum }_{\gamma \gamma }^{-1}{\sum }_{\gamma ,\delta }$ is the conditional variance of δ_i given γ_i.
   After updating β, we sample δ_i given β, Z, γ_i, and Σ for each i.

   $${\delta }_i|\beta ,{\gamma }_i\sim MVN\left({\xi }_i,{\left\{{\sum }_{\delta |\gamma }^{-1}+U_i^T{U}_i\right\}}^{-1}\right),$$

   where ${\xi }_i={\left\{{\sum }_{\delta |\gamma }^{-1}+U_i^T{U}_i\right\}}^{-1}\left({\sum }_{\delta |\gamma }^{-1}{\sum }_{\delta ,\gamma }{\sum }_{\gamma \gamma }^{-1}{\gamma }_i+U_i^T{z}_i-U_i^T{X}_i\beta \right)$.

3. 3. Severity model regression coefficients α: As conjugacy is not available for the CMP model, we use a pair of Metropolis-Hastings updates. We perform a global step that seeks to update the full α vector, as well as a local step that attempts to update each component of α one at a time.

   For the global step, we propose the candidate value α^c ~ MV N(α^t, Ω_q,α), where α^t is the current value of α at the t^th iteration. For ease of explanation, we use $P_{ij}^{+}$ to denote the probability mass function of the truncated CMP distribution of Y_ij in (1) and Π to be the prior density. We accept the candidate value α^c with probability A_α where

   $$A_{\alpha }=\mathit{min}\left(1,\left\{{\displaystyle \prod _{i,j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|{\alpha }^c,\upsilon ,{\gamma }_i\right)}\right\}\mathit{\prod }\left({\alpha }^c\right)/\left\{{\displaystyle \prod _{i,j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|{\alpha }^t,\upsilon ,{\gamma }_i\right)}\right\}\mathit{\prod }\left({\alpha }^t\right)\right);$$

   otherwise, we remain at α^t.
   For the local step that seeks to update the k^th element of the α, we propose ${\alpha }_k^c$ from $N\left({\alpha }_k^t,{\sigma }_{q,{\alpha }_k}^2\right)$, and for all other components of α, we keep the current value, i.e., ${\alpha }_j^c={\alpha }_j^t\left(j\ne k\right)$. We accept the proposed α^c with probability $A_{{\alpha }_k}$ where

   $$A_{{\alpha }_k}=\mathit{min}\left(1,\frac{\left\{{\displaystyle \prod _{i,j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|{\alpha }^c,\upsilon ,{\gamma }_i\right)}\right\}\mathit{\prod }\left({\alpha }_k^c\right)}{\left\{{\displaystyle \prod _{i,j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|{\alpha }^t,\upsilon ,{\gamma }_i\right)}\right\}\mathit{\prod }\left({\alpha }_k^t\right)}\right).$$

   Otherwise, we remain at the current value α^t. We repeat this for all components α_k.
4. Severity model dispersion parameter υ: We update υ using the Metropolis-Hastings algorithm. For the proposal distribution, we use a pseudo-random walk ${\upsilon }^c\sim LN\left(\mathit{log}\left({\upsilon }^t\right),{\sigma }_{q,\upsilon }^2\right)$, and accept the move with probability A_υ,

   $$A_{\upsilon }=\mathit{min}\left(1,\frac{\left\{{\displaystyle \prod _{i,j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|\alpha ,{\upsilon }^c,{\gamma }_i\right)}\right\}\mathit{\prod }\left({\upsilon }^c\right)q\left({\upsilon }^t|{\upsilon }^c\right)}{\left\{{\displaystyle \prod _{i,j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|\alpha ,{\upsilon }^t,{\gamma }_i\right)}\right\}\mathit{\prod }\left({\upsilon }^t\right)q\left({\upsilon }^c|{\upsilon }^t\right)}\right),$$

   where q(υ^c|υ^t) is the log-normal $LN\left(\mathit{log}\left({\upsilon }^t\right),{\sigma }_{q,\upsilon }^2\right)$ proposal density.

5. Severity model random effects γ: As with the regression coefficients α, there is no conjugacy, and generally, the Metropolis-Hastings algorithm is needed to update γ_i for each cluster i. However, in many situations this can be simplified by using only a MV N-Gibbs step for γ_i or a Metropolis step for part of γ_i with a MV N draw for the rest. This partially collapsed Gibbs step will lead to move efficient computation than a naive Metropolis-Hastings approach.

   Recall that only the non-zero Y_ijs appear in the CMP part, and hence, only the γ_i that contribute to the distribution of these Y_ijs are identified by the CMP distribution. The sampling distribution for γ_i is proportional to

   $$p\left({\gamma }_i|{\delta }_i,\alpha ,\upsilon ,\sum ,y_i\right)\propto p\left({\gamma }_i,{\delta }_i|\sum \right){\displaystyle \prod _{j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|\alpha ,\upsilon ,{\gamma }_i\right)}.$$

   In particular, for a cluster where all counts are zero, the data provide no information about γ_i, as the product over y_ij is empty. Hence, the sampling distribution for γ_i is $p\left({\gamma }_i|{\delta }_i.\sum \right)=N\left({\sum }_{\gamma \delta }{\sum }_{\delta \delta }^{-1}{\delta }_i,{\sum }_{\gamma \gamma }-{\sum }_{\gamma \delta }{\sum }_{\delta \delta }^{-1}{\sum }_{\delta \gamma }\right)$, which we can draw from exactly.
   More generally, we let ${\stackrel{\sim }{\gamma }}_i$ denote the portion of γ_i identified in ${\displaystyle \prod _{j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|\alpha ,\upsilon ,{\gamma }_i\right)}$, and ${\gamma }_i^{\ast }$ be the unidentified portion of γ_i. We will update ${\stackrel{\sim }{\gamma }}_i$ by Metropolis-Hastings, marginalized over ${\gamma }_i^{\ast }$, and then, sample ${\gamma }_i^{\ast }$ from MV N conditional on ${\stackrel{\sim }{\gamma }}_i$ and δ_i. To that end, we propose the candidate ${\stackrel{\sim }{\gamma }}_i^c\sim N\left({\stackrel{\sim }{\gamma }}_i,{\mathrm{\Omega }}_{\gamma ,q}\right)$, with a random walk around the current value ${\stackrel{\sim }{\gamma }}_i$. We accept the move with probability

   $$A_{{\stackrel{\sim }{\gamma }}_i}=\mathit{min}\left(1,\frac{\left\{{\displaystyle \prod _{j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|{\stackrel{\sim }{\gamma }}_i^c,\alpha ,\upsilon \right)}\right\}\mathit{\prod }\left({\stackrel{\sim }{\gamma }}_i^c,{\delta }_i|\sum \right)}{\left\{{\displaystyle \prod _{j:y_{ij}>0}{P}_{ij}^{+}\left(y_{ij}|{\stackrel{\sim }{\gamma }}_i^t,\alpha ,\upsilon \right)}\right\}\mathit{\prod }\left({\stackrel{\sim }{\gamma }}_i^t,{\delta }_i|\sum \right)}\right),$$

   where Π(γ_i, δ_i|Σ) represents the density of the MV N(0, Σ) random effects distribution after marginalizing over the unidentified components in ${\gamma }_i^{\ast }$. We then sample the remaining ${\gamma }_i^{\ast }$ from the conditional $p\left({\gamma }_i^{\ast }|{\delta }_i,{\stackrel{\sim }{\gamma }}_i\right)$ based on MV N(0, Σ).
6. Random effects covariance matrix Σ : The covariance matrix can be updated through conjugacy:

   $$\sum |\delta ,\gamma \sim IW\left(c+N,{\displaystyle \sum _{i=1}^N\left(\begin{array}{c}{\delta }_i\\ {\gamma }_i\end{array}\right){\left(\begin{array}{c}{\delta }_i\\ {\gamma }_i\end{array}\right)}^T}+\mathrm{\Psi }\right).$$

   Variance parameters in the Metropolis proposal distributions are chosen by trial and error so that acceptance rate is about 25% for multivariate steps and between 25% and 40% for univariate steps.²⁹ We further discuss the selection of these variance parameters in Web Appendix B.

4. Analysis of Iowa Fluoride Study

The Iowa Fluoride Study (IFS) is a longitudinal study which in 1991 began collecting dental examination data on children in Iowa starting at age 5. These children were followed up at 9, 13 and 17 years. In this paper, we focus on the 9-year-old children’s dataset which is particularly interesting due to the mixed dentition (composed of some primary teeth and some permanent teeth, which does not pose any complications with our approach).

This dataset consists of caries experience scores (CES) as a response variable and seven potential risk/protective factors for caries. Each surface of a tooth is scored 0 (sound), 1 (non-cavitated), or 2 (cavitated) depending on the level of caries involvement, and the CES is the sum over the five surfaces of the tooth. Thus, the response variable takes integer values from 0 to 10. A larger CES indicates more severe decay on the tooth. The dataset includes N = 464 clusters (representing 464 children) with cluster size n_i lying between 16 and 24 for the number of teeth per person. Altogether, we have 10,838 observations, with 9,616 zero counts, which is almost 89% of the dataset (Figure 1). Thus, this dataset appears to be zero-inflated.

In the dental field, the location of a tooth inside the mouth is known to have a great effect on the likelihood of dental carries, or cavities. In fact, cavities are more likely to occur on the molars than non-molars (incisors, canines, and premolars) because molars have irregular occlusal surfaces which more easily retain food. Additionally, the mesial and distal surfaces between the teeth of molars also are more likely to retain bacteria and have increased caries risk. To account for this, both the presence and severity models include a covariate for non-molar (relative to molar). Each model includes eight covariates which presumably affect cavities or caries as protective/risk factors (Table 1).

Table 1.

Description of potential risk/protective factors from the Iowa Fluoride Study (IFS)

Non-molar	Non-molar effect; non-molar is coded as 1.
Sex	Sex of the child; male is coded as 1.
ExamAge	Age in years at the time of the dental examination (centered at 9 years).
FlIntake	Daily fluoride intake (mg) from water, other beverages and selected foods, ingested dentifrice and fluoride supplements. Computed by AUC trapezoidal method from all available data within the time span 5 to 9 years.
SodaPop	Daily soda pop intake (oz.) computed with AUC trapezoidal method using all available data within the time span 5 to 9 years.
ToothBrush	Average of all tooth brushing frequencies reported for the period 5 to 9 years.
DentalVisit	Proportion of times a dental visit was reported with each individual point assessing the previous 6 months.
FlTrt	Average proportion of times a professional dental fluoride treatment was received with each individual point assessing the previous 6 months.
FlHome	Average home tap water fluoride level for all returned questionnaires for the period 5 to 9 years.

To define the dependence structure across teeth, we again focus on the two types of teeth: molar and non-molar. We introduce the clustering effect by tooth location as we expect that teeth within each class are more closely related than those across classes. We parameterize this by letting δ_i be a length 2 vector, where the first component is the overall cluster effect (random intercept) and the second represents the effect of non-molar teeth (relative to molars). For the severity model, we only include a cluster-specific random effect (random intercept), as there are fewer responses to inform the severity model and its random components (less than 12% of observations have positive Y). In addition, most cavities occur on molars (more than 95%), so there would be insufficient information to identify a non-molar term in this severity model. In total, we have three random effects (δ_i1, δ_i2, γ_i).

As discussed in Section 2, the hyperparameters for the priors are chosen to be Ω_α = Ω_β = 10 · I₁₁, c = 5, Ψ = I₃, and σ_υ = 0.5, yielding relatively disperse priors. The posterior samples of the model parameters are obtained by running the MCMC algorithm (Section 3) for 65,000 iterations. The samples are collected after first 25,000 burn-in iterations, yielding 40,000 samples to be used for inference.

MCMC convergence is assessed through trace plots and Geweke tests³⁰ for the individual parameters, as well as the log-likelihoods for the presence (logL₁) and severity (logL₂) models, where

$$L_1={\displaystyle \prod _{i=1}^N{\displaystyle \prod _{j=1}^{n_i}P{\left(y_{ij}=0\right)}^{I\left(y_{ij}=0\right)}P{\left(y_{ij}>0\right)}^{I\left(y_{ij}>0\right)}}},L_2={\displaystyle \prod _{i=1}^N{\displaystyle \prod _{j=1}^{n_i}P\left(Y_{ij}=y_{ij}|y_{ij}>0\right)}}.$$

The trace plots indicate adequate mixing (Figure 1 in Web Appendix B) and most parameters pass the Geweke test (Table 2 in Web Appendix B). The effective sample sizes³¹ for the log-likelihood functions of the presence and severity models are both found to be greater than 1,000. We also analyze the same dataset with a hurdle mixed Poisson model (i.e., fixing υ = 1) to compare with our hurdle CMP model. The posterior means and 95% equal-tailed credible intervals are given in Table 2.

Table 2.

Posterior means and 95% credible intervals (CI) for both presence and severity models as applied to the Iowa data

	hurdle mixed CMP		hurdle mixed Poisson
Presence Model
	posterior mean	CI	posterior mean	CI
Intercept	−0.555	(−1.130, 0.015)	−0.560	(−1.124, −0.007)
Non-molars	−2.608	(−3.314, −2.082)	−2.525	(−3.133, −2.026)
Sex	−0.191	(−0.404, 0.019)	−0.186	(−0.397, 0.024)
ExamAge	0.132	(−0.017, 0.283)	0.133	(−0.017, 0.281)
FlIntake	−0.423	(−0.774, −0.074)	−0.417	(−0.764, −0.080)
SodaPop	0.073	(0.029, 0.117)	0.074	(0.029, 0.118)
ToothBrush	−0.566	(−0.796, −0.339)	−0.567	(−0.796, −0.342)
DentalVisit	0.222	(−0.342, 0.785)	0.219	(−0.330, 0.775)
FlTrt	0.334	(−0.039, 0.710)	0.340	(−0.027, 0.710)
FlHome	0.122	(−0.128, 0.378)	0.116	(−0.131, 0.363)
Severity Model
	posterior mean	CI	posterior mean	CI
Intercept	0.904	(0.422, 1.406)	1.038	(0.560, 1.453)
Non-molars	−0.627	(−0.897, −0.373)	−0.668	(−0.951, −0.400)
Sex	−0.102	(−0.240, 0.039)	−0.108	(−0.257, 0.050)
ExamAge	0.103	(−0.001, 0.207)	0.112	(−0.001, 0.230)
FlIntake	−0.104	(−0.343, 0.136)	−0.115	(−0.359, 0.131)
SodaPop	0.015	(−0.014, 0.044)	0.018	(−0.014, 0.050)
ToothBrush	−0.189	(−0.360, −0.036)	−0.202	(−0.382, −0.024)
DentalVisit	−0.071	(−0.474, 0.357)	−0.058	(−0.457, 0.344)
FlTrt	0.259	(0.002, 0.554)	0.272	(−0.004, 0.538)
FlHome	−0.117	(−0.308, 0.064)	−0.123	(−0.306, 0.051)
υ	0.888	(0.772, 1.005)	1

Coinciding with our expectations, we find the molar/non-molar effect to be highly impactful in both the presence and severity models with both the CMP and Poisson frameworks. Non-molars are much less likely to develop caries, and of those teeth that do develop caries, they tend to have lower scores relative to a corresponding molar.

Considering predictors whose credible intervals (CI) exclude zero to be important factors, we find the same set of important covariates in the presence (zero) model for the CMP and the Poisson choices. This is reasonable and expected as the differences in the two models occur in the distribution of the positive counts. Daily fluoride intake (FlIntake) and tooth brushing frequency (ToothBrush) are protective factors, while greater soda pop intake (SodaPop) increases the risk of developing caries.

In the severity model of the CMP and Poisson frameworks, tooth brushing frequency (ToothBrush) is predictive of less caries. In the hurdle mixed CMP there is evidence that professional fluoride treatment (FlTrt) is associated with higher CES score but the effect size is small; in the Poisson model the CI contains zero. The estimated CMP dispersion parameter is $\widehat{\upsilon }=0.888$ with P(υ < 1|y) = 0.969, indicating the (positive) CES scores are overdispersed.

To evaluate the resulting dependence structure of our model, we consider the posterior mean of the random effect covariance matrix:

$${\widehat{\sum }}_{\text{CMP}}=\left[\begin{array}{ccc}0.937& -0.195& 0.258\\ -0.222& 0.830& -0.063\\ 0.565& -0.147& 0.222\end{array}\right],$$ (4)

and

$${\widehat{\sum }}_{\text{POISSON}}=\left[\begin{array}{ccc}0.936& -0.219& 0.277\\ -0.262& 0.749& -0.082\\ 0.558& -0.185& 0.263\end{array}\right],$$ (5)

where the variance-covariance components are displayed in the upper triangular part and the correlation coefficients in the lower off-diagonal part. Based on the CMP-estimated $\widehat{\sum }$, we can find the correlations between the latent variables Z to describe the dependence within cluster. The correlation between the Z_is of two molars is 0.484, between two non-molars is 0.579, and between a molar and non-molar is 0.346. Clearly, teeth within a location class are more highly correlated than across class, but there remains positive correlation across all observations in the cluster.

V ar(γ_i), is the variance component corresponding to the severity model in Equation 5, roughly 18% larger than the corresponding component in the CMP model. In addition to clustering, random effects are used in GLMs to induce overdispersion. Here, V ar(γ_i) the variance component is inflated to compensate for the overdispersion that the restrictive Poisson model cannot explain. Thus, the Poisson choice conflates overdispersion and the clustering effect. That is, it may overstate the correlation between teeth to account for true overdispersion. However, the mixed CMP is flexible enough to distinguish between the contributions of these two.

To determine the sensitivity of our conclusions to our prior choice, we perform a brief sensitivity study in Web Appendix A. We consider a more informative, strong prior choice using the hyperparameters: Ω_α = Ω_β = 1 × I₁₁ with c = 25, Ψ = 5 × I₃, and σ_υ = 0.2. Under this choice of prior on Σ, we have ${\left[E\left({\sum }^{-1}\right)\right]}^{-1}=\frac{1}{5}\times I$ as in the original prior. Additionally, we use a less-informative, weak prior using the values: Ω_α = Ω_β = 100 × I₁₁, and σ_υ = 0.8. Here, we use an improper prior for Σ, Π(Σ) ∝ |Σ|^{−(p+1)/2}. We find our parameter estimates and conclusions are consistent across these choices. Detailed results are contained in Web Appendix A.

5. Simulation Studies

To validate our method and better understand its operating characteristics, we consider two simulation experiments, one with overdispersion (υ = 0.7) and the other with equidispersion (υ = 1, leading to a Poisson distribution). For each setting, we consider N = 200 clusters with cluster size of n_i = 20. Similar to the role of molars and non-molars, each cluster contains two classes with 10 observations each. This setting enables us to compare our hurdle CMP mixed model and the hurdle Poisson mixed model. The simulation set-up of this section is guided by the Iowa data for the nine-year-old children.

For each scenario, we use the same design matrices for fixed effects in both binary and positive count parts. The design matrix for the fixed effects consists of four different covariates with an intercept. The first two are the intercept and a binary class indicator, 0 for the first 10 observations and 1 for the rest. Then, we consider three continuous factors corresponding to FlIntake, SodaPop, and ToothBrush chosen by sampling with replacement from the IFS data, respectively.

For the dependence, we take the first two columns from the fixed effects design matrix as random effects design matrix in both the binary and positive count parts. Hence, the random effect is (δ_i1, δ_i2, γ_i1, γ_i2), corresponding to an intercept and binary class effect in the presence model, and an intercept and binary class effect in the severity model. The true parameter values can be found in Tables 3–6.

Table 3.

Summary of fixed effect estimation in a simulation study described in Section 5; here the model is overdispersed, υ = 0.7.

		hurdle mixed CMP			hurdle mixed Poisson
	True	Bias	MSE	CR	Bias	MSE	CR
${\widehat{\beta }}_0$	−0.40	0.0178	0.1141	0.975	0.0188	0.1139	0.975
${\widehat{\beta }}_1$	−1.00	−0.0014	0.0136	0.940	−0.0017	0.0135	0.940
${\widehat{\beta }}_2$	−0.20	−0.0036	0.0429	0.955	−0.0042	0.0428	0.960
${\widehat{\beta }}_3$	0.20	−0.0002	0.0009	0.970	<0.0001	0.0009	0.970
${\widehat{\beta }}_4$	−0.60	−0.0122	0.0309	0.945	−0.0129	0.0309	0.930
${\widehat{\alpha }}_0$	0.20	0.0697	0.1032	0.955	0.3555	0.2127	0.635
${\widehat{\alpha }}_1$	−2.00	−0.0157	0.1116	0.980	−0.1121	0.1245	0.965
${\widehat{\alpha }}_2$	−0.20	−0.0151	0.0308	0.945	−0.0407	0.0390	0.925
${\widehat{\alpha }}_3$	0.05	0.0005	0.0006	0.965	0.0069	0.0008	0.945
${\widehat{\alpha }}_4$	−0.30	−0.0186	0.0212	0.955	−0.0557	0.0278	0.930
$\widehat{\upsilon }$	0.70	0.0490	0.0234	0.940	0.3000	N/A	N/A

Table 6.

Summary of variance component estimation in simulation study described in Section 5; here the model is equidispersed, υ = 1.

		hurdle mixed CMP		hurdle mixed Poisson
	True	Bias	MSE	Bias	MSE
${\widehat{\sigma }}_{11}$	0.80	−0.0171	0.0159	−0.0172	0.0159
${\widehat{\sigma }}_{12}$	−0.20	0.0245	0.0109	0.0245	0.0108
${\widehat{\sigma }}_{13}$	0.20	−0.0038	0.0051	−0.0070	0.0049
${\widehat{\sigma }}_{14}$	0.20	−0.0657	0.0262	−0.0658	0.0260
${\widehat{\sigma }}_{22}$	0.40	−0.0146	0.0120	−0.0147	0.0120
${\widehat{\sigma }}_{23}$	−0.10	0.0023	0.0032	0.0042	0.0031
${\widehat{\sigma }}_{24}$	−0.05	0.0144	0.0062	0.0131	0.0061
${\widehat{\sigma }}_{33}$	0.20	0.0124	0.0034	0.0042	0.0025
${\widehat{\sigma }}_{34}$	0.10	−0.0468	0.0066	−0.0463	0.0062
${\widehat{\sigma }}_{44}$	0.20	0.1483	0.0363	0.1444	0.0345

We generate 200 simulated datasets under the two choices of υ, 0.7 and 1.0. For each data set, we run MCMC to obtain 50,000 posterior iterations to use for inference. When the data are drawn from CMP (υ = 0.7), we first sample 5,000 burn-in iterations (55,000 total), and when the true data are conditionally Poisson (υ = 1.0), the MCMC chain takes longer to reach the stationary distribution and 15,000 burn-in iterations are used (65,000 total). Based on these samples over 200 datasets, bias and mean squared error (MSE) are calculated for all the fixed effect estimators and individual variance components for the random effects. We also calculate the sum of squared errors (SSE) for a block of the random effect variance matrix by summing the MSE over the appropriate (i, j) parameters corresponding to the relevant block of Σ.

For the overdispersion case (υ = 0.7), estimation of the β parameters in the binary component from the CMP model is similar to estimation in the Poisson model (Table 3). As noted in the previous section, this is expected, as the models are the same for this component. However, the positive part estimators α behave noticeably different for those two models. Table 3 shows that the CMP model estimates have smaller bias and smaller MSE than those estimators from the Poisson model.

As we use the 95% credible intervals to determine important factors, we also consider the coverage rate (CR) in Table 3. As we use only 200 datasets to evaluate these proportions, all are found to be within the margin of error of the nominal 0.95 rate with one exception (the theoretical Monte Carlo standard error is 0.015). In the hurdle Poisson model, the intercept α₀ displays very poor coverage due to the bias from model misspecification.

Estimation of the variance components is assessed in Table 4. As with the regression coefficients, estimation of the upper block of Σ corresponding to δ (σ₁₁, σ₁₂, σ₂₂), the random effects in the binary model, are roughly equivalent between the CMP and Poisson models; SSE in this block is 0.0416 for the CMP model and 0.0415 for the Poisson. However, differences between the models are apparent in the γ block of Σ (σ₃₃, σ₃₄, σ₄₄) describing the positive count model. SSE for this block is 0.0375 for CMP, compared to 0.0545 for Poisson. In particular, the variance terms for γ tend to be biased high in the hurdle Poisson model to recover overdispersion, as discussed in the previous section. Overall, we find the hurdle CMP mixed effects model performs significantly better for zero-inflated, dispersed data than the simpler Poisson choice.

Table 4.

Summary of variance component estimation in a simulation study described in Section 5; here the model is overdispersed, υ = 0.7.

		hurdle CMP		hurdle Poisson
	True	Bias	MSE	Bias	MSE
${\widehat{\sigma }}_{11}$	0.80	−0.0063	0.0141	−0.0066	0.0142
${\widehat{\sigma }}_{12}$	−0.20	0.0172	0.0087	0.0180	0.0087
${\widehat{\sigma }}_{13}$	0.20	0.0095	0.0044	0.0400	0.0072
${\widehat{\sigma }}_{14}$	0.20	−0.0425	0.0182	−0.0566	0.0208
${\widehat{\sigma }}_{22}$	0.40	−0.0163	0.0101	−0.0171	0.0100
${\widehat{\sigma }}_{23}$	−0.10	−0.0002	0.0026	−0.0165	0.0037
${\widehat{\sigma }}_{24}$	−0.05	0.0043	0.0064	0.0158	0.0072
${\widehat{\sigma }}_{33}$	0.20	0.0206	0.0031	0.0862	0.0115
${\widehat{\sigma }}_{34}$	0.10	−0.0324	0.0046	−0.0390	0.0073
${\widehat{\sigma }}_{44}$	0.20	0.1220	0.0252	0.1327	0.0284

The υ = 1 scenario is also considered, and the results are given in Tables 5 and 6. Overall, estimation of both the fixed effects and random effects variances perform similarly in both the CMP and Poisson models. We do see slightly inflated MSE of the regression coefficients in the severity component under the hurdle CMP model, but the difference is minor and the bias is still negligible. The coverage rates (CR) of 95% CI are also close to the nominal rate. In addition, a low bias in υ indicates the flexibility of our model. Thus, we conclude that even for υ = 1 case, the hurdle CMP mixed effects model is comparable to the hurdle Poisson mixed effects model.

Table 5.

Summary of fixed effect estimation in a simulation study described in Section 5; here the model is equidispersed, υ = 1.

		hurdle mixed CMP			hurdle mixed Poisson
	True	Bias	MSE	CR	Bias	MSE	CR
${\widehat{\beta }}_0$	−0.40	0.0242	0.1249	0.940	0.0250	0.1246	0.935
${\widehat{\beta }}_1$	−1.00	−0.0041	0.0134	0.960	−0.0041	0.0134	0.950
${\widehat{\beta }}_2$	−0.20	−0.0116	0.0442	0.940	−0.0116	0.0442	0.950
${\widehat{\beta }}_3$	0.20	−0.0009	0.0009	0.965	−0.0009	0.0009	0.965
${\widehat{\beta }}_4$	−0.60	−0.0065	0.0308	0.945	−0.0068	0.0308	0.945
${\widehat{\alpha }}_0$	0.20	0.0344	0.1504	0.940	−0.0064	0.0982	0.930
${\widehat{\alpha }}_1$	−2.00	−0.0118	0.1401	0.960	0.0014	0.1330	0.965
${\widehat{\alpha }}_2$	−0.20	−0.0101	0.0360	0.950	−0.0080	0.0348	0.950
${\widehat{\alpha }}_3$	0.05	0.0022	0.0007	0.965	0.0015	0.0007	0.975
${\widehat{\alpha }}_4$	−0.30	−0.0051	0.0271	0.945	−0.0027	0.0264	0.935
$\widehat{\upsilon }$	1.00	0.0461	0.0548	0.955	0.0000	N/A	N/A

In conclusion, our simulation studies demonstrate that the hurdle CMP mixed effects model fits significantly better for dispersed data and is comparable to the hurdle Poisson mixed effects model, when the data are equidispersed.

As suggested by a reviewer, we conducted another simulation study where data have no zero inflation to see how our hurdle mixed CMP model behaves compared with the true model, a mixed effects CMP. It turns out that most of all the corresponding estimators are reasonably close to the true values even under the no zero-inflation setting. For full detail, see details in Web Appendix C.

6. Discussion

We have proposed a new Bayesian approach for modeling dependent, zero-inflated count data by combining a probit component with the Conway-Maxwell-Poisson regression using shared random effects. Our approach is flexible in terms of allowing various types of dispersions from under- to over-dispersion (unlike negative binomial and many other count models), and the structure of the dependence across counts is adaptable to many correlation forms. Most frequentist approaches to this problem experience difficulties in approximating the likelihood with Laplacian/quadrature methods. However, our Bayesian approach avoids this by relying on an iterative sampling scheme that draws the values of the random effects each iteration. Consequently, such a sampling scheme-based framework gains the flexibility to choose a more versatile form of the random effects design matrix. The data application and simulation studies provide clear-cut evidence that our approach is superior to a more standard, random effects, hurdle Poisson model.

While the MCMC scheme we describe in Section 3 is found to perform successfully in the experiments we consider, one of the outstanding challenges is further improving and speeding up the computation. By using collapsed Gibbs steps, our sampler is designed to minimize auto-correlation when possible, but as with any Gibbs sampler in a complex modeling framework, mixing can be slow. One relevant contributor is that evaluation of the mass function requires the normalizing constant $\mathcal{Z}\left(\mathrm{\lambda },\upsilon \right)$, which is an infinite sum with no closed form representation; Gillispie and Christopher³² suggest an approximation of $\mathcal{Z}$, but it only works under certain ranges of the parameters, λ and υ. As all of the observed counts are less than or equal to 10, we instead choose to truncate the sum at 100 for computation, providing a high level of accuracy since P(Y > 100) is negligible under the υ and λ_ijs we encounter.

In the analysis of the IFS data, we include a tooth-location factor in the model to control the dependence across teeth. Another possibility might be to consider a spatial structure to define the dependence across teeth, perhaps along the lines of some previous work.^17,19 Intuitively, we may expect that adjacent teeth are highly correlated, and that the dependence decays the farther away the teeth are located. In principle, our model can handle this approach by defining a γ_ij and δ_ij term for every tooth, and the full vector is drawn from MVN with covariance matrix Σ_i that provides a (low-dimension) spatial structure based on tooth location. In practice, there are some challenges. First, as our data is so sparse (almost 89% zeros), we have very little information regarding the random effects for the count components. Secondly, the expansion of the random effect structure will require greater MCMC computational time. The continued use the partially collapsed steps for δ (see Step 5 in Section 3) may help manage this issue. Third, in the 9-year-old children’s dataset, there is a mix of primary and permanent teeth, and their locations do not exact align. Specification of the dependence for these terms will require additional considerations. Thus, with respect to these challenges, the random effects structure we chose is a more reasonable and flexible choice than equicorrelation as typically used. Additionally, we only focus on the data of the 9-year-old children. Further methodology can be developed to leverage the longitudinal information across the several study visits to understand the factors leading to improving or declining dental health across childhood and adolescence. We leave these as possibilities for future extensions.