Mechanistic Insights on Human Phosphoglucomutase Revealed by Transition Path Sampling and Molecular Dynamics Calculations

Abstract

Human α-phosphoglucomutase 1 (α-PGM) catalyzes the isomerization of glucose-1-phosphate into glucose-6-phosphate (G6P) through two sequential phosphoryl transfer steps with a glucose-1,6-bisphosphate (G16P) intermediate. Given that the release of G6P in the gluconeogenesis raises the glucose output levels, α-PGM represents a tempting pharmacological target for type 2 diabetes. Here, we provide the first theoretical study of the catalytic mechanism of human α-PGM. We performed transition-path sampling simulations to unveil the atomic details of the two catalytic chemical steps, which could be key for developing transition state (TS) analogue molecules with inhibitory properties. Our calculations revealed that both steps proceed through a concerted S_N2-like mechanism, with a loose metaphosphate-like TS. Even though experimental data suggests that the two steps are identical, we observed noticeable differences: 1) the transition state ensemble has a well-defined TS region and a late TS for the second step, and 2) larger coordinated protein motions are required to reach the TS of the second step. We have identified key residues (Arg23, Ser117, His118, Lys389), and the Mg²⁺ ion that contribute in different ways to the reaction coordinate. Accelerated molecular dynamics simulations suggest that the G16P intermediate may reorient without leaving the enzymatic binding pocket, through significant conformational rearrangements of the G16P and of specific loop regions of the human α-PGM.

Graphical abstract

Stepping out: The catalytic mechanism of the biosynthesis of glucose-6-phosphate by the human α-phosphoglucomutase 1 (α-PGM, see figure) has been computationally investigated by using quantum mechanics/molecular mechanics methodologies. Understanding this reaction mechanism will be important to foster the development of new drugs to target this enzyme.

Introduction

Enzymes that transfer phosphoryl groups are extremely efficient and are involved in almost all metabolic processes.^[1] Human α-phosphoglucomutase 1 (α-PGM, EC 5.4.2.2) has a pivotal role in the homeostasis of cellular glucose, by mediating the connection between glycogenolysis to gluconeogenesis and glycolysis. In the glycogenolysis, the glycogen phosphorylase catalyzes the breakdown of glycogen to glucose-1-phosphate (G1P), which is interconverted into glucose-6-phosphate (G6P) by α-PGM. This reaction is highly reversible. The G6P molecule is susceptible to go down the route of gluconeogenesis or glycolysis, whereas G1P can be used for protein N-glycosylation.^[2] In patients with type 2 diabetes, an increased glycogenolysis contributes to an excessive hepatic glucose output despite hyperglycemia. This raises the risk of microvascular damage and is also associated with reduced life expectancy.^[3] Hence, these enzymes have been the focus of novel pharmacological strategies. Furthermore, several mutations in α-PGM were recently identified as the cause of α-PGM deficiency in autosomal recessive inherited disease.^{[2b, 4]} Some of these mutations were classified as deleterious to catalysis, whereas others disturb the α-PGM folding. Mutants that affect the enzyme folding are more common than the ones that affect the catalysis.^[2b,4,5]

Human α-PGM is a cytoplasmic enzyme with 562 residues that belongs to the ubiquitous α-d-phosphohexomutase superfamily, and it requires a magnesium ion as a cofactor. Its structure was recently determined by X-ray diffraction.^[4] This monomeric enzyme is composed of four domains with similar size and organized in an overall heart shape (depicted in Figure 1). The domains converge in a large central cleft (molecular surface area of 1670 Ų), where the active site is located. The active site is composed by 70% of charged polar residues that accommodate the negative phosphocarbohydrate substrates.^[4] It was also suggested that each domain has a critical loop that has a specific function for catalysis: 1) the phosphoserine 117 (Ser117P) loop, 2) the magnesium-binding loop, 3) the sugar-binding loop, and 4) the phosphate-binding loop.

Figure 1.

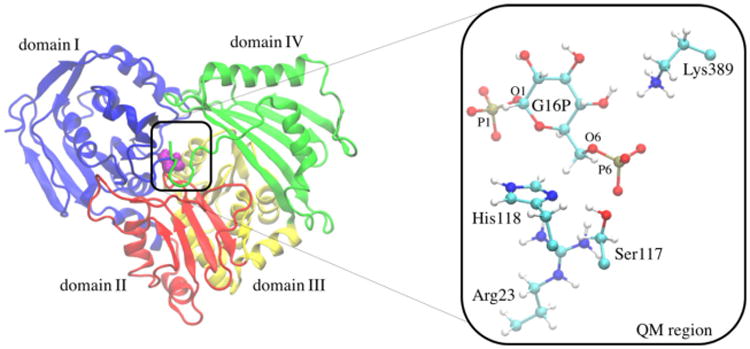
Representation of the four domains of the human α-PGM enzyme. Domains I, II, III, and IV are colored in blue, red, yellow, and green, respectively. The catalytic Ser117 residue is shown in purple. A close-up of the quantum mechanical region and the Mg²⁺ ion is shown on the right-hand side.

The sequence identity between human and rabbit α-PGM is 97%.^[6] Because of this, the catalytic mechanism of rabbit α-PGM was extensively studied.^{[1a, 7]} Scheme 1 illustrates the proposed catalytic mechanism that occurs in two consecutive phosphoryl transfers, separated by the formation of the stable glucose-1,6-bisphosphate (G16P) intermediate.

Scheme 1.

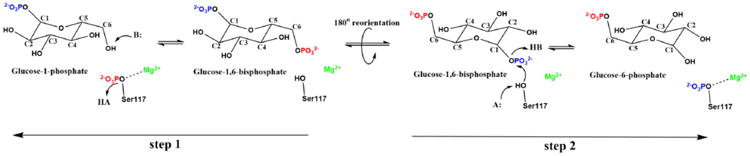
Schematic representation of the reversible reaction catalyzed by α-PGM. The two steps studied in the present work are also indicated.

In the first step, the Ser117P transfers the phosphoryl group to the C6 of the G1P substrate, producing G16P. After this, a reorientation of the intermediate in the active site is thought to occur, in order to place the molecule in a proper position to transfer the other phosphoryl back to the serine residue, thus returning the enzyme to its initial state. Both mechanistic steps are assisted by general acid and base residues that donate a proton to Ser117 and accept a proton from the O1/O6 hydroxyl groups of the G1P/G6P molecules, respectively. The nearby Arg23 and Lys389 residues were pointed out as potential candidates for the general acid and base catalysts, respectively.^{[4, 8]} Mutagenesis and kinetic studies on α-phosphomannomutase/phosphoglucomutase (α-PMM/PGM) from the prokaryotic Pseudomonas aeruginosa revealed that the conserved His329 (lysine in the α-PGM subfamily—Lys389 in human α-PGM), Arg20 (Arg23 in human α-PGM), and His119 (His118 in human α-PGM) residues are critical for catalysis.^[4,8,9] Similar results were obtained with mutagenesis studies on the analogous Lys409 in PGM from Salmonella typhimurium (Lys389 in human α-PGM).^[8] These lysine residues are adequately located to subtract a proton from the O1/O6 hydroxyl groups of the G1P/G6P molecules, respectively, which suggests that they may serve as the general base catalyst.

In the last decades, experimental and computational studies provided several reasonable mechanisms for phosphoryl transfer reactions. However, there are still some doubts regarding the precise mechanistic details of these reactions, and sometimes even different mechanistic pathways have been suggested for the same system.^[10] The most usual mechanism is the concerted S_N2-like mechanism that proceeds through a single step and has no intermediate.^[11] It is often observed in the catalytic mechanism of integrases, phosphatases, and α-d-phosphohexomutases.^{[11a,b, 12]} Because all members of the latter superfamily appear to have similar mechanisms of action, a concerted pathway is expected for the human-α-PGM-catalyzed reaction.^{[11a, 13]} However, phosphoryl transfer reaction mechanisms can also proceed through two other different pathways: 1) a stepwise associative mechanism (addition–elimination) in which the nucleophilic attack precedes the departure of the leaving group, and the reaction proceeds through a pentavalent phosphorane intermediate, and 2) a stepwise dissociative mechanism (elimination–addition) in which the leaving group departs prior to the nucleophilic attack with the formation of a metaphosphate intermediate.^{[11a,b, 14]} Furthermore, the mechanisms for phosphoryl transfer reactions can yet proceed through an inline or a non-inline attack at the phosphorus atom.^[15] Despite that it has been demonstrated that both processes have similar barriers, the direct inline displacement mechanism is more typical and more actively studied.^[15] Some factors have been described to influence the occurrence of a specific mechanism, such as the position of the nucleophile and an increasing nucleophilicity by metal ions.^[11a]

Regarding the reorientation of the G16P, it is expected that significant changes should occur in the enzyme and/or the intermediate at the large central cleft of α-PGM. However, there is currently no consensus on the precise details of this reorientation. Nuclear magnetic resonance (NMR) and kinetic studies of rabbit α-PGM indicated that the two-step reaction is uninterrupted and support the reorientation of the G16P without its release into solution.^[16] In addition, molecular dynamics (MD) simulations indicated a higher flexibility of the apo-de-phosphorylated than the apo-phosphorylated form of α-PMM/PGM from P. aeruginosa.^[17] In fact, an expansion on the transient dephosphorylated form that opens the binding pocket by improving rotational freedom of domain IV was observed, which could allow the rotation of the intermediate. The movement of this domain was suggested as the main motion, which is responsible for closing/opening the catalytic cleft.^[18] Therefore, the dephosphorylation of Ser117P in the first step is also crucial to improve the structural flexibility of α-PGM for the second step.^[16a] Several α-PMM/PGM structures suggest that the G16P dissociates from its binding pocket, diffuses into the larger active-site cleft, rotates and then re-binds in the opposite orientation.^[19] This challenging process could justify the greater conformational flexibility attributed to α-PGM proteins, as well as the larger active-site pocket of α-PGM and α-PMM/PGM (cavity dimensions of ≈1700 ų)^[20] as compared to that of β-PGM (cavity size of ≈730 ų).^[13c] Studies involving β-PGM proposed that the intermediate dissociates and leaves the active site, and then returns and binds with the other phosphorylated site directed towards the catalytic residues.^[13d] However, Zhang and colleagues^[21] identified several open–close motions of the β-PGM that occur during the catalytic turnover, which could allow the required reorientation of the intermediate.

To provide new insights on the human phosphoglucomutase reaction, we have studied its mechanism of action starting from the G16P intermediate in both directions (i.e., toward G1P and G6P), by using the hybrid quantum mechanics/molecular mechanics (QM/MM) transition path sampling (TPS) method. In addition, we have performed accelerated molecular dynamics simulations to assess the reorientation pathway of G16P within the active site of the enzyme.

Results and Discussion

The atomic details of the catalytic mechanism of the human α-PGM were revealed by the TPS method. This is a crucial enzyme for the glucose metabolism, so our results can have a significant impact for modulating its activity by using structure-based drug design strategies.

We started with two geometries for the enzyme:G16P complex, with the G16P intermediate in two possible orientations. Each orientation then proceeds in opposite directions in the two-step mechanistic cycle, in order to obtain both products, G1P and G6P (as proposed in Scheme 1). In the reactant state of both mechanistic steps, the two phosphate groups are co-valently bound to the O1 and O6 atoms of the glucose unit of the substrate.

For both mechanistic steps, a transition-state ensemble (TSE) of twelve uncorrelated reactive trajectories was generated from our TPS analysis. For that, the commitment probability (probability of a configuration to relax into reactant or product states) along each reactive trajectory was determined. Committor values of 0.0, 0.5, and 1.0 correspond to reactant, transition, and product states, respectively. In Figure 2, we show the commitment probability for one representative reactive trajectory (chosen based on the closer time to the average values) of each mechanistic step. In the first step (see Figure 2, black), the committor probability increases from 0.0 to 1.0 in approximately 35 fs. The plot, however, is not symmetric in relation to the transition state, as the system spends more time in the reactants state, followed by a quick increase after the TS (23 fs pre-TS and 12 fs post-TS). In contrast, the committor probability rising (from 0.0 to 1.0) for the second step is much faster (≈12 fs, Figure 2, gray). In addition, this curve is more symmetric in relation to the TS, crossing it halfway between reactants (0.0 probability) and products (1.0 probability). This difference on the committor probability possibly occurs due to the higher Ser117-O-PO3²⁻ distance in the first step (3.64 Å), in comparison to the second step (3.45 Å).

Figure 2.

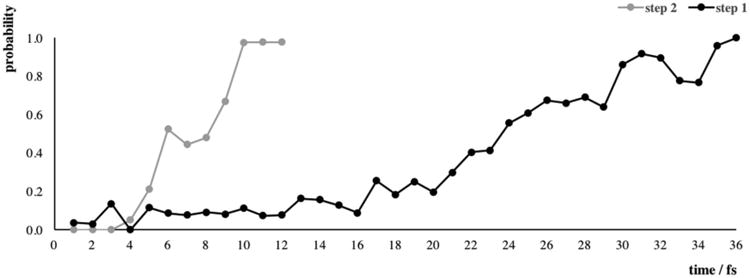
Commitment probability for the first (black) and the second (gray) mechanistic step of human α-PGM. The first time point at the x axis corresponds to frame number 235 (for step 1) and frame number 200 (for step 2), therefore, a comparison can be made.

In Figure SI-1 in the Supporting Information we provide the average root-mean-square fluctuation (RMSF) values of the Cα atoms over all reactive trajectories of the two mechanistic steps. The higher RMSF values obtained for the second step indicate that in the timescale of the reaction, the whole enzyme is more flexible in this step than in the first step. Figure 3 projects the twelve reactive trajectories per mechanistic steps by using the main bond-forming (Ser117-O-PO₃²⁻) and bond-breaking (O6/O1-sugar-PO₃²⁻) distances. We observed that the reaction tube formed in the transition-state region is narrower and better defined in the second step (Figure 3, right), which suggests the existence of a single pathway to reach the TS. The wider discrepancy observed in the first step (Figure 3, left) suggests the possibility of various pathways to reach the transition state. The two steps also differ in the maximum value for the bond-breaking distance, which is higher for the second step (6 vs. 4 Å). This probably happens due to the shorter substituent group linked to the sugar ring in the second step (–OPO₃²⁻ vs. –CH₂OPO₃²⁻). This may also contribute to the higher flexibility of the overall enzyme system during this step (Figure SI-1 in the Supporting Information).

Figure 3.

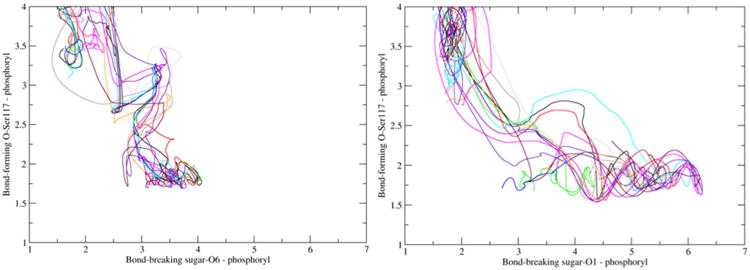
Twelve reactive trajectories projected on the plane of the bond-breaking and bond-forming distances for the first (left) and the second (right) mechanistic step.

Reaction coordinate identification

From the TSE of the uncorrelated reactive trajectories, we have identified the reaction coordinate of each mechanistic step. Six TS geometries for each step were used for this calculations. We used structures on the isocommittor surface, in which four different combinations of candidate atoms/residues to the reaction coordinate were constrained with a force of 2000 kcal mol⁻¹ Å⁻²: 1) the QM region, 2) the QM region and the magnesium cation, 3) the QM region, the Mg²⁺ ion, and Arg293, and 4) the QM region, the Mg²⁺ ion, Arg293, and Glu376. Afterwards, the system was propagated and the committor analysis was performed in order to evaluate if the commitment probability remained at 0.5. Figure 4 displays the histograms of the four tests for the first and second steps. Although the two selections (QM region or QM atoms plus the magnesium ion) give successful reaction coordinates for the first mechanistic step, the second option gives slightly better results. However, the inclusion of both Arg293 and Glu376 residues hinders the committor histograms, biasing this probability towards the products of the reaction. Interestingly, we obtained quite different results for the second step. The constrained region that gives a successful reaction coordinate was the one including the QM atoms, the Mg²⁺ ion, and Arg293. This indicates that at the TS1, there are protein-mediated vibrations that promote the catalytic residues and the Mg²⁺ cofactor, whereas the TS2 is characterized by additional protein motions on Arg293. In fact, a recent study proposed that the D263Y/G variants of human α-PGM interfere with the catalysis by an indirect propagated structural effect on Arg293. The mutation of the first residue causes the loss of the conserved salt bridge with the arginine residue that reorients its side chain towards the active site, thereby interfering with the substrate binding pocket.^[5] Our TPS calculations indicate additional important electrostatic roles for Arg293: 1) stabilization of the deprotonated Nδ atom of the catalytic His118 residue at the reactant state (2.48 and 3.06 Å in the steps 1 and 2 of the representative trajectory, respectively) and 2) stabilization of the HO–C4 (1.82, 1.95, and 1.80 Å in the reactant state, the TS, and the product state, respectively) and HO–C1 (3.05 Å in the product state) groups of the glucose in the second step.

Figure 4.

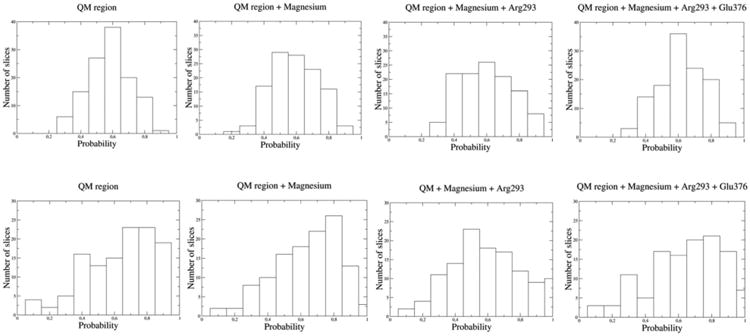
Different committor distributions for the first (top) and second (bottom) mechanistic steps of human α-PGM.

Overall, the identified residues contribute in different ways to the reaction coordinate: Ser117 directly interchanges the phosphoryl group with the substrate, His118 and Lys389 act as general acid/base catalysts, Arg23 and the Mg²⁺ ion have an electrostatic role by stabilizing the negative charge of the phosphoryl groups, and Arg293 possesses both structural and electrostatic functions.

G16P intermediate to G1P

First mechanistic step

In the reactants, the deprotonated Nδ atom of the catalytic His118 residue is stabilized by a hydrogen bond with Arg293, whereas the glucose C3–OH group also establishes short hydrogen bonds with the Glu376 and Ser378 residues through-out the entire chemical pathway. The large negative charge on the phosphoryl groups is stabilized by hydrogen bonds. The sugar-O1-PO₃²⁻ group interacts with Lys515 and water molecules in the vicinity, whereas the sugar-O6-PO₃²⁻ group interacts with the Lys389 residue and the magnesium cation. Interestingly, we noticed that in half of all reactive trajectories, the proton from Lys389 is already close to the O6 atom of the substrate (interacting with one oxygen atom of the phosphoryl group), which accounts for the larger error associated to this average distance (2.05 ±1.19 Å). This seems to indicate that this hydrogen transfer is the pioneer step that triggers the reaction pathway. Throughout the chemical step, the hydroxyl group of the nucleophilic Ser117 also transfers its proton to the deprotonated Nδ atom of the immediately adjacent His118. Table SI-1 in the Supporting Information displays the average lengths (and the individual values of each reactive trajectory) of the forming and breaking bonds along the two chemical steps. The reactant state, the TS, and the product state of one representative reactive trajectory (chosen based on the closer distances to the average bond length values) of this mechanistic step are illustrated in Figure 5.

Figure 5.

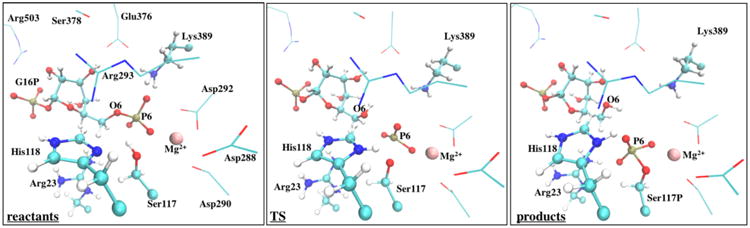
Representation of the reactant, transition-state, and product structures of one representative reactive trajectory, considering the first mechanistic step. The QM region is depicted in ball-and-stick, whereas the neighboring residues and the Mg²⁺ ion are shown as lines and sphere, respectively.

At the TSE, both proton transfers have already happened (the Nδ-His118-HO-Ser117 and HZ3-Lys389-O6 distances of approximately 1 Å). Hence, the His118 and Lys389 residues acquire protonated and neutral forms, respectively. Our calculations indicate that the His118 residue acts as the general base catalyst (considering the mechanism from the phosphorylated enzyme to the intermediate formation) instead of the Arg23 residue proposed in the literature.^[8,9] We also verified that the latter residue has an important role in stabilizing the negative charge of the phosphoserine in the products through hydrogen-bond interactions with one oxygen atom of the phosphate group. The bond length varies between (3.79±0.26) and (1.81 ±0.27) Å in the TS and the products, respectively. At the TSE, the sugar ring acquires a more energetically unstable boat conformation, which returns to an inverted twist-boat conformation in the product state. Figure SI-2 in the Supporting Information shows the superimposition of the sugar ring conformations in the three stationary points of the mechanistic step.

The distance between the Mg²⁺ ion and one oxygen atom of the PO₃²⁻ group was maintained along the entire catalytic pathway (bond lengths of (1.82 ±0.11), (1.69 ±0.33), and (1.75 ±0.02) Å in the reactant state, the TS, and the product state, respectively). On the one hand, this corroborates the crucial role played by this cation in guiding the phosphoryl group throughout the catalytic mechanism of human α-PGM, already proposed for β-PGM and α-PMM/PGM enzymes.^[13c,19] On the other hand, the Mg²⁺ ion also stabilizes and guides the catalytic serine residue by coordinating its hydroxyl group with a distance of (2.49±0.51) and (2.93±0.10) Å in the reactants and the TS, respectively, which decreases to (2.19±0.19) Å in the products.

As depicted in Figure 5, our mechanism does not follow the typical inline mechanism that proceeds with inversion of the configuration at the phosphorus atom,^[10,11] but resembles a non-inline mechanism. In fact, the two crystal structures used to build our reactant states have one Mg^II metal cofactor and O_{leaving group}-P-O_nuc angles of 127 and 128/134° (depending on the OD1/OD2 carboxylic oxygen atom present in the S108D mutation),^[9] and the structure of a rabbit α-PGM vanadate-based TS-analogue complex exhibits an angle of 150°.^[22] Despite that the latter angle does not prohibit an inline attack, the presence of different atoms (V instead of P and Co²⁺ instead of Mg²⁺) may lead to a geometry arrangement different from that of human α-PGM. Hence, even though Nam et al. have reported that PM3 presents deviations of the O_{leaving group}-P-O_nuc angle up to 208 in the TS geometry,^[23] our observations suggest that the inline mechanism may be sterically unlikely for α-PGM. In addition, a stereochemical experimental analysis of the products with isotopes shows that the PGM reaction proceeds with an overall retention of the phosphate ester configuration,^[24] which may occur in a non-inline mechanism.^[15b] Finally, despite that the inline mechanism has been observed for enzyme reactions with either one metal center and di- or triphosphates as substrates (e.g., Ras GTPase and some kinases),^[11b] two metal ions in the active site and mono-, di-, or triphosphates as substrates (e.g., alkaline phosphatase^[11c] and protein kinase A^[25]), or no metal ions and a monophosphate substrate (e.g., protein tyrosine phosphatase), we do not know of any attempt to characterize a reaction similar to the one of α-PGM (with one metal center coordinated to both the nucleophile group and the substrate).

On the other hand, as expected, we observed a concerted mechanism with no intermediates. The geometries of the transition-state ensemble show a planar PO₃²⁻ group that is not exactly midway between the two oxygen atoms of the nucleophile and the leaving group (distances of (2.54±0.12) and (3.07 ±0.22) Å, respectively). This geometry corresponds to a loose TS, in which the phosphorus atom has less net bonding to the leaving group and nucleophile atoms than in the ground state. Subsequently, larger forming and breaking P–O bond lengths were obtained, which seems to be promoted by the various hydrogen bonds between the hydroxyl groups of the glucose unit and the polar residues around it. Large values were also attained in computational studies of similar reactions, such as the enzymatic phosphoryl transfer of β-PGM as well as in models of monophosphate hydrolysis.^[10,13d] Additionally, computational studies have suggested that the pK_a value of the leaving group influences the geometry of the TSs in concerted mechanisms, becoming tighter or looser depending on whether they are associative or dissociative TSs, respectively^{[10, 11c]} The stable metaphosphate ion form is also supported by the larger fluctuation of the Mg²⁺–PO₃²⁻ distance at the TS, comparatively to the reactant and product structures. In agreement with past spectroscopic and theoretical studies, our results suggest that the reaction mechanism of human α-PGM proceeds through a concerted mechanism with a loose meta-phosphate-like TS: 1) the geometry of the vanadate-based TS-analogue complex of rabbit α-PGM seems to have a concerted S_N2-like character,^[22] 2) a computational study on the mechanism of β-PGM also proposed a concerted reaction path-way,^[13b] 3) in a 1.2 Å resolution X-ray structure of b-PGM from Lactococcus lactis obtained at cryogenic temperature,^[26] a species described as a stabilized metaphosphate was identified, and 4) the hydrolysis of phosphate monoester dianions was observed to occur through a concerted pathway with a loose (metaphosphate-like) TS, whereas the hydrolysis of phosphate di- and triesters tends to have a tight (phosphorane-like) TS.^[11a]

Second mechanistic step

Starting the second step from the reoriented bisphosphate G16P substrate, the reaction proceeds by transferring the phosphoryl group bound to the O1 atom of the sugar to Ser117, which simultaneously transfers its proton to the Nδ atom of the adjacent His118. At the same time, the O1 atom of the sugar carries one proton from Lys389 to complete the reaction. The geometries of both transition-state ensembles (TSE1 and TSE2) are very similar. However, the sugar conformations of TSE1 and TSE2 do not completely fit by simple positional interchange of the phosphate groups. A greater sugar ring conformation variation occurs in the second step, changing it from a twist-boat (at the reactants) to a half-chair conformation at the TS (a superimposition of the sugar ring conformations is depicted in Figure SI-2 in the Supporting Information). In addition, the C1-O1-P1/C6-O6-P6 angles of the reactive phosphate groups differ by approximately 40° between both transition-state structures. Other differences to the first step are 1) at the TSE, both proton transfers are not completed (Nδ–OH and H–Lys389-O1 bonds of (1.25 ±0.14) and (1.23± 0.26) Å, respectively); 2) the longer chain of the sugar–CH₂OPO₃²⁻ group is electrostatically stabilized by Lys503 and Lys515, and 3) at the product stage, the negative charge of the Ser117–PO₃²⁻ group is mainly neutralized by the Mg²⁺ ion and the double-protonated His118 (instead of the Arg23 residue in the first step). The present results differ from the ones obtained for β-PGM, in which the proton transfer from the general acid catalyst to the sugar–O1 group is faster than to the sugar–O6 group.^[13d] Interestingly, although the G16P molecule can adopt different orientations inside the active pocket, there are residues such as Glu376 and Ser378 that are specifically oriented to establish interactions with the OH and PO⁻ groups of the intermediate irrespectively of its direction. This likely contributes to the higher reversibility of the catalytic reaction of human α-PGM.^[4]

Accelerated molecular dynamics simulations

As mentioned previously, the two consecutive mechanistic steps are linked by a 180° reorientation of the stable intermediate G16P. In order to evaluate if the intermediate releases from the active site of the human α-PGM and re-binds without going to the bulk solution, two accelerated MD (aMD) simulations were performed. The two simulations (i.e., A and B) correspond to the same α-PGM/G16P system, but with the intermediate placed in different positions within the active site: in simulation A O1–PO₃²⁻ is facing the Ser117 residue and in simulation B O6–PO₃²⁻ is directed towards the Ser117 residue. Figures SI-3-SI-6 in the Supporting Information show the root-mean-square deviation (RMSD) values of the starting structures for the backbone atoms of α-PGM (for the complete enzyme and for each domain) and the G16P intermediate (for the complete molecule and for glucose and the phosphate groups) in both simulations. The behavior of both systems is quite similar. The RMSD values for the entire protein backbone increase to approximately 4 Å, stabilizing after about 150 ns. The motions of the domains II and IV are the main contributors to the global motion of the α-PGM enzyme. Higher RSMD values were obtained for the intermediate (maximum RMSD values of 6 and 9 Å around 100 ns for simulations A and B, respectively), which indicates a great mobility throughout the simulations. The motions that contribute the most to this rearrangement are those associated with the O6–PO₃²⁻ group. To measure the movement of the human α-PGM system relative to the average structure over the whole simulations, the RMSF values for each residue were determined for both simulations (Figure SI-7 in the Supporting Information). In both simulations, there are several peaks which in most cases match the main loop regions present in the domains I, II, and IV. Domain IV is the one with the highest RMSF values (5 and 8 Å for simulations A and B, respectively). These findings support previous work, in which the movement of domain IV is highlighted as the main contributor to the reorientation of the intermediate in the binding pocket.^[18] Because the catalytic Ser117 residue belongs to a region with higher RMSF values (loop of domain I), we followed the Mg²⁺–P1/P6 distances to inspect the orientation of the intermediate. These distances are shown in Figures SI-8 and SI-9 in the Supporting Information. As seen in Figure SI-8 in the Supporting Information, after approximately 100 ns of simulation, the overall position of the intermediate starts to change and seems to invert the distances (with the O6–PO₃²⁻ group becoming closer to the magnesium ion than the O1–PO₃²⁻ group). However, a larger timescale of simulation would be required to observe a possible full structural reorientation within the large binding site of the α-PGM.

Analyzing the binding of the intermediates in both simulations, we verified the existence of two regions populated by positively charged residues: 1)Arg23, Lys130, Arg293, and Lys389 and 2) Arg427, Arg503, and Arg515, which neutralize the anionic charge of the phosphoryl groups. These residues promote an electrostatic effect that appears to support and guide the reorientation of the intermediate. A detailed description of the rearrangement of the phosphoryl groups around these residues is given in the Supporting Information. All these results suggest that the reorientation of the G16P molecule may occur within the binding pocket of the human α-PGM through electrostatic effects and synchronized conformational rearrangements of both the enzyme and the intermediate.

Conclusions

Our calculations provided new insights on the reaction of human α-PGM: 1) we confirmed that this reaction occurs by two consecutive steps, connected by the intermediate; 2) in both steps, the nucleophilic Ser117 residue transfers its proton to the adjacent His118, while receiving the phosphoryl group from the G16P molecule; 3) simultaneously, another hydrogen transfer occurs from Lys389 to the O6 or O1 atoms of the sugar (depending on whether this is the first or second step, respectively); and iv) we concluded that the His118 and Lys389 residues act as general base and acid catalysts, whereas the role of Argf23 is to stabilize the phosphorylated enzyme by electrostatic interactions with the Ser117P residue. Furthermore, our calculations also propose that the phosphorylation of Ser117 proceeds through a concerted S_N2-like mechanism with a loose metaphosphate-like transition state.

The geometrical analysis of both TSEs and their committor probability calculations showed that the second step resembles a late transition state and has a quicker committor distribution. The narrower and well-defined TS region of the second step indicates the existence of a single pathway to reach the transition state, whereas various pathways are suggested for the first step. Our study also revealed that overall, α-PGM is more flexible in the second step, and it involves an additional residue on the reaction coordinate. This suggests that a greater degree of coordinated protein motions is required to reach the TS of the second step. With our commitment probability calculations, we highlight key residues for the catalytic chemical step, that is, Arg23, Ser117, His118, Arg293, Lys389, and the magnesium cofactor.

Our aMD simulations indicate that the overall position and conformation of G16P does change throughout the simulations, and G16P is able to invert the distances between its two P1 and P6 atoms and the magnesium ion. Concurrently, the main loops from domains I, II, and IV have also shown an increased flexibility, in particular considering the ones from domain IV. However, we could not observe a full reorientation of G16P within the enzyme—larger simulation times are likely required. Still, our results suggest that all these conformational rearrangements help the reorientation of the G16P to continue the catalytic path without leaving the active pocket. We also found that an electrostatic effect promoted by several positive residues located around the binding pocket (i.e., Arg23, Lys130, Lys389, Arg427, Arg503, Arg515, and Arg293) can help support the reorientation of the intermediate.

Computational Methods

Molecular modeling

The crystallographic structure of the human α-PGM (PDB ID: 5EPC, at a resolution of 1.85 Å) was used in the present study. Chain A was chosen from the two copies in the crystal.^[4] The G16P substrate (with the O6–PO₃²⁻ group oriented to Ser117) and the missing residues (507–510) were modeled from the 1C47.pdb structure (rabbit α-PGM crystallized with G16P). This structure was used to study the first step of the α-PGM reaction. To generate the α-PGM:G16P complex with the substrate repositioned in the opposite way, the 2FKM.pdb structure (P. aeruginosa α-PMM/PGM crystallized with G16P with the O1–PO₃²⁻ group directed to Ser117)^[9] was used. This structure was used to study the second step of the α-PGM reaction. The pK_a values of all ionizable residues were evaluated by using the PROPKA program.^[27] The proper hydrogen atoms were added, maintaining most residues in their physiological protonation state. The exceptions were Asp308 and Asp390 that were protonated due to their high pK_a values (>7.0) and the fact that these did not have any neighboring positively charged residue. Three sodium counterions were added to neutralize the system. All crystallographic water molecules were retained and additional explicit water molecules were employed, filling a spherical box with a distance of 12 Å between the edges of the sphere and any atom of the protein. The TIP3P water model was used to describe the solvent.^[28] A total of 27387 water molecules was added to the system. The final system was composed by 92 478 atoms that were divided into two layers: a high layer described with quantum mechanics (QM) and a low layer described with molecular mechanics (MM). The generalized hybrid orbital (GHO) method was used to couple both layers.^[29] The high layer includes the entire substrate and the side chains of Arg23, Ser117, His118, and Lys389, comprising a total of 72 atoms. The QM region was treated with the PM3 semi-empirical model.^[30] The low layer was described with MM additive force fields. Even though PM3 has been described to underperform when studying phosphate transfer reactions, the geometrical errors that have been reported by Nam et al.^[23] do not undermine the chemistry of the studied reactions. Thiel and Voityuk^[31] determined that the mean absolute errors for bond lengths and bond angles of molecules containing phosphorus were 0.056 Å and 4.9°, respectively, which indicates quite good accuracy. Its main limitation is to accurately describe the energetic pathway of reactions,^[23,32] which is not evaluated in this work. Moreover, the QM/MM PM3/MM approach has been successfully applied to study other enzymatic reactions involving phosphate groups.^[33] However, in order to validate the starting geometry of our model, we have optimized our reactant state of the first mechanistic step with the higher-level DFT method to describe the QM part. The QM/MM ONIOM formalism was used for this purpose, at the B3LYP/6-31G(d):PARM99SB level. Because the QM/MM approach is different from the TPS, we also re-calculated the geometry with the PM3/MM method in order to perform an adequate comparison. The details of this procedure and an image with the superimposition of the two optimized geometries (Figure SI-10 in the Supporting Information) are given in the Supporting Information. Visually, both optimized structures seem quite similar, except for the O6···Arg23 and Ser117···His118 distances. In both, the substrate moves significantly away from the Ser117, and the proton from Lys389 is bound to one oxygen atom from the phosphoryl group, becoming closer to the O6 atom (similarly to what happens in half of the previous TPS reactive trajectories). The RMSD value of the QM region is 0.789 Å, whereas the mean unsigned errors of the main geometric parameters are: bond lengths: P6–O6 0.09, P6–O-Ser117 0.14, O6–H-Lys389 0.09, O6–H-Arg23 0.21, and O–Ser117-N-His118 0.85 Å; and angles: O6-P6-O-Ser117 0.88, C6-O6-P6 0.29, and O6-P6-H-Lys389 0.82°. In light of these results, PM3 seems to be an adequate method to study the structural features of this enzyme reaction within the TPS methodology. Hence, our QM/MM model was described at the PM3/CHARMM36 level of theory. This and other QM/MM approaches have been extensively used for describing the reactions catalyzed by various enzymes.^[34] The CHARMM molecular dynamics package^[35] was used to perform the geometry optimization and equilibration of the systems considering the QM/MM multi-resolution model. Protein atoms of the MM layer were described with the CHARMM36 force field.^[36] We used results with two decimal places because both methods (semi-empirical PM3 and MM CHARMM) have been shown to attain this level of accuracy for bond lengths and angles.^[31] The geometry optimization of the α-PGM:G16P complex was performed in three stages: 1)only the water molecules were minimized (100 steps by using the adopted basis Newton-Raphson method (ABNR)); 2) the side-chain atoms and the QM region were constrained (100 steps by using the ABNR method); and 3) the entire system was minimized (100 steps by using the ABNR method). The heating was conducted slowly from 0 to 300 K: 1) 25 ps with the water molecules and hydrogen atoms constrained with a harmonic force constant of 20 kcalmol⁻¹ Å⁻²; 2) 25 ps with the water molecules and hydrogen atoms constrained with a harmonic force constant of 10 kcalmol⁻¹ Å⁻²; 3) 20 ps with the water molecules and hydrogen atoms constrained with a harmonic force constant of 5 kcalmol⁻¹ Å⁻²; and 4) 15 ps without constrains. After this, the system was equilibrated for 50 ps at 300 K. The microcanonical (NVE) ensemble was used. The SHAKE algorithm was employed to constrain the bond lengths involving hydrogen atoms,^[37] and the equations of motion were integrated with a 1 fs time step by using the Verlet leapfrog algorithm.

Transition path sampling calculations

The equilibrated α-PGM:G16P structures were used as starting geometries for the transition path sampling (TPS)^[38] calculations, in which the structures of the reactive trajectories were analyzed. TPS is a Monte–Carlo method that searches in the reactive trajectory space. The order parameters are defined by specific bond lengths that inform whether the system is in the reactant or product states. Although this approach does not consider the energetic details of the reaction, it represents an unbiased and accurate method to simulate how a reaction proceeds from the reactant state to the product state, thus identifying its expected catalytic pathway. We have considered the first and second mechanistic steps as G16P+α-PGM↔G1P+α-PGM-Ser117P and G16P+α-PGM↔G6P+α-PGM-Ser117P, respectively (see Scheme 1). Hence, for the first step, we have defined three order parameters: 1) bond-breaking P6(sugar)–O6(sugar) length <2.6 Å for the reactants and >2.6 Å for the products; 2) bond-forming OG(Ser117)–P6(sugar) length >2.6 Å for the reactants and <2.6 Å for the products; and 3) bond-forming HG1(Ser117)–Nδ(His118) length > 1.3 Å for the reactants and < 1.3 Å for the products. For the second step, we have used the first three order parameters by using the P1 and O1 atoms of the sugar instead of the P6 and O6 atoms, plus the fourth one, that is, 4) bond-forming HZ3(Lys389)–O1(sugar) length > 1.3 Å for the reactants and < 1.3 Å for the products. These order parameters were used to generate an initial reactive trajectory. For the first step, we have generated the first reactive trajectory by applying harmonic force constants of 40, 70, and 100 kcalmol⁻¹ Å⁻² on the three previously defined bond lengths, respectively. For the second step, the harmonic force constants applied on the four bond lengths were 55, 90, 55, and 25 kcalmol⁻¹ Å⁻², respectively. These harmonic force constants are those for which the reaction proceeds from the reactant state to the product state. The reactive trajectories were propagated for 250 fs, which was an appropriate time for both reactions to occur. The momenta of a randomly chosen slice of this reactive trajectory was perturbed and propagated from that slice by using new momenta chosen from a Boltz-mann distribution. This was repeated until a new reactive trajectory was generated. By using this new trajectory as a seed, we generated 180 reactive trajectories of 500 fs for both mechanistic steps. This large number of reactive trajectories was used to minimize the correlation between them. In each 500 fs trajectory of both steps the crossing barrier should be very small, as the system rapidly transitions from a reactant state to a product state. Most of the simulation time, the system samples the reactant state, and then it rapidly transitions to the products state.

Subsequently, we performed a committor analysis,^[39] in which we identified the slice of each reactive trajectory that has the ability to generate new trajectories with 50% of probability to reach the reactants or products. We carried out a sampling of 50 committors and all results converged in the same manner. The set of all iso-committor structures is the transition state ensemble (TSE), which is the appropriate statistical definition for a transition state.^[39] The TPS method can generate the TSE without any a priori knowledge of the reaction coordinate, so it is an unbiased method. From the collected reactive trajectories, we identified a transition state ensemble comprised of twelve uncorrelated transition-state structures for each mechanistic step. Following this, we identified the reaction coordinate for each mechanistic step. To do this, we started with structures on the isocommittor surface, in which some residues or atoms that are possible candidates for belonging to the reaction coordinate were constrained. Afterwards, the system was propagated, and if the selected atoms are indeed part of the reaction coordinate, the system would stay on the isocommittor surface (with commitment probabilities of 0.5 for the reactants and products). Hence, fifty trajectories were generated from the constrained simulation and the commitment probabilities were determined. Some assumptions on the reaction coordinate residues need to be tested, until the isocommittor process succeeds. We have used six uncorrelated TS geometries (randomly selected) as starting points for this procedure.

Accelerated molecular dynamics simulations

Two α-PGM:G16P structures with the substrate in two different orientations (O1–phosphoryl or O6–phosphoryl groups oriented to Ser117) were used as starting geometries for the accelerated molecular dynamics (aMD) calculations.^[40] This method enhances the sampling of conformational space by reducing the barriers that separate different states of a system. The potential-energy landscape was modified by applying a boost energy to the dihedral potentials, which accelerates the key internal degrees-of-freedom, and subsequently, produces large and slow motions in shorter simulation times.^[40a–c] The molecular modeling of both systems was similar to that previously described for the TPS calculations, except that instead of a spherical box, a rectangular TIP3P water^[28] box with edges of 15 Å was considered. For these simulations, we have used the isothermal-isobaric ensemble with periodic boundary conditions. All MM calculations were performed by using the NAMD 2.11^[41] with the CHARMM36 force-field parameters,^[36] for describing protein and carbohydrate residues. The geometry of each system was optimized (25 000 steps), heated (simulation of 400 ps to slowly increase the temperature from 0 to 310 K by using increments of 0.75 Kps⁻¹) and equilibrated for 400 ps. This was followed by 5 ns of conventional MD (cMD) simulations and 400 ns of dihedral boost aMD simulations with the NPT ensemble, in which Langevin dynamics and a Langevin piston were used to maintain the temperature at 300 K and the pressure at 1 atm, respectively. The boost parameters, the dihedral threshold energy (7372.5 and 7341.0 kcalmol⁻¹ for the two systems) and the dihedral alpha value (451.2 kcalmol⁻¹ for both systems) were computed from the cMD simulation. The SHAKE algorithm was employed to constrain the bond lengths involving hydrogen atoms^[37] and the equations of motion were integrated with a 2 fs time step. The long-range interactions were considered by the Particle–Mesh–Ewald (PME) method,^[42] and the non-bonded interactions were truncated with a 10 Å cutoff. The aMD trajectories were collected every 20 ps and were analyzed with the VMD 1.9.3 software.^[43]