A comparison of time-homogeneous Markov chain and Markov process multi-state models

Abstract

Time-homogeneous Markov models are widely used tools for analyzing longitudinal data about the progression of a chronic disease over time. There are advantages to modeling the true disease progression as a discrete time stationary Markov chain. However, one limitation of this method is its inability to handle uneven follow-up assessments or skipped visits. A continuous time version of a homogeneous Markov process multi-state model could be an alternative approach. In this article, we conduct comparisons of these two methods for unevenly spaced observations. Simulations compare the performance of the two methods and two applications illustrate the results.

1. Introduction

In most longitudinal medical studies on the progression of healthy individuals to chronic diseases, such as cancer, AIDS, and dementia, the natural development is often expressed in terms of distinct states. The analyses in such studies where individuals may transition among several states are often performed by using multi-state models (MSMs). There are two major types of multi-state models in the literature, one is based on discrete-time Markov chain, and the other one is based on continuous-time Markov process. These two types of modeling techniques are related in certain ways, and both enable researchers to study transitions between different disease states simultaneously. However, the two types of models are constructed under different assumptions, and might generate different results and conclusions under certain cases. Thus, researchers need to be careful when deciding which models to use in real data applications.

Multi-state models based on the discrete-time Markov chain have become popular in analyzing longitudinal data collected in chronic disease studies. Such models are also called Markov chain transitional models (Agresti 2002). Kryscio, Schmitt, and Salazar (2006) used a Markov chain model to identify risk factors associated with transitions from cognitively normal to various forms of mild cognitive impairment (MCI) and then from MCI into early dementia, with death before dementia as a competing state. A series of polytomous logistic models were used to model the one-step transition probabilities, and they focused on the effects of baseline age, education, sex, family history of dementia, and APOE4 status on the transition probabilities.

Use of continuous-time MSMs has grown quickly in the literature. A continuous-time MSM is a model for a continuous time stochastic process allowing individuals to move among a finite number of states (Meira-Machado et al. (2009). There exists an extensive literature on continuous-time MSMs (see, e.g., Hougard (1999) or Commenges (1999))., Hubbard and Zhou (2011), or Joly, Commenges, and Letenneur (1998), Joly, and Commenges (1999), Joly et al. (2002). Applications of continuous-time MSMs can be found in liver cirrhosis (Andersen, Esbjerg, and Sorensen. (2000)), dementia (Joly, Commenges, and Letenneur 1998, Joly, and Commenges 1999, Joly et al. 2002; Hubbard and Zhou 2011) among others.

In real-data applications, the observation schemes vary among different studies. In some studies, investigators are able to collect the data at equally spaced time points, for example, once a month or once a year. In this case, the resulting longitudinal data will be evenly spaced. In other studies, collecting the data at equal time intervals is unrealistic; in these cases, the longitudinal data will be unevenly spaced. Both types of MSMs are widely used in applications to model similar longitudinal data without considering the observation schemes. In this article, we will conduct a comparison study between the two types of models. To the best of our knowledge, there are few studies in the literature that compares these methods.

The rest of this article is structured as follows. In Section 2, the discrete-time MSM and continuous-time MSM are introduced respectively. In Section 3, a simulation study is conducted to compare the two modeling methods under different observation schemes. Section 4 applies the two methods to two real datasets, the Nun study and the BRAiNS study. Conclusion and discussion are provided in Section 5.

2. Discrete-time and continuous-time multi-state models

For a chronic disease with K possible outcome states, we could write the underlying disease process as X(t) ε {1, 2,…, K}, t ≥ 0. Here, the value of X(t) denotes the occupied disease state at time t. Suppose an individual has observations at time points T = (t₀, t₁,…, t_m), we write X = (X₀, X₁,…, X_m) the corresponding occupied states such that X_l = X (t_l), l = 1, 2, …, m. The initial state X₀ is usually given.

2.1. Discrete-time multi-state model

In a discrete-time multi-state model, the longitudinal data are modeled through a joint probability mass function P(X₀, X₁,…, X_m). The observation time points T = (t₀, t₁,…, t_m) are ignored under the assumption that the data are evenly spaced. In most applications, the outcome data (X₀, X₁,…, X_m) are assumed to follow a discrete-time Markov chain, in which we have

$$P\left(X_0,X_1,\dots ,X_m\right)=P\left(X_0\right)\times P\left(X_1|X_0\right)\times \dots \times P\left(X_m|X_{m-1}\right).$$

The one-step transition probability from state h to state j at lth step can be written as

$$P_{hj,l}=P\left(X_l=j|X_{l-1}=h\right).$$

Thus, the joint probability mass function P(X₀, X₁,…, X_m) can be characterized by the one-step transition probability matrix

$${\mathbf{P}}_l=\left(\begin{array}{ccc}{P}_{11}& \dots & P_{1K,l}\\ ⋮& \ddots & ⋮\\ P_{K1,l}& \cdots & P_{KK,l}\end{array}\right).$$

The rows of P_l satisfy the condition ${\displaystyle {\sum }_{j=1}^K{P}_{hj,l}=1}$. The Markov chain is often assumed to be time homogeneous. In this case, we have P_l = P and P_hj,l = P_hj, which is a constant of time.

Baseline covariates Z are usually linked to the transition probabilities through a series of polytomous logistic regressions

$$\log \left(\frac{P_{hj}}{P_{hh}}\right)={\beta }_{hj,0}+{\beta }_{hj}^T\mathbf{Z},j\ne h.$$

There are K possible polytomous logistic regressions, one model for each row of the transition probability matrix. When the model only involves baseline covariates, standard software such as PROC LOGISTIC and PROC CATMOD (SAS Institute (2011) can be used to fit each logistic model separately.

2.2. Continuous-time multi-state model

In a continuous-time multi-state model, the transition process is modeled as a stochastic process. The longitudinal data are allowed to be unevenly spaced. We can write the transition probability from state h at time s to state j at time t as

$$P_{hj}\left(s,t|H_{s-}\right)=P\left(X\left(t\right)=j|X\left(s\right)=h,H_{s-}\right),s<t.$$

Here, H_s− is the history of the process up to time s. For a Markov process, the transition probabilities are independent of the past history before time s. In this case, we have

$$P_{hj}\left(s,t\right)=P\left(X\left(t\right)=j|X\left(s\right)=h\right),\text{s < t}.$$

The transition probabilities can be fully characterized by the corresponding transition intensities, which have the following definition:

$${\alpha }_{hj}\left(t\right)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{P_{hj}\left(t+\mathrm{\Delta }t,t\right)}{\mathrm{\Delta }t},j\ne h$$

Similar to the hazard function in survival models, the transition intensities measure the instantaneous hazard of transition from the current state h to another state j. For j = h, we have

$${\alpha }_{hh}\left(t\right)=-{\displaystyle \sum _{j\ne h}{\alpha }_{hj}\left(t\right)}.$$

Different assumptions can be made about the dependence of the transition intensities on time. In this study, we focus on time-homogeneous models. In a time-homogeneous model, we have α_hj (t) = α_hj.

Covariates of interest can be incorporated into the transition intensities using the Cox proportional hazards regression model, which has the following form:

$${\alpha }_{hj}\left(\mathbf{Z}\right)={\alpha }_{hj,0}\exp \left({\mathbf{\beta }}_{\mathbf{h}j}^{\mathbf{T}}\mathbf{Z}\right)=\exp \left({\beta }_{hj,0}+{\mathbf{\beta }}_{\mathbf{h}j}^{\mathbf{T}}\mathbf{Z}\right).$$

Here, α_hj,0 = exp(β_hj,0) is called the baseline intensity from state h to state j.

Write the transition intensity matrix as

$$\mathbf{Q}=\left(\begin{array}{ccc}{\alpha }_{11}\left(\mathbf{Z}\right)& \dots & {\alpha }_{1K}\left(\mathbf{Z}\right)\\ ⋮& \ddots & ⋮\\ {\alpha }_{K1}\left(\mathbf{Z}\right)& \cdots & {\alpha }_{KK}\left(\mathbf{Z}\right)\end{array}\right),$$

and write the transition probability matrix as

$$\mathbf{P}\left(s,t\right)=\left(\begin{array}{ccc}{P}_{11}\left(s,t\right)& \dots & P_{1K}\left(s,t\right)\\ ⋮& \ddots & ⋮\\ P_{K1}\left(s,t\right)& \cdots & P_{KK}\left(s,t\right)\end{array}\right).$$

For a time-homogeneous model, P(s,t) can be calculated in terms of the transition intensity matrix Q using the Kolmogorov differential equation (Hougard (1999))

$$\mathbf{P}\left(s,t\right)=\mathbf{P}\left(t-s\right)=\text{Exp}\left(\left(t-s\right)\mathbf{Q}\right)$$

Estimation of the model can be done using the maximum likelihood method. Given an individual has observations at time points (t₀, t₁,…, t_m) and corresponding observed states (X₀, X₁,…, X_m), its likelihood contribution can be calculated as

$$L=P\left(X_0,X_1,\dots ,X_m\right)=P\left(X_0\right)\times P_{X_0{X}_1}\left(t_0,t_1\right)\times \cdot \cdot \cdot \times P_{Xm-1Xm}\left(t_{m-1},t_m\right).$$

Through the transition intensities, we are able to calculate the transition probabilities at any given time period. Thus, we are able to handle unevenly spaced longitudinal data.

We can also handle transitions with exact transition times. Death is an important competing risk in many chronic diseases and is often included in the model. The exact time of death will be recorded, while the state just before death might be unknown. Suppose the last state X_m = K is death and t_m is the time of death. In this case, the likelihood contribution can be calculated as

$$L=P\left(X_0,X_1,\dots ,X_m\right)=P\left(X_0\right)\times P_{X_0{X}_1}\left(t_0,t_1\right)\times \cdot \cdot \cdot \times \left({\displaystyle \sum _{j\ne K}{P}_{X_{m-1}j}\left(t_{m-1},t_m\right)}{\alpha }_{jk}\left(\mathbf{Z}\right)\right),$$

where j can be any possible state just before death (Jackson (2011)).

2.3. Relationship between the two models

Two types of models are constructed under different assumptions about the response data. The discretetime MSM assumes the transitions follow a Markov chain. However, the continuous-time MSM assumes the transitions follow a continuous-time Markov process. Thus, the covariates coefficients in the two types MSMs have different interpretations. The discrete-time MSM incorporates covariates into the model through a series of multinomial logit regressions; the corresponding coefficients have the log odds ratio interpretation. The continuous-time MSM incorporates covariates through transition intensity functions by proportional hazard regressions; the corresponding coefficients have the log hazard ratio interpretation.

The relationship between the two types of models is linked through their one-step transition probabilities. Note that in our notation P is the one step transition probability for the discrete-time model and P(t − s) is the transition probability matrix from time s to time t for the continuous-time model. Suppose the time interval between two assessments equals one time unit; thus we have P = P(1).

3. Simulation study

In chronic disease studies, the collected longitudinal data are often not evenly spaced. In this section, we conduct simulation studies to compare the performance of the two types of MSMs under different observation schemes. The comparisons are taken under three types of observed data:

• (1) Evenly spaced data: the time intervals between two consecutive observations are all equal to 1 year;

• (2) Unevenly spaced data 1: the time intervals between two consecutive observations follow a truncated Normal distribution with mean 1 and standard deviation 0.5, left truncated at 0.01.

• (3) Unevenly spaced data 2: the time intervals between two consecutive observations follow a Normal distribution with mean 1 and standard deviation 1.5, left truncated at 0.0125.

We focus on the one-year transition probability estimates (P_hj). Comparisons are made by their percent biases (% bias) for the two methods under these three types of observed data.

Data are generated from a four-state model with state 1 and state 2 representing two transient states, and state 3 and state 4 representing two absorbing states. The true model has the following transition intensity matrix:

$$\mathbf{Q}=\left(\begin{array}{cccc}{\alpha }_{11}& {\alpha }_{12,0}\exp \left({\beta }_{12}Z\right)& {\alpha }_{13,0}\exp \left({\beta }_{13}Z\right)& {\alpha }_{14,0}\\ {\alpha }_{21,0}\exp \left({\beta }_{21}Z\right)& {\alpha }_{22}& {\alpha }_{23,0}\exp \left({\beta }_{23}Z\right)& {\alpha }_{24,0}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right).$$

Here, Z is a binary baseline covariate. In our simulation study, Z follows a Bernoulli distribution with probability of 0.4 with value 1. We set the baseline intensities

$$\left({\alpha }_{12,0},{\alpha }_{13,0},{\alpha }_{14,0},{\alpha }_{21,0},{\alpha }_{23,0},{\alpha }_{24,0}\right)=\left(0.25,0.03,0.05,0.2,0.15,0.05\right)$$

and the regression coefficients

$$\left({\beta }_{12},{\beta }_{13},{\beta }_{21},{\beta }_{23}\right)=\left(0.5,-0.2,-0.3,0.15\right)$$

For all three observation schemes, each subject has up to 30 observations. If a patient is still at state 2 or state 3 after 30 years, it will be right censored at year 30. The exact transition times to state 4 are recorded, while the transition time to state 1, 2, or 3 are all interval censored because of the discrete time observations as we described above.

Simulations are set to 1000 iterations, with each containing 500 subjects. For simplicity, all subjects start at state 1. All calculations are done by using the “msm” package in R (Jackson (2011) and the PROC IML and PROC CATMOD procedures in SAS 9.3 system (SAS Institute (2011).

Tables 1 and 2 list the percent bias of the one year transition probabilities by discrete-time MSM and by continuous-time MSM, respectively. The results show that the discrete-time MSM and continuoustime MSM work equally well when the data are evenly spaced. Since the calculation of transition probabilities through the transition intensities are usually complicated, discrete-time MSM has the computational advantage over the continuous-time MSM.

Table 1.

Percent bias of one-year transition probability for each path by the discrete-time multi-state model under three observation schemes.

	Evenly spaced data		Unevenly spaced data 1		Unevenly spaced data 2
Transition	Z=0	Z=1	Z=0	Z=1	Z=0	Z=1
1 to 1	−0.29%	0.22%	1.10%	2.90%	−11.70%	−15.97%
1 to 2	0.40%	−0.42%	−2.90%	−11.00%	24.81%	12.58%
1 to 3	−0.74%	1.00%	−3.10%	19.00%	57.53%	89.89%
1 to 4	−0.38%	0.76%	−3.80%	6.50%	40.64%	52.35%
2 to 1	0.27%	−0.39%	−4.90%	−9.90%	22.99%	13.65%
2 to 2	−0.18%	0.21%	0.26%	3.50%	−15.69%	−10.50%
2 to 3	0.45%	−0.45%	2.00%	−6.70%	41.59%	32.47%
2 to 4	0.66%	−0.94%	5.40%	−11.00%	50.35%	29.00%

Table 2.

Percent bias of one-year transition probability for each path by the continuous-time multi-state model under three observation schemes.

	Evenly spaced data		Unevenly spaced data 1		Unevenly spaced data 2
Transition	Z=0	Z=1	Z=0	Z=1	Z=0	Z=1
1 to 1	−0.06%	−0.31%	−0.03%	−0.13%	−0.03%	−0.13%
1 to 2	0.42%	0.51%	0.23%	0.12%	0.23%	0.12%
1 to 3	−0.44%	1.50%	0.28%	1.59%	0.28%	1.59%
1 to 4	−0.23%	−0.31%	−0.56%	−0.57%	−0.56%	−0.57%
2 to 1	0.41%	0.23%	0.23%	−0.35%	0.23%	−0.35%
2 to 2	−0.08%	0.03%	−0.07%	−0.01%	−0.07%	−0.01%
2 to 3	0.22%	−0.08%	0.20%	0.36%	0.20%	0.36%
2 to 4	−0.72%	−0.72%	−0.23%	−0.24%	−0.23%	−0.24%

When the collected longitudinal data are unevenly spaced, the discrete-time MSM will provide biased estimates for the one year transition probabilities. We may observe that the biases of the estimations of one year transition probabilities increase as the spacing gets more uneven. For example, the percent bias of the transition probability estimate from state 1 to state 3 with the covariate Z = 1 by the discrete-time Markov MSM could be as large as 19% in unevenly spaced data with relative less the observation time interval variation (unevenly spaced data 1 in the tables), and increases to 90% in unevenly spaced data with relatively larger observation time interval variation (unevenly spaced data 2 in the tables). For the same case, the percent bias of transition probability estimate from state 1 to state 3 with the covariate Z = 1 by the continuous-time Markov MSM is only 1.6% in both unevenly spaced datasets. Thus, in those longitudinal chronic disease studies in which the actual visit times deviate from the planned visit times, with possible skipped visits, continuous-time MSMs are recommended.

4. Application to the NUN study and the BRAiNS study

In this section, we apply both the discrete-time MSM and continuous-time MSM to the Nun Study and the BRAiNS datasets. The NUN Study is a well-known cohort study designed to assess the influence of early life exposures and cognitive ability on the development of Alzheimer-type dementia and pathology in late life. The outcome of the NUN’s data include four states: Not Serious Impairment (NSI), Global Impairment (GI), Dementia, and Death. The purpose of the BRAiNS project is to study normal aging of the brain in contrast to Alzheimer’s disease. Subjects are recruited in phases and receive annual assessments with brain donation at death. In the current BRAiNS model, the outcome contains four states: normal cognition (Normal), mild cognitive impairment (MCI), dementia, and death. The transition flows and frequencies among states of both the NUN’s data and the BRAiNS data are shown in Figure 1.

Figure 1.

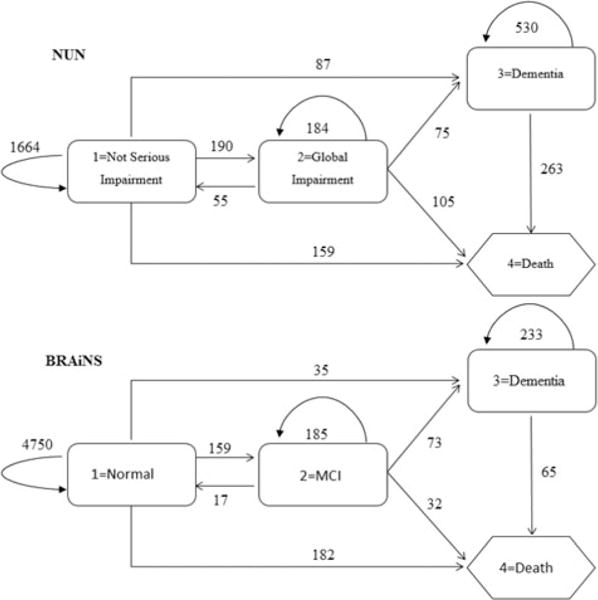
Transition flows and frequencies of the NUN’s data and the BRAiNS data.

The NUN’s data sample used in the study consists of 617 subjects having 3312 observations. At baseline, 440 (71.3%) subjects were in state NSI; 60 (9.7%) subjects were already in state GI and 117 (19.0%) subjects have already developed dementia. At the end of the study, there were 74 subjects who survived without dementia or censored before converting to dementia, 279 subjects who developed dementia, 264 who died without dementia, and 263 subjects who died with dementia. Even though the NUN study was designed to conduct cognitive assessments annually, the actual number of total assessments and the time interval between two consecutive assessments varied across subjects. The number of assessments ranges from 2 to 12 with an average of 6 assessments over 7.0 ± 4.3 years of follow up. The time interval between two assessments ranges from 0.01 year to 10 years, with an average of 1.4 ± 0.6 years.

The BRAiNS data sample used in this study consists of 525 subjects with total 5731 observations. At baseline, all 525 subjects were at state 1 (Normal). The number of assessments ranges from 2 to 24 with an average of 12 assessments over 10.6 ± 4.7 years of follow-up. The time interval between two assessments ranges from 0.01 year to 8 years, with an average of 1.07 ± 0.4 years. Figure 2 presents the histogram of the time intervals between two consecutive assessments up to 3 years for both the NUN and the BRAiNS datasets. It shows that the BRAiNS has more evenly assessments than the NUN study.

Figure 2.

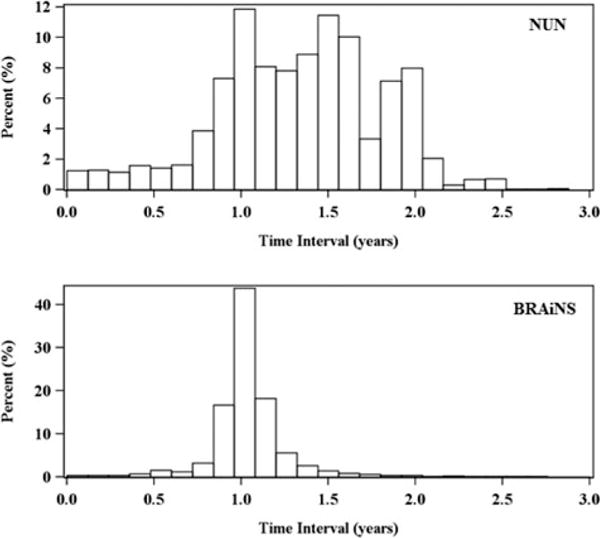
Histogram of time intervals between two consecutive assessments.

In the NUN’s data, the baseline ages range from 75.37 to 102.01 with mean 83.45 ± 5.53, and there are 141 (22.85%) subjects with at least one APOE4 allele. In the BRAiNS data, the baseline ages range from 60 to 98 with mean 73.3 ± 7.4. We assume the transition hazards remain constant over time by considering baseline age as a risk factor in the examples for two reasons. First, dementia is chronic and develops over a long period of time but the follow-up times are relatively short compared to their baseline age in the applications. Second, even though a non-homogeneous model may be more suitable, with interval censoring data and backward transitions, both the calculation of likelihood and the estimation process will be much more complicated and difficult without strong assumptions in such a model with more than three states (Mathieu et al. (2007). Thus, we will model both datasets using time- homogeneous MSMs.

Besides baseline age, we will also consider another risk factor in the four-state model: APOE4 (1 = at least one ε4 allele, 0 = no ε4 allele). There are 157 (29.9%) subjects with at least one APOE4 allele.

In the model, baseline ages were centered at age 75 for NUN and at age 60 for BRAiNS. The difference in centering for the cohorts is due to the difference in mean age at baseline: 73.2 ± 7.4 for BRAiNS versus 84.3 ± 5 years for Nun’s). Tables 3 and 4 list the parameter estimates of the discrete-time MSM and continuous- MSM on the NUN’s data and the BRAiNS’ data, respectively. Both discrete-time and continuous-time MSMs show similar effects of baseline age and APOE4 on the NUN’s and BRAiNS’ data. Baseline age has significant effects on increasing the hazard of all transition paths except for GI (or MCI) back to NSI (or Normal) and GI (or MCI) directly to Death. APOE4 has significant effects on increasing the hazard of transition from NSI (or Normal) to GI (or MCI). In the BRAiNS’ data, the discrete-time MSM also show APOE4 has significant effect of increasing the hazard of transition from Normal to Dementia.

Table 3.

MSM results on the NUN’s data.

		Discrete model			Continuous model
Covariates	Path	Coefficient	Std. err	P value	Coefficient	Std. err	P value
Intercept	1 to 2	−2.9425	0.1512	< .01	−2.8417	0.1515	< .01
	1 to 3	−3.9931	0.2213	< .01	−4.6231	0.3545	< .01
	1 to 4	−3.0251	0.1613	< .01	−3.8646	0.2856	< .01
	2 to 1	−1.1615	0.3001	< .01	−1.7183	0.2711	< .01
	2 to 3	−1.4880	0.2901	< .01	−1.8899	0.2428	< .01
	2 to 4	−0.6328	0.2429	< .01	−1.2368	0.2364	< .01
	3 to 4	−1.3189	0.1677	< .01	−1.6425	0.1382	< .01
Baseline age	1 to 2	0.1044	0.0171	< .01	0.0882	0.0168	< .01
	1 to 3	0.1405	0.0225	< .01	0.1277	0.0360	< .01
	1 to 4	0.0963	0.0186	< .01	0.0646	0.0321	0.04
	2 to 1	0.0101	0.0294	0.73	0.0100	0.0268	0.71
	2 to 3	0.0525	0.0254	0.04	0.0375	0.0183	0.04
	2 to 4	0.0161	0.0235	0.49	−0.0215	0.0246	0.38
	3 to 4	0.0632	0.0137	< .01	0.0364	0.0106	< .01
APOE4	1 to 2	0.5799	0.1940	< .01	0.4447	0.1968	0.02
	1 to 3	0.5064	0.2831	0.07	0.0403	0.7244	0.96
	1 to 4	0.3976	0.2191	0.07	0.3561	0.3711	0.34
	2 to 1	−0.6509	0.4233	0.12	−0.6053	0.3994	0.13
	2 to 3	0.5268	0.3066	0.09	0.4952	0.2611	0.06
	2 to 4	−0.2533	0.3018	0.40	−0.5631	0.3679	0.13
	3 to 4	0.0417	0.1661	0.80	0.0112	0.1331	0.93

P values in bold are statistically significant at p ≤ .05.

Table 4.

MSM results on the BRAiNS’data.

		Discrete model			Continuous model
Covariates	Path	Coefficient	Std. err	P value	Coefficient	Std. err	P value
Intercept	1 to 2	−4.1015	0.1904	< .01	−3.9794	0.1860	< .01
	1 to 3	−6.5050	0.4512	< .01	−8.2161	1.5140	< .01
	1 to 4	−4.5632	0.1948	< .01	−4.7157	0.2137	< .01
	2 to 1	−1.0981	0.5537	0.05	−1.6062	0.5032	< .01
	2 to 3	−0.7283	0.3605	0.04	−1.4084	0.2777	< .01
	2 to 4	−1.9591	0.5334	< .01	−2.4982	0.9356	< .01
	3 to 4	−2.3889	0.4331	< .01	−2.2894	0.3451	< .01
Baseline age	1 to 2	0.0445	0.0114	< .01	0.0463	0.0109	< .01
	1 to 3	0.0944	0.0233	< .01	0.1107	0.0538	0.04
	1 to 4	0.0946	0.0105	< .01	0.0921	0.0111	< .01
	2 to 1	−0.0814	0.0397	0.04	−0.0742	0.0371	0.05
	2 to 3	−0.0169	0.0217	0.44	0.0129	0.0166	0.44
	2 to 4	0.0232	0.0306	0.45	−0.0129	0.0633	0.84
	3 to 4	0.0677	0.0239	< .01	0.0464	0.0185	0.01
APOE4	1 to 2	0.4162	0.1692	0.01	0.3869	0.1699	0.02
	1 to 3	0.7573	0.3445	0.03	1.2111	1.4112	0.39
	1 to 4	−0.1593	0.1806	0.38	−0.2357	0.2067	0.25
	2 to 1	−0.6589	0.5953	0.27	−0.5767	0.5782	0.32
	2 to 3	0.1203	0.2823	0.67	0.1701	0.2329	0.46
	2 to 4	−0.4717	0.4217	0.26	−1.3741	2.0358	0.50
	3 to 4	0.1371	0.2916	0.64	0.1163	0.2400	0.63

P values in bold are statistically significant at p ≤.05.

Figure 3 plots the estimated transition probabilities from state 1 to state 3 and from state 2 to state 3 from both the NUN and BRAiNS data. The transition probabilities were estimated at 5 years baseline age (baseline age were center at age 75 for NUN and at 60 for BRAiNS), and with or without APOE4. The results show that the difference between discrete-time MSM and continuous-time MSM estimates is much smaller in BRAiNS’ data than in NUN’s data.

Figure 3.

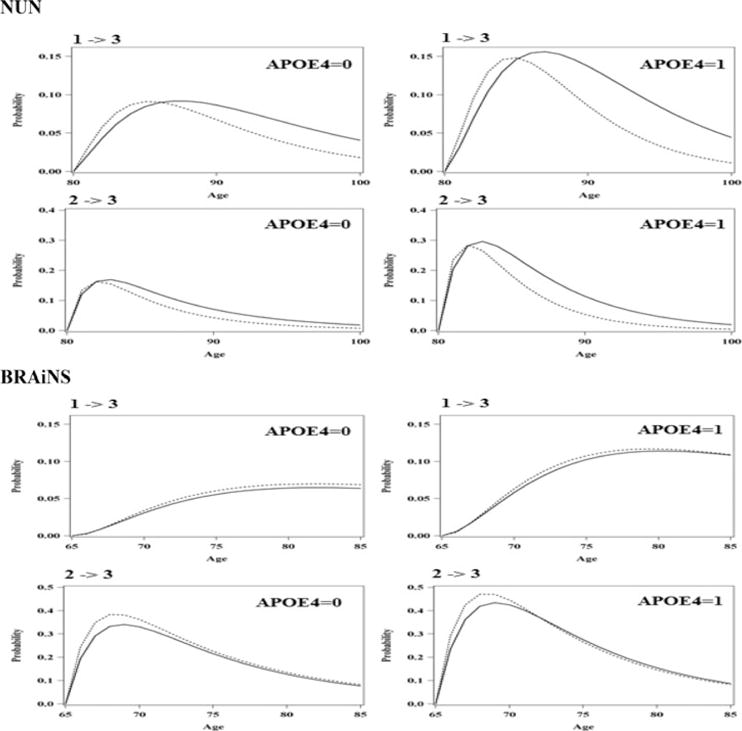
Estimated transition probabilities from state 1 to state 3 and from state 2 to state 3 from NUN and BRAiNS with and without APOE4. (Solid line: Transition probabilities estimated by the continuous-time model; and dashed line: transition probabilities estimated by the discrete-time model.)

5. Discussion

In longitudinal chronic disease studies, the natural development of a chronic disease is often expressed in terms of distinct states and MSMs are widely used to model the progression of individuals through these states. There are advantages to modeling the true disease progression as a discrete time Markov chain. For example, reverse transitions are much easier to study under the discrete model as illustrated by Abner et al. (2012). In addition, nonstationary risk factors such as a subject’s age can be incorporated into a Markov chain model (see, e.g., Yu et al. (2010)). However, while Markov chain models can accommodate the simultaneous analysis of multiple events of interest and inclusion of competing risks through the states defined in the model, use of Markov chains have some potential limitations. As it requires the time intervals between two consecutive assessments are all equal among subjects, and it does not allow unobserved transitions between two consecutive assessments. In real studies, the data are often unevenly spaced and multiple unobserved transitions may take place between cycle assessments. A more general model, continuous-time MSM could be an alternative approach which can accommodate the evenly spaced data under different types of observation schemes.

To the best of our knowledge, this research is the first to compare the performance of the widely used discrete-time multi-state model with the continuoustime multi-state model for unevenly spaced data. The simulation study compares the one-year transition probability under three types of observed data, one evenly spaced data and two unevenly spaced data. The results show that when the longitudinal observations are evenly spaced, both versions of MSMs work equally well. Since the calculation of transition probabilities through the transition intensities is usually complicated, the discrete-time MSMs have the computational advantage over the continuous-time version MSMs. When longitudinal observations are unevenly spaced, the discrete-time MSMs would be biased. In this case, the continuous-time MSMs are recommended.

In the application of the two types of models to the Nun’s data, the discrete-time model has relative worse performance compared to the continuous-time model. Both models provided similar results of the effects of baseline age and APOE4 in the model. However, the estimations of the transition probabilities are different by the two models. The discrete-time model has relative lower long-term transition probability estimations from state NSI to dementia and from state GI to dementia. The average time interval between two consecutive assessments was 1.4 ± 0.6 years (larger than 1 year assumption of the discrete-time model) in the Nun’s data, which is one of the reason the discrete-time model underestimates the long-term transition probabilities from NSI to dementia and from GI to dementia.

Different with the NUN’s data, the BRAiNS’ data contain more evenly spaced longitudinal observations. In the application of the two types of MSMs to the BRAiNS’ data, the discrete-time model and continuous-time model have very close results. Their transition probability estimates are close as shown in the transition probability plots. The prevalence estimates of the absorbing state (Death) by the two models are also very close.

In conclusion, discrete-time Markov chain models are useful tools for survival analysis that allow for more nuanced modeling that is available in most standard time to event methods. However, most journal readers and reviewers may readily comprehend the results from discrete-time Markov chain models, but they may lack familiarity with the underlying statistical assumptions. If so, they may neglect to challenge investigators to demonstrate these assumptions are tenable (Abner, Charnigo, and Kryscio 2013). A continuous time MSM could be an alternative approach and should have a potential to being used much more by practitioners, although the lack of knowledge of the available software may be responsible for its lack of popularity. Given that improper use of Markov models may result in biased estimation, perhaps some standardization in the reporting of MSM results and assumption verification is needed.