Abstract
Human microbiome studies use sequencing technologies to measure the abundance of bacterial species or Operational Taxonomic Units (OTUs) in samples of biological material. Typically the data are organized in contingency tables with OTU counts across heterogeneous biological samples. In the microbial ecology community, ordination methods are frequently used to investigate latent factors or clusters that capture and describe variations of OTU counts across biological samples. It remains important to evaluate how uncertainty in estimates of each biological sample’s microbial distribution propagates to ordination analyses, including visualization of clusters and projections of biological samples on low dimensional spaces. We propose a Bayesian analysis for dependent distributions to endow frequently used ordinations with estimates of uncertainty. A Bayesian nonparametric prior for dependent normalized random measures is constructed, which is marginally equivalent to the normalized generalized Gamma process, a well-known prior for nonparametric analyses. In our prior, the dependence and similarity between microbial distributions is represented by latent factors that concentrate in a low dimensional space. We use a shrinkage prior to tune the dimensionality of the latent factors. The resulting posterior samples of model parameters can be used to evaluate uncertainty in analyses routinely applied in microbiome studies. Specifically, by combining them with multivariate data analysis techniques we can visualize credible regions in ecological ordination plots. The characteristics of the proposed model are illustrated through a simulation study and applications in two microbiome datasets.
Keywords: Dependent Dirichlet processes, Bayesian factor analysis, Uncertainty of ordination, Microbiome data analysis
1 Introduction
Next generation sequencing (NGS) has transformed the study of microbial ecology. Through the availability of cheap efficient amplification and sequencing, marker genes such as 16S rRNA are used to provide inventories of bacteria in many different environments. For instance soil and waste water microbiota have been inventoried (DeSantis et al., 2006) as well as the human body (Dethlefsen et al., 2007). NGS also enables researchers to describe the metagenome by computing counts of DNA reads and matching them to the genes present in various environments.
Over the last ten years, numerous studies have shown the effects of environmental and clinical factors on the bacterial communities of the human microbiome. These studies enhance our understanding of how the microbiome is involved in obesity (Turnbaugh et al., 2009), Crohn’s disease (Quince et al., 2013), or diabetes (Kostic et al., 2015). Studies are currently underway to improve our understanding of the effects of antibiotics (Dethlefsen and Relman, 2011), pregnancy (DiGiulio et al., 2015), and other perturbations to the human microbiome.
Common microbial ecology pipelines either start by grouping the 16S rRNA sequences into known Operational Taxonomic Units (OTUs) or taxa as done in Caporaso et al. (2010), or denoising and grouping the reads into more refined strains sometimes referred to as oligotypes, phylotypes, or ribosomal variants (RSV) (Rosen et al., 2012; Eren et al., 2014; Callahan et al., 2016). We will call all types of groupings OTUs to maintain consistency. In all cases the data are analyzed in the form of contingency tables of read counts per sample for the different OTUs, as exemplified in Table 1. Associated to these contingency tables are clinical and environmental covariates such as time, treatment, and patients’ BMI, information collected on the same biological samples or environments. These are sometimes misnamed “metadata”; this contiguous information is usually fundamental in the analyses. The data are often assembled in multi-type structures, for instance phyloseq (McMurdie and Holmes, 2013) uses lists (S4 classes) to capture all the different aspects of the data at once.
Table 1.
An example of OTU table derived from data published in Morgan et al. (2012).
| OTU | Ctrl1 | Ctrl2 | Ctrl3 | Ctrl4 | Ctrl5 | IBD1 | IBD2 | IBD3 | IBD4 | IBD5 |
|---|---|---|---|---|---|---|---|---|---|---|
| Bacteroidesa | 1822 | 913 | 147 | 2988 | 4616 | 172 | 3516 | 657 | 550 | 1423 |
| Bifidobacterium | 0 | 162 | 0 | 0 | 84 | 0 | 85 | 1927 | 0 | 286 |
| Collinsella | 1359 | 0 | 0 | 206 | 0 | 327 | 0 | 0 | 160 | 122 |
| Enterococcus | 621 | 0 | 0 | 3 | 40 | 0 | 0 | 0 | 0 | 0 |
| Streptococcus | 75 | 139 | 2161 | 110 | 97 | 1820 | 85 | 58 | 5 | 294 |
Currently bioinformaticians and statisticians analyze the preprocessed microbiome data using linear ordination methods such as Correspondence Analysis (CA), Canonical or Constrained Correspondence Analysis (CCA), and Multidimensional Scaling (MDS) (Caporaso et al., 2010; Oksanen et al., 2015; McMurdie and Holmes, 2013). Distance-based ordination methods use measures of between-sample or Beta diversity, such as the Unifrac distance (Lozupone and Knight, 2005). These analyses can reveal clustering of biological samples or taxa, or meaningful ecological or clinical gradients in the community structure of the bacteria. Clustering, when it occurs indicates a latent variable which is discrete, whereas gradients correspond to latent continuous variables. Following these exploratory stages, confirmatory analyses can include differential abundance testing (McMurdie and Holmes, 2014), two-sample tests for Beta diversity scores (Anderson et al., 2006), ANOVA permutation tests in CCA (Oksanen et al., 2015), or tests based on generalized linear models that include adjustment for multiple confounders (Paulson et al., 2013).
The interaction between these tasks can be problematic. In particular, the uncertainty in the estimation of OTUs’ prevalence is often not propagated to subsequent steps (Peiffer et al., 2013). Moreover, unequal sequencing depths generate variations of the number of OTUs with zero counts across biological samples. Finally, the hypotheses tested in the inferential step are often formulated after significant exploration of the data and are sensitive to earlier choices in data preprocessing.
These issues motivate a Bayesian approach that enables us to integrate the steps of the analytical pipeline. Holmes et al. (2012); La Rosa et al. (2012); Ding and Schloss (2014) have suggested the use of a simple Dirichlet-Multinomial model for these data; however, in those analyses the multinomial probabilities for each biological sample are independent in the prior and posterior, which fails to capture underlying relationships between biological samples. The simple Dirichlet-Multinomial model is also not able to account for strong positive correlations (high co-occurrences (Faust et al., 2012)) or negative correlations (checker board effect (Koenig et al., 2011)) that can exist between different species (Gorvitovskaia et al., 2016).
We propose a Bayesian procedure, which jointly models the read counts from different OTUs and sample-specific latent multinomial distributions, allowing for correlations between OTUs. The prior assigned to these multinomial probabilities is highly flexible, such that the analysis learns the dependence structure from the data, rather than constraining it a priori. The method can deal with uncertainty coherently, provides model-based visualizations of the data, and is extensible to describe the effects of observed clinical and environmental covariates.
Bayesian analysis with Dirichlet priors is a convenient starting point for microbiome data, since the OTU distributions are inherently discrete. Moreover, Bayesian nonparametric priors for discrete distributions, suitable for an unbounded number of OTUs, have been the topic of intense research in recent years. General classes of priors such as normalized random measures have been developed, and their properties in relation to classical estimators of species diversity are well-understood (Ferguson, 1973; Lijoi and Prünster, 2010). The problem of modeling dependent distributions has also been extensively studied since the proposal of the Dependent Dirichlet Process (MacEachern, 2000) by Müller et al. (2004), Rodríguez et al. (2009), and Griffin et al. (2013)).
In this paper, we try to capture the variation in the composition of microbial communities as a result of a group of unobserved samples’ characteristics. With this goal we introduce a model which expresses the dependence between OTUs abundances in different environments through vectors embedded in a low dimensional space. Our model has aspects in common with nonparametric priors for dependent distributions, including a generalized Dirichlet type marginal prior on each distribution, but is also similar in spirit to the multivariate methods currently employed in the microbial ecology community. Namely, it allows us to visualize the relationship between biological samples through low dimensional projections.
The paper is organized as follows. Section 2 describes a prior for dependent microbial distributions, first constructing the marginal prior of a single discrete distribution through manipulation of a Gaussian process and then extending this to multiple correlated distributions. The extension is achieved through a set of continuous latent factors, one for each biological sample, whose prior has been frequently used in Bayesian factor analyses. Section 3 derives an MCMC sampling algorithm for posterior inference and a fast algorithm to estimate biological samples’ similarity. Section 4 discusses a method for visualizing the uncertainty in ordinations through conjoint analysis. Section 5 contains analyses of simulated data, which serve to demonstrate desirable properties of the method, followed by applications to real microbiome data in Section 6. Section 7 discusses potential improvement and concludes. The code for implementing the analyses discussed in this article is included in the Supplementary Materials.
2 Probability Model
In Table 1, we illustrate an example of a typical OTU table with 10 biological samples, where half are healthy subjects, and half are Inflammatory Bowel disease (IBD) patients. This contingency table is a subset of the data in Morgan et al. (2012) and records the observed frequencies of five most abundant genus level OTUs in all biological samples based on 16S rRNA sequencing results. Let Zi be the ith observed OTU (e.g. Z1 is Bacteroides) and ni,j be the observed frequency of OTU Zi in biological sample j. As an example, n11 = 1822 is the observed frequency of Bacteroides in the biological sample Ctrl1. We will denote an OTU table as (ni,j)i≤I,j≤J, where I is the number of observed OTUs and J the number of biological samples.
For the biological sample j, we will assume the vector (n1,j, …, nI,j) follows a multinomial distribution, noting that our analysis extends easily to the case in which the total count is a Poisson random variable. The unobserved multinomial probabilities of OTUs present in biological sample j determine the distribution of the frequencies ni,j. These probabilities form a discrete probability measure, which we call a microbial distribution, on the space of all OTUs.
We denote this discrete measure as Pj and Pj({Zi}) gives the probability of sampling Zi from biological sample j. If we consider all J biological samples, we expect there will be variation in the respective Pj’s. This variation usually can be explained by specific characteristics of the biological sample. For instance, in Table 1, we can see the empirical multinomial probability of Enterococcus is higher in healthy controls than in IBD patients on average. This variation has been discovered in prior publication (Morgan et al., 2012) and is attributed to the IBD status. Microbiome studies aim to elucidate the characteristics that explain these types of variations.
Our method focuses on modeling the distributions Pj’s and the variations among them. For biological samples labelled in , we assume they have the same infinite set of OTUs . We let the number of OTUs present in a biological sample be infinity to make our model nonparametric in consideration of the fact that there might be an unknown number of OTUs that are not observed in the experiment. We specify the probability mass assigned to a group of OTUs as
| (1) |
where σi ∈ (0, 1), Xi, Yj ∈ ℝm, is the indicator function, and . In addition, 〈·,·〉 is the standard inner product in ℝm.
In this model specification, σi is related to the average abundance of OTU i across all biological samples. When σi is large, the average probability mass assigned to OTU Zi will also be large. We refer to Xi and Yj as OTU vector and biological sample vectors respectively. The variation of the Pj’s is determined by the vectors Yj, which can be treated as latent characteristics of the biological samples that associate with microbial composition; for example, an unobserved feature of the subject’s diet, such as vegetarianism, could affect the abundance of certain OTUs. We assume there are m such characteristics, and the lth component in Yj is the measurement of the lth latent characteristic in biological sample j. The vector Xi denotes the effects of each of the m latent characteristics on the abundance of the OTU Zi. Therefore Xi has m entries.
In subsection 2.1 we consider a single microbial distribution Pj with fixed parameter Yj and define a prior on σ = (σ1, σ 2, …) and (Xi)i≥1 which makes Pj a Dirichlet process (Ferguson, 1973). The degree of similarity between the discrete distributions {Pj; } is summarized by the Gram matrix ( ; j, ). Subsection 2.2 discusses the interpretation of this matrix. Subsection 2.3 proposes a prior for the parameters {Yj, } which has been previously used in Bayesian factor analysis, and which has the effect of shrinking the dimensionality of the Gram matrix (ϕ(j, j′)) and is used to infer the number of latent characteristics m. The parameters {Yj, } or (ϕ(j, j′)) can be used to visualize and understand variations of microbial distributions across biological samples.
2.1 Construction of a Dirichlet Process
The prior on σ = (σ1, σ1, …) is the distribution of ordered points (σi > σi+1) in a Poisson process on (0, 1) with intensity
| (2) |
where α > 0 is a concentration parameter. Denote the index of component of Yj and Xi as l. Fix j, and let Yj = (Yl,j, l ≤ m) be a fixed vector in ℝm such that 〈Yj, Yj〉 = 1. We let Xi = (Xl,i, l ≤ m) be a random vector for i = 1, 2, … and Xl,i be independent and N(0, 1) a priori for l = 1, 2, …, m and i = 1, 2, … Finally, let G be a nonatomic probability measure on the measurable space ( , ℱ), where ℱ is the sigma-algebra on , and Z1, Z2, … is a sequence of independent random variables with distribution G. We claim that the probability distribution Pj defined in Equation (1) is a Dirichlet Process with base measure G.
We note that the point process σ defines an infinite sequence of positive numbers, the products 〈Xi, Yj〉, i = 1, 2, …, are independent Gaussian N(0, 1) variables, and that the intensity ν satisfies the inequality . These facts directly imply that with probability 1, 0 < Mj(A) < ∞ when G(A) > 0. It also follows that for any sequence of disjoint sets A1, A2, … ∈ ℱ the corresponding random variables Mj(Ai)’s are independent. In different words, Mj is a completely random measure (Kingman, 1967). The marginal Lévy intensity can be factorized as μM(ds) × G(dz), where
The above expression shows that Mj is a Gamma process. We recall that the Lévy intensity of a Gamma process is proportional to the map s ↦ exp(−c × s) × s−1, where c is a positive scale parameter. In Ferguson (1973) it is shown that a Dirichlet process can be defined by normalizing a Gamma process. It directly follows that Pj is a Dirichlet Process with base measure G.
Remark
Our construction can be extended to a wider class of normalized random measures (James, 2002; Regazzini et al., 2003) by changing the intensity ν that defines the Poisson process σ. If we set
β ∈ [0, 1), in our definition of Mj, then the Lévy intensity of the random measure in (1) becomes proportional to
In this case the Lévy intensity indicates that Mj is a generalized Gamma process (Brix, 1999). We recall that by normalizing this class one obtains normalized generalized Gamma processes (Lijoi et al., 2007), which include the Dirichlet process and the normalized Inverse Gaussian process (Lijoi et al., 2005) as special cases.
A few comments capture the relation between our definition of Pj(A) in (1) and alternative definitions of the Dirichlet Process. If we normalize h independent Gamma(α/h, 1/2) variables, we obtain a vector with Dirichlet(α/h,…, α/h) distribution. To interpret our construction we can note that, when α/h < 1/2, each of the Gamma(α/h, 1/2) components can be obtained by multiplying a Beta(α/h, 1/2 − α/h) variable and an independent Gamma(1/2, 1/2). The distribution of the 〈Xi, Yj〉+2 variables in (1) is in fact a mixture with a Gamma(1/2, 1/2) component and a point mass at zero. Finally if we let h increase to ∞, the law of the ordered Beta(α/h, 1/2 − α/h) converges weakly to the law of ordered points of a Poisson point process on (0, 1) with intensity ν (see Supplementary Document S1).
2.2 Dependent Dirichlet Processes
We use the representation for Dirichlet processes from Equation (1) to define a family of dependent Dirichlet processes labelled by a general index set . The dependency structure of this family is related to Send a message . Geometrically ϕ(j, j′) is the cosine of the angle between Yj and . The dependent Dirichlet processes is defined by setting
| (3) |
for every A ∈ ℱ. Here the sequence (Z1, Z2,…) and the array (X1, X2,…), as in Section 2.1, contain independent and identically distributed random variables, while σ is our Poisson process on the unit interval defined in (2). We will use the notation Qi,j = 〈Xi, Yj〉. This construction has an interpretable dependency structure between the Pj’s that we state in the next proposition.
Proposition 1
There exists a real function η : [0, 1] ⟶ [0, 1] such that the correlation between Pj(A) and (A) is equal to η (ϕ(j, j′)) for every A that satisfies G(A) > 0. In different words, the correlation between Pj(A) and (A) does not depend on the specific measurable set A, it is a function of the angle defined by Yj and .
The proof is in the Supplementary Document S2. The first panel of Figure 1 shows a simulation of Pj’s. In this figure . When ϕ(j, j′), the cosine of the angle between two vectors Yj and , corresponding to distinct biological samples j and j′, decreases to −1 the random measures tend to concentrate on two disjoint sets. The second panel shows the function η that maps the ϕ(j, j′)’s into the correlations . As expected the correlation increases with ϕ(j, j′).
Figure 1.
(Left) Realization of 4 microbial distributions from our dependent Dirichlet processes. We illustrate 10 representative OTUs and set α = 100. The miniature figure at the top-left corner shows the relative positions of the four biological sample vectors Yj. The OTUs are those associated to the 10 largest σ’s. As suggested by this panel, the larger the angle between two Yj’s, the more the corresponding random distributions tend to concentrate on distinct sets. (Right) Correlation of two random probability measures when the cosine ϕ(j, j′) between Yj and varies from −1 to 1. We consider five different values of the concentration parameter α. In the right panel we also mark with crosses the correlations between Pj(A) and (A) for pairs of biological samples j, j′ considered in the left panel.
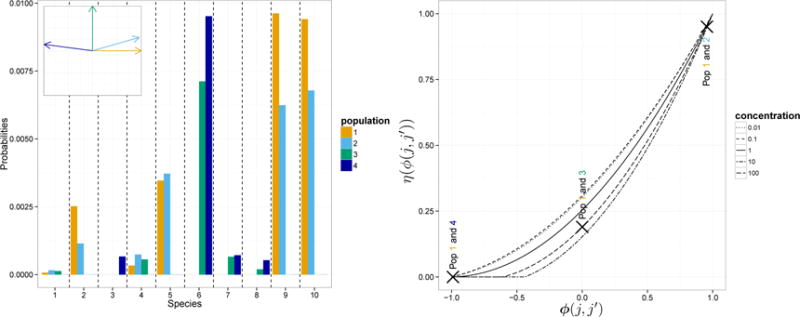
We want to point out that the construction in (3) extends easily to the setting where we are given any positive semi-definite kernel capturing the similarity between biological samples labelled by . Mercer’s theorem (Mercer, 1909) guarantees the kernel is represented by the inner product in an ℒ2 space, whose elements are infinite-dimensional analogues of the vectors Yj. The analysis presented in this section is unchanged in this general setting.
The next proposition provides mild conditions that guarantee a large support for the dependent Dirichlet processes that we defined.
Proposition 2
Consider a collection of probability measures (Fj, j = 1,…, J) on and a positive definite kernel ϕ. Assume that and the support of G coincides with . The prior distribution in (3) assigns strictly positive probability to the neighborhood , where ε > 0 and fi, i = 1,…, L, are bounded continuous functions.
In what follows we will replace the constraint 〈Yj, Yj〉 = 1 with the requirement 〈Yj, Yj〉 < ∞. The two constraints are equivalent for our purpose, because we normalize and 〈Yj, Yj〉 can be viewed as a scale parameter.
2.3 Prior on biological sample parameters
This subsection deals with the task of estimating the parameters Yj, , that capture most of the variability observed when comparing J biological samples with different OTU counts. We define a joint prior on these factors which makes them concentrate on a low dimensional space; equivalently, the prior tends to shrinks the nuclear norm of the Gram matrix . The problem of estimating low dimensional factor loadings or a low-rank covariance matrix is common in Bayesian factor analysis, and the prior defined below has been used in this area of research.
The parameters Yj can be interpreted as key characteristics of the biological samples that affect the relative abundance of OTUs. As in factor analysis, it is difficult to interpret these parameters unambiguously (Press and Shigemasu, 1989; Rowe, 2002); however, the angles between their directions have a clear interpretation. As observed in Figure 1, if the kernel , the two microbial distributions and will be very similar. If ϕ(j1, j2) ≈ 0, then there will be little correlation between OTUs’ abundances in the two samples. If , then the two microbial distributions are concentrated on disjoint sets. This interpretation suggests Principal component analysis (PCA) of the Gram matrix as a useful exploratory data analysis technique.
It is common in factor analysis to restrict the dimensionality of factor loadings. In our model, this is accomplished by assuming Yj to be in ℝm and adding an error term ε in the definition of Qi,j, the OTU-specific latent weights,
| (4) |
where the εi,j are independent standard normal variables. Recall that each sample-specific random distribution Pj is obtained by normalizing the random variables . If we denote the covariance matrix of (Qi,1, …, Qi,J) as Σ, this factor model specification indicates Σ = Y⊤Y + I conditioning on Y, where I is the identity matrix and Y = (Y1, …, YJ). As a result, the correlation matrix S induced by Σ only depends on Y.
In most applications the dimensionality m is unknown. Several approaches to estimate m have been proposed (Lopes and West, 2004; Lee and Song, 2002; Lucas et al., 2006; Carvalho et al., 2008; Ando, 2009). However, most of them involve either calculation of Bayes Factors or complex MCMC algorithms. Instead we use a normal shrinkage prior proposed by Bhattacharya and Dunson (2011). This prior includes an infinite sequence of factors (m = ∞), but the variability captured by this sequence of latent factors rapidly decreases to zero. A key advantage of the model is that it does not require the user to choose the number of factors. The prior is designed to replace direct selection of m with the shrinkage toward zero of the unnecessary latent factors. In addition, this prior is nearly conjugate, which simplifies computations. The prior is defined as follows,
| (5) |
where the random variables γ = (γl, ; l, j ≥ 1) are independent and, conditionally on these variables, the Yl,j’s are independent.
When al > 1, the shrinkage strength a priori increases with the index l, and therefore the variability captured by each latent factor tends to decrease with l. We refer to Bhattacharya and Dunson (2011) for a detailed analysis of the prior in (5). In practice, the assumption of infinitely many factors is replaced for data analysis and posterior computations by a finite and sufficiently large number m of factors. The choice of m is based on computational considerations. It is desirable that posterior variability of the last components (l ~ m) of the factor model in (4) is negligible. This prior model is conditionally conjugate when paired with the dependent Dirichlet processes prior in subsection 2.2, a relevant and convenient characteristic for posterior simulations. We summarize the full model with a plate diagram, shown in Figure 2.
Figure 2.
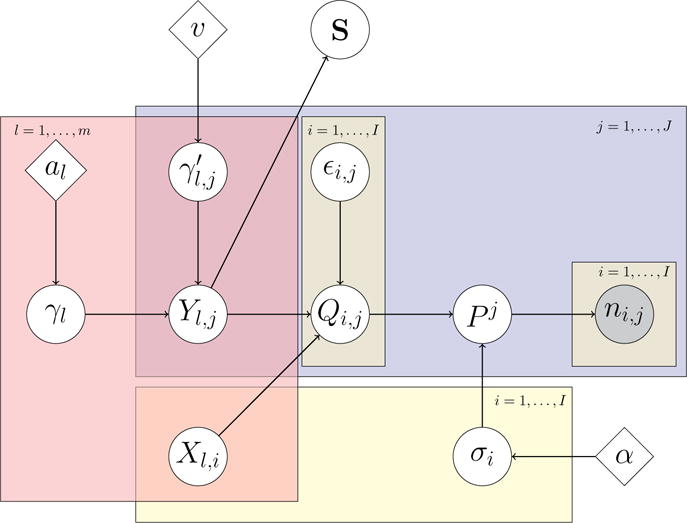
Plate diagram. We include the factor model for the latent variables Qi,j as well as the matrix S. Nodes encompassed by a rectangle are defined over the range of indices indicated at the corner of the rectangle, and the connections shown within the rectangle are between nodes with the same index. We use j to index biological samples, i to index microbial species and l to index the components of latent factors.
3 Posterior Analysis
Given an exchangeable sequence W1,…, Wn from as defined in subsection 2.1, we can rewrite the likelihood function using variable augmentation as in James et al. (2009),
| (6) |
Here is the list of distinct values in (W1,…Wn) and n1,…, nI are the occurrences in (W1,…Wn), so that . We use expression (6) to specify an algorithm that allows us to infer microbial abundances P1,…, PJ in J biological samples.
We proceed, similarly to Muliere and Tardella (1998) and Ishwaran and James (2001), using truncated versions of the processes in subsection 2.2. We replace σ= {σi, i ≥ 1} with a finite number I of independent Beta(εI, 1/2 −εI) points in (0, 1). Supplementary Document S1 shows that when I diverges, and εI = α/I, this finite dimensional version converges weakly to the process in (2). Each point σi is paired with a multivariate normal Qi = (Qi,1,…, Qi,J) with mean zero and covariance Σ. The distribution of is a mixture of a point mass at zero and a Gamma distribution. In this section Q and σ are finite dimensional, and the normalized vectors Pj, which assign random probabilities to I OTUs in J biological samples, are proportional to (M1,j,…, MI,j), j = 1,…, J. Note that Pj conditional on follows a Dirichlet distribution with parameters proportional to
The algorithm is based on iterative sampling from the full conditional distributions. We first provide a description assuming that Σ is known. We then extend the description to allow sampling under the shrinkage prior in Section 2.3 and to infer Σ.
With I OTUs and J biological samples, the typical dataset is n = (n1,…, nJ), where nj = (n1,j,…, nI,j) and ni,j is the absolute frequency of the ith OTU in the jth biological sample. We use the notation , , σ = (σ1,…, σI), Y = (Yj, j = 1,…, J) and Q = (Qi,j, 1 ≤ i ≤ I, 1 ≤ j ≤ J). By using the representation in (6) we introduce the latent random variables T = (T1,…, TJ) and rewrite the posterior distribution of (σ, Q):
| (7) |
| (8) |
where π is the prior. In order to obtain approximate (σ, Q) sampling we specify a Gibbs sampler for (σ, Q, T) with target distribution
| (9) |
The sampler iterates the following steps:
[Step 1] Sample Tj independently, one for each biological sample j = 1, …, J,
[Step 2] Sample Qi independently, one for each OTU i = 1, …, I. The conditional density of Qi = (Qi,1 … Qi,J) given σ, T, n is log-concave, and the random vectors Qi, i = 1, …, I, given σ, T, n are conditionally independent.
We simulate, for j = 1, …, J, from
| (10) |
where Qi, −j = (Qi,1, …, Qi,j−1, Qi,j+1, …, Qi,J), μi,j = E[Qi,j|Qi, −j], , with the proviso 0° = 1. Since Qi is a multivariate normal, both μi,j and sj have simple closed form expressions.
When ni,j = 0 the density in (10) reduces to a mixture of truncated normals:
and . Here N(·; μ, s2) and Φ(·; μ, s2) are the density and cumulative density functions of a normal variable with mean μ and variance s2.
When ni,j > 0 the density p[Qi,j|Qi,−j, σ, T, n] remains log-concave, and the support becomes (0, +∞). We update Qi,j using a Metropolis-Hastings step with proposal identical to the Laplace approximation of the density in (10),
| (11) |
Here maximizes the density (10), and is obtained from the second derivative of the log-density at . We found the approximation accurate. In Supplementary Document S4 we provide bounds of the total variation distance between the target (10) and the approximation (11). When ni,j increases, the bound of the total variation decreases to zero. See also Figure S1 in the Supplementary Document.
[Step 3] Sample σi independently, one for each OTU i = 1, …, I, from the density . The σi’s are a priori independent Beta(α/I, 1/2 −α/I) variables. We use piecewise constant bounds for , σ ∈ [0, 1] and an accept/reject step to sample from p(σi|Q, T, n).
We now consider inference on Σ using the prior on Y in subsection 2.3. The goal is to generate approximate samples of Y from the posterior. We exploit the identity of the conditional distributions of Y given (σ, T, Q, n) and Q. In order to sample Y from the posterior we can therefore directly apply the MCMC transitions in Bhattacharya and Dunson (2011), with Q replacing the observable variables in their work.
3.1 Self-consistent estimates of biological samples’ similarity
We discuss an EM-type algorithm to estimate the correlation matrix S of the vectors (Qi,1,…, Qi,J), i = 1,…, I. Under our construction in subsection 2.3, we interpret S as the normalized version of Gram matrix between biological samples. In this subsection we describe an alternative estimating procedure, distinct from the Gibbs sampler, which does not require tuning of the prior probability model. The algorithm can be used for MCMC initialization and for exploratory data analyses. It assumes that the observed OTU abundances are representative of the microbial distributions, i.e. Pj = (n1,j/nj,…, nI,j/nj). Under this assumption, for each biological sample j,
| (12) |
For σi, i = 1,…, I, we use a moment estimate . The procedure uses these estimates and at iteration t + 1 generates the following results:
[Expectation] Impute repeatedly Q, ℓ = 1,…, D times, consistently with the constraints (12) and using a N(0, Σt) joint distribution. Here Σt is the estimate of Σ, the covariance matrix of (Qi,1,…, Qi,J), after the t-th iteration. For each replicate ℓ = 1,…, D, we fix for all (i, j) pairs with strictly positive ni,j counts at and sample jointly, conditional on these values, negative values for the remaining (i, j) pa b irs with ni,j = 0. We use these values to approximate ℒ (Σ), the full data log-likelihood, our target function as in any other EM algorithm. [Maximization] Set Σt+1 equal to the empirical covariance matrix of the ( ,…, ) vectors, thus maximizing the ℒ (Σ) approximation.
We iterate until convergence of Σt. Then, after the last iteration, the inferred covariance matrix of (Qi,1,…, Qi,J) directly identifies an estimate of S. We evaluated the algorithm using in-silico datasets from the simulation study in Section 5. Overall it generates estimates that are slightly less accurate compared to posterior estimation based on MCMC simulations. We use the datasets considered in Figure 3(a), with number of factors fixed at three and nj at 100,000, for a representative example. In this case the average RV-coeffcient between the true S and the estimated matrix is 0.93 for the EM-type algorithm and 0.95 for posterior simulations. In our work the described procedure reduced the computing time to approximately 10% compared to the Gibbs sampler. More details on this procedure are provided in the Supplementary Document S5.
Figure 3.
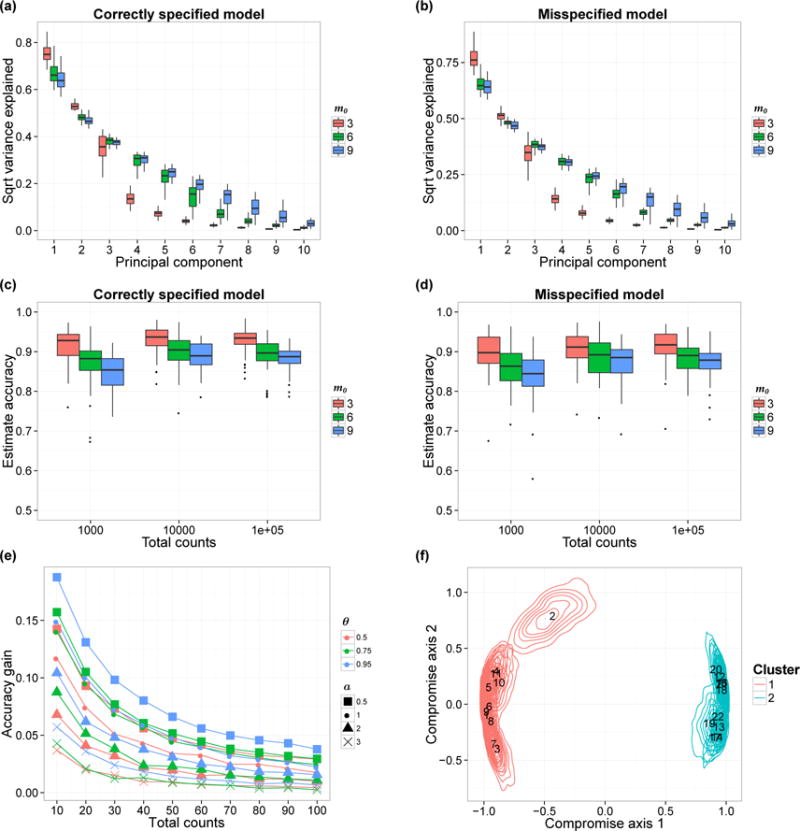
(a–b) Estimated proportion of variability captured by the first 10 PCs. Each box-plot here shows the variability of the estimated proportion across 50 simulation replicates. We show the results when the data are generated from the prior (Panel a) and from the model in (13) with a = 1 (Panel b). (c–d) Accuracy of the correlation matrix estimates The box-plots show the variability of the accuracy in 50 simulation replicates, with data generated from the prior (Panel c) and from model (13) with a = 1 (Panel d). We vary the true number of factors m0 (colors) and nj and show the corresponding accuracy variations. (e) Comparison between Bayesian estimates of the underlying microbial distributions Pj and the empirical estimates. We consider the average total variation difference, averaging across all J biological samples. Each curve shows the relationship between nj and average accuracy gain. We set m0 = 3 and the parameter a varies from 0.5 to 3 (shapes). The similarity parameter θ is equal to 0.5, 0.75 or 0.95 (colors). (f) PCoA plot with confidence regions. We visualize the confidence regions using the method in Section 4. Each contour illustrates the uncertainty of a single biological sample’s position. Colors indicate cluster membership and annotated numbers are biological samples’ IDs.
4 Visualizing uncertainty in ordination plots
Ordination methods such as Multidimensional Scaling of ecological distances or Canonical Correspondence Analysis are central in microbiome research. Given posterior samples of the model parameters, we use a procedure to plot credible regions in visualizations such as Fig 3(f). The methods that we consider here are all related to PCA and use the normalized Gram matrix S between biological samples. We recall that in our model S is the correlation matrix of (Qi,1,…, Qi,J). Based on a single posterior instance of S, we can visualize biological samples in a lower dimensional space through PCA, with each biological sample projected once. Naively, one could think that simply overlaying projections of the principal component loadings generated from different posterior samples of S on the same graph would show the variability of the projections. However, these super-impositions could be spurious if we carry out PCA for each S sample separately. One possible problem is principal component (PC) switching, when two PCs have similar eigenvalues. Another problem is the ambiguity of signs in PCA, which would lead to random signs of the loadings that result in symmetric groups of projections of the same biological sample at different sides of the axes. More generally PCA projections from different posterior samples of S are difficult to compare, as the different lower dimensional spaces are not aligned.
We alternatively identify a consensus lower dimensional space for all posterior samples of S (Escoufier, 1973; Lavit et al., 1994; Abdi et al., 2005). We list the three main steps used to visualize the variability of S.
Identify a normalized Gram matrix S0 that best summarizes K posterior samples of normalized Gram matrix S1,…, SK. One simple criterion is to minimize L2 loss element-wise. This leads to . Alternatively, we can define S0 as the normalized Gram matrix that maximizes similarity with S1,…, SK. One possible similarity metric between two symmetric square matrices A and B is the RV-coefficient (Robert and Escoufier, 1976), . We refer to Holmes (2008) for a discussion on RV-coefficients.
Identify the lower dimensional consensus space V based on S0. Assume we want dim(V) = 2; the basis of V will be the orthonormal eigenvectors v1 and v2 of S0 corresponding to the largest eigenvalues λ1 and λ2. The configuration of all biological samples in V is visualized by projecting rows of S0 onto . As in a standard PCA, this configuration best approximates the normalized Gram matrix in the L2 sense: .
Project the rows of posterior sample Sk onto V by . Over laying all the ψk displays uncertainty of S in the same linear subspace. Posterior variability of the biological samples’ projections is visualized in V by plotting each row of the matrices , k = 1,…, K, in the same figure. A contour plot is produced for each biological sample (see for example Fig 3(f)) to facilitate visualization of the posterior variability of its position in the consensus space V.
5 Simulation Study
In this section, we evaluate the procedure described in Section 3 and explore whether the shrinkage prior allows us to infer the number of factors and the normalized Gram matrix between biological samples S. We also consider the estimates E(Pj|n) obtained with our joint model, one for each biological sample j, and compare their precision with the empirical estimator. Throughout the section, we assumed the number of factors is m = 10 when running the posterior simulations.
We first defined a scenario with distributions Pj generated from the prior (1), with I = 68 OTUs and J = 22 biological samples. The true number of factors is m0, and for biological samples j = 1, …, m0/2, the vector Yj = (Yl,j, 1 ≤ l ≤ m0) has elements l = m0/2+1, …, m0 equal to zero, while symmetrically, for j = J/2+1, …, J, the vectors Yj have the elements l = 1, …, m0/2 equal to zero. The underlying normalized Gram matrix S is therefore block-diagonal. After generating the distributions Pj, we sampled with fixed total counts (nj) per biological sample nj= 1,000. We produced 50 replicates with m0 =3, 6, and 9. In our simulations the non-zero components Yl,j’s are independent standard normal.
We use PCA-type summaries for the posterior samples of Y generated from p(Y|n). Computations are based on the J × J normalized Gram matrix S. At each MCMC iteration we generate approximate samples Y from the posterior, compute S by normalizing the Gram matrix Y′Y, and operate standard spectral decomposition on S. This allows us to estimate the ranked eigenvalues, i.e. the principal components’ variance of our Q latent vectors (after normalization), by averaging over the MCMC iterations. Figure 3(a) shows the variability captured by the first 10 principal components, with the box-plots illustrating posterior means’ variability across our 50 replicates. The proportion of variability associated to each principal component decreases rapidly after the true number of factors m0 = 3, 6, 9. This suggests that the shrinkage model (Bhattacharya and Dunson, 2011) tends to produce posterior distributions for our Y latent variables that concentrates around a linear subspace.
Figure 3(c) illustrates the accuracy of the estimated normalized Gram matrix Ŝ with nj equal to 1,000, 10,000, and 100,000. We estimated the unknown J × J normalized Gram matrix S with the posterior mean of the normalized Gram matrix, which we approximate by averaging over MCMC iterations. We summarized the accuracy using the RV coefficient between Ŝ and S, see Robert and Escoufier (1976) for a discussion on this metric. The box-plots illustrate variability of estimates’ accuracy across 50 simulation replicates. As expected, when the total counts per sample increases from 10,000 to 100,000, we only observe limited gain in accuracy. Indeed the overall number of observed OTUs with positive counts per biological sample remains comparable, with expected values equal to 30 and 33 when the total counts per biological sample are fixed at 10,000 and 100,000 respectively. We also note that when m0 increases, the accuracy decreases.
We investigate interpretability of our model by using distributions Pj generated from a probability model that slightly differs from the prior. More precisely, the ith random weight in Pj, conditionally on Y and X, is defined proportional to a monotone function of 〈Xi, Yj〉+. We considered for example
| (13) |
When the monotone function is quadratic the probability model becomes identical to our prior. In Figure 3(b) and Figure 3(d) we used model (13) with a = 1 to generate datasets. We repeated the same simulation study summarized in the previous paragraphs.
We evaluated the effectiveness of borrowing information across biological samples for estimating the vectors Pj. The accuracy metric that we used is the total variation distance. We compared the Bayesian estimator E(Pj|n) and the empirical estimator which assigns mass ni,j/nj to the ith OTUs. The advantage of pooling information varies with the similarity between biological samples. To reflect this, we generated Pj with non-zero components of Y sampled from a zero mean multivariate normal with equal to θ. We considered the case when Pj is generated either from our prior or model (13) with a = 0.5, 1, 3. In addition, we considered θ = 0.5, 0.75, 0.95, I = 68, J = 22, and m0 = 3, while nj varies from 10 to 100.
The results are summarized in Figure 3(e) which shows the average difference in total variation, contrasting the Bayesian and empirical estimators. The results, both when the model is correctly specified, and when mis-specified, quantify the advantages in using a joint Bayesian model.
We complete this section with one illustration of the method in Section 4. We simulate a dataset with two clusters by generating Yl,j for l = 1, …, m0 from N(−3, 1) when j = 1, …, J/2 and from N(3, 1) when j = J/2 + 1, …, J. All Yl,j are different from zero. We expected a low nj to be sufficient for detecting the clusters. We sampled Pj from the prior and set J = 22, I = 68, m = 3, and nj = 100. The PC plot and the biological sample specific credible regions are shown in Figure 3(f). In the PC plot the two clusters are illustrated with different colors. In this simulation exercise the posterior credible regions leave little ambiguity both on the presence of clusters and also on samples-specific cluster membership. To compare this with the Principal Coordinates Analysis (PCoA) method used in microbiome studies, we plot the ordination results using PCoA based on the Bray-Curtis dissimilarity matrix derived from the empirical microbial distributions (See Figure S3). We can see that the PCoA point estimate is similar to the centroids identified by the proposed Bayesian ordination method.
6 Application to microbiome datasets
In this section, we apply our Bayesian analysis to two microbiome datasets. We show that our method gives results that are consistent with previous studies, and we show our novel visualization of uncertainty in ordination plots. We start with the Global Patterns data (Caporaso et al., 2011) where human-derived and environmental biological samples are included. We then considered data on the vaginal microbiome (Ravel et al., 2011).
6.1 Global Patterns dataset
The Global Patterns dataset includes 26 biological samples derived from both human and environmental specimens. There are a total of 19,216 OTUs, and the average total counts per biological sample is larger than 100,000. We collapsed all taxa OTUs to the genus level—a standard operation in microbiome studies—and yielded 996 distinct genera. We treated these genera as OTUs’ and fit our model to this collapsed dataset. We ran one MCMC chain for 50,000 iterations and recorded posterior samples every 10 iterations.
We first performed a cluster analysis of biological samples based on their microbial compositions. For each posterior sample of the model parameters, we computed Pj for j = 1, …, J and calculated the Bray-Curtis dissimilarity matrix between biological samples. We then clustered the biological samples using this dissimilarity matrix with Partitioning Among Medoids (PAM) (Tibshirani et al., 2002). By averaging over the MCMC iterations for the clustering results from each dissimilarity matrix, we obtained the posterior probability of two biological samples being clustered together. Figure 4(a) illustrates the clustering probabilities. We can see that biological samples belonging to a specific specimen type are tightly clustered together while different specimens tend to define separate clusters. This is consistent with the conclusion in Caporaso et al. (2011), where the authors suggest, that within specimen microbiome variations are limited when compared to variations across specimen types. We also observed that biological samples from the skin are clustered with those from the tongue. This is to some extent an expected result, because both specimens are derived from humans, and because the skin microbiome has often OTUs frequencies comparable to other body sites (Grice and Segre, 2011).
Figure 4.
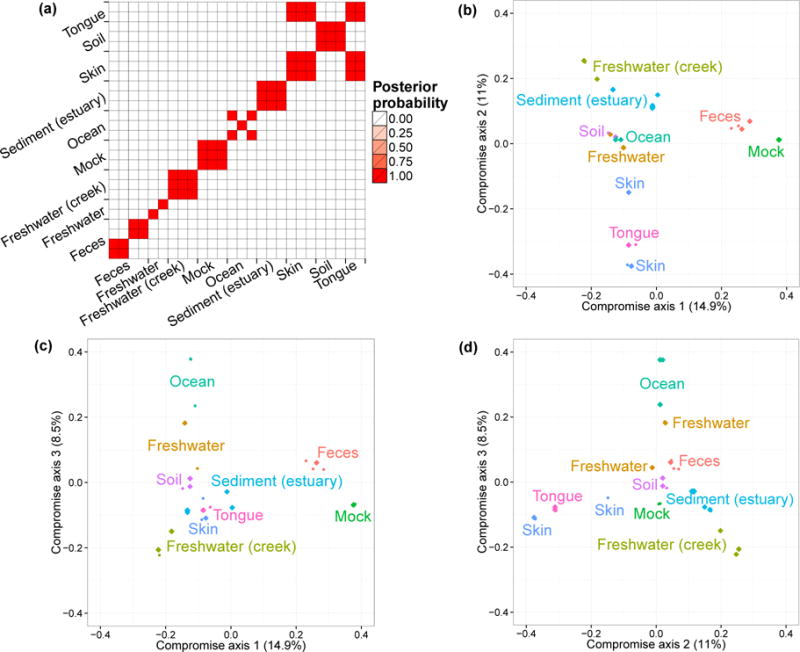
(a) Posterior Probability of each pair of biological samples (j, j′) being clustered together. The labels on axes indicate the environment of origin for each biological sample. (b–d) Ordination plots of biological samples and 95% posterior credible regions. We illustrate the first three compromise axes with three panels. Panel (b) plots projections on the first and second axes. Panel (c) plots projections on the first and third axes. Panel (d) plots projections on the second and third axes. The percentages on the three axes are the ratios of the corresponding S0 eigenvalues and the trace of the matrix. The credible regions for some biological samples are so small that appears as single points. Colors and annotated text indicate the environments.
We then visualized the biological samples using ordination plots and applying the method described in Section 4. We fixed the dimension of the consensus space V at three. We plotted all biological samples’ projections onto V along with contours to visualize their posterior variability. The results are shown in Figure 4(b–d). We observe a clear separation between human-derived (tongue, skin, and feces) biological samples and biological samples from free environments. This separation is mostly identified by the first two compromise axes. The third axis defines a saline/non-saline samples separation. Biological samples derived from saline environment (e.g. Ocean) are well separated when projected on this axis from those derived from non-saline environment (e.g. Creek freshwater). We observed small 95% credible regions for all biological samples projections. This low level of uncertainty captured by the small credible regions in Figure 4(b–d) is mainly explained by the large total counts nj for all biological samples. Finally, to compare the ordination results to those given by standard methods used in microbiome studies, we generated ordination results using PCoA. Figure S4 shows that the relative positions of different types of biological samples in PCoA plots and in the Bayesian ordination plots are similar.
6.2 The Vaginal Microbiome
We also consider a dataset previously presented in Ravel et al. (2011) which contains a larger number of biological samples (900) and a simpler bacterial community structure. These biological samples are derived from 54 healthy women. Multiple biological samples are taken from each individual, ranging from one to 32 biological samples per individual. Each woman has been classified, before our microbiome sequencing data were generated, into vaginal community state subtypes (CST). This dataset contains only species level taxonomic information, and we filtered OTUs by occurrence. We only retain species with more than five reads in at least 10% of biological samples. This filtering resulted in 31 distinct OTUs. We ran one MCMC chain with 50,000 iterations.
We performed the same analyses as in the previous subsection. The results are shown in Figure 5. Clustering probabilities indicate strong within CST similarity (panel a). There is one exception, CST IV-A samples, in some cases, presenting low levels of similarities when compared to each other and tend to cluster with CST I, CST III, and CST IV-B samples. This is because CST IV-A is characterized as a highly heterogeneous subtype (Ravel et al., 2011). The ordination plots are consistent with the discoveries in Ravel et al. (2011). A tetrahedron shape is recovered, and CST I, II, III, IV-B occupy the four vertices. CST II is well separated from other CSTs by the third axis. This pattern is similar to the one observed in the plots generated using PCoA (Figure S5). We also observed a sub-clustering in CST II which has not been detected and discussed in Ravel et al. (2011). This difference in the results can be due to distinct clustering metrics in the analyses.
Figure 5.
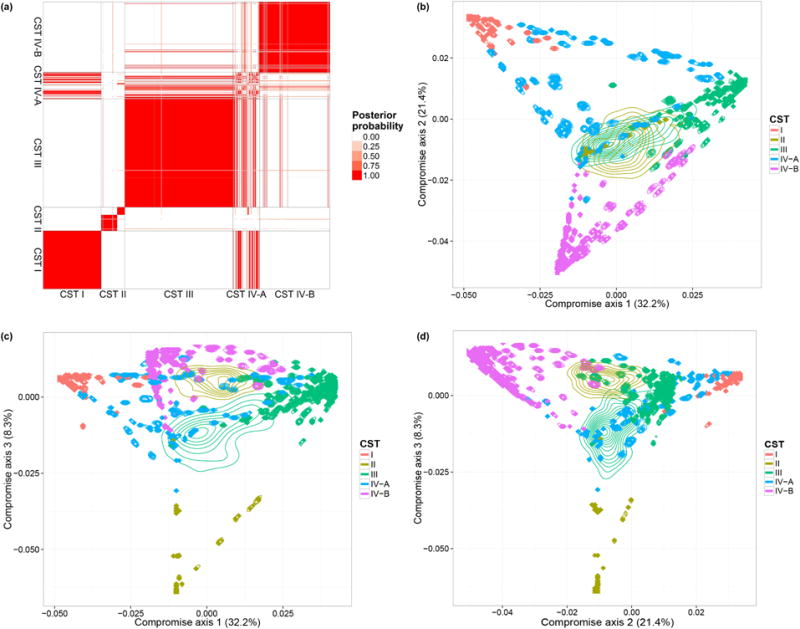
(a) Posterior Probability of each pair of biological samples (j, j′) being clustered together. The labels on axes indicate the CST for each biological sample. (b–d) Ordination plots of biological samples and posterior credible regions. We illustrate the first three compromise axes with three panels. The percentages on the three axes are the ratios of the corresponding S0 eigenvalues and the trace of the matrix. Colors and indicate CSTs.
Note that there are two biological samples with large credible regions, indicating high uncertainty of the corresponding positions. This uncertainty propagates on their cluster membership. Both biological samples have small total counts compared to the others. The lack of precision when using biological samples with small sequencing depth leads to high uncertainty in ordination and classification. It is therefore important to account for uncertainty in the validation of subgroups biological differences—in our case CST subtypes—based on microbiome profiling. Our example suggests also the importance of uncertainty summaries when microbiome profiles are used to classify samples. Uncertainty summaries allow us to retain all samples, including those with low counts, without the risk of overinterpreting the estimated locations and projections. This also argues for the retention of raw counts in microbiome studies (McMurdie and Holmes, 2014). By using raw counts, we can evaluate the uncertainty of our estimates and exploit the information and statistical power carried by the full dataset; whereas if we downsample the data we lose information and increase uncertainty on the projections.
It is ubiquitous to have biological samples with relevant differences in their total counts, and in some cases the number of OTUs and the total number of reads can be comparable. In this cases, the empirical estimates of microbial distributions are not reliable, and an assessment of the uncertainty is necessary for downstream analyses. The two biological samples with low total counts in the vaginal microbiome dataset are examples. For biological samples with a scarce amount of data our model provides measures of uncertainty and allows uncertainty visualizations with ordination plots.
7 Conclusion
We propose a joint model for multinomial sampling of OTUs in multiple biological samples. We apply a prior from Bayesian factor analysis to estimate the similarity between biological samples, which is summarized by a Gram matrix. Simulation studies give evidence that this parameter is recovered by the Bayes estimate, and in particular, the inherent dimensionality of the latent factors is effectively learned from the data. The simulation also demonstrated that the analysis yields more accurate estimates of the microbial distributions by borrowing information across biological samples.
In addition, we provide a robust method to visualize the uncertainty in ecological ordinations, furnishing each point in the plot with a credible region. Two published microbiome datasets were analyzed, and the results are consistent with previous findings. The second analysis demonstrates that the level of uncertainty can vary across biological samples due to differences in sampling depth, which underlines the importance of modeling multinomial sampling variations coherently. We believe our analysis will mitigate artifacts arising from rarefaction, thresholding of rare species, and other preprocessing steps.
There are several directions for development which are not explored here. We highlight the possibility of incorporating prior knowledge about the biological samples, such as the subject or group identifier in a clinical study. To achieve this, we can augment the latent factors Yj by a vector of covariates , whose coefficients b could be given a normal prior, for example. The posterior distribution of the coefficients could be used to infer the magnitude of covariates’ effects. A less straightforward extension involves moving away from the assumption of a priori exchangeability between OTUs to include prior information about phylogenetic or functional relationships between them. In our present analysis, these relationships are not taken into account in the definition of the prior for microbial distributions.
Supplementary Material
Acknowledgments
B. Ren is supported by National Science Foundation under Grant No. DMS-1042785. S. Favaro is supported by the European Research Council (ERC) through StG N-BNP 306406. L. Trippa has been supported by the Claudia Adams Barr Program in Innovative Basic Cancer Research. S. Holmes was supported by the NIH grant R01AI112401. We thank Persi Diaconis, Kris Sankaran and Lan Huong Nguyen for helpful suggestions and improvements.
Funding was provided by the National Science Foundation, European Research Council, Claudia Adams Barr Program in Innovative Basic Cancer Research and the National Institutes of Health.
Footnotes
SUPPLEMENTARY MATERIAL
Supplementary document This file contains the proofs for our propositions, details about the fast algorithm we described in subsection 3.1, the PCoA plots for the simulated data in Figure 3(f), Global Patterns dataset, and Ravel’s vaginal microbiome dataset, and a section to illustrate the computation time and convergence diagnosis of the MCMC sampler. (.pdf file)
R code for simulation study and applications The MCMC sampler is formatted into a R package and the code to reproduce Figure 3–5 can be found in the vignette of the package (DirFactor.zip). We also include the code for the algorithm described in subsection 3.1 and the code for supplementary Figure S2–S6 (Misc.zip). (zip file)
Contributor Information
Boyu Ren, Department of Biostatistics, Harvard University, Boston, MA 02115.
Sergio Bacallado, University academic staff, Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridgeshire CB2 1TN, UK.
Stefano Favaro, Associate Professor, University of Torino and Collegio Carlo, C.so Unione Sovietica 218/bis, Torino 10134, Italy.
Susan Holmes, Professor, Department of Statistics, Stanford University, Sequoia Hall, Stanford, CA 94305.
Lorenzo Trippa, Assistant Professor, Department of Biostatistics, Harvard University, Boston, MA 02115.
References
- Abdi H, O’Toole AJ, Valentin D, Edelman B. Computer Vision and Pattern Recognition-Workshops, 2005 CVPR Workshops IEEE Computer Society Conference on. IEEE; 2005. Distatis: The analysis of multiple distance matrices; pp. 42–42. [Google Scholar]
- Anderson MJ, Ellingsen KE, McArdle BH. Multivariate dispersion as a measure of beta diversity. Ecology Letters. 2006;9(6):683–693. doi: 10.1111/j.1461-0248.2006.00926.x. [DOI] [PubMed] [Google Scholar]
- Ando T. Bayesian factor analysis with fat-tailed factors and its exact marginal likelihood. Journal of Multivariate Analysis. 2009;100(8):1717–1726. [Google Scholar]
- Bhattacharya A, Dunson DB. Sparse Bayesian infinite factor models. Biometrika. 2011;98(2):291. doi: 10.1093/biomet/asr013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brix A. Generalized gamma measures and shot-noise cox processes. Advances in Applied Probability. 1999:929–953. [Google Scholar]
- Callahan BJ, McMurdie PJ, Rosen MJ, Han AW, Johnson AJA, Holmes SP. Dada2: High-resolution sample inference from illumina amplicon data. Nature methods. 2016;13(7):581–583. doi: 10.1038/nmeth.3869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caporaso JG, Kuczynski J, Stombaugh J, Bittinger K, Bushman FD, Costello EK, Fierer N, Pena AG, Goodrich JK, Gordon JI, Knight R. Qiime allows analysis of high-throughput community sequencing data. Nature methods. 2010;7(5):335–336. doi: 10.1038/nmeth.f.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caporaso JG, Lauber CL, Walters WA, Berg-Lyons D, Lozupone CA, Turnbaugh PJ, Fierer N, Knight R. Global patterns of 16s rRNA diversity at a depth of millions of sequences per sample. Proceedings of the National Academy of Sciences. 2011;108(Supplement 1):4516–4522. doi: 10.1073/pnas.1000080107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho CM, Chang J, Lucas JE, Nevins JR, Wang Q, West M. High-dimensional sparse factor modeling: applications in gene expression genomics. Journal of the American Statistical Association. 2008;103(484) doi: 10.1198/016214508000000869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeSantis TZ, Hugenholtz P, Larsen N, Rojas M, Brodie EL, Keller K, Huber T, Dalevi D, Hu P, Andersen GL. Greengenes, a chimera-checked 16s rRNA gene database and workbench compatible with arb. Applied and environmental microbiology. 2006;72(7):5069–5072. doi: 10.1128/AEM.03006-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dethlefsen L, McFall-Ngai M, Relman DA. An ecological and evolutionary perspective on human–microbe mutualism and disease. Nature. 2007;449(7164):811–818. doi: 10.1038/nature06245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dethlefsen L, Relman DA. Incomplete recovery and individualized responses of the human distal gut microbiota to repeated antibiotic perturbation. Proceedings of the National Academy of Sciences. 2011;108(Supplement 1):4554–4561. doi: 10.1073/pnas.1000087107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiGiulio D, Callahan BJ, McMurdie PJ, Costello EK, Lyell DJ, Robaczewska A, Sun CL, Goltsman DSA, Wong RJ, Shaw G, Stevenson DK, Holmes S, R DA. Temporal and spatial variation of the human microbiota during pregnancy. 2015 doi: 10.1073/pnas.1502875112. to appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding T, Schloss PD. Dynamics and associations of microbial community types across the human body. Nature. 2014;509(7500):357. doi: 10.1038/nature13178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eren AM, Borisy GG, Huse SM, Welch JLM. Oligotyping analysis of the human oral microbiome. Proceedings of the National Academy of Sciences. 2014;111(28):E2875–E2884. doi: 10.1073/pnas.1409644111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escoufier Y. Le traitement des variables vectorielles. Biometrics. 1973:751–760. [Google Scholar]
- Faust K, Sathirapongsasuti JF, Izard J, Segata N, Gevers D, Raes J, Huttenhower C. Microbial co-occurrence relationships in the human microbiome. PLoS Comput Biol. 2012;8(7):e1002606. doi: 10.1371/journal.pcbi.1002606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson TS. A Bayesian analysis of some nonparametric problems. The annals of statistics. 1973:209–230. [Google Scholar]
- Gorvitovskaia A, Holmes SP, Huse SM. Interpreting prevotella and bacteroides as biomarkers of diet and lifestyle. Microbiome. 2016;4(1):1. doi: 10.1186/s40168-016-0160-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grice EA, Segre JA. The skin microbiome. Nature Reviews Microbiology. 2011;9(4):244–253. doi: 10.1038/nrmicro2537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffin JE, Kolossiatis M, Steel MFJ. Comparing distributions by using dependent normalized random-measure mixtures. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2013;75(3):499–529. [Google Scholar]
- Holmes I, Harris K, Quince C. Dirichlet multinomial mixtures: generative models for microbial metagenomics. PloS one. 2012;7(2):e30126. doi: 10.1371/journal.pone.0030126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes S. Probability and statistics: Essays in honor of David A Freedman. Institute of Mathematical Statistics; 2008. Multivariate data analysis: the french way; pp. 219–233. [Google Scholar]
- Ishwaran H, James LF. Gibbs sampling methods for stick-breaking priors. Journal of the American Statistical Association. 2001;96(453):161–173. [Google Scholar]
- James LF. Poisson process partition calculus with applications to exchangeable models and bayesian nonparametrics. 2002 arXiv preprint math/0205093. [Google Scholar]
- James LF, Lijoi A, Prünster I. Posterior analysis for normalized random measures with independent increments. Scandinavian Journal of Statistics. 2009;36(1):76–97. [Google Scholar]
- Kingman J. Completely random measures. Pacific Journal of Mathematics. 1967;21(1):59–78. [Google Scholar]
- Koenig JE, Spor A, Scalfone N, Fricker AD, Stombaugh J, Knight R, Angenent LT, Ley RE. Succession of microbial consortia in the developing infant gut microbiome. Proceedings of the National Academy of Sciences. 2011;108(Supplement 1):4578–4585. doi: 10.1073/pnas.1000081107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kostic AD, Gevers D, Siljander H, Vatanen T, Hyötyläinen T, Hämäläinen A, Peet A, Tillmann V, Pöhö P, Mattila I. The dynamics of the human infant gut microbiome in development and in progression toward type 1 diabetes. Cell host & microbe. 2015;17(2):260–273. doi: 10.1016/j.chom.2015.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- La Rosa PS, Brooks JP, Deych E, Boone EL, Edwards DJ, Wang Q, Sodergren E, We-instock G, Shannon WD. Hypothesis testing and power calculations for taxonomic-based human microbiome data. PloS one. 2012;7(12):e52078. doi: 10.1371/journal.pone.0052078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavit C, Escoufier Y, Sabatier R, Traissac P. The ACT (statis method) Computational Statistics & Data Analysis. 1994;18(1):97–119. [Google Scholar]
- Lee S, Song X. Bayesian selection on the number of factors in a factor analysis model. Behaviormetrika. 2002;29(1):23–39. [Google Scholar]
- Lijoi A, Mena RH, Prünster I. Hierarchical mixture modeling with normalized inverse-gaussian priors. Journal of the American Statistical Association. 2005;100(472):1278–1291. [Google Scholar]
- Lijoi A, Mena RH, Prünster I. Controlling the reinforcement in Bayesian nonparametric mixture models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2007;69(4):715–740. [Google Scholar]
- Lijoi A, Prünster I. Models beyond the dirichlet process. In: Hjort NL, Holmes C, Müller P, Walker SG, editors. Bayesian nonparametrics. Cambridge University Press; 2010. pp. 80–136. Chapter 3. [Google Scholar]
- Lopes HF, West M. Bayesian model assessment in factor analysis. Statistica Sinica. 2004;14(1):41–68. [Google Scholar]
- Lozupone C, Knight R. Unifrac: a new phylogenetic method for comparing microbial communities. Applied and environmental microbiology. 2005;71(12):8228–8235. doi: 10.1128/AEM.71.12.8228-8235.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucas J, Carvalho C, Wang Q, Bild A, Nevins JR, West M. Sparse statistical modelling in gene expression genomics. Bayesian Inference for Gene Expression and Proteomics. 2006;1 [Google Scholar]
- MacEachern SN. Unpublished manuscript. Department of Statistics, The Ohio State University; 2000. Dependent dirichlet processes. [Google Scholar]
- McMurdie PJ, Holmes S. phyloseq: an r package for reproducible interactive analysis and graphics of microbiome census data. PLOS one. 2013;8(4):e61217. doi: 10.1371/journal.pone.0061217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMurdie PJ, Holmes S. Waste not, want not: why rarefying microbiome data is inadmissible. PLoS Comput Biol. 2014;10(4):e1003531. doi: 10.1371/journal.pcbi.1003531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mercer J. Functions of positive and negative type, and their connection with the theory of integral equations. Philosophical transactions of the royal society of London Series A, containing papers of a mathematical or physical character. 1909:415–446. [Google Scholar]
- Morgan XC, Tickle TL, Sokol H, Gevers D, Devaney KL, Ward DV, Reyes JA, Shah SA, LeLeiko N, Snapper SB, et al. Dysfunction of the intestinal microbiome in inflammatory bowel disease and treatment. Genome biology. 2012;13(9):1. doi: 10.1186/gb-2012-13-9-r79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muliere P, Tardella L. Approximating distributions of random functionals of ferguson-dirichlet priors. Canadian Journal of Statistics. 1998;26(2):283–297. [Google Scholar]
- Müller P, Quintana F, Rosner G. A method for combining inference across related nonparametric Bayesian models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2004;66(3):735–749. [Google Scholar]
- Oksanen J, Blanchet FG, Kindt R, Legendre P, Minchin PR, O’Hara RB, Simpson GL, Solymos P, Stevens MHH, Wagner H. vegan: Community Ecology Package 2015 Nov; [Google Scholar]
- Paulson JN, Stine OC, Bravo HC, Pop M. Diffierential abundance analysis for microbial marker-gene surveys. Nature methods. 2013;10(12):1200–1202. doi: 10.1038/nmeth.2658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peiffer JA, Spor A, Koren O, Jin Z, Tringe SG, Dangl JL, Buckler ES, Ley R. Diversity and heritability of the maize rhizosphere microbiome under field conditions. Proceedings of the National Academy of Sciences. 2013;110(16):6548–6553. doi: 10.1073/pnas.1302837110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press SJ, Shigemasu K. Contributions to probability and statistics. Springer; 1989. Bayesian inference in factor analysis; pp. 271–287. [Google Scholar]
- Quince C, Lundin EE, Andreasson AN, Greco D, Rafter J, Talley NJ, Agreus L, Andersson AF, Engstrand L, D’Amato M. The impact of crohn’s disease genes on healthy human gut microbiota: a pilot study. Gut. 2013:952–954. doi: 10.1136/gutjnl-2012-304214. [DOI] [PubMed] [Google Scholar]
- Ravel J, Gajer P, Abdo Z, Schneider GM, K SSK, McCulle SL, Karlebach S, Gorle R, Russell J, Tacket CO, Brotman RM. Vaginal microbiome of reproductive-age women. Proceedings of the National Academy of Sciences. 2011;108(Supplement 1):4680–4687. doi: 10.1073/pnas.1002611107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regazzini E, Lijoi A, Prünster I. Distributional results for means of normalized random measures with independent increments. Annals of Statistics. 2003:560–585. [Google Scholar]
- Robert P, Escoufier Y. A unifying tool for linear multivariate statistical methods: the RV-coefficient. Applied statistics. 1976:257–265. [Google Scholar]
- Rodríguez A, Dunson DB, Gelfand AE. Bayesian nonparametric functional data analysis through density estimation. Biometrika. 2009;96(1):149–162. doi: 10.1093/biomet/asn054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen MJ, Callahan BJ, Fisher DS, Holmes S. Denoising pcr-amplified metagenome data. BMC bioinformatics. 2012;13(1):283. doi: 10.1186/1471-2105-13-283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowe DB. Multivariate Bayesian statistics: models for source separation and signal unmixing CRC Press 2002 [Google Scholar]
- Tibshirani R, Hastie T, Narasimhan B, Chu G. Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proceedings of the National Academy of Sciences. 2002;99(10):6567–6572. doi: 10.1073/pnas.082099299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turnbaugh PJ, Hamady M, Yatsunenko T, Cantarel BL, Duncan A, Ley RE, Sogin ML, Jones WJ, Roe BA, Affourtit JP, Egholm M, Henrissat B, Heath AC, Knight R, Gordon JI. A core gut microbiome in obese and lean twins. Nature. 2009 Jan;457(7228):480–484. doi: 10.1038/nature07540. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


