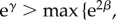Risk ratios for contagious outcomes

Abstract

Epidemiologists commonly use the risk ratio to summarize the relationship between a binary covariate and outcome, even when outcomes may be dependent. Investigations of transmissible diseases in clusters—households, villages or small groups—often report risk ratios. Epidemiologists have warned that risk ratios may be misleading when outcomes are contagious, but the nature of this error is poorly understood. In this study, we assess the meaning of the risk ratio when outcomes are contagious. We provide a mathematical definition of infectious disease transmission within clusters, based on the canonical stochastic susceptible–infective model. From this characterization, we define the individual-level ratio of instantaneous infection risks as the inferential target, and evaluate the properties of the risk ratio as an approximation of this quantity. We exhibit analytically and by simulation the circumstances under which the risk ratio implies an effect whose direction is opposite that of the true effect of the covariate. In particular, the risk ratio can be greater than one even when the covariate reduces both individual-level susceptibility to infection, and transmissibility once infected. We explain these findings in the epidemiologic language of confounding and Simpson's paradox, underscoring the pitfalls of failing to account for transmission when outcomes are contagious.

1. Introduction

Risk ratios are often recommended for summarizing the relationship between a covariate and an outcome in epidemiology [1–10]. They are simple and easy to compute [11–13], and when outcomes may exhibit correlation within clusters, ‘robust’ standard errors are available [10,14]. Many researchers report risk ratios in studies of infectious disease outcomes within clusters or communities of interacting individuals, including studies of H1N1 influenza [15,16], Ebola [17,18], leprosy [19] and varicella [20]. When the outcome is an infection indicator, the covariate of interest may correspond to a preventive treatment like vaccination, a risk factor like immune status or the presence of a co-morbid condition, or a demographic characteristic like age, sex or socio-economic status. Contagion within clusters may induce dependence in cluster members' infection outcomes [21], but the effect of a covariate under contagion may be complicated: different values might alter an individual's susceptibility to infection, or their infectiousness once infected, or both [22–24].

Infectious disease epidemiologists have repeatedly warned that when outcomes are contagious, simplistic summaries of risk may be misleading [24–35]. Researchers have argued that bias can arise when analytical methods do not separate the effects of a covariate on susceptibility to infection from infectiousness once infected [24,29,36], or when individual-level variation in exposure to infection is ignored [26,27,34,36–39]. Epidemiologists have suggested that risk ratios may not always give a reasonable summary of individual-level covariate effects. For example, risk ratios are often assumed to be time-invariant, but they can change over time in both observational [40] and experimental [41] studies. Likewise the risk ratio, as a measure of the effect of a vaccine, depends on both the time at which outcomes are observed and the population-level vaccine coverage [42]. However, epidemiologists have not explained how these issues are related, nor demonstrated formally why the risk ratio may be an unsatisfactory measure of association under contagion for empirical research on infectious diseases. Prior work does not provide guidance about the disease dynamics and study design features that are most likely to give rise to profoundly biased estimates.

In this paper, we investigate the properties of the risk ratio when outcomes are contagious within clusters, and explain how these properties depend on the covariate of interest and the epidemiologic features of disease transmission. We first introduce a canonical definition of infectious disease contagion, based on the widely used susceptible–infective epidemic model [43,44]. This structural description of disease transmission formalizes the epidemiologic intuition that a susceptible individual's risk of infection at a given time depends both on their own traits, and those of their infectious contacts [36,39,45]. We define the inferential target as the ratio of instantaneous individual-level risks (hazards) of infection under a one-unit change in the value of a covariate [28,34], and show that the risk ratio can be a profoundly biased approximation of this quantity. For the simplest setting of clusters of size two, we describe conditions under which the risk ratio exhibits the most egregious form of error, bias ‘across the null’, in which the direction of the estimated effect is in error. Further analytic results and simulations provide insight into the behaviour of the risk ratio under contagion in clusters of larger size and in randomized trials. These results provide the first formal description of the pathological properties of the risk ratio under common assumptions about contagion. Finally, we explain these findings in the epidemiologic language of bias induced by confounding.

2. Setting

Consider a collection of clusters (e.g. households, workplaces, villages), with n_i subjects in cluster i. Let Y_ij(t) be the binary indicator of infection for subject j in cluster i on or before time t ≥ 0. Let T_i be the time at which outcomes in cluster i are observed and recorded by researchers. We consider a single time-invariant binary covariate x_ij for subject j in cluster i. The risk ratio is defined as

2.1

The risk ratio is implicitly a function of the observation time T_i for each cluster i [46].

We describe a stochastic transmission model based on the canonical susceptible–infective model of infectious disease contagion within clusters [36,39,43–45], then characterize the hazard ratio corresponding to a one-unit change in a covariate associated with susceptibility to disease. The susceptible–infective model captures the intuition that the risk to a susceptible individual at a given time is given heuristically by

2.2

where ‘susceptibility’ is a function of the subject's own characteristics, and ‘force of infection’ summarizes the risk transmitted by that subject's infectious contacts, including from outside of the cluster.

To formalize this risk, let t_ij be the minimum of the infection time of subject j in cluster i and the observation time T_i, so that Y_ij(t) = 0 for t≤t_ij, and Y_ij(t) = 1 for t_ij < t ≤ T_i. A subject j in cluster i is called susceptible at time t if Y_ij(t) = 0, and infected if Y_ij(t) = 1. Consider the possible sources of transmission to a susceptible subject j in cluster i. First, j may be infected by exposure to an exogenous source of infection (sometimes called the community force of infection if clusters are households). Let τ^e_ij be the waiting time for j to be infected from this exogenous source, and let λ^e_ij(t) be the hazard of this event at time t. Second, suppose another subject k in cluster i becomes infected at a time t_ik ∈ [0, T_i), which is defined similarly to t_ij as the minimum of the infection time of subject k and cluster i observation time T_i. Suppose subject j is not infected at time t_ik, Y_ij(t_ik) = 0. Let τ^k_ij be the waiting time (measured since t_ik) for k to transmit the infection to j, and let λ^k_ij(t) be the hazard of this event at time t > t_ik. For each cluster i and susceptible subject j, the total hazard experienced by a susceptible individual j is the sum of these hazards,

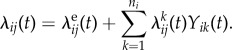2.3

The additive form of (2.3) arises because j experiences competing risks of infection: from the exogenous source, and from each of their infectious contacts. Under this simple generative process, subjects may not be re-infected.

We assume for simplicity that the hazards λ^e_ij(t) and λ^k_ij(t) are Cox-type models: each decomposes into the product of a possibly time-varying force of infection and a function of covariates. Let 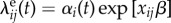, where α_i(t) is the possibly time-varying exogenous force of infection to cluster i, and β is a susceptibility parameter corresponding to the binary covariate x. Likewise, when t > t_ik, let 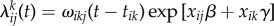where ω_ikj(t − t_ik) is the possibly time-varying force of infection from subject k to subject j in cluster i, and γ is an infectiousness parameter corresponding to the binary covariate x. Then the total infection hazard to susceptible subject j in cluster i at time t becomes

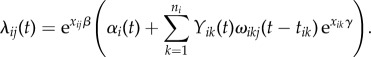2.4

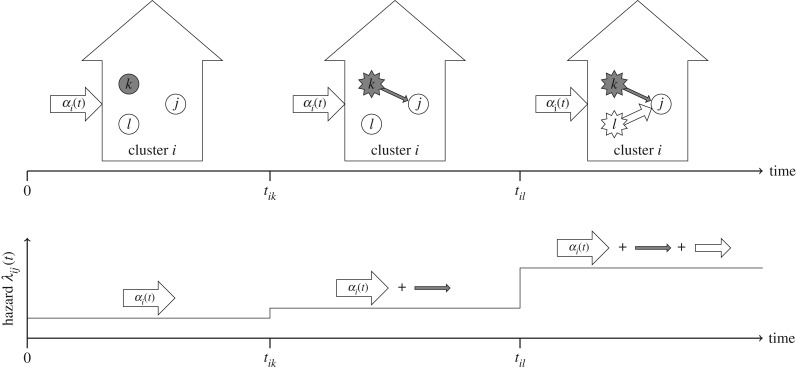
The multiplicative relationship between susceptibility 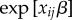and the total force of infection in (2.4) mirrors the heuristic description of infection risk given by (2.2). Figure 1 shows a schematic depiction of the transmission model in a cluster of size three. The risk of infection experienced by a susceptible subject j increases over time as individuals around j become infected. Since a covariate x may, in general, alter infectiousness, the magnitude of risk increase to j with every subsequent contact, who become infected, depends on that individual's covariate.

Figure 1.

Schematic of hazards in the transmission model for a cluster of size three. Grey colour indicates x = 1. Before the first infection, subject j experiences only an exogenous (community) force of infection α_i(t), because neither k nor l is infected. After k is infected, the hazard to j increases in proportion to the infectiousness of k, which is a function of x_ik = 1. Likewise, after l is infected, the hazard to j increases in proportion to the infectiousness of l, with x_il = 0. Below, the sum of hazards experienced by subject j is shown over time.

When x_ij = x is constant across individuals, α_i(t) = 0, and ω_ikj(t − t_ik) = ω, the process becomes the standard continuous-time Markov susceptible–infective model within clusters. The formulation of the hazard of infection in (2.4) mirrors a transmission model proposed for semi-parametric relative risk regression [36]. The model captures temporal changes in post-infection transmission via the functional form of ω_ikj(t − t_ik), which can accommodate latency or other changes in infectiousness over time.

The hazard ratio (HR) is the ratio of instantaneous risks given by (2.4) under different values of the covariate x, holding individual-level force of infection constant:

2.5

The hazard ratio summarizes the individual-level association between the covariate x and susceptibility to infection at time t [28,34,46].

We emphasize that we do not treat the transmission model characterized by (2.4) as an inferential model. We have not specified the possibly time-varying hazards α_i(t) and ω_ikj(t), nor showed that any feature of the process is identified by a particular observation scenario. Instead, (2.4) characterizes the transmission dynamics of infection by which the observable data are assumed to be generated. Table 1 summarizes the parameters that define this process.

Table 1.

Summary of parameters in the transmission model.

notation	definition
ni	size of cluster i
Ti	observation time for cluster i
tij	minimum of infection time of subject j in cluster i and cluster i observation time Ti
xij	covariate of interest, time-invariant
Yij(t)	binary indicator of infection by time t
β	susceptibility parameter for covariate x
γ	infectiousness parameter for covariate x
αi(t)	exogenous force of infection, a function of time
ωikj(t)	force of infection from infectious k to susceptible j, a function of time since infection of k

It seems reasonable to expect the risk ratio given by (2.1) for the binary variable x, as a marginal or population-level measure of association, to be meaningful for assessment of the ratio of conditional risks (2.5) experienced by an individual. Since the hazard ratio (2.5) evaluated at a time t is time-invariant, we might expect the risk ratio, as a cross-sectional measure of association at time t, to provide similar evidence about the relationship between x and the outcome. In particular, researchers may wish to avoid a particularly egregious form of bias, in which the direction of the estimated effect is opposite that of the true effect. For example, if x = 1 is associated with reduced susceptibility to infection, we would like to see that RR < 1. To make this notion more formal, we define a general property that we would like the risk ratio to satisfy.

Definition 2.1. —

(Direction-unbiasedness of risk ratio.) If HR < 1, then RR < 1, if HR = 1, then RR = 1, and if HR > 1, then RR > 1.

We say that for a particular study design and values of parameters in (2.4), the risk ratio is direction-unbiased if definition 2.1 holds. When definition 2.1 does not hold, we say that the risk ratio exhibits ‘bias across the null’ because its direction is opposite that of the true effect e^β. Definition 2.1 is a relatively weak requirement: it does not imply zero bias, nor monotonicity in the risk ratio as a function of the hazard ratio, nor any particular functional relationship between the two.

3. Results

3.1. Clusters of size two

We first consider a simple parametric version of (2.4) with two-person clusters and balanced covariate values for which a variety of precise analytic results can be derived. This setting is based on a two-person infectious disease contagion model introduced previously [47–49], and serves to illustrate the potential for the risk ratio to give a misleading summary of association under contagion. Clusters of size two appear in empirical study designs, including HIV transmission in couples [50,51], and mother-to-child transmission of Staphylococcus aureus [52,53]. Consider the transmission model characterized by (2.4), where each cluster i consists of exactly two subjects: n_i = 2. Assume also that the covariate is balanced within the cluster, subject 1 has x_i1 = 1 and subject 2 has x_i2 = 0; all subjects are uninfected at baseline, Y_ij(0) = 0; and follow-up time is constant, T_i = T for all i. Additionally, assume there is a constant exogenous force of infection α_i(t) = α, and constant within-cluster contagion ω_ikj(t − t_ik) = ω per susceptible j and infected k. The hazards of infection experienced by subjects 1 and 2 in cluster i become 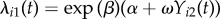and 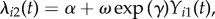respectively. The following results establish the properties of the risk ratio as an approximation to the hazard ratio in several relevant special cases. Unless otherwise stated, we assume α > 0 and ω > 0. Derivations and proofs of all results are given in the electronic supplementary material.

Result 3.1. —

(No within-cluster contagion.) Suppose ω = 0. For any T > 0, the risk ratio is direction-unbiased.

Thus when the outcome is not transmissible within clusters, the risk ratio is direction-unbiased.

Define the ‘null’ hypothesis under the transmission model as β = 0, so that all subjects are equally susceptible to infection.

Result 3.2. —

(Under the null.) Suppose β = 0 and T > 0. Then if γ < 0, RR > 1; if γ > 0, RR < 1; and if γ = 0, RR = 1.

This result means that when the covariate does not affect susceptibility to infection, the direction of the risk ratio is entirely determined by the infectiousness coefficient γ. In particular, when the covariate reduces infectiousness (γ < 0)—as many treatments do—the risk ratio can be greater than one.

Result 3.3. —

(Homogeneous infectiousness.) Suppose γ = 0. For any T > 0, the risk ratio is direction-unbiased.

Therefore, if the covariate does not alter infectiousness, direction-unbiasedness holds.

Result 3.4. —

(Bias across the null.) Suppose either β < 0 and , or β > 0 and . Then there exists t* > 0 such that for all T > t*, the risk ratio is not direction-unbiased.

This result states that the risk ratio can be biased across the null when β is non-zero. Figure 2 illustrates result 3.4.

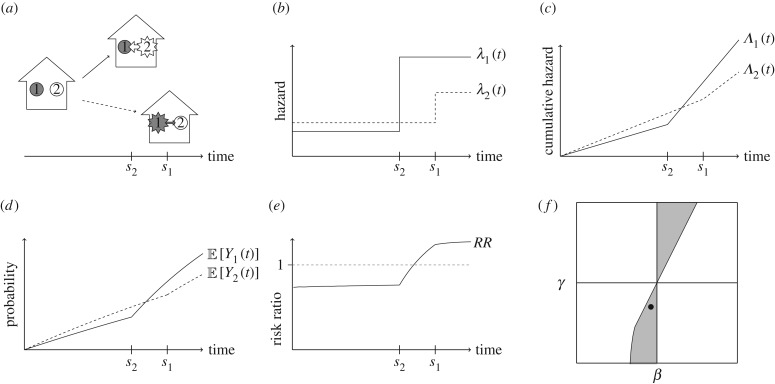
Figure 2.

Illustration of how the risk ratio can give misleading results under contagion in a cluster of size two. Suppose the conditions of result 3.4 hold with β < 0 and γ < 0 (such that the presence of the covariate, designated as value = 1, is associated with reduced susceptibility and transmissibility). Subject 1 (grey) has x₁ = 1, subject 2 (white) has x₂ = 0. (a) Either subject 2 becomes infected first (at time s₂), or subject 1 is infected first (at time s₁); depending on which is infected first, the other experiences a change in their hazard of infection. (b) If 1 is infected first, then 2 experiences only a small increase in hazard, because γ < 0. Alternatively, if 2 is infected first, then 1 experiences a large increase in hazard because x₂ = 0. (c) The relationship between the cumulative hazards in these scenarios, and hence the relationship between the expected infection outcomes (d), is eventually reversed at some time after s₂. Therefore, the risk ratio (e) eventually rises above one. Panel (f) shows the region of (β, γ) parameter space in which bias across the null may occur, where β and γ are plotted on the same scale. A black dot indicates the values of β and γ used in this illustration.

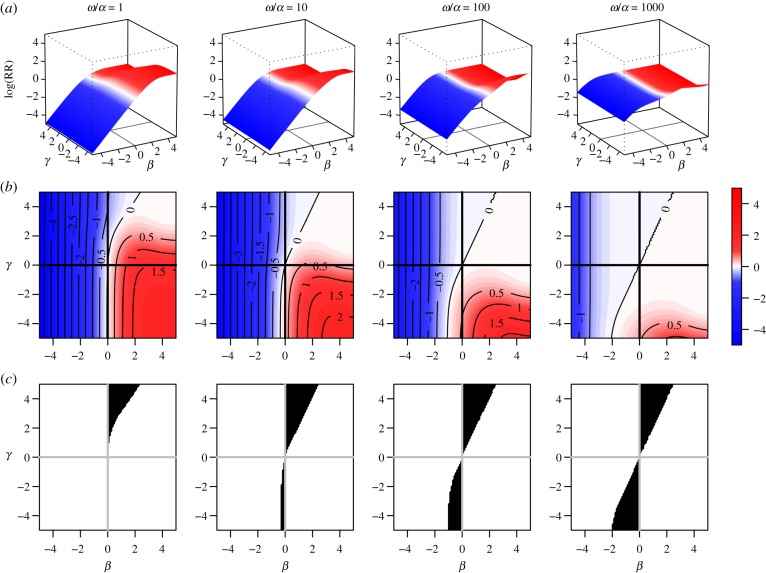
Direction-unbiasedness under definition 2.1 does not imply zero bias. Figure 3 shows log[RR] as a function of β and γ for several values of ω/α. Under the transmission model (2.4), any covariate can be represented by a point in this two-dimensional (β, γ) space, corresponding to its effects on susceptibility and infectiousness. Other study design parameters govern the behaviour of the risk ratio as a function of β and γ. The ratio ω/α summarizes the relative contribution of within-cluster transmission compared to transmission from the community. To make results comparable in every sub-figure, the observation time T is selected so that cumulative incidence at time T when β = 0 and γ = 0 is held constant at approximately 0.15. Figure 3a shows the magnitude of bias; as the ratio ω/α increases, the absolute value of the bias becomes larger even in regions where direction-unbiasedness holds. The electronic supplementary material provides a derivation of an exact expression for log[RR] and similar plots for a wider range of parameters α and ω. As an approximation to the hazard ratio, the risk ratio is always biased unless β = 0 and either ω = 0 or γ = 0 holds. For all other combinations of parameters, whenever the risk ratio is not biased across the null, it is biased towards the null hypothesis of β = 0.

Figure 3.

Risk ratio (log) as a function of true covariate effects β and γ. Row (a) shows the log risk ratio surface on (β, γ) space, and (b) shows the corresponding heat maps and contours for the log risk ratio. Row (c) shows the region of (β, γ) space in which the risk ratio is biased across the null hypothesis of β = 0. In the absence of bias, contour lines would be perfectly vertical and would match the value of β. In the absence of direction bias, heat maps for log[RR] would be entirely blue to the left of the β = 0 line, and red to the right of it. The greater the mismatch between β and the corresponding log[RR] contour line, the greater the bias. The bottom row shows the region of bias across the null, in which log[RR] and β have different signs. Study setup: clusters of size two with exactly one subject per cluster with x = 1. Values of the ω/α summarize the relative contribution of within-cluster transmission compared to transmission from the community. Observation time T was chosen such that cumulative incidence when β = 0 and γ = 0 is approximately 0.15 in all of the plots.

3.2. General clusters

The results derived above address performance of the risk ratio in clusters of size two. However, most empirical cluster cohort studies of infectious diseases involve variable cluster sizes and a more complex design. Several factors may influence the behaviour of the risk ratio in empirical studies, including epidemiologic features like the exogenous force of infection α_i(t), the force of contagion ω_ikj(t), and aspects of study design such as experimental assignment of the covariate x, the duration and variability of observation time T_i, cluster size distribution, or selection of clusters with or without infected individuals at baseline.

Result 3.5. —

(No within-cluster contagion.) Suppose ω_ikj(t) = 0 for all t and x_i = (x_i1, …, x_ini) is independent of {α_i(t), n_i, T_i}. Then the risk ratio is direction-unbiased.

Results 3.1 and 3.5 confirm the intuition that when there is no within-cluster contagion, and the covariate is independent of the force of infection and observation time, the risk ratio is direction-unbiased.

Result 3.6. —

(Independent x.) Suppose the covariates x_i = (x_i1, …, x_ini) are jointly independent and x_i is independent of {α_i(t), ω_ikj(t), n_i, T_i}. Then the risk ratio is direction-unbiased.

Joint independence of within-cluster covariates guarantees direction-unbiasedness for any parameter values.

The risk ratio is not generally direction-unbiased when the joint distribution of x_i is dependent. For example, bias across the null may occur under two common randomization schemes used in clinical trials: ‘block randomization’ within clusters, when a fixed number of subjects per cluster have x = 1 with 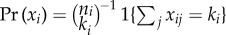, and ‘cluster randomization’ with x_ij = 1 for all j in some subset of clusters, and x_ij = 0 for all j in the remaining subset. In general, when the joint distribution of x_i is not independent, or when there is heterogeneity in n_i, α_i(t), or ω_ikj(t) across clusters, the risk ratio need not be direction-unbiased, even when γ = 0. Dependence in x_i may occur in observational studies, where x_i may be dependent due to shared environment, genetic factors or other forms of dependence within clusters. For example, an observational study of heterosexual partnerships might exhibit dependence on a covariate for gender.

3.3. Simulation results

Analytical expressions for the bias of the risk ratio as an approximation to the hazard ratio are intractable in general. However, simulations can provide further insight under particular epidemiologic and study design parameters. In simulations, we vary the distribution of covariates x_i, cluster size n_i, observation time T_i, infected cluster members at baseline and values of force of infection parameters α and ω, which are assumed to be constant over time and clusters. A comprehensive set of simulation results and R code [54] for replicating the simulations appear in the electronic supplementary material.

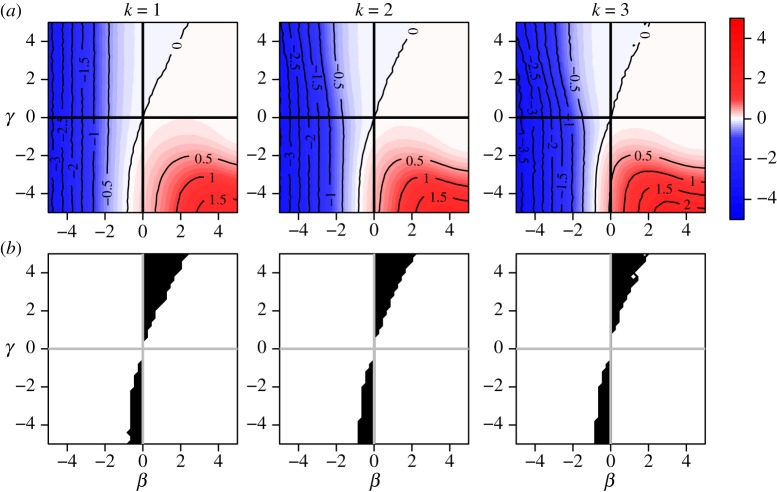
Some properties of the two person-cluster case hold in more complex scenarios. Figure 4 shows results for clusters of size four and block randomized distribution of x, such that each cluster has exactly k subjects with x = 1, k = 1, 2, 3. The behaviour of the bias in figure 4 mimics that of the two-person cluster case. We demonstrated analytically in result 3.5 that direction-unbiasedness under no within-cluster contagion holds under independence of x_i and cluster level parameters α_i(t), n_i and T_i. The simulation shows that results under constant cluster size and block randomized x are similar to those in the two-person cluster case for sufficiently large observation times T_i.

Figure 4.

Risk ratio (log) and region of bias across the null as a function of true covariate effects β and γ when cluster size is constant (n_i = 4 for all i) and distribution of x is block randomized: 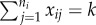. Row (a) shows log[RR], and (b) shows the region of bias across the null (where log[RR] and β have opposite signs). In all plots α = 0.0001, ω = 0.01, N = 500, T_i = 450 and no subjects are infected at time zero.

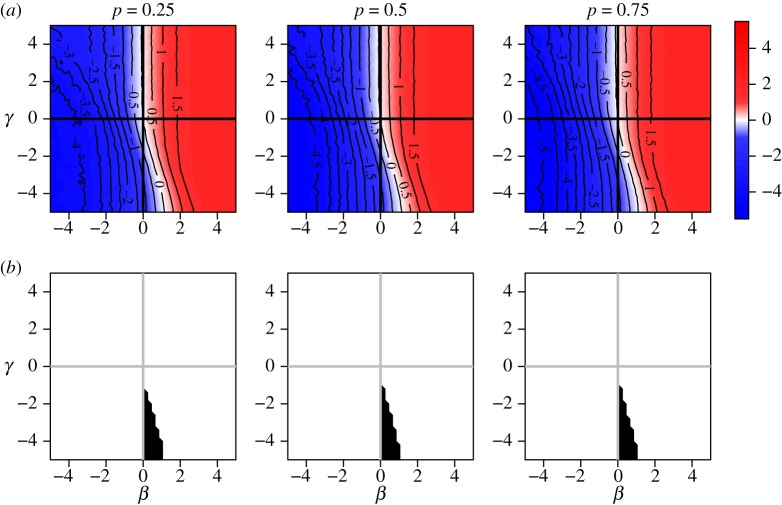
It follows from result 3.6 that the risk ratio is direction-unbiased under independent Bernoulli assignment of x_i. In practical intervention trials, many studies in small clusters employ block or cluster randomization. Simulation results show that both of these methods result in bias across the null in a region of (β, γ) space. Figure 4 shows that block randomized distribution of x_i can result in bias across the null when β and γ have the same sign and γ is more extreme than β. Figure 5 illustrates cluster randomized distribution of x_i, showing bias across the null in regions where β and γ have opposite sign.

Figure 5.

Risk ratio (log) and region of bias across the null as a function of true covariate effects β and γ when cluster size is constant and x is cluster randomized: proportion p of clusters have 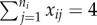, and remaining 1 − p have 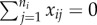. Row (a) shows the value of log[RR], and (b) shows the region of bias across the null. In all plots α = 0.0001, ω = 0.01, N = 500, n_i = 4, T_i = 450 and no subjects are infected at time zero.

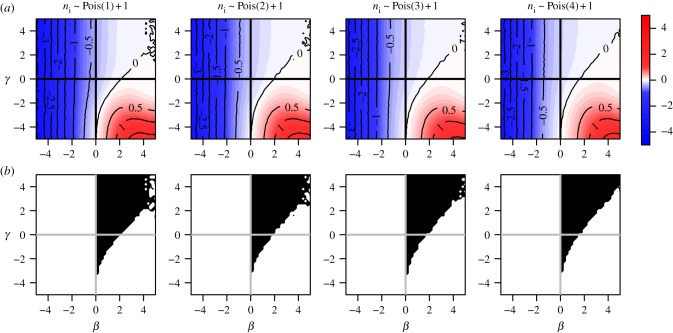
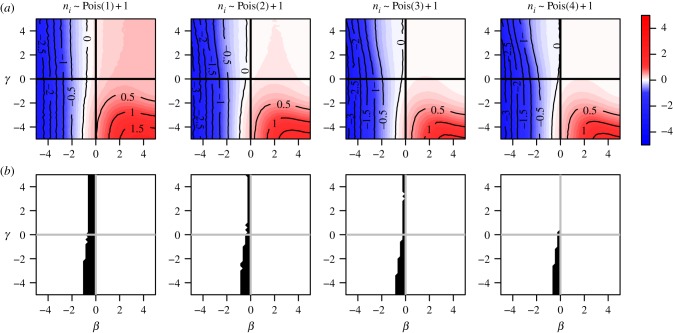
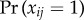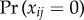When cluster size n_i varies, bias patterns can change substantially with the nature of dependence in the distribution of x_i. Even under block randomization, the pattern of bias across the null differs depending on allocation proportion, and generally worsens with imbalance between and . Figure 6 illustrates bias across the null under variable cluster sizes with exactly one subject per cluster having x = 1, and figure 7 shows balanced block randomized x under variable cluster sizes. It is not necessary for γ to be more extreme than β, nor must these parameters have the same sign, to observe bias across the null. While regions where the risk ratio exhibits bias across the null become smaller in figure 7 compared to figure 6, in both cases it is still present when γ = 0. Thus, the desirable property of direction-unbiasedness under homogeneous infectiousness (result 3.3 in two-person cluster case) disappears when cluster sizes vary.

Figure 6.

Risk ratio (log) and region of bias across the null as a function of true covariate effects β and γ when cluster size n_i ∼ Pois(μ) + 1 and x is block randomized such that 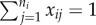for all i. Row (a) shows log[RR], and (b) shows the region of bias across the null. In all plots α = 0.0001, ω = 0.01, N = 500, no subjects are infected at time zero and observation time T_i is chosen such that cumulative incidence when β = 0 and γ = 0 is approximately 0.15.

Figure 7.

Risk ratio (log) and region of bias across the null as a function of true covariate effects β and γ when cluster size n_i ∼ Pois(μ) + 1 and x is block randomized such that 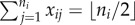for all i. Row (a) shows log[RR], and (b) shows the region of direction bias. In all plots α = 0.0001, ω = 0.01, N = 500, no subjects are infected at time zero, and observation time T_i is chosen such that cumulative incidence when β = 0 and γ = 0 is approximately 0.15.

The duration of observation influences the size of the region in (β, γ) parameter space where the risk ratio exhibits direction bias. Longer observation times increase the region of direction bias under block randomized distribution of x and reduce the size of this region under cluster randomized distribution of x. When the distribution of x is jointly independent, the risk ratio is always direction unbiased; however, increasing the observation time increases the absolute value of the bias. When observation time varies from cluster to cluster, the behaviour of the bias remains similar to the case where all clusters are observed for the same duration, when all other study design parameters are kept the same.

In real-world cohort studies of infectious disease outcomes, researchers often select clusters (e.g. households) based on infection outcomes detected at baseline (sometimes called ‘index’ cases), especially for diseases with low overall prevalence or community force of infection, and risk ratios are computed at follow-up for cluster members susceptible at baseline. Simulation results, given in the electronic supplementary material, show that when subjects are infected at baseline, resulting direction bias depends on the distribution of x among infected and uninfected subjects at baseline.

4. Discussion

We have applied a standard and widely accepted measure of association to outcomes generated by a canonical stochastic model of infectious disease contagion. Infectious disease epidemiologists have warned that simplistic summaries of association can be misleading in the presence of contagion, but none have explained formally how and why these summaries depend on the susceptibility and infectiousness effects of the covariate. The results presented here provide the first formal evidence of the pathological properties of the risk ratio under contagion. When the distribution of a covariate is dependent within clusters and associated with both susceptibility to infection and transmissibility once infected, the risk ratio for that covariate may imply an aggregate effect whose direction is opposite that of its individual-level effect on susceptibility to infection. This form of grossly misleading error may occur even when the covariate effects on susceptibility (β) and infectiousness (γ) have the same sign. For example, a vaccine might protect individuals who receive it from infection (β < 0), and reduce their infectiousness (γ < 0) if they become infected. Clearly such a vaccine should be regarded as helpful, but the risk ratio measured from a block-randomized trial could show RR ≥ 1.

Our findings apply to many other traditional measures of association between a covariate and outcome under contagion. For example, the odds ratio (OR) always indicates the same effect direction as the risk ratio. That is, if RR < 1 then OR < 1, and if RR > 1 then OR > 1. Therefore, the odds ratio can be expected to exhibit bias across the null under contagion whenever the risk ratio does. Likewise, the risk difference, attributable risk, and some measures of vaccine efficacy will suffer from direction bias under precisely the same conditions as the risk ratio.

Characterizing the bias of the risk ratio as an approximation to the susceptibility effect of a covariate gives clues about the performance of the risk ratio in a variety of empirical settings. Under the transmission model described by (2.4), the effect of any covariate x can be represented by a point in the two-dimensional (β, γ) space shown in figures 3–7 according to its true effect on susceptibility (β) and infectiousness (γ). In particular, when x = 1 denotes treatment or vaccination intended to reduce both susceptibility and infectiousness, we would expect its effect to be localized in the lower left quadrant of this space. For example, challenge studies have demonstrated the protective effect of influenza vaccine against infection (β < 0), and against infectiousness via reduction in viral shedding (γ < 0) [55]. We have shown that the risk ratio describing vaccine effect may be biased across the null in this setting (i.e. RR > 1 even though the vaccine protects against susceptibility and infectiousness). The likelihood of such egregious bias depends on disease parameters α and ω, and may be more likely to arise when using a block randomization study design. As another example, antiretroviral drugs may be given to people at risk for HIV infection as ‘pre-exposure prophylaxis’ to reduce susceptibility to HIV infection (β < 0) [56]. But antiretroviral HIV drugs also reduce viral load, and hence diminish infectiousness of people living with HIV (γ < 0) [57]. Susceptibility and infectiousness effect sizes of antiretrovirals are quite large, which could make it less likely that the risk ratio would exhibit direction bias in this setting.

When x is a variable associated with an increased risk of infection, it may be localized in the upper right quadrant of the (β, γ) covariate effect space. For example, a history of injection drug use is a risk factor for both acquiring (β > 0) and transmitting (γ > 0) HIV and hepatitis C infections [58], and the risk ratio may be biased across the null under some study designs, particularly block randomization, in this setting. The region in the (β, γ) space where risk factors exhibit direction bias is generally larger than that for protective covariates conditional on the study design and duration of observation.

Finally, a covariate may have differential effects on susceptibility and infectiousness. It may, for instance, increase susceptibility to infection, but reduce infectiousness, placing it in the lower right quadrant of the (β, γ) space. For example, HIV infection may increase susceptibility to tuberculosis infection and clinical disease (β > 0) [59]. At the same time, studies have shown that people with tuberculosis co-infected with HIV may be less infectious than HIV-negative individuals (γ < 0) [60]. We have shown in simulation that when all subjects in the cluster have the same value of a covariate (e.g. under cluster randomization), the risk ratio may be biased across the null in the regions of the (β, γ) space where the signs of β and γ are opposite. Bias across the null also occurs under some block randomized designs when cluster sizes vary.

The bias of the risk ratio as an approximation to the hazard ratio (2.5) can be readily understood in terms of concepts already familiar to epidemiologists [9]. When the covariate x is dependent within clusters, other subjects' covariate values can be regarded as a common cause of both a given subject's covariate value (via dependence), and that subject's outcome (via contagion). Omitting or failing to condition on this common cause can result in bias. In other words, the relationship between an individual's covariate x and their infection outcome is subject to confounding [9,61], and bias across the null in this scenario is an example of Simpson's paradox [62–65].

The risk ratio is a valid statistical estimand: it summarizes the marginal association between x and infection. However, if investigators are interested in the causal direct (i.e. susceptibility) effect of treatment on the person who receives it [24,28], the risk ratio may give a very misleading estimate of this quantity. One striking consequence of result 3.4 is that bias across the null can occur even when subjects are the same except for their value of x (exchangeable) and treatment (i.e. x = 1) is randomized and balanced within each cluster. The primary factor driving these results is contagion; bias across the null can occur even in the absence of unmodelled within-cluster heterogeneity, imbalance in covariate values, or heterogeneity in contact patterns [27].

Whether severe bias occurs in a particular empirical investigation depends on the epidemiologic features (i.e. α_i(t), ω_ikj(t)) of the disease under study, the distribution of cluster size n_i and observation time T_i, and the distribution of x within clusters. Recently, researchers have called for more comprehensive simulation models to assist in the design of intervention studies for infectious disease outcomes [66]. Simulations such as those presented here may give insight into the anticipated properties of effect measures like the risk ratio under realistic models of infectious disease transmission. When a disease is only weakly contagious within clusters or when within-cluster transmissibility is less than the exogenous force of infection, bias across the null may be less likely to occur. This may be the situation in many cohort studies of infectious diseases. Based on result 3.6, researchers who wish to report the naive risk ratio may avoid direction bias when they can ensure that treatment assignment has independent Bernoulli distribution. The use of the risk ratio may also be justified in observational studies in which covariates of interest are independent or only weakly dependent within clusters. In a wide variety of empirical dependence settings in which infection is only weakly contagious, the risk ratio may be a reasonable estimator of the ratio of instantaneous risks. However, in studies of highly contagious outcomes (e.g. Ebola) in which ω/α is large and the protective effect of the intervention is weak, the risk ratio may exhibit direction bias under some designs.

Our analysis is subject to several limitations. First, we have focused primarily on the conditions under which the risk ratio can exhibit the most misleading form of bias—bias across the null. But even when direction-unbiasedness holds, the risk ratio is almost always a biased approximation of the covariate effect on susceptibility [27,28,31,34,67]. When the magnitude of an estimated risk ratio is important for decision-making, a more detailed study of bias may be warranted. Second, the transmission model in this analysis is represented by a standard stochastic susceptible–infective model with subject-specific covariates and an exogenous force of infection. This setting provides a simple generative model that incorporates features of infectious disease contagion relevant to the properties of the risk ratio. However, this model does not capture several important aspects of infectious disease dynamics, including recovery, removal, re-infection or multiple infections. Further investigation is necessary to determine properties of the risk ratio under more complex assumptions about disease dynamics.

Finally, the purpose of this work is to explain why the risk ratio may not be a satisfactory measure of association for epidemiologic studies of infectious disease outcomes. We have not addressed correction of the risk ratio, nor proposed alternative strategies for estimating the hazard ratio. Fortunately, epidemiologists have developed deterministic and stochastic models of infectious disease transmission in groups that take exposure to infection into account [37,43,44]. Several researchers have developed inferential approaches that capture infectious disease transmission dynamics and permit adjustment for individual-level factors [36,37,68–70]. Some analyses of contagious outcomes adjust for variables that may be correlated with exposure to infectiousness [71–74]. It remains an open question whether standard regression adjustment using a summary of infection outcomes of other individuals can deliver risk ratio estimates that are direction-unbiased.

Data accessibility

This paper uses only simulated data. Electronic supplementary material includes the file simulation_functions.R, which is an R code that implements simulation; the file replication_code.pdf, which is an R markdown file that provides examples of the simulation functions used to produce figures; and the file rr_bias_supplement.pdf that provides formal description and proofs of analytic results, and a summary of simulation results.

Authors' contributions

O.M., T.C. and F.W.C. conceived and designed the study and reviewed and revised the paper and gave final approval for publication. O.M. and F.W.C. derived the technical results. O.M. wrote the simulation code, conducted the simulations and wrote the majority of the paper.

Competing interests

We have no competing interests.

Funding

This work was supported by grants R36 DA042643 from NIDA, R01 DA015612 from NIDA, DP2 OD022614 from NICHD, R01 AI112438-03 from NIAID, the Yale Center for Clinical Investigation, and the Center for Interdisciplinary Research on AIDS. Computing support was provided by the Yale Center for Research Computing and the W. M. Keck Biotechnology Laboratory, as well as grant nos. RR19895 and RR029676-01 from NIH.