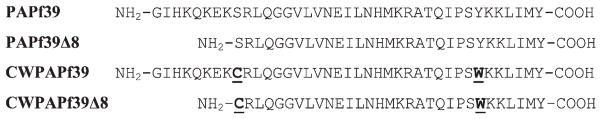Abstract
The 39-residue fragment of human prostatic acidic phosphatase (PAP) is found in high concentrations in semen and easily form fibrils. Previous work has shown that fibrillization is accelerated with a deletion of the first 8, mostly charged residues and it was hypothesized that fibrillization depended on the dynamics of these peptides. To test this hypothesis we have measured the intramolecular diffusion of the full length and 8-residue deletion peptides at two different pHs and found a correlation with fibrillization lag time. These results can be explained by a simple kinetic model of the early stages of aggregation in which oligomerization is controlled by the rate of peptide reconfiguration.
GRAPHICAL ABSTRACT
1. Introduction
Amyloid fibrils are pathogenically associated with a range of debilitating human diseases such as Alzheimer’s disease, Parkinson’s disease, prion diseases, type II diabetes, cancer, systemic amyloidosis, among others [1–3]. The assembly of monomers into fibrils occurs through a multi-step seeding nucleation process that sometimes involves oligomeric intermediates and protofibril states. A combination of theoretical and computational studies with experiments has provided a deeper understanding of the kinetics and thermodynamics underlying the mechanism for this process [4]. Although the exact series of molecular events that lead to this transformation is unknown, it has been proposed that a preference of monomers towards a certain conformational state is a prerequisite en route to fibril formation. Understanding this process is essential for designing therapeutics that target amyloid formation at early stages of the disease [3]. In this sense, the conformational diversity of the monomers is of particular interest, as it is the starting point for modeling any nucleation pathway. For amyloid fibrils formed by shorter polypeptides, such as Aβ40/42, insulin, IAPP, gelsolin or PAPf39 analyzed here, monomers exhibit large degrees of conformational heterogeneity (i.e. are “unstructured”) in solution. Most current experimental methods have many inherent limitations in characterizing conformational heterogeneity and dynamics of such unstructured peptides.
The relatively recently developed method of intramolecular contact quenching provides a much different view of the heterogeneity of unfolded proteins. Measuring the rate of tryptophan triplet state quenching by cysteine on the same peptide provides us with a measure of the distribution of Trp-Cys distances and the coefficient of intramolecular diffusion. Many studies of different unfolded proteins have revealed a wide range of diffusion coefficients depending on sequence, pH and other solvent conditions [5–11]. For example, the intramolecular diffusion coefficient of the Alzheimer’s peptide lacking residues 41 and 42 (Aβ40) was five times faster than the Alzheimer’s peptide containing those residues (Aβ42) [12]. This 5-fold change in intramolecular diffusion rate correlates with the difference in lag time of aggregation for Aβ40 vs. Aβ42, which suggests that aggregation is kinetically controlled by the reconfiguration of the monomer. If reconfiguration of the monomer is much faster than the rate of bimolecular association, aggregation is unlikely because one of the monomers can escape an encounter complex before stabilizing interactions can be made. However, if reconfiguration is on the same time scale as biomolecular association, then aggregation is more likely [13].
In this study we employ Trp-Cys triplet state quenching [14] to investigate the reconfiguration dynamics of PAPf39 (PAP fragment of 39 amino acid residues long) peptide corresponding to residues 248 to 286 of human prostatic acidic phosphatase (PAP). PAP is expressed in semen at high concentrations (>4 mg/ml) and following degradation by an unknown mechanism generates significant levels of PAPf39 [15]. PAPf39 has a tendency to readily form fibrils and it has been shown that these fibrils, instead of the PAPf39 monomer, appear to boost HIV infectivity in cultured cells [15–17]. We have previously characterized the mechanism of fibril formation by the PAPf39 peptide [18–20]. The effects of environmental factors such as agitation, seeding, pH, and ionic strength on the aggregation of this peptide were investigated using a battery of biophysical methods. It was found that PAPf39 peptide fibril formation follows a typical nucleation-dependent elongation mechanism at neutral pH but completely abolished or significantly slowed down at pH below 6 [20]. Using hydrogen exchange mass spectroscopy, the sequence of PAPf39 comprising the fibrillar core was identified and mapped to the central and C-terminal region (residues 13–39) of the peptide. Interestingly PAPf39 variants with the 8 and 13 residue N-terminal deletion (PAPf39Δ8 and PAPf39Δ13) form fibrils both at neutral pH and pH below 6. Additional experiments exploring other factors that can contribute to the observed pH dependence (i.e. difference in structure/morphology of the fibrils, electrostatic repulsion, etc.) led to the hypothesis that structural dynamics of the peptide monomers at different pHs may be responsible for such pH dependence of fibrillization [18]. This hypothesis was tested in this work by measuring Trp-Cys contact quenching within PAPf39 and PAPf39Δ8 at neutral and low pH. We find a correlation between the fibrillization lag time and intramolecular diffusion, suggesting that the first step of aggregation is kinetically controlled by monomer reconfiguration.
2. Experimental section
2.1. Peptides, fibrillization assays and AFM
PAPf39, PAPf39Δ8, CWPAPf39, CWPAPf39Δ8 were synthesized at the Penn State College of Medicine Macromolecular Core Facility using standard Fmoc chemistry. Peptides were dissolved in 0.05% trifluoroacetic acid (TFA) and purified on a C18 reverse-phase HPLC column (Discovery Bio Wide pore C18 10 μm, 25 cm by 10 mm, Supelco Sigma-Aldrich, Bellefonte, PA) using a methanol gradient in the presence of 0.05% TFA. For each peptide, the fractions containing the pure peptide were pooled and subjected to 3–5 cycles of lyophilization and resuspension in Milli-Q water to remove residual TFA. The mass of each peptide was confirmed using matrix-assisted laser desorption/ionization (MALDI) mass spectrometry. Concentrations of the peptides in solution were determined spectrophotometrically at 280 nm using a molar extinction coefficient of 2980 M−1 cm−1 for the PAPf39 and PAPf39Δ8 peptides, and 6990 M−1 cm−1 for the CWPAPf39 and CWPAPf39Δ8 peptides. Fibrillization kinetics assays were followed by monitoring the changes in thioflavin T (ThT) fluorescence as described in detail elsewhere [18–20]. Atomic force microscopy (AFM) images were acquired using AC tapping mode in air at room temperature and humidity on a MFP-3D, AFM (Asylum Research, Santa Barbara, CA), using a silicon coated cantilever (AC240TS, Olympus America Inc., Center Valley, PA) as previously described [18,21].
2.2. Trp-Cys contact quenching
Trp-Cys quenching experiments were carried out with 30 μMPAPf39 peptide variants either in 18 mM sodium phosphate (pH 7.0) or in 25 mM sodium acetate (pH 3.5) buffer, at different viscosities (0, 10, 20, or 30% sucrose (w/w)), and at five different temperatures (ranging from 0 to 40 °C). For each experiment, the desired solutions containing buffer, sucrose, and 1 mM TCEP (to prevent disulfide bond formation) were bubbled with N2O for 1 h to eliminate oxygen and scavenge solvated electrons created in the UV laser pulse. Immediately prior to the data acquisition, lyophilized peptide aliquots were re-suspended in 300 μL of 3.5 mM HCl, pH 2.5 to prepare a 300 μM stock of monomeric peptide. Freshly prepared peptide stocks were then added into the above mentioned degassed buffer solutions, and the mixtures were further degassed for 10 min on ice.
Contact quenching rates were measured by following the tryptophan triplet lifetime decay, due to quenching Cys in close proximity, using an in-house instrument described previously [14]. Briefly, the tryptophan triplet is populated simultaneously with the singlet state by a 10 ns laser pulse at 289 nm. The triplet state population is monitored by optical absorption at 450 nm(improving on previous measurements, the probe light is provided by 500mWdiode laser). The decay in optical absorption was detected by a silicon diode, compared to a reference beam, amplified 50× and recorded on 2 digital oscilloscopes covering a range from 1 ns to 10 ms. The lifetime of the Trp triplet state in water is ~40 μs, but can be much shorter in the presence of cysteine. The temperature was controlled using a Peltier temperature controller. Solvent viscosities at individual temperatures were measured with a viscometer (Brookfield Engineering, Middleboro, MA).
3. Results and discussion
The sequence of PAPf39 and PAPf39Δ8 does not contain Cys or Trp residues (Fig. 1). So in order to perform these experiments the sequence needs to be modified to incorporate these residues. Two criteria were used for identifying the sites for substitutions. First requirement is that the sequence separation must be large enough to increase the probability of Cys and Trp coming into direct contact. Previous experiments have shown that sequence separation on the order of 15–20 residues between Cys and Trp appears to be optimal [22]. Second, substitutions should have minimal possible effect on the fibrillization properties. For PAPf39 and PAPf39Δ8 peptides, considering their length, there was one possible solution: we replaced sterically similar Ser9 with Cys and aromatic Tyr27 with Trp. The sequences of the resulting CWPAPf39 and CWPAPf39Δ8 peptides are shown in Fig. 1.
Fig. 1.
Sequences of the studied peptides. Sites of substitutions for Cys-Trp pair in CW peptides are underlined.
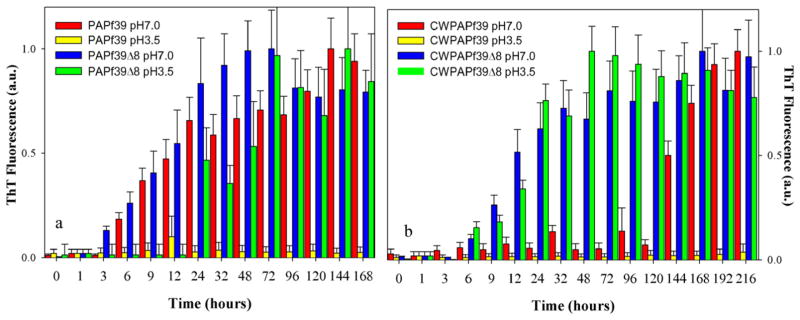
The CWPAPf39 and CWPAPf39Δ8 peptides, designed with these constraints, and PAPf39 and PAPf39Δ8 qualitatively show similar fibrillization patterns. PAPf39 and CWPAPf39 form fibrils at pH 7 but not at pH 3.5, while PAPf39Δ1-8 and CWPAPf39Δ8 fibrillate at both pH (Fig. 2). However, at pH 7, CWPAPf39 has much longer lag phase (~4–5 days) than wild type PAPf39 (<1 day). Similarly, at pH 7, the lag phase for CWPAPf39Δ8 (~6 h) is slightly longer than the lag phase for PAPf39Δ8 (~3 h). The results of fibrillization kinetics are further supported by AFM (Supplementary Fig. S1) which show that the fibrils formed by all four peptides have similar morphologies.
Fig. 2.
Fibrillization kinetics for a) PAPf39 and PAPf39Δ8 (wild-type sequences) and b) CWPAPf39 and CWPAPf39Δ8 at two different pH. See Materials and Methods for experimental details.
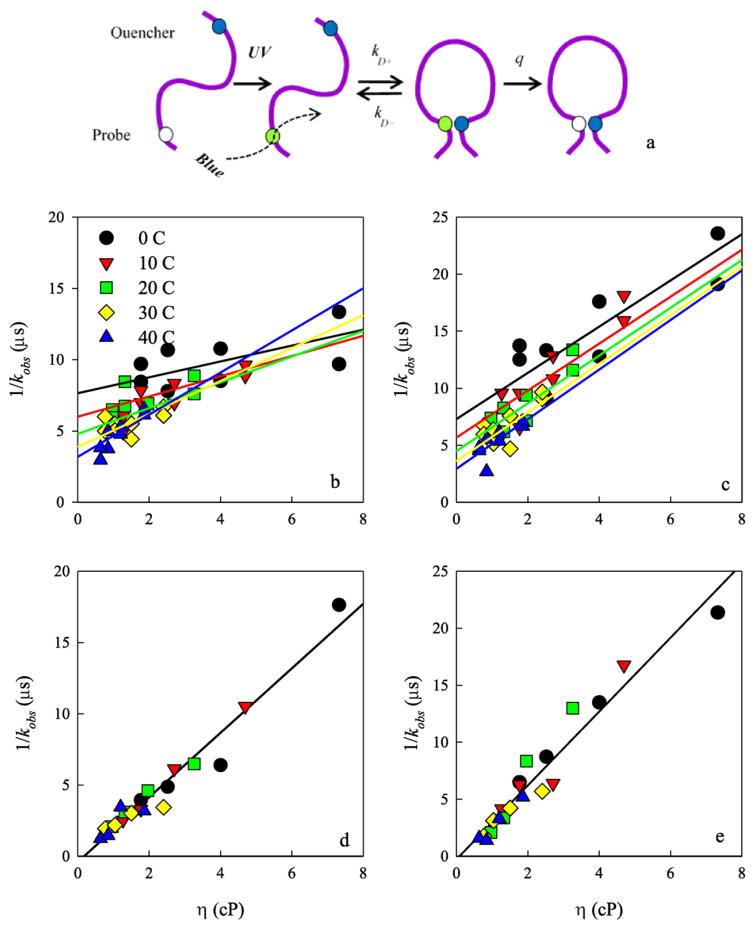
Trp-Cys contact quenching rates were measured for the variant full length CWPAPf39 and CWPAPf39Δ8 peptides. The general scheme of the experiment is shown in Fig. 3a. Tryptophan is excited to a long-lived excited state that typically has a lifetime of 40 μs in water but can be orders of magnitude shorter if it comes into contact with cysteine [14]. Cysteine has a much higher quenching efficiency than any other amino acids so that a peptide with one Trp and one Cys in the sequence will measure loop formation between those two positions [23]. The measurement can be modeled with a two-step process by which the Trp and Cys diffuse towards each other and then the Cys quenches the Trp only when in close contact. The observed rate of the triplet state is given by
Fig. 3.
a) Schematic of the Trp-Cys contact quenching measurement. (b–e) Observed tryptophan triplet lifetimes at various viscosities and temperatures. b) Full length CWPAPf39 peptide at pH 7. c) Full length CWPAPf39 peptide at pH 3.5. d) CWPAPf39Δ8 peptide at pH 7. e) CWPAPf39Δ8 peptide at pH 3.5. In the top panels, the data were globally fit to the temperature-dependent model described in the text. In the bottom panels, the data at all temperatures were fit to a single line.
| (1) |
The equation can be further rearranged
| (2) |
where the reaction-limited (kR) rate depends only on temperature, and the diffusion-limited (kD+) rate depends on both temperature and viscosity (η) of the solution. Measurements at various viscosities at the same temperature can be fitted to a line in which the intercept is 1/kR and the slope is 1/ηkD+. Fig. 3b–e shows the Trp triplet state decay lifetimes vs. viscosities at different temperatures for each peptide. For the CWPAPf39 peptide, lifetimes for different temperatures lie on distinct lines with respect to viscosity. Therefore, the data were globally fit to a model where the intercepts and slopes have an Arrhenius dependence on temperature given by
| (3) |
| (4) |
where T0=293 K and R is the gas constant. E1, E2, kR0, and kD+0 are the fitting parameters and are shown in Table 1. The data in Fig. 4 were calculated from Eqs. (3) and (4) and the error bars were calculated from the standard errors of linear fits given by:
| (5) |
| (6) |
| (7) |
| (8) |
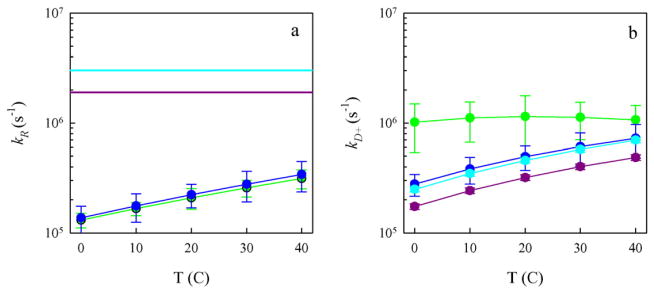
where N is the number of data points per line, y is the calculated lifetime and 1/kobs is the measured lifetime. The reaction-limited rates for CWPAPf39 are plotted in Fig. 4a vs. temperature. For the CWPAPf39Δ8 peptide, the lifetimes at different temperatures converge, so all the data is fit to a single, temperature-independent line with an intercept consistent with 1/kR = 0. From the error of the fit, the reaction-limited rates are plotted as lower limits in Fig. 4a. The actual diffusion-limited rates for both peptides were plotted with respect to temperature in Fig. 4b.
Table 1.
Fit parameters for lines plotted in Fig. 3b and c.
| Peptide | pH | E1 (kcal/mol) | E2 (kcal/K) | kR0 (s−1) | kD + 0 (cP s−1) |
|---|---|---|---|---|---|
| CWPAPf39 | 7 | 3.6995 | −0.0278 | 208,545 | 1,106,369 |
| CWPAPf39 | 3.5 | 3.8554 | −0.0052 | 222,998 | 477,639 |
Fig. 4.
Reaction-limited (a) and diffusion-limited (b) rates for the full-length CWPAPf39 peptide at pH 7 (green), full-length CWPAPf39 peptide at pH 3.5 (blue), CWPAPf39Δ8 peptide at pH 7 (cyan), and CWPAPf39Δ8 peptide at pH 3.5 (purple). The rates and error bars were determined from the linear fits in Fig. 3. The horizontal lines in (a) were determined from the error in the intercept of Fig. 3c and d and represent lower limits of the reaction-limited rates. The diffusion-limited rates in (b) have been normalized by the viscosity of water at each temperature. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
To further understand these measured rates, we used a theory by Szabo, Schulten and Schulten [24] which models intramolecular motion as diffusion on a one-dimensional potential which is determined by the probability distribution of Trp-Cys distances, P(r). From this theory, the reaction-limited and diffusion-limited rates are given by [25]
| (9) |
| (10) |
where D is the intramolecular diffusion coefficient, r is the distance between Trp and Cys, dα is the distance of closest approach and lc is the contour length of the protein between Trp and Cys. Generally, kR and kD+ are both inversely proportional to the average volume of the chain and kD+ is proportional to D. The distance-dependent quenching rate of Cys on Trp, q(r), has been determined experimentally to be extremely close-range [22].
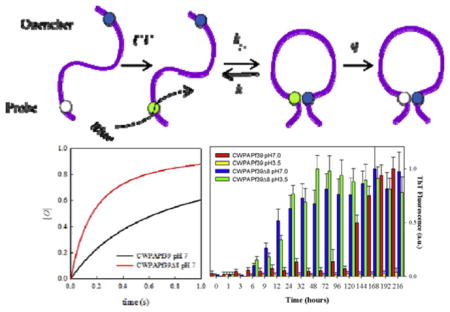
To determine the diffusion coefficient, D, we require a probability distribution of Trp-Cys distances, P(r), which accurately reproduces the measured reaction-limited rate using Eq. (9). This distribution can be obtained from a number of methods, including polymer models and molecular dynamics simulations. We conducted MD simulations of both the full length and truncated peptides at neutral and low pH and measured the Trp-Cys distance every 1 ns to create a histogram of distances. Using Eq. (9) and dα = 5 Å we calculate reaction-limited rates and compare them to the measured values in Fig. 5. While the measured and calculated rates had reasonable qualitative agreement, the quantitative agreement for the truncated peptides was not good enough to calculate diffusion coefficients using Eq. (9) accurately. Therefore we turn to a polymer model, the energy re-weighted wormlike chain (WLC) [26]. This model starts with 20 million chains constructed by a Monte Carlo method with a persistence length of 4 Å and an excluded volume diameter of 4 Å. This probability distribution produced a set of expanded chains that had reaction-limited rates (using Eq. (3)) lower than expected. Therefore, we reweighted the distribution to yield conformations that are more compact by assigning an energy (EH) for each chain based on favorable close-range interactions between residues of similar hydrophobicity using the following:
| (11) |
where σ is an adjustable weighting factor, and the hydropathy, h, for each residue in the sequence is given using the Miyazawa-Jernigan scale. We assumed that two residues with h values within 30% of each other contribute to hydrophobic or hydrophilic interactions which reduce the free energy of the system thereby making conformations containing such interactions favorable. We also apply a distance cut-off to EH such that EH=0 for |ri − rj | > 6.5 Å.
Fig. 5.
Comparison of measured and calculated values of kR for both peptides at 40 °C. For the re-weighted WLC model (green, yellow and blue bars), γ=5andσ=3 and the charge on the glutamic acid residue was adjusted as indicated. The charges on other residues were assigned as expected at pH 7 and pH 3.5. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
To account for charge–charge interactions, we calculated the charge, q, on each residue at the appropriate pH using the Henderson-Hasselbach equation and calculate the Coulombic energy
| (12) |
where γ is an adjustable weighting factor for the Coulombic interactions. Using the total interaction energy ETOT = EH + Ee, we can reweight the probability distribution P(r) to yield a new distribution Z(r),
| (13) |
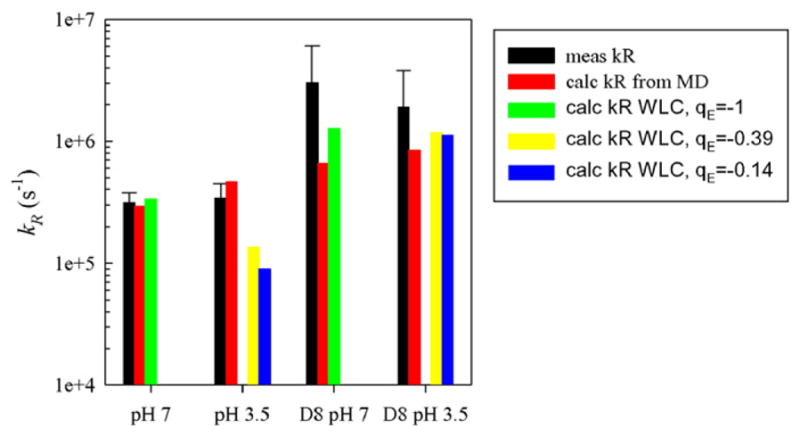
The reaction-limited rate was calculated using Eq. (3) and substituting Z(r) for P(r). The adjustable parameters, σ and γ, can be chosen such that the calculated kR matches the measured kR. However, for any peptide and pH we only have one reaction-limited rate and cannot constrain both parameters simultaneously. Therefore, we used the ratio of two rates to constrain γ and then set σ to exactly match each rate. An exploration of different values of σ and γ showed that the difference in sequence between the full length and Δ8 peptides only results in changes of Ee, (σ = 0) not EH (γ = 0). Fig. 6 shows this effect on the resulting probability distributions. Thus, the deletion of the charged amino acids (three lysines and one glutamic acid) leads to a significant increase in the reaction-limited rate and compaction of the peptide. Using the ratio of kR for CWPAPf39 and CWPAPf39Δ8 at pH 7 (~10×) we find γ=5. Setting σ= 3, a value that is typical for many sequences [10,26], gave rates that agreed well with the measured reaction-limited rates at 40 °C, as shown in Fig. 5. We assume that EH does not depend on pH as Ee obviously does. Comparing the full length peptide at pH 7 and pH 3.5, the lower pH expands the chain slightly, but not as much as Δ8 deletion compacts it. It is also dependent on the exact average partial charge assigned to the glutamic acid, qE. At pH 3.5, we expect the fractional charge on the Glu to be approximately qE ~ −0.15 (i.e. pKa ~ 4.3 see ref. [27]). However, if the charge is larger (i.e. pKa ~3.8 which will be consistent with a high number of basic groups in the peptide sequence), qE ~ −0.40, the reaction-limited rate is approximately two times higher, in better agreement with the measured value. Therefore it is possible the pKa of glutamic acids are lower in the sequence context of this peptide than the intrinsic pKa for this amino acid in solution.
Fig. 6.
Energy re-weighted probability distributions for both peptides calculated as discussed in the text for values of the adjustable parameters as indicated in the legend. For all distributions, the pH is 7 (qE ~ −1).
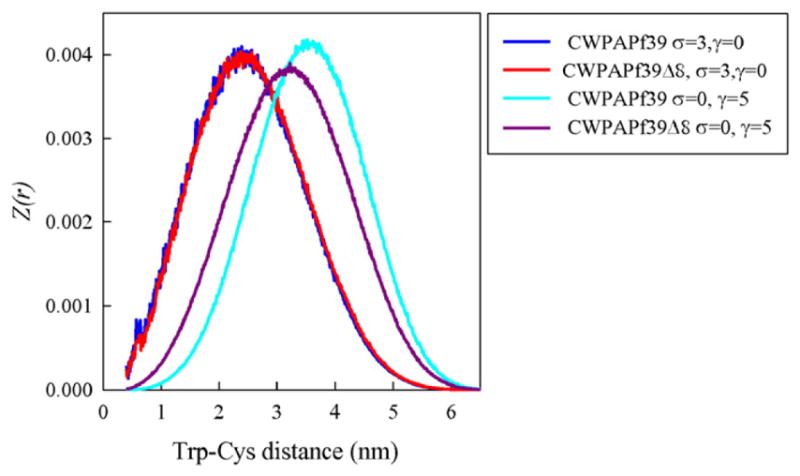
Finally, using the probability distributions that best match the experimentally derived reaction-limited rate (σ = 3, γ = 5 for all measurements except the full length peptide at pH 3.5 where σ = 3.8, γ = 5), the diffusion coefficient is calculated using Eq. (10). Fig. 7 shows the diffusion coefficients (D) calculated based on the probability distributions from the WLC model and the MD simulations. There is good qualitative agreement between the two methods, indicating that the choice of how the probability distribution is calculated does not strongly affect the diffusion coefficient, as long as there is reasonable agreement between measured and calculated reaction-limited rates. There is a large difference between the diffusion coefficients for the CWPAPf39Δ8 peptide compared to the full length CWPAPf39, particularly when comparing the values calculated with the re-weighted WLC distributions. This suggests that deleting the first eight mostly charged residues, compacts and slows intramolecular diffusion in the chain.
Fig. 7.
Calculated diffusion coefficients at T = 40 °C using the best energy re-weighted probability distributions (black) and the probability distributions produced by MD (grey). Error bars are calculated as proportional to the measured error in kD+.
These diffusion coefficients inversely correlate with the lag time of fibrillization: the truncated CWPAPf39Δ8 peptide, which has relatively slow diffusion coefficients at both pH 7 and 3.5, aggregates at least ten times faster than the full length peptide. This difference can be understood if one thinks of the first step of aggregation as being kinetically controlled by the reconfiguration of the monomer. The monomer population can be divided into two subpopulations, M and M* where M* is the ensemble of conformations prone to aggregation (i.e. having hydrophobic residues exposed to solvent). These subpopulations reconfigure at a rate proportional to the diffusion coefficient. If two M* come into close contact, an encounter complex is formed which may be broken if one M* reconfigures to M. However if the encounter complex is sufficiently stable, eventually a stable oligomer, O, is formed which may eventually nucleate a fibril, F. There are many ways for fibrillization to proceed from the oligomer, which will not be addressed here, but the simplest model to form an oligomer and incorporating the monomer dynamics is given by [8]
| (i) |
This model can be numerically solved. The concentration of peptide in the ThT experiments was ~500 μM, therefore we can assume Fick diffusion, giving kbi=1.9 × 106 s−1. kO is not directly measureable but for the purposes of modeling we assume that it is much lower than kbi and reconfiguration rates and is not affected by the pH or the length of the peptide. These assumptions imply that the oligomer formation rate will be similar for all conditions and is irrelevant to the comparison between conditions. Therefore we choose kO=100 s−1 for computational speed. The reconfiguration rate, k1 + k−1=D/<r > 2, can be calculated from the diffusion coefficients in Fig. 7 and the average distance from the MD simulations, <r > ~3.4 nm. For the full length peptide at pH 7, k1 + k−1 = 6.3 × 106 s−1 and for the CWPAPf39Δ8 peptide, k1+k−1=1.2×106 s−1. To separate k1 fromk−1, we need the equilibrium K=[M*]/[M]=k1/k−1, which can be estimated from the energy-reweighted WLC model as K=e−ΔETOT/kT ~0.2 for all conditions. Fig. 8 shows the formation of O vs. time for the full length CWPAPf39 and CWPAPf39Δ8 peptides at pH 7. Fitting these traces to second-order formation kinetics yields an oligomer formation rate of 2.8 s−1 for the full length CWPAPf39 peptide and 11.3 s−1 for CWPAPf39Δ8 peptide. This four-fold increase in oligomerization does not quite account for the ten-fold increase in fibrillization lag time, but since we were only able to measure the lower limit of kR and an upper limit of D for Δ8, this increase could be larger. It is also possible that there is a difference in the nucleation rate of fibrillization between the full length CWPAPf39 and CWPAPf39Δ8 peptides, independent of the monomer reconfiguration rate. Similarly, the difference in fibrillization for the full length peptide at pH 7 vs. pH 3.5, despite similar reconfiguration rates, could be due to the slow structural transformations of the oligomer during nucleation, not reconfiguration of the monomer.
Fig. 8.
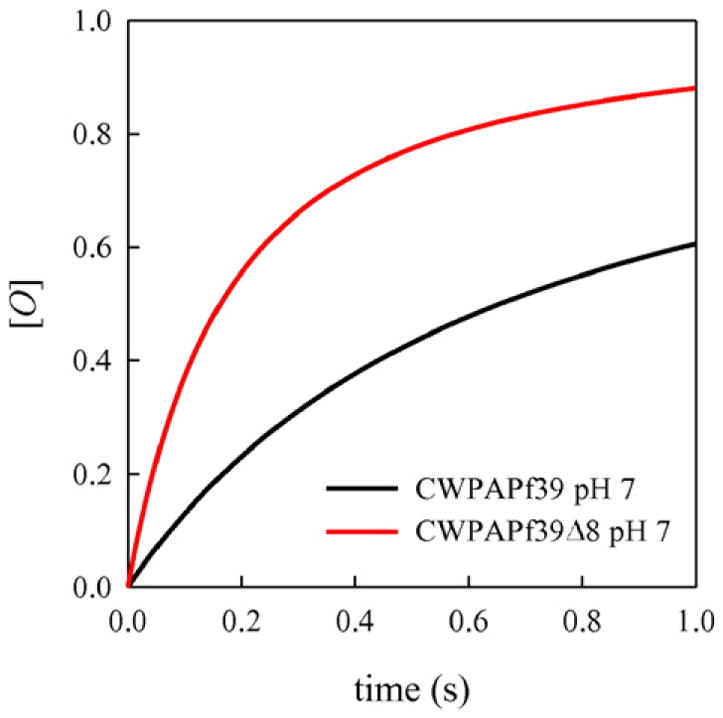
Formation of the oligomer [O] from scheme (i) using the rates indicated in the text.
3.1. Concluding remarks
In this work we have shown distinct dynamic differences in the PAPf39 peptide with the deletion of the first eight residues. The difference in intramolecular diffusion appears to be due to the deletion of charged residues, both positive and negative in the N-terminal region of the peptide. Changing the pH, which partially deprotonates the glutamic acids, does not seem to have as big an effect as the deletions in the full length peptide. Previously [18] and in this work, we demonstrated that aggregation is accelerated when the first eight residues of this peptide are deleted. We also showed that aggregation is slowed at low pH, but we did not observe significant differences in the diffusion coefficient at pH 7 and pH 3.5. However, since the lag time of fibril formation for CWPAPf39 is ten times slower than PAPf39 at pH 7 and the lag time is fairly similar for CWPAPf39Δ8 and PAPf39Δ8, regardless of pH, this immeasurable difference in diffusion coefficients is not surprising. With the caveat that the inclusion of the Cys/Trp residues in the peptides (necessary for the experiments) affected the fibrillization kinetics, the results presented here support the previous hypothesis that differences in the conformational dynamics between PAPf39 and PAPf39Δ8 caused the difference in the fibrillization kinetics of these two peptides at pH 7 [18]. Admittedly, the results presented here provide little support for the notion that the difference in conformational dynamics of these two peptides also leads to the difference in the pH dependence of fibrillization, namely that PAPf39 peptide fails to form fibrils at low pH while PAPf39Δ8 readily forms fibrils at low pH, albeit with longer lag phase than at pH 7.0. However, the pH-dependences of fibril formation suggest that residues that change ionization state upon titration from pH 7 to pH 3.5 may be responsible for structural transformations of the oligomer during nucleation. Investigation into these effects is currently in progress.
Atomic force microscopy images of fibrillized peptides. Supplementary data associated with this article can be found in the online version, at http://dx.doi.org/10.1016/j.bpc.2016.06.004.
HIGHLIGHTS.
The PAPf39 peptide is expressed in semen, is known to aggregate and the fibrils enhance HIV infectivity.
Previous work showed that an 8-residue N-terminal deletion aggregates much faster than the full-length peptide.
Measurement of intramolecular diffusion shows that the full-length peptide diffuses much faster than the truncated peptide.
The measured differences are explained by a kinetic model in which aggregation is controlled by peptide reconfiguration.
Acknowledgments
This work was supported by grants from the National Institutes of Health (R21GM101134 to G.I.M. and R01GM100908 to L.J.L).
Footnotes
Notes
The authors declare no competing financial interest.
References
- 1.Buxbaum JN, Linke RP. A molecular history of the amyloidoses. J Mol Biol. 2012;421:142–159. doi: 10.1016/j.jmb.2012.01.024. [DOI] [PubMed] [Google Scholar]
- 2.Chiti F, Dobson CM. Protein misfolding, functional amyloid, and human disease. Annu Rev Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 3.Knowles TP, Vendruscolo M, Dobson CM. The amyloid state and its association with protein misfolding diseases. Nat Rev Mol Cell Biol. 2014;15:384–396. doi: 10.1038/nrm3810. [DOI] [PubMed] [Google Scholar]
- 4.Radford SE, Weissman JS. Special issue: the molecular and cellular mechanisms of amyloidosis. J Mol Biol. 2012;421:139–141. doi: 10.1016/j.jmb.2012.05.042. [DOI] [PubMed] [Google Scholar]
- 5.Eaton WA, Munoz V, Hagen SJ, Jas GS, Lapidus LJ, Henry ER, Hofrichter J. Fast kinetics and mechanisms in protein folding. Annu Rev Biophys Biomol Struct. 2000;29:327–359. doi: 10.1146/annurev.biophys.29.1.327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Singh VR, Kopka M, Chen Y, Wedemeyer WJ, Lapidus LJ. Dynamic similarity of the unfolded states of proteins L and G. Biochemistry. 2007;46:10046–10054. doi: 10.1021/bi700270j. [DOI] [PubMed] [Google Scholar]
- 7.Singh VR, Lapidus LJ. The intrinsic stiffness of polyglutamine peptides. J Phys Chem B. 2008;112:13172–13176. doi: 10.1021/jp805636p. [DOI] [PubMed] [Google Scholar]
- 8.Chen Y, Parrini C, Taddei N, Lapidus LJ. Conformational properties of unfolded HypF-N. J Phys Chem B. 2009;113:16209–16213. doi: 10.1021/jp904189b. [DOI] [PubMed] [Google Scholar]
- 9.Waldauer SA, Bakajin O, Lapidus LJ. Extremely slow intramolecular diffusion in unfolded protein L. Proc Natl Acad Sci. 2010;107:13713–13717. doi: 10.1073/pnas.1005415107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ahmad B, Chen Y, Lapidus LJ. Aggregation of α-synuclein is kinetically controlled by intramolecular diffusion. Proc Natl Acad Sci. 2012;109:2336–2341. doi: 10.1073/pnas.1109526109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Acharya S, Saha S, Ahmad B, Lapidus LJ. Effects of mutations on the reconfiguration rate of α-synuclein. J Phys Chem B. 2015 doi: 10.1021/acs.jpcb.5b10136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Acharya S, Srivastava KR, Lapidus LJ. Monomer dynamics of aβ and kinetic control of early aggregation in Alzheimer’s disease. J Biol Chem. 2016 doi: 10.1002/cphc.201600706. (submitted for publication) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lapidus LJ. Understanding protein aggregation from the view of monomer dynamics. Mol BioSyst. 2013;9:29–35. doi: 10.1039/c2mb25334h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lapidus LJ, Eaton WA, Hofrichter J. Measuring the rate of intramolecular contact formation in polypeptides. Proc Natl Acad Sci U S A. 2000;97:7220–7225. doi: 10.1073/pnas.97.13.7220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Munch J, Rucker E, Standker L, Adermann K, Goffinet C, Schindler M, Wildum S, Chinnadurai R, Rajan D, Specht A, Gimenez-Gallego G, Sanchez PC, Fowler DM, Koulov A, Kelly JW, Mothes W, Grivel JC, Margolis L, Keppler OT, Forssmann WG, Kirchhoff F. Semen-derived amyloid fibrils drastically enhance HIV infection. Cell. 2007;131:1059–1071. doi: 10.1016/j.cell.2007.10.014. [DOI] [PubMed] [Google Scholar]
- 16.Arnold F, Schnell J, Zirafi O, Sturzel C, Meier C, Weil T, Standker L, Forssmann WG, Roan NR, Greene WC, Kirchhoff F, Munch J. Naturally occurring fragments from two distinct regions of the prostatic acid phosphatase form amyloidogenic enhancers of HIV infection. J Virol. 2012;86:1244–1249. doi: 10.1128/JVI.06121-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Usmani SM, Zirafi O, Muller JA, Sandi-Monroy NL, Yadav JK, Meier C, Weil T, Roan NR, Greene WC, Walther P, Nilsson KP, Hammarstrom P, Wetzel R, Pilcher CD, Gagsteiger F, Fandrich M, Kirchhoff F, Munch J. Direct visualization of HIV-enhancing endogenous amyloid fibrils in human semen. Nat Commun. 2014;5:3508. doi: 10.1038/ncomms4508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.French KC, Makhatadze GI. Core sequence of PAPf39 amyloid fibrils and mechanism of pH-dependent fibril formation: the role of monomer conformation. Biochemistry. 2012;51:10127–10136. doi: 10.1021/bi301406d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shanmuganathan A, Bishop AC, French KC, McCallum SA, Makhatadze GI. Bacterial expression and purification of the amyloidogenic peptide PAPf39 for multidimensional NMR spectroscopy. Protein Expr Purif. 2013;88:196–200. doi: 10.1016/j.pep.2013.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ye Z, French KC, Popova LA, Lednev IK, Lopez MM, Makhatadze GI. Mechanism of fibril formation by a 39-residue peptide (PAPf39) from human prostatic acidic phosphatase. Biochemistry. 2009;48:11582–11591. doi: 10.1021/bi901709j. [DOI] [PubMed] [Google Scholar]
- 21.French KC, Roan NR, Makhatadze GI. Structural characterization of semen coagulum- derived SEM1(86-107) amyloid fibrils that enhance HIV-1 infection. Biochemistry. 2014;53:3267–3277. doi: 10.1021/bi500427r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lapidus LJ, Eaton WA, Hofrichter J. Dynamics of intramolecular contact formation in polypeptides: distance dependence of quenching rates in a room-temperature glass. Phys Rev Lett. 2001;87:4. doi: 10.1103/PhysRevLett.87.258101. [DOI] [PubMed] [Google Scholar]
- 23.Gonnelli M, Strambini GB. Phosphorescence lifetime of tryptophan in proteins. Biochemistry. 1995;34:13847–13857. doi: 10.1021/bi00042a017. [DOI] [PubMed] [Google Scholar]
- 24.Szabo A, Schulten K, Schulten Z. 1st passage time approach to diffusion controlled reactions. J Chem Phys. 1980;72:4350–4357. [Google Scholar]
- 25.Lapidus LJ, Steinbach PJ, Eaton WA, Szabo A, Hofrichter J. Effects of chain stiffnesss on the dynamics of loop formation in polypeptides. Appendiz: testing a one dimentional diffusion model for peptide dynamics. J Phys Chem B. 2002;106:11628–11640. [Google Scholar]
- 26.Chen Y, Wedemeyer WJ, Lapidus LJ. A general polymer model of unfolded proteins under folding conditions. J Phys Chem B. 2010;114:15969–15975. doi: 10.1021/jp104746g. [DOI] [PubMed] [Google Scholar]
- 27.Thurlkill RL, Grimsley GR, Scholtz JM, Pace CN. pK values of the ionizable groups of proteins. Protein Sci. 2006;15:1214–1218. doi: 10.1110/ps.051840806. [DOI] [PMC free article] [PubMed] [Google Scholar]