Abstract
In mucosal drug delivery, two design goals are desirable: 1) insure drug passage through the mucosal barrier to the epithelium prior to drug removal from the respective organ via mucus clearance; and 2) design carrier particles to achieve a prescribed arrival time and drug uptake schedule at the epithelium. Both goals are achievable if one can control éone-sidedé diffusive passage times of drug carrier particles: from deposition at the mucus interface, through the mucosal barrier, to the epithelium. The passage time distribution must be, with high confidence, shorter than the timescales of mucus clearance to maximize drug uptake. For 100nm and smaller drug-loaded nanoparticulates, as well as pure drug powders or drug solutions, diffusion is normal (i.e., Brownian) and rapid, easily passing through the mucosal barrier prior to clearance. Major challenges in quantitative control over mucosal drug delivery lie with larger drug-loaded nanoparticulates that are comparable to or larger than the pores within the mucus gel network, for which diffusion is not simple Brownian motion and typically much less rapid; in these scenarios, a timescale competition ensues between particle passage through the mucus barrier and mucus clearance from the organ. In the lung, as a primary example, coordinated cilia and air drag continuously transport mucus toward the trachea, where mucus and trapped cargo are swallowed into the digestive tract. Mucus clearance times in lung airways range from minutes to hours or significantly longer depending on deposition in the upper, middle, lower airways and on lung health, giving a wide time window for drug-loaded particle design to achieve controlled delivery to the epithelium. We review the physical and chemical factors (of both particles and mucus) that dictate particle diffusion in mucus, and the technological strategies (theoretical and experimental) required to achieve the design goals. First we describe an idealized scenario — a homogeneous viscous fluid of uniform depth with a particle undergoing passive normal diffusion — where the theory of Brownian motion affords the ability to rigorously specify particle size distributions to meet a prescribed, one-sided, diffusive passage time distribution. Furthermore, we describe how the theory of Brownian motion provides the scaling of one-sided diffusive passage times with respect to mucus viscosity and layer depth, and under reasonable caveats, one can also prescribe passage time scaling due to heterogeneity in viscosity and layer depth. Small-molecule drugs and muco-inert, drug-loaded carrier particles 100nm and smaller fall into this class of rigorously controllable passage times for drug delivery. Second we describe the prevalent scenarios in which drug-loaded carrier particles in mucus violate simple Brownian motion, instead exhibiting anomalous sub-diffusion, for which all theoretical control over diffusive passage times is lost, and experiments are prohibitive if not impossible to measure one-sided passage times. We then discuss strategies to overcome these roadblocks, requiring new particle-tracking experiments and emerging advances in theory and computation of anomalous, sub-diffusive processes that are necessary to predict and control one-sided particle passage times from deposition at the mucosal interface to epithelial uptake. We highlight progress to date, remaining hurdles, and prospects for achieving the two design goals for 200nm and larger, drug-loaded, non-dissolving, nanoparticulates.
Graphical abstract
1. INTRODUCTION
Inhaled drug delivery must overcome the same primary defense mechanism that Nature has engineered to prevent all inhaled insults from engagement with and absorption by lung epithelial tissue: the mucosal barrier [1]. Mucus likewise coats the nasal, sinus, digestive, and reproductive tracts, and indeed all organs not covered by skin. Mucus layers present a diffusive barrier to viruses (~100 nm), bacteria (microns), environmental particulates and drug particles spanning nanometers to microns. For inhaled small molecule drugs typically delivered with nebulizer sprays, or with powder particles that dissolve instantly upon landing at the air-mucus interface, drug diffusion through the mucus layer obeys simple Brownian motion and is instantaneous relative to mucus clearance times. Drug molecules or particles that tightly bind to the mucus microstructure, or that diffuse sufficiently slowly, are removed by mucus clearance. (All organs not covered by skin have mucus barriers for muco-trapping of insults, with organ-specific mucus clearance mechanisms to remove trapped insults before they penetrate the barrier, and mucus replenishment sources to maintain the barrier.)
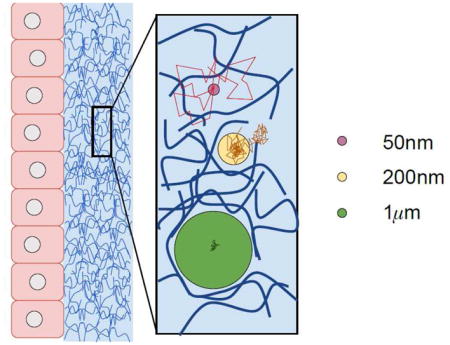
For all other drug-loaded carrier particles that are sufficiently large (200nm and larger), not permanently bound to the mucus mesh, and do not dissolve in mucus prior to contact with epithelial tissue or clearance from the protected organ, their diffusion in mucus is not described by simple Brownian motion. This has profound consequences for being able to control passage times through a mucus barrier. Particle diffusive passage times through a mucus barrier of known depth varies dramatically (potentially many orders of magnitude) depending on size and chemical properties of the particle and biophysical properties of the mucus. Furthermore, there is no theory for passage times, nor how they scale with depth of a layer or with heterogeneity of the fluid, for anomalous, transient, sub-diffusion. Mucus itself varies dramatically from human to human, organ to organ, health to disease. Figure 1 aims to provide intuition of the qualitative and quantitative differences in the diffusion of muco-inert particles of three Class sizes relative to the pore-network length scales of the mucus gel.
FIG. 1.
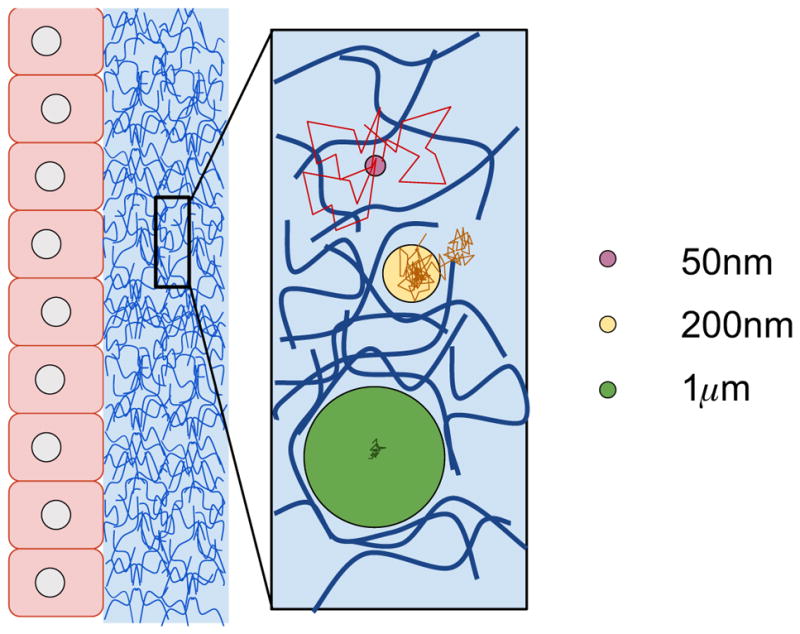
Diagram depicting the effect of particle size on the nature (Brownian vs. non-Brownian) of diffusive motion in mucus barriers. Class 1: Small molecules and drug-loaded nanoparticulates 100nm or smaller that do not chemically bind to the mucus mesh are minimally affected by the mucus microstructure and rapidly move via Brownian motion through the barrier. Class 2: Muco-inert particles of size proportional to mucus pores experience steric interactions with the mesh and entropic fluctuations from the mucus gel microstructure. Their increments are not only reduced relative to freely diffusing smaller particles, they are correlated, violating Brownian motion. Class 3: Muco-inert particles much larger than the mucus pores, e.g., 500nm to 1 micron depending on the mucus source, experience the full range of entropic fluctuations from the mucus microstructure, and are the ideal probes for particle-tracking microrheology. These particle increments are likewise correlated, reflecting elastic memory of the mucus gel, and exhibit transient, anomalous, sub-diffusive behavior. Class 2 and 3 particles with adhesive or repulsive interactions to the mucus mesh exhibit a wide range of mobilities that, with rare exception, also violate simple Brownian motion. Advanced particle-tracking experiments of drug-loaded nanoparticulates, ranging from 200nm to microns, are required to give sufficient data to select among possible models for transient, anomalous, sub-diffusion, and to properly estimate best-fit model parameters. From these results, due to the absence of theory for passage times of such non-Brownian processes, model computations become the required technology to estimate one-sided passage times through mucus barriers.
(Significant effort has gone into tuning the surface chemistry of drug-loaded nanoparticulates for mucosal delivery, aiming to disrupt the scenario of Figure 1 for muco-inert particles of Class 2 size especially, but also Class 3. With strong muco-repulsive interactions, 200–300nm particles that would otherwise have strong steric interactions with the mucus mesh, instead repel the mucin molecules, creating larger pores that minimize steric interactions, enhancing their diffusive mobility [2, 3]. Third party crosslinkers (e.g., antibodies) have been shown to possess the ability to anchor ~100nm nanoparticles to constituents of the mucus polymer network, thereby arresting its motion in a manner that is equivalent to a knockdown of the effective Brownian diffusivity [4]. We note possibilities of a cocktail surface chemistry strategy [5], with an exterior muco-inert coating to promote diffusion through the mucosal barrier that dissolves on the timescales of passage through the barrier, exposing a second surface coating for epithelial absorption. This strategy only raises the bar on the diffusive passage time focus of this review, since one must tune dissolution times of the exterior coating in mucus to diffusive passage times.)
In this review we discuss the theoretical technologies, and the experimental technologies for sufficient data acquistion, that are required to quantify and control one-sided diffusive passage times of drug-loaded carrier particles through mucosal barriers. In all organs, particles are deposited at the mucosal interface opposite the epithelium, and must diffuse through the barrier to the epithelial interface; thus the terminology used is “one-sided” diffusive passage time. We emphasize at the outset that the required theoretical and experimental technologies are not yet solved, but they are achievable. We strive to explain how emerging experimental and theoretical technologies promise to significantly narrow the gaps in current understanding of the non-Brownian diffusive processes governing many current drug carrier particles, and thereby to make strides toward predictive drug particle engineering design and control.
The present review does not address drug-loaded particle deposition strategies or the timescales of mucus clearance from a particular organ. For inhaled drug delivery and lung mucus clearance timescales, we defer to the vast and active literature on these assessments [6–14].
Herein, we focus on rigorous estimates of one-sided diffusive passage times from particle deposition at the exterior mucus interface through the barrier to the mucus-epithelium interface. After summarizing the precise control on passage times afforded by any particle undergoing simple Brownian motion in mucus, we address the conditions on particles and mucus for which this assumption is violated. We also assume particle size is sustained during diffusion in the layer; while we could incorporate dissolution of the shell radius, the complexities of mucus viscoelasticity and heterogeneity in depth and biophysical properties, and both size-dependence and chemical affinity of particles to mucus, are our priority for this review.
The race between transport through and transport of the mucosal barrier
For all deposited particles, including drug-loaded carrier particles, pathogens, and environmental particulates, spanning nanometer to micron scales, the mucus barrier imposes a limbo status, or delay, during which individual particles must penetrate the mucus barrier to encounter epithelial cells or vasculature. This time delay provided by the mucosal barrier gives the organ time to transport and clear the mucus layer plus all trapped cargo. Meanwhile, the organ continually replenishes the mucus barrier. For example, the lung produces on the order of a liter of mucus per day to maintain homeostasis [1, 15]. Mucus clearance is achieved by a combination of coordinated cilia and air drag from tidal breathing in normal circumstances, each biased toward the trachea, estimated at tens of microns per second in the small airways, and up to ten times faster in the upper airways and trachea [cf. [8]]. This experimental data translates to estimates of clearance times spanning minutes to hours in the upper airways and up to days in the central airways in healthy lungs. Thus it is important to know which branches in the airways a given inhaler will deposit particles of given sizes, since that sets the distribution of clearance times that drug particle diffusion through the mucosal barrier must outrace. (An interesting issue arises in the deep lung which has significant pulmonary surfactant. Raesch et al [16] studied the corona that forms around nanoparticles subjected to porcine pulmonary surfactant, revealing differences due to surface chemistries of the particles. Since mucus layers decrease to negligible in the deep lung, the impact of surfactant on passage times of particles that reach the deep lung is a very interesting, and to our knowledge, unexplored question.)
The mucus escalator picture implies that all trapped cargo in a local mucus patch is transported together, indiscriminately. As the conveyor moves, individual particle mobility will lead to repositioning among all the cargo, where the key issue for this review is any individual particle’s position relative to the deposition interface and epithelium. Cough is a totally different lung airway clearance mechanism (cf. [17]), with the obvious effect of violently forcing the mucus layer toward the larynx with turbulent air drag, including detaching and propelling droplets of mucus into the air stream toward the trachea. We do not address the impact of cough on drug particle delivery. There is a non-intuitive cough effect, consisting of stress-induced biochemical cascades that trigger ion transport and thereby stimulate hydration of the airway [18–22], allowing more efficient transport by cilia and normal breathing. These effects give a causal explanation for the persistent cough, day and night, of individuals with cystic fibrosis.
While particle diffusion in mucus is 3-dimensional, time to transport from the deposition interface to the epithelium is the key quantity of interest
While the diffusive mobility of particles in mucus is 3-dimensional, the only dimension that matters with respect to drug uptake is motion toward the epithelium. The time it takes for one-sided diffusion, from the deposition interface to epithelial tissue, is our definition of the particle passage time. As noted above, passage times of particles in mucus barriers vary dramatically depending on the diffusion process of that particle in that mucus. The processes range from simple Brownian motion for sufficiently small and non-interacting particles to a wide range of sub-diffusive, non-Brownian stochastic processes. The intimate interplay between physical and chemical properties of particles and mucus, their impact on particle passage times, and the technologies that are necessary to engineer predictive control over drug particle uptake at the epithelium, are the focus of our review.
The experimental techniques that have been applied to estimate particle diffusive mobility in mucus are summarized in Section 5, along with the emerging realizations within the drug delivery literature how particle size and surface chemistry have such a dramatic impact on diffusive mobility in mucus. The experimental methods—including Diffusion Chambers, FRAP, and Particle Tracking—each have limitations that are described in Section 5. However, at this junction we want to call attention to additional concerns that are subtle yet quite important in the overall goal to estimate particle diffusive passage times through mucosal barriers in the lung, sinus, digestive or reproductive tract where the particle is deposited at one boundary of the mucus barrier and has to diffuse through to the other boundary with the epithelium. This physiological “one-sided” diffusive passage time problem is typically not what is observed in ex vivo experiments.
If only particles would diffuse “normally”, physiological versus ex vivo experimental conditions would not matter
One subtle issue is extrapolation from experimental observation of particle motion in controlled settings to the geometry of lung airways or other organs. In diffusion chamber and FRAP experiments (see Section 5), the diffusion of small molecules and nanoparticles (1–100 nm diameter) are observed in mucus samples from a patient or assay, revealing a bulk effective diffusivity that was, surprisingly at the time, only a few times greater than pure buffer. However, small non-binding molecules and nanoparticles are mostly diffusing in the pores of the mucus gel, rarely interacting with the mucin network of entangled and crosslinked macromolecules. Therefore, the diffusion is consistent with normal, Brownian motion, and the concept of an effective diffusion coefficient for such particles in mucus is valid. This experimental confirmation has strong implications, because for normal Brownian motion, one can rigorously extrapolate from experimental initial and boundary conditions to the physiological “one-sided diffusion” conditions. The theory and numerical simulations for Brownian motion and one-sided passage times is presented in Sections 2 and 3, the ideal scenario.
The effective diffusivity approach to quantify mobility as a proxy for passage times
Almost all drug delivery experiments, analyses, and inferences rely on an “effective diffusivity” for a given particle mobility in mucus, which either explicitly or implicitly assumes that Brownian motion is an accurate physical model of particle diffusion through mucosal barriers. What predictions about passage times can, and cannot, be inferred from an effective diffusivity approach? A typical assessment of diffusive mobility of drug particles is to track particles using microscopy for a specific timescale, e.g., one second, and to estimate the effective diffusivity of that particle in that mucus sample for that timescale, typically one second.
Effective diffusivity breaks down for sufficiently large particles because of steric hindrance with, electrostatic and binding interactions with, viscoelastic properties of, and spatial heterogeneity of, the mucus barrier
The ability to extrapolate beyond the timescale of experimental observations is based on the fact that effective diffusivity for simple Brownian diffusion (explained and illustrated in Section 2) is independent of the observational timescale chosen: one second, one minute, or one hour. Sufficiently small molecules, nanoparticles, antibodies, and viruses (except those that become directly or indirectly crosslinked to the mucus mesh) diffuse normally through the pores of the mucus mesh, which by volume constitute 90–98%, with minimal hindrance due to the 2–10% volume of the large molecule network. However, particles above ~200nm in diameter typically do not exhibit normal Brownian motion, and the degree of departure from normal Brownian motion of any given particle in mucus depends on a multitude of health factors that influence the pore size distribution within the mucin molecular mesh as well as the attractive versus repulsive interactions between the mucin mesh, and particle size which determines whether the particle samples some or all entropic fluctuations of the mesh. For particles comparable in size to the local pore scales, equivalently the local length scales of the mucin-dominated mesh, steric interactions with the molecular mesh dominate mobility and change the qualitative character of the position increments of the particles. The entropic fluctuations of the mesh drive particle motion, so one still observes “movement” but it is strongly hindered relative to smaller particles that rarely encounter the molecular mesh.
Furthermore, surface chemistry of particles comparable in size, or larger than, the network mesh scales, becomes an important factor in mobility. This intuitive concept has been explored widely in engineering of surface-modified drug carrier particles that are mucoadhesive versus muco-repulsive, aiming toward prolonged versus shortened passage times through mucus barriers; we revisit these issues below. For particles much larger than the local mesh scales, elasticity of the mucus network strongly influences particle motion and induces clear departure from simple Brownian motion. Particle increments locally strain the mesh across all length scales probed by the particle, the strained mesh responds, attempting to relax (reverse the strain) and return to equilibrium, introducing negative correlations in the increments over the time scales of elastic relaxation probed by the particle size. If sufficiently large particles have “neutral” affinity to the network, then the observed displacements versus lag time, when transformed to frequency space, yield the viscous (loss) and elastic (storage) moduli of the mucus sample; this is indeed the basis of passive particle tracking microrheology that was introduced in the mid-1990s [23–27]. The microrheology reviews by Waigh [28, 29], separated by a decade, are highly recommended.
During the development of passive particle tracking microrheology, explorations of biomaterials such as entangled and crosslinked F-actin solutions led to important limitations on the ability to infer linear viscoelastic moduli from particle position time series. The observed motion of passively diffusing beads within the biomaterial was shown to be strongly influenced by the bead size and surface chemistry relative to the length scales and chemical properties of the mesh created by the entangled/crosslinked biomolecules; cf. [30]. These and related studies were critical for microrheology, since they shed light on the myriad factors that violate the generalized Stokes-Einstein relation, and thereby tracked particle time series do not yield the linear viscoelastic moduli of the biological material being studied. These observations compelled advances in theoretical microrheology in order to faithfully interpret experimental data, with particle size used to probe the length scales of the macromolecular mesh and the viscosity of the fluids filling the pores, particle surface chemistry used to probe affinity and phobicity of biomolecules relative to particle surface treatments, and multiple particle tracking (two-bead microrheology) used to screen particle-fluid chemical interactions and infer viscoelastic properties of the medium at intermediate length scales between particles. In Ref. [30], microbeads of varying diameter and surface treatment were compared in identical F-actin solutions, including bovine albumin coated, polyethelene-glycol (PEG) coated, and uncoated carboxylated microbeads.
All of these findings shed light on the critical factors influencing how foreign particles diffuse within mucus: small and large particles relative to the pore scales of the mucus molecular mesh, and particles that match the dominant mesh scales, all experience completely different diffusive motion, with only sufficiently small, non-bound particles exhibiting simple Brownian motion. Likewise, particles that have neutral, attractive, and repulsive interactions, especially those with diameters at the dominant mesh scales or larger, experience completely different diffusive motion. Furthermore, particles at or larger than the mucus mesh scales exhibit transient, sub-diffusive motion, converging to normal diffusive behavior only at observation lag times exceeding the longest timescales of memory of the mucus sample (rarely observed). The reviews by Ribbeck and collaborators [31, 32] give an excellent treatment of the remarkable diversity of particle mobility in mucin solutions. For microrheology, these lessons reveal that one can make huge, orders of magnitude, errors in inference of viscoelastic moduli with particle tracking by failure to select the right particle size and surface chemistry.
For particle drug delivery, the “correct” linear viscoelastic moduli of the mucosal barrier is irrelevant; the critical issue is the ability to control one-sided passage times from the particle deposition interface through the mucus layer to the epithelium. The particle size and surface chemistry lessons from particle tracking in soft biomaterials were immediately adopted in mucosal drug delivery, with two diametrically opposed strategies: mucoadhesive and muco-repulsive surface chemistry. When molecules with a binding affinity to the mucus mesh are tightly bound to the surface of drug particles, the particles are muco-adhesive, forcing prolonged passage times. The aim is to provide an extended time release of drugs within the particles, during which the particles slowly release their drug payload. However, this strategy is fraught with the high likelihood of drug particle clearance from the protected organ, with negative consequences, e.g., in inhaled drug delivery for asthma (immune suppression in the stomach instead of the lung) [33], cf. [34]. Surface chemistries such as polyethelene-glycol (PEG) have been shown to be muco-repulsive, with the ability to tune the particle size, as well as molecular weight and surface density of PEG, to control nanoparticle diffusion in mucus from diverse organs and mammals [35].
The mucus gel also utilizes a backup defense mechanism with active (i.e., highly mobile) binding or crosslinking agents, antibodies, that transiently bind to both the perceived invasive species and the mucus macromolecular mesh. The role played by antibodies in mucus has been the focus of the Lai lab at UNC for several years [36–39] for diverse applications including but not restricted to drug delivery. These small molecule anchors typically possess a weak affinity for the mucus microstructure so that their mobility in mucus is only slightly reduced. However, with a slightly stronger affinity to any invasive inhaled species (pathogens or particulates) in mucus, and the ability for many molecular anchors to crosslink to the invasive species and the mucus mesh, natural and engineered antibodies have the capacity to dramatically, and rapidly, decrease mobility and thereby increase the passage times of the invasive species well beyond the time window for mucus clearance [34, 35].
For particles that are larger than lung mucus network length scales, e.g., 500nm and 1 micron diameter beads, strongly non-Brownian, sub-diffusive particle motion is detected over a wide range of lag times (cf. [40]). This sub-diffusive behavior will persist up to the longest elastic memory timescales of the local network surrounding the particle, which typically exceed the total observation times of particle tracking. For such particles, surface treatment (attractive or repulsive to the mucus network) perturbs the particle motion, thus perturbs the inference of microrheology of the mucus sample if that was the purpose of particle tracking. However, for drug delivery purposes, inference of mucus rheology is not the goal; surface treatment of drug particles is a way to perturb mobility through electrostatic or binding interactions with the mucus network, and thereby influence passage times. This strategy is far more powerful for diffusion in viscoelastic media than simple viscous fluids precisely because passage times for transient sub-diffusive motion scale completely differently than simple diffusion. E.g., doubling effective diffusivity for Brownian motion leads to halving of the mean passage time through a given layer depth; changes in transient sub-diffusive motion can have a strongly nonlinear impact on passage times, inducing orders of magnitude changes rather than multiplicative factors (cf. [40]), discussed in more detail in the theoretical Sections below.
The timescales of memory in particle fluctuations are most easily recognized if one plots the mean-squared dis6 placements (MSD) versus lag time (time between particle position observations). MSD is the most-used summary statistic for diffusive mobility, including the drug delivery literature. Tracked particles above ~ 200nm in diameter are typically sub-diffusive (i.e., the MSD does not scale linearly with lag time) for lag times up to the longest memory timescale of the mucus network. The memory timescales of mucus, even in the equilibrium state of particle tracking experiments, are at least minutes, and typically hours or longer, far beyond the experimental timescales of particle tracking. The ability to assess the longest timescale of memory in mucus is an open problem, even if the mucus sample is homogeneous. Furthermore, if the passage time of a drug particle exceeds the mucus memory timescales, then there is a transition from sub-diffusive scaling to normal diffusion. There is no theory for passage times of transient sub-diffusive behavior, and no theory for passage times in heterogeneous viscoelastic media, as discussed later. This has many profound consequences, discussed throughout this review, with the upshot being that it is impossible to extrapolate from existing experimental data to passage times for controlled drug delivery. Prospects to overcome these hurdles are likewise addressed below.
Leading researchers in drug delivery make a rational compromise, giving up the ideal goal of accurate assessments of passage times for drug carrier particles in mucus, instead choosing a fixed timescale well within experimental capabilities, e.g., 1 s, and assessing mobility exclusively on that timescale, or lag time. This approach gives qualitative assessments, in particular, relative mobilities among candidate drug carrier particles. But it does not give quantitative assessments. To get a sense of the limitation of measuring mobility for a fixed lag time, consider the MSD of a tracked microbead in mucus. Due to viscoelasticity, the MSD is sub-linear, and lies below the linear MSD of normal diffusion for observational lag times up to 30 seconds or 1 minute, which is a typical duration for microbead particle tracking [40]. This means that fits over a chosen lag time to an “effective diffusivity”, i.e., a linear fit to a sub-linear MSD curve, will give a different line with a different slope (and thus a different inferred diffusivity) for every lag time! While it is perfectly acceptable to compare relative mobilities via an effective diffusion coefficient for a chosen timescale, say 1 s, one cannot extrapolate from effective diffusivity over that timescale to any other timescale, and especially not to passage times, even if the mucus barrier was perfectly homogeneous in physical properties (rheology) and in layer thickness.
The power to extrapolate, from a carefully designed experimental dataset to predictive engineering control of particle passage times in mucosal barriers, is made possible by the scaling laws of normal diffusion and Brownian motion, embodied in the Stokes-Einstein relation recalled in Sections 2, 4 below. In the remainder of this review, we first discuss the ideal conditions under which this is a valid assumption, followed by the long list of assumptions that are violated for drug particles in mucus, and the pitfalls (potentially dramatic errors) of any attempt to invoke an effective diffusivity for estimation of particle passage times through mucosal layers. We then present theoretical and computational modeling approaches, and the requisite experiments and data, to overcome each limitation and pitfall in the “effective diffusivity approach.” While not all of these technological solutions, either experimental or computational, are currently implemented in drug particle design and delivery, we review progress that has been made, as well as further progress on the horizon to overcome remaining hurdles. At the very least, this review outlines a strategy toward increased certainty in the design and control of drug particle delivery, with the caveat that some remaining hurdles represent significant challenges, experimentally and theoretically.
Why not eschew theory and measure passage times directly?
For anomalous sub-diffusion of 200nm and larger particles in mucus, little if anything is known about first passage times, or about how passage times scale with layer depth, and there is no theory that relates free diffusion to one-sided diffusion with reflection at the deposition interface. An empirical approach to drug particle design would be to simply eschew theory and directly measure passage times in mucus layers. The experimental technologies, time, and cost required for sufficiently many observations to infer a reliable one-sided passage time distribution, even for a given particle in a specific mucus sample of a fixed layer thickness, are prohibitive. The experimental limitations are, first and foremost, technological. Very few, if any, labs do particle tracking in a physiological geometry; e.g., depositing particles at one mucus layer interface and tracking their diffusion through the layer to the opposing interface. Furthermore, most labs only have 2D particle tracking capabilities, which only provides particle position time series in a focal plane, parallel to the plates that bound the sample; this limits observations of particles within a focal plane. As with flow of mucus along the airway, the sinus, digestive or reproductive tract, the measurement of interest for drug delivery is movement in the direction orthogonal to clearance; experimentally, that means through all focal planes from the top interface to a chosen depth. Thus, 3D particle tracking is essential to any empirical approach to measure passage times.
Piezoelectric stages and emerging light sheet microscopy allow, in principle, 3D particle tracking (by a rapid scan of focal planes). But 3D tracking generates huge video data files, 100s of gigabytes to terabytes depending on the number of particles and the duration required to observe passage through prescribed layer depths of 10–100 microns. For inhaled lung delivery, one can use human bronchial epithelial (HBE) cell cultures, place fluorescent particles at the air-mucus interface, and then track them until they reach the epithelial layer using 3D microscopy. This strategy is conceivable, but has not been carried out to our knowledge for micron-scale particles due to 3D tracking requirements and the time that would be required. Whether one-sided sub-diffusive transport in a cylinder geometry is equivalent to an annular geometry of the airway is another interesting question.
Thus one is faced with the following scenario. Experimental measurements of particle diffusive mobility in stationary mucus samples of sufficient volume are required to get particle position time series for sufficiently long timescales. Then one has to extrapolate from the particle tracking data to one-sided passage time distributions versus mucus depth. Finally, one must perform these 3D experiments, record and analyze the particle tracking data versus particle control parameters, diameter and surface chemistry. Even if one has the resources to perform all of these experiments, convert the particle tracking video data to particle position time series, and analyze the data: is this sufficient to extrapolate and estimate particle passage time distributions versus mucosal layer depths (see Table I). Furthermore, do experiments and passage time estimates for one organ mucus sample apply to the same organ but different mucus sample, e.g., versus age, disease and disease progression of the individual? How do the passage time estimates scale with particle diameter or mucus layer depth? Can one extrapolate across different particle surface chemistries?
TABLE I.
| Lung: central airway | 10–20 μm |
| Lung: upper airway | 50–100 μm |
| GI tract: stomach | 40–450 μm |
| GI tract: ilium | 10 μm |
| GI tract: colon | 110–160 μm |
Under ideal circumstances, the answer to all of the above questions is affirmative. The ideal assumptions are: mucus is a homogeneous, viscous fluid with a known viscosity (e.g., 10–100 times more viscous than water); and the diffusing particle is a passive tracer that moves solely due to entropic fluctuations of the simple fluid. For any interaction between the particle and fluid that does not corrupt the Brownian nature of particle diffusion, then there is an effective diffusivity. Under these assumptions, since exact scaling laws exist, one does not have to perform experiments or numerical simulations of passage times for all particle sizes and mucus viscosities and layer thicknesses. In fact, one does not have to observe even one passage time of one particle; the entire distribution of passage times is known for any particle diameter, fluid viscosity and thickness of the layer. This will be presented and illustrated in Section 2, 3. We then walk through evaluations of passage times as each of these idealized assumptions are relaxed in light of what we know about drug particles, human organ mucus, and particle-mucus interactions.
Recapitulation of factors that violate the ideal scenario with full control over one-sided passage times of particles through mucosal organ barriers
Airway, sinus, cervical, and intestinal mucus is not a simple viscous fluid. Mucus is a viscoelastic hydrogel, consisting of a mixture of water, salts, proteins, immune response agents such as antibodies and bacteriophages, DNA from dead cells, and a spectrum of mucin macromolecules. Mucins are large molecular weight glycoproteins with remarkable structure, including interspersed domains of different scales and charge density (cf. [7]) that convey the functionality of the mucosal barrier. Mucus forms a crosslinked, entangled, heterogeneous network, creating a distribution of fluid-filled pores ranging in size from 100nm to 500nm [41, 43, 44]. Dedicated experimental studies are required to identify the pore size distribution for a given mucus sample. The mucus pore size distribution has dramatic implications for size-dependent particle diffusive mobility, as illustrated in Figure 1 and discussed above. Particles much smaller than the local pore scales rarely interact with the mucus mesh network, and typically diffuse normally with diffusivity determined by the local fluid viscosity and particle diameter. This explains why small molecules and 50nm nanoparticles and 100nm viruses in diffusion chambers with mucus that has ~200–300nm mean pore diameter exhibit simple Brownian motion.
There is further evidence that the local fluid viscosity within pores is heterogeneous, owing possibly to density variations in small proteins or weak particle interactions with the local network that can be modeled as a local effective viscosity. We discuss the impact of viscous heterogeneity on Brownian diffusion and passage times in Section 3, 4.
As discussed above, particles with diameter sufficiently large (typically above 200 nm) relative to the length scales of the mucin network, if they have neutral interactions with the network, exhibit correlated fluctuations and sub-diffusive MSD scaling over long timescales that reveal the local, frequency-dependent, viscous and elastic moduli of the mucus gel. This scenario is the fundamental basis of passive particle tracking microrheology — to convert entropic fluctuations of passive microbeads to equilibrium viscoelastic moduli via the Generalized Stokes-Einstein Relation (GSER, cf. [23, 45]), which we recall and discuss in Section 3. If sufficiently large particles have attractive and/or repulsive interactions with the mucus network, their motion is some perturbation of neutral particle motion, which will typically not obey the GSER scaling behavior. In all cases, the particle diffusive behavior is not simple Brownian motion, and the only strategy for estimation of passage times is based on modeling and simulation. Such a strategy requires sophisticated modeling of transient, sub-diffusive processes together with significant experimental and theoretical challenges to identify the timescales of memory due to elasticity of the network (cf. [46–51]).
A higher level design task, our penultimate goal in this review, is to not only insure drug penetration through the mucus barrier with quantification of the inherent uncertainty, but to control the passage time distributions, i.e., arrival times to the epithelium, of drug carrier particles. We summarize the requisite technologies (experimental and theoretical) to achieve such a high-level design, both progress and challenges associated with each technology, toward a capability to dictate the dynamic schedule of drug dosage to the airway epithelium, including an assessment of the factors governing variability and uncertainty even if the full design task is fulfilled.
2. THE IDEAL SCENARIO WITH PRECISE CONTROL OVER INHALED PARTICLE PASSAGE TIMES THROUGH MUCUS BARRIERS
Assume a mucus layer of uniform thickness, L, uniform viscosity η, and particles of radius r. In this Section, we assume the simplest scenario, namely that particles undergo simple Brownian motion (a precise mathematical definition is presented in Section 2 2.1). We treat the mucus deposition interface as a reflecting boundary; particles start at the deposition interface, with movement only allowed into the mucus layer. The mucus-epithelium interface is modeled as an absorbing boundary; when a particle first encounters this boundary, the total elapsed time is recorded and the time series is terminated. A sample particle trajectory is shown in Figure 2.
FIG. 2.
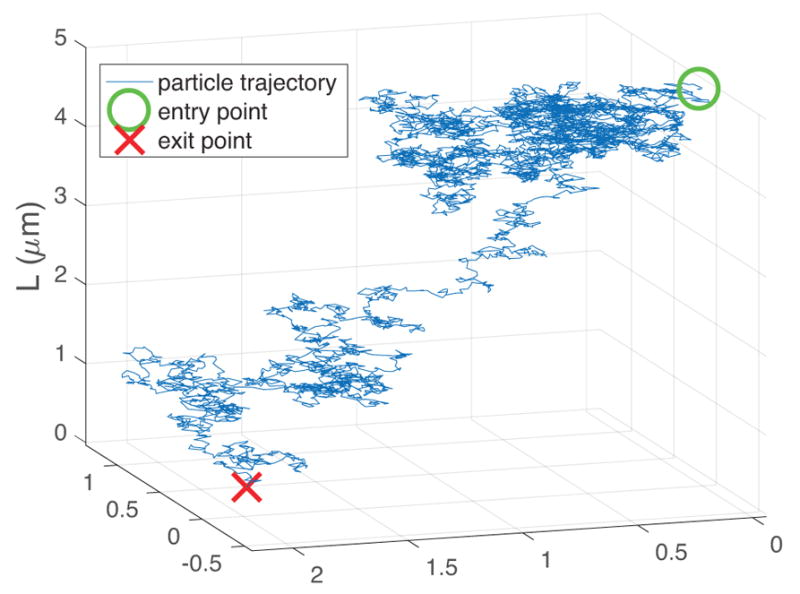
A sample Brownian particle trajectory in a layer of uniform depth L = 5μm and viscosity η = 25 times that of water, 2.34 × 10−8 μm2 s−1, with a time step, τ, of 1/60 s. As the particle of radius r = 0.5μm undergoes Brownian motion through the layer, it stays near the presumed air-fluid interface at early times, returning to and reflecting from the upper boundary. Gradually, the particle moves away from the boundary and eventually is absorbed at the lower boundary at T = 601 s for this simulation.
Many such particle trajectories are simulated, and the time it takes to pass from entry point to exit point, the one-sided particle passage time, is recorded for each simulated particle. In Figure 3, a histogram of passage times from 10,000 particle simulations is shown, along with the exact values of the probability density function and mean first passage time given in Section 3.
FIG. 3.
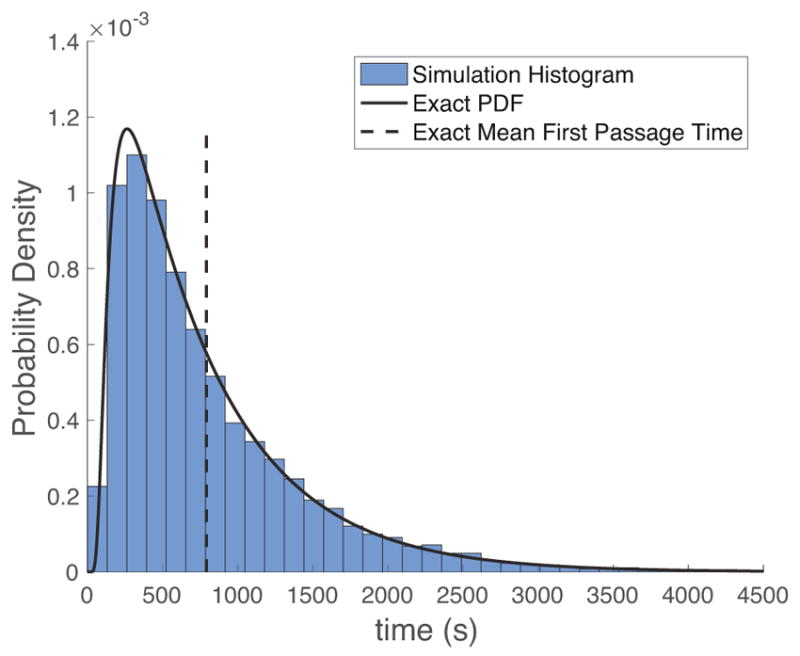
Probability Density histogram of passage times for particle simulations described in Figure 2, together with the exact PDF and mean first passage time. The PDF is closely approximated by a lognormal distribution.
A natural question arises at this point: What are the first passage time distributions and mean passage times for other particle radii r, mucus viscosities η and thicknesses L? We can, of course, compute the answers across the full 3-parameter space (r, η, L) for a relevant range of each parameter, just like we generated the passage time histogram in Figure 3 for the choice (r, η, L) = (0.5, 2.34 × 10−8, 5). Figures 4 and 5 illustrate the brute force results of direct simulations for (r, η, L) = (0.5, 2.34 × 10−8, L) for mucus depths L = 1, 2, 10μm, and (r, η, L) = (r, 2.34 × 10−8, 5) for r = 0.1R, 0.2R,R. Figures 4 and 5 correspond to sparse data along two line segments in a 3-dimensional parallelopiped, indicating how cumbersome it is to not only generate the data over a large parameter space, but then one has to mine the dataset for meaningful information. We shall come back to this onerous task when we discuss the realities of particles diffusing in mucus. Meanwhile, if one looks at the mean first passage times (MFPT) in Figures 4 and 5, a striking realization is evident: the MFPT scales linearly with r and quadratically with L. If we had computed the analog of Figures 4 and 5 for η, we would observe a linear scaling of MFPT with η.
FIG. 4.
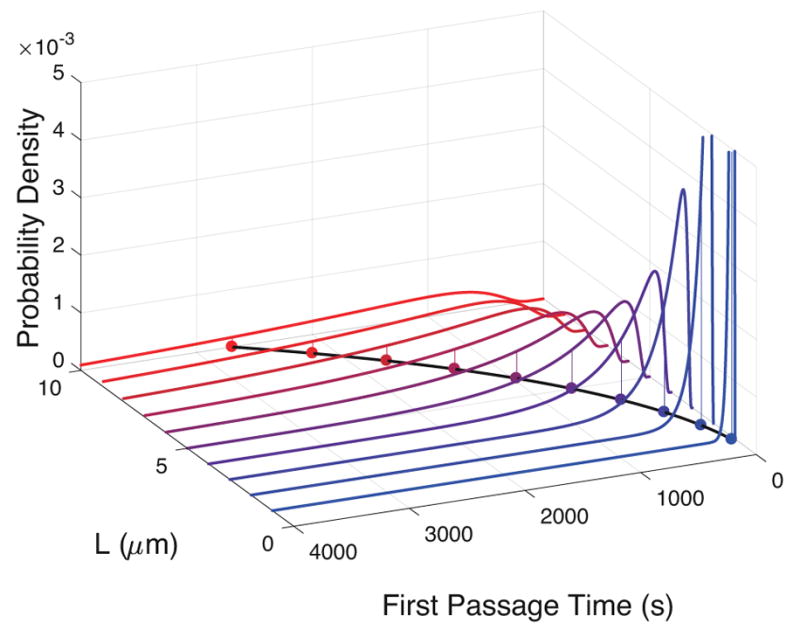
First passage time distributions for different values of the layer thickness, L. The means for the distributions are indicated by the dots below each, and they demonstrate that the times it takes to pass through the layer increases as a power law with respect to the thickness of the layer.
FIG. 5.
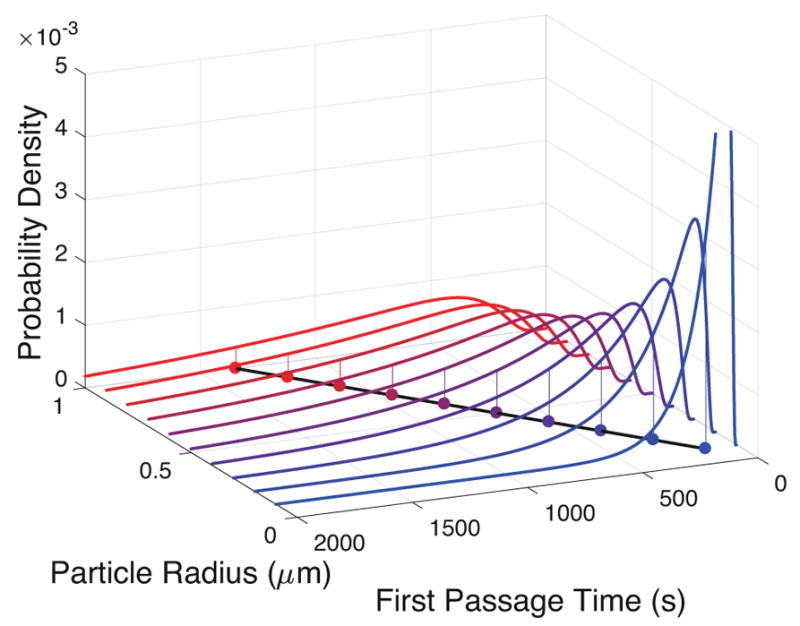
First passage time distributions as a function of particle radius, r. The mean first passage times have a linear relationship with both r and η.
Here is where a rigorous theory for the ideal scenario not only confirms these observations, but generalizes them across the entire 3-parameter space (r, η, L)! The exact formula for the MFPT of the one-sided diffusion of Brownian particles of radius r in a layer of uniform viscosity η and uniform depth L, starting at a reflecting boundary z = 0 and diffusing until hitting an absorbing boundary z = L, is
| (2.1) |
or
| (2.2) |
where EB = kBTK ≈ 4.1 pNnm (at 25 °C) is the natural energy scaling factor for molecular scale systems. Therefore we confirm that the MFPT scales linearly with r and η and quadratically with L, and given the precise particle size, mucus viscosity and thickness, the exact value of MFPT is known. Furthermore, there is an exact formula for the entire passage time distribution, given in Section 3, which is an infinite series but it can be calculated numerically to arbitrary precision, as illustrated in Figures 3 and 4.
With these precise results in hand, we return to the design goals for inhaled drug particle delivery, and assume the ideal scenario is applicable. For sufficiently small molecules and nanoparticles that do not interact with the mucus network in any significant way, their diffusion is normal with an effective diffusivity D = EB/(6πηr), the celebrated Stokes-Einstein relation. If particles are polydisperse with a known distribution of radii r, it is straightforward to generate the full passage time distribution and MFPT. In Section 3, we discuss analogous scenarios in which the layer thickness is non-uniform and the viscosity is heterogeneous, and show how the theory of Brownian motion can be extended, tediously yet straightforwardly, to rigorously compute the full passage time distributions and MFPTs for polydisperse particles in heterogeneous viscous fluids of variable thickness. This exercise illustrates the power of the direct application of the scaling laws for Brownian motion. For application of the fundamental theory to drug particle design, one designs the particle radius distribution and wants to prescribe the passage time distribution. The only unknowns that we need are the mucus viscosity distribution and the mucus thickness profile in the airways of deposition. As stated at the outset, we defer to other technologies to estimate the layer thickness profile; heterogeneous thickness profiles are addressed in Section 2.2 for this ideal scenario. Thus, our only remaining task is to infer the mucus viscosity distribution, an inverse problem, whose solution for viscous fluids is straightforward via particle tracking. One first must distribute particles of any fixed radius randomly throughout the mucus sample, and use particle tracking technology to get their position time series.
For each particle position time series, in a locally uniform viscous fluid, the maximum likelihood estimator of the diffusivity is
| (2.3) |
The increment statistics of each particle will give the local diffusivity D = EB/(6πηr) of the spatial mucus environment they are sampling. Since r,EB are known, one determines η at the random experimental sampling of the mucus volume. The only caveat is that the length scales of heterogeneity in viscosity should be larger than the distance traversed by each tracked particle. One can confirm this caveat by looking at the histograms of increments to confirm they are Gaussian and not a mixture of Gaussians (which would indicate the particle increments are from distinct viscosities); if necessary, one can reduce the observation time of each particle to resolve finer spatial scales of viscous heterogeneity. This adaptation to smaller observation times is possible for normal Brownian motion, with the only price being a larger error bar in the inferred diffusivity; for non-Brownian motion, fewer observations, i.e., shorter increment lag times of observed particles, severely limits the ability to perform model selection among all candidate non-Brownian, sub-diffusive processes.
Since exact relationships are known for all parameters of interest, all problems of this nature are precisely connected to one another. That is, one can normalize the probability density functions and time values by the mean first passage time, T, such that all of these curves collapse on each other, shown in Figure 6, below. Given the dimensionless curve shown in Figure 6, we can rescale the curve to represent the probability density function when we know the values of the parameters of interest (i.e., D and L).
FIG. 6.
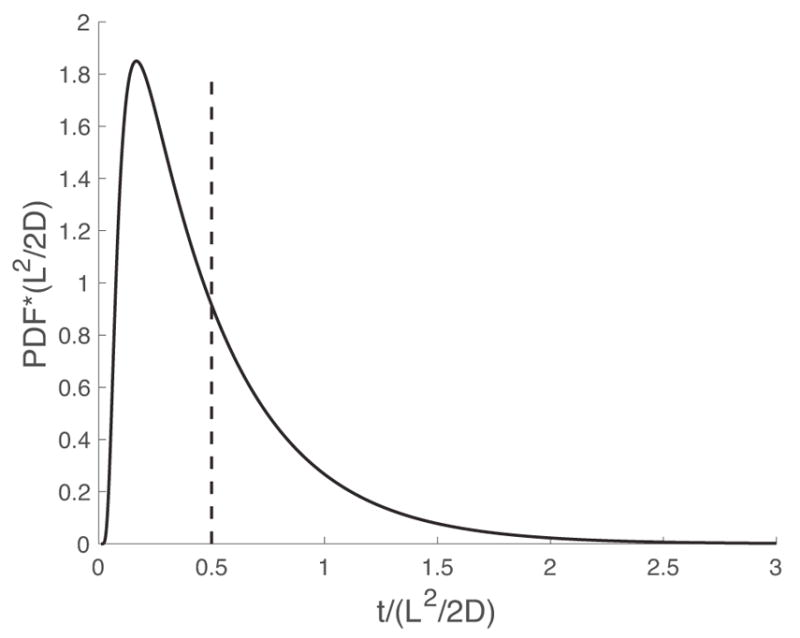
A master curve demonstrating the ability to scale first passage time distributions by L and D such that all curves are equivalent.
2.1. First passage time across a viscous mucus barrier
The development of first passage time theory for stochastic physics of submicron biological systems has advanced significantly in the last few decades [52–61]. The strength of the theory is its ability to explore how thermal fluctuations, chemical interactions, and mechanical forces on a particle play out in specific scenarios that include the complex geometries typical of living systems. For example, the first passage time for a transcription factor to locate a specific sequence of DNA involves random motion within the nucleoplasm, interspersed with random motion along DNA filaments. The combination of the two phases of motion substantially speeds up the first passage time [60].
In this section, we formulate penetration of a mucosal barrier by drug particles as a first passage time problem. For completeness, we include the basic formulation of a first passage time distribution.
Let X(t) be the distance of a given particle undergoing Brownian motion from the airway lumen. Let the random variable τ be the first passage time, defined as the first time at which the particle reaches the epithelium at X(t) = L (in mathematical terms the definition is τ = inf{t > 0 : X(t) = L}). Let p(x, x0, t) be a solution to the Fokker-Planck equation [62],
| (2.4) |
| (2.5) |
| (2.6) |
| (2.7) |
The solution to this equation can be regarded in two equivalent ways. First, p(·) can be viewed as the normalized concentration of a drug particle released instantaneously at a distance x0 from the airway lumen and absorbed at the epithelium. Second, from the perspective a single drug particle, we have
| (2.8) |
Given the solution to (2.4), the first passage time density is derived as follows. The probability the particle has not yet exited the layer at time t is called the survival probability and is given by
| (2.9) |
The first passage time distribution is then
| (2.10) |
where the last two lines made use of (2.4).
The FPT can be written in two equivalent forms, both of which are infinite series rather than an algebraic formula. Nonetheless, the terms of the series converge under most circumstances so that the series can be truncated to obtain an approximation with any desired accuracy. The truncation error gets smaller as more terms are included in the series. There are two different series representations [63]: one that converges quickly for short times and the other for large times. For fast convergence at small times (t < L2/(2D)), the first passage time density is
| (2.11) |
For fast convergence at large times ( ), the first passage time density is
| (2.12) |
where
| (2.13) |
At x0 = 0, the formulae for the first passage time density and cumulative distribution (denoted as F(t)) simplify to
| (2.14) |
| (2.15) |
and
| (2.16) |
| (2.17) |
In practice, either expression can be used, except for extreme values of very large or vary small values of t.
An explicit solution to (2.4) can only be found in limited circumstances. A simpler equation for the mean first passage time is available [62, 64], which allows us to extend our understanding, for example, to the case where the mucus layer has variable depth and/or viscosity. Denote the mean first passage time as T(r), where r is the initial position. One can show that the MFPT satisfies
| (2.18) |
| (2.19) |
| (2.20) |
In the absence of heterogeneity in D, the MFPT is
| (2.21) |
At x0 = 0, the above formula simplifies to (2.1).
To illustrate how the MFPT alone can be useful, we examine the effect of variability in the depth of the mucus barrier.
2.2. Heterogeneity in the layer depth
It is highly idealized to assume that the mucus barrier has a uniform depth across the entire surface of the organ. As we show in this section, the effect of variable depth on the MFPT is not as simple as one might expect. Suppose we compare the MFPT for two hypothetical scenarios: a constant depth layer and a variable depth layer, each having the same average depth. The following result tells us that even though the two layers contain the same volume of mucus, it takes longer on average for a particle to penetrate the variable depth layer. While some particles in the variable depth layer start closer to the epithelium and take less time to traverse the mucus barrier, an equal fraction of particles start farther away and require more time. Recall that the MFPT scales with the square of the depth L. Hence, the slow down for the fraction that start farther from the epithelium will be comparatively larger than the speed up for the fraction that start closer. This observation follows the general rule that diffusive transport is more efficient over short distances than long distances [65] for normal Brownian motion; for non-Brownian, transient, sub-diffusive processes, there is no analogous result.
Assume that the layer thickness is a function of y, the distance along the centerline of the airway. For simplicity, assume that the depth is a periodic function , with period λ > 0 and average depth 〈L〉:
| (2.22) |
If we assume that we have a slowly-varying depth then the MFPT is approximately
| (2.23) |
Averaging the MFPT over the initial position y then yields
| (2.24) |
Notice that this result is not the one we might expect from a naive guess, namely 〈T〉 ~ 〈L〉2 /(2D). Indeed, we can write where f(y) is a periodic function with zero average (〈f(y)〉 = 0). Then we have
| (2.25) |
The specific value of 〈f2〉 depends on the maximum amplitude. For example, if f(y) = Asin(2πy/λ), where 0 < A < L is the amplitude, then 〈f2〉 = A2/2.
3. HETEROGENEITY IN THE VISCOSITY OF A MUCUS BARRIER
Variation in the viscosity within the pores of a mucus barrier, relevant to sufficiently small particle diffusion, arises due to local density of proteins and other small molecules. The pore viscosity is potentially stratified from the mucus deposition interface to the epithelium, arising perhaps from mucus production in the epithelium or active forcing at the deposition or epithelial interface. The principal result of this section is that the MFPT across a variable viscosity mucus layer is roughly equivalent to a homogeneous layer with a spatially averaged viscosity. For a stratified layer, the MFPT is simply the sum of all the MFPTs through each sublayer, and the relative order of each layer does not affect the MFPT. Neither of these results is known to generalize to viscoelastic diffusion.
Suppose that the viscosity depends on the position within the mucus layer. We define
| (3.1) |
There are multiple formulations for stochastic models of particle motion with variable diffusivity, often refered to as multiplicative noise. Physical considerations are required to resolve the appropriate model. The most common approach is to require the model to satisfy a detailed balance constraint, which ensures that the particle distribution approaches a steady state that is consistent with the Boltzmann distribution [66, 67]. This is the correct approach, provided that there are no active (i.e., energy consuming) processes that establish concentration gradients under steady state conditions. Particle diffusion in a Newtonian fluid with variable viscosity is governed by
| (3.2) |
| (3.3) |
| (3.4) |
| (3.5) |
To derive a stochastic differential equation that can be used to simulate paths, we first rewrite (3.2) in Fokker-Planck form
| (3.6) |
The corresponding stochastic differential equation is
| (3.7) |
where dW is the standard Wiener process [62]. The simplest numerical scheme is Euler’s method,
| (3.8) |
where tn = nΔt and Z(tn) is a normal random variable with mean zero and unit variance. An efficient Euler-like scheme for simulating the process near reflecting boundaries is given by [68]. We want to examine two scenarios: viscosity periodic in y and viscosity periodic in x. For simplicity, we ignore the z direction.
3.0.1. Depth-wise variable viscosity
The extension of the MFPT equation (2.18) to variable viscosity (depth wise) is
| (3.9) |
| (3.10) |
The solution is
| (3.11) |
Starting at the interface,
| (3.12) |
If D(x) is piecewise constant, then the MFPT is simply the sum of all the MFPTs through each sublayer.
3.0.2. Variable viscosity along the centerline axis of an airway
Suppose that D(r) = D(y/λ), with λ > 0, is a λ periodic function. Variation of viscosity in the y coordinate yields the MFPT problem,
| (3.13) |
| (3.14) |
| (3.15) |
Both T and D are strictly positive, and we can assume that the two functions are anti-correlated in y, meaning that when D increases, we can expect a corresponding decrease in T. Hence, we can assume that
| (3.16) |
(One can show that this is asymptotically accurate for both λ ≪ L and λ ≫ L.) By averaging (3.13)–(3.15) with respect to a uniformly distributed initial position y0 and setting x0 = 0, we obtain
| (3.17) |
Hence, the MFPT is proportional to the averaged viscosity.
4. FIRST PASSAGE TIMES ACROSS A VISCOELASTIC MUCUS BARRIER
Unlike particles below 100nm diameter exhibiting viscous dynamics, particles of diameter ~200nm or larger interact with the mucosal mesh structure, thereby exhibiting dynamical “memory” that cannot be explained by Brownian motion alone. That is, if Xt is the position of the particle at time t, Brownian dynamics would predict that the mean squared displacement (MSD) of the particle scales linearly in time,
| (4.1) |
However, the MSD of these larger particles is almost always sub-diffusive on observational timescales of particle tracking, with
| (4.2) |
for 0 < α < 1 and on some timescale t ∈ (tmin, tmax). The fundamental laws of motion of such particles are described by a Generalized Langevin Equation (GLE) [69],
| (4.3) |
where m is the mass of the particle, Ẍt is its acceleration, κ is a spring-like potential force, γ(t) is the memory kernel for the frictional force on the velocity Ẋt, and Ft is the thermal force, a stationary stochastic process satisfying the Fluctuation-Dissipation theorem [69], such that its autocorrelation is given by
| (4.4) |
While the GLE interprets conveniently as the decomposition of the total force (mẌt) acting on the particle into potential, frictional, and thermal forces, it can be rigorously derived from the Hamiltonian equations of motion for any particle in a microcanonical physical ensemble [70]. As such, the GLE has often served as a foundational tool for physically valid modeling of viscoelastic particle dynamics [47, 49–51, 71]. Two GLE models have proved particularly useful in this respect.
The first assumes a Maxwellian linear viscoelastic regime [50], wherein the memory kernel γ(t) is composed of discrete, power-law distributed relaxation spectra,
| (4.5) |
Assuming a negligible potential force κ = 0, the so-called generalized Rouse spectrum (4.5) induces transient sub-diffusion [71],
| (4.6) |
where tmin and tmax are functions of τ and K.
The second major GLE model is that of fractional Brownian motion (fBM), a continuous Gaussian process with zero mean and covariance function
| (4.7) |
such that it exhibits uniform subdiffusion
| (4.8) |
It can be shown that fBM satisfies a GLE with negligible potential force κ = 0 and in the “zero-mass limit” m = 0, with γ(t) ∝ t−α [72].
4.1. Calculation of first passage times
Several analytic results for first passage times have been derived for fBM [cf. 73] and to a lesser extent, for GLEs as well [74]. However, almost none of the results we have surveyed account for the reflecting boundary condition required here. One notable exception is [75], which derives the MFPT for an fBM particle, but only when released far from the airway lumen, x0 ≫0. In contrast to these analytic results, the following method of simulating FPTs alleviates many restrictions, at a moderate cost of computational power and (controllable) approximation accuracy.
First, we note that the reflecting-boundary process X̃t corresponding to a general one-dimensional stochastic process Xt is given by [76]
| (4.9) |
which only for Brownian motion corresponds to X̃t = |Xt|. To simulate the reflected process one then employs a simple numerical discretization scheme [77]
| (4.10) |
where X0, · · · ,XN are observations of Xt with frequency Δt. [77] prove that for fBM, the strong discretization error is of order Δtα/2. On the other hand, both fBM and the Rouse-GLE with zero-mass limit are stationary-increment processes with closed-form auto-correlation functions [71], which can be simulated in O(N log N) operations using the circulant embedding method of [78, 79]. In the more general setting, the GLE can be solved explicitly in the Fourier domain:
| (4.11) |
where , F(ω) = 𝔉{Ft}, and , such that Xt can be simulated approximately using FFT methods. Employing a similar approach, [51] showed that the MFPT across a two-sided barrier of the Rouse-GLE (4.5) scales linearly in the particle radius r, and quadratically in the barrier depth L, which agrees with the analytic calculation for Brownian motion with reflecting boundary (2.1).
4.2. Parameter estimation from experimental data
In [46, 47], the two- or three-dimensional trajectory of the particle Xt is modeled as
| (4.12) |
where μ is a vector of coordinate-wise linear drifts, Σ is a variance matrix, and Zt are independent and identically distributed Gaussian continuous stationary-increments (CSI) processes, such that their covariance structure is entirely characterized by the coordinate-wise MSD,
| (4.13) |
Both fBM and the Rouse-GLE (4.5) with κ = 0 and m = 0 [71] are shown to be expressible in this form, with θ = α and θ = (α, τ,K). Let X = (X0, … ,XN) denote observations of the particle recorded at regular time intervals of Δt. Then under model (4.12), the maximum likelihood estimate of all parameters Θ = (μ,Σ, θ),
| (4.14) |
along with its error bars, can be calculated efficiently via the methods in [46, 47, 80]. In particular, [47] show that the generalized Rouse-GLE model provides a much better fit than fBM to tracer particles in 2.5% wt human bronchial epithelial (HBE) mucus, reliably detecting tmin, the transition time from ordinary to sub-diffusive MSD scaling. However, calibrating the number of modes K from experimental data remains a computational challenge, and the experimental timescales thus far offer virtually no information about tmax, the longest timescale of memory, a fundamental parameter for FPT calculations. The shortest timescale of memory in HBE mucus, tmin, is negligible (fractions of a second) for passage time estimates, whereas the longest timescale of memory, tmax, is minutes if not hours, and thereby is critical for passage time estimates. However, a dedicated experimental effort to track particles for minutes is required, where one can expand the lag time between observations but must track particles far beyond current tracking data. This will not only require experimental time and cost, video data storage expense, but also light sheet 3D particle tracking and automated conversion of video files to particle time series such as the convolutional neural net algorithm [81]. Given such 3D time series, methods in [47] will produce a fully parametrized, generalized Rouse-GLE model, which can then be simulated to predict physiological passage times versus mucus layer thickness, as illustrated in [51], assuming mucus viscoelasticity is homogeneous! Of course, mucus is heterogeneous, so future prospects to accommodate this reality are presented next.
4.3. Heterogeneous viscoelastic mucus barriers
Obtaining a physically valid description of particle dynamics reflecting both (i) a memory component due to interactions with the mucus network and (ii) the spatial heterogeneity of said network – is an open modeling challenge. One possible approach is to couple the GLE (4.3) with a nonlinear potential force, such that
| (4.15) |
The Boltzmann distribution of the particle is then
| (4.16) |
suggesting that the potential term U(x) can account for variations in the elasticity and/or mesh size of the mucus network, which affect the particle’s mobility. Eulertype discretization schemes for (4.16) have been discussed by [82, 83], although the scaling of these algorithms is 𝒪(N2), due to the presence of the memory kernel.
5. EXPERIMENTAL TECHNIQUES TO QUANTIFY “NANOPARTICLE” TRANSPORT IN MUCUS
Any mathematical modality and prediction of the timescales of “nanoparticle” penetration through mucosal barriers critically depends on accurate experimental measurements of transport properties. Here “nano” refers to particle scales ranging from nanometers to microns. This has motivated a number of techniques to assess the degree to which transport is hindered by the mucus barrier, and furthermore to use these techniques to test particle design parameters (size and surface chemistry) for their impact on diffusive transport in mucus. We introduce and briefly describe the most common experimental techniques used in recent years and their respective advantages as well as limitations.
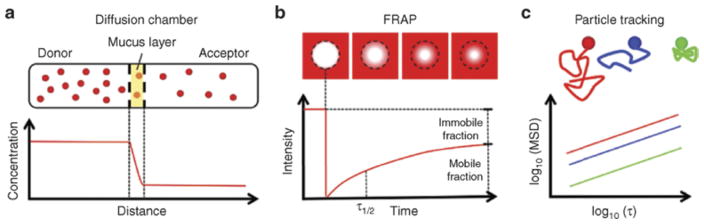
5.1. Diffusion chambers
One of the earliest techniques used to quantify the diffusion of small molecules and nanoparticles through mucus was the diffusion chamber [84–88], where a thin layer of mucus is sandwiched between a donor and an acceptor compartment (Figure 8.A). The rates with which a particle or molecule of interest in the donor compartment can diffuse through the mucus layer into the acceptor compartment, as a result of the concentration gradient, can be measured over time. At steady-state flux, an effective diffusion coefficient D can be calculated from the concentration profile within the mucus layer [89].
FIG. 8.
Experimental techniques commonly used to quantify nanoparticle transport in mucus. (a) Diffusion chamber schematic showing concentration-driven nanoparticle (NP) diffusion from a donor compartment into a similar acceptor compartment. NP diffuse across a thin mucus layer sandwiched between filters of the donor and acceptor compartments. The concentration profile of NP within the mucus layer can be used to calculate the diffusion coefficient. (b) Fluorescence recovery after photobleaching (FRAP) schematic showing photobleaching (white circle) of a mucus specimen (dosed with red fluorescent NP) at time zero followed by fluorescence recovery of the circular region by rapid diffusion of unbleached NP in the specimen. The time required to reach 50% fluorescence recovery (τ12) in the photobleached region can be used to calculate the effective diffusion coefficient of NP. Mobile and immobile fractions of NP are determined based on the ratio of the plateau intensity at the end of the recovery profile. (c) Multiple particle tracking (MFPT) schematic showing various representative NP trajectories in mucus.
Sinko and coworkers were among the first to use the diffusion chamber system (Transwell-Snapwell diffusion chamber apparatus) to study the one-dimensional effective diffusivity of nanoparticles of various sizes in mucus [90]. Using reconstituted porcine gastric mucin gel as a model for human mucus, the group observed a significant decrease in diffusive mobility (beyond the expected scaling with particle size from the Stokes-Einstein relation), as inferred from measured translocation permeability as the particle size approached 300 nm. Similarly, Sanders and coworkers reported decreasing penetration percentages of carboxylated polystyrene nanoparticles (0.24, 0.022, and 0.0017%) diffusing across a 220μm thick cystic fibrosis (CF) sputum layer as the particle size increased (124, 270, and 560 nm, respectively) [84]. From these results, the authors concluded that the bulk viscoelasticity of the CF sputum effectively limited the diffusion of nanoparticles. To paraphrase, the nanoparticle diffusion data in CF sputum was violating the Stokes-Einstein scaling behavior of the diffusion coefficient D with particle size, from which the authors concluded that particles in mucus above a certain size, e.g.,200–300 nm, fail to adhere to normal Brownian motion. These observations were a few years into the rapidly growing field of particle-tracking microrheology, where it was widely observed that particles at or above the lengthscales of the microstructure in colloids and polymer solutions exhibit non-Brownian, indeed sub-diffusive scaling, which was consistent with some mechanism of hindered diffusion relative to Brownian motion.
Although the diffusion chamber technique for measuring drug and particle diffusion across mucus barriers is simple and allows quantification of the effective flux from which average effective diffusion coefficients can be calculate, there are a number of important limitations. For example, these measurements are typically taken over the course of several hours, which limits insights into the transport behavior over short durations [84]. There are also experimental setup challenges that can strongly influence the measurements but are very difficult to control, such as controlling the thickness of the mucus layer, ensuring uniformity of the mucus thickness over the entire surface of the filters, potential blockage of filter pores by mucins, and alterations in mucus properties during preparation [91]. Indeed, the diffusion chamber filter is often able to non-specifically adhere to nanoparticles [84] and/or allow significant amounts of mucin molecules to diffuse into either the donor or acceptor compartments, thereby reducing the barrier properties of the mucus layer [90]. Finally, diffusion chamber measurements only provide bulk average estimates of an effective diffusivity. Thus, such measurements rely on the fundamental assumption of normal Brownian motion (otherwise, there is no known relation between measured flux and diffusion law parameters such as diffusivity), and further fail to provide insights into distributions and heterogeneity in the diffusive mobility of nanoparticles. Both issues confound mathematical efforts to predict passage times on the basis of experimental data, which require one to accurately identify a diffusion process consistent with measured data, to select among all candidate processes, and to estimate parameters of the best-fit process. Due to these significant challenges, many investigators turned to high-resolution microscopy techniques to characterize transport through mucus.
5.2. Fluorescence recovery after photobleaching
Fluorescence recovery after photobleaching (FRAP) has been used to quantify the effective diffusion rates of proteins, viruses, nanoparticles, and many other macromolecules in various biological tissues, including mucus [91–95]. The basis of FRAP involves using strong fluorescence intensity to effectively photobleach a small defined area within a specimen containing a fluorescent entity of interest (e.g., a protein), followed by quantifying the recovery of fluorescence into the defined area over time (Figure 8.B). An effective diffusion coefficient can be calculated for the molecule of interest, generally based on the time required to reach 50% recovery of pre-bleached fluorescence. The immobile fractions can also be determined based on the ratio of the plateau intensity in the FRAP recovery profile compared to the intensity in a neighboring non-bleached area [92]. Each FRAP measurement typically takes a few minutes compared to the multiple hours required with diffusion chambers, and multiple measurements are performed on each specimen (8–20) to arrive at an average diffusivity measurement. As emphasized throughout this review, for small molecules and sufficiently small nanoparticles below the length scales of the entangled and crosslinked mucin network, and that do not bind significantly to the mucus network, their diffusion is reasonably modeled by simple Brownian motion, for which an effective diffusivity is relevant.
The landmark work by the Saltzman and Cone groups on diffusion in human mid-cycle cervical mucus utilized FRAP to measure the diffusion coefficients of antibodies (IgG and IgA) and select capsid viruses (Norwalk and human papilloma). Prior to their work, the prevailing dogma was that the bulk viscosity of mucus greatly limited the diffusion of proteins and viruses across mucus. The FRAP technique enabled them to discover that both antibodies and viruses can undergo rapid diffusion in mucus at rates comparable to those in buffer [91, 93]. In a different study using FRAP, Braeckmans and coworkers observed rapid and nearly complete fluorescence recovery (> 90%) of different-sized fluorescent labeled dextran (hydrodynamic radii of 9, 15, and 33 nm) in CF sputum, which further verifies that CF sputum pores are filled with relatively low viscosity interstitial fluids (only 4- to 6-fold higher viscosity than that of pure water) [92]. In the same study, FRAP was also used to measure the immobile fractions of 37 and 89 nm polystyrene nanoparticles in CF mucus (38% and 56%, respectively); the authors attributed the high immobile fractions to adhesive interactions between the hydrophobic domains of mucins and hydrophobic polystyrene particle surface. More recently, nanoparticle transport in native and highly purified mucus matrices was assessed in the presence of guluronate oligomers using FRAP. By decreasing the density of mucin network crosslinks and consequently increasing the network pore size, the authors found that guluronate oligomers increased mobility of the nanoparticles across mucus layers [95].
As described above, due to its ability to quantify real-time transport over very small distances and durations (i.e., high spatiotemporal resolution), FRAP has provided valuable insights into the effective diffusion of sufficiently small molecules and nanoparticles in mucus. It is possible to measure spatial variability in transport, thus heterogeneity in effective diffusivity, by performing multiple measurements in different regions of a specimen, which represents another improvement over diffusion chamber studies that yield only one measured transport value per specimen. Nevertheless, it is important to note that each FRAP measurement still represents only an ensemble-averaged diffusion rate within that region, and hence fails to provide quantitative insights into the heterogeneity of transport among different populations of particles. Insight into heterogeneity is particularly important for diffusion in heterogeneous media such as mucus, where the same particles can exhibit orders of magnitude variations in diffusion coefficients [96]. Another concern with FRAP is the high concentration of fluorescent particles required within the mucus sample to produce a bright and uniform fluorescent background [97], which generally promotes a smooth recovery curve for accurate estimation of diffusion coefficients. At high concentrations, nanoparticles can cause mucin fibers to aggregate, resulting in significant microstructural changes to the mucus mesh, such as increased mesh pore size [93, 98]. We reiterate that the overall successes in understanding diffusive transport in mucus using FRAP are exclusively for sufficiently small particles, Class 1 in Figure 1.
5.3. Particle Tracking
To circumvent issues with and limitations of FRAP, researchers are increasingly adopting another microscopy method, particle tracking (PT), for quantifying transport of drug and gene carrier particles in various tissues, including nanoparticle transport in mucus [3, 34, 35, 44, 99–107]. PT involves capturing videos of nanoparticle diffusion with high frame rates, and subsequently converting the real-time motion of individual nanoparticles into position time series (“tracks”), from which data analysis can be performed. If the particles are sufficiently small and their tracks are consistent with Brownian motion, then an effective diffusivity of the mucus (or any fluid) sample can be inferred, locally from individual nanoparticles and volume averaged for an ensemble of particles in any chosen volume that contains the tracked particles. In order to ensure high fidelity tracking of the same nanoparticles, PT is typically performed with an epifluorescence or confocal microscope equipped with a high magnification objective (63× or 100×) and a high-speed camera capable of up to 60 frames per second (fps) imaging [108]. Unlike FRAP, PT does not require high concentrations of nanoparticles in the mucus sample, minimizing concerns with mucus dilution or mucin bundling and with particle-particle interactions. The common statistic for PT experiments is the mean-squared-displacement (MSD) of individual or ensemble-averaged particle traces (Figure 8.C). The MSD statistic can be used to quantitatively estimate how far particles move over given timescales if the particles obey Brownian motion, as explained in Sections 2 and 3, but only qualitative, relative estimates can be inferred from the MSD statistic for non-Brownian motion [41, 96, 108–110], and even then, all relative mobilities are restricted to the duration of the particle tracks, which are typically at most one minute.
There are additional drawbacks and shortcomings of focusing on MSD to understand particle mobility. First, the common understanding of MSD scaling (linear, sub-linear, etc.) is based on “free diffusion in unbounded domains”, which eliminates virtually all biologically relevant scenarios. Second, correlations in the increments of a path can be influenced by a host of factors, and often several completely different mechanisms can have the same effect on the “shape” (i.e., scaling) of the MSD locally and globally versus lag time (time between increments). Third, standard methods for calculating the MSD (e.g., using overlapping lag times to get enough data for longer lag times, and estimating particle by a non-zero mean of the increments, then subtraction of drift from the increments) impose correlations that skew the MSD estimate [46, 47].
The modern theory of statistical physics for micron scale biological systems has largely eliminated the need for the traditional MSD-based analysis. There is a wide range of mechanistic stochastic models that describe a particle and the factors within the physical system that influence its motion. Moreover, there is a highly developed mathematical framework for formulating new stochastic models or revising existing ones as our understanding evolves [62, 111, 112]. A stochastic model can be used to predict particle mobility in realistic biological contexts, including boundary effects, with first passage time theory [60, 64, 112]. These advances were illustrated in Section 3. Modern statistical methods can be used in conjunction with a stochastic model to analyze particle tracking data in order to extract relevant parameter values and quantitatively compare competing models [46, 47]. These advances and remaining challenges were addressed in Section 4.
In one of the first PT experiments studying transport of nanoparticles in mucus, Dawson and co-workers measured the movements of carboxylate- and amine-modified polystyrene nanoparticles sized 100–500 nm in sputum obtained from patients with CF [107]. The authors used the PT data to calculate effective diffusion coefficients for these nanoparticles (notwithstanding the strong likelihood that many of the particles were undergoing non-Brownian motion). They concluded an order of magnitude greater diffusion rates than predicted based on macrorheology of CF sputum, but still more than 300-fold slower than the diffusion of the same particles in water. These conclusions are subject to the concerns raised throughout the review, namely that effective diffusivity is not well-defined for transient sub-diffusion, giving a different diffusivity at every timescale. Indeed, identical 500nm particles have been studied in reconstituted human bronchial epithelial mucus, across a range of mucus wt% solids spanning healthy to moderate CF disease progression, and all PT data reveal transient sub-diffusive behavior [40]. Furthermore, there is no study to date that confirms equivalence of micro and macro rheology of CF sputum. Nonetheless, the trends revealed in this study are valuable, i.e., relative mobilities based on effective diffusivity at a common fixed timescale are valid qualitative metrics of diffusive mobility.
PT has further been a powerful tool in facilitating the development of methods to enhance nanoparticle diffusion through mucus, such as developing muco-inert particles coated with hydrophilic polymers [35] or the use of mucolytics to aid nanoparticle transport [105, 113]. Rather than measuring only ensemble-averaged diffusion rates, such as with FRAP, the ability of PT to resolve motions on an individual particle basis has enabled a sensitive method to assess the performance of different particle formulations. For example, Wang and Lai found that high grafting density of low MW polyethylene glycol (PEG) on polymeric nanoparticle surfaces could enable rapid particle diffusion in mucus compared to particles coated with PEG at lower grafting densities, achieving effective diffusivities over 1 second timescales in mucus only 7-fold reduced compared to in water [2].
While PT is a robust technique for quantifying transport of a large number of individual particles in mucus and other extracellular barriers, there are a number of limitations to note. First, the tracked object must be sufficiently bright and retain adequate signal-to-noise ratio during microscopy (i.e. limited photobleaching). Thus, it is difficult if not impossible to employ PT to measure the transport of proteins and very small biological systems. Second, current microscopy methods are typically limited to 2D rather than 3D video microscopy.
Due to the limited thickness of the focal plane, small nanoparticles that inherently have greater diffusivity quickly diffuse out of the focal plane, limiting the duration over which particles can be tracked to no more than a few seconds. This naturally raises concerns whether diffusion measurements made on the order of only a few seconds can accurately predict the transport of particles over physiologically relevant time scales of several to many minutes or even longer. This potential discrepancy was highlighted recently when comparing the transport of 100nm nanoparticles using PT (shorter-time scale diffusion) versus FRAP (longer-time scale diffusion), which yielded significant differences in the calculated mobile fractions (43% versus 24%, respectively) [114]. The lack of proper statistical weighting of particle traces can also significantly bias the calculated averages and distributions of nanoparticle diffusivities [48].
For the purposes of assessing passage times of all drug carrier particles above ~200nm in mucus barriers, which do not exhibit Brownian motion, a serious challenge arises that is discussed in greater detail in Section 4. Suffice to say, such non-Brownian, transient sub-diffusive motion is due to the viscoelasticity of the mucus gel, whose entropic fluctuations are not simply white noise. Rather, the fluctuations have colored noise arising from the timescales of memory in the elastic network; particle diffusion that feels these elastic network fluctuations will be sub-diffusive over all timescales of memory, and then transition to simple Brownian motion for timescales beyond the longest memory of the mucus gel. This situation requires extreme care in modeling the underlying stochastic process, in validating models based on experimental data, in parameter estimation, and especially in predicting passage times through layers of varying thick nesses, since there are virtually no theoretical analogs of the Brownian motion formulas for mean passage times and passage time distributions! These challenges are discussed in Section 4. However, a fundamental requirement for transient sub-diffusive processes, which describe all particles above 200nm in mucus, is to capture sufficiently long particle trajectories via PT such that one can assess the longest timescales of memory across the fluid volume. For this purpose, much longer observations of the particles of interest in mucus are required than the current 30 s duration particle tracks at 60 fps in most of our studies thus far [40].
Finally, particle tracking analysis, despite the aid of tracking software, continues to require substantial user supervision and intervention to ensure accurate extraction of position-time series. There has been significant progress toward the goal of fully automated tracking, and dozens of effective methods have been developed that are capable, given ideal conditions, automatically converting image data into position-time series particle paths [108, 115, 116]. However, given the conditions commonly encountered in experimental data—such as spatiotemporal heterogeneity, variable background intensity, photobleaching, and low signal-to-noise ratio (SNR)—analyzing PT videos remains a labor intensive process. This not only limits the throughput of the experiments, but also introduces user-variations in tracking analysis [81]. Over the last decade, machine learning tools have rapidly advanced the field of computer imaging [117, 118]. This emerging technology has been adapted to the task of automated particle tracking, processing 4D image data into position-time series particle paths [81]. Using a type of computer algorithm called a convolutional neural network, the neural network tracker provides full automation with substantially improved accuracy over existing methods, over a broad range of experimental conditions commonly encountered in the field of drug delivery. This technology promises to enable broad adoption of PT as a standard laboratory tool for quantifying particle mobility in micron scale biological systems.
6. CONCLUSION
Our aim in this review has been to frame the goals of mucosal drug-loaded particle delivery in terms of technologies required to control physiologically relevant, one-sided diffusive passage times: from deposition at the mucus interface, through the mucosal barrier, to the epithelium. If one can control particle passage times from deposition to absorption by epithelial tissue, then one can control drug dosage and rate of uptake via drug carrier particle design. The design space of particles consists of size, surface chemistry, and stability while transporting in mucus. The states-of-the-art for the requisite experimental and theoretical technologies for control of one-sided passage times of drug carrier particles through mucosal barriers have been reviewed, highlighting remaining hurdles and prospects for overcoming them.
The passage-time perspective is an extension of the prevalent assessment in mucosal drug delivery based on effective diffusivity, estimated from experimental data over a fixed timescale (cf. [3, 31, 32, 35, 44, 96, 99–107]. When particle diffusion is Brownian, e.g., small molecules and Class 1 (Figure 1) nanoparticles in a homogeneous mucus of a prescribed thickness, then the full theoretical power of Brownian motion (exact formulas for mean first passage time and passage time distribution) can be applied to gain a rigorous quantitative assessment of one-sided passage times from free diffusion experiments on a short, fixed timescale. Furthermore, the scaling of passage times with respect to particle size, mucus viscosity and layer thickness, are all explicitly known. We further discussed how to generalize these results for two physiologically relevant violations of the ideal scenario: heterogeneity in the viscosity and thickness of the mucus layer. The scaling behavior of the Stokes-Einstein relation already gives hints at the averaging results we presented: heterogeneity in viscosity can be replaced with an averaged viscosity, due to the linear scaling of mean first passage time with viscosity (and with particle size), whereas the scaling with depth of the layer is quadratic, yielding non-intuitive mean first passage time results due to modulations in the air-mucus interface.
For non-Brownian motion typical of Class 2 and 3 particles in mucus depicted in Figure 1, the fixed timescale, effective diffusivity approach is only qualitative, and only applicable for the timescales of experimental observation, which are typically much shorter than passage times through organ mucosal barriers. Thus, effective diffusivity does not provide quantitative estimates of passage times for 200nm and larger drug-carrier particles for mucosal drug delivery. In Section 4 we summarize a theoretical strategy to rigorously assess physiologically relevant, one-sided passage time distributions, relying on data from emerging 4D (3D + time) particle tracking technologies discussed in Section 5. When simple Brownian motion is violated (essentially all particles 200nm in size or larger in typical human mucus) due to a combination of steric interactions with, entropic fluctuations of, electrostatic interactions with, and transient binding interactions (directly or through third party molecular anchors) with, the mucus macromolecular network. We likewise discussed viscoelastic heterogeneity of mucus and non-uniformity in layer depth. In all such particlemucus scenarios, mobility is strongly time-dependent, so that none of the fixed timescale experiments and mobility characterizations are sufficient to extrapolate to passage times. Intriguing open questions remain as to how to simulate passage times for transient, sub-diffusive motion through a heterogeneous viscoelastic medium. Solutions to these questions and the development of the requisite experimental and theoretical technologies are the focus of current research among the authors and collaborators.
Finally, we cannot overemphasize the importance of the mucus source. We have described the experimental and theoretical technologies that will, hopefully within a few years, give the capability to predict passage times for given particles in a given mucus sample. However, the predictions are strongly dependent on the individuality of the mucus source, with very different outcomes depending on the organ, the individual’s health versus disease, age, and many factors that have yet to be resolved. We note, for example, the dramatic changes in the diffusive mobility and estimates of passage times for identical micron beads in human bronchial epithelial mucus over a range of weight percent solids of [40], a proposed biomarker in disease progression for cystic fibrosis and COPD. Identification of lung mucus profiles for subpopulations that stand to benefit from drug therapies has certainly been pursued, e.g., for asthma, diabetes, gene therapy, and COPD, and the technologies reviewed here stand to benefit the drug particle design strategies. Such studies reveal the importance of the mucus source in the design of drug carrier particles, and how diffusion in mucus of identical particles in any human organ can vary dramatically with age, health factors, disease and disease progression.
FIG. 7.
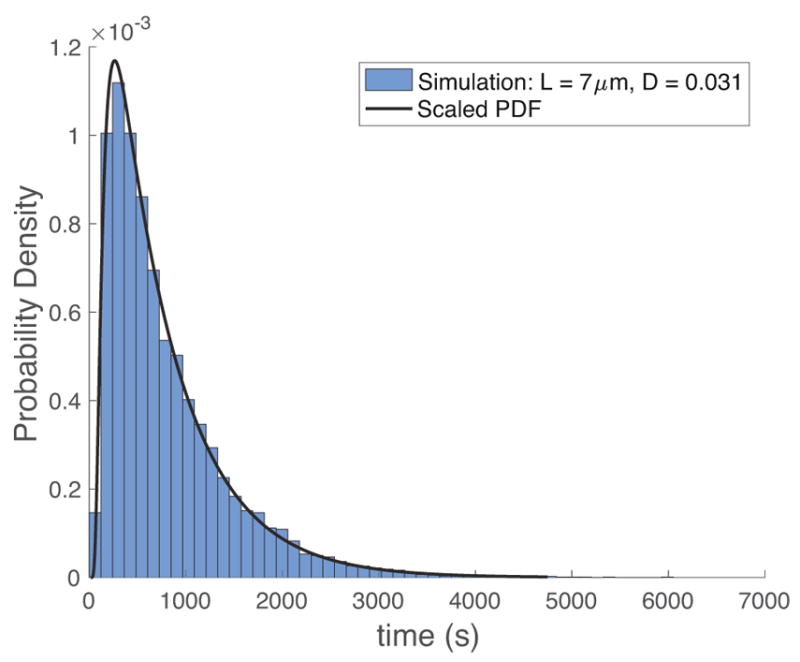
The dimensionless PDF in Figure 6 scaled to represent specific values of L and D.
Acknowledgments
JMN and MGF were funded by the National Science Foundation (NSF) DMS-1462992. ML and YL were funded by the Natural Sciences and Engineering Research Council of Canada RGPIN-2014-04255. MGF was also funded by the NSF DMS-1412844, DMS-1517274, DMS-1664645.. SKL was funded by a NSF CAREER Award DMR-1151477; the David and Lucile Packard Foundation (http://www.packard.org/); the Eshelman Institute of Innovation (https://unceii.org/); and the National Institute of Health R41GM123897, R56HD095629. JTH was supported by an NSF Graduate Research Fellowship DGE-1650116. The authors would like to especially acknowledge colleagues whose collaborations have positively influenced this review: David Hill, Rich Superfine, Ric Boucher, John Sheehan, Bill Davis, Scott McKinley, Natesh Pillai, Paula Vasquez, John Fricks, Tim Elston, Lingxing Yao, and Christel Hohenegger.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Knowles Michael R, Boucher Richard C. Mucus clearance as a primary innate defense mechanism for mammalian airways. The Journal of clinical investigation. 2002;109:571. doi: 10.1172/JCI15217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang Ying-Ying, Lai Samuel K, Suk Jung Soo, Pace Amanda, Cone Richard, Hanes Justin. Addressing the peg mucoadhesivity paradox to engineer nanoparticles that aĂIJslipaĂİ through the human mucus barrier. Angewandte Chemie International Edition. 2008;47:9726–9729. doi: 10.1002/anie.200803526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Maisel Katharina, Reddy Mihika, Xu Qingguo, Chattopadhyay Sumon, Cone Richard, Ensign Laura M, Hanes Justin. Nanoparticles coated with high molecular weight peg penetrate mucus and provide uniform vaginal and colorectal distribution in vivo. Nanomedicine. 2016;11:1337–1343. doi: 10.2217/nnm-2016-0047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Newby Jay, Schiller Jennifer L, Wessler Timothy, Edelstein Jasmine, Gregory Forest M, Lai Samuel K. A blueprint for robust crosslinking of mobile species in biogels with weakly adhesive molecular anchors. Nature Communications. 2017;8:833. doi: 10.1038/s41467-017-00739-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shan Wei, Zhu Xi, Liu Min, Li Lian, Zhong Jiaju, Sun Wei, Zhang Zhirong, Huang Yuan. Overcoming the diffusion barrier of mucus and absorption barrier of epithelium by self-assembled nanoparticles for oral delivery of insulin. ACS nano. 2015;9:2345–2356. doi: 10.1021/acsnano.5b00028. [DOI] [PubMed] [Google Scholar]
- 6.Matsui Hirotoshi, Randell Scott H, Peretti Steven W, William Davis C, Boucher Richard C. Coordinated clearance of periciliary liquid and mucus from airway surfaces. Journal of Clinical Investigation. 1998;102:1125. doi: 10.1172/JCI2687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Thornton David J, Sheehan John K. From mucins to mucus: toward a more coherent understanding of this essential barrier. Proceedings of the American Thoracic Society. 2004;1:54–61. doi: 10.1513/pats.2306016. [DOI] [PubMed] [Google Scholar]
- 8.Donaldson Scott H, Corcoran Timothy E, Laube Beth L, Bennett William D. Mucociliary clearance as an outcome measure for cystic fibrosis clinical research. Proceedings of the American thoracic society. 2007;4:399–405. doi: 10.1513/pats.200703-042BR. [DOI] [PubMed] [Google Scholar]
- 9.Thiagarajah Jay R, Song Yuanlin, Derichs Nico, Verkman AS. Airway surface liquid depth imaged by surface laser reflectance microscopy. The Journal of general physiology. 2010 doi: 10.1085/jgp.201010490. jgp–201010490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Newman Stephen, Bennett William D, Biddiscombe Martyn, Devadason Sunalene G, Dolovich Myrna B, Fleming John, Haeussermann Sabine, Kietzig Claudius, Kuehl Philip J, Laube Beth L, et al. Standardization of techniques for using planar (2d) imaging for aerosol deposition assessment of orally inhaled products. Journal of aerosol medicine and pulmonary drug delivery. 2012;25:S–10. doi: 10.1089/jamp.2012.1Su4. [DOI] [PubMed] [Google Scholar]
- 11.Bennett William D, Laube Beth L, Corcoran Timothy, Zeman Kirby, Sharpless Gail, Thomas Kristina, Wu Jihong, Mogayzel Peter J, Jr, Pilewski Joseph, Donaldson Scott. Multisite comparison of mucociliary and cough clearance measures using standardized methods. Journal of aerosol medicine and pulmonary drug delivery. 2013;26:157–164. doi: 10.1089/jamp.2011.0909. [DOI] [PubMed] [Google Scholar]
- 12.Conway Joy, Fleming John, Bennett Michael, Havelock Tom. The co-imaging of gamma camera measurements of aerosol deposition and respiratory anatomy. Journal of aerosol medicine and pulmonary drug delivery. 2013;26:123–130. doi: 10.1089/jamp.2011.0960. [DOI] [PubMed] [Google Scholar]
- 13.Bennett William D, Xie Miao, Zeman Kirby, Hurd Harry, Donaldson Scott. Heterogeneity of particle deposition by pixel analysis of 2d gamma scintigraphy images. Journal of aerosol medicine and pulmonary drug delivery. 2015;28:211–218. doi: 10.1089/jamp.2013.1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fuchs Susanne I, Gappa Monika. Lung clearance index: clinical and research applications in children. Paediatric respiratory reviews. 2011;12:264–270. doi: 10.1016/j.prrv.2011.05.001. [DOI] [PubMed] [Google Scholar]
- 15.Kis Adrian, Krick Stefanie, Baumlin Nathalie, Salathe Matthias. Airway hydration, apical k+ secretion, and the large-conductance, ca2+-activated and voltage-dependent potassium (bk) channel. Annals of the American Thoracic Society. 2016;13:S163–S168. doi: 10.1513/AnnalsATS.201507-405KV. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Raesch Simon Sebastian, Tenzer Stefan, Storck Wiebke, Rurainski Alexander, Selzer Dominik, Ruge Christian Arnold, Perez-Gil Jesus, Schaefer Ulrich Friedrich, Lehr Claus-Michael. Proteomic and lipidomic analysis of nanoparticle corona upon contact with lung surfactant reveals differences in protein, but not lipid composition. ACS nano. 2015;9:11872–11885. doi: 10.1021/acsnano.5b04215. [DOI] [PubMed] [Google Scholar]
- 17.Basser PJ, McMahon TA, Griffith P. The mechanism of mucus clearance in cough. Journal of biomechanical engineering. 1989;111:288–297. doi: 10.1115/1.3168381. [DOI] [PubMed] [Google Scholar]
- 18.Fredberg Jeffrey J, Hoenig A. Mechanical response of the lungs at high frequencies. Journal of Biomechanical Engineering. 1978;100:57–66. [Google Scholar]
- 19.Boucher RC. Human airway ion transport. part two. American journal of respiratory and critical care medicine. 1994;150:581–593. doi: 10.1164/ajrccm.150.2.8049852. [DOI] [PubMed] [Google Scholar]
- 20.Tarran Robert, Grubb Barbara R, Gatzy John T, William Davis C, Boucher Richard C. The relative roles of passive surface forces and active ion transport in the modulation of airway surface liquid volume and composition. The Journal of general physiology. 2001;118:223–236. doi: 10.1085/jgp.118.2.223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tarran Robert, Button Brian, Boucher Richard C. Regulation of normal and cystic fibrosis airway surface liquid volume by phasic shear stress. Annu Rev Physiol. 2006;68:543–561. doi: 10.1146/annurev.physiol.68.072304.112754. [DOI] [PubMed] [Google Scholar]
- 22.Herschlag Gregory, Garcia Guilherme JM, Button Brian, Tarran Robert, Lindley Brandon, Reinhardt Benjamin, Elston Timothy C, Gregory Forest M. A mechanochemical model for auto-regulation of lung airway surface layer volume. Journal of theoretical biology. 2013;325:42–51. doi: 10.1016/j.jtbi.2013.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mason Thomas G, Weitz DA. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Physical review letters. 1995;74:1250. doi: 10.1103/PhysRevLett.74.1250. [DOI] [PubMed] [Google Scholar]
- 24.Dhont Jan KG. An introduction to dynamics of colloids. Vol. 2. Elsevier; 1996. [Google Scholar]
- 25.Schnurr B, Gittes F, MacKintosh FC, Schmidt CF. Determining microscopic viscoelasticity in flexible and semiflexible polymer networks from thermal fluctuations. Macromolecules. 1997;30:7781–7792. [Google Scholar]
- 26.Gittes F, Schnurr B, Olmsted PD, MacKintosh Fred C, Schmidt Christoph F. Microscopic viscoelasticity: shear moduli of soft materials determined from thermal fluctuations. Physical review letters. 1997;79:3286. [Google Scholar]
- 27.Mason TG, Ganesan K, Van Zanten JH, Wirtz D, Kuo SC. Particle tracking microrheology of complex fluids. Physical Review Letters. 1997;79:3282. [Google Scholar]
- 28.Waigh Thomas A. Microrheology of complex fluids. Reports on progress in physics. 2005;68:685. doi: 10.1088/0034-4885/79/7/074601. [DOI] [PubMed] [Google Scholar]
- 29.Waigh Thomas Andrew. Advances in the microrheology of complex fluids. Reports on Progress in Physics. 2016;79:074601. doi: 10.1088/0034-4885/79/7/074601. [DOI] [PubMed] [Google Scholar]
- 30.Valentine MT, Perlman ZE, Gardel ML, Shin JH, Matsudaira P, Mitchison TJ, Weitz DA. Colloid surface chemistry critically affects multiple particle tracking measurements of biomaterials. Biophysical journal. 2004;86:4004–4014. doi: 10.1529/biophysj.103.037812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Witten Jacob, Ribbeck Katharina. The particle in the spider’s web: transport through biological hydrogels. Nanoscale. 2017 doi: 10.1039/c6nr09736g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lieleg Oliver, Ribbeck Katharina. Biological hydrogels as selective diffusion barriers. Trends in cell biology. 2011;21:543–551. doi: 10.1016/j.tcb.2011.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lai Samuel K, Hanes Justin. Real-time multiple particle tracking of gene nanocarriers in complex biological environments. Gene Therapy Protocols: Design and Characterization of Gene Transfer Vectors. 2008:81–97. doi: 10.1007/978-1-60327-248-3_6. [DOI] [PubMed] [Google Scholar]
- 34.Schneider Craig S, Xu Qingguo, Boylan Nicholas J, Chisholm Jane, Tang Benjamin C, Schuster Benjamin S, Henning Andreas, Ensign Laura M, Lee Ethan, Adstamongkonkul Pichet, et al. Nanoparticles that do not adhere to mucus provide uniform and long-lasting drug delivery to airways following inhalation. Science Advances. 2017;3:e1601556. doi: 10.1126/sciadv.1601556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lai Samuel K, Elizabeth O’Hanlon D, Harrold Suzanne, Man Stan T, Wang Ying-Ying, Cone Richard, Hanes Justin. Rapid transport of large polymeric nanoparticles in fresh undiluted human mucus. Proceedings of the National Academy of Sciences. 2007;104:1482–1487. doi: 10.1073/pnas.0608611104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.McKinley Scott A, Chen Alex, Shi Feng, Wang Simi, Mucha Peter J, Gregory Forest M, Lai Samuel K. Modeling neutralization kinetics of hiv by broadly neutralizing monoclonal antibodies in genital secretions coating the cervicovaginal mucosa. PloS one. 2014;9:e100598. doi: 10.1371/journal.pone.0100598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chen Alex, McKinley Scott A, Wang Simi, Shi Feng, Mucha Peter J, Gregory Forest M, Lai Samuel K. Transient antibody-mucin interactions produce a dynamic molecular shield against viral invasion. Biophysical Journal. 2014;106:2028–2036. doi: 10.1016/j.bpj.2014.02.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chen Alex, McKinley Scott A, Shi Feng, Wang Simi, Mucha Peter J, Harit Dimple, Gregory Forest M, Lai Samuel K. Modeling of virion collisions in cervicovaginal mucus reveals limits on agglutination as the protective mechanism of secretory immunoglobulin a. PloS one. 2015;10:e0131351. doi: 10.1371/journal.pone.0131351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wessler Timothy, Chen Alex, McKinley Scott A, Cone Richard, Gregory Forest M, Lai Samuel K. Using computational modeling to optimize the design of antibodies that trap viruses in mucus. ACS infectious diseases. 2015;2:82–92. doi: 10.1021/acsinfecdis.5b00108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hill David B, Vasquez Paula A, Mellnik John, McKinley Scott A, Vose Aaron, Mu Frank, Henderson Ashley G, Donaldson Scott H, Alexis Neil E, Boucher Richard C, Gregory Forest M. A biophysical basis for mucus solids concentration as a candidate biomarker for airways disease. PloS one. 2014;9:e87681. doi: 10.1371/journal.pone.0087681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lai Samuel K, Wang Ying-Ying, Hanes Justin. Mucus-penetrating nanoparticles for drug and gene delivery to mucosal tissues. Advanced drug delivery reviews. 2009;61:158–171. doi: 10.1016/j.addr.2008.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ensign Laura M, Cone Richard, Hanes Justin. Oral drug delivery with polymeric nanoparticles: the gastrointestinal mucus barriers. Advanced drug delivery reviews. 2012;64:557–570. doi: 10.1016/j.addr.2011.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lai Samuel K, Wang Ying-Ying, Hida Kaoru, Cone Richard, Hanes Justin. Nanoparticles reveal that human cervicovaginal mucus is riddled with pores larger than viruses. Proceedings of the National Academy of Sciences. 2010;107:598–603. doi: 10.1073/pnas.0911748107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schuster Benjamin S, Suk Jung Soo, Woodworth Graeme F, Hanes Justin. Nanoparticle diffusion in respiratory mucus from humans without lung disease. Biomaterials. 2013;34:3439–3446. doi: 10.1016/j.biomaterials.2013.01.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mason Thomas G. Estimating the viscoelastic moduli of complex fluids using the generalized stokes–einstein equation. Rheologica Acta. 2000;39:371–378. [Google Scholar]
- 46.Mellnik John WR, Lysy Martin, Vasquez Paula A, Pillai Natesh S, Hill David B, Cribb Jeremy, McKinley Scott A, Gregory Forest M. Maximum likelihood estimation for single particle, passive microrheology data with drift. Journal of Rheology. 2016;60:379–392. [Google Scholar]
- 47.Lysy Martin, Pillai Natesh S, Hill David B, Gregory Forest M, Mellnik John WR, Vasquez Paula A, McKinley Scott A. Model comparison and assessment for single particle tracking in biological fluids. Journal of the American Statistical Association. 2016;111:1413–1426. [Google Scholar]
- 48.Wang Ying-Ying, Nunn Kenetta L, Harit Dimple, McKinley Scott A, Lai Samuel K. Minimizing biases associated with tracking analysis of submicron particles in heterogeneous biological fluids. Journal of Controlled Release. 2015;220:37–43. doi: 10.1016/j.jconrel.2015.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Didier Gustavo, McKinley Scott A, Hill David B, Fricks John. Statistical challenges in microrheology. Journal of Time Series Analysis. 2012;33:724–743. [Google Scholar]
- 50.Fricks John, Yao Lingxing, Elston Timothy C, Gregory Forest M. Time-domain methods for diffusive transport in soft matter. SIAM JOURNAL ON APPLIED MATHEMATICS. 2008;69:1277–1308. doi: 10.1137/070695186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hohenegger C, Durr R, Senter DM. Mean first passage time in a thermally fluctuating viscoelastic fluid. Journal of Non-Newtonian Fluid Mechanics. 2017;242:48–56. [Google Scholar]
- 52.Szabo Attila, Schulten Klaus, Schulten Zan. First passage time approach to diffusion controlled reactions. The Journal of chemical physics. 1980;72:4350–4357. [Google Scholar]
- 53.Bicout DJ. Green’s functions and first passage time distributions for dynamic instability of microtubules. Phys Rev E. 1997;56:6656–6667. [Google Scholar]
- 54.Benichou O, Coppey M, Moreau M, Suet PH, Voituriez R. Optimal search strategies for hidden targets. Phys Rev Lett. 2005;94:198101. doi: 10.1103/PhysRevLett.94.198101. [DOI] [PubMed] [Google Scholar]
- 55.Holcman D, Schuss Z. Stochastic chemical reactions in microdomains. JOURNAL OF CHEMICAL PHYSICS. 2005;122 doi: 10.1063/1.1849155. [DOI] [PubMed] [Google Scholar]
- 56.Bressloff Paul C, Earnshaw Berton A, Ward Michael J. Diffusion of protein receptors on a cylindrical dendritic membrane with partially absorbing traps. SIAM J Appl Math. 2007;68:1223–1246. [Google Scholar]
- 57.Condamin S, Benichou O, Tejedor V, Voituriez R, Klafter J. First-passage times in complex scale-invariant media. Nature. 2007;450:77–80. doi: 10.1038/nature06201. [DOI] [PubMed] [Google Scholar]
- 58.Condamin S, Tejedor V, Voituriez R, Benichou O, Klafter J. Probing microscopic origins of confined subdiffusion by first-passage observables. Proc Natl Acad Sci U S A. 2008;105:5675–5680. doi: 10.1073/pnas.0712158105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Coombs Daniel, Straube Ronny, Ward Michael. Diffusion on a sphere with localized traps: mean first passage time, eigenvalue asymptotics, and Fekete points. SIAM J Appl Math. 2009;70:302–332. [Google Scholar]
- 60.Bressloff Paul C, Newby Jay M. Stochastic models of intracellular transport. Reviews of Modern Physics. 2013;85:135. [Google Scholar]
- 61.Metzler Ralf, Oshanin Gleb, Redner Sidney. First-passage phenomena and their applications. Vol. 35. World Scientific; 2014. [Google Scholar]
- 62.Gardiner CW. Handbook of stochastic methods for physics, chemistry, and the natural sciences. Vol. 13. Springer-Verlag; Berlin: 1983. [Google Scholar]
- 63.Carslaw HS, Jaeger JC. Conduction of heat in solids. 2. Clarendon Press; Oxford: 1959. [Google Scholar]
- 64.Redner Sidney. A guide to first-passage processes. Cambridge University Press; Cambridge, UK: 2001. [Google Scholar]
- 65.Berg HC, Purcell EM. Physics of chemoreception. Biophys J. 1977;20:193–219. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lau Andy WC, Lubensky Tom C. State-dependent diffusion: Thermodynamic consistency and its path integral formulation. Physical Review E. 2007;76:011123. doi: 10.1103/PhysRevE.76.011123. [DOI] [PubMed] [Google Scholar]
- 67.Sattin F. Fick’s law and fokker–planck equation in inhomogeneous environments. Physics Letters A. 2008;372:3941–3945. [Google Scholar]
- 68.Bossy Mireille, Gobet Emmanuel, Talay Denis. A symmetrized Euler scheme for an efficient approximation of reflected diffusions. Journal of Applied Probability. 2004;41:877–889. [Google Scholar]
- 69.Kubo R. The fluctuation-dissipation theorem. Reports on Progress in Physics. 1966;29:255–284. [Google Scholar]
- 70.Zwanzig R. Nonequilibrium statistical mechanics. Oxford University Press; 2001. [Google Scholar]
- 71.McKinley Scott A, Yao Lingxing, Gregory Forest M. Transient anomalous diffusion of tracer particles in soft matter. Journal of Rheology. 2009;53:1487–1506. [Google Scholar]
- 72.Henry BI, Langlands TAM, Straka P. An Introduction to Fractional Diffusion. In: Dewar RL, Detering F, editors. Complex Physical, Biophysical and Econophysical Systems. 2010. pp. 37–89. [Google Scholar]
- 73.Jeon JH, Chechkin AV, Metzler R. First Passage Phenomena and Their Applications. World Scientific; 2014. First passage behavior of multi-dimensional fractional Brownian motion and application to reaction phenomena; pp. 175–202. [Google Scholar]
- 74.Chaudhury Srabanti, Cherayil Binny J. Approximate first passage time distribution for barrier crossing in a double well under fractional gaussian noise. The Journal of Chemical Physics. 2006;125:114106. doi: 10.1063/1.2354089. [DOI] [PubMed] [Google Scholar]
- 75.Guérin T, Levernier N, Bénichou O, Voituriez R. Mean first-passage times of non-markovian random walkers in confinement. Nature. 2016;534:356–359. doi: 10.1038/nature18272. [DOI] [PubMed] [Google Scholar]
- 76.Whitt Ward. Stochastic-process limits: an introduction to stochastic-process limits and their application to queues. Springer Science & Business Media; 2002. [Google Scholar]
- 77.McGlaughlin Peter, Chronopoulou Alexandra. Discretization error of reflected fractional Brownian motion. Proceedings of the 2016 Winter Simulation Conference; Piscataway, NJ, USA: IEEE Press; 2016. pp. 270–276. [Google Scholar]
- 78.Dietrich CR, Newsam GN. A fast and exact method for multidimensional Gaussian stochastic simulations. Water Resources Research. 1993;29:2861–2869. [Google Scholar]
- 79.Wood Andrew TA, Chan Grace. Simulation of stationary Gaussian processes in [0, 1]d. Journal of Computational and Graphical Statistics. 1994;3:409–432. [Google Scholar]
- 80.Ling Yun, Lysy Martin. r package version 1.0. 2017. SuperGauss: Superfast Likelihood Inference for Stationary Gaussian Time Series. [Google Scholar]
- 81.Newby Jay M, Schaefer Alison M, Lee Phoebe T, Gregory Forest M, Lai Samuel K. Deep neural networks automate detection for tracking of submicron scale particles in 2d and 3d. 2017 doi: 10.1073/pnas.1804420115. arXiv preprint arXiv:1704.03009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Berkowitz M, Morgan JD, Andrew McCammon J. Generalized langevin dynamics simulations with arbitrary time-dependent memory kernels. The Journal of Chemical Physics. 1983;78:3256–3261. [Google Scholar]
- 83.Mukhopadhyay Abhishek, Xing Jianhua. Tech Rep. Virginia Polytechnic Institute and State University; 2013. A numerical procedure for model reduction using the generalized Langevin equation formalism. [Google Scholar]
- 84.Sanders Niek N, DE SMEDT STEFAANC, Van Rompaey Elsa, Simoens Paul, De Baets Frans, Demeester Joseph. Cystic fibrosis sputum: a barrier to the transport of nanospheres. American journal of respiratory and critical care medicine. 2000;162:1905–1911. doi: 10.1164/ajrccm.162.5.9909009. [DOI] [PubMed] [Google Scholar]
- 85.Sanders Niek N, De Smedt Stefaan C, Demeester Joseph. Mobility and stability of gene complexes in biogels. Journal of controlled release. 2003;87:117–129. doi: 10.1016/s0168-3659(02)00355-3. [DOI] [PubMed] [Google Scholar]
- 86.Khanvilkar Kavita, Donovan Maureen D, Flanagan Douglas R. Drug transfer through mucus. Advanced drug delivery reviews. 2001;48:173–193. doi: 10.1016/s0169-409x(01)00115-6. [DOI] [PubMed] [Google Scholar]
- 87.Desai MA, Mutlu M, Vadgama P. A study of macromolecular diffusion through native porcine mucus. Cellular and Molecular Life Sciences. 1992;48:22–26. doi: 10.1007/BF01923598. [DOI] [PubMed] [Google Scholar]
- 88.Larhed Agneta Wikman, Artursson Per, Gråsjö Johan, Björk Erik. Diffusion of drugs in native and purified gastrointestinal mucus. Journal of pharmaceutical sciences. 1997;86:660–665. doi: 10.1021/js960503w. [DOI] [PubMed] [Google Scholar]
- 89.Sanders Niek N, De Smedt Stefaan C, Demeester Joseph. The physical properties of biogels and their permeability for macromolecular drugs and colloidal drug carriers. Journal of pharmaceutical sciences. 2000;89:835–849. doi: 10.1002/1520-6017(200007)89:7<835::AID-JPS1>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 90.Norris Daniel A, Sinko Patrick J. Effect of size, surface charge, and hydrophobicity on the translocation of polystyrene microspheres through gastrointestinal mucin. Journal of applied polymer science. 1997;63:1481–1492. [Google Scholar]
- 91.Mark Saltzman W, Radomsky Michael L, Whaley Kevin J, Cone Richard A. Antibody diffusion in human cervical mucus. Biophysical journal. 1994;66:508–515. doi: 10.1016/s0006-3495(94)80802-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Braeckmans Kevin, Peeters Liesbeth, Sanders Niek N, De Smedt Stefaan C, Demeester Joseph. Three-dimensional fluorescence recovery after photobleaching with the confocal scanning laser microscope. Biophysical journal. 2003;85:2240–2252. doi: 10.1016/s0006-3495(03)74649-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Olmsted Stuart S, Padgett Janet L, Yudin Ashley I, Whaley Kevin J, Moench Thomas R, Cone Richard A. Diffusion of macromolecules and virus-like particles in human cervical mucus. Biophysical journal. 2001;81:1930–1937. doi: 10.1016/S0006-3495(01)75844-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Wang Ying-Ying, Schroeder Holly A, Nunn Kenetta L, Woods Karen, Anderson Deborah J, Lai Samuel K, Cone Richard A. Diffusion of immunoglobulin g in shed vaginal epithelial cells and in cell-free regions of human cervicovaginal mucus. PloS one. 2016;11:e0158338. doi: 10.1371/journal.pone.0158338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Nordgard Catherine Taylor, Nonstad Unni, Olderøy Magnus Ø, Espevik Terje, Draget Kurt I. Alterations in mucus barrier function and matrix structure induced by guluronate oligomers. Biomacromolecules. 2014;15:2294–2300. doi: 10.1021/bm500464b. [DOI] [PubMed] [Google Scholar]
- 96.Suh Junghae, Dawson Michelle, Hanes Justin. Real-time multiple-particle tracking: applications to drug and gene delivery. Advanced drug delivery reviews. 2005;57:63–78. doi: 10.1016/j.addr.2004.06.001. [DOI] [PubMed] [Google Scholar]
- 97.Vasconcellos Carol A, Allen Phillip G, Wohl Mary Ellen, Drazen Jeffrey M, Janmey Paul A, Stossel Thomas P, et al. Reduction in viscosity of cystic fibrosis sputum in vitro by gelsolin. Science-AAAS-Weekly Paper Edition-including Guide to Scientific Information. 1994;263:969–970. doi: 10.1126/science.8310295. [DOI] [PubMed] [Google Scholar]
- 98.Wang Ying-Ying, Lai Samuel K, So Conan, Schneider Craig, Cone Richard, Hanes Justin. Mucoadhesive nanoparticles may disrupt the protective human mucus barrier by altering its microstructure. PloS one. 2011;6:e21547. doi: 10.1371/journal.pone.0021547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Zhang Clark, Nance Elizabeth A, Mastorakos Panagiotis, Chisholm Jane, Berry Sneha, Eberhart Charles, Tyler Betty, Brem Henry, Suk Jung Soo, Hanes Justin. Convection enhanced delivery of cisplatin-loaded brain penetrating nanoparticles cures malignant glioma in rats. Journal of Controlled Release. 2017 doi: 10.1016/j.jconrel.2017.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Mastorakos Panagiotis, Da Silva Adriana L, Chisholm Jane, Song Eric, Choi Won Kyu, Boyle Michael P, Morales Marcelo M, Hanes Justin, Suk Jung Soo. Highly compacted biodegradable dna nanoparticles capable of overcoming the mucus barrier for inhaled lung gene therapy. Proceedings of the National Academy of Sciences. 2015;112:8720–8725. doi: 10.1073/pnas.1502281112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Duncan Gregg A, Jung James, Joseph Andrea, Thaxton Abigail L, West Natalie E, Boyle Michael P, Hanes Justin, Suk Jung Soo. Microstructural alterations of sputum in cystic fibrosis lung disease. JCI insight. 2016;1 doi: 10.1172/jci.insight.88198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Maisel Katharina, Ensign Laura, Reddy Mihika, Cone Richard, Hanes Justin. Effect of surface chemistry on nanoparticle interaction with gastrointestinal mucus and distribution in the gastrointestinal tract following oral and rectal administration in the mouse. Journal of Controlled Release. 2015;197:48–57. doi: 10.1016/j.jconrel.2014.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Nance Elizabeth, Zhang Clark, Shih Ting-Yu, Xu Qingguo, Schuster Benjamin S, Hanes Justin. Brain-penetrating nanoparticles improve paclitaxel efficacy in malignant glioma following local administration. ACS nano. 2014;8:10655–10664. doi: 10.1021/nn504210g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Ensign Laura M, Henning Andreas, Schneider Craig S, Maisel Katharina, Wang Ying-Ying, Porosoff Marc D, Cone Richard, Hanes Justin. Ex vivo characterization of particle transport in mucus secretions coating freshly excised mucosal tissues. Molecular pharmaceutics. 2013;10:2176–2182. doi: 10.1021/mp400087y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Suk Jung Soo, Lai Samuel K, Boylan Nicholas J, Dawson Michelle R, Boyle Michael P, Hanes Justin. Rapid transport of muco-inert nanoparticles in cystic fibrosis sputum treated with n-acetyl cysteine. Nanomedicine. 2011;6:365–375. doi: 10.2217/nnm.10.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Lai Samuel K, Suk Jung Soo, Pace Amanda, Wang Ying-Ying, Yang Ming, Mert Olcay, Chen Jeane, Kim Jean, Hanes Justin. Drug carrier nanoparticles that penetrate human chronic rhinosinusitis mucus. Biomaterials. 2011;32:6285–6290. doi: 10.1016/j.biomaterials.2011.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Dawson Michelle, Wirtz Denis, Hanes Justin. Enhanced viscoelasticity of human cystic fibrotic sputum correlates with increasing microheterogeneity in particle transport. Journal of Biological Chemistry. 2003;278:50393–50401. doi: 10.1074/jbc.M309026200. [DOI] [PubMed] [Google Scholar]
- 108.Schuster Benjamin S, Ensign Laura M, Allan Daniel B, Suk Jung Soo, Hanes Justin. Particle tracking in drug and gene delivery research: State-of-the-art applications and methods. Advanced drug delivery reviews. 2015;91:70–91. doi: 10.1016/j.addr.2015.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Lai Samuel K, Wang Ying-Ying, Wirtz Denis, Hanes Justin. Micro-and macrorheology of mucus. Advanced drug delivery reviews. 2009;61:86–100. doi: 10.1016/j.addr.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Ensign Laura M, Schneider Craig, Suk Jung Soo, Cone Richard, Hanes Justin. Mucus penetrating nanoparticles: biophysical tool and method of drug and gene delivery. Advanced Materials. 2012;24:3887–3894. doi: 10.1002/adma.201201800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.van Kampen NG. North-Holland personal library. 3. Elsevier; Amsterdam: 2007. Stochastic processes in physics and chemistry. [Google Scholar]
- 112.Bressloff Paul C. Stochastic processes in cell biology. Springer; 2014. [Google Scholar]
- 113.Suk Jung Soo, Boylan Nicholas J, Trehan Kanika, Tang Benjamin C, Schneider Craig S, Lin Jung-Ming G, Boyle Michael P, Zeitlin Pamela L, Lai Samuel K, Cooper Mark J, et al. N-acetylcysteine enhances cystic fibrosis sputum penetration and airway gene transfer by highly compacted dna nanoparticles. Molecular Therapy. 2011;19:1981–1989. doi: 10.1038/mt.2011.160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Murgia Xabier, Pawelzyk Paul, Schaefer Ulrich F, Wagner Christian, Willenbacher Norbert, Lehr Claus-Michael. Size-limited penetration of nanoparticles into porcine respiratory mucus after aerosol deposition. Biomacromolecules. 2016;17:1536–1542. doi: 10.1021/acs.biomac.6b00164. [DOI] [PubMed] [Google Scholar]
- 115.Crocker John C, Grier David G. Methods of digital video microscopy for colloidal studies. Journal of colloid and interface science. 1996;179:298–310. [Google Scholar]
- 116.Parthasarathy Raghuveer. Rapid, accurate particle tracking by calculation of radial symmetry centers. Nature Methods. 2012;9:724–726. doi: 10.1038/nmeth.2071. [DOI] [PubMed] [Google Scholar]
- 117.Krizhevsky Alex, Sutskever Ilya, Hinton Geoffrey E. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems. 2012:1097–1105. [Google Scholar]
- 118.Long Jonathan, Shelhamer Evan, Darrell Trevor. Fully convolutional networks for semantic segmentation. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015:3431–3440. doi: 10.1109/TPAMI.2016.2572683. [DOI] [PubMed] [Google Scholar]