Properties of Global and Local Ancestry Adjustments in Genetic Association Tests in Admixed Populations

Abstract

Population substructure can lead to confounding in tests for genetic association, and failure to adjust properly can result in spurious findings. Here we address this issue of confounding by considering the impact of global ancestry (average ancestry across the genome) and local ancestry (ancestry at a specific chromosomal location) on regression parameters and relative power in ancestry adjusted and unadjusted models. We examine theoretical expectations under different scenarios for population substructure; applying different regression models, verifying and generalizing using simulations, and exploring the findings in real-world admixed populations. We show that admixture does not lead to confounding when the trait locus is tested directly in a single admixed population. However, if there is more complex population structure or a marker locus in linkage disequilibrium (LD) with the trait locus is tested, both global and local ancestry can be confounders. Additionally, we show the genotype parameters of adjusted and unadjusted models all provide tests for LD between the marker and trait locus, but in different contexts. The local-ancestry adjusted model tests for LD in the ancestral populations; while tests using the unadjusted and the global-ancestry adjusted models depend on LD in the admixed population(s), which may be enriched due to different ancestral allele frequencies. Practically, this implies that global-ancestry adjustment should be used for screening, but local-ancestry adjustment may better inform fine-mapping and provide better effect estimates at trait loci.

1. INTRODUCTION

It is well known that ancestry differences among individuals can lead to confounding in tests of association between genes and a phenotype (Chakraborty & Weiss, 1988). Allele frequencies may differ depending on ancestry, as may trait values or disease prevalence, and this can lead to spurious associations if not properly accounted for in analyses. For this reason, it has become standard practice for genetic association tests to adjust for covariates that capture the background ancestry of study subjects. Prior to the genome-wide association study (GWAS) era, studies often relied on self-reported race and ethnicity. With the availability of dense, genome-wide genotyping, it became feasible to estimate ancestry from genetic markers, giving an assessment of ancestry that reflects the true genetic ancestry of the individual, rather than assessment that reflects cultural or societal perceptions (Burnett et al., 2006; Pasaniuc et al., 2011; Rosenberg, Li, Ward, & Pritchard, 2003). Often GWAS use principal component analysis to model ancestry differences among study participants (Price et al., 2006), though other methods are available (Alexander, Novembre, & Lange, 2009; Alexander & Lange, 2011; Cox & Cox, 2001; Falush, Stephens, & Pritchard, 2003; Hubisz, Falush, Stephens, & Pritchard, 2009; Pritchard, Stephens, & Donnelly, 2000; Tang, Peng, Wang, & Risch, 2005). Under many scenarios, the top principal components (PCs) from genome-wide array data are highly correlated with underlying ancestry. Thus, such PCs provide surrogate measures of “global” ancestry—that is, a picture of an individual’s average ancestral origin across the genome—and can be used as covariates in regression models for association analysis (Adeyemo et al., 2015; Armstrong et al., 2014; Beecham et al., 2014; Cruchaga et al., 2013; Melton et al., 2013; Naj et al., 2011; Nalls et al., 2014). However, global ancestry is not always representative of ancestry at individual genomic loci. The genome of admixed individuals is composed of stretches of DNA from different ancestral origins that are not always consistent with the global measure. This “local” ancestry can be estimated using a variety of statistical methods (Baran et al., 2012; Maples, Gravel, Kenny, & Bustamante, 2013) and offers a more fine-scale measure of genetic ancestry. However, outside of admixture mapping, few GWAS have used local ancestry in their association analyses (Baran et al., 2012; Pino-Yanes et al., 2015).

Recently some studies have begun to examine the properties of models adjusted for local ancestry and compare the behavior of hypothesis tests (e.g., power and Type I error) using local- and global-ancestry adjusted models. Liu et al (Liu, Lewinger, Gilliland, Gauderman, & Conti, 2013) argued that global-ancestry adjustment is sufficient to control Type I error, but local-ancestry adjustment can improve power when the LD in the ancestral populations and the correlation between genotype and ancestry in the admixed population are in the opposite direction. Zhang and Stram (2014) showed that adjusting for global ancestry is largely sufficient to control Type I error in their simulated model, but found that adjusting for local ancestry generally leads to lower power compared to adjusting for global ancestry, particularly for markers with large ancestral allele frequency differences. Wang et al (2011) pointed out that adjustment for global ancestry may not be sufficient to control Type I error when forces such as selection may be acting to create a local-ancestry effect near the test locus.

Here we seek to expand on these studies and develop a comprehensive picture of the impact of global- and local-ancestry adjustment in regression analysis for genetic studies in admixed populations. This includes a taking a formal look at statistical confounding, the forms of regression parameters under different adjustments, and approximations for relative power. Formulating these properties in terms of genetic parameters (e.g., allele frequencies, coefficients of linkage disequilibrium (LD), admixture proportions) under specific models of population structure allows us both to address questions of when and how to adjust for ancestry and to better interpret hypothesis tests and regression parameter estimates. Throughout, we consider both a single admixed population and a stratified admixed population (composed of two non-intermating admixed subpopulations), under a quantitative genetic model. We use simulations to validate our theoretical results and illustrate findings with numerical examples. Finally, because we find that LD in the ancestral populations and admixed populations are key parameters driving differences in regression models, we use genome-wide single-nucleotide polymorphism (SNP) data generated in samples from the Genomic Origins and Admixture in Latinos (GOAL) study and other public data to examine LD in admixed and non-admixed samples; thereby placing our findings in the context of contemporary admixed populations.

2. METHODS

2.1 Confounding in linear regression models

The definition of a confounding variable is one that is related to both the outcome (dependent variable) and the predictor (independent variable). Consider the adjusted linear model:

$$E(Y|X_1,X_2)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2,$$ (1)

where Y is the outcome variable (a continuous quantitative variable), X₁ is the predictor variable being tested and X₂ is a potential confounder for which we are adjusting. Formally, X₂ is a confounder if and only if both of the following conditions hold:

1. $${\rho }_{12}^2\ne 0$$
2. $${\rho }_{Y2,1}^2\ne 0(\text{equivalent to }{\beta }_2\ne 0),$$ (2)

where ${\rho }_{12}^2$ is the squared correlation coefficient between X₁ and X₂, and ${\rho }_{Y2,1}^2=\frac{{({\rho }_{Y2}-{\rho }_{Y1}{\rho }_{12})}^2}{(1-{\rho }_{Y1}^2)(1-{\rho }_{12}^2)}$ is the partial squared correlation coefficient of Y and X₂ with X₁ fixed (Robinson & Jewell, 1991). This means that X₂ is a confounder if it is correlated with both the predictor (X₁) and with the outcome Y after removing the effect of the predictor. Note that condition (ii) is not the same as saying that X₂ and Y are correlated. They may in fact be correlated, but if that correlation is explained solely by the relationship between X₁ and X₂ and the effect of X₁ on Y, then X₂ is not a true confounder.

If the conditions in (2) both hold, so that X₂ is a confounder, then we must include X₂ in the model to ensure valid inference about the effect of X₁ on Y; otherwise, adjustment for X₂ is not necessary to obtain valid inference about the effect of X₁ on Y. There are cases, however in which it may still be desirable with respect to power to adjust for a non-confounding variable (Robinson & Jewell, 1991). Specifically, suppose we consider testing the null hypothesis β₁ = 0. If condition (ii) holds but (i) does not, then adjusting for X₂ will increase power relative to power in the unadjusted model. If condition (i) holds but (ii) does not, then the adjusting for X₂ will decrease power relative to the unadjusted model. If neither condition holds, then the powers of the adjusted and unadjusted models are largely equivalent. This leads to the general conclusion for linear regression that adjusting for a covariate that is correlated with outcome (after removing the effect of variable of interest) is desirable with respect to power. However, there is no benefit to adjusting for a variable that is not correlated with outcome; and furthermore, such adjustment is undesirable when the covariate is also correlated with the predictor of interest.

2.2 Regression parameters

In the multiple regression equation shown above (1), the unstandardized regression coefficient β₁ takes the following form:

$${\beta }_1=\sqrt{\frac{V_Y}{V_1}}\left(\frac{{\rho }_{Y1}-{\rho }_{Y2}{\rho }_{12}}{1-{\rho }_{12}^2}\right),$$ (3)

where V_Y and V₁ are the variances of Y and X₁ respectively, and the other terms are correlation coefficients. If X₂ is not a confounder (i.e., either condition i or ii of (2) fail), then the regression coefficient is equivalent to the coefficient from the univariate model with X₁ alone:

$${\beta }_1=\frac{C_{Y1}}{V_1},$$ (4)

where C_Y1 is the covariance between Y and X₁. However, if X₂ is a confounder, the equivalence no longer holds. Thus, adjusting by a confounding variable changes the interpretation of β₁ in the adjusted model compared to the coefficient in the unadjusted model. Understanding how the form of the regression coefficient being tested changes in terms of population genetic parameters, in unadjusted models or with covariate adjustment in the presence of confounding, is key to interpreting hypothesis tests. Failure to include confounding variables in the model can lead to what is known as specification bias, when parameters do not correctly model the desired effect because their relationship is confounded by an important omitted variable.

2.3 Asymptotic relative precision (ARP) and power

To compare the performance of estimators from adjusted and unadjusted regression models, we examined the asymptotic relative precision (ARP) of the models. This is the ratio of the variance of the estimate of the regression parameter (β̂_UN) in an unadjusted model containing only X₁ to the variance of the parameter estimate β̂₁ in the adjusted model (1):

$$\text{ARP}({\hat{\beta }}_1,{\hat{\beta }}_{\mathit{\text{UN}}})=\frac{\mathit{\text{Var}}({\hat{\beta }}_{\mathit{\text{UN}}})}{\mathit{\text{Var}}({\hat{\beta }}_1)}=\frac{1-{\rho }_{12}^2}{1-{\rho }_{Y2,1}^2}.$$ (5)

When ARP(β̂₁, β̂_UN) > 1, the adjusted model leads to greater precision (smaller variance for beta estimate); when ARP(β̂₁, β̂_UN) < 1, the unadjusted model leads to greater precision. Precision is a measure of variance of the beta estimator. When the expected values of the beta estimators in the adjusted and unadjusted models are the same (which happens when there is no confounding), then ARP is related directly to relative power. Specifically in this case, ARP is equivalent to Asymptotic Relative Efficiency (ARE), which represents the ratio of required sample sizes for the tests to have equivalent power asymptotically (Serfling, 2009). We note that these statements are about the large-sample (asymptotic) behavior of tests, and conclusions may not hold in small samples.

2.4 Population and genetic models

We examined the correlation coefficients (2), regression parameters (3), and ARP (5) in the context of two different genetic models of population structure: (1) a single admixed population with two source ancestral populations (e.g., African Americans); and (2) a stratified admixed population composed of two subpopulations, each of which is itself admixed from two source ancestral populations (e.g., Haitians and Dominicans in Hispañola). We considered a quantitative trait locus (QTL) and “marker” loci with varying levels of LD dependent on recombination and population dynamics. Table I defines the notation used in the following sections.

Table I.

Table of Notation

Single Admixed Population
Random Variables
G		QTL Genotype
L		Marker Genotype
Y		Quantitative Trait
A		Local Ancestry
Ā		Global Ancestry
Constants
K		number of chromosomes
m		number of markers per chromosome
M = mK		total number of markers
Parameters
a		genetic effect of QTL
σ2		Within-genotype variance of quantitative trait
q		probability any locus on a random haplotype is from ancestral population 1
rjk		recombination probability between locus j and k
ru		recombination probability between loci on different chromosomes
$\phi =1-\left(\frac{K-1}{K}\right)r_U-\frac{1}{\mathit{\text{Mm}}}{\sum }_{j=1}^m{\sum }_{k\ne j}^m{r}_{\mathit{\text{jk}}};$		Functions of recombination probabilities, where g is QTL and l is marker locus
${\phi }_g=1-\left(\frac{K-1}{K}\right)r_U-\frac{1}{M}{\sum }_{j\ne g}^m{r}_{\mathit{\text{gj}}};$
${\phi }_l=1-\left(\frac{K-1}{K}\right)r_U-\frac{1}{M}{\sum }_{j\ne l}^m{r}_{\mathit{\text{lj}}}$
QTL	Marker
pi	pLi	allele frequency in ancestral population i, for i = 0,1
Δ = p1 − p0	ΔL = pL1 − pL0	ancestral allele frequency difference
p* = qp1 + (1 − q)p0	$p_L^{\ast }={\mathit{\text{qp}}}_{L1}+(1-q)p_{L0}$	allele frequency in the admixed population
γ = qp1(1 − p1) + (1 − q)p0(1 − p0)	γL = qpL1(1 − pL1) + (1 − q)pL0(1 − pL0)	average variance of allele frequency in the admixed population
Di = PTLi − pLipi		disequilibrium coefficient between marker and QTL alleles in ancestral population i
D* = (1 − rgl)(W + q(1 − q)ΔΔL)		disequilibrium coefficient in admixed population
W = qD1 + (1 − q)D0		average disequilibrium coefficient
Stratified Admixed Populations
Random Variables
S		admixed subpopulation membership
Parameters
c		shift in mean quantitative trait value in subpopulation 1 compared to subpopulation 0
Q		probability of being in subpopulation 1
qs		probability any locus on a random haplotype in subpopulation s is from ancestral population 1
α = Qq1 + (1 − Q)q0		average ancestry in stratified population
δ = Q(1 − Q)(q1 − q0)2		covariance of ancestry of different haplotypes at the same locus within an individual
ω = α(1 − α) − δ = Qq1(1 − q1) + (1 − Q)q0(1 − q0)		convenient function of population structure parameters
QTL	Marker
$p_s^{\ast }=q_s{p}_1+(1-q_s)p_0$	$p_{\mathit{\text{Ls}}}^{\ast }=q_s{p}_{L1}+(1-q_s)p_{L0}$	allele frequency in subpopulation s, for s = 0,1
$p\prime ={\mathit{\text{Qp}}}_1^{\ast }+(1-Q)p_0^{\ast }=\alpha p_1+(1-\alpha )p_0$	$p_L^{\prime }={\mathit{\text{Qp}}}_{L1}^{\ast }+(1-Q)p_{L0}^{\ast }=\alpha p_{L1}+(1-\alpha )p_{L0}$	allele frequency in stratified population
γ′ = αp1(1 − p1) + (1 − α)p0(1 − p0)	γL′ = αpL1(1 − pL1) + (1 − α)pL0(1 − pL0)	average variance of allele frequency in stratified population
$D_s^{\ast }=(1-r_{\mathit{\text{gl}}})(W_s+q_s(1-q_s)\mathrm{\Delta }{\mathrm{\Delta }}_L)$		disequilibrium coefficient in sth subpopulation
Ws = qsD1 + (1 − qs)D0		average disequilibrium coefficient in subpopulation s
$D^{\ast \ast }={\mathit{\text{QD}}}_1^{\ast }+(1-Q)D_0^{\ast }+Q(1-Q){(q_1-q_0)}^2\mathrm{\Delta }{\mathrm{\Delta }}_L=(1-r_{\mathit{\text{gl}}})(W^{\ast }+\omega \mathrm{\Delta }{\mathrm{\Delta }}_L)+\delta \mathrm{\Delta }{\mathrm{\Delta }}_L$		disequilibrium coefficient in stratified population
W* = QW1 + (1 − Q)W0		average disequilibrium coefficient over subpopulations

2.4.1 Single admixed population model

For this model, we assume that there is initial mixing of two diploid ancestral populations with proportion q of the chromosomes originating from ancestral population 1. Following the initial mixing, we assume that there has been random mating within the admixed population for some number of generations, but for simplicity no additional migration. Suppose that each haplotype of an individual is broken into K chromosomes, each with m distinct biallelic loci (total M = mK loci). Here we use the term “haplotype” to refer to the entire set of chromosomes inherited from one parent (parental gamete). We define the recombination probability between any two loci j and k on the same chromosome, r_jk, as the chance that there has been some crossover event between the two loci since the initial mixing. For any pair of loci on different chromosomes (on the same haplotype), r_u is the probability that the gamete has recombined (or assorted with a non-gametic allele) since the initial admixture. For a single generation, r_u is expect to be ½. In general, the probabilities r_jk and r_u are functions of the crossover rate between a pair of loci and the number of generations since initial admixture.

In the admixed population, at each locus, the alleles of the two haplotypes each descend from ancestral population 1 or 0. For the hth haplotype at the jth locus, we define

$$\begin{array}{cc}\hfill A_{\mathit{\text{hj}}}=& 1\text{ if the jth locus descends from ancestral population }1\hfill \\ \hfill & 0\text{ if the jth locus descends from ancestral population }0.\hfill \end{array}$$ (6)

Initially the A_hj are the same for all j, but recombination begins to break down the correlation across the genome. Averaging over the two haplotypes within an individual, A_·j = (A_1j + A_2j)/2, gives a measure of local ancestry for the jth locus for the individual. As a global measure of ancestry, we use the average of local ancestry measures across all loci (and both haplotypes):

$$\overline{A}=\frac{{\sum }_{j=1}^M{A}_{·j}}{M},$$ (7)

where M is the total number of loci across the genome.

We suppose that there is a biallelic QTL with alleles T₁ and T₂, where p_i =the frequency of allele T₁ in ancestral population i, for i = 0,1. For the trait model, we assume allele effects at the QTL are additive so that the trait has the following conditional distribution:

$$Y~\{\begin{array}{c}\hfill N(a,{\sigma }^2)\text{ if }{T}_1{T}_1\hfill \\ \hfill N(0,{\sigma }^2)\text{ if }{T}_1{T}_2\hfill \\ \hfill N(-a,{\sigma }^2)\text{ if }{T}_2{T}_2\hfill \end{array}.$$ (8)

We define the genotypic random variable for the QTL:

$$G=\{\begin{array}{c}\hfill 1\text{ if }{T}_1{T}_1\hfill \\ \hfill 0\text{ if }{T}_1{T}_2\hfill \\ \hfill -1\text{ if }{T}_2{T}_2\hfill \end{array}.$$ (9)

We also consider a marker locus with two alleles (L₁ and L₂), where p_Li =the frequency of allele L₁ in ancestral population i, for i = 0,1, and define the genotypic random variable:

$$L=\{\begin{array}{c}\hfill 1\text{ if }{L}_1{L}_1\hfill \\ \hfill 0\text{ if }{L}_1{L}_2\hfill \\ \hfill -1\text{ if }{L}_2{L}_2\hfill \end{array}.$$ (10)

The LD coefficient between alleles at the QTL (T₁) and marker (L₁) in ancestral population i is defined as follows:

$$D_i=P_{\mathit{\text{TLi}}}-p_{\mathit{\text{Li}}}{p}_i,$$ (11)

where P_TLi is the frequency of the haplotype carrying T₁ and L₁ in ancestral population i. The LD in the admixed population depends on the LD in ancestral populations, the mixing proportion (q), the ancestral allele frequency differences at the QTL (Δ = p₁ − p₀) and marker (Δ_L = p_L1 − p_L0), and probability that there has been a recombination event between QTL and marker (r_gl):

$$D^{\ast }=(1-r_{\mathit{\text{gl}}})(W+q(1-q)\mathrm{\Delta }{\mathrm{\Delta }}_L),$$ (12)

where W = qD₁ + (1 − q)D₀ is the weighted average of LD coefficients in the ancestral populations.

2.4.2 Stratified admixed population model

For this model, we assume a population stratified into two admixed subpopulations: subpopulation 0 and 1 (Appendix B.3 extends the model to >2 subpopulations). Let Q be the probability that a random individual sampled from the whole population is from subpopulation 0. Suppose that for subpopulation s (s = 0,1), each locus is sampled from one of the two ancestral populations, and let q_s be the probability a locus is from ancestral population 1. For the QTL, we assume Hardy-Weinberg equilibrium (HWE) within each subpopulation, but not necessarily in the overall population (e.g., no intermating between subpopulations). Let subpopulation membership for an individual be denoted by the random variable,

$$\begin{array}{cc}\hfill S=& 1\text{ if the individual is in subpopulation }1\hfill \\ \hfill & 0\text{ if the individual is in subpopulation }0.\hfill \end{array}$$

We let the trait within subpopulation 0 be defined as above in the single admixed population (8), but for subpopulation 1, assume the following trait model:

$$Y~\{\begin{array}{cc}N(c+a,{\sigma }^2)\hfill & \text{if }{T}_1{T}_1\hfill \\ N(c,{\sigma }^2)\hfill & \text{if }{T}_1{T}_2\hfill \\ N(c-a,{\sigma }^2)\hfill & \text{if }{T}_2{T}_2\hfill \end{array}.$$ (13)

That is, both subpopulations have the same additive genetic effect (a), but subpopulation 1 has its mean trait value increased by a constant, c. This model would be reasonable, for example, if there was an independent environmental factor that increased the baseline value of the trait in subpopulation 1 (or lowered it in population 0) or independent genes that increased/decreased the baseline trait value.

Genotypic variables (G and L) for the trait locus and marker loci are defined as above (9 and 10). For marker loci in the stratified admixed population we must consider LD between marker and trait loci in the ancestral populations, D₀ and D₁, and LD in the admixed subpopulations, s=0 and 1 (similar to equation 12):

$$D_s^{\ast }=(1-r_{\mathit{\text{gl}}})(W_s+q_s(1-q_s)\mathrm{\Delta }{\mathrm{\Delta }}_L),$$

where W_s = q_sD₁ + (1 − q_s)D₀, the weighted disequilibrium coefficient in subpopulation s. The LD coefficient for the stratified population as a whole depends on LD in the ancestral populations (W* = QW₁ + (1 − Q)W₀), the ancestral allele frequency differences (Δ and Δ_L), and functions of both the mixing parameters and relative size of the subpopulations (ω = Qq₁(1 − q₁) + (1 − Q)q₀(1 − q₀) and δ = Q(1 − Q)(q₁ − q₀)²). The LD coefficient in the stratified population can be written as follows (see Appendix B.2.1):

$$D^{\ast \ast }=(1-r_{\mathit{\text{gl}}})(W^{\ast }+\mathrm{\omega }\mathrm{\Delta }{\mathrm{\Delta }}_L)+\mathrm{\delta }\mathrm{\Delta }{\mathrm{\Delta }}_L.$$ (14)

We see that like D*, the coefficient D** also depends on the recombination probability, r_gl, and decreases with increasing recombination; however, the term δΔΔ_L represents LD that results from the stratification (as a result of non-intermating between subpopulations) and is not influenced by recombination within the subpopulations.

2.5 Simulations

We performed simulations to test our theoretical conclusions using simuPOP (Peng & Kimmel, 2005), a forward-time population genetics simulation program. Genotype data and phenotype data were generated for single admixed and stratified admixed populations; then data were analyzed with regression models using different ancestry adjustments. Details of simulations are provided in Supplemental Material.

2.6 Analysis of LD in admixed and non-admixed datasets

2.6.1 Datasets

We estimated LD in seven different admixed datasets and three non-admixed “ancestral” datasets. Each of these would be comparable to our single-admixed population model but with three-way admixture rather than the simpler two-way admixture considered in our theory. Datasets included primarily family trios and parent-child pairs. The admixed datasets include samples from the GOAL study (Moreno-Estrada et al., 2013) sampled in South Florida with origins from five Caribbean countries: Colombia (39 individuals from 18 families), Honduras (24 individuals from 8 families), Cuba (60 individuals from 20 families), Puerto Rico (48 individuals from 16 families), Dominican Republic (27 individuals from 9 families). We also included four datasets from the 1000-Genomes Project (1000 Genomes Project Consortium et al., 2015): Mexican (MXL 64 individuals) and African American (ASW 61 individuals) admixed datasets, and two non-admixed datasets of European (CEU 99 individuals) and West African (YRI 107 individuals) individuals. Finally, a third ancestral population was included: 56 Native American samples from the Human Genome Diversity Project (includes Colombians, Karitiana, Maya, and Pima) (Cann et al., 2002). GWAS array data (1000 Genomes Project Consortium et al., 2015; Moreno-Estrada et al., 2013) were merged across datasets and 500 SNPs were selected on chromosome 20 to provide a range of intermarker distances. To represent unlinked markers, 500 SNPs were also selected on chromosome 21. SNPs were not selected on the basis of allele frequency. Genotypes from these SNPs were used for LD calculations.

2.6.2 Estimation of disequilibrium coefficient

Plink version 1.07 was used to estimate haplotype frequencies in the nine different datasets (Purcell et al., 2007). First, all founders were phased by Plink using the E-M algorithm; then all descendants of these founders were phased given the set of possible parental phases and assuming random-mating. Haplotype frequencies were then estimated from phased data and the LD coefficient was computed from these estimates as the difference between haplotype frequency and the product of respective allele frequencies. Haplotypes were matched across datasets to ensure consistency of the sign of the LD coefficient. R version 3.0.1 was used for computations with haplotype frequencies and plots of LD. In addition, we computed an estimate of W for each admixed population using previous estimates of mixing proportions (Bryc, Durand, Macpherson, Reich, & Mountain, 2015; Johnson et al., 2011; Moreno-Estrada et al., 2013) and LD estimates from the three ancestral datasets.

3. RESULTS

3.1 Observations based on theory

For each of the population models, we evaluated the conditions of confounding on measures of local and global ancestry, and examined the form of the regression parameters from unadjusted and adjusted regression models (Table II). We considered tests of genotype-phenotype association at the QTL itself and at marker locus, taking into account LD. Where appropriate we examined ARP to compare the relative power of tests with different adjustments.

Table II.

Regression models for tests at the QTL and marker adjusted by ancestry or subpopulation membership covariates.

	Testing QTL	Testing Marker
Unadjusted (UN)	E(Y|G) = β0 + βG G	E(Y|L) = βL0 + βL L
Local-ancestry adjusted (LA)	$E(Y|G,A_{·g})={\beta }_0^{\ast }+{\beta }_G^{\ast }G+{\beta }_A^{\ast }{A}_{·g}$	$E(Y|L,A_{·l})={\beta }_{L0}^{\ast }+{\beta }_L^{\ast }L+{\beta }_{\mathit{\text{LA}}}^{\ast }{A}_{·l}$
Global-ancestry adjusted (GA)	$E(Y|G,\overline{A})={\beta }_0^{\prime }+{\beta }_G^{\prime }G+{\beta }_{\overline{A}}^{\prime }\overline{A}$	$E(Y|L,\overline{A})={\beta }_{L0}^{\prime }+{\beta }_L^{\prime }L+{\beta }_{\mathit{\text{L}}\overline{\mathit{\text{A}}}}^{\prime }\overline{A}$
Subpopulation-membership adjusted (MA)	$E(Y|G,S)={\beta }_0^{″}+{\beta }_G^{″}G+{\beta }_S^{″}S$	$E(Y|L,S)={\beta }_{L0}^{″}+{\beta }_L^{″}L+{\beta }_{\mathit{\text{LS}}}^{″}S$

3.1.1 Single admixed population

3.1.1.1 Testing at the QTL

Suppose that we have measured the trait and the QTL genotype. We first asked whether local and/or global measures of ancestry are confounders by evaluating the conditions i and ii in (2). The relevant correlations for the two conditions are derived in Appendix A.1. We found that for both local and global ancestry, the partial correlations required to evaluate condition 2ii are always $0({\rho }_{\mathit{\text{YA}},G}^2=0\text{ and }{\rho }_{Y\overline{A},G}^2=0)$. This makes sense because at the QTL, once genotype is known, ancestry provides no additional information. It follows that neither local nor global ancestry are confounders for the relationship between the QTL genotype and trait in this scenario.

Since neither local nor global ancestry measures are confounders, the regression parameters in the unadjusted and both adjusted models should all take the same form. It is easy to show (see Appendix A.1.5) that the genotype-term regression parameters for the unadjusted, local-ancestry adjusted and global-ancestry adjusted models are ${\beta }_G={\beta }_G^{\ast }={\beta }_G^{\prime }=a$, respectively (Table III); thus all models correctly model the true genetic effect.

Table III.

Regression coefficients for the genotype term in single admixed and stratified admixed populations. Regression models are the unadjusted model (UN) and models adjusted for local ancestry (LA), global ancestry (GA), and subpopulation membership (MA) (only for stratified admixed populations).

Model	Regression Coefficient
Single Admixed Population
At QTL
UN	βG = a
LA	${\beta }_G^{\ast }=a$
GA	${\beta }_G^{\prime }=a$
At Marker
UN	${\beta }_L=\frac{{\mathit{\text{aD}}}^{\ast }}{q(1-q){\mathrm{\Delta }}_L^2+{\gamma }_L}$
LA	${\beta }_L^{\ast }=\frac{a(1-r_{\mathit{\text{gl}}})W}{{\gamma }_L}$
GA	${\beta }_L^{\prime }=\frac{a[D^{\ast }-q(1-q)\mathrm{\Delta }{\mathrm{\Delta }}_L\frac{{\phi }_g{\phi }_l}{\phi }]}{q(1-q){\mathrm{\Delta }}_L^2(1-\frac{{\phi }_l^2}{\phi })+{\gamma }_L}$
Stratified Admixed Population
At QTL
UN	${\beta }_G=a+\frac{cQ(1-Q)(q_1-q_0)\mathrm{\Delta }}{(\omega +2\delta ){\mathrm{\Delta }}^2+\gamma \prime }$
LA	${\beta }_G^{\ast }=a$
GA	${\beta }_G^{\prime }=a+c\frac{Q(1-Q)(q_1-q_0)\omega \mathrm{\Delta }\frac{(\phi -{\phi }_g)}{(\omega \phi +2\delta )}}{[(\omega +2\delta )-\frac{{(\omega {\phi }_g+2\delta )}^2}{(\omega \phi +2\delta )}]{\mathrm{\Delta }}^2+\gamma \prime }$
MA	${\beta }_G^{″}=a$
At Marker
UN	${\beta }_L=\frac{a(D^{\ast \ast }+\delta \mathrm{\Delta }{\mathrm{\Delta }}_L)+\mathit{\text{cQ}}(1-Q)(q_1-q_0){\mathrm{\Delta }}_L}{(\omega +2\delta ){\mathrm{\Delta }}_L^2+{\gamma }_L^{\prime }}$
LA	${\beta }_L^{\ast }=\frac{a(1-r_{\mathit{\text{gl}}})W^{\ast }}{{\gamma }_L^{\prime }}$
GA	${\beta }_L^{\prime }=\frac{a[(D^{\ast \ast }+\delta \mathrm{\Delta }{\mathrm{\Delta }}_L)-\mathrm{\Delta }{\mathrm{\Delta }}_L\frac{(\omega {\phi }_g+2\delta )(\omega {\phi }_l+2\delta )}{(\omega \phi +2\delta )}]+cQ(1-Q)(q_1-q_0){\mathrm{\Delta }}_L\omega \frac{(\phi -{\phi }_l)}{(\omega \phi +2\delta )}}{{\mathrm{\Delta }}_L^2[(\omega +2\delta )-\frac{{(\omega {\phi }_l+2\delta )}^2}{(\omega \phi +2\delta )}]+{\gamma }_L^{\prime }}$
MA	${\beta }_L^{″}=\frac{a(D^{\ast \ast }-\delta \mathrm{\Delta }{\mathrm{\Delta }}_L)}{\omega {\mathrm{\Delta }}_L^2+{\gamma }_L^{\prime }}$

Even though ancestry is not a confounder, and thus not a necessary covariate, we can explore the consequence of adjustment on statistical power. Since each model correctly estimates the same parameter, we can use ARP as a measure of relative power (or more precisely, the relative sample size required to achieve equivalent power). Because the partial correlations are 0 for both the local and global ancestry measures, the ARPs comparing the estimates from the adjusted models to unadjusted models are the following:

$$\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G)=1-{\rho }_{\mathit{\text{GA}}}^2\text{ and ARP}({\hat{\beta }}_G^{\prime },{\hat{\beta }}_G)=1-{\rho }_{G\overline{A}}^2.$$

These ARPs are clearly both always less than or equal to 1, and it follows that the test of the genetic effect in either ancestry adjusted model will always be less powerful than the test based on the unadjusted model.

We can further describe the relationship between $\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G)$ and $\text{ARP}({\hat{\beta }}_G^{\prime },{\hat{\beta }}_G)$, by noticing that ${\rho }_{G\overline{A}}^2=\left(\frac{{\phi }_g^2}{\phi }\right){\rho }_{\mathit{\text{GA}}}^2$, where $\phi =1-\left(\frac{K-1}{K}\right)r_U-\frac{1}{\mathit{\text{Mm}}}{\sum }_{j=1}^m{\sum }_{k\ne j}^m{r}_{\mathit{\text{jk}}}$ and ${\phi }_g=1-\left(\frac{K-1}{K}\right)r_U-\frac{1}{M}{\sum }_{j\ne g}^m{r}_{\mathit{\text{gj}}}$ (see Appendix A.1.5). The first equation, φ, involves the sum over all pairwise recombination probabilities and the second equation, φ_g, involves the sum of recombination probabilities between each locus and the QTL (locus g). We show in Appendix C and Supplemental Figure 2 that $1\ge \left(\frac{{\phi }_g^2}{\phi }\right)\ge \frac{1}{M}$; the ratio is largest when there is little recombination and smallest when there is lots of recombination. This gives the following relationship: $\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G)\le \text{ARP}({\hat{\beta }}_G^{\prime },{\hat{\beta }}_G)\le 1$, meaning the unadjusted model will have the most power, followed by the global adjusted model and then the local-adjusted model. At the extremes, when r_jk = r_U = 0∀j,k (which would be expected immediately after the initial admixture event), then $\left(\frac{{\phi }_g^2}{\phi }\right)=1$ and $\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G)=\text{ARP}({\hat{\beta }}_G^{\prime },{\hat{\beta }}_G)\le 1$, which implies that adjusting for global or local ancestry would give equivalent power. This makes intuitive sense because in this case of no recombination, global ancestry and local ancestry are equivalent. For the other extreme, when r_jk = r_U = 1∀j,k, then $\left(\frac{{\phi }_g^2}{\phi }\right)=\frac{1}{M}$ and $\text{ARP}({\hat{\beta }}_G^{\prime },{\hat{\beta }}_G)=1-\frac{1}{M}{\rho }_{\mathit{\text{GA}}}^2\approx 1$, for large M. In this case, little is lost by using the global-adjusted model relative to the unadjusted model, but the local adjusted model loses power due to the correlation between QTL genotype and local ancestry.

We examined the magnitude of the adjusted models’ power loss relative to the unadjusted model (Supplemental Figures 3 and 4) over a range of parameter values. We found that the power loss with the local-ancestry adjusted model can be substantial, particularly when allele frequencies are very different between the ancestral populations (Supplemental Figure 3). The global-ancestry adjusted model (Supplemental Figure 4) still loses power, but less power than the local-ancestry adjusted model. Additionally, we find that when recombination increases (Supplemental Figure 4B), $\text{ARP}({\hat{\beta }}_G^{\prime },{\hat{\beta }}_G)$ is very close to 1. This illustrates that as the amount of recombination across the genome increases (such as after several generations of random mating), the power of the global-ancestry adjusted model approaches the power of the unadjusted model.

3.1.1.2 Testing at a marker

For tests at a marker locus, we also evaluated the confounding conditions (2), but with respect to marker genotype, local ancestry at the marker, and global ancestry. The correlation between the marker genotype and local ancestry at the marker (required for condition 2i) is analogous to that derived for the QTL: ${\rho }_{\mathit{\text{LA}}}^2=\frac{q(1-q){{\mathrm{\Delta }}_L}^2}{q(1-q){{\mathrm{\Delta }}_L}^2+{\gamma }_L}$, where γ_L = qp_L1(1 − p_L1) + (1 − q)p_L0(1 − p_L0). However, unlike the case of testing at the QTL, the partial correlation necessary to evaluate condition 2ii can be non-zero because it involves both the LD between QTL and marker alleles and the correlation between QTL and marker ancestries. Specifically, we can show that the numerator of ${\rho }_{\mathit{\text{YA}},L}^2$ is proportional to Ψ², where $\mathrm{\Psi }=\sqrt{2q(1-q)}a(1-r_{\mathit{\text{gl}}})(\mathrm{\Delta }{\gamma }_L-{\mathrm{\Delta }}_{L}W)$ (see Appendix A.2.4 for full form).

As a validation, we can see that when there is complete LD in the ancestral populations (so that marker and QTL alleles are completely correlated), then Δ = Δ_L and W = γ_L, and these correlations reduce to the equations that we derived for testing the QTL itself. In that special case, there is no confounding. In general the partial correlation is 0 (and local ancestry is not a confounder) when any one of the following conditions holds: (1) a = 0 or (2) r_gl = 1 or (3) Δγ_L = Δ_LW. The last condition holds when Δ = 0 and either Δ_L = 0 or W = 0 (or if there is complete LD in the ancestral populations). If any of these conditions hold, local ancestry at the marker will not be a confounder. Alternatively the correlation between marker genotype and local ancestry will be 0 (which would also lead to no confounding) if Δ_L = 0.

The correlation between marker genotype and global ancestry also has the same form shown before for the QTL:

$${\rho }_{L\overline{A}}^2={\rho }_{\mathit{\text{LA}}}^2\left(\frac{{\phi }_l^2}{\phi }\right),$$

where ${\phi }_l=1-(\frac{K-1}{K})r_U-\frac{1}{M}{\sum }_{j\ne l}^m{r}_{\mathit{\text{lj}}}$ and φ is as defined previously. The numerator of ${\rho }_{Y\overline{A},L}^2$ is proportional to (Ψ + ψ)², where $\psi =2\mathit{\text{aq}}(1-q)[D^{\ast }{\mathrm{\Delta }}_L(1-{\phi }_l)-p_L^{\ast }(1-p_L^{\ast })\mathrm{\Delta }(1-{\phi }_g)]$ (see Appendix A.2.4). If there has been little recombination, φ_l and φ_g will both be close to 1 and the numerator will look like Ψ² as with local ancestry. In general, the partial correlation is 0 if either of the following conditions hold: (1) a = 0 or (2) Δ = 0 and either Δ_L = 0 or W = 0. The correlation between marker genotype and local ancestry is 0 if Δ_L = 0. Taken together, this means global ancestry will not be a confounder if either: (1) a = 0 or (2) Δ_L = 0 or (3) Δ = 0 and W = 0. Unlike adjusting for local ancestry, this partial correlation is not necessarily 0 when r_gl = 1. These observations show that when we are testing at a marker locus (not in perfect LD with the QTL), both local ancestry at the marker and global ancestry can be confounders, and adjusting may be required to obtain valid inference.

We can gain more insight by examining the regression parameters for the unadjusted and adjusted models (Table III). For the unadjusted model, we can show (see Appendix A.2.5) that β_L is a function of the LD between alleles T₁ at the QTL and L₁ at the marker locus in the admixed population, D* (equation 12). Specifically, we see (Table III) that the genotype coefficient in the unadjusted model is 0 if either there is no genetic effect (a = 0) or there is no LD in the admixed population (D* = 0). It is well known the admixture can generate LD even in the absence of LD in the ancestral populations. LD in the admixed population depends on the LD in the ancestral populations (W), the difference between allele frequencies in the ancestral populations (Δ and Δ_L), as well as recombination between the QTL and marker (r_gl). We expect no LD (D* = 0) if either (1) r_gl = 1 or (2) W = 0 and either Δ = 0 or Δ_L = 0. Either of these conditions or the condition that a = 0 satisfies the criteria for no confounding by local ancestry discussed above. Therefore, we can conclude that the unadjusted model will provide a valid test of the null hypothesis of no genetic effect (a = 0) or no LD in the admixed population (D* = 0).

For the local-ancestry adjusted model, we can show that ${\beta }_L^{\ast }$ is a function of genetic effect (a), LD in the ancestral populations (W) and recombination between the marker and QTL (r_gl) (see Appendix A.2.5). Specifically we see (Table III) that ${\beta }_L^{\ast }=0$ if a = 0, W = 0 or r_gl = 1; thus the model adjusted for local ancestry provides a valid test of either no genetic effect (a = 0) or no LD in the ancestral populations (W = 0). Since the parameter is also 0 when there has been recombination between the marker and trait loci, we can view this test as having power only for markers linked to the QTL (or for very recent admixture).

The genotype coefficient for the global-ancestry adjusted model is shown in Table III (see Appendix A.2.5 for derivation). We see that, in general, ${\beta }_L^{\prime }=0$ if either a = 0 or D* = 0 and either Δ = 0 or Δ_L = 0. This means that a test of genotypic effect using the model adjusted by global ancestry is valid as a test of no genetic effect, but is not generally a valid test of D* = 0 (unlike the unadjusted model) or W = 0 (unlike the local-ancestry adjusted model). In Appendix C and Supplemental Figure 2, we show the behavior of the functions $\frac{{\phi }_g{\phi }_l}{\phi }$ and $\frac{{\phi }_l^2}{\phi }$, which appear in the numerator and denominator of ${\beta }_L^{\prime }$, as a function of the amount of pairwise recombination. We see that when of the amount of recombination increases (e.g., Supp Fig 2B as s increases), the functions will both approach 0, and then ${\beta }_L^{\prime }$ will approximate the parameter from the unadjusted model. On the other extreme, when there has been little recombination (e.g., Supp Fig 2D for small s), both $\frac{{\phi }_g{\phi }_l}{\phi }$ and $\frac{{\phi }_l^2}{\phi }$ will be close to 1, and then ${\beta }_L^{\prime }$ will approximate parameter from the local-ancestry adjusted model.

In general power comparisons between the different models using ARP are not appropriate since the genotype regression parameters differ for the different models. However, relative rejection rates can be addressed with simulations, results following.

3.1.2 Stratified admixed population

3.1.2.1 Testing at the QTL

In the stratified population model, the two admixed populations may have different ancestry proportions (q₁, q₀) and different phenotypic means (shifted by a constant c). For the linear model adjusted for local ancestry at the QTL, the squared correlation coefficients relevant to assess confounding by local ancestry are as follows (see Appendix B.1.4):

$${\rho }_{\mathit{\text{GA}}}^2=\frac{(\omega +2\delta ){\mathrm{\Delta }}^2}{(\omega +2\delta ){\mathrm{\Delta }}^2+\gamma \prime }$$

$${\rho }_{\mathit{\text{YA}},G}^2=\frac{2c^{2}Q(1-Q)\delta \gamma \prime }{2c^{2}Q(1-Q)\delta \gamma \prime +((\omega +2\delta ){\mathrm{\Delta }}^2+\gamma \prime )(c^{2}Q(1-Q)\omega +(\omega +2\delta ){\sigma }^2)},$$

where Δ = p₁ − p₀ as defined before, γ′ = αp₁(1 − p₁) + (1 − α)p₀(1 − p₀), δ = Q(1 − Q)(q₁ − q₀)², and ω = Qq₁(1 − q₁) + (1 − Q)q₀(1 − q₀).

As in the single admixed population, ${\rho }_{\mathit{\text{GA}}}^2=0$ if the allele frequencies at the QTL are the same in the two ancestral populations (Δ = 0). It is also 0 if the mixing proportions are the same in the subpopulations, q₁ = q₀. Unlike the single admixed population model, we see that the partial correlation is non-zero in the stratified population when there are different ancestry proportions between the subpopulations (q₁ ≠ q₀) and different phenotypic means (c ≠ 0). Thus in general, if there are differences between ancestral allele frequencies at the QTL and differences in ancestry proportions and phenotypic means in the subpopulations, then local ancestry will be a confounder.

For global ancestry, the correlations to assess confounding are the following (see Appendix B.1.4 for details):

$${\rho }_{G\overline{A}}^2=\frac{{(\omega {\phi }_g+2\delta )}^2{\mathrm{\Delta }}^2}{[(\omega +2\delta ){\mathrm{\Delta }}^2+\gamma \prime ](\omega \phi +2\delta )}$$

$$\mathit{\text{numerator}}({\rho }_{Y\overline{A},G}^2)\propto 2Q(1-Q)c^2\delta {[\omega {\mathrm{\Delta }}^2(1-{\phi }_g)+\gamma \prime ]}^2.$$

where φ and φ_g are functions of the recombination probabilities defined previously. The conclusions are the same as for local ancestry: if there are differences between ancestral allele frequencies at the QTL (Δ ≠ 0) and differences in ancestry proportions (δ ≠ 0) and phenotypic means (c ≠ 0) in the subpopulations, then global ancestry will be a confounder.

The parameter estimates for the genotypic term in the unadjusted and ancestry adjusted models are shown in Table III (see Appendix B.1.5 for derivations). For the unadjusted model, we see that the regression parameter does not generally provide an estimate of the true genetic effect of the QTL, a (except in the case c = 0 or Δ = 0 or q₁ = q₀). On the other hand, the model adjusted by local ancestry does correctly model the true genetic effect. Like the unadjusted model, the regression parameter model adjusted by global ancestry, ${\beta }_G^{\prime }$, does not estimate the genetic effect, a, when c ≠ 0, Δ ≠ 0 and q₁ ≠ q₀. However, this bias also depends on pairwise recombination through φ and φ_g. Supplemental Figure 1 shows that 0 < φ ≤ 1 and the difference φ − φ_g approaches 0 as recombination increases or decreases (and tends to be small in general). Therefore, unless c is very large relative to a, the bias is expected to be small.

Although, subpopulation membership is often unknown, it is interesting to consider the properties of the model adjusted for membership. For the regression model adjusted for subpopulation membership (Table II), it is not hard to show (see Appendix B.1.5) that, like the local-ancestry adjusted model, using membership as a covariate also correctly models the true genetic effect: ${\beta }_G^{″}=a$ (Table III).

Since adjusting for local ancestry or subpopulation membership both provide estimates of the genetic effect, a, we can use ARP to compare power. Using the correlations derived in Appendix B.1.3 we have,

$$\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G^{″})=\left(\frac{\gamma \prime {\sigma }^2(\omega +2\delta )}{\gamma \prime {\sigma }^2(\omega +2\delta )+{\mathrm{\Delta }}^2\omega {\sigma }^2(\omega +2\delta )+c^{2}Q(1-Q)\omega (\omega {\mathrm{\Delta }}^2+\gamma \prime )}\right).$$

All parameters in the second and third terms of the denominator are positive, and consequently $\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G^{″})\le 1$. Thus the model adjusting for subpopulation membership is at least as powerful as the local-ancestry adjusted. Supplemental Figure 5 shows examples of $\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G^{″})$ for various parameter values. Power of the tests in the two models is most similar ( $\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G^{″})$ closest to 1) when q₀ and q₁ are most different (Supplemental Figure 5, red line q₁ = 1). Though not shown in this figure, when |q₁ − q₀| = 1, we have ω = 0, and it can be seen from the formula above that $\text{ARP}({\hat{\beta }}_G^{\ast },{\hat{\beta }}_G^{″})=1$. This makes sense because when local ancestries come from distinct ancestral populations in the strata, the local ancestry variable will be the same as the subpopulation membership variable. On the other hand, when q₁ − q₀ = 0 (Supplemental Figure 5, purple line q₁ = 0.65), local ancestry gives no information about subpopulation membership, and we see the greatest loss in power for the local-ancestry adjusted model relative to the membership-adjusted model. As with the single admixed population, for each value of q_i, the loss in power using local ancestry instead of subpopulation membership increases with more divergent ancestral allele frequencies (|Δ|). In Supplemental Figure 5, we also see that the ARPs increase (and hence the powers of the local ancestry and membership adjusted models become more similar) if the difference in trait means between populations is smaller (e.g., c = 1 vs c = 2).

3.1.2.2 Testing at a Marker

To assess confounding by local ancestry when testing at a marker, we derive the following correlation coefficients (see Appendix B.2.4):

$${\rho }_{\mathit{\text{LA}}}^2=\frac{(\omega +2\delta ){{\mathrm{\Delta }}_L}^2}{(\omega +2\delta ){{\mathrm{\Delta }}_L}^2+{\gamma }_L^{\prime }}$$

$$\mathit{\text{numerator}}\left({\rho }_{\mathit{\text{YA}},L}^2\right)\propto {\mathrm{\Phi }}^2,$$

where $\mathrm{\Phi }=a\{(1-r_{\mathit{\text{gl}}})(\omega +2\delta )(\mathrm{\Delta }{\gamma }_L^{\prime }-W^{\ast }{\mathrm{\Delta }}_L)+2\delta \mathrm{\Delta }{r}_{\mathit{\text{gl}}}{\gamma }_L^{\prime }\}+\mathit{\text{cQ}}(1-Q)(q_1-q_0){\gamma }_L^{\prime }$. Similar to the case of testing at the QTL, we see that local ancestry will be a confounder if there are differences between ancestral allele frequencies at the marker (Δ_L ≠ 0), differences in ancestry proportions (q₁ ≠ q₀) and phenotypic means in the subpopulations (c ≠ 0). However, when testing at a marker, the partial correlation ${\rho }_{\mathit{\text{YA}},L}^2$ can also be non-zero even when q₁ = q₀ or c = 0 if a ≠ 0.

For global ancestry, the relevant correlation coefficients are derived in Appendix B.2.4:

$${\rho }_{L\overline{A}}^2=\frac{{({\phi }_l\omega +2\delta )}^2{\mathrm{\Delta }}_L^2}{[(\omega +2\delta ){\mathrm{\Delta }}_L^2+{\gamma }_L^{\prime }][\omega \phi +2\delta ]}$$

$$\mathit{\text{numerator}}\left({\rho }_{Y\overline{A},L}^2\right)\propto {(\mathrm{\Phi }+\Upsilon )}^2,$$

where

$$\Upsilon =2\omega \{a\{(1-r_{\mathit{\text{gl}}})(W^{\ast }{\mathrm{\Delta }}_L(1-{\phi }_l)-\mathrm{\Delta }{\gamma }_L^{\prime })+\mathrm{\Delta }{\gamma }_L^{\prime }{\phi }_g+\mathrm{\Delta }{\mathrm{\Delta }}_L^2\{r_{\mathit{\text{gl}}}(\omega {\phi }_l+2\delta )+({\phi }_g-{\phi }_l)(\omega +2\delta )\}\}-[\mathit{\text{cQ}}(1-Q)(q_1-q_0){\mathrm{\Delta }}_L^2][({\phi }_l-1)]\}.$$

If there is complete LD between QTL and marker, then Υ = 0 and the correlations are the same as derived for local ancestry. We see that like local ancestry, global ancestry can be a confounder in general.

Examining the regression coefficients from the unadjusted and adjusted models (Table III), we see that the coefficient for the unadjusted model does not estimate the true genetic effect, and will not provide a valid test of a = 0 if c ≠ 0, Δ_L ≠ 0 and q₀ ≠ q₁. Unlike the unadjusted model in the single admixed population examples, in stratified populations the unadjusted model does not generally provide a test of LD in the population as a whole either, D** ≠ 0 because the regression parameter can be non-zero even when D** = 0 if Δ_L ≠ 0 and q₀ ≠ q₁. Therefore, when testing a marker locus, the unadjusted model generally provides neither a test for no genetic effect or of no LD in the stratified population.

For the model adjusted for local ancestry, the form of the regression parameter ${\beta }_L^{\ast }$ is similar to that in the single admixed population (Table III). We see that ${\beta }_L^{\ast }=0$ if a = 0 or W* = 0 or r_gl = 0; thus the model adjusted for local ancestry provides a valid test of either no genetic effect or no LD in the ancestral populations (independent of the value of c). Notably it is also possible for the regression parameter to be 0 even when the LD coefficients in the ancestral populations are non-zero if the LD in the ancestral populations is in opposite directions such that QW₀ = (1 − Q)W₁, or equivalently αD₀ = (1 − α)D₁.

As for the unadjusted model, the coefficient for the model adjusted for global ancestry also has a bias that depends on c, and so does not generally provide a test for no genetic effect (a = 0). The bias term will be 0 if $\mathit{\text{cQ}}(1-Q)(q_1-q_0)\omega {\mathrm{\Delta }}_L\frac{(\phi -{\phi }_l)}{(\omega \phi +2\delta )}=0$, which happens if c = 0, Δ_L = 0, q₁ = q₀, or $\frac{(\phi -{\phi }_l)}{(\omega \phi +2\delta )}=0$. We show in Supplemental Figure 1 that φ and φ_l approach 0 as the amount of recombination increases and approach 1 as recombination decreases; thus (φ − φ_l) → 0 at the extremes of recombination and the bias term disappears. However, the bias may be non-negligible for modest amounts of recombination (as with moderately recent populations) if c is large. Notably, as recombination decreases (φ and φ_l approach 1), we can show that ${\beta }_L^{\prime }\to {\beta }_L^{\ast }$. This makes sense because with little recombination, local ancestry and global ancestry measures should be similar for each individual. As recombination increases (φ and φ_l approach 1), we find that ${\beta }_L^{\prime }\to \frac{a(D^{\ast \ast }-\delta \mathrm{\Delta }{\mathrm{\Delta }}_L)}{\omega {\mathrm{\Delta }}_L^2+{\gamma }_L^{\prime }}$, which is the marker-genotype coefficient for the model adjusted for subpopulation membership (Table III).

For the subpopulation-membership adjusted model, we see that ${\beta }_L^{″}$ is 0 if a = 0 (Table III), showing that it is a valid test of genetic effect regardless of the value of c. It is also 0 if there is no LD in both of the admixed subpopulations, $D_0^{\ast }=D_1^{\ast }=0$. The coefficient is not 0, however, if D** = 0, unless Δ = 0 or Δ_L = 0, nor is it 0 if W* = 0, unless Δ = 0 or Δ_L = 0 or r_gl = 1. This means adjusting for subpopulation membership does not generally provide a valid test of LD in the stratified population or LD in the ancestral populations, but does provide a valid test of no genetic effect or of no LD in both admixed subpopulations.

3.2 Simulation results

We conducted simulations of single admixed and stratified admixed populations to validate our theoretical findings (Supplemental Methods and Results). Consistent with the theoretical conclusions above, our simulations of a single admixed population show that all models result in valid tests of the null hypothesis a = 0 (at the QTL and marker loci). For a ≠ 0, the rejection rates depend on LD as expected. The local-ancestry model, but not necessarily the unadjusted or global adjusted models, provides valid tests of W = 0. The unadjusted model provides valid tests of the null hypothesis of D* = 0. In general we found that power depends on the relative size of W and D*. When D* > W the unadjusted tends to be most powerful and when W > D* the local-ancestry adjusted model tends to be most powerful. In general, we found that the global-ancestry adjusted model performs similarly to the unadjusted model or has power between the unadjusted and local-ancestry adjusted model. This agrees with our theory that the regression parameter for the global-adjusted model should be close to the unadjusted model if there has been sufficient recombination, which is the case with our simulations involving 20 generations of random mating following admixture.

Results from simulations of stratified populations are also consistent with theory. When c ≠ 0, such that there is a difference in trait mean between strata, only the local-ancestry and membership adjusted models are valid for the null hypothesis of a = 0. Interestingly, the global-ancestry adjusted model also shows correct rejection rates, suggesting that the specification bias discussed in the methods section is small for these examples. When a > 0, we show that the local-ancestry adjusted model is valid as a test of the null hypothesis of W* = 0 (or r_gl = 0) and the membership-adjusted model provides a valid test of no LD in both subpopulations. Rejection rates for the unadjusted model are greater than the nominal rate, even for distant markers. The exceptions are markers in low LD with the QTL in the stratified population (D**) and with small differences between marker allele frequencies in the ancestral populations. Power again depends on the relative level of LD in the ancestral populations and in the stratified population.

3.3 Estimates of LD in admixed datasets

When testing at a marker, we have seen that the regression coefficient for the genetic effect depends on the genetic effect at the QTL and LD between the QTL and marker genotypes. To put these results into the context of actual admixed populations, we examined the relationship between estimates of LD (disequilibrium coefficient: D* or D_i) and intermarker distance for six admixed Hispanic datasets (Colombian, Honduran, Cuban, Puerto Rican, Dominican and Mexican), an admixed non-Hispanic dataset (African-American), and non-admixed “ancestral” datasets (European, African and Native American). As expected, the estimates of LD tend to be larger (in absolute value) and more variable in the admixed datasets relative to the non-admixed datasets (Supplemental Figure 6). Colombian, Honduran and Dominican datasets show the largest variation in LD estimates. Cuban, Mexican, and African-American datasets show the least variation and are similar to estimates in non-admixed datasets. For all datasets, LD values get closer to 0 as intermarker distance increases. Within each dataset, pairs beyond ~100–200kb demonstrate LD values with a similar distribution to unlinked pairs, but the range remains relatively wide in Colombians, Hondurans and Dominicans, even for unlinked pairs (e.g., 17–20% of unlinked pairs in these admixed datasets have estimates of |D*|<0.05 compared to <4% of unlinked pairs in non-admixed datasets).

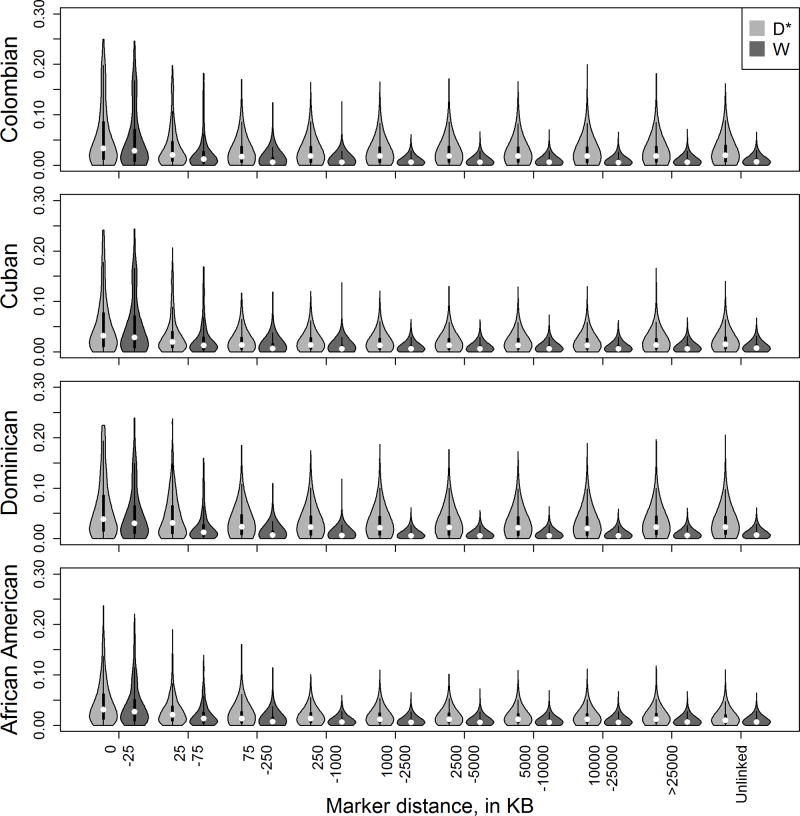
We have shown that the key quantities in the formulas for the regression coefficients of the unadjusted and local-ancestry adjusted models (as well as global-adjusted but in a more complex way) are D*, computed directly in an admixed population, and W, computed as an average of LD in the ancestral populations weighted by mixing proportions. Simulations also demonstrated that these have strong influences on relative power. Figure 1 compares estimates of W and D* across varying intermarker distances in Colombians, Cubans, Dominicans and African Americans (results in Hondurans, Puerto Ricans and Mexicans are shown in Supplemental Figure 7). We see as expected a smaller median and tighter distribution (smaller IQR) for W compared to D* for all admixed populations; however there is variability among populations, with the Dominicans being most strikingly different (e.g., for unlinked markers in Dominicans the median |D*| is about 3 times the median of |W| 0.023 vs 0.008). Interestingly, the differences in distribution are most apparent for distant markers; for nearby markers (e.g., <~25kb) the distributions of W and D* are fairly similar for all admixed populations.

Figure 1.

Violin plots for absolute value of estimates of disequilibrium coefficients three admixed datasets. D* is the estimate in the admixed dataset and W is the average of disequilibrium coefficients in the ancestral populations, weighted by estimates of mixing proportions: Colombian (0.68 European, 0.07 African, 0.25 Native American), Cuban (0.81 European, 0.15 African, 0.04 Native American), Dominican (0.70 European, 0.27 African, 0.03 Native American), African American (0.24 European, 0.75 African, 0.01 Native American). Results are binned by intermarker distance, with the final bin being pairs of unlinked markers.

4. DISCUSSION

Our aim was to better understand the properties of global- and local-ancestry adjustments in linear regression models used for genetic association studies. Specifically, we examined statistical confounding, the forms of regression parameters, and relative power in terms of genetic parameters. Our results regarding confounding are not surprising. When testing a QTL itself in a single admixed population, (global or local) ancestry is not a confounder because, in our model, the QTL explains all of the non-random phenotypic variation. However, in all other scenarios considered (testing at marker loci or in stratified admixed populations), ancestry can be a confounder, and our formulas shed light on when this is the case. Since typically we assume we are not testing the QTL directly, we must consider ancestry a potential confounder, and should adjust for it at some level.

Studying the forms of the regression parameters for unadjusted and adjusted regression models was particularly informative, as it shed light on our implicit assumptions in hypothesis testing. We saw that tests of the genotype coefficient can correspond to tests of different null hypotheses in terms of genetic parameters. In a single admixed population, we have shown that the unadjusted model and the models adjusted for local and global ancestry all provide valid tests for the hypothesis of no genetic effect; however, in the presence of a genetic effect, tests at marker loci depend on LD between the marker and QTL in different ways. The unadjusted model provides a valid test of the null hypothesis of no LD in the admixed population, while the local-ancestry adjusted model provides a valid test of no LD in the ancestral populations. The global-adjusted model will perform similarly to the unadjusted model as recombination increases and similarly to the local-ancestry adjusted model if there has been little recombination.

In a stratified population, only adjusting for local ancestry or subpopulation membership guarantees valid tests of no genetic effect. As in the single admixed population, in the presence of a genetic effect, the different adjustments provide tests of different null hypotheses with respect to LD. The model adjusted for subpopulation membership provides a valid test for no LD in both of the admixed subpopulations, while the local-ancestry adjusted model provides a valid test of no LD in the ancestral populations. The coefficient for the global-ancestry adjusted model ranges between that for the local-ancestry adjusted and population-membership adjusted models, depending on the amount of recombination across the genome. The unadjusted model is generally invalid, even at the QTL itself, since it is sensitive to phenotypic differences between the subpopulations not explained by the QTL.

Our estimates of disequilibrium coefficients in data from actual admixed and “ancestral” populations provide insight into how these different hypothesis tests may behave in real data. Though we cannot go directly from these estimates to statements about power, we can make some useful observations: (1) Values of W (average LD from the ancestral populations) get closer to 0 quite rapidly with increasing distance, suggesting that local-ancestry adjusted models will likely only have power at markers close to the QTL (<~1Mb for our examples); (2) The admixed populations show more extreme values of LD (D*) than the ancestral populations, suggesting that unadjusted (and sometimes global-adjusted models) will have more power in admixed populations than non-admixed populations; (3) The more extreme values of LD seen in the admixed populations persist even between distant and unlinked loci, suggesting there will be a lot of noise at distant markers when using unadjusted tests.

Our results are in agreement with previous studies that considered global vs. local ancestry adjustment in association tests. Like others (Liu et al., 2013; Zhang & Stram, 2014), we find that using global ancestry as a covariate works well to weed out spurious associations at distant loci and control type I error. Also in agreement, we show that the local-ancestry adjusted models will result in tests that generally have lower rejection rates than the global-adjusted model. Our derivation of explicit formulas for the regression coefficients helps us to understand these findings, and in particular understand that these models actually provide tests of different null hypotheses. For example, when testing at a marker in a single-admixed population, we have shown that the unadjusted model provides a test of LD in the admixed population while the local-ancestry adjusted model provides a test of LD in the ancestral populations. Since LD in admixed populations tends to be larger and span larger distances than the LD in the ancestral populations, it makes sense that the unadjusted model has a higher rejection rate. As we show, the coefficient for the global model is intermediate to the unadjusted and local adjusted model, depending on the admixture dynamics (in particular the amount of recombination). We did not explore the scenario posed by Wang et al (2011) in which forces such as selection lead to local-ancestry effects at the test marker, but this would appear to be a case for which additional adjustment for local-ancestry may be required. We also did not consider inclusion of a genotype × ancestry interaction term, which Liu et al (2013) show can improve power when LD varies in ancestral populations. Examining the forms of this interaction and main effect coefficients under these models will be the subject of future work.

We have made several assumptions to simplify the theoretical calculations. The model of admixture and population evolution assumes only two mixing populations as well as specific pulses of admixture followed by random mating. These assumptions may not be valid for Hispanic populations, which often show three-way admixture. Other assumptions include a known (not estimated) haplotype ancestry and equal trait variance. Perhaps the most unrealistic simplification is that of a single common QTL. We expect variation of quantitative traits to be influenced by multiple genetic and environmental factors as well as their potential interactions. The relationship of these factors to ancestry may influence our conclusions about ancestry adjustment. For example, we have assumed that the trait mean depends only on genotype at the QTL, but if the trait depends on ancestry -specific factors (genetic or environmental), our conclusions may not hold. Such considerations are particularly important as we think about the contributions of multiple rare variants within a gene to a trait. Rare variants are likely to be ancestry-specific, and thus trait means with respect to a particular variant genotype will depend on both the genotype and ancestry of the gene region. This relationship complicates theoretical calculations but is an important topic for future exploration.

We have focused here on analysis of continuous traits, but many studies use a case-control design that focuses on a binary outcome and use logistic regression. There has been interesting discussion on the properties of covariate adjustment in linear regression models versus randomized and retrospective case-control logistic regression models (Mefford & Witte, 2012; Pirinen, Donnelly, & Spencer, 2012; Robinson & Jewell, 1991). In particular, the conclusions with respect to relative power of adjusted and unadjusted models when considering a non-confounding, predictive covariate are similar for randomized studies with continuous or binary traits; but for a case-control design, where selection is based on phenotype, the relative power depends on disease prevalence (Pirinen et al., 2012; Robinson & Jewell, 1991). It is not clear how our findings will generalize to commonly used case-control designs. Extension of our theory to such designs, particularly approximations of relative power, are more difficult since the selection of subjects can induce a bias that must be accounted for in addition to relative variance (Robinson & Jewell, 1991). Nevertheless, such extensions would be interesting and informative.

As practical recommendations based on our results, we suggest that global-adjusted models should be used for initial association analyses. Though we did show that in stratified admixed populations, the parameter can be biased, we demonstrate that this bias is typically small. If one can be relatively certain that the population under study represents a single admixed population, e.g. African American, an unadjusted model may be used for this initial scan as it will be sensitive to LD in the admixed population. However, it is likely that more distant markers with LD driven by ancestral allele frequency differences will also be detected. For fine-mapping and to exclude results due entirely to LD induced by admixture; local-ancestry adjusted models should be used, given that in the presence of a genetic effect, they provide a valid test of LD in the ancestral populations. Our results also suggest that local-ancestry models should also be used to characterize effect size when we believe we have found the underlying QTL. This will more appropriately estimate the true genetic effect if there is population stratification than the global-adjusted or unadjusted model and more closely reflect the effect in non-admixed ancestral populations.