Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Dec 20;14(2):894–904. doi: 10.1021/acs.jctc.7b01099

Saturation Mutagenesis by Efficient Free-Energy Calculation

Zuzana Jandova 1, Daniel Fast 1, Martina Setz 1, Maria Pechlaner 1, Chris Oostenbrink 1,*
PMCID: PMC5813279  PMID: 29262673

Abstract

graphic file with name ct-2017-010993_0006.jpg

Single-point mutations in proteins can greatly influence protein stability, binding affinity, protein function or its expression per se. Here, we present accurate and efficient predictions of the free energy of mutation of amino acids. We divided the complete mutational free energy into an uncharging step, which we approximate by a third-power fitting (TPF) approach, and an annihilation step, which we approximate using the one-step perturbation (OSP) method. As a diverse set of test systems, we computed the solvation free energy of all amino acid side chain analogues and obtained an excellent agreement with thermodynamic integration (TI) data. Moreover, we calculated mutational free energies in model tripeptides and established an efficient protocol involving a single reference state. Again, the approximate methods agreed excellently with the TI references, with a root-mean-square error of only 3.6 kJ/mol over 17 mutations. Our combined TPF+OSP approach does show not only a very good agreement but also a 2-fold higher efficiency than full blown TI calculations.

Introduction

One-point mutation in a carefully chosen position in a protein may have a huge impact on a number of various properties, such as protein stability,1 protein secondary structure,2 catalytic function,3 oligomerization,4 binding of small ligands,5 DNA,6 or protein–protein interactions.7 It is of a great interest to understand and be able to predict these effects, for which it is highly relevant to compute the associated free energy of mutation.

Plentiful methods to calculate the change of the free energy in different systems have been described. By far the fastest are the empirical scoring functions. They gain their speed by working with rigid molecules, thereby largely neglecting the entropic term.8 A class of relatively fast free-energy methods is formed by the so-called end-point methods. As the name suggests, end-point methods save time by omitting intermediates and simulating solely two end states (e.g., bound and unbound, folded and unfolded, or charged and neutral states). Nonetheless, proper sampling in the end states is necessary for convergence of the free energies and accurate results. Sharir-Ivry et al.9 were able to correctly predict the trend of the free energy of mutation for variants of haloalkane dehalogenase via the linear response approximation (LRA) and Almlöf et al.10 accurately predicted the relative binding free energy of two proteins upon mutations using a similar approach. Other methods, such as molecular mechanics/Poisson–Boltzmann surface area (MM-PBSA)11,12 and molecular mechanics/generalized Born surface area (MM-GBSA)13 decompose the free energy term into various thermodynamic contributions and have been applied for a quick alanine scan with a good agreement with alchemical methods or experiments.14,15 Somewhat less efficient, yet theoretically robust, are alchemical free-energy calculation methods. They work, in contrast to the end-point methods, with physical or unphysical intermediates, often employing noninteracting dummy atoms. Thus, computationally more accessible processes can be simulated and, because free energy is a state function, relevant free-energy differences can be calculated from thermodynamic cycles. As the value around the cycle is equal to zero, the nature of the intermediate does not influence the final free energy value but can significantly affect the efficiency of the calculation.16−19 In thermodynamic integration (TI)20 the free energy is computed along a continuous path connecting state A and state B. TI has been proven to be accurate at calculating pKa values,21 relative22,23 or absolute binding free energies24 of protein–ligand or protein–protein complexes, and the free energy of mutation in DNA.25

Various methods that are still derived from robust statistical mechanics but can lead to more efficient free-energy calculations have been reported in the past. One prominent example is an one-step perturbation (OSP) approach in which a judiciously chosen reference state is designed, such that the free-energy difference to multiple relevant end states can be computed in a single step.26−28 The reference state itself does not have to represent a physical molecule, but the molecular sampling can be enhanced by using soft-core potential energy functions18,29 or floppy molecules.30 With OSP one can compare the free energy difference of two end states A and B from the differences to the reference state. OSP has found applications in design of BACE-1 inhibitors,31 in binding free energy calculations of α-thrombin and p38-MAP kinase ligands,32 in combination with quantum mechanics,33 and in a number of automated programs.34,35 Chiang and Wang used OSP to predict the free energy changes of benzene to its derivatives with different substituents on the ring.36 Without using any soft-core potential, however, only predictions for small neutral substituents meet accuracy requirements (<2.5 kJ/mol), whereas larger changes may be accommodated by using more elaborate reference states.28,37 Still, OSP was repeatedly shown to perform best for nonpolar changes, whereas large changes in polarity lead to poor overlap in the conformational ensembles of the reference state and the end states.18,37−39

The free energy of charging a neutral compound may be more appropriately approximated by the end-state methods, e.g., based on linear response or the linear interaction energies method.40−42 Some years ago, we introduced the third-power fitting method, which approximates the thermodynamic integration profile for charging or uncharging from simulations at the end states by using a cumulant expansion to determine second derivatives of the free energy.26,43 De Ruiter accurately calculated charging free energies of benzamidines in water and trypsin using third power fitting (TPF) method.43 As TPF only takes the two end points of a TI trajectory, it still significantly decreases the necessary simulation time while maintaining a comparable accuracy.

The aim of the current work is 2-fold. On the one hand, we want to systematically investigate the use of OSP and TPF on a chemically diverse set of compounds, calculating the solvation free energy of the amino acid side chain analogues. On the other hand, we aim to efficiently compute the free energy of mutation in a model peptide, with an eye to computational saturation mutagenesis in future work. We will use the fast and inexpensive OSP approach to calculate the van der Waals contributions to the free energy (nonpolar free energy, ΔGR>NOSP) and the third power fitting method (TPF) to calculate the Coulombic contributions to the free energy (uncharging free energy, ΔGQ>N).

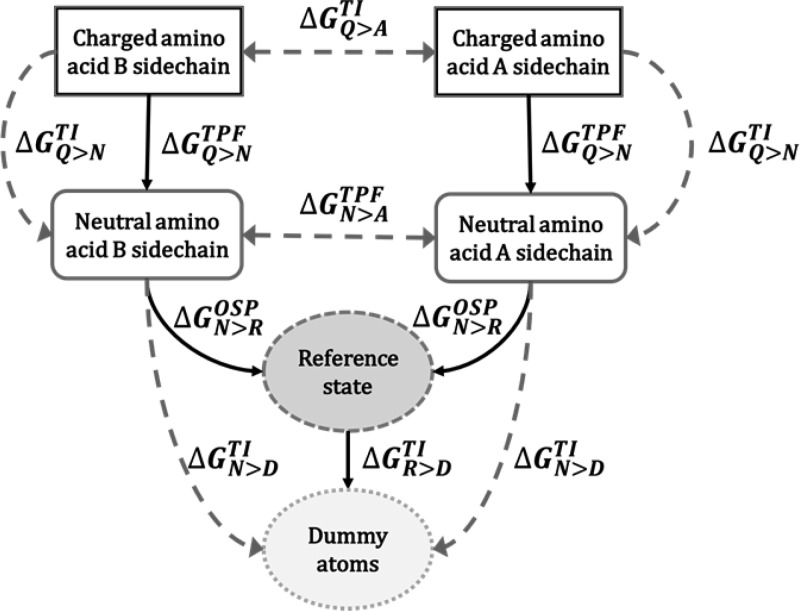
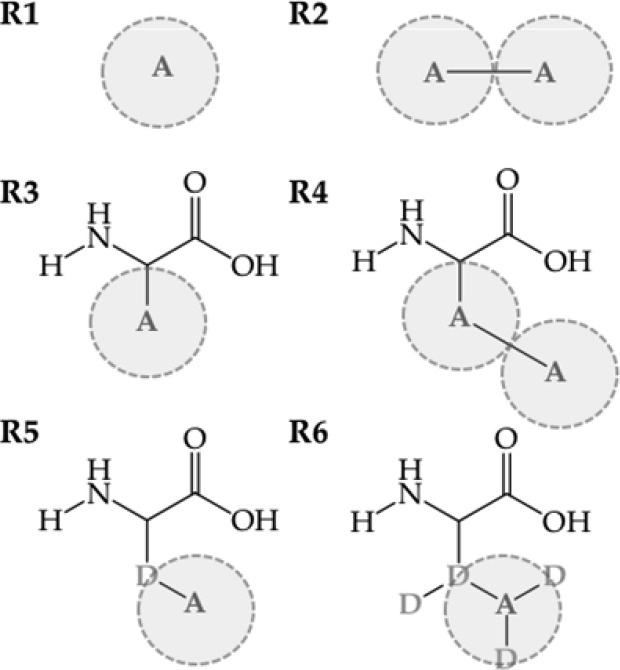
Our work can be divided into two parts. In the first part, we calculate the free energy of solvation of amino acid side chains. The free energy of desolvation (negative solvation free energy) can be computed by transforming an amino acid side chain in solution into a noninteracting dummy particle. Though this can be done using an alchemical method using 10–20 intermediate states, we here propose to use the scheme in Figure 1. First, the free energy of annihilation of the reference state into dummy atoms (ΔGR>DTI) is calculated via TI, so that the entire desolvation free energy of side chain analogues is calculated as the sum of the annihilation free energy of the reference state ΔGR>D, the van der Waals contribution to the free energy, ΔGN>ROSP, and the Coulombic contributions to the free energy, ΔGQ>N. The reference states for OSP calculation of the solvation free energies are formed by one or two soft spheres, noted as R1 and R2, respectively (Figure 2). As indicated in Figure 1, the uncharging and annihilation of all compounds is also calculated using TI, yielding ΔGQ>NTI and ΔGN>D, respectively.

Figure 1.

Figure 1

Open in a new tab

Solvation free energy is calculated by turning the electrostatic and van der Waals interactions of the amino acid side chain analogues off. This is done in two steps: (1) the uncharging free energy (Q > N) is computed by TI and TPF and (2) the decoupling free energy (N > D), is computed by TI and OSP, using R1 or R2 as reference states.

Figure 2.

Figure 2

Open in a new tab

Chemical structure of the reference states used for the OSP approach. Atom A represents a soft-core particle as defined in ref (18).

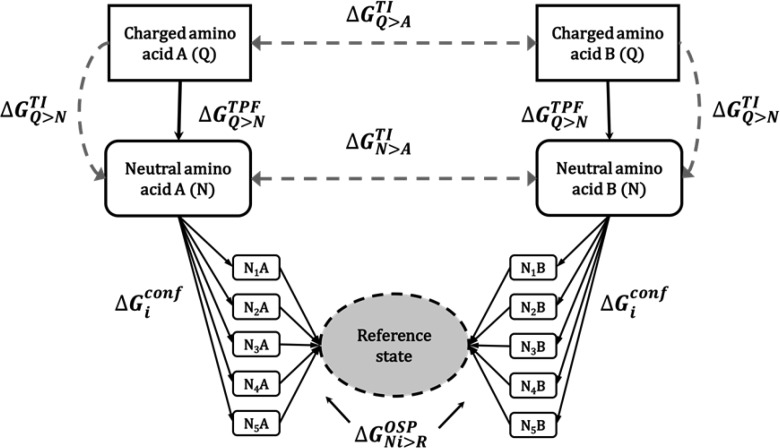
In the second part of this work, we calculate the free energy of mutation of the tripeptide Ala–ref–Ala, where ref represents the reference state. To compare calculations from the tripeptides with the ones of side chains, the first two reference states consist of one (R3) and two soft spheres (R4) connected to the peptide backbone. However, the conformational sampling of the side chains, relative to the backbone appears to play a large role, for which we have designed an additional reference state with one noninteracting dummy atom and one soft atom (R5) and one with the same construct but with three additional dummy atoms, R6. The additional dummy atoms in R6 are remnants from previous simulations but should not influence the free energies, such that these simulations can be considered independent repeats. Furthermore, a more elaborate thermodynamic cycle (Figure 3) is devised, employing a conformational library of amino acid side chains, which was developed in the GROMOS force field and can be further used for future applications.

Figure 3.

Figure 3

Open in a new tab

Free energy of mutation is computed using TI and the TPF and OSP approaches. In the OSP approach, multiple side chain conformations are considered, which are subsequently averaged appropriately (see Methods).

Methods

MD Simulations of Reference States

All MD simulations were carried out using the GROMOS11 software simulation package,44 employing the GROMOS 54a8 force field.45 The molecular topology building blocks for the reference states (Figure 2) are provided in the Supporting Information. The van der Waals parameters for soft reference atoms, noted as A, were modified according to Schafer18 to (C6)1/2 = 0.27322 (kJ mol–1 nm6)1/2 and (C12)1/2 = 0.056143 (kJ mol–1 nm12)1/2. This amounts to an interactions between water and the soft reference atoms with a radius, σ = 0.43 nm and a well depth, ε, of 0.536 kJ/mol. In the reference state R3 a bond of 0.252 nm was used between the Cα and A, which corresponds to the average distance between Cα and A in R5, in which the side chain bonds have a length of 0.153 nm and the Cα–D–A angle has an optimal value of 111°. For the reference states R2 and R4 a bond of length of 0.351 nm was used between the soft atoms. This distance was calculated as the regular CH–CH bond (0.153 nm) subtracted from twice the distance of Cα and A in R3 (2 × 0.252 nm). To enhance the sampling of the reference, a Lennard-Jones soft core parameter of 1.51 was used for the reference atoms.18,29

Initial structures of the reference states were modeled in MOE.46 Reference states were energy-minimized in a vacuum using the steepest-descent algorithm and subsequently solvated in a rectangular, periodic and pre-equilibrated box of simple point charge (SPC) water.47 Minimum solute to wall distances were set to 1.8 nm and the minimum solute–solvent distance to 0.23 nm. This led to systems containing around 6000 atoms.

During equilibration, initial velocities were randomly assigned according to a Maxwell–Boltzmann distribution at 60 K. All solute atoms were positionally restrained with a harmonic potential using a force constant of 2.5 × 104 kJ mol–1 nm–2. In each of the four subsequent 20 ps MD simulations, the force constant of the positional restraints was reduced by 1 order of magnitude and the temperature was increased by 60 K. Subsequently, the positional restraints were removed and rototranslational constraints were introduced on all solute atoms.48 To ensure that the systems are equilibrated, the simulations at 300 K were prolonged for another 10 ns while keeping the temperature (300 K) as well as the pressure constant (1 atm). To sustain a constant temperature, we used the weak-coupling thermostat49 with a coupling time of 0.1 ps. The pressure was maintained using a weak coupling barostat with a coupling time of 0.5 ps and an isothermal compressibility of 7.627 × 10–4 kJ–1 mol nm3 for reference states R1 and R2 and 4.575 × 10–4 kJ–1 mol nm3 for reference states R3–R6. Solute and solvent were coupled to separate temperature baths. Implementation of the SHAKE algorithm50 to constrain bond lengths of solute and solvent to their optimal values allowed for a 2 fs time-step. Nonbonded interactions were calculated using a triple range scheme. Interactions within a short-range cutoff of 0.8 nm were calculated at every time step from a pair list that was updated every fifth step. At these points, interactions between 0.8 and 1.4 nm were also calculated explicitly and kept constant between updates. A reaction field51 contribution was added to the electrostatic interactions and forces to account for a homogeneous medium outside the long-range cutoff using a relative dielectric constant of 61 as appropriate for the SPC water model.52 Coordinate and energy trajectories were stored every 0.5 ps for subsequent analysis. Production runs of reference states R1 and R2 in water were subsequently performed for 10 ns, whereas the production runs of tripeptides (reference states R3–R6) were performed for 50 ns.

MD Simulations of Tripeptides for Conformational Library

To obtain a conformational library of the real amino acids, simulations of all Ala–X–Ala tripeptides except for glycine and proline were performed. We followed the simulation protocol of the reference states, with production simulations of 100 ns. These trajectories were subsequently clustered using the algorithm by Daura53 according to the conformation of the side chain of the second residue after a rotational fit on the backbone atoms. The cutoff for clustering varied depending on the size of the side chain, so that the first five clusters cover ∼90% of trajectories. This clustering led to five central member structures (CMSs) for each amino acid which were subsequently used for fitting in OSP.

Thermodynamic Integration

Solvation free energies of amino acid side chain analogues and mutation free energies for tripeptides were calculated in two steps. In the first step the uncharging of the molecules was performed (ΔGQ>NTI), which was followed by disappearing of the van der Waals radii, i.e., turning the neutral side chains into dummy atoms (ΔGN>D) or to the alanine residue (ΔGN>ATI). The side chain analogues were prepared by breaking the Cα–Cβ bond and increasing the number of (united atom) hydrogen atoms on Cβ. Thermodynamic integration allows us to calculate the free energy difference between states A and B via multiple discrete intermediate steps using a coupling parameter λ.

graphic file with name ct-2017-010993_m001.jpg 1

In state A, represented by Hamiltonian HA, λ is equal to 0, and in state B, represented by HB, λ is equal to 1. These two states are linked via H(λ) and the free energy difference between them is calculated from the derivative of the free energy with respect to λ.

The uncharging simulations were performed at 11 evenly spaced λ points, using a linear coupling of the states, without soft-core potentials,

graphic file with name ct-2017-010993_m002.jpg 2

such that

graphic file with name ct-2017-010993_m003.jpg 3

HQ and HN indicate the Hamiltonians from the charged and neutral states, λ denotes an ensemble average obtained from a simulation at λ, and Vlsel is the electrostatic energy of the molecule with its surroundings. The intramolecular interactions are not included in the equation, as they are not expected to change significantly with the surrounding and cancel in the thermodynamic cycle to compute, e.g., the solvation free energy or the relative free energy of mutation in the folded and unfolded state.

Twenty picoseconds of equilibration at each λ value were followed by 1 ns of production run. To reach an estimated error smaller than 1.0 kJ/mol in the TI-calculations for every amino acid analogue, two more λ points (0.05 and 0.95) were added to the systems where the solutes carry either a positive or negative net charge. No counter charge was introduced to neutralize these systems upon creation or annihilation of the full charge. The simulations at the end states were prolonged to 10 ns and used to estimate the uncharging free energies with LRA (ΔGQ>NLRA) and TPF (ΔGQ>N) as well (see below). The calculations of the free energies of annihilation were performed using a similar scheme. Here, soft-core parameters of 0.5 for the van der Waals29 were used for the perturbed atoms, such that a nonlinear path in λ is taken.

Linear Response Approximation

To approximate the electrostatic contribution to the free energy, ΔGQ>N, we applied the linear response approximation (LRA).54,55

graphic file with name ct-2017-010993_m004.jpg 4

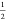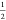The neutral and charged side chains are simulated explicitly to obtain the appropriate ensemble averages in eq 4. According to the linear response theory, the parameter β takes a theoretical value of Inline graphic.54,55 The term ⟨−Vlsel⟩N is also referred to as the electrostatic preorganization energy.56 Note that eq 4 with β = Inline graphic gives exactly the same result as eq 1 with the parametrization of H(λ) in eqs 2 and 3 if ⟨−Vls⟩λ is linear in λ.

The LRA estimates were based on 10 ns of simulations in the charged and neutral states, which were the prolonged end states of the TI calculations.

Third Power Fitting

In the work of de Ruiter43 we observed that the derivative of the electrostatic contribution to the free energy with respect to λ does not always correlate linearly with λ. Rather, it shows a slight curvature, which can be described with a third order polynomial. In the third-power fitting approach, we approximate the integration in eq 1 by

graphic file with name ct-2017-010993_m007.jpg 5

with

graphic file with name ct-2017-010993_m008.jpg 6

and the parameters are fitted to the first and second derivative of the free energy with respect to λ in the end states (λ = 0 and λ = 1). Using the Hamiltonian of eq 2, the first derivative is given by eq 3 and through a cumulant expansion,57 the second derivative of the free energy, is given by

graphic file with name ct-2017-010993_m009.jpg 7

Here, kB is Bolzmann’s constant, and T is the temperature in K. The second derivative of the free energy with respect to λ is equal to the negative of the fluctuations of the derivative of the Hamiltonian with respect to λ.

The TPF estimates were based on 10 ns of simulations in the charged (λ = 0) and neutral states (λ = 1), which were the prolonged end states of the TI calculations.

One-Step Perturbation

The one-step perturbation is based on Zwanzig’s free-energy perturbation equation:58

graphic file with name ct-2017-010993_m010.jpg 8

where HN refers to the Hamiltonian of an end state, HR to the Hamiltonian of a reference state, ⟨⟩R to the ensemble average from a simulation of the reference state. Here, the relevant end state is the neutral amino acid side chain N. The efficiency of this method results from the fact that there is only one reference-state simulation needed to compute the free-energy differences to multiple end states. However, the appropriate reference state has to be chosen very carefully. One precondition for accurate free-energy estimates is that all of the reference-state Hamiltonian singularities should be shared by the Hamiltonians of all end states,59 i.e., that all the relevant conformations of the end states should be covered by the reference state. To avoid intermolecular singularities between the end-state atoms and their surroundings, we use the soft-core interaction.29 Liu et al.26,60 and Schäfer18 showed that atoms with a soft-core potential in reference-state simulation help to accurately predict the solvation free energies of nonpolar molecules in water.

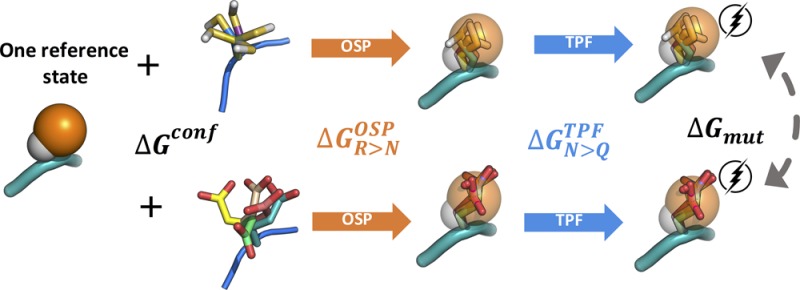
In the current work 10 ns MD trajectories of the R1 or R2 reference state were used for the OSP calculation of the amino acid side chain analogues. In the case of R1, the center of geometry of the side chain was fitted onto the center of geometry of the reference-state atom. In the case of R2, the line between the two atoms with the longest intramolecular distance in the side chain analogue was aligned with the bond between the two atoms of the reference state. This way, we ensured that the amino acid side chain would fit into both atoms of the reference state. Additionally, to improve statistics, this fit was repeated every 36°, leading to 10 rotations for every side chain.38

For the tripeptides, 50 ns of simulations of the reference states R3–R6 was used. Because of the common backbone, the fitting was not that straightforward. In a first step, the Cα atom of the fitted amino acid was aligned with the Cα atom of the reference state. In the second step, the center of geometry of the side chain was aligned to the center of geometry of the soft atoms in the reference state. Next, the interaction energies were calculated for the side chain conformation attached to the backbone of the reference state.

In the tripeptides, the fitting procedure was repeated for each of the central member structures obtained from separate plain MD simulations, to include multiple conformations of the side chains. This procedure leads to five separate ΔGR>NiOSP values per side chain. The relative free energies between the conformations i, was computed using

graphic file with name ct-2017-010993_m011.jpg 9

where Pi is the relative occurrence of this conformation, as obtained from the conformational clustering. ΔGiconf is added to ΔGR>Ni and the resulting sum was exponentially averaged to obtain a single estimate of ΔGR>NOSP

graphic file with name ct-2017-010993_m012.jpg 10

This equation represents the proper averaging of the multiple paths from the reference state to the real, neutral state of the amino acid in Figure 3.

Results and Discussion

Solvation Free Energies

Uncharging Free Energies

In the first step, we calculated the solvation free energies of amino acid side chain analogues in water. As outlined in Figure 1, this process is split up into an uncharging and a cavity formation, or decoupling, step. For the uncharging process, we compare two end-point methods, LRA and TPF, with TI (Table 1). Table S1 shows the individual ligand surrounding energies and their fluctuations in the neutral and charged states, which are used to compute the TPF free-energy differences. The convergence of the fluctuations is represented graphically in Figure S1. All fluctuations seem well converged within about 5 ns. For all molecules studied, the agreement between TPF and TI is significantly better than between LRA and TI. As a representative example, Figure 4 shows the free-energy profiles for the uncharging of methionine. It can be seen that the curve of dG/dλ vs λ (in black) is not strictly linear but shows some curvature. Although LRA assumes linearity, with TPF we approximate the TI profile better, leading to a better free-energy estimate from the end-state simulations. The total root-mean-square error (RMSE) over all compounds in Table 1 between ΔGQ>NLRA and ΔGQ>N amounts to 11.8 kJ/mol, whereas between ΔGQ>NTPF and ΔGQ>N this is reduced to 3.3 kJ/mol. The only two cases where TPF deviates from TI by more than 4 kJ/mol are the compounds with a full positive charge (Arg and Lys side chain analogues). TPF outperforms LRA especially in the case of compounds bearing a full negative charge (Asp and Glu side chain analogues), where LRA deviates from TI by around 20 kJ/mol.

Table 1. Calculated Uncharging Free Energies of Side Chain Analogues (kJ/mol) via TI, LRA, and TPF and Their Absolute Differences (ΔΔGQ>NLRA–TI and ΔΔGQ>N)a.
a.a. ΔGQ>NTI ΔGQ>NLRA ΔΔGQ>NLRA–TI ΔGQ>NTPF ΔΔGQ>NTPF–TI
arg 138.9 ± 0.3 152.6 ± 0.1 13.8 144.0 ± 0.2 5.1
asn 52.1 ± 0.2 64.8 ± 0.04 12.7 54.0 ± 0.1 1.9
asp 338.6 ± 0.4 359.2 ± 0.1 20.6 339.5 ± 0.3 0.9
cys 10.2 ± 0.1 12.7 ± 0.02 2.5 10.4 ± 0.03 0.2
gln 51.8 ± 0.2 64.9 ± 0.04 13.1 54.3 ± 0.1 2.5
glu 337.7 ± 0.4 356.9 ± 0.1 19.2 339.2 ± 0.3 1.5
hisa 51.5 ± 0.2 61.9 ± 0.1 10.4 54.2 ± 0.3 2.8
hisb 66.3 ± 0.2 76.0 ± 0.04 9.7 68.6 ± 0.1 2.3
lys 178.4 ± 0.3 192.0 ± 0.1 13.7 187.3 ± 0.3 8.9
met 14.7 ± 0.1 17.4 ± 0.02 2.8 14.9 ± 0.03 0.2
phe 9.0 ± 0.1 10.7 ± 0.02 1.8 9.3 ± 0.02 0.3
ser 29.5 ± 0.1 40.4 ± 0.03 10.8 32.5 ± 0.1 3.0
thr 28.6 ± 0.1 39.3 ± 0.03 10.7 31.7 ± 0.1 3.1
trp 32.1 ± 0.1 35.9 ± 0.03 3.8 32.7 ± 0.1 0.6
tyr 32.5 ± 0.1 43.0 ± 0.03 10.5 35.9 ± 0.1 3.4
RMSE             11.8       3.3
Open in a new tab
a

Statistical error estimates are obtained from 1000 bootstrap replicates on the original data. The root mean square error (RMSE) is computed between TI and LRA and between TI and TPF.

Figure 4.

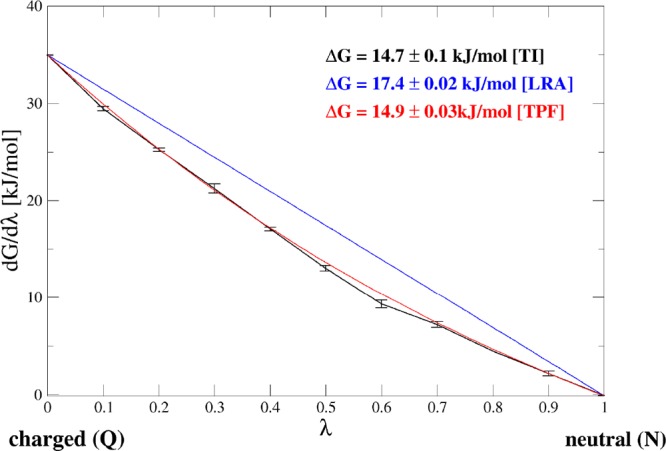
Figure 4

Open in a new tab

Example of the uncharging free energy computed by TI (black curve), LRA (blue curve), and TPF (red curve) for the side chain analogue of Met.

Decoupling Free Energies

The second step toward the solvation free energy involves the cavity formation step, here computed as the decoupling of the neutral side chain analogues by turning off the van der Waals interactions of all atoms with their surroundings. Following Figure 1, this process was performed by the TI approach, yielding ΔGN>DTI and a combination of TI and OSP, which is computed as ΔGN>D = ΔGN>ROSP + ΔGR>D. The value of ΔGR>DTI was −11.5 ± 0.1 kJ/mol for R1 and −16.5 ± 0.2 kJ/mol for R2. Note that these values only need to be computed once to obtain the complete solvation free energy, whereas it is not needed to represent relative solvation free energies. The annihilation free energies are collected in Table 2 and compared between TI and OSP with reference states R1 and R2. For reference state R1 it is clear that ΔGN>R amounts to extremely high values for larger molecules, such as the side chain analogues of Arg, Gln, Met, Tyr, and Trp. This is a clear indication that no relevant conformations for these compounds are observed in the simulation of R1. Table S3 in the Supporting Information shows the percentage of snapshots in the reference-state simulations that contribute significantly to the free-energy estimates. This value is obtained by counting the number of configurations for which (HN – HR) in eq 8 is less than ΔGN>ROSP + kBT. For the indicated compounds, no significant number of contributing snapshots is obtained, suggesting that the extremely high free-energy estimates.

Table 2. Decoupling Free Energies (kJ/mol) of the Neutral Amino Acid Side Chain Analogues via TI and OSP (ΔGN>DOSP = −ΔGR>N + ΔGR>DTI) Using Reference States R1 and R2, Together with Their Absolute Differences (ΔΔGN>D).
  R1
 R2
a.a. ΔGN>DTI ΔGN>DOSP ΔΔGN>DOSP–TI ΔGN>DOSP ΔΔGN>DOSP–TI
ala –9.1 ± 0.3 –9.3 ± 0.1 0.2        
arg –15.0 ± 0.8 –1408 ± 3 1393 –21.2 ± 0.3 6.2
asn –9.5 ± 0.5 –9.8 ± 0.4 0.3 –20.7 ± 0.2 11.2
asp –11.0 ± 0.6 –10.9 ± 0.4 0.1 –19.0 ± 0.3 8.1
cys –2.9 ± 0.4 –5.6 ± 0.4 2.7 –21.3 ± 0.2 18.4
gln –11.1 ± 0.6 –1325 ± 3 1314 –16.2 ± 0.2 5.1
glu –12.2 ± 0.6 –9.4 ± 0.7 2.8 –13.2 ± 0.2 1.1
hisa –7.5 ± 0.7 –11.8 ± 1.2 4.3 –13.1 ± 0.2 5.6
hisb –7.2 ± 0.6 –9.2 ± 1.3 2.0 –14.0 ± 0.2 6.8
ile –9.2 ± 0.6 –6.5 ± 1.4 2.7 –9.4 ± 0.2 0.2
leu –10.3 ± 0.7 –10.7 ± 1.1 0.4 –12.5 ± 0.3 2.2
lys –12.4 ± 0.6 –16.9 ± 2.0 4.5 –16.8 ± 0.3 4.4
met –6.6 ± 0.6 –438 ± 3 431 –7.2 ± 0.2 0.5
phe –7.6 ± 0.8 –12.7 ± 2.4 5.1 –10.0 ± 0.3 2.4
ser –5.4 ± 0.3 –7.1 ± 0.4 1.7 –25.4 ± 0.25 20.0
thr –6.3 ± 0.4 –8.6 ± 0.3 2.3 –10.5 ± 0.57 4.2
trp –7.0 ± 1.0 –149 ± 3 142 –1.3 ± 0.51 5.7
tyr –6.9 ± 0.9 –8583 ± 3 8576 –6.5 ± 0.62 0.5
val –8.5 ± 0.5 –9.3 ± 0.4 0.8 –15.0 ± 0.24 6.5
RMSE             2018       8.1
Open in a new tab

To accommodate larger compounds better, we introduced reference state R2 and included 10 rotational states of the molecules in the calculations, as outlined in the Methods. Table 2 shows that the agreement between ΔGN>RTI and ΔGN>R is much better for the large compounds, giving a RMS error over the indicated five compounds of 4.4 kJ/mol. However, some of the smaller compounds (e.g., the side chain anlogues of Cys and Ser) are not so well accommodated in the larger reference state, yielding deviations of roughly 20 kJ/mol. A viable strategy to choose the optimal reference state for a compound seems to be to pick the larger reference state, only if the percentage of contributing frames from Table S3 is less than 0.1% for simulation R1. The RMSE between the TI and OSP data is reduced to 3.1 kJ/mol when this rule of thumb is followed.

Combining the uncharging and the decoupling simulations into the full transfer of the side chain analogues from the hydrated to the vacuum state, we can compare the solvation free energies from experiment61 to the value obtained with TI and using the OSP-TPF approach. Table 3 collects these data, using the reference states R1 and R2 in the OSP approach. Note that for the side chains of Ala, Leu, Ile, and Val no TPF contribution was added, as these side chains are completely neutral in the united atom GROMOS 54a8 force field. No experimental data are given for the charged compounds (Arg, Asp, Glu, and Lys), as both the experimental and the computational ones require extensive processing before they can be compared directly.62,63 In this work, we did not attempt to compensate for the artifacts that arise in free-energy calculations involving a full charge change. These artifacts are identical between the various approaches and are hence irrelevant for a comparison between the TI and TPF+OSP data. The large deviations between the TI data and the TPF+OSP approach are due to the corresponding deviations in the decoupling states. Figure 5 compares the solvation free energies calculated via TI and TPF+OSP to the experimental values. Except for the bulky outliers, which could not be shown in the figure, the calculations using the R1 reference state agree better with the experimental as well as with the TI results. Using the same rule of thumb as above, applying reference state R2 only when the percentage of contributing frames drops below 0.1% for R1, the RMSE between TI and TPF+OSP is reduced to 2.6 kJ/mol, due to a fortuitous cancellation of the small errors in OSP (RMSE 3.1 kJ/mol) and TPF (RMSE 3.3 kJ/mol). The largest remaining deviations are for Trp (using R2; 6.4 kJ/mol), Lys (using R1; 4.4 kJ/mol), and Glu (using R1; 4.3 kJ/mol). For Trp the deviation still largely comes from the OSP calculation, as this compound is still relatively large for the (larger) reference state as reflected by the lowest percentage of contributing frames for R2 in Table S3. For Lys, however, the deviation largely comes from the TPF calculation (8.9 kJ/mol), one of the two compounds with a full positive charge, for which TPF was seen to perform worst (even though still better than LIE or LRA). For Glu, finally, the deviation of 4.3 kJ/mol is the result of errors of 2.8 kJ/mol for the charging free energy, which is quite reasonable for generating a full charge, and 1.5 kJ/mol for the decoupling free energy.

Table 3. Solvation Free Energies of Amino Acid Side Chains (kJ/mol)a.
      R1
 R2
a.a. ΔGsolvexp ΔGQ>DTI ΔGQ>DTPF+OSP ΔΔGQ>DT+O–TI ΔGQ>DTPF+OSP ΔΔGQ>DT+O–TI
ala 8.1 9.1 9.3 0.2    
ile 9.0 9.2 6.5 2.7 9.3 0.2
leu 9.5 10.3 10.7 0.4 12.5 2.2
val 8.3 8.5 9.3 0.8 14.9 6.4
arg   –123.9 1264 1388 –122.8 1.1
asn –40.5 –42.6 –44.2 1.6 –33.3 9.2
asp   –327.6 –328.6 1.0 –320.5 7.1
cys –5.2 –7.3 –4.8 2.5 10.8 18.1
gln –39.3 –40.6 1271 1312 –38.1 2.5
glu   –325.5 –329.8 4.3 –326.0 0.5
hisa –43.0 –44.0 –42.4 1.6 –41.2 2.8
hisb   –59.1 –59.5 0.4 –54.6 4.5
lys   –166.0 –170.4 4.4 –170.5 4.5
met –6.2 –8.0 423 432 –7.8 0.3
phe –3.2 –1.4 3.4 4.8 0.7 2.1
ser –21.2 –24.1 –25.4 1.3 –7.1 17.0
thr –20.4 –22.3 –23.2 0.9 –21.2 1.1
trp –24.6 –25.1 116 142 –31.4 6.4
tyr –25.6 –25.5 8547 8572 –29.5 3.9
RMSE       2018   7.2
Open in a new tab
a

ΔGsolvexp are experimentally measured solvation energies,61 ΔGQ>D are obtained from thermodynamic integration, and ΔGQ>DTPF+OSP are obtained with the combined TPF+OSP approach. ΔΔGQ>D are the absolute differences between ΔGQ>DTPF+OSP and ΔGQ>D.

Figure 5.

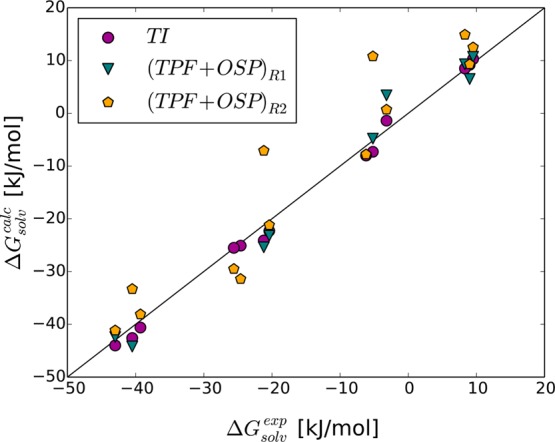
Figure 5

Open in a new tab

Comparison of experimental (ΔGsolvexp) and calculated (ΔGQ>D) solvation free energies of amino acid side chain analogues that do not carry a net charge. Calculations using TI are compared to using the TPF+OSP approach with reference states R1 and R2. Outliers Gln, Met, Trp, and Tyr are not shown for the calculations using R1 (Table 3).

Mutation Free Energies

Eventually, we aim to calculate the free energies of mutation in a protein; therefore, we here validate the TPF+OSP method using a tripeptide of Ala–ref–Ala. All of the amino acids except for proline and glycine were mutated into Ala via TI or the combination of TPF+OSP, following the scheme in Figure 3.

TI was performed in the tripeptide Ala–X–Ala, X being the mutated amino acid, in two separate steps. First, the partial charges of amino acid side chains were removed followed by the changing of Cß atom of the side chain into a united CH3 atom and annihilation of all remaining side chain atoms into dummy atoms. End points of the uncharging TI, i.e., λ = 0 and λ = 1 were simulated for 10 ns and used for the LRA and TPF calculation.

Simulations of the tripeptide with four reference states, R3–R6 were carried out for 50 ns in water. Seeing that in a tripeptide the conformation of a side chain can, through interactions with the backbone, significantly influence the mutation free energies, we created and used a library of the most relevant side chain conformations. A simulation of 100 ns of each tripeptide Ala–X–Ala was performed and subsequently clustered to obtain the five most relevant side chain conformations for each amino acid. CMSs from the five clusters were then fitted into the reference states to apply the OSP. The contributions for the individual conformations and a contribution due to the size of the cluster were exponentially averaged using eq 10 to obtain an overall estimate. An example of the conformational diversity of the five CMSs of Arg is shown in Figure 6.

Figure 6.

Figure 6

Open in a new tab

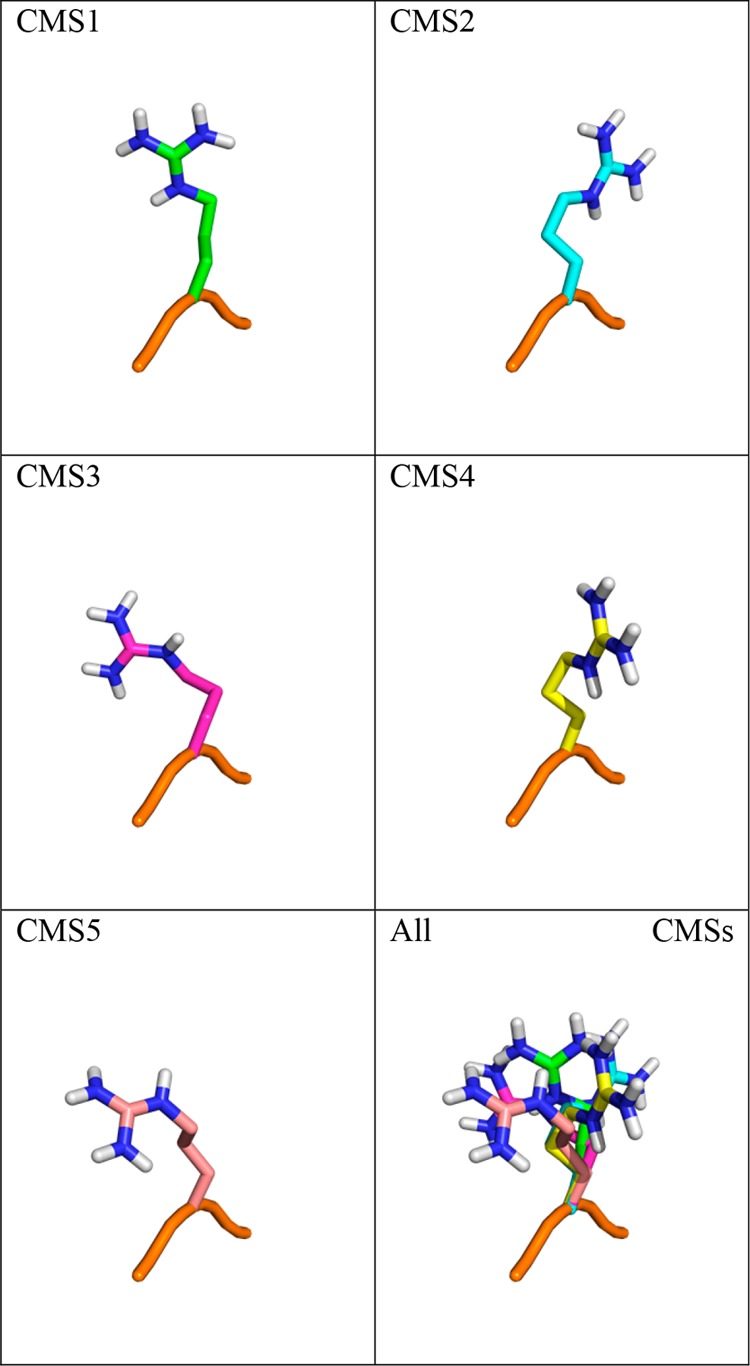
Overlay of central member structures of arginine side chains in the tripeptide. The backbone of the first CMS of the tripeptide Ala–Arg–Ala shown in orange and five central member structures of the side chain of Arg in differently colored sticks.

Uncharging Free Energies

Table 4 shows the comparison of uncharging free energies using TI, LRA, and TPF and Table S2 shows the individual ligand surrounding energies and their fluctuations in the neutral and charged states, which are used to compute the TPF free-energy differences. The results are very comparable to the values obtained for the individual side chain analogues. As before, the LRA values agree poorly, with an overall RMSE value of 12 kJ/mol. Similarly, we observe a good agreement between TPF and TI uncharging free energies with an overall RMSE of 3.4 kJ/mol. The biggest differences, of more than 5 kJ/mol, are for Arg, Gln, and Lys. Amino acids with a full charge show large uncharging free energies of more than 100 kJ/mol. Surprisingly, we found comparable values for the neutral residues Asn and Gln, for which uncharging free energies reach more than 250 kJ/mol. This could be traced to very strong intramolecular interactions of the acetamide group.

Table 4. Calculated Uncharging Free Energies of Side Chains in the Tripeptides (kJ/mol) via TI, LRA, and TPF and Their Absolute Differences (ΔΔGQ>NLRA–TI and ΔΔGQ>N)a.
a.a. ΔGQ>NTI ΔGQ>NIRA ΔΔGQ>NLRA–TI ΔGQ>NTPF ΔΔGQ>NTPF–TI
arg 217.0 ± 0.1 230.8 ± 0.1 13.8 222.5 ± 0.3 5.5
asn 252.0 ± 0.1 263.8 ± 0.1 11.9 253.9 ± 0.1 1.9
asp 415.9 ± 0.2 437.3 ± 0.1 21.5 416.9 ± 0.5 1.1
cys 18.3 ± 0.03 21.0 ± 0.03 2.7 18.7 ± 0.04 0.4
gln 268.2 ± 0.1 284.6 ± 0.1 16.5 274.3 ± 0.1 6.2
glu 406.1 ± 0.2 425.8 ± 0.1 19.7 407.1 ± 0.5 1.0
hisa 29.3 ± 0.1 40.0 ± 0.1 10.7 32.2 ± 0.1 2.8
hisb 60.9 ± 0.1 71.8 ± 0.1 10.9 64.0 ± 0.1 3.1
lysh 250.4 ± 0.1 264.4 ± 0.1 14.0 258.5 ± 0.4 8.1
met 12.6 ± 0.04 15.1 ± 0.03 2.6 12.7 ± 0.04 0.1
phe 0.6 ± 0.03 2.4 ± 0.02 1.7 1.0 ± 0.03 0.3
ser 44.4 ± 0.1 53.5 ± 0.04 9.1 46.2 ± 0.1 1.7
thr 44.0 ± 0.1 51.9 ± 0.04 7.9 45.4 ± 0.1 1.4
trp 53.0 ± 0.1 57.6 ± 0.04 4.6 54.1 ± 0.1 1.1
tyr 97.9 ± 0.1 108.0 ± 0.05 10.1 100.8 ± 0.1 2.9
RMSE             12.0       3.4
Open in a new tab
a

Statistical error estimates are obtained from 1000 bootstrap replicates on the original data. The root mean square error (RMSE) is computed between TI and LRA and between TI and TPF.

Free Energies of Annihilation

In the calculation of the free energies of annihilation, we compare the value obtained by TI, ΔGN>ATI to the corresponding free energy obtained from OSP as ΔΔGN>A = ΔGR>AOSP – ΔGR>N in Table 5. Following up on the OSP calculation for the solvation free energies in the previous section, we here included reference states R3 and R4. Considering that the smaller R1 gave reasonable results for most of the side chains, we furthermore introduced two additional reference states, R5 and R6. Both of them contain one dummy atom between the soft sphere and Cα, for the sake of a broader sampling of the soft sphere with respect to the backbone. As noted before, R6 is identical to R5, except for some additional dummy particles that may influence the dynamics, but not the conformational ensemble. All five CMSs were fitted into the configurations collected for the four reference states in the Ala–ref–Ala tripeptide and interaction energies were recalculated. Subsequently, the results from the individual CMS were averaged into one final value, using eq 10. This approach worked reasonably well for most of the side chains, but in Ile we could see a discrepancy between TI and OSP approach by more than 4 kJ/mol in all reference states. This could be avoided by including eight CMSs instead of five, better representing the conformational ensemble of Ile. Also the largest side chain of Trp seems most difficult to accommodate in all of the reference states, with deviations from the TI data of 5.7–16 kJ/mol.

Table 5. Absolute Difference between the Free Energy of Annihilation Calculated via TI and OSP, ΔΔGN>AOSP–TI = |ΔΔGN>A – ΔΔGN>ATI|, for the Different Reference Statesa.
  ΔΔGN>AOSP–TI [kJ/mol]
tripeptides R3 R4 R5 R6
arg 2.2 4.3 1.8 2.7
asn 2.8 2.3 1.2 1.1
asp 6.2 3.6 0.8 1.3
cys 1.7 1.5 2.6 2.3
gln 1.6 4.8 0.3 0.1
glu 1.8 2.8 1.5 0.7
hisa 4.3 4.4 0.0 0.6
hisb 1.0 0.3 2.3 1.3
ilea 6.8 8.6 3.1 6.6
leu 3.5 7.4 0.3 0.3
lysh 4.3 3.8 1.7 3.6
met 7.0 6.0 0.6 1.3
phe 6.3 4.7 1.2 1.1
ser 2.6 3.3 2.8 2.5
thr 4.8 3.2 2.1 1.8
trp 16.0 6.3 5.7 8.0
tyr 4.5 2.8 0.3 1.6
val 2.7 4.5 2.2 2.4
RMSE 5.6 4.6 2.2 3.0
Open in a new tab
a

Eight CMSs were used instead of five.

Overall, Table 5 shows that reference state R3 shows the worst agreement between TI and OSP with RMSE of 5.6 kJ/mol, followed by R4 with RMSE of 4.6 kJ/mol. R5 and R6, however, show very good agreement between the OSP and TPF values. R5 shows excellent agreement with TI, with RMSE of 2.2 kJ/mol, which is below kBT at 300 K.

Free Energies of Mutation

Combing the data from the uncharging and the annihilation of nonpolar side chains, the total free energy of mutation to Ala was calculated and correlated in Figure 7. The difference from the TI data (ΔΔGQ>A(TPF+OSP)–TI) is given in Table 6. Following the trend observed for the annihilation of nonpolar particles with OSP, the reference states showing the best agreement with TI are R5 and R6, with RMSE of 3.2 and 4.1 kJ/mol, respectively. R3 and R4 show RMSE of 6.7 and 6.4 kJ/mol, respectively. In all cases the biggest outlier is Lys, with a deviation of more than 9 kJ/mol, Gln, with a deviation of at least 6 kJ/mol and Trp, with a difference of at least 5 kJ/mol. The reasons for these deviations are different. As for the amino acid side chain analogues, the full positive charge hampers the accuracy of the TPF approach, whereas for Trp the large size limits the accuracy of the OSP approach. Not surprisingly, the large TPF estimates for Gln described above, lead to a large remaining deviation in the mutation free energy. An average overall deviation that is on the order of 4 kJ/mol (∼1 kcal/mol) is quite acceptable considering the wide range of the mutational free energies in Figure 7.

Figure 7.

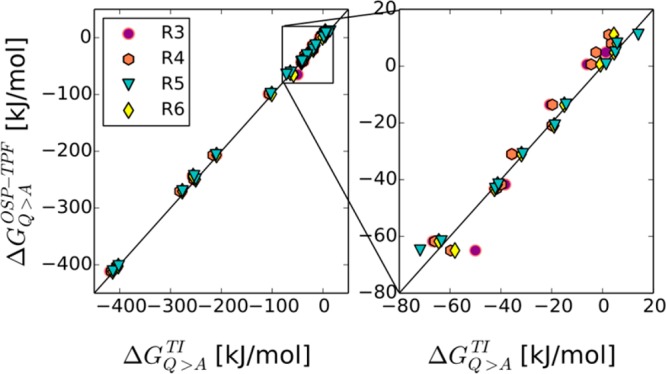
Figure 7

Open in a new tab

Comparison of the free energies of mutation of amino acids into alanine in the tripeptide calculated via TI (ΔGQ>ATI) and TPF+OSP approach with all reference states (ΔΔGQ>A). The right panel is a zoom of the indicated square in the left panel.

Table 6. Absolute Difference between the Mutational Free Energy Calculated via TI and OSP, ΔΔGQ>A(TPF+OSP)–TI = |ΔΔGQ>A – ΔΔGQ>ATI|, for the Different Reference Statesa.
  ΔΔGQ>A(TPF+OSP)–TI [kJ/mol]
tripeptides R3 R4 R5 R6
ilea 6.8 8.6 3.1 6.6
leu 3.5 7.4 0.3 0.3
val 2.8 4.5 2.2 2.4
arg 3.2 9.7 3.6 2.7
asn 4.7 4.2 0.7 0.8
asp 7.1 4.5 1.7 2.2
cys 1.3 1.1 2.2 1.9
gln 7.9 11.2 6.0 6.4
glu 2.8 3.8 0.5 0.3
hisa 4.6 4.7 0.3 0.9
hisb 5.0 4.3 1.6 2.7
lys 12.5 12.0 9.9 11.8
met 7.1 6.1 0.7 1.4
phe 6.7 5.1 0.8 1.4
ser 0.8 1.5 1.0 0.7
thr 3.4 1.9 0.8 0.4
trp 14.9 5.2 6.8 6.9
tyr 7.9 6.2 3.7 1.8
RMSE 6.7 6.4 3.6 4.1
Open in a new tab
a

Eight CMSs were used instead of five.

Efficiency of the Method

The combined TPF+OSP approach has the potential to significantly reduce the amount of computational time needed for calculation of the free energy of mutation. In TI, 10–20 simulations at different λ-values are needed for every pair of mutants that is studied. Most of the simulation time is spent on unphysical intermediate states. In the TPF+OSP approach, the charging free energy is collected from only two simulations in the end states, of which the charged state is a simulation of the actual mutants one is interested in, giving access to structural properties of the mutant. Furthermore, the OSP contribution is calculated from a single (longer) simulation of the reference state, which is efficiently reused for all mutants. Taken together, the TPF+OSP approach requires less overall simulation time, and a larger fraction of the simulation time is spent on simulations that have physical relevance and can be further used to study, e.g., the interactions of the amino acids.

Without an optimized simulation time for either of the approaches, Table S4 summarizes the overall simulation time used in the TI calculations and the TPF+OSP calculations of the tripeptides. The latter approach was based on approximately half the simulation length as the TI data.

It is important to mention that the computational resources spent on creating of the side chain conformation library amounted to 100 ns for each amino acid. This library is, however, already created and can be further used in future calculations. Alternatively, if necessary, the end-point trajectories of TPF could be used to create additional libraries in future calculations of the free energy of mutation in very different systems.

Conclusion

In the current work, we systematically studied the performance of an approach combining third-power fitting (TPF) and one-step perturbation (OSP) approaches, as compared to more robust thermodynamic integration (TI) data. The solvation free energies of a large range of compounds (charged, polar, nonpolar, small aliphatic, aromatic, ...) were computed and compare excellently to the TI data. When two reference states are considered, depending on the size of the solute, a root-mean-square deviation of only 2.6 kJ/mol was obtained. Furthermore, we extended this approach to the calculation of mutational free energies in model tripeptides and could establish an efficient protocol involving a single reference state. The overall deviation between the TI data and the TPF+OSP approach amounts to a very good 3–4 kJ/mol, which is still very acceptable considering the large range of free energies considered. Without explicit optimization of the method, the TPF+OSP approach can be about 2 times more efficient than full TI calculations.

Acknowledgments

Financial support of the Austrian Science Fund, project I 1999 is gratefully acknowledged.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b01099.

  • Tables S1 and S2, the individual energy terms and their fluctuations as used in the TPF method; Table S3, the percentage of contributing configurations in the OSP calculations for all amino acid side chain analogues (reference states R1 and R2) and for all amino acids (reference states R3, R4, R5 and R6); Table S4, comparison of the computational efforts of TI and the TPF+OSP approach; Figure S1, the convergence of the energy fluctuations as a function of time for selected amino acid side chain analogues; building blocks of all reference states for use in the GROMOS 54a8 force field (PDF)

Author Present Address

† Laboratory of Physical Chemistry, Swiss Federal Institute of Technology, ETH, 8093 Zürich, Switzerland.

The authors declare no competing financial interest.

Supplementary Material

ct7b01099_si_001.pdf (1.2MB, pdf)

References

  1. Zhang X. F.; Yang G. Y.; Zhang Y.; Xie Y.; Withers S. G.; Feng Y. A general and efficient strategy for generating the stable enzymes. Sci. Rep. 2016, 6, 12. 10.1038/srep33797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Won A.; Pripotnev S.; Ruscito A.; Ianoul A. Effect of Point Mutations on the Secondary Structure and Membrane Interaction of Antimicrobial Peptide Anoplin. J. Phys. Chem. B 2011, 115 (10), 2371–2379. 10.1021/jp108343g. [DOI] [PubMed] [Google Scholar]
  3. Acevedo J. P.; Reetz M. T.; Asenjo J. A.; Parra L. P. One-step combined focused epPCR and saturation mutagenesis for thermostability evolution of a new cold-active xylanase. Enzyme Microb. Technol. 2017, 100, 60–70. 10.1016/j.enzmictec.2017.02.005. [DOI] [PubMed] [Google Scholar]
  4. Moutaoufik M. T.; Morrow G.; Maaroufi H.; Ferard C.; Finet S.; Tanguay R. M. Oligomerization and chaperone-like activity of Drosophila melanogaster small heat shock protein DmHsp27 and three arginine mutants in the alpha-Crystallin domain. Cell Stress Chaperones 2017, 22 (4), 455–466. 10.1007/s12192-016-0748-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cortina G. A.; Kasson P. M. Excess positional mutual information predicts both local and allosteric mutations affecting beta lactamase drug resistance. Bioinformatics 2016, 32 (22), 3420–3427. 10.1093/bioinformatics/btw492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Budzko L.; Jackowiak P.; Kamel K.; Sarzynska J.; Bujnicki J. M.; Figlerowicz M. Mutations in human AID differentially affect its ability to deaminate cytidine and 5-methylcytidine in ssDNA substrates in vitro. Sci. Rep. 2017, 7 (1), 3873. 10.1038/s41598-017-03936-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bogan A. A.; Thorn K. S. Anatomy of hot spots in protein interfaces. J. Mol. Biol. 1998, 280 (1), 1–9. 10.1006/jmbi.1998.1843. [DOI] [PubMed] [Google Scholar]
  8. Du X.; Li Y.; Xia Y. L.; Ai S. M.; Liang J.; Sang P.; Ji X. L.; Liu S. Q. Insights into Protein-Ligand Interactions: Mechanisms, Models, and Methods. Int. J. Mol. Sci. 2016, 17 (2), 144. 10.3390/ijms17020144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Sharir-Ivry A.; Varatharaj R.; Shurki A. Challenges within the Linear Response Approximation When Studying Enzyme Catalysis and Effects of Mutations. J. Chem. Theory Comput. 2015, 11 (1), 293–302. 10.1021/ct500751f. [DOI] [PubMed] [Google Scholar]
  10. Almlof M.; Aqvist J.; Smalas A. O.; Brandsdal B. O. Probing the effect of point mutations at protein-protein interfaces with free energy calculations. Biophys. J. 2006, 90 (2), 433–442. 10.1529/biophysj.105.073239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S. H.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33 (12), 889–897. 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
  12. Honig B.; Nicholls A. Classical electrostatic in biology and chemistry. Science 1995, 268 (5214), 1144–1149. 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
  13. Onufriev A.; Bashford D.; Case D. A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins: Struct., Funct., Genet. 2004, 55 (2), 383–394. 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
  14. Martins S. A.; Perez M. A. S.; Moreira I. S.; Sousa S. F.; Ramos M. J.; Fernandes P. A. Computational Alanine Scanning Mutagenesis: MM-PBSA vs TI. J. Chem. Theory Comput. 2013, 9 (3), 1311–1319. 10.1021/ct4000372. [DOI] [PubMed] [Google Scholar]
  15. Simoes I. C. M.; Costa I. P. D.; Coimbra J. T. S.; Ramos M. J.; Fernandes P. A. New Parameters for Higher Accuracy in the Computation of Binding Free Energy Differences upon Alanine Scanning Mutagenesis on Protein-Protein Interfaces. J. Chem. Inf. Model. 2017, 57 (1), 60–72. 10.1021/acs.jcim.6b00378. [DOI] [PubMed] [Google Scholar]
  16. Chodera J. D.; Mobley D. L.; Shirts M. R.; Dixon R. W.; Branson K.; Pande V. S. Alchemical free energy methods for drug discovery: progress and challenges. Curr. Opin. Struct. Biol. 2011, 21 (2), 150–160. 10.1016/j.sbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Steinbrecher T.; Mobley D. L.; Case D. A. Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J. Chem. Phys. 2007, 127 (21), 214108. 10.1063/1.2799191. [DOI] [PubMed] [Google Scholar]
  18. Schafer H.; Van Gunsteren W. F.; Mark A. E. Estimating relative free energies from a single ensemble: Hydration free energies. J. Comput. Chem. 1999, 20 (15), 1604–1617. . [DOI] [Google Scholar]
  19. Steinbrecher T.; Joung I.; Case D. A. Soft-Core Potentials in Thermodynamic Integration: Comparing One- and Two-Step Transformations. J. Comput. Chem. 2011, 32 (15), 3253–3263. 10.1002/jcc.21909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kirkwood J. G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3 (5), 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
  21. Liu Y. L.; Patel A. H. G.; Burger S. K.; Ayers P. W. Benchmarking pK(a) prediction methods for Lys115 in acetoacetate decarboxylase. J. Mol. Model. 2017, 23 (5), 8. 10.1007/s00894-017-3324-x. [DOI] [PubMed] [Google Scholar]
  22. Maurer M.; de Beer S. B. A.; Oostenbrink C. Calculation of Relative Binding Free Energy in the Water-Filled Active Site of Oligopeptide-Binding Protein. Molecules 2016, 21 (4), 499. 10.3390/molecules21040499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Bekker G. J.; Kamiya N.; Araki M.; Fukuda I.; Okuno Y.; Nakamura H. Accurate Prediction of Complex Structure and Affinity for a Flexible Protein Receptor and Its Inhibitor. J. Chem. Theory Comput. 2017, 13 (6), 2389–2399. 10.1021/acs.jctc.6b01127. [DOI] [PubMed] [Google Scholar]
  24. Tanida Y.; Ito M. S.; Fujitani H. Calculation of absolute free energy of binding for theophylline and its analogs to RNA aptamer using nonequilibrium work values. Chem. Phys. 2007, 337 (1–3), 135–143. 10.1016/j.chemphys.2007.07.014. [DOI] [Google Scholar]
  25. Beierlein F. R.; Kneale G. G.; Clark T. Predicting the Effects of Basepair Mutations in DNA-Protein Complexes by Thermodynamic Integration. Biophys. J. 2011, 101 (5), 1130–1138. 10.1016/j.bpj.2011.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Liu H. Y.; Mark A. E.; van Gunsteren W. F. Estimating the relative free energy of different molecular states with respect to a single reference state. J. Phys. Chem. 1996, 100 (22), 9485–9494. 10.1021/jp9605212. [DOI] [Google Scholar]
  27. Oostenbrink C.; van Gunsteren W. F. Free energies of binding of polychlorinated biphenyls to the estrogen receptor from a single simulation. Proteins: Struct., Funct., Genet. 2004, 54 (2), 237–246. 10.1002/prot.10558. [DOI] [PubMed] [Google Scholar]
  28. Oostenbrink C.; van Gunsteren W. F. Free energies of ligand binding for structurally diverse compounds. Proc. Natl. Acad. Sci. U. S. A. 2005, 102 (19), 6750–4. 10.1073/pnas.0407404102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Beutler T. C.; Mark A. E.; van Schaik R. C.; Gerber P. R.; van Gunsteren W. F. Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett. 1994, 222 (6), 529–539. 10.1016/0009-2614(94)00397-1. [DOI] [Google Scholar]
  30. Graf M. M. H.; Lin Z. X.; Bren U.; Haltrich D.; van Gunsteren W. F.; Oostenbrink C. Pyranose Dehydrogenase Ligand Promiscuity: A Generalized Approach to Simulate Monosaccharide Solvation, Binding, and Product Formation. PLoS Comput. Biol. 2014, 10 (12), e1003995. 10.1371/journal.pcbi.1003995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ciordia M.; Perez-Benito L.; Delgado F.; Trabanco A. A.; Tresadern G. Application of Free Energy Perturbation for the Design of BACE1 Inhibitors. J. Chem. Inf. Model. 2016, 56 (9), 1856–1871. 10.1021/acs.jcim.6b00220. [DOI] [PubMed] [Google Scholar]
  32. Raman E. P.; Vanommeslaeghe K.; MacKerell A. D. Site-Specific Fragment Identification Guided by Single-Step Free Energy Perturbation Calculations. J. Chem. Theory Comput. 2012, 8 (10), 3513–3525. 10.1021/ct300088r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Cave-Ayland C.; Skylaris C. K.; Essex J. W. Direct Validation of the Single Step Classical to Quantum Free Energy Perturbation. J. Phys. Chem. B 2015, 119 (3), 1017–1025. 10.1021/jp506459v. [DOI] [PubMed] [Google Scholar]
  34. Loeffler H. H.; Michel J.; Woods C. FESetup: Automating Setup for Alchemical Free Energy Simulations. J. Chem. Inf. Model. 2015, 55 (12), 2485–2490. 10.1021/acs.jcim.5b00368. [DOI] [PubMed] [Google Scholar]
  35. Gapsys V.; Michielssens S.; Seeliger D.; de Groot B. L. pmx: Automated Protein Structure and Topology Generation for Alchemical Perturbations. J. Comput. Chem. 2015, 36 (5), 348–354. 10.1002/jcc.23804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Chiang Y. C.; Wang Y. Virtual Substitution Scan Via Single-Step Free Energy Perturbation. Biopolymers 2016, 105 (6), 324–336. 10.1002/bip.22820. [DOI] [PubMed] [Google Scholar]
  37. Oostenbrink C.; Van Gunsteren W. F. Single-step perturbations to calculate free energy differences from unphysical reference states: Limits on size, flexibility, and character. J. Comput. Chem. 2003, 24 (14), 1730–1739. 10.1002/jcc.10304. [DOI] [PubMed] [Google Scholar]
  38. Pitera J. W.; van Gunsteren W. F. One-step perturbation methods for solvation free energies of polar solutes. J. Phys. Chem. B 2001, 105 (45), 11264–11274. 10.1021/jp012003j. [DOI] [Google Scholar]
  39. Oostenbrink C. Efficient free energy calculations on small molecule host-guest systems - a combined linear interaction energy/one-step perturbation approach. J. Comput. Chem. 2009, 30 (2), 212–21. 10.1002/jcc.21116. [DOI] [PubMed] [Google Scholar]
  40. Sham Y. Y.; Chu Z. T.; Tao H.; Warshel A. Examining methods for calculations of binding free energies: LRA, LIE, PDLD-LRA, and PDLD/S-LRA calculations of ligands binding to an HIV protease. Proteins: Struct., Funct., Genet. 2000, 39 (4), 393–407. . [DOI] [PubMed] [Google Scholar]
  41. Aqvist J.; Medina C.; Samuelsson J. E. A new method for predicting binding affinity in computer-aided drug design. Protein Eng., Des. Sel. 1994, 7 (3), 385–91. 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
  42. Aqvist J.; Hansson T. On the validity of electrostatic linear response in polar solvents. J. Phys. Chem. 1996, 100 (22), 9512–9521. 10.1021/jp953640a. [DOI] [Google Scholar]
  43. de Ruiter A.; Oostenbrink C. Efficient and Accurate Free Energy Calculations on Trypsin Inhibitors. J. Chem. Theory Comput. 2012, 8 (10), 3686–3695. 10.1021/ct200750p. [DOI] [PubMed] [Google Scholar]
  44. Schmid N.; Christ C. D.; Christen M.; Eichenberger A. P.; van Gunsteren W. F. Architecture, implementation and parallelisation of the GROMOS software for biomolecular simulation. Comput. Phys. Commun. 2012, 183 (4), 890–903. 10.1016/j.cpc.2011.12.014. [DOI] [Google Scholar]
  45. Reif M. M.; Winger M.; Oostenbrink C. Testing of the GROMOS Force-Field Parameter Set 54A8: Structural Properties of Electrolyte Solutions, Lipid Bilayers, and Proteins. J. Chem. Theory Comput. 2013, 9 (2), 1247–1264. 10.1021/ct300874c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Chemical Computing Group ULC Molecular Operating Environment (MOE), 2013.08; 1010 Sherbooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7, 2017.
  47. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J.. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces: Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry, held in Jerusalem, Israel, April 13–16, 1981; Pullman B., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp 331–342. [Google Scholar]
  48. Amadei A.; Chillemi G.; Ceruso M. A.; Grottesi A.; Di Nola A. Molecular dynamics simulations with constrained roto-translational motions: Theoretical basis and statistical mechanical consistency. J. Chem. Phys. 2000, 112 (1), 9–23. 10.1063/1.480557. [DOI] [Google Scholar]
  49. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Dinola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81 (8), 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  50. Ryckaert J. P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of cartesian equations of motion of a system with constraints - molecular dynamics of N-alkanes. J. Comput. Phys. 1977, 23 (3), 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  51. Tironi I. G.; Sperb R.; Smith P. E.; van Gunsteren W. F. A generalized reaction field method for molecular dynamics simulations. J. Chem. Phys. 1995, 102 (13), 5451–5459. 10.1063/1.469273. [DOI] [Google Scholar]
  52. Heinz T. N.; van Gunsteren W. F.; Hünenberger P. H. Comparison of four methods to compute the dielectric permittivity of liquids from molecular dynamics simulations. J. Chem. Phys. 2001, 115 (3), 1125–1136. 10.1063/1.1379764. [DOI] [Google Scholar]
  53. Daura X.; van Gunsteren W. F.; Mark A. E. Folding-unfolding thermodynamics of a beta-heptapeptide from equilibrium simulations. Proteins: Struct., Funct., Genet. 1999, 34 (3), 269–80. . [DOI] [PubMed] [Google Scholar]
  54. Lee F. S.; Chu Z. T.; Bolger M. B.; Warshel A. Calculations of antibody-antigen interactions: microscopic and semi-microscopic evaluation of the free energies of binding of phosphorylcholine analogs to McPC603. Protein Eng., Des. Sel. 1992, 5 (3), 215–28. 10.1093/protein/5.3.215. [DOI] [PubMed] [Google Scholar]
  55. Sham Y. Y.; Chu Z. T.; Tao H.; Warshel A. Examining methods for calculations of binding free energies: LRA, LIE, PDLD-LRA, and PDLD/S-LRA calculations of ligands binding to an HIV protease. Proteins: Struct., Funct., Genet. 2000, 39 (4), 393–407. . [DOI] [PubMed] [Google Scholar]
  56. Warshel A.; Russell S. T. Calculations of electrostatic interactions in biological systems and in solutions. Q. Rev. Biophys. 1984, 17 (3), 283–422. 10.1017/S0033583500005333. [DOI] [PubMed] [Google Scholar]
  57. Chipot C.; Pohorille A.. Free energy calculations: Theory and applications in chemistry and biology; Springer: Berlin, 2007. [Google Scholar]
  58. Zwanzig R. W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22 (8), 1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
  59. Pitera J. W.; van Gunsteren W. F. One-step perturbation methods for solvation free energies of polar solutes. J. Phys. Chem. B 2001, 105 (45), 11264–11274. 10.1021/jp012003j. [DOI] [Google Scholar]
  60. Mark A. E.; Xu Y. W.; Liu H. Y.; van Gunsteren W. F. Rapid non-empirical approaches for estimating relative binding free energies. Acta Biochim. Polym. 1995, 42 (4), 525–535. [PubMed] [Google Scholar]
  61. Wolfenden R.; Andersson L.; Cullis P. M.; Southgate C. C. B. Affinities of amino-acid side-chains for solvent water. Biochemistry 1981, 20 (4), 849–855. 10.1021/bi00507a030. [DOI] [PubMed] [Google Scholar]
  62. Reif M. M.; Hünenberger P. H. Computation of methodology-independent single-ion solvation properties from molecular simulations. IV. Optimized Lennard-Jones interaction parameter sets for the alkali and halide ions in water. J. Chem. Phys. 2011, 134 (14), 144104. 10.1063/1.3567022. [DOI] [PubMed] [Google Scholar]
  63. Reif M. M.; Hünenberger P. H.; Oostenbrink C. New Interaction Parameters for Charged Amino Acid Side Chains in the GROMOS Force Field. J. Chem. Theory Comput. 2012, 8 (10), 3705–3723. 10.1021/ct300156h. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct7b01099_si_001.pdf (1.2MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES