Infectious Disease Dynamics Inferred from Genetic Data via Sequential Monte Carlo

Abstract

Genetic sequences from pathogens can provide information about infectious disease dynamics that may supplement or replace information from other epidemiological observations. Most currently available methods first estimate phylogenetic trees from sequence data, then estimate a transmission model conditional on these phylogenies. Outside limited classes of models, existing methods are unable to enforce logical consistency between the model of transmission and that underlying the phylogenetic reconstruction. Such conflicts in assumptions can lead to bias in the resulting inferences. Here, we develop a general, statistically efficient, plug-and-play method to jointly estimate both disease transmission and phylogeny using genetic data and, if desired, other epidemiological observations. This method explicitly connects the model of transmission and the model of phylogeny so as to avoid the aforementioned inconsistency. We demonstrate the feasibility of our approach through simulation and apply it to estimate stage-specific infectiousness in a subepidemic of human immunodeficiency virus in Detroit, Michigan. In a supplement, we prove that our approach is a valid sequential Monte Carlo algorithm. While we focus on how these methods may be applied to population-level models of infectious disease, their scope is more general. These methods may be applied in other biological systems where one seeks to infer population dynamics from genetic sequences, and they may also find application for evolutionary models with phenotypic rather than genotypic data.

Introduction

Phylodynamic methods extract information from pathogen genetic sequences and epidemiological data to infer the determinants of infectious disease transmission (Grenfell et al. 2004). For successful phylodynamic inference, mechanisms of transmission must leave their signature in genetic sequences. This occurs when pathogen transmission, and evolution occurs on similar timescales (Drummond et al. 2003). By explicitly relating models of disease dynamics to their predictions with respect to pathogen sequences, it is possible to estimate aspects of the mechanisms of transmission (Rasmussen et al. 2011; Stadler et al. 2013; Volz, Koelle, et al. 2013; Frost et al. 2015; Poon 2015; Karcher et al. 2016). Most existing phylodynamic inference methods proceed in three stages. First, one estimates the pathogen phylogeny using sequence data. Next, one fits models of disease dynamics to properties of the pathogen phylogeny, such as coalescent times or summary statistics on the tree. Finally, one assesses the robustness of the results to variation in the estimated phylogeny to account for phylogenetic uncertainty. Frequently, such methods harbor logical inconsistencies between the assumptions of the model used to estimate the phylogeny and those of the model of disease dynamics. In particular, it may happen that population dynamics, as estimated by the transmission model, are inconsistent with those assumed when estimating the phylogeny. In the absence of consistent methods, it may be difficult to assess the loss of accuracy due to the use of inconsistent methods.

Researchers developing Markov chain Monte Carlo (MCMC) approaches to phylodynamic inference have recognized the need to develop fully consistent approaches. In particular, Lau et al. (2015) have proposed a Bayesian method for joint inference. This work builds off phylodynamic inference that uses MCMC to fit deterministic population models (Bouckaert et al. 2014). However, to achieve efficiency, it is typically necessary to tailor an MCMC sampler to the specific model being fit (Vaughan et al. 2014). The required investment makes it costly to entertain competing models and to base inference directly on the models of greatest scientific interest. In practice, phylodynamic inference for infectious diseases has therefore tended to focus on the three-stage methods described above.

In this paper, we develop methodology for jointly inferring both phylogeny and transmission, as well as estimating unknown model parameters. Our central contribution is an algorithm which we call GenSMC, an abbreviation of sequential Monte Carlo with genetic sequence data. Sequential Monte Carlo (SMC), also known as the particle filter, provides a widely used basis for inference on complex dynamic systems (Kantas et al. 2015) with several appealing properties. Because basic SMC methods rely only on forward-in-time simulation of stochastic processes, they can accommodate a wide variety of models: Essentially any model that can be simulated is formally admissible. Thus, the algorithm enjoys a variant of the plug-and-play property (Bretó et al. 2009; He et al. 2010). An SMC computation results in an evaluation of the likelihood, which is a well understood and powerful basis for both frequentist and Bayesian inference. Finally, again because SMC requires only forward-in-time computation, it is straightforward to construct a model of genetic sequence evolution upon the basis of a transmission model, thus avoiding all conflict between these models.

SMC techniques have previously been used for inferring phylogenies (Bouchard-Côté et al. 2012) and for phylodynamic inference conditional on a phylogeny (Rasmussen et al. 2011). However, using SMC to solve the joint inference problem through forward-in-time simulation of tree-valued processes is a high-dimensional, computationally challenging problem. We found that several innovations were necessary to realize a SMC approach that is computationally feasible on models and datasets of scientific interest. The key innovations that provided a path to feasibility were: Just-in-time construction of state variables, hierarchical sampling, algorithm parallelization, restriction to a class of physical molecular clocks, and maximization of the likelihood using the iterated filtering algorithm of Ionides et al. (2015).

In the following, we first give an overview of the class of models for which our SMC algorithms are applicable. A formal specification is given in the supplement, and the source code for our implementation is also available. Next, we present a study on a simulated dataset as evidence of the algorithm’s feasibility. Finally, we use our methods to estimate determinants of the epidemic of human immunodeficiency virus (HIV) among the population of young, black, men who have sex with men (MSM) in Detroit, Michigan from 2004 to 2011. This analysis uses time-of-diagnosis and consensus protease sequences to estimate the rates of infection attributable to sources inside and outside the focal population.

New Approaches

The key novelty in our approach to phylodynamics is in formulating a flexible class of phylodynamic models and a class of SMC algorithms in such a way that the latter can be efficiently applied to the former. We refer to our phylodynamic model class as GenPOMP models, in recognition of the fact that they are partially observed Markov processes (POMPs). As such, a GenPOMP model consists of an unobserved Markov process—called the latent process—and an observable process. In the following sections, we specify the structure of each of these components. An additional, more formal, description of the GenPOMP model is given in the supplement (supplementary section S1, Supplementary Material online). Our GenSMC algorithm for GenPOMP models is introduced in the Materials and Methods section. GenSMC is presented at greater length in the supplement (supplementary section S2, Supplementary Material online) and also provided with a mathematical justification (supplementary section S3, Supplementary Material online). Our extension of GenSMC to parameter estimation, via iterated filtering, is called the GenIF algorithm and is discussed briefly in the Materials and Methods section and at greater length in supplementary section S2.2, Supplementary Material online. For computational implementation of the GenPOMP framework and the GenSMC and GenIF algorithms, we wrote the open-source genPomp program discussed further in supplementary section S1.1, Supplementary Material online.

For concreteness, we focus here on an infectious disease scenario, wherein the model describes transmission of infections among hosts and the sequences come from pathogens in those infections. In this context, measurements on infected individuals are called diagnoses. In the concluding Discussion section, we briefly consider other contexts within which the models and methods we have developed may prove useful.

The Latent Process

We adopt the convention of denoting random variables using uppercase symbols; we denote specific values assumed by random variables using the corresponding lowercase symbol. We use an asterisk to denote the data, which are treated as a specific realization of random variables in the model.

The latent Markov process, $\{X(t),\hspace{0.17em}t\in \mathbb{T}\}$, defined over a time interval $\mathbb{T}=[t_0,\hspace{0.17em}{t}_{\text{end}}]$, explicitly models the population dynamics and also includes any other processes needed to describe the evolution of the pathogen. Specifically, we suppose that we can write $X(t)=(\mathcal{T}(t),\hspace{0.17em}\mathcal{P}(t),\hspace{0.17em}\mathcal{U}(t))$, where $\mathcal{T}(t)$ is the transmission forest, $\mathcal{P}(t)$ is the pathogen phylogeny equipped with a relaxed molecular clock, and $\mathcal{U}(t)$ represents the state of the pathogen and host populations. For example, $\mathcal{U}(t)$ may categorize each individual in the host population into classes representing different stages of infection. We suppose that $\{\mathcal{U}(t),t\in \mathbb{T}\}$ is itself a Markov process.

The transmission forest represents the history of transmission among hosts. We assume that hosts cannot be multiply infected; this implies that $\mathcal{T}(t)$ is a forest, that is, a collection of trees. Nodes in $\mathcal{T}(t)$ are time-stamped and of several types. Internal nodes represent transmission events. Terminal nodes are of three types: 1) active nodes represent infections active at time t; 2) observed nodes correspond to diagnosis events, possibly associated with genetic sequences; 3) dead nodes correspond to death or emigration events. Root nodes at time t₀ correspond to infections present in the initial population; root nodes at times $t>t_0$ correspond to immigration events. Since all nodes are time-stamped, edges of $\mathcal{T}(t)$ have lengths measured in units of calendar time.

The pathogen phylogeny $\mathcal{P}(t)$ represents the history of divergences of pathogen lineages. Internal nodes of $\mathcal{P}(t)$ represent branch-points of pathogen lineages, which, we assume, coincide with transmission events. The terminal nodes of $\mathcal{P}(t)$ are in 1–1 correspondence with the terminal nodes of $\mathcal{T}(t)$. The distinction between $\mathcal{P}(t)$ and $\mathcal{T}(t)$ allows for random variation in the rate of molecular evolution, that is, relaxed molecular clocks (see below). Specifically, the edge lengths of $\mathcal{T}(t)$ measure calendar time between events, whereas edge lengths in $\mathcal{P}(t)$ can have additional random variation describing nonconstant rates of evolution.

The transmission forest $\mathcal{T}(t)$ can grow in only five distinct ways: 1) active nodes can split in two, when a transmission event occurs, 2) active nodes can become dead nodes, upon emigration, recovery, or death of the corresponding host, 3) immigration events can give rise to new active nodes, each with its own distinct root, 4) sampling events cause active nodes to spawn diagnosis nodes, and 5) active nodes for which none of the above occur simply grow older. Likewise, the pathogen phylogeny $\mathcal{P}(t)$ grows along with $\mathcal{T}(t)$ (fig. 1). The Markov process $\{\mathcal{U}(t)\}$ can contain additional information about the system at time t, for example, states of individual hosts. $\{\mathcal{U}(t)\}$ can affect, but must not be affected by, the $\{\mathcal{T}(t)\}$ and $\{\mathcal{P}(t)\}$ processes. That is, given any sequence of times $t_1<\dots <t_k<t,\hspace{0.17em}\{\mathcal{U}(t)\}$ is independent of {$(\mathcal{T}(t_j),\mathcal{P}(t_j)),\hspace{0.17em}j=1,\dots ,k$} conditional on $\{\mathcal{U}(t_j),\hspace{0.17em}{t}_1<\dots <t_k<t\}$. The dependence relationships among $\mathcal{T},\hspace{0.17em}\mathcal{P},\hspace{0.17em}\mathcal{U}$, and the data are diagrammed in supplementary figure S1, Supplementary Material online.

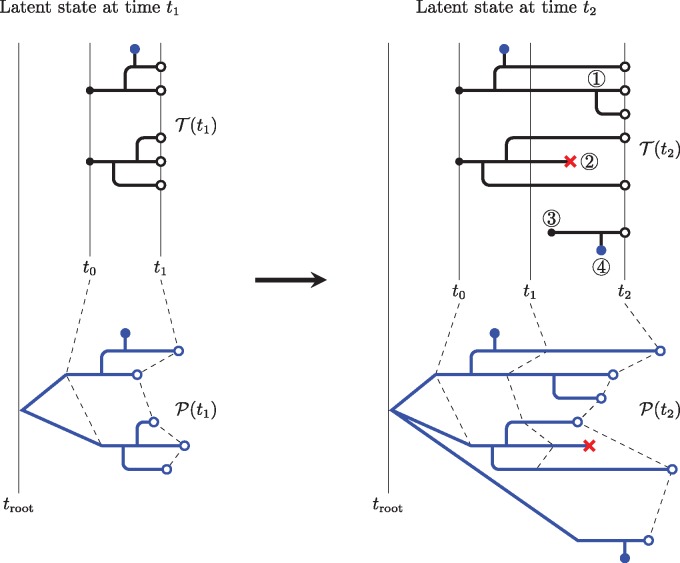
Fig. 1.

A schematic showing the nature and evolution of the latent transmission and phylogeny processes. The transmission forest, $\mathcal{T}(t)$, is shown in black; the pathogen phylogeny, $\mathcal{P}(t)$, in blue. On the left, we see the latent state at time t₁; it evolves by time t₂ to the state shown on the right. At time t₁, $\mathcal{T}(t_1)$ consists of two disconnected trees, representing the transmission histories of five active infections ($○$). These infections derive from two infections present at t₀ (black dots). The branching pattern of the pathogen phylogeny mirrors that of $\mathcal{T}(t)$ over the interval $[t_0,t_1]$. This diagram assumes that pathogen lineages branch exactly at transmission events; alternative models could allow for differences in the branching pattern between $\mathcal{T}(t)$ and $\mathcal{P}(t)$. This diagram displays a model with a relaxed molecular clock; randomness in the rate of evolution along lineages is depicted via random edge lengths in $\mathcal{P}(t)$. Over the time interval $[t_1,t_2]$, changes of each of the five permissible types are shown. At ①, an active node splits in two when a transmission event occurs. At ②, an active node becomes a dead node (×) when an infected host emigrates, recovers, or dies. At ③, an immigration event gives rise to a new active node with its own root. At ④, a sequence node (●) is spawned when a sample is taken. Finally, active nodes for which none of the above occur simply persist. The Markovian property insists that the latent state at time t₂ be an extension of the latent state at time t₁. In other words, changes to the latent state over the interval $[t_1,t_2]$ must not retroactively modify elements of the latent state prior to time t₁.

We assume subsequently that $\mathcal{P}(t)$ and $\mathcal{T}(t)$ agree topologically, but we note that this assumption is not essential. In particular, the SMC algorithms we apply could be straightforwardly extended to allow the topology and timing of genetic lineage divergences to deviate from those of transmission events and to allow multiple pathogen lineages within each host. Such extensions might be useful, for example, in accounting for within-host pathogen diversity.

The Observable Process

We now describe the model explicitly linking the latent process to the data. Let $\mathbb{Y}$ be the set of all finite collections of dated genetic sequences, with an element of $\mathbb{Y}$ being a collection $\{(g_k,t_k),\hspace{0.17em}k=1,\dots ,n\}$ where g_k is a sequence and t_k is the associated diagnosis time. We allow g_k to be an empty sequence, in the event that the corresponding diagnosis had no associated sequence. The observable process is a $\mathbb{Y}$-valued process, $\{Y(t),\hspace{0.17em}t\in \mathbb{T}\}$, where Y(t) consists of all sequences that have accumulated up to time t. Thus, Y(t) is expanding, that is, $Y(t)\subset \subset Y(t\prime )$ whenever $t\le t\prime$, and if $Y(t)=\{(G_k,T_k),\hspace{0.17em}k=1,\dots ,N\}$, then $T_k\le t$ for all k. The data are modeled as a realization of the observable process, $Y(t_{\text{end}})=y^{*}$.

Suppose each diagnosis has an equal and independent chance to give rise to a pathogen sequence, and each diagnosis event in Y(t) corresponds to a unique diagnosis node in $\mathcal{T}(t)$. Suppose also that some time-reversible molecular substitution model is defined to describe sequence evolution on the pathogen phylogeny $\mathcal{P}(t)$. These modeling assumptions implicitly define a conditional distribution for Y(t) given X(t).

Relaxed Molecular Clocks

A strict molecular clock assumes that the rate of evolution is constant through time and across lineages. Relaxation of this assumption has been shown to improve the fit of phylogenetic models to observed genetic sequences in many cases (Drummond et al. 2006) and for HIV in particular (Posada and Crandall 2001). A relaxed molecular clock models the rate of evolution as random. In our approach, this corresponds to constructing each edge length of $\mathcal{P}(t)$ as a stochastic process on the corresponding edge of $\mathcal{T}(t)$. Various forms of such processes have been assumed in the literature (Lepage et al. 2007; Ho and Duchne 2014), but not all of these are compatible with a mechanistic approach. In particular, a mechanistic molecular clock must be defined at all times and must have non-negative increments. Many relaxed clocks commonly employed in the literature do not enjoy the latter property: In effect, such clocks allow evolutionary time to run backward. The class of suitable random processes includes the class of nondecreasing Lévy processes, that is, continuous-time processes with independent, stationary, non-negative increments.

The Plug and Play Property

The formulation of the latent and observable processes as above is flexible enough to embrace a wide range of individual-based models. In particular, models that describe actual or hypothetical mechanisms of transmission and disease progression are readily formulated in this framework. Moreover, with this formulation, it becomes clear that the models described are POMPs (Bretó et al. 2009). This fact makes SMC methods for likelihood-based inference available for use in the present context. The supplementary material S1, Supplementary Material online makes the formal connections between this class of models and SMC methodology.

It is worth noting that models formulated as above are compatible with inference techniques that only require simulation from the model, not closed-form expressions for transition probabilities. Such algorithms are said to have the plug-and-play property (Bretó et al. 2009; He et al. 2010). The particle filter and iterated filtering, which we describe in the Materials and Methods section, are two algorithms that have this property. Because these algorithms only require the ability to simulate from the model, they allow for consideration of a wide class of models. Greater freedom in choice of the form of the model allows one to pose scientific questions closed to non-plug-and-play approaches. In the following, we demonstrate this potential in a study of HIV transmission dynamics.

A Model of HIV Transmission

Our study focuses on the expanding HIV epidemic among young, black, MSM within the Detroit metropolitan area. Specifically, we ask two questions: 1) How much transmission originates inside the study population relative to that originating outside? 2) Within the study population, how does transmission vary with respect to stage of disease (e.g., early, chronic, AIDS) and diagnosis status? To address these questions we construct a basic model of HIV transmission, similar to that of Volz, Ionides, et al. (2013). We describe our model as a special case of the general class of models described above. This model contains assumptions that can be altered and examined within our methodological framework. In the following, we describe both the form of the model and how we relate it to two data types: Diagnosis times and genetic sequences.

The Latent and Observable Processes

The latent state of the system at time t, ($\mathcal{T}(t),\hspace{0.17em}\mathcal{P}(t),\hspace{0.17em}\mathcal{U}(t)$), is of the form described above. To specify it completely, it remains to describe the Markov process $\{\mathcal{U}(t)\}$ and the transitions of $\{\mathcal{T}(t)\}$ and $\{\mathcal{P}(t)\}$. $\mathcal{U}(t)$ contains information about all infected individuals in the population. Following Volz, Ionides, et al. (2013), we do not explicitly track uninfected individuals and thus disallow depletion of the susceptible pool. There are reasons to suspect that this assumption may be problematic (Kenah et al. 2016), but its adoption here facilitates comparison of our results with those of Volz, Ionides, et al. (2013). Specifically, $\mathcal{U}(t)=\{({\tau }_i,B_i(t)):\hspace{0.17em}i\text{infected at time}\hspace{0.17em}t\}$, where τ_i is the time at which individual i was infected and $B_i(t)\in ℂ$ is the class of individual i at time t, where $ℂ=\{I_0,I_1,I_2,J_0,J_1,J_2\}$. $B_i(t)=I_k$ indicates that individual i has an infection at stage $k\in \{0,1,2\}$ but has not yet been diagnosed; $B_i(t)=J_k$ indicates that individual i has been diagnosed and has an infection at stage k. We think of k = 0 as indicating the early stage of infection; k = 1, the chronic stage; k = 2, AIDS. Individuals move between classes according to figure 2. New infections can occur, as can deaths, emigrations, and diagnosis events. Transmission events, immigration events, deaths, and diagnoses all result in events of the corresponding type being recorded in the structure of $\mathcal{T}(t)$.

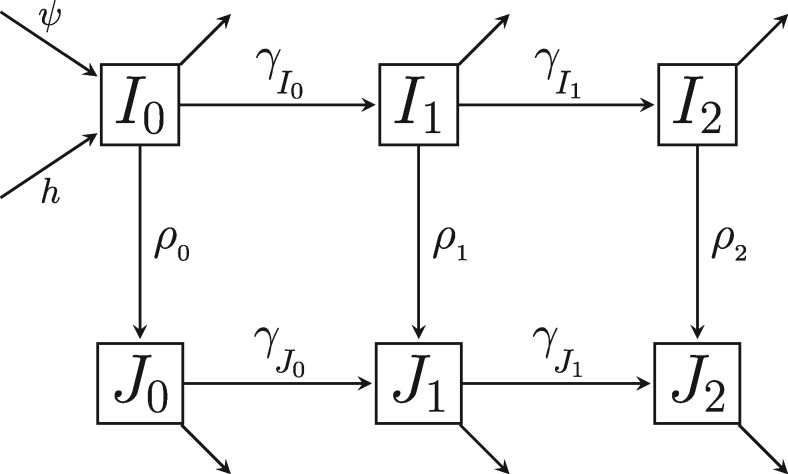
Fig. 2.

A flow diagram showing the possible classes for infected individuals. The columns represent stage of disease: With subscripts 0, 1, and 2 representing early, chronic, and AIDS stages respectively. The rows represent diagnosis status, with the top row representing undiagnosed individuals, I_k, and the bottom row representing diagnosed individuals, J_k, where $k\in \{0,1,2\}$. ρ_k are per capita rates of diagnosis and γ_c are rates of disease progression. Arrows out of classes that do not flow into other classes represent the combined flow out of the infected population due to death and emigration.

New infections arise from two distinct sources: Immigration and transmission within the population. Immigrations occur at a constant rate, ψ. Each currently infected individual inside the population seeds new infections at rate ${\varepsilon }_c$, where $c\in ℂ$ indicates infection class. Thus, we allow transmissibility to vary between different infection classes, but assume homogeneous transmissibility within each class. It follows that the incidence of new infections is $h(t)+\psi$, where $h(t)={\varepsilon }_{I_0}{N}_{I_0}(t)+{\varepsilon }_{I_1}{N}_{I_1}(t)+{\varepsilon }_{I_2}{N}_{I_2}(t)+{\varepsilon }_{J_0}{N}_{J_0}(t)+{\varepsilon }_{J_1}{N}_{J_1}(t)+{\varepsilon }_{J_2}{N}_{J_2}(t)$, and $N_c(t)$ is the number of individuals in class c at time t. Defining all nonzero transition rates between states is sufficient to specify a Markov process; a full set of model equations for $\{\mathcal{U}(t)\}$ is presented in the supplement (supplementary section S4, Supplementary Material online).

The inclusion of individual time-of-infection, τ_i, within $\{\mathcal{U}(t)\}$ allows us to model within-host pathogen evolution. In particular, when an individual is diagnosed at time t, a diagnosis node is added to $\mathcal{T}(t)$, together with a diagnosis edge, the length of which is linearly related to how long the diagnosed individual has been infected (fig. 1). This edge may account for sequencing error; it can also describe the emergence of new pathogen strains within a host having reduced between-host transmission potential (Lythgoe and Fraser 2012).

We assume for simplicity that the topology of $\mathcal{P}(t)$ matches that of $\mathcal{T}(t)$. Thus, we explicitly disallow the possibility of incomplete lineage sorting, though, as mentioned before, this choice is not forced by the algorithm. We assume a relaxed molecular clock: The edge lengths of $\mathcal{P}(t)$ are random. Specifically, each edge of $\mathcal{P}(t)$ has length conditionally Gamma distributed with expectation equal, and variance proportional, to the corresponding edge of $\mathcal{T}(t)$. That is, if L is the length of an edge of $\mathcal{P}(t)$ corresponding to an edge of length D in $\mathcal{T}(t)$, we posit that $L|D$ is Gamma distributed with $\mathbb{E}[L|D=d]=d$ and $\text{Var}[L|D=d]=\sigma \hspace{0.17em}d$. The parameter σ scales the noise on the rate of evolution. This relaxation, identical to the white noise model of Lepage et al. (2007), is a Lévy process with non-negative increments, as we require. Having specified $\mathcal{P}(t)$, the joint distribution of observed sequences is determined by the choice of the time-reversible molecular substitution model. Here, we used the TN93 model of molecular evolution (Tamura and Nei 1993). This model distinguishes between the rate of transitions between purines, the rate of transitions between pyrimidines, and the rate of transversions. It is fully specified by the following rate matrix (see also table 2):

$$Q=\left[\begin{array}{cccc}*& \beta {\pi }_T& \beta {\pi }_C& {\alpha }_R{\pi }_G\\ \beta {\pi }_A& *& {\alpha }_Y{\pi }_C& \beta {\pi }_G\\ \beta {\pi }_A& {\alpha }_Y{\pi }_T& *& \beta {\pi }_G\\ {\alpha }_R{\pi }_A& \beta {\pi }_T& \beta {\pi }_C& *\end{array}\right]$$

Table 2.

Parameters of the Genetic Model Used in Simulation of Datasets.

Parameter	Interpretation	Value
β	Rate of transversions	0.013 year−1
αY	Rate of transitions between purines	0.03 year−1
αR	Rate of transitions between pyrimidines	0.1 year−1
πA	Equilibrium frequency of adenine	0.37
πG	Equilibrium frequency of guanine	0.23
πC	Equilibrium frequency of cytosine	0.18
πT	Equilibrium frequency of thymine	0.22
${\sigma }_{\text{site}}$	Relaxation of the molecular clock with respect to sites	0
σ	Relaxation of the molecular clock with respect to edges	0.1 year
δfixed	The initial component of the sequence stem	0.001 year
δprop	Proportion of time since infection to add to the sequence stem	0.05

Results

We present results from both a study on simulated data and an analysis of actual data. The primary goal of the simulation study is to show how our methods can be used to extract information about transmission dynamics from pathogen genetic sequence data within the framework of likelihood-based inference. This study was carried out with 30 sequences of length 100 bases. The goals of the data analysis are to demonstrate the numerical feasibility of our implementation as well as illustrate the role of likelihood-based inference as part of the cycle of data-informed model development for a phylodynamic model. The data analysis was carried out using 100 protease consensus sequences of length 297 bases. Due to the intensive nature of the computations, further developments will be required to handle considerably larger datasets. Some empirical results concerning how our GenSMC implementation scales with number of sequences are given in the supplement (supplementary section S2.3, Supplementary Material online). We discuss applicability to the range of current phylodynamic challenges in the Discussion section.

A Study on Simulated Data

Using the individual-based, stochastic model of HIV described above (fig. 2), we set parameters governing the rate of evolution at relatively high values to generate a high proportion of variable sites. As computation scales with the number of variable sites, the computational effort in this simulation study could be comparable to fitting real sequences of greater length. Parameters values and their interpretations are specified in tables 1 and 2. Algorithmic parameters are specified in supplementary section S4.2, Supplementary Material online. Each simulated epidemic consisted of a transmission forest and a set of pathogen genetic sequences. We randomly selected 5 epidemics to fit. Each dataset consists of two types of data: Times of diagnoses and pathogen genetic sequences. A representative simulated transmission forest and its associated pathogen genetic sequences are shown in figure 3.

Table 1.

Parameters of the Transmission Model Used in Simulation of Datasets.

Parameter	Interpretation	Value
${\varepsilon }_{I_1}$	Infectiousness of undiagnosed chronic stage individuals	0.25 year–1
${\varepsilon }_{I_2}$	Infectiousness of undiagnosed AIDS individuals	0 year–1
${\varepsilon }_{J_0}$	Infectiousness of diagnosed acute stage individuals	0.125 year–1
${\varepsilon }_{J_1}$	Infectiousness of diagnosed chronic stage individuals	0.025 year–1
${\varepsilon }_{J_2}$	Infectiousness of diagnosed AIDS individuals	0 year–1
${\mu }_{I_0}$	Death rate+aging rate of undiagnosed acute stage individuals	1/3 year–1
${\mu }_{I_1}$	Death rate+aging rate of undiagnosed chronic stage individuals	1/3 year–1
${\mu }_{I_2}$	Death rate+aging rate of undiagnosed AIDS individuals	5/6 year–1
${\mu }_{J_0}$	Death rate+aging rate of diagnosed acute stage individuals	1/3 year–1
${\mu }_{J_1}$	Death rate+aging rate of diagnosed chronic stage individuals	1/3 year–1
${\mu }_{J_2}$	Death rate+aging rate of diagnosed AIDS individuals	2/3 year–1
${\gamma }_{I_0}$	Progression rate from undiagnosed acute to undiagnosed chronic	1 year–1
${\gamma }_{I_1}$	Progression rate from undiagnosed chronic to undiagnosed AIDS	1/6.3 year–1
${\gamma }_{J_0}$	Progression rate from diagnosed acute to diagnosed chronic	1 year–1
${\gamma }_{J_1}$	Progression rate from diagnosed chronic to diagnosed AIDS	1/6.3 year–1
ρ0	Diagnosis rate of acute stage individuals	0.5 year–1
ρ1	Diagnosis rate of chronic stage individuals	0.225 year–1
ρ2	Diagnosis rate of AIDS individuals	50 year–1
ψ	Immigration rate of infected individuals	0 year–1
$\varphi$	Emigration rate of infected individuals	0 year–1
troot	Root (polytomy) time	0 year
t0	Time to begin simulation of the transmission model	2 year
tend	Time to end simulation of the transmission model	10 year
nloci	Length of the sequences to simulate	100 base pairs
pG	Probability of a sequence given diagnosis	0.48
$N_{I_0}(t_0)$	Number of undiagnosed early-stage individuals at t0	11
$N_{I_1}(t_0)$	Number of undiagnosed chronic-stage individuals at t0	15
$N_{I_2}(t_0)$	Number of undiagnosed AIDS individuals at t0	0
$N_{J_0}(t_0)$	Number of diagnosed early-stage individuals at t0	4
$N_{J_1}(t_0)$	Number of diagnosed chronic-stage individuals at t0	8
$N_{J_2}(t_0)$	Number of diagnosed AIDS individuals at t0	6

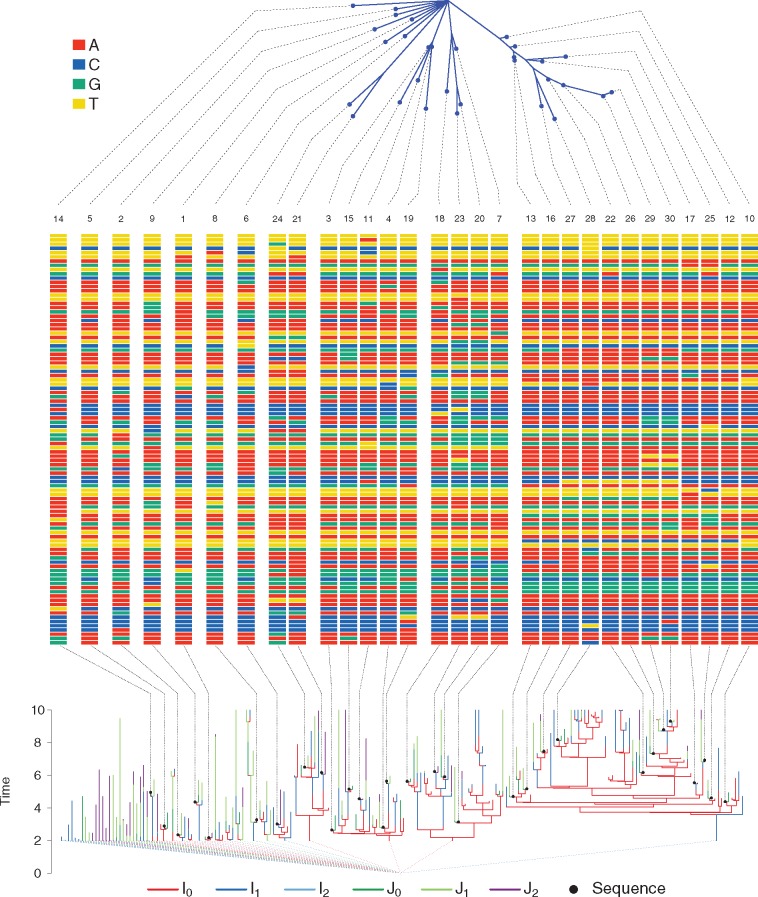
Fig. 3.

A simulated transmission forest (bottom), its associated pathogen genetic sequences (middle), and the phylogeny of the sequences (top). The class of the infected individual in the transmission forest is indicated by its color. Black dots represent genetic sequences. Black dashed lines connect sequence locations on the transmission tree, or the phylogeny, to visualizations of the sequences in the middle panel. Colored dashed lines from the roots of transmission trees connect at the polytomy at t_root = 0. Numbers at the top of the sequences indicate the rank of the sequence, with rank 1 being the first observed.

For each of the selected epidemics we ask two questions. First, when all other parameters are known, is it possible to infer ${\varepsilon }_{I_0}$ and ${\varepsilon }_{I_1}$ using only diagnosis times? Second, how does inference change when we supplement the diagnosis data with pathogen genetic sequences? To perform this comparison we estimated two likelihood surfaces for each epidemic: One using only the diagnosis likelihood, and one using both the diagnosis likelihood and the genetic likelihood. We estimated each surface by using the particle filter to compute a grid of likelihood estimates with respect to the two parameters of interest: ${\varepsilon }_{I_0}$, the infectiousness of early-stage undiagnosed individuals, and ${\varepsilon }_{I_1}$, the infectiousness of chronic-stage undiagnosed individuals. Equilibrium base frequencies were set to the empirical values in the simulated data. All other parameters were fixed at the known values used for simulation. We extracted grid-based likelihood profiles for each parameter by taking maxima over the columns or rows of the grid. For each parameter we therefore obtained two profiles: One using only the diagnosis likelihood and one using the joint likelihood. The difference in curvature between these profiles tells how much the genetic data improves, or weakens, inference on the parameters.

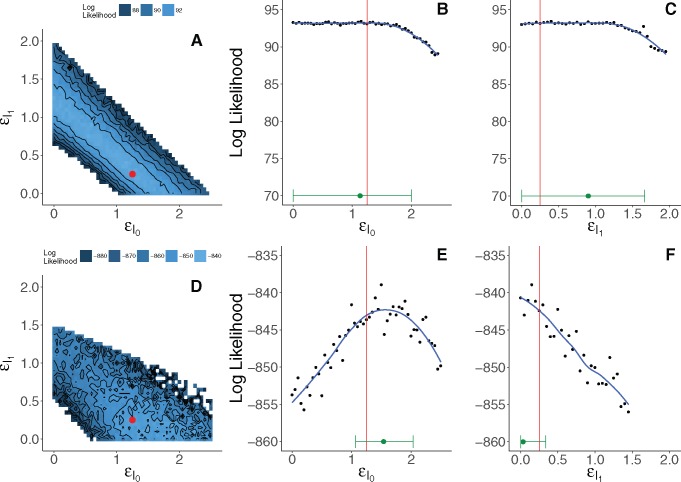
When only the diagnosis data are used, we find a tradeoff between ${\varepsilon }_{I_0}$ and ${\varepsilon }_{I_1}$ (fig. 4). The diagnoses provide information on upper bounds for each infectiousness parameter, but otherwise only inform their sum. In other words, when estimated using only the diagnosis times, ${\varepsilon }_{I_0}$ and ${\varepsilon }_{I_1}$ are nonidentifiable. Supplementing the data on diagnoses with pathogen genetic sequences resolves this uncertainty (fig. 4). Note that including the genetic data increases noise in the likelihood estimate. This is expected, as computing the likelihood estimate for the genetic sequences requires a numerical approximation to an integral over tree space. Nevertheless, the genetic data increase the curvature of the likelihood surface. From figure 4, we see that this additional curvature leads to more precise identification of the parameters despite the increased Monte Carlo noise. In principle, Monte Carlo variation can be reduced to negligibility by increased computational effort. This may not be practical when computational expense is high, as it is here. Therefore, it is necessary to bear in mind the tradeoff between the benefits of the information accessed for inference versus the computational burden of extracting this information.

Fig. 4.

Grid-based estimates of likelihood surfaces and likelihood profiles from fitting to simulated data. The top row shows the surface (A) and profiles (B and C) estimated using only the diagnosis likelihood. The bottom row shows the surface (D) and profiles (E and F) estimated using both the diagnosis and the genetic likelihood. Red dots and red lines indicate true values of ${\varepsilon }_{I_0}$ and ${\varepsilon }_{I_1}$ used in simulation. Point estimates and 95% confidence intervals are shown in green just above the horizontal axis of the likelihood profile plots. Confidence intervals for (E) and (F) account for both statistical uncertainty and Monte Carlo noise (Ionides et al. 2016) using a square root transformation appropriate for non-negative parameters. Augmenting the diagnosis data with genetic data yields smaller confidence intervals for ${\varepsilon }_{I_0}$ and ${\varepsilon }_{I_1}$, and resolves the nonidentifiability of these parameters when estimated using only the diagnoses. Note that scales of the likelihood surfaces shown in (A) and (D) are not the same; (E) and (F) have the same scale as (B) and (C) but with a vertical shift.

Analysis of an HIV Subepidemic in Detroit, MI

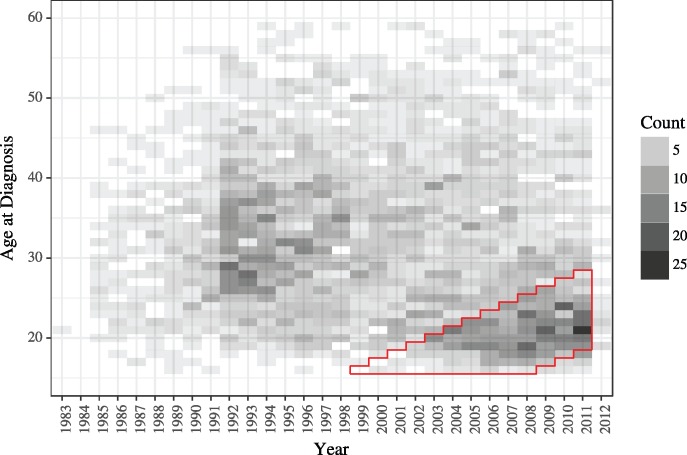
In this data analysis, we explored whether our full-information approach could estimate key transmission parameters using HIV protease consensus sequences and diagnosis times. We focused our analysis on a subepidemic in the young, black, MSM community. The cohort of individuals that we chose to study is shown in figure 5. See Materials and Methods for details on how we selected the subepidemic and cleaned the sequence data.

Fig. 5.

The distribution of age at diagnosis through time for black MSM in Detroit, MI. The cohort that we selected for analysis is outlined in red. We excluded the data from 2012 to limit effects from delays in updating the MDCH database. Twenty-nine individuals that were diagnosed at ages greater than or equal to 60 years are not shown on this plot.

As in the study on simulated data, we were interested in what the genetic data yield beyond what we can see using the diagnoses alone. Therefore, we again estimated likelihood profiles in two ways: Using only the diagnosis data and using both the diagnosis data and the genetic sequences. We estimated likelihood profiles for three parameters of interest: ${\varepsilon }_{I_0},\hspace{0.17em}{\varepsilon }_{J_0}$, and ψ. In contrast to the simulation study, in this analysis we were faced with a parameter space of much higher dimension. To reduce the dimension of the problem we fixed some parameters: Rates of disease progression, rates of diagnosis, and the rate of emigration. Parameters that were fixed and fit are shown in tables 3 and 4, respectively. Algorithmic parameters are specified in supplementary section S4.2, Supplementary Material online. For each likelihood profile we first used iterated filtering (Ionides et al. 2015) to maximize the likelihood for a sequence of values that spanned the reasonable range of the parameter. Second, we used the particle filter to estimate likelihoods for each parameter set obtained from iterated filtering. We repeated this process of maximization followed by evaluation until the profile stabilized. All initial-value parameters were fixed, with the exception of t_root. Initial counts for individuals in each class were fixed. See the supplement for details on how we arrived at these counts.

Table 3.

Parameters Fixed in the Data Analysis.

Parameter	Interpretation	Value
${\mu }_{I_0}$	Death rate of undiagnosed acute stage individuals	1/70 year−1
${\mu }_{I_1}$	Death rate of undiagnosed chronic stage individuals	1/70 year−1
${\mu }_{I_2}$	Death rate of undiagnosed AIDS individuals	1/2 year−1
${\mu }_{J_0}$	Death rate of diagnosed acute stage individuals	1/70 year−1
${\mu }_{J_1}$	Death rate of diagnosed chronic stage individuals	1/70 year−1
${\mu }_{J_2}$	Death rate of diagnosed AIDS individuals	1/70 year−1
${\gamma }_{I_0}$	Progression rate from undiagnosed acute to undiagnosed chronic	1 year−1
${\gamma }_{I_1}$	Progression rate from undiagnosed chronic to undiagnosed AIDS	1/6.3 year−1
${\gamma }_{J_0}$	Progression rate from diagnosed acute to diagnosed chronic	1 year−1
${\gamma }_{J_1}$	Progression rate from diagnosed chronic to diagnosed AIDS	1/6.3 year−1
ρ0	Diagnosis rate of acute stage individuals	0.225 year−1
ρ1	Diagnosis rate of chronic stage individuals	0.225 year−1
ρ2	Diagnosis rate of AIDS individuals	50 year−1
$\phi$	Emigration rate of infected individuals	0 year−1
$N_{I_0}(t_0)$	Number of undiagnosed early-stage individuals at t0	20
$N_{I_1}(t_0)$	Number of undiagnosed chronic-stage individuals at t0	36
$N_{I_2}(t_0)$	Number of undiagnosed AIDS individuals at t0	0
$N_{J_0}(t_0)$	Number of diagnosed early-stage individuals at t0	4
$N_{J_1}(t_0)$	Number of diagnosed chronic-stage individuals at t0	22
$N_{J_2}(t_0)$	Number of diagnosed AIDS individuals at t0	16
σsite	Relaxation of molecular clock with respect to sites	0 year
t0	Time to start filtering	January 1, 2004

Table 4.

Parameters Fit in the Data Analysis.

Parameter	Interpretation	Diagnosis data	Diagnosis data and genetic sequences	Diagnosis data, with ψ fixed at 0
ψ	Immigration rate of infected individuals	120 (104, 134) year–1	5.82 (2.55, 11.2) year–1	0 year–1
${\varepsilon }_{I_0}$	Infectiousness of undiagnosed acute stage individuals	0 (0, 0.413)	0.257 (0.0399, 0.623)	0 (0, 0.192)
${\varepsilon }_{I_1}$	Infectiousness of undiagnosed chronic stage individuals	0.0042	0.00048	0.0056
${\varepsilon }_{I_2}$	Infectiousness of undiagnosed AIDS individuals	0	0	0
${\varepsilon }_{J_0}$	Infectiousness of diagnosed acute stage individuals	0.0675 (0, 1.17)	3.36 (3.13, 4.2)	7.34 (5.78, 9.25)
${\varepsilon }_{J_1}$	Infectiousness of diagnosed chronic stage individuals	0.0089	0.17	0.032
${\varepsilon }_{J_2}$	Infectiousness of diagnosed AIDS individuals	0	0	0
β	Rate of transversions	—	0.0042 year–1	—
αY	Rate of transitions between purines	—	0.047 year–1	—
αR	Rate of transitions between pyrimidines	—	0.043 year–1	—
πA	Equilibrium frequency of adenine	—	0.37	—
πG	Equilibrium frequency of guanine	—	0.24	—
πC	Equilibrium frequency of cytosine	—	0.18	—
πT	Equilibrium frequency of thymine	—	0.21	—
σ	Relaxation of molecular clock with respect to edges	—	2 year	—
δprop	Proportion of time since infection to use for diagnosis edge	—	0.064	—
δfixed	Amount of calendar time to add on to diagnosis edge	—	0.00049 year	—
troot	Time of the polytomy that joins all genetic lineages	—	August 27, 2000	—

We present confidences intervals for parameters for which we computed likelihood profiles. For all other parameters, we present only the point estimate.

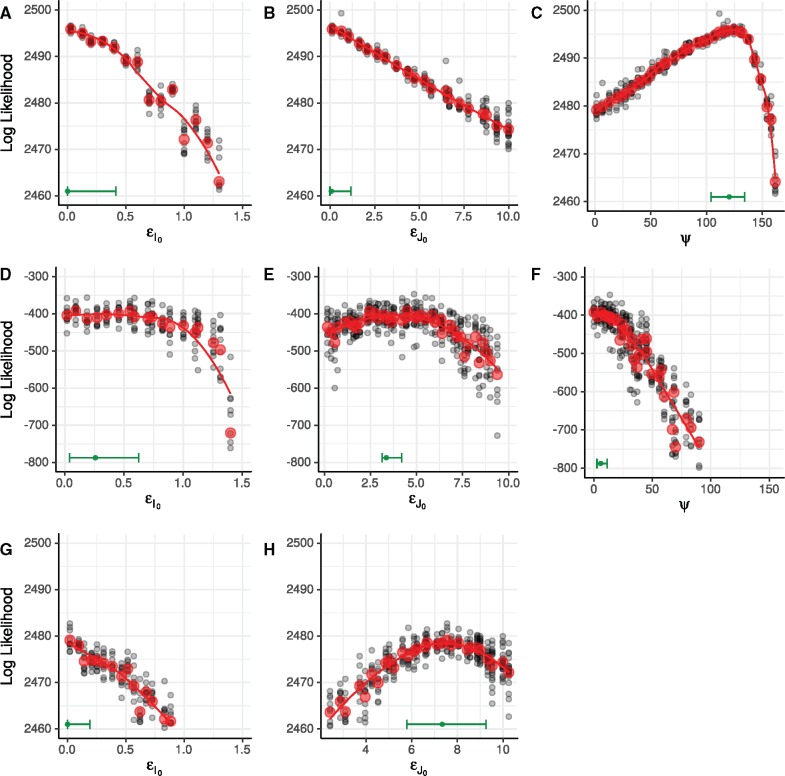
When only the diagnosis data are used, we find that the model prefers to explain all infections as originating outside the cohort, with the maximum likelihood estimate (MLE) for $\psi \hspace{0.17em}\approx \hspace{0.17em}120$ infections per year (fig. 6). Under this explanation for the data, little or no transmission occurs inside the cohort: This covariate-defined subgroup acts as a sentinel of the broader epidemic. Equivalently, this result would imply that the covariates we used to select these cases do not define a meaningful subepidemic.

Fig. 6.

Estimated likelihood profiles from fits to data from the black, MSM cohort. (A–C) show likelihood profiles computed using only the diagnosis likelihood. (D–F) show likelihood profiles computed using both the diagnosis likelihood and the genetic likelihood. (G, H) show likelihood profiles computed using only the diagnosis likelihood when ψ is fixed at zero. Black dots represent particle filter likelihood evaluations of parameter sets obtained using iterated filtering. Red dots represent mean log likelihoods of the multiple likelihood evaluations (black dots) at each point in the profile. Red lines are loess fits to the red dots. Green bars along the lower margin of each panel encompass 95% confidence intervals for each parameter. Confidence intervals account for both statistical uncertainty and Monte Carlo noise (Ionides et al. 2016). The smoothed profile was calculated on the square root scale, appropriate for non-negative parameters, with a green dot indicating the maximum.

On the other hand, when the genetic data are folded in, the estimate of ψ is greatly revised: The MLE for ψ becomes $\approx 6$ infections per year. On its face, this is evidence for a low rate of transmission into the cohort and, therefore, evidence that the cohort subepidemic is much more self-contained. Although this may in part be true, the lower estimate of ψ is also potentially driven by assumptions of the genetic model. Supposing, as it does, that all immigrant lineages coalesce at a single, global polytomy, the model insists that sequences from immigrant infections derive from a broad genetic pool. The breadth of this pool—the average genetic distance between an imported infection and any other observed sequence—is determined by the depth of the polytomy, an estimated parameter. Nevertheless, the low estimate of ψ implies that few infections derive from this broader pool. The model’s disallowance of a more structured immigrant pool makes it difficult to say more, however. In particular, the low value of ψ is not inconsistent with the existence of chains of transmission originating within the cohort, leaving it, and returning. Such chains would produce sequence clustering despite the openness of the cohort to transmission. Future work, incorporating genetic and diagnosis information from the broader epidemic will be needed to better quantify the latter effect.

Joint likelihood profiles over ${\varepsilon }_{I_0}$ and ${\varepsilon }_{J_0}$ show support for transmission from both of the early-stage groups, with evidence for higher infectiousness in the early-stage diagnosed class than in the early-stage undiagnosed class. However, it is epidemiologically implausible that diagnosis increases transmission: This is a paradox. Since the paradox did not arise in the simulation study, it cannot be due to a coding error in the implementation of the model or the statistical methodology. Assuming no errors in the data, therefore, it must derive from some inappropriate feature of the model. We propose two possible explanations for how the model and data combine to yield this result.

One possibility is that temporal clusters of genetically related diagnoses favor high infectiousness for the early-stage diagnosed. For example, this could be an artifact of unmodeled clusters in HIV testing. We searched the data for such clusters, but found no conclusive evidence for their presence.

A second possibility is understood by noting that, under the model, any significant amount of transmission from the undiagnosed classes leads necessarily to an exponentially growing accumulation of diagnoses, in conflict with the data. When the genetic data were left out, the model accounted for the observed, roughly linear, ramp-up in diagnoses using immigration, hence the relatively high estimated ψ. Incorporating the genetic data eliminates this option, forcing the model to explain the epidemic’s sub-exponential growth as a consequence of diagnosis itself.

To illustrate the second possibility, we estimated likelihood profiles using only the diagnosis likelihood, fixing the immigration rate, ψ, at zero. These profiles show that, when forced to explain the diagnoses without any imported infection, the model prefers to do so by making the early-stage diagnosed class most infectious (fig. 6). This suggests that the model lacks flexibility to explain the pattern in the diagnoses without immigration; this constraint likely limits efficient use of information in the genetic sequences. To remedy this problem, one could modify the model by explicitly introducing a small and ephemeral population of susceptible hosts.

In this methodological paper, we display but one iteration of the scientific method and it is clear that our motivating scientific questions remain incompletely answered. Our principal goal, however, is to illustrate how the methodology facilitates the formulation and testing of scientific hypotheses. For example, the results above suggest a number of straightforward model modifications: The plug-and-play property of the methodology makes it nearly as straightforward to evaluate the evidence for these new hypotheses just as we have done for the old. Moreover, we have shown how probing the data with a mechanistic model can lead to clear identification of flaws in model structure, along with indications for improvements.

Discussion

We demonstrated, via a simulation study, that our algorithms provide access to the likelihood surface of a population dynamic model fit to genetic sequence data. This opens the door to likelihood-based phylodynamic inference. As this study shows, incorporating information from genetic data has the potential to improve on inference that we obtain using diagnosis data alone.

In our analysis of an HIV subepidemic in Detroit, MI, we showed that our methods can be used to ask questions of current public health interest by fitting practical models to data of nontrivial size. This study illustrates how the ability to confront the model with different data types, alone or in combination, can be essential to understanding how the model interacts with the data, to uncovering shortcomings of the model, and to pointing the way toward improved model formulations. The ability of our methods to incorporate different data types made it possible to assess each source of information’s contribution to the overall inference. In turn, the ability to easily restructure the model, guaranteed by the plug-and-play property, will allow us to push forward model development.

The scope of our methodology goes beyond the examples presented: The algorithms described here are applicable across a wide range of host-pathogen systems and may find application in realms beyond genetics. From an abstract perspective, these algorithms provide the ability to relate demographic processes with a growing tree-like structure to the evolution of discrete characters that are carried and passed along the branches of that tree. So long as this evolution occurs on a similar timescale to that of the demographic process, and measurements of the discrete process are heterochronous, the methods presented here apply.

In this paper, we demonstrated the methods using relatively short consensus sequences derived from Sanger sequencing. While our methods may be well suited to analysis of data from fast-evolving RNA viruses, they may also apply in studies of pathogens that evolve more slowly. Advances in sequencing are increasing the range of problems for which phylodynamic inference is applicable (Biek et al. 2015). The ability to apply phylodynamic inference to bacterial and protozoan genomes opens the door to many epidemiological applications. One area that may be particularly interesting to explore using our methods is hospital outbreaks of drug resistant bacteria. Hospital records on location and duration of stay may provide fine-scale information on populations of susceptible and infected individuals. Accurate measures of these demographic quantities may allow for efficient use of information held in genetic data. Furthermore, the relatively small size of outbreaks in hospitals means that stochasticity may play a large role in their dynamics, and our methods are designed to explicitly account for the role of different sources of stochasticity.

We conclude by placing our new methodology in the context of the eight current challenges identified by Frost et al. (2015) for inferring disease dynamics from pathogen sequences. We will make some relevant comments on each challenge, in order.

1. Accounting for sequence sampling patterns. Our methodology explicitly models sequence sampling. The chance of an individual being diagnosed, or subsequently having their pathogen sequenced, is permitted to depend on the state of the individual. This state could contain geographic information, or whatever other aspect of the sampling procedure one desires to investigate. Sampling issues revolve around how the dynamics and the measurement process affect the relatedness of sequences, and are more naturally handled in a framework that deals jointly with estimation of the population dynamics and the phylogeny. Thus, our main innovation of joint estimation is directly relevant to this challenge.

2. Using more realistic evolutionary models to improve phylodynamic inferences. In this paper, we have used simple evolutionary models that have been widely used for previous phylodynamic inference investigations. Our methodology does not particularly facilitate the use of more complex evolutionary models, since the large number of trees under consideration puts a premium on rapid likelihood computation. However, our methodology is primarily targeted at drawing inference on the population dynamics rather than the micro-evolutionary processes. For this purpose, it may be sufficient to employ an evolutionary model which captures the statistical relationship between genetic distance and temporal distance on the transmission tree, together with an appropriate estimate of the uncertainty in this relationship. Better evolutionary models would be able to extract information more efficiently from the data, but from our perspective this challenge may not be a primary concern.

3. The role of stochastic effects in phylodynamics. Our methodology explicitly allows for stochastic effects in the population dynamics and sequence collection.

4. Relating the structure of the host population to pathogen genetic variation. Our framework explicitly models this joint relationship. Further scientific investigations, fitting models using methods accounting properly for the joint relationship, will lead to progress in understanding which aspects of dynamics (such as super-spreading) might be especially important to include when carrying out phylodynamic inference.

5. Incorporating recombination and reassortment. In principle, our methodology is flexible enough to include co-infection and its evolutionary consequences. Due to computational considerations, it will be important to capture parsimoniously the key aspects of these processes.

6. Including phenotypic as well as genotypic information. Our framework naturally combines genotypic information with other information sources. For example, in our data analysis we complemented genetic sequence data with diagnosis times for unsequenced patients.

7. Capturing pathogen evolution at both within-host and between-host scales. The diagnosis edges on our phylogenetic tree allow for differences between observed and transmissible strains, and therefore give a representation of within-host diversity or measurement noise. Other approaches to within-host pathogen diversity are possible within our general framework. For example, one could include within-host branching of the phylogenetic tree. More complete investigation of within-host pathogen dynamics will require additional modeling. Due to the larger models and datasets involved, applying our methodology to such investigations will require further methodological work on scaling.

8. Scaling analytical approaches to keep up with advances in sequencing. In this manuscript, our goal was to develop generally applicable and statistically efficient methodology. Our methodology is structured with computational efficiency in mind, subject to that goal. Our approach combines various algorithms that have favorable computational properties: Peeling, particle filtering with hierarchical resampling and just-in-time variable construction, and iterated filtering. There is scope for computational enhancement by adapting the methodology to high performance architectures. In particular, parallel particle filtering is an active research topic (Paige et al. 2014) that is directly applicable to our methodology. There are also possibilities for improving scaling by imposing suitable situation-specific approximations; for example, it might be appropriate to reduce the computational burden by supposing that some deep branches in the phylogeny are known.

In summary, our new methodology has potential for making progress on many of the challenges identified by Frost et al. (2015). Beyond that, the methodology offers a full-information, plug-and-play approach to phylodynamic inference that gives the scientist flexibility in selecting appropriate models for the research question and dataset at hand. Although technical challenges remain, especially in scaling these methods to large data, these algorithms hold the potential to ask and answer questions not accessible by alternative approaches.

Materials and Methods

Overview of SMC Estimation of the Likelihood

SMC is a family of stochastic algorithms originally designed to estimate imperfectly observed states of a system via a collection of dynamically interacting simulations (Arulampalam et al. 2002). Each such simulation is called a particle; SMC is often referred to as the particle filter. The simplest SMC algorithm sequentially estimates the latent state at the time of each observation by iteratively repeating three steps: 1) for each particle, simulate the latent process forward in time to the next data point, 2) for each particle, compute the conditional probability density of the observation given the proposed latent state, and 3) resample the particles with replacement with probabilities proportional to their conditional probabilities. While inference of unobserved states is one use of the particle filter, we are primarily interested in using the filter for likelihood estimation. The average of the conditional likelihoods across particles is an estimator of the conditional likelihood of each observation, and the product of these conditional likelihoods is an unbiased estimator of the full likelihood of the data (Del Moral 2004, Theorem 7.4.2 on p. 239).

The basic particle filter described above requires only the ability to simulate realizations of the latent state and to evaluate the density of an observation given the latent state. As explained above, in the present case, the latent state contains both the full transmission forest and the phylogeny of the pathogen lineages. At minimum, the observations consist of a time-ordered set of pathogen genetic sequences. Although in principle these methods could be applied to homochronous sequences, we primarily envision using them to fit models to heterochronous sequences. Additional datatypes can be incorporated into the likelihood evaluation if desired so long as there is a means to relate these data to the latent state.

We implemented the particle filter such that the algorithmic code is independent of the code that specifies the model. This structure allows for realizing the advantanges of the plug-and-play paradigm by facilitating quick comparisons between models of different forms. Pseudocode for the algorithm is provided in the supplement. In Algorithm 1 we give an outline of the pseudocode, and we show a schematic of simplest form of the algorithm in figure 7. In our framework, the user specifies the model by writing three functions:

Fig. 7.

A schematic of the particle filter. Here, we show steps to run the filter from the first sequence to the second. Transmission forests are shown in black and phylogenies that connect observed sequences, $\tilde{\mathcal{P}}(t)$, are shown in blue. Observed sequences are depicted as blue dots. This schematic shows how the algorithm uses just-in-time construction of state variables to ease computational costs. Although the model describes how $\mathcal{P}(t)$ relates to $\mathcal{T}(t)$ across all branches of the transmission tree, the algorithm only constructs the subtree of the phylogeny needed to connect the observations (and therefore evaluate conditional probabilities of sequences). Note that in our implementation of the particle filter we introduce additional procedures in the proposal and weighting steps. These procedures, which are detailed below, allow for more accurate assessment of a particle’s weight (through hierarchical sampling) and estimation of the conditional probability of a sequence under a relaxed clock. In our current implementation (supplementary algorithm S1, Supplementary Material online), assimilation of each data point is followed by systematic resampling (Arulampalam et al. 2002; Douc et al. 2005); future developments may aim to increase efficiency further using alternative resampling schemes.

1. A simulator for the initial state of the latent process. This function initializes $\mathcal{T}(t_0)$ and $\mathcal{U}(t_0)$. For example, in a model with only one class of infected individuals, this function would initialize $\mathcal{T}(t_0)$ by specifying the number of infected individuals at t₀. Additional information about the states of those individuals may be contained in $\mathcal{U}(t_0)$. Each of these individuals then becomes a root of a tree in the transmission forest. Each root of the transmission forest has its own genetic lineage; these comprise $\mathcal{P}(t_0)$. In our implementation, the initializer does not construct $\mathcal{P}(t_0)$; the structure of $\mathcal{P}(t)$ is built as needed (see Just-in-Time Construction of State Variables).

2. A forward simulator for the latent state. This function simulates $\mathcal{T}(t)$ and $\mathcal{U}(t)$ forward in time from one observation to the next. This function also places the next observation on $\mathcal{T}(t)$, assigning the sequence to an individual by augmenting $\mathcal{T}(t)$ with a diagnosis edge and a sequence node. Note that this function does not simulate evolution of genetic sequences. Rather, the algorithm proposes ancestral relationships between genetic sequences via the simulated transmission forest. While formally, the pathogen phylogeny $\mathcal{P}(t)$ is part of the latent state, for computational efficiency we choose not to simulate its structure in full. The function in 3) builds the necessary components of $\mathcal{P}(t)$ given the simulated transmission forest and placement of sequences on the forest.

3. An evaluator for the conditional probability of observing a sequence. This function returns the conditional probability of observing a sequence given the latent state and all previously observed sequences. In particular, this function conditions on the structure of the subtree of $\mathcal{P}(t)$ that connects the observed sequences. The simplest choice for this function is to 1) make the strong assumption that $\mathcal{P}(t)$ maps directly onto $\mathcal{T}(t)$, and therefore build the phylogeny based strictly on the topology of $\mathcal{T}(t)$ and 2) evaluate the conditional likelihood of the genetic sequence using the peeling algorithm (Felsenstein 1981). These two choices are equivalent to assuming a strict molecular clock. However, one may choose more complicated functions, such as mappings that allow for discrepancy between $\mathcal{T}(t)$ and $\mathcal{P}(t)$ or a relaxed molecular clock, to better match the mechanistic processes that generate real data. The branching pattern of the transmission forest and of the phylogeny may differ for a number of reasons (Romero-Severson et al. 2014), so there may be strong arguments for allowing for discrepancy between these trees.

Algorithm 1.

GenSMC [Corresponding step numbers for the complete description in supplementary section S2, Supplementary Material online are in brackets]

input: simulator for the initial state; a dynamic model; diagnosis times; genetic sequence data; number of particles; number of nested particles; number of relaxed clock samples.

  initialize filter particles [step 1]

for each diagnosis time do [step 2]

 simulate particles through to next diagnosis time [steps 3, 5]

 propose multiple candidate individuals for the next diagnosis [steps 6, 7]

 propose multiple relaxed clock edge lengths for each candidate assignment [steps 8–11]

 compute particle weights: the probability density of the diagnosis and sequence [steps 4, 12, 13]

 resample according to particle weights [steps 14–21]

 compute conditional log likelihood [step 22]

end for

output: log likelihood estimate; latent states estimates.

Maximization of the Likelihood via Iterated Filtering

The particle filter provides access to the likelihood surface, but it does not provide an efficient way to maximize the likelihood. A closely related class of algorithms, iterated filtering, allows for maximizing the likelihood. Iterated filtering incorporates perturbation of unknown parameters into the particle filter. Repeatedly passing the filter over the data while shrinking the size of the perturbations allows the parameters to converge to their MLEs. The setup here, with the use of just-in-time construction of unobserved states, does not perfectly match the framework used to develop iterated filtering by Ionides et al. (2015). However, the basic iterated filtering approach of perturbing parameters and filtering repeatedly can be applied, and can be assessed on its empirical success at maximizing the likelihood.

Computational Structure

One way our algorithms differ from a standard SMC approach is that each particle maintains a latent state comprising of tree structures that reach back to t_root. As the algorithm incorporates each additional data point its memory requirement grows. From a practical perspective, the necessity of maintaining a deep structure in the particles presents challenges for writing a computationally feasible implementation of the algorithm. We developed several innovations to meet the computational challenges posed by numerically integrating over tree space. In this section, we give an overview of key components of our implementation that contributed to numerical tractability. For details, see the source code at https://github.com/kingaa/genpomp. Scripts and data that allow for reproducing the simulation study are archived at Dryad (doi:10.5061/dryad.3634m).

Data Structures and Their Relationship to Model Specification

Our implementation holds two tree structures in memory for each particle: 1) $\mathcal{T}(t)$, the transmission tree, and 2) $\tilde{\mathcal{P}}(t)$, the subtree of $\mathcal{P}(t)$ that connects all sequences observed up to time t. We represent $\mathcal{T}(t)$ as a vector of nodes, where each node contains the index of its mother, a timestamp, and the index of the genetic lineage with which it is associated (if any). Although the model of the latent state includes the full phylogeny of the pathogen, $\mathcal{P}(t)$, our algorithms only need to keep a subtree of the phylogeny, $\tilde{\mathcal{P}}(t)$, in memory. We also represent $\tilde{\mathcal{P}}(t)$ as a vector of nodes. However, nodes of $\tilde{\mathcal{P}}(t)$ require more memory than the nodes of $\mathcal{T}(t)$. In addition to the information in a transmission tree node, each node of $\tilde{\mathcal{P}}(t)$ contains the indices of the node’s daughters, an array of probabilities, and an evolutionary edge length. These additional components allow for computing the likelihood of observing the sequences at the tips of $\tilde{\mathcal{P}}(t)$.

Our implementation provides a set of functions that allow for specifying the model via forward-in-time simulation of the latent state. These functions provide access to the latent state and allow for modifying the latent state by branching lineages in $\mathcal{T}(t)$, terminating leaves in $\mathcal{T}(t)$, etc. Our code does not provide access to $\tilde{\mathcal{P}}(t)$. Instead, internal functions update the structure of $\tilde{\mathcal{P}}(t)$ as necessary (detailed in the following section on Just-in-Time Construction of State Variables). The structure of $\tilde{\mathcal{P}}(t)$ is in part determined by the molecular clock model. Our current implementation supports strict molecular clock models and relaxed molecular clocks with Gamma distributed edge lengths (as we use in this paper). Alternative models for $\mathcal{P}(t)$ are possible, and the plug-and-play structure of our algorithms allows the user to explore a wide range of alternative models.

Just-in-Time Construction of State Variables

Although the model of the latent process includes the full phylogeny of the pathogen, $\mathcal{P}(t)$, for the purposes of computation we need only store $\tilde{\mathcal{P}}(t)$ in memory. In our implementation, we add new edges to $\tilde{\mathcal{P}}(t)$ at the time of measurement; it is not until a sequence is placed on a lineage of $\mathcal{T}(t)$ that we have enough information to update $\tilde{\mathcal{P}}(t)$. We call this approach just-in-time construction of state variables because simulation of part of the state is postponed until the last moment. An alternative approach would include simulation of $\mathcal{P}(t)$ in tandem with the transmission forest. Then, when a sequence is attached to $\mathcal{T}(t)$ the necessary components of $\mathcal{P}(t)$ to relate the new sequence to all previously observed sequences would be guaranteed to be present. When the transmission forest is large relative to the phylogeny such an approach would be costly in both computation and memory.

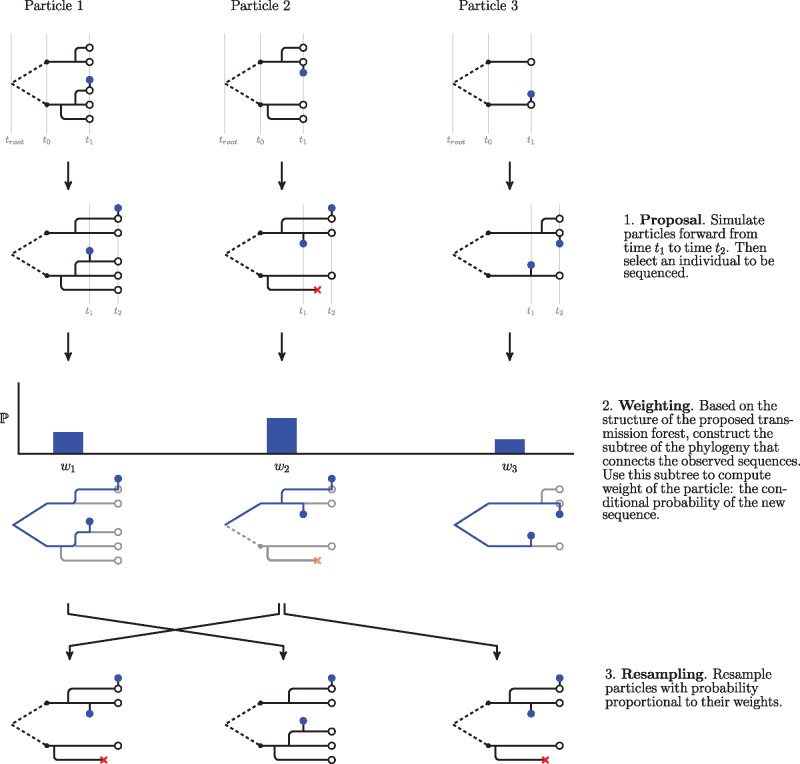
A Hierarchical Sampling Scheme

We developed a hierarchical sampling scheme to allow for scaling the effective number of particles while holding only a fraction of the effective number of particles in memory. This sampling scheme allows for holding J particles in memory while approaching effective sample sizes approaching JK, where J is the number of base particles and K is the number of nested particles. In this hierarchical scheme, we split the proposal into two steps: 1) proposal of the transmission forest and 2) proposal of the location of the sampled sequence on the transmission forest. Each of J particles first proposes a transmission forest. Then each of the J particles calculates the likelihood of the observed sequence for K possible locations of the observed sequence (fig. 8). One of the K-nested particles is kept, sampled with weight proportional to its conditional likelihood, and the remaining K−1 particles are discarded. The weight of the surviving particle is the average of the conditional likelihoods of the K-nested particles.

Fig. 8.

A schematic of our hierarchical sampling scheme. In this scheme, we split the proposal into two steps: 1) simulation of the transmission forest and 2) selecting an eligible individual to be sequenced. When each particle is expensive, it may pay to invest more effort in evaluating the conditional probability of a sequence given the latent state. This procedure is easily nested within the simpler form of the particle filter shown in figure 7. In turn, one can add additional Monte Carlo steps to the weighting step in this procedure to evaluate the conditional probability of a sequence under a relaxed clock (see fig. 9).

A Monte Carlo Procedure for the Relaxed Molecular Clock

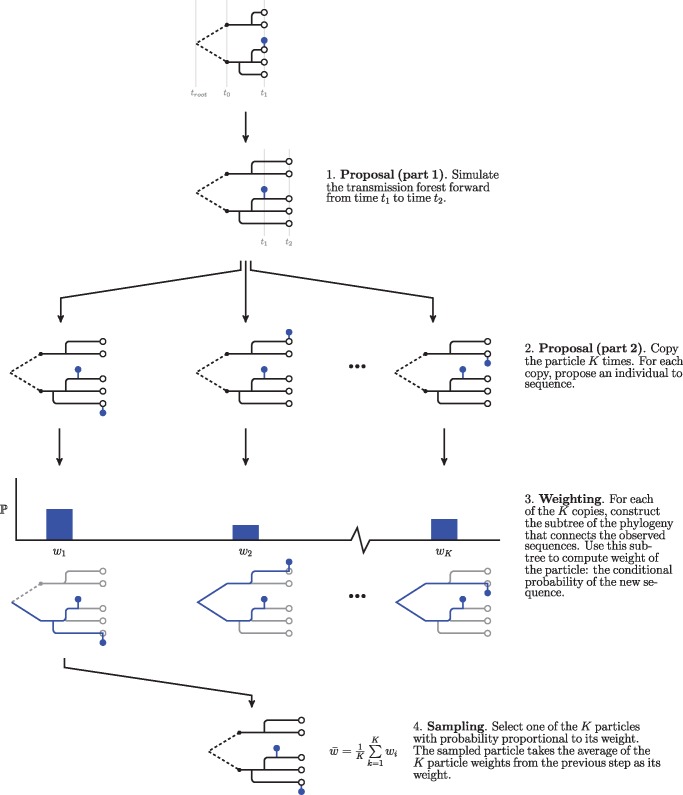
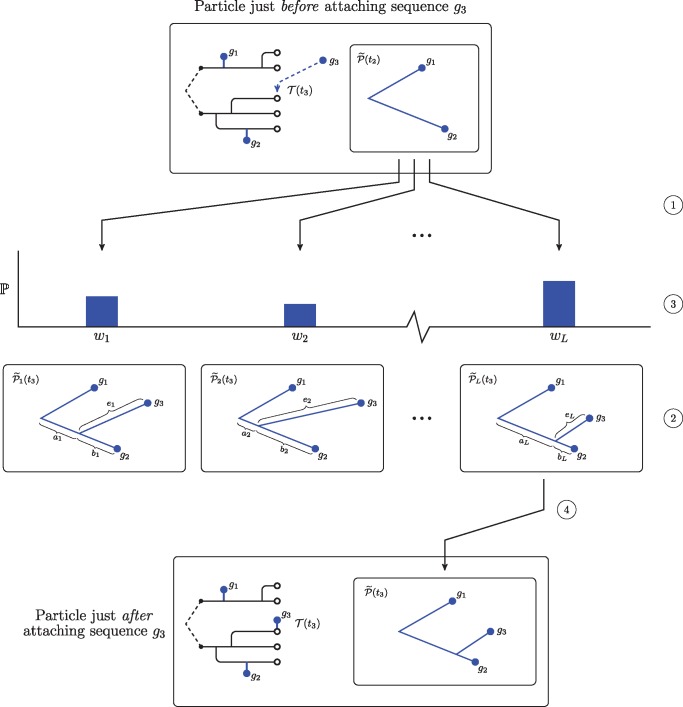
As we have no closed-form expression for the conditional probability of an observed sequence under a relaxed clock, we estimate this probability via simulation. Figure 9 shows how we incorporate this Monte Carlo procedure into our SMC framework. We generate L instances of the subtree of the phylogeny that connects all previously observed sequences up to time t, $\tilde{\mathcal{P}}(t)$. We then augment each subtree with an edge to accommodate the new sequence. The length of this edge is Gamma distributed as described above. When connecting the new edge to the existing phylogeny, there are two cases: Either the edge connects at the root or the new edge splits an existing edge. In the case of a split edge, we allocate edge length to either side of the split according to a beta distribution. This procedure maintains Gamma distributed edge lengths. Having constructed the phylogeny connecting all sequences up to the new sequence, we then use the peeling algorithm (Felsenstein 1981) to compute the conditional probability of the new sequence. The average of the conditional probability given each of the L subtrees is an estimate of the conditional probability of the new sequence under a relaxed clock.

Fig. 9.

A schematic showing our Monte Carlo approach to estimate the conditional probability of a sequence under a relaxed clock. Note that this procedure only modifies the subtree of the phylogeny that joins the sequences, $\tilde{\mathcal{P}}(t)$. At the top, we show a particle just before attaching a new sequence. In this case, the particle has already incorporated two sequences, and the location of the third sequence on the transmission forest has already been selected. First, we make L copies of $\tilde{\mathcal{P}}(t_2)$, the subtree of the phylogeny that connects all sequences observed up to time t₂ (at ①). For each of these phylogenies we propose an attachment site and an edge length for sequence g₃ (at ②). The edge length of the edge subtending sequence g₃, $e_{\ell }$, is drawn from a Gamma distribution parameterized as described in the text. We split the edge between the root and sequence g₂ according to a Beta distribution into two lengths, $a_{\ell }$ and $b_{\ell }$; this procedure preserves Gamma distributed edge lengths for two components of the split edge. Then, for each proposed phylogeny, we use the peeling algorithm to compute the conditional probability of sequence g₃ (at ③). Finally, we sample one of these proposed phylogenies with probability proportional to its weight (at ④). The unsampled proposals are discarded and the particle takes the average of the conditional probabilities as its weight.

Parallelization

We used openMP (Dagum and Menon, 1998) to parallelize the algorithm at the level of a single machine to reduce runtimes. In particular, we parallelized the outer loop of the hierarchical sampling scheme described above. Each processor handles one base particle at a time. The cost in memory for n processors handling J particles with a nested sample size of K is therefore at worst J + nK, as each processor may have at most K additional particles in memory.

A Model of HIV Transmission: Computation of the Measurement Model

Each diagnosis event consists of a diagnosis time and, possibly, an associated genetic sequence. In the case where the diagnosis event has no sequence, the measurement model is only the conditional density of the diagnosis time. When there is an associated sequence, it is the product of the conditional density of the diagnosis time and the conditional probability of the genetic sequence.

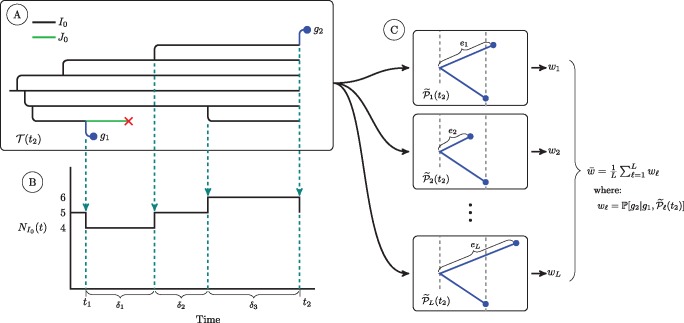
We compute the conditional density of a diagnosis time as follows. We decompose the density into two terms: 1) The probability of no diagnosis over the last interdiagnosis interval: $\text{exp}\hspace{0.17em}(-{\sum }_{k=0}^2{\Lambda }_k)$ where Λ_k is the cumulative hazard of a diagnosis from class I_k, $k\in \{0,1,2\}$. That is, ${\Lambda }_k={\rho }_k{\sum }_{r=1}^R{\delta }_r{N}_{I_k,r}$, where, ρ_k is the diagnosis rate for class I_k, δ_r is length of the rth subinterval in the interdiagnosis interval over which the count of class I_k, $N_{I_k,r}$, is constant, and 2) the hazard of a diagnosis at the time of diagnosis: ${\sum }_{k=0}^2{\rho }_k{N}_{I_k}$. The conditional density of a diagnosis time is the product of these two quantities, and is therefore a mixture of a probability and a density. To compute the first, each particle accumulates the person-years of undiagnosed individuals over the last diagnosis interval (fig. 10). The second is easily computed given the number of each class of undiagnosed individual at the time of diagnosis.

Fig. 10.

A schematic of quantities used in calculation of the conditional density of a diagnosis and the conditional probability of a genetic sequence. At (A) we show a simulated transmission tree. For simplicity, this tree only has individuals of class I₀ and class J₀. Dashed arrows fall from events in the transmission tree that change the count of I₀ individuals in the population. At (B) we show a plot of the trajectory of the I₀ class. This plot shows the quantities we use to calculate the cumulative hazard of diagnosis for the I₀ class, ${\Lambda }_0$, over an interval of time from t₁ to t₂. We first subdivide the time interval into R subintervals over which the number of I₀ individuals is constant (indicated with dashed lines). We let the number of I₀ individuals in the rth subinterval be $N_{I_0,r}$. The cumulative hazard of diagnosis is then: ${\Lambda }_0={\rho }_0{\sum }_{r=1}^R{\delta }_r{N}_{I_0,r}$. The cumulative hazards of diagnosis for the other two classes of undiagnosed individuals are computed in the same fashion. At (C) we show the set of L subtrees of the phylogeny that we use to numerically estimate the conditional probability of sequence g₂ under our relaxed clock model. The $\ell \text{th}$ subtree is constructed by augmenting $\tilde{\mathcal{P}}(t_1)$ with a new edge with length $e_{\ell }$ drawn from a Gamma distribution parameterized as described in the text. For each of these L subtrees we use the peeling algorithm to compute $w_{\ell }=\mathbb{P}[g_2|g_1,{\tilde{\mathcal{P}}}_{\ell }(t_2)]$, the conditional probability of observing sequence g₂ given sequence g₁ and the structure of ${\tilde{\mathcal{P}}}_{\ell }(t_2)$. The average of these conditional probabilities is a numerical estimate of the conditional probability of g₂ under our relaxed clock model. For simplicity, here we do not show the case in which the edge length of g₂ splits an existing edge; this case requires a beta bridge to apportion the length of the split edge so as to maintain Gamma distributed edge lengths. For this more complicated case, see figure 9.

The conditional probability of a genetic sequence is the probability of observing that sequence given the latent state of the system and all previously observed sequences. Our Monte Carlo approach for computing this probability under a relaxed clock is detailed in the Computational Structure section.

Data Analysis Methods: The Sequence Data

We preprocessed the sequence data following Volz, Ionides, et al. (2013) to facilitate comparison with that work. We excluded poor quality sequences and recombinant sequences, and accounted for known sources of selection. We first aligned all sequences to the reference sequence for the pol gene of HIV subtype-B. We then masked known drug resistant sites, as specified in the Stanford database of HIV drug resistance (Bennett et al. 2009). We used the program HyPhy (Pond et al. 2005) to identify the type of each sequence and then excluded recombinant sequences and nonsubtype-B sequences. M any individuals in the dataset have multiple sequences. To limit the complexity of the problem, we chose to keep only first available sequences that were collected within 1 year of diagnosis. Our methods could, in principle, allow for multiple sequences from each individual. However, this extension has not yet been implemented. We took the time of diagnosis as the time of sequencing—for most sequences this is a reasonable approximation. Poor quality sequencing often manifests as sequences with clipped ends. We therefore considered the length of a sequence as a proxy for quality, and we excluded sequences whose concatenated length was shorter than 1,100 base pairs.

Data Analysis Methods: Selecting a Subepidemic

The Michigan Department of Community Health (MDCH) maintains an extensive dataset on HIV positive individuals living in the state of Michigan. This dataset stretches back to the beginnings of the HIV epidemic in the United States, and includes over 30,000 diagnoses and nearly 9,000 genetic sequences. Analysis of the full dataset is beyond the scope of our current implementation. Further developments, possibly including preliminary splitting of the full phylogeny into clusters, will be necessary to apply our methods to larger-scale situations. We therefore selected a subset of the cases based on a number of clinical covariates. We chose to focus on the young, black, MSM, subepidemic, which has been of recent concern in Detroit and elsewhere in the United States (Maulsby et al. 2014). In selecting this subset, one of our goals was to choose a well-defined subpopulation. We selected records of individuals from the MDCH dataset that met the following criteria: Black, MSM, known not to be an intravenous drug user, and diagnosed in one of 10 counties that comprise the Detroit Metropolitan Area. For this subpopulation, the distribution of the age at diagnosis through time shows striking patterns. In particular, it there is evidence for cohorts of infected individuals that may be clusters of transmission within the young, black, MSM community. We selected a cohort from this population that may represent such a cluster of transmission: Individuals that were between the ages of 19 and 28 inclusive in the year 2011 (a span of 10 years) and were diagnosed between January 1, 1999 and December 31, 2011 (fig. 5). We selected this particular cohort of individuals because it contains what appears to be a pulse of transmission, and because it coincides with when we have high rates of sampling for the genetic sequence data. Counts of individuals diagnosed between January 1, 1999 and December 31, 2003 were used to determine initial conditions (detailed in the supplement). We fit models to data from January 1, 2004 to December 31, 2011. This portion of the cohort has 709 diagnoses and 253 primary genetic sequences. We subsampled the genetic sequences, randomly selecting 100 sequences to keep in the analysis. For the current implementation of our methodology, and in the context of this HIV model, 100 sequences was around the limit of computational tractability.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.