Significance
-Barrel membrane proteins (MPs) are drawing increasing attention because of their promising potential in bionanotechnology. However, their structures are notoriously hard to determine experimentally. Here we develop a method to achieve accurate prediction of MP structures, including those for which no prediction has been attempted before. The method is general and can be applied to genome-wide structural prediction of MPs, which will enable research into bionanotechnology and drugability of MPs.
Keywords: structure prediction, β-barrel membrane proteins, strand register, Covariation, loop prediction
Abstract
-Barrel membrane proteins (MPs) play important roles, but knowledge of their structures is limited. We have developed a method to predict their 3D structures. We predict strand registers and construct transmembrane (TM) domains of MPs accurately, including proteins for which no prediction has been attempted before. Our method also accurately predicts structures from protein families with a limited number of sequences and proteins with novel folds. An average main-chain rmsd of 3.48 Å is achieved between predicted and experimentally resolved structures of TM domains, which is a significant improvement (3 Å) over a recent study. For MPs with NMR structures, the deviation between predictions and experimentally solved structures is similar to the difference among the NMR structures, indicating excellent prediction accuracy. Moreover, we can now accurately model the extended -barrels and loops in non-TM domains, increasing the overall coverage of structure prediction by %. Our method is general and can be applied to genome-wide structural prediction of MPs.
The outer membrane proteins are found in the gram-negative bacteria, mitochondria, and chloroplast (1). They form -barrels, so are also known as -barrel membrane proteins (MPs). MPs are involved in outer membrane biogenesis, membrane anchoring, pore formation, translocation of virulence factors, and enzyme activities (2–5). Recent progress in engineering protein nanopores using MPs for protein profiling (6–8), DNA sequencing (9, 10), small molecule detection (11), and targeted drug delivery for cancer therapy (12) has increased the significance of understanding the organizing principles of MPs.
A major obstacle in studies of MPs is the limited availability of structural data. Only 320 MP structures, of which 59 are nonhomologous, have been deposited in the Protein Data Bank (PDB) that contains protein structures (13). Computational studies have contributed to expand our knowledge of MPs by successfully predicting MP sequences at a genome-wide scale (14, 15), identifying transmembrane (TM) segments (16, 17) and uncovering sequence and spatial motifs (18, 19). The stability, oligomerization state, protein–protein interaction interfaces, and the transfer free energy of residues in the TM regions of MPs can also be accurately computed (20–26).
Template-based methods for structure prediction have been successfully applied in studies of globular proteins (27). They have also been used to predict 3D structures of MPs but have achieved limited success with novel folds like the ones found in VDAC, FimD, PapC, and LptD proteins (28) due to the limited availability of templates for MPs. General purpose template-free structure prediction methods do not generate accurate structures of MPs, as these proteins can be large, with the number of residues reaching 800.
A recently published MP-specific method that combines sequence covariation for contact prediction with a machine-learning–based method achieved limited progress, with a main-chain rmsd of 6.66 Å for predicted structures of TM regions, before it was adjusted to a better published value of 4.45 Å when only a subset of residues were aligned instead of all TM residues (29). Another template-free MP-specific method, 3D-SPoT (3D structure predictor of transmembrane β-barrels), can predict the TM regions of MPs with an average main-chain rmsd of 4.14 Å (30). Despite such progress, further improvement in prediction methods to generate accurate structural models is required to bridge the gap between identified MP sequences and resolved MP structures, so that modeled structures can be used directly for applications such as nanopore engineering and drug design/delivery.
In this study, we describe a template-free method for predicting 3D structures of MPs, which provides significant improvement over previous methods. Our approach, named 3D beta-barrel membrane protein predictor (3D-BMPP), is based on a statistical mechanical model (31) that incorporates sequence covariation information and is built upon a parametric structural model of intertwined zigzag coils. In a blind test of 51 nonhomologous MPs, our prediction generates accurate 3D structures of TM regions with an average main-chain rmsd of 3.48 Å. This represents a significant improvement of 3.1 Å compared with a recent study (29) over a much bigger dataset (51 proteins vs. 17 proteins). In addition, predictions are expanded to include non-TM regions, including both extended -sheets and loops, resulting in significant increase in the coverage of residues compared with previous methods. Furthermore, our method can be applied to model structures of MPs with novel folds, including those from mitochondria of eukaryotes, as evidenced by the accurately modeled structures of VDAC and FimD. Our method is general and can be applied to genome-wide structural prediction of MPs.
Results
MPs have strong thermal and chemical resistance due to the well-knit hydrogen bond network (32), in which each residue in the TM strand is hydrogen bonded to residues on the adjacent TM strands (SI Appendix, Fig. S1). We use a physical model that accounts for strong hydrogen bonds, weak hydrogen bonds, and side-chain interactions between adjacent strands in the barrel domain (20, 31, 33, 34). In addition, we incorporate interstrand loop entropy, right-handedness of the MP, and medium-to-long–range contacts predicted from sequence covariation information. Details of our model can be found in SI Appendix, section 3.
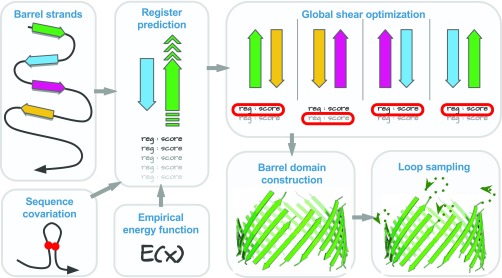
To predict structures of MPs, we proceed in three steps: predicting strand registers (interstrand hydrogen bond contacts), predicting 3D coordinates of TM residues, and modeling non-TM residues (Fig. 1).
Fig. 1.
The flowchart of MP structure prediction method 3D-BMPP. The strand registers are predicted using a combination of empirical energy function and sequence covariation information. Global shear optimization is then performed upon the predicted register candidates. The 3D coordinates of Cα atoms of TM and non-TM residues are then predicted using a parametric structural model. We also predict ensembles of loop conformations.
Predicting Strand Registers
Predicting strand registers of adjacent strands.
We use a discrete model of reduced states to represent the conformational space of the strands, in which the relative position between a pair of adjacent strands can adopt different registers, where and are the lengths of the two strands (Fig. 1 and SI Appendix, Fig. S1) (20). For each adjacent strand pair, we generate all possible conformations in the discrete state space, each with a different register of hydrogen bonds with its next sequentially adjacent strand (Fig. 1). Every conformation is evaluated by summing up the contribution from terms representing different strand-interaction types (strong hydrogen bonds, weak hydrogen bonds, and side-chain interactions), a term for the loop entropy, a term for bias toward right-handedness, and a term for sequence covariation. Sequence covariation is calculated using the sparse inverse covariation estimation method of protein sparse inverse covariance (PSICOV) (35). For a pair of strands, the register is predicted to be the one with the lowest score.
The results of strand register prediction for 51 MPs show that overall 655 of 771 registers are predicted correctly, representing an accuracy of 85% (see SI Appendix, Table S4 for details). This is a significant improvement over previous MP register prediction methods of Jackups and Liang (%) (31), Randall et al. (%) (28), Naveed et al. (%) (30), and Hayat et al. (%) (29). It is also important to note that the dataset used is much larger than those used in the previous studies (Table 1). For eight MPs (OpA60, autotransporter Hbp, TodX, EstA, FhuA, FecA, FptA, and HasR that contain 8, 12, 14, 12, 22, 22, 22, and 22 strands, respectively), we are able to predict all of the strand registers correctly.
Table 1.
Comparison of different methods for strand register and 3D structure prediction for TM regions of MPs
| Method | No. MPs | No. strands | Strand register accuracy, % | Average main-chain TM-rmsd, Å | Average all-atom TM-rmsd, Å |
| Jackups and Liang (31) | 19 | 256 | 46 | — | — |
| TMBpro-server (28) | 14 | 214 | 48 | — | 7.3 |
| 3D-SPoT (30) | 23 | 324 | 73 | 4.12 | 5.6 |
| EVfold_bb (29) | 17 | 265 | 44 | 6.66 | — |
| 3D-BMPP (this study) | 51 | 771 | 85 | 3.48 | 4.26 |
3D-BMPP can predict strand registers with an accuracy of ∼85% and 3D structures of TM regions with an average main-chain rmsd of 3.48 Å and average all-atom rmsd of 4.26 Å for a much bigger dataset (51 βMPs vs. 14–23 βMPs).
To assess the contribution of the sequence covariation information and the patterns of hydrogen bonds and side-chain interactions (HSC), we predicted the strand registers using sequence covariation data and a reduced state space (SC+RSS). The strand register prediction accuracy with SC+RSS was found to be 52%, representing significant deterioration from the accuracy of 69% (30) using HSC+RSS. This result indicates that patterns of hydrogen bonds and side-chain interactions derived from structural data can predict local strand registers more accurately than sequence covariation information. This conclusion is consistent with that of Hayat et al. (29), in which machine learning and sequence covariation were used to predict the strand register at an accuracy of 44%.
The side-chain orientation of the TM residues is an important determinant of the structure of MPs. A residue can be either lipid facing or pore facing, with consecutive residues in the TM region taking alternating orientations. Pore-facing residues are predominantly responsible for protein function (e.g., flux control of metabolites and ion sensing), while lipid-facing residues are mostly responsible for protein insertion and stability. Residues on adjacent strands have the same side-chain orientation when they share strong hydrogen bonds or side-chain interactions. Incorrect strand register can lead to erroneous side-chain orientation prediction. The correct prediction of strand register is therefore an important requirement in structure prediction of MPs and is well recognized in the literature (28). Our method can predict strand register at 85% accuracy. In contrast, the criteria were relaxed to allow +1 or −1 difference in strand register in a previous study (29). While this relaxation made the register prediction results more presentable (65% after relaxation vs. 44% before relaxation), it is problematic, as it would lead to prediction of TM residues to adopt erroneous orientation opposite to that of the native structures. Such incorrect TM residue orientations would imply completely different properties of the barrel interior and exterior. Here we report correct prediction only when we are able to exactly match the register with the experimentally resolved structure.
Predicting side-chain orientations.
We use the reduced state space and a single body potential (20) calculated from the updated dataset to predict the side-chain orientation of each strand. Since the side-chain orientations of a strand follow an alternative lipid-facing–pore-facing pattern, only the orientation of the first residue of each strand needs to be predicted. The accuracy of our prediction is 98% (see SI Appendix, section 3.4 for details).
Optimizing protein shear.
We next optimize the shear number which characterizes the global hydrogen bond pattern of a MP. The shear number is the displacement of the relative positions in the TM strands if one starts to follow the strong hydrogen bond or side-chain interaction between strands, beginning from one strand and returning after a full circle to the same strand (SI Appendix, Fig. S5). The predicted shear number of a MP can be calculated as the sum of the predicted strand registers.
In the step of register prediction, we keep the register with the lowest score and the one with the second lowest score as candidates for each strand pair. They are then evaluated against the predicted side-chain orientations of the strand, based on the fact that residues sharing a strong hydrogen bond or side-chain interaction have the same side-chain orientation. One of the two registers is then selected so that the predicted shear number is as close as possible to the most common shear number of the MPs of the same strand number (SI Appendix, Table S3), while keeping the sum of the strand register scores as small as possible (see SI Appendix, section 3.5 for technical details). After optimization, the error in predicted shear numbers is decreased from to . The improved global shear accuracy will lead to overall more accurate 3D structure prediction of MPs.
Predicting 3D Structures of TM Regions of MPs
Parametric model for 3D structures of the TM regions.
Parametric models have had recent successes in modeling and designing structures of -helical proteins (36, 37). We have developed a parametric structural model, named the intertwined zigzag coil model, to generate 3D structures of MPs from predicted strand registers (SI Appendix, Fig. S4). Following previous studies (30, 38), we model the overall shape of the -barrel as an ideal cylinder. The Cα trace of each strand is described as a coiled zigzag wrapping around the hypothetical cylinder (see SI Appendix, section 4.1 for details). This model captures the zigzag nature of a polypeptide in the MP and the varied distance between Cα atoms on adjacent strands (SI Appendix, Fig. S3), which improves positioning of Cα atoms.
Predicting 3D atomic structures.
We then use these Cα atoms to construct the main-chain atoms using Gront et al.’s (39) algorithm. The side-chain atoms are then added using side-chains with a rotamer library 4 (Scwrl4) (40).
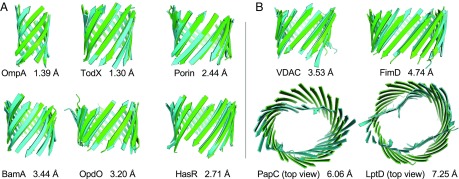
Fig. 2A depicts the predicted structures (green) of the TM regions of proteins OmpA, TodX, Porin, BamA, OpdO, and HasR, which are shown superimposed on experimentally determined structures (cyan). The rmsds of the main-chain atoms between the computed and experimentally resolved structures are 1.39 Å, 1.30 Å, 2.44 Å, 3.44 Å, 3.20 Å, and 2.71 Å for OmpA, TodX, Porin, BamA, OpdO, and HasR, respectively. The structures of the TM regions of 51 MPs are predicted with an average rmsd of 3.48 Å for main-chain atoms and 4.26 Å for all atoms (see SI Appendix, Table S4 and Fig. S7 for details). The accuracy of predicted structures is maintained for large proteins such as Iron(III) dicitrate transport protein FecA protein (237 TM residues). This is in contrast to other prediction methods, where there is considerable deterioration in the quality of predicted structures (SI Appendix, Table S5 and Fig. S6). The average TM scores of our predicted structures also compare favorably with those of a recent study (0.73 vs. 0.54) (29). Furthermore, our results are over a much bigger dataset (51 proteins vs. 17 proteins). Thus, these results represent a very significant improvement. Moreover, the parametric structural model of intertwined zigzag coils improves accuracy of side chains, as the all-atom rmsd has improved by more than 1.30 Å (4.26 Å vs. 5.60 Å) compared with a previous study (30).
Fig. 2.
Structure prediction of TM regions. (A) Predicted structures of the TM regions (green) superimposed on experimentally determined structures (cyan): OmpA (1bxw), TodX (3bs0), Porin (1prn), BamA (4n75), OpdO (3szv), and HasR (3csl). (B) Predicted structures of the TM regions of proteins with novel folds (green) superimposed on experimentally determined structures (cyan): VDAC (3emn), FimD (3rfz), PapC (2vqi), and LptD (4q35). PapC and LptD are shown in top view.
TM regions of MPs have considerable intrinsic flexibility: The NMR structures have an average mutual Cα-rmsd of Å for the seven MPs with known NMR data (Table 2, column 2). The difference between the NMR and X-ray structures is more pronounced, with an average Cα-rmsd of Å (Table 2, column 3). In contrast, the average Cα-rmsds of our predicted structures against NMR and X-ray structures are and , respectively (Table 2, columns 4 and 5). These differences are similar to the structural differences originating from the intrinsic flexibility of the proteins, suggesting that our prediction of TM regions of MPs has excellent accuracy comparable to NMR structures.
Table 2.
Flexibility of TM regions of MPs and the accuracy of the prediction of 3D-BMPP
| PDB ID | ||||
| 1bxw | 1.41 0.42 | 1.99 0.31 | 1.83 0.15 | 1.36 |
| 1qj8 | 2.50 0.74 | 2.48 0.80 | 3.11 0.46 | 2.65 |
| 1thq | 1.99 0.58 | 4.53 0.38 | 5.30 0.42 | 3.32 |
| 2f1c | 2.42 0.37 | 2.80 0.21 | 3.93 0.21 | 3.06 |
| 2f1t | 2.13 0.35 | 4.30 0.11 | 4.08 0.14 | 3.12 |
| 2lhf | 0.82 0.22 | No X-ray | 1.60 0.08 | 1.48∗ |
| 2mlh | 1.48 0.28 | No X-ray | 1.49 0.14 | 1.44∗ |
| Mean | 2.11 0.79 | 3.18 1.16 | 3.09 1.39 | 2.35 0.82 |
is the average of the mutual Cα-rmsd between structures s1 and s2.
As no X-ray structures for these proteins are available, we used the first model of the NMR data.
Predicting structures of MPs with novel folds.
It is challenging to predict the structures of MPs with novel folds. MPs were considered to have even numbers of strands from 8 to 22 (41). A MP is considered to have a novel fold when its number of strands has not been observed in other experimentally determined structures. For example, VDAC in mitochondria has an odd number (19) of strands (42); PapC, FimD, and LptD all have more than 22 strands (24, 24, and 26, respectively). Predicting structures of a number of MPs including VDAC, FimD, and LptD with reasonable accuracy was not possible in a recent study (29), likely due to inaccurate residue contact predictions and limitations in the machine-learning–based procedure. Template-based prediction methods either fail to build any model or generate very poor structures. With the improved modeling procedure of 3D-BMPP, we are able to model the TM regions of the VDAC, FimD, PapC, and LptD proteins with a main-chain rmsd of 3.53 Å, 4.74 Å, 6.06 Å, and 7.25 Å, respectively (Fig. 2B). While the structure of VDAC was previously predicted with an accuracy of 3.9 Å (30) and 7.41 Å (29), to the best of our knowledge the structures of FimD, PapC, and LptD have not been successfully predicted before this study. The large rmsds of predicted structures of PapC and LptD show that our current idealized cylindrical structural model cannot yet model deformed barrels effectively.
Predicting Structure of non-TM Regions of MPs
Predicting structures of extended -sheets.
We also model the structures of the non-TM regions of MPs, including the extended -sheets (extended barrels) and loops connecting adjacent strands. The extended barrels have overall similar structures to those of the TM barrels. Including the extended barrel in our prediction increases the coverage of the modeled structures by 20% when measured by the average number of residues modeled in the 51 structures (159 in TM regions vs. 191 in whole-barrel regions, with the largest modeled barrel structure containing 350 residues), with little deterioration in the average main-chain rmsd (3.48 Å vs. 3.80 Å).
Predicting structures of loops.
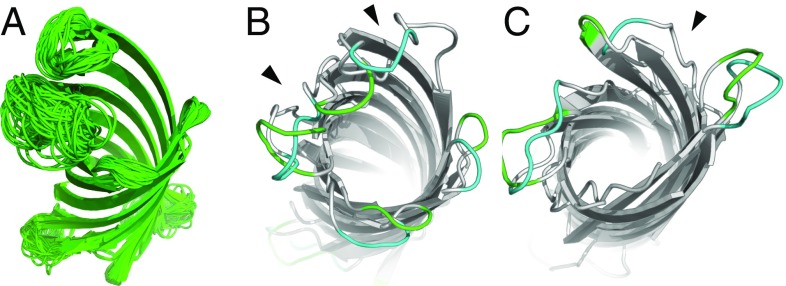
Loops are the most flexible regions of MPs and are important for their functions (43). NMR structures of MPs show that these loops adopt multiple conformations (44, 45), which likely contribute to the challenges in predicting binding affinity of MP–ligand interactions (46). We model loops by investigating a large ensemble of loop conformations generated using an improved version of the multi-loop distance-guided sequential chain-growth Monte Carlo (m-DiSGro) algorithm (47) that guarantees clash-free conformations of the sampled loops. For each of the seven MPs with available NMR structures, once the structure of the barrel domain is predicted, we sample – multiloop conformations, with the specific number of conformations dictated by the number and the lengths of loops. We then perform clustering to generate an ensemble of multiloop conformations as a prediction for each protein. The predicted loop conformations are diverse (Fig. 3A) and represent the broad conformational space that is accessible to loops (48). Examples of predicted loops are shown in Fig. 3.
Fig. 3.
Structure prediction of loop regions. (A) Ensemble of predicted loop structures of OmpX (1qj8). (B and C) Examples of predicted loops on the extracellular side (B, green) and on the periplasmic side (C, green) superimposed on the corresponding NMR structure (cyan) (49). The black arrowheads indicate the big fluctuations in the barrel region.
To assess the quality of the predicted loop conformations, we define a metric that measures how Cα-rmsd between structures and is changed upon incorporation of the loop regions: where is the Cα-rmsd between the structures and including both the barrel and loop regions, and is the Cα-rmsd between the barrel domains only. Since the number of available NMR structures for each protein is limited compared with our predictions (10–20 vs. 400), we selected predicted conformations closest to the NMR structures by from the modeled ensemble for each protein. The resulting s calculated using these structures are Å, with an average of (Table 3, column 5), which is on par with the values of (Table 3, column 3), suggesting that we are able to sample the loop conformations observed in the NMR structures accurately.
Table 3.
Comparison of the accuracy of loop prediction for MPs
| PDB id | ||||
| 1bxw | 2.78 0.72 | 3.83 1.25 | 3.35 0.51 | 3.00 0.55 |
| 1qj8 | 3.31 0.80 | 0.61 0.26 | 4.14 0.57 | 0.67 0.27 |
| 1thq | 1.99 0.58 | 0.79 0.35 | 5.30 0.42 | 0.52 0.21 |
| 2f1c | 3.33 0.61 | 3.76 0.94 | 5.29 0.50 | 2.78 0.48 |
| 2f1t | 2.58 0.54 | 1.01 0.55 | 4.35 0.15 | 0.45 0.20 |
| 2lhf | 0.85 0.24 | 1.94 0.60 | 1.63 0.09 | 2.05 0.27 |
| 2mlh | 1.48 0.28 | 1.51 0.64 | 1.49 0.14 | 0.99 0.26 |
| Mean | 3.65 1.21 | 1.03 0.89 | 3.64 1.46 | 1.12 0.89 |
We are able to sample most of the loop conformations seen in the NMR structures with <3 Å deterioration in Cα-rmsd.
Discussion
Due to the difficulties in experimental determination of membrane protein structures, there are a limited number of structures of nonhomologous MPs. However, it is estimated that there are 15,000 MPs across 600 different gram-negative chromosomes (50). Computational modeling has the promise to provide working 3D models for these sequences, enabling novel applications in nanopore engineering and drug design/delivery, as well as furthering understanding of the structural basis of the function and mechanism of these MPs. We have developed a method for predicting structures of MPs, which combines a statistical mechanical model, sequence covariation information, and global register optimization with a parametric structural model of intertwined zigzag coils. The results show that we can accurately predict structures of MPs with a significantly expanded coverage of extended -sheets and loops.
The incorporation of global register optimization increases the accuracy of the predicted structures by 0.24 Å on average, suggesting that the global hydrogen bond network cannot be approximated accurately using local strand register alone. As an example, for the MPs OmpA (PDB ID: 1bxw), hypothetical protein HB27 (PDB ID: 3dzm), and PagL (PDB ID: 2erv), the strand registers were predicted correctly for six of eight strands before global register optimization, with an error in shear number of , , and , respectively. After global register optimization, the strand register was predicted correctly for eight, six, four strands, respectively, and the error in shear number becomes 0 in all three cases. Moreover, the main-chain rmsd of these predicted structures is improved by 2.7 Å, 2.5 Å, and 1.5 Å, respectively.
Our parametric model of intertwined zigzag coils captures the zigzag nature of a polypeptide and the varied distance between Cα atoms of two adjacent strands, which depends on whether the respective residues share a main-chain hydrogen bond. This results in significant improvement in rmsd for all atoms in general and side-chain atoms in particular. When we constructed structures of all 51 MPs using our parametric model with true registers, the average main-chain rmsd of these structures was 2.5 Å. Given our prediction accuracy of 3.48Å in this study, only 1 Å error on average is due to incorrect register prediction, while the 2.5-Å error is due to the structural deviation of MPs from the ideal cylindrical shape.
Currently this ideal cylindrical model cannot capture ellipticity, twist, and curvature of local surface of the deformed barrel domains such as those observed in PapC and LptD (Fig. 2B), and alternative hyperboloid models have been discussed in the literature (51, 52). However, as current understanding of the physical factors determining these geometric properties is incomplete, further investigation of the heterogeneity of interactions in the TM region is required to develop a more accurate geometric model that can account for the deformed barrel domain.
In a recent study, structures for only 17 proteins (compared with 51 proteins in this study) were predicted (29), as the number of sequences available for the remaining proteins was insufficient to analyze sequence covariation. Here, we show that this limitation can be removed by combining patterns of hydrogen bond and side-chain interactions derived from experimentally determined 3D structures with the sequence covariation information (SI Appendix, Fig. S8). Our method predicts the 3D structures of 51 MPs with an average rmsd of 3.48 Å, which compares favorably with the recent study that has an average rmsd of 6.66 Å (29). Detailed technical issues comparing the two methods are discussed in SI Appendix, section 6.
Our method revealed basic organizational principles of MPs and requires no template structures. In addition, TM regions of MPs with a novel fold can also be modeled effectively, as evidenced by the predicted structures of VDAC and FimD. Furthermore, non-TM regions including both extended -sheets and loops can be predicted accurately. Overall, our method opens the possibility of structural studies of many MPs, including those in eukaryotic mitochondria and chloroplasts.
Materials and Methods
We use 59 MPs with known structures as our dataset. The mutual sequence similarity is below . Predictions are made only for 51 MPs, after excluding multichain -barrels to avoid overestimation of repeated interaction types. Leave-one-out cross-validation is performed to assess the accuracy of the predictions.
Here, we describe our methods briefly. More details of the methods can be found in SI Appendix, sections 2–5. We take the canonical model of TM strands based on the physical interactions between strands described in refs. 31 and 33. The energetic contributions incorporate interactions with adjacent strands, interstrand loop entropy, a penalty for left-handedness, and sequence covariation. For each pair of adjacent strands, we enumerate all possible registers in a reduced conformational space and predict the registers. This is followed by the global shear optimization. We use a parametric structural model of intertwined zigzag coils to calculate the positions of Cα atoms. Main-chain atoms and side chains are added using Gront et al.’s (39) algorithm and Scwrl4 (40). We then use an improved version of the m-DiSGro algorithm (47) to sample loop ensembles.
The 3D-BMPP code and the corresponding data are available at sts.bioe.uic.edu/3dbmpp/.
Supplementary Material
Acknowledgments
The authors thank Drs. Jinbo Xu, Aly Azeem Khan, and Jianzhu Ma for helpful discussions. The authors also thank Alan Perez-Rathke for providing the loop modeling code of the improved version of the m-DiSGro algorithm. This work was supported by Toyota Technological Institute at Chicago and NIH Grants R01GM079804, R01CA204962, R01GM126558, and R21AI126308.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1716817115/-/DCSupplemental.
References
- 1.Freeman T, Jr, Landry S, Wimley W. The prediction and characterization of YshA, an unknown outer-membrane protein from Salmonella typhimurium. Biochim Biophys Acta. 2011;1808:287–297. doi: 10.1016/j.bbamem.2010.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Delcour A. Structure and function of pore-forming beta-barrels from bacteria. J Mol Microbiol Biotechnol. 2002;4:1–10. [PubMed] [Google Scholar]
- 3.Bishop R. Structural biology of membrane-intrinsic beta-barrel enzymes: Sentinels of the bacterial outer membrane. Biochim Biophys Acta. 2008;1778:1881–1896. doi: 10.1016/j.bbamem.2007.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Song L, et al. Structure of staphylococcal alpha-hemolysin, a heptameric transmembrane pore. Science. 1996;274:1859–1866. doi: 10.1126/science.274.5294.1859. [DOI] [PubMed] [Google Scholar]
- 5.Noinaj N, et al. Structural insight into the biogenesis of beta-barrel membrane proteins. Nature. 2013;501:385–390. doi: 10.1038/nature12521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fahie M, Yang B, Mullis M, Holden M, Chen M. Selective detection of protein homologues in serum using an OmpG nanopore. Anal Chem. 2015;87:11143–11149. doi: 10.1021/acs.analchem.5b03350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fahie M, Chisholm C, Chen M. Resolved single-molecule detection of individual species within a mixture of anti-biotin antibodies using an engineered monomeric nanopore. ACS Nano. 2015;9:1089–1098. doi: 10.1021/nn506606e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Oukhaled A, Bacri L, Pastoriza-Gallego M, Betton J, Pelta J. Sensing proteins through nanopores: Fundamental to applications. ACS Chem Biol. 2012;7:1935–1949. doi: 10.1021/cb300449t. [DOI] [PubMed] [Google Scholar]
- 9.Farimani A, Heiranian M, Aluru N. Electromechanical signatures for DNA sequencing through a mechanosensitive nanopore. J Phys Chem Lett. 2015;6:650–657. doi: 10.1021/jz5025417. [DOI] [PubMed] [Google Scholar]
- 10.Ayub M, Stoddart D, Bayley H. Nucleobase recognition by truncated alpha-hemolysin pores. ACS Nano. 2015;9:7895–7903. doi: 10.1021/nn5060317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Campos E, et al. Sensing single mixed-monolayer protected gold nanoparticles by the alpha-hemolysin nanopore. Anal Chem. 2013;85:10149–10158. doi: 10.1021/ac4014836. [DOI] [PubMed] [Google Scholar]
- 12.Panchal R, Cusack E, Cheley S, Bayley H. Tumor protease-activated, pore-forming toxins from a combinatorial library. Nat Biotechnol. 1996;14:852–856. doi: 10.1038/nbt0796-852. [DOI] [PubMed] [Google Scholar]
- 13.Berman H, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ou Y, Gromiha M, Chen S, Suwa M. TMBETADISC-RBF: Discrimination of beta-barrel membrane proteins using RBF networks and PSSM profiles. Comput Biol Chem. 2008;32:227–231. doi: 10.1016/j.compbiolchem.2008.03.002. [DOI] [PubMed] [Google Scholar]
- 15.Freeman T, Jr, Wimley W. A highly accurate statistical approach for the prediction of transmembrane beta-barrels. Bioinformatics. 2010;26:1965–1974. doi: 10.1093/bioinformatics/btq308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ou Y, Chen S, Gromiha M. Prediction of membrane spanning segments and topology in beta-barrel membrane proteins at better accuracy. J Comput Chem. 2010;31:217–223. doi: 10.1002/jcc.21281. [DOI] [PubMed] [Google Scholar]
- 17.Hayat S, Peters C, Shu N, Tsirigos K, Elofsson A. Inclusion of dyad-repeat pattern improves topology prediction of transmembrane beta-barrel proteins. Bioinformatics. 2016;32:1571–1573. doi: 10.1093/bioinformatics/btw025. [DOI] [PubMed] [Google Scholar]
- 18.Jackups R, Jr, Cheng S, Liang J. Sequence motifs and antimotifs in beta-barrel membrane proteins from a genome-wide analysis: The Ala-Tyr dichotomy and chaperone binding motifs. J Mol Biol. 2006;363:611–623. doi: 10.1016/j.jmb.2006.07.095. [DOI] [PubMed] [Google Scholar]
- 19.Jackups R, Jr, Liang J. Combinatorial analysis for sequence and spatial motif discovery in short sequence fragments. IEEE/ACM Trans Comput Biol Bioinform. 2010;7:524–536. doi: 10.1109/TCBB.2008.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Naveed H, Jackups R, Jr, Liang J. Predicting weakly stable regions, oligomerization state, and protein-protein interfaces in transmembrane domains of outer membrane proteins. Proc Natl Acad Sci USA. 2009;106:12735–12740. doi: 10.1073/pnas.0902169106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Naveed H, Liang J. Weakly stable regions and protein-protein interactions in beta-barrel membrane proteins. Curr Pharm Des. 2014;20:1268–1273. doi: 10.2174/13816128113199990071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Geula S, Naveed H, Liang J, Shoshan-Barmatz V. Structure-based analysis of VDAC1: Defining oligomer contact sites. J Biol Chem. 2011;287:2179–2190. doi: 10.1074/jbc.M111.268920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Naveed H, et al. Engineered oligomerization state of OmpF protein through computational design decouples oligomer dissociation from unfolding. J Mol Biol. 2012;419:89–101. doi: 10.1016/j.jmb.2012.02.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lin M, Gessmann D, Naveed H, Liang J. Outer membrane protein folding and topology from a computational transfer free energy scale. J Am Chem Soc. 2016;138:2592–2601. doi: 10.1021/jacs.5b10307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tian W, Lin M, Naveed H, Liang J. Efficient computation of transfer free energies of amino acids in beta-barrel membrane proteins. Bioinformatics. 2017;33:1664–1671. doi: 10.1093/bioinformatics/btx053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tian W, Naveed H, Lin M, Liang J. 2017. GeTFEP: A general transfer free energy profile for transmembrane proteins. bioRxiv:191650.
- 27.Yang J, et al. Template-based protein structure prediction in casp11 and retrospect of i-tasser in the last decade. Proteins Struct Funct Bioinformatics. 2016;84:233–246. doi: 10.1002/prot.24918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Randall A, Cheng J, Sweredoski M, Baldi P. TMBpro: Secondary structure, beta-contact and tertiary structure prediction of transmembrane beta-barrel proteins. Bioinformatics. 2008;24:513–520. doi: 10.1093/bioinformatics/btm548. [DOI] [PubMed] [Google Scholar]
- 29.Hayat S, Sander C, Marks D, Elofsson A. All-atom 3D structure prediction of transmembrane β-barrel proteins from sequences. Proc Natl Acad Sci USA. 2015;112:5413–5418. doi: 10.1073/pnas.1419956112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Naveed H, Xu Y, Jackups R, Jr, Liang J. Predicting three-dimensional structures of transmembrane domains of beta-barrel membrane proteins. J Am Chem Soc. 2012;134:1775–1781. doi: 10.1021/ja209895m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jackups R, Jr, Liang J. Interstrand pairing patterns in beta-barrel membrane proteins: The positive-outside rule, aromatic rescue, and strand registration prediction. J Mol Biol. 2005;354:979–993. doi: 10.1016/j.jmb.2005.09.094. [DOI] [PubMed] [Google Scholar]
- 32.Gessmann D, et al. Improving the resistance of a eukaryotic beta-barrel protein to thermal and chemical perturbations. J Mol Biol. 2011;413:150–161. doi: 10.1016/j.jmb.2011.07.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ho B, Curmi P. Twist and shear in beta-sheets and beta-ribbons. J Mol Biol. 2002;317:291–308. doi: 10.1006/jmbi.2001.5385. [DOI] [PubMed] [Google Scholar]
- 34.Jackups R, Jr, Liang J. Combinatorial model for sequence and spatial motif discovery in short sequence fragments: Examples from beta-barrel membrane proteins. Conf Proc IEEE Eng Med Biol Soc. 2006;1:3470–3473. doi: 10.1109/IEMBS.2006.259727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jones D, Buchan D, Cozzetto D, Pontil M. PSICOV: Precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics. 2012;28:184–190. doi: 10.1093/bioinformatics/btr638. [DOI] [PubMed] [Google Scholar]
- 36.Schmidt N, Grigoryan G, DeGrado W. The accommodation index measures the perturbation associated with insertions and deletions in coiled-coils: Application to understand signaling in histidine kinases. Protein Sci. 2016;26:414–435. doi: 10.1002/pro.3095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Huang P, et al. High thermodynamic stability of parametrically designed helical bundles. Science. 2014;346:481–485. doi: 10.1126/science.1257481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McLachlan A. Gene duplications in the structural evolution of chymotrypsin. J Mol Biol. 1979;128:49–79. doi: 10.1016/0022-2836(79)90308-5. [DOI] [PubMed] [Google Scholar]
- 39.Gront D, Kmiecik S, Kolinski A. Backbone building from quadrilaterals: A fast and accurate algorithm for protein backbone reconstruction from alpha carbon coordinates. J Comput Chem. 2007;28:1593–1597. doi: 10.1002/jcc.20624. [DOI] [PubMed] [Google Scholar]
- 40.Krivov G, Shapovalov M, Dunbrack R., Jr Improved prediction of protein side-chain conformations with SCWRL4. Proteins. 2009;77:778–795. doi: 10.1002/prot.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fioroni M, Dworeck T, Rodriguez-Ropero F. Beta-Barrel Channel Proteins As Tools in Nanotechnology: Biology, Basic Science and Advanced Applications. Springer; Dordrecht, The Netherlands: 2013. [Google Scholar]
- 42.Ujwal R, et al. The crystal structure of mouse VDAC1 at 2.3 Å resolution reveals mechanistic insights into metabolite gating. Proc Natl Acad Sci USA. 2008;105:17742–17747. doi: 10.1073/pnas.0809634105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Koebnik R. Structural and functional roles of the surface-exposed loops of the beta-barrel membrane protein OmpA from Escherichia coli. J Bacteriol. 1999;181:3688–3694. doi: 10.1128/jb.181.12.3688-3694.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Arora A, Abildgaard F, Bushweller J, Tamm L. Structure of outer membrane protein A transmembrane domain by NMR spectroscopy. Nat Struct Biol. 2001;8:334–338. doi: 10.1038/86214. [DOI] [PubMed] [Google Scholar]
- 45.Cierpicki T, Liang B, Tamm L, Bushweller J. Increasing the accuracy of solution NMR structures of membrane proteins by application of residual dipolar couplings. High-resolution structure of outer membrane protein A. J Am Chem Soc. 2006;128:6947–6951. doi: 10.1021/ja0608343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Koehler Leman J, Ulmschneider M, Gray J. Computational modeling of membrane proteins. Proteins. 2015;83:1–24. doi: 10.1002/prot.24703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tang K, Wong S, Liu J, Zhang J, Liang J. Conformational sampling and structure prediction of multiple interacting loops in soluble and beta-barrel membrane proteins using multi-loop distance-guided chain-growth Monte Carlo method. Bioinformatics. 2015;31:2646–2652. doi: 10.1093/bioinformatics/btv198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tang K, Zhang J, Liang J. Distance-guided forward and backward chain-growth Monte Carlo method for conformational sampling and structural prediction of antibody CDR-H3 loops. J Chem Theor Comput. 2017;13:380–388. doi: 10.1021/acs.jctc.6b00845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fernandez C, Hilty C, Wider G, Guntert P, Wuthrich K. NMR structure of the integral membrane protein OmpX. J Mol Biol. 2004;336:1211–1221. doi: 10.1016/j.jmb.2003.09.014. [DOI] [PubMed] [Google Scholar]
- 50.Freeman T, Jr, Wimley W. TMBB-DB: A transmembrane beta-barrel proteome database. Bioinformatics. 2012;28:2425–2430. doi: 10.1093/bioinformatics/bts478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Novotný J, Bruccoleri RE, Newell J. Twisted hyperboloid (strophoid) as a model of -barrels in proteins. J Mol Biol. 1984;177:567–573. doi: 10.1016/0022-2836(84)90301-2. [DOI] [PubMed] [Google Scholar]
- 52.Lasters I, Wodak SJ, Alard P, van Cutsem E. Structural principles of parallel beta-barrels in proteins. Proc Natl Acad Sci USA. 1988;85:3338–3342. doi: 10.1073/pnas.85.10.3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.