Multidimensional photon correlation spectroscopy of cavity polaritons

Significance

We propose a spectroscopic technique that can track the time-dependent state of a dressed molecule in an optical cavity (polariton) by measuring coincidence of two emitted photons. The proposed technique offers an independent control of the spectral and temporal resolution; single-photon detection allows for low-intensity measurements, which do not disturb the state of the cavity field, and time-dependent atom/cavity coupling provides a control tool. Tracking the evolution of the polariton states with time-dependent atom/cavity coupling should be of interest in photochemistry and photobiology and could improve fundamental understanding of many physical processes in strongly coupled atom/radiation states. Possible applications include chemical sensors and quantum information processing.

Abstract

The strong coupling of atoms and molecules to radiation field modes in optical cavities creates dressed matter/field states known as polaritons with controllable dynamical and energy transfer properties. We propose a multidimensional optical spectroscopy technique for monitoring polariton dynamics. The response of a two-level atom to the time-dependent coupling to a single-cavity mode is monitored through time-and-frequency–resolved single-photon coincidence measurements of spontaneous emission. Polariton population and coherence dynamics and its variation with cavity photon number and controlled by gating parameters are predicted by solving the Jaynes–Cummings model.

Cavity quantum electrodynamics (QED) provides a powerful tool for studying quantum effects in matter (1–6). Due to strong coupling between electronic and nuclear degrees of freedom, molecular systems can undergo nonadiabatic dynamics, which is hard to detect. The nonadiabatic dynamics can be manipulated (7) when a molecule is coupled to a localized cavity mode. Earlier studies in atomic systems showed that the cavity photons can enhance cooperative signals, such as superradiance and subradiance (8, 9). The description of these phenomena is based on the joint photon–matter states known as polaritons (10, 11). Cavity polaritons have been applied to trapping and cooling of atoms (12) and prescribe a new recipe for cooling molecules (13, 14). Cavity effects can provide a tool to probe larger molecules (15, 16), where various many-body quantum effects play an important role. For instance, the polariton–polariton interaction strength can be directly probed in a high-quality microcavity (17). Strong coupling in cavity QED has been recently demonstrated for organic molecules (18–21) and photosynthetic light harvesting (22). Polaritons have been further investigated in chromophore aggregates (11) arising from electronic transitions (10) as well as from vibrational transitions (23), which in turn, allow the manipulation of chemical reaction rates and outcomes (24–27).

Cavity polariton dynamics can be investigated by nonlinear spectroscopy. IR and Raman spectroscopies have been recently used to show the enhancement of the spectra of vibrational polaritons in molecular aggregates (11, 28–31). More elaborate two-dimensional spectroscopic measurements have further provided experimental demonstration for multiexciton correlation effects (32). Coherent multidimensional spectroscopy can reveal correlations of matter dynamics during several time intervals controlled by sequences of short pulses to reveal material information (33, 34) by a coherent measurement of a signal optical field. Such correlation plots carry qualitatively higher levels of information than single-interval (1D) techniques. A recent theoretical study of vibrational polaritons using coherent 2D IR spectroscopy (35) has been reported.

In this paper, we propose to study polariton dynamics using a different class of incoherent multidimensional signals. Unlike coherent multidimensional techniques, which is based on carefully timed laser pulse sequences, incoherent techniques detect spontaneously emitted light, and the control knobs of such signals are based on single-photon gated detection. Time-and-frequency (TF)–gated $N$-photon measurement provides a $2N$-dimensional parameter ${\omega }_j{t}_j$ space. An adequate microscopic description where joint matter and field information could be retrieved by a proper description of the detection process is required for, e.g., single-photon spectroscopy of single molecules (36–38). These photon counting techniques performed on bulk ensembles or at the single-molecule level offer unique windows into molecular events and relaxation processes that are complementary to coherent multidimensional techniques (34). The proposed incoherent photon coincidence counting measurements (5, 39) can monitor the joint system–cavity mode state as well as the cavity mode statistics. The independent control of the TF photon gating parameters can capture detailed features of polariton dynamics. We consider a two-level system strongly coupled to the quantized cavity modes. The strong coupling is attributed to the enhanced density of radiation states inside the cavity governed by the Purcell effect (1), which results in the strong enhancement of the photon emission into the cavity modes. The joint atom plus photon states (polaritons) can be described by the Jaynes–Cummings (JC) model (2), which is a pillar of quantum optics. In addition, strong coupling requires large absorption oscillator strength, narrow exciton absorption line width, and small cavity losses into leaky modes. It is, therefore, expected that dissipation does not affect the ladder dynamics. Furthermore, for typical molecular polaritons, the dynamics occurs on a picosecond timescale, whereas the cavity linewidth is usually in the nanosecond range. The quantum nature of the field has been shown to result in revival of damped Rabi oscillations, which is missed by a classical field (40). We shall use a generalized JC model, where the system–cavity field coupling is time dependent (41–43). To achieve temporal modulation, cavity mirror must be manipulated on a similar timescale to the molecular dynamics that needs to be controlled. It is hard to achieve this by mechanical devices. However, terahertz scanning tunneling microscope (THz-STM) techniques may provide necessary modulation speed down to picosecond timescale (44).

Analytical solutions for the time evolution of the population inversion for the time-dependent JC model can be derived for specific time profiles of the system–cavity coupling (41, 42, 45). The gated number of photons spontaneously emitted into noncavity modes and photon coincidence signals for this analytically solvable time-dependent JC model are given by two-point and four-point correlation functions of the dipole operator, respectively. We shall use a compact time ordered superoperator formalism in these calculations (46–49). These correlation functions and the corresponding Green’s functions that describe dynamics in the dressed field–matter (polariton) space will be calculated. The proposed signals provide a unique observation window for the population and coherence polariton dynamics.

The spontaneously emitted photons will be detected by a TF–resolved photon gating obtained by consecutive spectral and temporal gates with bandwidths ${\mathrm{\Gamma }}_{\omega }$ and ${\mathrm{\Gamma }}_T$, respectively. Optimization of the temporal and spectral resolutions is required when the field–matter coupling variation is faster than the inverse magnitude of the change of the coupling. We compare this gating with a simpler commonly used “physical spectrum” (PS) (50), which only uses a spectral gate characterized by a single parameter ${\mathrm{\Gamma }}_{ps}$ that controls both spectral ${\mathrm{\Gamma }}_{ps}$ and temporal resolution $1/{\mathrm{\Gamma }}_{ps}$. We find that the TF gating can resolve a variety of dynamical features that are missed by the PS.

Evolution of Polaritons in Time-Modulated Cavities

The two-level molecular system can be described by the Pauli matrices, which satisfy ${\sigma }_i{\sigma }_j={\delta }_{ij}+i{ϵ}_{ijk}{\sigma }_k$, where $i,j,k=x,y,z$. We denote the eigenstates of ${\sigma }_z$ by $|\uparrow ⟩$ and $|\downarrow ⟩$ with eigenvalues $1$ and $-1$; the operators ${\sigma }_{\pm }=\frac{1}{2}({\sigma }_x\pm i{\sigma }_y)$ represent dipole raising $V^{†}={\mu }^{\ast }{\sigma }_{+}$ and lowering $V=\mu {\sigma }_{-}$ operators, where $\mu$ is the transition dipole. Using this notation, the time-dependent JC model Hamiltonian reads

$$H_{JC}=\omega A_{+}{A}_{-}+\frac{{\omega }_0}{2}{\sigma }_z+\lambda (t)(A_{+}{\sigma }_{-}+A_{-}{\sigma }_{+}),$$ [1]

where ${\omega }_0$ is the transition frequency, $\lambda (t)$ is the time-modulated system–cavity coupling, and $A_{+}$ ($A_{-}$) is a creation (annihilation) operator for the cavity mode. The first two terms represent the cavity field and the molecule, respectively, while the third term corresponds to the interaction between molecule and cavity field. The matter plus field dressed (polariton) state energies that form the JC ladder obtained by diagonalizing Eq. 1 $E_{n\pm }=\omega (n+1/2)\pm \sqrt{{({\omega }_0-\omega )}^2/4+{\lambda }^2(t)(n+1)}$ are shown in Fig. 1. We adopt the following coupling profile:

$$\lambda (t)={\lambda }_0\text{sech}[(t-T)/(2\tau )].$$ [2]

This represents pulsed modulation of duration $2\tau$ centered at time $T$ with magnitude ${\lambda }_0^2=\frac{{\omega }_0^2{|\mu |}^2}{2\omega {ϵ}_0\mathcal{V}\mathrm{\hslash }}$, where $\mathcal{V}$ is the cavity volume. The sech profile allows for exact analytical solution for the time evolution using special functions (SI Text). Our approach, however, is general and can treat an arbitrary time profile.

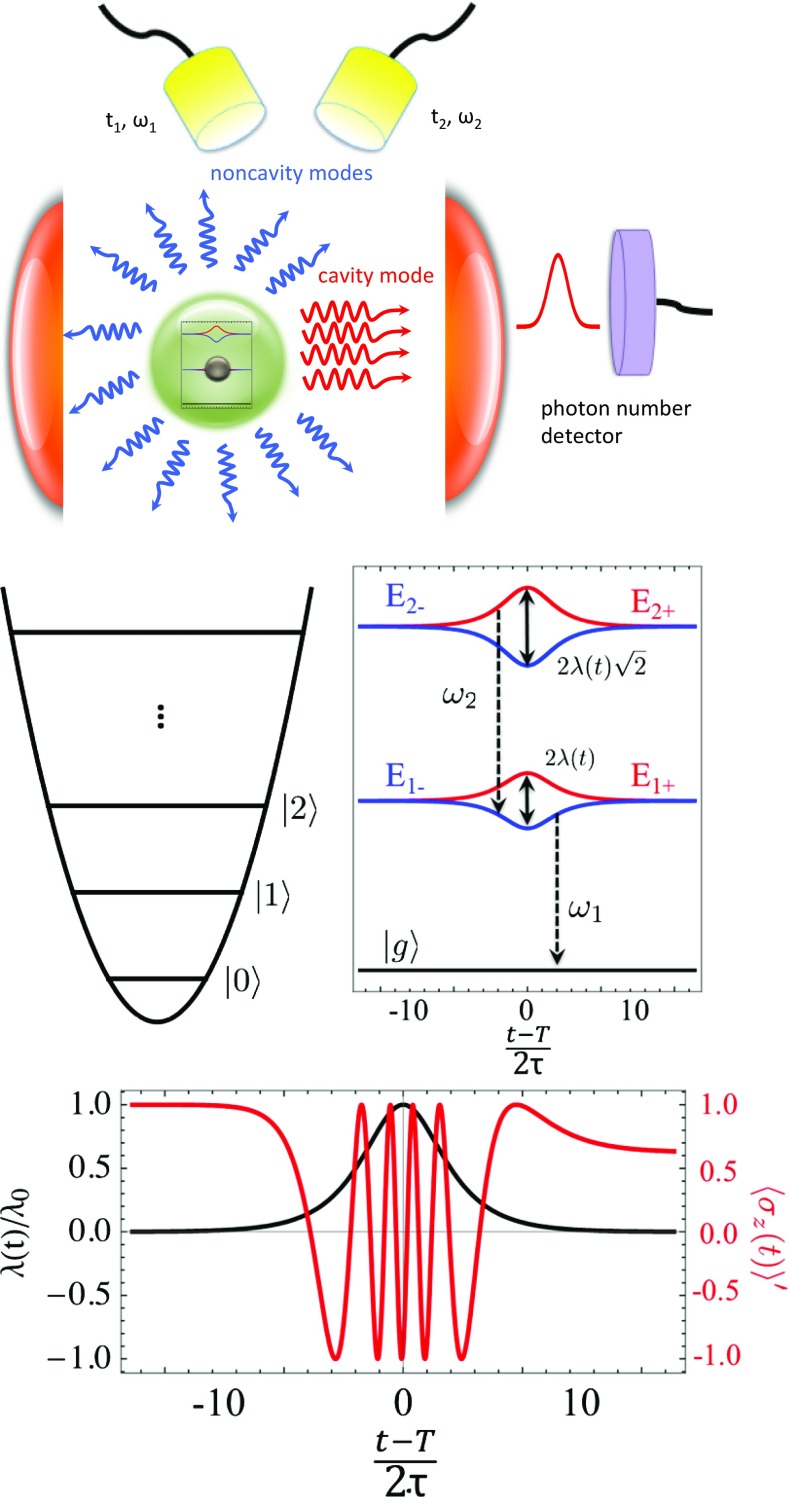
Fig. 1.

(Top) Atom in the cavity emitting photons into the longitudinal cavity mode as well as noncavity vertical modes. Two TF-resolved detectors outside of the cavity register noncavity modes photon coincidence events. One photon number-resolving detector on the main optical axis measures photon number of the cavity mode photons. (Middle Left) Fock states. (Middle Right) Time evolution of the dressed atom plus cavity (polariton) states of the JC subject to the coupling Eq. 2. Vertical black dashed lines represent transition between different ladder states captured by spectroscopic measurements. (Bottom) Time evolution of the atom–cavity mode coupling $\lambda (t)$ (black line) and population inversion ${⟨{\sigma }_z(t)⟩}^{\prime }$ Eq. 3 (red line) for an atom initially in the excited state with cavity mode being initially in the vacuum state.

In addition to the strong coupling to the single-longitudinal cavity mode, the atom is weakly coupled to the vacuum modes described by $H_{vac}=V{\sum }_{𝐤}{g}_{𝐤}{a}_{𝐤}^{†}+H.c.$, where $a_{𝐤}$ is a field operator for vacuum modes that is responsible for the spontaneous emission into noncavity modes. The spontaneous emission rate into the cavity mode (vertical lines in Fig. 1) at resonance $\omega ={\omega }_c={\omega }_0$ is ${\gamma }_{cav}=\frac{2Q{|\mu |}^2}{\mathrm{\hslash }{ϵ}_0\mathcal{V}}$ (3), where $Q={\omega }_0/2\kappa$ is the quality factor of a mode at frequency ${\omega }_c$ with cavity loss rate $\kappa$. The typical solid angle extended by the cavity mirrors is very small, and therefore, the atomic decay rate governed by $H_{vac}$ into noncavity modes is then comparable with the rate of atomic decay rate in free space ${\gamma }_0=\frac{{\omega }_0^3{|\mu |}^2}{3\mathrm{\hslash }{ϵ}_0\pi c^3}$. The Purcell factor $f=\frac{{\gamma }_{cav}}{{\gamma }_0}=\frac{3Q}{\mathcal{V}}\frac{2\pi c^3}{{\omega }_0^3}$ (1, 3) is much greater than one, and the cavity leads to a strong enhancement of the atom’s ability to emit photons into the cavity mode. Details are in SI Text. We use perturbation theory in $H_{vac}$ and trace over the vacuum field. We shall calculate various photon counting signals by placing the detectors off the cavity axis. These signals are governed by multipoint correlation functions of the dipole operators, and the corresponding Green’s functions are determined by an exact solution of the equation of motion governed by $H_{JC}$ alone.

Gated Photon Counting Signals

Atomic Inversion.

We first present the atomic inversion (population difference of the two-level system) ${⟨{\sigma }_z(t)⟩}^{\prime }=⟨{\psi }_0|U(t)F_0{U}^{†}(t)|{\psi }_0⟩$ given in Eq. S51. Assuming that, initially, the atom is in the excited state ($w_n=1$, $v_n=0$) and the cavity mode in the vacuum state $n=0$, the inversion

$${⟨{\sigma }_z(t)⟩}^{\prime }=\mathrm{\hspace{0.17em}1}-2{|{\mathcal{F}}_1(t)|}^2$$ [3]

undergoes oscillation between $\pm 1$ as seen in Fig. 1. $\mathcal{F}$ depends on the atom–field interaction time $\tau$. We note that, although initially, the cavity is empty (no photons), the atom will Rabi flip between the ground and excited states during the interaction time due to the fact that continuum of modes of the free space modes is replaced by a single cavity mode. This results in Rabi oscillations rather than dissipative spontaneous emission.

Gated Photon Counting Signals.

In the following, we denote a general Nth-order correlation measurement as photon counting. Gated photon number and gated photon coincidence correspond to $g^{(1)}$ and $g^{(2)}$ measurements, respectively, where each photon has its own detector. We thus calculated the gated photon number and photon coincidence signals using the formalism of ref. 48. TF-resolved photon number is detected by placing a sequence of temporal and spectral filters in front of the bucket photon detector, whereas the photon coincidence is detected by simultaneous monitoring of a pair of the gated photons, which is a single-photon version of the intensity–intensity correlation measurement. Assuming Lorentzian gating (Eq. S32), we obtain (for the TF-resolved photon number signal)

$$n(t,\omega )={\int }_0^{\mathrm{\infty }}d{t}_1^{\prime }{\int }_0^{\mathrm{\infty }}d{t}_1^{″}D(\omega ;t_1^{\prime },t_1^{″}){⟨V^{†}(t-t_1^{″})V(t-t_1^{\prime })⟩}^{\prime }.$$ [4]

The coincidence counting signal is similarly given by

$$g^{(2)}(t_1,{\omega }_1;t_2,{\omega }_2)={\int }_0^{\mathrm{\infty }}d{t}_1^{\prime }{\int }_0^{\mathrm{\infty }}d{t}_1^{″}{\int }_0^{\mathrm{\infty }}d{t}_2^{\prime }{\int }_0^{\mathrm{\infty }}d{t}_2^{″}\times D({\omega }_1;t_1^{\prime },t_1^{″})D({\omega }_2;t_2^{\prime },t_2^{″}){⟨V^{†}(t-t_1^{″})\times V^{†}(t-t_2^{″})V(t-t_2^{\prime })V(t-t_1^{\prime })⟩}^{\prime }.$$ [5]

For the TF gated signals $D_{TF}(\omega ,t\prime ,t^{″})=\theta (t^{″}-t\prime )F_{\mathrm{\Gamma }+}^{\ast }(t^{″},\omega )F_{\mathrm{\Gamma }-}(t\prime ,\omega )$, where exponential gate $F_{\mathrm{\Gamma }}(t\prime ,\omega )=e^{[i(\omega -{\omega }_0)-\mathrm{\Gamma }]t\prime }$. The gating bandwidth in $D_{TF}$ is given by a combination of temporal and spectral gates ${\mathrm{\Gamma }}_{\pm }={\mathrm{\Gamma }}_T\pm {\mathrm{\Gamma }}_{\omega }$. Details of the derivation of the signals via matter correlation functions defined by Eqs. S45 and S48 are given in SI Text.

Results and Discussion

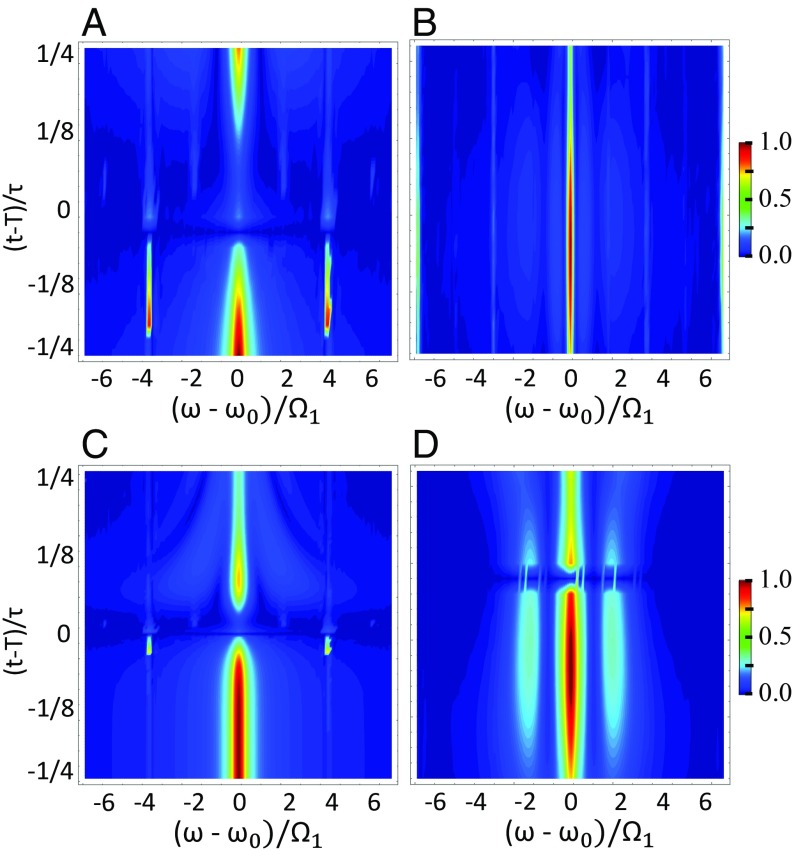
Using Eqs. 4 and 5, we have simulated the photon number $n$ and the photon coincidence rate $g^{(2)}$; the time-dependent coupling profile given by Eq. 2 is shown in Fig. 1 for the parameters given in Materials and Methods. Fig. 2 depicts the time–frequency dependence of the TF gated photon number. Consider first a fast variation $\tau$, such that $\mathrm{\Delta }t\mathrm{\Delta }\omega \simeq \tau 2{\mathrm{\Omega }}_1=1$, where $2{\mathrm{\Omega }}_1$ is a spectral interval between neighboring lines of the first-order JC ladder (e.g., at $\omega ={\omega }_0$ and ${\omega }_0\pm 2{\mathrm{\Omega }}_1$, where ${\mathrm{\Omega }}_n=\pi {\alpha }_n/4\tau$). The photon number signal shown in Fig. 2A now shows a dominant peak at $\omega ={\omega }_0$ and two strong side peaks at $\omega ={\omega }_0\pm 4{\mathrm{\Omega }}_1$, which evolve for the entire range of $t$. We also see weak peaks at $\omega ={\omega }_0\pm 2{\mathrm{\Omega }}_1$. For a slow modulation $\mathrm{\Delta }t\mathrm{\Delta }\omega =3.7$ due to the extra time gate, the TF signal yields no time resolution and very weak side peaks at $\omega ={\omega }_0\pm 2{\mathrm{\Omega }}_1$ as shown in Fig. 2B. The side peaks signify the coherence origin of the photon coming from the superposition of the dressed atom–cavity states, which can only be observed during the time modulation of the coupling.

Fig. 2.

(A and B) A 2D depiction of TF gated photon number $n_{TF}(t,\omega )$ [S60] using the gating parameters ${\mathrm{\Gamma }}_{\omega }=2{\lambda }_0$ and ${\mathrm{\Gamma }}_T=2.5{\lambda }_0$ for the fast modulation with ${\tau }^{-1}=2.2{\lambda }_0$ (A) and ${\mathrm{\Gamma }}_{\omega }=0.8{\lambda }_0$ and ${\mathrm{\Gamma }}_T=0.95{\lambda }_0$ along with slow modulation ${\tau }^{-1}=0.6{\lambda }_0$ (B). (C and D) Same coupling duration as in A and B but for PS gated photon number $n_{PS}(t,\omega )$ [S59] for gated bandwidths ${\mathrm{\Gamma }}_{ps}=2{\lambda }_0$ (C) and ${\mathrm{\Gamma }}_{ps}=0.8{\lambda }_0$ (D).

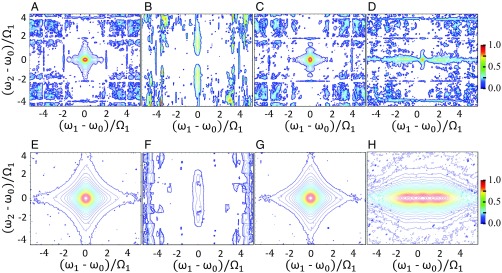
The photon coincidence signals are shown in Fig. 3 A–D. For rapid coupling variation corresponding to Fig. 2A, the coincidence counting depicted in Fig. 3A contains side peaks at ${\omega }_{\mathrm{1,2}}={\omega }_0\pm 2{\mathrm{\Omega }}_1$, ${\omega }_0\pm 4{\mathrm{\Omega }}_1$. These are well-resolved and form a grid similar to that reported by del Valle and coworkers (51–53). For gating times $t_1=T$, $t_2=T-20\tau$, the signal shows high spectral resolution with well-pronounced peaks at ${\omega }_2={\omega }_0\pm 2{\mathrm{\Omega }}_1$ and a single peak for ${\omega }_1={\omega }_0$. In addition, it contains peaks for ${\omega }_1={\omega }_0\pm 2{\mathrm{\Omega }}_1$ and ${\omega }_0\pm 4{\mathrm{\Omega }}_1$ as depicted in Fig. 3B. At $t_1=T+20\tau$, $t_2=T-20\tau$, Fig. 3C is similar to Fig. 3A. Finally, for $t_1=T+20\tau$, $t_2=T$, Fig. 3D shows a full grid of well-pronounced resonances with three prominent peaks for ${\omega }_1={\omega }_0,{\omega }_0\pm 2{\mathrm{\Omega }}_1$ and ${\omega }_2={\omega }_0$ and a set of weaker peaks for ${\omega }_2={\omega }_0\pm 2{\mathrm{\Omega }}_1$ and ${\omega }_0\pm 4{\mathrm{\Omega }}_1$.

Fig. 3.

(A–D) TF gated photon coincidence counting $g_{TF}^{(2)}(t_1,{\omega }_1;t_2,{\omega }_2)$ [S62] vs. ${\omega }_1$ and ${\omega }_2$ using gating parameters ${\mathrm{\Gamma }}_{\omega 1}={\mathrm{\Gamma }}_{\omega 2}=2{\lambda }_0$, ${\mathrm{\Gamma }}_{T1}={\mathrm{\Gamma }}_{T2}=2.5{\lambda }_0$ for $t_1=T-20\tau$, $t_2=T+20\tau$ (A); $t_1=T$, $t_2=T-20\tau$ (B); $t_1=T+20\tau$, $t_2=T-20\tau$ (C); and $t_1=T+20\tau$, $t_2=T$ (D). (E–H) Same but for PS gating $g_{PS}^{(2)}(t_1,{\omega }_1;t_2,{\omega }_2)$ [S61] using gated bandwidth ${\mathrm{\Gamma }}_{ps1}={\mathrm{\Gamma }}_{ps2}=2{\lambda }_0$ cm⁻¹.

We next compare the commonly used TF gated results of Figs. 2 A and B and 3 A–D with the simpler PS gating (50, 51), which uses the gating function $D_{PS}(\omega ;t\prime ,t^{″})=F_{{\mathrm{\Gamma }}_{ps}}^{\ast }(t^{″},\omega )F_{{\mathrm{\Gamma }}_{ps}}(t\prime ,\omega )$. The PS photon number signal (4) shown in Fig. 2C has a single dominant peak at $\omega ={\omega }_0$ and two very weak peaks at $\omega ={\omega }_0\pm 4{\mathrm{\Omega }}_1$ visible only at $t\simeq T$. This is due to the limited resolution allowed by the model ($\mathrm{\Delta }t\mathrm{\Delta }\omega =2$). Higher-order resonances at $\omega ={\omega }_0\pm 2{\mathrm{\Omega }}_1$ and $\omega ={\omega }_0\pm 6{\mathrm{\Omega }}_1$ are not resolved by this gate. For the slow process depicted in Fig. 2D, the stationary PS gate might have higher spectral resolution, allowing us to visualize the strong side peaks at $\omega ={\omega }_0\pm 2{\mathrm{\Omega }}_1$. Therefore, for slow cavity modulation, the temporal gate is not necessary, and the PS is adequate. However, rapid modulation requires separately controlled time gate when $\mathrm{\Delta }t\mathrm{\Delta }\omega \le 1$, where PS fails and TF is required. Note that the key parameter is not an absolute value of the modulation depth ${\lambda }_0$ and duration $\tau$ but is their product for a given cavity photon number via $\tau {\mathrm{\Omega }}_1\sim \tau {\lambda }_0\sqrt{n+1}$, which governs the temporal and spectral resolution via the product $\mathrm{\Delta }t\mathrm{\Delta }\omega$.

Turning to coincidence counting, we note that the PS Eq. 5 has a low temporal and spectral resolution and misses some spectral features. For instance, the JC ladder of various peaks cannot be observed in Fig. 3 E and G for $n=1$, $t_1=T-20\tau$, $t_2=T+20\tau$ and $t_1=T+20\tau$, $t_2=T-20\tau$, respectively, other than the zero-order peak at ${\omega }_1={\omega }_2={\omega }_0$. For $t_1=T$, $t_2=T-20\tau$, the PS signal shows two weak peaks at ${\omega }_2={\omega }_0\pm 2{\mathrm{\Omega }}_1$ and a single peak for ${\omega }_1={\omega }_0$ as depicted in Fig. 3F, with much less contrast compared with the case of TF. Finally, for $t_1=T+20\tau$, $t_2=T$, the PS signal has three overlapping peaks for ${\omega }_1={\omega }_0,{\omega }_0\pm 2{\mathrm{\Omega }}_1$ but a single peak for ${\omega }_2={\omega }_0$ as depicted in Fig. 3H vs. well-resolved peaks shown in Fig. 3D for TF. Therefore, the TF coincidence counting signal shows how the response to the time modulation of the coupling changes the configuration of the JC states participating in the photon emission for a given cavity photon number, which is missed by the PS. The resonances that manifest as cross-peaks in Fig. 3 A, C, and D mark the role of coherence between different dressed atom–cavity states that are governed by the coupling temporal profile, since the pair of photons can be generated from the superposition of two JC ladder states.

Note on the Joint Temporal/Spectral Resolution

We identify two main differences between the PS and TF signals. In PS, both frequency and time resolutions are determined by a single parameter ${\mathrm{\Gamma }}_{ps}$. The two time integrations in Eq. S59 are independent, so that each field operator is gated separately. In contrast, the TF signal in Eq. S60 depends on two gating parameters ${\mathrm{\Gamma }}_{\pm }$. In addition, there is an extra $\theta (t_1^{″}-t_1^{\prime })$ factor, which couples the two time integrations in Eq. S60. To examine how these parameters determine the temporal and spectral resolutions of the signal, we performed an asymptotic expansion of Eq. 7, such that, in zeroth order, one can approximate it at $t_0=0$ as Eq. S63. This contains terms of the form (details are in SI Text) $e^{(i{\omega }_{n\pm }-1/(2\tau )-{\mathrm{\Gamma }}_{ps}/2)(t-T)}/({\omega }_{n\pm }-i{\mathrm{\Gamma }}_{ps}/2)$, where ${\omega }_{n\pm }=\omega -{\omega }_0\pm 2{\mathrm{\Omega }}_n$. This term yields two side peaks due to Rabi splitting. Clearly, the spectral resolution is given by $\mathrm{\Delta }{\omega }_{PS}={\mathrm{\Gamma }}_{ps}/2$, whereas the temporal resolution is given by $\mathrm{\Delta }{t}_{PS}=2/{\mathrm{\Gamma }}_{ps}$. The product of the two gives the Fourier limit $\mathrm{\Delta }{t}_{PS}\cdot \mathrm{\Delta }{\omega }_{PS}=1$. The corresponding product of uncertainties for the TF gated signal reads $e^{(i{\omega }_{n\pm }-1/(2\tau )-{\mathrm{\Gamma }}_T/2)(t-T)}/({\omega }_{n\pm }-i{\mathrm{\Gamma }}_{+}/2)$. The spectral resolution is now given by ${\mathrm{\Gamma }}_{+}/2$, the combined spectral and temporal gate bandwidth. The temporal resolution is ${({\mathrm{\Gamma }}_{+}/2+{\mathrm{\Gamma }}_{-}/2)}^{-1}=2/{\mathrm{\Gamma }}_T$, which is a temporal gate alone. Therefore, $\mathrm{\Delta }{t}_{TF}\cdot \mathrm{\Delta }{\omega }_{PS}=1+{\mathrm{\Gamma }}_{\omega }/{\mathrm{\Gamma }}_T$. An important point is related to the fact that we achieve the sum ${\mathrm{\Gamma }}_{+}+{\mathrm{\Gamma }}_{-}$ for the temporal resolution. This is due to the nested time integrations and the $\theta (t_1^{″}-t_1^{\prime })$ factor in Eq. S33. To illustrate the role of the time gate, we can consider a high spectral resolution, so that ${\mathrm{\Gamma }}_{\omega }+{\mathrm{\Gamma }}_T={\mathrm{\Gamma }}_{ps}<2{\mathrm{\Omega }}_n$. We also take $2/{\mathrm{\Gamma }}_T<\tau <2/{\mathrm{\Gamma }}_{ps}$, such that the PS temporal resolution is low, whereas the TF gated signal gives high temporal resolution. Ultrafast temporal resolution of single photons can be readily achieved in strongly coupled quantum dot–cavity systems (54) or up-conversion schemes (55). The pure time-resolved photon counting can be also used to probe temporal evolution of the cavity polaritons. However, similar to coherent spectroscopy, where time-resolved measurement alone can only provide partial information about the system vs. multidimensional four wave mixing spectroscopy that can distinguish signal generated from the molecular populations and from the molecular coherences (due to intermolecular coupling), simultaneous TF gating allows us to distinguish signals originated from polariton coherences and populations as follows from Fig. 3.

In summary, we have demonstrated how multidimensional photon counting can be used to reveal polariton dynamics in a cavity. The TF gated photon number and photon coincidence detection can capture subtle time-evolving features, such as dressed JC ladder polariton states and their correlations via cross-peaks in the 2D photon coincidence spectra. Note that, in the strong dissipation limit, the oscillations shown in Fig. 1 and contributing to the polariton dynamics would be significantly damped. This means that, for systems with the dynamics of the timescale similar to the cavity damping rate, one has to take into account the cavity leakage when evaluating the signals. Recent experiments in light harvesting molecules placed in a microcavity (22) observe large amounts of scattering into the microcavity system; however, the observed damping is not strong enough to destroy the strong coupling. The technique described in this paper can be useful for laser stabilization, where the cavity photon distribution and gain medium dynamics are monitored simultaneously. In this scenario, cavity photon statistics acts as an input into the polariton configuration captured by the photon counting signals, which consequently monitors the stability of the cavity radiation. The time-dependent coupling offers a versatile coherent control tool. Similarly to the pulse shaping technique used in ordinary spectroscopy, one can optimize the coupling temporal profile in a generic algorithm setup to optimize the control. To implement this control scheme, one has to match the coupling duration and profile to the timescale of the nuclear motion. In addition to the suppression of the dephasing and changing of the dynamical rates that are observed in the systems with the stationary cavity coupling, time-dependent coupling provides a unique control mechanism for tracking the polariton–polariton and other many-body correlation effects via optimizing the corresponding coherences visualized as the cross-peaks in 2D spectra in photon coincidence signals.

Materials and Methods

The Hamiltonian [1] can be recast as $H=H_0+H_i$, where $H_0=\omega (\mathrm{\Delta })$ and $\mathrm{\Delta }=n+\frac{1+{\sigma }_z}{2}$ is the field energy function given by Eq. S2, while $H_i=\delta (\mathrm{\Delta }){\sigma }_z+\lambda (t)(A_{+}{\sigma }_{-}+A_{-}{\sigma }_{+})$, and the $\delta (\mathrm{\Delta })$ is given by Eq. S3. For the one-photon JC ladder, $\omega (\mathrm{\Delta })=(\mathrm{\Delta }-1/2)\omega$ and $\delta (\mathrm{\Delta })=\delta /2$, where $\delta ={\omega }_0-\omega$. A more general $m$-photon JC ladder, which can be used for describing multiphoton processes, is presented in SI Text. The subspace in which $n$, the eigenvalue of $\mathrm{\Delta }$, satisfies for $n\ne 0$ the special unitary group of the second degree [SU(2)] symmetry of $\mathrm{\Delta }$. In many molecular polariton applications that involve, for example, nonadiabatic dynamics, the inclusion of the counterrotating terms is required, which results in band-diagonal structure of the Hamiltonian. While purely analytic, a solution without the rotating wave approximation is possible only in certain cases (56), and the problem can be treated in Fock space to allow for a numerically exact solution (57). The time evolution operator may be recast as $U(t)=e^{-i\omega (\mathrm{\Delta })t}{U}_i(t)$, where $U_i(t)$ is the evolution operator corresponding to $H_i$. Using the SU(2) algebra and the Wei–Norman formalism (42, 58, 59), we can recast the evolution operator in the form $U_i(t)=e^{h(t)F_0}{e}^{g(t)F_{+}}{e}^{f(t)F_{-}}$, where $F_{\pm }=\pm A_{\mp }{\sigma }_{\pm }/\sqrt{\mathrm{\Delta }}$, $F_0={\sigma }_z$, and $f(t)$, $g(t)$, and $h(t)$ are generally complex functions, such that $x^{\ast }(t)=-x(t)$, $x=f,g,h$. Introducing $\mathcal{G}(t)=g(t)e^{h(t)}$, $\mathcal{F}(t)=f(t)e^{-h(t)}$, and $\mathcal{H}(t)=e^{-h(t)}$ using unitary condition, we obtain $\mathcal{G}(t)={\mathcal{F}}^{\ast }(t)$. For simplicity in the following, we assume that the atom is driven on resonance, such that $\delta =0$. The functions $X=\mathcal{F},\mathcal{H}$ satisfy the differential equation:

$$\ddot{X}-\frac{\dot{\lambda }}{\lambda }\dot{X}+4(n+1){\lambda }^{2}X=0.$$ [6]

The initial conditions for $\mathcal{F},\mathcal{H}$ are $\mathcal{H}(t_0)=1$, $\dot{\mathcal{H}}(t_0)=0$, $\mathcal{F}(t_0)=0$, and $\dot{\mathcal{F}}(t_0)=i\sqrt{n+1}\lambda (t_0)=-i\alpha /(2\tau )$, where $\alpha =2{\lambda }_0\tau \sqrt{n+1}$. Normalization implies ${|\mathcal{H}(t)|}^2+{|\mathcal{F}(t)|}^2=1$. Eq. 6 can be solved analytically for the sech function coupling $\lambda (t)$. Changing the variable to $z(t)=e^{(t-T)/\tau }/[1+e^{(t-T)/\tau }]$, we obtain a hypergeometric equation with $\beta =-\alpha =1/2$. The solution of Eq. 6 subject to initial conditions above is given by a simplified hypergeometric function

$$\mathcal{H}(z)=\cosh \left[2\alpha \log \left(\frac{\sqrt{z}+\sqrt{z-1}}{\sqrt{z_0}+\sqrt{z_0-1}}\right)\right],\mathcal{F}(z)=\sinh \left[2\alpha \log \left(\frac{\sqrt{z}+\sqrt{z-1}}{\sqrt{z_0}+\sqrt{z_0-1}}\right)\right],$$ [7]

where $z_0\equiv z(t_0)$.

The matter correlation functions in Eqs. 4 and 5 are traced over the noncavity modes. Assuming initial wave function $|{\psi }_0⟩={\sum }_n[w_n|n,\uparrow ⟩+v_n|n,\downarrow ⟩]$, where the coefficients $w_n$ ($v_n$) represent the probability amplitude of the atom to be in the excited (ground) state, the field is in a Fock state with $n$ quanta. These amplitudes satisfy the normalization ${\sum }_n({|w_n|}^2+{|v_n|}^2)=1$. The atomic inversion ${⟨{\sigma }_z(t)⟩}^{\prime }$ has been calculated previously (41) and is given by Eq. S51.

To get the photon counting signal, we have calculated two-point [4] and four-point [5] correlation functions:

$${⟨V^{†}(t_1)V(t_2)⟩}^{\prime }={|\mu |}^2{e}^{-i{\omega }_0(t_1-t_2)}\sum _n{G}_{in}^{\ast }(t_1)G_{pn}(t_1,t_2)G_{in}(t_2),$$ [8]

$${⟨V^{†}(t_1)V^{†}(t_2)V(t_3)V(t_4)⟩}^{\prime }={|\mu |}^4{e}^{-i{\omega }_0(t_1+t_2-t_3-t_4)}\sum _n{G}_{in}^{\ast }(t_1)G_{cn}^{\ast }(t_2,t_1)\times G_{pn}(t_2,t_3)G_{cn}(t_3,t_4)G_{in}(t_4),$$ [9]

where the “initial state” Green’s function $G_i$, “coherence” $G_c$, and “population” $G_p$ Green’s functions are defined, respectively, as

$$\begin{array}{c}{G}_{in}(t)=w{}_n\mathcal{H}_{n+1}(t)-v{}_{n+1}\mathcal{F}_{n+1}^{\ast }(t),\\ G_{cn}(t_i,t_j)={\mathcal{H}}_{n+1}(t_i){\mathcal{F}}_{n+1}^{\ast }(t_j)-{\mathcal{F}}_{n+1}^{\ast }(t_i){\mathcal{H}}_{n+1}(t_j),\\ G_{pn}(t_i,t_j)={\mathcal{H}}_{n+1}^{\ast }(t_i){\mathcal{H}}_{n+1}(t_j)+{\mathcal{F}}_{n+1}(t_i){\mathcal{F}}_{n+1}^{\ast }(t_j).\end{array}$$ [10]

Making use of the closed form expressions [7], we have made use of Eqs. 8–10 to calculate the gated emission [4] and the coincidence counting [5]. Note that Eqs. 8–10 reduce to the simple Rabi oscillations $\cos (\mathrm{\Omega }t)$ in the $\tau \to 0$ limit given by Eqs. S57 and S58, respectively. Additional details are summarized in SI Text.

The simulations shown in Figs. 1–3 use typical parameters related to vibrational spectroscopy: vibrational frequency ${\omega }_0=12600$ cm⁻¹, coupling modulation ${\lambda }_0=100$ cm⁻¹, and centered at $T=111.5$ ps. The coupling timescale in Figs. 1 and 3 is $\tau =150$ fs.