Shape-directed dynamics of active colloids powered by induced-charge electrophoresis

Significance

Despite recent advances in the ability to “program” the self-assembly of colloidal components, the resulting structures are often static and therefore incapable of performing dynamic functions such as the ability to actuate, heal, replicate, and compute. The realization of colloidal machines that organize in space and time to perform such functions requires new strategies for encoding the dynamic behaviors of colloidal components. Focusing on active colloids powered by induced-charge electrophoresis, we use theory and simulation to show how the shape of a colloidal particle can be rationally tailored to specify complex motions powered by simple energy inputs.

Abstract

The symmetry and shape of colloidal particles can direct complex particle motions through fluid environments powered by simple energy inputs. The ability to rationally design or “program” the dynamics of such active colloids is an important step toward the realization of colloidal machines, in which components assemble spontaneously in space and time to perform dynamic (dissipative) functions such as actuation and transport. Here, we systematically investigate the dynamics of polarizable particles of different shapes moving in an oscillating electric field via induced-charge electrophoresis (ICEP). We consider particles from each point group in three dimensions (3D) and identify the different rotational and translational motions allowed by symmetry. We describe how the 3D shape of rigid particles can be tailored to achieve desired dynamics including oscillatory motions, helical trajectories, and complex periodic orbits. The methodology we develop is generally applicable to the design of shape-directed particle motions powered by other energy inputs.

The creation of colloidal machines (1)—that is, dynamic assemblies of colloidal components that perform useful functions—requires advances in our ability to rationally engineer the dynamics of active colloids (2, 3) operating outside of thermodynamic equilibrium. Owing to their small size (nanometers to micrometers), such machines must assemble spontaneously and operate autonomously in response to simple energy inputs due to chemical fuels or external fields. Achieving nontrivial dynamical behaviors and ultimately function demands the use of complex components, into which the desired behaviors can be effectively encoded. The challenge is conceptually similar to that of programmable self-assembly (4), whereby assembly information encoded in the building blocks directs their organization into a specific structure. For equilibrium assemblies, this information takes the form of colloidal interactions, which can be designed by controlling particle shape (5, 6) and surface chemistry (7–11). Extending this approach to design colloidal machines will require control over particle organization in time as well as space—that is, over dynamics as well as structure. In this context, it is instructive to consider first the dynamics of a single particle and how it might be programed to perform increasingly complex tasks [e.g., the weaving of microscopic braids (12)]. Understanding the complex motions of individual units is a critical prerequisite to the design of dynamic assemblies of active particles.

The motion of colloidal particles relative to their fluid surroundings can be driven by a variety of different physicochemical mechanisms. Self-phoretic particles (13) induce local gradients (e.g., in the electric potential) that propel particle motions through interfacial “phoretic” effects (e.g., electrophoresis) (14). By engineering the shape and symmetry of such particles, different dynamical behaviors have been realized, including linear (15–17), rotational (18, 19), and circular (20) motions. The variety of possible dynamics for self-phoretic particles in isotropic media is significantly limited by the translational and rotational invariance of particle motions (only helical trajectories have yet to be reported). By contrast, rigid particles within uniform shear flows move relative to the fluid at velocities that depend on their orientation, which can lead to complex—even chaotic—rotational and translational motions (21, 22). Similarly, asymmetric polarizable particles within uniform electric fields are known to swim through conductive fluids by means of induced-charge electrophoresis (ICEP) (23). Such motions are well understood (24) and depend on the symmetry of the particle and its orientation in the applied field (25, 26). Notably, metallodielectric Janus particles ($C_{\mathrm{\infty }v}$ symmetry) translate away from their metallic hemispheres and perpendicular to the applied field (27); Janus doublets ($C_{2h}$) (28) or active colloidal clusters ($C_{nh}$) (29, 30) rotate steadily about the axis of the field. These previous experimental realizations only hint at the diversity of possible particle dynamics accessible via ICEP in three dimensions.

Here, we systematically investigate the ICEP dynamics of particles of different symmetries and discuss how particle shape can be used to encode a variety of complex dynamical behaviors. We consider particles from each point group in 3D (31) and identify the rotational and translational motions allowed by symmetry. For each qualitatively distinct motion, we create specific realizations of the dynamics, using rigid polarizable particles of a particular shape. The dynamics of such particles are computed numerically using a boundary integral formulation of the electrostatic and hydrodynamic problems governing ICEP motion. In addition to linear, rotational, and circular motions reported previously, our analysis suggests that particles of appropriate shapes are capable of oscillatory motions, helical trajectories, and complex periodic orbits. We show how the complexity of the dynamics grows as the symmetry of the particle is reduced. We discuss how complex particle trajectories can be rationally engineered into asymmetric particles through a careful combination of simpler shapes and their accompanying motions. In particular, we demonstrate how ICEP particles can be designed to achieve effective “foraging” motions within liquid environments for applications in chemical sensing or remediation (32, 33). While the present focus is ICEP, our approach is readily extended to other shape-directed particle motions powered by self-phoresis, hydrodynamic shear, and ultrasonic actuation (34–36). Overall, this work represents one step toward a broader goal of programing the organization of active particles in space and time to create colloidal machines with bio-inspired function.

Results and Discussion

ICEP Dynamics.

We consider the motion of an ideally polarizable particle immersed in an unbounded electrolyte and subject to an oscillating electric field, ${\mathrm{𝑬}}^{\mathrm{\infty }}(t)=E^{\mathrm{\infty }}\cos (\omega t){\mathrm{𝒆}}_z$, with magnitude $E^{\mathrm{\infty }}$ and frequency $\omega$ (Fig. 1). For sufficiently small frequencies and field strengths, the translational and rotational velocity of the particle can be expressed as

$$\mathrm{𝑼}=\frac{\epsilon a}{\eta }𝕮:{\mathrm{𝑬}}^{\mathrm{\infty }}{\mathrm{𝑬}}^{\mathrm{\infty }},$$ [1]

$$𝛀=\frac{\epsilon }{\eta }𝕯:{\mathrm{𝑬}}^{\mathrm{\infty }}{\mathrm{𝑬}}^{\mathrm{\infty }},$$ [2]

where $\epsilon$ and $\eta$ are, respectively, the permittivity and the viscosity of the electrolyte, $a$ is the size of the particle, and $𝕮$ and $𝕯$ are dimensionless tensors (25). Importantly, these tensors share the symmetry of the particle and are uniquely specified by its shape and orientation. Below, we explore the space of possible particle shapes to enumerate the different types of particle trajectories implicit in these dynamics.

Fig. 1.

(A) A rigid, polarizable particle of complex shape is immersed in an electrolyte and subject to an oscillating electric field, $\mathrm{𝑬}(t)$. The force on the field-induced double layer results in steady streaming flows and the concomitant motion of the particle. The dynamical trajectory of the particle (A, Right) can be “programed” by engineering its symmetry and shape. Here, the $x\prime$ (red), $y\prime$ (green), and $z\prime$ (blue) axes carve out similarly colored ribbons to help visualize particle motion. (B) Particle shapes of different symmetries organized into their ICEP rotation classes. Particle colors are mapped to denote the radial distance from the surface to the particle center.

The frequency of the ac field is assumed to be slower than the rate of ion accumulation at the particle–electrolyte interface—that is, $\omega \ll \kappa /\epsilon$, where $\kappa$ is the conductivity of the electrolyte. At the same time, we assume that the frequency is fast enough that oscillatory particle displacements due to electrophoresis are small compared with the particle size—that is, $\epsilon \zeta E^{\mathrm{\infty }}/\omega \eta \ll a$, where $\zeta \sim k_{B}T/e$ is the particle zeta potential, $k_B$ is the Boltzmann constant, $T$ is the temperature, and $e$ is the elementary charge (27, 28). Under these conditions, the oscillating field results in steady particle motions independent of the applied frequency; the results below describe these steady (time-averaged) motions. The validity of the model also requires that the surface potential induced by the field be smaller than the thermal potential—that is, $E^{\mathrm{\infty }}<k_{B}T/ea$. The use of large fields can lead to chaotic flows that disrupt the double-layer structure and greatly reduce the particle velocity (37). In practice, however, this simple model accurately captures the physical features of ICEP motions at intermediate fields in dilute electrolytes (38).

To describe the rigid-body motion of the particle, we introduce two coordinate systems: a stationary system and a moving system, which is fixed to the particle and participates in its motion (Fig. 1). A vector $\text{𝐯}\prime$ expressed in the moving system is related to the same vector v in the stationary system as $v_i^{\prime }=R_{ij}{v}_j$, where R is an orthogonal rotation matrix that depends on the orientation of the particle (e.g., on the Euler angles $\varphi$, $\theta$, $\psi$; Fig. 1A). Similarly, the components of the shape tensors, $𝕮$ and $𝕯$, in the stationary system are related to those in the moving system as

$${ℭ}_{ijk}=R_{pi}{R}_{qj}{R}_{rk}{ℭ}_{pqr}^{\prime },$$ [3]

$${𝔇}_{ijk}=R_{pi}{R}_{qj}{R}_{rk}{𝔇}_{pqr}^{\prime }.$$ [4]

The components ${ℭ}_{pqr}^{\prime }$ and ${𝔇}_{pqr}^{\prime }$ are independent of particle orientation and depend only on particle shape. Knowledge of these constants allows for computation of the particle trajectory in accordance with Eqs. 1 and 2 and the kinematics of rigid-body motion (Materials and Methods). In general, there are 18 quantities associated with each shape tensor (27 components less 9 relations of the form ${ℭ}_{ijk}={ℭ}_{ikj}$ due to the fact that $E_j^{\mathrm{\infty }}{E}_k^{\mathrm{\infty }}=E_k^{\mathrm{\infty }}{E}_j^{\mathrm{\infty }}$). As previously observed (25), particle symmetries can be used to further simplify these tensors and thereby constrain the types of accessible particle motions.

Particle Symmetry and Shape.

The symmetry of a particle is characterized by the set of operations such as reflections, rotations, and inversions that leave the particle unchanged; each such operation can be specified by an orthogonal matrix Q. Invariance of the particle shape with respect to the operation Q implies the following relationships among the components of the shape tensors:

$${ℭ}_{ijk}^{\prime }=Q_{ip}{Q}_{jq}{Q}_{kr}{ℭ}_{pqr}^{\prime },$$ [5]

$${𝔇}_{ijk}^{\prime }=|\text{𝑸}|Q_{ip}{Q}_{jq}{Q}_{kr}{𝔇}_{pqr}^{\prime }.$$ [6]

These symmetry relations can be used to reduce the number of independent quantities needed to specify the shape tensors. As a specific example, consider a particle which is invariant under reflection about the $z$ axis:

$$\text{𝑸}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right].$$ [7]

Eq. 5 implies that ${ℭ}_{ijk}^{\prime }=0$ for components with an odd number of indexes equal to three (e.g., ${ℭ}_{113}^{\prime }$, ${ℭ}_{333}^{\prime }$, etc.); similarly, Eq. 6 implies ${𝔇}_{ijk}^{\prime }=0$ for components with an even number of indexes equal to three (e.g., ${𝔇}_{111}^{\prime }$, ${𝔇}_{133}^{\prime }$, etc.). In this way, the number of independent quantities needed to specify the shape tensors is reduced from 36 to 18; additional symmetries afford further simplifications.

We consider particles from each of the possible point groups in three dimensions, visualized in Fig. 1B and represented by their Schoenflies notation (31) in Table 1 (SI Appendix, Fig. S1). For each point group, we define a representation of the associated shape tensors ${ℭ}_{ijk}^{\prime }$ and ${𝔇}_{ijk}^{\prime }$ with a minimal number of parameters. For example, shape tensors of particles in the prismatic groups $D_{nh}$ with $n\ge 3$ can be expressed using a single parameter: $-{𝔇}_{123}^{\prime }=-{𝔇}_{132}^{\prime }={𝔇}_{231}^{\prime }={𝔇}_{213}^{\prime }=d$ with all other ${ℭ}_{ijk}^{\prime }$ and ${𝔇}_{ijk}^{\prime }$ equal to zero. Particles from different point groups can exhibit identical ICEP dynamics—e.g., the polyhedral groups $O_h$ and $I_h$ exhibit the same behavior as the sphere with no rotational or translational motion. It is therefore convenient to organize the different point groups into classes that share the same dynamics.

Table 1.

Summary of ICEP dynamics organized by rotation class and symmetry group

Rotation class	Point group	Primary axis	Name	Description
Sphere	$O_h$, $I_h$	None	Unresponsive	Does not translate or rotate.
	$T_d$	None	Cruiser	Translates steadily in a constant direction.
$D_{\mathrm{\infty }h}$	$D_{nh}$, $D_{nd}$*	$C_n$ axis	$\parallel$ aligner	Aligns $\parallel$ to field.
			$\perp$ aligner	Aligns $\perp$ to field.
	$D_n$*	$C_n$ axis	$\parallel$ aligner	Aligns $\parallel$ to field with transient translation.
			$\perp$ aligner	Aligns $\perp$ to field with transient translation.
	$C_{nv}$*	$C_n$ axis	$\parallel$ rocket	Translates $\parallel$ to axis ($\parallel$ to field).
			$\perp$ rocket	Translates $\parallel$ to axis ($\perp$ to field).
	$D_{2d}$	$S_4$ axis	$\parallel$ aligner	Aligns $\parallel$ to field with transient translation.
			$\perp$ shuttle	Translates $\parallel$ to axis with $\varphi$-dependent rate.
	$D_{3h}$	$C_3$ axis	$\parallel$ aligner	Aligns $\parallel$ to field with transient translation.
			$\perp$ glider	Translates $\perp$ to axis in $\varphi$-dependent direction.
$D_{2h}$	$D_{2h}$	$C_2$ axis†	$\parallel$ aligner	Aligns $\parallel$ to field.
	$D_2$	$C_2$ axis†	$\parallel$ aligner	Aligns $\parallel$ to field with transient translation.
	$C_{2v}$	$C_2$ axis	$\parallel$ rocket	Translates $\parallel$ to axis ($\parallel$ to field).
			$\perp$ rocket	Translates $\parallel$ to axis ($\perp$ to field).
$D_{3d}$	$D_{3d}$	$C_3$ axis	$\parallel$ aligner	Aligns $\parallel$ to field.
			$\perp$ flipper	Aligns $\perp$ to field and particle rotates about field.
	$D_3$	$C_3$ axis	$\parallel$ aligner	Aligns $\parallel$ to field with transient translation.
			$\perp$ flipping glider	Rotates and translates $\perp$ to axis ($\parallel$ to field).
	$C_{3v}$	$C_3$ axis	$\parallel$ rocket	Translates $\parallel$ to axis ($\parallel$ to field).
			$\perp$ flipping cruiser	Traces circular orbits in plane $\perp$ to field.
$C_{4h}$	$C_{nh}$*, $S_{2n}$	$C_n$ axis	$\parallel$ spinner	Aligns $\parallel$ to field and rotates about axis.
			$\perp$ spinner	Aligns $\perp$ to field and rotates about axis.
	$C_n$*	$C_n$ axis	$\parallel$ spinning rocket	Rotates and translates $\parallel$ to axis ($\parallel$ to field).
			$\perp$ spinning rocket	Rotates and translates $\parallel$ to axis ($\perp$ to field).
	$C_{3h}$	$C_3$ axis	$\parallel$ spinner	Aligns $\parallel$ to field and rotates about axis.
			$\perp$ spinning glider	Traces circular orbits in plane $\parallel$ to field.
	$S_4$	$S_4$ axis	$\parallel$ spinner	Aligns $\parallel$ to field and rotates about axis.
			$\perp$ spinning shuttle	Rotates and oscillates $\parallel$ to axis ($\perp$ to field).
$S_6$	$S_6$	$S_6$ axis	$\parallel$ spinner	Aligns $\parallel$ to field and rotates about axis.
			Precesser	Aligns oblique to field and rotates about field.
			Wobbler	Axis wobbles about direction $\perp$ to field.
	$C_3$	$C_3$ axis	$\parallel$ spinning rocket	Rotates and translates $\parallel$gto axis.
			Precessing cruiser	Traces helical paths aligned $\parallel$ to field.
			Wobbling cruiser	Traces complex paths with net translation.
$C_{2h}$	$C_{2h}$	$C_2$ axis	$\parallel$ spinner	Aligns $\parallel$ to field and rotates about axis.
			$\perp$ spinner	Aligns $\perp$ to field and rotates with an oscillatory rate.
			Aligner	Aligns oblique to field with no motion.
	$C_2$	$C_2$ axis	$\parallel$ spinning rocket	Rotates and translates $\parallel$ to axis at a constant rate.
			$\perp$ spinning shuttle	Rotates and translates $\parallel$ to axis with oscillatory rate.
			Cruiser	Translates steadily in a constant direction.
	$C_s$	$\perp$ to $\sigma$	$\parallel$ spinning glider	Traces circular orbits in plane $\perp$ to field.
			$\perp$ spinning glider	Traces complex orbits in plane $\parallel$ to field.
			Cruiser	Translates steadily in a constant direction.

For each particle symmetry, we identify a primary axis and describe the motion relative to this axis. Note that multiple motions are possible within each symmetry group, depending on the specific geometry of the particle. Names have three components: (i) the stable orientation of the particle axis relative to the field (parallel, ∥; perpendicular, ⊥; or other), (ii) the type of rotational motion (align, spin, flip, wobble, precess), and (iii) the type of translational motion (rocket, glide, shuttle, cruise). Each motion is described in more detail in SI Appendix.

^*Refers to n ≥ 4.

^†Refers specifically to the major C₂ axis of the particle.

While the symmetry of a particle can significantly constrain its dynamics, the detailed particle shape is needed to uniquely specify the shape tensors $𝕮\prime$ and $𝕯\prime$. Here, we consider the family of sphere-like particles for which the radial distance is equal to a linear combination of spherical harmonics

$$r(\theta ,\varphi )=\sum _{\mathrm{\ell }=0}^{\mathrm{\infty }}\sum _{m=0}^{\mathrm{\ell }}\text{Re}\left(B_{\mathrm{\ell }m}{Y}_{\mathrm{\ell }}^m(\theta ,\varphi )\right)>0.$$ [8]

For each particle, the shape tensors are computed numerically using a boundary integral scheme to solve the electrostatic and hydrodynamic problems governing particle motion (Materials and Methods). Finally, we compute the particle dynamics by integrating Eqs. 1 and 2 starting from a specified orientation. We neglect effects due to Brownian motion, such that particle dynamics are fully deterministic. Physically, this approximation is appropriate for sufficiently large particles and fields such that $\epsilon a^3{E}^2\gg k_{B}T$. Fig. 1A shows the computed trajectory for a particle with $D_{3d}$ symmetry.

Possible Particle Dynamics.

We now survey the variety of possible ICEP motions for particles of different symmetries and shapes. Owing to the translational invariance of the particle dynamics, it is possible to fully describe the rotational motion of a given particle independent of any translational motions. It is therefore convenient to organize particles of different point groups into classes that share common rotational dynamics. Within each rotation class, the point groups can be further divided based on the different possible translational motions. This organizational scheme is illustrated in Table 1 and serves to guide our exploration through the space of different particle shapes. Each rotation class is denoted by a prototypical member that possesses inversion symmetry and therefore exhibits no translational motion.

Sphere Rotation Class.

The electrokinetic flows induced around a spherical particle are highly symmetric and result in no translation or rotational motion of the particle. Similarly, particles with octahedral ($O_h$) or icosahedral ($I_h$) symmetry do not translate or rotate by ICEP. Particles with tetrahedral symmetry ($T_d$) do not rotate but can translate in a manner similar to $D_{2d}$ particles described in the next section.

${\mathrm{𝑫}}_{\infty \mathrm{𝒉}}$ Rotation Class.

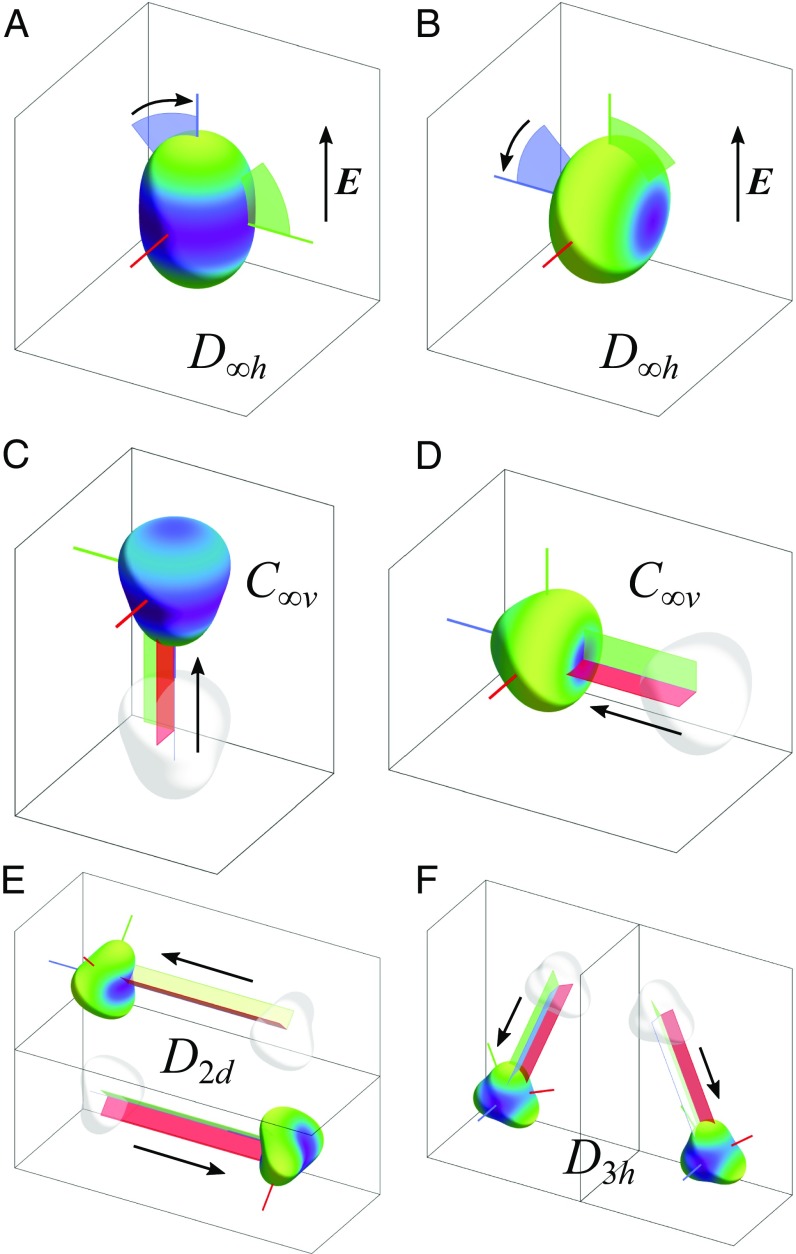
Particles in the $D_{\mathrm{\infty }h}$ rotation class exhibit rotational motions characteristic of anisotropic particles with axial symmetry (e.g., cylindrical rods or spheroids). Such particles rotate to align their primary axis either parallel or perpendicular to the applied field. The rotation pseudotensor $𝕯\prime$ can be specified by a single parameter, which determines the stable orientation of the particle and the speed at which it approaches that orientation. Taller particles (e.g., prolate spheroids) align parallel to the field while shorter particles (e.g., oblate spheroids) orient perpendicular to the field (Fig. 2 A and B). More generally, we find that a particle’s aspect ratio is key to specifying its preferred orientation in the field.

Fig. 2.

Representative dynamics of particles in the $D_{\mathrm{\infty }h}$ rotation class. (A and B) Parallel and perpendicular aligners orient their primary axes parallel and perpendicular to the field E. Particle shapes are characterized by the nonzero coefficients $B_{20}=0.4$ and $-0.4$, respectively. (C and D) Parallel and perpendicular rockets align in the field and translate along their primary axes; here, $B_{30}=\pm B_{20}=0.2$. (E) A perpendicular shuttle translates along its primary axis in a direction perpendicular to the field. The velocity depends on the particle’s orientation about that axis; here, $\varphi =\frac{1}{4}\pi$ (Top) and $\varphi =-\frac{1}{4}\pi$ (Bottom) with $B_{32}=-B_{20}=0.5$. (F) A perpendicular glider translates perpendicular to its axis along a direction that depends on the particle’s orientation about that axis; here, $\varphi =\frac{1}{8}\pi$ (Left) and $\varphi =\frac{5}{24}\pi$ (Right) with $B_{33}=-B_{20}=0.4$ (Movie S1).

Members of this rotation class that exhibit no translational motion include the point groups $D_{nh}$ and $D_{nd}$ with $n\ge 4$ (e.g., an eight-tooth gear). Other point groups—namely, $D_n$ with $n\ge 4$ (e.g., a quadruple helix)—exhibit transient motions that cease upon reaching their stable orientation. In Table 1, these particles are labeled as aligners, which are further distinguished by their preferred orientation parallel ($\parallel$) or perpendicular ($\perp$) to the applied field. By contrast, particles of $C_{nv}$ symmetry with $n\ge 4$ (e.g., a pear) translate steadily in a direction parallel to their primary axis upon reaching their final orientation. We refer to such particles as rockets, which can move parallel or perpendicular to the applied field, depending on their aspect ratio (Fig. 2 C and D). Such steady translational motion has been explored in experimental studies on Janus particles, which belong to the $C_{\mathrm{\infty }v}$ point group (27).

While the members of the $D_{\mathrm{\infty }h}$ rotation class have no preferred orientation about their primary axis (i.e., no preferred $\varphi$ in Fig. 1), some members exhibit translational motions that depend on this orientation. When aligned perpendicular to the field, particles with $D_{2d}$ symmetry will translate forward or backward along their primary axis, depending on their orientation about that axis (Fig. 2E). We refer to such particles as shuttles, which are capable of bidirectional motion. When aligned perpendicular to the field, $D_{3h}$ particles will translate perpendicular to their primary axis in a direction that depends on their orientation about that axis (Fig. 2F). We refer to such particles as gliders.

To summarize, particles in this rotation class are all capable of aligning parallel or perpendicular to the applied field. We further distinguish three particle types capable of steady translation: Rockets move parallel to their primary axis at a constant velocity; shuttles move parallel to their axis with a velocity that depends on the orientation $\varphi$; and gliders move perpendicular to their axis in a $\varphi$-dependent direction.

$D_{2\hspace{0.17em}h}$ Rotation Class.

Particles in the $D_{2h}$ rotation class (e.g., ellipsoids) also rotate to align their primary axis parallel to the applied field. However, owing to their lack of axial symmetry, these particles exhibit transient rotations about the major axis as they orient in the field. The translational motions of particles in this class are similar to those of the $D_{\mathrm{\infty }h}$ class described above. $D_2$ particles exhibit transient translational motions that cease upon reaching their stable orientation; $C_{2v}$ particles translate steadily in a direction parallel or perpendicular to the applied field depending on their aspect ratio.

$D_{3\hspace{0.17em}d}$ Rotation Class.

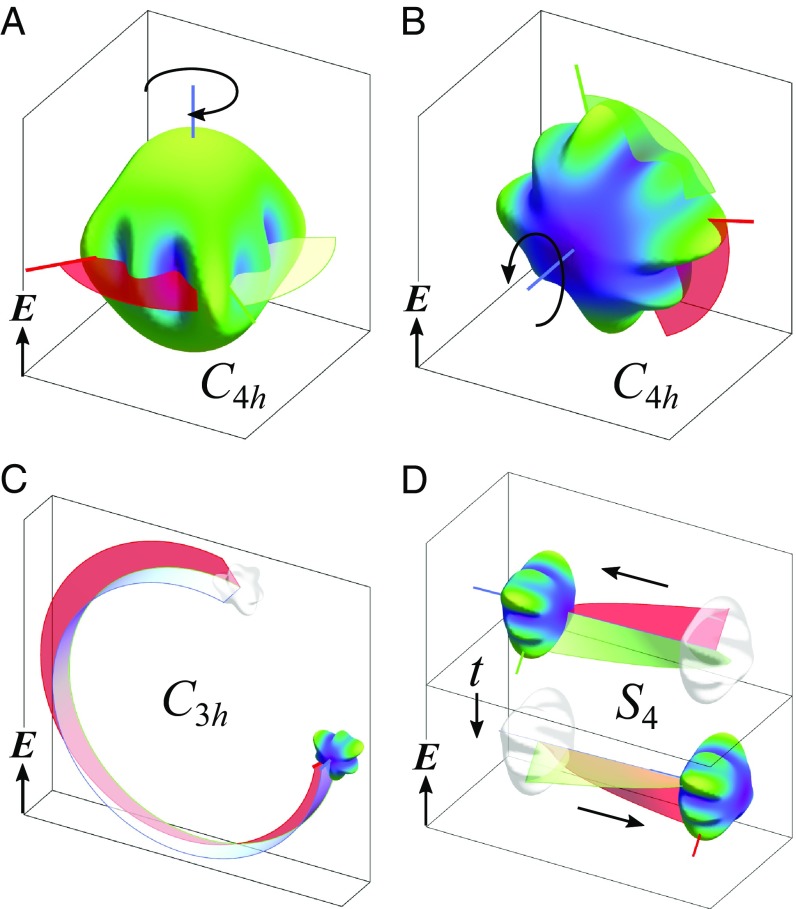
Particles in the $D_{3d}$ rotation class (e.g., an ethane molecule) are capable of an additional elemental motion we call flipping. When such particles align their primary axis perpendicular to the field, they rotate or flip head over tail at a steady rate about the axis of the field (Fig. 3A). Particles in the $D_{3d}$ point group possess inversion symmetry and therefore do not translate. By breaking this symmetry, however, one can combine flipping motions with the translational motions characteristic of gliders and rockets.

Fig. 3.

Representative dynamics of particles in the $D_{3d}$ rotation class. (A) Perpendicular flippers rotate steadily about the field axis; here, $i{B}_{43}=B_{20}=-0.3$. (B) Perpendicular flipping gliders translate parallel to the field while rotating about an axis parallel to the field; here, $B_{53}=-i{B}_{43}=-B_{20}=0.2$. (C) Perpendicular flipping cruisers orient perpendicular to the field and translate perpendicular to the field while rotating about an axis parallel to the field; here, $i{B}_{43}=i{B}_{33}=-B_{30}=B_{20}=-0.2$ (Movie S2).

When $D_3$ particles orient perpendicular to the field, they glide perpendicular to their axis while flipping (Fig. 3B). The net motion is reminiscent of a rotating corkscrew that swims through viscous surroundings. This example shows how similar motions are achieved using very different particles—e.g., $C_{nv}$ rockets and $D_3$ flipping gliders both translate at a steady rate along the field axis (compare Figs. 2C and 3B). In another example, $C_{3v}$ particles that orient perpendicular to the field exhibit steady flipping motions while translating along a constant direction oblique to the particle axis. We refer to this most general form of translational motion as cruising. Such $C_{3v}$ flipping cruisers swim along circular orbits within the plane perpendicular to the field (Fig. 3C). The size of the circular orbit is determined by the relative rates of rotation and translation, which can be tuned by varying the particle shape.

$C_{4\hspace{0.17em}h}$ Rotation Class.

Particles in the $C_{4h}$ rotational class (e.g., a twisted star) exhibit steady rotational motions we call spinning (Fig. 4 A and B). In contrast to flipping, spinning refers to rotational motion about the primary axis of the particle, which can be oriented either parallel or perpendicular to the field. Particles of $C_{nh}$ or $S_{2n}$ symmetry with $n\ge 4$ exhibit these rotational motions without translation. By contrast, $C_n$ particles (e.g., a pinwheel) lack the fore–aft symmetry of $C_{nh}$ particles and therefore rocket along their primary axis while spinning. These spinning rockets move at a constant rate either parallel or perpendicular to the field.

Fig. 4.

Representative dynamics of particles in the $C_{4h}$ rotation class. (A and B) Spinners orient parallel or perpendicular to the field and rotate about their primary axis; here, $-i{B}_{88}=B_{44}=\pm B_{20}=0.3$. (C) Spinning gliders can trace circular orbits within planes parallel to the field; here, $i{B}_{66}=-B_{33}=B_{20}=-0.4$. (D) Spinning shuttles can oscillate along a line perpendicular to the field; here, $-i{B}_{88}=B_{44}=-B_{20}=0.3$ and $B_{32}=0.1$ (Movie S3).

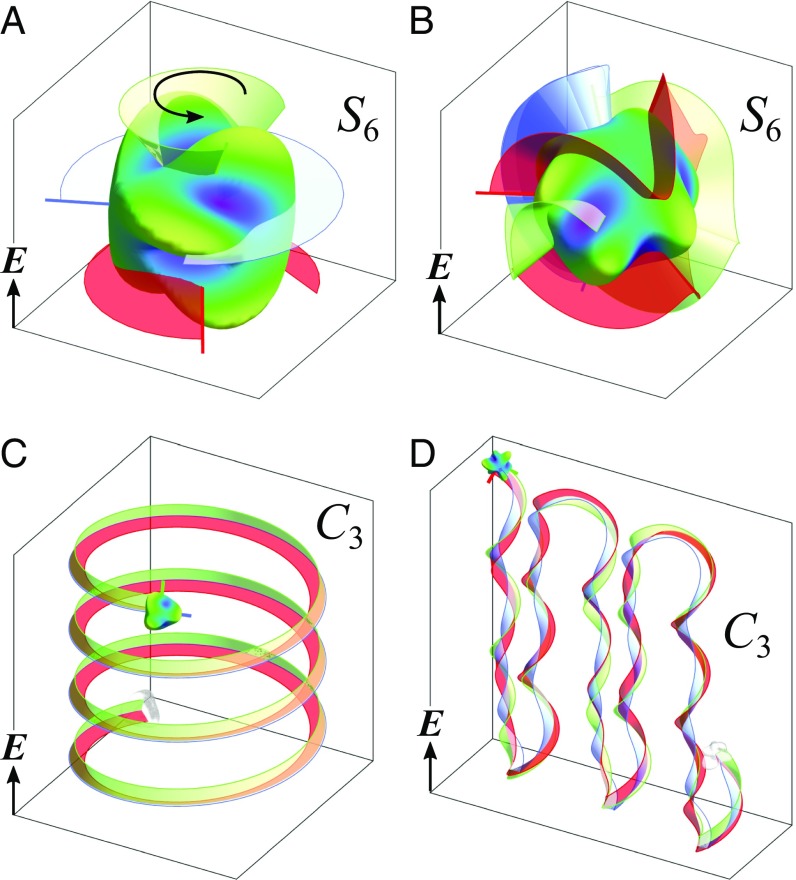
${\mathrm{𝑺}}_{\mathrm{𝟔}}$ Rotation Class.

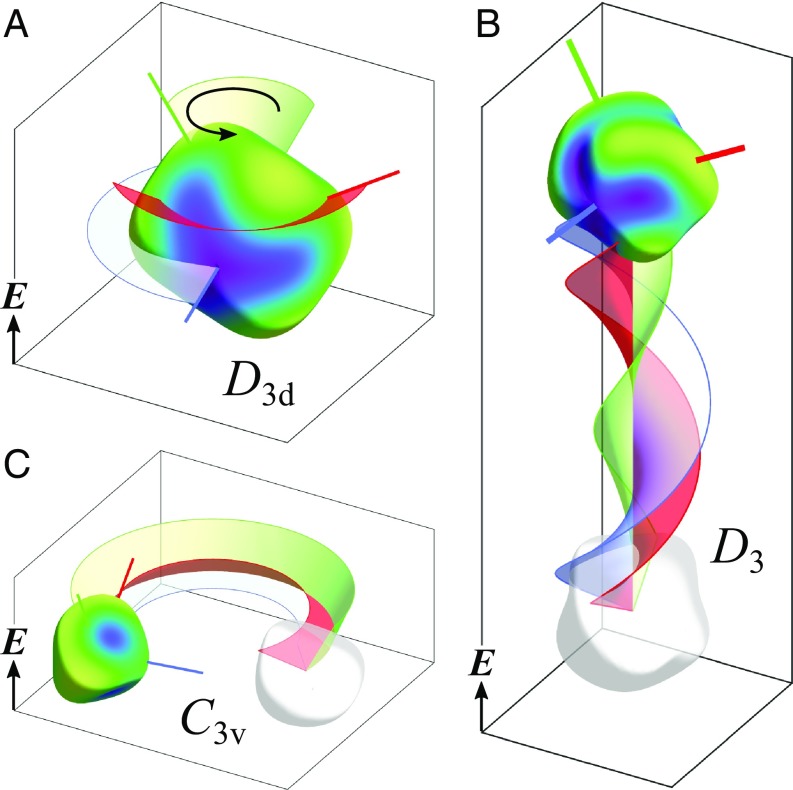
Particles in the $S_6$ rotational class are capable of increasingly complex rotational motions, which can be viewed as a combination of spinning and flipping. Indeed, the rotation tensor for these particles can be expressed as a superposition of the $C_{4h}$ and $D_{3d}$ tensors. When such particles align their threefold rotation axis parallel to the field, they spin steadily just like particles from the $C_{4h}$ group. Other $S_6$ particles orient their rotation axis oblique to the field and rotate steadily about the field axis (Fig. 5A). This motion—termed precessing—is similar to flipping but with the particle axis tilted with respect to the field. Finally, some $S_6$ particles are capable of simultaneous rotation about multiple axes, which we called wobbling (Fig. 5B). The specific conditions for which each motion occurs are detailed in SI Appendix.

Fig. 5.

Characteristic dynamics of particles in the $S_6$ rotation class. (A) A precesser aligns its primary axis oblique to the field and rotates about an axis parallel to the field; here, $-i{B}_{66}=B_{43}=0.7$ and $B_{20}=0.1$. (B) The primary axis of a wobbler traces periodic orbits as the particle spins about that axis; here, $-i{B}_{66}=B_{43}=0.3$ and $B_{20}=0.04$. (C) A precessing cruiser aligns its primary axis oblique to the field and translates along a helical trajectory; here, $i{B}_{66}=B_{20}=-0.09726$, $B_{43}=0.2024$, and $B_{30}=0.3889$. (D) A wobbling cruiser translates in different directions, depending on its orientation as it rotates; here, $-i{B}_{66}=B_{43}=B_{33}=0.5$ and $B_{20}=-0.1$ (Movie S4).

Breaking the fore–aft symmetry of the $S_6$ particles to create $C_3$ particles allows for translational motions. For $C_3$ particles in the precessing regime, the addition of steady translation oblique to the particle axis results in helical trajectories oriented parallel to the field (Fig. 5C). For $C_3$ particles in the wobbling regime, we encounter complex trajectories that combine periodic rotational motions about multiple axes with orientation-dependent translation. During each rotation cycle, the particle translates some net distance along a common direction. The translational motions performed during each cycle vary widely, depending on details of the particle shape. Fig. 5D shows one example where a $C_3$ particle follows a zig-zag trajectory reminiscent of the patterns used in search and rescue operations. Such complex motions may offer desirable characteristics for improving mass transfer to/from active colloids for applications in sensing or remediation (32, 33).

$C_{2\hspace{0.17em}h}$ Rotation Class.

Particles in the $C_{2h}$ rotational class (e.g., the letter S) introduce a new capability—namely rotation at a time-varying rate. The rotation tensor for these particles can be expressed as a superposition of the $C_{4h}$ and $D_{2h}$ tensors. When oriented perpendicular to the field, $C_{2h}$ particles exhibit two competing tendencies: the steady spinning motion of $C_{4h}$ particles and the major-axis alignment of $D_{2h}$ particles. When the former tendency dominates, the particle rotates about its axis with a speed that oscillates between fast and slow over a period of $\pi$ radians (Movie S5). Alternatively, when alignment dominates, the particle approaches a fixed orientation (Movie S5). $C_{2h}$ particles that orient parallel to the field spin at a constant rate as demonstrated experimentally for doublets of metallodielectric Janus particles (28). The conditions for each possible motion are detailed in SI Appendix.

Within this rotation class, particles of $C_2$ or $C_s$ ($C_{1h}$) symmetry are capable of translational motions. As in the classes above, the breaking of fore–aft symmetry ($C_{2h}$ to $C_2$) allows for translation along the particle axis to create spinning rockets that move parallel to the field. Interestingly, those $C_2$ particles that move perpendicular to the field do so at an oscillatory rate as spinning shuttles (Fig. 6A). Particles with one plane of mirror symmetry ($C_s$) are of particular practical interest as they are readily fabricated using common lithographic methods. When such particles are short (plate-like), they orient their axis perpendicular to the field and trace complex periodic orbits within a plane parallel to the field (Fig. 6B). Tall particles orient parallel to the field and trace circular orbits in the plane perpendicular to the field (Fig. 6C). Both $C_2$ and $C_s$ particles are capable of steady translation in a fixed direction relative to the field.

Fig. 6.

(A) A perpendicular spinning shuttle translates along its primary axis in a direction perpendicular to the field while rotating about that axis at an oscillatory rate; here, $-i{B}_{44}=B_{32}=0.5$, $B_{30}=0.01$, and $B_{20}=-0.4$. (B) A perpendicular spinning glider translates perpendicular to its axis as it rotates about its axis; here, $-i{B}_{88}=B_{4}4=0.3$, $B_{33}=0.1$, and $B_{20}=-0.2$. (C) A parallel spinning glider translates perpendicular to its axis as it rotates about its axis, leading to orbital motions in a plane perpendicular to the field; here, $-i{B}_{88}=B_{44}=0.3$, $B_{33}=0.5$, and $B_{20}=0.2$ (Movie S5).

Programing Particle Motion.

So far, we have shown how the symmetry of a particle can constrain its dynamics to permit certain translational and rotational motions; the detailed shape of the particle further specifies its unique trajectory. We now consider the inverse problem: Given a desired dynamical behavior, we seek to determine the particle shape that “encodes” those dynamics. We limit our discussion to those motions described in the previous section such that the necessary particle symmetry is implied by the desired particle motion. For example, to achieve helical motions along the field axis, one would select particles of $C_3$ symmetry (Fig. 5C).

The desired motion is characterized by a set of features F such as the radius, pitch, and speed of the helical trajectory. More generally, particle trajectories can be well approximated by truncated Fourier series. The particle shape is specified by some weighted combination of basis functions, which are chosen to preserve the desired symmetry of the particle. Here, we use linear combinations of spherical harmonics; however, other choices are possible. In the forward problem, the basis function weights B are used to specify the particle shape, compute the shape tensors, integrate the particle motion, and determine the features of the particle trajectory. The features are therefore a function of the weights, $\text{𝑭}=\text{𝑭}(\text{𝑩})$.

In designing a $C_3$ particle, one might consider contributions such as $Y_2^0$ to tune the aspect ratio, $Y_3^0$ to break the fore–aft symmetry, and a combination of $Y_3^3$ and $Y_6^6$ to control the threefold rotational symmetry. For near-spherical particles, increasing the magnitude of a particular basis function increases the speed of the associated particle motions. Increasing the $Y_2^0$ contribution ($D_{\mathrm{\infty }h}$ symmetry) causes the particle to align more quickly in the field; increasing the $Y_3^0$ contribution ($C_{\mathrm{\infty }v}$ symmetry) results in faster translation; and increasing the $Y_3^3$ and $Y_6^6$ contributions ($C_{3h}$ symmetry) drives faster spinning motions. In general, these changes in the particle velocity are neither linear nor independent from one another.

In the inverse problem, we are given the desired features ${\text{𝑭}}_0$ and seek to determine a set of weights such that $\text{𝑭}(\text{𝑩})={\text{𝑭}}_0$. When the number of weights is equal to the number of features, this problem involves solving a system of nonlinear equations, which can be solved numerically (e.g., using Newton’s method). When the number of weights is greater than the number of features, the problem is underdetermined, and the constraints must be augmented by an additional objective function to be minimized. We solved this optimization problem using sequential quadratic programing (SQP) (39) with the objective function $O(\text{𝑩})=\text{𝑩}\cdot \text{𝑩}$. This choice ensures that the particle is as “sphere-like” as possible while retaining the desired dynamical features. Fig. 5C shows the helical trajectory of a $C_3$ particle that was rationally designed to have a radius of precisely $7a$, a pitch of $5a$, and a speed of $0.05\epsilon a{E}_{\mathrm{\infty }}^2/\eta$.

It is important to note that there are particle motions which cannot be accessed by ICEP. Owing to the invariance of the dynamics with respect to rotation about the axis of the field, the angular velocity of the particle depends on only two variables (e.g., Euler angles $\varphi$ and $\theta$). Chaotic motions are therefore prohibited by the Poincare–Bendixson theorem (40); the particle orientation evolves in time to a constant value (a fixed point) or to a periodic function of time (a limit cycle).

In experimental practice, the “encoding” of colloidal motions into particle shapes remains challenging. Recent advances in colloidal synthesis offer routes to low-symmetry particles such as colloidal doublets, trimers, and tetramers (5, 6, 41); however, most of the particles described here are currently inaccessible to bottom–up synthetic approaches. By contrast, top–down fabrication techniques such as two-photon lithography (42, 43) now enable one to “print” micrometer-scale particles of arbitrary, 3D shapes with features on the scale of tens of nanometers. As a demonstration, we printed a $C_2$ particle of prescribed shape with a radius of 5 $\mu$m (SI Appendix, Fig. S20). Such polymeric particles could be coated with a metal layer by electroless deposition to create the kinds of polarizable particles studied here (44, 45).

Sensitivity on Particle Shape.

The ability to precisely prescribe a particle’s motion demands similar precision over the particle’s shape, which may be difficult to achieve in experiment. It is therefore important to consider the sensitivity of such motions with respect to perturbations in the particle shape. Specifically, we consider how the shape tensors, $𝕮\prime$ and $𝕯\prime$, respond to small changes in the basis function weights B (here, the coefficients $B_{\mathrm{\ell }m}$). We limit our discussion to small perturbations, for which the shape tensors are linear functions of the perturbations $\mathrm{\Delta }\text{𝑩}$ about the desired shape ${\text{𝑩}}_0$,

$$𝕮\prime (\text{𝑩})\approx 𝕮\prime ({\text{𝑩}}_0)+\mathrm{\Delta }\text{𝑩}\cdot {\nabla }_{\text{𝑩}}𝕮\prime ({\text{𝑩}}_0).$$ [9]

The sensitivity matrix ${\nabla }_{\text{𝑩}}𝕮\prime ({\text{𝑩}}_0)$ characterizes how the particle velocity changes upon small changes in its shape.

For a spherical particle (${\text{𝑩}}_0=0$), there are only few basis functions that contribute to particle motions at first order. The addition of spherical harmonics $Y_{\mathrm{\ell }}^m$ with $\mathrm{\ell }=2$ leads to rotational motions like those of aligners with $D_{\mathrm{\infty }h}$ or $D_{2h}$ symmetry. Perturbations with $\mathrm{\ell }=3$ lead to translational motions like those of rockets ($C_{\mathrm{\infty }v}$, $C_{2v}$), gliders ($C_{3h}$), and shuttles ($D_{2d}$). Motions associated with other rotation classes (e.g., flipping, spinning, wobbling, etc.) are prohibited at this order (SI Appendix, Fig. S16).

A particle’s sensitivity to small perturbations depends on its shape (i.e., on ${\text{𝑩}}_0)$. Spheroidal particles with $D_{\mathrm{\infty }h}$ symmetry are susceptible to the same perturbations that affect spheres but also to new perturbations of lower symmetry. In particular, the addition of spherical harmonics $Y_4^1$ and $Y_4^3$ leads to spinning and flipping motions characteristic of $C_{2h}$ and $D_{3d}$ particles, respectively. In general, particles of lower symmetry are susceptible to more types of perturbations in their shape.

In the linear regime, the effects of individual perturbations can be added together to describe the particle’s response. Higher-order mixing of two or more perturbations is prohibited. For example, there exists no small defect that will cause a $D_{\mathrm{\infty }h}$ aligner to spin about its axis like a $C_{4h}$ particle. Creating fourfold rotation symmetry without the mirror symmetries of $D_{4h}$ particles cannot be achieved by a single spherical harmonic. By contrast, $D_{4h}$ aligners, whose dynamics are otherwise indistinguishable from those of $D_{\mathrm{\infty }h}$ particles, are susceptible to linear perturbations that lead to spinning motions.

For low-symmetry shapes, just about any perturbation will alter the shape tensors at first order but by different amounts. The addition of spherical harmonics of low order $\mathrm{\ell }$ has a larger impact on particle motions than the addition of those of higher order. This observation suggests that large-scale defects accompanying particle fabrication are more likely to disrupt the desired particle motions than small-scale defects due to surface roughness. The sensitivity of particle motions to defects could likely be mitigated by altering the objective function $O(\text{𝑩})$ to favor particle shapes that are less sensitive to specified perturbations.

Brownian Motion.

The effects of Brownian motion may be significant for smaller particles or weaker fields. The relative importance of electrokinetic vs. diffusive particle motions is quantified by dimensionless Péclet numbers for translation and rotation: ${\mathrm{Pe}}_t=Ua/D_t$ and ${\mathrm{Pe}}_r=\mathrm{\Omega }/D_r$, respectively, where $D_t=k_{B}T/6\pi \eta a$ and $D_r=k_{B}T/8\pi \eta a^3$ are the translational and rotational diffusivities for spherical particles of comparable size. The above analysis assumes that the Péclet numbers are large (${\mathrm{Pe}}_t\gg 1$ and ${\mathrm{Pe}}_r\gg 1$), which is often the case in experiment (e.g., $\mathrm{Pe}\sim {10}^3$ in ref. 27). Nevertheless, it is interesting to consider how shape-dependent diffusive motions may interact with those due to ICEP of smaller particles subject to weaker fields.

We therefore simulated the Brownian dynamics of particles subject to applied fields at various dimensionless temperatures $\beta =k_{B}T/a^3\epsilon E_{\mathrm{\infty }}^2$ corresponding to different Péclet numbers ($\mathrm{Pe}\sim {\beta }^{-1}$; Materials and Methods). At long times, particles exhibit anisotropic enhancements in their translational diffusion due to the applied field. Such motions are characterized by diffusion coefficients $D_{\parallel }$ and $D_{\perp }$ for displacements parallel and perpendicular to the field. In general, these coefficients are different from one another and greater than that of passive particles in the absence of the field. To understand these trends, it is instructive to consider the dynamics of a parallel rocket (Fig. 2C). In the absence of Brownian motion, such particles align and translate parallel to the field. At finite temperatures $\beta \sim 1$, the particle orientation fluctuates, causing it to translate sometimes with and other times against the direction of the field. The particle thereby performs a random walk along the field axis, resulting in field-enhanced diffusion, $D_{\parallel }>D_t$ (SI Appendix, Fig. S18). Motions perpendicular to the field can be similarly enhanced (SI Appendix, Fig. S19). The specific values of $D_{\parallel }$ and $D_{\perp }$ depend on the particle shape and the dimensionless temperature $\beta$.

Boundaries and Interactions.

Realizing the 3D motions described here would likely require density-matched materials to avoid sedimentation of the microparticles onto system boundaries. The presence of such boundaries—neglected in the present analysis—can alter the dynamics of active colloids by modifying the electric field and the accompanying fluid flows (46). For a single planar wall oriented normal to the applied field ($z$ direction), the particle velocity is still described by Eqs. 1 and 2 such that $U_i\propto {ℭ\prime }_{i33}$ and ${\mathrm{\Omega }}_i\propto {𝔇\prime }_{i33}$. However, the shape tensors are no longer constant; they depend on the orientation and position of the particle relative to the wall. As a result, new types of particle motions become possible.

Such motions are constrained by the symmetry of the particle–wall system, not just the particle itself. For example, a sphere near a wall has $C_{\mathrm{\infty }v}$ symmetry; the particle velocity must share this symmetry such that $\mathrm{𝑼}=[0,0,U_3]$ and $𝛀=0$. Spheres are attracted or repelled by walls at a rate dependent on the surface separation. Additional physical considerations reveal that conductive spheres are attracted to conducting walls normal to the field but repelled by insulating walls parallel to the field (46). Notably, the symmetry constraints of ICEP motions near a planar wall are identical to those of self-phoretic colloids near a wall, as illustrated by the specific case of Janus spheres (46–48).

The symmetry of the particle–wall system can change, depending on the particle orientation. A $C_{4h}$ spinner might orient its rotation axis parallel or perpendicular to the field to create a system with $C_4$ or $C_s$ symmetry, respectively. In the parallel orientation, $C_{4h}$ particles are expected to spin about their axis while translating to or away from the wall. In the perpendicular orientation, particles of the same symmetry can spin while translating perpendicular to the particle axis to perform complex periodic orbits superimposed on steady motions parallel and/or perpendicular to the field (compare Fig. 6B). Interestingly, the same particle may even switch its preferred orientation as a function the surface separation, thereby changing the symmetry of the system in time.

Within bulk dispersions, long-ranged particle interactions can also influence ICEP motions. In the far field, each particle creates an electrostatic disturbance like that of a charge dipole as well as a hydrodynamic disturbance like that of a force dipole [a so-called stresslet of the “puller” variety (49)]. These disturbances cause particles to attract one another along the direction of the field and then repel along a perpendicular direction (50, 51). Combined with linear self-propulsion, such hydrodynamic interactions can lead to stable “flocks” of particles moving in a common direction (52). These and other collective motions should depend on the individual particle trajectories and their near-field interactions, both of which are controlled by particle shape. It may therefore be possible to extend the present concept of shape-based programing to direct colloidal dynamics within ensembles of active particles. Recent experimental results highlight opportunities for creating complex dynamic assemblies using shape-directed ICEP motions (29, 30, 53, 54).

Conclusions

Low-symmetry particles can exhibit complex dynamics powered by induced-charge electrophoresis in three dimensions. In contrast to motions of self-phoretic particles, the ICEP velocity depends on the particle orientation relative to the applied field. The field can therefore serve to guide particle motions along intricate cycles of rotation and translation. These motions are largely dictated by particle symmetry and can be uniquely prescribed by engineering particle shape. The diversity of particle trajectories described here may offer useful functions as colloidal clocks ($C_{2h}$), oscillators ($S_4$), and foragers ($C_3$), as well as switchable dispersions, in which the application of a field introduces new length scales (e.g., the radius and pitch of a helical trajectory) and thereby new properties (e.g., a change in optical response). Beyond ICEP, it will be interesting to systematically explore the types of shape-directed particle motions powered by other energy inputs such as hydrodynamic shear and asymmetric acoustic streaming. Beyond the motions of individual particles, shape is also expected to influence the collective dynamics of more concentrated dispersions of active colloids. Just as particle shape has played an essential role in directing colloidal assemblies at equilibrium, we anticipate the role of shape will only grow in pursuit of dissipative assemblies or colloidal machines capable of dynamic functions.

Materials and Methods

The formulation of the ICEP problem below follows closely that of Squires and Bazant (26). Additionally, we introduce a boundary integral formulation of the problem and describe its numerical solution.

Electrostatics.

The electric potential $\mathrm{\Phi }(\mathrm{𝒙})$ surrounding the particle satisfies the Laplace equation

$${\nabla }^2\mathrm{\Phi }(\mathrm{𝒙})=0,$$ [10]

where the origin of the position vector x is chosen as the center of the particle. This expression assumes that the electric double-layer thickness is much smaller than the size of the particle, such that there is no free charge in solution. At the particle surface $S_p$, the normal component of the ionic current is zero such that

$$\text{𝒏}\cdot \nabla \mathrm{\Phi }(\mathrm{𝒙})=0\hspace{0.17em}\text{for}\hspace{0.17em}\mathrm{𝒙}\in S_p,$$ [11]

where n is the unit normal vector directed out from the surface. Far from the particle, the potential approaches the externally applied potential ${\mathrm{\Phi }}^{\mathrm{\infty }}(\mathrm{𝒙})$,

$$\mathrm{\Phi }(\mathrm{𝒙})={\mathrm{\Phi }}^{\mathrm{\infty }}(\mathrm{𝒙})=-{\mathrm{𝑬}}^{\mathrm{\infty }}\cdot \mathrm{𝒙}\hspace{0.17em}\text{for}\hspace{0.17em}|\mathrm{𝒙}|\to \mathrm{\infty },$$ [12]

where ${\mathrm{𝑬}}^{\mathrm{\infty }}$ is the constant electric field. Eqs. 10–12 imply that the electric potential on the surface of the particle is governed by the integral equation

$$\mathrm{\Phi }(\mathrm{𝒙})={\mathrm{\Phi }}^{\mathrm{\infty }}(\mathrm{𝒙})-{\int }_{S_p}\left[\mathrm{\Phi }(\text{𝒚})-\mathrm{\Phi }(\mathrm{𝒙})\right]\frac{\text{𝒏}(\text{𝒚})\cdot \text{𝒓}}{4\pi r^3}dS(\text{𝒚}),$$ [13]

where $\text{𝒓}=\text{𝒚}-\mathrm{𝒙}$ (see SI Appendix for details) (55). As detailed below, the integral Eq. 13 is solved numerically to determine the potential and the potential gradient on the particle surface.

Hydrodynamics.

The fluid flows around the particle are described by the Stokes equations for creeping flow,

$$\nabla \cdot 𝝈=-\nabla p+\eta {\nabla }^2\mathrm{𝒖}=0\hspace{0.17em}\text{and}\hspace{0.17em}\nabla \cdot \mathrm{𝒖}=0,$$ [14]

where $\mathrm{𝒖}(\mathrm{𝒙})$ is the velocity, $p(\mathrm{𝒙})$ is the pressure, $𝝈(\mathrm{𝒙})$ is the stress tensor, and $\eta$ is the fluid viscosity. The particle moves as a rigid body with a translational velocity U and angular velocity $𝛀$. Here, we adopt a moving frame of reference centered on the particle. In this frame, there is no flow normal to the particle surface

$$\text{𝒏}\cdot \mathrm{𝒖}=0\hspace{0.17em}\text{for}\hspace{0.17em}\mathrm{𝒙}\in S_p.$$ [15]

The force of the electric field on the field-induced double layer induces a slip velocity ${\mathrm{𝒖}}_s$ tangential to the particle surface

$$\text{𝒕}\cdot \mathrm{𝒖}=\text{𝒕}\cdot {\mathrm{𝒖}}_s=\text{𝒕}\cdot \left(\frac{\epsilon }{\eta }\zeta (\mathrm{𝒙})\nabla \mathrm{\Phi }(\mathrm{𝒙})\right)\hspace{0.17em}\text{for}\hspace{0.17em}\mathrm{𝒙}\in S_p,$$ [16]

where t is a unit vector tangent to the surface, and $\zeta (\mathrm{𝒙})$ is the spatially dependent zeta potential. Here, $\zeta (\mathrm{𝒙})=C-\mathrm{\Phi }(\mathrm{𝒙})$, where $C$ is a constant chosen such that surface averaged zeta potential is zero. Far from the particle, the velocity approaches

$$\mathrm{𝒖}(\text{𝒙})=-(\text{𝑼}+𝛀\times \mathrm{𝒙})\hspace{0.17em}\text{for}\hspace{0.17em}\mathrm{𝒙}\to \mathrm{\infty }.$$ [17]

The translational and rotational velocities are determined by the constraints that there is no net force or torque acting on the particle,

$$\text{𝑭}={\int }_{S_p}\text{𝒇}(\text{𝒚})dS(\text{𝒚})=0\hspace{0.17em}\text{and}\hspace{0.17em}\text{𝑳}={\int }_{S_p}\text{𝒚}\times \text{𝒇}(\text{𝒚})dS(\text{𝒚})=0,$$ [18]

where $\text{𝒇}=𝝈\cdot \text{𝒏}$ is the stress on the surface. Rather than solve this problem directly, it is convenient to make use of the Lorentz reciprocal theorem to obtain (26, 56)

$$\widehat{\text{𝑭}}\cdot \mathrm{𝑼}+\widehat{\text{𝑳}}\cdot 𝛀=-{\int }_{S_p}{\mathrm{𝒖}}_s(\text{𝒚})\cdot \widehat{\text{𝒇}}(\text{𝒚})dS(\text{𝒚}),$$ [19]

where $\widehat{\text{𝒇}}=\widehat{𝝈}\cdot \text{𝒏}$ is the stress due to the same particle undergoing pure translational or rotational motion through a quiescent fluid; $\widehat{\text{𝑭}}$ and $\widehat{\text{𝑳}}$ are the force and torque due to this associated Stokes flow. The stress $\widehat{\text{𝒇}}(\mathrm{𝒙})$ is given by the integral equation

$$0={\widehat{u}}_j^{\mathrm{\infty }}(\mathrm{𝒙})-\frac{1}{8\pi \eta }{\int }_{S_p}\left(\frac{{\delta }_{ij}}{r}+\frac{r_i{r}_j}{r^3}\right){\widehat{f}}_i(\text{𝒚})dS(\text{𝒚}),$$ [20]

(see SI Appendix for details). The velocity far from the particle is that due to pure translation and/or rotation

$${\widehat{\mathrm{𝒖}}}^{\mathrm{\infty }}(\mathrm{𝒙})=-(\widehat{\mathrm{𝑼}}+\widehat{𝛀}\times \mathrm{𝒙})\hspace{0.17em}\text{for}\hspace{0.17em}\mathrm{𝒙}\to \mathrm{\infty }.$$ [21]

Solving the integral Eq. 20 numerically gives the stress $\widehat{\text{𝒇}}(\mathrm{𝒙})$, from which the force $\widehat{\text{𝑭}}$ and torque $\widehat{\text{𝑻}}$ are evaluated. The desired particle velocity U and $𝛀$ are computed using Eq. 19.

Numerical Solution.

The integral equations above are solved numerically using Lebedev quadrature (57) over surfaces parameterized by the spherical angles $\theta$ and $\varphi$. In this approach, integrals are approximated as

$${\int }_0^{2\pi }{\int }_0^{\pi }g(\theta ,\varphi )\sin \theta d\hspace{0.17em}\theta d\varphi \approx \sum _{q=1}^N{w}_{q}g({\theta }_q,{\varphi }_q),$$ [22]

where the grid points $({\theta }_q,{\varphi }_q)$ have octahedral rotation and inversion symmetry, and the grid weights $w_i$ enable the exact integration of spherical harmonics up to a given order. To circumvent the challenges associated with the singular integrand in Eq. 13, we introduce an alternative Green’s-like function ${\mathcal{G}}_{\alpha }(\mathrm{𝒙},\text{𝒚})$ for the potential at point y due to a Gaussian charge distribution of width ${\alpha }^{1/2}$ centered at point x. This function approaches the standard Green’s function for a point charge in an unbounded medium in the limit as $\alpha \to 0$. The integral Eq. 13 for the potential is then divided into two components: (i) a far-field contribution using the Gaussian-modulated Green’s function and (ii) a near-field correction that contains the singularity. The first component is nonsingular and can be computed numerically using Lebedev quadrature and a linear solver [MATLAB’s gmres() function]; the second one is nonzero only in the vicinity of the singularity and can be approximated analytically. We use an analogous approach for computing the hydrodynamic integral Eq. 20 with a similarly filtered Green’s function (58) (see SI Appendix for details).

For a given orientation of the applied field, the above approach was used to compute the translational and rotational velocity of the particle. This process was repeated for multiple orientations—typically, the 38 points of the ninth-order Lebedev grid. The nonzero tensor coefficients were then estimated by linear regression of Eqs. 1 and 2. Given the shape tensors, the equations of motion were integrated numerically using MATLAB’s ode113() Adams–Bashforth–Moulton solver (59); particle orientation was represented and integrated using unit quaternions (60).

Effects of Brownian Motion.

To describe the effects of Brownian motion on the shape-directed dynamics of particles moving by ICEP, we start from the Langevin equation for translational and rotational motion,

$$\text{𝒎}\cdot \frac{\mathrm{d}\mathcal{𝓤}}{\mathrm{d}t}={\mathcal{𝓕}}_E+{\mathcal{𝓕}}_H+{\mathcal{𝓕}}_B,$$ [23]

where m is a generalized mass/moment-of-inertia tensor, $\mathcal{𝓤}=\left(\mathrm{𝑼},𝛀\right)$ is the particle translational/rotational velocity vector, ${\mathcal{𝓕}}_E=\left({\text{𝑭}}_E{,\text{𝑳}}_E\right)$ is the electric force/torque vector, ${\mathcal{𝓕}}_H$ is the hydrodynamic force/torque vector, and ${\mathcal{𝓕}}_B$ is the stochastic force/torque that gives rise to Brownian motion (61). At low Reynolds numbers, the hydrodynamic force on the particle is linearly related to its velocity as $ve{\mathcal{F}}_H=-\mathcal{𝓡}\cdot \mathcal{𝓤}$, where $\mathcal{𝓡}$ is the hydrodynamic resistance tensor. Consistent with Eqs. 1 and 2 for the ICEP velocity, the electric force is equal and opposite to the hydrodynamic force, ${\mathcal{𝓕}}_E=-{\mathcal{𝓕}}_H$. The stochastic force/torque ${\mathcal{𝓕}}_B$ arises from thermal fluctuations and is characterized by

$$⟨{\mathcal{𝓕}}_B⟩=0\hspace{0.17em}\text{and}\hspace{0.17em}⟨{\mathcal{𝓕}}_B(0){\mathcal{𝓕}}_B(t)⟩=2k_{B}T\mathcal{𝓡}\delta (t),$$ [24]

where $k_{B}T$ is the thermal energy, the angle brackets denote an ensemble average, and $\delta (t)$ denotes the delta function.

Like the shape tensors $𝕮\prime$ and $𝕯\prime$, the resistance tensor in the particle frame is constrained by the particle symmetry (62). In particular, the symmetric resistance tensor can be divided as

$$\mathcal{𝓡}=\left(\begin{array}{cc}\hfill {\text{𝑹}}_{FU}\hfill & \hfill {\text{𝑹}}_{F\mathrm{\Omega }}\hfill \\ \hfill {\text{𝑹}}_{LU}\hfill & \hfill {\text{𝑹}}_{L\mathrm{\Omega }}\hfill \end{array}\right),$$ [25]

where ${\text{𝑹}}_{FU}$ is the symmetric translation tensor, ${\text{𝑹}}_{L\mathrm{\Omega }}$ is the symmetric rotation tensor, and ${\text{𝑹}}_{LU}={\text{𝑹}}_{F\mathrm{\Omega }}^T$ is the coupling pseudotensor. These tensors and pseudotensors satisfy symmetry relations analogous to Eqs. 5 and 6. With these constraints, the resistance tensors were computed numerically, using the boundary integral formulation detailed in the previous section. The Langevin equation Eq. 23) was integrated numerically in the overdamped regime, using Fixman’s midpoint scheme with a constant time step of $\mathrm{\Delta }t=0.1\eta /\epsilon E_{\mathrm{\infty }}^2$ (63). As in the deterministic simulations, the particle orientation was parameterized using normalized quaternions.