Evolution of vertical and oblique transmission under fluctuating selection

Significance

Evolutionary dynamics of phenotypes in populations depend on how the traits are transmitted across generations and how the environments that cause selection on the traits fluctuate over time. We show that, under periodically fluctuating selection, a gene that increases the rate of vertical transmission is disfavored when the periods are short but approaches an intermediate stable rate for longer periods. This stable rate differs markedly from the rate that maximizes the geometric mean fitness. The evolution of learning rules thus differs qualitatively from the evolution of genetically modified rules of genetic transmission.

Abstract

The evolution and maintenance of social learning, in competition with individual learning, under fluctuating selection have been well-studied in the theory of cultural evolution. Here, we study competition between vertical and oblique cultural transmission of a dichotomous phenotype under constant, periodically cycling, and randomly fluctuating selection. Conditions are derived for the existence of a stable polymorphism in a periodically cycling selection regime. Under such a selection regime, the fate of a genetic modifier of the rate of vertical transmission depends on the length of the cycle and the strength of selection. In general, the evolutionarily stable rate of vertical transmission differs markedly from the rate that maximizes the geometric mean fitness of the population. The evolution of rules of transmission has dramatically different dynamics from the more frequently studied modifiers of recombination, mutation, or migration.

Cavalli-Sforza and Feldman (1) distinguished two forms of nonparental phenotypic transmission in the context of cultural evolution. Horizontal transmission occurs when a trait is passed between members of the same generation and is analogous to transmission of an infectious agent. Oblique transmission to offspring is from nonparental members of the parental generation. Evolution under either of these is expected to be more rapid than under purely vertical (i.e., parent-to-offspring) transmission (2, 3).

Oblique transmission occurs via some mechanism of social learning, which may include imitation or active teaching. There has been an interesting debate over the past 30 y concerning the conditions under which social learning would have an advantage over individual learning or vertical (including genetic) transmission. This debate is usually couched in terms of the mode and tempo of environmental fluctuations that would affect fitness and hence, evolution (4–11). Mathematical analyses of models of competition between individual and social learning have generally shown that social learning has an advantage when the environment does not fluctuate too frequently. However, when environmental changes are very frequent, individual learning is favored, while innate (genetic) determination of the trait does best when periods between environmental change are long on average.

In some situations, oblique transmission of biological material is possible. In bacteria, phenotypes might be determined by heritable mobile genetic elements, such as phages (12), plasmids (13), integrons (14), and transposons (15). Similarly, some phenotypes are determined by genes that are commonly converted by uptake of foreign DNA (i.e., transformation) (16). In these cases, inheritance of a phenotype may combine vertical transmission from the parent cell and oblique transmission from other cells.

In some animals, transmission of microbes may occur during sharing or manipulation of food or other consumable resources during a social interaction. Although transmission of the microbiome in humans is likely to be mostly vertical (17), in other organisms, there is multigenerational food sharing, during which symbionts from the parental cohort may be transmitted obliquely to younger individuals (18). In such cases, fluctuations in the resource type or availability may have fitness effects that depend on features of the transmitted microbiome. This ecological perspective on community transmission is stressed by van Opstal and Bordenstein (19), who emphasize the “need to consider the relative roles of vertical and horizontal transmission of microbial communities.”

Another perspective on the evolutionary consequences of fluctuating environments (and as a result, fluctuating selection) derives from the phenomenon of phenotypic switching (20–25). In these studies, mutation causes the organism to switch phenotypes (usually treated as haploid genotypes), and the problem has usually been couched in terms of the optimal rate of mutation in models where the phenotypic fitness fluctuates over time. These models did not include social learning, and the evolution was regarded as a mode of bet-hedging against future environmental change. Optimal (that is, evolutionarily stable) mutation rates depend on many features of the fluctuations (for example, degree of fitness symmetry, strength of selection, and variance in the period of fluctuation) (23).

In a recent analysis of evolution under fluctuating selection, Xue and Leibler (26) allowed an organism to absorb information about the distribution of possible environments by learning the phenotypes of members of its parental lineage from previous generations. They describe this as “positive feedback that enhances the probability that the offspring expresses the same phenotype as the parent” (26). In this formulation, there was “reinforcement of the parent phenotype” in an offspring, such as might occur through epigenetic inheritance. Although their analysis was not couched in terms of oblique and vertical transmission, as defined by Cavalli-Sforza and Feldman (1), we have been stimulated by their analysis to develop a model in which oblique transmission, at a rate dependent on the trait frequency in the parental generation, occurs in addition to classical vertical transmission. We then ask how fluctuations in selection interact with the rate of oblique transmission to affect evolutionary dynamics and how the rate of oblique transmission itself might evolve.

In our formulation, both the parental phenotype and the distribution of phenotypes in the whole population contribute to an offspring’s phenotype. Using conventional modifier theory (27), we show that, in a symmetric cyclic selection regime with cycles of periods 1 or 2, an allele reducing the rate of vertical transmission is expected to increase in frequency when rare and in so doing, to increase the mean fitness of the population. However, for cycles of greater length or period asymmetry, interesting nonmonotonicities emerge both in the uninvadable rate of vertical transmission and in the rate that maximizes the geometric time average of the population mean fitness, which we will refer to as the “geometric mean fitness.” We develop the models in very large populations with cyclic selection and with random fitness and also in the case where drift occurs via sampling from generation to generation in a finite population.

Model

Consider an infinite population whose members are characterized by their phenotype $\varphi$, which can be of two types, $\varphi =A$ or $\varphi =B$, with associated frequencies $x$ and $(1-x)$, respectively. We follow the evolution of $x$ over discrete nonoverlapping generations. In each generation, individuals are subject to selection, where the fitnesses of $A$ and $B$ are $w_A$ and $w_B$, respectively.

An offspring inherits its phenotype from its parent via vertical transmission with probability $\rho$ and from a random individual in the parental population via oblique transmission with probability $(1-\rho )$. Therefore, given that the parent phenotype is $\varphi$ and assuming uniparental inheritance (28), the conditional probability that the phenotype $\varphi \prime$ of the offspring is $A$ is

$$P(\varphi \prime =A|\varphi )=\{\begin{array}{cc}\hfill (1-\rho )x+\rho \hfill & \hfill \text{if}\varphi =A\hfill \\ \hfill (1-\rho )x\hfill & \hfill \text{if}\varphi =B\hfill \end{array},$$ [1]

where $x=P(\varphi =A)$ in the parent’s generation before selection.

Therefore, the frequency $x\prime$ of phenotype $A$ after one generation is given by the recursion equation

$$x\prime =\rho {\displaystyle \frac{w_A}{\overline{w}}}x+(1-\rho )x={\displaystyle \frac{w_A}{\overline{w}}}x\left[(1-\rho )x+\rho \right]+{\displaystyle \frac{w_B}{\overline{w}}}(1-x)\left[(1-\rho )x\right],$$ [2]

where $\overline{w}$ is the mean fitness, namely

$$\overline{w}=w_{A}x+w_B(1-x).$$ [3]

Eq. 2 can be rewritten as

$$x\prime =x\left[1+\rho (1-x){\displaystyle \frac{w_A-w_B}{\overline{w}}}\right]=x\cdot {\displaystyle \frac{x(1-\rho )(w_A-w_B)+\rho w_A+(1-\rho )w_B}{x(w_A-w_B)+w_B}}.$$ [4]

In what follows, we explore the evolution of the recursion Eq. 4, namely the equilibria and their stability properties, in the cases of constant environments and changing environments.

Constant Environment.

When the environment is constant, the fitness parameters $w_A$ and $w_B$ do not change between generations, and we have the following result.

Result 1.

If $0<\rho \le 1$ and both $w_A$ and $w_B$ are positive with $w_A\ne w_B$, then fixation in the phenotype $A(B)$ is globally stable when $w_A>w_B$ $(w_A<w_B)$.

Proof:

If we rewrite Eq. 4 as $x\prime =x\cdot f(x)$, it can be seen that $f(1)=1$, and for $\rho >0$ and $0<x<1$,

$$\begin{array}{ccc}\hfill f(x)>1\hfill & \hfill \text{when}\hfill & \hfill w_A>w_B,\hfill \\ \hfill f(x)<1\hfill & \hfill \text{when}\hfill & \hfill w_A<w_B.\hfill \end{array}$$ [5]

Hence, as $w_A>0$ and $w_B>0$, both fixations in $A$ or in $B$ ($x^{\ast }=1$ for fixation in $A$ and $x^{\ast }=0$ for fixation in $B$) are equilibrium points of Eq. 4. Moreover, if $x_t$ is the value of $x$ at the $t$th generation $(t=\mathrm{0,1,2},\mathrm{\dots })$, from Eqs. 4 and 5, we have, for any $0<x_0<1$ and all $t=\mathrm{0,1,2},\mathrm{\dots }$,

$$\begin{array}{ccc}\hfill x_{t+1}>x_t\hfill & \hfill \text{when}\hfill & \hfill w_A>w_B,\hfill \\ \hfill x_{t+1}<x_t\hfill & \hfill \text{when}\hfill & \hfill w_A<w_B,\hfill \end{array}$$ [6]

and since $x^{\ast }=1$ or $x^{\ast }=0$ is the only equilibrium point, we have

$$\begin{array}{ccc}\hfill {lim}_{t\to \mathrm{\infty }}{x}_t=1,\hfill & \hfill \text{for all}\hspace{0.17em}0<x_0\le 1,\hfill & \hfill \text{when}\hspace{1em}{w}_A>w_B,\hfill \\ \hfill {lim}_{t\to \mathrm{\infty }}{x}_t=0,\hfill & \hfill \text{for all}\hspace{0.17em}0\le x_0<1,\hfill & \hfill \text{when}\hspace{1em}{w}_A<w_B.\hfill \end{array}$$ [7]

Therefore, fixation of the favored phenotype is globally stable.

Periodically Changing Environment.

Suppose the environment changes periodically, such that the favored phenotype changes after a fixed number of generations. Simple examples are $A1B1=ABABAB\mathrm{\dots }$, in which the favored phenotype switches every generation, or $A2B1=AABAABAAB\mathrm{\dots }$, where every two generations, in which selection favors $A$, are followed by a single generation, in which selection favors $B$. In general, $AkBl$ denotes a selection regime, in which the period is of $(k+l)$ generations, with $k$ generations favoring phenotype $A$ followed by $l$ generations favoring $B$.

Let $W$ be the fitness of the favored phenotype and $w$ be that of the other phenotype, where $0<w<W$. Rewrite Eq. 4 as $x\prime =F_A(x)=x{f}_A(x)$ when $A$ is favored and $x\prime =F_B(x)=x{f}_B(x)$ when $B$ is favored. Then,

$$\begin{array}{c}{f}_A(x)={\displaystyle \frac{x(1-\rho )(W-w)+\rho W+(1-\rho )w}{x(W-w)+w}}=1+\rho (1-x){\displaystyle \frac{W-w}{Wx+w(1-x)}},\\ f_B(x)={\displaystyle \frac{x(1-\rho )(w-W)+\rho w+(1-\rho )W}{x(w-W)+W}}=1+\rho (1-x){\displaystyle \frac{w-W}{wx+W(1-x)}}.\end{array}$$ [8]

If $x_t$ denotes the frequency of the phenotype $A$ at generation $t$ starting with $x_0$ initially, then as we are interested in the values of $x_t$ for $t=n(k+l)$ with $n=\mathrm{0,1},\mathrm{\dots }$ at the end of complete periods, we can write

$$x_{(n+1)(k+l)}=F(x_{n(k+l)}),n=\mathrm{0,1,2},\mathrm{\dots },$$ [9]

where $F$ is the composed function

$$F=\underset{l\hspace{0.17em}\text{times}}{\underbrace{F_B\circ F_B\circ \mathrm{\cdots }\circ F_B}}\circ \underset{k\hspace{0.17em}\text{times}}{\underbrace{F_A\circ F_A\circ \mathrm{\cdots }\circ F_A}}.$$ [10]

Clearly, since $F_A(0)=F_B(0)=0$ and $F_A(1)=F_B(1)=1$, both fixations in $A$ or in $B$ are equilibrium points. An interesting question is when these fixations are locally stable. We concentrate on $x^{\ast }=0$, the fixation of the phenotype $B$. As $x\prime =F_A(x)=x{f}_A(x)$ for $k$ generations and $x\prime =F_B(x)=x{f}_B(x)$ for $l$ generations, the linear approximation of $F(x)$ “near” $x=0$ is

$$F(x)\simeq {\left[f_A(0)\right]}^k{\left[f_B(0)\right]}^{l}x.$$ [11]

Hence, the local stability of $x^{\ast }=0$ is determined by the product ${\left[f_A(0)\right]}^k{\left[f_B(0)\right]}^l$; $x^{\ast }=0$ is locally stable if this product is less than one and unstable if it is larger than one.

From Eq. 8, we have

$$f_A(0)=1+\rho \frac{W-w}{w},\hspace{1em}{f}_B(0)=1+\rho \frac{w-W}{W}.$$ [12]

We start with the case $k=l$.

Result 2.

If $k=l$ and $0<w<W$ with $0<\rho <1$, fixation of $B$ is unstable.

Proof:

The local stability of $x^{\ast }=0$, the fixation of $B$, is determined by the product

$${\left[f_A(0)\right]}^k{\left[f_B(0)\right]}^k={\left[\left(1+\rho \frac{W-w}{w}\right)\left(1+\rho \frac{w-W}{W}\right)\right]}^k.$$ [13]

Observe that

$$\left(1+\rho \frac{W-w}{w}\right)\left(1+\rho \frac{w-W}{W}\right)=1+\rho (1-\rho )\frac{{\left(W-w\right)}^2}{wW}>1.$$ [14]

Since $0<\rho <1$ and $0<w<W$, fixation on $B$ is unstable.

Conclusions.

• i)Since $k=l$ and the above result also holds when $0<W<w$, there is total symmetry between the two fixations in $A$ and $B$, and fixation in $A$ is also unstable. Thus, neither phenotype can be lost, and there is a protected polymorphism (29).
• ii)
  For general $k$, $l$, the condition for local stability of fixation in $A$ is

  $${\left[f_A(0)\right]}^l{\left[f_B(0)\right]}^k<1,$$ [15]

  and that of B is

  $${\left[f_A(0)\right]}^k{\left[f_B(0)\right]}^l<1.$$ [16]

  Therefore, following Result 2,

  $${\left[f_A(0)\right]}^{k+l}{\left[f_B(0)\right]}^{k+l}>1,$$ [17]

  and it is impossible that both fixations are stable. Furthermore, since by Eq. 12, $f_A(0)$> and 0>f_B(0)>1 when 0>w >W, by choosing k and l appropriately, fixation on A or fixation on B (but not both) can be stable. In addition, we can have both fixations unstable giving the following result.

Result 3.

With $0<\rho <1$ and $0<w<W$ in the case of $AkBl$ periodically changing environments, both fixations may be unstable, producing a protected polymorphism.

Proof:

Let $a=1+\rho \frac{W-w}{w}$ and $b=1+\rho \frac{w-W}{W}$, and our assumption entails $a>1$ and $0<b<1$. Following Eq. 11, fixation in $B$ is unstable if $a^k{b}^l>1$, and similarly, fixation in $A$ is unstable if $a^l{b}^k>1$. Therefore, both fixations are unstable if

$$a^k{b}^l>1\hspace{1em}\text{and}\hspace{1em}{a}^l{b}^k>1$$ [18]

or equivalently, if

$$k\log a+l\log b>0\hspace{1em}\text{and}\hspace{1em}l\log a+k\log b>0.$$ [19]

Now the inequalities of Eq. 19 hold if and only if

$$k\frac{\log (1/b)}{\log a}<l<k\frac{\log a}{\log (1/b)}.$$ [20]

These inequalities are consistent if and only if $\log (1/b)<\log a$ (i.e., $ab>1$), which is true by Eq. 14.

The linear approximation of $F(x)$ near $x^{\ast }=0$ (Eq. 11) does not depend on the order in which phenotypes $A$ and $B$ are favored within a cycle of $k+l$ generations. Therefore, the local stability properties of the two fixations depend only on the fact that, in a cycle of $(k+l)$ generations,$A$ is favored $k$ times and $B$ is favored $l$ times and not their order in the cycle. When neither fixation in $A$ nor that in $B$ are stable, there is a protected polymorphism, and we expect to have one or more polymorphic equilibria. Fig. S1 illustrates the relationship between $k,l$ and $\rho$ that gives polymorphism of $A$ and $B$, or fixation, for different values of $s=W-w$.

For the simple case of $A1B1$ periodically changing environment, we have the following.

Result 4.

In the case $A1B1$ with $0<\rho <1$ and $0<w<W$, the two fixations are unstable, and there exists a unique stable polymorphism.

Proof:

Let $x$ be the initial frequency of $A$ and $x\prime$ be its frequency after one cycle of $A1B1$ selection. Then, $x\prime =F_B\left(F_A(x)\right)$, where, by Eq. 8,

$$\begin{array}{c}{F}_A(x)=x{\displaystyle \frac{x(1-\rho )(W-w)+\rho W+(1-\rho )w}{x(W-w)+w}},\\ F_B(y)=y{\displaystyle \frac{y(1-\rho )(w-W)+\rho w+(1-\rho )W}{y(w-W)+W}}.\end{array}$$ [21]

The equilibrium equation is $x=F_B\left(F_A(x)\right)$, which reduces to a fourth degree polynomial equation in $x$. Since the fixations in $B$ and $A$ are equilibria corresponding to the solutions $x=0$ and $x=1$, the other equilibria correspond to solutions of a quadratic equation $Q(x)={\alpha }_2{x}^2+{\alpha }_{1}x+{\alpha }_0=0$, with ${\alpha }_2=1$ and

$${\alpha }_1=\frac{W+w}{(2-\rho )(W-w)}-1,{\alpha }_0=\frac{-w}{(2-\rho )(W-w)}.$$ [22]

As $0<\rho <1$ and $0<w<W$, we have

$$\begin{array}{c}Q(0)={\displaystyle \frac{-w}{(2-\rho )(W-w)}}<0\\ \text{and}\hspace{0.17em}Q(1)={\displaystyle \frac{W}{(2-\rho )(W-w)}}>0.\end{array}$$ [23]

Also, as ${\alpha }_2=1$ and ${\alpha }_0<0$, the quadratic equation $Q(x)=0$ has two real roots, one negative and one positive $x^{\ast }$, satisfying $0<x^{\ast }<1$. The latter determines a unique polymorphism. Let $H(x)=F_B\left(F_A(x)\right)$. Then,

$$H(0)=0,H(x^{\ast })=x^{\ast },H(1)=1.$$ [24]

Also,

$$F_A^{\prime }(x)=\frac{x^2(1-\rho ){(W-w)}^2+2xw(1-\rho )(W-w)+w[\rho W+(1-\rho )w]}{{[x(W-w)+w]}^2}$$ [25]

and

$$F_B^{\prime }(x)=\frac{x^2(1-\rho ){(w-W)}^2+2xW(1-\rho )(w-W)+W[\rho w+(1-\rho )W]}{{[x(w-W)+W]}^2}.$$ [26]

From our assumptions on $\rho$, $w$, and $W$, we have $F_A^{\prime }(x)>0$ for $0\le x\le 1$. Observe that the numerator of $F_B^{\prime }(x)$ is linear in $\rho$; its value when $\rho =1$ is $wW>0$, and when $\rho =0$, it is

$$x^2{\left(w-W\right)}^2+2xW(w-W)+W^2={[x(w-W)+W]}^2>0.$$ [27]

Hence, $F_B^{\prime }(x)>0$ for all $0\le x\le 1$, and $H\prime (x)=F_B^{\prime }\left(F_A(x)\right)F_A^{\prime }(x)$ is positive when $0\le x\le 1$. Thus, $H(x)$ is monotone increasing for $0\le x\le 1$; $H(x)>x$ is monotone increasing for $0<x<x^{\ast }$, and $H(x)<x$ is monotone increasing for $x^{\ast }<x<1$. Starting from any initial value $0<x_0<1$, we have $x_t\to x^{\ast }$ as $t\to \mathrm{\infty }$. Fig. S2 A, C, and E illustrates how the frequency of $A$ changes over time in the $A1B1$ regime of cycling selection.

For more general cyclic fitness regimes, the polynomial that gives the equilibria is of higher order, and it is conceivable that more than one stable polymorphism could exist for given values of $\rho$, $W$, and $w$. We have been able to show that, when neither fixation in $A$ nor fixation in $B$ are stable, in the $AkBk$ case, this cannot occur. In fact, we have the following.

Result 5.

In the $AkBk$ selection regimes, if the fixations in $A$ and $B$ are locally unstable, a single stable polymorphic equilibrium exists.

The proof of Result 5 is in SI Text. Fig. S3A shows the stable equilibrium frequencies $x^{\ast }$ as a function of $\rho$, $W$, and $w$ in the $A1B1$ regime. For $AkBk$ selection regimes from $k=1$ to $k=40$, Fig. S4 illustrates the convergence to a single stable polymorphism.

We have not been able to prove that, for selection regimes $AkBl$ with $l\ne k$, there is a single stable polymorphic equilibrium when the two fixations are unstable. However, the numerical examples in Fig. S1 for $AkBl$ and in Fig. 1 and Fig. S5 for the special case $A1B2$ all exhibit a single stable polymorphic equilibrium when fixations in $A$ and $B$ are unstable. These numerical results suggest that, for $W>w>0$ and $0<\rho <1$, the high-order equilibrium polynomial has only a single root corresponding to a globally stable polymorphism. Fig. S6 shows that this is the case for the $A3B10$ regime.

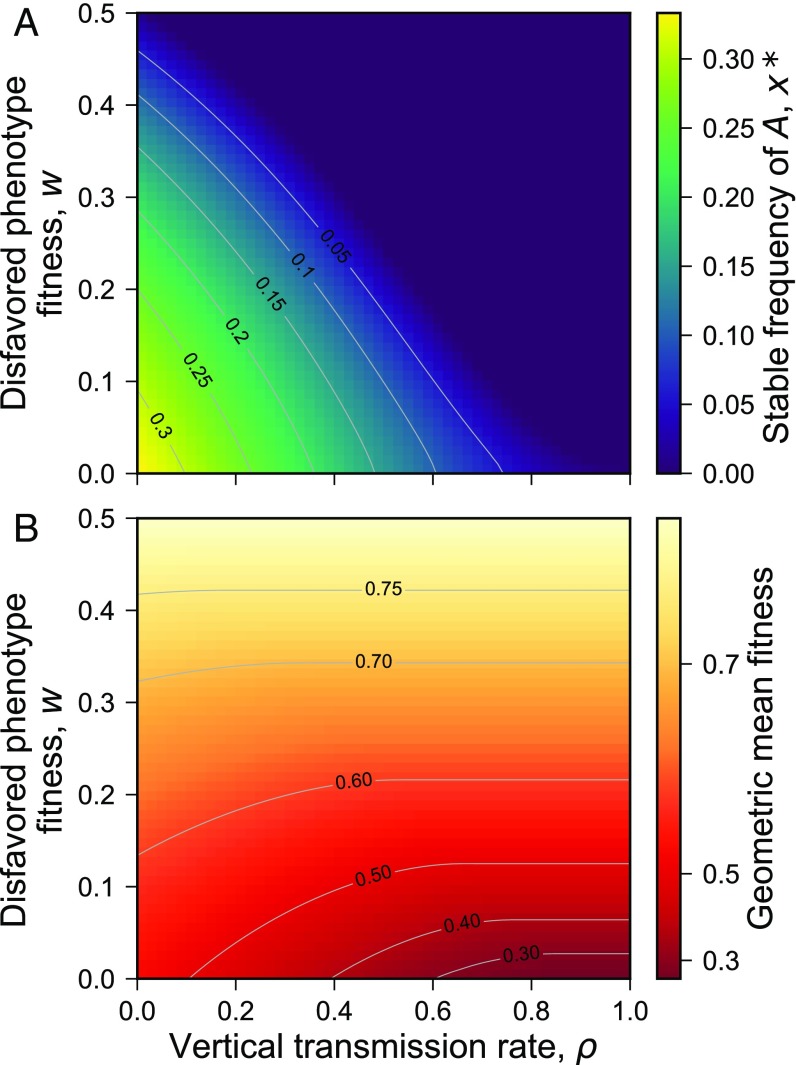
Fig. 1.

Stable frequency of phenotype A and geometric mean fitness in selection regime $A1B2$ as a function of the vertical transmission rate $\rho$ and the fitness of the disfavored phenotype $w$. (A) Stable frequency of phenotype $A$ at the end of each three-generation cycle. (B) Geometric average of the stable population mean fitness over the three-generation cycle: ${(\overline{w}\text{*}\cdot \overline{w}\text{**}\cdot \overline{w}\text{***})}^{1/3}$. Gray contour lines join $\rho$ and $w$ combinations that result in the same stable value. In all cases, W = 1.

Randomly Changing Environment.

We now consider the case where the environment changes according to a stochastic process. Without loss of generality, assume that the fitness parameters at generation $t$ ($t=\mathrm{0,1,2},\mathrm{\dots }$) are $1+s_t$ for phenotype $A$ and $1$ for phenotype $B$, where the random variables $s_t$ for $t=\mathrm{0,1,2},\mathrm{\dots }$ are independent and identically distributed. Also assume that there are positive constants $C$ and $D$, such that $P(-1+C<s_t<D)=1$.

Corresponding to Eq. 4, with $w_A=1+s_t$ and $w_B=1$, the recursion equation is

$$x_{t+1}=x_t\frac{1+\rho s_t+x_t(1-\rho )s_t}{1+x_t{s}_t}\hspace{0.17em}t=\mathrm{0,1,2},\mathrm{\dots }.$$ [28]

As $\{x_t\}$ for $t=\mathrm{0,1,2},\mathrm{\dots }$ is a sequence of random variables, the notion of stability of the two fixation states needs clarification. Following Karlin and Lieberman (30) and Karlin and Liberman (31), we make the following definition.

Definition:

“Stochastic local stability” is defined as follows. A constant equilibrium state $x^{\ast }$ is said to be stochastically locally stable if, for any $\epsilon >0$, there exists a $\delta >0$, such that $|x_0-x^{\ast }|<\delta$ implies

$$P(\underset{t\to \mathrm{\infty }}{lim}{x}_t=x^{\ast })\ge 1-\epsilon .$$ [29]

Thus, $x^{\ast }$ is stochastically locally stable if for any initial $x_0$ sufficiently near $x^{\ast }$ the process $x_t$ converges to $x^{\ast }$ with high probability.

In our case, there are two constant equilibria $x^{\ast }=0$ and $x^{\ast }=1$ corresponding to fixation in $B$ and $A$, respectively. We can characterize the stochastic local stability of these fixations with the following results, and proofs are in SI Text.

Result 6.

Suppose $E\left[\log (1+\rho s_t)\right]>0$. Then, $x^{\ast }=0$, the fixation of phenotype $B$, is not stochastically locally stable. In fact, $P({lim}_{t\to \mathrm{\infty }}{x}_t=0)=0$.

Result 7.

Suppose $E[\log (1+\rho s_t)]<0$. Then, $x^{\ast }=0$, the fixation of phenotype $B$, is stochastically locally stable. In particular, if $E(s_t)\le 0$, $x^{\ast }=0$ is stochastically locally stable.

Using the general notation for the fitness parameters $w_A$ and $w_B$, the stochastic local stability of fixation in $B$ is determined by the sign of $E\left[\log \left(1-\rho +\rho \frac{w_A}{w_B}\right)\right]$, and that of fixation in $A$ is determined by the sign of $E\left[\log \left(1-\rho +\rho \frac{w_B}{w_A}\right)\right]$. For example, if the sign of the first is negative, fixation in $B$ is stochastically locally stable, and when it is positive, with probability of one, convergence to fixation in $B$ does not occur. It is also true that, if $E(w_A/w_B)\le 1$, then fixation of $B$ is stochastically locally stable. Following Eq. 14, for all realizations of $w_A$ and $w_B$,

$$\log \left(1-\rho +\rho \frac{w_A}{w_B}\right)+\log \left(1-\rho +\rho \frac{w_B}{w_A}\right)>0.$$ [30]

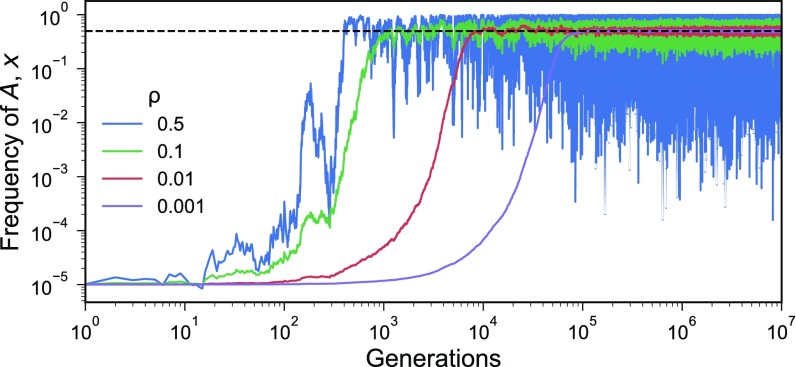
Therefore, as in the case of periodically changing environments $AkBl$, it is impossible that both fixations are simultaneously stochastically locally stable. It is possible, however, that neither fixation is stochastically locally stable, in which case, we expect the population to converge to a polymorphic distribution. Fig. 2 illustrates how the properties of $s_t$ in Eq. 28 affect the frequency of phenotype $A$ and in particular, the stochastic local stability of fixation in phenotype $B$. Fig. 3 shows the dynamics of the frequency of $A$ in a case where $w_A$ and $w_B$ are identically distributed and independent; in this case, the expectation of the stationary distribution is $\frac{1}{2}$, and its variance increases as $\rho$ increases.

Fig. 2.

Stochastic local stability. The figure shows the frequency of phenotype A after ${10}^6$ generations in a very large population evolving in a stochastic environment (Eq. 28). The fitnesses of phenotypes A and B are $w_A=1+s_t$ and $w_B=1$, respectively, where $s_t$ is s with probability p and $-s$ with probability $1-p$. The gray lines mark combinations of p and s for which $E[\log (1-\rho +\rho \frac{w_A}{w_B})]=0$ and $E[\log (1-\rho +\rho \frac{w_B}{w_A})]=0$. According to Result 6, between these lines, fixation of either phenotype is not stochastically locally stable, and we expect a stationary polymorphism between the lines. Here, initial frequency of $A$ is $x_0=1/10,000$, and the vertical transmission rate is $\rho =0.1$.

Fig. 3.

Effect of vertical transmission rate $\rho$ on phenotype polymorphism in a randomly changing environment. Dynamics of the frequency of phenotype $A$ over time starting at $x_0={10}^{-5}$ when the fitnesses of phenotypes $A$ and $B$ are identically and independently distributed random variables. As the vertical transmission rate $\rho$ increases from 0.001 to 0.5, the frequency reaches a polymorphic distribution with $E(x_t)\to 0.5$ faster, but the variance also increases. The fitnesses of phenotypes $A$ and $B$, $w_A$ and $w_B$, respectively, are both exponential random variables with expected values of two.

Evolutionary Stability of Oblique Transmission

An interesting question concerns the evolution of oblique transmission itself. For example, is there an evolutionarily stable rate of oblique transmission? To answer this question, we use a modifier model, in which we suppose that the vertical transmission rate is controlled by a genetic locus with two possible alleles $m$ and $M$. Let the vertical transmission rates determined by $m$ and $M$ be $\rho$ and $P$, respectively. Thus, there are four pheno-genotypes: $mA$, $mB$, $MA$, and $MB$, with frequencies that, at a given generation, are denoted by $x_1$, $x_2$, $x_3$, and $x_4$, respectively. As the fitnesses are determined by the two phenotypes $A$ and $B$ and the modifier locus is selectively neutral, we have the following table:

$$\begin{array}{ccccc}\hfill \text{pheno}-\text{genotype}\hfill & \hfill mA\hfill & \hfill mB\hfill & \hfill MA\hfill & \hfill MB\hfill \\ \hfill \text{frequency}\hfill & \hfill x_1\hfill & \hfill x_2\hfill & \hfill x_3\hfill & \hfill x_4\hfill \\ \hfill \text{fitness}\hfill & \hfill w_A\hfill & \hfill w_B\hfill & \hfill w_A\hfill & \hfill w_B\hfill \\ \hfill \text{vertical transmission rate}\hfill & \hfill \rho \hfill & \hfill \rho \hfill & \hfill P\hfill & \hfill P\hfill \end{array}.$$ [31]

Following the rationale leading to Eq. 2, the next generation pheno-genotype frequencies $x_1^{\prime }$, $x_2^{\prime }$, $x_3^{\prime }$, and $x_4^{\prime }$ are

$$\begin{array}{c}\overline{w}{x}_1^{\prime }=w_A{x}_1\left[(1-\rho )(x_1+x_3)+\rho \right]+w_B{x}_2(1-\rho )(x_1+x_3)\hfill \\ \overline{w}{x}_2^{\prime }=w_A{x}_1(1-\rho )(x_2+x_4)+w_B{x}_2\left[(1-\rho )(x_2+x_4)+\rho \right]\hfill \\ \overline{w}{x}_3^{\prime }=w_A{x}_3\left[(1-P)(x_1+x_3)+P\right]+w_B{x}_4(1-P)(x_1+x_3)\hfill \\ \overline{w}{x}_4^{\prime }=w_A{x}_3(1-P)(x_2+x_4)+w_B{x}_4\left[(1-P)(x_2+x_4)+P\right],\hfill \end{array}$$ [32]

with $\overline{w}$, the mean fitness, given by

$$\overline{w}=w_A(x_1+x_3)+w_B(x_2+x_4).$$ [33]

Note that, under these assumptions, the $M/m$ locus and the $A/B$ phenotypic dichotomy do not undergo anything analogous to recombination, which might be introduced if $A/B$ phenotypes were viewed as haploid genetic variants.

Starting with a stable equilibrium, where only the $m$ allele is present, we check its external stability (27, 32) to invasion by allele $M$. A constant environment always leads to fixation of the favored type, independent of $\rho$. We, therefore, assume changing environments and in particular, the simple case of the $A1B1$ cycling environment, where a unique stable polymorphism exists and depends on $\rho$ (SI Text has a computational analysis of the general $AkBl$ case). Specifically, from Eq. 32 with $w_A=W$, $w_B=w$ in the first generation and $w_A=w$, $w_B=W$ in the second generation, after two generations, we have

$${\underset{¯}{x}}^{″}=T_2(T_1\underset{¯}{x}),$$ [34]

where the nonlinear transformation $\underset{¯}{x}\prime =T_1\underset{¯}{x}$ is given by Eq. 32 with $w_A=W$, $w_B=w$ and the nonlinear transformation ${\underset{¯}{x}}^{″}=T_2\underset{¯}{x}\prime$ is given by Eq. 32 with $w_A=w$, $w_B=W$. Here, $\underset{¯}{x}$, $\underset{¯}{x}\prime$, and ${\underset{¯}{x}}^{″}$ are the frequency vectors.

For the $A1B1$ case, when only the $m$ allele is present with associated rate $\rho$, $0<\rho <1$, and $0<w<W$, a unique stable equilibrium ${\underset{¯}{x}}^{\ast }=(x_1^{\ast },1-x_1^{\ast },\mathrm{0,0})$ exists. $x_1^{\ast }$ is the only positive root of the quadratic equation $Q(x)={\alpha }_2{x}^2+{\alpha }_{1}x+{\alpha }_0=0$, with ${\alpha }_2,{\alpha }_1,{\alpha }_0$ specified in Eq. 22. Solving $Q(x)=0$ gives

$$x_1^{\ast }=\frac{1}{2}-\frac{W+w-\sqrt{{\left(1-\rho \right)}^2{\left(W-w\right)}^2+4Ww}}{2\cdot (2-\rho )(W-w)},$$ [35]

and it can be seen that

$$\frac{\sqrt{Ww}-w}{W-w}<x_1^{\ast }<\frac{1}{2}.$$ [36]

The external stability of ${\underset{¯}{x}}^{\ast }$ to the introduction of the modifier allele $M$ with rate $P$ is determined by the linear approximation matrix $𝐋$. We prove the following result in SI Text.

Result 8.

$𝐋$ has two positive eigenvalues, and

• i)when $P>\rho$, the two eigenvalues are less than one;
• ii)when $P<\rho$, the largest eigenvalue is larger than one; and
• iii)when $P=\rho$, the largest eigenvalue is one.

We conclude that, in the $A1B1$ selection regime, an allele $m$ producing vertical transmission rate $\rho$ is stable to the introduction of a modifier allele $M$ with associated rate $P$ if $P>\rho$, and it is unstable if $P<\rho$. Thus, in this case, evolution tends to reduce vertical transmission and hence, increase the rate of oblique transmission, and there is a reduction principle for the rate of vertical transmission (27, 32). The evolutionary dynamics of the reduction in $\rho$ under the $A1B1$ cycling regime are shown in Fig. 4, which also illustrates the change in phenotype frequencies over time.

Fig. 4.

Consecutive fixation of modifiers that reduce the vertical transmission rate in selection regime A1B1. The figure shows results of numerical simulations of evolution with two modifier alleles (Eq. 32). When a modifier allele fixes (frequency $>$ 99.9%), a new modifier allele is introduced with a vertical transmission rate one order of magnitude lower (vertical dashed lines). (A) The frequency of phenotype A in the population over time. (B) The frequency of the invading modifier allele over time. (C) The population geometric mean fitness over time; Inset zooms in to show that the mean fitness increases slightly with each invasion. Invading alleles are introduced at frequency 0.01%; whenever their frequency drops below 0.01%, they are reintroduced. Parameters: vertical transmission rate of the initial resident modifier allele, ${\rho }_0=0.1$; fitness values: $W=1$ and $w=0.5$. The x axis is on a log scale, as each sequential invasion takes an order of magnitude longer to complete. Fig. S12 shows $w=0.1$ and $0.9$.

In the case of identically distributed random fitnesses $w_A$ and $w_B$, Fig. 5 shows an example of the success of modifiers that reduce $\rho$. We have not, however, been able to prove that there is a reduction principle for this class of fluctuating fitnesses.

Fig. 5.

Consecutive fixation of modifiers that reduce the vertical transmission rate $\rho$ under symmetric randomly changing selection. The figure shows results of numerical simulations of evolution with two modifier alleles (Eq. 32). When a modifier allele fixes (frequency > 99.9%), a new modifier allele is introduced with a vertical transmission rate one order of magnitude lower (vertical dashed lines). (A) The frequency of phenotype A in the population over time. (B) The frequency of the invading modifier allele over time. Invading alleles are introduced at frequency 0.01%; whenever their frequency drops below 0.01%, they are reintroduced. Parameters: vertical transmission rate of the initial resident modifier allele is ${\rho }_0=0.1$, and the ratio of fitness values is $w_A/w_B=10$ with probability 0.5 and $w_A/w_B=0.1$ also with probability 0.5. The x axis is on a log scale, as each sequential invasion takes an order of magnitude longer to complete.

Values of the evolutionarily stable vertical transmission rate, ${\rho }^{\ast }$, for some $AkBl$ examples (SI Text and Fig. S10 have analytical details) are recorded in Table 1 for different values of $w$ relative to $W=1$. Interestingly, with $w=0.1$, the evolutionarily stable value of $\rho$ is zero for the $A1B2$ regime but not for the $A3B10$ and $A5B30$ regimes, in which the only stable values are those that lead to fixation of phenotype $B$ (e.g., $\rho >0.4625$ and $\rho >0.1489$, respectively); these are, therefore, neutrally stable (Fig. S10). $AkBk$ results are plotted in Fig. 6B. In the $A2B2$ regime, ${\rho }^{\ast }=0$, and there is reduction of vertical transmission for all selection values tested. However, for $AkBk$ regimes with $k>2$, we find ${\rho }^{\ast }\ne 0$, and depending on $w$, ${\rho }^{\ast }$ can be as high as 0.95. In Table 1, blank values for ${\rho }^{\ast }$ indicate that our method was numerically unstable and that a precise value for ${\rho }^{\ast }$ could not be obtained. This is why, in Fig. 6B, no ${\rho }^{\ast }$ points are shown for $AkBk$ with $k>19$. In Table 1, the word “fixation” indicates that fixation of $B$ occurs, at which point there can be no effect of modification of $\rho$; ${\rho }^{\ast }$ cannot be calculated in such cases.

Table 1.

Values of $\rho \text{*}$ (stable $\rho$) and $\widehat{\rho }$ (optimal $\rho$)

$k$	$l$	$\{w\}$ †	$\rho *$	$\widehat{\rho }$
1	1	0.1	0.000000	0.000000
1	1	0.5	0.000000	0.000000
1	1	0.9	0.000000	0.000000
1	2	0.1	0.000000	0.00065
1	2	0.5	Fixation	Fixation
1	2	0.9	Fixation	Fixation
2	2	0.1	0.000000	0.000000
2	2	0.5	0.000000	0.000000
2	2	0.9	0.000000	0.000000
3	10	0.1	>0.4265	0.00031
3	10	0.5	Fixation	Fixation
3	10	0.9	Fixation	Fixation
5	30	0.1	>0.1489	0.00027
5	30	0.5	Fixation	Fixation
5	30	0.9	Fixation	Fixation
12	12	0.1	0.84924	0.24347
12	12	0.5	0.91209	0.000000
12	12	0.9	0.95686	0.000000
20	20	0.1		0.223925
20	20	0.5	0.94643	0.000000
20	20	0.9	0.98304	0.000000
30	30	0.1		0.193280
30	30	0.5	0.96331	0.000000
30	30	0.9	0.99136	0.000000
50	50	0.1		0.15419
50	50	0.5	0.9768	0.22107
50	50	0.9	0.99581	0.000000

ρ* is the uninvadable value of the vertical transmission rate. $\widehat{\rho }$ is the rate that maximizes the geometric mean fitness at the stable equilibrium of the AkBl cycle

^†Note that $W=1$.

Fig. 6.

Fitness “optimal” and evolutionary stable vertical transmission rate in $AkBk$ selection regime. (A) The vertical transmission rate $\widehat{\rho }$ that maximized the geometric average of the population mean fitness is zero (complete oblique transmission) when selection cycles quickly between favoring phenotype $A$ and $B$ and then abruptly transitions to $\approx 0.2$ followed by a slow decrease (Figs. S5 and S6 have details on the abrupt transition). (B) The evolutionary stable rate $\rho \text{*}$, which cannot be invaded by modifiers with either higher or lower vertical transmission rate $P$, rapidly increases from zero when selection cycles are short ($k=1$ or $2$) to roughly one when selection cycles are longer. The dashed line shows $1-\frac{1}{k-1}$, which fits the values for $w=0.5$ (41). The values for $w=0.1$ (blue) could not be calculated for $k>19$ due to numerical instability when selection is strong and the duration between selection fluctuations is long. In all cases, $W=1$. SI Text has details on how we calculated the stable rate.

Geometric Mean Fitness and Rate of Vertical Transmission

Under fluctuating selection, the geometric mean fitness of genotypes has been shown to determine their evolutionary dynamics (8, 30, 33). For the evolution of mutation rates that are controlled by genetic modifiers, the stable mutation rate and the mutation rate that maximizes the geometric mean fitness of the population seem to be the same when the period of environmental fluctuation is low enough (24). We can ask the same question here: is the stable rate ${\rho }^{\ast }$ the same as the rate $\widehat{\rho }$ that maximizes the equilibrium value of the geometric mean fitness under fluctuating selection? For the $A1B1$ selection regime, we have the following result.

Result 9.

If $W>w$ and $0\le \rho \le 1$, then the mean fitness at the stable equilibrium in the $A1B1$ environment is a decreasing function of $\rho$.

Proof:

In $A1B1$, the stable frequency of phenotype $A$ is, by Eq. 35,

$$x^{\ast }=\frac{1}{2}-\frac{W+w-Z}{2(2-\rho )(W-w)},$$ [37]

where $Z=\sqrt{{(1-\rho )}^2{(W-w)}^2+4Ww}>0$. The geometric mean fitness at the stable equilibrium is ${\overline{w}}^{\ast }\cdot {\overline{w}}^{\ast \ast }$, where ${\overline{w}}^{\ast \ast }$ is the mean fitness at the middle of the $A1B1$ cycle; in this case ${\overline{w}}^{\ast }={\overline{w}}^{\ast \ast }$ due to the symmetry between the two phenotypes $A$ and $B$, which allows us to reduce the problem to properties of ${\overline{w}}^{\ast }$. Now, because $W>w$, ${\overline{w}}^{\ast }$ is an increasing linear function of $x^{\ast }$:

$${\overline{w}}^{\ast }=x^{\ast }W+(1-x^{\ast })w=x^{\ast }(W-w)+w.$$ [38]

Thus, ${\overline{w}}^{\ast }$ is decreasing in $\rho$ if $d{x}^{\ast }/d\rho$ is negative. Using Eq. 37,

$${\displaystyle \frac{d{x}^{\ast }}{d\rho }}=-{\displaystyle \frac{(1-\rho )(W-w)}{2(2-\rho )Z}}-{\displaystyle \frac{W+w-Z}{2(2-\rho )(W-w)}}={\displaystyle \frac{x^{\ast }-\frac{1}{2}}{2-\rho }}-{\displaystyle \frac{(1-\rho )(W-w)}{2(2-\rho )Z}}.$$ [39]

From Eq. 36, $0<x^{\ast }\le \frac{1}{2}$, and therefore, $d{x}^{\ast }/d\rho <0$, which completes the proof.

Fig. 4 illustrates the increase over time of the geometric mean fitness with decreasing $\rho$ at a polymorphic equilibrium in the $A1B1$ regime. The values of $\widehat{\rho }$ and ${\rho }^{\ast }$ are the same in $A1B1$ and $A2B2$ regimes, namely both are zero. Fig. 1B shows the geometric mean fitness in the $A1B2$ regime, and we see that, for small values of $w$, this mean fitness increases as $\rho$ decreases. At $w=0.1$, Table 1 shows that $\widehat{\rho }$ and ${\rho }^{\ast }$ are roughly zero. In all $AkBk$ regimes that we tested with $w=0.9$, the value of $\widehat{\rho }$ was also zero, substantially different from the values of ${\rho }^{\ast }$, as shown in Fig. 6. Also in Fig. 6A, we see that, with $w=0.1$, $\widehat{\rho }$ changes from zero to positive in the $AkBk$ regimes with $k\ge 12$, while with $w=0.5$, the change occurs at $k=31$. In Fig. 6, with $w=0.1$, $\widehat{\rho }$ is between 0.15 and 0.24 for $12\le k\le 50$, while with $w=0.5$, $\widehat{\rho }$ exceeds 0.2 for $31\le k\le 50$. More details on the mismatch between ${\rho }^{\ast }$, which cannot be invaded, and $\widehat{\rho }$, which maximizes geometric mean fitness, are given in Table 1, Figs. S7 and S8, and SI Text.

Finite Population Size

To include the effect of random drift due to finite population size in the above deterministic model, we use the Wright–Fisher model. Let $X_t$ denote the number of individuals with phenotype $A$ in a population of fixed size $N$ at the $t$th generation, and suppose that $X_t=Nx$. Also, let $x\prime$ represent the frequency of the phenotype $A$ in the infinite population model in the next generation, namely (Eq. 2)

$$x\prime =\rho \frac{w_A}{\overline{w}}x+(1-\rho )x.$$ [40]

Then, according to the Wright–Fisher model (34), $X_{t+1}$, the number of individuals of phenotype $A$ at generation $(t+1)$, is determined by the probability

$$P(X_{t+1}=j\mid X_t=Nx)=\left(\begin{array}{c}\hfill N\hfill \\ \hfill j\hfill \end{array}\right)(x\prime )j(1-x\prime )N-j$$ [41]

for $j=\mathrm{0,1,2},\mathrm{\dots },N$. Thus, the fluctuations in the numbers of phenotypes $A$ and $B$ in the population of size $N$ are generated by the Wright–Fisher Markov chain, where, given that $X_t=Nx$, $X_{t+1}$ has a binomial distribution with parameters $(N,x\prime )$.

This Markov chain has two absorbing states, $X_t=N$ and $X_t=0$, corresponding to the two fixations in $A$ and $B$, respectively, and we are interested in the fixation probabilities and the time to fixation of these two absorbing states as functions of the initial frequency $x$ and also of $\rho$, $w_A$, and $w_B$. To these ends, we use a diffusion approximation to the process $\{X_t\}$, which allows us to compute $u(x)$, the probability that phenotype $A$ goes to fixation when its initial frequency is $x$, namely

$$u(x)=\frac{1-e^{-2\rho sx}}{1-e^{-2\rho s}}.$$ [42]

The expected time to fixation in $A$ starting from an initial frequency of $x$ is given by

$$T(x)=\frac{1-u(x)}{\rho s}{\int }_0^x\frac{e^{2\rho s\xi }-1}{\xi (1-\xi )}d\xi +\frac{u(x)}{\rho s}{\int }_x^1\frac{1-e^{-2\rho s(1-\xi )}}{\xi (1-\xi )}d\xi ,$$ [43]

where $u(x)$ is given in Eq. 42, and in generations, $T(x)$ is multiplied by $N$ (the derivation is in SI Text). Unfortunately, the integrals in Eq. 43 cannot be done in closed form unless $\rho s=0$, in which case $u(x)=x$ and $T(x)=-2x\ln x-2(1-x)\ln (1-x)$ (ref. 34, p. 160), and only numerical computation of $T(x)$ is possible for specified values of $x$, $\rho$, and $s$.

For the fixation probability $u(x)$, we have the following result.

Result 10.

When $s>0$, so that the phenotype $A$ is favored, the fixation probability $u(x)$ is monotone increasing in $\rho$.

The proof of Result 10 is in SI Text. Fig. S9 compares the fixation probability and time to fixation derived numerically from simulating the Wright–Fisher Markov chain with the diffusion-derived values of $u(x)$ and $T(x)$. The fit is seen to be very good. Note that, when $N$ is large, the Wright–Fisher model exhibits persistent fluctuation around the deterministic expectation, as shown by the orange traces in Fig. S2.

We can also develop a diffusion approximation for the case of a cycling environment. Suppose that selection changes in cycles of length $n$, such that, within the cycle, the fitness parameters are $w_A^t$, $w_B^t$ for $t=\mathrm{1,2},\mathrm{\dots },n$. Also, let

$$\frac{1}{N}{s}_t\simeq w_A^t-w_B^t,\hspace{1em}{S}_t=\sum _{i=1}^t{s}_i,\hspace{1em}t=\mathrm{1,2},\mathrm{\dots },n.$$ [44]

Following Karlin and Levikson (35), we have the following result.

Result 11.

The mean $\mu (x)$ and variance ${\sigma }^2(x)$ of the change in the frequency of $A$ in one generation for the diffusion approximation in the case of a cycling environment $AkBl$, where $k+l=n$, are

$$\begin{array}{c}\mu (x)=\rho S_{n}x(1-x)\\ {\sigma }^2(x)=nx(1-x).\end{array}$$ [45]

The proof of Result 11, based on induction on $n$, is given in SI Text.

Using the moments in Eq. 45, the fixation probability $u(x)$ and the expected time $T(x)$ to fixation from an initial frequency of $x$ can be computed, where $s$ is replaced by $s_n/n$. We find

$$u(x)=\frac{1-e^{-2\rho \frac{S_n}{n}x}}{1-e^{-2\rho \frac{S_n}{n}}},$$ [46]

and $T(x)$ can be computed similarly.

In the case of the $AkBl$ cycling environment, we write $n=k+l$, and if $w_A=W$, $w_B=w$ for $k$ generations and $w_A=w$, $w_B=W$ for $l$ generations, we have

$$S_n=S_{k+l}=N(k-l)(W-w).$$ [47]

Fig. 7 shows an example of how $(k-l)$, $\rho$, and $(W-w)$ in Eq. 46 for $u(x)$ interact to affect fixation probabilities. More examples are illustrated in Fig. S11.

Fig. 7.

Fixation in a finite population with different ratios of selection periods $\frac{k}{l}$. Fixation probability of phenotype $A$ when starting with a single copy in a population of size $N$: $u(1/N)=(1-\exp (-2\rho \frac{k-l}{k+l}(W-w))/(1-\exp (-2N\rho \frac{k-l}{k+l}(W-w))$ (Eqs. 46 and 47). k and l are the numbers of generations in which phenotypes A and B, respectively, are favored by selection. Here, fitness of the favored phenotype is $W=1$, fitness of the disfavored phenotype is $w=0.5$, and the population size is $N=\mathrm{10,000}$. Fig. S11 shows additional examples.

Discussion

Nonchromosomal modes of phenotypic transmission are receiving increasing attention (36–38), especially with respect to their potential role in adaptation and maintenance of diversity (39). Here, we have focused on a dichotomous phenotype transmitted through a combination of parental and nonparental transmission. In addition to the roles that these transmission modes play in the dynamics of phenotypic diversity in large and small populations, we have also investigated a genetic model for the evolution of the transmission mode itself.

Our model differs markedly from that of Xue and Leibler (26), who took the individual phenotypic distribution (i.e., the probability that an individual develops one of a set of phenotypes) to be the inherited trait. In our model, the transmitted trait is the phenotype itself. Thus, with two phenotypic states $A$ and $B$, we track the frequency $x$ of $A$, whereas Xue and Leibler (26) focus on the dynamics of the per-individual probability ${\pi }_A$ of learning the phenotype $A$. One interpretation of our model is as a mean value approximation to the model of Xue and Leibler (26), where $x$, the state in our model, is the average of the population distribution of individual phenotype probabilities.

In a constant environment, the higher the vertical transmission rate $\rho$, the faster the approach to fixation of the favored phenotype: $A$ if $w_A>w_B$ or $B$ if $w_B>w_A$. Here, $1-\rho$, the oblique transmission rate, represents the added chance that an offspring becomes $A$ by learning from the parent’s population after learning from the parents who have undergone selection (Eq. 2). This simple phenotypic model does not allow a polymorphism to be achieved in a constant environment, but with more oblique transmission, approach to fixation is retarded.

With fluctuating environments, the dynamics of the phenotype frequencies are, in general, much more complicated. In particular, with deterministically cycling symmetric fitness values (the $AkBl$ model), it is impossible for fixation in $A$ and $B$ to both be stable. If $k=l$, for example, neither fixation is stable, and there is a single stable polymorphic equilibrium (with phenotypes $A$ and $B$ present) (Result 5). In the $A1B1$ case, this polymorphism is globally stable. In the $AkBl$ case, bounds on $l/k$ that determine the instability of both fixations and hence, the protection of polymorphism are given by the inequalities of Eq. 20, which depend on both the fitness differences and the rate $\rho$ of vertical transmission. We conjecture that, with $k\ne l$, there is a unique stable polymorphism if both fixations are unstable. This result is similar to the storage effect (40), in which protection from selection maintains species coexistence: consider two species, $A$ and $B$, with overlapping generations, an equal death rate $\rho$, and different growth rates $w_A$ and $w_B$; then, Eq. 2 describes the change in frequency of species $A$. In our model, oblique transmission can be said to protect the disfavored phenotype from selection, because it allows transmission without reproduction.

In deterministic one-locus, two-allele diploid population genetic models with cycling fitness regimes, Haldane and Jayakar (33) first showed the relevance of the geometric mean of genotypic fitness (compare Eqs. 16 and 17) for the maintenance (or loss) of polymorphism. However, with equal homozygote fitness, alternating in strength as a two-generation cycle (compare with $A1B1$), Karlin and Liberman (31) extended the results of Haldane and Jayakar (33) and found conditions under which both allelic fixations and polymorphic equilibrium could all be stable, with the evolution depending on initial allele frequencies as well as the homozygote fitness differences between alternate generations. Our haploid model does not seem to produce such dependence on the initial conditions.

When the fitnesses $w_A$ and $w_B$ are treated as random variables rather than varying cyclically, stochastic local stability is the appropriate analog to local stability in the case of cyclic fitness variation. While fixations in phenotypes $A$ and $B$ cannot both be stochastically stable in this case, both may be unstable, and a polymorphic distribution may result. The variance of this distribution is greater for larger values of $\rho$. This is because the stochastic local stability conditions involve $E\left\{\log [1-\rho +\rho (w_A/w_B)]\right\}$, and the effect of the variance of $(w_A/w_B)$ will clearly increase as $\rho$ increases. In the finite population case, a greater level of vertical transmission makes selection more effective, increasing the probability $u(x)$ of fixation and reducing the expected time to fixation.

We have shown that, in the $A1B1$ case, the rate of vertical transmission tends to decrease when it is under the control of a genetic modifier. From numerical iteration, it seems that this is also true in the random selection case when the fitnesses of $A$ and $B$ are identically distributed and independent between generations. However, for $AkBl$ selection regimes more complicated than $A1B1$, evolution of a modifier of vertical transmission is not straightforward. While reduction of $\rho$ occurs in the $A2B2$ regime, the uninvadable value ${\rho }^{\ast }$ is not zero for all of the fitness values explored in $AkBk$ regimes with $k>2$ (Fig. 6B and Table 1). In fact, ${\rho }^{\ast }$ increases sharply as $k$ increases beyond $k=2$. This is an unusual scenario for genetic modifiers, although it must be noted that a modifier of $\rho$ is not neutral; it affects primary selection, while neutral modifiers of recombination, mutation, and migration affect induced or secondary selection.

The dependence of the modifier dynamics on the strength of selection (that is, $w$ when $W=1$) is complicated by the approach of the system to fixation. When the phenotype frequencies become exceedingly small, dependence of the dynamics of the modifier of $\rho$ becomes extremely difficult to detect due to numerical instability; this is especially true for larger values of $k$ in $AkBk$ regimes when $w$ is small (Fig. 6B and Table 1) (with $k\ge 19$).

Fig. 6A (Table 1) shows that the value $\widehat{\rho }$ that maximizes the geometric mean fitness is the same as the evolutionarily stable value ${\rho }^{\ast }$ in the $A1B1$ and $A2B2$ selection regimes. For $AkBk$ regimes with $k>2$, our numerical analysis shows that $\widehat{\rho }$ depends strongly on the strength of selection (i.e., the value of $w$ relative to $W=1$). For $AkBl$ regimes with $w=0.1$, the difference between $\widehat{\rho }$ and ${\rho }^{\ast }$ is seen even with the $A1B2$ environment. For $AkBk$ regimes and $w=0.9$, we find $\widehat{\rho }=0$, while ${\rho }^{\ast }$ is close to $0.9$. For larger values of $k$, $\widehat{\rho }$ is between 0.15 and 0.25, while ${\rho }^{\ast }$ remains above 0.8 and can reach 0.99 for very large $k$. Comparing Fig. 6A with the asymptotic growth rate (AGR) of Xue and Leibler (26), whose parameter $\eta$ is the rate at which an individual learns from its parental lineage, there is a similarity of our curves for $w=0.1$ and $0.5$ with their curve in the $AkBk$ environment. They show the AGR decreasing with $\eta$ in the $AkBk$ regime for small $k$, but larger values of $k$ entail that the AGR has a maximum for an intermediate value of $\eta$.

Although the models of Xue and Leibler (26) and that analyzed here both incorporate parental and nonparental transmission, they do so in qualitatively different ways. The model treated in this paper is squarely in the tradition of gene–culture coevolutionary theory together with modifier theory from population genetics. The different findings from the two classes of models are interesting and suggest that additional exploration of the overlaps and discrepancies between the two approaches would be worthwhile.