Key Points
Question
What is the discriminative accuracy of deep learning algorithms compared with the diagnoses of pathologists in detecting lymph node metastases in tissue sections of women with breast cancer?
Finding
In cross-sectional analyses that evaluated 32 algorithms submitted as part of a challenge competition, 7 deep learning algorithms showed greater discrimination than a panel of 11 pathologists in a simulated time-constrained diagnostic setting, with an area under the curve of 0.994 (best algorithm) vs 0.884 (best pathologist).
Meaning
These findings suggest the potential utility of deep learning algorithms for pathological diagnosis, but require assessment in a clinical setting.
Abstract
Importance
Application of deep learning algorithms to whole-slide pathology images can potentially improve diagnostic accuracy and efficiency.
Objective
Assess the performance of automated deep learning algorithms at detecting metastases in hematoxylin and eosin–stained tissue sections of lymph nodes of women with breast cancer and compare it with pathologists’ diagnoses in a diagnostic setting.
Design, Setting, and Participants
Researcher challenge competition (CAMELYON16) to develop automated solutions for detecting lymph node metastases (November 2015-November 2016). A training data set of whole-slide images from 2 centers in the Netherlands with (n = 110) and without (n = 160) nodal metastases verified by immunohistochemical staining were provided to challenge participants to build algorithms. Algorithm performance was evaluated in an independent test set of 129 whole-slide images (49 with and 80 without metastases). The same test set of corresponding glass slides was also evaluated by a panel of 11 pathologists with time constraint (WTC) from the Netherlands to ascertain likelihood of nodal metastases for each slide in a flexible 2-hour session, simulating routine pathology workflow, and by 1 pathologist without time constraint (WOTC).
Exposures
Deep learning algorithms submitted as part of a challenge competition or pathologist interpretation.
Main Outcomes and Measures
The presence of specific metastatic foci and the absence vs presence of lymph node metastasis in a slide or image using receiver operating characteristic curve analysis. The 11 pathologists participating in the simulation exercise rated their diagnostic confidence as definitely normal, probably normal, equivocal, probably tumor, or definitely tumor.
Results
The area under the receiver operating characteristic curve (AUC) for the algorithms ranged from 0.556 to 0.994. The top-performing algorithm achieved a lesion-level, true-positive fraction comparable with that of the pathologist WOTC (72.4% [95% CI, 64.3%-80.4%]) at a mean of 0.0125 false-positives per normal whole-slide image. For the whole-slide image classification task, the best algorithm (AUC, 0.994 [95% CI, 0.983-0.999]) performed significantly better than the pathologists WTC in a diagnostic simulation (mean AUC, 0.810 [range, 0.738-0.884]; P < .001). The top 5 algorithms had a mean AUC that was comparable with the pathologist interpreting the slides in the absence of time constraints (mean AUC, 0.960 [range, 0.923-0.994] for the top 5 algorithms vs 0.966 [95% CI, 0.927-0.998] for the pathologist WOTC).
Conclusions and Relevance
In the setting of a challenge competition, some deep learning algorithms achieved better diagnostic performance than a panel of 11 pathologists participating in a simulation exercise designed to mimic routine pathology workflow; algorithm performance was comparable with an expert pathologist interpreting whole-slide images without time constraints. Whether this approach has clinical utility will require evaluation in a clinical setting.
This diagnostic accuracy study compares the ability of machine learning algorithms vs clinical pathologists to detect cancer metastases in whole-slide images of axillary lymph nodes dissected from women with breast cancer.
Introduction
Full digitalization of the microscopic evaluation of stained tissue sections in histopathology has become feasible in recent years because of advances in slide scanning technology and cost reduction in digital storage. Advantages of digital pathology include remote diagnostics, immediate availability of archival cases, and easier consultations with expert pathologists. Also, the possibility for computer-aided diagnostics may be advantageous.
Computerized analysis based on deep learning (a machine learning method; eAppendix in the Supplement) has shown potential benefits as a diagnostic strategy. Gulshan et al and Esteva et al demonstrated the potential of deep learning for diabetic retinopathy screening and skin lesion classification, respectively. Analysis of pathology slides is also an important application of deep learning, but requires evaluation for diagnostic performance.
Accurate breast cancer staging is an essential task performed by pathologists worldwide to inform clinical management. Assessing the extent of cancer spread by histopathological analysis of sentinel axillary lymph nodes (SLNs) is an important part of breast cancer staging. The sensitivity of SLN assessment by pathologists, however, is not optimal. A retrospective study showed that pathology review by experts changed the nodal status in 24% of patients. Furthermore, SLN assessment is tedious and time-consuming. It has been shown that deep learning algorithms could identify metastases in SLN slides with 100% sensitivity, whereas 40% of the slides without metastases could be identified as such. This could result in a significant reduction in the workload of pathologists.
The aim of this study was to investigate the potential of machine learning algorithms for detection of metastases in SLN slides and compare these with the diagnoses of pathologists. To this end, the Cancer Metastases in Lymph Nodes Challenge 2016 (CAMELYON16) competition was organized. Research groups around the world were invited to produce an automated solution for breast cancer metastases detection in SLNs. Once developed, the performance of each algorithm was compared with the performance of a panel of 11 pathologists participating in a simulation exercise intended to mimic pathology workflow.
Methods
Image Data Sets
To enable the development of diagnostic machine learning algorithms, we collected 399 whole-slide images and corresponding glass slides of SLNs during the first half of 2015. SLNs were retrospectively sampled from 399 patients that underwent surgery for breast cancer at 2 hospitals in the Netherlands: Radboud University Medical Center (RUMC) and University Medical Center Utrecht (UMCU). The need for informed consent was waived by the institutional review board of RUMC. Whole-slide images were deidentified before making them available. To enable the assessment of algorithm performance for slides with and without micrometastases and macrometastases, stratified random sampling was performed on the basis of the original pathology reports.
The whole-slide images were acquired at 2 different centers using 2 different scanners. RUMC images were produced with a digital slide scanner (Pannoramic 250 Flash II; 3DHISTECH) with a 20x objective lens (specimen-level pixel size, 0.243 μm × 0.243 μm). UMCU images were produced using a digital slide scanner (NanoZoomer-XR Digital slide scanner C12000-01; Hamamatsu Photonics) with a 40x objective lens (specimen-level pixel size, 0.226 μm × 0.226 μm).
Reference Standard
All metastases present in the slides were annotated under the supervision of expert pathologists. The annotations were first manually drawn by 2 students (1 from each hospital) and then every slide was checked in detail by 1 of the 2 pathologists (PB from RUMC and PvD from UMCU; eFigure 1 in the Supplement). In clinical practice, pathologists may opt to use immunohistochemistry (IHC) to resolve diagnostic uncertainty. In this study, obvious metastases were annotated without the use of IHC, whereas for all difficult cases and all cases appearing negative on hematoxylin and eosin–stained slides, IHC (anti-cytokeratin [CAM 5.2], BD Biosciences) was used (eFigure 2 in the Supplement). This minimizes false-negative interpretations. IHC is the most accurate method for metastasis evaluation and has little interpretation variability.
In clinical practice, pathologists differentiate between macrometastases (tumor cell cluster diameter ≥2 mm), micrometastases (tumor cell cluster diameter from >0.2 mm to <2 mm) and isolated tumor cells (solitary tumor cells or tumor cell clusters with diameter ≤0.2 mm or less than 200 cells). The largest available metastasis determines the slide-based diagnosis. Because the clinical value of having only isolated tumor cells in an SLN is disputed, we did not include such slides in our study and also did not penalize missing isolated tumor cells in slides containing micrometastases or macrometastases. Isolated tumor cells were, however, annotated in slides containing micrometastases and macrometastases by the pathologists and included in the training whole-slide images. The set of images was randomly divided into a training (n = 270) and a test set (n = 129; details in Table 1). Both sets included slides with both micrometastatic and macrometastatic tumor foci as encountered in routine pathology practice.
Table 1. Characteristics of the Whole-Slide Images and Glass Slides in the Data Sets Used in the CAMELYON16 Challenge.
| Data Set (N = 399 Slides and Images)a |
Hospital Providing the Slides and Images | Primary Tumor Histotypeb | Slides Containing Metastases, No. | No. of Lesions per Slide or Image, Median (Range) |
Total Slides or Images | |||
|---|---|---|---|---|---|---|---|---|
| IDC | Non-IDC | None | Macro | Micro | ||||
| Training (n = 270 images) |
RUMC | 54 | 16 | 100 | 35 | 35 | 2 (1-20) | 170 |
| UMCU | 30 | 10 | 60 | 26 | 14 | 3 (1-27) | 100 | |
| Test (n=129 slides and images) |
RUMC | 23 | 6 | 50 | 14 | 15 | 2 (1-14) | 79 |
| UMCU | 15 | 5 | 30 | 8 | 12 | 3 (1-25) | 50 | |
Abbreviations: CAMELYON16, Cancer Metastases in Lymph Nodes Challenge 2016; IDC, infiltrating ductal carcinoma; RUMC, Radboud University Medical Center; UMCU, University Medical Center Utrecht.
All analyses in the training set were determined with whole-slide images. Analyses in the test were determined with whole-slide images by the algorithms and with glass slides by the panel of 11 pathologists (because diagnosing is most commonly done using a microscope in pathology labs).
Primary tumor histotypes included IDC and other histotypes (non-IDC).
Coding Challenge
In the first stage (training) of the CAMELYON16 competition, participants were given access to 270 whole-slide images (training data set: 110 with nodal metastases, 160 without nodal metastases) of digitally scanned tissue sections. Each SLN metastasis in these images was annotated enabling participants to build their algorithms. In the second stage (evaluation) of the competition, the performance of the participants’ algorithms was tested on a second set of 129 whole-slide images (test data set: 49 with nodal metastases, 80 without nodal metastases) lacking annotation of SLN metastases. The output of each algorithm was sent to the challenge organizers by the participants for independent evaluation. Each team was allowed to make a maximum of 3 submissions. The submission number was indicated in each team’s algorithm name by Roman numeral. Multiple submissions were only allowed if the methodology of the new submission was distinct.
Tasks and Evaluation Metrics
Two tasks were defined: identification of individual metastases in whole-slide images (task 1) and classification of every whole-slide image as either containing or lacking SLN metastases (task 2). The tasks had different evaluation metrics and consequently resulted in 2 independent algorithm rankings.
Task 1: Identification of Individual Metastases
In task 1, algorithms were evaluated for their ability to identify specific metastatic foci in a whole-slide image. Challenge participants provided a list of metastasis locations. For each location participants provided a confidence score that could range from 0 (indicating certainty that metastasis was absent) to 1 (certainty that metastasis was present) and could take on any real-number value in between. Algorithms were compared using a measure derived from the free-response receiver operator characteristic curve (FROC). The FROC curve shows the lesion-level, true-positive fraction (sensitivity) vs the mean number of false-positive detections in metastasis-free slides only. The FROC true-positive fraction score that ranked teams in the first task was defined as the mean true-positive fraction at 6 predefined false-positive rates: ¼ (meaning 1 false-positive result in every 4 whole-slide images), ½, 1, 2, 4, and 8 false-positive findings per whole-slide image. Details on detection criteria for individual lesions can be found in the eMethods in the Supplement. All analyses in task 1 were determined with whole-slide images (algorithms and the pathologist without time constraint [WOTC]).
Task 2: Classification of Metastases
Task 2 evaluated the ability of the algorithms to discriminate between 49 whole-slide images with SLN metastases vs 80 without SLN metastases (control). In this case, identification of specific foci within images was not required. Participants provided a confidence score, using the same rating schema as task 1, indicating the probability that each whole-slide image contained any evidence of SLN metastasis from breast cancer. The area under the receiver operating characteristic curve (AUC) was used to compare the performance of the algorithms. Algorithms assessed whole-slide images, as did the pathologist WOTC. The panel of 11 pathologists with time constraint (pathologists WTC), however, did their assessment on the corresponding glass slides for those images because diagnosing is most commonly done using a microscope in pathology labs.
Performance of Pathologists
Pathologist Without Time Constraint
To establish a baseline for pathologist performance, 2 experiments were conducted using the 129 slides in the test set, corresponding to the tasks defined above. In the first experiment, 1 pathologist (MCRFvD, >10 years of experience in pathology diagnostics, >2 years of experience in assessing digitized tissue sections) marked every single metastasis on a computer screen using high magnification. This task was performed without any time constraint. For comparison with the algorithms on task 2, the pathologist WOTC indicated (during the same session) the locations of any (micro or macro) metastases per whole-slide image.
Panel of Pathologists With Time Constraint
Assessment without time constraint does not yield a fair measure of the accuracy of the routine diagnostic process. Preliminary experiments with 4 independent pathologists determined that 2 hours was a realistic amount of time for reviewing these 129 whole-slide images. To mimic routine diagnostic pathology workflow, we asked 11 pathologists to independently assess the 129 slides in the test set in a simulation exercise with time constraint (pathologists WTC) for task 2. A flexible 2-hour time limit was set (exceeding this limit was not penalized and every pathologist was allowed time to finish the entire set). All pathologists participating in this study were informed of and agreed with the rationale and goals of this study and participated on a voluntary basis. The research ethics committee determined that the pathologists who participated in the review panel did not have to provide written informed consent. The panel of the 11 pathologists (mean age, 47.7 years [range, 31-61]) included 1 resident pathologist (3-year resident) and 10 practicing pathologists (mean practicing years, 16.4 [range, 0-30]; 0 indicates 1 pathologist who just finished a 5-year residency program). Three of these pathologists had breast pathology as a special interest area.
The panel of 11 pathologists WTC assessed the glass slides using a conventional light microscope and determined whether there was any evidence of SLN metastasis in each image. This diagnostic task was identical to that performed by the algorithms in task 2. The pathologists WTC assessed the same set of glass slides used for testing the algorithms (which used digitized whole-slide images of these glass slides). Pathologists indicated the level of confidence in their interpretation for each slide using 5 levels: definitely normal, probably normal, equivocal, probably tumor, definitely tumor. To obtain an empirical ROC curve, the threshold was varied to cover the entire range of possible ratings by the pathologists, and the sensitivity was plotted as a function of the false-positive fraction (1-specificity). To get estimates of sensitivity and specificity for each pathologist, the 5 levels of confidence were dichotomized by considering the confidence levels of definitely normal and probably normal as a negative finding and all other levels as positive findings.
Algorithm Teams
Between November 2015 and November 2016, 390 research teams signed up for the challenge. Twenty-three teams submitted 32 algorithms for evaluation by the closing date (for details, see eTable 3 and eMethods in the Supplement).
Statistical Analysis
All statistical tests used in this study were 2-sided and a P value less than .05 was considered significant.
For tasks 1 and 2, CIs of the FROC true-positive fraction scores and AUCs were obtained using the percentile bootstrap method for the algorithms, the pathologists WTC, and the pathologist WOTC. The AUC values for the pathologists (WTC and WOTC) were calculated based on their provided 5-point confidence scores.
To compare the AUC of the individual algorithms with the pathologists WTC in task 2, multiple-reader, multiple-case (MRMC) ROC analysis was used. The MRMC ROC analysis paradigm is frequently used for evaluating the performance of medical image interpretation and allows the comparison of multiple readers analyzing the same cases while accounting for the different components of variance contributing to the interpretations. Both the panel of readers and the algorithms as well as the cases were treated as random effects in this analysis. The pathologists WTC represent the multiple readers for modality 1 (diagnosing on glass slides; modality represents the technology with which the dataset is shown to the readers) and an algorithm represents the reader for modality 2 (diagnosing on whole-slide images). Cases were the same set of slides or images seen by the panel and the algorithm. The AUC was the quantitative measure of performance in this analysis. The Dorfman-Berbaum-Metz significance testing with Hillis improvements was performed to test the null hypothesis that all effects were 0. The Bonferroni correction was used to adjust the P values for multiple comparisons in the MRMC ROC analysis (independent comparison of each of the 32 algorithms and the pathologists WTC).
Additionally, a permutation test was performed to assess whether there was a statistically significant difference between the AUC of the pathologists (WTC and WOTC) detecting macrometastases compared with micrometastases. This test was also repeated for comparing the performance of pathologists for different histotypes: infiltrating ductal cancer vs all other histotypes. Because the 80 control slides (not containing metastases) were the same in both groups, the permutation was only performed across the slides containing metastases. This test was performed for each individual pathologist and, subsequently, Bonferroni correction was applied to the obtained P values.
No prior data were available for the performance of algorithms in this task. Therefore, no power analysis was used to predetermine the sample size.
The iMRMC (Food and Drug Administration), version 3.2, was used for MRMC analysis. An in-house developed script in Python (Babak Ehteshami Bejnordi, MS; Radboud University Medical Center), version 2.7, was used to obtain the percentile bootstrap CIs for the FROC and AUC scores. A custom script was written to perform the permutation tests and can be found at the same location.
Results
The pathologist WOTC required approximately 30 hours for assessing 129 whole-slide images. No false-positives were produced in task 1 (ie, nontumorous tissue indicated as metastasis) by the pathologist WOTC, but 27.6% of individual metastases were not identified (lesion level, true-positive fraction, 72.4% [95% CI, 64.3%-80.4%]) that manifested when IHC staining was performed. At the slide level in task 2, the pathologist WOTC achieved a sensitivity of 93.8% (95% CI, 86.9%-100.0%), a specificity of 98.7% (95% CI, 96.0%-100.0%), and an AUC of 0.966 (95% CI, 0.927-0.998). The pathologists WTC in the simulation exercise spent a median of 120 minutes (range, 72-180 minutes) for 129 slides. They achieved a mean sensitivity of 62.8% (95% CI, 58.9%-71.9%) with a mean specificity of 98.5% (95% CI, 97.9%-99.1%). The mean AUC was 0.810 (range, 0.738-0.884) (eTables 1-2 in the Supplement show results for individual pathologists WTC). eFigure 3 in the Supplement shows the ROC curves for each of the 11 pathologists WTC and the pathologist WOTC.
The results of the pathologists WTC were further analyzed for their ability to detect micrometastases vs macrometastases (eResults in the Supplement). The panel of 11 pathologists had a mean sensitivity of 92.9% (95% CI, 90.5%-95.8%) and mean AUC of 0.964 (range, 0.924-1.0) for detecting macrometastases compared with a mean sensitivity of 38.3% (95% CI, 32.6%-52.9%) and a mean AUC of 0.685 (range, 0.582-0.808) for micrometastases. Even the best performing pathologist in the panel missed 37.1% of the cases with only micrometastases.
Algorithm Performance
Of the 23 teams, the majority of submitted algorithms (25 of 32 algorithms) were based on deep convolutional neural networks (eAppendix in the Supplement). Besides deep learning, a variety of other approaches were attempted by CAMELYON16 participants. Different statistical and structural texture features were extracted (eg, color scale-invariant feature transform [SIFT] features, local binary patterns, features based on gray-level co-occurrence matrix) combined with widely used supervised classifiers (eg, support vector machines, random forest classifiers). The performance and ranking of the entries for the 2 tasks are shown in Table 2. Overall, deep learning–based algorithms performed significantly better than other methods: the 19 top-performing algorithms in both tasks all used deep convolutional neural networks as the underlying methodology (Table 2). Detailed method description for the participating teams can be found in the eMethods in the Supplement.
Table 2. Test Data Set Results of the 32 Submitted Algorithms vs Pathologists for Tasks 1 and 2 in the CAMELYON16 Challengea.
| Codenameb | Task 1: Metastasis Identification | Task 2: Metastases Classification | P Value for Comparison of the Algorithm vs Pathologists WTCd | Algorithm Model | Comments | |
|---|---|---|---|---|---|---|
| FROC Score (95% CI)c |
AUC (95% CI)c |
Deep Learning | Architecture | |||
| HMS and MIT II | 0.807 (0.732-0.889) |
0.994 (0.983-0.999) |
<.001 | ✓ | GoogLeNet | Ensemble of 2 networks; stain standardization; extensive data augmentation; hard negative mining |
| HMS and MGH III | 0.760 (0.692-0.857) |
0.976 (0.941-0.999 |
<.001 | ✓ | ResNet | Fine-tuned pretrained network; fully convolutional network |
| HMS and MGH I | 0.596 (0.578-0.734) |
0.964 (0.928-0.989) |
<.001 | ✓ | GoogLeNet | Fine-tuned pretrained network |
| CULab III | 0.703 (0.605-0.799) |
0.940 (0.888-0.980) |
<.001 | ✓ | VGG-16 | Fine-tuned pretrained network; fully convolutional network |
| HMS and MIT I | 0.693 (0.600-0.819) |
0.923 (0.855-0.977) |
.11 | ✓ | GoogLeNet | Ensemble of 2 networks; hard negative mining |
| ExB I | 0.511 (0.363-0.620) |
0.916 (0.858-0.962) |
.02 | ✓ | ResNet | Varied class balance during training |
| CULab I | 0.544 (0.467-0.629) |
0.909 (0.851-0.954) |
.04 | ✓ | VGG-Net | Fine-tuned pretrained network |
| HMS and MGH II | 0.729 (0.596-0.788) |
0.908 (0.846-0.961) |
.04 | ✓ | ResNet | Fine-tuned pretrained network |
| CULab II | 0.527 (0.335-0.627) |
0.906 (0.841-0.957) |
.16 | ✓ | VGG-Net & ResNet | Fine-tuned pretrained network; cascaded a VGG-Net that operated on low magnification images and a ResNet model that refined the results |
| DeepCare I | 0.243 (0.197-0.356) |
0.883 (0.806-0.943) |
>.99 | ✓ | GoogLeNet | Fine-tuned pretrained network |
| Quincy Wong I | 0.367 (0.250-0.521) |
0.865 (0.789-0.924) |
>.99 | ✓ | SegNet | Fine-tuned pretrained network |
| Middle East Technical University I | 0.389 (0.272-0.512) |
0.864 (0.786-0.927) |
>.99 | ✓ | 4-layer CNN | Custom confidence filtering for postprocessing |
| NLP LOGIX I | 0.386 (0.255-0.511) |
0.830 (0.742-0.899) |
>.99 | ✓ | AlexNet | Used a second-stage random forest classifier to generate slide scores |
| Smart Imaging II | 0.339 (0.239-0.420) |
0.821 (0.753-0.894) |
>.99 | ✓ | GoogLeNet | Used an ensemble of the output from the team’s first entry and the GoogLeNet model |
| University of Toronto I | 0.382 (0.286-0.515) |
0.815 (0.722-0.886) |
>.99 | ✓ | VGG-Net | Combined the output of multiple CNNs trained on different magnifications by computing their mean |
| Warwick-Qatar University I | 0.305 (0.219-0.397) |
0.796 (0.711-0.871) |
>.99 | ✓ | U-Net | Used stain normalization |
| Radboudumc I | 0.575 (0.446-0.659) |
0.779 (0.694-0.860) |
>.99 | ✓ | VGG-Net | Extensive data augmentation; second-stage CNN to generate slide-level scores |
| Hochschule für Technik und Wirtschaft-Berlin I | 0.187 (0.112-0.250) |
0.768 (0.665-0.853) |
>.99 | ✓ | CRFasRNN | Fine-tuned pretrained network |
| University of Toronto II | 0.352 (0.292-0.511) |
0.762 (0.659-0.846) |
>.99 | ✓ | VGG-Net | Combined the output of multiple CNNs trained on different magnifications by using an additional CNN |
| Tampere I | 0.257 (0.171-0.376) |
0.761 (0.662-0.837) |
>.99 | Random Forests | Used a large set of intensity and texture features | |
| Smart Imaging I | 0.208 (0.119-0.306) |
0.757 (0.663-0.839) |
>.99 | SVM & Adaboost | Cascaded SVM and Adaboost classifiers using texture features | |
| Osaka University I | 0.347 (0.234-0.463) |
0.732 (0.629-0.824) |
>.99 | ✓ | GoogLeNet | |
| CAMP-TUM II | 0.273 (0.194-0.379) |
0.735 (0.633-0.819) |
>.99 | ✓ | GoogLeNet | Hard negative mining |
| University of South Florida I | 0.179 (0.116-0.242) |
0.727 (0.611-0.823) |
>.99 | Random Forests | Used various intensity and texture features | |
| NSS I | 0.165 (0.116-0.195) |
0.727 (0.635-0.81) |
>.99 | Rule-based | Multiple thresholds on several nucleus-based features | |
| Tampere II | 0.252 (0.149-0.350) |
0.713 (0.612-0.801) |
>.99 | ✓ | 7-layer CNN | Self-designed network architecture |
| CAMP-TUM I | 0.184 (0.127-0.243) |
0.691 (0.580-0.787) |
>.99 | ✓ | Agg-Net | Multiscale approach for analyzing the images |
| Minsk Team I | 0.227 (0.181-0.264) |
0.689 (0.568-0.804) |
>.99 | ✓ | GoogLeNet | Separate models for different data sets; hard negative mining |
| VISILAB I | 0.142 (0.080-0.203) |
0.653 (0.551-0.748) |
>.99 | Random Forests | Used Haralick texture features | |
| VISILAB II | 0.116 (0.063-0.177) |
0.651 (0.549-0.742) |
>.99 | ✓ | 3-layer CNN | Self-designed network architecture |
| Anonymous I | 0.097 (0.049-0.158) |
0.628 (0.530-0.717) |
>.99 | Random Forests | ||
| Laboratoire d'Imagerie Biomédicale I | 0.120 (0.079-0.182) |
0.556 (0.434-0.654) |
>.99 | SVM | Used various color and texture features | |
| Pathologist WOTC | 0.724 (0.643-0.804) |
0.966 (0.927-0.998) |
Expert pathologist who assessed without a time constraint | |||
| Mean pathologists WTC | 0.810 (0.750-0.869) |
The mean performance of 11 pathologists in a simulation exercise designed to mimic the routine workflow of diagnostic pathology with a flexible 2-h time limit | ||||
Abbreviations: AUC, area under the receiver operating characteristic curve; CAMELYON16, Cancer Metastases in Lymph Nodes Challenge 2016; CAMP-TUM, Computer Aided Medical Procedures and Augmented Reality-Technical University of Munich; CNN, convolutional neural network; CULab, Chinese University Lab; FROC, free-response receiver operator characteristic; HMS, Harvard Medical School; MGH, Massachusetts General Hospital; MIT, Massachusetts Institute of Technology; WOTC, without time constraint; WTC, with time constraint.
For algorithms, contact information, and detailed a description of each algorithm, see eTable 3 and eMethods in the Supplement. For a glossary of deep learning terminology, see eAppendix in the Supplement.
Algorithms are shown ranked highest (top of Table) to lowest (bottom of Table) according to their performance on task 2. The submission number was indicated in each team’s algorithm name by Roman numeral. Teams were allowed a maximum of 3 submissions.
The percentile bootstrap method was used to construct 95% CIs for FROC true-positive fraction scores (FROC scores) and AUCs.
The results of the significant test with MRMC ROC analysis for the comparison of each individual algorithm with the pathologists WTC. The P values were adjusted for multiple comparisons using the Bonferroni correction, in which the P values are multiplied by the number of comparisons (32; comparison of the 32 submitted algorithms with the panel of pathologists).
Task 1: Metastasis Identification
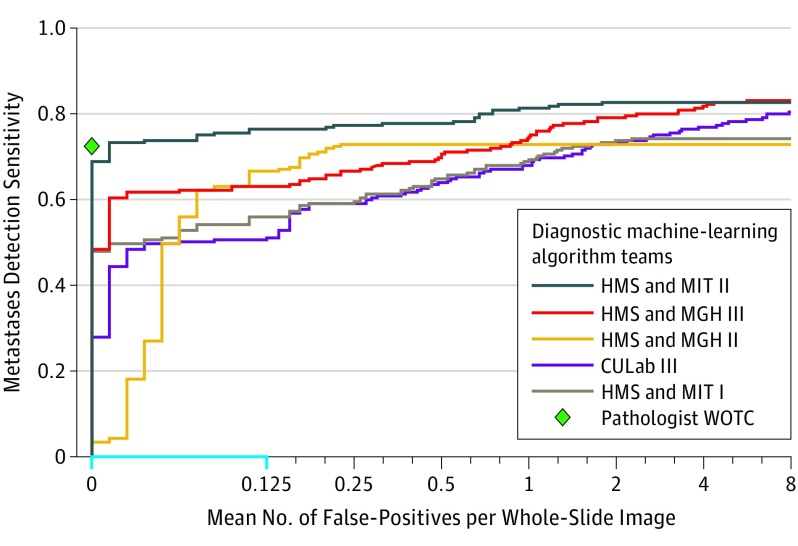
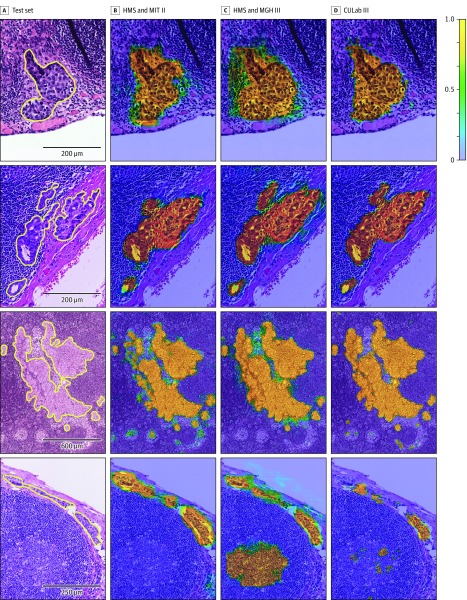
The results of metastasis identification, as measured by the FROC true-positive fraction score, are presented in Table 2 (eTable 4 in the Supplement provides a more detailed summary of the results for the FROC analysis). The best algorithm, from team Harvard Medical School (HMS) and Massachusetts Institute of Technology (MIT) II, achieved an overall FROC true-positive fraction score of 0.807 (95% CI, 0.732-0.889). The algorithm by team HMS and Massachusetts General Hospital (MGH) III ranked second in task 1, with an overall score of 0.760 (95% CI, 0.692-0.857). Figure 1 presents the FROC curves for the top 5 performing systems in task 1 (for FROC curves of all algorithms, see eFigure 4 in the Supplement). Figure 2 shows several examples of metastases in the test set of CAMELYON16 and the probability maps produced by the top 3 ranked algorithms (eFigure 5 in the Supplement).
Figure 1. FROC Curves of the Top 5 Performing Algorithms vs Pathologist WOTC for the Metastases Identification Task (Task 1) From the CAMELYON16 Competition.
CAMELYON16 indicates Cancer Metastases in Lymph Nodes Challenge 2016; CULab, Chinese University Lab; FROC, free-response receiver operator characteristic; HMS, Harvard Medical School; MGH, Massachusetts General Hospital; MIT, Massachusetts Institute of Technology; WOTC, without time constraint. The range on the x-axis is linear between 0 and 0.125 (blue) and base 2 logarithmic scale between 0.125 and 8. Teams were those organized in the CAMELYON16 competition. Task 1 was measured on the 129 whole-slide images in the test data set, of which 49 contained metastatic regions. The pathologist did not produce any false-positives and achieved a true-positive fraction of 0.724 for detecting and localizing metastatic regions.
Figure 2. Probability Maps Generated by the Top 3 Algorithms From the CAMELYON16 Competition.
For abbreviations, see the legend of Figure 3. The color scale bar (top right) indicates the probability for each pixel to be part of a metastatic region. For additional examples, see eFigure 5 in the Supplement. A, Four annotated micrometastatic regions in whole-slide images of hematoxylin and eosin–stained lymph node tissue sections taken from the test set of Cancer Metastases in Lymph Nodes Challenge 2016 (CAMELYON16) dataset. B-D, Probability maps from each team overlaid on the original images.
Task 2: Whole-Slide Image Classification
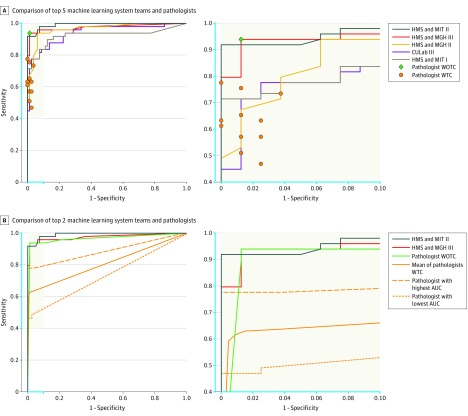
The results for all automated systems, sorted by their performance, are presented in Table 2. Figure 3A-B show the ROC curves of the top 5 teams along with the operating points of the pathologists (WOTC and WTC). eFigure 6 in the Supplement shows the ROC curves for all algorithms. All 32 algorithms were compared with the panel of pathologists using MRMC ROC analysis (Table 2).
Figure 3. ROC Curves of the Top-Performing Algorithms vs Pathologists for Metastases Classification (Task 2) From the CAMELYON16 Competition.
AUC indicates area under the receiver operating characteristic curve; CAMELYON16, Cancer Metastases in Lymph Nodes Challenge 2016; CULab, Chinese University Lab; HMS, Harvard Medical School; MGH, Massachusetts General Hospital; MIT, Massachusetts Institute of Technology; WOTC, without time constraint; WTC, with time constraint; ROC, receiver operator characteristic. The blue in the axes on the left panels correspond with the blue on the axes in the right panels. Task 2 was measured on the 129 whole-slide images (for algorithms and the pathologist WTC) and corresponding glass slides (for 11 pathologists WOTC) in the test data set, which 49 contained metastatic regions. A, A machine-learning system achieves superior performance to a pathologist if the operating point of the pathologist lies below the ROC curve of the system. The top 2 deep learning–based systems outperform all the pathologists WTC in this study. All the pathologists WTC scored glass slide images using 5 levels of confidence: definitely normal, probably normal, equivocal, probably tumor, definitely tumor. To generate estimates of sensitivity and specificity for each pathologist, negative was defined as confidence levels of definitely normal and probably normal; all others as positive. B, The mean ROC curve was computed using the pooled mean technique. This mean is obtained by joining all the diagnoses of the pathologists WTC and computing the resulting ROC curve as if it were 1 person analyzing 11 × 129 = 1419 cases.
The top-performing algorithm by team HMS and MIT II used a GoogLeNet architecture, which outperformed all other CAMELYON16 submissions with an AUC of 0.994 (95% CI, 0.983-0.999). This AUC exceeded the mean performance of the pathologists WTC (mean AUC, 0.810 [range, 0.738-0.884]) in the diagnostic simulation exercise (P < .001, calculated using MRMC ROC analysis) (Table 2). The top-performing algorithm had an AUC comparable with that of the pathologist WOTC (AUC, 0.966 [95% CI, 0.927-0.998]). Additionally, the operating points of all pathologists WTC were below the ROC curve of this method (Figure 3A-B). The ROC curves for the 2 leading algorithms, the pathologist WOTC, the mean ROC curve of the pathologists WTC, and the pathologists WTC with the highest and lowest AUCs are shown in Figure 3C-D.
The second-best performing algorithm by team HMS and MGH III used a fully convolutional ResNet-101 architecture. This algorithm achieved an overall AUC of 0.976 (95% CI, 0.941-0.999), and yielded the highest AUC in detecting macrometastases (AUC, 1.0). An earlier submission by this team, HMS and MGH I, achieved an overall AUC of 0.964 (95% CI, 0.928-0.989) and ranked third. The fourth highest–ranked team was CULab (Chinese University Lab) III with a 16-layer VGG-net architecture, followed by HMS and MIT I, with a 22-layer GoogLeNet architecture. Overall, 7 of the 32 submitted algorithms had significantly higher AUCs than the pathologists WTC (see Table 2 for the individual P values calculated using MRMC ROC analysis).
The results of the algorithms were further analyzed for comparing their performance in detecting micrometastases and macrometastases (eResults and eTable 5 in the Supplement). The top-performing algorithms performed similarly to the best performing pathologists WTC in detecting macrometastases. Ten of the top-performing algorithms achieved a better mean AUC in detecting micrometastases than the AUC for the best pathologist WTC (0.885 [range, 0.812-0.997] for the top 10 algorithms vs 0.808 [95% CI, 0.704-0.908] for the best pathologist WTC).
Discussion
The CAMELYON16 challenge demonstrated that some deep learning algorithms were able to achieve a better AUC than a panel of 11 pathologists WTC participating in a simulation exercise for detection of lymph node metastases of breast cancer. To our knowledge, this is the first study that shows that interpretation of pathology images can be performed by deep learning algorithms at an accuracy level that rivals human performance.
To obtain an upper limit on what level of performance could be achieved by visual assessment of hematoxylin and eosin–stained tissue sections, a single pathologist WOTC evaluated whole-slide images at high magnification in details and marked every single cluster of tumor cells. This took the pathologist WOTC 30 hours for 129 slides, which is infeasible in clinical practice. Although this pathologist was very good at differentiating metastases from false-positive findings, 27.6% of metastases were missed compared with the reference standard obtained with the use of IHC staining to confirm the presence of tumor cells in cases for which interpretation of slides was not clear. This illustrates the relatively high probability of overlooking tumor cells in hematoxylin and eosin–stained tissue sections. At the slide level, a high overall sensitivity and specificity for the pathologist WOTC was observed.
To estimate the accuracy of pathologists in a routine diagnostic setting, 11 pathologists WTC assessed the SLNs in a simulated exercise. The setting resembled diagnostic practice in the Netherlands, where use of IHC is mandatory for cases with negative findings on hematoxylin and eosin–stained slides. Compared with the pathologist WOTC interpreting the slides, these pathologists WTC were less accurate, especially on the slides which only contained micrometastases. Even the best-performing pathologist on the panel missed more than 37% of the cases with only micrometastases. Macrometastases were much less often missed. Specificity remained high, indicating that the task did not lead to a high rate of false-positives.
The best algorithm achieved similar true-positive fraction as the pathologist WOTC when producing a mean of 1.25 false-positive lesions in 100 whole-slide images and performed better when allowing for slightly more false-positive findings. On the slide level, the leading algorithms performed better than the pathologists WTC in the simulation exercise.
All of the 32 algorithms submitted to CAMELYON16 used a discriminative learning approach to identify metastases in whole-slide images. The common denominator for the algorithms in the higher echelons of the ranking was that they used advanced convolutional neural networks. Algorithms based on manually engineered features performed less well.
Despite the use of advanced convolutional neural network architectures, such as 16-layer VGG-Net, 22-layer GoogLeNet, and 101-layer ResNet, the ranking among teams using these techniques varied significantly, ranging from 1st to 29th. However, auxiliary strategies to improve system generalization and performance seemed more important. For example, team HMS and MIT improved their AUC in task 2 from 0.923 (HMS and MIT I) to 0.994 (HMS and MIT II) by adding a standardization technique to help them deal with stain variations. Other strategies include exploiting invariances to augment training data (eg, tissue specimens are rotation invariant) and addressing class imbalance (ie, more normal tissue than metastases) by different training data sampling strategies (for further examples of properties that distinguish the best-performing methods, see eDiscussion in the Supplement).
Previous studies on diagnostic imaging tasks in which deep learning reached human-level performance, such as detection of diabetic retinopathy in retinal fundus photographs, used a reference standard based on the consensus of human experts. This study, in comparison, generated a reference standard using additional immunohistochemical staining, yielding an independent reference against which human pathologists could also be compared.
Limitations
This study has several limitations, most related to the conduct of these analyses as part of a simulation exercise rather than routine pathology workflow. The test data set on which algorithms and pathologists were evaluated was enriched with cases containing metastases and, specifically, micrometastases and, thus, is not directly comparable with the mix of cases pathologists encounter in clinical practice. Given the reality that most SLNs do not contain metastases, the data set curation was needed to achieve a well-rounded representation of what is encountered in clinical practice without including an exorbitant number of slides. To validate the performance of machine learning algorithms, such as those developed in the CAMELYON16 competition, a prospective study is required. In addition, algorithms were specifically trained to discriminate between normal and cancerous tissue in the background of lymph node histological architecture, but they might be unable to identify rare events such as co-occurring pathologies (eg, lymphoma, sarcoma, or infection). The detection of other pathologies in the SLN, which is relevant in routine diagnostics, was not included in this study. In addition, algorithm run-time was not recorded nor included as a factor in the evaluation, but it might influence the suitability for use in, for example, frozen section analysis.
In this study, every pathologist was given 1 single hematoxylin and eosin–stained slide per patient to determine the presence or absence of breast cancer metastasis. In a real clinical setting, sections from multiple levels are evaluated for every lymph node. Also, in most hospitals pathologists request additional IHC staining in equivocal cases. Especially for slides containing only micrometastases, this is a relevant factor affecting diagnostic performance.
In addition, the simulation exercise invited pathologists WTC to review a series of 129 hematoxylin and eosin–stained slides in about 2 hours to determine the presence of macroscopic or microscopic SLN metastasis. Although feasible in the context of this simulation, this does not represent the work pace in other settings. Less time constraint on task completion may increase the accuracy of SLN diagnostic review. In addition, pathologists may rely on IHC staining and the knowledge that all hematoxylin and eosin–slides with negative findings will undergo additional review with the use of IHC.
Conclusions
In the setting of a challenge competition, some deep learning algorithms achieved better diagnostic performance than a panel of 11 pathologists participating in a simulation exercise designed to mimic routine pathology workflow; algorithm performance was comparable with an expert pathologist interpreting slides without time constraints. Whether this approach has clinical utility will require evaluation in a clinical setting.
eAppendix. Deep Learning and Glossary
eFigure 1. Two Example Annotated Areas of Whole-Slide Images Taken From the CAMELYON16 Dataset
eFigure 2. Use of Immunohistochemistry Staining to Generate Reference Standard
eFigure 3. ROC Curves of the Panel of 11 Pathologists for Task 2
eFigure 4. FROC Curves of All Participating Teams for Task 1
eFigure 5. Example Probability Maps Generated by the Top-Three Performing Systems
eFigure 6. ROC Curves of All Participating Teams for Task 2
eTable 1. Classification Results by Pathologists for the Whole-Slide Image Classification Task (Sensitivity and Specificity)
eTable 2. Classification Results by Pathologists for the Whole-Slide Image Classification Task (Area Under the ROC Curve)
eTable 3. Participating Teams in CAMELYON16
eTable 4. Summary of Results for the Metastasis Identification Task (Task 1)
eTable 5. Summary of Results for the Whole-Slide Image Classification Task (Task 2)
eMethods. Methods 1 Through 30
eResults.
eDiscussion.
eReferences.
References
- 1.Griffin J, Treanor D. Digital pathology in clinical use: where are we now and what is holding us back? Histopathology. 2017;70(1):134-145. [DOI] [PubMed] [Google Scholar]
- 2.Madabhushi A, Lee G. Image analysis and machine learning in digital pathology: challenges and opportunities. Med Image Anal. 2016;33:170-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gulshan V, Peng L, Coram M, et al. Development and validation of a deep learning algorithm for detection of diabetic retinopathy in retinal fundus photographs. JAMA. 2016;316(22):2402-2410. [DOI] [PubMed] [Google Scholar]
- 4.Esteva A, Kuprel B, Novoa RA, et al. Dermatologist-level classification of skin cancer with deep neural networks. Nature. 2017;542(7639):115-118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vestjens JHMJ, Pepels MJ, de Boer M, et al. Relevant impact of central pathology review on nodal classification in individual breast cancer patients. Ann Oncol. 2012;23(10):2561-2566. [DOI] [PubMed] [Google Scholar]
- 6.Litjens G, Sánchez CI, Timofeeva N, et al. Deep learning as a tool for increased accuracy and efficiency of histopathological diagnosis. Sci Rep. 2016;6:26286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reed J, Rosman M, Verbanac KM, Mannie A, Cheng Z, Tafra L. Prognostic implications of isolated tumor cells and micrometastases in sentinel nodes of patients with invasive breast cancer: 10-year analysis of patients enrolled in the Prospective East Carolina University/Anne Arundel Medical Center Sentinel Node Multicenter Study. J Am Coll Surg. 2009;208(3):333-340. [DOI] [PubMed] [Google Scholar]
- 8.Chagpar A, Middleton LP, Sahin AA, et al. Clinical outcome of patients with lymph node-negative breast carcinoma who have sentinel lymph node micrometastases detected by immunohistochemistry. Cancer. 2005;103(8):1581-1586. [DOI] [PubMed] [Google Scholar]
- 9.Pendas S, Dauway E, Cox CE, et al. Sentinel node biopsy and cytokeratin staining for the accurate staging of 478 breast cancer patients. Am Surg. 1999;65(6):500-505. [PubMed] [Google Scholar]
- 10.Chakraborty DP. Recent developments in imaging system assessment methodology, FROC analysis and the search model. Nucl Instrum Methods Phys Res A. 2011;648 supplement 1:S297-S301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Efron B. Bootstrap methods: another look at the jackknife. Ann Stat. 1979;7(1):1-26. [Google Scholar]
- 12.Gallas BD, Chan H-P, D’Orsi CJ, et al. Evaluating imaging and computer-aided detection and diagnosis devices at the FDA. Acad Radiol. 2012;19(4):463-477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Obuchowski NA, Beiden SV, Berbaum KS, et al. Multireader, multicase receiver operating characteristic analysis: an empirical comparison of five methods. Acad Radiol. 2004;11(9):980-995. [DOI] [PubMed] [Google Scholar]
- 14.Hillis SL, Obuchowski NA, Berbaum KS. Power estimation for multireader ROC methods. Acad Radiol. 2011;18(2):129-142. doi: 10.1016/j.acra.2010.09.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Upton G, Cook I. A Dictionary of Statistics 3e. Oxford, UK: Oxford University Press; 2014. [Google Scholar]
- 16.Mason SJ, Graham NE. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: statistical significance and interpretation. Q J R Meteorol Soc. 2002;128(584):2145-2166. doi: 10.1256/003590002320603584 [DOI] [Google Scholar]
- 17.GitHub DIDSR/iMRMC. https://github.com/DIDSR/iMRMC. Accessed November 14, 2017.
- 18.GitHub CAMELYON16. https://github.com/computationalpathologygroup/CAMELYON16. Accessed November 14, 2017.
- 19.Lowe DG. Distinctive image features from scale-invariant keypoints. Int J Comput Vis. 2004;60(2):91-110. https://people.eecs.berkeley.edu/~malik/cs294/lowe-ijcv04.pdf. Accessed November 13, 2017. [Google Scholar]
- 20.Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans Pattern Anal Mach Intell. 2002;24(7):971-987. doi: 10.1109/TPAMI.2002.1017623 [DOI] [Google Scholar]
- 21.Haralick RM, Shanmugam K, Dinstein I. Textural features for image classification. IEEE Trans Syst Man Cybern. 1973;SMC-3(6):610-621. http://haralick.org/journals/TexturalFeatures.pdf. Accessed November 13, 2017. [Google Scholar]
- 22.Cortes C, Vapnik V. Support-vector networks. Mach Learn. 1995;20(3):273-297. http://image.diku.dk/imagecanon/material/cortes_vapnik95.pdf. Accessed November 13, 2017. [Google Scholar]
- 23.Breiman L. Random forests. Mach Learn. 2001;45(1):5-32. http://www.math.univ-toulouse.fr/~agarivie/Telecom/apprentissage/articles/randomforest2001.pdf. Accessed November 13, 2017. [Google Scholar]
- 24.Szegedy C, Wei L, Yangqing J, et al. Going deeper with convolutions. Paper presented at: IEEE Conference on Computer Vision and Pattern Recognition; June 7-12, 2015; Boston, MA. http://ieeexplore.ieee.org/document/7298594/. Accessed November 13, 2017. [Google Scholar]
- 25.He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. Paper presented at: IEEE Conference on Computer Vision and Pattern Recognition; June 27-30, 2016; Las Vegas, NV. https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf. Accessed November 13, 2017. [Google Scholar]
- 26.Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. https://arxiv.org/pdf/1409.1556.pdf. Accessed November 13, 2017.
- 27.Kendall A, Badrinarayanan V, Cipolla R. Bayesian segnet: model uncertainty in deep convolutional encoder-decoder architectures for scene understanding. http://mi.eng.cam.ac.uk/~cipolla/publications/inproceedings/2017-BMVC-bayesian-SegNet.pdf. Accessed November 13, 2017. [DOI] [PubMed]
- 28.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Paper presented at: Advances in Neural Information Processing Systems 25; December 3-8, 2012; Lake Tahoe, NV. https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf. Accessed November 13, 2017. [Google Scholar]
- 29.Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. Paper presented at: International Conference on Medical Image Computing and Computer-Assisted Intervention; October 5-9, 2015; Munich, Germany. https://pdfs.semanticscholar.org/0704/5f87709d0b7b998794e9fa912c0aba912281.pdf. Accessed November 13, 2017. [Google Scholar]
- 30.Zheng S, Jayasumana S, Romera-Paredes B, et al. Conditional random fields as recurrent neural networks. Paper presented at: IEEE Conference on Computer Vision and Pattern Recognition; June 7-12, 2015; Boston, MA. http://www.robots.ox.ac.uk/~szheng/papers/CRFasRNN.pdf. Accessed November 13, 2017. [Google Scholar]
- 31.Viola P, Jones M. Fast and robust classification using asymmetric adaboost and a detector cascade. Paper presented at: Advances in Neural Information Processing Systems 15; December 9-14, 2002; Vancouver, British Columbia, Canada. https://pdfs.semanticscholar.org/90f6/e2c454909f819f20d9eb6c731ba709bbe8b6.pdf. Accessed November 13, 2017. [Google Scholar]
- 32.Albarqouni S, Baur C, Achilles F, Belagiannis V, Demirci S, Navab N. AggNet: deep learning from crowds for mitosis detection in breast cancer histology images. IEEE Trans Med Imaging. 2016;35(5):1313-1321. [DOI] [PubMed] [Google Scholar]
- 33.Dorfman DD, Berbaum KS, Metz CE. Receiver operating characteristic rating analysis: generalization to the population of readers and patients with the jackknife method. Invest Radiol. 1992;27(9):723-731. [PubMed] [Google Scholar]
- 34.Bejnordi BE, Litjens G, Timofeeva N, et al. Stain specific standardization of whole-slide histopathological images. IEEE Trans Med Imaging. 2016;35(2):404-415. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
eAppendix. Deep Learning and Glossary
eFigure 1. Two Example Annotated Areas of Whole-Slide Images Taken From the CAMELYON16 Dataset
eFigure 2. Use of Immunohistochemistry Staining to Generate Reference Standard
eFigure 3. ROC Curves of the Panel of 11 Pathologists for Task 2
eFigure 4. FROC Curves of All Participating Teams for Task 1
eFigure 5. Example Probability Maps Generated by the Top-Three Performing Systems
eFigure 6. ROC Curves of All Participating Teams for Task 2
eTable 1. Classification Results by Pathologists for the Whole-Slide Image Classification Task (Sensitivity and Specificity)
eTable 2. Classification Results by Pathologists for the Whole-Slide Image Classification Task (Area Under the ROC Curve)
eTable 3. Participating Teams in CAMELYON16
eTable 4. Summary of Results for the Metastasis Identification Task (Task 1)
eTable 5. Summary of Results for the Whole-Slide Image Classification Task (Task 2)
eMethods. Methods 1 Through 30
eResults.
eDiscussion.
eReferences.