Joint arterial input function and tracker kinetic parameter estimation from under-sampled DCE-MRI using a model consistency constraint

Abstract

Purpose

To develop and evaluate a model-based reconstruction framework for joint arterial input function (AIF) and kinetic parameter estimation from under-sampled brain tumor DCE-MRI data.

Methods

The proposed method poses the tracer-kinetic (TK) model as a model consistency constraint, enabling the flexible inclusion of different TK models and TK solvers, and the joint estimation of the AIF. The proposed method is evaluated using an anatomic realistic digital reference object (DRO), and nine retrospectively downsampled brain tumor DCE-MRI datasets. We also demonstrate application to 30-fold prospectively under-sampled brain tumor DCE-MRI.

Results

In DRO studies with up to 60-fold under-sampling, this method provided TK maps with low error that are comparable to fully sampled data, and is demonstrated to be compatible with a third-party TK solver. In retrospective under-sampling studies, this method provided patient-specific AIF with normalized root mean-squared-error (nRMSE, normalized by the 90%ile value) less than 8% at up to 100-fold under-sampling. In the 30-fold under-sampled prospective study, the proposed method provided high-resolution whole-brain TK maps and patient-specific AIF.

Conclusion

The proposed model-based DCE-MRI reconstruction enables the use of different TK solvers with a model consistency constraint, and enables joint estimation of patient-specific AIF. TK maps and patient-specific AIF with high fidelity can be reconstructed at up to 100-fold under-sampling in k,t-space.

Introduction

Dynamic contrast enhanced (DCE) MRI is a powerful technique for probing sub-voxel vascular properties of tissue including fractional plasma volume, fractional extracellular-extravascular volume, and clinically important transfer constants. DCE-MRI involves capturing a series of images before, during, and after administration of a T1-shortening contrast agent. Tracer-kinetic (TK) parameter maps are then computed from the dynamic images, and provide information for diagnosis and monitoring treatment response (1–3). DCE-MRI is used throughout the body, most commonly in the prostate, breast, liver, and brain. In the brain, DCE-MRI has shown value in the assessment of brain tumor, multiple sclerosis, and Alzheimer disease (4–6).

With conventional Nyquist sampling, DCE-MRI is often unable to simultaneously provide adequate spatiotemporal resolution and spatial coverage. A typical brain DCE-MRI provides 5 second temporal resolution, which is a minimum requirement for accurate TK modeling (7, 8). Using Cartesian sampling at the Nyquist rate, only 5-10 slices are achievable. This is typically inadequate in large Glioblastoma cases, and cases with scattered metastatic disease that may be spread throughout the brain (9). It is possible to coarsen spatial resolution in order to achieve greater spatial coverage, but this compromises the ability to evaluate the narrow (1-2mm) enhancing margin of glioblastomas and the ability to evaluate small lesions.

Thus, techniques involving under-sampling and constrained reconstruction have been proposed to simultaneously provide high spatial resolution and whole-brain coverage. Early work used compressed sensing and parallel imaging to reconstruct dynamic images from under-sampled k,t-space data (10–12). Standard TK modeling software was then used to generate high-resolution whole-brain TK maps based on the reconstructed images (9, 13). A more recent proposed approach was to enforce the TK model and directly estimate TK parameters from under-sampled k,t-space data (14). Similar model-based reconstruction approaches have been used for MRI relaxometry (15, 16), PET kinetic parameter estimation (17, 18), and recently, in DCE-MRI kinetic parameter estimation (14, 19–21). Compared to conventional compressed sensing techniques that reconstruct dynamic images first, the model-based approach provides superior results and allows higher under-sampling rates (14, 21). Direct kinetic parameter estimation makes most efficient use of acquired information, however it is sensitive to inaccuracy of the forward model. Two major issues with this are variations in the arterial input function (22), and prior knowledge of the appropriate TK model (23–25).

In conventional DCE-MRI, images are reconstructed for each time point. Patient-specific arterial input functions (AIF) can be identified from vessel pixels using either manual region of interest (ROI) selection or automatic cluster-based ROI selection (26). Some centers use a fixed population-averaged AIF (27), an institutionally-derived population AIF, or a delay and dispersion corrected version of these (9). The use of a patient-specific AIF (pat-AIF) is generally preferred, as it is known to provide more accurate TK mapping (22). The estimation of pat-AIF from under-sampled data is extremely challenging due to under-sampling artifacts. Current model-based TK reconstruction approaches rely on the use of a population-averaged AIF (pop-AIF) (14, 21). This is considered a major limitation of these approaches because the use of a pop-AIF can lead to significant errors in the resulting TK maps (22).

In this work, we develop a DCE-MRI reconstruction approach that allows for integration of different TK models and/or different TK solvers, and allows for joint estimation of the patient-specific AIF and TK parameter maps. We evaluate the performance of the proposed method using simulated DCE-MRI data from a physiologically-realistic digital reference object (DRO) and in-vivo DCE-MRI data from brain tumor patients. We also demonstrate its application to prospectively under-sampled high-resolution whole-brain DCE-MRI data.

We propose simultaneous reconstruction of TK maps and dynamic images, where TK model consistency is applied as a penalized reconstruction constraint, and the patient-specific AIF can be iteratively estimated from the dynamic images. This approach is inspired by recent works in accelerated quantitative MR relaxometry (28, 29), where physical or physiological model consistency was applied as a penalized reconstruction constraint (not strictly enforced). This consistency constraint allowed for the data fit to deviate from the model, which made the scheme robust to scenarios with model inconsistencies (e.g. motion). For DCE-MRI, TK model is applied as a consistency constraint with a regularization parameter that balances the tradeoff between data consistency and model consistency. We will show that this approach provides a much more flexible framework for direct model-based reconstruction of accelerated DCE-MRI.

Theory

Model consistency constraint

This method jointly estimates contrast concentration vs time images (C) and TK parameter maps (θ) from the under-sampled data (y) by solving a least-squares problem:

$$(C,\theta )=\underset{C,\theta }{\text{arg}\min }||\mathit{UFE}(\psi C+S_0)-y|{|}_2^2+\beta ||P(\theta )-C|{|}_2^2$$ [1]

The first l₂ norm represents data consistency, where C should be consistent with the measured data y by Ψ (signal equation), U (under-sampling mask), F (Fourier transform), and E (sensitivity encoding). The second l₂ norm represents model consistency, where C is consistent to the forward modeling (P) of TK parameter maps (Patlak, eTofts etc.). This formulation can be simplified to:

$$(C,\theta )=\underset{C,\theta }{\text{arg}\min }||AC-b|{|}_2^2+\beta ||P(\theta )-C|{|}_2^2$$ [2]

where A=UFEΨ represents data consistency modeling, b=(y+UFES₀) is the known data, S₋₀ is the first temporal frame images that are fully sampled.

To solve the least-square optimization problem in Eqn [2], we alternatively solve for each variable while keeping others constant. For each iteration n:

$$C^{n+1}=\underset{C}{\text{arg}\min }||AC-b|{|}_2^2+\beta ||P({\theta }^n)-C|{|}_2^2$$ [3]

$${\theta }^{n+1}=P^{-1}(C^{n+1})$$ [4]

Note that Eqn [3] is regularized SENSE reconstruction with an l₂ norm constraint that can be solved efficiently using conjugate gradients (CG) (30). Eqn [4] is backward TK modeling that can be solved using any DCE-MRI modeling toolbox. Because forward modeling (P) and backward modeling (P⁻¹) are used iteratively, the modeling solver should not utilize linearization or other forms of approximation. For example, Rocketship (31) and TOPPCAT (32) are two suitable solvers. Detailed sub-steps and variants of Eqn [3] and [4] can be found in Appendix I.

Joint AIF and TK parameter estimation

The proposed formulation allows for joint estimation of the patient-specific AIF. Eqn [2] can be modified to estimate C, θ and AIF from under-sampled data by solving the following least-squares problem:

$$(C,\theta ,\mathit{AIF})=\underset{C,\theta ,\mathit{AIF}}{\text{arg}\min }||AC-b|{|}_2^2+\beta ||P(\theta ,\mathit{AIF})-C|{|}_2^2$$ [5]

Similar to the above, we solve each variable alternatively as follows (n^th iteration):

$$C^{n+1}=\underset{C}{\text{arg}\min }||AC-b|{|}_2^2+\beta ||P({\theta }^n,AI{F}^n)-C|{|}_2^2$$ [6]

$${\theta }^{n+1},AI{F}^n=P^{-1}(C^{n+1})$$ [7]

Eqn [7] is backward TK modeling from contrast concentration including pat-AIF estimation. This can be performed by identifying an arterial ROI once, using the time-averaged image or post-contrast image. Within each iteration, it is then possible to: 1) apply this ROI to C to estimate the AIF (averaging the pixels), and 2) use the updated AIF during TK modeling. This is a common procedure in TK modeling for DCE-MRI. The only difference is identification of the arterial ROI prior to the reconstruction of the dynamic images.

Theoretical Benefits

The proposed method formulates model consistency as a constraint with a penalty β, and decouples it from data consistency. There are multiple benefits of this formulation: 1. algorithm complexity is reduced compared to recently proposed direct reconstruction techniques that require complex cost function gradient evaluations (14, 20, 33); 2. different TK models can easily be included in this formulation, as described above; 3. patient-specific AIFs can be estimated jointly with TK maps, as described above; and 4. the penalty β can allow for TK model deviation, reducing errors that may be caused by strict model enforcement (29). This work specifically demonstrates #2 and #3.

Methods

Data Sources

Digital Reference Object

Anatomically-realistic brain tumor DCE-MRI digital reference object (DRO) was generated based on the method and data provided by Bosca and Jackson (34). The Extended-Tofts (eTofts) model was used to generate contrast concentration curves with known TK parameter maps and pop-AIF (27). Coil sensitivity maps measured on our MRI scanner (3T, 8-channel head coil) were co-registered to the DRO and used to generate realistic MRI k-space data (35). Gaussian noise were added to the image space to simulate noise levels typical of DCE-MRI at 3T and 1.5T.

Retrospective

Nine anonymized fully sampled brain tumor DCE-MRI raw data sets were obtained from patients who had received routine brain MRI with contrast (including DCE-MRI) at our Institution. The study protocol was approved by our Institutional Review Board. The acquisition was based on a 3D Cartesian fast spoiled gradient echo sequence (SPGR) with FOV: 22×22×4.2cm³, spatial resolution: 0.9×1.3×7.0mm³, temporal resolution: 5s, 50 time frames, and 8 receiver coils. The flip angle was 15°, and TE was 1.3ms, TR was 6ms. DESPOT1 was performed prior DCE-MRI, with flip angle of 2°, 5°, 10° to estimate pre-contrast T1 and M0 maps. The contrast agent, Gadobenate dimeglumine (MultiHance Bracco Inc., relaxivity r₁=4.39 s-1mM-1 at 37°C at 3 Tesla (36)) was administered with a dose of 0.05 mMol/kg, followed by a 20 ml saline flush in the left arm by intravenous injection.

Prospective

Prospectively under-sampled data were acquired in one brain tumor patient (65 M, Glioblastoma) with Cartesian golden-angle radial k-space sampling (9, 37). 3D SPGR data was acquired continuously for 5 minutes. Whole-brain coverage was achieved with a FOV of 22*22*20 cm³ and spatial resolution of 0.9*0.9*1.9 mm³. The prospective study protocol was approved by our Institutional Review Board. Written informed consent was provided by the participant.

Demonstration of TK Solver Flexibility

To demonstrate TK solver flexibility, DRO data was retrospectively under-sampled using a randomized golden-angle sampling pattern at R=60x (37). Gaussian noise were added to the image space, creating SNR levels of 20 and 10 (white matter based) for simulation of DCE-MRI image quality at 3T and 1.5T. The proposed method with eTofts modeling was used to reconstruct TK parameter maps at R=60x and SNR=20 and 10 respectively. An in-house gradient-based algorithm and an open-source TK modeling toolbox, Rocketship (31), were used for the eTofts solver in the proposed algorithm (Eqn [4]). Tumor ROI K^trans correlation coefficient, R² and normalized root mean-squared-error (nRMSE, normalized by the 90%ile value within the tumor ROI) between the estimated and true values were calculated and compared. Note that tumor ROI 90%ile K^trans value has been found to be a sensitive and clinically valuable DCE-MRI biomarker (38, 39), hence normalization of RMSE(root mean-squared-error) by this value. TK maps estimated from the noisy fully sampled images (SNR=20, R=1x) were also compared to the true TK maps to evaluate the performance of the proposed method with respect to errors found in conventional DCE-MRI.

Demonstration of TK Model Flexibility

The nine fully sampled patient data were fitted to both Patlak and eTofts model to calculate model fitting error, and F-test was performed in the tumor ROI to determine whether Patlak or eTofts model is an appropriate fit (23–25). In the F-test (40, 41), the null hypothesis is that the two samples of sum-of-squared modeling errors were drawn from the same pool. The failure of this hypothesis leads to acceptance of the higher-order model. Thus for each pixel F-test will show whether a higher-order model (eTofts model) should be used (23–25). If more than 50% of the tumor pixels were appropriately fitted for certain model, this model was selected for the data set. We reconstructed the corresponding TK parameter maps for fully sampled data (used as reference) and at under-sampling rates of 20x, 60x and 100x for all 9 cases. A randomized golden-angle sampling pattern (37) was used in the k_x-k_y plane, simulating k_y-k_z phase encoding in a 3D whole-brain acquisition. Images were reconstructed using a pop-AIF (27) with patient-specific delay corrected by the delay estimated from k-space center (42). ROI-based K^trans nRMSE and K^trans histograms were calculated based on the reference K^trans maps. K^trans histogram skewness and 90%ile K^trans values were also measured for evaluation, as they have been shown to be valuable in the clinical assessment of brain tumors by DCE-MRI (38, 39, 43).

Demonstration of Joint AIF and TK estimation

The cases following Patlak model were reviewed with special attention to vessel signal. Cases that showed significant pre-contrast inflow enhancement were identified and subsequently excluded. With the remaining cases, we performed joint estimation of AIF and Patlak parameter maps from under-sampled data across sampling rates of 20x, 60x, and 100x. For each under-sampling rate, 15 realizations were generated by varying the initial angle of the golden-angle radial sampling pattern (37). The golden-angle radial sampling with different initial angle will create mostly non-overlapped k-space coverage, effectively providing different noise realizations with the same noise level (white matter SNR=20). Reconstructed patient-specific AIFs were compared to the fully sampled reference using nRMSE (normalized to the 90%ile AIF value over time) and bolus peak difference. ROI-based K^trans nRMSE (normalized to the 90%ile K^trans value over the tumor ROI) were also calculated for evaluation.

Demonstration with Prospectively Under-sampled Data

We demonstrate application of the proposed method for joint AIF and TK parameter estimation on prospectively 30x under-sampled high-resolution whole-brain DCE-MRI data. Five second temporal resolution was achieved by grouping raw (k,t)-space data acquired within consecutive 5 sec intervals, effectively 30x under-sampling compared to Nyquist sampling (44). Patient-specific AIF and TK maps were jointly reconstructed using the proposed model consistency constraint approach. Pat-AIF ROI was selected based on time-averaged images. Three-plane of K^trans and v_p maps and pat-AIF are presented for visual assessment.

Results

Figure 1 shows the DRO reconstruction results at R=60x for SNR=20 and 10. E-tofts model was used to generate the simulated DCE-MRI data, and also for model-based reconstruction. TK maps estimated from fully sampled (R=1x) noisy images are also shown to evaluate the performance in the context of normal DCE-MRI modeling with noise. β=0.1 and iteration=100 were chosen based on prior experiments. Computation time for the conversion from concentration vs time to TK maps, was 3.44s for the in-house gradient-based method, and 31.62s for Rocketship with parallel computing turned on (4 workers). Pixel-wise correlation plots between the true and estimated K^trans values are shown at the bottom row, with calculated R² at upper left corner, and correlation coefficient at lower right corner. Both methods were able to restore K^trans maps with less than 50% error, and the in-house solver is able to restore the TK maps at the quality close to fully sampled noisy results. Rocketship solver is more sensitive to increased noise level, especially for K_ep and v_p maps. These results show that the proposed method can restore TK maps from highly under-sampled data (R=60x) with quality close to modeling results from fully sampled noisy images. It also shows that this method is compatible with a third-party TK solver.

Figure 1.

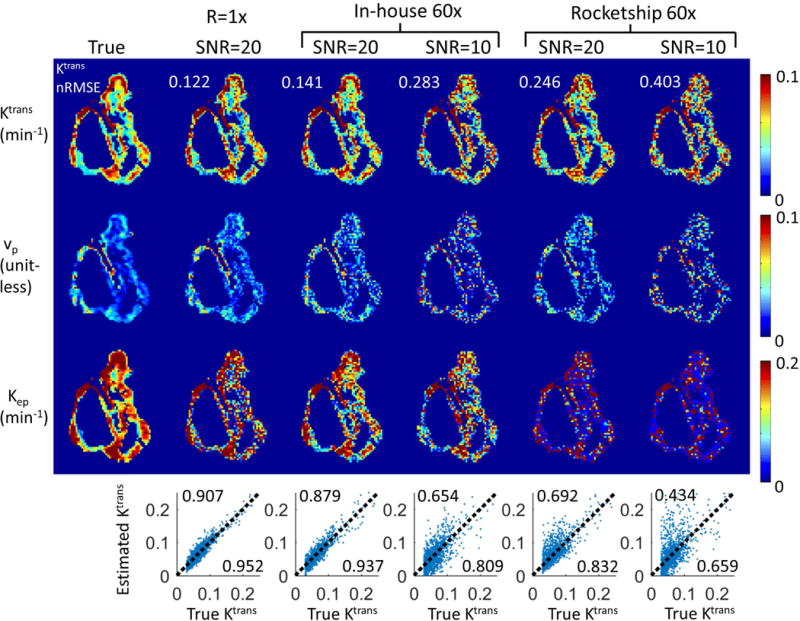
The proposed method is compatible with third-party TK solvers. Shown are results from an anatomically-realistic brain-tumor DCE-MRI digital reference object using an in-house solver and the Rocketship solver, both using the model consistency constraint method. R=60x were tested at white matter SNR level of 20 and 10. Tumor ROI K^trans nRMSE (normalized to 90%ile value) were shown on the upper left corner of respective K^trans maps. Correlation plots are shown at the bottom of each respective result, where the upper left corner shows the R² value, and lower right corner shows the correlation coefficient. Both methods were able to restore K^trans maps with less than 50% nRMSE, while the Rocketship solver yielded K^trans maps with higher errors, especially at SNR=10. K_ep and v_p maps are more sensitive to noise, especially when using the Rocketship solver.

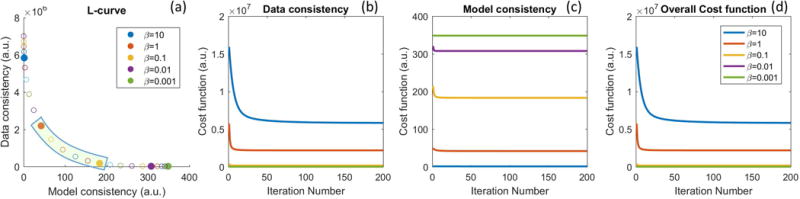
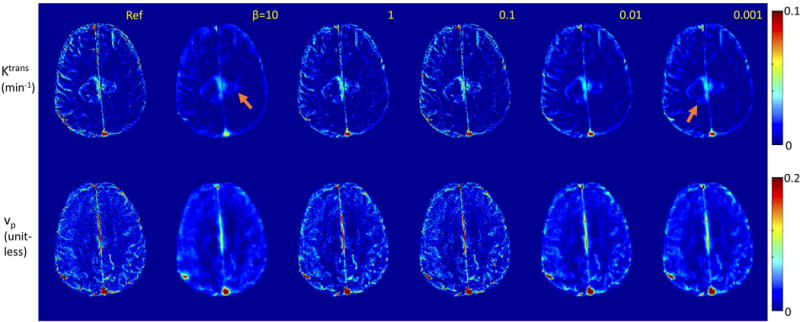
Figure 2 and Figure 3 illustrate the impact of regularization parameter β for one representative in-vivo brain tumor dataset, using the Patlak model, at R=20x. The cost function values as a function of iteration number, l-curve, and the final reconstructed TK maps are plotted for different β values. A large β resulted in slow convergence, while a smaller β provided fast convergence. This behavior is expected as ill-conditioning of the problem in Eqn [3] increases with β (45). TK maps obtained with a large β show poor fidelity as data consistency is violated, while the maps with a small β is equivalent to a SENSE reconstruction without constraints, and demonstrated g-factor related artifacts at R=20x. The L-curve shows the balance between the data consistency and model consistency, based on which the β values in the range of 0.1 to 1 (green highlighted) show similar performance. We then tune the β value in this range for different cases. We found the acceptable range to be roughly 1 order of magnitude, and consistent among the 4 cases that we carefully examined.

Figure 2.

Performance for different β values at R=20x for one representative in-vivo data set. (a) The l-curve shows that β value controls the balance between model and data consistency. (b, c, d) Convergence of the cost function to within 1% of its final value required 116, 24, 10, 4, and 2 iterations for β values of 10, 1, 0.1, 0.01, and 0.001, respectively. The actual reconstructed TK maps for different β values are shown in Figure 3.

Figure 3.

TK maps reconstructed for different β values using the case in Figure 2. Tumor ROI nRMSE (K^trans) are 0.102, 0.073,0.072, 0.098, 0.105 respectively for β values 10, 1, 0.1, 0.01, 0.001. Reconstruction with small β values converged quickly, and is closer to a SENSE reconstruction with associated g-factor losses and under-sampling artifacts. Reconstruction with large β values shows slow convergence, and provides less accurate TK maps since the data consistency is violated.

Based on the tumor ROI F-test, the Patlak model was appropriate for 6 in-vivo cases, while the e-Tofts model was appropriate for 3 in-vivo cases. Figure 4 and Figure 5 show representative cases of Patlak and eTofts model, respectively, at R=60x and R=100x. K^trans and v_p maps on the zoomed-in tumor region are shown (K_ep for eTofts is not shown). Histograms of the K^trans values within the tumor ROI are plotted for respective case at the bottom row. Figure 6 shows quantitative evaluation of all the in-vivo reconstruction results focusing on K^trans values. For Patlak model reconstruction, the 90%ile K^trans values matched well with the reference values across all cases, the histogram skewness were also reasonably matched. Across all cases and under-sampling rates, nRMSE was less than 32%. For the eTofts model, the 90%ile K^trans matched well with reference for one case, and had larger deviation for the other cases at R=100x. The nRMSE also increased considerably as the under-sampling rate is increased.

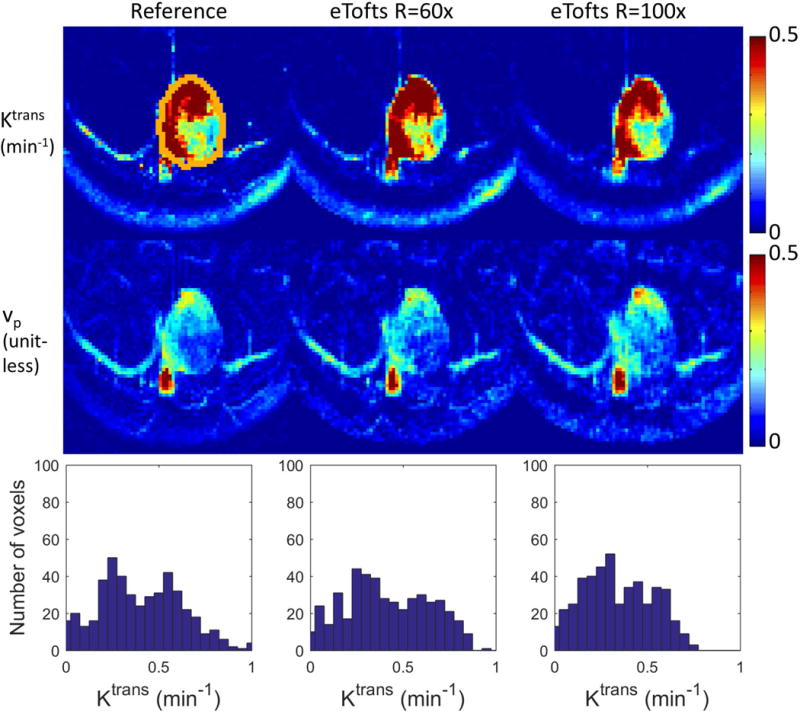
Figure 4.

Reconstruction of the TK maps of one representative in-vivo brain tumor case using the Patlak model at R=60x and 100x. Tumor ROI (indicated in the reference images) histograms are shown below the respective cases. Detailed evaluation of the ROI K^trans histograms by skewness, 90%ile, and nRMSE are shown in Figure 6.

Figure 5.

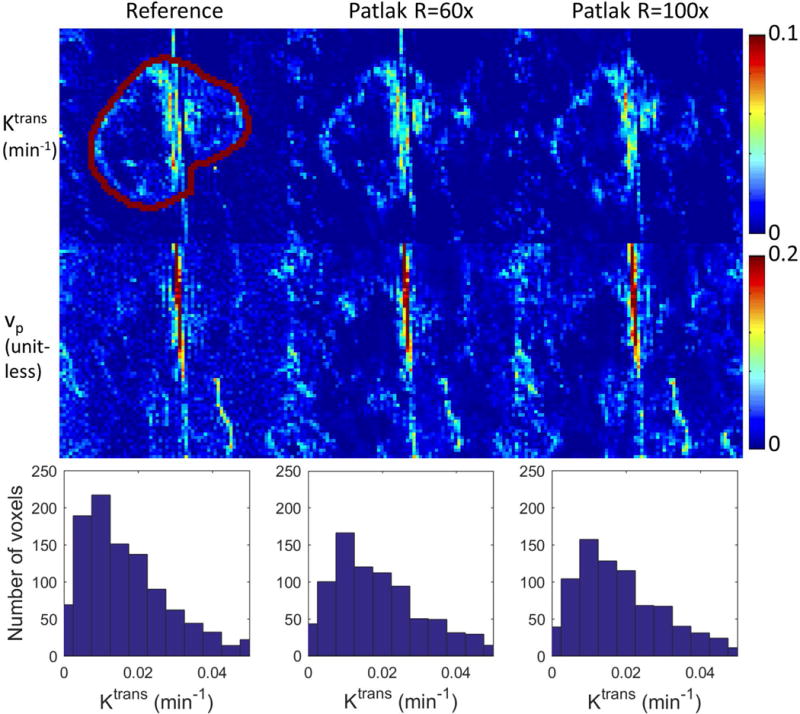
Reconstruction of the TK maps of one representative in-vivo brain tumor case using the eTofts model at R=60x and 100x. Tumor ROI (indicated in the reference images) histograms are shown below the respective cases. Detailed evaluation of the ROI K^trans histograms by skewness, 90%ile, and nRMSE are shown in Figure 6.

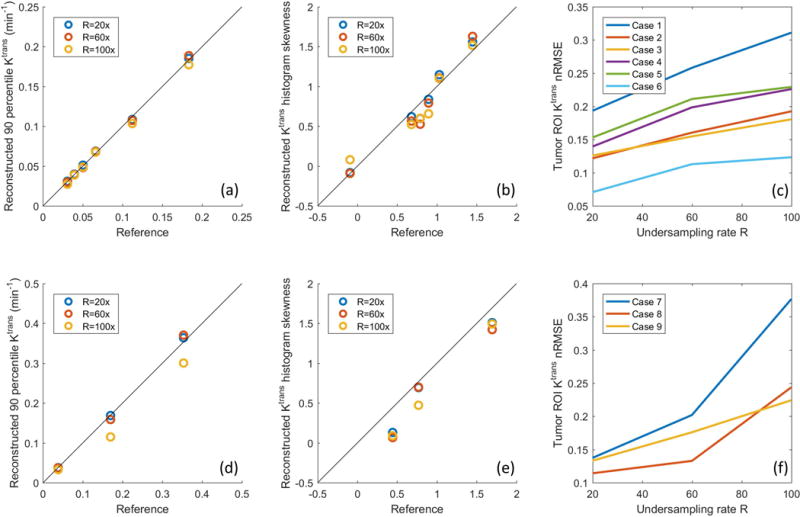
Figure 6.

Quantitative evaluation of Patlak (top row) and eTofts (bottom row) reconstruction on 9 retrospective under-sampled in-vivo cases. 90%ile of the reconstructed K^trans values for different cases were plotted against the reference 90%ile K^trans. For Patlak model the values matched well for all cases and under-sampling rates (a). For eTofts model the values matched well for R=20x and 60x, and have larger deviation for R=100x (d). The K^trans histogram skewness were also plotted against the reference histogram skewness (b), (e). The tumor ROI K^trans nRMSE (normalized based on reference 90%ile K^trans value) were plotted against different R’s across different cases. For Patlak reconstruction, the nRMSE are less than 32% consistently for all cases and under-sampling factors (c). For eTofts reconstruction, the nRMSE are less than 15% at lower under-sampling rates, then increase considerably at higher under-sampling rates (f).

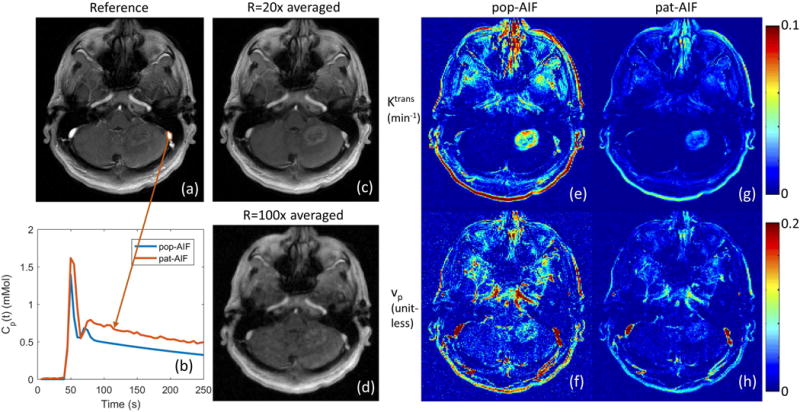
Figure 7 shows the selection of AIF ROI from under-sampled data, and the comparison of pop-AIF and pat-AIF, and the resulting TK maps in one representative in-vivo data set. This figure shows that the ROI of pat-AIF can be easily selected based on average of under-sampled data. This ROI can then be used for joint reconstruction of AIF and TK parameters in the proposed method. Figure 8 shows the reconstruction results of TK maps and pat-AIF (same case as Figure 7) at different under-sampling rates. Comparing to the AIF extracted from fully sampled data, the proposed method was able to provide clear depiction of AIF peak up to R=100x, with good-quality TK maps restored at the same time.

Figure 7.

Left: Extraction of pat-AIF (b) from a manually selected ROI on the peak contrast frame of fully sampled in-vivo data set (a). The pop-AIF show in (b) was delay corrected. In under-sampling scenario, a time averaged image can be generated (c), and even at R=100x (d), it is straightforward to select an artery ROI from this image for the joint AIF and TK maps reconstruction. Right: Different AIFs can result in different TK maps (e, f, g, h), and pat-AIF is preferred for more accurate TK modeling.

Figure 8.

Joint reconstruction of TK maps (cropped portion of the case in Figure 5) and AIF at R=20x, 60x and 100x for one representative in-vivo case. Comparing to the fully sampled reference, the proposed method is able to restore both AIF and TK maps at the same time, even at a high under-sampling rate of 100x. Quantitative evaluation of TK maps and AIF, including this case, are presented in Figure 7. See Supplemental Material for a movie of the estimated pat-AIF vs. iteration number.

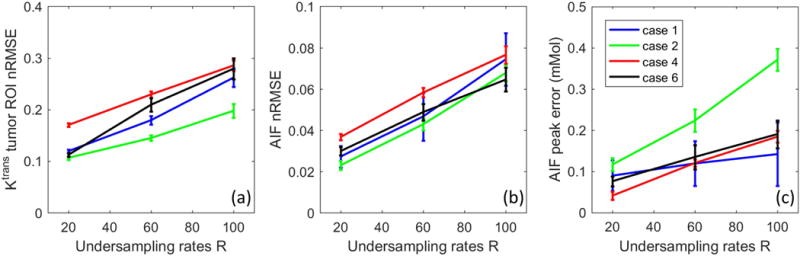
Figure 9 show the quantitative evaluation of joint AIF and TK reconstruction across the 4 in-vivo data sets. Based on the nRMSE of the TK maps, TK maps can be restored with error less than 30% at for all cases and under-sampling rates. Radial sampling patterns with different initial angle created different noise realization for each case, and multiple noise realizations show that the method is robust to noise, with an expected increase in variance at higher under-sampling rates. The shape of the AIF can be estimated at up to R=100x, with AIF nRMSE below 8% for all cases. The peak of the AIF shows larger variance for different noise realization, since the peak is only one point. However, the proposed method is still able to restore the AIF peak up to R=60x with the error at most 0.25 mMol across all cases.

Figure 9.

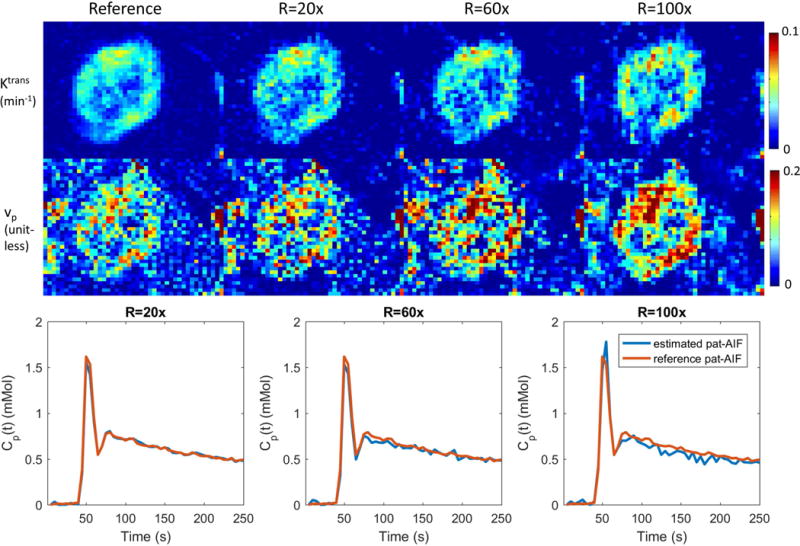
Quantitative evaluation of the joint AIF and TK reconstruction for the 4 in-vivo retrospective under-sampled cases across R=20x, 60x, and 100x. (a) K^trans nRMSE was calculated as the spatial RMSE across all tumor pixels, divided by the 90%ile of the reference tumor K^trans value. (b) AIF nRMSE was calculated as the temporal RMSE divided by the 90%ile of the reference AIF. (c) AIF peak error was calculated as the reference peak minus the estimated peak. Across different ceases, the nRMSE mean and variance all increased with under-sampling rate, as expected.

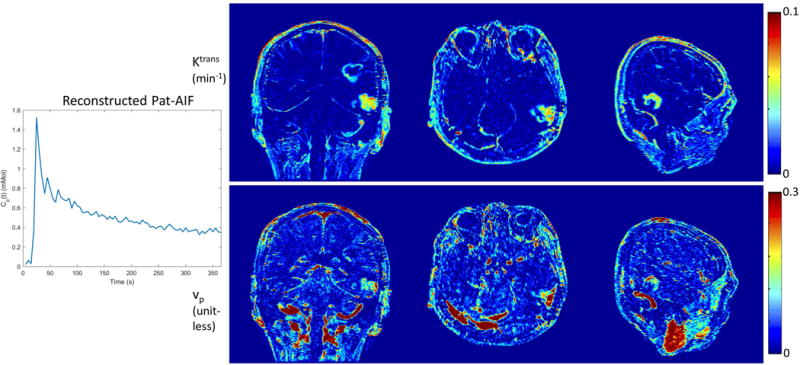
Figure 10 shows reconstruction of pat-AIF and TK maps from prospectively under-sampled in-vivo data from a brain tumor patient. This demonstrates that whole-brain TK maps can be reconstructed jointly with patient-specific AIF, with no obvious under-sampling artifacts in the final TK maps. The clinically-meaningful benefits of under-sampling can be best demonstrated in prospective study, where arbitrary reformats of the 3D TK maps are made possible thanks to the ability to achieve high spatial resolution and whole-brain coverage.

Figure 10.

Joint reconstruction of Pat-AIF and TK maps from in-vivo prospective under-sampled data. Whole-brain high-resolution TK maps can be provided together with patient-specific AIF using the proposed model-based reconstruction approach.

Discussion

We have described, demonstrated, and evaluated a novel model-based reconstruction approach for DCE-MRI, where the TK model is posed as a penalized consistency constraint. By this formulation, we decoupled the TK model consistency from the k,t space data consistency. The two sub-problems can be solved using existing techniques, namely TK modeling (including AIF estimation) and regularized SENSE reconstruction. The proposed approach allows for easy inclusion of different TK solvers, including third-party solvers, and also allows for joint estimation of the patient-specific AIF. We have demonstrated the robustness of the proposed method in one anatomically-realistic brain-tumor DRO, and a retrospective study of nine brain tumor DCE-MRI datasets. The DRO study demonstrated that the proposed method provides performance comparable to conventional TK modeling results from fully sampled noisy images, with only a 2% higher error at 60-fold under-sampling. The retrospective study shows that the proposed method is robust to noise across different cases, and can provide accurate TK maps with less than 32% error, and AIF with less than 8% error up to 100-fold under-sampling. We also demonstrated the application of the proposed method to prospectively under-sampled data, where whole-brain high-resolution TK maps can be jointly reconstructed with patient-specific AIF.

Limitations of the Study

The proposed method also has a few important limitations. First, the alternating algorithm proposed is a two-loop iteration, where an iterative solver is needed for each sub-problem. Comparing to a gradient-based direct reconstruction (14), this formulation takes longer computing time. This issue can be addressed by using more powerful computers, implementing in C, and/or using GPU acceleration.

Second, although we demonstrate that the proposed method is compatible with a third-party solver, it requires that the solver not use any approximation for the modeling. This is because the proposed approach requires the backward and forward modeling operators to be exact inverses of each other, otherwise error will accumulate during the iteration process. For higher-order TK models, a few linearized approximation approaches have been proposed for fast computation (46, 47). Unfortunately, those approximation methods are not compatible with this framework.

Third, although we have shown that this method can include different TK solver, it may be difficult to use a nested model that selects between several different local model based on local fitting errors (23–25). This type of approach has been shown in recent literature to be advantageous. The quality of intermediate anatomic images in the proposed method, especially in the first few iterations, may make it challenging to generate a modeling mask needed for nested models.

Fourth, we have not accounted for phase that can be induced by the contrast agent (primarily in vessels). Many centers, including ours, use a half dose for DCE-MRI which makes this effect negligible. If a full dose is used, the potential phase effects on the AIF signal can and should be modeled using the closed-form solution by Simonis et al. (48).

Conclusion

We have demonstrated a novel model-based reconstruction approach for accelerated DCE-MRI. Posing the TK model as a model consistency constraint, this formulation provides flexible use of different TK solvers, joint estimation of patient-specific AIF, and straightforward implementation. In anatomically realistic brain tumor DRO studies, this method provides TK maps with low error that are comparable to fully sampled data. In retrospective under-sampling studies, this method provides TK maps with nRMSE less than 32% and patient-specific AIF with nRMSE less than 8% at under-sampling rates up to 100x.

Supplementary Material

Supp VideoS1

1. (VIDEO) Supporting Video S1: Movie of estimated pat-AIF vs. iteration number at under-sampling rate R=20x, 40x, 60x, 80x, 100x, 120x.

Appendix I

The proposed method uses an alternating approach to solve for C and θ from under-sampled k,t-space data. This appendix details the steps involved in solving the two sub-problems shown in Eqn [3] and Eqn [4].

In Eqn [3], we solve for the contrast concentration vs time from the measured data using the following equation:

$$C^{n+1}=\underset{C}{\text{arg}\min }||AC-b|{|}_2^2+\beta ||P({\theta }^n)-C|{|}_2^2$$ [3]

where A=UFEΨ. We first solve for the image difference (ΔS) from b (since the pre-constrast signal S₀ is included in b) by solving the following least-square problems using CG (or another iterative algorithm for least-square problems). We use the result from the previous iteration as an initial guess for faster convergence.

$$\mathrm{\Delta }S=\underset{\mathrm{\Delta }S}{\text{arg}\min }||\mathit{UFE}(\mathrm{\Delta }S)-b|{|}_2^2+||\mathrm{\Delta }S-\psi P({\theta }^n)|{|}_2^2$$ [A.1]

where first term represents SENSE, and the second term is an identity constraint to ΨP(θⁿ) that is constant in this step. P is the forward modeling from TK maps to contrast concentration vs time C, and Ψ is the conversion from contrast concentration C to signal difference ΔS following the steady-state SPGR signal equation:

$$\mathrm{\Delta }S=\psi (C)=\frac{M_0\sin \alpha (1-e^{-TR\cdot (R_0+C\cdot r_1)})}{1-\cos \alpha e^{-TR\cdot (R_0+C\cdot r_1)}}-\frac{M_0\sin \alpha (1-e^{-TR\cdot R_0})}{1-\cos \alpha e^{-TR\cdot R_0}}$$ [A.2]

where TR is the repetition time, α is the flip angle, r₁ is the contrast agent relaxivity. R₀ and M₀ are the pre-contrast R₁ (reciprocal of T₁) and the equilibrium longitudinal magnetization that are estimated from a T₁ mapping sequence. In this work, we used DESPOT1 (49) prior to the DCE-MRI scan.

Note that Ψ is a one-to-one mapping for each voxel, and its inversion (C= Ψ⁻¹(ΔS)) is:

$$\begin{array}{l}{R}_t=-\frac{1}{TR}\ln \frac{1-\left(\frac{\mathrm{\Delta }S}{M_0\sin \alpha }+\frac{1-e^{-TR\cdot R_0}}{1-\cos \alpha e^{-TR\cdot R_0}}\right)}{1-\cos \alpha \left(\frac{\mathrm{\Delta }S}{M_0\sin \alpha }+\frac{1-e^{-TR\cdot R_0}}{1-\cos \alpha e^{-TR\cdot R_0}}\right)}\\ C=(R_t-R_0)/r_1\end{array}$$ [A.3]

Eqn [A.3] is used to compute C after solving for ΔS using Eqn [A.1], this completes the detailed algorithm for solving Eqn [3].

After C is estimated, Eqn [4] represents backward TK modelling. C(t) is used in the equation below to avoid confusion. For the Patlak model, Eqn [4] is expressed as:

$$C(t)=P(\theta )=P(K^{\mathit{trans}},v_p)=K^{\mathit{trans}}{\displaystyle \underset{0}{\overset{t}{\int }}{C}_p(\tau )\mathrm{d}\tau +v_p{C}_p(t)}$$ [A.4]

Where C_p(t) is the arterial input function (AIF). The Patlak model is linear, and a pseudo-inverse can be used to solve θ=P⁻¹(C).

For the extended-Tofts (eTofts) model, Eqn [4] is expressed as:

$$C(t)=P(\theta )=P(K^{\mathit{trans}},v_p,K_{ep})=K^{\mathit{trans}}{\displaystyle \underset{0}{\overset{t}{\int }}{C}_p(\tau )e^{-K_{ep}(t-\tau )}\mathrm{d}\tau +v_p{C}_p(t)}$$ [A.5]

where an extra TK parameter K_ep is modeled for better fitting. eTofts is nonlinear, and an iterative algorithm can be used to solve this model fitting:

$$\theta =\underset{\theta }{\text{arg}\min }||P(\theta )-C|{|}_2^2$$ [A.6]

We use a gradient-based l-BFGS algorithm to solve Eqn [A.6], where we derive the gradient for each TK parameter. In this study, we also used an open-source DCE-MRI TK modeling toolbox, Rocketship (31), for comparison.

We have made the code and examples of the proposed algorithm publicly available at the following GitHub Link: https://github.com/usc-mrel/DCE_MOCCO