Abstract
In this article, we evaluate Parallel Level Sets (PLS) and Bowsher’s method as segmentation-free anatomical priors for regularized brain PET reconstruction. We derive the proximity operators for two PLS priors and use the EM-TV algorithm in combination with the first order primal-dual algorithm by Chambolle and Pock to solve the non-smooth optimization problem for PET reconstruction with PLS regularization. In addition, we compare the performance of two PLS versions against the symmetric and asymmetric Bowsher priors with quadratic and relative difference penalty function. For this aim, we first evaluate reconstructions of 30 noise realizations of simulated PET data derived from a real PET/MRI acquisition in terms of regional bias and noise. Second, we evaluate reconstructions of a real brain PET/MR data set acquired on a GE Signa TOF PET/MR in a similar way. The reconstructions of simulated and real 3D PET/MRI data show that all priors were superior to post-smoothed Maximum Likelihood Expectation Maximization with ordered subsets (OSEM) in terms of bias-noise characteristics in different regions of interest where the PET uptake follows anatomical boundaries. Our implementation of the asymmetric Bowsher prior showed slightly superior performance compared to the two versions of PLS and the symmetric Bowsher prior. At very high regularization weights, all investigated anatomical priors suffer from the transfer of non-shared gradients.
Index Terms: image reconstruction, positron emission tomography (PET), anatomical priors
I. Introduction
Image reconstruction in Positron Emission Tomography (PET) is challenged by different factors. First of all, due to limited acquisition time and injected dose, the acquired coincidence data are subject to high Poisson noise that propagates into the reconstructed image. Second, the resolution of PET systems is limited (ca 4.5mm for the latest clinical systems [1]) due to finite detector size and photon acollinearity.
This limited resolution in the reconstructed images causes partial volume effects (PVEs) that affect quantification [2]–[6]. The PVEs can be partly compensated by incorporating a suitable resolution model into the forward model during iterative reconstruction [7]. However, resolution modeling causes Gibbs artifacts (overshoots and undershoots near sharp edges) which affect quantification as well [7].
Regularization in combination with resolution modeling in PET image reconstruction can be used to reduce PVEs and noise. In addition, regularization can help to suppress Gibbs artifacts caused by resolution modeling [8]. Under the assumption that the PET tracer distribution follows anatomical boundaries that can be determined with high spatial resolution with other imaging modalities such as magnetic resonance imaging (MR), penalized-likelihood reconstructions using anatomical information have been investigated by several groups to suppress noise and Gibbs artifacts while limiting the loss of resolution caused by this regularization.
Those methods can be divided into two groups: (i) methods that require a segmentation of the anatomical image [9]–[12], and (ii) segmentation-free methods [13]–[22]. The latter methods have the advantage that they are insensitive to potential errors in the segmentation of the anatomical images.
Recently, Ehrhardt et al. [21] (see also [23]) compared different segmentation-free anatomical priors for PET reconstruction in 2D simulations and a 2D reconstruction of a clinical data set. The authors conclude that their proposed method of Parallel Level Sets (PLS) is superior to the segmentation-free priors by Kaipio [14], Bowsher [15], Kazentsev [20], and to joint total variation [19].
In this work, which is an extension of [24], we show how to efficiently apply PLS regularization for the reconstruction of 3D clinical time-of-flight PET data. We evaluate a variant of PLS which was proposed in [25] for color imaging for PET reconstruction as well as a modified PLS version that is independent of the gradient magnitude of the anatomical image. In contrast to [21], [23], [25], both investigated PLS versions are an extension of the original, non-smooth total variation (TV) functional instead of a smoothed TV functional. We present an algorithm for the PLS regularized PET reconstruction problem that is very suitable from a practical point of view, in particular for 3D TOF PET, due to its memory efficiency and because it allows to incorporate ordered subsets.
In addition, we aim to evaluate the performance of PLS against Bowsher’s method in 3D simulations and a clinical data set. Particularly, we include the asymmetrical version of the Bowsher prior [16] as well. This heuristic modification of the Bowsher prior was shown to give superior results to the symmetrical Bowsher prior used by Ehrhardt et al. in [21]. In the following subsections we formulate the penalized-likelihood PET reconstruction problem and provide details about PLS and Bowsher’s method as segmentation-free anatomical priors.
II. Theory
A. Penalized-likelihood PET reconstruction
The penalized-likelihood PET reconstruction problem can be written as
| (1) |
where yi are measured coincidences for line of response i 1, LPET is the negative of the Poisson log-likelihood, u is the non-negative discretized PET image to be reconstructed, R is a penalty function (prior) and β is a non-negative scalar controlling the weight of the regularization. The forward model u ↦ ŷ(u) for the estimated measured data ŷ is given by
| (2) |
In (2), the operator P with matrix elements Pij is the geometrical forward projection including the effects of sensitivity, attenuation, and finite spatial resolution. Its adjoint operator P* is the back projection. Additive contaminations such as random and scattered events are denoted as s.
In the case of anatomy-guided PET reconstruction R is a function that incorporates information from a discretized anatomical prior image v. Popular choices for those joint images are high resolution MR images with low noise. Assuming that for certain tracers and applications the PET tracer distribution follows anatomical boundaries, we aim to design a function R that transfers knowledge about anatomical boundaries into the PET reconstruction. In the case of MR-guided PET reconstruction the following properties of R are desirable:
Since we aim to share information about boundaries, R should incorporate the gradients of the PET and MR image.
R should encourage neighboring voxels to have the same intensity (to suppress noise and Gibbs artifacts) unless they are separated by anatomical boundaries.
R should not depend on the sign of the gradient of the MR image. This is important since the MR image contrast might be inverted compared to the contrast in the PET tracer uptake.
R should be convex in u which makes it possible to obtain global solutions of (1) using efficient convex optimization methods.
In the following we will discuss two promising choices for R that have been proposed before.
B. Parallel Level Sets
The concept of Parallel Level Sets (PLS) was introduced by Ehrhardt et al. [25] and applied to 2D PET and MR reconstruction [21], [23], [26]. The assumption behind PLS is that the gradients in the PET (u) and MR images (v) are either parallel or anti-parallel which means that the level sets (isocontour lines) of both images are parallel. In [25], a generalized version of PLS for continuously differentiable images u(x) and v(x) was defined as
| (3) |
where d(∇u(x),∇v(x)) is a general measure of the parallelism of two gradient vectors at every point x in the domain Ω given by
| (4) |
with arbitrary strictly increasing functions φ, ψ : [0,∞) ↦ [0,∞). |∇u(x)| denotes the Euclidean norm of the gradient of u at point x given by
| (5) |
Choosing and ψ(t) = t2 we obtain
| (6) |
where θ(x) is the angle between ∇u(x) and ∇v(x) at point x. Using (6) we obtain a version of PLS that is similar to the quadratic level sets version proposed in [23]2
| (7) |
In the case of discrete images u and v with voxels j we obtain
| (8) |
which is the first version of PLS that we include in this study. In the discrete setting, we use finite forward differences to calculate the discrete gradient operator (∇u)j of the discretized image u in every voxel j.
That is, reindexing the PET signal points uj with j = 1, … , K×L×M according to the voxel position in space such that uk,l,m for k = 1, … , K, l = 1, … , L, m = 1, … , M is the signal value at position (k, l,m) in space, we define ∇u = (δxu, δyu, δzu) with
and δy, δz accordingly.
We see that the PLS1 penalty depends on the relative orientation between the two gradients but also on the magnitude of the (∇v)j which might be undesirable for MR-guided PET reconstruction3. Hence, we define a second version of PLS as
| (9) |
where we define sin θj = 1 if |(∇v)j | = 0. In contrast to PLS1, PLS2 is completely independent of the magnitude of (∇v)j. In addition, it reduces to Total Variation (TV) in regions where |(∇v)j | = 0 4. We remark that this second version of PLS cannot be regarded as a special case of [23], [25], but is rather related to [21]. In [21], the functional is employed as prior, where ξj = (∇v)j/|(∇v)j |η, with the edge parameter η > 0 and the smoothing parameter β > 0. The PLS2 functional used here corresponds to the choice β = 0 (no additional smoothing of the objective functional) and ξj = (∇v)j/|(∇v)j | if (∇v)j ≠ 0 and ξ = 0 otherwise.
Both our definitions of PLS are non-differentiable and convex in u. See Section II-D for more details about the convexity. However, as pointed out in [23], they are not jointly convex in (u, v). In contrast to the proposed PLS versions for PET reconstruction in [21], [23], [25] we do not use smoothed versions of PLS to solve (1). In [26], Ehrhardt et al. use the alternating direction method of multipliers (ADMM) to solve the non-smooth PLS-regularized MR reconstruction problem. In Section II-D of this article (see also [24]), we show how to solve the non-smooth optimization problem for PLS-regularized PET reconstruction using the EM-TV algorithm in combination with the first-order primal dual algorithm by Chambolle and Pock. The proposed algorithm is efficient and suitable for reconstruction of clinical 3D time of flight PET data.
C. Bowsher Prior
The Bowsher prior proposed in [15] is a smoothing Markov prior operating on a position dependent set of voxels. In the discrete setting, it can be written as
| (10) |
where M(uj, uk) is a function penalizing differences between the reconstructed PET uptake in voxels k and j. The neighbor weights wjk are 1 if the voxel k is in a set Bj, which consists of the n most similar voxels around j, and 0 otherwise. In all reconstructions shown in this work this set Bj includes the 4 out of the 18 nearest voxels around j that, according to the MR image intensity v, are most similar to voxel j. The absolute MR intensity difference was used as the similarity measure.
Popular choices for M are the quadratic difference [27]
| (11) |
or the relative difference [28]
| (12) |
We denote the respective versions of the Bowsher prior with BOWquad and BOWrd. To solve (1) with the Bowsher prior as penalty function R we used the preconditioned gradient descent algorithm proposed in [28]. The required first derivative for the Bowsher priors is given by
| (13) |
In the last equation, the partial derivatives of M with respect to a and b represent the partial derivatives with respect to the first and second argument of M, respectively.
The first sum in (13) involves the 4 voxels uj that are most similar neighbors of ul. The second sum involves all voxels uj for which ul is one of their most similar neighbors. These terms are not identical because wlj can be different from wjl. Intuitively, it makes sense to only use the first term when updating ul (if the second term introduces additional neighbors, they will always be less similar). This leads to the following heuristic modification resulting in improved quantification in [18F]Fluorodeoxyglucose (FDG) PET imaging5, as shown in [16]
| (14) |
In the following we will refer to the original Bowsher prior as symmetrical Bowsher (BOW) and the algorithm using the heuristic modification as asymmetrical Bowsher (aBOW). Note that, while RBOW indeed is a convex function, we are not aware of any function whose derivative corresponds to (14). Consequently, the result of the gradient descent algorithm in [28] with the asymmetrical Bowsher prior cannot be regarded as the solution of a convex optimization problem. However, since the performance of the asymmetrical version seems superior and no convergence issues of the gradient descent algorithm were observed in practice [16], [17], we included this method in our comparison.
D. Algorithm for PET reconstruction with PLS
To solve (1) with TV regularization, Sawatzki et al. [29] proposed the iterative EM-TV Algorithm shown in Algorithm 1. In the EM-TV algorithm every iteration consists of two main steps. The first step (step 5) is a normal expectation maximization (EM) step that results in the intermediate update d. The second step (step 7) consists of a weighted denoising problem that uses d as noisy input image. The main advantage of the EM-TV algorithm is the fact that the EM step can be performed with any existing Maximum Likelihood Expectation Maximization (MLEM) implementation (including list-mode MLEM). In addition, the incorporation of acceleration techniques such as ordered subsets is straightforward.
Algorithm 1.
EM-TV [29] with ordered subsets
| 1: | input y and s |
| 2: | initialize u > 0 |
| 3: | for n = 1… ni do |
| 4: | for k = 1… ns do |
| 5: | |
| 6: | |
| 7: | |
| 8: | u = u+ |
| 9: | end for |
| 10: | end for |
| 11: | return u |
When using ns subsets, the EM step and the denoising step are performed ns times in each iteration n. In the EM step, Pk denotes the PET forward operator for the k-th subset. yk and sk denote the data and contamination sinogram of the k-th subset, respectively. To investigate the number of iterations and subsets needed to achieve convergence in a practical feasible setting, we performed the bias-noise analysis for the different priors for 21 subsets with 20 and 40 iterations. Since the difference in the results when using 40 compared to 20 iterations were small, we decided to use 20 iterations in practice. Note that the weights wj become infinite if uj = 0. To keep the weights finite, we first calculate the inverse of the weights. In voxels where uj = 0, we replace the inverse weights by the average weight divided by 104. Subsequently, we calculate the weights for the denoising problem from the modified inverse weights.
The weighted denoising problem in the step 7 can be solved with the primal-dual algorithm by Chambolle and Pock [30] which results in the iterative scheme shown in Algorithm 2.
Note that the accelerated Algorithm 2 of [30] was used because the data fidelity term given by sum of the weighted squared differences is uniformly convex with convexity parameter γ = min(w). For the initialization of the dual variable q in the denoising problem after every EM step we use q from the previous denoising problem. In the first denoising problem we use q = 0. The constant L in step 3 (the norm of the 3D gradient operator) can be estimated to be [31]. In this study we always use nd = 10 when applying Algorithm 2. In step 6, div denotes the negative adjoint of ∇.
Algorithm 2.
Chambolle-Pock weighted image denoising [30]
| 1: | input d and w from EM step |
| 2: | initialize u = ū = d, q |
| 3: | initialize γ = min(w), τ = 1/γ, σ = 1/(τL2) |
| 4: | for l = 1… nd do |
| 5: | q+ = proxσ,R* (q + σ∇ū) |
| 6: | u+ = proju≥0 ((u + τ (divq+ + wd))/(1 + τw)) |
| 7: | , τ ← τϑ, σ ← σ/ϑ |
| 8: | ū+ = u+ + θ(u+ − u) |
| 9: | u = u+, ū = ū+, q = q+ |
| 10: | end for |
| 11: | return u |
In order to apply the iterative scheme to solve the weighted denoising problem, the proximity operator proxσ,R* needs to be known. To derive the proximity operators for PLS1 and PLS2, we define a candidate for the conjugate function of PLS to be
| (15) |
where gj = (∇v)j and rj is a positive real number, which we will determine below. The corresponding proximity operator of is then given by
| (16) |
where (q⊥)j is the component of qj that is perpendicular to gj given by
| (17) |
This proximity operator first removes the component of qj that is parallel to gj and then projects the residual perpendicular component to have Euclidean norm less or equal rj. The convex conjugate of is given by
| (18) |
| (19) |
| (20) |
where sin θj is the sine of the angle between the gradient of the PET reconstruction and the gradient field g in voxel j. sin θj is set to 1 when |gj | = 0. Choosing rj = |gj | we obtain and for rj = 1 we get . Hence both RPLS1 and RPLS2 are convex as being the pointwise supremum of a family of affine functions [32]. Since is convex and lower semi-continuous, their proximity maps are given as in (16).
Remark
By introducing a dual variable for the estimated measured data in the data fidelity term of (1), it is possible to directly use the first order primal-dual algorithm of Chambolle and Pock [30] to solve (1) as shown in [22]. However, since for modern PET scanners with good time of flight resolution the size of data sinograms is big (ca. 20GB for the GE Signa TOF PET/MR [1]), it is desirable to use algorithms that do not require keeping a second sinogram (the one of the dual variable) in memory. In addition, we are convinced that the fact that the use of listmode data in the EM-TV is straight forward is of great practical value for the reconstruction of current and future time of flight PET scanners whose data sinograms are highly sparse.
Remark
We note that a disadvantage of Algorithm 1 is the fact that for most priors, step 7 requires inner iterations and that convergence can only be guaranteed under some restrictive assumptions (see [33]). As alternative, one can also employ the primal-dual algorithm of [34], which uses an explicit descent on the data fidelity, for the numerical solution of (1).
III. Materials and Methods
A. Reconstruction of simulated PET data
To investigate the performance of different segmentation-free anatomical priors, we first created a 3D PET/MR software phantom based on a T1-weighted MR image of a healthy volunteer acquired on a GE Signa PET/MR scanner with an 8 channel head coil. The parameters of the T1-weighted sequence were: pulse sequence BRAVO (3D gradient echo sequence with magnetization preparation), imaging mode 3D, flip angle 12°, TI 450 ms, voxel size 0.7×1×1mm3, TE 3.2 ms, TR 8.5 ms. The raw k-space data were fully sampled and reconstructed with the vendor-provided MR reconstruction software implemented on the Signa PET/MR.
The T1 MR was segmented into fuzzy gray matter (GM), white matter (WM) and cerebral spinal fluid (CSF) compartments using SPM12 (Wellcome Trust Centre for Neuroimaging, UCL, UK) [35] and resampled to the voxel size of the PET reconstruction (1 × 1 × 1mm3). This required resampling along the x axis only, which was done by linear interpolation from the 0.7mm to a 0.5mm grid, followed by averaging pairs of neighbors into the final 1mm grid. In the PET image, fixed ground truth values for a [18F]FDG-like tracer uptake in all tissue classes (white matter 1 arbitrary unit (arb.u.), gray matter 4 arb.u., CSF 0 arb.u.) were assigned. We artificially decreased the uptake by 40% in three gyri to simulate regional hypometabolism. In addition, we added two lesions with increased uptake. The first ellipsoidal lesion was placed between GM and WM in the PET ground truth to study the influence of an MR gradient crossing a PET lesion. The second (standalone) ellipsoidal PET lesion was placed into WM where the MR is very homogeneous. Lastly, we placed a hypointense ellipsoidal MR lesion in a white matter region with constant PET uptake to study the influence of an MR gradient in a homogeneous PET region.
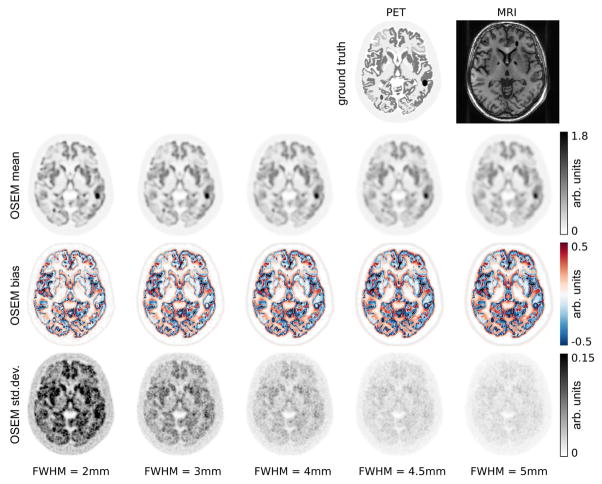
The top row of Fig. 2 shows a transversal slice of the simulated PET/MR software phantom.
Fig. 2.
Top row: transversal slice of PET and MR ground truth images that were used to generate the simulated data. The following rows show mean, bias and standard deviation images of post-smoothed OSEM reconstructions of 30 noise realizations with 108 true coincidences of the simulated 3D PET data set. All reconstructions were done with 20 iterations and 21 subsets. For post-smoothed OSEM the results after 8 iterations and 21 subsets are shown as well. The amount of post-smoothing is shown in the bottom and increases from left to right.
We simulated measured PET data by forward projecting the simulated ground truth PET. The effects of limited resolution, attenuation, realistic detector sensitivities, and a smooth scatter distribution were included. Random coincidence events were not simulated. A forward projector with the geometry of the Siemens mCT [36] (4mm crystal size) was used in the data simulation and reconstruction. The resolution of the PET scanner was modeled by a convolution with a 2D Gaussian kernel of 4.4mm in sinogram space operating along the radial and axial dimensions. The simulated TOF resolution was 400 ps which mimics the TOF resolution of current state-of-the-art PET detectors. We also simulated a smooth contamination (scatter) sinogram with a scatter fraction of 20% by convolving the forward projected PET ground truth image with a Gaussian kernel of 50 mm.
We generated 30 Poisson noise realizations each containing 108 true coincidence events which corresponds approximately to a 5 min (60 min p.i.) [18F]FDG acquisition with an injected activity of 150MBq on the GE Signa PET/MR which has a similar detector pixel size and time-of-flight resolution. For each noise realization, we performed a standard Ordered Subset Maximum Likelihood Expectation Maximization (OSEM) [37] reconstruction without anatomical information and different levels of Gaussian post-smoothing as regularization. In addition, we performed reconstructions with the following anatomical priors:
Parallel Level Sets version 1 (PLS1),
Parallel Level Sets version 2 (PLS2),
symmetrical Bowsher prior combined with quadratic penalty function (BOWquad),
asymmetrical Bowsher prior combined with quadratic penalty function (aBOWquad),
asymmetrical Bowsher prior combined with relative difference penalty function (aBOWrd).
In all reconstructions with anatomical priors the original T1-weighted MR image that was resampled to the voxel size of the PET reconstruction was used as anatomical prior image. The exact attenuation and detector sensitivities were included in the system matrix as well, and the noise-free scatter sinogram was used as the scatter estimate. For each anatomical prior reconstruction we used eight different levels of prior strength. Between two neighboring levels the prior strength was increased by a factor of three. In all reconstructions 20 iterations with 21 subsets and a voxel size of 1×1×1mm3 were used. To evaluate the different reconstructions we first of all performed a visual comparison of all reconstructions. Subsequently, we calculated bias-noise curves in different anatomical regions of interest (ROIs). The ROI averaged relative voxel bias that was used in the bias noise curves was calculated as follows: First, we calculated the bias bj in each voxel j using all reconstructions ur of the nR noise realizations and the ground truth image p as
| (21) |
Subsequently, in each ROI the average bias was calculated as the regional mean of the voxel bias. Finally, this value was divided by the ROI mean of the ground truth image to obtain the ROI averaged relative voxel bias as
| (22) |
Similarly, we calculated the standard deviation σj in each voxel j using all reconstructions ur of the nR noise realizations as
| (23) |
Subsequently, the ROI-averaged voxel noise was calculated as:
| (24) |
All reconstructions were implemented in IDL v.8.4 and C.
B. Reconstruction of clinical PET/MR data set
In addition to the reconstructions of the simulated data, we also reconstructed a clinical [18F]FDG PET/MR examination of a patient suspected for neurodegeneration. The patient had a thrombosis visible in the PET and T1 MR image in the left temporal lobe. The patient was injected with 167.5MBq of [18F]FDG and examined 78 min p.i. with a GE Signa time-of-flight PET/MR. The PET acquisition time was 20 min. The parameters of the T1 MR acquisition were the same as in the case of the healthy volunteer that was used to generate the simulated PET/MR data set. We performed a standard OSEM reconstruction without anatomical information and different levels of post-smoothing as regularization. Gaussian kernels with a full width at half maximum (FWHM) of 2, 3, 4, and 5mm were used for the post-smoothing. In addition, we performed reconstructions with the PLS2 and aBOWrd priors with different prior strengths. We chose PLS2 and aBOWrd for the clinical reconstructions since their performance in the simulations was most promising. All reconstructions used 20 iterations with 28 subsets and an image-based resolution modeling with a Gaussian kernel of 4.5 mm. After visual inspection of all reconstructions, we calculated the mean uptake in four different anatomical ROIs (right middle frontal gyrus, right superior frontal gyrus, left putamen, and cerebral white matter). The ROIs were defined in PMOD v.3.6 (PMOD, Zurich, Switzerland) using the Hammers atlas [38]. The image noise in each reconstruction was estimated by the coefficient of variation calculated over all voxels in a central white matter ROI. All reconstructions were implemented in IDL v.8.4 and C. The GE PET reconstruction toolbox v.1.26 was used to estimate the scatter and randoms contributions and to extract the sensitivity and emission sinograms, enabling image reconstruction with our research software.
IV. Results
A. Reconstruction of simulated PET data
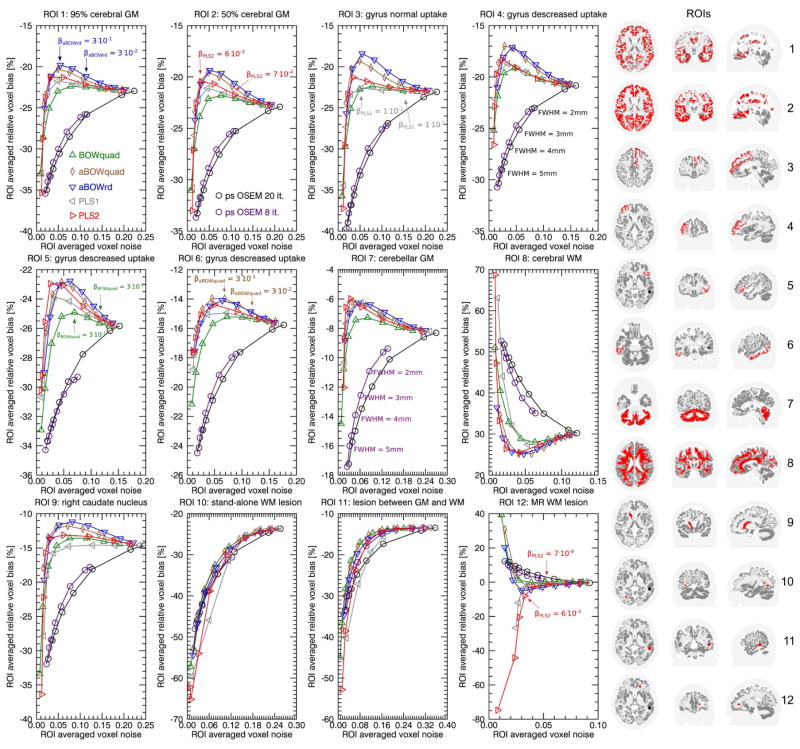
Figure 1 shows regional bias noise curves for the reconstructions of the simulated 3D PET data set. In all cerebral gray matter (GM) ROIs (top row) and in the right caudate nucleus, the reconstructions with the asymmetrical Bowsher prior with relative difference penalty (aBOWrd) shows the smallest bias at a given noise level. In the same ROIs, PLS2 reconstructions show slightly less bias than PLS1 reconstructions. Both PLS versions have less bias than the symmetrical Bowsher with quadratic penalty (BOWquad) in the cerebral GM ROIs. In the cerebellar GM ROI the difference between aBOWrd and both PLS versions is small. In the cerebral white matter (WM) ROI, aBOWrd and PLS2 show the smallest bias at a given noise level. By comparing the bias-noise curves of aBOWrd, aBOWquad, and BOWquad it can be seen that the main improvement between aBOWrd and BOWquad is due to the asymmetry and not due to the penalty function.
Fig. 1.
Regional bias-noise curves generated from 30 noise realizations with 108 true coincidences of the simulated 3D PET data set. The panel in the right shows transaxial, coronal and sagittal slices through the ROIs that were used in each subplot. For the reconstructions using anatomical priors there is factor of 3 difference in the prior strength between each data point. ROI 1 (95% cerebral GM) consists of all cerebral voxel with a gray matter fraction greater equal 95%. ROI 2 (50% cerebral GM) consists of all cerebral voxel with a gray matter fraction greater equal 50%. Note that the transversal, coronal, and sagittal slices that visualize the ROIs on the right differ between the ROIs.
In the first seven ROIs, where the simulated PET uptake coincides with the anatomical boundaries in the MR, all reconstructions with anatomical priors show less bias than post-smoothed OSEM at a given noise level. In those ROIs, all anatomical prior reconstructions allow suppression of noise without increasing the bias (due to smoothing over anatomical boundaries) up to a certain prior strength (kink in the biasnoise curve). At the noise level of minimal bias in the aBOWrd reconstructions, the bias in the post-smoothed OSEM reconstructions is approximately 10 percentage points bigger (e.g. -20% vs. -30% in the 95% GM ROI 1). The comparison between the cerebral GM, cerebellar GM and right caudate nucleus ROIs shows that the minimal achievable bias in a given ROI is object dependent. In the stand-alone PET lesion in WM (ROI 8), where the simulated PET uptake does not follow the anatomical boundaries of the MR, the difference between post-smoothed OSEM and all anatomical prior reconstructions is small.
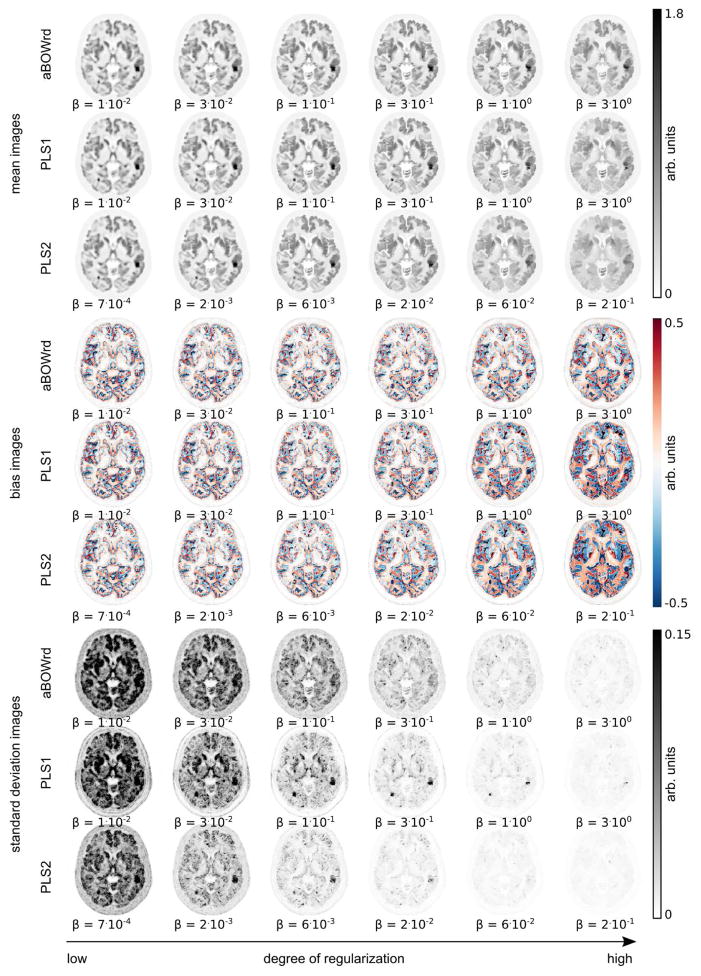
Figures 2 and 3 show a transversal slice of mean, bias, and standard deviation images over 30 noise realizations derived from reconstructions with post-smoothed OSEM, aBOWrd, PLS1, and PLS2 with different degrees of regularization. Figures 4, 5, and 6 show zoomed versions of the same transversal slice for the mean of all noise realizations.
Fig. 3.
Same as Fig. 2 but for reconstructions with different anatomical priors (aBOWrd, PLS1, PLS2). All reconstructions were done with 20 iterations and 21 subsets. The amount of regularization increases from left to right.
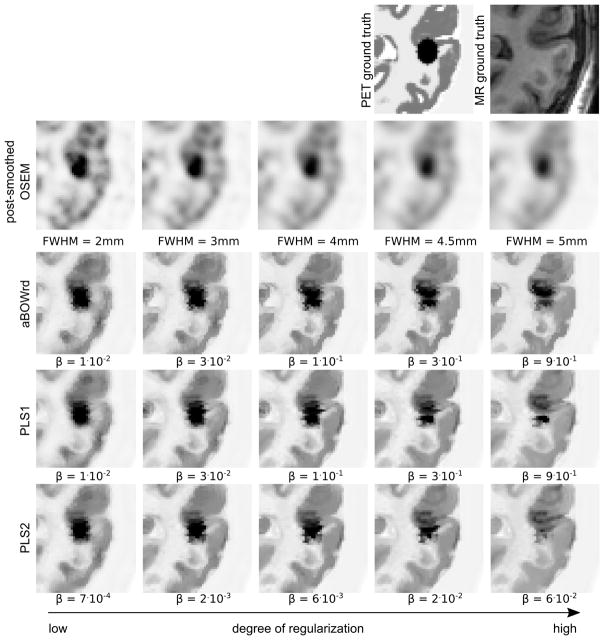
Fig. 4.
Cropped transversal slice of mean images over 30 noise realization with 108 true coincidences of the simulated 3D PET data set. In the PET ground truth the added ellipsoidal lesion that is located between GM and WM which results in an MR gradient crossing the PET lesion is visible. The top row shows the ground truth images that were used to simulate the data. The following rows show OSEM reconstructions with different levels of post-smoothing, and reconstructions with different levels of PLS1, PLS2, and asymmetrical Bowsher prior with relative difference penalty (aBOWrd). All reconstructions were done with 20 iterations and 21 subsets. The amount of regularization increases from left to right.
Fig. 5.
Same as Fig. 4 for a different region. The PET ground truth shows a small simulated standalone lesion that is not present in the MR.
Fig. 6.
Same as Fig. 4 for a different region. The MR ground truth shows a simulated lesion (signal void) in a region where the PET uptake is constant.
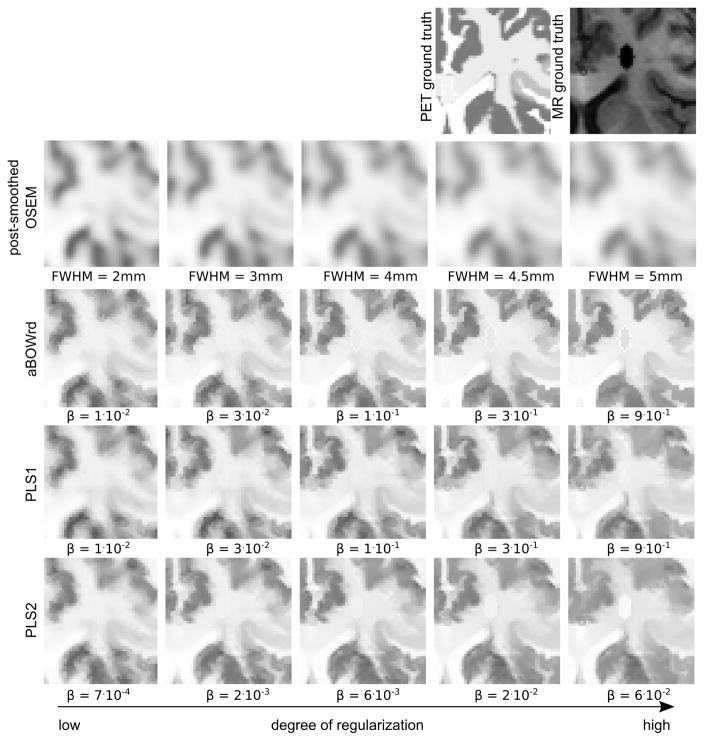
It is obvious that all anatomical prior reconstructions suffer from the transfer of non-shared MR gradients at high degrees of regularization. As shown in Figure 6, the transfer of the stand-alone MR lesion to the PET reconstruction is less pronounced with PLS1. In addition, at high degrees of regularization, the detectability of the stand-alone PET lesion is best in the PLS1 images as shown in Fig. 5.
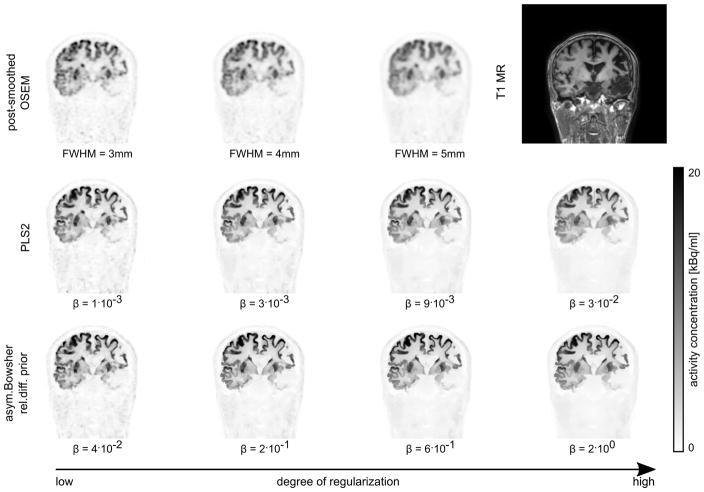
B. Reconstruction of clinical PET/MR data set
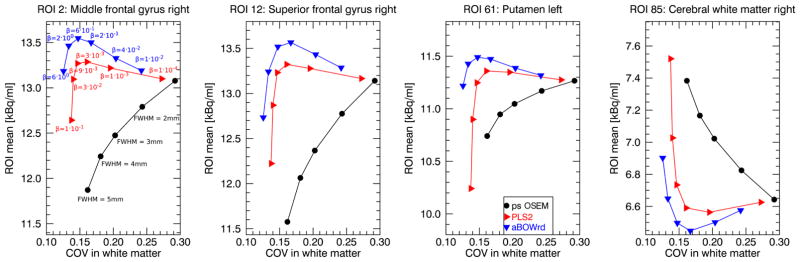
Figure 7 and supplemental figures S1 and S2 show a coronal, transversal, and sagittal slice of post-smoothed OSEM, PLS2 and aBOWrd reconstructions with different degrees of regularization for the patient data set acquired on the GE SIGNA PET/MR. Supplementary materials are available in the supplementary files/multimedia tab. Figure 8 shows a comparison of the mean reconstructed uptake in two gyri, the left putamen, and in the right cerebral white matter against the image noise. The image noise was estimated by the coefficient of variation in a central white matter ROI. At the same noise level, the reconstructions with aBOWrd show higher uptake than reconstructions with PLS2 in the first three ROIs (ROIs with lower uptake in the surrounding background). The difference in the mean uptake in the middle frontal gyrus between post-smoothed OSEM and aBOWrd reconstructions is approximately 10% at the noise level corresponding to the highest mean uptake of the aBOWrd reconstructions. At low to intermediate degrees of regularization (before the kink in the bias-noise curves), the difference in the reconstructed mean uptake between PLS2 and aBOWrd is small (less than 3%). In the cerebral white matter ROI which is influenced by spill-in from gray matter, reconstructions with aBOWrd show lower uptake than reconstructions with PLS2.
Fig. 7.
Post-smoothed OSEM, PLS2 and asymmetrical Bowsher reconstructions of a 20 min (at 78 min p.i., injected dose 167.5 MBq) clinical [18F]FDG acquisition of a patient with thrombosis in the left hemisphere. In all reconstructions 20 iterations with 28 subsets were used. The amount of regularization increases from left to right.
Fig. 8.
Plots of mean uptake in four different ROIs versus coefficient of variation in cerebral white matter ROI for the clinical data set shown in Fig. 7. For the post-smoothed OSEM, PLS2, and aBOWrd 20 iterations with 28 subsets were used.
V. Discussion
In this article we have presented two versions of Parallel Level Sets that can be used as segmentation-free anatomical priors for PET reconstruction. The application of the EM-TV algorithm [29] in combination with the first-order primal-dual algorithm by Chambolle and Pock [30] makes it possible to efficiently solve the associated convex optimization without the need to introduce smoothing parameters. As discussed in Section II-D, the introduced computational overhead by the additional denoising problem in every EM-TV iteration is small, especially when reconstructing 3D time-of-flight PET data sets.
Our proposed prior PLS2 has the advantage that it is completely independent of the magnitude of (∇v)j. In addition, as shown in Section II-D, its proximity map can be calculated efficiently which facilitates the solution of the PLS2-regularized PET reconstruction problem. Because there is no straightforward general way to derive the edge parameter η from a realistic MR image, we believe that independence of the magnitude of (∇v)j without the need of tuning the parameter η is a useful property of PLS2. A disadvantage of PLS2 is the fact that it is also sensitive to small gradients in v. However, in all PLS2 reconstructions of the simulated and clinical data we did not observe artifacts that were introduced by gradients due to noise in the MR image.
The analysis of the bias-noise curves of the reconstructions of the simulated data sets confirms the finding of [21] (where a PLS version that is similar to PLS2 was proposed) that PLS2 is superior to the symmetric Bowsher prior with quadratic penalty function (BOWquad). However, as demonstrated in the reconstructions of our simulated and in the clinical data sets, both proposed PLS versions seem slightly inferior compared to the asymmetrical Bowsher prior with relative difference penalty (aBOWrd). At noise levels obtained with algorithms typically applied in clinical routine (e.g. early-stopped OSEM with 4mm post-smoothing) the difference in the bias between PLS2 and aBOWrd is small (less than 3%) compared to the bias of post-smoothed OSEM. PLS2 has no internal parameters that have to be optimized. In contrast, Bowsher’s method depends on the chosen neighborhood and the penalty function.
When using the quadratic or relative difference penalties, the Bowsher prior is differentiable. This is advantageous because simple preconditioned gradient descent algorithms as proposed in [28] can be used to solve the optimization problem. We are aware that the iterative scheme of [28] used in combination with the asymmetric Bowsher derivative may not be the solution of a convex optimization problem. However, as observed in our analysis and shown in [16], this scheme is stable and gives better results compared to the symmetric Bowsher prior.
We believe that the reason for the difference in the performance of PLS1 compared to PLS2 can be found in the pointwise rescaling: At any point, PLS1 weighs the (anisotropic) penalization of the gradient by the magnitude of the gradient of the prior images. In contrast, PLS2 does not perform any weighting. A first, direct consequence of this is that the overall cost of the PLS1 and PLS2 regularizer are different (PLS1 has lower cost if (|∇v)j| ≤ 1), which explains that different values of β lead to comparable results. Furthermore, compared to PLS2, PLS1 potentially penalizes different edges, depending on the gradient magnitude of the prior image. On the other hand, in regions where the prior image is flat, the regularizing effect of PLS1 is very small, while PLS2 always has some regularizing effect.
The choice of the regularization parameter β is non-trivial and should be done task-dependently. For example, for some applications, such as kinetic modeling, minimal bias might be more important than low voxel noise. On the other hand, for visual evaluation the noise level plays an important role. In all cases when using anatomical prior information, the possible transfer of non-shared gradients should be considered. As shown in Figures 4, 5 and 6, the transfer of non-shared gradients is a problem for all investigated segmentation-free anatomical priors at high degrees of regularization. This fact should always be kept in mind when choosing the degree of anatomical regularization.
The analysis of the simulated reconstructions has shown that the bias in post-smoothed OSEM reconstructions introduced by partial volume effects can be reduced by approximately 10 percentage points. However, it should be noted that the minimal achievable bias was still object dependent. The difference in the mean ROI values between post-smoothed OSEM and the anatomical prior reconstructions at a given noise level was very similar in the simulations and the clinical data set. This indicates that the simulated conditions are a good approximation of real acquisitions. In the future, we aim to investigate the clinical value of PET reconstructions with different anatomical priors in the diagnosis of patients suspected for neurodegenerative diseases.
As mentioned in the introduction, the main advantage of segmentation-free over segmentation-based anatomical priors is the fact they are insensitive to segmentation errors which to our experience mostly occur in the subcortical regions when using SPM12. Advances in brain segmentation algorithms might reduce those segmentation errors leading to improved results with segmentation-based anatomical priors. For a review of state-of-the-art brain tissue segmentation methods we refer to [39].
VI. Conclusion
The method of Parallel Level Sets (PLS) is a promising segmentation-free anatomical prior for iterative PET reconstruction. The EM-TV algorithm in combination with first-order primal-dual algorithm by Chambolle and Pock makes it possible to apply PLS in clinical 3D TOF PET imaging. Our simulations and reconstructions of a clinical data set have confirmed that PLS has superior bias-noise characteristics compared to the symmetric Bowsher prior as reported in [21]. However, we found that PLS was slightly inferior compared to the asymmetrical Bowsher prior. At very high regularization weights, all investigated anatomical priors suffer from the transfer of non-shared gradients.
Supplementary Material
Footnotes
In the case of time-of-flight (TOF) PET reconstruction, i is a master index that includes the physical lines of response and the TOF bins.
The quadratic Parallel Levels Sets function in [23] uses ψ(t) = t2 and in order to obtain a smooth objective functional.
The magnitude of the gradient between different tissue classes (e.g. GM and WM) is strongly sequence dependent in MR imaging and completely unrelated to the PET tracer uptake.
Note that the case |(∇v)j | = 0 almost never occurs in real MR images.
The second derivative needed in the gradient descent algorithm was modified in a similar way.
References
- 1.Grant AM, Deller TW, Khalighi MM, Maramraju SH, Delso G, Levin CS. NEMA NU 2-2012 performance studies for the SiPM-based TOF-PET component of the GE SIGNA PET/MR system. Med Phys. 2016;43(5):2334–2343. doi: 10.1118/1.4945416. [DOI] [PubMed] [Google Scholar]
- 2.Müller-Gärtner HW, Links JM, Prince JL, Bryan RN, McVeigh E, Leal JP, Davatzikos C, Frost JJ. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects. J Cereb Blood Flow Metab. 1992;12(4):571–583. doi: 10.1038/jcbfm.1992.81. [DOI] [PubMed] [Google Scholar]
- 3.Yang J, Huang S, Mega M, Lin K, Toga A, Small G, Phelps M. Investigation of partial volume correction methods for brain FDG PET studies. IEEE Trans Nucl Sci. 1996;43(6):3322–3327. [Google Scholar]
- 4.Meltzer CC, Kinahan PE, Greer PJ, Nichols TE, Comtat C, Cantwell MN, Lin MP, Price JC. Comparative evaluation of MR-based partial-volume correction schemes for PET. J Nucl Med. 1999;40(12):2053–65. [PubMed] [Google Scholar]
- 5.Fazio F, Perani D. Importance of partial-volume correction in brain PET studies. J Nucl Med. 2000;41(11):1849–50. [PubMed] [Google Scholar]
- 6.Erlandsson K, Buvat I, Pretorius PH, Thomas BA, Hutton BF. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys Med Biol. 2012;57(21):R119–R159. doi: 10.1088/0031-9155/57/21/R119. [DOI] [PubMed] [Google Scholar]
- 7.Rahmim A. Resolution modeling in PET imaging: theory, practice, benefits, and pitfalls. Med Phys. 2013;40(6):1–15. doi: 10.1118/1.4800806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rapisarda E, Bettinardi V, Thielemans K, Gilardi MC. Evaluation of a new regularization prior for 3-d PET reconstruction including PSF modeling. IEEE Trans Nucl Sci. 2012;59(1):88–101. [Google Scholar]
- 9.Baete K, Nuyts J, Laere KV, Van Paesschen W, Ceyssens S, De Ceuninck L, Gheysens O, Kelles A, Van Den Eynden J, Suetens P, Dupont P. Evaluation of anatomy based reconstruction for partial volume correction in brain FDG-PET. Neuroimage. 2004;23(1):305–317. doi: 10.1016/j.neuroimage.2004.04.041. [DOI] [PubMed] [Google Scholar]
- 10.Baete K, Nuyts J, Van Paesschen W, Suetens P, Dupont P. Anatomical-based FDG-PET reconstruction for the detection of hypometabolic regions in epilepsy. IEEE Trans Med Imaging. 2004;23(4):510–519. doi: 10.1109/TMI.2004.825623. [DOI] [PubMed] [Google Scholar]
- 11.Nuyts J, Baete K, Beque D, Dupont P. Comparison between MAP and postprocessed ML for image reconstruction in emission tomography when anatomical knowledge is available. IEEE Trans Med Imaging. 2005;24(5):667–675. doi: 10.1109/TMI.2005.846850. [DOI] [PubMed] [Google Scholar]
- 12.Goffin K, Van Paesschen W, Dupont P, Baete K, Palmini A, Nuyts J, Van Laere K. Anatomy-based reconstruction of FDG-PET images with implicit partial volume correction improves detection of hypometabolic regions in patients with epilepsy due to focal cortical dysplasia diagnosed on MRI. Eur J Nucl Med Mol Imaging. 2010;37(6):1148–1155. doi: 10.1007/s00259-010-1405-5. [DOI] [PubMed] [Google Scholar]
- 13.Lipinski B, Herzog H, Rota Kops E, Oberschelp W, Müller-Gärtner HW. Expectation maximization reconstruction of positron emission tomography images using anatomical magnetic resonance information. IEEE Trans Med Imaging. 1997;16(2):129–136. doi: 10.1109/42.563658. [DOI] [PubMed] [Google Scholar]
- 14.Kaipio JP, Kolehmainen V, Vauhkonen M, Somersalo E. Inverse problems with structural prior information. Inverse Probl. 1999;15:713–729. [Google Scholar]
- 15.Bowsher JE, Yuan H, Hedlung LW, Turkington TG, Akabani G, Badea A, Kurylo WC, Wheeler CT, Cofer GP, Dewhirst MW, Johnson A. Utilizing MRI information to estimate F18-FDG distributions in rat flank tumors. Nucl Sci Symp Conf Rec 2004 IEEE. 2004;4(C):2488–2492. [Google Scholar]
- 16.Vunckx K, Nuyts J. Heuristic modification of an anatomical Markov prior improves its performance. Nucl Sci Symp Conf Rec 2010 IEEE; 2010. pp. 1–5. [Google Scholar]
- 17.Vunckx K, Atre A, Baete K, Reilhac A, Deroose CM, Van Laere K, Nuyts J. Evaluation of three MRI-based anatomical priors for quantitative PET brain imaging. IEEE Trans Med Imaging. 2012;31(3):599–612. doi: 10.1109/TMI.2011.2173766. [DOI] [PubMed] [Google Scholar]
- 18.Vunckx K, Dupont P, Goffin K, Paesschen WV, Laere KV, Nuyts J. Voxel-based comparison of state-of-the-art reconstruction algorithms for 18F-FDG PET brain imaging using simulated and clinical data. Neuroimage. 2014;102:875–884. doi: 10.1016/j.neuroimage.2014.06.068. [DOI] [PubMed] [Google Scholar]
- 19.Haber E, Holtzman Gazit M. Model fusion and joint inversion. Surv Geophys. 2013;34(5):675–695. [Google Scholar]
- 20.Kazantsev D, Ourselin S, Hutton BF, Dobson KJ, Kaestner AP, Lionheart WRB, Withers PJ, Lee PD, Arridge SR. A novel technique to incorporate structural prior information into multi-modal tomographic reconstruction. Inverse Probl. 2014;30(6):065004. [Google Scholar]
- 21.Ehrhardt M, Markiewicz P, Liljeroth M, Barnes A, Kolehmainen V, Duncan J, Pizarro L, Atkinson D, Hutton BF, Ourselin S, Thielemans K, Arridge SR. PET reconstruction with an anatomical MRI prior using parallel level sets. IEEE Trans Med Imaging. 2016;35(9):2189–2199. doi: 10.1109/TMI.2016.2549601. [DOI] [PubMed] [Google Scholar]
- 22.Knoll F, Holler M, Koesters T, Otazo R, Bredies K, Sodickson DK. Joint MR-PET reconstruction using a multi-channel image regularizer. IEEE Trans Med Imaging. 2016;36(1):1–16. doi: 10.1109/TMI.2016.2564989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ehrhardt MJ, Thielemans K, Pizarro L, Atkinson D, Ourselin S, Hutton BF, Arridge SR. Joint reconstruction of PET-MRI by exploiting structural similarity. Inverse Probl. 2014;31(1):15001. [Google Scholar]
- 24.Schramm G, Holler M, Koesters T, Boada F, Knoll F, Bredies K, Nuyts J. PET reconstruction with non-smooth gradient-based priors. IEEE Nucl Sci Symp Med Imaging Conf Rec; 2016. [Google Scholar]
- 25.Ehrhardt MJ, Arridge SR. Vector-valued image processing by parallel level sets. IEEE Trans Image Process. 2014;23(1):9–18. doi: 10.1109/TIP.2013.2277775. [DOI] [PubMed] [Google Scholar]
- 26.Ehrhardt MJ, Betcke MM. Multicontrast MRI reconstruction with structure-guided total variation. SIAM J Imaging Sci. 2016;9(3):1084–1106. [Google Scholar]
- 27.Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell. 1984;PAMI-6(6):721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 28.Nuyts J, Beqúe D, Dupont P, Mortelmans L. A concave prior penalizing relative differences for maximum-a-posteriori reconstruction in emission tomography. IEEE Trans Nucl Sci. 2002;49(1):56–60. [Google Scholar]
- 29.Sawatzky A, Brune C, Wübbeling F, Kosters T, Schäfers K, Martin B. Accurate EM-TV algorithm in PET with low SNR. IEEE Nucl Sci Symp Conf Rec; 2008; pp. 5133–5137. [Google Scholar]
- 30.Chambolle A, Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. J Math Imaging Vis. 2011;40(1):120–145. [Google Scholar]
- 31.Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans Image Process. 2009;18(11):2419–2434. doi: 10.1109/TIP.2009.2028250. [DOI] [PubMed] [Google Scholar]
- 32.Ekeland I, Témam R. Convex Analysis and Variational Problems. SIAM; 1999. [Google Scholar]
- 33.Burger M, Mennucci AC, Osher S, Rumpf M. Level Set and PDE Based Reconstruction Methods in Imaging. 2008. p. 110. [Google Scholar]
- 34.Chambolle A, Pock T. On the ergodic convergence rates of a first-order primal-dual algorithm. Math Program. 2016;159(1–2):253–287. [Google Scholar]
- 35.Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26(3):839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- 36.Jakoby BW, Bercier Y, Conti M, Casey ME, Bendriem B, Townsend DW. Physical and clinical performance of the mCT time-of-flight PET/CT scanner. Phys Med Biol. 2011;56(8):2375–2389. doi: 10.1088/0031-9155/56/8/004. [DOI] [PubMed] [Google Scholar]
- 37.Hudson HM, Larkin RS. Ordered subsets of projection data. IEEE Trans Med Imaging. 1994;13(4):601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- 38.Hammers A, Allom R, Koepp MJ, Free SL, Myers R, Lemieux L, Mitchell TN, Brooks DJ, Duncan JS. Three-dimensional maximum probability atlas of the human brain, with particular reference to the temporal lobe. Hum Brain Mapp. 2003;19(4):224–247. doi: 10.1002/hbm.10123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dora L, Agrawal S, Panda R, Abraham A. State of the art methods for brain tissue segmentation: A review. IEEE Rev Biomed Eng. 2017;99:1–14. doi: 10.1109/RBME.2017.2715350. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.