Grid scale drives the scale and long-term stability of place maps

Abstract

Medial entorhinal cortex (MEC) grid cells fire at regular spatial intervals and project to the hippocampus, where place cells are active in spatially restricted locations. One feature of the grid population is the increase in grid spatial scale along the dorsal-ventral MEC axis. However, the difficulty in perturbing grid scale without impacting the properties of other functionally-defined MEC cell types has obscured how grid scale influences hippocampal coding and spatial memory. Here, we use a targeted viral approach to knock out HCN1 channels selectively in MEC, causing grid scale to expand while leaving other MEC spatial and velocity signals intact. Grid scale expansion resulted in place scale expansion in fields located far from environmental boundaries, reduced long-term place field stability and impaired spatial learning. These observations, combined with simulations of a grid-to-place cell model and position decoding of place cells, illuminate how grid scale impacts place coding and spatial memory.

Proposed to serve as a neural metric for self-localization, grid cells in medial entorhinal cortex (MEC) fire in periodic patterns to form hexagonal arrays that tile the environment¹. Grid scale, the spacing between the grid vertices and the size of grid fields, increases along the dorsal-ventral MEC axis¹. Computational work^2–6 has proposed that this diversity in grid scale provides a spatial input capable of generating hippocampal place cells, which fire in spatially restricted locations⁷. However, while grid cells project to the hippocampus⁸, the examination of place cells in the absence of grid cells has produced mixed results. Temporally-restricted MEC inactivation induced place cell re-mapping^{9, 10} and larger interventions, such as MEC lesions, resulted in place field expansion^{11, 12}. However, these manipulations eliminated, in addition to grid cells, other functionally-defined MEC neurons, such as border cells that encode environmental boundaries and head direction cells that fire when an animal faces a particular direction^{13, 14}. More selective manipulations of grid cells have revealed they are not necessary for the formation of place cells. For example, the loss of grid periodicity after medial septal inactivation does not disrupt place cell firing and developmental work demonstrated that place cells have stable fields before the emergence of grid cell firing patterns^15–18.

Importantly, previous studies that examined the impact of grid cells on place coding involved a total loss of grid cells^{9–11, 17, 19}, degradation of the grid structure^{15, 16, 20}, or manipulation of multiple functionally defined cell-types²¹. This could obscure how grid cells normally effect place cells when their periodicity is intact. Place cells likely receive inputs uniformly distributed across space, with non-linear amplification of certain inputs driving field formation^{22, 23}. Removal versus modification of an input could have different effects, with each manipulation revealing principles for how inputs drive place cells. Thus, while grid cells are not necessary for place cells to form coherent and stable fields^{15, 16}, this does not negate the idea that grid cells play an important role in controlling place cells when present and spatially stable.

Yet, selectively perturbing a specific grid cell feature, such as spatial scale, remains challenging. Grid cells are anatomically intermingled with multiple functionally-defined cell types^{13, 14, 24} and genetic markers tightly corresponding to specific MEC cell classes are lacking^{25, 26}. These issues have not only made it difficult to study how grid scale impacts the place code but have left the role of grid scale in spatial navigation and memory unresolved. Theoretical and computational work suggest that the representation of space at multiple scales allows the grid population to provide a map of space that is simultaneously high in spatial resolution and large in its spatial range, features which could have implications for how different grid scales support behavior^{27, 28}. To experimentally test the impact of grid scale on place cell coding and behavior we took advantage of the expansion in grid scale observed after the loss of HCN1 channels^{29, 30}, which leaves grid periodicity and other functionally-defined MEC neurons intact. While previous work deleted HCN1 across the forebrain^29–31, we used a viral approach to knockout HCN1 in the MEC of adult mice, allowing us to examine how grid scale controls place codes, navigation and memory.

Results

Selective knockout of MEC HCN1 channels

Previous work demonstrated that germline knockout of forebrain HCN1 channels increased both grid and place scale^{30, 31}. To selectively examine how grid scale impacts place coding and behavior, we regulated HCN1 channel expression specifically in the MEC by injecting Cre-expressing AAV (AAV-DJ CMV cre-GFP) into the MEC of adult floxed HCN1 knockout mice (iCre-KO) and their wildtype littermates (iWT) (Fig. 1a). GFP was well constricted to and detected in a large portion of MEC (Fig. 1b–c, Online Methods and Supplementary Figs. 1–4). Whole-cell patch clamp recordings confirmed that the Cre-mediated knockout of HCN1 reduced I(h) (Supplementary Fig. 5).

Figure 1.

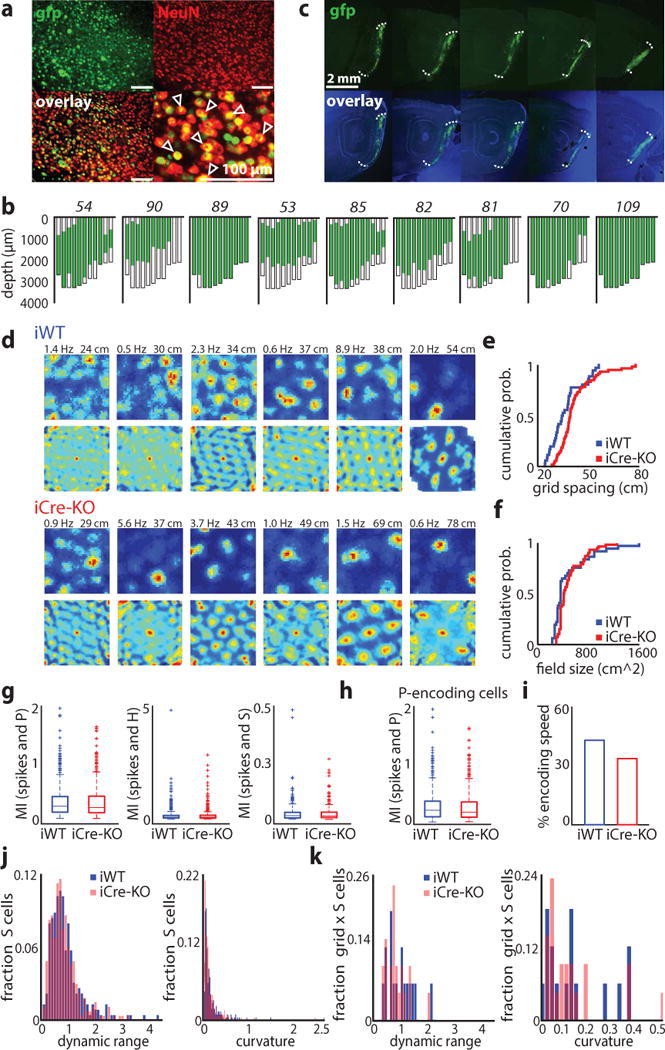
Knockout of HCN1 in MEC increases grid scale. (a) Virus expression near the injection site. Sections were stained against NeuN (red). The majority of neurons also express the nuclear fusion protein Cre-GFP (green). Scale bars: 100 μm. Arrows indicate virus-infected neurons. The rate of virus infection was determined from brain slices from 6 mice (mean ± SD, 71 ± 18%, n = 24 ROIs from 12 brain slices from 6 mice). (b) Flat maps from nine mice showing the extent of MEC infection; maps are plotted from lateral (left) to medial (right). Mouse identification number in italics. In these mice, virus was present within the majority of MEC (mean ± SD; 60 ± 20% of total volume) and across the medial-lateral and dorsal-ventral axes (medial-lateral: 98 ± 2.4%, dorsal-ventral: 75 ± 17.8%; n = 9 mice). (c) Example of virus expression across the medial-lateral axis of MEC in an individual mouse. Images of dapi and GFP were taken separately and then combined in Photoshop. The intensity of the blue and green channels were adjusted separately to allow for clear visualization of the GFP expression. Similar results were obtained in nine mice randomly selected for virus expression quantification. (d) Examples of grid cells recorded in iWT and iCre-KO mice. Rate maps (top rows) and autocorrelation maps (bottom rows) are color coded for minimum (blue) and maximum (red) values. Peak firing rates (left) and grid spacing (right) are marked at the top of each plot. Grid score, firing rates, and stability did not differ significantly between groups (mean ± SD; grid score: iWT = 0.49 ± 0.12, iCre-KO = 0.59 ± 0.25, Z = −0.98, p = 0.33, two-tailed WRS; FR: iWT = 1.11 ± 2.66 Hz, iCre-KO = 1.75 ± 6.43 Hz, Z = 0.054, p = 0.96, two-tailed WRS; Stability controlled for grid scale F(1, 96) = 0.66, p = 0.42, ɳ² = 0.007, ANCOVA). (e-f) Cumulative distributions of grid spacing (e) and grid field size (f) in iWT (blue) and iCre-KO (red) mice (n = 37 iWT cells, 62 iCre-KO cells). Grid field size was determined from the radius of the circle around the center field of the autocorrelation map. See Table 1 for statistics. (g) Cells identified as significantly encoding P, H or S using the LN model did not differ in mutual information (MI) between iWT and iCre-KO mice (mean ± SD; P cells spatial information iWT = 0.31 ± 0.29, n = 464, iCre-KO = 0.30 ± 0.29, n = 544, Z = 0.77, p = 0.44; H cells angular information iWT = 0.16 ± 0.35, n = 351, iCre-KO = 0.16 ± 0.30, n = 434, Z = −1.57, p = 0.12; S cells speed information iWT = 0.034 ± 0.045, n = 227, iCre-KO = 0.034 ± 0.046, n = 264, Z = 0.50, p = 0.62, two-tailed WRS tests). Boxes show the first and third quartiles, lines show the median. Whiskers indicate the range, except for data falling above the third quartile or below the first quartile by at least 1.5 times the interquartile range (plotted separately by a plus sign). (h) P cells not classified as border or grid cells in iWT and iCre-KO mice did not differ in MI (mean ± SD; iWT = 0.30 ± 0.29, iCre-KO = 0.27 ± 0.27, Z = 1.33, p = 0.18, two-tailed WRS; n = 355 iWT cells, 419 iCre-KO cells), percent of the environment covered by a field, or spatial stability (mean ± SD; % environment covered: iWT = 35.17 ± 32.52%, iCre-KO = 38.02 ± 33.53%, Z = −1.04, p = 0.30; stability: iWT = 0.18 ± 0.16, iCre-KO = 0.19 ± 0.16, Z = −0.48, p = 0.63, two-tailed WRS tests). Box plots are depicted as in (g). (i) A similar proportion of grid cells in each group significantly encoded speed (16/37 iWT grid cells, 21/62 iCre-KO grid cells; Z = 0.93, p = 0.35, two-tailed binomial test). (j) S encoding cells in iWT and iCre-KO mice did not differ in their speed modulation (defined as (minimum FR – maximum FR)/mean FR) or curvature (mean ± SD; speed modulation: iWT = 0.90 ± 0.62, iCre-KO = 0.85 ± 0.53, Z = 1.01, p = 0.31; curvature: iWT = 0.15 ± 0.25, iCre-KO = 0.13 ± 0.20, Z = 0.95, p = 0.34, two-tailed WRS tests; n = 227 iWT cells, 264 iCre-KO cells). (k) iWT and iCre-KO grid cells that also significantly encoded S did not differ in their speed modulation or curvature (mean ± SD; speed modulation: iWT = 0.93 ± 0.49, iCre-KO = 0.79 ± 0.39, Z = 0.78, p = 0.43; curvature: iWT = 0.13 ± 0.13, iCre-KO = 0.12 ± 0.13, Z = 0.17, p = 0.87, two-tailed WRS tests; n = 16 iWT cells, 21 iCre-KO cells).

Loss of MEC HCN1 channels selectively impacts grid scale

To investigate if the loss of MEC HCN1 in adult mice specifically impacted grid scale, we implanted tetrodes into 29 mice (12 iWT; 17 iCre-KO) and recorded cells in MEC (iWT n = 527; iCre-KO n = 600) as mice explored open arenas. We considered MEC coding properties in two ways. First, we identified grid, border, spatially-stable, head direction and speed cells by performing a shuffling analysis (Online Methods) (Supplementary Fig. 6). Using this approach, we found 37 iWT and 62 iCre-KO grid cells (Fig. 1d). While the magnitude of periodicity, mean firing rate (FR) and spatial stability of grid cells did not differ between groups, both grid spacing and field size were significantly expanded in iCre-KO compared to iWT mice (mean ± SD; spacing: iWT = 36.26 ± 9.27 cm, iCre-KO = 42.16 ± 10.53 cm, Z = −3.09, p = 0.0020; field size: iWT = 489.29 ± 301.62 cm², iCre-KO = 502.64 ± 207.26 cm², Z = −2.20, p = 0.028, two-tailed Wilcoxon rank sum [WRS] tests) (Fig. 1d–f). This difference in scale did not reflect different dorsal-ventral (DV) recording locations between the two groups (Supplementary Fig. 7). We did not detect any significant changes in the coding properties of other functionally-defined MEC cell types, including: border cells, spatially stable cells not classified as grid or border cells, putative interneurons (mean FR > 10 Hz)²⁴, head direction cells and speed cells (Table 1, Supplementary Fig. 8–9).

Table 1.

Firing and EEG-properties in medial entorhinal cortex and hippocampus

	iWT	iCre-KO
border cells
n	86	71
border score	0.62 ± 0.092	0.61 ± 0.080	WRS Z = −0.20, p = 0.84
mean firing rate	1.13 ± 2.50 Hz	1.01 ± 1.73 Hz	WRS Z = 0.34, p = 0.73
peak firing rate	3.69 ± 5.09 Hz	3.53 ± 5.00 Hz	WRS Z = 0.22, p = 0.83
spatial stability	0.31 ± 0.22	0.27 ± 0.22	WRS Z = 0.87, p = 0.38
border width	14.43 ± 6.53 cm	14.23 ± 5.22 cm	WRS Z =−0.30, p = 0.76
spatially stable cells
n	32	38
mean firing rate	1.15 ± 1.11 Hz	1.99 ± 2.21 Hz	WRS Z = −1.20, p = 0.23
peak firing rate	5.00 ± 4.37 Hz	6.15 ± 1.00 Hz	WRS Z = −1.73, p = 0.084
spatial stability	0.37 ± 0.15	0.37 ± 0.17	WRS Z = 0.19, p = 0.85
mean field size	2473.45 ± 2233.2 cm2	2692.29 ± 2768.8 cm2	WRS Z = 0.12, p = 0.90
% box covered by fields	43.24 ± 30.72 %	45.58 ± 31.62 %	WRS Z = −0.15, p = 0.88
interneurons
n	15	22
mean firing rate	23.33 ± 26.46 Hz	23.37 ± 16.11 Hz	WRS Z = −1.38, p = 0.17
peak firing rate	37.22 ± 36.48 Hz	38.85 ± 19.89 Hz	WRS Z = −1.50, p = 0.13
bursting	19.33 ± 14.55 %	21.50 ± 16.20 %	WRS Z = 0, p > 0.99
theta-modulated interneurons, n	13	16
interspike interval	96.92 ± 14.65 s	98.75 ± 16.07 s	WRS Z = −0.36, p = 0.72
head direction cells
layer II/III, n	176	185
head direction score	0.36 ± 0.21	0.37 ± 0.20	WRS Z = −1.32, p = 0.19
mean firing rate	1.24 ± 7.62 Hz	0.72 ± 1.22 Hz	WRS Z = 0.15, p = 0.88
peak firing rate	3.66 ± 11.37 Hz	2.98 ± 3.81 Hz	WRS Z = −0.50, p = 0.62
directional stability	0.46 ± 0.29	0.46 ± 0.29	WRS Z = −0.18, p = 0.86
tuning width	124.77 ± 72.86°	128.43 ± 81.51°	WRS Z = 0.0071, p = 0.99
layer V, n	49	55
head direction score	0.41 ± 0.26	0.40 ± 0.20	WRS Z = −0.64, p = 0.52
mean firing rate	0.54 ± 0.75 Hz	0.84 ± 1.70 Hz	WRS Z = −0.036, p = 0.97
peak firing rate	2.08 ± 2.34 Hz	3.00 ± 4.49 Hz	WRS Z = −0.35, p = 0.73
directional stability	0.55 ± 0.27	0.52 ± 0.20	WRS Z = 0.83, p = 0.41
tuning width	126.61 ± 80.08°	126.55 ± 78.98°	WRS Z = −0.42, p = 0.67
speed cells
n	69	89
speed score	0.11 ± 0.056	0.11 ± 0.055	WRS Z = −0.074, p = 0.94
mean firing rate	3.39 ± 12.41 Hz	3.088 ± 9.72 Hz	WRS Z = 0.11, p = 0.92
peak firing rate	6.89 ± 18.39 Hz	6.40 ± 13.12 Hz	WRS Z = −0.50, p = 0.61
slope (hz/cm/s)	0.018 ± 0.025	0.024 ± 0.047	WRS Z = −0.070, p = 0.94
MEC EEG (layer II)
n	12	16
theta power	0.75 ± 0.34	0.80 ± 0.47	WRS Z = 0, p > 0.99
theta frequency	8.82 ± 0.22 Hz	8.79 ± 0.25 Hz	WRS Z = 0.35, p = 0.73
theta slope (Hz/cm/s)	0.011 ± 0.0067	0.014 ± 0.0081	WRS Z = −1.27, p = 0.20
fast gamma power	0.092 ± 0.024	0.092 ± 0.039	WRS Z = 0.023, p = 0.98
slow gamma power	0.27 ± 0.068	0.23 ± 0.085	WRS Z = 1.18, p = 0.24
hippocampal EEG
n	11	8	*p-value using exact method
theta power	0.89 ± 0.40	0.85 ± 0.32	WRS, p > 0.99
theta frequency	8.74 ± 0.29 Hz	8.77 ± 0.12 Hz	WRS, p = 0.86
theta slope (Hz/cm/s)	0.016 ± 0.01	0.015 ± 0.0053	WRS, p = 0.90
fast gamma power	0.082 ± 0.049	0.087 ± 0.026	WRS, p = 0.60
slow gamma power	0.25 ± 0.097	0.32 ± 0.066	WRS, p = 0.091
place cells
n	113	126
number of fields	1.95 ± 1.16	1.71 ± 1.09	WRS Z = 1.66, p = 0.10
peak firing rate	3.50 ± 2.55 Hz	4.38 ± 4.32 Hz	WRS Z = −1.30, p = 0.19
mean in-field firing rate	1.41 ± 1.02 Hz	1.84 ± 1.98 Hz	WRS Z = −1.09, p = 0.27
bursting	4.76 ± 6.40 %,	5.52 ± 4.29 %	WRS Z = −1.00, p = 0.32

Mean ± SD. Cells are used as experimental units except for EEG measures, where mice are used. All WRS tests were two tailed.

Second, we used a general statistical approach to capture the coding properties of MEC neurons³². We fit multiple, nested linear-nonlinear-Poisson (LN) models to the spike train of each cell, enabling us to quantify how well the position (P), head direction (H) or running speed (S) of the animal predicted single cell spiking activity (Figure 1g–k, Supplementary Fig. 10, Online Methods). This model-based approach does not classify neurons based on specific pre-defined firing rate patterns and thus, captures coding in a significantly larger proportion of MEC neurons than shuffling analyses (# classified cells: shuffled = 879/1127, LN model = 1025/1127, Z = −8.49, p ≪ 0.0001, 1-sided Binomial test). Using the LN model approach, we found equal proportions of MEC neurons encoding P, H, or S in iWT and iCre-KO mice (Supplementary Fig. 10). For cells that significantly encoded P, H or S, there was no significant difference between groups in the mutual information between the navigation variable and neural spikes (Fig. 1g). As MEC contains a large number of cells that encode the spatial location of the animal but do not show grid or border firing patterns^{32, 33}, we then considered cells that significantly encoded P but were not classified as grid or border cells. We found no significant differences in multiple coding features of this population of P-encoding cells, consistent with our analyses of spatially modulated cells identified using shuffling (Fig. 1h). Finally, given the reported heterogeneity in how MEC neurons encode speed³², we examined cells S-encoding cells, many of which were not detected by our shuffling analysis. These included, for example, speed cells that had a negative or non-monotonic firing rate relationship with running speed (Supplementary Fig. 10). We found no significant differences in the speed modulation of speed cells or the degree of curvature in their firing rate profiles (Fig. 1i–k). This result held for grid cells that significantly encoded S (Fig. 1k). Combined, these findings are consistent with our analyses using the shuffling approach to classify cell-types.

Finally, we examined if MEC HCN1 deletion impacted MEC or hippocampal temporal signals (Table 1, Supplementary Fig. 9). Theta power, frequency, and the running speed modulation of theta, as well as slow and fast gamma power, were all comparable between iCre-KO and iWT mice (all p > 0.05). Taken together, these data indicate that the impact of HCN1 on MEC coding properties is highly specific to grid scale, pointing to this experimental model as an ideal entry point for the investigation of how grid scale impacts place coding and behavior.

Place and grid cell scale expansion occur in concert

We next asked how an increase in grid scale influenced spatial coding in dorsal hippocampus⁸. We recorded CA1 place cells in iWT (n = 11) and iCre-KO mice (n = 8) as they explored open arenas (Fig. 2a, Supplementary Fig. 2). Place field size was significantly larger in iCre-KO compared to iWT mice (Fig. 2b–c, Supplementary Fig. 11–12). Consistent with this, the percentage of the environment covered by firing fields and the mean firing rate (FR) across the environment were higher in iCre-KO place cells (Fig. 2d–e). This FR difference reflected the increased place field size in iCre-KO mice rather than increased firing outside of fields, as the spatial selectivity index was not significantly different between groups (mean ± SD; iWT = 1.08 ± 0.26, iCre-KO = 1.06 ± 0.27, Z = 0.53, p = 0.60, two-tailed WRS). In addition, in a separate group of iWT and iCre-KO mice trained to run on a linear track, analysis of individual passes through place fields demonstrated that the expansion in field size represented a true scale expansion, rather than place fields slowly drifting over the course of the session (Supplementary Fig. 11–12).

Figure 2.

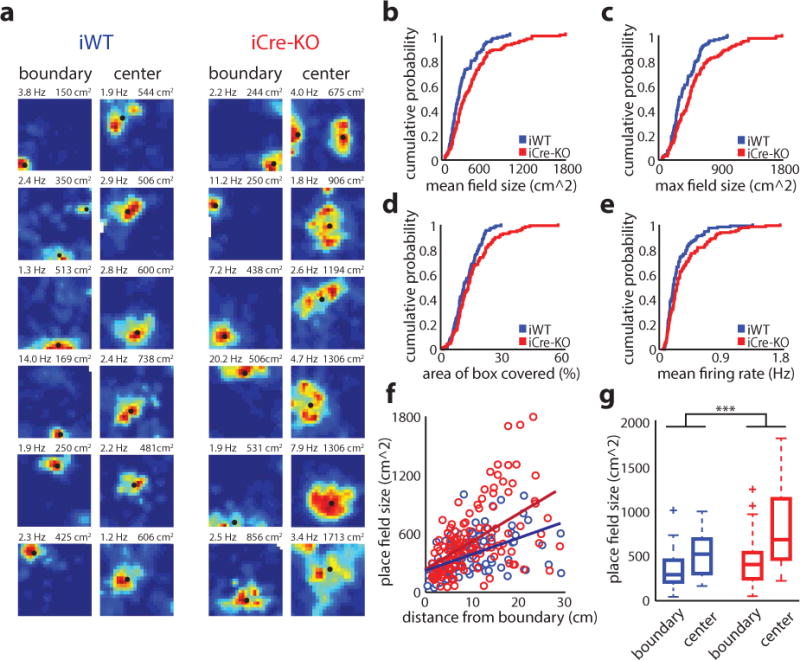
Place scale expands in mice with an expanded grid scale. (a) Examples of place cells with fields within the boundary (left) and center (right) regions of the arena. The boundary width was set to 14 cm, the average width of all recorded border cells. Classification was based on the position of the largest field detected. Rate maps coded as in Figure 1. Peak firing rate (left) and maximum field size (right) are indicated at the top of each plot. Black dots denote firing fields. (b-e) Cumulative distributions of the mean place field sizes (mean ± SD; iWT = 303.75 ± 204.07 cm², iCre-KO = 438.71 ± 337.04 cm², Z = −3.34, p = 8.3e-4, two-tailed WRS) (b), maximum place field sizes (mean ± SD; iWT = 373.34 ± 205.71 cm², iCre-KO = 524.40 ± 352.82 cm², Z = −3.24, p = 0.0012, two-tailed WRS) (c), percentage of environment covered by fields (mean ± SD; iWT = 12.27 ± 6.1 %, iCre-KO = 15.3 ± 9.6 %, Z = −2.14, p = 0.033, two-tailed WRS) (d), and mean firing rate (mean ± SD; iWT = 0.28 ± 0.21 Hz, iCre-KO = 0.37 ± 0.32 Hz, Z = −2.38, p = 0.017, two-tailed WRS) (e), in iWT (blue) and iCre-KO (red) mice (n = 113 iWT place cells, 126 iCre-KO place cells). (f) Scatterplot demonstrating the increase in place field size as a function of the field’s distance from the nearest arena edge (iWT r(111) = 0.49, p = 3.5e-8, iCre-KO r(124) = 0.53, p = 1.5e-10, Pearson’s correlation). The slope was significantly greater among iCre-KO cells (F(1,235) = 6.01, p = 0.015, ɳ² = 0.025, ANCOVA; n = 113 iWT cells, 126 iCre-KO cells). (g) Boxplot showing the sizes of place fields near the center (> 14 cm; 22 iWT cells, n = 35 iCre-KO cells) versus the boundaries (< 14 cm; n = 91 iWT cells, 91 iCre-KO cells) of the environment. The difference in size between place fields located near the arena boundaries versus the arena center was larger for iCre-KO (red) compared to iWT (blue) place cells, as assessed by a two-tailed t-test on bootstrapped distributions of the mean difference (t(19998) = 192.30, p ≪ 0.0001; see Online Methods). Box shows first and third quartiles, a line shows the median. Whiskers indicate the range, except for data falling above the third quartile or below the first quartile by at least 1.5 times the interquartile range (plotted separately by a plus sign). *p<0.05, ***p<0.001

Despite the increased place scale, other spiking features of place cells were similar between groups (Table 1). In addition, the temporal dynamics of place cell phase precession remained intact in iCre-KO mice, consistent with previous work demonstrating both that MEC is necessary for hippocampal phase precession³⁴ and that the loss of forebrain HCN1 did not impact MEC theta phase precession²⁹ (Supplementary Fig. 11).

Developmental and pharmacological approaches have suggested that grid cells predominately influence place cells with fields located far from environmental boundaries^{15, 20, 35}. To examine this idea, we quantified place field size as a function of the field’s distance from the boundaries of the arena. In both iWT and iCre-KO mice, place field size was positively correlated with distance from the nearest boundary (Fig. 2f). However, the slope of this correlation was significantly steeper in iCre-KO mice, suggesting that the increase in grid scale primarily effected the size of place fields located far from boundaries. To further investigate this, we compared the size of place fields located near the center versus the boundaries of the arena. The difference in field size between these locations was more pronounced for iCre-KO compared to iWT mice (Fig. 2g). Taken together these data indicate that, when present, grid scale is an important determinant of place scale, with the strength of this influence likely dependent on the location of place fields relative to environmental landmarks.

Grid scale expansion impacts long-term place stability

While the scale of the place code could impact how accurately an animal can decode its current position, the long-term maintenance of place field stability across multiple exposures to the same environment has been proposed as a vital element of the spatial memory system. MEC input likely plays a role in the maintenance of the place map, as inactivation of MEC induces a near instantaneous change in the configuration of place fields, a phenomenon referred to as remapping^{9, 10, 34}. However, which features of entorhinal coding drive place stability versus remapping, as well as what impact place cell stability might have on memory, remain unresolved.

To address the role of grid scale in place cell stability, we compared the stability of iWT and iCre-KO place cells within a single session and across days within the same spatial context (Fig. 3a and Supplementary Fig. 13, 14). While stability did not differ across a single session (mean ± SD; Pearson’s correlation coefficient: iWT = 0.56 ± 0.23, iCre-KO = 0.60 ± 0.23, Z = −1.24, p = 0.21, two-tailed WRS), place cell stability across 24 hours was significantly lower in iCre-KO compared to iWT place cells (Fig. 3b). Suggesting that this decrease in iCre-KO long-term place stability reflected remapping, rather than degeneration, spatial information content remained similar across days (iWT Z = 0.013, p = 0.99; iCre-KO Z = 0.64, p = 0.52, two-tailed Wilcoxon signed-rank tests).

Figure 3.

Long-term place field stability is reduced after the loss of MEC HCN1 channels. (a) Examples of iWT (left) and iCre-KO (right) place cells recorded across two sessions separated by 24 hours. Rate maps coded as in Figure 2. Pearson’s correlation coefficient between maps is shown at top. Black dots denote firing fields. Right-most plots: cross-correlograms between rate maps, coded for minimum (blue) and maximum (red) correlations; the peak correlation is indicated by a black dot. The difference between the center bin and the bin containing the peak correlation is shown at top. This measure describes the degree of place field shift across days. (b) Cumulative distribution of stability for sessions separated by 24 hours in iWT (blue; n = 25) and iCre-KO (red; n = 36) place cells. Across-day stability was significantly higher in iWT cells than in iCre-KO cells (mean ± SD; iWT = 0.52 ± 0.20, iCre-KO = 0.33 ± 0.25; Z = 2.81, p = 0.005, two-tailed WRS). Distributions of shuffled scores were obtained by randomly pairing place maps across days. Shuffled distributions for each group are show in black and gray, respectively (n = 1000 iWT shuffles, 1000 iCre-KO shuffles). (c) Histogram showing shift magnitude of place maps across 24 hours (D = 0.49, p = 8.33e-4, two-sample Kolmogorov-Smirnov test [KS]; n = 25 iWT cells, 36 iCre-KO cells). Inset: The distributions of shift magnitudes for iWT and iCre-KO were both larger than the corresponding shuffled distributions (iWT D = 0.68, p = 8.6e-11, two-sample KS; iCre-KO D = 0.38, p = 6.0e-5, two-sample KS; n = 25 iWT cells, 36 iCre-KO cells, 1000 iWT shuffles, 1000 iCre-KO shuffles). (d) The Pearson’s correlation coefficient of place cells recorded across sessions was inversely correlated with shift magnitude (iWT r(23) = −0.53, p = 0.0061; iCre-KO r(34) = −0.69, p = 3.9e-6, Pearson’s correlation; n = 25 iWT cells, 36 iCre-KO cells). Colors as in (b). Filled circles represent cells with correlations coefficients exceeding the 95^th percentile of shuffled correlations.

We then examined the degree to which place cells remapped across days in iWT and iCre-KO mice, which can consist of a change in firing rate or a shift in the location of a place field^{36, 37}. While changes in firing rate across days were similar between iWT and iCre-KO (mean ± SD; rate difference index iWT = 0.37 ± 0.26, iCre-KO = 0.36 ± 0.39, Z = −0.42, p = 0.68, two-tailed WRS), iCre-KO place fields shifted across days to a larger degree than iWT place fields, with 80% of iWT place cells shifting less than 8 cm across days (median shift iWT = 2.50 cm, iCre-KO = 14.58 cm, Z = −3.27, p = 0.0011, two-tailed WRS) (Fig. 3c). This suggests that shifts in place field location drove the reduction in iCre-KO across-day stability values, an idea supported by the correlation between shift-magnitudes and across-day correlation coefficients in both groups (Fig. 3d). Cells that were simultaneously recorded shifted independently of one another (Supplementary Fig. 14d), consistent with previous place cell remapping work^{37, 38}. The distributions of across-day correlation coefficients for iWT and iCre-KO mice were significantly greater than shuffled distributions (Fig. 3b), indicating that place maps across days were not completely independent. However, significantly fewer place cells remained stable across days in iCre-KO compared to iWT mice (place cells with an across-day correlation coefficient > 95^th percentile of the shuffled distribution: iWT = 17/25 [68%], iCre-KO = 11/36 [31%], Z = 2.89, p = 0.0039, two-tailed binomial test). Taken together, these data indicate that larger grid scales increase the propensity of place cells to remap across days, and that this remapping reflects changes in place field location.

Winner-take-all dynamics, grid scale and remapping

How does grid scale influence the propensity of place cells to remap even when spatial context remains the same across days? Computational and experimental works have suggested that place cell remapping can be induced by rotation or phase shift in the grid pattern, or a change in grid firing rate^{3, 21, 39}. However, we found that grid cells remained spatially stable across days in iWT and iCre-KO mice (Supplementary Fig. 14). To better understand how grid scale influences long-term place stability we next implemented a computational model of place cell formation, where place fields are formed via a winner-take-all competition⁴⁰. In the model, place cells received two types of input: modular grid cell inputs and “unstable spatial” inputs. Grid cell inputs remained constant across two consecutive simulations (i.e. days). The activity of unstable spatial inputs was represented by Gaussian fields and were re-drawn from one simulation to the next, representing the long-term spatial instability of some place cell inputs^{41, 42}. Competitive inhibition between place cells limited the number of cells active at any given location of the environment. Although the exact number of grid inputs received by place cells is unknown, studies suggest a range up to ~1000⁴³. To explore values near this range, we varied the number of grid and unstable spatial inputs, as well as the ratio between each input type, across different iterations of this model (i.e. “conditions”).

To test the impact of increased grid scale on place cell remapping we ran simulations over which we varied the spacing of the smallest grid module, which set the spacing for all successive modules (Fig. 4a). The model recapitulated our experimental findings. First, increasing the scale of grid inputs increased the size of place fields (Supplementary Fig. 15). Second, the simulations revealed a reduction in the Pearson’s correlation of place maps across days as the scale of the grid inputs increased. This result was robust and independent of the exact parameters used in the model: reduced stability with increased grid scale was observed across all conditions tested, in which we varied the number of grid and unstable spatial inputs (Fig. 4b–d) or the size of the unstable spatial inputs (Supplementary Fig. 15).

Figure 4.

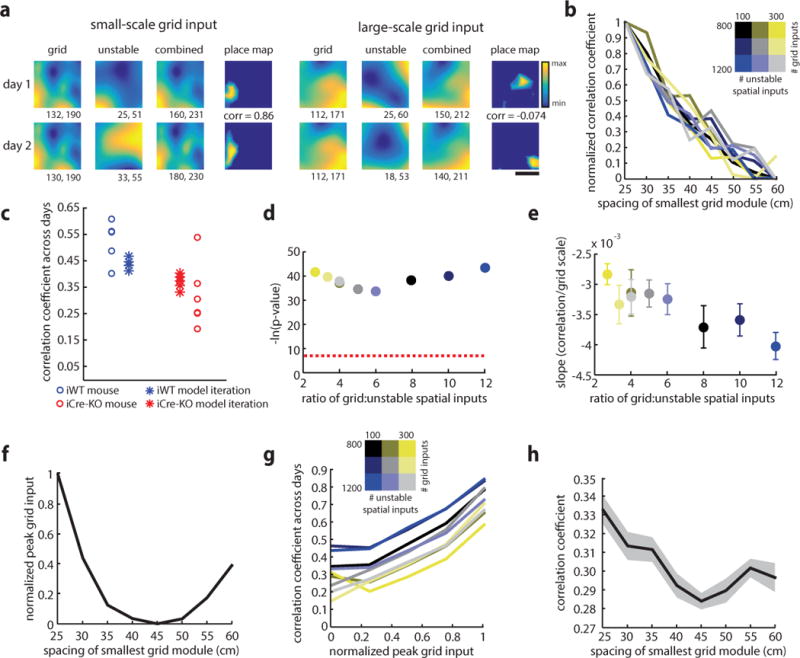
Increasing grid scale reduces long-term place cell stability in a winner-take-all model of place field formation. (a) Individual examples of place cells simulated from small and large-scale grid inputs (left: smallest grid module = 30 cm, right: smallest grid module = 60 cm). For each cell, the activity map resulting from grid input (left), unstable spatial input (middle) and the combination of grid and unstable spatial inputs (right) are shown, with warmer colors indicating regions of stronger input. The units of activity are a measure proportional to firing rate. Minimum and maximum activity values are reported below each map. The place maps resulting after winner-take-all dynamics are shown at right, with the Pearson’s correlation coefficient between the two maps indicated. Scale bar = 25 cm. (b) Across 9 simulation conditions, in which the number of grid and unstable spatial inputs received by each place cell varied, the correlation coefficients for place maps across days declined with as the spacing of the smallest grid module increased. Each colored line shows the average of ten iterations for one condition (for each of the 9 conditions tested separately, all r(78) < −0.74, p < 2.51e-15, Pearson’s correlations). (c) Place cell correlations observed in individual animals compared to correlations predicted by the model. Each circle represents the average correlation between place cells recorded across days in an individual animal (iWT shown in blue, n = 5 mice, iCre-KO shown in red, n = 6 mice). Each asterisk represents the average correlation obtained in one iteration of the model (n = 5 iterations), using parameters chosen to best match the experimental data (minimum grid spacings: 27 cm for iWT, 37 cm for iWT; number of grid inputs: 1000; number of LEC inputs: 200). There was not a significant difference between the stability values for the experimental and simulated iWT data (p = 0.15, two-tailed WRS test) or the stability values for the experimental and simulated iCre-KO data (p = 0.18, two-tailed WRS test). However, there was a significant decrease in the stability values between simulated iWT and simulated iCre-KO data (p = 0.0079, two-tailed WRS test). (d) The p-value for the Pearson’s correlation between grid scale and the correlation coefficient between place maps across days (n = 9 simulation conditions). Each color represents a different simulation condition, as in (b). Dashed line indicates p = 0.001. (e) The slope between grid scale and the correlation coefficient between place maps across days becomes significantly steeper as the ratio of grid to unstable spatial inputs increases (r(7) = −0.91, p = 6.73e-04; Pearson’s correlation; n = 9 simulation conditions). Mean ± SEM of 10 iterations is shown for each condition. (f) Peak total grid input decreases as the spacing of the smallest grid module increases (r(22) = −0.51, p = 0.011; Pearson’s correlation; n = 3 conditions [each with a different number of grid inputs], 8 grid scales). For each condition, the mean of 10 iterations is shown. Each of the 3 conditions tested individually also showed a significant correlation (n = 2000 place cells, 10 iterations, 8 grid scales; all r(159998) < −0.34, p ≪ 0.0001). (g) The correlation coefficient for place maps across days increases with peak total grid input, a finding that was consistent over all conditions and grid scales tested. Each line represents the average for one condition across all active place cells, 8 grid scales, and 10 iterations per scale (all r > 0.25, all p << 0.0001; Pearson’s correlation). A significant, positive correlation was also observed for all grid scales (all r > 0.20, all p < 3.5e-38). (h) The correlation between the activity maps of summed grid input, as in (a), and the place map resulting after winner-take-all dynamics decreased with the spacing of the smallest grid module (r(70) = −0.44, p = 9.4e-05, Pearson’s correlation). For each of the 9 simulation conditions, the average of 10 iterations is shown. For each condition tested separately, all r < −0.012, all p < 0.0090.

How does grid scale control place cell stability in the presence of winner-take-all dynamics? We hypothesized that linear combinations of smaller-scaled grid cells result in an input pattern that has large peak values in specific spatial locations. This type of input then forms place fields resistant to changes in lower-amplitude unstable spatial inputs, allowing them to remain stable across simulations. We found several features in our simulation consistent with this hypothesis. First, the effect of grid scale on place cell remapping strengthened as the ratio of grid to unstable spatial inputs increased (Fig. 4e). Second, we examined the activity maps resulting from grid inputs, which represent the strength of the grid cell input to a single place cell at any given point in physical space (Fig. 4a). We found that the peak value for this grid input declined with increased grid spacing, as the likelihood of grid fields spatially coinciding decreased (Fig. 4f and Supplementary Fig. 15). Further, we found a significant relationship between the peak value of the grid input and the correlation coefficient of place maps across days (Fig. 4g). Finally, the correlation between the activity map for grid inputs and the resulting place map became less coupled as the scale of grid inputs increased, suggesting that grid input had less influence on the resulting place field location as grid scale increased (Fig. 4h). Together, these observations suggest that the activity profile of grid input across the environment changes with scale, impacting the degree to which grid inputs determine the location of the place field. Place cells receiving smaller-scale grid input may be driven strongly by grid inputs, whereas those receiving larger-scale grid inputs may be more heavily influenced by unstable spatial inputs that change over time.

Decoding accuracy after changes in place scale and stability

Given our experimental findings, we next asked how place scale versus long-term stability impact an animal’s ability to estimate its current position. Using a maximum-likelihood decoding framework, we computed the accuracy of decoders trained on simulated iWT and iCre-KO place cell datasets (Fig. 5a). These simulated data sets allowed us to examine how features of the place code impact position decoding assuming more realistic numbers of active place cells, which is higher than what our data captured. First, we matched simulated field sizes for iWT and iCre-KO datasets to the experimentally observed distributions. For small populations of place cells (less than ~100), the iCre-KO model outperformed the iWT model, as the larger scaled iCre-KO place cells covered more of the environment. However, the difference in error between models decreased with cell number (5000 shuffles, p = 6.0e–4) (Fig. 5b–c) and at more realistic place cell numbers (1000 neurons), decoding from iWT cells was only slightly better (< 1 cm difference) than from iCre-KO cells (Fig. 5c). These results suggest that the increased size of iCre-KO place fields is unlikely to impair the resolution of encoded position to a degree that is behaviorally relevant, consistent with theoretical work showing that in 2-dimensions (for 2-dimensional variables), the width of tuning curves does not affect the amount of information conveyed once there is coverage of the whole space⁴⁴.

Figure 5.

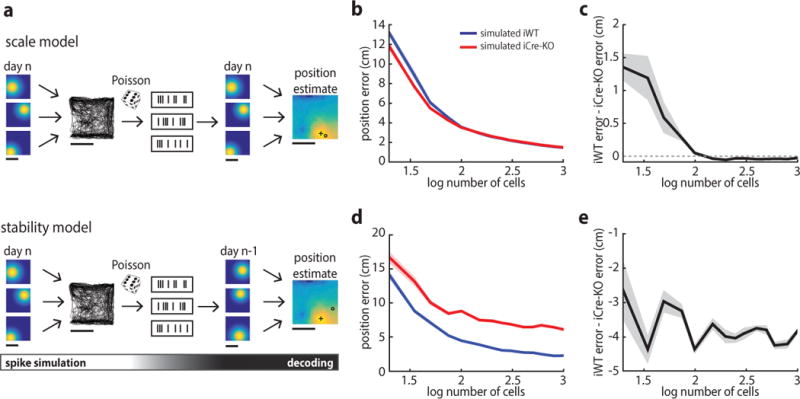
Impaired decoding accuracy in iCre-KO mice. (a) Schematic of the decoding scheme used to estimate position. Top: depiction of the model used to assess the impact of place field size on decoding accuracy. Simulated spike trains were generated by combining simulated iWT or iCre-KO place field maps with the position trajectory. Spiking was assumed to follow a Poisson distribution. In the decoding phase, the simulated spike trains were passed through the decoder to generate an estimate of the animal’s position. A plus sign denotes the estimated position, an open circle denotes the actual position of the animal. Bottom: depiction of the model used to assess the impact of long-term place field stability on decoding accuracy. All aspects of the model are the same as those described above, except that the decoder was trained on simulated place maps from the previous day (n-1). The shifts in place maps across days were selected from those observed experimentally. Scale bars: 50 cm. (b) Errors in estimated position for the scale model using simulated iWT (blue) and iCre-KO (red) datasets with varying numbers of cells. Here and in (c-e), the solid line represents the mean of 10 model iterations; shaded lines indicate the SEM. (c) In the scale model, the simulated iCre-KO dataset performed slightly more accurately at low cell numbers, but this advantage diminished with cell number. Difference in error using 1000 cells [iWT - iCre-KO] ± SD: −0.027 ± 0.025 cm, t(18) = −3.41, p = 0.0031, two-tailed unpaired t-test. (d) Errors in estimated position for the stability model using simulated iWT (blue) and iCre-KO (red) datasets. (e) In the stability model, the error in estimated position was greater for the iCre-KO dataset at all cell numbers. Difference in error using 1000 cells [iWT - iCre-KO] ± SD: −3.85 ± 0.4, t(18) = −30.63, p = 5.6e-17, two-tailed unpaired t-test.

Next, to explore how the reduced long-term stability of iCre-KO place cells impacts decoding accuracy, the decoder was trained on datasets simulating iWT and iCre-KO place maps, but performance was assessed on a second day in which the field locations of each cell were shifted by values we observed experimentally. The iCre-KO model exhibited reduced decoding accuracy compared to the iWT model across the entire range of simulations, with the absolute difference increasing with cell number (5000 shuffles, p = 0.031) until reaching ~4 cm at 1000 cells (Fig. 5d–e). Together, these results suggest that the instability, rather than the size, of iCre-KO place cells would have a larger impact on the accuracy of position coding.

Impaired rapid place learning in iCre-KO mice

Finally, to examine how impaired position decoding impacts behavior, we examined animals’ performance on the delayed-match-to-place (DMP) task, a hippocampal-dependent water maze variant that demands a flexible knowledge of the environment (Fig. 6, Supplementary Fig. 3)⁴⁵. The task assesses the ability of rodents to rapidly learn the position of a hidden platform, whose location changes each day, within the context of a familiar environment. DMP testing began after five days of training, in which mice learned to swim to a hidden platform whose location remained constant. Suggesting that iCre-KO mice can accurately navigate to a fixed goal location, there were no differences in performance between the two groups on the training task (Fig. 6a–b and Supplementary Fig. 3) and both groups retained long-term memory for the goal location on a probe test administered 24 hours after the last training session (Fig. 6c).

Figure 6.

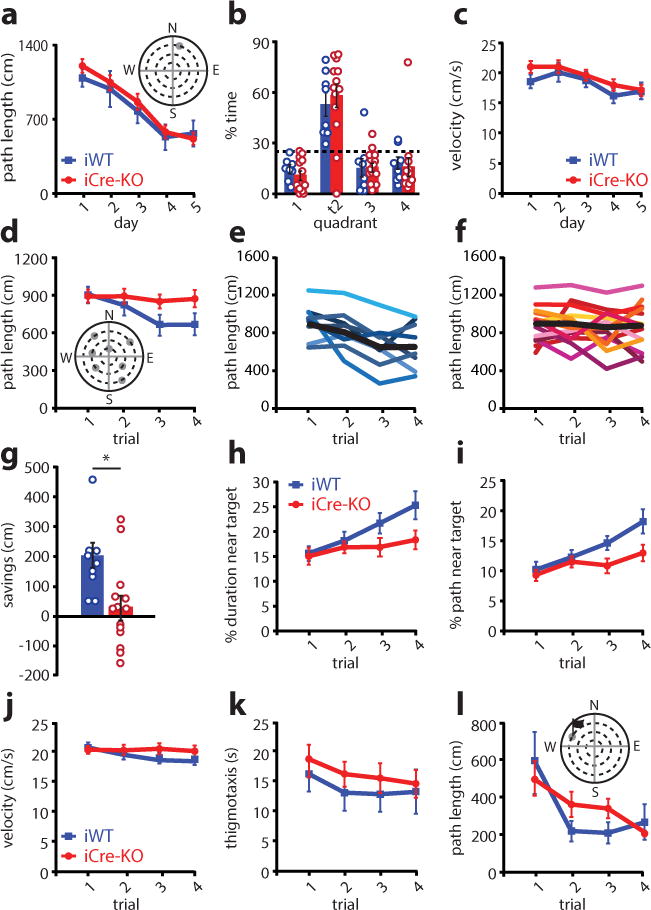
Rapid place learning is impaired with the loss of MEC HCN1 channels. (a) Distance traveled during the pre-training MWM task was not significantly different between iWT (blue; n = 8) and iCre-KO (red; n = 13) mice (group×day interaction for distance traveled: F(4,76) = 0.36, p = 0.84, main effect of group: F(1,19) = 0.32, p = 0.58, repeated measures ANOVA). Plot shows mean ± SEM with individual data points overlaid. Inset: schematic of the MWM task. (b) Velocity did not differ between groups (main effect of group: F(1,19) = 0.69, p = 0.42; repeated measures ANOVA; n = 8 iWT, 13 iCre-KO mice). Plot shows mean ± SEM with individual data points overlaid. (c) Both groups spent significantly more time in the target quadrant than the other quadrants in a probe test conducted 24 hours after the last session of the MWM task (mean ± SEM; % time in correct quadrant: iWT = 52.70 ± 6.77, iCre-KO = 57.50 ± 6.76; main effect of quadrant type: F(1,19) = 21.94 p = 1.6e-4; main effect of group: F(1,19) = 1.15, p = 0.30, repeated measures ANOVA with group and quadrant type as factors). The dashed line represents chance. Circles show individual data points (n = 8 iWT, 13 iCre-KO mice). Colored bars represent the means and black bars ± SEM. Additionally, for times when the animal was exploring the correct quadrant, the animals’ average distance from the previous platform location did not significantly differ between groups (mean ± SEM; iWT = 42.7 ± 5.66 cm, iCre-KO = 38.0 ± 4.88 cm, t(19) = 0.61, p = 0.55, two-tailed unpaired t-test). (d) Distance traveled on the DMP task decreased across trials in iWT (blue, n = 8) but not iCre-KO (red; n = 13) mice (group×trial interaction: F(3,57) = 2.87, p = 0.044, repeated measures ANOVA with group and trial as factors). The distance traveled by iWT mice, but not iCre-KO mice, decreased over the four trials (main effect of trial: iWT F(3,21) = 6.70, p = 0.0024; iCre-KO F(3,36) = 0.23, p = 0.87; one way repeated measures ANOVAs). Plot shows mean ± SEM with individual data points overlaid. Inset: schematic of the DMP task. Grey circles mark the potential locations of the platform. (e-f) Distance traveled on the DMP by all iWT (e) and all iCre-KO (f) mice. Each colored line represents one subject. The black line shows the mean. (g) iCre-KO (red; n = 13) mice showed significantly less savings (difference in path length late versus early trials) than iWT (blue; n = 8) mice (mean ± SEM; iWT = 200.80 ± 41.46 cm, iCre-KO = 30.03 ± 40.35 cm, t(19) = 2.80, p = 0.011, two tailed t-test). Circles show individual data points. Colored bars represent the means and black bars ± SEM. *p<0.05. (h-i) The improvement of iWT on later trials was reflected in their search strategy. iWT (blue; n = 8), but not iCre-KO (red, n = 13) mice spent an significantly increasing proportion of their search path in the area surrounding the target platform (% path in target area, group×trial interaction: F(3,57) = 3.16, p = 0.031, repeated measures ANOVA) (h), and a similar trend was observed for duration (% duration in area surrounding, group×trial interaction: F(3,57) = 2.59, p = 0.062, repeated measures ANOVA) (i). Plots show mean ± SEM with individual data points overlaid. (j) The average velocity was not significantly different between groups (mean ± SEM; iWT = 19.62 ± 0.83 cm/s, iCre-KO = 20.60 ± 0.76 cm/s, main effect of group: F(1,19) = 0.71 p = 0.41, repeated measures ANOVA). Plot shows mean ± SEM with individual data points overlaid. (k) Time spent in thigmotaxis was not significantly different between groups (main effect of group: F(1,19) = 0.44, p = 0.51, repeated measures ANOVA). Plot shows mean ± SEM with individual data points overlaid. (l) The distance traveled by iWT and iCre-KO mice was comparable on a cued-version of the DMP, in which a prominent proximal visual cue was erected above the platform (group×trial interaction: F(3,57) = 1.64, p = 0.19, repeated measures ANOVA; n = 8 iWT mice, 13 iCre-KO mice). Plot shows mean ± SEM with individual data points overlaid.

For the DMP task, the platform was moved to a new location each day, and the average performance on each of the four daily trials averaged across seven days of testing. The performance of iWT and iCre-KO mice was similar on the first trial of each day (t(19) = 0.15, p = 0.88, two-tailed t-test). However, the rate of learning across trials significantly differed between the groups. The distance traveled by iWT mice to locate the platform decreased over the four trials, whereas iCre-KO mice did not show significant improvement across trials (Fig. 6d–f, Supplementary Fig. 3). Consistent with this finding, the average ‘savings’ (reduction in path length between trials 1–2 and 3–4) was significantly greater in iWT compared to iCre-KO mice (Fig. 6g, Supplementary Fig. 3). The improved performance of iWT mice in later trials was also reflected in their search strategies: compared to iCre-KO mice, iWT mice became increasingly focused on the area surrounding the platform location (Fig. 6h–i).

Deficits in rapid place learning in iCre-KO mice were not attributable to an overall difference in velocity or thigmotaxis (Fig. 6j–k). In addition, iCre-KO mice did not display visual, sensorimotor, or motivational impairments, performing comparably to iWTs on a cued version of the DMP task (Fig. 6l and Supplementary Fig. 3). Deficits did not reflect increased perseveration for the previous day’s platform location or the training platform location (visits to training platform iCre-KO, t(19) = 0.24, p = 0.81; visits to previous day’s platform, t(19) = 0.78, p = 0.45; two-tailed t-tests). Taken together with the intact performance on the training task (Fig. 6a), this suggests that iCre-KO mice can learn the general structure of the DMP task (e.g. that the environment contains a hidden platform and that finding this platform terminates the trial). However, unlike the training task, the DMP task requires that the mouse distinguish the current platform position (recent memory) from previous platform positions (remote memory). While precisely how place code stability supports recent versus remote memories remains incompletely understood, decreased long-term place stability may result in interference between encoding of the current platform location and recall of remote spatial information regarding the environment or previous platforms.

Alternatively, it is possible that the iCre-KO manipulation impacted working memory. However, we found no difference in the performance of these same iWT and iCre-KO mice on a spontaneous Y maze alternation task (Supplementary Fig. 3). Thus, as a combined set of results, these data raise the possibility that increasing grid scale leads to decreased place stability, which in turn impacts the ability of mice to encode changing spatial goal locations within a single spatial context.

Discussion

While theoretical and computational works have proposed that grid scale impacts hippocampal coding and behavior^{2–5, 27, 28}, the difficulty in selectively perturbing specific grid cell features has left these ideas experimentally untested. Here, we used a viral approach to knock out HCN1 channels in the MEC of adult mice, which increased grid scale but left the coding features of spatial, velocity and temporal MEC signals intact. In iCre-KO mice, the increase in grid scale expanded CA1 place scale and decreased long-term place stability. Simulations of large place cell populations, revealed that the experimentally observed decrease in iCre-KO long-term place stability led to larger decoding errors when estimating the animal’s position across days. The behavioral impact of this reduction in decoding accuracy became apparent in a task requiring mice to flexibly navigate to a goal location that moved each day. Combined, our data and simulations point to grid scale as a determinant of place scale and long-term stability, features that likely support an animal’s ability to rapidly learn multiple goal locations within a single spatial context.

These findings have implications for computational models that generate place cells. First, previous work that examined place cells in the absence of grid cells indicated that grid cells did not impact the formation or maintenance of place fields^{15, 16}, a finding inconsistent with models that use linear summation of grid cell input to drive place field formation^{2, 5, 6}. At the same time, our data support the idea that, when present, grid scale is a significant feature of entorhinal input that is capable of shaping the place code. Our findings taken together with previous reports^{9, 15, 16} thus support models in which place cells receive inputs distributed across space, with spatial selectivity arising from the potentiation of subsets of these inputs²² or local hippocampal circuit computation⁴⁰. In such a model, grid cells could influence the formation of place fields when present but have little impact on this process when absent. Moreover, the idea that place cell spatial selectivity reflects input-potentiating mechanisms is consistent with the expansion of place size we observed after grid scale expansion. Recent data points to coincidental activity between MEC and CA3 as a mechanism for generating large regenerative events in CA1 neurons called plateau potentials, with the prevalence of such events capable of creating place fields²². Inputs from grid cells with larger fields could thus interact with intrinsic hippocampal dynamics to cause an increase in the probability or duration of CA1 plateau potentials, leading to larger place fields, an idea future experiments could address.

The importance of local hippocampal dynamics in determining place field spatial selectivity is also reflected in our simulations of a winner-take-all model⁴⁰. These simulations demonstrate how, in the context of a competitive hippocampal network, place cells that receive inputs from larger grid scales are more prone to remap in response to changes in unstable spatial inputs. The mechanism underlying this observation likely lies in the fact that inputs from large grid scales are less likely to overlap in a way that would create a strong spatial signal, allowing other inputs to dominate the location of the place field. This relationship however, likely depends on the degree of plasticity associated with various inputs, as previous manipulations that expanded grid scale and enhanced hippocampal plasticity at synapses receiving MEC input resulted in increased long-term place stability^{30, 31, 46}. Even so, as grid spacing in ventral MEC is at least five times wider than spacing in dorsal MEC⁴⁷ and a general dorsal to ventral topography exists in the projections from MEC to CA1⁴⁸, our simulations thus predict that, in the normal animal, ventral place cells should show more remapping than dorsal place cells when non-spatial cues change. This idea is consistent with experimental work demonstrating more remapping in ventral place cells after non-spatial manipulations, such as a change to the olfactory context⁴⁹. Although we do not specify what anatomical sources might provide this unstable-spatial input, likely sources include the lateral entorhinal cortex, which encodes non-spatial contextual features⁴¹ or the hippocampal CA2 region, where neurons gradually change their coding features to reflect the passage of hours to days⁴². Our model predicts that elimination of these inputs would increase the stability of place maps, an idea future work could explore.

The decrease in long-term place stability we observed in iCre-KO mice had a clear behavioral impact when mice were required to encode novel goal locations within a single spatial context. Our data indicates a large subset of place cells in wildtype mice remain stable over days. However, the proportion of place cells that retained stable fields across days significantly decreased in iCre-KO mice. This decrease in long-term place stability could lead to errors when the mouse must integrate its current position and the location of a new goal within a familiar spatial context. As place maps in iCre-KO mice change substantially from day to day, one possibility is that the map used to decode the animal’s current position did not match the map used to form a representation of the spatial context, or the map used to encode the location of the new goal. This mismatch between maps as a possible mechanism underlying the poor performance of iCre-KO mice on the DMP task is consistent with two other findings of the present study. First, it is consistent with our simulations of place cell networks, which demonstrates that the degree of iCre-KO place instability leads to significantly larger decoding errors across days in iCre-KO compared to iWT mice. Second, it is consistent with the fact that iCre-KO mice can navigate as well as iWT mice when the goal location can be located based on a visual cue, a strategy that likely supported their accurate behavior on the training task with a fixed goal location and on the cued version of the DMP task.

Together, our data reconciles studies describing varied effects of grid cell manipulations on place cells. Previously, the most selective manipulations of the grid network were achieved by inactivating the medial septum and thus triggering a loss of grid periodicity while preserving other MEC signals, causing a transient expansion in grid scale by introducing an animal to a novel environment, or lesioning MEC. First, with medial septal inactivation, the size of the environment appeared to determine the degree to which the loss of grid cells impacted place coding. When boundary information was readily available, for example in a small arena, the loss of grid cell periodicity did not impact the maintenance or formation of place fields^{15, 20}. In larger open arenas however, place cells in the absence of grid periodicity did not form fields in the center of the box, where boundary information was less apparent²⁰. Second, grid and place scale transiently expanded in novel environments and then contracted in concert as the environment becomes more familiar⁵⁰. Combined, these findings are complementary to our work demonstrating grid cells play a stronger role in controlling place scale in conditions where input from border cells is weaker. In addition, our results of increased place scale and decreased place stability after grid scale expansion most closely mirror spatial changes in the place code observed after complete MEC lesions³⁴. Taken together, these studies highlight a critical contribution for MEC spatial codes to the hippocampal place code. We take these findings further however, by both experimentally and computationally demonstrating how grid scale uniquely impacts long-term place stability and the ability to encode multiple spatial locations within a single spatial context.