Protein Folding Transition Path Times from Single Molecule FRET

Abstract

The transition path is the tiny segment of a single molecule trajectory when the free energy barrier between states is crossed and for protein folding contains all of the information about the self-assembly mechanism. As a first step toward obtaining structural information during the transition path from experiments, single molecule FRET spectroscopy has been used to determine average transition path times from a photon-by-photon analysis of fluorescence trajectories. These results, obtained for several different proteins, have already provided new and demanding tests that support both the accuracy of all-atom molecular dynamics simulations and the basic postulates of energy landscape theory of protein folding.

Introduction

There have been several milestones over the past three decades in understanding how proteins fold that have created an active subfield of biological physics and biophysical chemistry. They have come from all three branches of science - experiment, theory and computation. Experimental advances have included the application of linear free energy relations and protein engineering to obtain structural information on the transition state ensemble [1,2] and the introduction of nanosecond laser-triggering to dramatically improve time-resolution in kinetic experiments [3–5]. Theoretical advances have included the statistical mechanical description of folding as diffusion on a low dimensional free energy surface with order parameters as coordinates [6–8], the development of theoretical models based on explicit consideration of only native contacts (i.e., intramolecular contacts present in the folded structure) [9–12] and the application of concepts from polymer physics [13]. The most unexpected advance has been in the area of computation, specifically all-atom molecular dynamics (MD) simulations, in which Newton’s equations of motion are solved for all heavy atoms of the polypeptide and solvent [14,15]. These simulations are now capable of folding a polypeptide from an initially disordered state into a protein with the correct structure for many small proteins [16]. The importance of the MD simulations cannot be overstated. If accurate, with long trajectories to observe a statistically sufficient number of folding/unfolding transitions, the simulations contain everything one would want to know on how a specific protein folds in atomistic detail. These simulations have already provided critical testing grounds for universal theoretical concepts [17] and statistical mechanical models of protein folding [18]. Therefore, new kinds of experiments that further test the accuracy of these simulations are extremely important. One such class of experiments employs single molecule fluorescence spectroscopy, with the ultimate goal of watching the evolution of structure for individual molecules as they self-assemble on transition paths. In this article we describe the first steps toward this goal using single molecule Förster resonance energy transfer (FRET) spectroscopy that have allowed determination of the average duration of transition paths from photon trajectories.

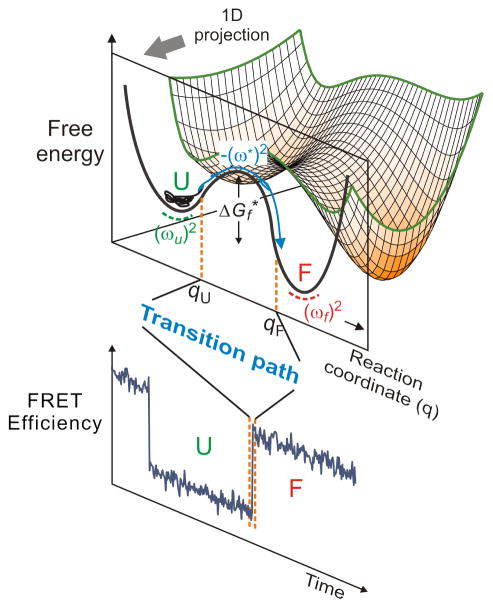
First, what is a transition path? The transition path corresponds to a successful reactant to product crossing of the free energy barrier separating states (free energy minima). For folding of a protein with just two populated states - unfolded and folded - Figure 1 shows that the transition path corresponds to the segment of the molecular trajectory from unfolded to folded for which a position q_U close to the unfolded minimum on the reaction coordinate q is crossed and reaches position q_F close to the folded minimum without ever re-crossing q_U [19]. Consequently, in this case, the transition path contains all of the structural information on how the unfolded polypeptide self-assembles to form the folded, biologically-active structure. Since the transition path is a property of an individual molecule, it can only be observed by watching one molecule at a time. The zeroth order question about transition paths, then, is: what is the average duration of the barrier crossing, i.e. what is the average transition path time? What we have learned from the experimental determination of this time using single molecule FRET is the subject of this article.

Figure 1.

Free-energy surface of protein folding. Protein folding can be described as diffusion on a low-dimensional free energy surface with order parameters as coordinates and has been described successfully as diffusion on a 1D free energy surface, here projected onto the coordinate q. For a two-state protein, the folded and unfolded states are separated by a free energy barrier with the height of $\mathrm{\Delta }{G}_f^{\ast }$. (ω_u)², (ω_f)², and (ω^*)², are curvatures at the bottom of the unfolded and folded state wells and at the top of the barrier, respectively. An unfolded molecule spends the vast majority of time fluctuating in the unfolded well before making a very rapid folding transition over the barrier. The transition path is that part of the molecular trajectory that leaves a position q_U on the unfolded side of the barrier and reaches q_F on the folded side without re-crossing q_U (blue portion of the trajectory). The transition path appears as a near-instantaneous jump in a binned FRET efficiency trajectory (Bottom).

Definition of Transition Path Time

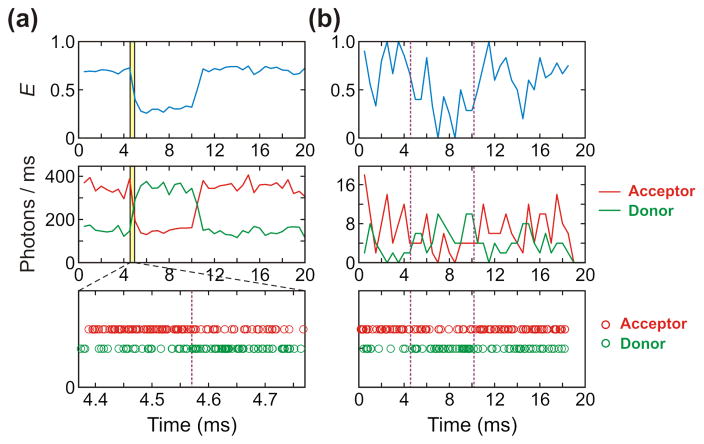
In single molecule experiments it is important to distinguish between the average folding time, t_f (the inverse of the rate coefficient for folding, k_f) and the average transition path time, t_TP. Unlike the average folding and unfolding times, the average transition path time is the same for folding and unfolding regardless of the shape of a free energy barrier. The folding time is the average time that the molecule spends in the unfolded state before a successful barrier crossing to the folded state, which appears as an almost instantaneous jump in the trajectory in Figure 1, while the unfolding time (t_u) is the average time that the molecule spends in the folded state before crossing the barrier to the unfolded state. These waiting times are exponentially distributed and their average is the inverse of the corresponding rate coefficients (k_f and k_u; note that in ensemble experiments, the observed rate is the sum of the two rate coefficients, while in single molecule experiments they are determined individually). The transition path time, on the other hand, is the time actually spent in a successful barrier crossing (the apparent “jump” in Figure 2a).

Figure 2.

Photon (Bottom), binned fluorescence (Middle) and FRET efficiency (Top) trajectories simulated with (a) high (500 ms⁻¹) and (b) low (10 ms⁻¹) photon count rates and the FRET efficiencies of 0.7 and 0.3. The FRET efficiency (E) is the fraction of photons in a bin that are emitted by the acceptor (E = n_A/(n_A + n_D), where n_A is the number of acceptor photons and n_D is the number of donor photons). The bin time of the FRET efficiency and fluorescence trajectories is 0.5 ms. Purple vertical dashed lines indicate positions of transition between folded and unfolded states. Transition time points are the same in (a) and (b). The photon trajectory in (a) shows photons near the first transition (yellow shaded area in the binned trajectory).

In addition to the large difference in time scales, a major difference between folding times and transition path times is their dependence on the height of the free energy barrier (Figure 1). The folding time is given by the Kramers’ theory [20] as

$$t_f=\frac{1}{k_f}=\frac{2\pi }{\beta D^{\ast }{\omega }^{\ast }{\omega }_{\mathrm{u}}}exp(\beta \mathrm{\Delta }{G}_f^{\ast }),$$ (1)

where D^* is the diffusion coefficient at the barrier top, (ω^*)² and (ω_u)² are the curvatures of the free energy surface at the top of the barrier and bottom of the unfolded well, respectively, $\mathrm{\Delta }{G}_f^{\ast }$ is the barrier height, β = 1/k_BT, k_B is the Boltzmann constant, and T is the absolute temperature. With the same one-dimensional (1D) diffusion theory, the average transition path time (for a high parabolic barrier) is [19,21]

$$t_{TP}=\frac{1}{\beta D^{\ast }{({\omega }^{\ast })}^2}ln(2e^{\gamma }\beta \mathrm{\Delta }{G}_f^{\ast }),$$ (2)

where γ (= 0.577 …) is Euler’s constant. These two equations are similar in that both times are inversely proportional to the diffusion coefficient D^* and depend on the free energy barrier height $\mathrm{\Delta }{G}_f^{\ast }$. However, the folding time is extremely sensitive to the barrier height (exponentially dependent) while the transition path time is insensitive (logarithmically dependent).

The justification for using equations 1 and 2 for one-dimensional free energy surfaces began with results of early simulations of folding lattice model representations of proteins [22]. These simulations showed that the rates of folding could be accurately reproduced by Kramers’ theory for escape over a one-dimensional free energy barrier with the fraction of native contacts (Q) as the reaction coordinate. Calculation of the barrier height from the relative populations of structures (the potential of mean force) for a given Q, and the decay time for the Q-Q correlation function in the unfolded well as the Kramers pre-exponential factor, resulted in rates within a factor of 2 of the mean first passage times to the folded state observed in the simulations [22]. It is an enormous simplification to project the many degrees of freedom onto this one-dimensional picture, so the results of the lattice simulation were quite surprising. Subsequently, all-atom MD simulations have shown that the one-dimensional free energy surface with an order parameter as reaction coordinate is indeed sufficient to describe both equilibria, i.e. the number and relative free energy of populated minima, and the kinetics [23]. That it is possible to represent the dynamics of a system with so many degrees of freedom as diffusion on a one-dimensional surface may be a consequence of the fraction of native contacts Q being a good reaction coordinate, owing to the dominant role of native contacts in determining folding mechanism [17].

Determination of Transition Path Times from Single Molecule FRET

Förster resonance energy transfer (FRET) [24] has been the most useful single molecule fluorescence method [25–27] for studying protein folding [21,28–59]. Single molecule FRET has also made numerous contributions toward understanding the structure and dynamics of unfolded and intrinsically disorderd proteins (see [60] for recent review). In FRET experiments, a protein molecule is labeled at specific positions with one donor and one acceptor fluorophore. For observing folding/unfolding trajectories, the molecule is immobilized on a coated glass surface. After laser excitation of the donor, emission of both the donor or, if the excitation energy has been transferred, of the acceptor is detected. Since the transfer efficiency (E) depends on the distance (R) between the two fluorophores [E = R₀⁶/(R₀⁶ + R⁶), where the constant R₀ is the Förster radius], folded and unfolded states are distinguished by the higher FRET efficiency for the folded molecule compared to the unfolded molecule. By performing experiments near the denaturation mid-point, the trajectory contains a roughly equal number of folding and unfolding transitions. If the waiting times are sufficiently long and the photon detection rate is sufficiently high, as in Fig. 2(a), the photons can be binned and the FRET efficiency for each bin is plotted as a function of time. This FRET efficiency trajectory readily yields the individual rate coefficients for folding and unfolding. On the other hand, for waiting times that are too short or photon detection rates are too low, the FRET efficiency trajectory is too noisy to obtain any information about rate coefficients. In this case, the unbinned photon trajectory must be analyzed [37]. According to MD simulations, transition path times are in the nanosecond-microsecond time scale, which poses an enormous challenge for single molecule FRET experiments [16]. Consequently, acquisition of data sufficient to obtain even average transition path times requires photon trajectories with the highest possible detection rate and a robust method of analysis.

Szabo and Gopich have developed a very powerful maximum likelihood method for analyzing such photon trajectories [21,61,62]. The analysis with their method is considerably simplified if a model has already been firmly established in ensemble measurements. Given the number of states contained in the trajectory, the method determines the most likely parameters of the model (FRET efficiencies and rate coefficients) that best reproduce the photon trajectory. For the kinetics of a two-state model, for example, the 4 parameters are the folding and unfolding rate coefficients and the FRET efficiencies for the folded and unfolded states. To obtain average transition path times, a third virtual state is introduced with a FRET efficiency that is assumed to be midway between the folded and unfolded state. The only additional parameter to add to this model is the lifetime of the virtual state, which corresponds to the average transition path time [63]. The likelihood of a two-state model, which implicitly assumes that the transition path time is instantaneous, is then compared with the likelihood of a three-state model with a finite lifetime for the virtual intermediate. If the plot of the difference in log likelihoods for the two- and three-state models versus assumed lifetime for the virtual intermediate shows a statistically-significant difference at a peak in the likelihood-time plot, the value of the assumed lifetime at the peak is the average transition path time. If there is no statistically-significant peak, an upper bound for the average transition path time can be determined.

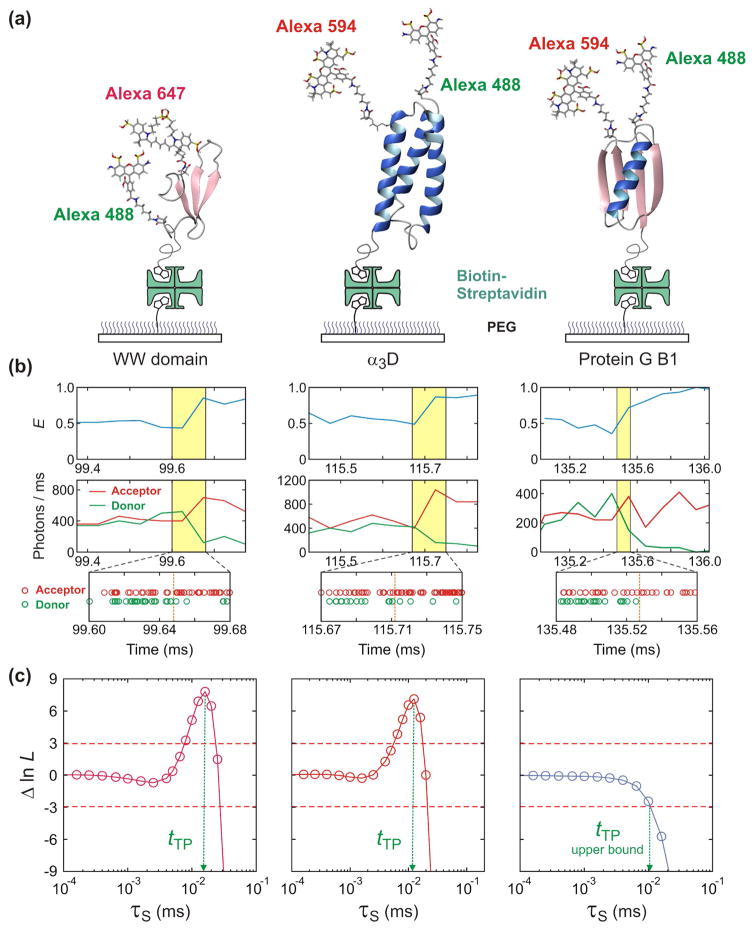
Figure 3 shows the results for three two-state proteins - the 35-residue all-β WW domain [63], the 56-residue α/β protein GB1 [63], and the 73-residue, designed all-α protein α₃D [43,64]. The WW domain is a fast folder (t_f = 100 μs), so to slow the rates and increase the transition path times making them more easily measurable, the experiments were performed at a viscosity (η) 10-times higher than water. After correcting for the higher viscosity, the average transition path time in water at 22°C was determined to be 1.6 μs [63]. No viscogen was necessary to resolve the average transition path time for α₃D, for which the folding time at 22^oC is 3 ms and the average transition path time is 12 μs. There were too few transitions to determine the average transition path time for the slow folding protein GB1 with a folding time of 1 s. However, the analysis gave the initially surprising result that it must be less than 10 μs [63].

Figure 3.

Measurement of average transition path times of folding of the FBP28 WW domain (Left), α₃D (Middle), and GB1 (Right). (a) Proteins are labeled with a donor (Alexa 488) and an acceptor (Alexa 594 or Alexa 647) dyes and immobilized on a polyethylene glycol-coated glass surface. (b) Binned donor and acceptor fluorescence trajectories (Top) (bin times of 50 μs for the WW domain and α₃D and 100 μs for protein G) and photon trajectories near the folding transition (Bottom). (c) The transition path time is determined by analyzing photon trajectories near transitions using the maximum likelihood method with the three-state model. The average transition path time (t_TP) is equal to the lifetime of a virtual intermediate state S (τ_S), which is determined from the maximum of the difference of the log likelihood, Δln L = ln L(τ_s) − ln L(0). L(0) is the likelihood for the two-state model, in which transitions are instantaneous (τ_S = 0). The transition path time of the WW domain is 16 μs (at the viscosity of 10 cP). The transition path time of α₃D (12 μs) can be measured without increasing solvent viscosity because its diffusion on the one-dimensional free energy surface is much slower than those of the WW domain and protein GB1. Only the upper bound for the transition path time of 10 μs can be determined for GB1 because no peak is observed. Figure is adapted from refs. [63]. and [43].

Comparison of Transition Path Times with Theory and Simulations

Even though only average transition path times were determined, the results turn out to be quite interesting and important. First is the excellent agreement of t_TP determined from the experiments and those observed in the simulations. After correcting for the higher temperature and lower viscosity of the water in the MD simulations, t_TP simulations for a WW domain with the same structure, but different sequence, is 1.5 μs compared to 1.6 μs from the experiments [16,63]. In the case of α₃D, the measurement of the temperature dependence of t_TP allowed extrapolation to the temperature 370 K of the simulations. The experimental value is 1.7 – 2.3 μs, while the simulation t_TP is ~1.3 μs after a viscosity (η^0.3; see below) correction [43]. From this comparison, one can conclude that the experiments and simulations are mutually consistent.

The transition path times are remarkably similar for the WW domain and protein GB1 even though their folding rates differ by ~10⁴-fold (100 μs vs. 1 s). Equation 2 readily explains this result by showing that t_TP is insensitive to the free energy barrier height, which is the primary factor in determining t_f in equation 1. Equation 2 was derived with the very same assumptions of Kramers theory, namely that the rate of escape over the barrier top is determined by diffusion of a Brownian particle on a one-dimensional free energy surface. Given the importance of the one-dimensional diffusion picture for describing protein folding kinetics [6], the finding of similar transition path times for the fast and slow folder provides additional support for this theoretical description.

Determination of free energy barrier heights has always been a challenging problem for experiments [65]. α₃D presented a unique opportunity. When both the folding and transition path times are known, equations 1 and 2 show that the ratio of these two quantities allows the determination of the free energy barrier height, $\mathrm{\Delta }{G}_f^{\ast }$, if the ratio ω*/ω_u is known. ω*/ω_u has not yet been determined by experiments, but the success of the MD simulations in reproducing experimental folding mechanisms [66] suggests that the simulated ratio of ~1.3 can be used, which results in a value $\mathrm{\Delta }{G}_f^{\ast }=4.2\pm 1.0k_{B}T$ at the midpoint denaturant concentration [43]. From the denaturant dependence of the folding rate [37], it is predicted that the folding barrier height is close to zero in the absence of denaturant, consistent with the theoretical prediction that free energy barriers in protein folding can become quite small and even disappear [6].

The folding time for the WW domain is proportional to the first power of the viscosity (t_f ∝ η), as expected from the results for a β hairpin [67] and for all-β proteins [68], while the dependence of both the folding time and average transition path time for α₃D at neutral pH is extremely weak, t ∝ η^α, with α = 0.2 for t_f and α = 0.3 for t_TP. Subsequent experiments at low pH, where the salt bridges involving aspartates and glutamates are eliminated by protonating the negatively-charged carboxylic acid groups, showed that both t_f and t_TP markedly decrease [64]. At low pH, t_f decreases over 10-fold and t_TP also decreases by a similar amount, indicating that the pre-exponential factor in Kramers’ equation 1 is responsible for the decrease in t_f rather than the barrier height. The low pH experiments also showed that α, the exponent in the viscosity dependence of the folding time increases from 0.3 to 0.7, the value found for isolated α helices [67]. The exponent less than 1.0 has been explained by dihedral angle rotations occurring faster than the solvent relaxation time [67–69], which is a breakdown of Kramers’ theory in which solvent relaxation is assumed to be instantaneous and therefore α = 1.0.

Extensive MD simulations were performed, which are consistent with the experimental results in that both t_TP and t_f decrease at low pH in spite of an increase in the free energy barrier height, because the diffusion coefficient D* increases [64]. Moreover, as found in the experiments, the viscosity dependence of both t_TP and t_f increase at low pH. The experimental and simulation results both point to a rougher underlying energy landscape for α₃D at neutral pH compared to the WW domain and protein GB1, confirming a key prediction on the difference in roughness between evolved and designed protein landscapes [70,71].

The pre-exponential factor in Eq. (1) is usually ignored in interpreting rate coefficients because of its much greater sensitivity to ΔG* than to D*. However, it should be pointed out that the pre-exponetial factor provides an estimate of the fastest rate that a particular protein can fold, the so-called protein folding “speed limit” [72]. Moreover, changes in the pre-exponential factor can potentially complicate the interpretation of Φ-values (discussed below). The results for α₃D provide a cautionary note.

Significance of Transition Path Experiments for Understanding How Proteins Fold

The answer to the question - how do proteins fold? - depends very much on the discipline of the scientist asking the question. Prior to the discovery of the role of chaperones [73,74], a biologist might argue that, since Anfinsen demonstrated proteins fold to a structure determined only by the amino acid sequence and do so spontaneously, there is no question and nothing more to know. A structural biologist or biochemist will of course want to know more, such as: what is the order of assembly of the various secondary structural elements, such as α helices and β hairpins? A biophysical scientist, on the other hand, seeks universal principles and a theoretical model based on these principles that can quantitatively explain the results of equilibrium and kinetic experiments, as well as those of all-atom molecular dynamics calculations. Only then, is the assembly order of the parts explained or predicted by the model believable.

To appreciate the importance of transition paths for understanding how proteins fold from this biophysical perspective, it is first instructive to point out what has been meant by a protein folding mechanism. The early approach was similar to that of classical organic chemistry, namely determine the number and connectivity of intermediates in kinetic experiments in which the initial condition is the unfolded polypeptide. In this description, the mechanism is a simple sequence (often incorrectly cited as solving the Levinthal paradox[75]): U → I₁ → I₂ → …N, with off pathway intermediates also permitted [76]. Having identified the number of intermediates, the next step is to characterize their structure. There are two major problems with this scenario. One is that theoretical considerations and MD simulations clearly show that, if viewed at atomistic resolution, no two transition paths are identical. Consequently, all intermediates are enormously large ensembles of structures and folding must proceed via a comparably large ensemble of pathways. For this reason, comprehension of an assembly pathway must involve some level of coarse graining, so the number of pathways in the ensemble is a function of the extent of coarse graining. For example, if the mechanism of the 3-helical villin subdomain is described in terms of the order in which the 3 helices form on the transition path, all 6 possible pathways are populated according to both state-of-the art MD simulations [18,77] and an Ising-like theoretical model [18].

The second problem with the sequential model, U → I₁ → I₂ → …N, is that many single domain proteins exhibit no detectable intermediates. These so-called two-state proteins exhibit only folded and unfolded states at equilibrium and at all times in kinetic experiments [78]. In this case, Φ-value analysis, in which the effect of a single amino acid replacement on rates and equilibrium constants is commonly used to infer the degree of native structure around the substituted amino acid in the transition state ensemble [1,2]. Although this experiment produces the only detailed structural information on the folding mechanism for two-state proteins, the information is for the average structural environment at a single position along the transition path, i.e. the average degree of native structure in the transition state ensemble at the top of the free energy barrier.

Additional structural information on a two-state folding mechanism can be obtained from NMR experiments [79–81]. These experiments delineate regions of the structure protected from hydrogen-deuterium (HD) exchange in high-lying free energy minima on the folded side of the free energy barrier. To translate the results of these equilibrium experiments into a kinetic mechanism, it is necessary to make the critical assumption that the order of, albeit average, structure formation is determined solely by the relative free energies of the minima. Given the success of a one-dimensional free energy surface description of folding discussed above, the assumption is not unreasonable. However, the order of structure formation is for the segment of the transition path on the folded side of the barrier, with no information on the more important segment between the unfolded state and the top of the free energy barrier, which describes how the protein reaches the barrier top (transition state).

Finally, there is one case where the average properties of a transition path ensemble can be probed in temperature-jump experiments. It is for two-state proteins that fold without a barrier when the temperature is increased - so called “downhill” or “one-state” folders [82–86]. These proteins fold very fast and therefore require probes with high time-resolution, but they do have the potential of yielding considerable average three-dimensional structural information all along the transition path and not just at the top of the barrier, as in Φ-value analysis, or on the folded side of the barrier, as in the HD exchange NMR experiments.

The above discussion points out why we have focused our single molecule FRET studies on measuring properties of transition paths.

Future Directions

Although determining average transition path times is only the first step in the investigation of transition paths in protein folding, these experiments have already played a significant part in motivating numerous interesting theoretical investigations, see, e.g. ref [87–91]. For the slower transition path times found for nucleic acids, advances in single molecule force spectroscopy now permit resolution of the duration of a single barrier crossing, making it possible to obtain a complete distribution of transition path times [92–97]. This is more difficult for single molecule FRET experiments of proteins, where currently only the very longest individual transition path times can be observed (HS Chung and WA Eaton, unpublished results) because of bleaching of the fluorophores at the high illumination intensities that must be employed. So, to observe structure during an individual transition path will require methods that significantly decrease the excited state chemistry that destroys the fluorophores [98,99]. With such improvements it should then be possible to obtain three-dimensional structural information during the transition path from an experiment in which 3 fluorophores are attached to the protein, which can yield 3 distances (Figure 4). Knowing three long-range distances as a function of time during the transition path may place sufficiently severe constraints on polypeptide conformations to provide a demanding test of transition paths calculated from simulations or theoretical models. With technical improvements, it should be fairly straightforward, as shown in Fig. 4, to determine the order of helix formation for helical proteins such as the villin subdomain, which has been predicted by both simulations and a theoretical model [18]. While this can potentially be done for the average pathway by ensemble experiments, observation of the complete distribution, as predicted by simulations and a theoretical model, will require watching folding one molecule at a time.

Figure 4.

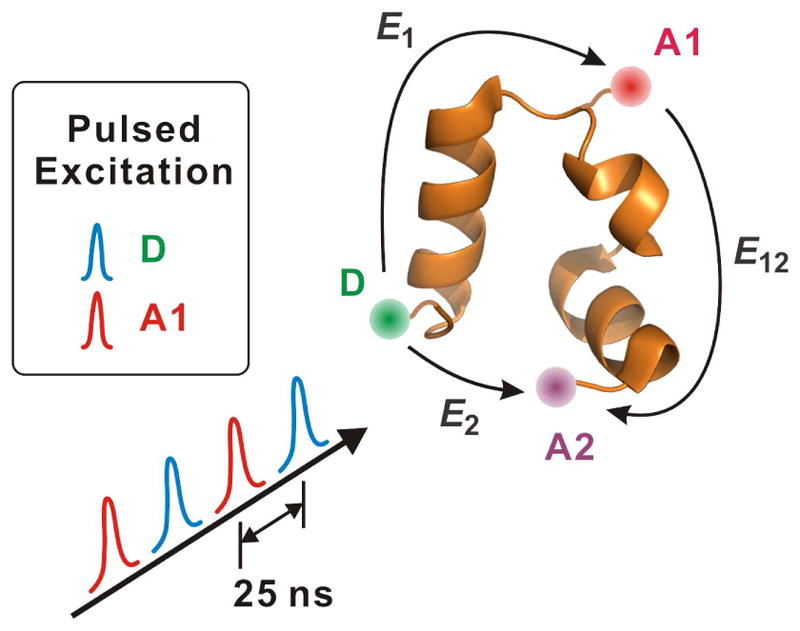
Three-color FRET for observing three-dimensional structure during transition paths. Calling the 3 fluorophores donor (D), acceptor 1 (A1) and acceptor 2 (A2), the idea of the experiment is to alternately excite D and A1 with two different pulsed lasers, which can be done with simple time delays so each dye is excited once every 50 ns. Excitation of D results in transfer of the excitation energy to A1 (E₁) and also, albeit less, directly to A2 (E₂). However, A1 can transfer excitation energy that it has received from D to A2 (E₁₂). To determine directly the efficiency of transfer from A1 to A2, the second laser excites A1, which can only transfer excitation energy to A2. The alternating excitation therefore allows disentanglement of the results to yield 3 FRET efficiencies, D to A1, D to A2, and A1 to A2, thereby yielding 3 distances [100]. Because the protein is so small, the experiment will require development of fluorophores that have smaller R₀’s than those currently employed and are also more resistant to photochemistry.

Highlights.

• Single molecule FRET experiments determine average transition path times

• Observed times are extremely close to those found in all-atom MD simulations.

• Times are very similar for fast- and slow-folding proteins

• Longer times for designed protein are due to slower reaction coordinate diffusion

• Slower diffusion on reaction coordinate results from non-native interactions