Significance
Soft solids such as gels are routinely used to coat solid surfaces to control wetting and adhesion. While wetting statics on these coatings have received a lot of attention, the dynamics have hardly been studied. Here, we show that energy dissipation during spreading depends not only on the viscoelasticity of the gel but also on the thickness of the coating. We provide both an analytical model and a scaling law that predict the dynamic contact angle—i.e., the signature of dissipation in the droplet–substrate–atmosphere system—as a function of the mechanical properties of the gel and the thickness of the coating. Finally, we show that droplets moving on coatings having thickness gradients drift toward regions of higher dissipation.
Keywords: interface science, wetting, soft materials
Abstract
Gel layers bound to a rigid substrate are used in cell culture to control differentiation and migration and to lower the friction and tailor the wetting of solids. Their thickness, often considered a negligible parameter, affects cell mechanosensing or the shape of sessile droplets. Here, we show that the adjustment of coating thickness provides control over energy dissipation during the spreading of flowing matter on a gel layer. We combine experiments and theory to provide an analytical description of both the statics and the dynamics of the contact line between the gel, the liquid, and the surrounding atmosphere. We extract from this analysis a hitherto-unknown scaling law that predicts the dynamic contact angle between the three phases as a function of the properties of the coating and the velocity of the contact line. Finally, we show that droplets moving on vertical substrates coated with gel layers having linear thickness gradients drift toward regions of higher energy dissipation. Thus, thickness control opens the opportunity to design a priori the path followed by large droplets moving on gel-coated substrates. Our study shows that thickness is another parameter, besides surface energy and substrate mechanics, to tune the dynamics of liquid spreading and wetting on a compliant coating, with potential applications in dew collection and free-surface flow control.
Gels are soft complex materials made of a polymeric scaffold in which a liquid may be embedded (1). They can be obtained from a broad catalog of macromolecules and solvents such as poly(dimethylsiloxane) (PDMS) or water-based solutions of poly(vinyl alcohol). In turn, gels offer great flexibility with respect to the tuning of their mechanical and physicochemical properties. These materials find uses in a diverse range of applications, such as cell culture (2), regenerative medicine, drug delivery (3), or the modification of solid surfaces to control friction, wetting, and heterogeneous nucleation (4–6). Finally, gels as coatings have attracted renewed interest in recent years due to the opportunity they offer to generalize existing descriptions of the wetting of solids to arbitrary materials (7–19).
Most of the reports dealing with wetting involve a sessile droplet sitting on a solid with a large shear modulus (20, 21). In this context, the normal component of the resulting capillary force at the contact line between the droplet, the rigid substrate, and the atmosphere deforms the interfacial region of the solid on molecular scales. As a result, this contribution is neglected in the rationalization of wetting on solids, and the problem is usually described with the Young–Dupré equation. In contrast, gels can be soft enough ( Pa) that deforms their surface on micrometer scales, much larger than the size of the polymers and of the solvent molecules. Due to progress in experimental methods, many recent studies have investigated how the presence of this deformation, known as a ridge, may alter the force balance at the contact line and modify the shape of both the sessile drop and the substrate (13, 14, 16–18, 22).
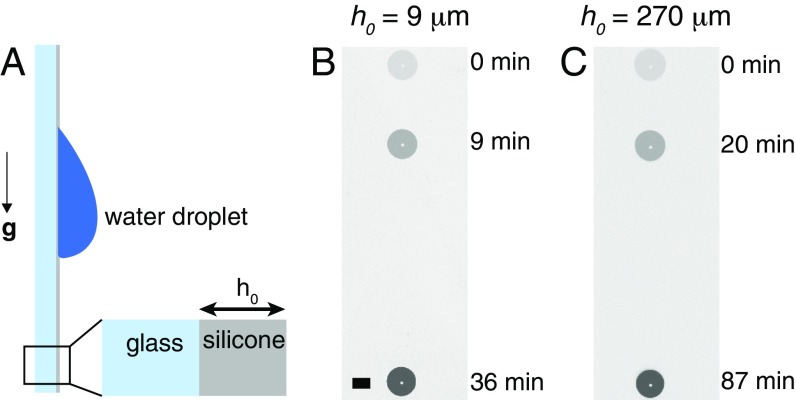
The presence of a soft coating also modifies wetting dynamics. The velocity at which a contact line between a solid, a liquid, and a gas moves on a rigid substrate coated with a soft elastomeric layer is smaller than the velocity of the contact line on the bare substrate. This velocity reduction, known as viscoelastic braking (23), results from an additional mechanism of energy dissipation due to the viscoelasticity of the gel. As a consequence, the spreading of liquids and the motion of droplets are slowed down. Nonetheless, this description of the problem is incomplete: Fig. 1 B and C demonstrate that the velocity of a water droplet moving down a vertical glass slide coated with a soft viscoelastic silicone layer ( kPa, used for all experiments in this study; see Materials and Methods for a rheological characterization) also decreases as the elastomer thickness increases. The purpose of this work is to uncover the link between substrate thickness and the motion of a contact line.
Fig. 1.
Sliding of a droplet on a soft layer. (A) A water droplet is deposited on the surface of a glass slide covered with a PDMS layer of thickness . The glass slide is inclined to the vertical at . (B and C) Motion of 2-L droplets on glass slides covered with PDMS layers 9 and 270 m thick. Labels: time in minutes elapsed since inclination. (Scale bar: 1 mm.)
Results
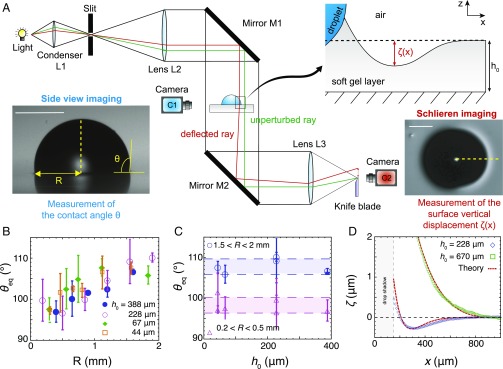
As we want to understand a dynamic wetting observation, we must characterize the reference state, that is, the statics of wetting. We investigate the properties of the region surrounding the contact line between a sessile droplet and a silicone elastomer layer using both side-view microscopy to measure the apparent contact angle at equilibrium and a noninvasive optical method based on Schlieren photography (24) (Fig. 2A). We find that depends on the contact radius of the droplet on the elastomer at constant sample thickness , but it is independent of for constant (Fig. 2 B and C), accounting for measurement uncertainties. For large droplets, tends toward a saturation at a value The Schlieren results show that the connection between the ridge and the flat elastomer surface far from the droplet is monotonically decreasing for large thicknesses, while the surface profile shows a submicrometer surface depression in the vicinity of the ridge at small thicknesses, known as a microtrough (13, 14). The microtrough results from the incompressibility of the gel, which has to accommodate the Poisson effect at small thicknesses under the zero-motion constraint at its basis due to its bonding to a rigid substrate. Its depth increases with a decrease of and an increase of the droplet radius (SI Appendix).
Fig. 2.
Experimental setup and characterization of the static three-phase contact line. (A) The region surrounding the contact line between water, the elastomer, and the atmosphere is visualized simultaneously from the side with camera C1 and from the bottom with camera C2 that captures the output of a Schlieren photography setup. The former allows us to measure the contact angle and the contact radius between the droplet and the solid . The latter is used as a surface profilometer along the yellow dashed line. (Scale bars: 0.5 mm.) (B and C) Dependence of the equilibrium value of the contact angle on for four different layer thicknesses and on the thickness of the soft layer for submillimetric and supramillimetric droplets. In C, the dashed lines represent a spread of 1 standard deviation around the average value of over all thicknesses. (D) Dependence of the surface position on the distance to the contact line for two different thicknesses. The origin of the axis is arbitrary; we use it to note that part of the contact line is hidden to the Schlieren setup by the droplet as . Dashed lines: predictions of our model.
We interpret these observations with an analytical theoretical description of the statics of elastowetting in the limit of linear elasticity developed recently by Dervaux and Limat (25) that we extend to account for finite-depth effects (SI Appendix). The model (and the model used in the dynamic context later) considers a rivulet, that is, a column of liquid whose axis of symmetry is parallel to the surface of the gel, sitting on the surface of the coating. As the angles that we measure are close to , we assume that the interfacial tensions of the solid with the liquid and the gas are identical, , and this quantity is the only fitting parameter. The model is able to capture the surface profiles of the elastomer for all of the thicknesses that we investigate (Fig. 2D), as well as the evolution of as a function of and (SI Appendix). The model indicates that mNm−1, a value comparable to those reported earlier (17, 26). To sum up, the surface profile of the elastomer layer in the vicinity of the contact line depends on layer thickness. In contrast, the apparent equilibrium contact angle is independent of the geometry of the gel layer; it depends only on the surface energies of the materials, a feature that is predicted by the model (SI Appendix). The analysis of the statics of wetting allows us to define the reference state of the study of wetting dynamics as a function of the thickness of the elastomer layer, to which we now turn.
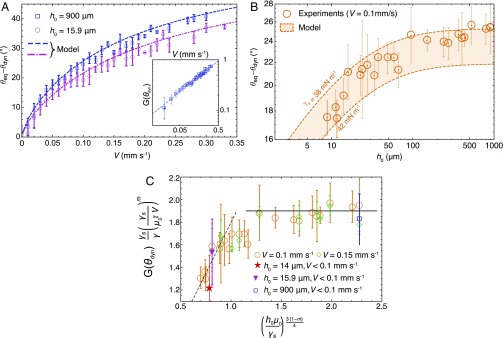
Wetting dynamics are characterized by the measurement of the dependence of the difference , the latter being the dynamic contact angle, on the velocity of the contact line (21). As , we study a receding contact line surrounding a droplet with an initial contact radius mm that we deflate at a constant flow rate. We recall that reaches its saturation value for such large droplets. For all thicknesses, increases with an increase of (Fig. 3A). The dynamic contact angle differs by almost 30° from the static equilibrium contact angle for the largest velocities we investigated. The two curves show that is also a function of thickness: It grows by 30% with an augmentation of from 10 to ∼100 m (Fig. 3B). saturates to its velocity-dependent value when m. To interpret these observations, we recall that, in general, large energy dissipation induces large values for at fixed contact line velocity (21). In this context, our results show that the thinner the elastomer is, the more energy dissipation is reduced. Voué et al. (27) reported a similar observation for a silicone oil wetting a silicone elastomer. As the liquid can permeate through the gel in their system, the wetting dynamics they report are difficult to interpret, especially since the thickness of their elastomer layers is of the order of 10 m. Permeation does not occur in our system. We now unveil how thickness and dissipation are related in elastowetting.
Fig. 3.
Characterization of the dynamics of the receding three-phase contact line on soft elastic layers. (A) Dependence of the contact angle difference on the velocity of the receding contact line on two layers of thickness and 900 m. Dashed lines: predictions based on our model. (A, Inset) Log–log plot of the function as a function of the contact-line velocity for the same systems. Dashed line: power-law fit with an exponent . (B) Dependence of on at constant receding velocity mms−1. Dashed lines: predictions of our model for two values of the solid surface tension . (C) Test of Eq. 11, relating the dynamic contact angle to the velocity of the contact line and the thickness of the sample in the small-thickness regime against experimental data. Dashed line: Eq. 11, with and a slope of 2. The horizontal line is a guide for the eyes.
To identify the mechanism relating dissipation to the thickness of the coating, we develop an analytical model based on linear viscoelasticity that is a generalization to large velocities and arbitrary rheology of a framework proposed by Long et al. (10). In this model, dissipation in the solid balances the energy that sets the contact line in motion. We assume that the shear relaxation modulus of the soft layer is described by the Chasset–Thirion model, (10). We find this assumption to be valid for our material with Pa, and ms (Materials and Methods). We also use the surface tension of the solid mNm−1 obtained from the statics. The model predicts that the function describing the dependence of the dynamic contact angle on the properties of the substrate and the velocity of the contact line is proportional to , in excellent agreement with the data (Fig. 3A), with an adjusted exponent close to the experimental value of we obtain from rheology (Fig. 3 A, Inset). The full model also captures the dependence of on at constant velocity of the contact line (Fig. 3B). Finally, we note that we do not observe effects related to the Laplace pressure inside the droplet. Thus, the 2D results we obtain with the model are valid in 3D (SI Appendix).
We can extract from the model scaling laws that describe the asymptotic behavior of for thick and thin coatings. We assume that the problem is invariant with a translation along the contact line. Our considerations are based on the Fourier transform of the problem. The power per unit length of the contact line injected by the driving capillary force is:
| [1] |
where is the interfacial tension of the liquid–gas interface. Power is balanced by dissipation in the gel. Using the Chasset–Thirion model, we estimate the power dissipated in the gel per unit volume:
| [2] |
where is a typical frequency that we assume to be of the order of , with a length scale to be determined. The dissipated power per unit length of the contact line is obtained by integrating Eq. 2 over , as this length scale also corresponds to the typical vertical displacement experienced by the solid as well as the horizontal extent of the moving ridge. Taking as a typical scale for strains:
| [3] |
Equating Eqs. 1 and 3, we find that:
| [4] |
The length is related to the balance between capillarity and elasticity in the system. Its expression depends on whether the coating has a finite thickness or not. We can express in the limit of thin and thick samples by investigating the asymptotics of the amplitude of the Fourier transform of the surface vertical displacement field (SI Appendix, Eq. S20):
| [5] |
where is the wavenumber and:
| [6] |
For large thicknesses, , and we obtain that . Then:
| [7] |
The characteristic length scale in Eq. 7 is , that is, the elastocapillary length. Injecting this value of in Eq. 4, we find the scaling predicted 20 y ago by Long et al. (10):
| [8] |
In the limit of thin coatings, we carry out the Taylor expansion of around , and we keep the first nonvanishing term:
| [9] |
We find that the characteristic length scale is in this case. Injecting in Eq. 3, we obtain the following expression for the dissipated power:
| [10] |
and we obtain a scaling law reflecting thickness effects on the dynamic contact angle for thin coatings:
| [11] |
Eq. 11 can be tested by rescaling the experimental data as in Fig. 3C. We see that the data follow Eq. 11 when . When , the data are independent of , and they follow Eq. 8, thus validating Long et al.’s model (10). Thus, our results show that dissipation during the wetting of a soft coating by a liquid can be engineered in a predictable way by adjusting the thickness of the layer. Finally, the range of thicknesses over which we observe a dependence of dissipation on corresponds to the typical range of coating thicknesses in applications.
Discussion
The prediction that the dynamic contact angle at a contact line moving on a soft coating is closer to the value of the static contact angle as the thickness of the coating decreases may seem counterintuitive at first. To gain more insight, we shall now compare contact line motion for a rivulet on a gel layer and on a liquid substrate of similar thickness . In the latter case, continuity of stresses and velocities is enforced at all of the interfaces. Momentum diffuses from the droplet to the bulk of the liquid substrate through the droplet–substrate interface, and stresses and dissipation do not diverge at the contact line. Energy dissipation occurs in the bulk of both the droplet and the substrate. In the latter, the dissipation power per unit length along the contact line between the rivulet and the gel scales as (28), where is the radius of the spreading rivulet; we assume that remains constant over time. Thus, dissipation increases with a decrease of (29, 30). In contrast, at the interface between a gel coating and a liquid, we enforce the no-slip boundary condition. Thus, velocities are zero everywhere along this interface, and the contact line is the locus of most dissipation. In this context, we show that dissipation follows Eq. 10. As , dissipation decreases with a decrease of the thickness of the sample.
We also compute the prediction for the dependence of using another model proposed recently by Karpitschka et al. (26). This model captures well the data for at large thickness, provided we adjust the surface tension of the solid to a value different from the one we obtain in our study of the statics of wetting. Nonetheless, it does not capture the decreasing trend of at small thicknesses (SI Appendix). In their model, Karpitschka et al. impose that capillary forces are at equilibrium at the moving contact line at all times. The failure of their model to capture our data suggests that this constraint is not true anymore for droplets moving on thin coatings. The question of the validity of this assumption at all thicknesses remains open, as its answer lies in a second-order analysis of the dynamics of elastowetting that has yet to be performed.
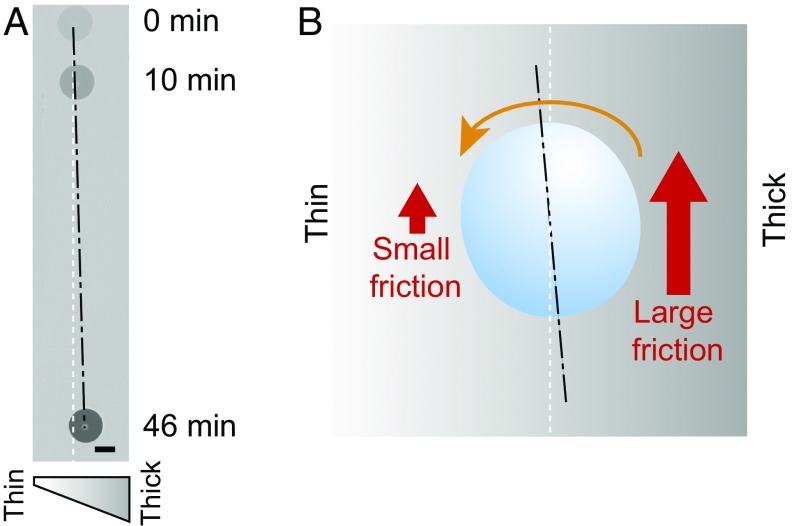
We take advantage of our findings to control the trajectory of liquids moving at the surface of solid substrates. We coat a glass slide with a soft elastomeric layer with a thickness gradient (Fig. 4A). We place a water droplet at one extremity of the glass slide above the thinnest part of the coating. Then, we incline the glass slide to the vertical, the thickness gradient being perpendicular to gravity. The droplet slides down, and it drifts from the thinnest regions toward the thickest ones. Drift results from the dependence of dissipation in the gel on : the droplet experiences a larger braking over the thick part of the coating than over the thin region (Fig. 4B). Thus, the droplet is subject to a torque that leads to a global drift toward the thick region. In our system, drift will be observed if the gradient starts from m. If the thin part of the thickness gradient is thicker than m, we expect no drift, as is observed in the experiments. Finally, we observe no spontaneous motion of droplets when the glass slide remains horizontal for a long time. This fact highlights the difference between our results, whose origin lies in the variation of the dynamic contact angle around the droplet, and those reported by Style et al. (31) concerning droplet durotaxis, which occurs due to changes of the static contact angle along the droplet perimeter.
Fig. 4.
Drifting of a droplet moving down a vertical glass slide covered with a soft layer of increasing thickness. (A) A 2-L droplet moving over a coating with a thickness gradient mmm−1. (Scale bar: 1 mm.) (B) Schematic explaining the mechanism leading to droplet drift during forced motion. The black dashed line is the trajectory of the droplet; the white dashed line is the vertical. The orange arrow represents the rotation of the droplet as it moves down the coating and experiences differences in dissipation along its contour, in a fashion analogous to a car experiencing braking only on one of its sides.
Our findings open the possibility to design soft coatings whose mechanical dissipation can be adjusted not only by formulation but also by an appropriate choice of thickness. We envision improvements in applications such as dew collection, where the use of soft layers has been shown to improve the nucleation rate of condensation droplets (5); the use of thin layers will help increase the up-time of the condensation cell. We also anticipate the use of our results to control free-surface flows such as droplet impact or gravity currents passively with thickness-gradient coatings.
Materials and Methods
Gel Preparation and Characterization.
All of the experiments are performed with Millipore-Q purified water ( = 72 mN/m) on PDMS substrates made from the commercial elastomer Sylgard 527 (Dow Corning). Sylgard 527 is a two-component elastomer kit composed of a base and a cross-linker. The two liquids are mixed at a manufacturer-recommended 1:1 ratio, to respect cross-linking stoichiometry, with a magnetic stirrer for ∼30 min. The mixture is then left to degas under vacuum ( mbar) for at least 1 h. We obtain thin flat PDMS gel films (thickness m) by spin-coating directly the degassed mixture on glass slides. Thickness is controlled by tuning the spinning speed from 100 to 3,400 rpm. For thick flat films (thickness m), the thickness is tuned by changing the elastomer volume poured onto the glass slide mounted with movable walls.
For the thickness gradient experiment, the Sylgard mixture is poured into a mold containing a titled glass slide. Next, the elastomer is cross-linked at 65 °C in an oven for 24 h. This protocol produces transparent PDMS films strongly bound to glass slides. The thickness of the films is measured with a 3D Profiler (FOCAL 3D Pilot; FOCAL Nanotech) operating in white light scanning mode with a precision of the order of a nanometer.
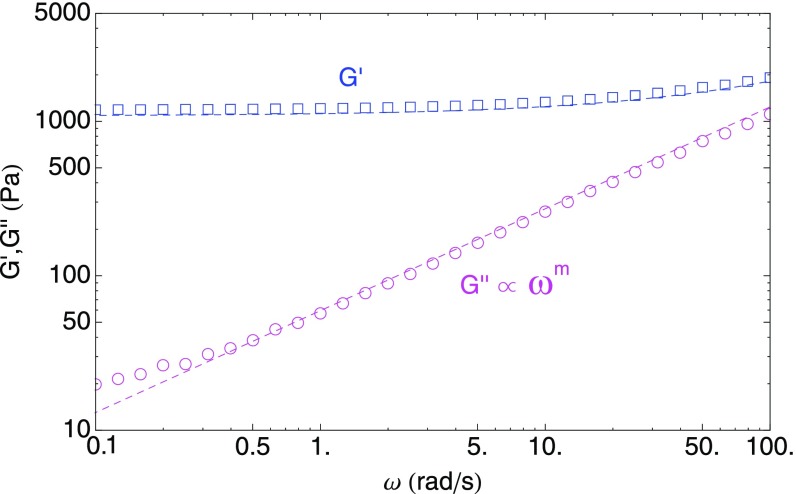
Fig. 5 shows the rheological data we obtain for Sylgard 527 measured with a strain-controlled rheometer (Physica MCR 500; Anton Paar). The elastomer is cross-linked directly between the Peltier plate and the plate tool (PP20-MRD, mm; Anton Paar) at C for 4 h. The sample is then left to cool down to C before running the test. The gap is set at 0.6 mm, and the strain is fixed at 1%. A fit of the Chasset–Thirion model, , to the experimental data provides the parameters for the frequency-dependent mechanical response of the gel. We also characterize the contact angle hysteresis of water on Sylgard 527, and we find it to be of the order of 3–4°.
Fig. 5.
Small-amplitude oscillatory shear measurement of the mechanical properties of the Sylgard 527 elastomer with a strain-controlled rheometer (Physica MCR 500; Anton Paar). Dashed line: best fit of the Chasset–Thirion model, , to the experimental data. Pa, and ms.
Quantitative Schlieren Optics.
We build an observation platform for the measurements of out-of-plane deformations of the soft film based on Schlieren optics. A white LED light source (Luxeon; Lumileds) is focused on a mechanical slit (VA100/M; Thor Labs; size mm) by a condenser L1. The light beam from the slit is then collimated by a lens L2 (diameter mm; focal length mm; MPD 149-P01; Thor Labs). The parallel light beam goes through the sample between mirror prisms M1 and M2. It is then collected by a third lens L3 (LB1374-B; Thor Labs). To obtain a Schlieren setup, a knife blade is placed at the focal point of lens L3 and hides part of the focal region. The blade filters those light beams that are deviated because of surface deformations of the gel sample due to the presence of the droplet. Images of the filtered focal point are captured with a digital camera (DFK 23UX174; Imaging Source) equipped with a lens (Avenir TV Zoom Lens F1.8). The CCD sensor of the camera has a dimension of pixels, resulting in a lateral spatial resolution of 10.2 mpx−1.
In principle, the slit light source is perfectly refocused on the knife blade plane as illustrated by the green light beam drawn in Fig. 2A, as long as there is no disturbance on the light path. However, changes in the surface slope of the gel film deflect the light beam, and the conjugated image is thus shifted by a distance in the focal plane, as illustrated by the red beam shown in Fig. 2A. Under the small angle approximation, this distance is related to the deflection of the light beam through the Schlieren object by the formula , where is the focal length of L3. For an accurate quantification of the surface profile, we carry out a three-step measurement. First, a sequence of pictures is recorded at different vertical blade positions, and a map relating the pixel grayscale value to the deflection by the knife cutoff is built. During this step, the Schlieren object is absent. Second, all of the camera parameters are kept identical, and pictures are taken 5 min after the drop fully relaxes on the soft substrate (for the static deformation measurement). Then, the grayscale value of the Schlieren picture is compared with the calibration map, and we obtain a deflection map. Finally, by combining the deflection relation and Snell’s law, the map of the surface slope is reconstructed. Our system has a deflection angle sensitivity of 0.0007 rad, and we could measure angles up to 0.05 rad.
Data Acquisition.
To study the statics of wetting, we enclose the sample in a transparent glass chamber ( mm) to control humidity and avoid evaporation. Its lid could easily be removed to place drops. For experiments, a reservoir of water is enclosed together with the PDMS slides to saturate the atmosphere of the glass chamber. All of the measurements are performed 5 min after deposition. For the spreading dynamic experiments, a side view camera (DMK 23UV024; Imaging Source; C1 in Fig. 2A) equipped with a lens (TV Lens 50 mm, f1:2.8; Ricoh) and two tube sets (C Mount TV Lens Extension Tube Set; 40 mm) is used. The spatial resolution of C1 is 5.5 mpx−1. By using a Gaussian subpixel detection technique, the error in the contact line velocity determination is ∼10 ms−1. All of the drops are deposited by using a syringe which is connected to a pump (PUMP 33; Harvard Apparatus) at room temperature. For the sliding and drifting experiments on tilted slides, droplets are deposited by using a micropipette (0.5–10 L; FinnPipette) at ambient temperature. A front view camera (DFK 23UX174; Imaging Source) equipped with a lens (TV Lens; 50 mm f1:2.8; Ricoh) and one tube set (C Mount TV Lens Extension Tube Set; 20 mm), with a spatial resolution of 15.9 mpx−1 is used to track the sliding droplets.
Model.
We use two models, one for the statics and one for the dynamics. The model describing the statics is built in the framework of linear elasticity, and we account for the surface tension of the solid. We assume that the system is translation-invariant, and we describe an x–y slice of the substrate subjected to the capillary force of a liquid. We model the latter as a concentrated load on an elastic half-space of depth . We are interested in two situations, the single contact line and the rivulet, that is, a column of liquid that has two straight contact lines with the substrates. We focus on the far-field vertical displacement, for which possible divergences in the displacements at the contact line do not matter (25). We use Fourier transforms to solve the biharmonic equation that describes the problem, and we compare the data with the outcomes of the description of the rivulet. The static model also accounts for the small hysteresis that we measure in experiments in the form of a force tangential to the surface.
The model for the dynamics is built in the framework of linear viscoelasticity. We use the surface tension of the solid deduced from the study of the statics as an input to the model. As experiments indicate that the properties of the motion of the contact line are independent of the size of the droplet, we focus on the case of a single contact line. We compute the dependence of the vertical displacement on the velocity of the contact line using a similar procedure to the statics resorting to Fourier transforms. We then compare the power injected in the system due to capillarity with the dissipated power in the substrate due to its viscoelasticity.
Supplementary Material
Acknowledgments
We thank Bruno Andreotti and Jacco Snoeijer for interesting discussions. M.Z. was supported by a China Scholarship Council PhD fellowship. This work was supported by Agence Nationale de la Recherche and Commissariat à l’Investissement d’Avenir Multiscale Modeling of Material Interfaces (MMEMI) Grant (LabEx Science and Engineering for Advanced Materials and Devices) ANR-11-LABX-086, ANR-11-IDEX-05-02 and Poroelasticity and Non-linearity in Gel Wetting (GELWET) Grant ANR-17-CE30-0016.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. R.W.S. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1712562115/-/DCSupplemental.
References
- 1.Larson RG. The Structure and Rheology of Complex Fluids. 1st Ed Oxford Univ Press; Oxford: 1999. [Google Scholar]
- 2.Tibbitt MW, Anseth KS. Hydrogels as extracellular matrix mimics for 3D cell culture. Biotechnol Bioeng. 2009;103:655–663. doi: 10.1002/bit.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jagur-Grodzinski J. Polymeric gels and hydrogels for biomedical and pharmaceutical applications. Polym Adv Technol. 2010;21:27–47. [Google Scholar]
- 4.Gong JP. Friction and lubrication of hydrogels—its richness and complexity. Soft Matter. 2006;2:544–552. doi: 10.1039/b603209p. [DOI] [PubMed] [Google Scholar]
- 5.Sokuler M, et al. The softer the better: Fast condensation on soft surfaces. Langmuir. 2010;26:1544–1547. doi: 10.1021/la903996j. [DOI] [PubMed] [Google Scholar]
- 6.Style RW, Jagota A, Hui CY, Dufresne ER. Elastocapillarity: Surface tension and the mechanics of soft solids. Annu Rev Condens Matter Phys. 2017;8:99–118. [Google Scholar]
- 7.Lester GR. Contact angles of liquids at deformable solid surfaces. J Colloid Sci. 1961;16:315–326. [Google Scholar]
- 8.Shanahan MER, de Gennes PG. L’arête produite par un coin liquide près de la ligne triple de contact solide/liquide/fluide. C R Acad Sci Paris. 1986;302:517–521. [Google Scholar]
- 9.Shanahan MER. The influence of solid micro-deformation on contact angle equilibrium. J Phys D. 1987;20:945–950. [Google Scholar]
- 10.Long D, Ajdari A, Leibler L. Static and dynamic wetting properties of thin rubber films. Langmuir. 1996;12:5221–5230. [Google Scholar]
- 11.Yu YS, Yang Z, Zhao YP. Role of vertical component of surface tension of the droplet on the elastic deformation of PDMS membrane. J Adhes Sci Technol. 2008;22:687–698. [Google Scholar]
- 12.Yu YS, Zhao YP. Elastic deformation of soft membrane with finite thickness induced by a sessile liquid droplet. J Colloid Interface Sci. 2009;339:489–494. doi: 10.1016/j.jcis.2009.08.001. [DOI] [PubMed] [Google Scholar]
- 13.Pericet-Camara R, et al. Solid-supported thin elastomer films deformed by microdrops. Soft Matter. 2009;5:3611–3617. [Google Scholar]
- 14.Jerison E, Xu Y, Wilen L, Dufresne E. Deformation of an elastic substrate by a three-phase contact line. Phys Rev Lett. 2011;106:186103. doi: 10.1103/PhysRevLett.106.186103. [DOI] [PubMed] [Google Scholar]
- 15.Limat L. Straight contact lines on a soft, incompressible solid. EPJ E. 2012;35:134–147. doi: 10.1140/epje/i2012-12134-6. [DOI] [PubMed] [Google Scholar]
- 16.Style RW, Dufresne ER. Static wetting on deformable substrates, from liquids to soft solids. Soft Matter. 2012;8:7177. [Google Scholar]
- 17.Style RW, et al. Universal deformation of soft substrates near a contact line and the direct measurement of solid surface stresses. Phys Rev Lett. 2013;110:066103. doi: 10.1103/PhysRevLett.110.066103. [DOI] [PubMed] [Google Scholar]
- 18.Style RW, Hyland C, Boltyanskiy R, Wettlaufer JS, Dufresne ER. Surface tension and contact with soft elastic solids. Nat Commun. 2013;4:2728. doi: 10.1038/ncomms3728. [DOI] [PubMed] [Google Scholar]
- 19.Bostwick JB, Shearer M, Daniels KE. Elastocapillary deformations on partially-wetting substrates: Rival contact-line models. Soft Matter. 2014;10:7361. doi: 10.1039/c4sm00891j. [DOI] [PubMed] [Google Scholar]
- 20.de Gennes PG. Wetting: Statics and dynamics. Rev Mod Phys. 1985;57:827–863. [Google Scholar]
- 21.Bonn D, Eggers J, Indekeu J, Meunier J, Rolley E. Wetting and spreading. Rev Mod Phys. 2009;81:739–805. [Google Scholar]
- 22.Marchand A, Das S, Snoeijer J, Andreotti B. Capillary pressure and contact line force on a soft solid. Phys Rev Lett. 2012;108:094301. doi: 10.1103/PhysRevLett.108.094301. [DOI] [PubMed] [Google Scholar]
- 23.Carré A, Gastel JC, Shanahan MER. Viscoelastic effects in the spreading of liquids. Nature. 1996;379:432–434. [Google Scholar]
- 24.Settles GS. 2001. Schlieren and Shadowgraph techniques. (Springer, Berlin), Vol 1.
- 25.Dervaux J, Limat L. Contact lines on soft solids with uniform surface tension: Analytical solutions and double transition for increasing deformability. Proc R Soc A. 2015;471:20140813. [Google Scholar]
- 26.Karpitschka S, et al. Droplets move over viscoelastic substrates by surfing a ridge. Nat Commun. 2015;6:7891. doi: 10.1038/ncomms8891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Voué M, et al. Dissipation and moving contact lines on non-rigid substrates. J Euro Ceram Soc. 2003;23:2769–2775. [Google Scholar]
- 28.Landau LD, Lifshitz EM. Fluid Mechanics. 2nd Ed Butterworth-Heinemann; Oxford: 1987. [Google Scholar]
- 29.Craster RV, Matar OK. On the dynamics of liquid lenses. J Colloid Interface Sci. 2006;303:503–516. doi: 10.1016/j.jcis.2006.08.009. [DOI] [PubMed] [Google Scholar]
- 30.Karapetsas G, Craster RV, Matar OK. Surfactant-driven dynamics of liquid lenses. Phys Fluids. 2011;23:122106. [Google Scholar]
- 31.Style RW, et al. Patterning droplets with durotaxis. Proc Natl Acad Sci USA. 2013;110:12541–12544. doi: 10.1073/pnas.1307122110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.