Maximizing the information learned from finite data selects a simple model

Significance

Most physical theories are effective theories, descriptions at the scale visible to our experiments which ignore microscopic details. Seeking general ways to motivate such theories, we find an information theory perspective: If we select the model which can learn as much information as possible from the data, then we are naturally led to a simpler model, by a path independent of concerns about overfitting. This is encoded as a Bayesian prior which is nonzero only on a subspace of the original parameter space. We differ from earlier prior selection work by not considering an infinite quantity of data. Having finite data is always a limit on the resolution of an experiment, and in our framework this selects how complicated a theory is appropriate.

Abstract

We use the language of uninformative Bayesian prior choice to study the selection of appropriately simple effective models. We advocate for the prior which maximizes the mutual information between parameters and predictions, learning as much as possible from limited data. When many parameters are poorly constrained by the available data, we find that this prior puts weight only on boundaries of the parameter space. Thus, it selects a lower-dimensional effective theory in a principled way, ignoring irrelevant parameter directions. In the limit where there are sufficient data to tightly constrain any number of parameters, this reduces to the Jeffreys prior. However, we argue that this limit is pathological when applied to the hyperribbon parameter manifolds generic in science, because it leads to dramatic dependence on effects invisible to experiment.

Physicists prefer simple models not because nature is simple, but because most of its complication is usually irrelevant. Our most rigorous understanding of this idea comes from the Wilsonian renormalization group (1–3), which describes mathematically the process of zooming out and losing sight of microscopic details. These details influence the effective theory which describes macroscopic observables only through a few relevant parameter combinations, such as the critical temperature or the proton mass. The remaining irrelevant parameters can be ignored, as they are neither constrained by past data nor useful for predictions. Such models can now be understood as part of a large class called sloppy models (4–14), whose usefulness relies on a similar compression of a large microscopic parameter space down to just a few relevant directions.

This justification for model simplicity is different from the one more often discussed in statistics, motivated by the desire to avoid overfitting (15–21). Since irrelevant parameters have an almost invisible effect on predicted data, they cannot be excluded on these grounds. Here we motivate their exclusion differently: We show that simplifying a model can often allow it to extract more information from a limited dataset and that this offers a guide for choosing appropriate effective theories.

We phrase the question of model selection as part of the choice of a Bayesian prior on some high-dimensional parameter space. In a set of nested models, we can always move to a simpler model by using a prior which is nonzero only on some subspace. Recent work has suggested that interpretable effective models are typically obtained by taking some parameters to their limiting values, often $0$ or $\mathrm{\infty }$, thus restricting to lower-dimensional boundaries of the parameter manifold (22).

Our setup is that we wish to learn about a theory by performing some experiment which produces data $x\in X$. The theory and the experiment are together described by a probability distribution $p(x|\theta )$, for each value of the theory’s parameters $\theta \in \mathrm{\Theta }$. This function encodes both the quality and the quantity of data to be collected.

The mutual information (MI) between the parameters and their expected data is defined as $\mathrm{MI}=I(X;\mathrm{\Theta })=S(\mathrm{\Theta })-S(\mathrm{\Theta }|X)$, where $S$ is the Shannon entropy (23). The MI thus quantifies the information which can be learned about the parameters by measuring the data, or equivalently, the information about the data which can be encoded in the parameters (24, 25). Defining $p_{\star }(\theta )$ by maximizing this, we see the following:

• i)The prior $p_{\star }(\theta )$ is almost always discrete (26–30), with weight only on a finite number $K$ of points or atoms (Figs. 1 and 2): $p_{\star }(\theta )={\sum }_{a=1}^K{\lambda }_a\delta (\theta -{\theta }_a).$
• ii)When data are abundant, $p_{\star }(\theta )$ approaches the Jeffreys prior $p_{\mathrm{J}}(\theta )$ (31–33). As this continuum limit is approached, the proper spacing of the atoms shrinks as a power law (Fig. 3).
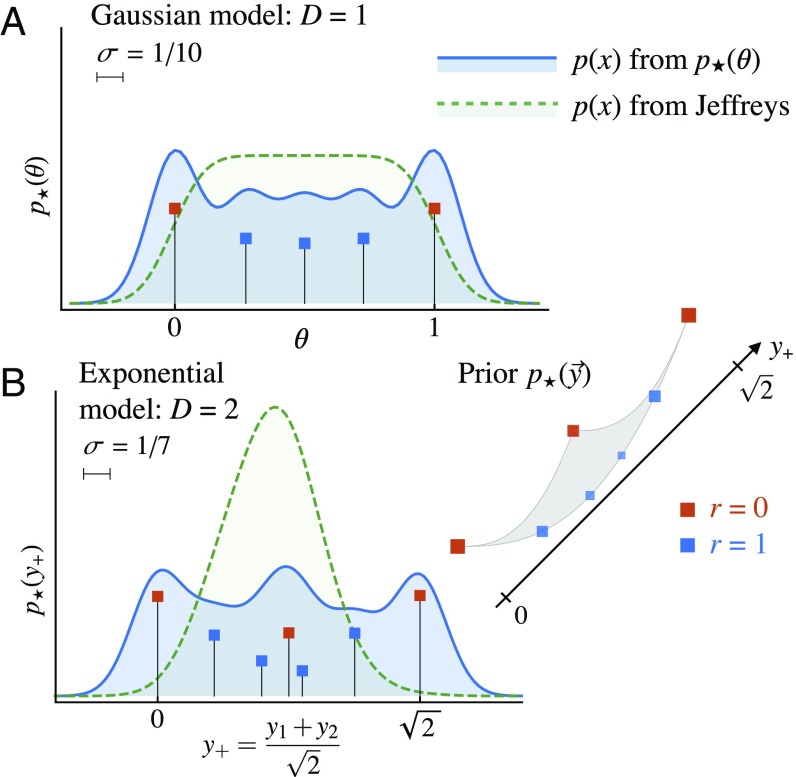
• iii)When data are scarce, most atoms lie on boundaries of the parameter space, corresponding to effective models with fewer parameters (Fig. 4). The resulting distribution of weight along relevant directions is much more even than that given by the Jeffreys prior (Fig. 5).

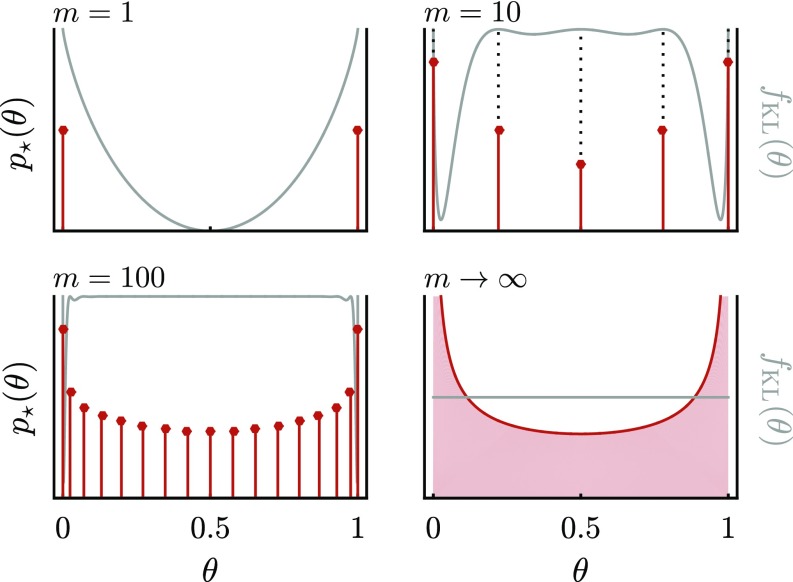
Fig. 1.

Optimal priors for the Bernoulli model (Eq. 1). Red lines indicate the positions of delta functions in $p_{\star }(\theta )$, which are at the maxima of $f_{\mathrm{KL}}(\theta )$, Eq. 3. As $m\to \mathrm{\infty }$ these coalesce into the Jeffreys prior $p_{\mathrm{J}}(\theta )$.

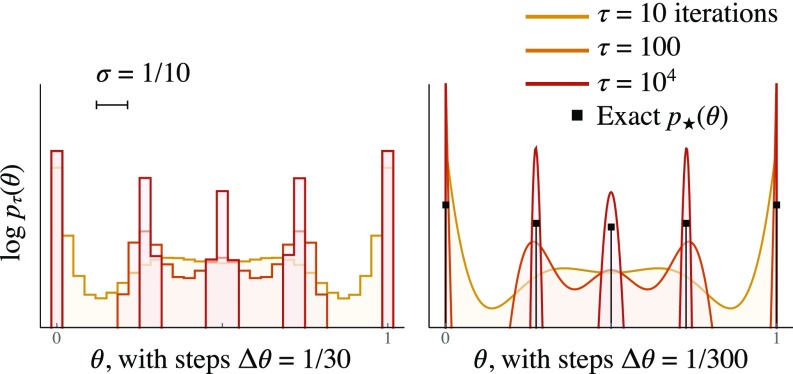
Fig. 2.

Convergence of the BA algorithm. This is for the one-parameter Gaussian model Eq. 2 with $L=10$ (comparable to $m=10$ in Fig. 1). Right shows $\theta$ discretized into 10 times as many points, but $p_{\tau }(\theta )$ clearly converges to the same 5 delta functions.

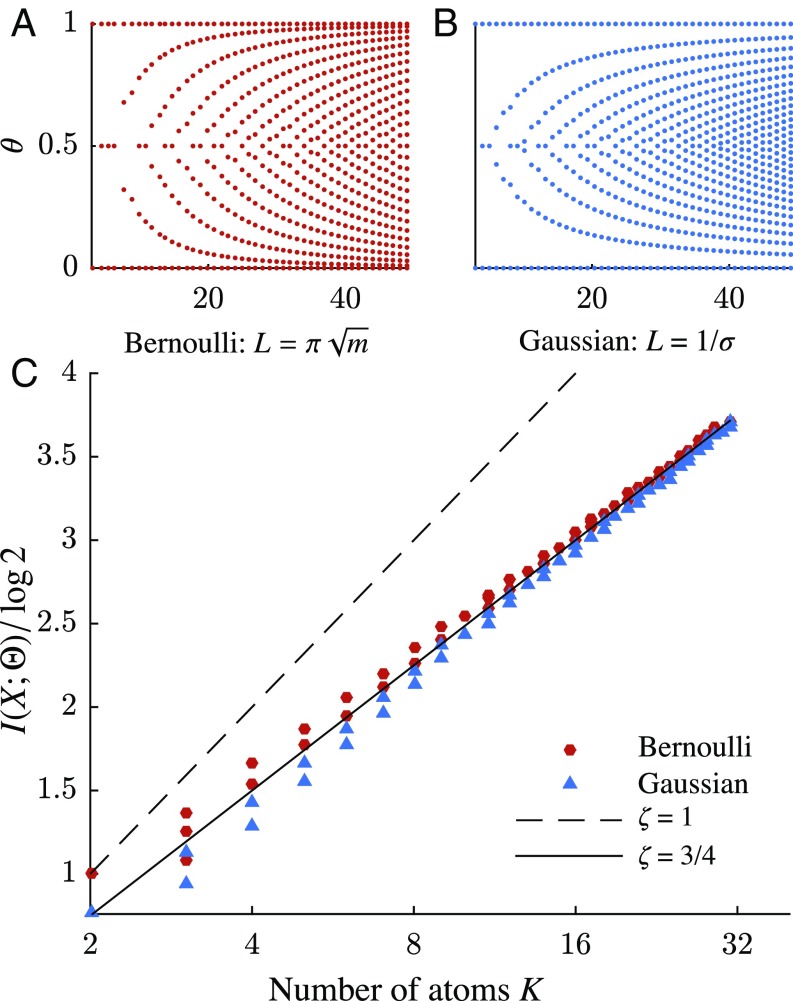
Fig. 3.

Behavior of $p_{\star }(\theta )$ with increasing Fisher length. A and B show the atoms of $p_{\star }(\theta )$ for the two one-dimensional models as $L$ is increased (i.e., we perform more repetitions $m$ or have smaller noise $\sigma$). C shows the scaling of the MI (in bits) with the number of atoms $K$. The dashed line is the bound $\mathrm{MI}\le \log K$, and the solid line is the scaling law $\mathrm{MI}\sim 3/4\log K$.

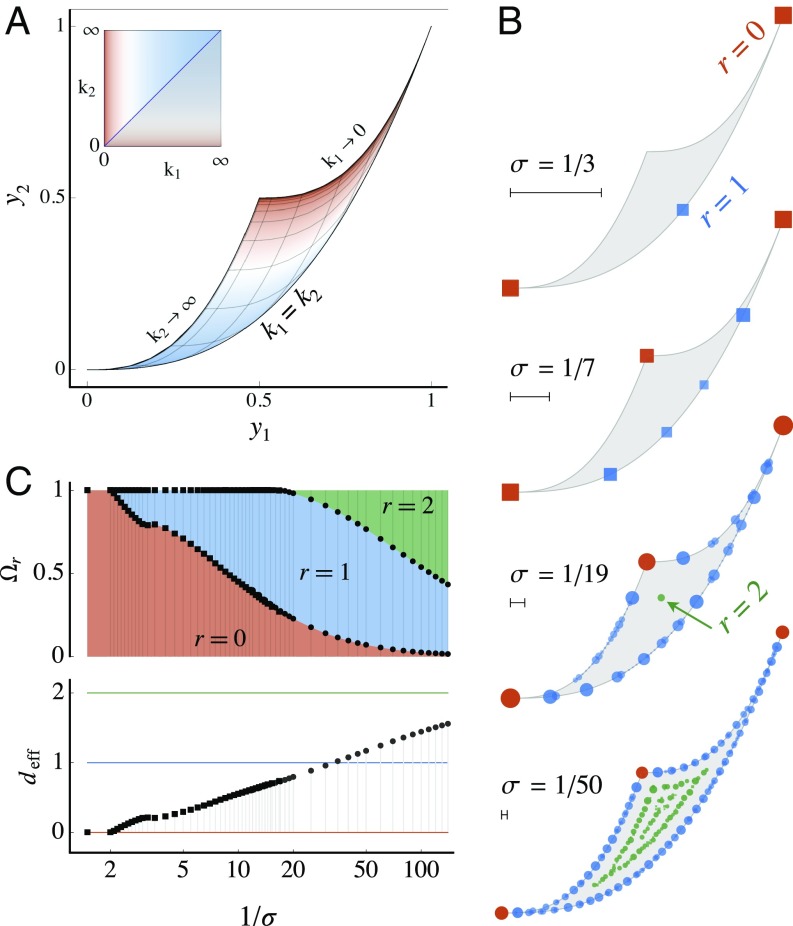
Fig. 4.

Parameters and priors for the exponential model (Eq. 5). A shows the area of the $\overrightarrow{y}$ plane covered by all decay constants $k_1,k_2\ge 0$. B shows the positions of the delta functions of the optimal prior $p_{\star }(\overrightarrow{y})$ for several values of $\sigma$, with colors indicating the dimensionality $r$ at each point. C shows the proportion of weight on these dimensionalities.

Fig. 5.

Distributions of expected data $p(x)$ from different priors. A is the one-parameter Gaussian model, with $L=10$. B projects the two-parameter exponential model onto the $y_1+y_2$ direction, for $\sigma =1/7$ where the perpendicular direction should be irrelevant. The length of the relevant direction is about the same as the one-parameter case: $L_{+}=7\sqrt{2}$. Note that the distribution of expected data $p(x_{+})$ from the Jeffreys prior here is quite different, with almost no weight at the ends of the range ($0$ and $\sqrt{2}$), because this prior still weights the area and not the length.

After some preliminaries, we demonstrate these properties in three simple examples, each a stylized version of a realistic experiment. To see the origin of discreteness, we study the bias of an unfair coin and the value of a single variable corrupted with Gaussian noise. To see how models of lower dimension arise, we then study the problem of inferring decay rates in a sum of exponentials.

In Supporting Information, we discuss the algorithms used for finding $p_{\star }(\theta )$, and we apply some more traditional model selection tools to the sum of exponentials example.

Priors and Geometry

Bayes’ theorem tells us how to update our knowledge of $\theta$ upon observing data $x$, from prior $p(\theta )$ to posterior $p(\theta |x)=p(x|\theta )p(\theta )/p(x)$, where $p(x)=\int d\theta p(\theta )p(x|\theta )$. In the absence of better knowledge we must pick an uninformative prior which codifies our ignorance. The naive choice of a flat prior $p(\theta )=\text{const}.$ has undesirable features, in particular making $p(x)$ depend on the choice of parameterization, through the measure $d\theta$.

The Jeffreys prior $p_{\mathrm{J}}(\theta )$ is invariant under changes of parameterization because it is constructed from some properties of the experiment (34). This $p_{\mathrm{J}}(\theta )\propto \sqrt{det{g}_{\mu \nu }}$ is, up to normalization, the volume form arising from the Fisher information metric or matrix (FIM):

$$g_{\mu \nu }(\overrightarrow{\theta })=\int dx\hspace{0.17em}p(x|\overrightarrow{\theta })\frac{\partial \log p(x|\overrightarrow{\theta })}{\partial {\theta }^{\mu }}\frac{\partial \log p(x|\overrightarrow{\theta })}{\partial {\theta }^{\nu }}.$$

This Riemannian metric defines a reparameterization-invariant distance between points, $d{s}^2={\sum }_{\mu ,\nu =1}^D\hspace{0.17em}{g}_{\mu \nu }\hspace{0.17em}d{\theta }^{\mu }\hspace{0.17em}d{\theta }^{\nu }$. It measures the distinguishability of the data which $\theta$ and $\theta +d\theta$ are expected to produce, in units of standard deviations. Repeating an (identical and independently distributed) experiment $m$ times means considering $p^m(\overrightarrow{x}|\theta )={\prod }_{j=1}^{m}p(x_j|\theta )$, which leads to metric $g_{\mu \nu }^m(\theta )=m\hspace{0.17em}{g}_{\mu \nu }(\theta )$. However, the factor $m^{D/2}$ in the volume is lost by normalizing $p_{\mathrm{J}}(\theta )$. Thus, the Jeffreys prior depends on the type of experiment, but not the quantity of data.

Bernardo defined a prior $p_{\star }(\theta )$ by maximizing the MI between parameters $\mathrm{\Theta }$ and the expected data $X^m$ from $m$ repetitions and then a reference prior by taking the limit $m\to \mathrm{\infty }$ (29, 31). Under certain benign assumptions, this reference prior is exactly the Jeffreys prior (31–33), providing an alternative justification for $p_{\mathrm{J}}(\theta )$.

We differ in taking seriously that the amount of data collected is always finite.* Besides being physically unrealistic, the limit $m\to \mathrm{\infty }$ is pathological both for model selection and for prior choice. In this limit any number of parameters can be perfectly inferred, justifying an arbitrarily complicated model. In addition, in this limit the posterior $p(\theta |x)$ becomes independent of any smooth prior.^†

Geometrically, the defining feature of sloppy models is that they have a parameter manifold with hyperribbon structure (6–9): There are some long directions (corresponding to $d$ relevant, or stiff, parameters) and many shorter directions ($D-d$ irrelevant, or sloppy, parameter combinations). These lengths are often estimated using the eigenvalues of $g_{\mu \nu }$ and have logarithms that are roughly evenly spaced over many orders of magnitude (4, 5). The effect of coarse graining is to shrink irrelevant directions (here using the technical meaning of irrelevant: a parameter which shrinks under renormalization group flow) while leaving relevant directions extended, producing a sloppy manifold (8, 14). By contrast, the limit $m\to \mathrm{\infty }$ has the effect of expanding all directions, thus erasing the distinction between directions longer and shorter than the critical length scale of (approximately) 1 SD.

On such a hyperribbon, the Jeffreys prior has an undesirable feature: Since it is constructed from the $D$-dimensional notion of volume, its weight along the relevant directions always depends on the volume of the $D-d$ irrelevant directions. This gives it extreme dependence on which irrelevant parameters are included in the model.^‡ The optimal prior $p_{\star }(\theta )$ avoids this dependence because it is almost always discrete, at finite $m$.^§ It puts weight on a set of nearly distinguishable points, closely spaced along the relevant directions, but ignoring the irrelevant ones. Yet being the solution to a reparameterization-invariant optimization problem, the prior $p_{\star }(\theta )$ retains this good feature of $p_{\mathrm{J}}(\theta )$.

Maximizing the MI was originally done to calculate the capacity of a communication channel, and we can borrow techniques from rate-distortion theory here: The algorithms we use were developed there (37, 38), and the discreteness we exploit was discovered several times in engineering (26–28, 39). In statistics, this problem is more often discussed as an equivalent minimax problem (40). Discreteness was also observed in other minimax problems (41–43) and later in directly maximizing MI (29, 30, 33, 44). However, it does not seem to have been seen as useful, and none of these papers explicitly find discrete priors in dimension $D>1$, which is where we see attractive properties. Discreteness has been useful, although for different reasons, in the idea of rational inattention in economics (45, 46). There, market actors have a finite bandwidth for news, and this drives them to make discrete choices despite all the dynamics being continuous. Rate-distortion theory has also been useful in several areas of biology (47–49), and discreteness emerges in a recent theoretical model of the immune system (50).

We view this procedure of constructing the optimal prior as a form of model selection, picking out the subspace of $\mathrm{\Theta }$ on which $p_{\star }(\theta )$ has support. This depends on the likelihood function $p(x|\theta )$ and the data space $X$, but not on the observed data $x$. In this regard it is closer to Jeffreys’ perspective on prior selection than to tools like the information criteria and Bayes factors, which are used at the stage of fitting to data. We discuss this difference at length in Model Selection from Data.

One-Parameter Examples

We begin with some problems with a single bounded parameter, of length $L$ in the Fisher metric. These tractable cases illustrate the generic behavior along either short (irrelevant) or long (relevant, $L\gg 1$) parameter directions in higher-dimensional examples.

Our first example is the Bernoulli problem, in which we wish to determine the probability $\theta \in [\mathrm{0,1}]$ that an unfair coin gives heads, using the data from $m$ trials. It is sufficient to record the total number of heads $x$, which occurs with probability

$$p(x|\theta )=\frac{m!}{x!(m-x)!}{\theta }^x{(1-\theta )}^{m-x}.$$ [1]

This gives $g_{\theta \theta }=\frac{m}{\theta (1-\theta )}$, thus $p_{\mathrm{J}}(\theta )={[\pi \sqrt{\theta (1-\theta )}]}^{-1}$, and proper parameter space length $L=\int \sqrt{d{s}^2}=\pi \sqrt{m}$.

In the extreme case $m=1$, the optimal prior is two delta functions, $p_{\star }(\theta )=\frac{1}{2}\delta (\theta )+\frac{1}{2}\delta (\theta -1)$, and $\mathrm{MI}=\log 2$, exactly one bit (29, 30, 33). Before an experiment that will run only once, this places equal weight on both outcomes; afterward it records the outcome. As $m$ increases, weight is moved from the boundary onto interior points, which increase in number and ultimately approach the smooth $p_{\mathrm{J}}(\theta )$ (Figs. 1 and 3A).

Similar behavior is seen in a second example, in which we measure one real number $x$, normally distributed with known $\sigma$ about the parameter $\theta \in [0,1]$:

$$p(x|\theta )=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-{(x-\theta )}^2/2{\sigma }^2}.$$ [2]

Repeated measurements are equivalent to smaller $\sigma$ (by $\sigma \to \sigma /\sqrt{m}$), so we fix $m=1$ here. The Fisher metric is $g_{\theta \theta }=1/{\sigma }^2$, and thus $L=1/\sigma$. An optimal prior is shown in Fig. 2; in Fig. 5A it is shown along with its implied distribution of expected data. This $p(x)$ is similar to that implied by the Jeffreys prior, here $p_{\mathrm{J}}(\theta )=1$.

We calculated $p_{\star }(\theta )$ numerically in two ways. After discretizing both $\theta$ and $x$, we can use the Blahut–Arimoto (BA) algorithm (37, 38). This converges to the global maximum, which is a discrete distribution (Fig. 2). Alternatively, using our knowledge that $p_{\star }(\theta )$ is discrete, we can instead adjust the positions ${\theta }_a$ and weights ${\lambda }_a$ of a finite number of atoms. See Algorithms for more details.

To see analytically why discreteness arises, we write the MI as

$$\begin{array}{l}\mathrm{MI}=I(X;\mathrm{\Theta })=\int d\theta \hspace{0.17em}p(\theta )f_{\mathrm{KL}}(\theta ),\\ f_{\mathrm{KL}}(\theta )=D_{\mathrm{KL}}[p(x|\theta )\parallel p(x)]=\int dx\hspace{0.17em}p(x|\theta )\log \frac{p(x|\theta )}{p(x)},\end{array}$$ [3]

where $D_{\mathrm{KL}}$ is the Kullback–Leibler divergence.^¶ Maximizing MI over all functions $p(\theta )$ with $\int d\theta \hspace{0.17em}p(\theta )$ = 1 gives $f_{\mathrm{KL}}(\theta )$ = const. But the maximizing function will not, in general, obey $p(\theta )\ge 0$. Subject to this inequality $p_{\star }(\theta )$ must satisfy

$$\{p_{\star }(\theta )>0,f_{\mathrm{KL}}(\theta )=\mathrm{MI}\}\hspace{0.17em}\text{or}\hspace{0.17em}\{p_{\star }(\theta )=0,f_{\mathrm{KL}}(\theta )<\mathrm{MI}\}$$

at every $\theta$. With finite data $f_{\mathrm{KL}}(\theta )-\mathrm{MI}$ must be an analytic function of $\theta$ and therefore must be smooth with a finite number of zeros, corresponding to the atoms of $p_{\star }(\theta )$ (Fig. 1). See refs. 28, 29, and 46 for related arguments for discreteness and refs. 41–43 for other approaches.

The number of atoms occurring in $p_{\star }(\theta )$ increases as the data improve. For $K$ atoms there is an absolute bound $\mathrm{MI}\le \log K$, saturated if they are perfectly distinguishable. In Fig. 3C we observe that the optimal priors instead approach a line $\mathrm{MI}\to \zeta \log K$, with slope $\zeta \approx 0.75$. At large $L$ the length of parameter space is proportional to the number of distinguishable points, and hence $\mathrm{MI}\to \log L$. Together these imply $K\sim L^{1/\zeta }$, and so the average number density of atoms grows as

$${\rho }_0=K/L\sim L^{1/\zeta -1}\approx L^{1/3},\hspace{1em}L\gg 1.$$ [4]

Thus, the proper spacing between atoms shrinks to zero in the limit of infinite data; i.e., neighboring atoms cease to be distinguishable.

To derive this scaling law analytically, in a related paper (51) we consider a field theory for the number density of atoms, in which the entropy density (omitting numerical factors) is $\mathcal{S}=\text{const.}-e^{-{\rho }^2}[{\rho }^4{(\rho \prime )}^2+1]$. From this we find $\zeta =3/4$, which is consistent with both examples presented above.

Multiparameter Example

In the examples above, $p_{\star }(\theta )$ concentrates weight on the edges of its allowed domain when data are scarce (i.e., when $m$ is small or $\sigma$ is large, and hence $L$ is small). We next turn to a multiparameter model in which some parameter combinations are ill-constrained and where edges correspond to reduced models.

The physical picture is that we wish to determine the composition of an unknown radioactive source, from data of $x_t$ Geiger counter clicks at some times $t$. As parameters we have the quantities $A_{\mu }$ and decay constants $k_{\mu }$ of isotopes $\mu$. The probability of observing $x_t$ should be a Poisson distribution (of mean $y_t$) at each time, but we approximate these by Gaussians of fixed $\sigma$ to write^#

$$p(\overrightarrow{x}|\overrightarrow{y})\propto \prod _t{e}^{-{(x_t-y_t)}^2/2{\sigma }^2},\hspace{1em}{y}_t=\sum _{\mu }{A}_{\mu }{e}^{-k_{\mu }t}.$$ [5]

We can see the essential behavior with just two isotopes in fixed quantities: $A_{\mu }=\frac{1}{2}$, and thus $y_t=\frac{1}{2}(e^{-k_{1}t}+e^{-k_{2}t})$. Measuring at only two times $t_1$ and $t_2$, we almost have a 2D version of Eq. 2, in which the center of the distribution $\overrightarrow{y}=(y_1,y_2)$ plays the role of $\theta$ above. The mapping between $\overrightarrow{k}$ and $\overrightarrow{y}$ is shown in Fig. 4A, fixing $t_2/t_1=e$. The FIM is proportional to the ordinary Euclidean metric for $\overrightarrow{y}$, but not for $\overrightarrow{k}$:

$$g_{\mu \nu }(\overrightarrow{k})=\frac{1}{{\sigma }^2}\sum _t\frac{\partial y_t}{\partial k_{\mu }}\frac{\partial y_t}{\partial k_{\nu }}\hspace{1em}⟺\hspace{1em}{g}_{st}(\overrightarrow{y})=\frac{1}{{\sigma }^2}{\delta }_{st}.$$ [6]

Thus, the Jeffreys prior is a constant on the allowed region of the $\overrightarrow{y}$ plane.

Then we proceed to find the optimum $p_{\star }(\overrightarrow{y})$ for this model, shown in Fig. 4B for various values of $\sigma$. When $\sigma$ is large, this has delta functions only in two of the corners, allowing only $k_1,k_2=0$ and $k_1,k_2=\mathrm{\infty }$. As $\sigma$ is decreased, new atoms appear first along the lower boundary (corresponding to the one-dimensional model where $k_1=k_2$) and then along the other boundaries. At sufficiently small $\sigma$, atoms start filling in the (2D) interior.

To show this progression in Fig. 4C, we define ${\mathrm{\Omega }}_r$ as the total weight on all edges of dimension $r$ and an effective dimensionality $d_{\mathrm{eff}}={\sum }_{r=1}^{D}r{\mathrm{\Omega }}_r$. This increases smoothly from 0 toward $D=2$ as the data improve.

At medium values of $\sigma$, the prior $p_{\star }(\overrightarrow{y})$ almost ignores the width of the parameter manifold and cares mostly about its length ($L_{+}=\sqrt{2}/\sigma$ along the diagonal). This behavior is very different from that of the Jeffreys prior: In Fig. 5B we demonstrate this by plotting the distributions of data implied by these two priors. Jeffreys puts almost no weight near the ends of the long (i.e., stiff or relevant) parameter’s range because the (sloppy or irrelevant) width happens to be even narrower there than in the middle. By contrast, our effective model puts significant weight on each end, much like the one-parameter model in Fig. 5A.

The difference between one and two parameters being relevant (in Fig. 4B) is very roughly $\sigma =1/7$ to $\sigma =1/50$, a factor 7 in Fisher length and thus a factor 50 in the number of repetitions $m$—perhaps the difference between a week’s data and a year’s. These numbers are artificially small to demonstrate the appearance of models away from the boundary: More realistic models often have manifold lengths spread over many orders of magnitude (5, 8) and thus have some parameters inaccessible even with centuries of data. To measure these we need a qualitatively different experiment, justifying a different effective theory.

The one-dimensional model along the lower edge of Fig. 4A is the effective theory with equal decay constants. This remains true if we allow more parameters $k_3,k_4,\mathrm{\dots }$ in Eq. 5, and $p_{\star }(\overrightarrow{y})$ will still place a similar weight there.^‖ Measuring $x_t$ also at later times $t_3,t_4,\mathrm{\dots }$ will add more thin directions to the manifold (7), but the one-dimensional boundary corresponding to equal decay constants will still have significant weight. The fact that such edges give human-readable simpler models (unlike arbitrary submanifolds) was the original motivation for preferring them in ref. 22, and it is very interesting that our optimization procedure has the same preference.**

Discussion

While the three examples we have studied here are very simple, they demonstrate a principled way of selecting optimal effective theories, especially in high-dimensional settings. Following ref. 45, we may call this rational ignorance.

The prior $p_{\star }(\theta )$ which encodes this selection is the maximally uninformative prior, in the sense of leaving maximum headroom for learning from data. But its construction depends on the likelihood function $p(x|\theta )$, and thus it contains knowledge about the experiment through which we are probing nature. The Jeffreys prior $p_{\mathrm{J}}(\theta )$ also depends on the experiment, but more weakly: It is independent of the number of repetitions $m$, precisely because it is the limit $m\to \mathrm{\infty }$ of the optimal prior (32, 33).

Under either of these prescriptions, performing a second experiment may necessitate a change in the prior, leading to a change in the posterior not described by Bayes’ theorem. If the second experiment is different from the first one, then changing to the Jeffreys prior for the combined experiment (and then applying Bayes’ rule just once) will have this effect (55, 56).^†† Our prescription differs from that of Jeffreys in also regarding more repetitions of an identical experiment as being different. Many experiments would have much higher resolution if they could be repeated for all eternity. The fact that they cannot is an important limit on the accuracy of our knowledge, and our proposal treats this limitation on the same footing as the rest of the specification of the experiment.

Keeping $m$ finite is where we differ from earlier work on prior selection. Bernardo’s reference prior (31) maximizes the same MI, but always in the $m\to \mathrm{\infty }$ limit where it gives a smooth analytically tractable function. Using $I(X;\mathrm{\Theta })$ to quantify what can be learned from an experiment goes back to Lindley (24). That finite information implies a discrete distribution was known at least since refs. 26 and 27. What has been overlooked is that this discreteness is useful for avoiding a problem with the Jeffreys prior on the hyperribbon parameter spaces generic in science (5): Because it weights the irrelevant parameter volume, the Jeffreys prior has strong dependence on microscopic effects invisible to experiment. The limit $m\to \mathrm{\infty }$ has erased the divide between relevant and irrelevant parameters, by throwing away the natural length scale on the parameter manifold. By contrast, $p_{\star }(\theta )$ retains discreteness at roughly this scale, allowing it to ignore irrelevant directions. Along a relevant parameter direction this discreteness is no worse than rounding $\theta$ to as many digits as we can hope to measure, and we showed that in fact the spacing of atoms decreases faster than our accuracy improves.

Model selection is more often studied not as part of prior selection, but at the stage of fitting the parameters to data. From noisy data, one is tempted to fit a model which is more complicated than reality; avoiding such overfitting improves predictions. The Akaike information criterion (AIC), Bayesian information criterion (BIC) (15, 61), and related criteria (19, 20, 62–64) are subleading terms of various measures in the $m\to \mathrm{\infty }$ limit, in which all (nonsingular) parameters of the true model can be accurately measured. Techniques like minimum description length (MDL), normalized maximum likelihood (NML), and cross-validation (62, 65, 66) need not take this limit, but all are applied after seeing the data. They favor minimally flexible models close to the data seen, while our procedure favors one answer which can distinguish as many different outcomes as possible. It is curious that both approaches can point toward simplicity. We explore this contrast in more detail in Model Selection from Data.^‡‡

Being discrete, the prior $p_{\star }(\theta )$ is very likely to exclude the true value of the parameter, if such a ${\theta }_{\mathrm{true}}\in \mathrm{\Theta }$ exists. This is not a flaw: The spirit of effective theory is to focus on what is relevant for describing the data, deliberately ignoring microscopic effects which we know to exist (67). Thus, the same effective theory can emerge from different microscopic physics [as in the universality of critical points describing phase transitions (68)]. The relevant degrees of freedom are often quasiparticles [such as the Cooper pairs of superconductivity (69)] which do not exist in the microscopic theory, but give a natural and simple description at the scale being observed. We argued here for such simplicity not on the grounds of the difficulty of simulating ${10}^{23}$ electrons or of human limitations, but based on the natural measure of information learned.

There is similar simplicity to be found outside of physics. For example, the Michaelis–Menten law for enzyme kinetics (70) is derived as a limit in which only the ratios of some reaction rates matter and is useful regardless of the underlying system. In more complicated systems which we cannot solve by hand and, for which the symmetries and scaling arguments used in physics cannot be applied, we hope that our information approach may be useful for identifying the appropriately detailed theory.