Coral reef structural complexity provides important coastal protection from waves under rising sea levels

If coral reefs continue to degrade, waves on coastlines may substantially increase, leading to greater coastal erosion.

Abstract

Coral reefs are diverse ecosystems that support millions of people worldwide by providing coastal protection from waves. Climate change and human impacts are leading to degraded coral reefs and to rising sea levels, posing concerns for the protection of tropical coastal regions in the near future. We use a wave dissipation model calibrated with empirical wave data to calculate the future increase of back-reef wave height. We show that, in the near future, the structural complexity of coral reefs is more important than sea-level rise in determining the coastal protection provided by coral reefs from average waves. We also show that a significant increase in average wave heights could occur at present sea level if there is sustained degradation of benthic structural complexity. Our results highlight that maintaining the structural complexity of coral reefs is key to ensure coastal protection on tropical coastlines in the future.

INTRODUCTION

Coral reefs are an effective natural barrier from waves (1, 2), which has allowed human populations to settle on tropical coasts and reef islands (3). The predicted future increase of sea level is often seen as the most crucial threat to these low-lying areas (4). However, the interaction between higher sea levels and wave climate on coral reef flats is likely to be an important mechanism governing coastal inundation and erosion on tropical coastlines in the future (5, 6). The three-dimensional structure of live coral communities on coral reefs (hereafter structural complexity) plays a crucial role in dissipating wave energy and protecting tropical coastlines (2, 7). The high structural complexity of coral reefs results in high hydraulic roughness and greater frictional dissipation of waves when compared to other coastal settings (8). The high frictional dissipation on coral reefs, in conjunction with wave breaking on the reef rim, results in high rates of wave energy dissipation over relatively short distances when compared to other coastal systems (1, 2, 7, 9). The coastal protection service provided by coral reefs is therefore greater than many other marine ecosystems (3). However, there is now an increasing concern regarding the capacity of degraded and stressed coral reefs to maintain coastal protection from waves at present and under rising sea levels (3, 6, 10–14). The observed widespread loss of reef-building corals will affect the efficiency of coral reefs in dissipating wave energy (6) and growing vertically in response to rising sea levels (15–17). A significant loss of living corals leads to a reduction in structural complexity of coral reefs (18, 19) and frictional dissipation of waves (6, 20). Lower frictional dissipation results in larger wave heights in back-reef environments and erosion of the near-shore zones of tropical reef islands and beaches (6, 21). Furthermore, if vertical reef accretion is unable to keep pace with the predicted rate of sea-level rise, then the reduction in breaker dissipation of the reef crest will also allow larger waves to propagate into back-reef environments (5, 21).

Here, we investigate the future ability of coral reefs at Moorea and Tahiti, French Polynesia, to protect coastal zones from average wave conditions under scenarios of changing coral reef structural complexity and sea-level rise. We use a one-dimensional wave dissipation model (22) calibrated from surf zone field data to examine the dissipation of waves by coral reefs (see Materials and Methods and the Supplementary Materials). Coastal protection in this study therefore refers to change in average back-reef wave conditions, which is a common approach taken in previous research (3, 20, 23). Three coral reef sites in Moorea (Tiahura, Ha’apiti, and Temae) and one in Tahiti (Teahupo’o) were selected for this study, each with different average wave exposure (from low to high energy; see Materials and Methods). The coral reefs in Moorea are also the focus of long-term ecological and oceanographic monitoring and have previously shown an ability to recover live coral cover in response to environmental disturbances such as bleaching and cyclones (see Materials and Methods). The response of coral reefs in Tahiti to sea-level rise is also well studied, with numerous geological reef cores showing likely growth rates under different reef flat water depths (24). We use these data to inform future reef growth and structural complexity scenarios in the Monte Carlo wave dissipation simulations (see Materials and Methods).

The three main inputs to the model simulations were sea level (in meters), reef response in terms of vertical reef accretion or erosion (RR; in meters), and the structural complexity of coral assemblages [f_w (-)] (Fig. 1 and Materials and Methods). f_w was calibrated for each reef site and was site-specific to each reef for the subsequent Monte Carlo simulations. A Reef Health Index (RHI) was defined as the sum of RR and f_w and measures the capacity of coral reefs to accrete vertically and maintain structural complexity (Fig. 1). Monte Carlo simulations of 10,000 individual model runs were conducted for six scenarios (a total of 240,000 individual model runs were conducted) of changing RHI and sea level at each reef site (low to high energy; see Materials and Methods and the Supplementary Materials). We report three primary results here (P1 to P3) and the three supplementary scenarios (S1 to S3) in the Supplementary Materials (fig. S2). Our primary scenarios simulated wave dissipation under the following conditions:

Fig. 1. Conceptual diagram showing the future scenarios of coral reef structural complexity and vertical reef accretion.

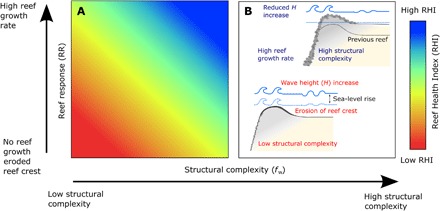
The RHI measures the capacity of a coral reef to accrete vertically and maintain structurally complex coral communities, with red indicating a low RHI and blue indicating a high RHI.

(1) P1 models wave dissipation on a degraded reef at present sea level that has a persistent state of low structural complexity [for example, coral reef flattening (19)]. P1 is a degraded coral reef scenario.

(2) P2 models wave dissipation on a degraded coral reef of scenario P1 under higher–sea level conditions (mean, 0.48 m), from the Intergovernmental Panel on Climate Change (IPCC) Representative Concentration Pathway (RCP) 4.5 emission scenario (25). P2 is the worst-case scenario.

(3) P3 is the full model simulation of wave dissipation using the complete ranges of predicted sea level by 2100 and the potential changes in structural complexity and vertical reef accretion or erosion. For our simulations, P3 represents the most likely range of wave conditions in the future.

To compare our modeling under different scenarios and between reef sites, we standardized our results by calculating the increase in back-reef wave height as a nondimensional scaling factor, referred to as H(-). H(-) is defined as the future root mean square wave height (H_rms) divided by the H_rms at present-day sea level and coral reef structural complexity. For example, an H(-) of 2 indicates back-reef wave heights that are twice as large as those at present, whereas an H(-) = 1 indicates that there will be no increase in back-reef wave height from present conditions. This metric is indicative of the likely increase in wave height and, therefore, erosion potential under average conditions. The average probability of wave height increase in the back-reef, for scenarios P1 to P3, is shown in Fig. 2. The coastal protection service provided by structurally complex live coral communities is further shown in Fig. 2 as the difference between present conditions and P1 for present sea levels, as well as P2 and P3 for forecasted higher sea levels. To examine the likely increase of sediment transport and coastal erosion under different scenarios, the change in H_rms² was also assessed. H_rms² is proportional to the potential sediment entrainment from waves and is therefore often used as a proxy for sediment transport in coastal systems (26–28). It is used here to examine the change in erosion and sediment transport potential of each scenario compared to present conditions.

Fig. 2. Changes in back-reef wave height for three scenarios.

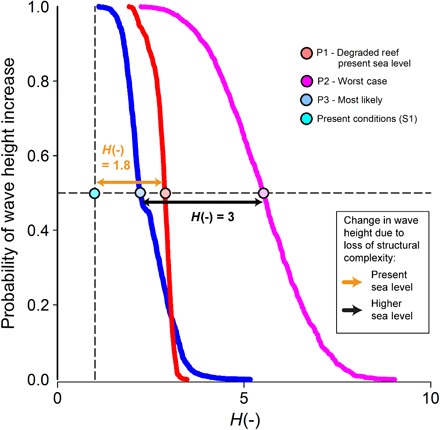
P1, coral reef degradation at present sea level; P2, the worst-case scenario by 2100; and P3, the most likely scenario by 2100. The circle markers show the mean result for each scenario. The mean of the present wave conditions (scenario S1 in the Supplementary Materials) is also shown as the cyan marker. The wave dissipation [in terms of H(-)] provided by coral reef structural complexity (f_w) is shown by the orange arrowed line (present sea level) and black arrowed line (higher sea levels). The vertical dashed line represents present wave conditions where H(-) = 1, and the horizontal dashed line is the 50% probability line (P = 0.5).

RESULTS

Under the most likely scenario (P3), we found that the average back-reef wave heights across all sites were 2.4 times greater than those under present conditions [H(-) = 2.4; Fig. 2]. These results were similar to the changes in average H_rms² under the P3 scenario where H_rms² = 0.04, which was 2.6 times greater than that under present conditions (scenario S1, H_rms² = 0.015; Fig. 3). The increase in average back-reef wave heights in the P3 scenarios was primarily influenced by changes to the RHI score (R² = 0.53) rather than changes in sea level (R² = 0.09) (Fig. 4). Change in f_w was the main component of the RHI that governed the change in H(-) (R² = 0.44). Wave height increase due to the loss of structural complexity was greatest on the lower-energy coral reefs (Tiahura and Temae, Moorea) with initially high structural complexity (fig. S2). These reefs were reliant on greater bed frictional dissipation, due to their high structural complexity, to maintain present back-reef wave conditions. High-energy reef environments (Ha’apiti, Moorea and Teahupo’o, Tahiti), with lower structural complexity, had a greater reliance on wave breaking to dissipate waves and were therefore more susceptible to slow rates of vertical reef accretion but were still mostly influenced by a reduction in structural complexity for the P3 scenario (fig. S2). Although there was some variation in the dominant controls on the future ability to dissipate waves for each reef site, on average, the degradation of structurally diverse coral communities leading to persistently low values of f_w (scenario P1) resulted in larger waves [H(-) = 2.8] than those predicted under the most likely scenario that included a rise of sea level (scenario P3). This indicates that frictional dissipation of wave energy by structurally complex corals had a greater effect on average back-reef wave heights than sea-level rise. There was a similar increase in the likely sediment transport for P1 where H_rms² = 0.043, which was 2.9 times larger than that under present conditions (Fig. 3).

Fig. 3. Box plots and distribution of H_rms² for the three scenarios.

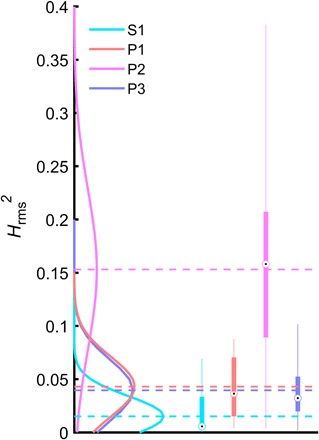
P1, coral reef degradation at present sea level; P2, the worst-case scenario by 2100; P3, the most likely scenario by 2100; and S1, the coral reef under present conditions. Boxes show the interquartile range (IQR, 25th and 75th percentiles) of the H_rms² values. Whiskers represent the distance of 1.5 IQR from the 25th and 75th percentiles, and circle markers show the median values. Dashed lines show the mean H_rms² values of which correspond with the peak of the wave height distributions shown as solid lines. Wave height distributions were calculated probability density functions in MATLAB.

Fig. 4. Controls on future back-reef wave heights in coral reefs for scenario P3.

The influence of sea-level rise (SLR), RR, structural complexity (f_w), and RHI on wave height is shown for 40,000 model runs. (A) Scatterplot showing the influence of sea-level rise on normalized back-reef wave height (H_n, subscript n indicating normalized values between 0 and 1), with marker colors indicating the normalized values of structural complexity (fw_n) for the model run, with blue indicating high fw_n and red indicating low fw_n. The dashed trend line is the linear regression result where H_n = 0.81SLR − 0.06 (R² = 0.09). (B) Strong relationship between RHI and back-reef wave height with the dashed black line showing the fitted curve H_n = −0.66RHI_n + 0.66 (R² = 0.53). The dashed red line is the 1:−1 ratio shown for comparison. (C) Distribution of H_n due to changes in f_w and RR.

The addition of predicted sea-level rise by 2100 to the degraded-reef scenario (scenario P2, the worst-case scenario) led to a substantial increase in wave height when compared to present conditions with H(-) = 5.5. The increase in H_rms² was much larger for P2, where H_rms² = 0.15 or 10.15 times greater than that under present conditions. Structurally complex coral communities were determined to reduce wave heights by almost half under present sea levels and by three times under higher sea levels by 2100, suggesting a greater protection service from average wave conditions provided by structural complex coral communities in the future.

DISCUSSION

Our results show that wave heights in back-reef environments will increase in the future at the four reef sites in French Polynesia. We calculate that, by 2100, average wave heights and sediment transport potential will most likely be over twice as large as those under present conditions (scenario P3; Figs. 2 and 4). This is likely to be similar in other reef sites worldwide; however, the specific increase in H(-) and H_rms² will depend on local rates of sea-level rise, vertical accretion of coral reef flats, and variation in benthic structural complexity. The primary control on future wave energy dissipation was not sea level but the structural complexity of coral communities (Fig. 4). This suggests that successfully maintaining structurally complex coral communities can mitigate some of the erosion risks in the future as a result of higher sea levels (Figs. 2 and 4). Maintaining the structural complexity of corals under higher sea level in the future reduced back-reef wave heights by three times (Fig. 2). This suggests that coral reefs may have some control over future energy regimes in the back-reef environment but require healthy coral communities that can recover their structural complexity after environmental disturbances, such as cyclones or severe coral bleaching (17). The coral reefs of Tahiti and Moorea have shown remarkable recovery of live coral cover from environmental disturbances (29) and also have some of the fastest vertical reef accretion rates under rising sea levels (24). However, it is also likely that these coral reefs will degrade in the future on the basis of current global trends of reduced reef-building coral cover and predictions of continued coral reef degradation in the 21st century (13, 30, 31). Our results indicate that the combination of reef degradation and sea-level rise may result in average back-reef wave heights at Moorea and Tahiti that are over five times larger by 2100 and potential sediment transport (based on H_rms² values) that is 10 times larger when compared to that under present conditions. There are also likely to be important additional threats to coastal erosion and inundation that are not examined here. Although we show that structural complexity is a dominant driver of future back-reef wave heights on average, it does not reduce the importance of the increased risk from high-energy events, such as cyclones and storm surges, due to higher sea levels (5).

However, the increased risk of coastal erosion is not solely reserved for a future of higher sea levels. The degradation of structurally complex live coral communities at present sea level (scenario P1) resulted in modeled back-reef wave heights that are greater than those predicted under higher sea levels by 2100 (scenario P3) (Fig. 2). Substantial coastal erosion could therefore occur under present sea levels (32, 33) and is in agreement with observations of coastal change after the severe bleaching of corals in 1998 (20). The coastal protection value of structurally complex coral communities is therefore immense, but potentially overlooked (3), and is a critically important service provided to the tropical coastal regions both at present and in the future.

Our results are focused on the reefs of Tahiti and Moorea but are relevant for coral reefs globally because sea-level rise and reduced coral cover are likely to affect coral reefs worldwide. The results present potential divergent futures for tropical coastlines that are highly dependent on structurally complex and healthy coral reefs. The increase in average wave height due to higher sea levels could either (i) occur in the near future due to rapid coral reef degradation that leads to persistent states of low structural complexity or (ii) be partially mitigated by maintaining coral reef structural complexity throughout the 21st century. However, an increase in average back-reef wave heights is a likely outcome in the future regardless of the health status and structural complexity of coral reef communities and should therefore be a focus of future management of tropical shorelines. These results further support the calls for reducing the global and local stressors on coral reefs through the curbing of greenhouse emissions and successful local management. The combination of these actions will help maintain some of the natural protection of tropical coastlines in the future.

MATERIALS AND METHODS

Wave conditions were measured on the fore-reef slopes and reef flats of four coral reef sites in French Polynesia, three in Moorea (Tiahura, Ha’apiti, and Temae) and one in Tahiti (Teahupo’o) (see Supplementary Materials). The four sampling locations were selected to provide low- to high-energy sites for analysis based on exposure from the dominant swell direction. Tiahura is a low-energy site, Temae is an intermediate-energy site, and Ha’apiti and Teahupo’o are high-energy sites.

Pressure records were measured in cross-reef transects from the fore-reef slope to the reef flat using INW PT2X Aquistar and DHI SensorONE pressure transducers (PTs) both logging at 4 Hz. Pressure records were corrected for pressure attenuation with depth (34) and split into 15-min ensembles (35). Wave statistics were then calculated from the 15-min pressure records on a wave-by-wave basis using zero down-crossing analysis (36). Significant wave height (H_s) and H_rms, as well as wave period (T), were calculated from the wave record for each 15-min run. The wave statistics recorded by the PTs were used to calibrate the wave dissipation model. The waves measured during this period were similar to the mean of the long-term wave records at Moorea and Tahiti and representative of common winter southwest swell conditions (figs. S8 and S9). However, large swell and storm events were not recorded and were therefore not included in the analysis.

The wave dissipation model

A one-dimensional morphodynamic model (XBeach; https://oss.deltares.nl/web/xbeach/) was used to model future wave climates across reef flats (22). XBeach is a depth-averaged model that solves coupled cross-shore and alongshore equations for wave propagation, flow, sediment transport, and bed level changes. XBeach was chosen because it was used extensively in coral reef and coastal studies (37–39). The main free parameters of the XBeach stationary wave dissipation model, the breaker criterion (γ_b) and the wave friction factor (f_w), were calibrated using the wave records recorded by the PTs (Table 1). The wave friction factor has been directly linked to the cover of living corals and the structural complexity of coral reefs (2, 9, 40). Therefore, we used the wave friction factor as a proxy for changes in live coral cover and structural complexity based on similar strategies from previous publications (2, 6, 21, 41, 42). The breaker index was set between 0.9 and 1, which were similar to values found previously for coral reefs using stationary breaker dissipation models (43). This is also supported by the field data that show that wave height–to–water depth ratios can be high on the fore-reef slope (see Supplementary Materials). The model predictions were shown to be accurate with strong correlations and low RMSEs between measured and modeled reef flat and back-reef wave heights (Table 1).

Table 1. Calibrated free parameters $(\overline{{\mathit{f}}_{\mathrm{w}}} \text{and} {\mathrm{\gamma }}_{\mathrm{b}})$ in the wave dissipation model for each reef type (low to high energy).

The mean wave friction factor ($\overline{{\mathit{f}}_{\mathrm{w}}}$) and breaker criterion inputs for XBeach are shown. The root mean square error (RMSE) and the R² correlation derived from linear regression between the modeled and measured reef flat and back-reef wave heights are also shown.

Coral reef (energy)	$\overline{{\mathit{f}}_{\mathbf{w}}}$	γb	R2	RMSE
Tiahura (low)	0.3	0.9	0.98	0.006
Temae (intermediate)	0.24	1	0.88	0.02
Ha’apiti (high)	0.11	0.9	0.94	0.02
Teahupo’o (high)	0.03	1	0.92	0.028

The calibrated XBeach model was used to run Monte Carlo simulations under different scenarios relating to future climate and coral reef states based on regional estimates of sea-level rise by 2100 (25), reef growth in response to higher sea levels (15, 16, 24), and changes in live coral cover and structural complexity (6, 7). The wave boundary conditions (H_s and T) used in the model were based on average values recorded from a Sea-Bird SBE6+ wave and tide recorder operated by Centre de Recherches Insulaires et Observatoire de l’Environnement (CRIOBE) (Tiahura, 2012–2013), two acoustic Doppler current profilers (Ha’apiti and Temae, 2003–2015) operated by Moorea Long-Term Ecological Research (LTER) (44) and a regional-scale wave hindcast model for the last 35 years (Teahupo’o, 1979–2014) (45).

Model inputs

Wave dissipation across low- to high-energy coral reefs was examined under numerous scenarios depending on coral reef structural complexity, vertical growth, or potential erosion, and the likely sea-level rise for French Polynesia in the 21st century. Monte Carlo simulations were conducted with 10,000 random samples for each model run, under five different scenarios, resulting in a total of 240,000 individual runs (6 × 10,000 at each site). The description of the model inputs below mostly focused on the justification of the maximum and minimum values used within the Monte Carlo simulations. The values between these ranges were normally distributed. Therefore, the maximum and minimum values only occurred in very rare circumstances (<1% of all model runs), with most of the model runs occurring at the mean between the two extrema.

Sea-level rise

To take into account the spatially variable nature of sea-level predictions, in our wave simulations, we used IPCC AR5 relative sea-level predictions for Moorea and Tahiti (and related uncertainties) under the RCP4.5 emission scenario, which foresaw an average global temperature rise of 1.8°C for 2081–2100 (25). We also used the RCP8.5 emission scenario to simulate wave conditions where sea levels exceeded the RCP4.5 range of predictions. The corresponding RCP4.5 and RCP8.5 sea-level rise scenarios modeled in the IPCC AR5 are presented in fig. S4. The predicted sea-level rise under the RCP4.5 emission scenarios for the period 2081–2100 was equal to the global average of 0.48 m, with the likely range of 0.63 to 0.32 m, respectively (66% confidence interval or 1σ). The predicted sea-level rise under the RCP8.5 scenarios for the same period was an average of 0.62 m, with the likely range of 0.45 to 0.82 m, respectively. For our model, we used a random sample set from a normal distribution of future sea-level scenarios generated from the mean and likely range (1σ) of the RCP4.5 and RCP8.5 sea-level predictions.

Coral reef structural complexity and hydrodynamic roughness

The observed loss of wave height during propagation across the reef flats that was not accounted for by breaker dissipation was attributed to frictional dissipation (D_f)

$${\mathit{D}}_{\mathrm{f}}=\frac{2}{3\mathrm{\pi }}\mathrm{\rho }{\mathit{f}}_{\mathrm{w}}{(\mathit{A}\mathrm{\omega })}^3$$ (1)

where A is the near bed wave orbital amplitude, ω is the radian frequency, and ρ is the density of salt water. From the observed bed frictional dissipation of wave height, the present f_w value for each reef could be determined. The mean f_w for each site ($\overline{{\mathit{f}}_{\mathrm{w}}}$) is shown in Table 1. The f_w values used in the model simulations were based on scenarios of changing structural complexity. This was based on observations of significant changes in benthic structure of coral reefs in Moorea. The three coral sites on Moorea underwent cycles of loss and gain of live coral cover since the beginning of systemic observations in 1979 at Tiahura (46–48), which was linked, albeit anecdotally, to changes in structural complexity (48). The specific measurement of benthic structural complexity was not conducted, but the links between greater percentage coral cover and higher structural complexity scores are well established (19, 49). We therefore considered the fluctuation of structural complexity a natural background condition on the coral reefs of Moorea and Tahiti. To assess the wave conditions of coral reef that were in a persistent state of degradation and low structural complexity, we used a minimum of f_w = 0.01. This value represented a smooth reef with low coral cover and structural complexity (50) and was lower than the observed values on coral reefs with live coral cover (2, 7, 9, 51) and at Teahupo’o in this study (f_w = 0.03) but greater than siliciclastic settings where f_w ≈ 0.001 (52). The maximum value of f_w was twice that of the present value ($2\overline{{\mathit{f}}_{\mathrm{w}}}$) for each reef site and represented an increase in structural complexity measured at present (that is, from the time of survey in August 2015). We assumed that f_w could be larger than that at present because Moorea and Tahiti were in recovery from major cyclone and crown-of-thorns events at the time of surveying and previously had greater levels of live coral cover (46, 48). The direct relationship between live coral cover and structural complexity in other reef sites suggested that the coral reefs at Moorea and Tahiti were likely to have displayed much higher structural complexity in the past (46, 48, 49). The maximum f_w values used for this study were well within the range of observations of previously research (2, 6, 7, 9, 51). We note that the current modeling did not assess the likely lag times between an extreme event, such as mass coral bleaching or cyclones, and subsequent reduction in structural complexity but modeled the possible response of coral reefs that underwent sustained degradation over a significant period (for example, over decades) based on well-known examples in the Caribbean and Indian Ocean (17, 19, 20, 49, 53). In the degraded-reef scenario, this state has occurred in the near future where sea levels are still comparable to present. A scenario similar to this was previously observed at the Seychelles (20). The worst-case scenario assumed that a persistent state of low structural complexity was established at some point before 2100.

Coral reef vertical accretion and erosion

The rate of sea-level rise by 2100 at the Tahiti and Moorea sites was predicted to be 7.6 and 10.1 mm year⁻¹ by the IPCC under the upper most likely range in the RCP4.5 and 8.5 emission scenarios, respectively. The average rates of vertical coral reef growth found in cores at Tahiti for the last 5.5 Ka were approximately 0.04 to 1 mm year⁻¹ (54, 55), with an estimated rate of 2 mm year⁻¹ (16) during the Holocene for coral reefs and 4 mm year⁻¹ at most (56). We therefore considered that the best-case scenario was a reef accretion rate of 2 mm year⁻¹, or a total growth of 16.6 cm by 2100. However, increased stressors, such as increases in temperature, are likely to inhibit the vertical growth rates of coral reefs (13). In addition, the degradation of coral reefs, due to events like coral bleaching, may result in rapid reductions in reef crest height of up to 0.5 m (20, 53). Research in potential erosion rates of reef crests due to reduced carbonate production by stressed reefs found a loss of carbonate material equivalent to a 6 mm year⁻¹ erosion of the reef crest, which would result in about 0.5 m of erosion by 2100 (57). In addition, previous research also observed the erosion of reef crests by a similar height of the coral colonies that were lost after severe bleaching in 1998 (20). Therefore, the model inputs assumed that, at best, coral reefs would accrete at a rate of 2 mm year⁻¹ and, at worst, would incur a conservative estimate of reef crest erosion of up to 0.2 m, which was the approximate size of the dominant Pocillopora sp. colonies observed on the reef crests in August 2015.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/2/eaao4350/DC1

Description of model scenarios and results

Model inputs

Wave data collection

Model calibration

Offshore wave climate

fig. S1. Schematic representation of the inputs into the wave dissipation simulations for the six scenarios (P1 to P3 and S1 to S3) described in the main text.

fig. S2. Changes in back-reef wave height for different scenarios and energy regimes.

fig. S3. Locations of the cross-reef bathymetric profiles and of the wave measurements for the four reef sites in Moorea and Tahiti.

fig. S4. Global map of sea-level rise predictions by 2100 by the IPCC for the RCP4.5 and RCP8.5 scenarios.

fig. S5. Example of time-averaged and individual wave heights for Tiahura near breakpoint.

fig. S6. Comparison of the modeled and measured wave for each deployment location on the reef flats and lagoon of the four sites in Moorea and Tahiti.

fig. S7. Example time series for Ha’apiti, Moorea.

fig. S8. Summary of long-term offshore wave data (1979–2013) for Tahiti and Moorea from National Oceanic and Atmospheric Administration WAVEWATCH III (http://polar.ncep.noaa.gov/waves/index2.shtml) (150.05°W, 17.94°S).

fig. S9. Comparison of the measrured offshore significant wave height (H_so) used to calibrate the XBeach wave model (study period) and the long-term averages from CRIOBE and Moorea LTER (4) measurements (long-term) for each reef site.

table S1. Sources of bathymetric data sets for Moorea and Tahiti.

References (58, 59)