Scikit-ribo enables accurate estimation and robust modeling of translation dynamics at codon resolution

Summary

Ribosome profiling (Riboseq) is a powerful technique for measuring protein translation, however, sampling errors and biological biases are prevalent and poorly understand. Addressing these issues, we present Scikit-ribo (https://github.com/schatzlab/scikit-ribo), an open-source analysis package for accurate genome-wide A-site prediction and translation efficiency (TE) estimation from Riboseq and RNAseq data. Scikit-ribo accurately identifies A-site locations and reproduces codon elongation rates using several digestion protocols (r = 0.99). Next we show commonly used RPKM-derived TE estimation is prone to biases, especially for low-abundance genes. Scikit-ribo introduces a codon-level generalized linear model with ridge penalty that correctly estimates TE while accommodating variable codon elongation rates and mRNA secondary structure. This corrects the TE errors for over 2000 genes in S. cerevisiae, which we validate using mass spectrometry of protein abundances (r = 0.81) and allows us to determine the Kozak-like sequence directly from Riboseq. We conclude with an analysis of coverage requirements needed for robust codon-level analysis, and quantify the artifacts that can occur from cycloheximide treatment.

eTOC Description

New open-source statistical learning software package enables accurate analysis of translational efficiency from Riboseq and RNAseq data. Using it corrects the biases for thousands of genes in S. cerevisiae, which enables improved estimates of relative protein abundances and the discovery of the Kozak-like regulatory sequence in yeast from Riboseq data.

Introduction

First introduced by Ingolia et al in 2009(Ingolia et al., 2009), ribosome profiling (Riboseq) allows researchers to investigate genome-wide in vivo protein synthesis through deep sequencing of ribosome-protected mRNA footprints(Ingolia, 2014). Since the original introduction, several improved versions have been developed to mitigate biases(Gerashchenko and Gladyshev, 2014, 2017; Weinberg et al., 2016) and address new biological questions(Archer et al., 2016; Oh et al., 2011). After the protocol became standardized in 2012, there was a rapid increase in adoption(Ingolia et al., 2012), leading to discoveries of translational defects in different forms of cancer(Hsieh et al., 2012; Sendoel et al., 2017; Wurth et al., 2016), other important human diseases(Schafer et al., 2015), and the identification of novel drug targets(Su et al., 2015). Riboseq has also revealed new insights into many steps in the translation process itself(Brar and Weissman, 2015; Michel and Baranov, 2013).

Riboseq provides genome-wide insights into the regulation of gene expression at the level of translation. A key metric of measuring translational control is translational efficiency (TE), defined as the level of protein production per mRNA(Ingolia et al., 2009; Li, 2015). Assuming minimal ribosome fall-off, Li showed that TE effectively measures translation initiation efficiency (TIE) in the steady state(Li, 2015). Shah et al showed that TIE is the rate limiting factor for translation(Shah et al., 2013). In practice, this metric is calculated for a given gene as the ratio of the ribosome density from Riboseq to the mRNA abundance measured by RNAseq. We refer to this ratio as RPKM-derived TE (ribosome density per mRNA, Equation 1), because both values have RPKM units, reads per kilobase of transcript per million mapped reads (Equation 2). Although this metric is commonly used in the literature, it is not a direct measure of protein output but ribosome density, and the two are only correlated assuming the same elongation rate across genes(Li, 2015). However, this assumption does not hold in many cases, especially genes with extensive ribosome pausing(Mohammad et al., 2016; Quax et al., 2013; Radhakrishnan et al., 2016; Zhang et al., 2016).

Technical shortcomings in the Riboseq workflow can introduce bias and systematic error into the analysis. Ribosome footprints vary depending on the organism, nuclease, and cell lysis conditions, making it difficult to identify the ribosome position on the fragment and potentially yielding misleading results(Mohammad et al., 2016). Another source of the noise is ligation bias in cloning ribosome footprints and amplification by PCR(Lecanda et al., 2016). Finally, early protocols used antibiotics such as cycloheximide (CHX) to arrest translation prior to cell lysis but CHX treatment distorts ribosome profiles because initiation continues even though elongation is blocked(Gerashchenko and Gladyshev, 2014). This artifact leads to high levels of ribosome density at alternative initiation sites at the 5’-end of ORFs, and masks the local translational landscape (Hussmann et al., 2015). Weinberg et al produced excellent quality reference datasets and showed that RNAseq libraries are also subject to their own problems including isolating mRNA through interaction with the poly-A tail (Weinberg et al., 2016).

Addressing these problems analytically, it is first essential to correctly determine the location of the codon bound in the ribosomal A-site within the Riboseq reads. Decoding of the A-site codon by incoming aminoacyl-tRNAs is rate limiting during elongation(Michel and Baranov, 2013); low levels of specific aminoacyl-tRNA species lead to pausing as indicated by changes in the codon-specific elongation rate (ER). Precise determination of the A-site codon is needed to determine whether a given read belongs to the canonical open reading frame (ORF) of a gene, especially when genes are overlapping. RiboDeblur(Wang et al., 2016) models ribosome profiles as blurred position signals, but it is not suitable for downstream analysis. Most other studies followed the 15-nucleotide (nt) rule from Ingolia et al(Ingolia et al., 2009), based on the work of Wolin and Walter(Wolin and Walter, 1988); the A-site codon starts at 15 nt in 28mer reads produced by RNase I. Reads of other lengths are commonly excluded from consideration, significantly reducing the data available, and perhaps missing important signals that affect footprint size. Correct identification of the ribosome position is particularly problematic in bacteria(Hwang and Buskirk, 2017; Mohammad et al., 2016) and Arabidopsis(Hsu et al., 2016) where MNase generates a broad distribution of footprints(Hwang and Buskirk, 2017).

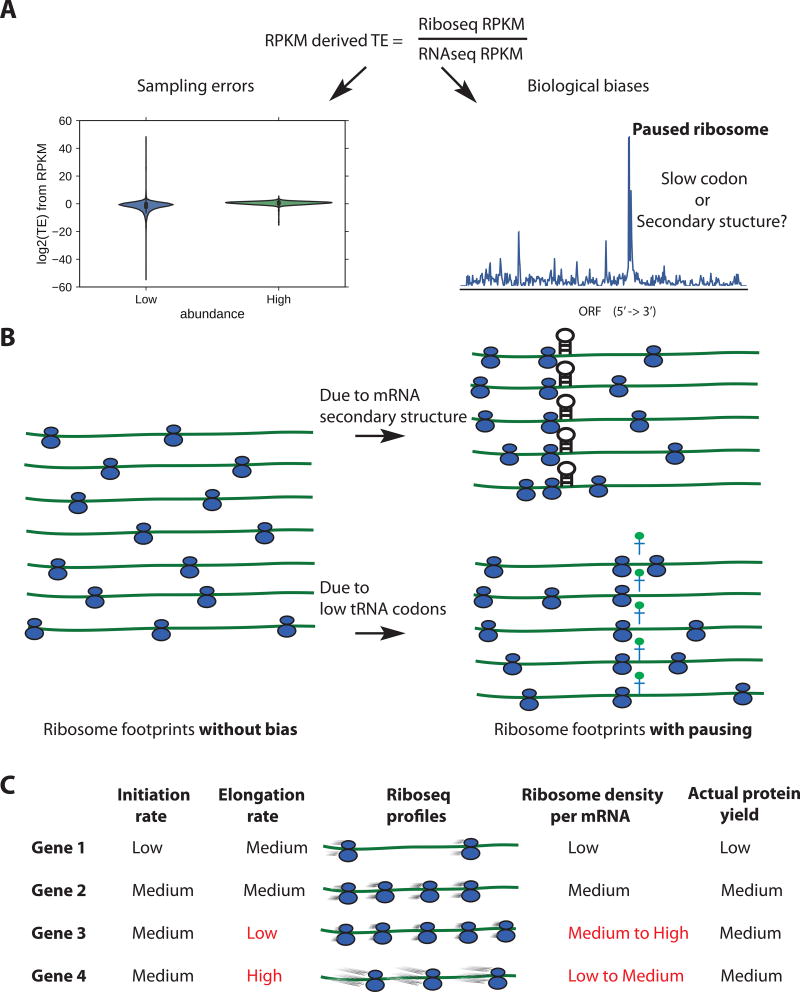
Secondly, in almost every published Riboseq study, the distributions of RPKM-derived log TE are severely skewed with a long tail on the negative side(Dunn et al., 2013; Gonzalez et al., 2014; Ingolia et al., 2009) (Figure S1A). This observation is also reported by Weinberg et al in their analysis of wild-type S. cerevisiae data from ten different labs(Weinberg et al., 2016). One of the main reasons for the skewed distribution is sampling error from low-abundance genes: the range of gene expression level spans 8 to 11 orders of magnitude, but a limited amount of sequencing coverage is available. As a result, the sampling of low-abundance transcripts is more error-prone (Figure 1A), yielding higher dispersion of RPKM among low-abundance genes, and subsequently even higher dispersion of RPKM-derived TE (Figure 1A). To address this problem in analyses of RNAseq data, fold change shrinkage methods (e.g. empirical Bayesian shrinkage) have been widely adapted in differential expression (DE) methods such as DEseq2(Love et al., 2014) and edgeR(Robinson et al., 2010). In order to perform shrinkage with between-sample normalization, these methods rely on at least three replicates, which are not typically available in Riboseq studies. Even where multiple replicates are available, it is not appropriate to use RNAseq DE methods to compute TE, because those methods were developed to estimate changes of gene expression under perturbation, while TE reflects the level of translation control under a single condition (Albert et al., 2014; Csardi et al., 2015).

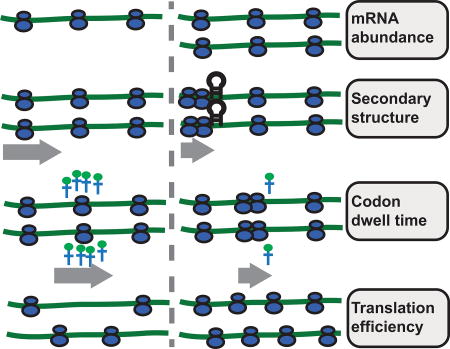
Figure 1. Sources of biases using ribosomes densities per mRNA (RPKM-derived TE) as a proxy for TE.

(A) Sampling biases towards low abundance genes (left), and biological biases due to paused ribosomes (right). (B) Idealized ribosome footprints distribution without biases (left), or with downstream mRNA secondary structure and low conjugate tRNA availability for the A-site codon (right). (C) Confounding effects of translation initiation and elongation on Riboseq profiles, figure adapted from Quax et al 2013. Initiation rate should be proportional to actual protein yield.

Finally, traditional techniques for mRNA quantification and DE testing rely on a strong assumption: random fragmentation and uniform sequencing of mRNA molecules. However, this assumption does not apply to Riboseq data given that the abundance of ribosome-protected fragments is strongly influenced by local translational elongation rates, causing peaks due to paused ribosomes (Figure 1B) (Schuller et al., 2017; Woolstenhulme et al., 2015; Zhang et al., 2016). Two major determinants of ribosome pausing are slow codons(Thanaraj and Argos, 1996) and downstream mRNA secondary structure(Doma and Parker, 2006) (Figure 1B), although their importance and relative contributions have been controversial (Chen et al., 2013; Gorochowski et al., 2015; Mohammad et al., 2016). The presence of paused ribosomes problematizes the use of ribosome density for calculating TE(Quax et al., 2015) (Figure 1C). Genes with paused ribosomes have more reads than expected, depleting coverage on other genes. Traditional read counting methods do not control for these biases (when using RPKM to derive TE).

Earlier attempts to more accurately model TE have significant restrictions and have seen limited application so far. Pop et al developed a queuing model for translation, but it failed to recover significant correlation between codon dwell time and cognate tRNA availability, and the source code is not available(Pop et al., 2014). Weinberg et al proposed a comprehensive model to estimate TE(Weinberg et al., 2016) in S. cerevisiae using the analytical approximations of initiation probability, but this required parameterizations from a whole-cell simulation from Shah et al(Shah et al., 2013), making it difficult to apply to other organisms. Duc and Song developed a simulation-based inference algorithm to estimate translation initiation and local elongation rates, but it could only be applied to ~900 (13%) genes in S. cerevisiae, because it requires extensive filtering (Dao Duc and Song, 2017). None of these methods addressed the prevalent sampling errors and biological biases in Riboseq data described above.

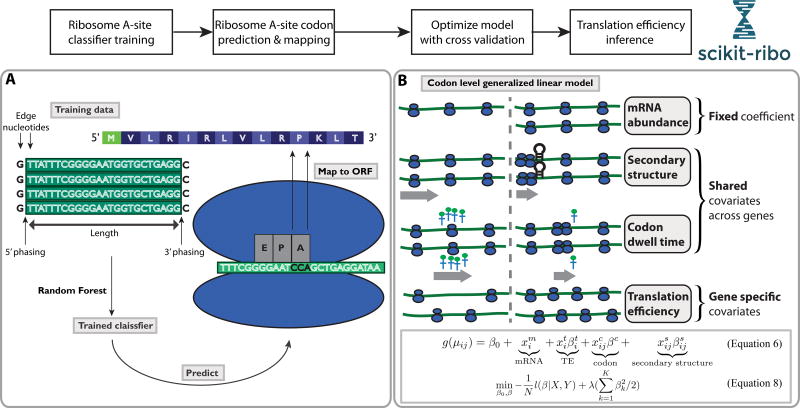
Here, we present Scikit-ribo (https://github.com/schatzlab/scikit-ribo), an open-source software package for accurate genome-wide TE inference from Riboseq data (Figure 2). Scikit-ribo is very fast; it can analyze more than 6000 genes from a high-coverage S. cerevisiae Riboseq data (over 75 million reads) in less than one hour with single-codon resolution. We applied it to 10 Riboseq data sets and demonstrated its robustness to a variety of different mRNA digestion methods and low-abundance genes while automatically correcting biases across different genes. We next show that the commonly used RPKM-derived TE is sensitive to sampling errors and biological biases, creating substantial discrepancies in previous studies. To address this, we developed a codon-level generalized linear model (GLM) with a ridge penalty to shrink the TE estimates. The GLM also serves as a mechanistic model for translation elongation and initiation, incorporating codon-specific elongation rates, local mRNA secondary structure, and gene-specific translational initiation efficiencies. We validate the model using in silico analysis and experimental mass spectrometry data and show a high correlation in predicted protein abundance (r=0.81). This successfully corrects the biases for ~2000 genes, and resolves the negative skew in TE observed in previous studies. Finally, we show the importance of accurate TE estimation for interpreting Riboseq data, including recovering the Kozak-like consensus sequence in S. cerevisiae.

Figure 2. Overview of the analysis workflow in Scikit-ribo.

The complete workflow consists of Ribosome A-site classifier training, A-site codon prediction and mapping, and translation efficiency inference. (A) Ribosome A-site training and prediction, gray text boxes denote the major steps. (B) Illustration of the covariates in the codon level generalized linear model. In the model, the mRNA abundance (in TPM) are considered as offset with fixed coefficient equal to one. Codon dwell time and mRNA secondary structure are shared covariates across genes. Translation efficiencies are gene specific covariates.

Results

Accurate A-site codon prediction with different organisms and nuclease digestion

Using a supervised learning approach, Scikit-ribo trains a model for identifying the A-site codon using reads that contain start codons (Figure 2A). The algorithm uses a random forest model to evaluate eight features of how the Riboseq reads align to the genome: the length of the read, the distance from the 5’ or 3’ end of the read to the start codon, and the nucleotides flanking the ends of the Riboseq reads (STAR Methods). Unlike other methods, Scikit-ribo can accommodate different types of Riboseq data using a recursive feature selection technique and cross validation (CV). For a given dataset, Scikit-ribo finds the optimal features with the lowest prediction error. This helps remove irrelevant features and avoids overfitting an unnecessarily complex model.

Using this approach on the S. cerevisiae data prepared with RNase I by Weinberg et al, the accuracy of the prediction of the A-site codon was extremely high (mean accuracy=0.98, SD=0.003, 10-fold CV)(Weinberg et al., 2016). Unlike the basic 15-nt rule, our model’s predictions are consistent across reads with different lengths or A-site locations (Figure S2A). This means that it can utilize the full complement of reads for downstream analysis; this is especially helpful for low-abundance genes. Our model also achieved high accuracies in seven other S. cerevisiae datasets (Table S1). Interestingly, for all eight S. cerevisiae datasets the most important features were the phase of the 5’-end of a read (whether it falls in the first, second, or third frame) and the read length (Figure S3A). This is consistent with the previous findings that RNase I was not always precise in generating ribosome footprints(Gerashchenko and Gladyshev, 2017). By examining elongating ribosomes within the canonical ORF (not overlapping the start codon), 94.3% of the predicted A-sites are in the correct frame, confirming Scikit-ribo’s high accuracy.

To test how Scikit-ribo performs in different model organisms or with different digestions protocols, we next applied it to the Riboseq data from E. coli. Bacterial ribosome profiling protocols use MNase instead of RNase I because RNase I is inhibited by bacterial ribosomes. The resulting read distributions are broad and have posed challenges in assigning ribosome position(Li et al., 2012; Woolstenhulme et al., 2015). One promising approach is to employ MNase together with the endonuclease RelE, taking advantage of RelE’s ability to precisely cleave the A-site codon within the ribosome. In the resulting ribosome footprints, the A-site codon is found at the 3’-end of reads, rather than 12 to 18 nt away from the 5’-end of a read as in S. cerevisiae. In spite of these differences, the accuracy of Scikit-ribo was still high (mean accuracy=0.91, SD=0.041, 10-fold CV, Figure S3B) and showed 99.8% assignment of the A-site codon to canonical ORFs for reads not overlapping the start codons. Interestingly, for the RelE data, the optimal feature was the phase of 3’-end of a read, while the 5’-end did not have a strong effect (Figure S3B). This is consistent with the report in Hwang et al that RelE preferentially cleaves at the ribosome A-site codon, generating precise 3’-ends(Hwang and Buskirk, 2017). Using Scikit-ribo, we also analyzed E. coli Riboseq libraries prepared with MNase alone, but the accuracy was lower (0.70) than those with RelE. This indicates that RelE improves the precision of the ribosome sub-codon position and thus is a better nuclease for analyses requiring codon resolution.

Paused ribosomes and biological biases of TE

Ribosome pausing (RP) events are prevalent in many organisms(Zhang et al., 2016), occurring for several reasons, including slow recruitment of tRNAs and mRNA secondary structure(Gorochowski et al., 2015). These biological effects can introduce biases in ribosome profiles and lead to overestimation of TE in genes with high levels of pausing. In Weinberg et al(Weinberg et al., 2016), the distribution of RPKM-derived log₂ TE is negatively skewed with a mean of −0.5 (Figure S1B). We hypothesized that the distribution of RPKM-derived TE was skewed largely due to RP events. To illustrate this, we simulated both Riboseq and RNAseq data, with and without paused ribosomes in S. cerevisiae (STAR Methods). Upon comparing log₂ TE_RP (i.e. the log₂ TE in the data with RP) with log₂ TE_Baseline (i.e. the log₂ TE in the data without RP), we observed that several genes had inflated TEs, while the remaining majority had decreased estimates. We also observed that the log₂ TE_RP distribution for paused data was broader and negatively skewed, similar to what has been observed in previous reports. These results show that this skew can arise from genes with significant pausing as they will have more Riboseq reads and higher RPKM-derived TE, although their protein abundance remains the same. Pausing also reduces the available Riboseq reads available on other non-paused genes, so that their TE estimates are deflated.

Since pauses can be induced by non-optimal codons and downstream mRNA secondary structure(Gorochowski et al., 2015), we developed a statistical model to jointly correct for these effects that we refer to as biological biases. Since the observed ribosome profiles are affected by changes in elongation rates, and not simply initiation rates, Scikit-ribo uses a codon-level generalized linear model (GLM) to separate out these two processes, considering three categorical covariates and one continuous covariate (STAR Methods, Equation 5–6). This models that at a codon position, the ribosome coverage is proportional to mRNA abundance and gene specific TE, reflecting initiation levels, as well as downstream mRNA secondary structure and codon specific dwell time, reflecting limiting steps in elongation rates (Figure 2B).

Sampling errors for low abundance genes using Riboseq

Another difficulty in estimating TE is sampling error for low-abundance genes due to lack of sequencing depth. Similar trends have been reported in DE analysis of RNAseq data, where low abundance genes can have extreme fold changes if not corrected (Love et al., 2014). This is a side-effect of modeling high-dispersion count data; measurements are inherently noisier when counts are low(Love et al., 2014). Riboseq data shares the same issue, and since most Riboseq experiments are done with two or fewer replicates, estimation of between-sample variability and subsequent shrinkage of dispersion has not been feasible(Albert et al., 2014). Thus, most published Riboseq studies used the RPKM-derived TE: RPKM^Ribo/RPKM^mRNA (Equation 1)(Ingolia et al., 2009). However, low abundance genes, especially those with a “transcripts per million” (TPM, Equation 3) value less than one, show much more dispersed TE values compared with other genes (Figure 1A). This is true even if the TPM cutoff is increased to 10 (Figure S1D). Consequently, the standard deviation (SD) of log₂ TE in low abundance genes from the Weinberg et al(Weinberg et al., 2016) data was 3-fold higher than for other genes (Levene test, p-value=3 × 10⁻⁸⁹), the overall range in TE was 5-fold larger (99 vs 20), and the median absolute deviation (MAD) was also larger (1.9 vs 1.0). The high dispersion of TEs was driven by the high variance of the ratio between the numbers of reads per gene (Equation 4).

One ad-hoc solution is to remove low abundance genes from downstream analysis, although the threshold is arbitrary and cannot be determined rigorously. Furthermore, this approach reduces the sensitivity of finding genuinely extreme TE genes and reduces the power of finding significance. Instead of imposing arbitrary thresholds, Scikit-ribo uses a shrinkage method based on ridge penalty to account for the sampling uncertainty for low abundance genes (STAR Methods, Equation 7–8). This method helps address the sampling issues even without replicates, and enables Scikit-ribo to report balanced log₂ TE distributions (Figure S1).

Accurate inference reveals the interplay between cognate tRNA availability and mRNA secondary structure

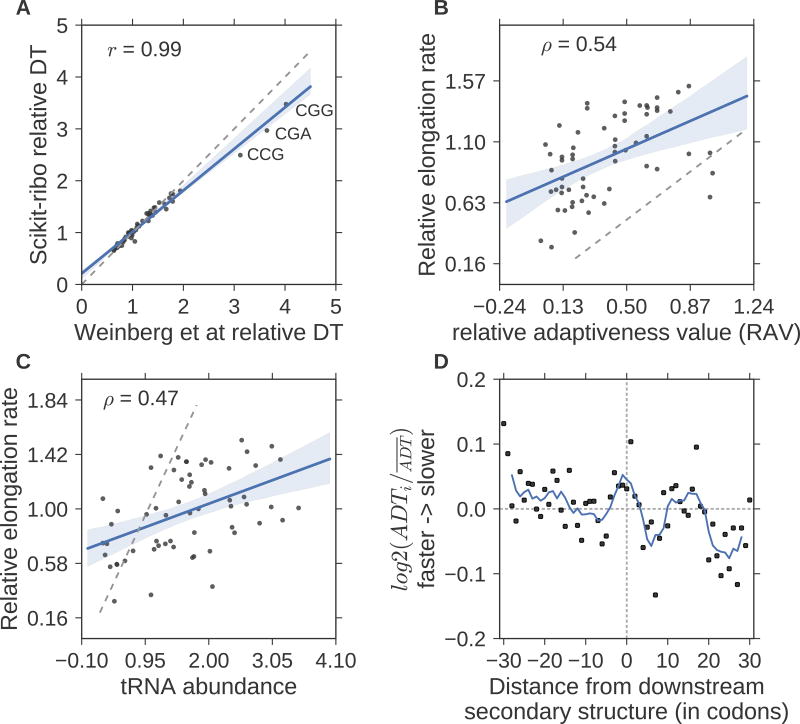
Having described how Scikit-ribo addressed the errors and biases, we analyzed the CHX-free S. cerevisiae Riboseq data from Weinberg et al(Weinberg et al., 2016). The codon dwell time (DT) estimates from the GLM are the inverse of the codon elongation rates (ER). Scikit-ribo almost perfectly reproduced the codon DT (Pearson r = 0.99) from Weinberg et al(Weinberg et al., 2016), in which the three slowest codons are CGG, CGA, and CCG (Figure 3A). The tRNA adaptation index (tAI) measures the efficiency of a coding sequence recognized by the intra-cellular tRNA pool, taking into account each gene’s codon compositions, mRNA expression levels, and the availability of the conjugate tRNA(dos Reis et al., 2004). Reis et al(dos Reis et al., 2004) estimates tAI as the geometric mean of its codons’ relative adaptiveness value (RAV). A codon with lower RAV is sub-optimal for translation elongation, i.e. slower codon. We found CGG, CGA, and CCG have low RAV values(dos Reis et al., 2004) and are among the rarest codons in the S. cerevisiae transcriptome. Following Weinberg et al and others(Dao Duc and Song, 2017; Gorochowski et al., 2015; Weinberg et al., 2016; Zhang et al., 2016), we compared the relative codon ERs with RAV and their cognate tRNA abundance measured by microarray(Weinberg et al., 2016), and reproduced a positive correlation against both (Spearman ρ_tAI = 0.54, ρ_tRNA = 0.47, Figure 3B–C).

Figure 3. Accurate inference of codon elongation rates and mRNA secondary structure.

(A) Almost perfectly reproduced codon dwell time (DT), inverse of elongation rate) from Weinberg et al (r=0.99). (B) Correlation with the codon’s adaptiveness value (RAV, r=0.5), (C) Correlation with tRNA abundance (r=0.47). In A–C, the gray dashed line denotes the diagonal line; y=x. The RAV scales from 0 to 1. A codon with lower RAV means that it is less optimal for translation elongation, i.e. slower codons. (D) Meta gene analysis of the log ratio of adjusted DT (ADT), divided by the mean adjusted DT. The solid line denotes the average ADT in a five-codon sliding window. A log ratio greater than zero means ribosomes at this position are faster than average. The log ratios on the left were significantly higher than the ones on the right (T-test, p-value= 5 × 10⁻³). The unit of the distance is codon.

Although our findings confirm that ribosomes have lower DT on codons with higher cognate tRNA levels, it cannot solely explain the variation in ER given the imperfect correlation. We hypothesize part of the missing contribution was from downstream mRNA secondary structure, and adjusted the within-gene ribosome densities by the inferred codon ERs, which controlled for the codon-specific effects on local translational elongation. We also used RNAfold(Lorenz et al., 2011) to predict the optimal mRNA secondary structure and test if large downstream stem-loops would increase ribosome density (STAR Methods). We found that the ribosomes move slower in the presence of downstream mRNA stem-loops (t-test, p-value= 5 × 10⁻³), and noted a peak in the average adjusted ribosome density in a five-codon sliding window at the junction (Figure 3D). This finding is consistent with previous reports that downstream stem-loops decrease the ribosome ER, i.e. increase the DT as ribosomes wait for the downstream stem-loops to be unfolded(Chen et al., 2013; Mao et al., 2014; Zur and Tuller, 2016). Together our analyses show that ribosome elongation rates are affected by a complex interplay of cognate tRNA availability and downstream mRNA secondary structure. These results also confirm that Scikit-ribo accurately estimates codon-specific DT and the effect of mRNA secondary structure, after it correctly predicted the A-site codon and fit the GLM.

Simultaneously correcting sampling errors and biological biases for TEs

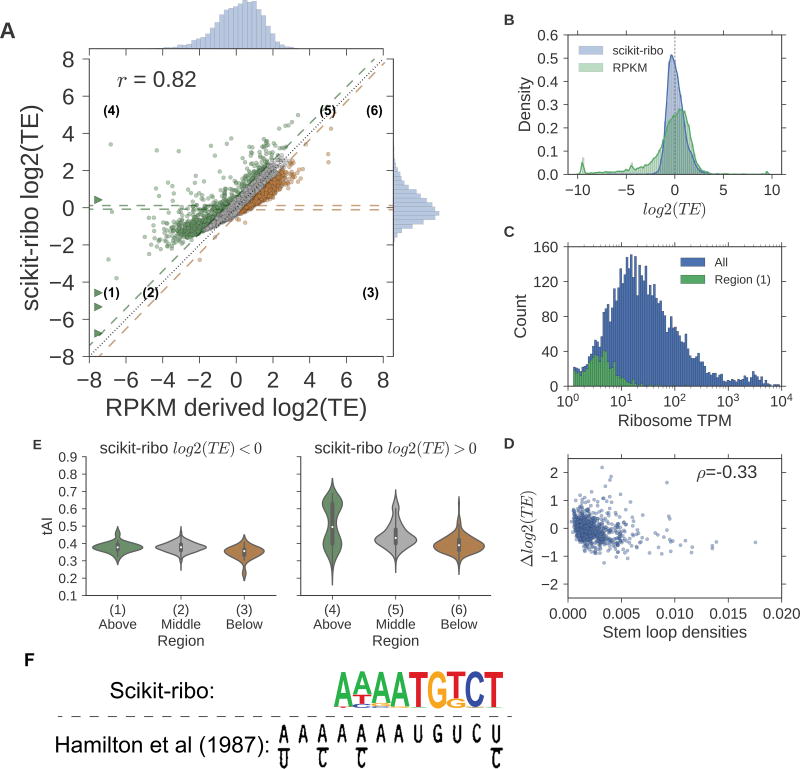
To understand how Scikit-ribo corrects the biases in the Riboseq analysis, we compared the Scikit-ribo log₂ TE with the RPKM-derived log₂ TE from the Weinberg et al data (Figure 4A). The correlation between the estimates was high (r=0.82), but the RPKM-derived TE estimates showed clear trends of systematic biases (negative skew) that were corrected by Scikit-ribo (Figure 4B). We calculated the differences between the two estimates, Δ log₂ TE = log₂ TE_{scikit–ribo} – log₂ TE_RPKM, and colored them as green for Δ log₂ TE > 0.5, previously underestimated; orange for Δ log₂ TE < −0.5, previously overestimated; and gray for neutral genes (Table S2). The green points in the left half of the plot shifted upward from the diagonal line, while the points in the right half were more consistent (Figure 4A). There were 1957 genes with large differences (|Δ log₂ TE| > 0.5); 897 being under-estimated and 1060 being over-estimated. Compared with RPKM-derived TE, we found the log₂ TE of some genes were previously underestimated by as much as 11 (2048 fold), while other genes were overestimated by almost 3 (8 fold) (Figure S4B).

Figure 4. Pair-wise comparisons of estimates between Scikit-ribo and RPKM-derived TE.

(A) Scatter plot of Scikit-ribo and RPKM derived log2(TE). Difference in log2(TE): Δ log2(TE). Δ log2(TE) > 0.5, previously underestimated (green), Δ log2(TE) < −0.5, previously overestimated (orange), and other genes in between (gray). The genes with Δ log2(TE) less than −8 are indicated by triangles. (B) Histograms of scikit-ribo and RPKM-derived log2(TE), log2(TE) values less than −10 are adjusted to −10 (C) Histograms of ribosome TPM in all genes (blue), and region 1 (green). (D) Violin plots of Δ log2(TE) by the number stem loops. (E) Violin plots of tAI for genes in the six regions, left: Δ log2(TE) < 0, right: log2(TE) > 0. (F) The Kozak consensus sequence, AAAATGTCT, found with the TE estimates from Scikit-ribo (p-value=1 × 10⁻²¹). The lower panel is adapted from the original paper, Hamilton et al (1987).

We further defined six regions based on Δ log₂ TE and the sign of Scikit-ribo log₂ TE. For example, region 1 corresponds to genes with Δ log₂ TE greater than 0.5 with negative Scikit-ribo log₂ TE (n=629); most of these genes were of low abundance with a TPM less than 10 (Figure 4C, Figure S4). This means given 75 million reads, these genes had fewer than 750 reads on average, i.e. ~2 reads per codon. The sampling of such genes is highly unstable, causing the ratio of the read counts to have high variance. As a result, the RPKM-derived TE reports a high dispersion and incorrect TE estimates in region 1, while Scikit-ribo successfully corrected the sampling errors with its shrinkage estimates.

While improvements in TE estimates in region 1 arise from a better correction of sampling error on low abundance genes, how can we address differences in regions with more highly expressed genes? For this analysis, we excluded low abundance genes (TPM < 10) to focus on the effects on biological covariates, codon specific ER and mRNA structure. There were 268 and 981 genes in the highly-translated regions 4 and 6, respectively. If downstream mRNA secondary structure had an effect, the RPKM-derived log₂ TE of genes with high levels of structure would be inflated as additional ribosomes are paused at the loop; the Δ log₂ TE becomes smaller with a higher stem loop density (normalized by ORF length). We found this was indeed the case: there is a negative correlation between Δ log₂ TE and stem loop density (Figure 4D, Spearman ρ = −0.33). This bias was corrected by the mRNA secondary structure covariate of the GLM as we found an enrichment of 15% greater ribosome density when there was a downstream secondary structure.

Second, we investigated the influences of variation in codon-specific ER values. The gene level tRNA-adaptation index (tAI) indicates whether a gene is enriched for optimal or non-optimal codons: higher tAI means the gene is enriched for faster codons, while a lower tAI means it is enriched for slower codons. The middle regions, 2 and 5, served as baseline for genes with negative and positive log₂ TE, respectively (Figure 4E). For negative log₂ TE, genes, there were no significant difference of tAI between genes in regions 1 and 2, but the region 3 genes had significantly lower tAI than those in region 2 (Table S2, t-test, p-value=2 × 10⁻⁶). We conclude that the differences in TE for region 1 is not due to tAI but is instead due to the shrinkage estimates via the ridge penalty of the Scikit-ribo model. In contrast, the TE values of region 3 genes were previously overestimated because they contained more slow codons. When log₂ TE is positive, tAI values have a stronger effect: region 4 genes had much higher tAI values than region 5 genes (t-test, p-value=1 × 10⁻¹⁷) while genes in region 6 had lower tAI (t-test, p-value=5 × 10⁻⁵⁵). This means the genes in the region 4 and 6 were previously underestimated and overestimated, respectively, because their genes tend to enrich for fast and slow codons.

We further found the region 4 genes are enriched for the biological process of cytoplasmic translation [GO:0002181] (Table S3, p-value=3 × 10⁻²⁵), consistent with previous reports showing genes encoding ribosomal proteins are enriched for optimal codons (Gingold and Pilpel, 2011). Since ribosomes move faster on mRNAs encoding ribosome proteins, RPKM-derived TE values are underestimated but are corrected by Scikit-ribo. These observations do not depend on the use of the tAI metric that is based on gene expression data, including ribosome proteins: the same conclusion holds true using the species-specific tAI (stAI)(Sabi and Tuller, 2014) metric developed to provide a similar measurement of codon efficiency without gene expression data (Figure S5).

Scikit-ribo discovers Kozak-like consensus in S. cerevisiae

The Kozak consensus sequence, GCCRCCATGG, promotes translation initiation in vertebrates(Kozak, 1987). In S. cerevisiae, the Kozak-like sequence was shown to be AAAAAAATGTCT(Hamilton et al., 1987), and has been widely used as a positive control to train translation initiation start (TIS) site prediction methods(Lee et al., 2012; Michel et al., 2014; Raj et al., 2016). The Kozak sequence has been re-discovered in Riboseq studies in humans (homo sapiens), mice (Mus musculus) and maize (Zea mays) (Cenik et al., 2015; Chew et al., 2016; Lei et al., 2015). However, it has not been found using Riboseq data in S. cerevisiae, and only a weak resemblance of it, 4 out of 12 bases, has been reported(Pop et al., 2014).

We examined whether the improved TE estimates from Scikit-ribo can discover this mRNA element as it is associated with high TE. We collected the 5’UTR sequences from genes with log₂ TE > 2, and scanned for enriched sequences using HOMER(Heinz et al., 2010). Based on HOMER’s suggested p-value threshold, there were two statistically significant sequences. Strikingly, the top hit exactly matches the Kozak-like sequence from Hamilton et al(Hamilton et al., 1987), AAAATGTCT (p-value=1 × 10⁻²¹, Figure 4F). This is the first report of the exact Kozak-like sequence in the S. cerevisiae Riboseq analyses. The other enriched sequence was AAATAAGCTCCC, which has not been reported in vivo (p-value=1 × 10⁻¹¹, Figure S6). Interestingly, this sequence contains the motif ATAAG, one of the top five sequences that leads to higher TE in a large-scale HIS3 reporter assay from Cuperus et al(Cuperus et al., 2017). In contrast, using the same threshold, RPKM-derived TE failed to discover either of these sequences, and found a weak signal for CAACATGGCT with a much less significant p-value (1 × 10⁻¹¹) and weak resemblance to the Kozak-like sequence (Figure S6). This failure of RPKM-derived TE to yield the Kozak-like motif was likely because that approach provided skewed estimates where some lower TE genes had artificially high RPKM-derived TE. This contaminated the gene set for enrichment analysis, and prevented it from finding the correct motif.

Large-scale validation showed Scikit-ribo’s accurate TE estimation, especially for low-abundance genes

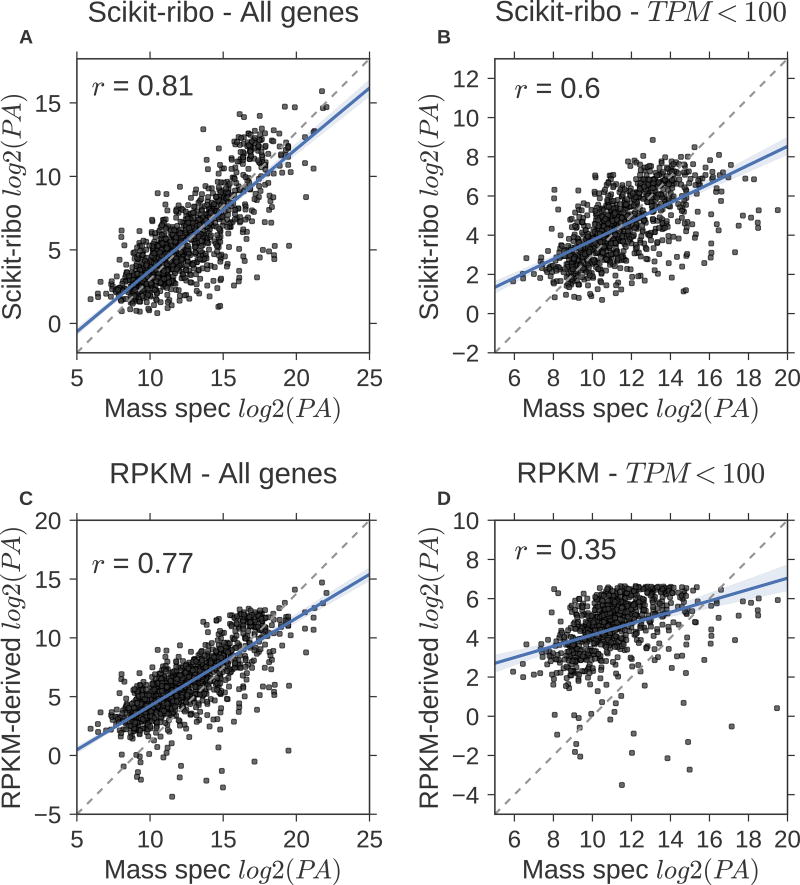
To further understand the discrepancies between Scikit-ribo and RPKM-derived TE, we performed a large-scale validation using the selected reaction monitoring (SRM) mass spectrometry data from a recent reference proteome dataset containing high quality measurements in S. cerevisiae(Lawless et al., 2016). Based on the master equations relating mRNA transcription and protein translation (Equation 9)(Li, 2015), the relative protein abundance (PA) is proportional to the product of mRNA abundance and TE, assuming a consistent protein degradation rate across genes (Equation 10). There were 1,180 genes in the validation set, with a mean of 55,012 copies per cell, ranging from 6 to 4,366,751. The correlation between the protein abundance derived by Scikit-ribo and by mass spectrometry was high (Pearson r = 0.81, Figure 5A) and the fitted line was close to the diagonal (linear regression, β = 0.83). When we further considered protein degradation rates from Christiano et al(Christiano et al., 2014), the correlation became even higher (Pearson r = 0.83, Figure S8). In contrast, RPKM-derived log PA reported a lower correlation (Pearson r = 0.77) and the fitted line is more distant from the diagonal (β = 0.75, Figure 5C). In addition, many of the outliers in the RPKM-derived PA were low abundance genes, suggesting a systematic bias (Figure 5C). Focusing on a set of 933 lower abundance genes with a TPM less than 100, the Scikit-ribo derived log PA maintained a high correlation with mass spectrometry derived log PA (Pearson r = 0.6, β = 0.48, Figure 5B) while the RPKM-derived PA became more inaccurate with a much lower correlation (Pearson r = 0.35, β = 0.29, Figure 5D). This demonstrates that Scikit-ribo more accurately estimates genome-wide TE regardless of mRNA abundance, including low abundance mRNAs.

Figure 5. Large-scale validation with mass spectrometry data confirmed Scikit-ribo’s accurate TE estimates, especially for low-abundance genes.

(A) Scikit-ribo derived protein abundance (PA) for all genes in the validation set (r = 0.81, β = 0.83). (B) Scikit-ribo derived PA for genes with TPM less than 100 (r = 0.6, β = 0.48). (C) RPKM-derived PA for all genes in the validation set (r = 0.77, β = 0.75). (D) RPKM-derived PA for genes with TPM less than 100 (r = 0.35, β = 0.29). The black dashed line denotes the identity line; y=x.

Coverage and data quality requirements for accurate Riboseq analysis

Above we showed how Scikit-ribo can recover many additional insights from the codon-level analysis of the Riboseq data. However, it is of crucial importance to understand the practical requirements of our method, especially: 1) How much coverage is needed for robust codon-level analysis; and 2) What kind of artifacts may be present, especially those from CHX treatment?

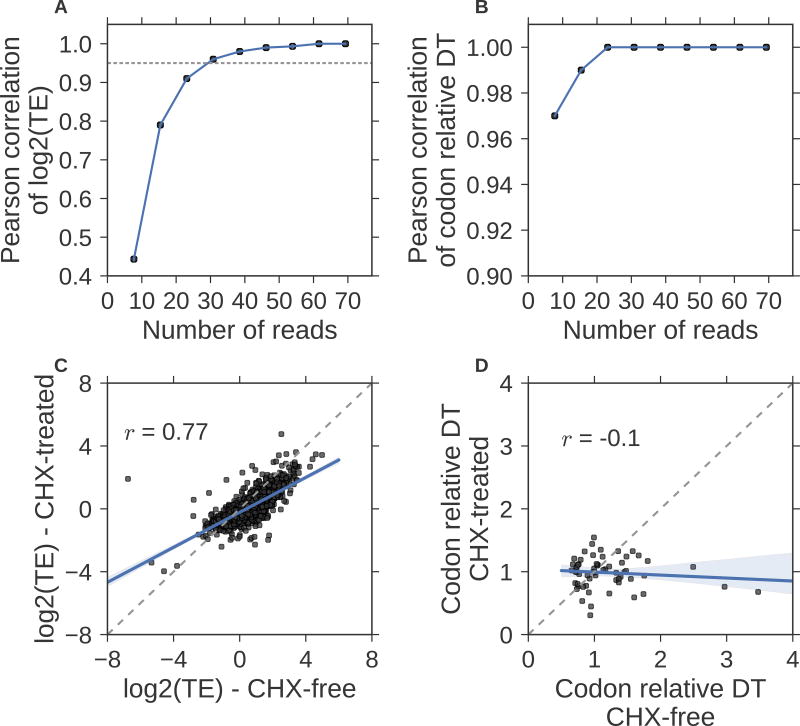
To answer the first question, we performed an in silico down-sampling of the Weinberg et al(Weinberg et al., 2016) Riboseq data using between 10% to 90% of its original coverage (77 million reads) in 10% increments. We found that the correlation drastically increases between 7.7 million (Pearson r = 0.44) to 30.8 million (Pearson r = 0.96) reads, while the improvement saturates with 38.5 million or more reads (Pearson r = 0.98, Figure 6A). This observation is consistent with our analysis of two biological replicates in Radhakrishnan et al which had a Pearson correlation of 0.96 between the 80-million and 39-million read datasets (Figure S9). Interestingly, the estimation of codon relative DT does not require as much coverage and a Pearson r = 0.97 is achieved with only 7.7 million reads and a Pearson r = 1.0 is achieved with only 23.1 million reads (Figure 6B), consistent with the biological replicate analysis (Figure S10). This is because the codon relative DT is the coefficient of a shared covariate across genes, with on average 48,666 occurrences of each codon across the S. cerevisiae transcriptome. In contrast, the log₂ TE is the coefficient of the gene-specific covariate with only ~467 codons per gene. Thus, for a fixed amount of overall coverage, Scikit-ribo’s statistical model effectively has ~100 times as much information to estimate codon relative DT than to estimate TE. Overall, in S. cerevisiae, at least 30 million reads are needed to achieve the highest accuracy of TE estimation. The requirements for other species will scale linearly with the total transcriptome length, and about 200 million reads will be needed for Homo sapiens and Mus musculus.

Figure 6. Practical considerations of using Scikit-ribo for Riboseq analysis.

Pearson correlations between the down-sampled data and the original data (Weinberg et al) on (A) log2(TE), the gray dashed horizontal line denotes Pearson r = 0.95. (B) The same down-sampling comparison for the codon relative dwell time (DT). (C) Scatter plot of log₂ TE on Riboseq experiments treated with cycloheximide (CHX) and CHX free data, (D) Same comparison for the codon relative dwell time (DT). The CHX free data is from Weinberg et al, and the CHX-treated Riboseq data is from McManus et al. Both data are in S. cerevisiae. The black dashed line denotes the identity line; y=x.

Cycloheximide (CHX) has been shown to distort ribosome profiles and dramatically alter codon-specific elongation rates, including downstream “waves” of artificial ribosome densities(Hussmann et al., 2015). Because of these waves, the measured positions of ribosomes after CHX treatment do not reflect the amount of time ribosomes spend at each position in vivo(Hussmann et al., 2015). These artifacts can be problematic for Scikit-ribo, as it relies on the accurate ribosome positioning for the codon-level analysis.

To investigate, we compared the CHX-treated data in McManus et al(McManus et al., 2014) (41 million reads) with the CHX-free data in Weinberg et al (both from S. cerevisiae). Even after excluding genes with RNA TPM less than 10, we observed a poor correlation of log₂ TE estimates (Pearson r = 0.77) between CHX-treated and CHX-free data (Figure 6C). Compared to the SRM mass spectrometry data the log₂ TE estimates from the CHX-treated data had an appreciably lower correlation than those from the CHX-free data (Pearson r: 0.73 vs 0.81); the CHX treatment reduces the accuracy of TE estimation. To further investigate this artifact, we compared the codon relative DT between these two datasets, and observed a low and negative Pearson correlation (Pearson r = −0.1, Figure 6D). This means that CHX substantially disrupts the positioning of the ribosomes, leading to the incorrect codon relative DT estimates and subsequently reducing the accuracy of log₂ TE estimates. Consequently, we recommend using Scikit-ribo with CHX-free Riboseq data only.

Discussion

For nearly 60 years, the central dogma of molecular biology has been the guiding model for explaining how genetic information flows from DNA to RNA and then to proteins. Through widespread genome and transcriptome sequencing, the first half of this process has been extensively explored, however relatively little is known about the later phases of this process, largely because of the difficulties in acquiring high throughput and high quality data about translation and translational control. Riboseq is a powerful approach poised to fill this void.

Several methods have been developed for selected aspects of Riboseq analysis, including differential TE testing(Larsson et al., 2011; Olshen et al., 2013; Xiao et al., 2016; Zhong et al., 2017), identifying ORFs and alternative translation initiation sites(Malone et al., 2017; Zhang et al., 2017), and predicting the shape of ribosome profiles(Liu and Song, 2016). But few practical methods have been developed for robust TE estimation and most previous analyses were not performed in a systematic fashion. This had led to conflicted findings about the roles of codons and mRNA secondary structure on translation, and has prevented biological discoveries from being made. Here, through a systematical characterization and validation using mass spectrometry data, we exposed some of the more troubling issues of RPKM-derived TEs, including sampling errors and biological biases, especially for the low abundance genes.

We demonstrated that Scikit-ribo is a statistically robust model and open-source software package for accurate genome-wide TE inference from Riboseq data. The core of Scikit-ribo is a codon-level generalized linear model that unifies our study of translation elongation and initiation. When paired with a powerful ridge regression regularization method, Scikit-ribo corrects the negative skew in TE observed in most previous papers, especially for low expressed genes. Using three case studies involving ten different datasets, we showed how these advances allow universal improvement to Riboseq data analysis. This particularly improves the estimation of genome-wide TE, allowing us to discover the Kozak-like consensus sequence in S. cerevisiae. From a practical perspective, we demonstrated that at least 30 million reads are needed to achieve a high accuracy of TE estimation in S. cerevisiae. We further demonstrated that CHX-treatment can induce substantial artifacts and recommend only using CHX-free data with Scikit-ribo. Once CHX-free mammalian Riboseq data become available, Scikit-ribo can be used to deepen our understanding of mammalian translational control.

Our findings showcase the interplay between biology and statistics; biological knowledge informs statistical methods development, and statistical improvement yields novel biological insights. Together, we demonstrate that Scikit-ribo substantially improves Riboseq analysis and our understanding of translation control. In the future, we foresee more researchers applying Riboseq to address their biological questions related to protein translation in many samples and conditions, and Scikit-ribo can unlock the full potential of this technique.

STAR Methods

Overview of Scikit-ribo

Scikit-ribo has two major modules (Figure 2): (1) Ribosome A-site codon location prediction, and (2) TE inference using a codon-level generalized linear model (GLM) with ridge penalty. A complete analysis with Scikit-ribo involves two steps: 1) data preprocessing to prepare the ORFs and codons for a genome of interest, 2) the actual model training and fitting. The few inputs to Scikit-ribo includes the alignments of Riboseq reads (i.e. BAM file), gene-level quantification of RNAseq reads (i.e. from Salmon(Patro et al., 2017) and Kallisto(Bray et al., 2016)), a gene annotation file (i.e. gtf file) and a reference genome (i.e. fasta file) for the model organism of interest. The main outputs include log₂ TE estimates for the genes, and the translation elongation rates for the 61-sense codons. Scikit-ribo also has modules to automatically produce diagnostic plots of the random forest model and the GLM. The ribosome profile plots for each gene can also be plotted using Scikit-ribo. For details of preparing the inputs, see data processing steps in Methods. For a complete workflow from raw sequencing reads to results, see Figure S11.

Ribosome A-site codon prediction

Scikit-ribo uses a random forest(Breiman, 2001) classifier from Scikit-learn(Pedregosa et al., 2011) to predict the ribosome A-site locations over the 61-sense codons in the ORFs after excluding the start and stop codons. (Figure 2A). Low mapping quality (MAPQ<20) and clipped alignments are removed from downstream analysis. After filtering out overlapping genes, it collects all reads that intersect the start codons as training data. In the Weinberg et al data, the sample size of the training data is ~700,000, with ~85,00 in each class. The feature set of the classifier include 1) read length, 2) reading frame phase of the 5’-end and 3’-end nucleotides (1st, 2nd, or 3rd), 3) the edge and the flanking nucleotides of the Riboseq reads. In the RNase I data, the label of the training data is the distance between the 3’-end of the start codon and the 5’-end of the read. In the RelE data, the label of the training data is the distance between the 3’-end of the start codon and the 3’-end of the read, which is enabled by the flag –r of the Scikit-ribo program.

The training of the random forest classifier involved two steps: recursive feature selection with CV, and training the classifier with reduced feature set. The first step of the training uses CV to find the optimal features that gives the lowest prediction error. During each step of the CV, the features are re-ranked and the lowest ranked feature is dropped. This is similar to finding the “elbow” point in the feature importance plot (Figure S3), which indicates the last sharp decrease of feature importance. Once the optimal feature set is selected, Scikit-ribo performs another ten-fold CV to measure the accuracy (1 - error rate) of the model and learns the weights for each feature. After this, the learned classifier is applied to all the reads in the ORF and the A-site location on each read is predicted. Finally, Scikit-ribo compares the A-site locations to the canonical ORF, and reads that do not match it will be dropped from downstream analysis.

Calculating RPKM-derived TE

We refer to ribosome density per mRNA as RPKM-derived TE. It is a commonly used proxy for TE, which can be calculated by the ratio of RPKM for a given gene i(Ingolia et al., 2009; Li, 2015):

$${\text{Ribosome density per mRNA}}_i=\frac{{\text{RPKM}}_i^{\text{Ribo}}}{{\text{RPKM}}_i^{\text{mRNA}}}$$ Equation 1

where ${\text{RPKM}}_i^{\text{Ribo}}$ and ${\text{RPKM}}_i^{\text{mRNA}}$ are the relative abundance of gene i in the Riboseq data and RNAseq data, respectively.

RPKM and TPM are defined by:

$${\text{RPKM}}_i=\frac{R_i}{\left(\frac{l_i}{{10}^3}\right)\left(\frac{{\sum }_i{R}_i}{{10}^6}\right)}=\frac{R_i}{l_i·{\sum }_i{R}_i}·{10}^9$$ Equation 2

$${\text{TPM}}_i=(\frac{{\text{RPKM}}_i}{{\sum }_i{\text{RPKM}}_i})·{10}^6$$ Equation 3

where R_i, l_i are the sequencing coverage and coding sequence length of a gene, respectively.

In Riboseq studies, rather than using fragments per kilobase of gene per million reads mapped (FPKM), RPKM is employed (Equation 1). This is because the Riboseq reads are single stranded, and the companion RNAseq libraries were also made using a single stranded protocol to mimic the Riboseq data. Since l_i is a shared term between the two data, RPKM – derived TE_i can be further derived as:

$$\text{RPKM}–{\text{derived TE}}_i=\frac{\raisebox{1ex}{$R_i^{\mathit{\text{Ribo}}}$}\!\left/ \!\raisebox{-1ex}{${\sum }_i{R}_i^{\mathit{\text{Ribo}}}$}\right.}{\raisebox{1ex}{$R_i^{\mathit{\text{mRNA}}}$}\!\left/ \!\raisebox{-1ex}{${\sum }_i{R}_i^{\mathit{\text{mRNA}}}$}\right.}=\frac{\raisebox{1ex}{$R_i^{\mathit{\text{Ribo}}}$}\!\left/ \!\raisebox{-1ex}{$R_i^{\mathit{\text{mRNA}}}$}\right.}{\raisebox{1ex}{${\sum }_i{R}_i^{\mathit{\text{Ribo}}}$}\!\left/ \!\raisebox{-1ex}{${\sum }_i{R}_i^{\mathit{\text{mRNA}}}$}\right.}$$ Equation 4

The total number of reads ${\sum }_i{R}_i^{\mathit{\text{Ribo}}}$ and ${\sum }_i{R}_i^{\mathit{\text{mRNA}}}$ are fixed normalization factors shared between genes. Thus, the variance of the nominator, the ratio of the number of reads, determines the dispersion of RPKM – derived TE_i. That is why low abundance genes, either in the Riboseq or RNAseq data, report highly dispersed TE derived with RPKM.

Correcting for biological biases with the Scikit-ribo GLM

The joint inference of TE and codon DT is achieved via a codon-level GLM with a penalized likelihood function(Friedman et al., 2010) (Equation 5). The model can be fit using a python implementation of glmnet (https://github.com/hanfang/glmnet_python(Balakumar, 2017)). In Scikit-ribo, the design matrix is loaded as a scipy(Jones et al., 2001) compressed sparse column matrix. This can effectively reduce memory usage, as the size of the design matrix grows exponentially with respect to the number of categorical variables. As a quality control, low MAPQ regions and genes with TPM less than one are excluded from the analysis. If a gene has fewer than 10 effective codons remaining, it is also excluded. The model assumes that the number of ribosomes Y_ij for each codon at position j of gene i follows a Poisson distribution with the mean equal to μ_ij (Equation 5). A log link function is employed.

$$Y_{\mathit{\text{ij}}}~\mathit{\text{Poisson }}(\mathit{\text{mean}}={\mu }_{\mathit{\text{ij}}})\text{ for position }j\text{ of gene }i$$

$$\mathit{\text{log }}{\mu }_{\mathit{\text{ij}}}={\beta }_0+{\beta }^T{x}_{\mathit{\text{ij}}}$$ Equation 5

$$\text{where }i\in [0,I],j\in [0,J]$$

To correct for the biological biases, Scikit-ribo considers the below three categorical covariates and a continuous covariate (Figure 2B, Equation 6). The first continuous covariate $X_i^m$ represents mRNA abundance in TPM and its coefficient is fixed to be one, indicating the ribosomes are proportional to mRNA abundance. Before putting into the model, the log TPM_i values are normalized by their mean and SD. The coefficients ${\beta }_i^t$ (in log_e scale) of the first categorical covariate $X_i^t$ represent TE/TIE for each gene. The log₂ TE_i can further be computed by using median normalization: ${\text{log}}_2{\mathit{\text{TE}}}_i=({\beta }_i^t-\mathit{\text{median}}(\overrightarrow{{\beta }_i^t}))/{\text{log}}_{e}2$. The second categorical covariate $X_{\mathit{\text{ij}}}^c$ represent the 61-sense codons. Their coefficients, β^c (in log_e scale) are proportional to the relative codon DT, which are the inverse of codon ERs. The start and stop codons in each ORF are excluded, because of their relevance to translation initiation and termination, rather than elongation. Finally, the third categorical covariate $X_{\mathit{\text{ij}}}^s$ indicates whether a likely double-stranded stem loop exists within 18 nt downstream of the current ribosome, as predicted from the optimal minimum free energy structure from RNAfold(Lorenz et al., 2011). The current ribosome is likely to reside at a single strand part of the mRNA molecule.

$$g\left({\mu }_{\mathit{\text{ij}}}\right)={\beta }_0+\underset{\mathit{\text{mRNA}}}{\underbrace{x_i^m}}+\underset{\mathit{\text{TE}}}{\underbrace{x_i^t{\beta }_i^t}}+\underset{\mathit{\text{codon}}}{\underbrace{x_{\mathit{\text{ij}}}^c{\beta }^c}}+\underset{\mathit{\text{secondary structure}}}{\underbrace{x_{\mathit{\text{ij}}}^s{\beta }_{\mathit{\text{ij}}}^s}}$$ Equation 6

where g(․) is a log link function, μ_ij = E[Y_ij],

• $X_i^m$ is the mRNA abundance for gene i with its coefficient fixed to 1,

• ${\mathrm{\beta }}_{\mathrm{i}}^{\mathrm{t}}$ is the translational efficiency coefficient for gene i,

• β^c is the codon dwell time (inverse of elongation rate) for codon c,

• ${\mathrm{x}}_{\text{ij}}^{\mathrm{s}}$ denotes whether secondary structure exists downstream of position j in gene i,

• β₀ is the intercept.

Correcting for sampling errors with ridge penalty

To correct for the sampling errors, i.e. the high dispersion of TE among low-abundance genes, Scikit-ribo employs a GLM with a ridge penalty(Friedman et al., 2010) (l₂ norm) to provide shrinkage estimates of TEs (Equation 7 and 8). This is computed by setting the α parameter in glmnet to zero. The lasso penalty is not considered here because we wish to infer all the coefficients (e.g. TEs of all genes), rather than performing variable selection. To optimize the log-likelihood, Scikit-ribo calls glmnet(Friedman et al., 2010), which uses a Newton quadratic approximation (outer loop) and then coordinate descent on the resulting penalized weighted least-squares problem (inner loop). A ten-fold CV is performed to find the optimal λ, which controls the strength of l₂ norm regularization. If one wishes to utilize or inspect the coefficients from an un-penalized GLM, this could be done by setting λ = 0 when printing the coefficients.

The log likelihood for the observations {x_ij, y_ij} is given by

$$l(\beta |X,Y)=\sum _{i=0}^I\sum _{j=0}^J(y_{\mathit{\text{ij}}}({\beta }_0+{\beta }^T{x}_{\mathit{\text{ij}}})-e^{{\beta }_0+{\beta }^T{x}_{\mathit{\text{ij}}}})$$ Equation 7

We optimize the l₂ norm penalized log likelihood w. r. t. a total of N observations and K parameters:

$${\mathit{\text{argmin}}}_{{\beta }_0,\beta }-\frac{1}{N}l(\beta |X,Y)+\lambda (\sum _{k=1}^K{\beta }_k^2/2)$$ Equation 8

where the optimal λ with the smallest Poisson deviance is decided via CV.

Deriving relative protein abundance

As per the master equations for mRNA transcription and protein translation from Li(Li, 2015), for a gene i,

$$\frac{d}{\mathit{\text{dt}}}{P}_i=k_i^2{M}_i-{\lambda }_i^2{P}_i$$ Equation 9

where M_i and P_i are the concentration of mRNA and protein, respectively. $k_i^1$ and $k_i^2$ are the transcription and translation efficiency, while ${\lambda }_i^1$ and ${\lambda }_i^2$ are the degradation rates of mRNA and protein. Under steady state, $\frac{d}{\mathit{\text{dt}}}{P}_i=\mathbf{0}$, thus, the relative protein abundance (PA) can be derived from Riboseq and RNAseq data using:

$$P_i=\frac{k_i^2}{{\lambda }_i^2}{M}_i=\frac{{\mathit{\text{TE}}}_i}{{\mathit{\text{DR}}}_i}{M}_i\propto {\mathit{\text{TE}}}_i{M}_i$$ Equation 10

where TE_i is the translation efficiency, M_i is the relative mRNA abundance in TPM, and DR_i is the relative protein degradation rates, which can be assumed identical across genes. For the Riboseq data alone, P_i approximates to the relative ribosome density/abundance in TPM.

Sequencing reads processing

The complete sequencing reads processing workflow is shown in Figure S15. Each time a new fastq file is generated, it is recommended to run fastqc to ensure the expected outcome and replace runs with excessive quality errors. For both Riboseq and RNA-seq data, the first step is to identify and trim the 3’-end adapters from each read using cutadapt(Martin, 2011) (v1.13). The first base of the reads’ 5’-end is also clipped to avoid contamination on the 5’-end. To filter out ribosomal RNA (rRNA) sequences, the resulting reads are aligned to the known rRNA using Bowtie(Langmead, 2010) (v1.2.0). As a quality control, the reads that are too short or too long are removed using Prinseq(Schmieder and Edwards, 2011), keeping reads in a range from 15nt to 35nt (v0.20.4). In E. coli, the size range of the Riboseq reads is larger, so this filtering step on read size should be adjusted accordingly. The remaining reads are then aligned with STAR(Dobin et al., 2013) (v2.4.0j) in a single pass mode with parameters tuned for short reads (--sjdbOverhang 35). The quality control report file of the resulting bam is generated using Qualimap(Okonechnikov et al., 2016) (v2.0.2). From there, the RNAseq data is used to quantify the gene-level mRNA abundance in TPM using a quantifier. Salmon(Patro et al., 2017) and Kallisto(Bray et al., 2016) are recommended here because they are extremely fast and their file formats are automatically supported by Scikit-ribo.

Scikit-ribo input processing

Scikit-ribo uses the pandas(McKinney, 2010) data frame as the main data structure: a codon-level data frame for the GLM, and a read-level data frame for A-site prediction. The codon-level data frame consists of the following variables: chromosome, start, end, codon, secondary structure pairing probability, mRNA abundance in TPM, number of ribosomes at this codon. Scikit-ribo filters and converts the provided Riboseq bam file into a bed file using pysam(v0.10.0)(Li et al., 2009) and pybedtools(v0.7.9)(Dale et al., 2011; Quinlan and Hall, 2010), which is subsequently converted into a read-level data frame. To prepare the codon-level data frame, it retrieves the cDNA sequence (includes ORF, 5’/3’-UTR) given a reference genome and a gene annotation file. The 24 nucleotides in both the 5’UTR and 3’-UTR are included for calculating mRNA secondary structure. The cDNA sequence is then used to predict the optimal secondary structure under minimal free energy using RNAfold(v2.3.4)(Lorenz et al., 2011). By parsing the postscript files, Scikit-ribo finds the lbox entries, which represent the pairing of nucleotides in the optimal structure. With that, it identifies the positions on the ORF with a likely stem loop downstream (i.e. nine nucleotides downstream of the A-site), while the ribosome is residing at a likely single-strand region (i.e. from six nucleotides upstream to nine nucleotides downstream). Due to the uncertainty of RNAfold prediction, a likely stem loop requires at least 17 out of the 18 nucleotides to be paired, while a single-strand region requires no more than three nucleotides paired. Given the canonical ORF of a gene, Scikit-ribo splits the sequences into tri-nucleotides as codons.

Data and statistical analysis in this paper

For the wild-type S. cerevisiae analysis and validation, the Riboseq (flash-freeze protocol) and RNA-seq (Ribo-zero protocol) data were from Weinberg et al(Weinberg et al., 2016). The accession numbers are GSM1289257, GSM1289256. For the CHX comparison, the CHX-treated data is SRR948553 and the RNA-seq data is SRR948551, from McManus et al(McManus et al., 2014). The reference genome of S. cerevisiae used is S288C R64-2-1. The gene annotation file was the SGD annotation downloaded from UCSC. For the E. coli analysis, the Riboseq (RelE protocol) and RNA-seq data were from Hwang et al(Hwang and Buskirk, 2017). The accession number is GSE85540. The reference genome of E. coli used is the MG1655 genome. For more details of how these data were generated, please refer to the original papers. All the figures in the paper were plotted using matplotlib(Hunter, 2007) (v2.0.0) and seaborn(Waskom and Wagner, 2017) (v0.7.1). The Pearson correlation and Spearman correlation are denoted as r and ρ, respectively.

Simulation, sequence enrichment, and gene enrichment analysis

The simulation of the S. cerevisiae Riboseq and RNAseq data were done with polyester(Frazee et al., 2015) and the log TE_baseline, followed a balanced normal distribution. To mimic paused ribosomes, we randomly sampled 2500 sites (occurring within ~20% of the genes) and added 1000 additional reads into these locations of the Riboseq data. We then sampled back to the same number of reads as the original data and computed the new RPKM-derived log TE_RP. For the sequence enrichment analysis, we collected 5’UTR sequences from genes with log₂ TE greater than two. The 5’UTR region is from 50 nt upstream to 6nt downstream of the translation start site. Then we used HOMER (v4.9) to scan for enriched sequences from the 56nt windows(Heinz et al., 2010), using the HOMER recommended p-value cutoff of 1 × 10⁻¹⁰ Gene set enrichment analysis was done on the website: http://www.yeastgenome.org/(Cherry et al., 2012).

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Michael C Schatz (mschatz@cs.jhu.edu).

DATA AND SOFTWARE AVAILABILITY

The source code of Scikit-ribo is freely available at https://github.com/schatzlab/scikit-ribo. Scikit-ribo can be easily installed with a single command: “pip install scikit-ribo”. The documentation of Scikit-ribo is available at http://scikit-ribo.readthedocs.io/. To ensure reproducibility, all source codes for data processing, statistical analyses and figure plotting are available in the iPython notebooks under the GitHub repository: https://github.com/schatzlab/scikit-ribo_manuscript

Highlights.

• -Scikit-ribo predicts A-sites and estimates translation efficiency from Riboseq data
• -TE estimation is prone to biases, especially for low-abundance genes
• -Scikit-ribo corrects the biases using a generalized linear model with ridge penalty
• -Results validated by mass-spec and quantifies the artifacts from cycloheximide